Effect of Solid Volume Concentration on the Rheological Properties of Debris Flow: A Case Study of Jiangjiagou Debris Flow in China

Abstract

The Anton Paar MCR 52 intelligent high-speed rheometer was utilized in this paper to conduct rheological tests on the Jiangjiagou debris flow slurry via linear loading. The relationship curves between shear rate and shear stress at different solid volume concentrations were obtained, and predictive formulas for yield stress and viscosity coefficient variations with the shear rate are proposed. Furthermore, the evolution mechanisms of yield stress and viscosity coefficient with changes in solid volume concentration of the debris flow were thoroughly analyzed. The results indicated that the rheological curves of the Jiangjiagou debris flow conformed to the Bingham fluid model. An increase in solid volume concentration continuously promoted the upward trend of the rheological curves, with significant increments observed only at high volume concentrations. A predictive model for debris flow rheological parameters was established based on the linear relationship between the rheological parameters and the solid volume concentration. The rise in solid volume concentration inhibited turbulence in the debris flow, while clay minerals enhanced the debris flow slurry’s ability to capture pore water. Significant shear-thinning effects were observed within the debris flow, which were particularly more pronounced at lower shear rates. The study outcomes hold crucial engineering significance for a better understanding of debris flow rheological properties, the calculation of debris flow dynamic parameters, and disaster prevention and control.

1. Introduction

Debris flow is a solid–liquid–gas mixture that occurs in mountainous areas, and its properties lie between those of water-laden flows and those of landslides, being it usually characterized by sudden outbreaks, fierceness, and strong destructive power [1,2,3,4,5]. Its catastrophic nature poses a significant threat to infrastructure, economic development, and lives and properties of people in mountainous regions, making it one of the main natural disasters in these areas [6]. Debris flow differs from water-laden flows and landslides; yet, it exhibits certain characteristics of both landslides and water-laden flows, due to its wide range of grain size distribution [7]. The wide grain size distribution causes significant internal resistance, influencing the transport characteristics of debris flow [8,9,10]. The rheological characteristics of debris flow, reflecting its structural properties and movement laws, affect the calculation of dynamic parameters, such as impact force and flow velocity, and are correlated with the erosion–deposition features and delineation of hazardous zones. Therefore, the rheological properties of debris flow remain an essential basis for researchers exploring its internal movement mechanisms [11,12,13].

The influence factors of debris flows are very complex; they can basically be categorized into background factors and triggering factors. The background factors mainly refer to the mechanical characteristics of geo-materials, topography and landscape, and soil vegetation, while the triggering factors include hydrological and rainfall conditions and human activities. Numerous scholars so far have extensively researched the rheological characteristics and influence factors of debris flow, aiming to unveil its internal mechanisms. Takahashi [14] and Bagnold [15] employed granular flow theory to explain the shear mechanisms of debris flow. Wang et al. [16] utilized large-scale rotating plate rheometers to conduct on-site tests on the viscous debris flow of Jiangjiagou, revealing phenomena like stress overshoot and shear thinning under low shear rates. Yang et al. [17] analyzed the shear deformation of debris flow slurries with different maximum particle sizes, obtaining the variation rules of rheological parameters. The results indicated that mixing coarse particles with fine ones can enhance the yield stress of debris flow slurries, mitigating the occurrence of shear thinning. Sosio and Crosta [18] observed the transformation of suspensions from initially shear-thinning fluids to progressively shear-thickening fluids by adding sands of varying concentrations and particle sizes (<0.425 mm) into clay and silt suspensions. Based on the relationship between the rheological parameters and the grading parameters of debris flow, Yang reversed-calculated its rheological characteristics, inferred the rheological curve, and established a dynamic equation, uncovering the particle effects of debris flow rheological characteristics [19].

In summary, the existing studies indicate that the solid content and composition of debris flow slurries are the main factors affecting their rheological relationships. This paper, therefore, employs the state-of-the-art Anton Paar intelligent high-speed rheometer to explore the relationship between shear rate and shear stress of debris flow slurries at different solid volume concentrations and discusses the evolution of rheological parameters with changes in solid volume concentration, aiming to provide practical reference for a deeper understanding of debris flow movement laws and for effective disaster prevention and control.

2. Materials and Methods

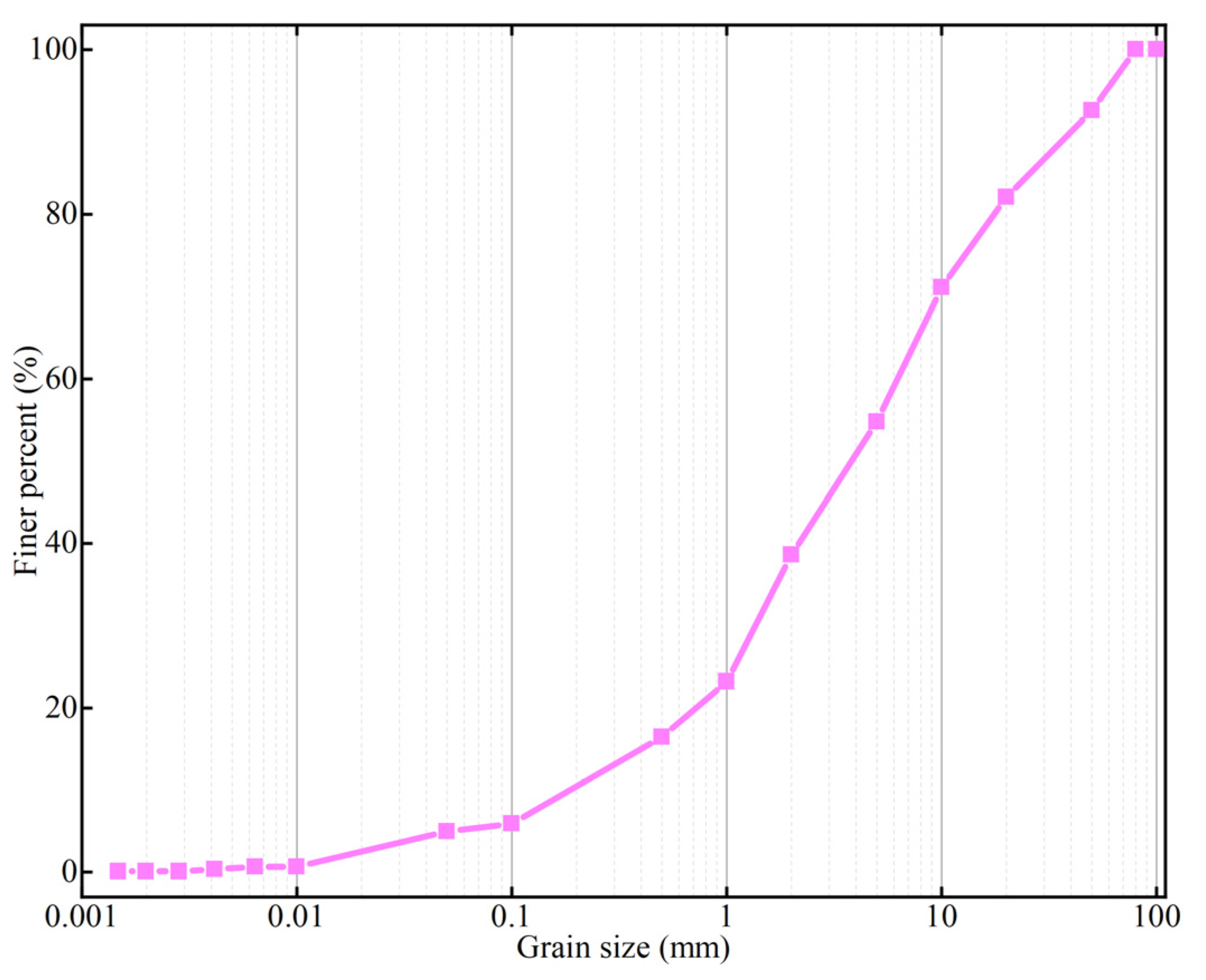
2.1. Experimental Materials

The materials examined in this study were obtained from a debris flow event that occurred in Jiangjiagou, located in Kunming City, Yunnan Province of China, which is a typical debris flow gully in the Xiaojiang River Basin, a tributary of the Jinsha River. Approximately 1.5 tons of samples were collected from different locations in the same region and transported back to the laboratory for further research. The region experiences frequent and large-scale debris flow outbreaks of various types, making it known as the “debris flow museum” among domestic and foreign scholars [20]. In terms of topographic and geomorphologic conditions, the average elevation of the Jiangjiagou Basin is 2200 m, with a relative elevation difference of 2181 m, and many longitudinal slopes upstream are more than 35°. The terrain rises like a ladder from west to east, and the landform has obvious stratification. The common feature of the landforms is that there are thick loose accumulations (including eluvium, residual slope accumulation and debris flow accumulation), which provide favorable topographic conditions for the development of debris flow. Figure 1 shows the sample collection locations. The samples were collected from an accumulation downstream of the debris flow. To prevent the fine particles from leaching out due to precipitation, a surficial deposit of 30 cm was removed using an iron shovel before sampling, to obtain well-preserved debris flow raw materials. Subsequently, these samples were dried and sieved to obtain raw materials with a maximum particle size of 2 mm. Additionally, particles below 0.075 mm were obtained through water sieving, and XRD (X-ray diffraction) tests were used to determine the mineral composition of the raw materials. As

Table 1. Major mineral composition of the debris flow raw materials.

Minerals	Quartz	Illite	Plagioclase	Chlorite	Potassium Feldspar
Content (%)	4.4	57	4.3	31.6	2.7

shows, the main clay minerals in the Jiangjiagou debris flow were illite and chlorite.

In accordance with the “soil test method standards” (GB/T50123-2019) [21] for grain size distribution tests, the grading curve of the raw samples in this study was determined. Particles above 0.075 mm were tested using sieving methods, while particles below 0.075 mm were analyzed using a lase r particle size analyzer. The obtained grading parameters are listed in

Table 2. Primary granular parameters of the debris flow raw materials.

Granular Parameters	d60	d30	d10	d50	Cu	Cc
Particle Size (mm)	6.682	1.196	0.238	3.795	28.076	0.899

, and based on these data, the grading curve was plotted, as shown in Figure 2. The coefficient of uniformity C_u reflects the degree of particle uniformity, and the curvature coefficient C_c reflects the shape of the particle size distribution curve, which are both crucial grading parameters. According to the test results, the C_u of the samples in this study was higher than 5, yet the C_c did not fall between 1 and 3; so, the debris flow material in this study was categorized as poorly graded soil.

2.2. Sample Preparation

Based on the field-collected original debris flow, indoor test specimens were prepared according to the testing requirements. The specific steps for sample preparation were as follows:

(1) The debris flow raw materials obtained from the field site were sieved through a 2 mm sieve and subjected to drying indoors.

(2) The debris flow raw materials below 2 mm were mixed with air-free water in certain proportions to prepare debris flow slurries with varying volume concentrations. Equation (1) was used to calculate the volume concentration (C_v) of the debris flow slurry mixtures

$$C_{\mathrm{v}}=\frac{{\rho }_{\mathrm{h}}+{\rho }_{\mathrm{w}}}{{\rho }_{\mathrm{s}}-{\rho }_{\mathrm{w}}}$$

(1)

where ${\rho }_{\mathrm{h}}$ and ${\rho }_{\mathrm{w}}$ represent the density of the mixture and water, respectively (kg/m³); ${\rho }_{\mathrm{s}}$ stands for particle density (kg/m³).

2.3. Experimental Method

The relationship between stress and strain for debris flow is referred to as the rheological relationship. Hence, the parameters in the rheological relationship are known as the rheological parameters and mainly include the viscosity coefficient and the yield stress [22]. The viscosity coefficient is a fundamental physical index that characterizes the frictional properties of fluids, reflecting the ability of a fluid to resist deformation when it undergoes relative motion. Its generalized model is as follows: fluid layers are divided into many elemental layers which are parallel to the flow direction, and due to varying velocities between adjacent layers, there exists resistance to movement opposite to the flow direction, defined as viscosity. The value surpassed when an object undergoes deformation beyond its elastic limit is termed the yield value. In rheology, only when stress reaches a certain value does fluidity occur; this is known as the critical stress.

As shown in Figure 3, the experimental equipment for this study was an Anton Paar MCR 52 intelligent high-speed rheometer (made in Austria), equipped with an automatic data acquisition system for real-time test data reading. The temperature range was controlled by Peltier elements from 5 °C to 70 °C. The air bearing contained an embedded normal force sensor, accurately determining the interface position. The rheometer allowed a maximum particle size of 10 mm for test samples and a shear rate measurement range of 0.1 s⁻¹ < γ < 100 s⁻¹. The cylindrical loading container was 115 mm in diameter, 48 mm in height, and 500 mL in volume. After loading the sample, the instrument was activated; pressure was outputted by an air compressor until the semiconductor refrigeration cycle controlled the temperature at a constant 20 °C. The rotor was controlled by software; it was gradually moved to the center of the debris flow slurry mixture, and its rotational shear function was rapidly activated to shear the debris flow slurry mixture, generating data for the rheological curve. This process allowed for obtaining the relationship curve between shear stress and shear rate of the Jiangjiagou debris flow slurry at different volume concentrations (C_v). The shear rate gradually increased from 0 s⁻¹ to 30 s⁻¹, which typically corresponds to the real shear rate range for debris flow under natural conditions. The loading mode was set as uniform acceleration loading, i.e., linear loading. The total test time was 213.5 s, with a sampling interval of 3.5 s per data point, totaling 61 data points. In total, nine samples were tested, from a low C_v value to a high C_v value. This aimed to ensure the regularity of the sampled data points and indirectly monitor the acceleration stability of the rheometer based on the shear rate at different sampling points.

Numerous studies have indicated that the majority of debris flow fluids can be described using the Bingham fluid, which combines the rheological equations of the Saint-Venant plastic body and the Newtonian viscous body, as shown in Equation (2)

$$\tau ={\tau }_{\mathrm{s}}+\eta \gamma$$

(2)

where τ represents the shear stress (Pa), τ_s is the yield stress (Pa), γ stands for the shear rate gradient (s⁻¹), η denotes the viscosity coefficient (Pa·s), and 1/η is the flow coefficient, reflecting the strength of the flow. Thus, a larger viscosity coefficient indicates poorer fluidity, while a smaller coefficient signifies higher fluidity.

3. Experimental Results and Analysis

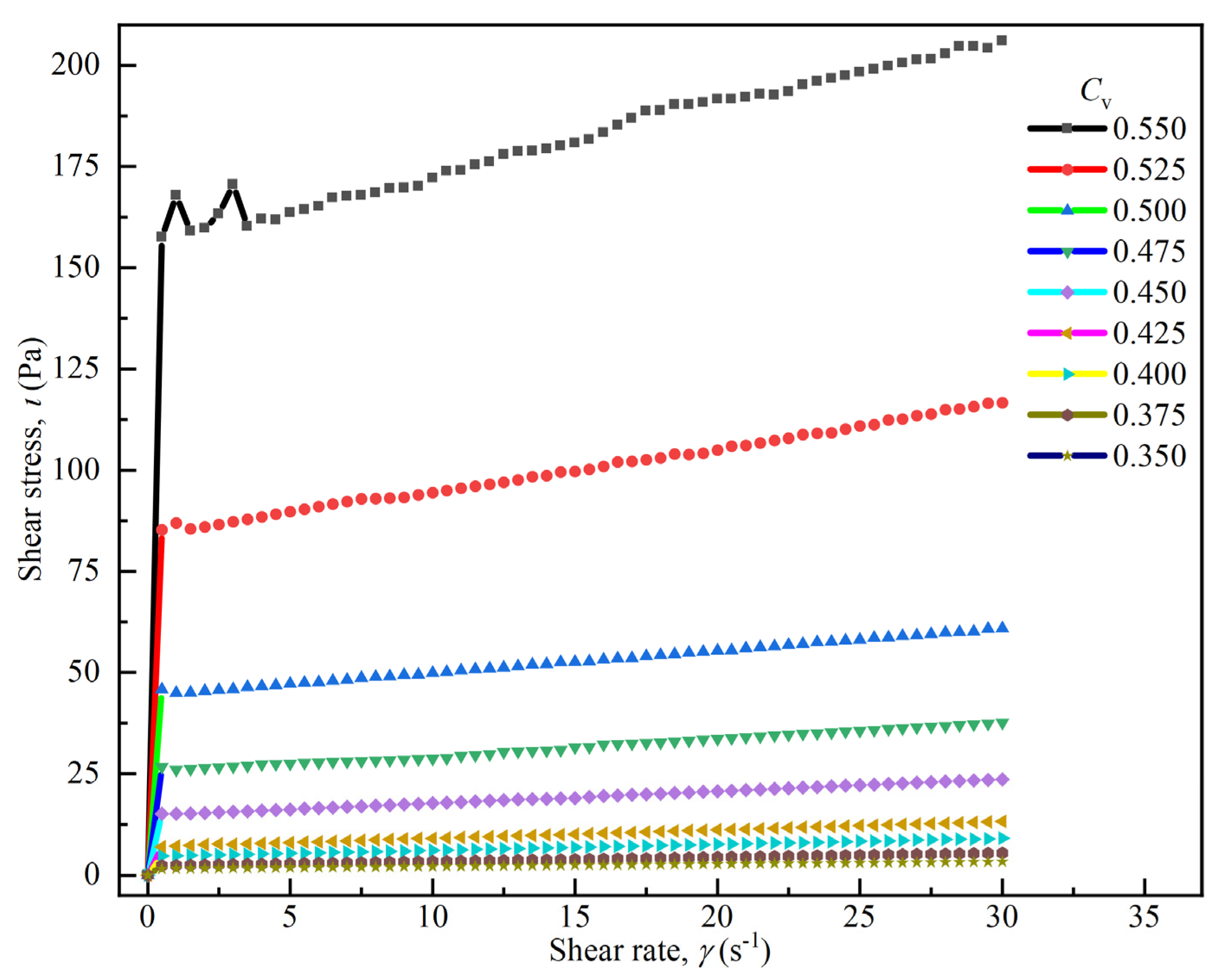
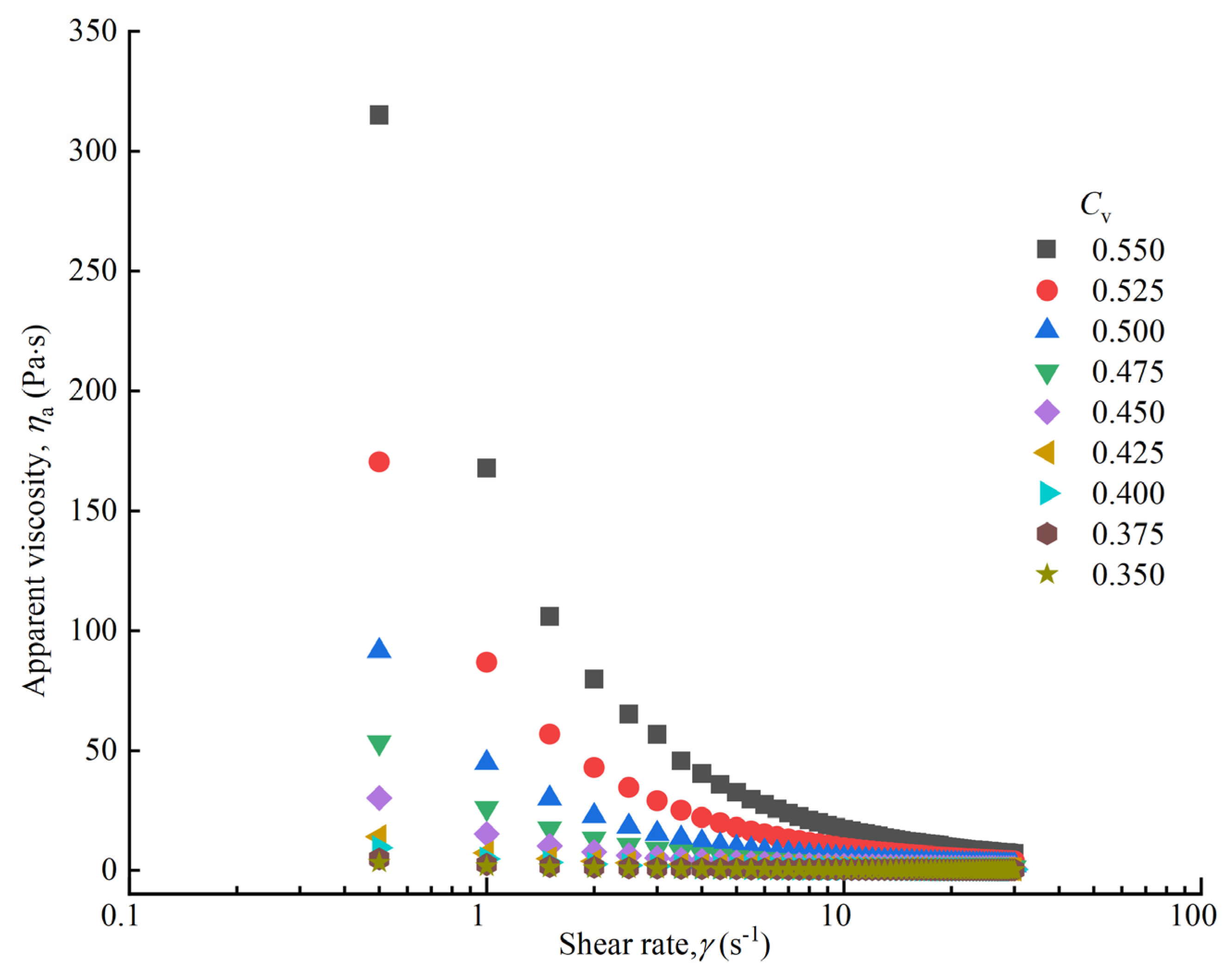
3.1. Rheological Curves at Different Volume Concentrations

Figure 4 presents the rheological curves of the debris flow at various solid volume concentration (C_v) conditions. It can be observed that, at different C_v levels, the shear stress demonstrates a linear relationship with shear rate, conforming to the Bingham fluid model for all curves. Furthermore, with increasing C_v values, the rheological curves increase continuously and become steeper. It is noteworthy that at lower C_v values, the rheological curves remain relatively stable without significant fluctuations. However, as the C_v values increase gradually, fluctuations begin to emerge in the initial shear stage of the rheological curves. Particularly, when C_v = 0.550, the overall rheological curve shows a fluctuating upward trend. This is primarily due to the increased solid particle content, which enhances the likelihood of collisions between the rotor and the particles in the sample, resulting in increased resistance and, thus, data fluctuations.

We found that compared with many debris flows of other regions, the shear stress of the Jiangjiagou debris flow is significantly greater than that of viscous debris flow under the same gravity and shear rate, which indicates that the Jiangjiagou debris flow has greater movement resistance. The main reason for this phenomenon is that the content of clay in the Jiangjiagou debris flow is high, and the slurry forming the debris flow is more abundant. Once the glacier debris flow breaks out, its movement velocity will be far greater than that of debris flows of other regions in the same state. Therefore, protection should be improved to ensure the safety of buildings and construction sites.

To assess the influence of solid volume concentration on the shear stress of the debris flow under various shear rate conditions, the shear stress increment Δτ (Equation (3)) at each solid volume concentration, relative to C_v = 0.350, was calculated by subtracting the shear stress at a specific C_v (τ(C_vi)) from the shear stress at C_v = 0.350 (τ(C_v0))

$$\Delta \tau =\tau \left(C_{\mathrm{vi}}\right)-\tau \left(C_{\mathrm{v}0}\right)$$

(3)

Here, τ(C_vi) represents the shear stress at a given solid volume concentration at the same shear rate, while τ(C_v0) denotes the shear stress at C_v = 0.350 for that particular shear rate.

Figure 5 depicts the variation in the shear stress increment Δτ with solid volume concentration at different shear rates. It is evident that the increment Δτ gradually increased with the rising solid concentration. Notably, during the transition of C_v from 0.350 to 0.425, the differences in the increment at various shear rates were indistinct; the curve changed mildly, and the data points among different sets almost overlapped, suggesting a minimal impact of the shear rate elevation in this phase. However, as the solid volume concentration continued to rise from 0.450 to 0.550, the elevation in shear rate distinctly led to varying shear stress increments. Specifically, at higher shear rates and the same volume concentration, greater shear stress increments were observed.

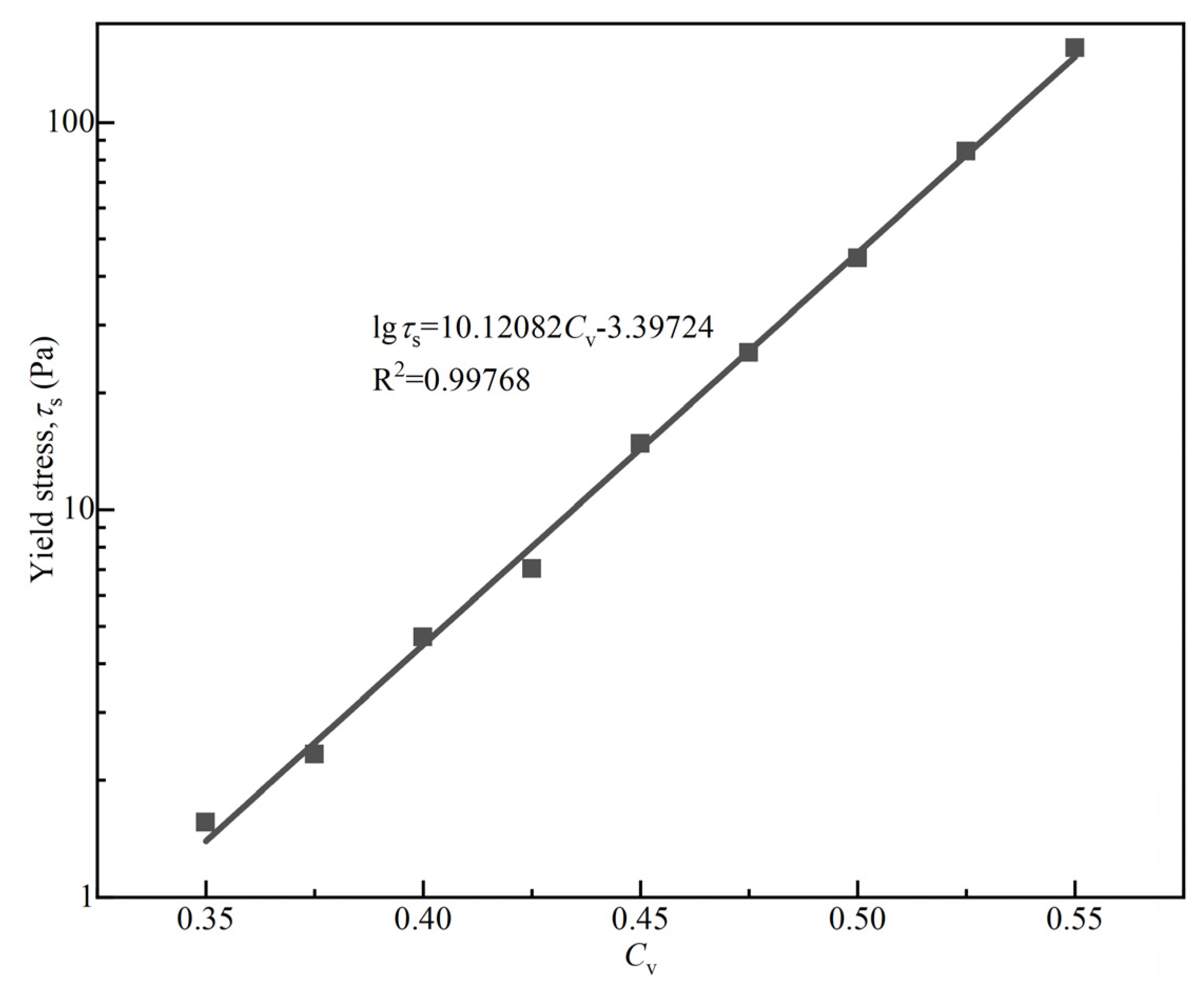
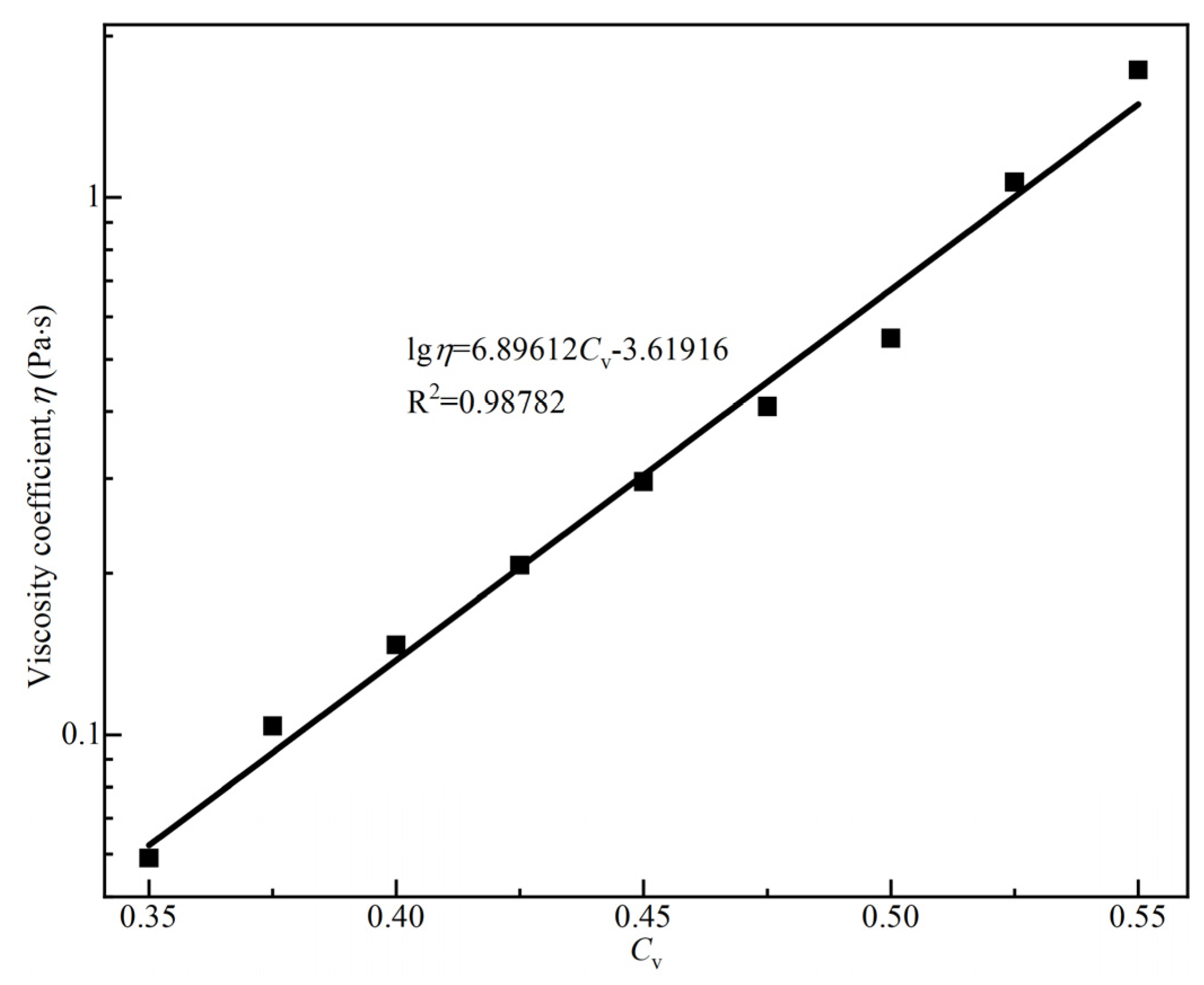
3.2. The Influence of Volume Concentration on the Rheological Parameters of the Debris Flow

Using Equation (2) to fit the rheological curves, the rheological parameters of the debris flow, namely, yield stress (τ_s) and viscosity (η), were obtained at various solid volume concentrations. The specific fitted data are presented in

Table 3. Fitting parameters of the rheological curves at different solid volume concentrations.

Cv	0.350	0.375	0.400	0.425	0.450	0.475	0.500	0.525	0.550
τs (Pa)	1.5579	2.3315	4.6737	7.0227	14.767	25.376	44.452	84.125	155.34
η (Pa·s)	0.0589	0.1039	0.1471	0.2068	0.2959	0.4081	0.5475	1.0686	1.7291
R2	0.9997	0.9980	0.9998	0.9995	0.9976	0.9931	0.9987	0.9975	0.9934

.

A debris flow is a non-Newtonian fluid composed of two phases: liquid and solid. The liquid phase is a slurry formed by the combination of water and fine particles, while the solid phase consists of the solid particles. Due to the complex interaction between the solid and the liquid phases during motion, currently, an effective mechanical model that adequately describes the debris flow movement mechanism is not available. However, through experimental analysis and research, we could quantitatively express the impact of the debris content on the yield stress. Figure 6 illustrates the variation in yield stress with solid volume concentration, demonstrating that as the solid volume concentration in the debris flow slurry gradually increased, the yield stress rose. Notably, on a semi-logarithmic scale, the yield stress exhibited a linear trend in relation to the solid volume concentration, with a correlation coefficient reaching 0.998, indicating a strong correlation between these parameters. The relationship between the yield stress of the debris flow slurry in Jiangjiagou and the volume concentration is expressed by Equation (4)

lgτ_s = 10.12082C_v − 3.39724

(4)

Figure 7 depicts the relationship between the viscosity coefficient and the solid volume concentration. It is evident that with an increase in solid volume concentration, the viscosity coefficient continuously rose. Similar to the trend observed for the yield stress in relation to the volume concentration, the viscosity coefficient also showed a linear relationship with the volume concentration on a semi-logarithmic scale. Consequently, the relationship between the viscosity coefficient of the debris flow slurry in Jiangjiagou and the volume concentration is represented by Equation (5)

lgη = 6.89612C_v − 3.61916

(5)

3.3. Shear-Thinning Behavior Characterization

Shear rheology introduces another key variable, the apparent viscosity η_a, defined as the ratio of shear stress to shear rate. As depicted in Figure 8, with increasing shear rates in the rheometer, slurries at different volume concentrations exhibited a continuous decrease in apparent viscosity, indicating a shear-thinning behavior of the debris flow slurry. Observing the relative positions of these curves revealed that higher volume concentrations corresponded to higher positions on the graphs, showing a positive correlation between apparent viscosity and volume concentration. This suggested that altering the solid volume concentration influenced the shear-thinning process of the slurry. Further analysis of these curves revealed distinct shear-thinning behaviors at different shear rates. At lower shear rates (γ < 10 s⁻¹), the apparent viscosity of the slurry drastically decreased with increasing shear rates, whereas at higher shear rates (γ > 10 s⁻¹), the apparent viscosity decreased more gradually. Overall, the rate of the decrease in apparent viscosity augmented initially with an increasing shear rate and then slowed down gradually, and the decrement in apparent viscosity diminished as the shear rate increased, approaching zero. Therefore, it is evident that lower shear rates exacerbated the shear-thinning behavior of the debris flow.

As shown in Figure 9a, in a logarithmic coordinate system, the relationship between apparent viscosity and shear rate for the debris flow complied with the expression:

lgη_a = a + blgγ

(6)

where a and b are fitting parameters, with specific values listed in

Table 4. Fitting parameters of the η_a–γ curves at different solid volume concentrations.

Cv	0.350	0.375	0.400	0.425	0.450	0.475	0.500	0.525	0.550
a	0.14058	0.31336	0.6224	0.80036	1.13374	1.3773	1.6229	1.89992	2.17517
b	−0.7746	−0.7486	−0.8027	−0.8117	−0.8614	−0.8875	−0.9079	−0.9059	−0.9211
R2	0.98838	0.98507	0.99095	0.99200	0.99529	0.99584	0.99785	0.99768	0.99796

. Plotting the data from Table 4 in Figure 9b revealed that both a and b were linearly correlated, respectively, with the solid volume concentration of the debris flow. Notably, the correlation coefficient (R²) for a surpassed 0.997, indicating a stronger association between a and the solid volume concentration of the debris flow. In fact, b describes the variation in apparent viscosity in relation to shear rate, specifically reflecting the fluid’s shear-thinning behavior, making it an indicator of the extent of this thinning behavior.

In conclusion, Equation (6) can be expressed as a function involving both solid volume concentration and shear rate, yielding the new Equation (7) capable of predicting the shear-thinning behavior of the debris flow in this study

lgη_a = −3.52216 + 10.31732C_v + (−0.39272 + 0.96176 C_v)lgγ

(7)

3.4. The Effects of Solid Volume Concentration on the Rheological Behavior of Debris Flows

The variation law of rheological parameters in debris flow slurry is mainly based on the relationship between yield stress, viscosity, and solid volume concentration, which are significantly affected by factors such as volume concentration, particle size distribution, and fine particle mineral composition [23]. Coarse and fine particles in a debris flow are the main solid components, and the maintenance and movement of a debris flow is related to their mixing with water and the buoyancy effect. Under certain concentration conditions, the interaction between fine particles and water can form a kind of non-sorting solid–liquid flow (i.e., a one-phase flow), which has a certain yield stress, and this is significant for the movement of the debris flow. Apart from buoyancy, the support force of solid particles can be the inter-particle discrete force generated by particle shear motion or the yield shear force of a high-concentration slurry that prevents particles from sinking, generating the so-called neutral suspension movement even at low slope conditions in the channel.

The volume concentration of a debris flow slurry directly reflects the influence of the slurry moisture content on the slurry flow and transport capacity. As the solid volume concentration increases, the volume fraction of the solid phase increases, reducing the internal water content of the debris flow, increasing viscosity, and suppressing the turbulence of the debris flow. In Figure 4, it can be observed that most curves show a relatively smooth upward trend, which indirectly indicates that, for the Jiangjiagou diluted debris flow (with low solid volume concentration) and viscous debris flow (with high solid volume concentration) in this study, the impact of discrete stress generated by particle collision on the resistance of the debris flow is lower than that of particle contact friction and viscous shear. The enhanced viscosity of the liquid phase slurry in the Jiangjiagou debris flow reduces the flow turbulence and increases the viscous shear. Moreover, as the solid volume concentration of the viscous debris flow in Jiangjiagou increases, the amount of solid particles increases, resulting in a denser structure. The adhesive force between coarse particles also increases, leading to greater frictional force when the particles contact each other, hence, continuously increasing resistance.

On another note, as the solid volume concentration gradually increases in the debris flow slurry, it becomes easier for particles to adhere to each other, forming aggregates. Moreover, the particles adhere to each other and to aggregates, forming a mesh-like structure. At this point, water is trapped in the grid structure formed between particles, which further increases with the concentration of the solid particles. Clusters combine to form cluster aggregates, thereby forming a flocculent network structure, and the density of this network structure increases with the rise in solid volume concentration. As the adhesive force between particles strengthens continuously, the viscosity of the slurry gradually increases. Coarse and fine particles adhere to each other, forming mud films on the surface of coarse particles. Collisions and compression occur between solid particles, and the internal friction of the slurry gradually increases, leading to an increase in the yield stress.

Considering physical and chemical properties such as particle size distribution, clay content, mineral and elemental composition, the influence of clay mineral content is also an important factor that cannot be ignored [24]. This is mainly because clay minerals themselves have significant properties such as a large specific surface area, a double electric layer, hydrophilicity, and surface features like cation adsorption. Regarding the clay minerals in the raw materials of the debris flow from Jiangjiagou in this study, the main ones are illite and chlorite (Table 1). These typical clay minerals are superior to non-typical clay minerals in terms of specific surface area, hydrophilicity, expansibility, and surface adsorption capacity. Although a significant solid–liquid phase separation is prone to occur in the debris flow slurry at low volume concentrations, as the solid volume concentration increases, the proportion of clay minerals gradually rises, leading to an eventual continuous enhancement in capturing pore water. Hence, a debris flow with strong fluidity and viscosity can form. Consequently, clay minerals are also crucial factors in the establishment of a strong structure, great stability, and minimal sedimentation in debris flows.

Furthermore, experiments have also shown that there is a significant shear-thinning phenomenon in debris flows, and the shear-thinning is more pronounced at low shear rates than at high shear rates, greatly reducing the viscous resistance of debris flows. Therefore, when the sediment stagnant in a channel bed is triggered according to its rheological properties, the flow velocity may suddenly increase. The head of the debris flow is disturbed, which hinders the formation of a mesh structure in the slurry, enhancing the shear-thinning performance and reducing resistance; however, the flow at the tail of the debris flow is small, which weakens the disturbance, allowing for the developing of a good mesh structure and easily leading to a shear-thickening behavior, thereby increasing the movement resistance.

4. Conclusions

This study, based on indoor rheological tests, used raw materials of the debris flow from Jiangjiagou as the research subject to obtain the rheological curves of the debris flow slurry at different solid volume concentrations. It discussed the evolution laws of yield stress and viscosity at different solid volume concentrations, constructed a predictive model for the rheological parameters of the Jiangjiagou debris flow based on fitting regression, and thoroughly analyzed the influence mechanism of solid volume concentration on the rheological characteristics of the debris flow slurry. Our conclusions are as follows:

(1)

The rheological curves of the debris flow from Jiangjiagou generally conformed to the Bingham fluid model, where shear stress consistently increases linearly with shear rate. The elevation in solid volume concentration continuously increased the rheological curves’ upward trend; yet, the increase in shear stress was not particularly significant at low volume concentrations and became more pronounced only at high volume concentration.

(2)

In a semi-log coordinate system, both the yield stress and the viscosity of the debris flow from Jiangjiagou exhibited a linear relationship with the solid volume concentration, which formed the basis for establishing a predictive formula for the rheological parameters of the debris flow in relation to the solid volume concentration.

(3)

The increase in solid volume concentration led to a higher solid phase volume fraction in the debris flow, resulting in reduced water content, increased viscosity, inhibited turbulence in the debris flow, a tighter structure, mutual adhesion of coarse and fine particles, greater friction between particle contacts, and hence, a continuous increase in resistance.

(4)

Typical clay minerals with high content exhibit superior properties in specific surface area, hydrophilicity, expansibility, and surface adsorption capability compared to atypical clay minerals, thereby endowing the debris flow slurry under high volume concentration conditions with strong capture ability of pore water, resulting in a debris flow with strong fluidity and viscosity.

(5)

The debris flow exhibited a significant shear-thinning effect, which was more pronounced at lower shear rates, greatly reducing the viscous resistance of the debris flow.