Analysis of Pressure Distribution on a Single-Family Building Caused by Standard and Heavy Winds Based on a Numerical Approach
Abstract
:Highlights
- Model of strong wind flow around sharp edges;
- Analysis of the impact of strong wind on structures.
- Theoretical and numerical analysis;
- Observations and measurements of impacts on existing facilities;
- Comparison of results depending on the solutions used.
Abstract
1. Introduction
2. Theoretical Assumptions in the Ansys Fluent Program [17,18,19,20,21,22]
- The air leaving the fan is set in turbulent motion, so the use of stabilizers is necessary;
- To eliminate the effect of viscosity on the tunnel walls and obtain the most linear flow, smooth walls are used, and the cross-section is often circular;
- If the model is suspended on cables or stands on a platform, their contribution should be taken into account using correction factors;
- When using a scale other than 1:1 to interpret the results, remember to maintain similarity numbers (e.g., Mach number, Froude number, Strouhal number, Reynolds number).
2.1. Straight-Line Flows
- (a)
- Principle of conservation of mass;
- (b)
- The principle of conservation of momentum;
- (c)
- User-defined scalar transport equations (UDS);
- Single-phase flow
- Multi-phase flow
2.2. Vortex and Rotational Flows
- Axisymmetric flows with swirling or rotation;
- Fully three-dimensional vortex or rotational flows;
- Flows requiring a moving reference frame;
- Flows requiring multiple moving reference frames or mixing planes;
- Flows requiring sliding grids.
- (d)
- The principle of conservation of momentum for the vortex speed;
- (e)
- Compressible flows (Mach’s law);
- (f)
- Physics of compressible flows;
- (g)
- Compressible form of the gas law.
3. Numerical Example and Program Comparison
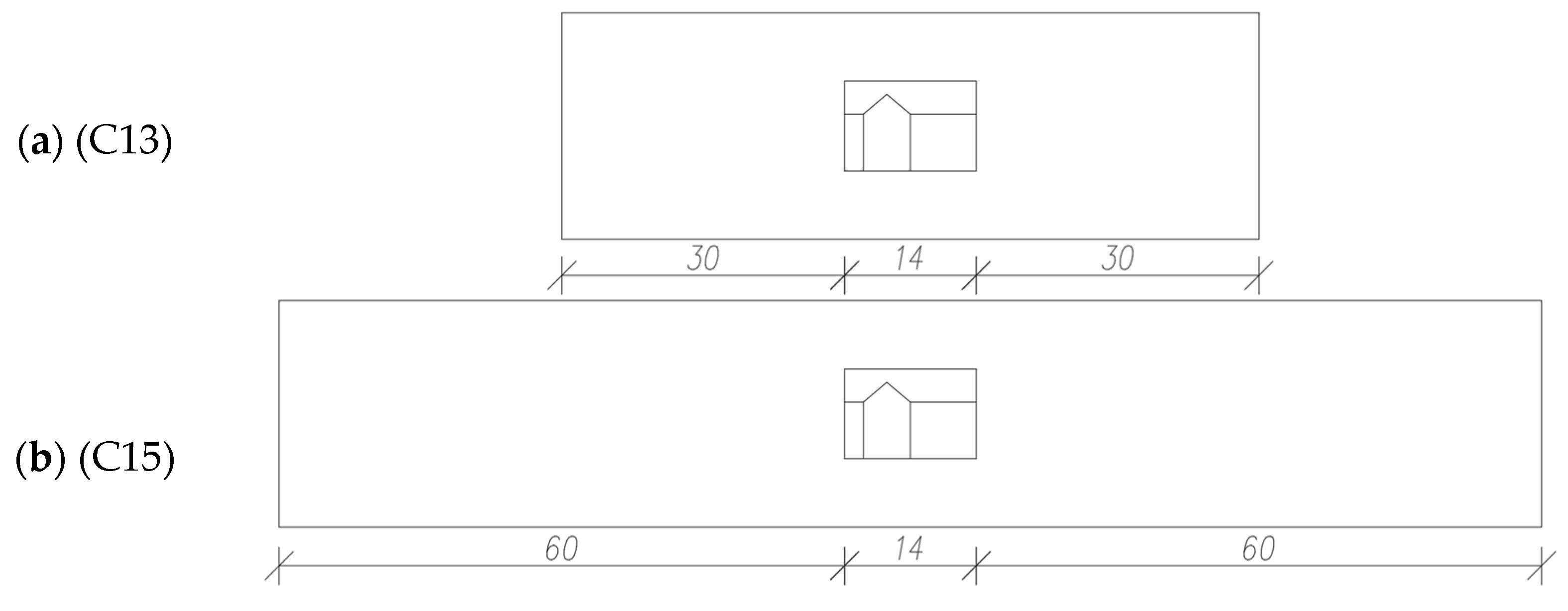
3.1. Description of the Research Subject and the Model Being Created [29,30]
3.2. Scheme of the Conducted Analysis [31,32]
3.3. Comparison of Ansys with Robot
4. Dependence of Results on Boundary Conditions
- The shape of the wind tunnel cross-section;
- Internal width;
- Location of the tested object;
- Tunnel length;
- Load duration.
4.1. The Shape of the Wind Tunnel Cross-Section
4.2. Internal Width
4.3. Setting the Object on the Ground
4.4. Tunnel Length
4.5. Load Duration
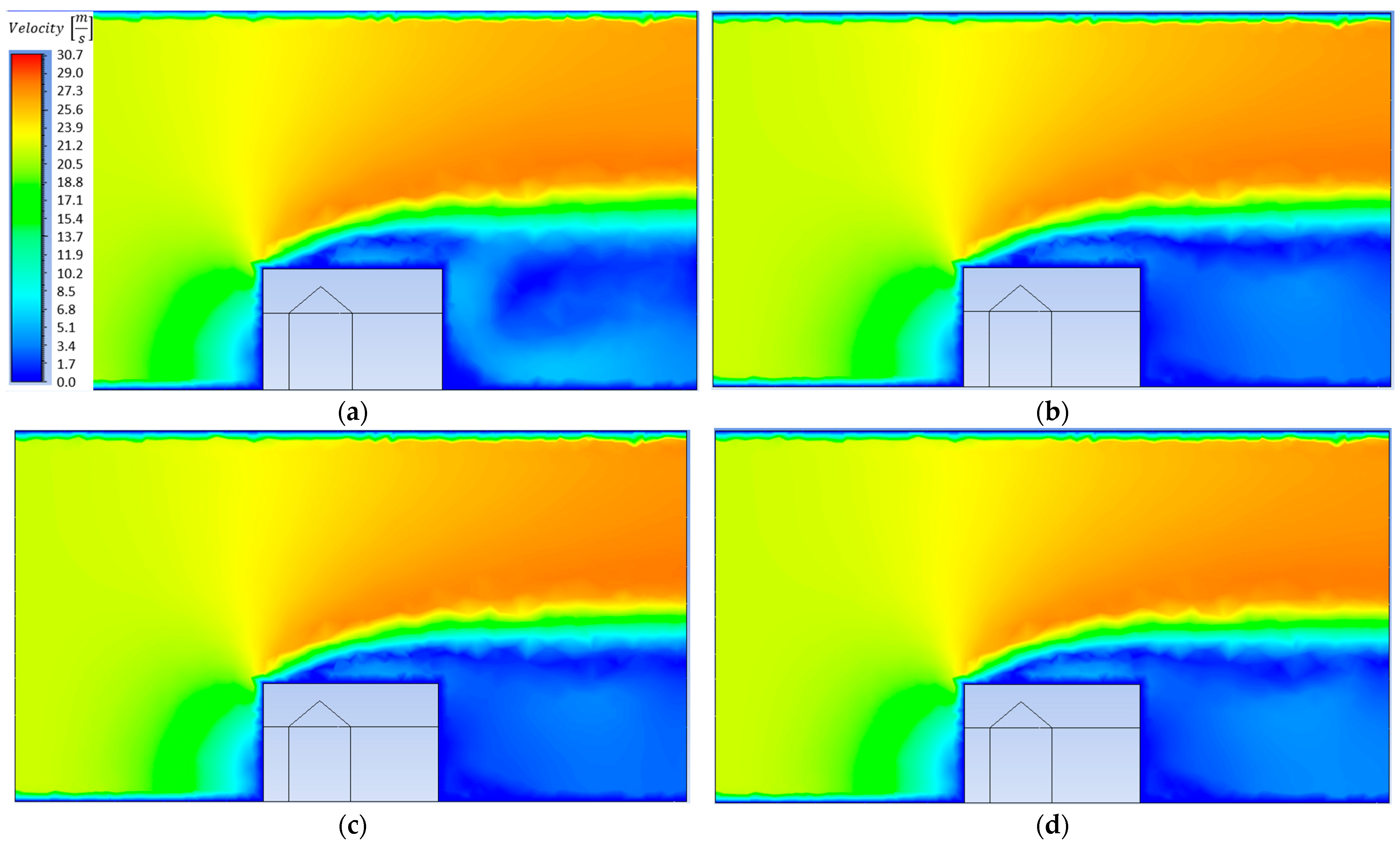
5. Received Results
6. Strong Wind Analysis in the Best Parameter Configuration
- (a)
- 38 m/s (138 km/h) above which the wind can be classified as EF1—case C21;
- (b)
- 50 m/s (178 km/h) above which the wind can be classified as EF2—case C22;
- (c)
- 60 m/s (218 km/h) above which the wind can be classified as EF3—case C23.
7. Summary and Conclusions
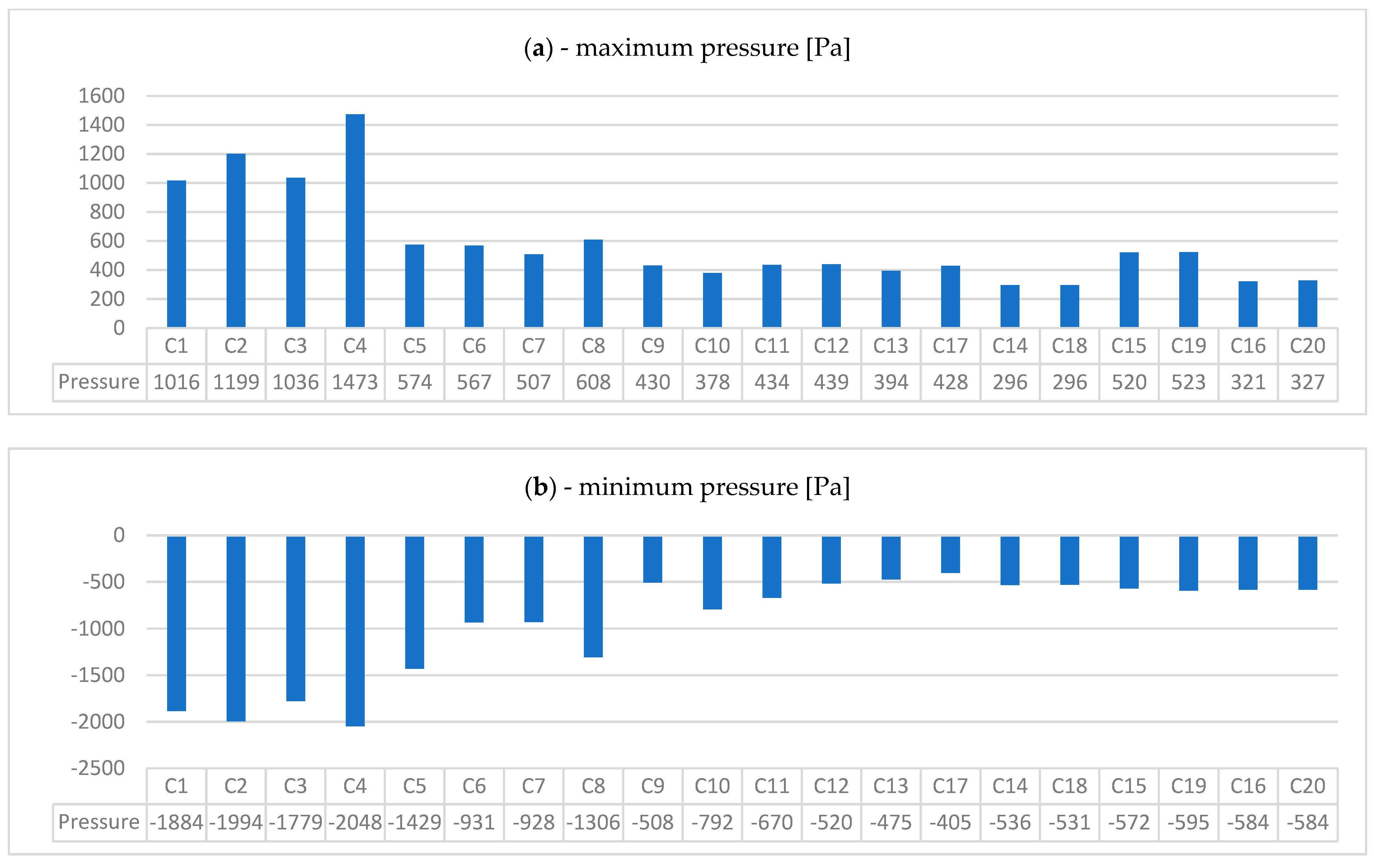
- The results of the obtained pressures, both positive and negative, differ significantly depending on the parameters used: the shape and dimensions (lateral and longitudinal) of the wind tunnel. The initial results were disturbed by the interference of the initial stream and the wave reflected from the building and tunnel walls, which resulted in values of 1473 Pa (C4 model), while the expected value was at the level of 322–325 Pa. Subsequent models created to eliminate the influence of boundary conditions reduced these stresses gradually from 574 Pa (C5 model) to the expected value of 321 Pa (C16 model).
- The location of the tested object (introducing the ground level on which the building is built) (C14 and C16 models) affects not only the pressure values obtained in characteristic places (corners of the object) but also the maximum pressure (pressure on the windward wall). We can analyze the difference in results with one variable (location on the ground) by comparing model C13 versus C14, a decrease from 394 Pa to 296 Pa (24.87%), and C15 versus C16, a decrease from 520 Pa to 321 Pa (38.26%).
- There is a specific (i = 200), easily achievable number of iterations of the computational process (corresponding to the passage of time), after which the impact on the results can be considered negligible. The results can be analyzed by comparing C13 versus C17, an increase from 394 Pa to 428 Pa (8.63%), then C14 versus C18, the value does not change 296 Pa, then C15 versus C19, an increase from 520 Pa to 523 Pa (0.57%), and C16 relative to C20, an increase from 321 Pa to 327 Pa (1.87%).
- It is clearly visible that smaller cross-sections (C1–C4) (average 1181 Pa) significantly overestimate the obtained results due to the concentration of stresses between the model and the tunnel wall. In the next 4 models (C5–C8) (average 564 Pa), the results are normalized, and only in the last part, we obtain reliable results close to the expected value of 320 Pa.
- The shape of the cross-section has a much smaller impact on the values than the size and, above all, the surface corresponding to the free space around the object. The results can be analyzed by comparing models C1–C4 among themselves, then C5–C8 among themselves, and C9–C12 among themselves.
- With a large increase in the cross-section parameters (case C16), it is possible to achieve values independent of the boundary disturbances.
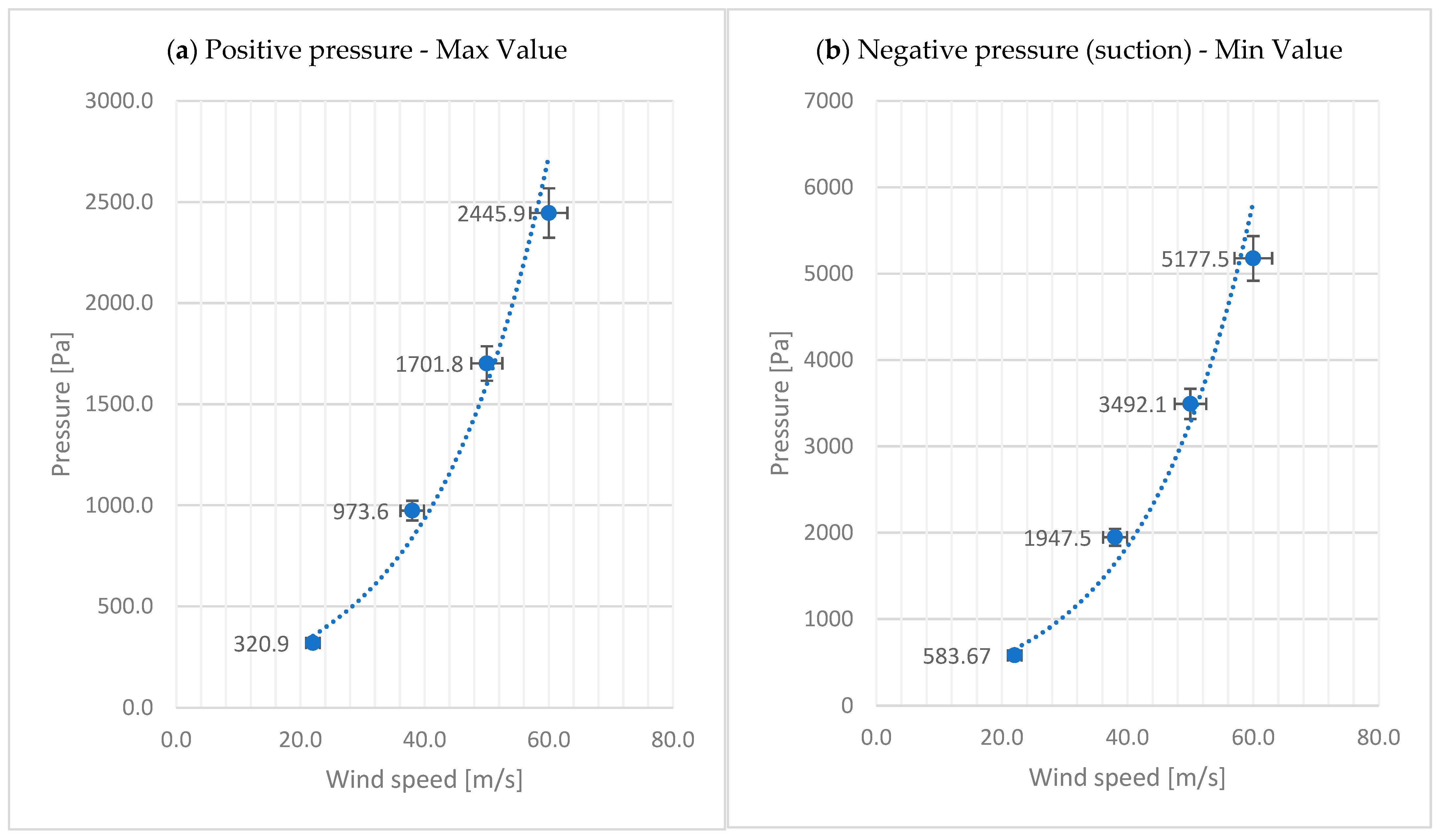
- The analysis of strong wind (presented by trend lines in extreme force diagrams) indicates the non-linearity of the resulting stresses with subsequent increases in output speed.
- The percentage influence on the obtained results depends on the mesh size of the numerical program;
- Changing the material parameters of the facility and the wind tunnel, such as viscosity, surface type (siding), and roughness.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Dutkiewicz, M.; Lamparski, T. Ultimate and serviceability limit States of a wooden roof under the wind speed that may cause potential damage to the structure. AIP Conf. Proc. 2023, 2928, 150038. [Google Scholar]
- Dutkiewicz, M.; Hajyalikhani, P.; Lamparski, T.; Whitman, L.; Covarrubias, J. Structural bracing of wooden roofs under the extreme wind. IOP Conf. Ser. Mater. Sci. Eng. 2021, 1203, 022024. [Google Scholar] [CrossRef]
- Dutkiewicz, M. Models of strong wind acting on buildings and infrastructure. IOP Conf. Ser. Mater. Sci. Eng. 2019, 471, 052030. [Google Scholar] [CrossRef]
- Fricker, T.; Friesenhahn, C. Tornado Fatalities in Context: 1995–2018. Weather. Clim. Soc. 2022, 14, 81–93. [Google Scholar] [CrossRef]
- Karstens, C.D.; Samaras, T.M.; Lee, B.D.; Gallus, W.A.; Finley, C.A. Near-ground pressure and wind measurements in tornadoes. Mon. Weather Rev. 2010, 138, 2570–2588. [Google Scholar] [CrossRef]
- Bjerknes, V. The meteorology of the temperate zone and the general atmospheric circulation. Mon. Weather. Rev. 1929, 49, 1–3. [Google Scholar] [CrossRef]
- Alexander, C.R.; Wurman, J.M. Updated mobile radar climatology of supercell tornado structures and dynamics. In Proceedings of the 24th Conference on Severe Local Storms, Savannah, GA, USA, 27–31 October 2008. [Google Scholar]
- A Photo Showing the Movement of a Tornado. Available online: https://nypost.com/wp-content/uploads/sites/2/2018/10/istock-923092852.jpg?quality=75&strip=all (accessed on 20 November 2023).
- Gołębiowska, I.; Dutkiewicz, M.; Lamparski, T.; Hajyalikhani, P. Vibrations of Slender Structures Caused by Vortices. IOP Conf. Ser. Mater. Sci. Eng. 2021, 1203, 022025. [Google Scholar] [CrossRef]
- Haan, F.L., Jr.; Balaramudu, V.K.; Sarkar, P.P. Tornado-induced wind loads on a low-rise building. J. Struct. Eng. 2010, 136, 106–116. [Google Scholar] [CrossRef]
- Horia, H.; Kim, J.D. Swirl ratio effects on tornado vortices in relation to the Fujita scale. Wind. Struct. 2008, 11, 291–302. [Google Scholar]
- Dutta, P.K.; Ghosh, A.K.; Agarwal, B.L. Dynamic response of structures subjected to tornado loads by FEM. J. Wind. Eng. Ind. Aerodyn. 2002, 90, 55–69. [Google Scholar] [CrossRef]
- Jaffe, A.L.; Kopp, G.A. Internal pressure modelling for low-rise buildings in tornadoes. J. Wind. Eng. Ind. Aerodyn. 2021, 209, 104454. [Google Scholar] [CrossRef]
- Kopp, G.A.; Wu, C.-H. A framework to compare wind loads on low-rise buildings in tornadoes and atmospheric boundary layers. J. Wind. Eng. Ind. Aerodyn. 2020, 204, 104269. [Google Scholar] [CrossRef]
- Rizzo, F.; D’Alessandro, V.; Montelpare, S.; Giammichele, L. Computational study of a bluff body aerodynamics: Impact of the laminar-to-turbulent transition modelling. Int. J. Mech. Sci. 2020, 178, 105620. [Google Scholar] [CrossRef]
- Rizzo, F.; Caracoglia, L. Examination of Artificial Neural Networks to predict wind-induced displacements of cable net roofs. Eng. Struct. 2021, 245, 112956. [Google Scholar] [CrossRef]
- Ansys Fluent 12.0 Theory Guide. Available online: https://www.afs.enea.it/project/neptunius/docs/fluent/html/th/main_pre.htm (accessed on 20 November 2023).
- CFD EXPERTS. Ansys Fluent Theory Guide. Available online: https://dl.cfdexperts.net/cfd_resources/Ansys_Documentation/Fluent/Ansys_Fluent_Theory_Guide.pdf (accessed on 20 November 2023).
- Rott, N. On the viscous core of a line vortex. Z. Für Angew. Math. Und Phys. ZAMP 1958, 9, 543–553. [Google Scholar] [CrossRef]
- Sullivan, R.D. A two-cell vortex solution of the navier-stokes equations. J. Aero. Sci. 1959, 26, 767–768. [Google Scholar] [CrossRef]
- Burgers, J.M. A mathematical model illustrating the theory of turbulence. Adv. Appl. Mech. 1948, 1, 171–199. [Google Scholar]
- Rankine, W.J.M. A Manual of Applied Physics, 10th ed.; Charles Griff and Co.: Burbank, IL, USA, 1882; p. 663. [Google Scholar]
- Elementary Knowledge of Real Wind Tunnels. Available online: https://en.wikipedia.org/wiki/Wind_tunnel (accessed on 20 November 2023).
- Takashi, M. Simulation of flying debris using a numerically generated tornado-like vortex. J. Wind. Eng. Ind. Aerodyn. 2011, 99, 249–256. [Google Scholar]
- Lewellen, W.S.; Lewellen, D.C.; Sykes, R.I. Large-eddy simulation of a tornado’s interaction with the surface. J. Atmos. Sci. 1997, 54, 581–605. [Google Scholar] [CrossRef]
- Diwakar, N.; Hangan, H. Numerical study on the effects of surface roughness on tornado-like flows. In Proceedings of the 11th Americas conference on wind engineering (11ACWE), San Juan, Puerto Rico, 22–26 June 2009. [Google Scholar]
- Panneer, S.R.; Millett, P.C. Computer modeling of tornado forces on buildings. Wind. Struct. 2003, 6, 209–220. [Google Scholar]
- Soares Fernandes, Y.M.; Rodrigues Machado, M.; Dutkiewicz, M. The Spectral Approach of Love and Mindlin-Herrmann Theory in the Dynamical Simulations of the Tower-Cable Interactions under the Wind and Rain Loads. Energies 2022, 15, 7725. [Google Scholar] [CrossRef]
- Lamparski, T.; Dutkiewicz, M. The Action of Tornadoes on the Structural Elements of a Wooden Low-Rise Building Roof and Surrounding Objects—Review and Case Study. Appl. Sci. 2023, 13, 4661. [Google Scholar] [CrossRef]
- Lewellen, W.S. Tornado Vortex Theory, the Tornado: Its Structure, Dynamics, Prediction, and Hazards; Geophysical Monograph Series; AGU: Washington, DC, USA, 1993; Volume 79, pp. 19–39. [Google Scholar]
- Alekseenko, S.V.; Kuibin, P.A.; Okulov, V.L. Theory of Concentrated Vortices; Springer: Berlin/Heidelberg, Germany, 2003. [Google Scholar]
- Davies-Jones, R.; Wood, V.T. Simulated Doppler velocity signature of evolving tornado-like vortices. J. Atmos. Ocean. Technol. 2006, 23, 1029–1048. [Google Scholar] [CrossRef]
- EN 1991: Eurocode 1: Actions on Structures Parts 1-1 to 1-7. Available online: https://www.phd.eng.br/wp-content/uploads/2015/12/en.1991.1.1.2002.pdf (accessed on 20 November 2023).
- EN 1990: Eurocode 0: Basis of Structural Design. Available online: https://www.phd.eng.br/wp-content/uploads/2015/12/en.1990.2002.pdf (accessed on 20 November 2023).
- EN 1995: Eurocode 5: Design of Timber Structures. Parts 1-1 to 1-2 and 2. Available online: https://www.phd.eng.br/wp-content/uploads/2015/12/en.1995.1.1.2004.pdf (accessed on 20 November 2023).
- Fujita, T.T. Proposed Characterization of Tornadoes and Hurricanes by Area and Intensity; SMRP Research Paper Number 91; University of Chicago: Chicago, IL, USA, 1970. [Google Scholar]
- Fujita Tornado Damage Scale. Available online: https://www.spc.noaa.gov/faq/tornado/f-scale.html (accessed on 20 November 2023).
- Enhanced Fujita Scale. Available online: https://en.wikipedia.org/wiki/Enhanced_Fujita_scale (accessed on 20 November 2023).
- McDonald, J.R.; Mehta, K.C.; Mani, S. A Recommendation for an Enhanced Fujita Scale (EF-Scale), Revision 2; Wind Science and Engineering, Texas Tech. Univ.: Lubbock, TX, USA, 2006. [Google Scholar]


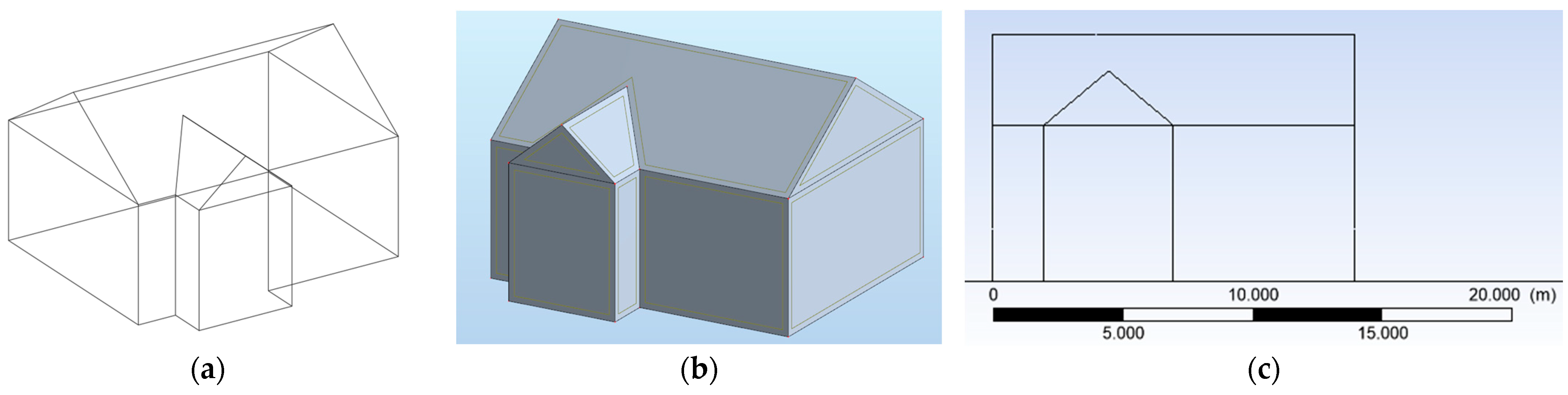
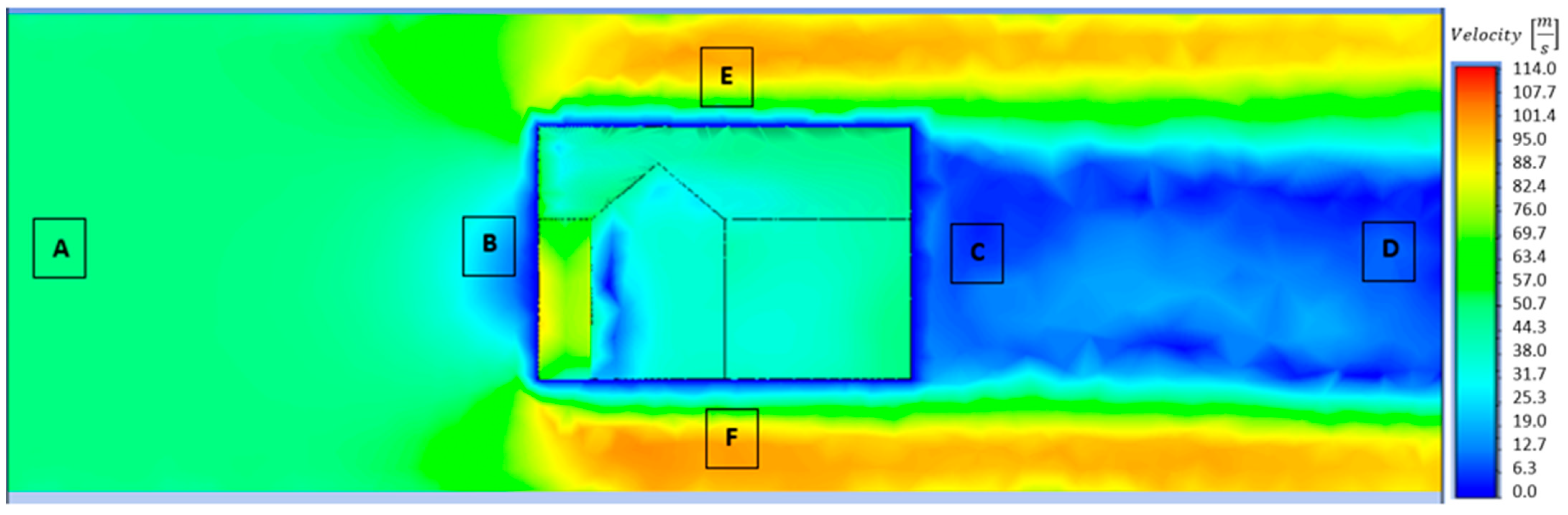

| Program: | Stress Values: | Graphic Representation: |
|---|---|---|
| Ansys | 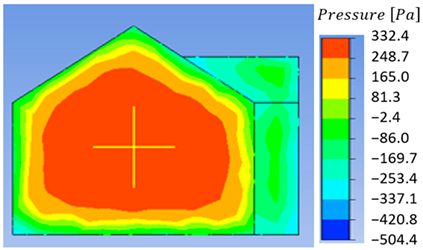 | |
| Robot | 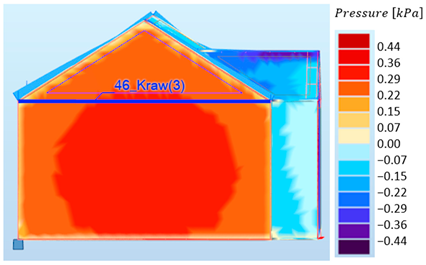 |
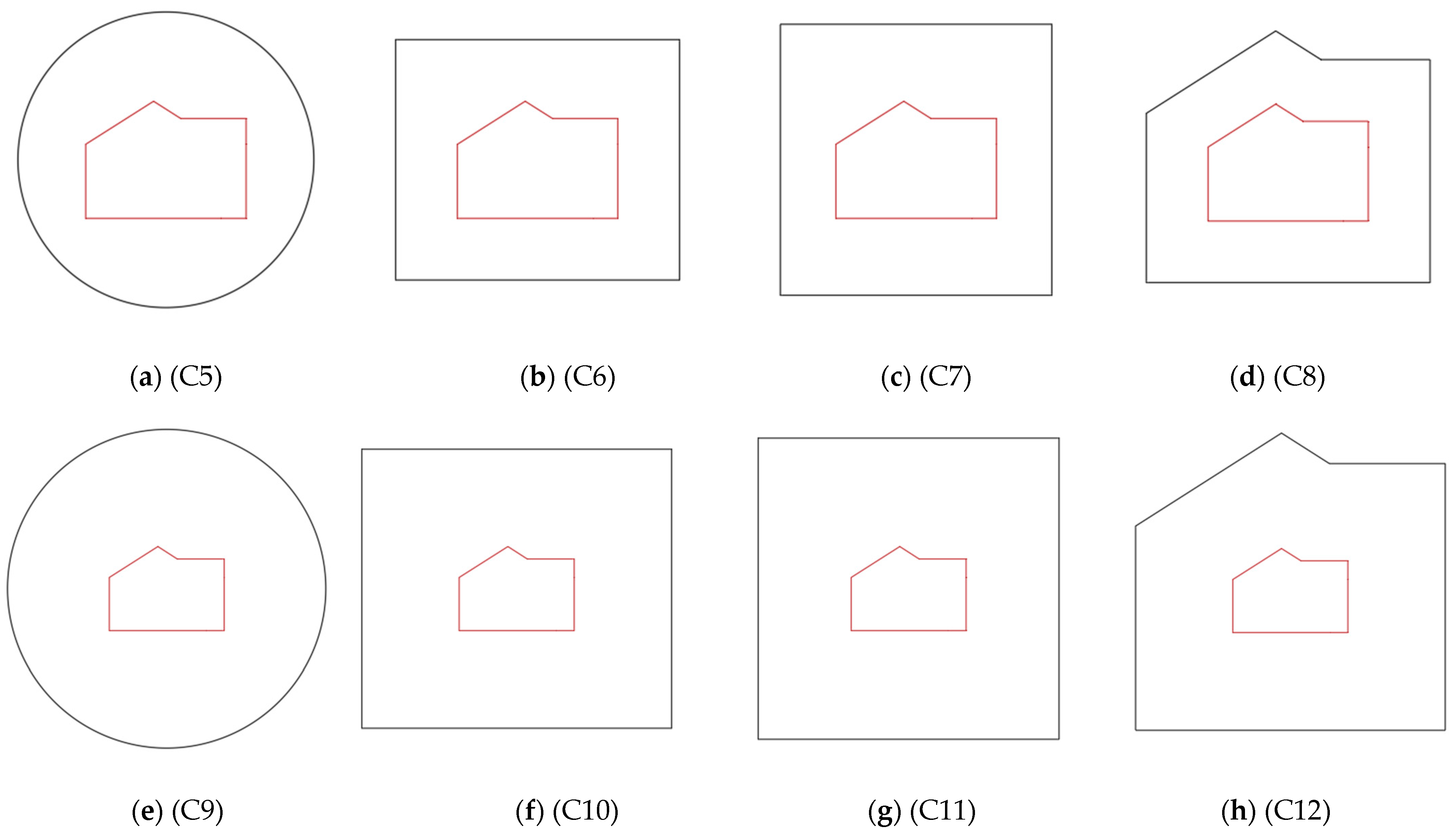
| Case | Shape | Width/Diameter [m] | Area [m2] | Free Space around [m2] |
|---|---|---|---|---|
| C1 | Circle | ø18 | 254.5 | 149.6 |
| C2 | Rectangle | 17 × 13.5 | 229.5 | 124.6 |
| C3 | Square | 16 × 16 | 256 | 151.1 |
| C4 | Building | 17 × 13.9 | 203.5 | 98.6 |
| C5 | Circle | ø24 | 452.4 | 347.5 |
| C6 | Rectangle | 23 × 19.5 | 448.5 | 343.6 |
| C7 | Square | 22 | 484 | 379.1 |
| C8 | Building | 23 × 20.4 | 409.9 | 305.0 |
| C9 | Circle | ø36 | 1017.9 | 913.0 |
| C10 | Rectangle | 35 × 31.5 | 1102.5 | 997.6 |
| C11 | Square | 34 | 1156 | 1051.1 |
| C12 | Building | 35 × 33.5 | 1032.9 | 928.0 |
| C13 | Square | 50 × 50 | 2500 | 2395.1 |
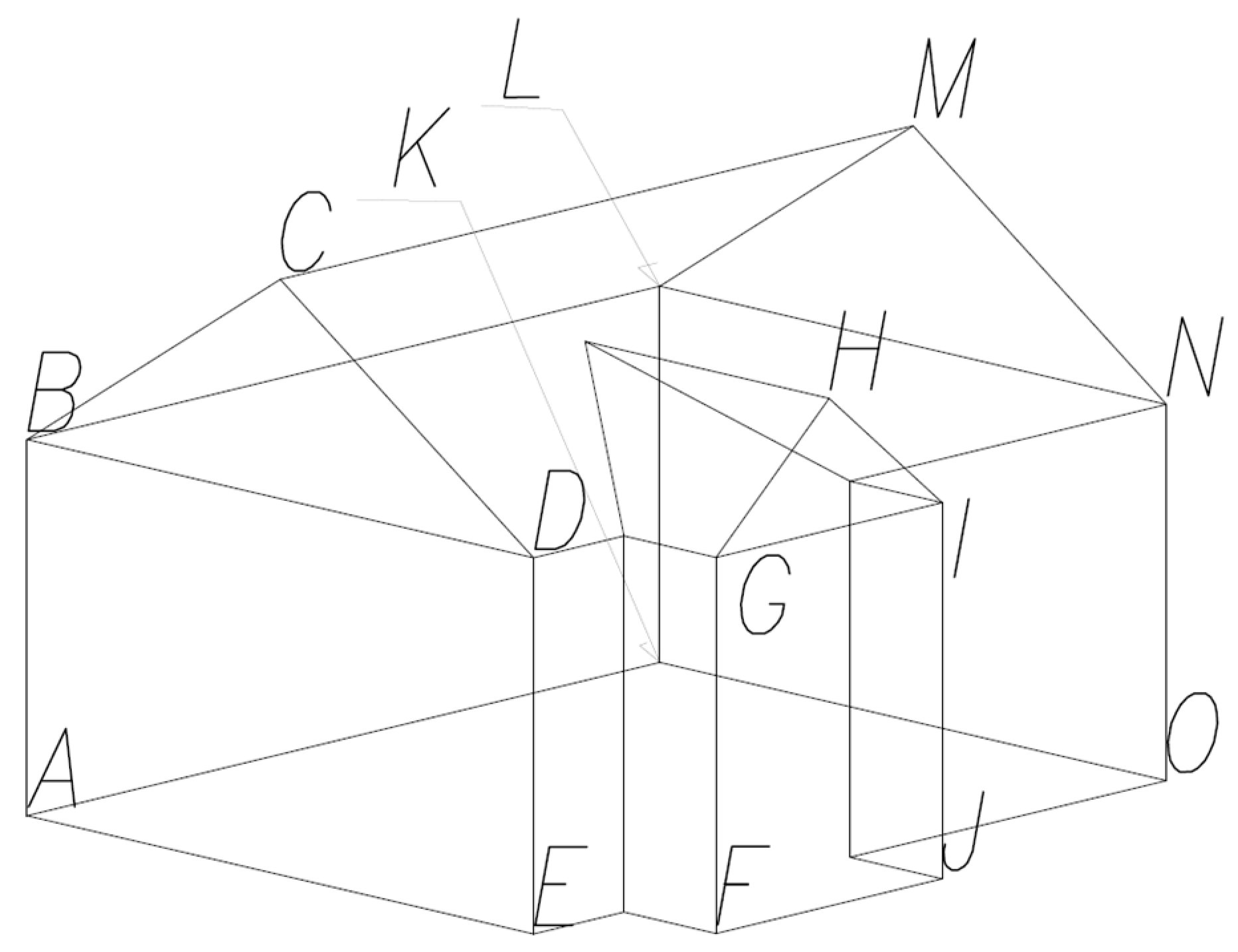
| Case\Point | A | B | C | D | E | F | G | H | I | J | K | L | M | N | O |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| C1 | −479.7 | −114.1 | −193.9 | 55.2 | 136.8 | −618.8 | −44.3 | −242.0 | −330.9 | −290.9 | −92.9 | −69.1 | −101.4 | −165.7 | −94.2 |
| C2 | −353.4 | −39.1 | −172.5 | 304.0 | 104.9 | −445.0 | −54.6 | −221.4 | −375.8 | −384.9 | −50.9 | −45.5 | −86.5 | −198.5 | −90.3 |
| C3 | −366.2 | 102.7 | −237.4 | 55.3 | 96.0 | −521.2 | −22.2 | −172.9 | −286.5 | −286.3 | −66.5 | −41.7 | −76.1 | −180.4 | −120.4 |
| C4 | −648.3 | −90.4 | −139.0 | 386.4 | 204.9 | −587.0 | 3.9 | −543.9 | −688.0 | −400.5 | −109.8 | −55.4 | −82.3 | −180.8 | −191.5 |
| C5 | −192.4 | −48.8 | −138.9 | −10.7 | −91.8 | −350.6 | −202.6 | −155.4 | −170.6 | −195.5 | −43.4 | −58.3 | −55.4 | −77.5 | −60.2 |
| C6 | −277.9 | −195.8 | −236.9 | −36.4 | −108.4 | −334.9 | −210.3 | −144.5 | −177.1 | −167.7 | −43.8 | −52.8 | −52.4 | −91.5 | −61.7 |
| C7 | −276.5 | −128.0 | −213.7 | −175.1 | −135.9 | −436.3 | −198.0 | −207.5 | −219.1 | −217.8 | −96.3 | −96.9 | −83.1 | −119.8 | −89.5 |
| C8 | −266.0 | 25.5 | −252.6 | −60.8 | −103.6 | −418.5 | −155.7 | −307.7 | −132.1 | −154.5 | −46.6 | −66.3 | −38.8 | −93.2 | −39.2 |
| C9 | −151.4 | −34.4 | −99.9 | −89.8 | −67.7 | −234.2 | −92.7 | −95.3 | −90.7 | −94.9 | −29.4 | −44.9 | −80.3 | −63.2 | −50.0 |
| C10 | −96.9 | 21.8 | −112.1 | −109.1 | −93.2 | −256.9 | −288.9 | −151.4 | −159.7 | −146.6 | −141.6 | −138.8 | −130.8 | −121.8 | −118.8 |
| C11 | −126.1 | 25.5 | −45.3 | −8.7 | −52.7 | −234.4 | −205.5 | −93.4 | −91.1 | −133.1 | −43.5 | −29.1 | −54.0 | −83.0 | −80.7 |
| C12 | −98.7 | −20.6 | −96.3 | −66.6 | −66.4 | −189.7 | −120.4 | −161.7 | −116.3 | −96.0 | −45.4 | −60.8 | −59.9 | −89.2 | −63.9 |
| C13 | −116.4 | 19.5 | −100.1 | 23.8 | −3.5 | −148.1 | −129.9 | −64.2 | −52.1 | −54.8 | −59.5 | −72.4 | −48.2 | −44.4 | −75.8 |
| C17 | −41.5 | 94.9 | −49.9 | 47.9 | 30.5 | −94.8 | −80.8 | −40.0 | −33.0 | −27.8 | −19.8 | −18.3 | −15.6 | −16.5 | −20.5 |
| C14 | 88.1 | 99.3 | −34.1 | −16.8 | 104.8 | 9.3 | −134.5 | −36.9 | −18.2 | −40.2 | −19.0 | −21.6 | −22.3 | −21.4 | −19.9 |
| C18 | 87.4 | 102.3 | −41.6 | −15.0 | 111.0 | 2.6 | −127.5 | −28.6 | −21.9 | −19.3 | −17.5 | −20.1 | −18.1 | −17.4 | −14.6 |
| C15 | −49.1 | −66.5 | −115.9 | −110.5 | −97.9 | −202.7 | −272.7 | −177.7 | −116.2 | −111.0 | −59.8 | −60.1 | −67.9 | −66.6 | −63.9 |
| C19 | −53.4 | −73.4 | −140.7 | −112.3 | −102.9 | −202.5 | −269.5 | −159.5 | −112.3 | −112.7 | −50.1 | −56.6 | −55.3 | −57.1 | −53.1 |
| C16 | −54.4 | −34.9 | −108.9 | −81.7 | −11.5 | −256.0 | −276.3 | −173.6 | −154.7 | −112.6 | −125.5 | −133.2 | −131.3 | −111.9 | −92.9 |
| C20 | −48.3 | −27.6 | −100.1 | −75.0 | −3.7 | −250.8 | −268.8 | −164.2 | −154.7 | −114.0 | −120.4 | −118.8 | −118.4 | −108.5 | −93.8 |
| Case\Value | C1 | C2 | C3 | C4 | C5 | C6 | C7 | C8 | C9 | C10 |
|---|---|---|---|---|---|---|---|---|---|---|
| Max | 1016.2 | 1199.5 | 1035.7 | 1472.5 | 573.9 | 567.3 | 507.4 | 608.0 | 430.4 | 378.5 |
| Min | −1884.3 | −1993.6 | −1779.1 | −2047.7 | −1429.0 | −930.7 | −928.0 | −1306.0 | −507.8 | −792.2 |
| Case\Value | C11 | C12 | C13 | C17 | C14 | C18 | C15 | C19 | C16 | C20 |
| Max | 433.7 | 438.5 | 393.9 | 427.9 | 296.0 | 296.0 | 519.7 | 523.4 | 320.9 | 327.1 |
| Min | −669.7 | −519.8 | −475.0 | −404.8 | −536.2 | −531.5 | −572.1 | −595.5 | −583.7 | −584.5 |
| Case\Point | Velocity [m/s] | A | B | C | D | E | F | G | H |
|---|---|---|---|---|---|---|---|---|---|
| C16 | 22 | −54.4 | −34.9 | −108.9 | −81.7 | −11.5 | −256.0 | −276.3 | −173.6 |
| C21 | 38 | −137.9 | −49.7 | −235.4 | −234.8 | −52.1 | −851.7 | −898.4 | −577.8 |
| C22 | 50 | −200.5 | −46.3 | −583.7 | −450.1 | −96.1 | −1516.0 | −1536.2 | −1073.4 |
| C23 | 60 | −361.5 | −280.4 | −698.5 | −614.9 | −155.9 | −2245.1 | −2258.5 | −1603.6 |
| Case\Point | I | J | K | L | M | N | O | Max | Min |
| C16 | −154.7 | −112.6 | −125.5 | −133.2 | −131.3 | −111.9 | −92.9 | 320.9 | −583.7 |
| C21 | −504.0 | −421.0 | −344.8 | −392.9 | −378.1 | −340.1 | −334.5 | 973.6 | −1947.5 |
| C22 | −908.5 | −830.0 | −572.7 | −575.4 | −604.4 | −651.6 | −704.3 | 1701.8 | −3492.1 |
| C23 | −1303.0 | −1340.2 | −726.7 | −767.5 | −918.7 | −890.8 | −932.7 | 2445.9 | −5177.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lamparski, T.; Dutkiewicz, M. Analysis of Pressure Distribution on a Single-Family Building Caused by Standard and Heavy Winds Based on a Numerical Approach. Appl. Sci. 2024, 14, 1976. https://doi.org/10.3390/app14051976
Lamparski T, Dutkiewicz M. Analysis of Pressure Distribution on a Single-Family Building Caused by Standard and Heavy Winds Based on a Numerical Approach. Applied Sciences. 2024; 14(5):1976. https://doi.org/10.3390/app14051976
Chicago/Turabian StyleLamparski, Tomasz, and Maciej Dutkiewicz. 2024. "Analysis of Pressure Distribution on a Single-Family Building Caused by Standard and Heavy Winds Based on a Numerical Approach" Applied Sciences 14, no. 5: 1976. https://doi.org/10.3390/app14051976
APA StyleLamparski, T., & Dutkiewicz, M. (2024). Analysis of Pressure Distribution on a Single-Family Building Caused by Standard and Heavy Winds Based on a Numerical Approach. Applied Sciences, 14(5), 1976. https://doi.org/10.3390/app14051976










