Overview of FEM-Based Resistance Models for Local Buckling of Welded Steel Box Section Columns
Abstract
:1. Introduction
2. Literature Review
2.1. Pure Local Buckling
- Clarin [1] examined a total of 48 experiments using materials with three different yield stresses. The findings indicated that the absolute magnitudes of residual tensile stresses were higher in high-strength plates compared to low-strength plates. However, the residual-stress-to-yield-stress ratio was lower for high-strength materials.
- Schillo and Feldmann [3] studied 34 stub column specimens with yield strengths of 500, 700, and 960 MPa, which were tested to compare the results with the EN1993-1-5 [4] design procedure. This work was supported by finite element analysis (FEA) that considered equivalent imperfections and realistic imperfections. The work presented in [6] introduces a buckling curve proposal that addresses the discrepancy between values obtained from EN1993-1-5 [4] and those derived from experimental tests, specifically when dealing with plate slenderness exceeding 1.55. Given the similarity in methodology between their research and the approach employed in this work, the buckling curve of Schillo will be further considered in the results.
- Hämäläinen et al. [5] conducted a study involving 12 specimens made from ultra-high-strength materials, with a yield strength exceeding 1100 MPa. The outcomes from these experiments were used to propose a simplification of factors designed to account for uncertainties specific to this type of material.
- Rasmussen and Hancock [7] used 18 specimens, which included cruciform, box, and I-sections, to investigate the effects of additional restraints along one or two edges and the residual stresses resulting from the welding process.
- In the work by Shi et al. [8], four box sections made of 460 MPa steel were tested, and the results were compared with FEA models that accounted for initial imperfections. The conclusion drawn was that the residual-stress-to-yield-strength ratio holds significant importance in the design moment of thin-walled structures.
2.2. Interaction between Local and Overall Buckling
- Chiew et al. [9] conducted tests on 20 welded box section columns to validate the applicability of empirical equations.
- In the research carried out by Usami et al. [10], 24 specimens were tested to verify an enhancement of an equation published by the same authors.
- Nishino et al. [11] examined eight specimens to verify theoretical values concerning elastic–plastic buckling in plates.
- The study by Schillo [6] aimed to investigate the interaction buckling phenomenon for welded box section columns made of different steel grades involving tests on 34 specimens.
- Liew and Shanmugam [12] conducted experiments on 28 large-scale square and rectangular sections with yield stresses ranging between 235 and 355 MPa. The research considered residual stresses and local and overall imperfections, and aimed to propose a load resistance equation.
2.3. Further Related Research Activities
- The research conducted by Vieira et al. [15] studied the interaction between the flanges and the web of a hollow section columns, considering the independent buckling behavior in each plate. To achieve this, they performed a parametric study to derive a local buckling coefficient for the combined effects of axial compression and bending actions. The numerical tools employed in their investigation included GBTUL 2.0 and CUFSM 3.13.
- Degée et al. [16] explored the influence of imperfections, such as residual stresses resulting from the welding process and initial global bow imperfection. Their work was supported by a combination of experimental and numerical investigations, leading to a proposal for modifying the non-dimensional slenderness equation used in global buckling verification. Additionally, they proposed an alternative to the current European buckling curve for welded box section columns.
- In the study by Johansson et al. [17], the effective width of the plate in thin-walled sections was investigated, and an evaluation of Winter’s formula was conducted. This research was carried out with the aid of FEA.
- Pircher et al. [18] presented their research findings on the influence of the fabrication process on buckling phenomena in thin-walled steel sections. Their aim was to propose a buckling curve specific to welded thin-walled members.
- Kövesdi and Somodi [19] studied and modified the Ayrton–Perry-type buckling formula to implement the effects of residual stresses and geometrical imperfections in the design procedure. This study was based on theoretical reviews and numerical analyses.

- To validate the numerical model;
- To evaluate the already existing models;
- To develop a new proposal for improved imperfections and a residual stress pattern.
3. Finite Element Model
3.1. General Details
3.2. Material Model
3.2.1. Material Model Used for Normal-Strength Steel

- “cut-off” strain to avoid over-prediction;
- coefficient to compute strain hardening modulus;
- strain-hardening;
- ultimate strain;
- strain hardening modulus.
3.2.2. Ramberg–Osgood-Type Material Model Used for High Strength Steel (HSS)
- [N/mm2];
- E Young´s modulus of steel [N/mm2];
- ;
- stress [N/mm2].

3.3. Boundary Conditions
3.4. Imperfections and Residual Stresses
3.4.1. Equivalent Geometric Imperfections
3.4.2. Residual Stress Distribution
3.4.3. Geometrical Imperfection
4. Verification and Validation of the Numerical Model
4.1. Model Verification—Mesh Sensitivity Analysis
- Ultimate local buckling resistance at “i” iteration;
- Ultimate local buckling resistance at “i − 1” iteration.

4.2. Model Validation and Evaluation of Imperfection and RS Models
4.2.1. Evaluation Strategy
- Testing different geometrical imperfection models (using the same residual stress model for all cases, called ECCS_Eq model—see details later)—Section 4.2.2;
- Modifying the already existing geometrical imperfection models to develop more general models that can more accurately reproduce experimental resistances—Section 4.2.2;
- Testing the different residual stress models (using the best two geometrical models based on previous step)—Section 4.2.3;
- Modifying the already existing residual stress models to develop general model that can more accurately reproduce experimental resistances—Section 4.2.4;
- Execute the final validation step using the best geometrical imperfection and residual stress models but using the actual measured residual stress values published in the corresponding papers (so at this step only the shape of the residual stress pattern according to the model is used, but the actual compressive and tensile stresses are taken from the measurements)—Section 4.2.5.
4.2.2. Evaluation of Realistic Geometric Imperfection Models
4.2.3. Evaluation of Residual Stress Models
4.2.4. Improvement in Residual Stress Models
4.2.5. Validation Using the Improved Residual Stress Model
5. Evaluation of the Numerical Results
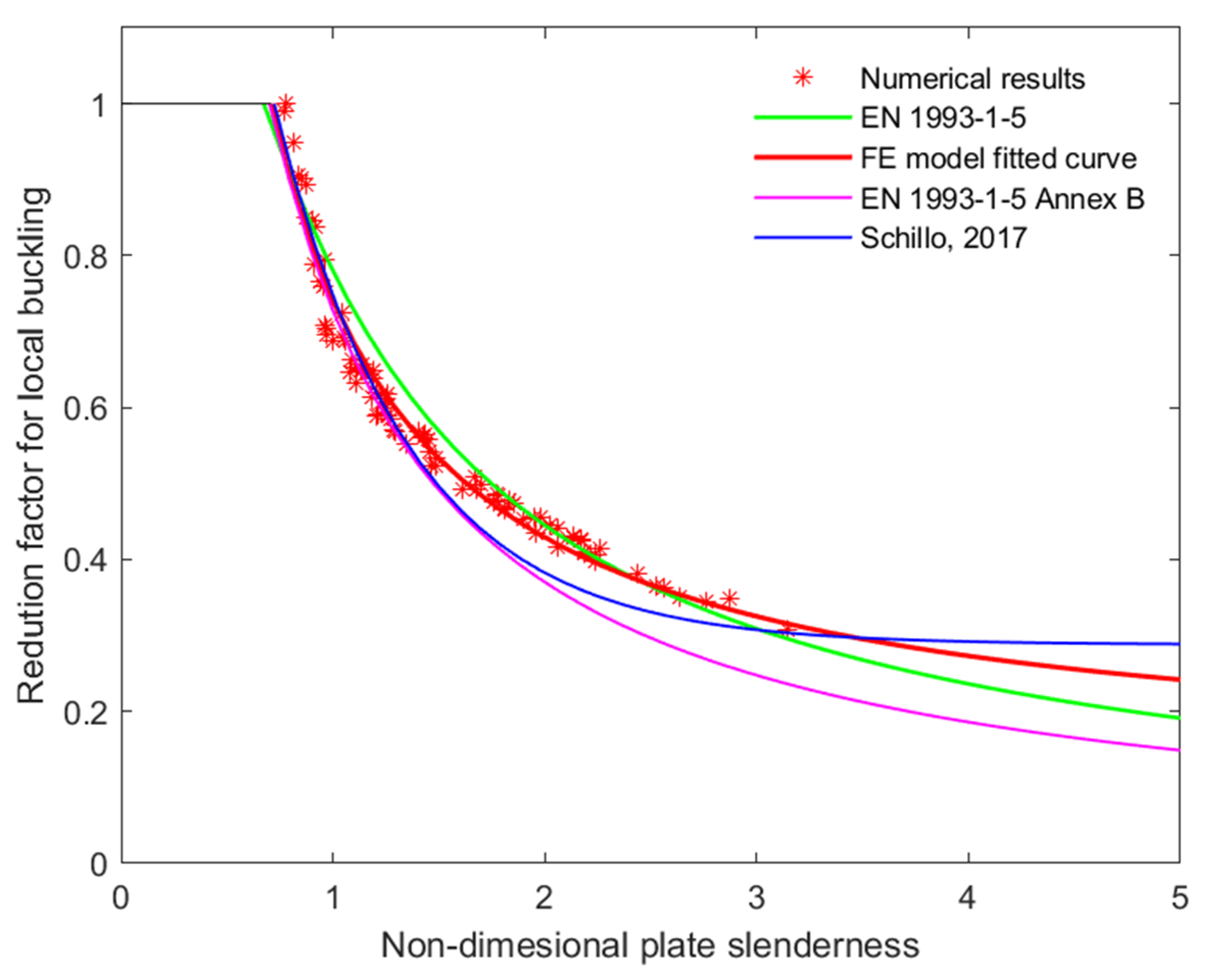
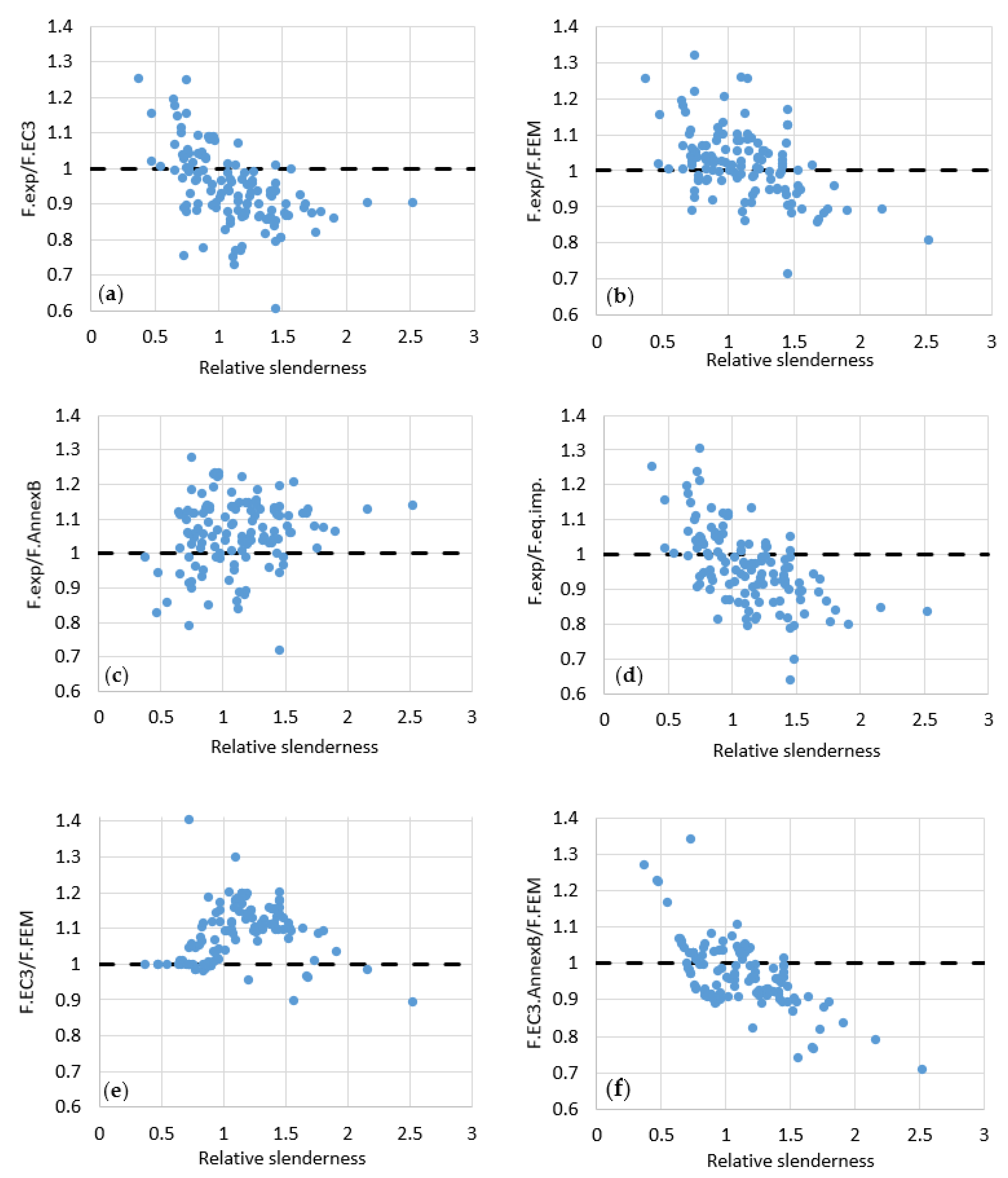
5.1. Comparison to Different Calculation Methods
5.2. Comparison to Analytical Buckling Curves
6. Conclusions
- The best analytical approach closest to the calculated data points obtained by the most accurate numerical model was the buckling curve proposed by Schillo [6];
- The buckling curve given by Annex B of EN 1993-1-5 [4] leads to safe side resistances, especially for very slender plates;
- The Winter-type buckling curve would overestimate the buckling resistance for the welded box section columns, as proven by previous research results as well.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
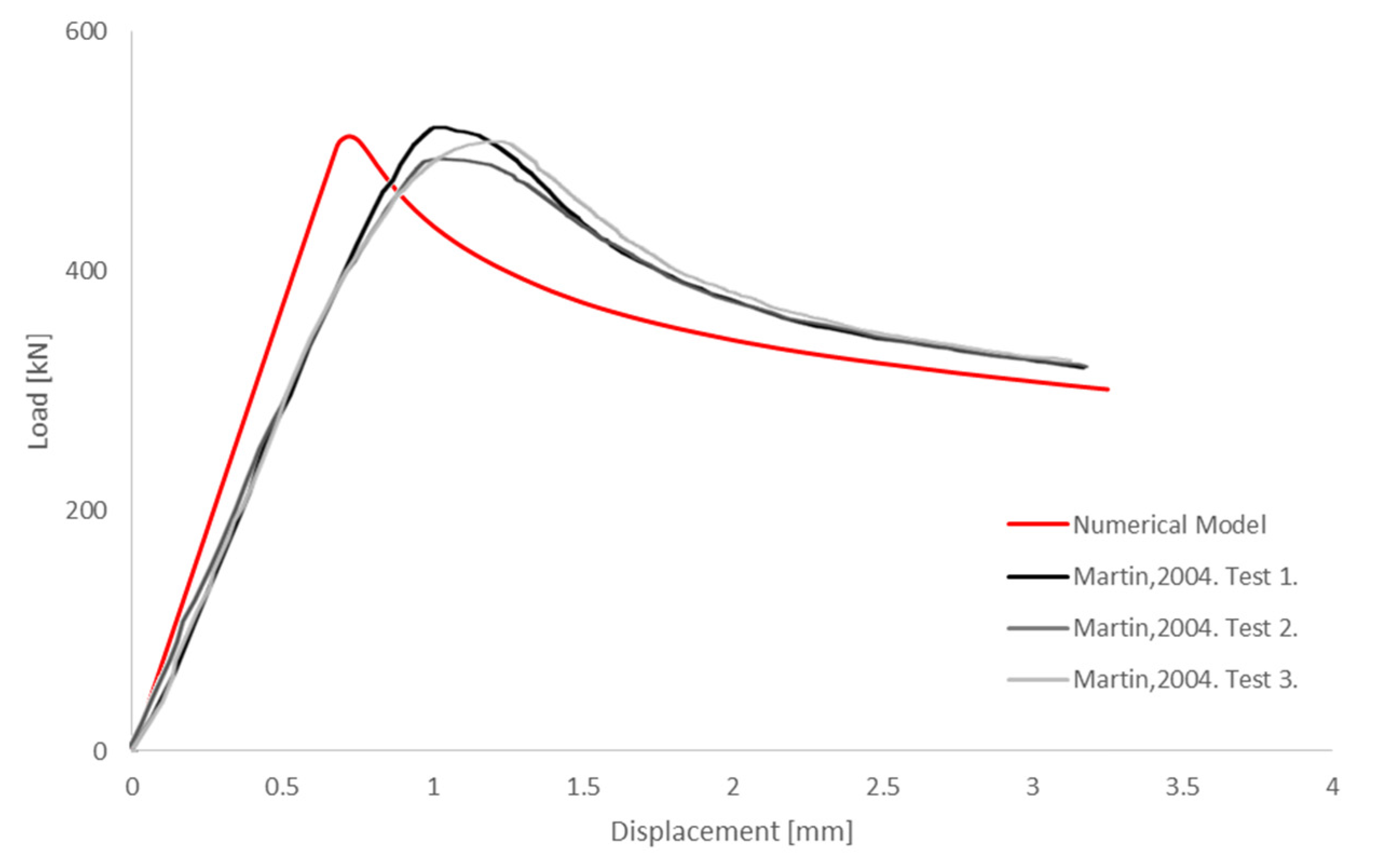
- Clarin, M. High Strength Steel: Local Buckling and Residual Stresses. Ph.D. Thesis, Luleå Tekniska Universitet, Luleå, Sweden, 2004. [Google Scholar]
- Bridge, R.Q.; O’Shea, M.D. Behaviour of thin-walled steel box sections with or without internal restraint. J. Constr. Steel Res. 1998, 47, 73–91. [Google Scholar] [CrossRef]
- Schillo, N.; Feldmann, M. Local buckling behaviour of welded box sections made of high-strength steel: Comparing experiments with EC3 and general method. Steel Constr. 2015, 8, 179–186. [Google Scholar] [CrossRef]
- EN 1993-1-5; Eurocode 3—Design of Steel Structures—Part 1-5: Plated Structural Elements. European Committee for Standardization (CEN): Brussels, Belgium, 2006.
- Hämäläinen, O.-P.; Halme, T.; Björk, T. Local Buckling of Welded Box Beams Made of Ultrahigh-Strength Steels. J. Struct. Eng. 2018, 144, 06018003. [Google Scholar] [CrossRef]
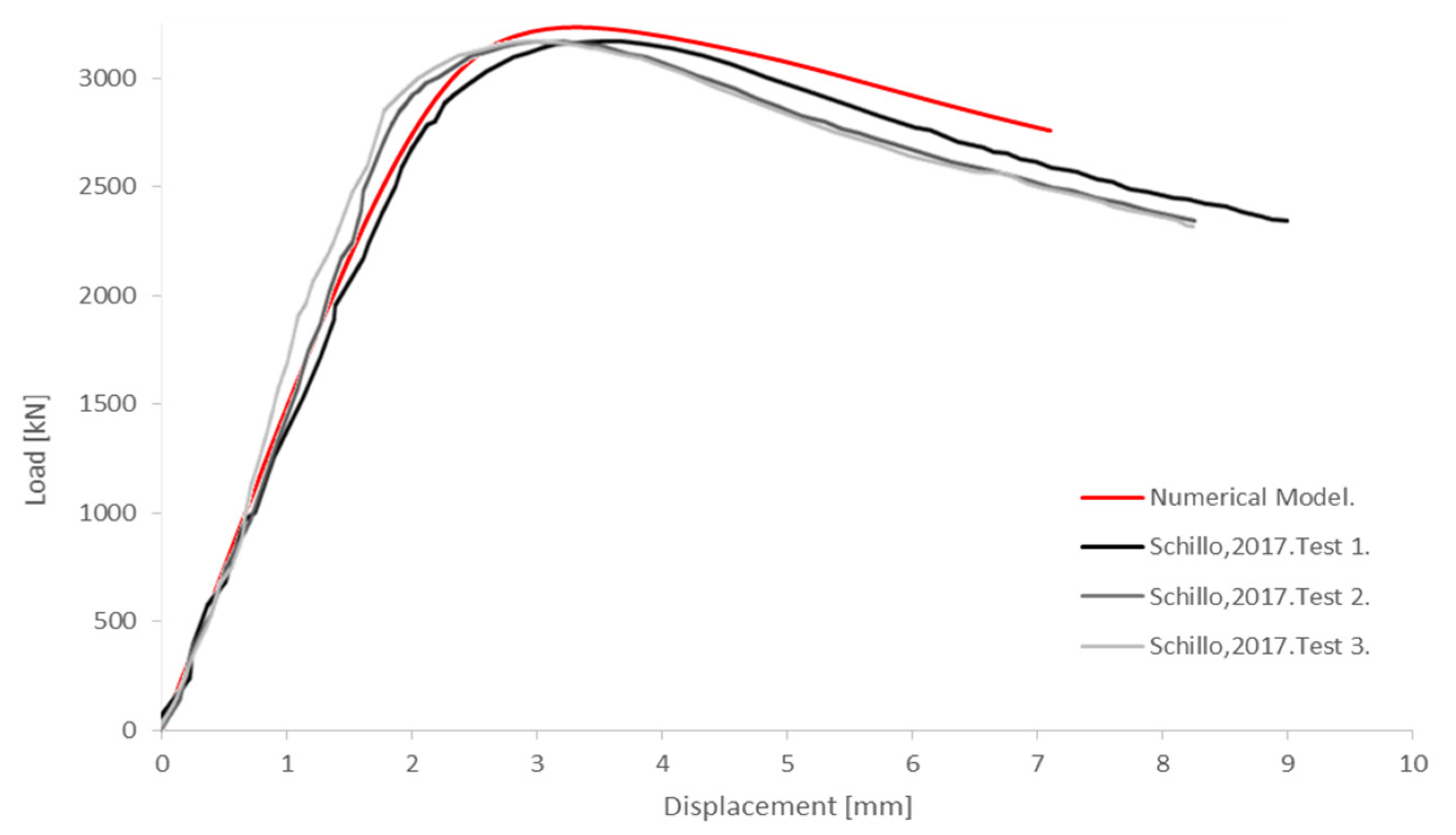
- Schillo, N. Local and global buckling of box columns made of high strength steel. In Schriftenreihe des Lehrstuhls für Stahlbau und Leichtmetallbau der RWTH Aachen; No. Heft 81; Shaker Verlag: Aachen, Germany, 2017. [Google Scholar]
- Rasmussen, K.J.R.; Hancock, G.J. Plate slenderness limits for high strength steel sections. J. Constr. Steel Res. 1992, 23, 73–96. [Google Scholar] [CrossRef]
- Shi, G.; Zhou, W.; Bai, Y.; Lin, C. Local buckling of 460 MPa high strength steel welded section stub columns under axial compression. J. Constr. Steel Res. 2014, 100, 60–70. [Google Scholar] [CrossRef]
- Chiew, S.; Lee, S.; Shanmugam, N.E. Experimental Study of Thin-Walled Steel Box Columns. J. Struct. Eng. 1987, 113, 2208–2220. [Google Scholar] [CrossRef]
- Usami, T.; Fukumoto, Y.; Aoki, T. Tests on the interaction strength between local and overall buckling of welded box columns. Proc. Jpn. Soc. Civ. Eng. 1981, 308, 47–58. [Google Scholar] [CrossRef] [PubMed]
- Nishino, F.; Ueda, Y.; Tall, L.; Nishino, F.; Deda, Y. Experimental Investigation of the Buckling of Plates with Residual Stresses. 1966. Available online: https://www.semanticscholar.org/paper/Experimental-investigation-of-the-buckling-of-with-Nishino-Ueda/7765ec8597cd6598095285396c382b34680d22d6 (accessed on 16 January 2024).
- Liew, J.Y.R.; Shanmugam, N.E.; Lee, S.L. Behavior of Thin-Walled Steel Box Columns Under Biaxial Loading. J. Struct. Eng. 1989, 115, 3076–3094. [Google Scholar] [CrossRef]
- Wright, H.D. Buckling of plates in contact with a rigid medium. Struct. Eng. 1993, 71, 209–215. Available online: https://trid.trb.org/View/383081 (accessed on 16 January 2024).
- Ge, H.; Usami, T. Strength of Concrete-Filled Thin-Walled Steel Box Columns: Experiment. J. Struct. Eng. 1992, 118, 3036–3054. [Google Scholar] [CrossRef]
- Vieira, L.; Gonçalves, R.; Camotim, D. On the local buckling of RHS members under axial force and biaxial bending. Thin-Walled Struct. 2018, 129, 10–19. [Google Scholar] [CrossRef]
- Degée, H.; Detzel, A.; Kuhlmann, U. Interaction of global and local buckling in welded RHS compression members. J. Constr. Steel Res. 2008, 64, 755–765. [Google Scholar] [CrossRef]
- Johansson, B.; Maquoi, R.; Sedlacek, G.; Müller, C.; Beg, D. Commentary and Worked Examples to EN 1993-1-5 “Plated Structural Elements”. JRC Publications Repository. Available online: https://publications.jrc.ec.europa.eu/repository/handle/JRC38239 (accessed on 16 January 2024).
- Pircher, M.; O’Shea, M.D.; Bridge, R.Q. The influence of the fabrication process on the buckling of thin-walled steel box sections. Thin-Walled Struct. 2002, 40, 109–123. [Google Scholar] [CrossRef]
- Kövesdi, B.; Somodi, B. Buckling resistance of HSS box section columns Part II: Analytical study. J. Constr. Steel Res. 2018, 140, 25–33. [Google Scholar] [CrossRef]
- Somodi, B.; Kövesdi, B. Residual stress measurements on welded square box sections using steel grades of S235–S960. Thin-Walled Struct. 2018, 123, 142–154. [Google Scholar] [CrossRef]
- Dwight and Bradfield. Local Buckling Rules for RHS; Technical note; University of Cambridge: Cambridge, UK, 1975. [Google Scholar]
- He, X.; Ke, K.; Zhou, X. Closed-form design solutions for parallelogram hollow structural sections under bending scenarios. J. Constr. Steel Res. 2023, 207, 107934. [Google Scholar] [CrossRef]
- Zhu, J.Y.; Chan, T.M.; Young, B. Cross-sectional capacity of octagonal tubular steel stub columns under uniaxial compression. Eng. Struct. 2019, 184, 480–494. [Google Scholar] [CrossRef]
- Chen, J.; Chan, T.M.; Varma, A.H. Stub Column Behavior of Cold-Formed High-Strength Steel Circular Hollow Sections under Compression. J. Struct. Eng. 2020, 146, 04020277. [Google Scholar] [CrossRef]
- Chen, J.; Chan, T.M. Material properties and residual stresses of cold-formed high strength steel circular hollow sections. J. Constr. Steel Res. 2020, 170, 106099. [Google Scholar] [CrossRef]
- Jiao, H.; Imperfection, X.L.Z. residual stress and yield slenderness limit of very high strength (VHS) circular steel tubes. J. Constr. Steel Res. 2003, 59, 233–249. [Google Scholar] [CrossRef]
- Ma, J.L.; Chan, T.M.; Young, B. Material properties and residual stresses of cold-formed high strength steel hollow sections. J. Constr. Steel Res. 2015, 109, 152–165. [Google Scholar] [CrossRef]
- Ma, J.L.; Chan, T.M.; Young, B. Experimental investigation on stub-column behavior of cold-formed high-strength steel tubular sections. J. Struct. Eng. 2016, 142, 04015174. [Google Scholar] [CrossRef]
- Sun, M.; Packer, J.A. Direct-formed and continuous-formed rectangular hollow sections. J. Constr. Steel Res. 2014, 92, 67–78. [Google Scholar] [CrossRef]
- Key, P.W.; Hancock, G.J. A Theoretical Investigation of the Column Behaviour of Cold-Formed Square Hollow Sections. Thin-Walled Struct. 1993, 16, 31–64. [Google Scholar] [CrossRef]
- Jandera, M.; Gardner, L.; Machacek, J. Residual stresses in cold-rolled stainless steel hollow sections. J. Constr. Steel Res. 2008, 64, 1255–1263. [Google Scholar] [CrossRef]
- Cruise, R.B.; Gardner, L. Residual stress analysis of structural stainless steel sections. J. Constr. Steel Res. 2008, 64, 352–366. [Google Scholar] [CrossRef]
- Huang, Y.; Young, B. Material properties of cold-formed lean duplex stainless steel sections. Thin-Walled Struct. 2012, 52, 72–81. [Google Scholar] [CrossRef]
- Limkatanyu, S.; Sae-Long, W.; Rungamornrat, J.; Buachart, C.; Sukontasukkul, P.; Keawsawasvong, S.; Bending, P.C. Buckling and free vibration analyses of nanobeam-substrate medium systems. Facta Univ. Ser. Mech. Eng. 2022, 20, 561–587. [Google Scholar] [CrossRef]
- Safaei, B.; Onyibo, E.C.; Hurdoganoglu, D. Thermal buckling and bending analyses of carbon foam beams sandwiched by composite faces under axial compression. Facta Univ. Ser. Mech. Eng. 2022, 20, 589–615. [Google Scholar] [CrossRef]
- Shahani, F. Kiarasi. Numerical and Experimental Investigation on Post-buckling Behavior of Stiffened Cylindrical Shells with Cutout subject to Uniform Axial Compression. J. Appl. Comput. Mech. 2023, 9, 25–44. [Google Scholar] [CrossRef]
- ANSYS® 2023 R2, ANSYS: Canonsburg, PA, USA.
- Somodi, B.; Kövesdi, B. Flexural buckling resistance of welded HSS box section members. Thin-Walled Struct. 2017, 119, 266–281. [Google Scholar] [CrossRef]
- prEN1993-1-14; Eurocode 3: Design of Steel Structures—Part 1-14: Design Assisted by Finite Element Analysis. European Committee for Standardization (CEN): Brussels, Belgium, 2022.
- Gardner, L.; Yun, X.; Fieber, A.; Macorini, L. Steel Design by Advanced Analysis: Material Modeling and Strain Limits. Engineering 2019, 5, 243–249. [Google Scholar] [CrossRef]
- Ramberg, W.; Osgood, W.R. Description of Stress-Strain Curves by Three Parameters. 1 July 1943. Available online: https://ntrs.nasa.gov/citations/19930081614 (accessed on 17 January 2024).
- Radwan, M.; Kövesdi, B. Local plate buckling type imperfections for NSS and HSS welded box-section columns. Structures 2021, 34, 2628–2643. [Google Scholar] [CrossRef]
- Couto, C.; Real, P.V. Numerical investigation on the influence of imperfections in the local buckling of thin-walled I-shaped sections. Thin-Walled Struct. 2019, 135, 89–108. [Google Scholar] [CrossRef]
- ECCS—European Convention for Constructional Steelwork. Available online: https://www.steelconstruct.com/ (accessed on 17 January 2024).
- BSK “Boverkets Handbok om Stålkonstruktioner”; Boverket, Byggavdelningen: Karlskrona, Sweden, 1997; ISBN 91-7147-337-8. (In Swedish)
- Code for Design of Steel Structures Committee. Application Construal of Code for Design of Steel Structures in China; China Planning Press: Beijing, China, 2003. (In Chinese) [Google Scholar]
- Ban, H.; Shi, G.; Shi, Y.; Wang, Y. Residual stress of 460 MPa high strength steel welded box section: Experimental investigation and modeling. Thin-Walled Struct. 2013, 64, 73–82. [Google Scholar] [CrossRef]
- Khan, M.; Paradowska, A.; Uy, B.; Mashiri, F.; Tao, Z. Residual stresses in high strength steel welded box sections. J. Constr. Steel Res. 2016, 116, 55–64. [Google Scholar] [CrossRef]
- MGrams, R.; Mendez, P.F. A General Expression for the Welding Tendon Force. J. Manuf. Sci. Eng. 2021, 143, 121002. [Google Scholar] [CrossRef]
- Somodi, B.; Kövesdi, B.; Hornyák, T. Partial factor for local buckling of welded box sections. Structures 2021, 30, 440–454. [Google Scholar] [CrossRef]
- Hassan, M.S.; Salawdeh, S.; Goggins, J. Determination of geometrical imperfection models in finite element analysis of structural steel hollow sections under cyclic axial loading. J. Constr. Steel Res. 2018, 141, 189–203. [Google Scholar] [CrossRef]
- BS EN 1090-2:2018-TC; BSI Knowledge. 2018. Available online: https://knowledge.bsigroup.com/products/execution-of-steel-structures-and-aluminium-structures-technical-requirements-for-steel-structures-1?version=tracked (accessed on 17 January 2024).
- Demkowicz, L.; Devloo, P.; Oden, J.T. On an h-type mesh-refinement strategy based on minimization of interpolation errors. Comput. Methods Appl. Mech. Eng. 1985, 53, 67–89. [Google Scholar] [CrossRef]
- EN 1993-1-1; Eurocode 3—Design of Steel Structures—Part 1-1: General Rules and Rules for Buildings. 2005. European Committee for Standardization (CEN): Brussels, Belgium, 2005.
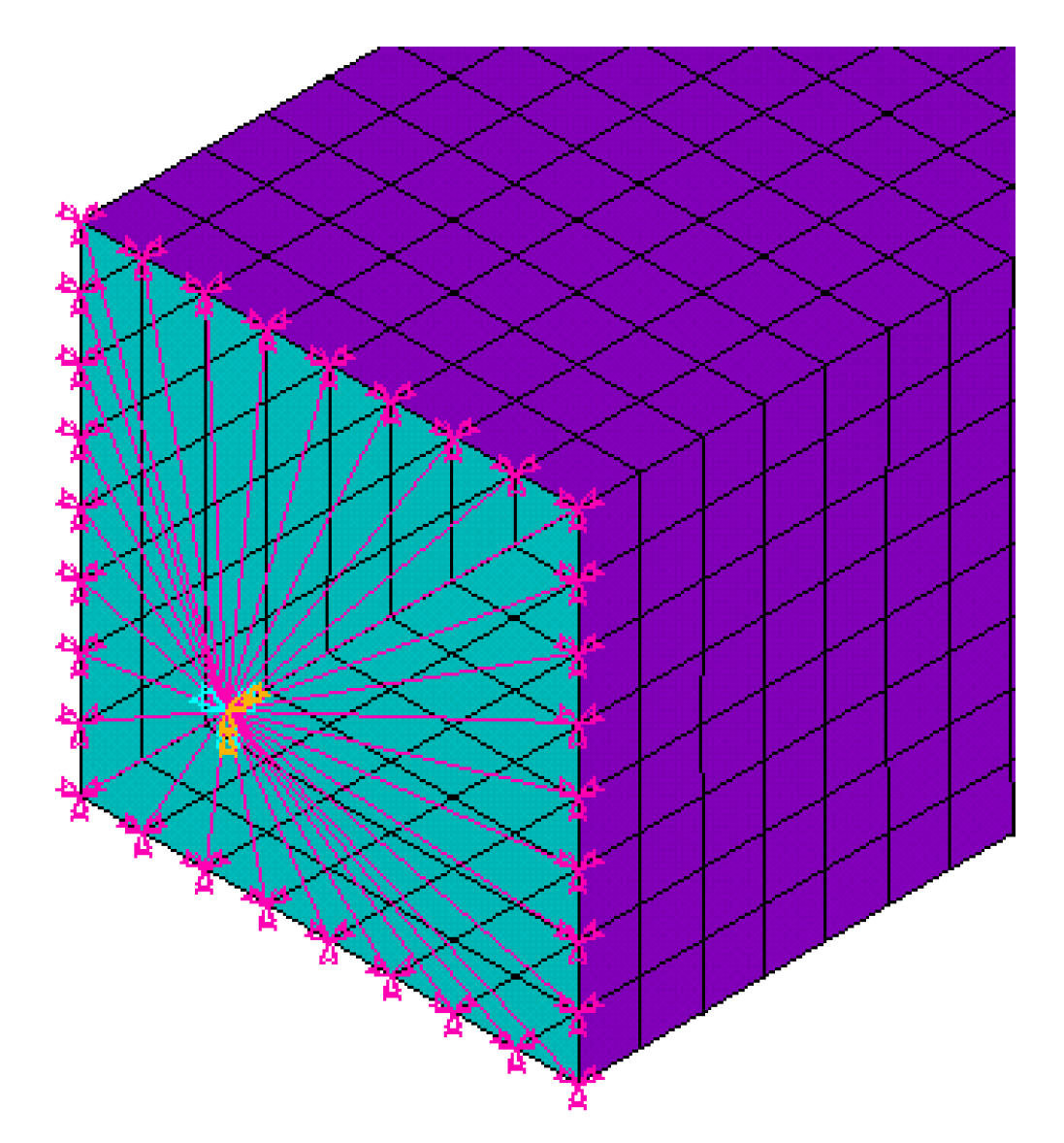

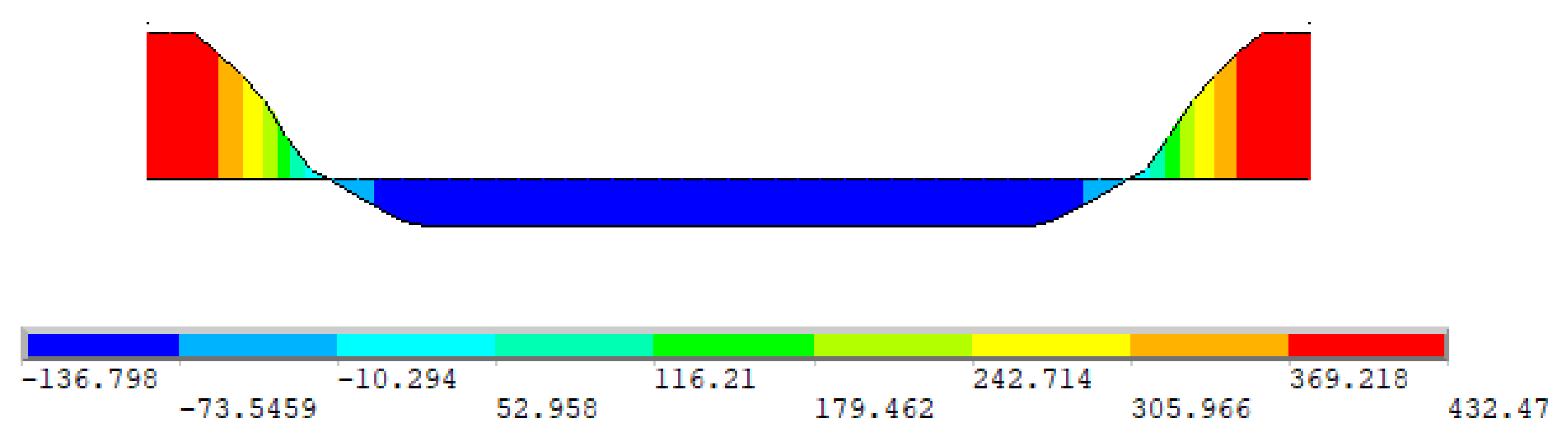
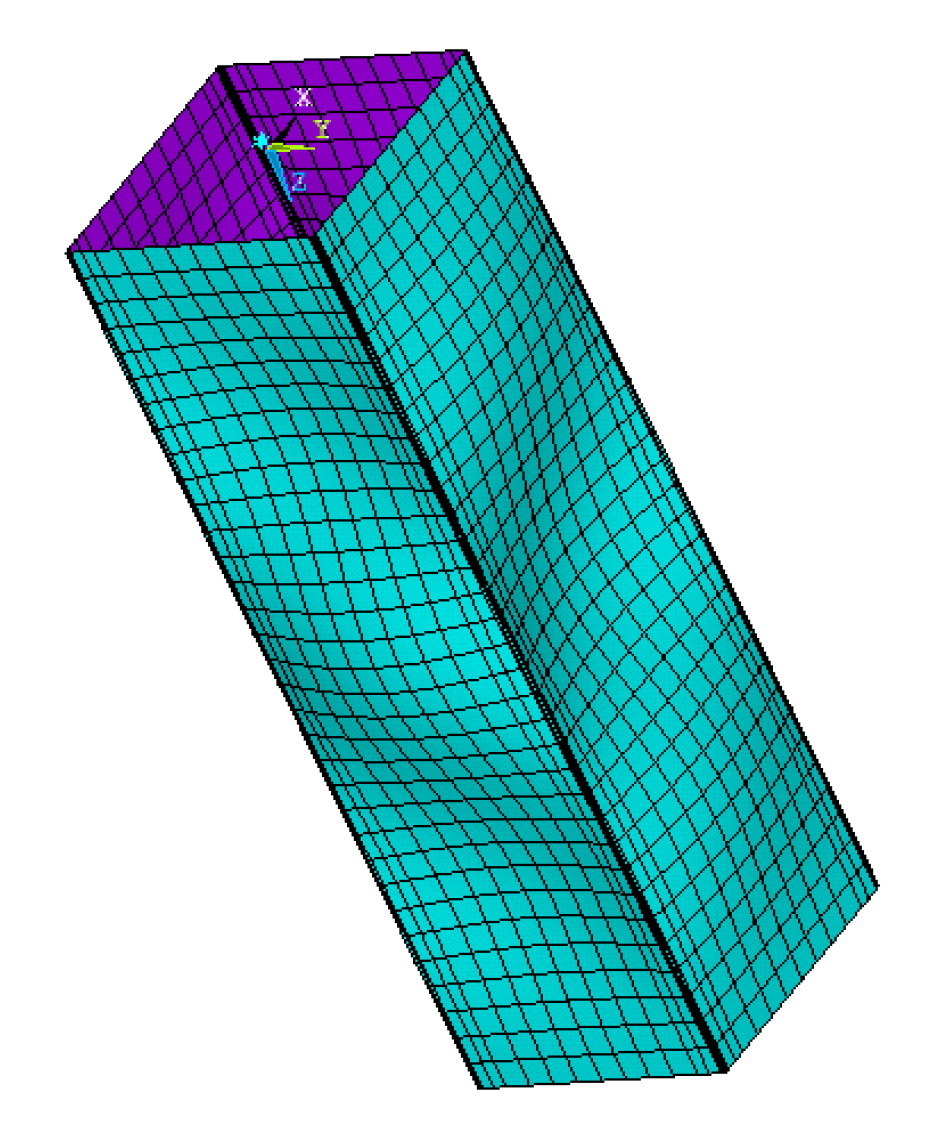

| Source | Total Number of Tests | Failure by Local Buckling | Section Type | fy [MPa] | Loading Type |
|---|---|---|---|---|---|
| Clarin, M. (2004) [1]. | 49 | 24 | 1 | 441.3 471 772.7 794 1335 1350.7 | Quasi-static Deformation-controlled |
| Russell Q. et al. (1998) [2]. | 11 | 6 | 2 | 282 | Quasi-static Displacement-controlled |
| Schillo, N. and Feldmann, M. (2015) [3]. | 32 | 8 | 2 | 561 610 760 991 | Quasi-static Displacement-controlled |
| Hämäläinen, O et al. (2018) [5]. | 12 | 12 | 1 | 1100 1121 | no data |
| Schillo, N. (2017) [6]. | 26 | 16 | 2 | 562 610 760 980 991 | Quasi-static Displacement-controlled |
| Rasmussen, K and Hancock, G. (1992) [7]. | 6 | 3 | 1 | 670 | Quasi-static Displacement-controlled |
| Shi, G. et al. (2014) [8]. | 4 | 4 | 2 | 460 | Displacement-controlled |
| Chiew. et al. (1987) [9]. | 13 | 13 | 3 | 248.6 253.6 261.2 | Quasi-static Displacement-controlled Load-controlled |
| Usami, T. (1981) [10]. | 13 | 12 | 3 | 743.8 | Load-controlled |
| Nishino, F, and Ueda. (1967) [11]. | 8 | 8 | 2 | 273.1 266.1 714.3 799.8 | Displacement-controlled |
| Liew, J. et al. (1989) [12]. | 6 | 6 | 3 | 268 293 353 | Static Displacement-controlled |
| Ge, H. et al. (1992) [14]. | 3 | 3 | 3 | 266 | Cyclic Load-controlled Displacement-controlled |
| Dwight, J., and Bradfield, C. (1975) [21]. | 17 | 9 | no data 1 | 250 275 312 403 | no data 1 |
| H/t | Welding Type | σrt/fy | σrc/fy | Tensile Zone | Transition Zone |
|---|---|---|---|---|---|
| 10 | ----- | 1 | −0.6 | 0 | from equilibrium |
| 20 | Heavy weld | 1 | −0.85 | 3t | 3t |
| 20 | Light weld | 1 | −0.29 | 1.5t | 1.5t |
| 40 | Heavy weld | 1 | −0.29 | 3t | 3t |
| 40 | Light weld | 1 | −0.13 | 1.5t | 1.5t |
| Ref. | Experiment | b/125 [52] | 2021 Model [50] | 2023 Model | Hassan et al. [51]. | Radwan et al. [42]. | 2021_mod | |
|---|---|---|---|---|---|---|---|---|
| [1] | 0.47 | 5460 | 5290 | 5357 | 5357 | 5357 | 5357 | 5357 |
| 0.84 | 8923 | 8072 | 8746 | 8605 | 8761 | 8589 | 8844 | |
| 1.20 | 7035 | 6831 | 6919 | 6863 | 7049 | 6991 | 7018 | |
| 1.56 | 7579 | 7891 | 7500 | 7510 | 7888 | 7891 | 7924 | |
| [2] | 0.72 | 182 | 151 | 174 | 150 | 164 | 171 | 177 |
| 1.09 | 184 | 176 | 173 | 171 | 178 | 178 | 177 | |
| 1.45 | 184 | 197 | 176 | 179 | 197 | 197 | 196 | |
| 1.80 | 211 | 214 | 173 | 178 | 211 | 214 | 211 | |
| [3] | 0.83 | 1833 | 1446 | 1677 | 1560 | 1492 | 1613 | 1687 |
| [6] | 0.80 | 506 | 426 | 480 | 437 | 439 | 454 | 470 |
| 0.86 | 1280 | 1070 | 1206 | 1126 | 1098 | 1159 | 1215 | |
| 0.93 | 1651 | 1311 | 1403 | 1353 | 1297 | 1372 | 1403 | |
| [11] | 0.83 | 1608 | 1417 | 1572 | 1506 | 1491 | 1500 | 1557 |
| 1.18 | 1510 | 1580 | 1510 | 1516 | 1587 | 1587 | 1588 | |
| 1.40 | 3101 | 3008 | 2972 | 2975 | 3010 | 3008 | 3004 | |
| 0.77 | 2909 | 2530 | 2942 | 2834 | 2435 | 2830 | 2947 | |
| [21] | 0.65 | 381 | 329 | 378 | 342 | 354 | 368 | 379 |
| 0.98 | 433 | 383 | 395 | 382 | 390 | 389 | 390 | |
| 1.15 | 442 | 401 | 389 | 389 | 403 | 402 | 404 | |
| 1.23 | 150 | 139 | 132 | 131 | 139 | 139 | 139 | |
| 1.44 | 160 | 144 | 129 | 130 | 144 | 144 | 143 | |
| 1.64 | 159 | 153 | 151 | 152 | 151 | 153 | 151 |
| Model | b/125 [52] | 2021 Model [50] | 2023 Model | Hassan et al. [51]. | Radwan et al. [42] | 2021_mod |
|---|---|---|---|---|---|---|
| Mean value | 1.095 | 1.070 | 1.100 | 1.076 | 1.052 | 1.039 |
| Standard deviation | 0.094 | 0.069 | 0.074 | 0.087 | 0.064 | 0.057 |
| Min. | 0.933 | 0.989 | 0.996 | 0.937 | 0.933 | 0.941 |
| Max. | 1.268 | 1.241 | 1.229 | 1.272 | 1.203 | 1.176 |
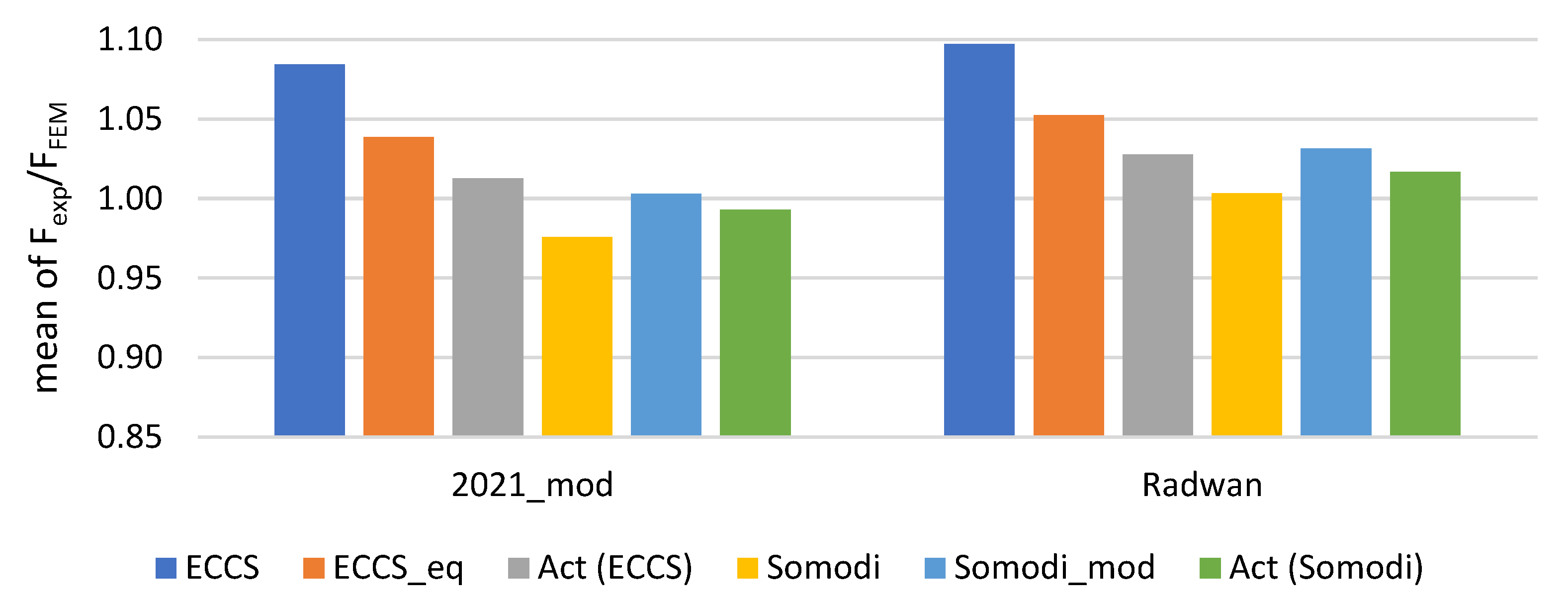
| Model | ECCS [44] + Radwan et al. [42] | Somodi et al. + Radwan et al. [42] | Khan et al. [48] + Radwan et al. [42] | ECCS_Eq + Radwan et al. [42] | Somodi_mod + Radwan et al. [42] |
|---|---|---|---|---|---|
| Mean | 1.097 | 1.003 1 | 0.976 | 1.052 | 1.032 |
| Standard Deviation | 0.068 | 0.065 1 | 0.079 | 0.064 | 0.087 |
| Model | ECCS [44] + 2021_mod | Somodi et al. [20] + 2021_mod | Khan et al. [48] + 2021_mod | ECCS_Eq + 2021_mod | Somodi_mod + 2021_mod |
|---|---|---|---|---|---|
| Mean | 1.084 | 0.976 1 | 0.947 | 1.039 | 1.003 |
| Standard Deviation | 0.078 | 0.056 1 | 0.080 | 0.057 | 0.056 |
| Steel Material | Original Model | Modified Model |
|---|---|---|
| fy < S235 | --- 1 | (20) |
| S235 | 2.5t | 2.5t |
| S355–S460 | 2t | 2t |
| S500 | 1.5t | 1.5t |
| S700 | 0.75t | 0.75t |
| S960 | 0 | 0 |
| fy > S960 | --- 1 | 0 |
| Specimen | Research Work | b/t | fy [MPa] | ECCS Model | ECCS_Eq Model | ||||
|---|---|---|---|---|---|---|---|---|---|
| a [mm] | b [mm] | Force-Remain [N] | a [mm] | b [mm] | Force-Remain [N] | ||||
| W72-0b | Clarin, M. (2004) [1] | 26.8 | 772.7 | 6.14 | 6.14 | −6213.71 | 8.21 | 8.21 | −4.4 |
| #3 | Russell et al. (1998) [2] | 75.0 | 282.0 | 6.43 | 6.43 | −6136.38 | 12.06 | 12.06 | 1.6 |
| T2A-T2B | Nishino et al. (1967) [11] | 25.5 | 714.3 | 9.75 | 9.75 | −7309.76 | 12.39 | 12.39 | −6 |
| S.52.10 | Liew et al. (1989) [12] | 53.4 | 353.0 | 9.15 | 9.15 | −4186.40 | 12.21 | 12.21 | −3.1 |
| Model | ECCS_Eq + 2021_mod | Somodi_mod. + 2021 mod | ECCS_Eq + Radwan [42] | Somodi_mod + Radwan [42] |
|---|---|---|---|---|
| Mean | 1.012 | 0.993 | 1.028 | 1.017 |
| Standard Deviation | 0.051 | 0.049 | 0.060 | 0.055 |
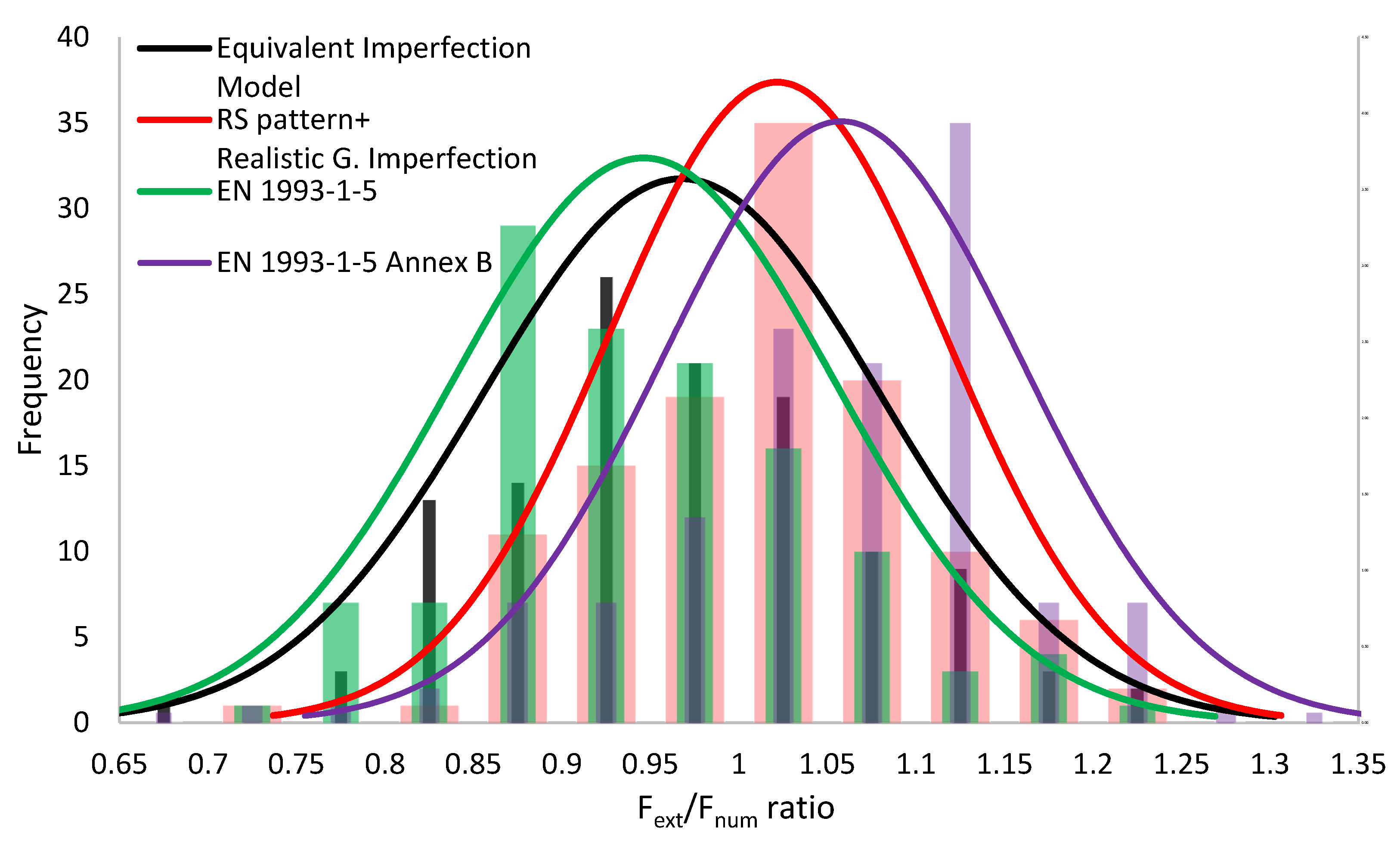
| Model | Advanced FEM with RS + imp. (Somodi_mod + 2021_mod) | FEM with Equivalent Imperfection (b/200) | EN 1993-1-5 Annex B [4] | EN 1993-1-5 [4] (Winter Curve) |
|---|---|---|---|---|
| Mean | 1.022 | 0.967 | 1.058 | 0.946 |
| Standard deviation | 0.095 | 0.112 | 0.101 | 0.108 |
| Maximum value | 1.318 | 1.304 | 1.279 | 1.255 |
| Minimum value | 0.808 | 0.640 | 0.718 | 0.606 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Quillupangui, I.; Somodi, B.; Kövesdi, B. Overview of FEM-Based Resistance Models for Local Buckling of Welded Steel Box Section Columns. Appl. Sci. 2024, 14, 2029. https://doi.org/10.3390/app14052029
Quillupangui I, Somodi B, Kövesdi B. Overview of FEM-Based Resistance Models for Local Buckling of Welded Steel Box Section Columns. Applied Sciences. 2024; 14(5):2029. https://doi.org/10.3390/app14052029
Chicago/Turabian StyleQuillupangui, Irvin, Balázs Somodi, and Balázs Kövesdi. 2024. "Overview of FEM-Based Resistance Models for Local Buckling of Welded Steel Box Section Columns" Applied Sciences 14, no. 5: 2029. https://doi.org/10.3390/app14052029
APA StyleQuillupangui, I., Somodi, B., & Kövesdi, B. (2024). Overview of FEM-Based Resistance Models for Local Buckling of Welded Steel Box Section Columns. Applied Sciences, 14(5), 2029. https://doi.org/10.3390/app14052029