Pockels Effect of Interfacial Water on a Mono-Electrode Induced by Current Parallel to the Electrode Surface
Abstract
:Featured Application
Abstract
1. Introduction
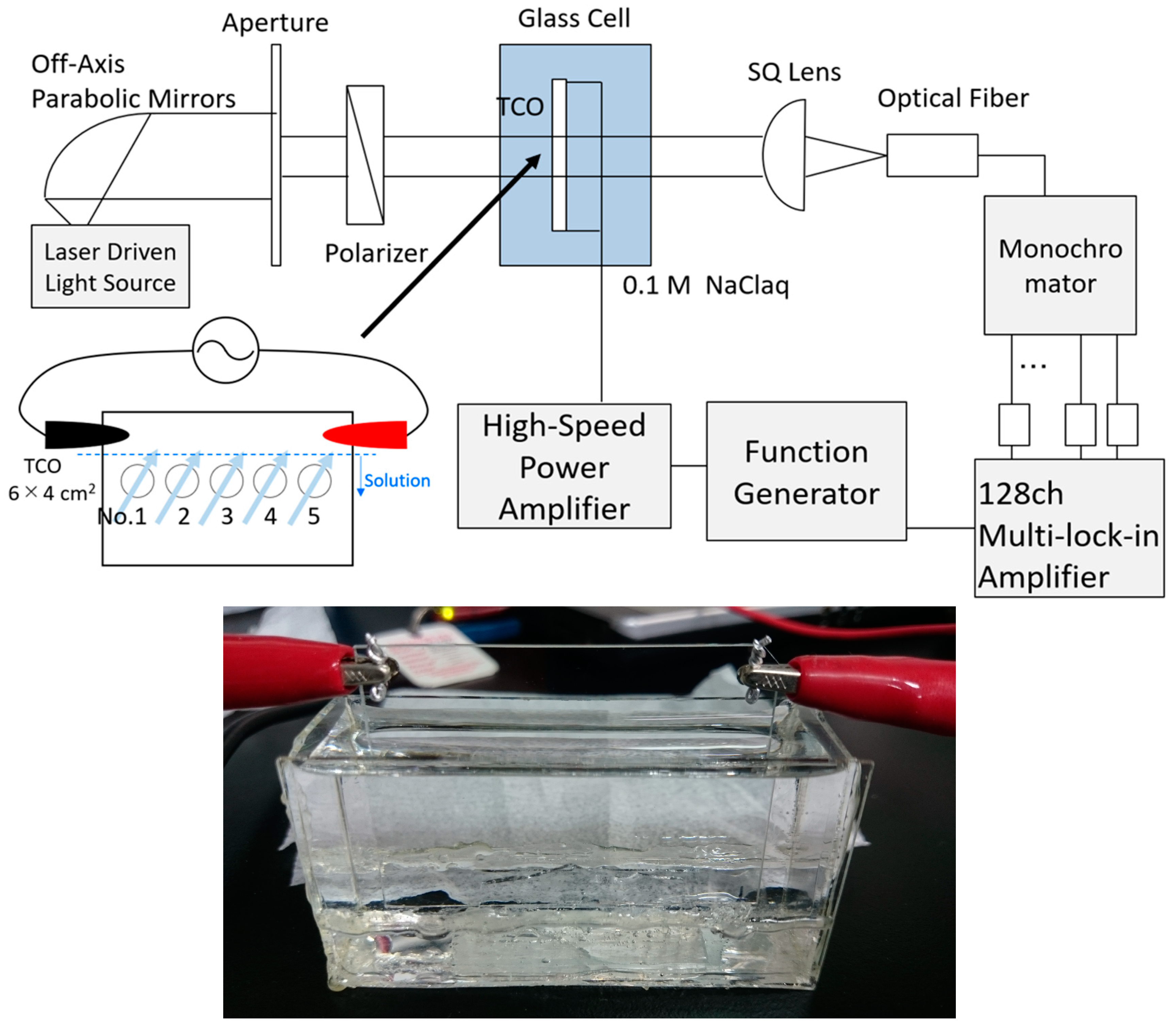
2. Materials and Methods
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Position Dependence on a Single Copper Electrode of the Pockels Signal Induced by Current Parallel to the Electrode Surface







References
- Parsons, R. The Electrical Double Layer: Recent Experimental and Theoretical Developments. Chem. Rev. 1990, 90, 813–826. [Google Scholar] [CrossRef]
- Schmickler, W. Electronic Effects in the Electric Double Layer. Chem. Rev. 1996, 96, 3177–3200. [Google Scholar] [CrossRef] [PubMed]
- Brown, G.E.; Henrich, V.E.; Casey, W.H.; Clark, D.L.; Eggleston, C.; Felmy, A.; Goodman, D.W.; Grätzel, M.; Maciel, G.; McCarthy, M.I.; et al. Metal Oxide Surfaces and Their Interactions with Aqueous Solutions and Microbial Organisms. Chem. Rev. 1999, 99, 77–174. [Google Scholar] [CrossRef]
- Groß, A.; Sakong, S. Modelling the Electric Double Layer at Electrode/Electrolyte Interfaces. Curr. Opin. Electrochem. 2019, 14, 1–6. [Google Scholar] [CrossRef]
- Burt, R.; Birkett, G.; Zhao, X.S. A Review of Molecular Modelling of Electric Double Layer Capacitors. Phys. Chem. Chem. Phys. 2014, 16, 6519–6538. [Google Scholar] [CrossRef]
- Shimotani, H.; Asanuma, H.; Tsukazaki, A.; Ohtomo, A.; Kawasaki, M.; Iwasa, Y. Insulator-to-Metal Transition in ZnO by Electric Double Layer Gating. Appl. Phys. Lett. 2007, 91, 082106. [Google Scholar] [CrossRef]
- Scherwitzl, R.; Zubko, P.; Lezama, I.G.; Ono, S.; Morpurgo, A.F.; Catalan, G.; Triscone, J.-M. Electric-Field Control of the Metal-Insulator Transition in Ultrathin NdNiO3 Films. Adv. Mater. 2010, 22, 5517–5520. [Google Scholar] [CrossRef]
- Du, H.; Lin, X.; Xu, Z.; Chu, D. Electric Double-Layer Transistors: A Review of Recent Progress. J. Mater. Sci. 2015, 50, 5641–5673. [Google Scholar] [CrossRef]
- Pei, Q.; Yu, G.; Zhang, C.; Yang, Y.; Heeger, A.J. Polymer Light-Emitting Electrochemical Cells. Science 1995, 269, 1086–1088. [Google Scholar] [CrossRef]
- Ono, S.; Miwa, K.; Iori, J.; Mitsuya, H.; Ishibashi, K.; Sano, C.; Toshiyoshi, H.; Fujita, H. A Novel Vibrational Energy Harvester with Electric Double Layer Electrets. J. Phys. Conf. Ser. 2016, 773, 012074. [Google Scholar] [CrossRef]
- Electrically Induced Ferromagnetism at Room Temperature in Cobalt-Doped Titanium Dioxide|Science. Available online: https://science.sciencemag.org/content/332/6033/1065 (accessed on 22 June 2021).
- Shimamura, K.; Chiba, D.; Ono, S.; Fukami, S.; Ishiwata, N.; Kawaguchi, M.; Kobayashi, K.; Ono, T. Electrical Control of Curie Temperature in Cobalt Using an Ionic Liquid Film. Appl. Phys. Lett. 2012, 100, 122402. [Google Scholar] [CrossRef]
- Ueno, K.; Nakamura, S.; Shimotani, H.; Ohtomo, A.; Kimura, N.; Nojima, T.; Aoki, H.; Iwasa, Y.; Kawasaki, M. Electric-Field-Induced Superconductivity in an Insulator. Nat. Mater. 2008, 7, 855–858. [Google Scholar] [CrossRef]
- Ueno, K.; Shimotani, H.; Yuan, H.; Ye, J.; Kawasaki, M.; Iwasa, Y. Field-Induced Superconductivity in Electric Double Layer Transistors. J. Phys. Soc. Jpn. 2014, 83, 032001. [Google Scholar] [CrossRef]
- Shen, Y.R. The Principles of Nonlinear Optics; Wiley: Hoboken, NJ, USA, 1984; ISBN 978-0-471-88998-4. [Google Scholar]
- Yariv, A. Quantum Electronics; Wiley: Hoboken, NJ, USA, 1989; ISBN 978-0-471-60997-1. [Google Scholar]
- Boyd, R.W. Nonlinear Optics; Elsevier: Amsterdam, The Netherlands, 2008; ISBN 978-0-08-048596-6. [Google Scholar]
- Du, Q.; Superfine, R.; Freysz, E.; Shen, Y.R. Vibrational Spectroscopy of Water at the Vapor/Water Interface. Phys. Rev. Lett. 1993, 70, 2313–2316. [Google Scholar] [CrossRef] [PubMed]
- Shen, Y.R. Fundamentals of Sum-Frequency Spectroscopy; Cambridge University Press: Cambridge, UK, 2016; ISBN 978-1-316-47304-7. [Google Scholar]
- Tokunaga, E.; Nosaka, Y.; Hirabayashi, M.; Kobayashi, T. Pockels Effect of Water in the Electric Double Layer at the Interface between Water and Transparent Electrode. Surf. Sci. 2007, 601, 735–741. [Google Scholar] [CrossRef]
- Nosaka, Y.; Hirabayashi, M.; Kobayashi, T.; Tokunaga, E. Gigantic Optical Pockels Effect in Water within the Electric Double Layer at the Electrode-Solution Interface. Phys. Rev. B 2008, 77, 241401. [Google Scholar] [CrossRef]
- Kanemaru, H.; Nosaka, Y.; Hirako, A.; Ohkawa, K.; Kobayashi, T.; Tokunaga, E. Electrooptic Effect of Water in Electric Double Layer at Interface of GaN Electrode. Opt. Rev. 2010, 17, 352–356. [Google Scholar] [CrossRef]
- Yukita, S.; Suzuki, Y.; Shiokawa, N.; Kobayashi, T.; Tokunaga, E. Mechanisms of the Anomalous Pockels Effect in Bulk Water. Opt. Rev. 2018, 25, 205–214. [Google Scholar] [CrossRef]
- Nishi, Y.; Watanabe, R.; Sasaki, S.; Okada, A.; Seto, K.; Kobayashi, T.; Tokunaga, E. Electric-Field Induced Shift in the Plasmon Resonance Due to the Interfacial Pockels Effect of Water on a Silver Surface. Appl. Sci. 2021, 11, 2152. [Google Scholar] [CrossRef]
- Tanimoto, S.; Okada, A.; Kobayashi, T.; Tokunaga, E. Pockels Effect at the Interface between Water and Ti Electrode. Appl. Sci. 2023, 13, 10284. [Google Scholar] [CrossRef]
- Kanemaru, H.; Yukita, S.; Namiki, H.; Nosaka, Y.; Kobayashi, T.; Tokunaga, E. Giant Pockels Effect of Polar Organic Solvents and Water in the Electric Double Layer on a Transparent Electrode. RSC Adv. 2017, 7, 45682–45690. [Google Scholar] [CrossRef]
- Sur, S.; Venkataraman, V. Observation of Electro-Optic Pockels Effect at the Amorphous TiO2 and Metal Interface. Phys. Rev. Appl. 2018, 10, 014020. [Google Scholar] [CrossRef]
- Hayama, D.; Seto, K.; Yamashita, K.; Yukita, S.; Kobayashi, T.; Kobayashi, T.; Kobayashi, T.; Tokunaga, E.; Tokunaga, E. Giant Pockels Effect in an Electrode-Water Interface for a “liquid” Light Modulator. OSA Contin. 2019, 2, 3358–3373. [Google Scholar] [CrossRef]
- Teng, P.; Luo, M.; Yang, X.; Gao, D.; Copner, N.; Liu, Z.; Liu, Z.; Yang, J.; Li, Z.; Gao, S.; et al. All-Fiber Bidirectional Optical Modulator Derives from the Microfiber Coated with ITO Electrode. Opt. Lett. 2021, 46, 2497–2500. [Google Scholar] [CrossRef]
- Kumar, S.; Tiwari, P.; Zymbler, M. Internet of Things Is a Revolutionary Approach for Future Technology Enhancement: A Review. J. Big Data 2019, 6, 111. [Google Scholar] [CrossRef]
- Twaha, S.; Zhu, J.; Yan, Y.; Li, B. A Comprehensive Review of Thermoelectric Technology: Materials, Applications, Modelling and Performance Improvement. Renew. Sustain. Energy Rev. 2016, 65, 698–726. [Google Scholar] [CrossRef]
- García-Cañadas, J.; Adkins, N.J.E.; McCain, S.; Hauptstein, B.; Brew, A.; Jarvis, D.J.; Min, G. Accelerated Discovery of Thermoelectric Materials: Combinatorial Facility and High-Throughput Measurement of Thermoelectric Power Factor. ACS Comb. Sci. 2016, 18, 314–319. [Google Scholar] [CrossRef]
- Gaultois, M.W.; Oliynyk, A.O.; Mar, A.; Sparks, T.D.; Mulholland, G.J.; Meredig, B. Perspective: Web-Based Machine Learning Models for Real-Time Screening of Thermoelectric Materials Properties. APL Mater. 2016, 4, 053213. [Google Scholar] [CrossRef]
- Iwasaki, Y.; Takeuchi, I.; Stanev, V.; Kusne, A.G.; Ishida, M.; Kirihara, A.; Ihara, K.; Sawada, R.; Terashima, K.; Someya, H.; et al. Machine-Learning Guided Discovery of a New Thermoelectric Material. Sci. Rep. 2019, 9, 2751. [Google Scholar] [CrossRef]
- Suzuki, Y.; Osawa, K.; Yukita, S.; Kobayashi, T.; Tokunaga, E. Anomalously Large Electro-Optic Pockels Effect at the Air-Water Interface with an Electric Field Applied Parallel to the Interface. Appl. Phys. Lett. 2016, 108, 191103. [Google Scholar] [CrossRef]
- Stahrenberg, K.; Herrmann, T.; Wilmers, K.; Esser, N.; Richter, W.; Lee, M.J.G. Optical Properties of Copper and Silver in the Energy Range 2.5–9.0 eV. Phys. Rev. B 2001, 64, 115111. [Google Scholar] [CrossRef]
- Babar, S.; Weaver, J.H. Optical Constants of Cu, Ag, and Au Revisited. Appl. Opt. 2015, 54, 477–481. [Google Scholar] [CrossRef]
- Rakhshani, A.E. Preparation, Characteristics and Photovoltaic Properties of Cuprous Oxide—A Review. Solid-State Electron. 1986, 29, 7–17. [Google Scholar] [CrossRef]





Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Morozumi, K.; Kanemaru, H.; Okada, A.; Ichimiya, T.; Kobayashi, T.; Tokunaga, E. Pockels Effect of Interfacial Water on a Mono-Electrode Induced by Current Parallel to the Electrode Surface. Appl. Sci. 2024, 14, 2076. https://doi.org/10.3390/app14052076
Morozumi K, Kanemaru H, Okada A, Ichimiya T, Kobayashi T, Tokunaga E. Pockels Effect of Interfacial Water on a Mono-Electrode Induced by Current Parallel to the Electrode Surface. Applied Sciences. 2024; 14(5):2076. https://doi.org/10.3390/app14052076
Chicago/Turabian StyleMorozumi, Kairi, Hironori Kanemaru, Akihiro Okada, Tomonari Ichimiya, Takayoshi Kobayashi, and Eiji Tokunaga. 2024. "Pockels Effect of Interfacial Water on a Mono-Electrode Induced by Current Parallel to the Electrode Surface" Applied Sciences 14, no. 5: 2076. https://doi.org/10.3390/app14052076
APA StyleMorozumi, K., Kanemaru, H., Okada, A., Ichimiya, T., Kobayashi, T., & Tokunaga, E. (2024). Pockels Effect of Interfacial Water on a Mono-Electrode Induced by Current Parallel to the Electrode Surface. Applied Sciences, 14(5), 2076. https://doi.org/10.3390/app14052076







