Low-Cost Data-Driven Robot Collision Localization Using a Sparse Modular Point Matrix
Abstract
:1. Introduction
- Building upon the collision point matrix template, the SMPM is first introduced to achieve local sparsity of the template, thereby reducing the data scale required for the data-driven collision localization method;
- Comparative experiments are conducted by constructing SMPMs of various forms and degrees of sparsity, exploring the optimal way to build SMPMs effectively while maintaining high collision localization performance with a reduced data scale;
- A data-driven collision localization method combining a convolutional neural network (CNN), an echo state network (ESN), and a support vector machine (SVM) is proposed to enable the SMPM to achieve optimal performance in collision localization.
2. Materials and Methods
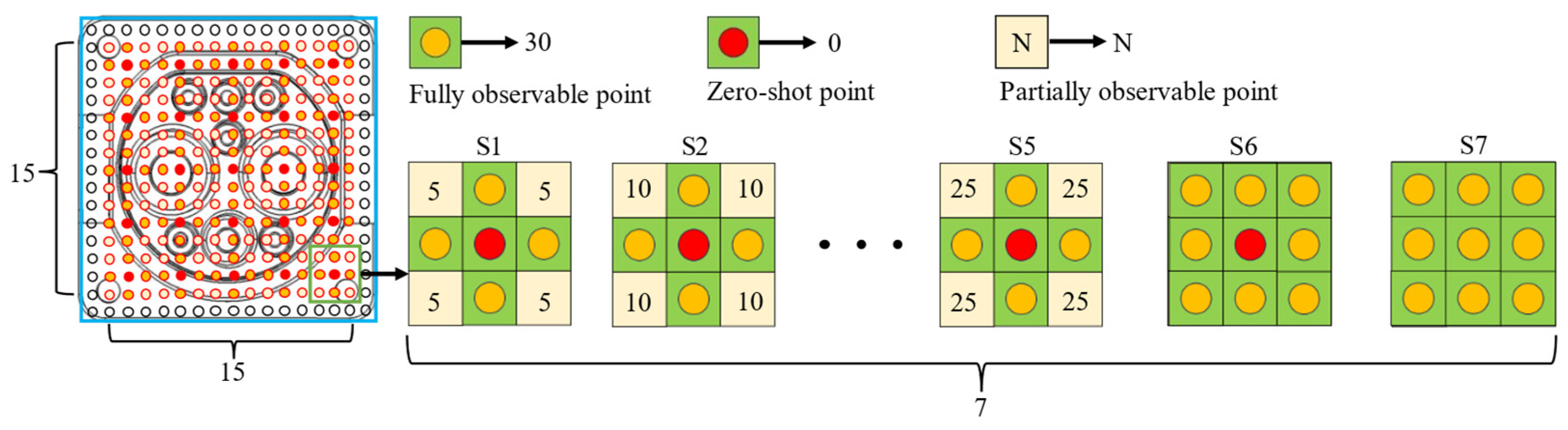
2.1. Dataset Description
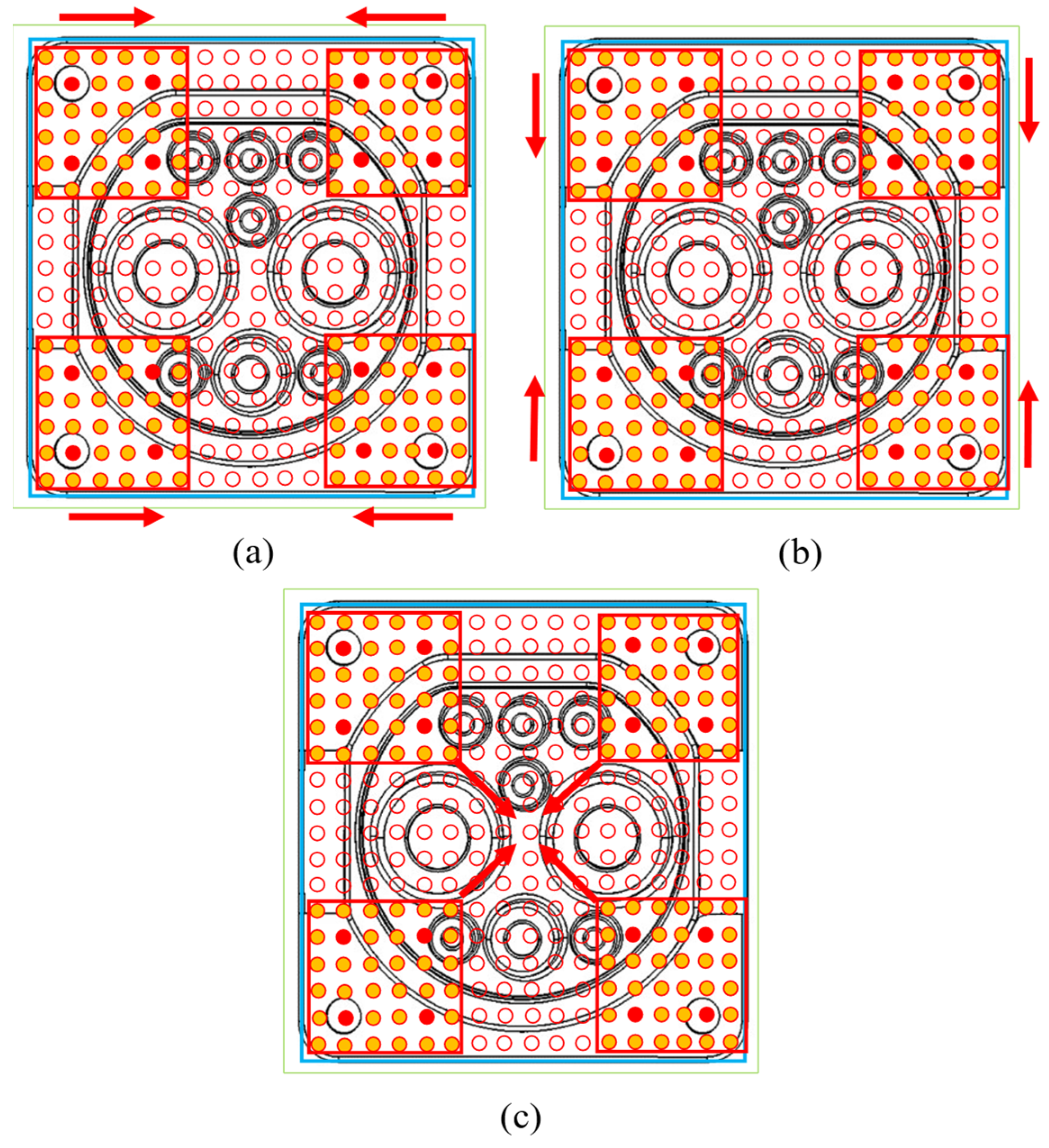
2.2. SMPM Method
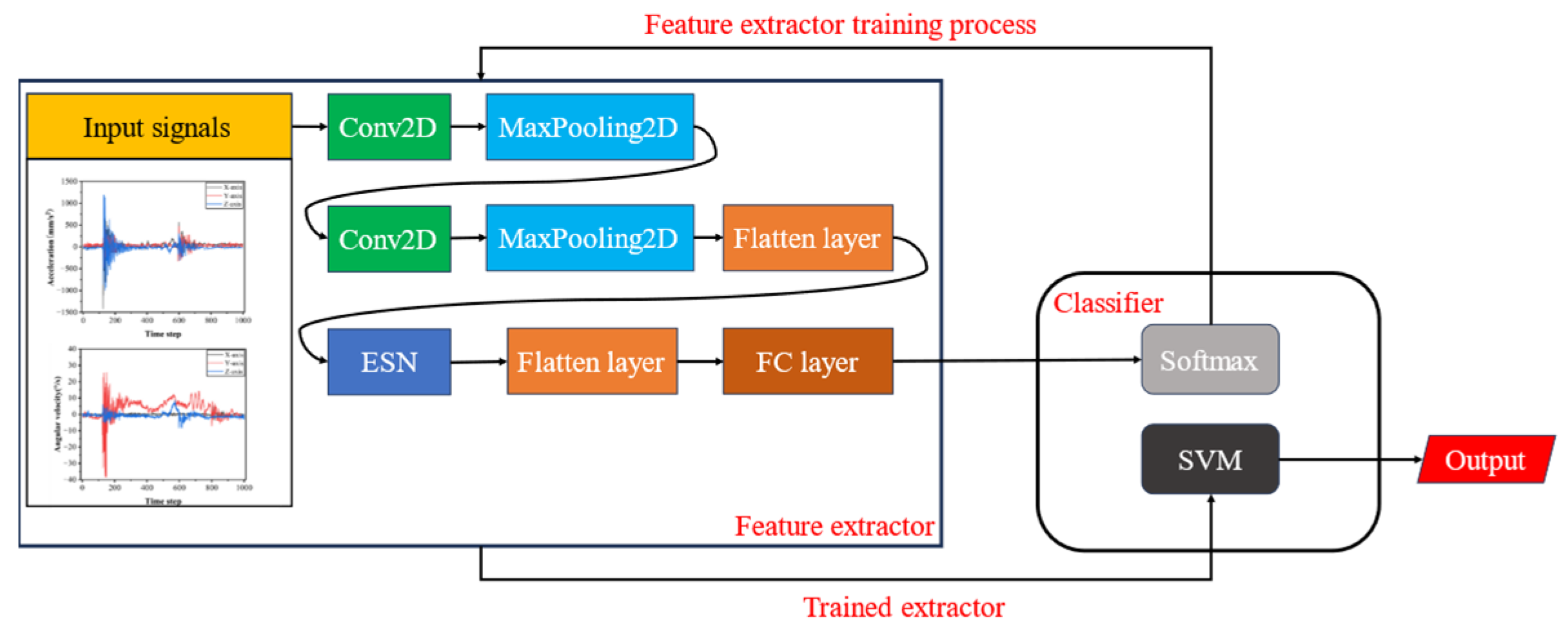
2.3. Collision Localization Model
2.3.1. CNN
2.3.2. ESN
2.3.3. Framework of CE-SVM
3. Results and Discussion
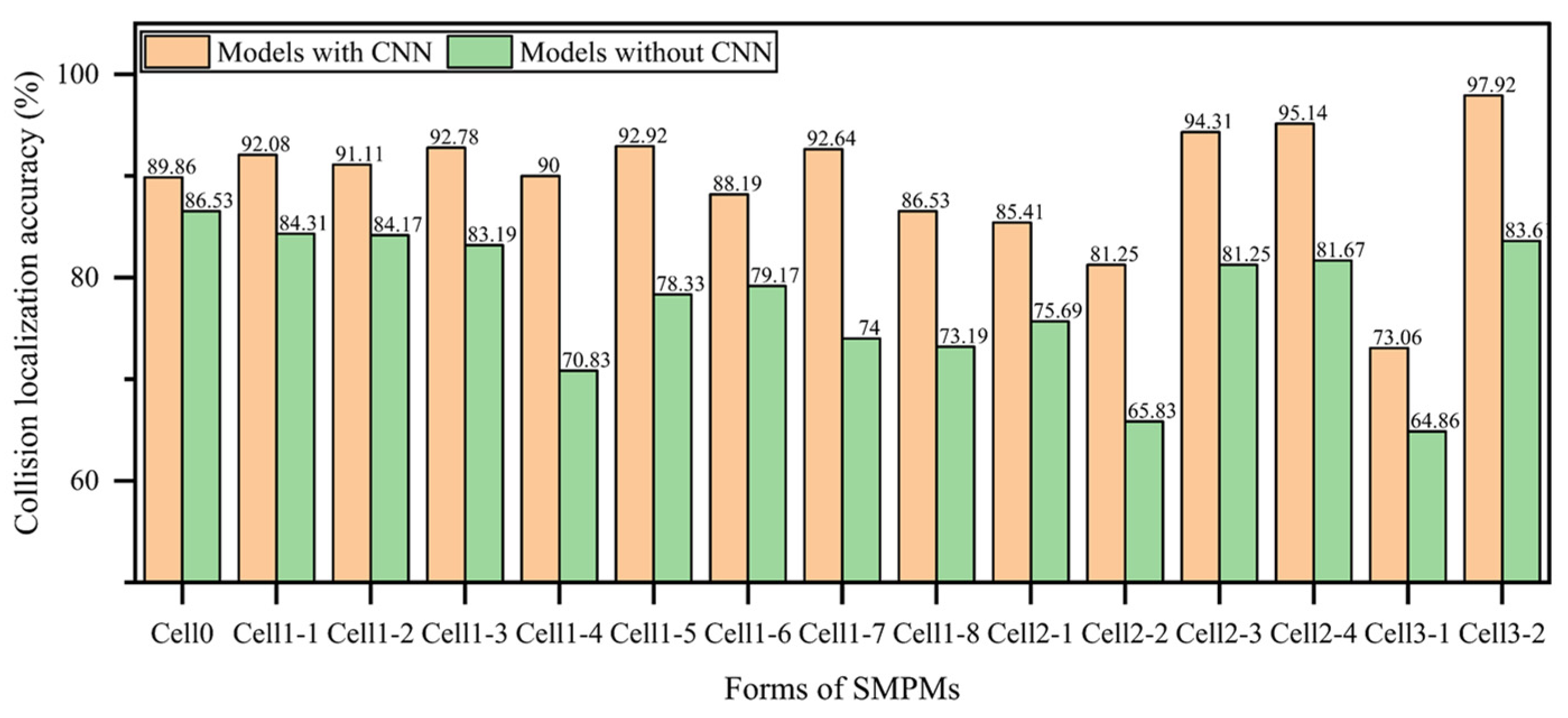
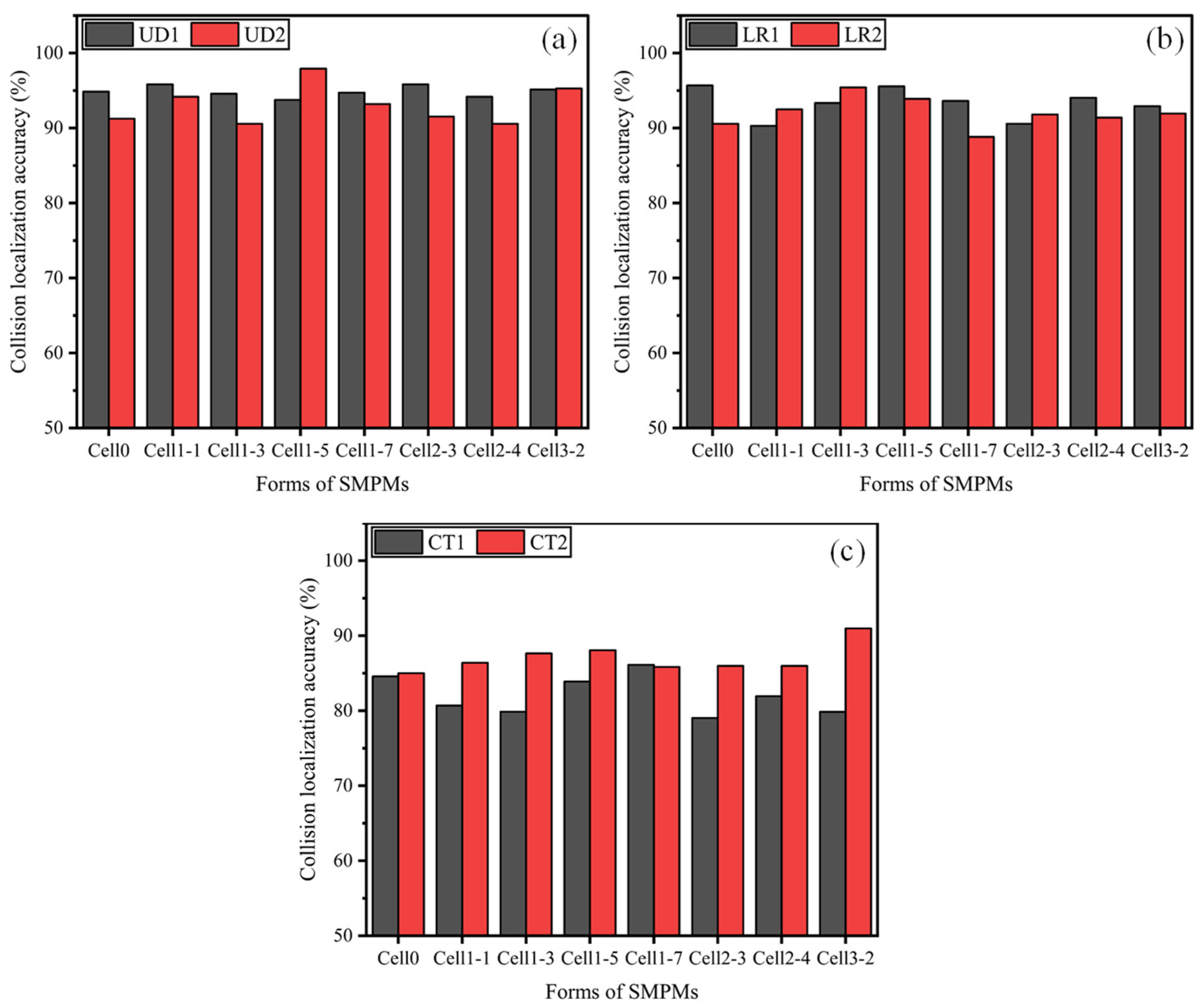
3.1. Optimal SMPM Structure
3.2. Collision Localization Results across the Entire Template
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Pan, M.; Sun, C.; Liu, J.; Wang, Y. Automatic Recognition and Location System for Electric Vehicle Charging Port in Complex Environment. IET Image Process 2020, 14, 2263–2272. [Google Scholar] [CrossRef]
- Zhang, H.; Zhu, W.; Huang, Y. A Research on the Control Strategy of Automatic Charging Robot for Electric Vehicles Based on Impedance Control. J. Phys. Conf. Ser. 2022, 2303, 012085. [Google Scholar] [CrossRef]
- Lin, H.; Quan, P.; Liang, Z.; Lou, Y.; Wei, D.; Di, S. Collision Localization and Classification on the End-Effector of a Cable-Driven Manipulator Applied to EV Auto-Charging Based on DCNN–SVM. Sensors 2022, 22, 3439. [Google Scholar] [CrossRef]
- Lin, H.; Quan, P.; Liang, Z.; Lou, Y.; Wei, D.; Di, S. Precision Data-Driven Collision Localization with a Dedicated Matrix Template for Electric Vehicle Automatic Charging. Electronics 2024, 13, 638. [Google Scholar] [CrossRef]
- Vorndamme, J.; Schappler, M.; Haddadin, S. Collision Detection, Isolation and Identification for Humanoids. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Singapore, 29 May–3 June 2017; pp. 4754–4761. [Google Scholar]
- Iskandar, M.; Eiberger, O.; Albu-Schaffer, A.; Luca, A.D.; Dietrich, A. Collision Detection, Identification, and Localization on the DLR SARA Robot with Sensing Redundancy. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Xi’an, China, 30 May–5 June 2021. [Google Scholar]
- Zurlo, D.; Heitmann, T.; Morlock, M.; De Luca, A. Collision Detection and Contact Point Estimation Using Virtual Joint Torque Sensing Applied to a Cobot. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), London, UK, 29 May 2023; pp. 7533–7539. [Google Scholar]
- Piacenza, P.; Dang, W.; Hannigan, E.; Espinal, J.; Hussain, I.; Kymissis, I.; Ciocarlie, M. Accurate Contact Localization and Indentation Depth Prediction with an Optics-Based Tactile Sensor. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Singapore, 29 May–3 June 2017. [Google Scholar]
- Fan, X.; Lee, D.; Jackel, L.; Howard, R.; Lee, D.; Isler, V. Enabling Low-Cost Full Surface Tactile Skin for Human Robot Interaction. IEEE Robot. Autom. Lett. 2022, 7, 1800–1807. [Google Scholar] [CrossRef]
- Mittendorfer, P.; Yoshida, E.; Cheng, G. Realizing Whole-Body Tactile Interactions with a Self-Organizing, Multi-Modal Artificial Skin on a Humanoid Robot. Adv. Robot. 2015, 29, 51–67. [Google Scholar] [CrossRef]
- Li, X.; Zhang, Y.; Xie, X.; Li, J.; Shi, G. Improving Robotic Tactile Localization Super-Resolution via Spatiotemporal Continuity Learning and Overlapping Air Chambers. AAAI 2023, 37, 6192–6199. [Google Scholar] [CrossRef]
- Popov, D.; Klimchik, A.; Mavridis, N. Collision Detection, Localization & Classification for Industrial Robots with Joint Torque Sensors. In Proceedings of the 26th IEEE International Symposium on Robot and Human Interactive Communication (RO-MAN), Lisbon, Portugal, 28–31 August 2017; pp. 838–843. [Google Scholar]
- Ha, X.T.; Wu, D.; Lai, C.-F.; Ourak, M.; Borghesan, G.; Menciassi, A.; Poorten, E.V. Contact Localization of Continuum and Flexible Robot Using Data-Driven Approach. IEEE Robot. Autom. Lett. 2022, 7, 6910–6917. [Google Scholar] [CrossRef]
- Min, F.; Wang, G.; Liu, N. Collision Detection and Identification on Robot Manipulators Based on Vibration Analysis. Sensors 2019, 19, 1080. [Google Scholar] [CrossRef]
- McMahan, W.; Romano, J.M.; Kuchenbecker, K.J. Using Accelerometers to Localize Tactile Contact Events on a Robot Arm. In Proceedings of the Workshop on Advances in Tactile Sensing and Touch-Based Human-Robot Interaction, ACM/IEEE International Conference on Human-Robot Interaction, Boston, MA, USA, 5–8 March 2012. [Google Scholar]
- Livieris, I.E.; Pintelas, E.; Pintelas, P. A CNN–LSTM Model for Gold Price Time-Series Forecasting. Neural Comput. Appl. 2020, 32, 17351–17360. [Google Scholar] [CrossRef]
- Sun, Y.; Xue, B.; Zhang, M.; Yen, G.G.; Lv, J. Automatically Designing CNN Architectures Using the Genetic Algorithm for Image Classification. IEEE Trans. Cybern. 2020, 50, 3840–3854. [Google Scholar] [CrossRef]
- Zha, W.; Liu, Y.; Wan, Y.; Luo, R.; Li, D.; Yang, S.; Xu, Y. Forecasting Monthly Gas Field Production Based on the CNN-LSTM Model. Energy 2022, 260, 124889. [Google Scholar] [CrossRef]
- Jaeger, H. Adaptive Nonlinear System Identification with Echo State Networks. In Proceedings of the Advances in Neural Information Processing Systems 15 (NIPS 2002), Vancouver, BC, Canada, 9–14 December 2002. [Google Scholar]
- Hua, Z.; Zheng, Z.; Péra, M.-C.; Gao, F. Remaining Useful Life Prediction of PEMFC Systems Based on the Multi-Input Echo State Network. Appl. Energy 2020, 265, 114791. [Google Scholar] [CrossRef]
- Montaha, S.; Azam, S.; Rafid, A.K.M.R.H.; Hasan, M.Z.; Karim, A.; Islam, A. TimeDistributed-CNN-LSTM: A Hybrid Approach Combining CNN and LSTM to Classify Brain Tumor on 3D MRI Scans Performing Ablation Study. IEEE Access 2022, 10, 60039–60059. [Google Scholar] [CrossRef]




| Parameters | Symbolic Representations | Values |
|---|---|---|
| Weight matrices from the input layer to the reservoir | [−0.5, 0.5] | |
| Weight matrices within the reservoir | [−0.5, 0.5] | |
| Leakage rate | 0.5 | |
| Spectral radius | 1 | |
| Numbers of neurons in the reservoir | 64 |
| Type | Name of Parameter | Values |
|---|---|---|
| Number of filters | 64 | |
| Conv2D | Kernel size | (10, 3) |
| Stride | 1 | |
| Batch normalization | - | - |
| ReLU | - | - |
| Pool size | (2, 2) | |
| Maxpooling | Stride | 1 |
| Padding | same | |
| Conv2D | Number of filters | 64 |
| Kernel size | (10, 3) | |
| Stride | 2 | |
| Padding | same | |
| Batch normalization | - | - |
| ReLU | - | - |
| Pool size | (2, 2) | |
| Maxpooling | Stride | 1 |
| Padding | same | |
| Time-distributed flattening | - | - |
| 64 | ||
| ESN | 0.5 | |
| 1 | ||
| FC | Number of hidden units | 512 |
| SVM | Regularization parameter | 100 |
| Kernel function | rbf |
| Case | CE-SVM | CNN-SVM | LSTM-SVM | ENS-SVM | GRU-SVM | Data Scale |
|---|---|---|---|---|---|---|
| S1 | 91.27% | 89.29% | 88.33% | 89.53% | 88.73% | 51.85% |
| S2 | 94.29% | 91.79% | 90.62% | 91.54% | 90.8% | 59.26% |
| S3 | 95% | 94.17% | 93.24% | 93.27% | 93.06% | 66.67% |
| S4 | 96.2% | 95% | 93.92% | 94.2% | 93.88% | 74.07% |
| S5 | 97.07% | 95.12% | 94.44% | 95.22% | 94.72% | 81.48% |
| S6 | 96.73% | 95.74% | 94.78% | 95.65% | 95.28% | 88.89% |
| S7 | 98.49% | 98.67% | 96.7% | 98.64% | 98.27% | 100% |
| Case | CE-SVM | CNN-SVM | LSTM-SVM | ENS-SVM | GRU-SVM |
|---|---|---|---|---|---|
| S1 | 1.46 | 1.62 | 1.73 | 1.63 | 1.75 |
| S2 | 1.4 | 1.52 | 1.59 | 1.54 | 1.61 |
| S3 | 1.37 | 1.46 | 1.51 | 1.5 | 1.49 |
| S4 | 1.33 | 1.45 | 1.48 | 1.47 | 1.48 |
| S5 | 1.34 | 1.39 | 1.54 | 1.42 | 1.42 |
| S6 | 1.3 | 1.39 | 1.45 | 1.42 | 1.44 |
| S7 | 1.25 | 1.24 | 1.35 | 1.26 | 1.26 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lin, H.; Quan, P.; Liang, Z.; Wei, D.; Di, S. Low-Cost Data-Driven Robot Collision Localization Using a Sparse Modular Point Matrix. Appl. Sci. 2024, 14, 2131. https://doi.org/10.3390/app14052131
Lin H, Quan P, Liang Z, Wei D, Di S. Low-Cost Data-Driven Robot Collision Localization Using a Sparse Modular Point Matrix. Applied Sciences. 2024; 14(5):2131. https://doi.org/10.3390/app14052131
Chicago/Turabian StyleLin, Haoyu, Pengkun Quan, Zhuo Liang, Dongbo Wei, and Shichun Di. 2024. "Low-Cost Data-Driven Robot Collision Localization Using a Sparse Modular Point Matrix" Applied Sciences 14, no. 5: 2131. https://doi.org/10.3390/app14052131
APA StyleLin, H., Quan, P., Liang, Z., Wei, D., & Di, S. (2024). Low-Cost Data-Driven Robot Collision Localization Using a Sparse Modular Point Matrix. Applied Sciences, 14(5), 2131. https://doi.org/10.3390/app14052131






