MRAS Using Lyapunov Theory with Sliding Modes for a Fixed-Wing MAV
Abstract
1. Introduction
- A new design of the adjustment mechanism for an MRAS is obtained based on Lyapunov theory and sliding mode theory, with the control objective to achieve the desired values in attitude and altitude in a fixed-wing MAV despite unknown wind gusts.
- The significant reduction in the oscillations in the system with the sliding mode theory to the design of the adjustment mechanism.
- Achieve the control objective in attitude and altitude by designing two adjustment mechanisms for the proportional and derivative gains.
- The stability proof of the adjustment mechanisms considering the Lyapunov and sliding modes theory and the stability proof of the controller.
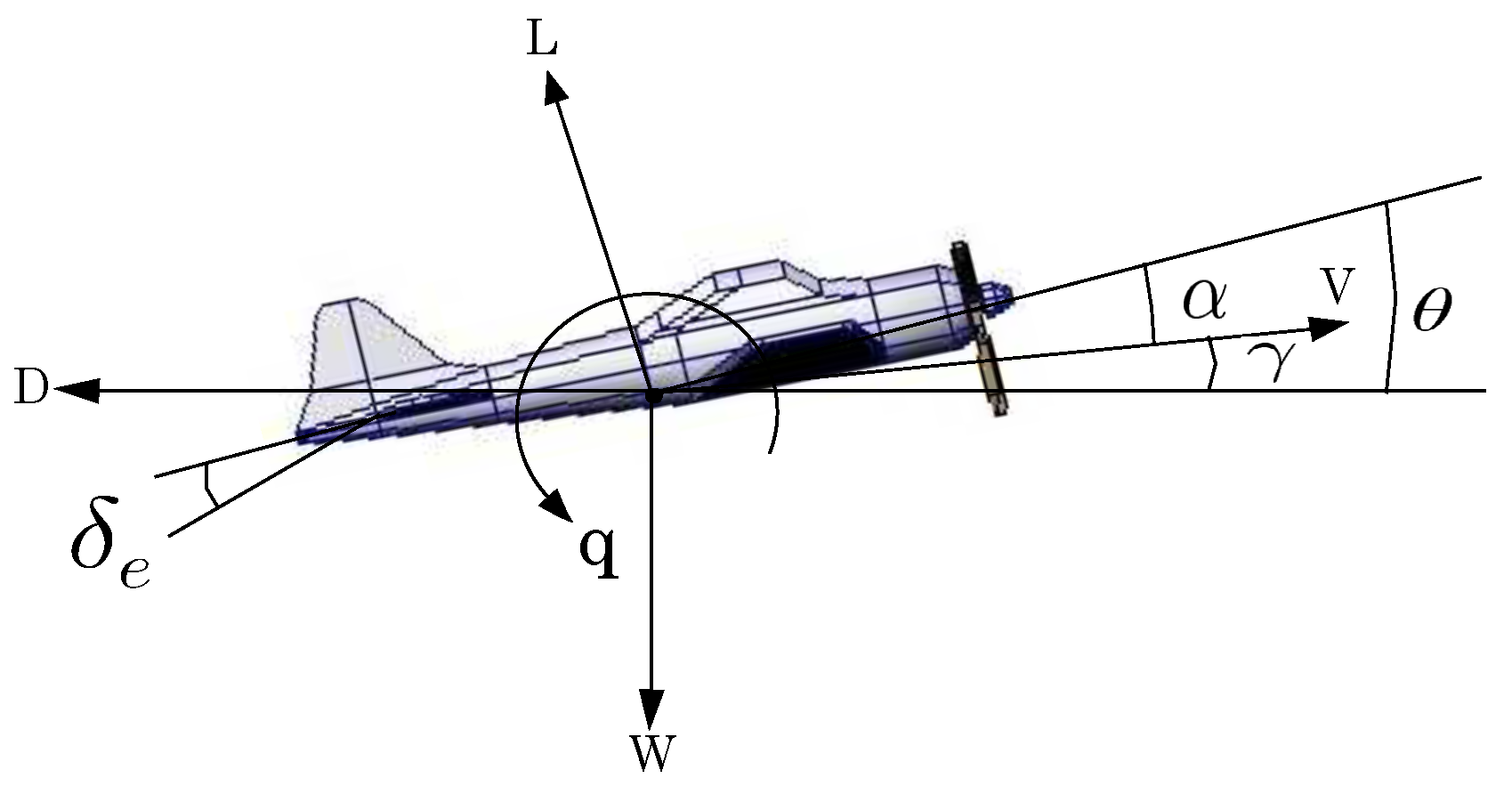
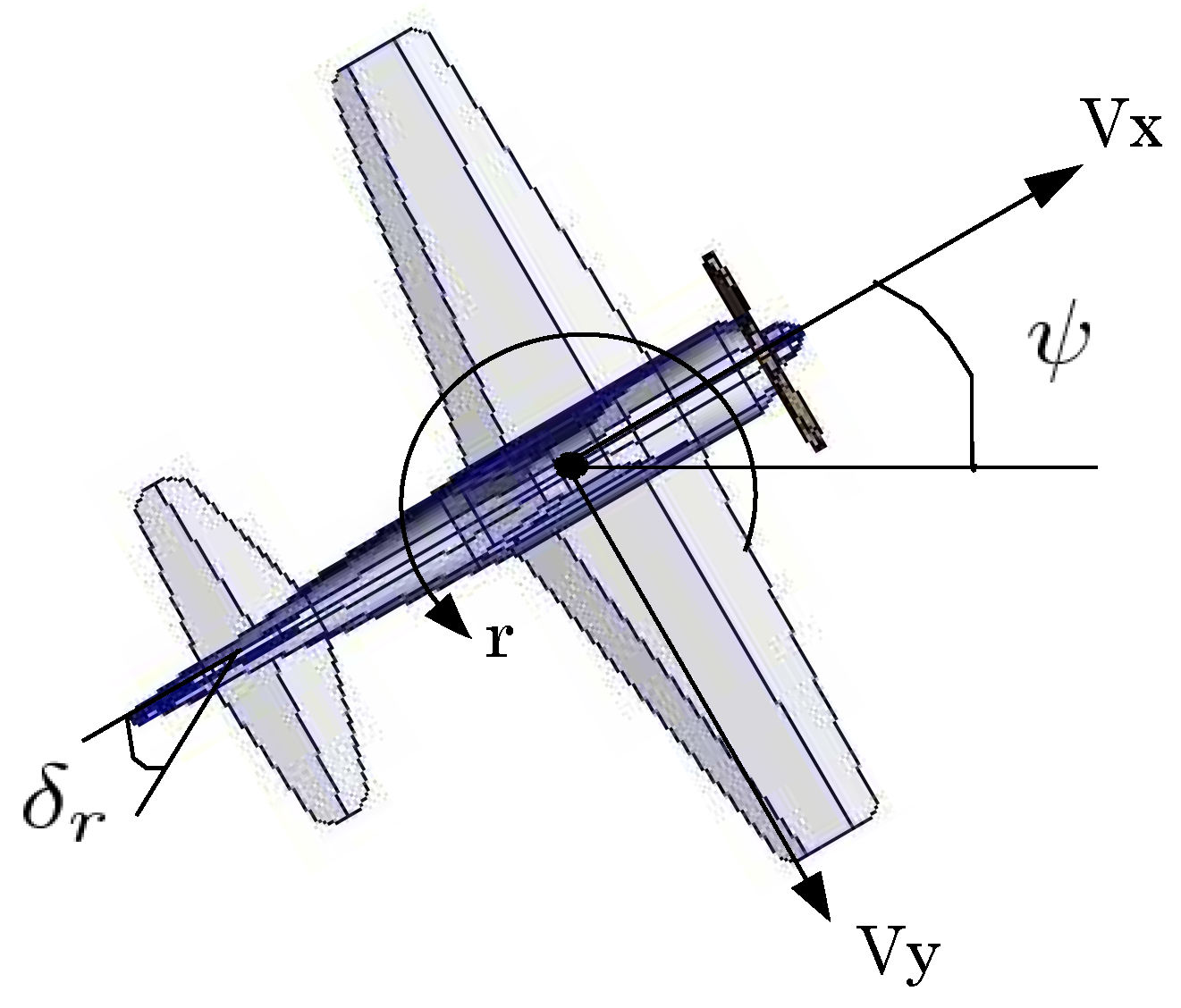
2. Fixed-Wing MAV Mathematical Model
2.1. Longitudinal Dynamics
2.2. Directional-Lateral Dynamic
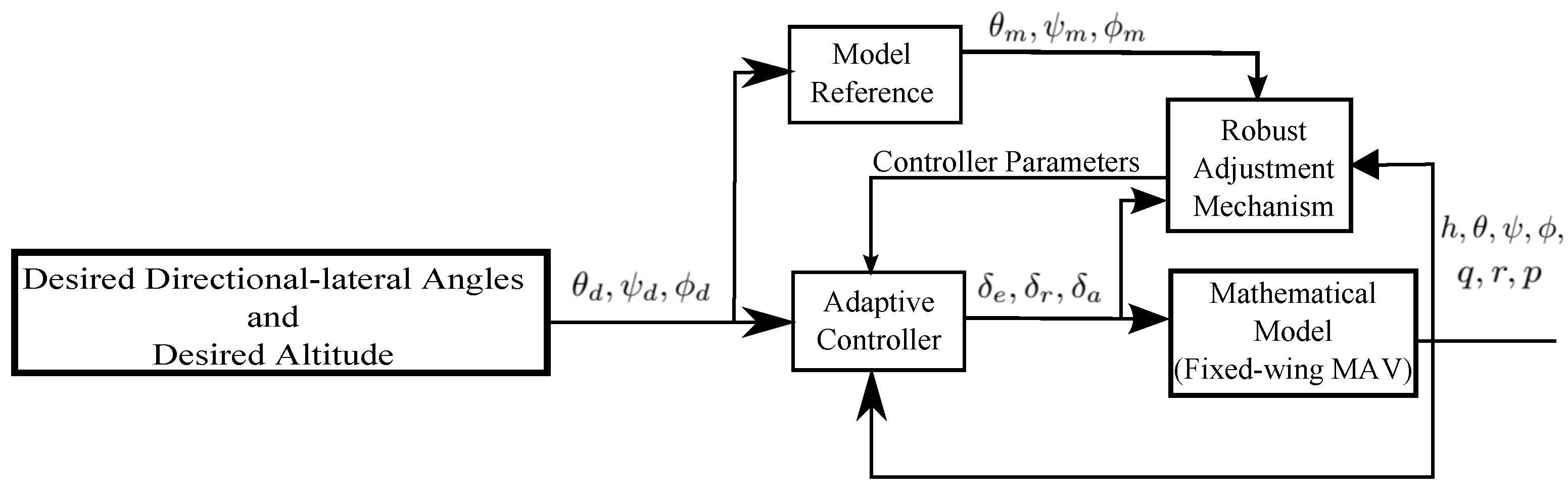
3. Adaptive Controller Design and Stability Proof
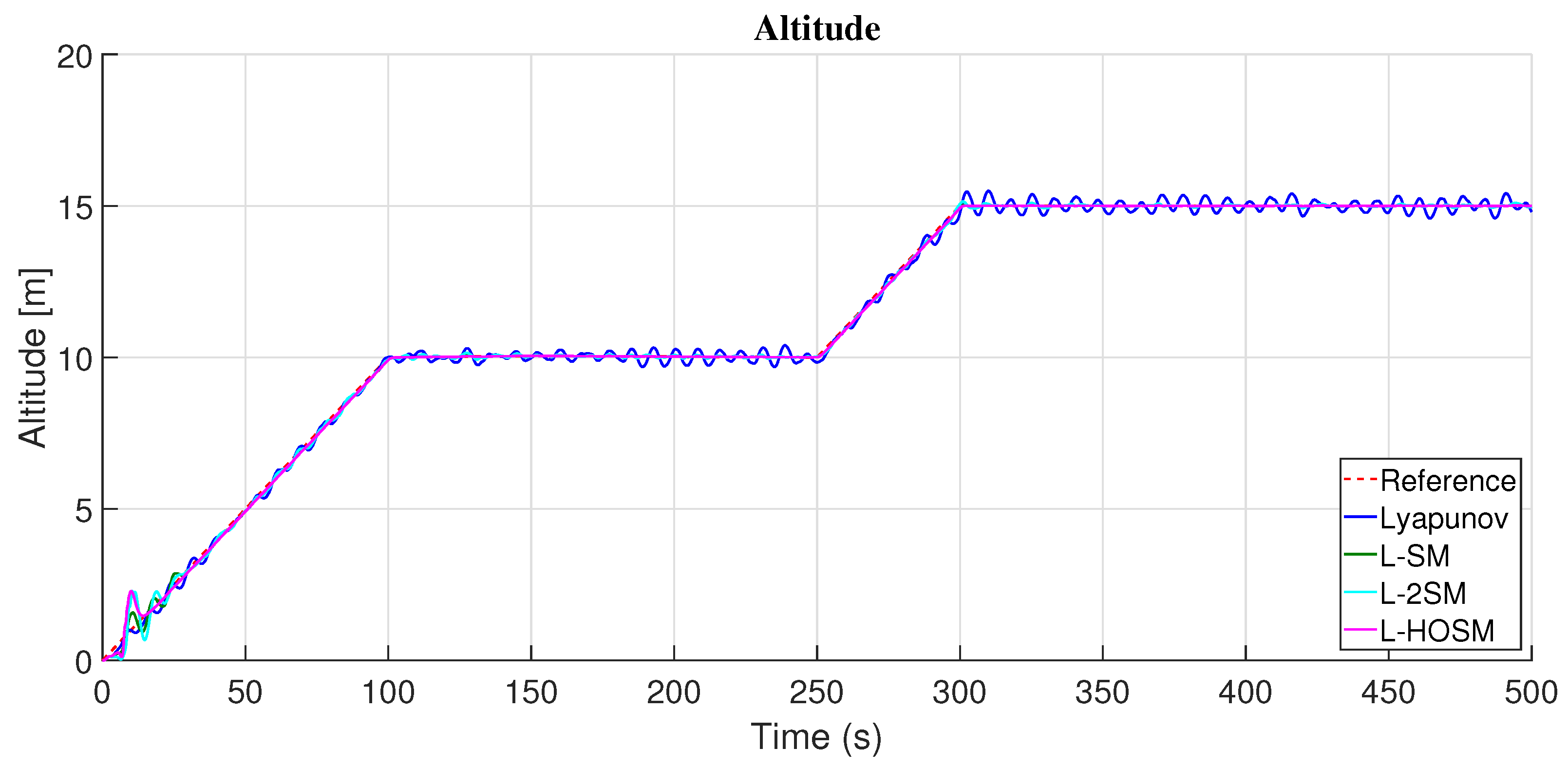
4. Simulation Results
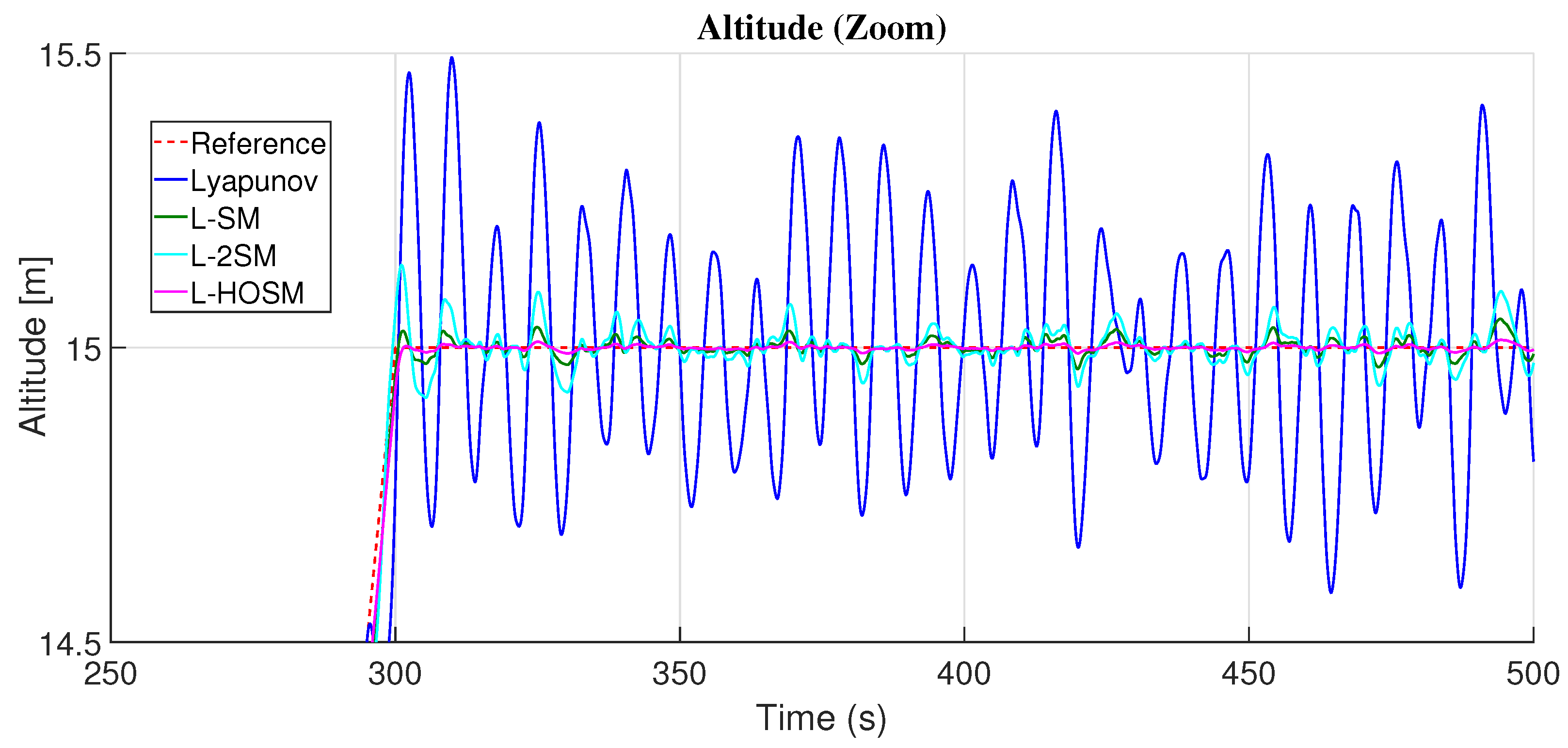
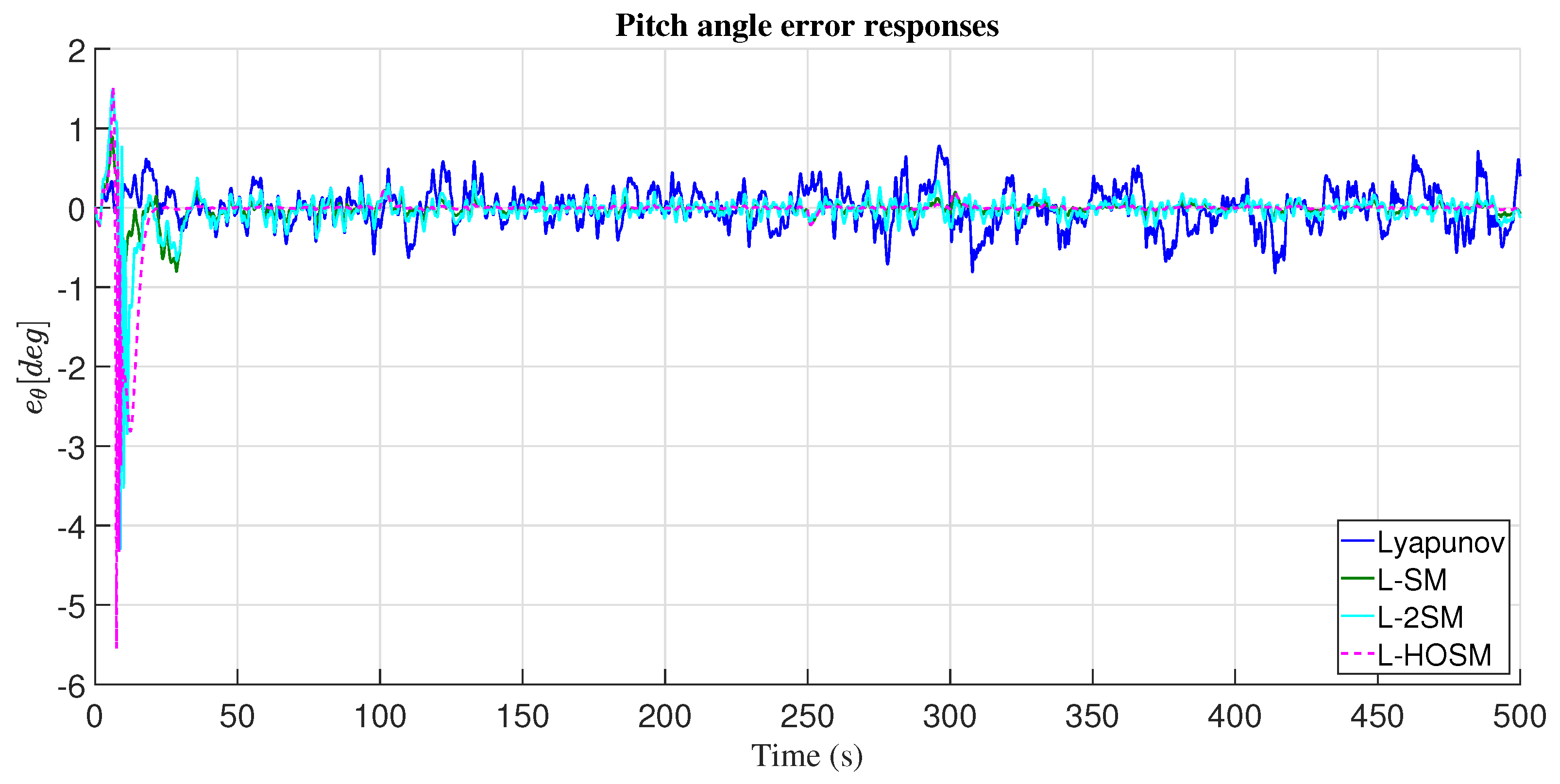
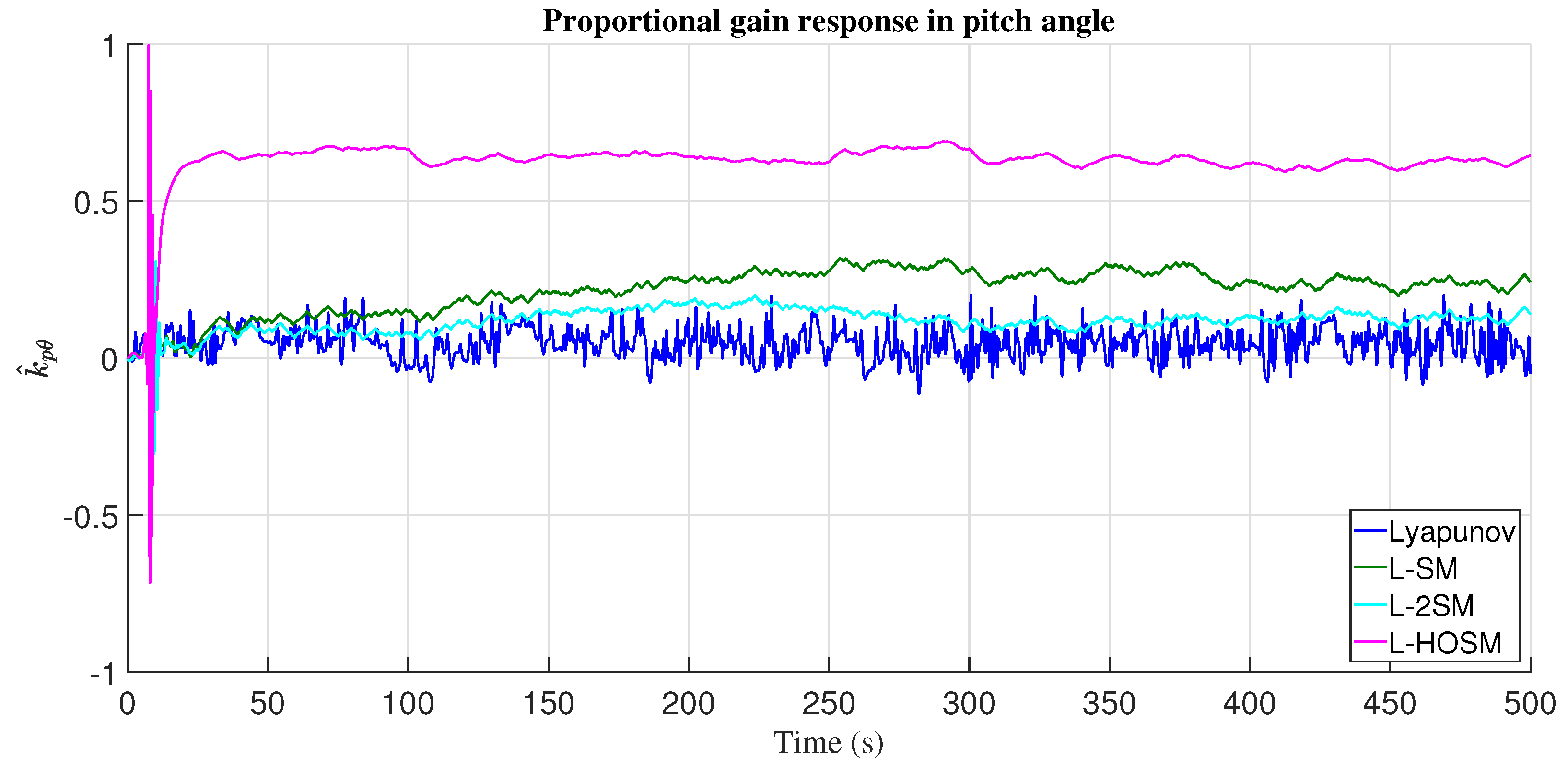
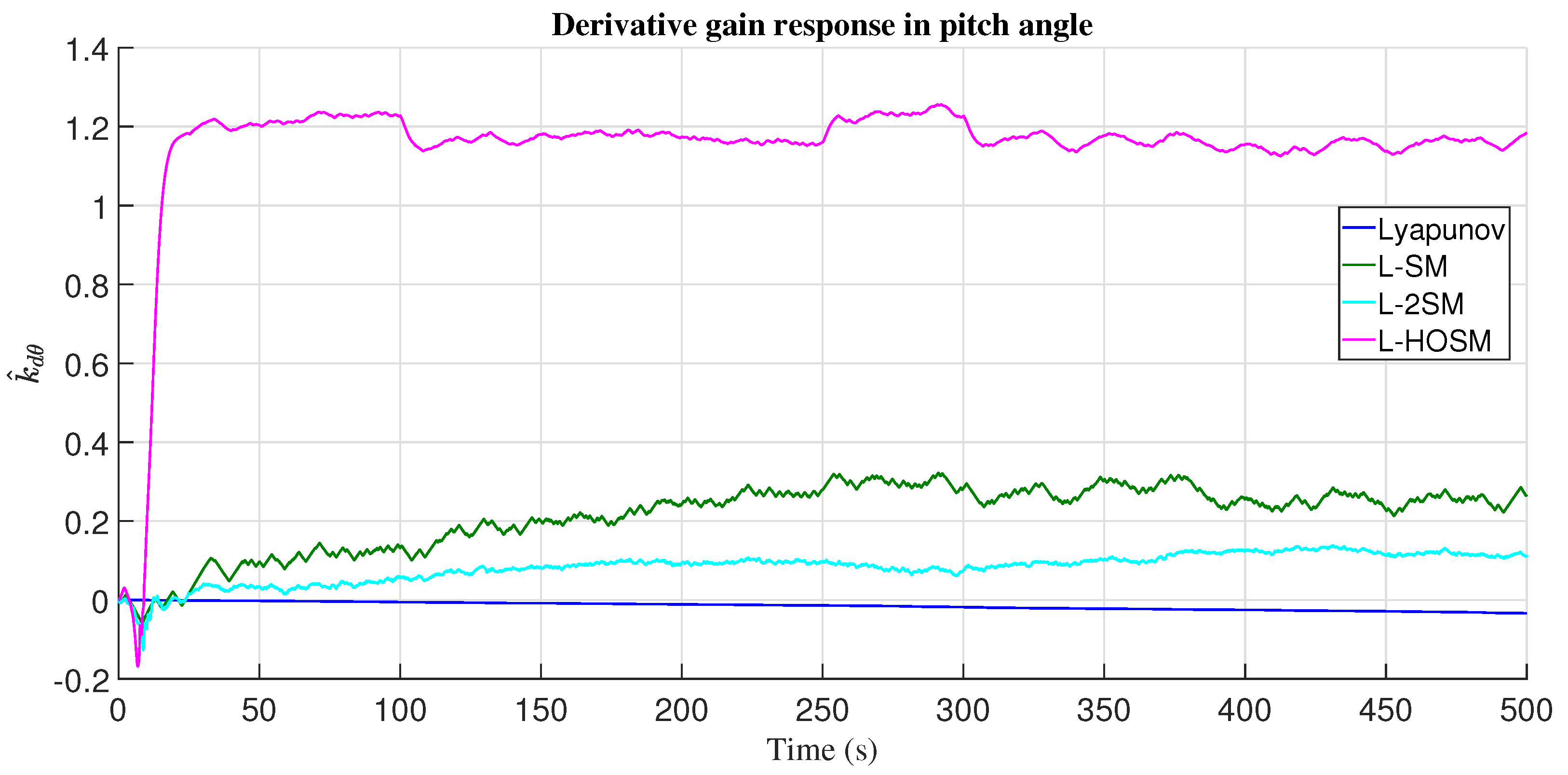
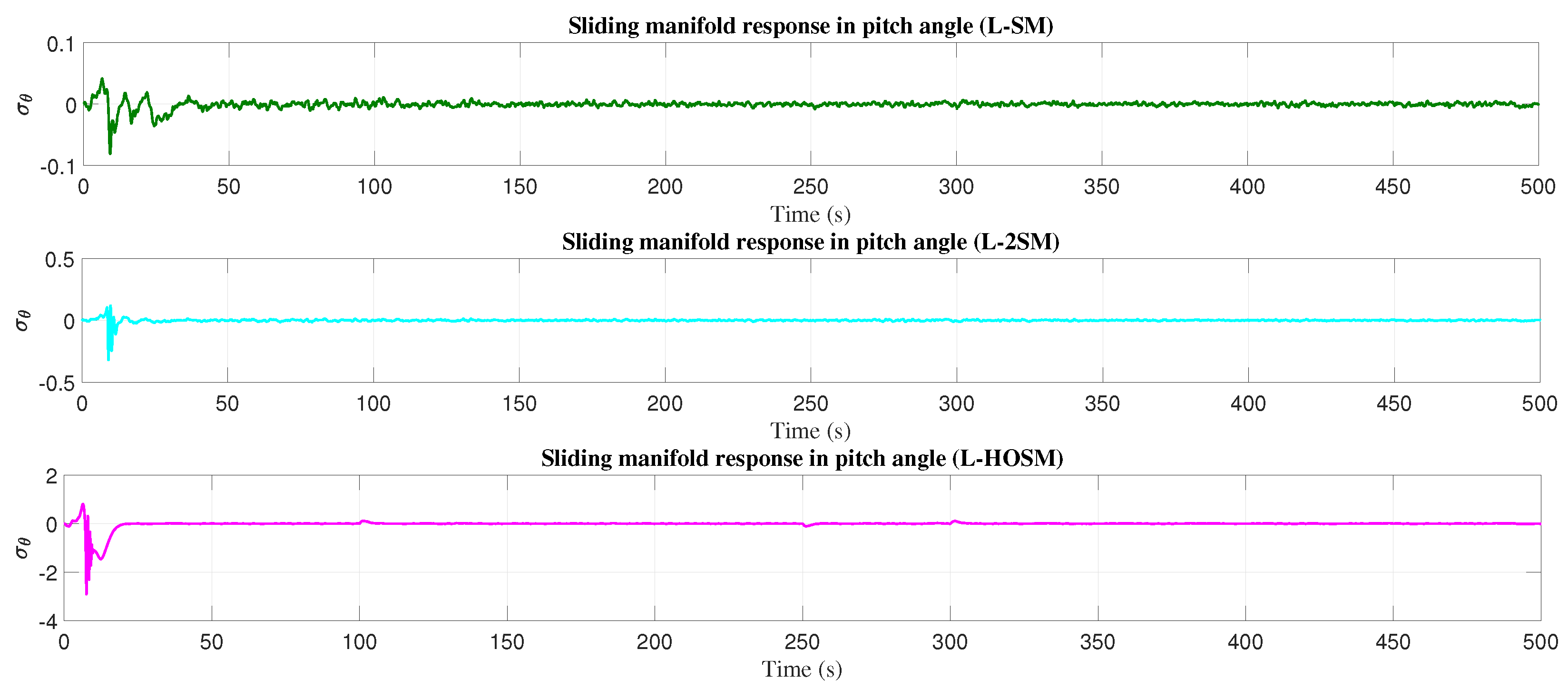
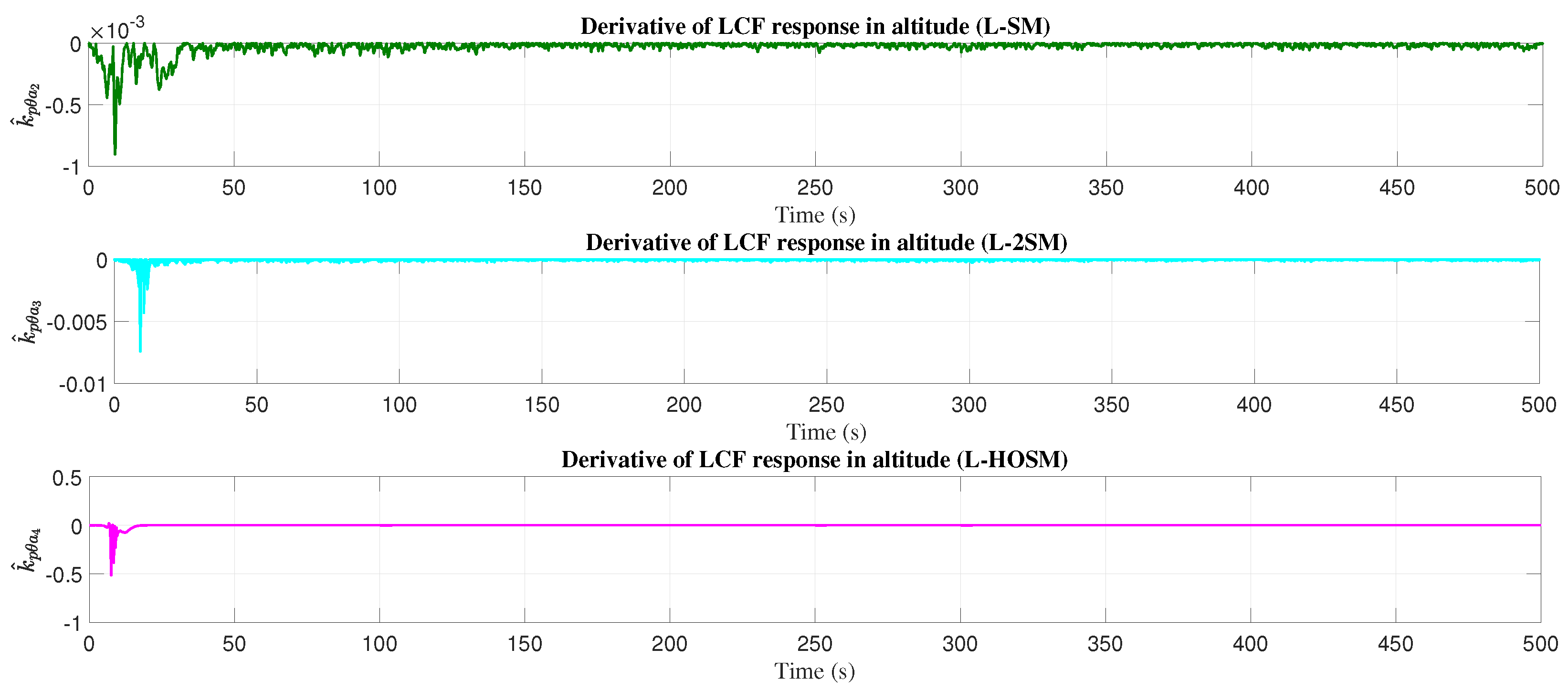
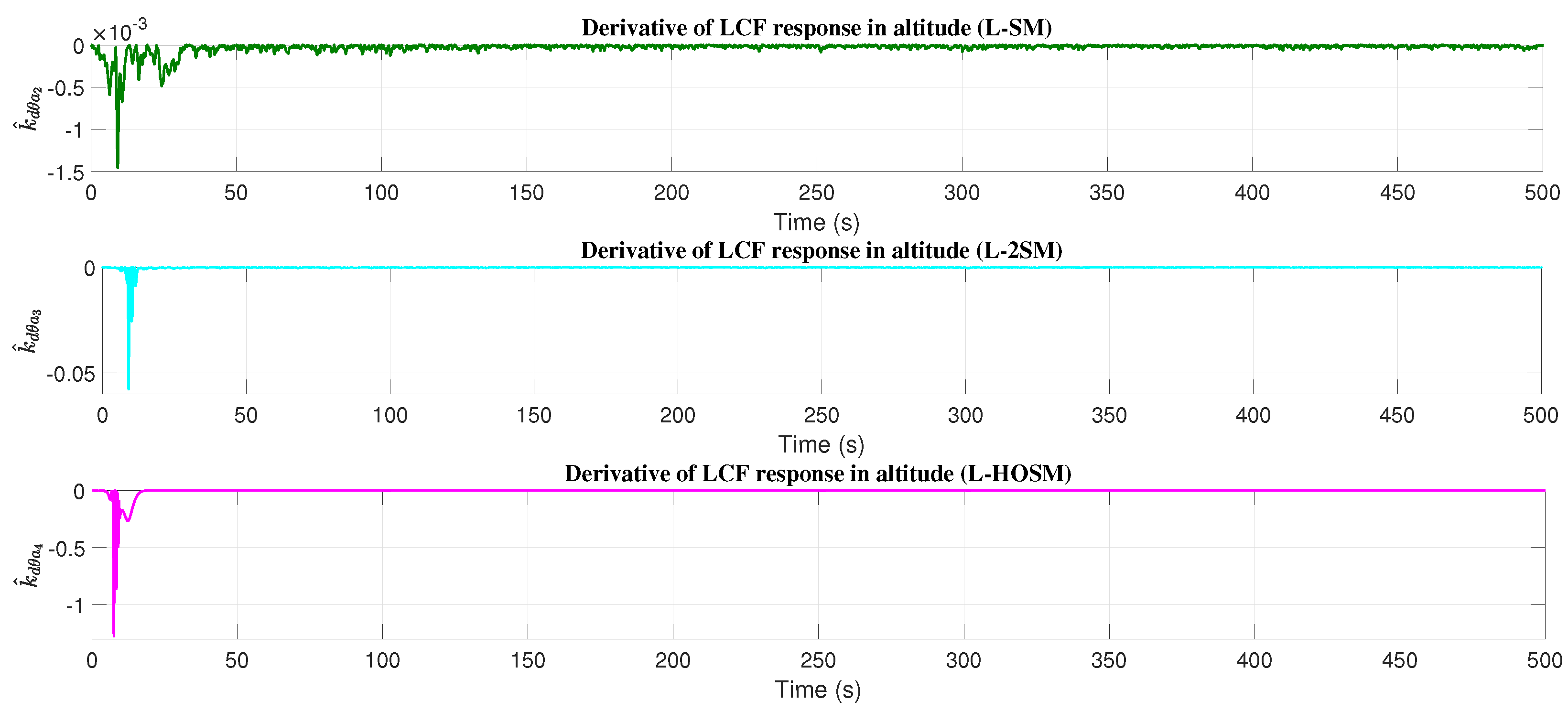
4.1. Altitude Movement
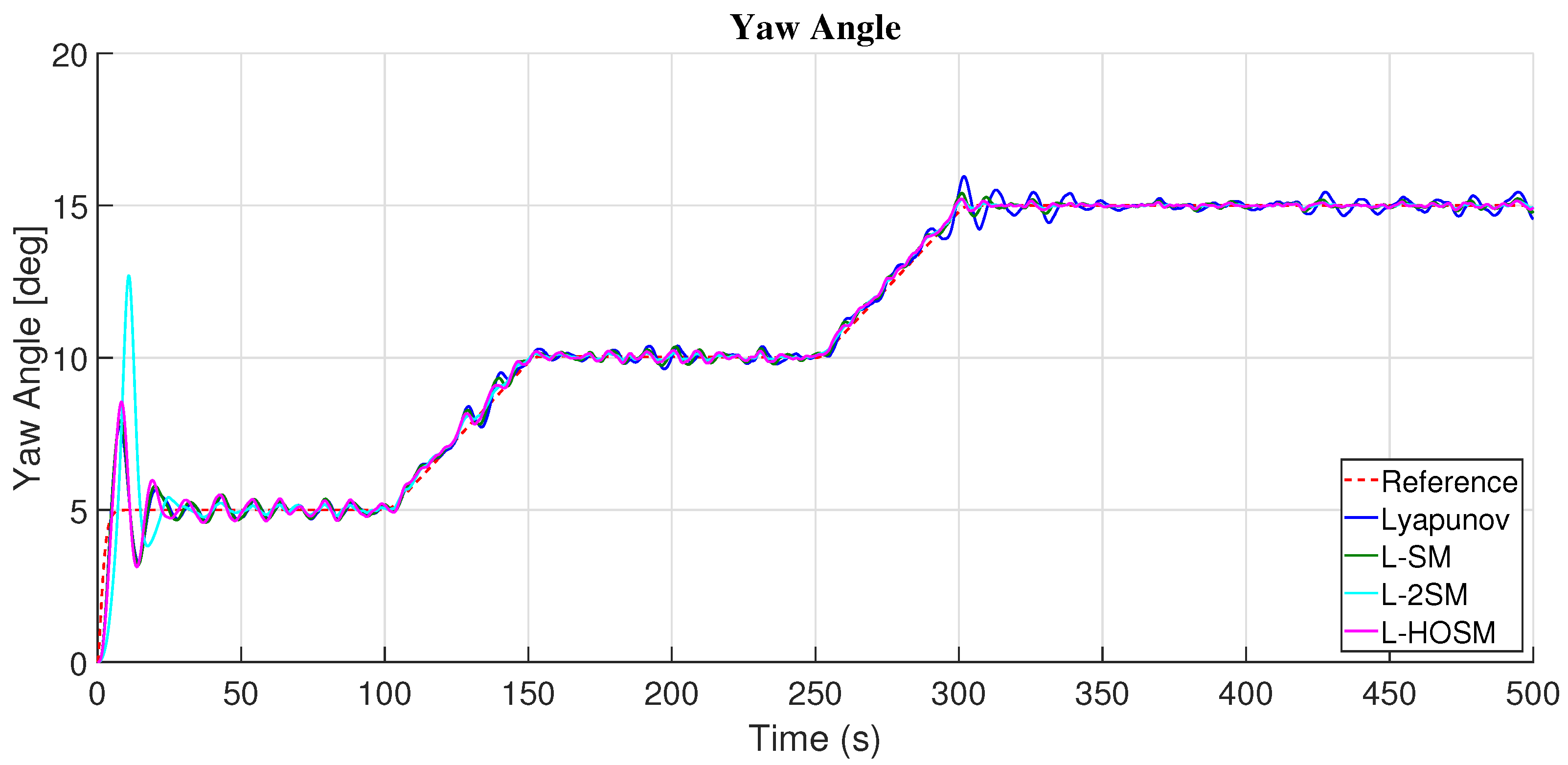
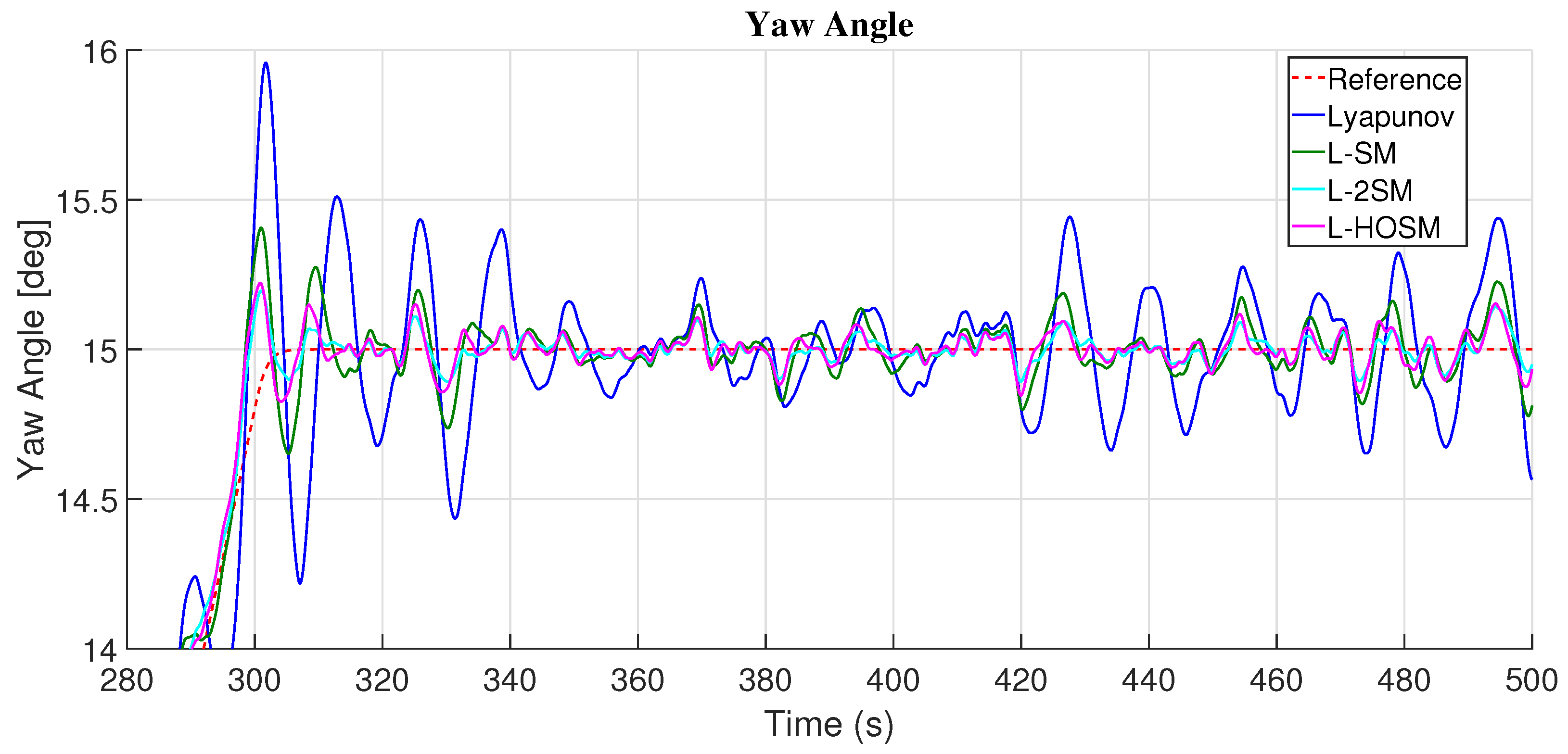
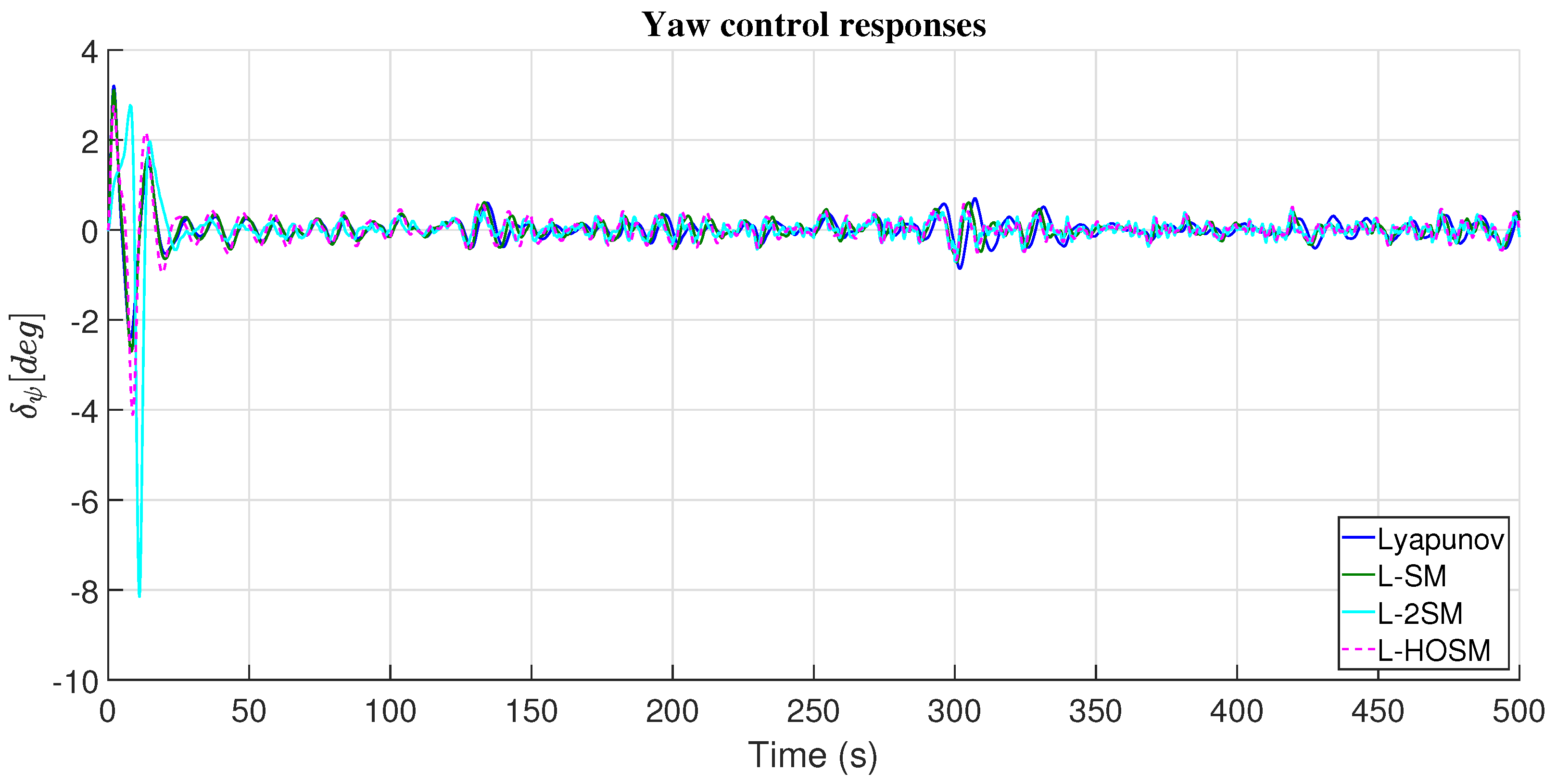
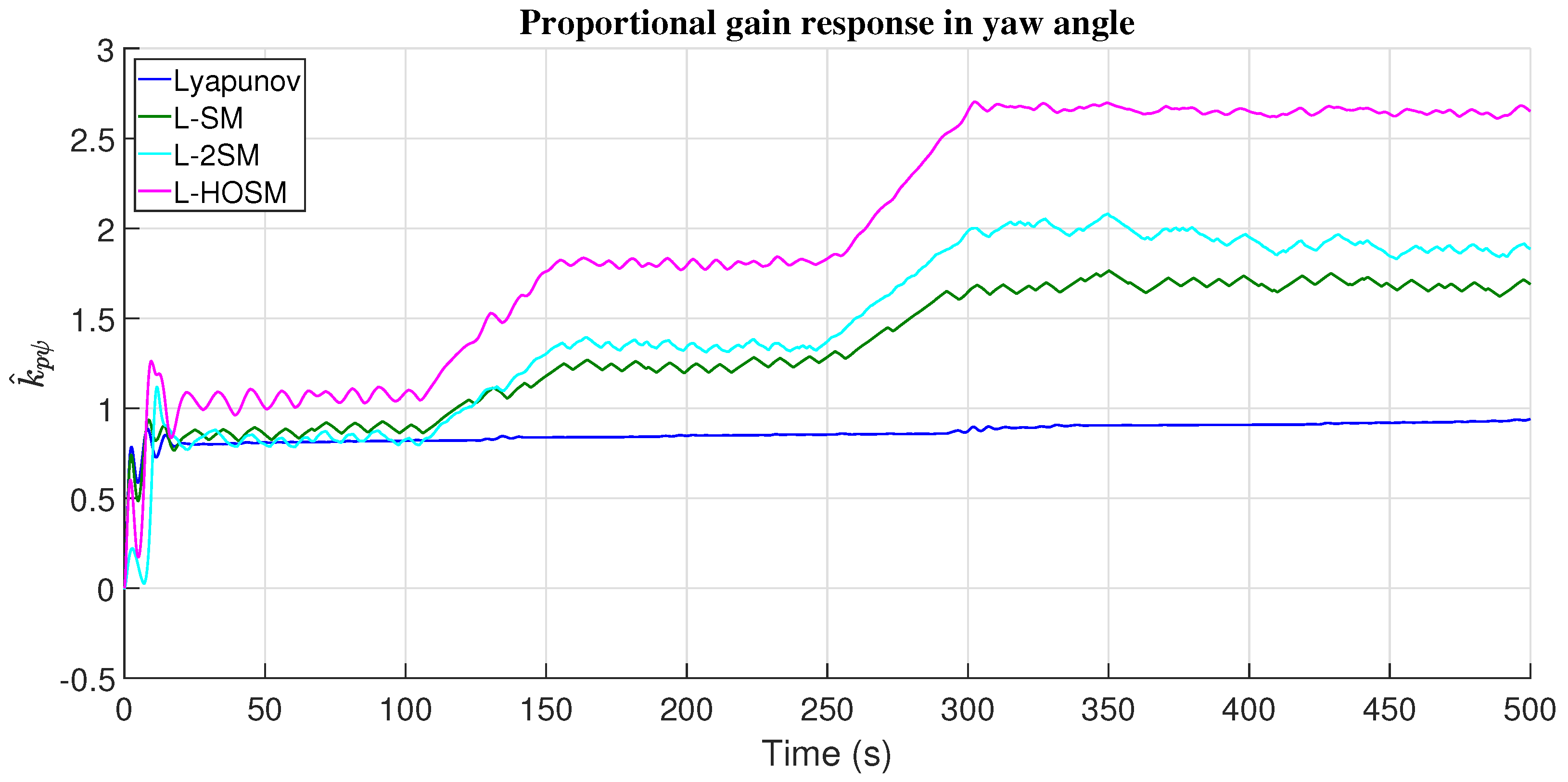
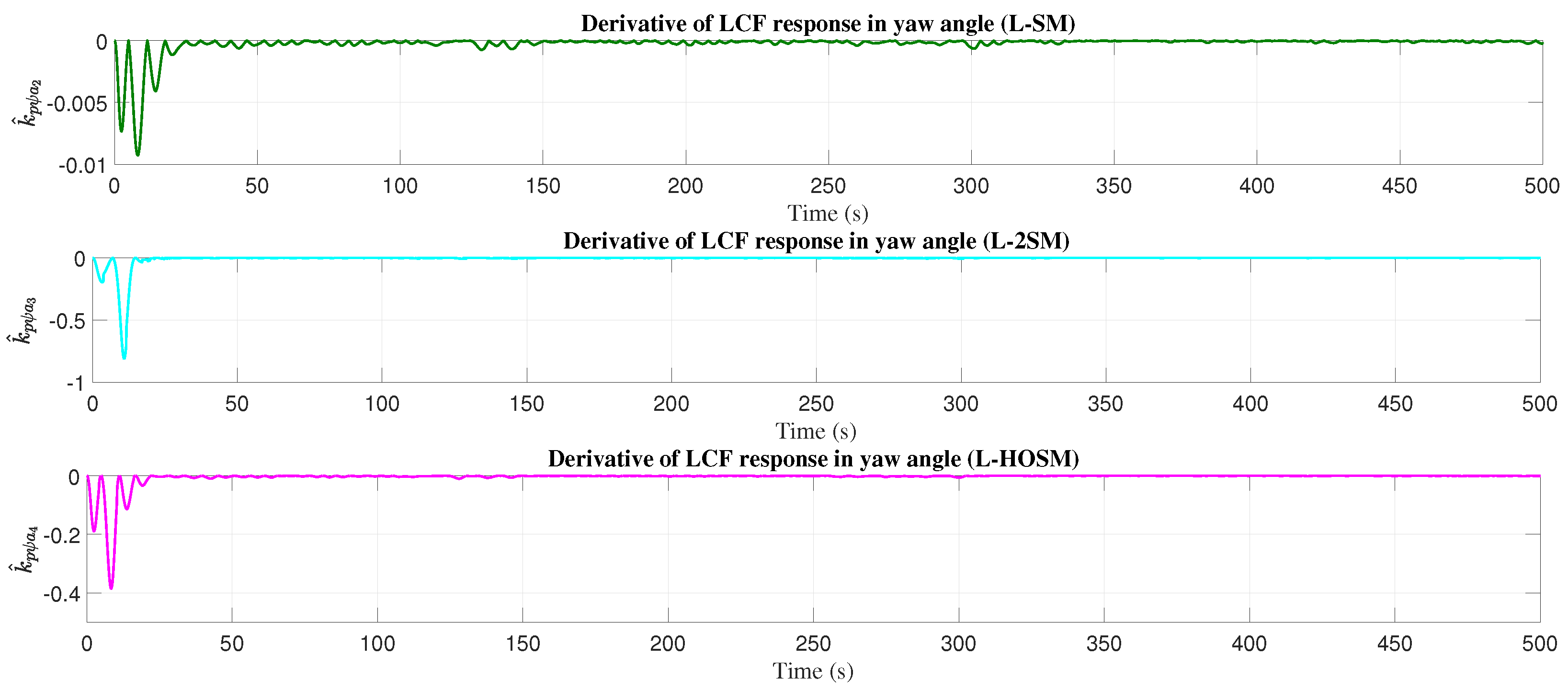
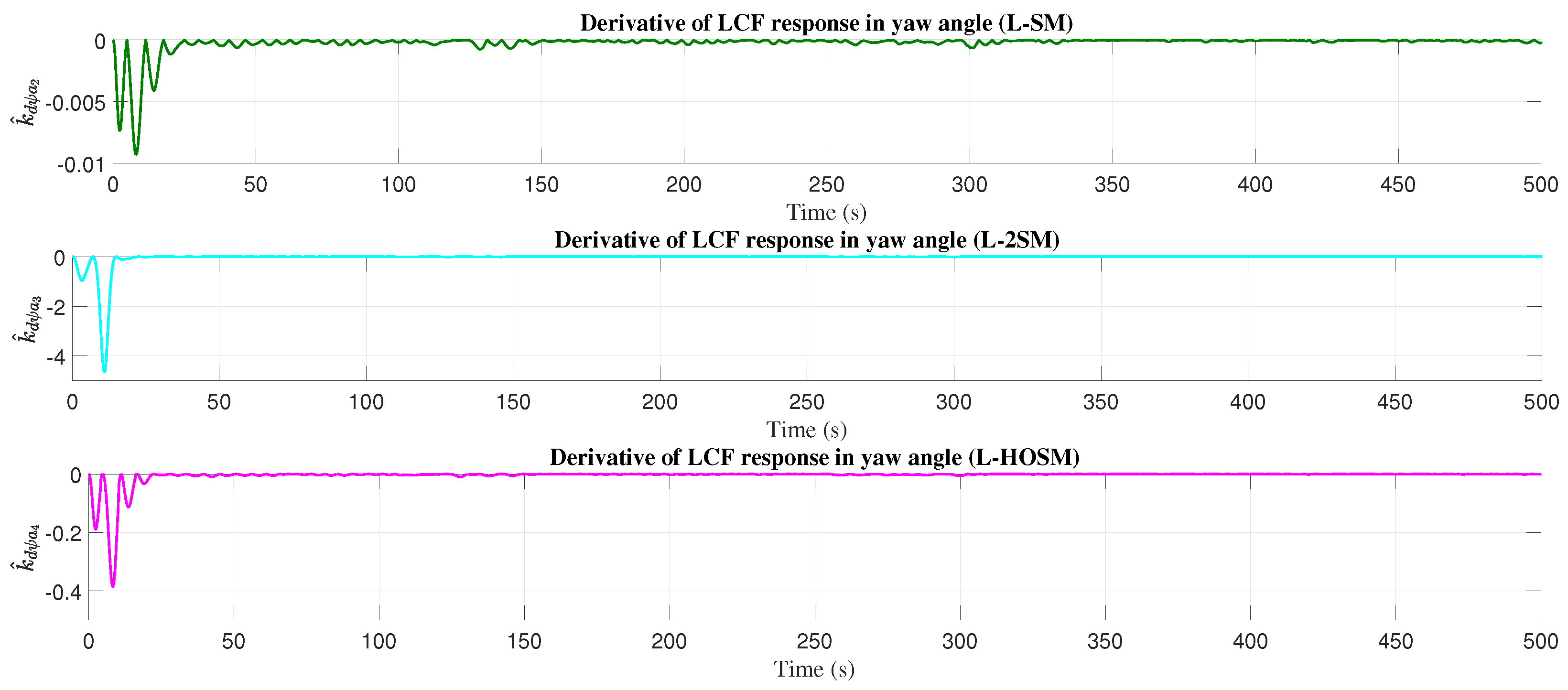
4.2. Yaw Angle
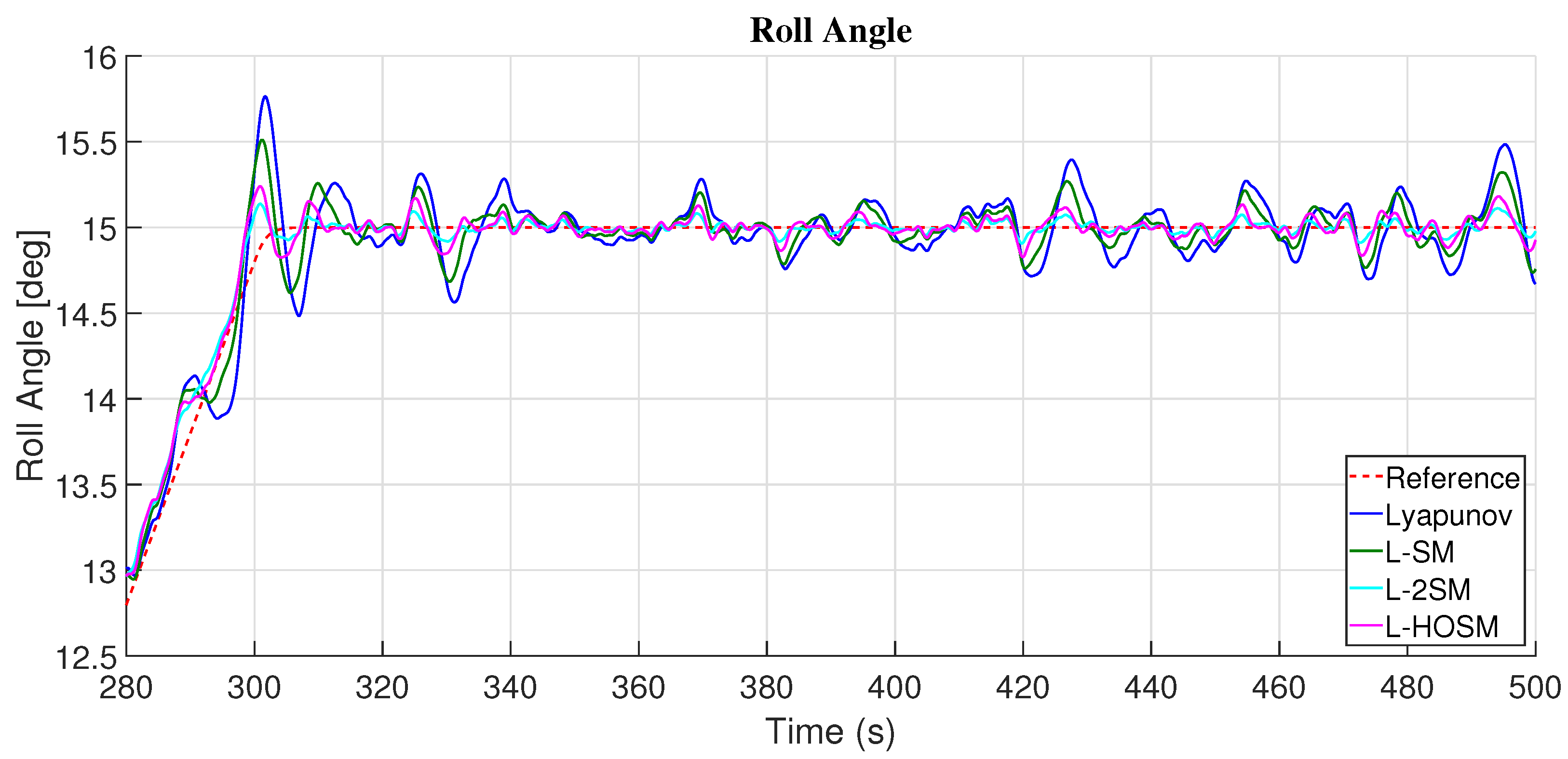
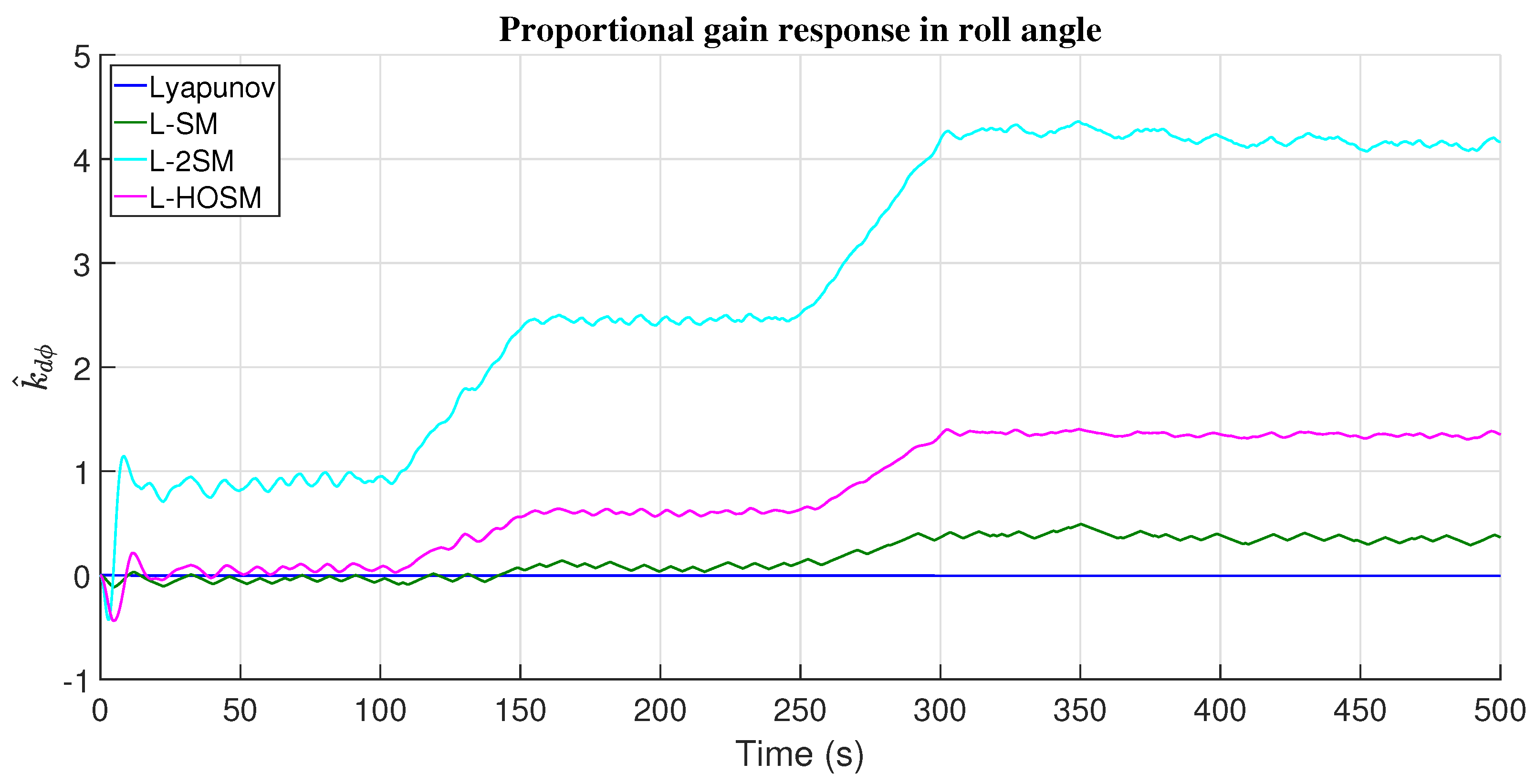
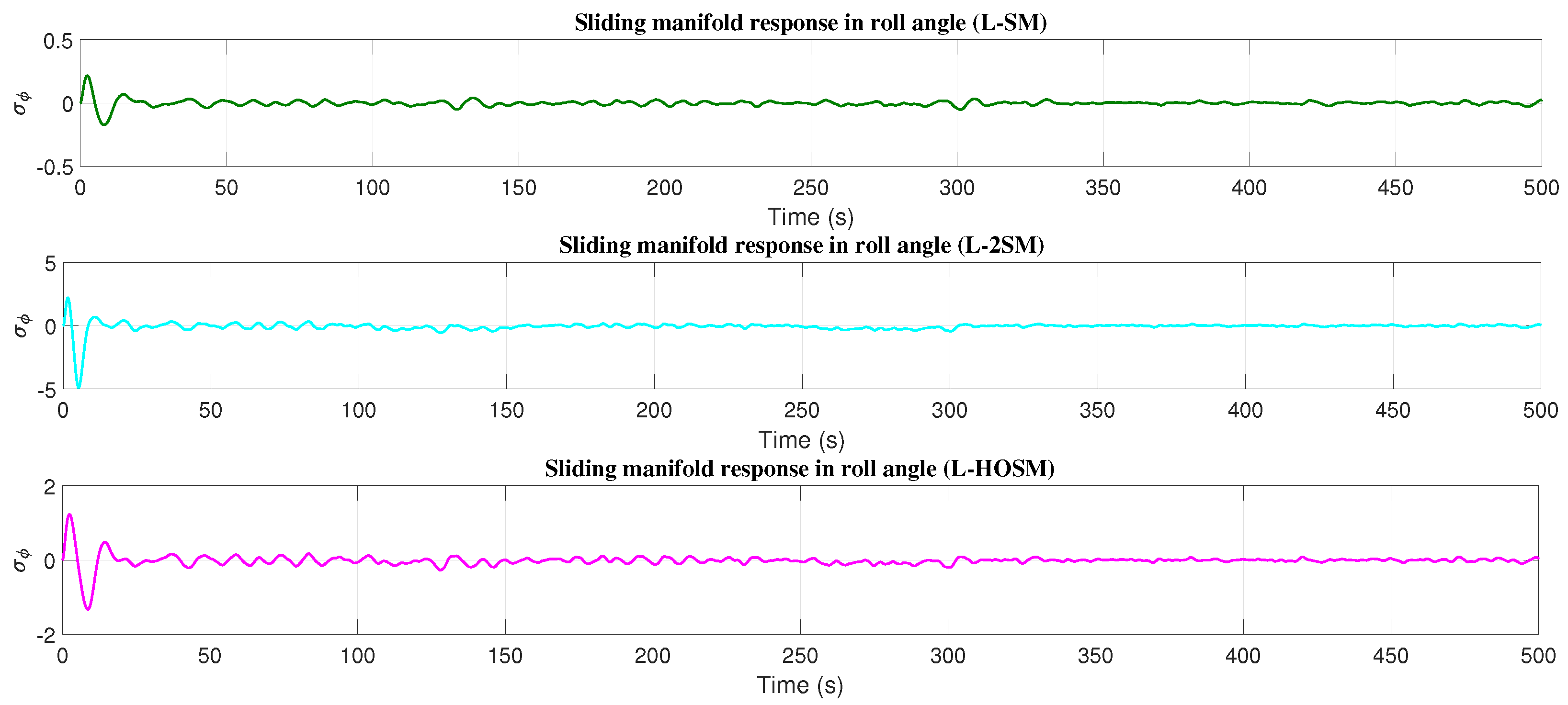
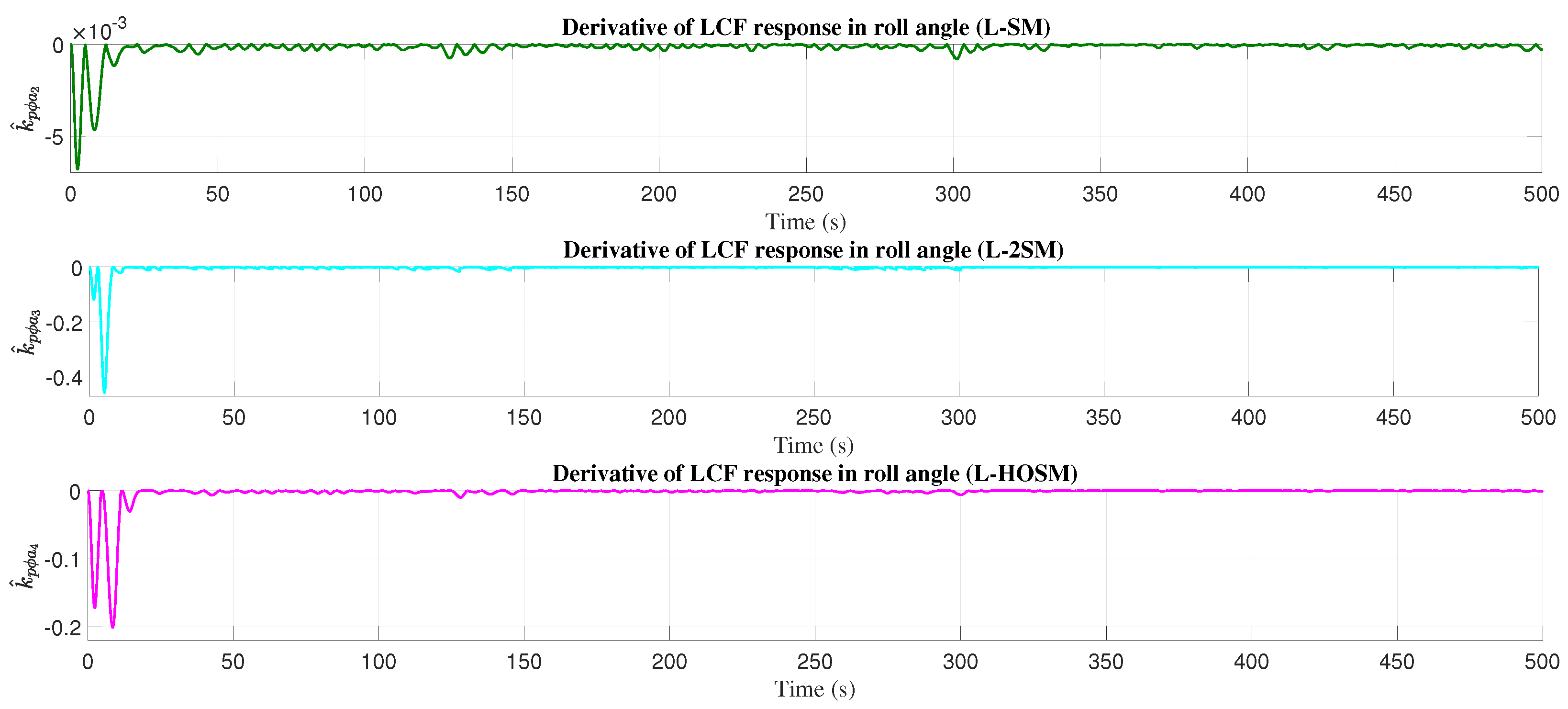
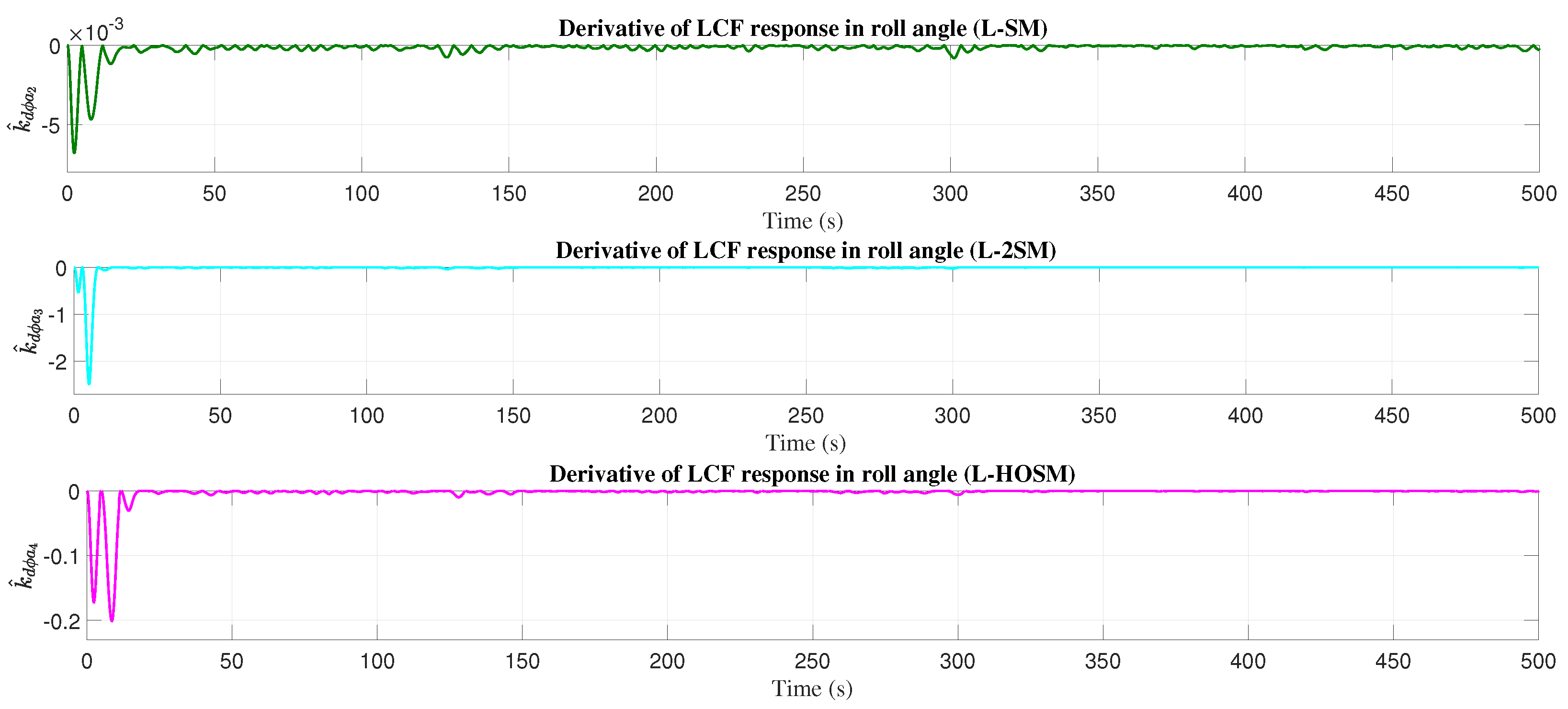
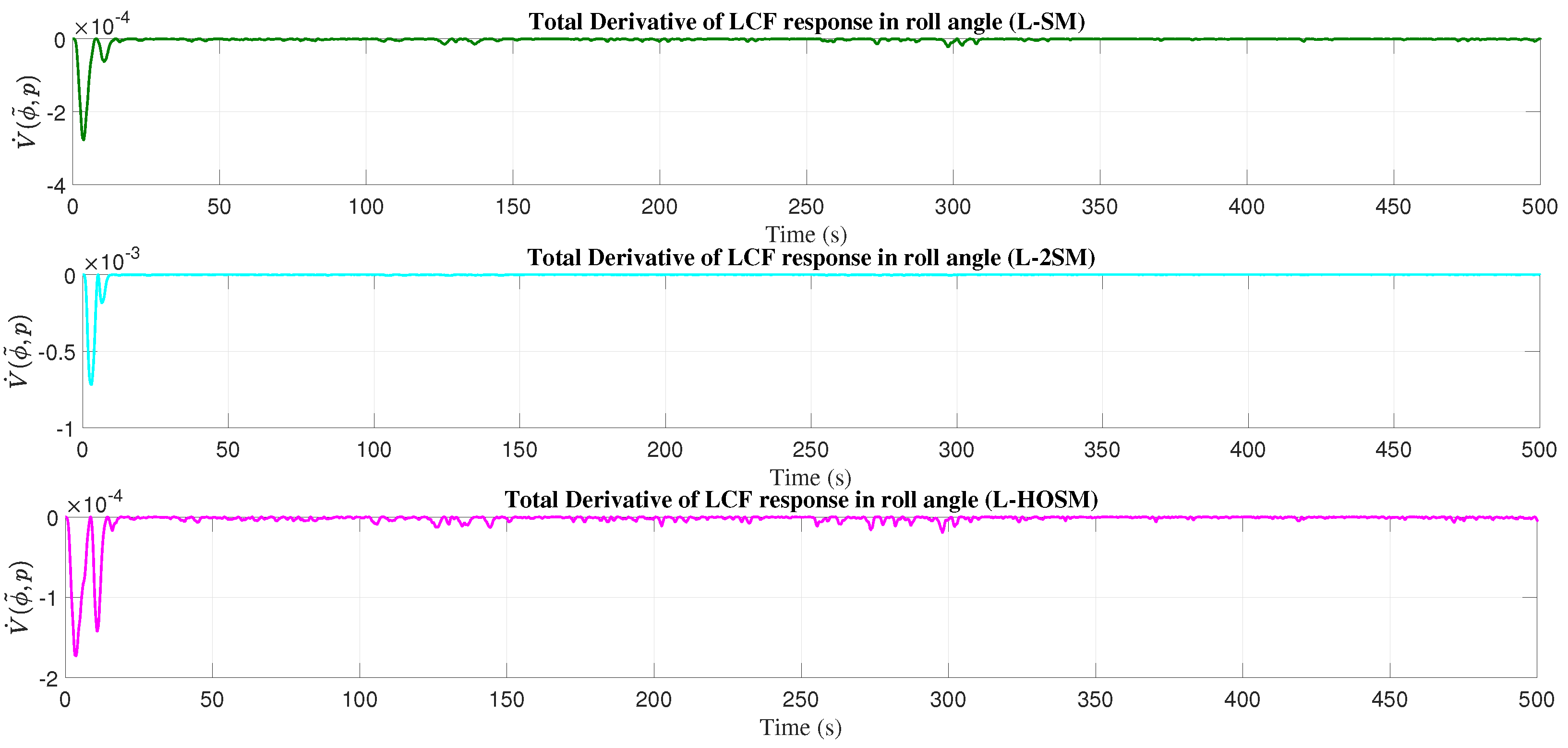
4.3. Roll Angle
5. Discussion
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| MRAS | Model Reference Adaptive System |
| MAV | Mini Aerial Vehicle |
| DOF | Degrees of Freedom |
| SMC | Sliding Mode Control |
| HOSM | High Order Sliding Mode |
| PD | Proportional-Derivative |
| PID | Proportional-Integral-Derivative |
| L-SM | Lyapunov with Sliding Mode |
| L-2SM | Lyapunov with second-order Sliding Mode |
| L-HOSM | Lyapunov with High Order Sliding Mode |
References
- Guo, Y.; Luo, L.; Bao, C. Design of a Fixed-Wing UAV Controller Combined Fuzzy Adaptive Method and Sliding Mode Control. Hindawi Math. Probl. Eng. 2022, 2022, 2812671. [Google Scholar] [CrossRef]
- Castañeda, H.; Salas-Peña, O.; León-Morales, J. Extended observer based on adaptive second order sliding mode control for a fixed wing UAV. ISA Trans. 2017, 66, 226–232. [Google Scholar] [CrossRef]
- Zheng, Z.; Jin, Z.; Sun, L.; Zhu, M. Adaptive Sliding Mode Relative Motion Control for Autonomous Carrier Landing of Fixed-wing Unmanned Aerial Vehicles. IEEE Access 2017, 5, 5556–5565. [Google Scholar] [CrossRef]
- Poksawat, P.; Wang, L.; Mohamed, A. Automatic Tuning of Attitude Control System for Fixed-wing Unmanned Aerial Vehicles. IET Control Theory Appl. 2016, 10, 2233–2242. [Google Scholar] [CrossRef]
- Thai, S.; Theodoulis, S.; Ross, C.; Biannic, J. Robust Gain-scheduled Autopilot Design with Anti-windup Compensation for a Guided Projectile. CEAS Aeronaut. J. 2023, 42, 765–786. [Google Scholar] [CrossRef]
- Poksawat, P.; Wang, L.; Mohamed, A. Gain Scheduled Attitude Control of Fixed-Wing UAV With Automatic Controller Tuning. IEEE Trans. Control Syst. Technol. 2018, 26, 1192–1203. [Google Scholar] [CrossRef]
- Chen, M.; Wang, Y. A Data-Driven Adaptive Method for Attitude Control of Fixed-Wing Unmanned Aerial Vehicles. Adv. Aerosp. Sci. Technol. 2019, 4, 1–15. [Google Scholar] [CrossRef][Green Version]
- Bao, C.; Guo, Y.; Luo, L.; Su, G. Design of a Fixed-Wing UAV Controller Based on Adaptive Backstepping Sliding Mode Control Method. IEEE Access 2021, 9, 157825–157841. [Google Scholar] [CrossRef]
- Souanef, T. L1 Adaptive Path-Following of Small Fixed-wing Unmanned Aerial Vehicles in Wind. IEEE Trans. Aerosp. Electron. Syst. 2022, 58, 3708–3716. [Google Scholar] [CrossRef]
- Hussien, M.; Elnaggar, M.; Kamel, A.; Fattah, H. Unmanned Aerial Vehicle Attitude Control using L1 Adaptive Controller. IEEE Access 2021, 9, 131916–131925. [Google Scholar] [CrossRef]
- Melkou, L.; Hamerlain, M.; Rezoug, M. Fixed-Wing UAV Attitude and Altitude Control via Adaptive Second-Order Sliding Mode. Arab. J. Sci. Eng. 2018, 43, 6837–6848. [Google Scholar] [CrossRef]
- Sungjae, L.; Yosoon, C. Comparison of Topographic Surveying Results using a Fixed-wing and a Popular Rotary-wing Unmanned Aerial Vehicle (Drone). Tunn. Undergr. Space 2016, 26, 24–31. [Google Scholar]
- Espinoza, A.T.; Saenz, J.A.; del Río, O.; de Jesús Gómez, F.; López, N.V. Aplicaciones de Drones en Ingeniería Civil: Topografía, Inspección de Obra y Estructuras; Grupo, A., Ed.; AlfaOmega Editor: Ciudad de México, Mexico, 2021. [Google Scholar]
- Carabassa, V.; Montero, P.; Alcañiz, M.; Padró, J. Soil Erosion Monitoring in Quarry Restoration Using Drones. Minerals 2021, 11, 949. [Google Scholar] [CrossRef]
- Gulch, E. Photogeammetric measurements in Fixed-wing UAV Imagery. In Proceedings of the XXII ISPRS Congress, Melbourne, Australia, 25 August–1 September 2012. [Google Scholar]
- Martins, A.; Almeida, J.; Almeida, C.; Figueiredo, A.; Santos, F.; Bento, D.; Silva, H.; Silva, E. Forest Fire Detection with a Small Fixed-wing Autonomous Aerial Vehicle. IFAC Proc. Vol. 2007, 40, 168–173. [Google Scholar] [CrossRef]
- Mohsan, S.; Othman, N.; Li, Y.; Li, Y.; Alsharif, M.H.; Khan, M.A. Unmanned aerial vehicles (UAVs): Practical aspects, applications, open challenges, security issues, and future trends. Intell. Serv. Robot. 2023, 16, 109–137. [Google Scholar] [CrossRef]
- Templin, T.; Popielarczyk, D.; Kosecki, R. Application of Low-Cost Fixed-wing UAV for Inland Shoreline Investigation. Pure Appl. Geophys. 2018, 175, 3263–3283. [Google Scholar] [CrossRef]
- Šiljeg, A.; Marinovic, R.; Domazetovic, F.; Jurišic, M.; Marić, I.; Panđa, L.; Radočaj, D.; Milošević, R. GEOBIA and Vegetation Indices in Extracting Olive Tree Canopies Based on Very High-Resolution UAV Multispectral Imagery. Appl. Sci. 2023, 13, 739. [Google Scholar] [CrossRef]
- Alfonso-Torreño, A.; Gómez-Gutiérrez, A.; Schnabel, S. Dynamics of Erosion and Deposition in a Partially Restored Valley-Bottom Gully. Land 2021, 10, 26. [Google Scholar] [CrossRef]
- Stengel, R.F. Flight Dynamics; Princeton University Press: Princeton, NJ, USA, 2004. [Google Scholar]
- Goldstein, H.; Poole, C.; Safko, J. Classical Mechanics; Adison-Wesley: Boston, MA, USA, 1983. [Google Scholar]
- Stevens, B.; Lewis, F.; Johnson, E. Aircraft Control and Simulation, 3rd ed.; John Wiley and Sons: Hoboken, NJ, USA, 2015; ISBN 978-1-118-87098-3. [Google Scholar]
- Mclean, D. Automatic Flight Control Systems; Prentice Hall International: Hoboken, NJ, USA, 1990. [Google Scholar]
- Cook, M. Flight Dynamics Principles, 2nd ed.; Elsevier: Amsterdam, The Netherlands, 2007. [Google Scholar]
- Parada, R.; Espinoza, T.; Dzul, A.; Salas, F. Performance analysis of nonlinear observers applied to the fixed-wing unmanned aerial vehicles flight under decoupled-reduced model. Int. J. Micro Air Veh. 2017, 9, 111–123. [Google Scholar] [CrossRef]
- Espinoza, T.; Parada, R.; Dzul, A.; Lozano, R. Linear controllers implementation for a fixed-wing MAV. In Proceedings of the 2014 International Conference on Unmanned Aircraft Systems (ICUAS), Orlando, FL, USA, 27–30 May 2014. [Google Scholar]
- Espinoza, T.; Dzul, A.; Llama, M. Linear and Nonlinear Controllers Applied to Fixed-Wing UAV. Int. J. Adv. Robot. Syst. 2013, 10, 33. [Google Scholar] [CrossRef]
- Åström, K.; Wittenmark, B. Adaptive Control, 2nd ed.; Prentice Hall: Hoboken, NJ, USA, 1994. [Google Scholar]
- Kelly, R.; Santibañez, V.; Loría, L. Control of Robot Manipulators in Joint Space; Springer: London, UK, 2005. [Google Scholar]
- Shtessel, Y.; Shkolnikov, A. Aeronautical and Space Vehicle Control in Dynamic Sliding Manifolds; IFAC Robust Control Design: Milan, Italy, 2003. [Google Scholar]
- Sanchez, T.; Moreno, J. Design of lyapunov functions for a class of homogeneous systems: Generalized forms approach. Int. J. Robust Nonlinear Control 2018, 29, 661–681. [Google Scholar] [CrossRef]
- Levant, A.; Livne, M. Globally convergent differentiators with variable gains. Int. J. Control 2018, 91, 1994–2008. [Google Scholar] [CrossRef]
- Levant, A. Robust exact differentition via sliding mode technique. Automatica 1998, 34, 379–384. [Google Scholar] [CrossRef]
- Shtessel, Y.; Edwards, C.; Fridman, L.; Levant, A. Sliding Mode Control and Observation; Birkhäuser: New York, NY, USA, 2015. [Google Scholar]











| Parameter | Value |
|---|---|
| 1.05 kg/m3 | |
| S | 0.09 m2 |
| 0.14 m | |
| b | 0.914 m |
| 0.16 kg·m2 | |
| 0.17 kg·m2 | |
| 0.02 kg·m2 | |
| −50 | |
| 0.25 | |
| −0.01 | |
| 0.0005 | |
| −0.15 | |
| 0.005 | |
| V | 60 km/h |
| Adaptive Mechanism (Altitude) | ||
|---|---|---|
| Lyapunov | 0.0184 | 0.0060 |
| Lyapunov-SM (L-SM) | 0.0081 | 0.0036 |
| Lyapunov-2SM (L-2SM) | 0.0217 | 0.0150 |
| Lyapunov-HOSM (L-HOSM) | 0.0451 | 0.0274 |
| Adaptive Mechanism (Yaw angle) | ||
| Lyapunov | 0.0379 | 0.0351 |
| Lyapunov-SM (L-SM) | 0.0362 | 0.0360 |
| Lyapunov-2SM (L-2SM) | 0.0714 | 0.0591 |
| Lyapunov-HOSM (L-HOSM) | 0.2976 | 0.2881 |
| Adaptive Mechanism
(Roll angle) | ||
| Lyapunov | 0.0284 | 0.0249 |
| Lyapunov-SM (L-SM) | 0.0279 | 0.0253 |
| Lyapunov-2SM (L-2SM) | 0.0261 | 0.0470 |
| Lyapunov-HOSM (L-HOSM) | 0.2528 | 0.2386 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Espinoza-Fraire, T.; Saenz, A.; Gandarilla, I.; Giernacki, W. MRAS Using Lyapunov Theory with Sliding Modes for a Fixed-Wing MAV. Appl. Sci. 2024, 14, 2198. https://doi.org/10.3390/app14052198
Espinoza-Fraire T, Saenz A, Gandarilla I, Giernacki W. MRAS Using Lyapunov Theory with Sliding Modes for a Fixed-Wing MAV. Applied Sciences. 2024; 14(5):2198. https://doi.org/10.3390/app14052198
Chicago/Turabian StyleEspinoza-Fraire, T., Armando Saenz, Isaac Gandarilla, and Wojciech Giernacki. 2024. "MRAS Using Lyapunov Theory with Sliding Modes for a Fixed-Wing MAV" Applied Sciences 14, no. 5: 2198. https://doi.org/10.3390/app14052198
APA StyleEspinoza-Fraire, T., Saenz, A., Gandarilla, I., & Giernacki, W. (2024). MRAS Using Lyapunov Theory with Sliding Modes for a Fixed-Wing MAV. Applied Sciences, 14(5), 2198. https://doi.org/10.3390/app14052198







