A Lightweight Chaotic Map-Based Key Agreement Scheme for the Advanced Metering Infrastructure

Abstract

In the advanced metering infrastructure (AMI), impersonation, eavesdropping, man-in-the-middle and other attacks occur in the process of communication between entities through public channels, which will lead to the leakage of user privacy or the incorrect issuance of control instructions, resulting in economic losses and even power system operation failures. In view of this situation, we design a lightweight key agreement scheme based on a chaotic map for the AMI. We use the chaotic map to replace the time-consuming bilinear pairing and elliptic curve method and establish a secure communication channel between legal entities. In addition, we also design a multicast key generation mechanism for message transmission in AMI. The security analysis proves the security of the proposed scheme in the random oracle model, which can meet the security characteristics of anonymity and forward secrecy, and can effectively resist common attacks such as impersonation, replay and man-in-the-middle. The performance analysis results show that the proposed scheme requires lower computational and communication costs than related schemes, so it is more suitable for AMI scenarios with limited resources.

1. Introduction

The advanced metering infrastructure (AMI) is a complete network processing system for collecting, storing and analyzing user electricity data, which is mainly composed of smart meters (SMs), data concentrators (DCs), the measurement data management system (MDMS), the local communication network, and the communication network connecting power company data center [1]. Among them, the communication network in the AMI includes uplink and downlink networks. The smart meter collects electricity consumption information from the user side and uploads the message to the MDMS through the DC, which belongs to the uplink network, and the process of MDMS transmitting command information from DC to SM belongs to the downlink network [2]. Eavesdropping, tampering and other attacks on the uplink network will lead to the exposure of electricity data and billing fraud, resulting in privacy leakage (such as whether the user is at home, whether the house is idle) and economic losses. Attacks on the downlink network will lead to errors in the command information, which will destroy the normal operation of the power system and can even lead to the paralysis of the whole power system [3,4]. For example, in 2014, Spanish hackers used meter vulnerabilities to conduct billing fraud and even shut down the entire circuit system, causing a large-scale power outage. In 2019, hackers used a firewall vulnerability to launch a denial-of-service attack against the American electrical company, resulting in equipment communication interruption.

In [5], the security vulnerabilities in the AMI were analyzed, and authentication and encryption were pointed out to be effective means to ensure the secure communication of the AMI. The secure communication scheme based on asymmetric cryptography has problems such as high communication overheads and multiple interactions during asymmetric encryption and decryption, making it unsuitable for smart meters with limited computing and communication resources. The key agreement mechanism allows both parties to negotiate the same session key before communication and uses symmetric encryption to communicate, which has less computation power and a faster speed. The certificateless key agreement scheme can not only avoid the complex certificate management in public key infrastructure (PKI), but also avoid the key escrow in identity-based cryptography (IBC). It is very suitable for entities in AMI with limited computation and communication resources such as smart meters [6].

In certificateless key agreement schemes, the scheme based on the hash algorithm [7] uses ultra-lightweight hash functions to achieve key agreements, which is suitable for scenarios with very limited communication resources, but cannot meet the security requirements well. In order to enhance security, many key agreement schemes based on bilinear pairing and an elliptic curve have been proposed. Bilinear mapping is simply a mapping e, which can map two elements in the cyclic group $G_1$ and $G_2$ of order n to one element in $G_3$, and the mapping satisfies bilinearity. The elliptic curve cryptosystem is based on the generalized discrete logarithm problem, and the use of shorter operands can provide the same security level as RSA.

In [8], anonymous communication between edge computing infrastructures in smart grid was realized, but the complexity of pairing operation increases the computational overhead. In addition, [9] proved that the scheme struggles to resist impersonation and transient key exposure attacks. In [10], a key exchange scheme named AAS-IoTaSG was proposed for the smart grid environment in the Internet of Things. This scheme is based on the anonymous signature, which allows the dynamic addition of nodes. However, it is proved by [9] that the scheme struggles to resist man-in-the-middle attacks and impersonation attacks. In [11], a key agreement scheme based on the elliptic curve was designed for the smart grid, but it was proved by [12] that the scheme cannot complete the authentication process in practical application scenarios. In [13], an authentication and key agreement scheme based on elliptic curves was proposed for smart grid environments that can satisfy forward confidentiality. In [14], a DRMAS scheme for identity authentication in demand response management in smart grid environment was proposed, which is based on the elliptic curve and the certificate. The use of the certificate and elliptic curve cryptosystem results in higher overheads. In [15], a lightweight authentication protocol was proposed for the smart metering infrastructure. The protocol is based on one-way hash and an elliptic curve, which can meet the security characteristics such as anonymity and mutual authentication. However, the scheme proved to be fragile in the face of impersonation attacks and key leakage attacks, and could not provide forward secrecy. In [16], in order to protect the secure communication between users and substations, an authentication scheme was designed using the elliptic curve cryptosystem. It was proved in [2] that the scheme could not provide anonymous and forward secrecy security features and could not resist ESL (Ephemeral Secret Leakage) attacks. In [17], a privacy protection and lightweight authentication scheme based on elliptic curves was proposed to achieve secure communication between SMs and neighbor area network gateways. In [18], Kumar et al.’s scheme [19] was proven to fail to satisfy security characteristics such as anonymity, and a lightweight key agreement scheme based on elliptic curves was proposed to establish a secure channel for data transmission in the smart grid environment. In [20], a blockchain-based privacy preserving authentication scheme was proposed for demand response management in the smart grid environment, establishing a secure channel between smart meters and service providers. However, the above schemes still have deficiencies in security, and still need more computational and communication overheads compared with other non-bilinear mapping and non-elliptic curve schemes.

In recent years, many scholars have proposed key agreement schemes based on chaotic maps. The chaotic map is a kind of random nonlinear process with high initial value sensitivity, high complexity and good confidentiality. The chaotic map based on the Chebyshev polynomial originates from the expansion of a multi-angle cosine function and sine function, which is very suitable for the design of cryptography and secure communication schemes. The definition and properties are shown in Section 2. According to relevant research, the cost of chaotic mapping is only about one-third of the elliptic curve point multiplication operation, which can greatly reduce the operation cost. Compared with bilinear pairing and elliptic curves, chaotic maps have lower computational complexity and higher security. Wang et al. [21] proposed a lightweight authentication scheme for electric vehicle charging, but it was proved that the scheme had errors in the registration and key agreement stages, and could not achieve secure communication [22]. In [23], for the Internet of Vehicles environment, a group key agreement scheme based on chaotic map and bilinear pairing was designed which can support batch authentication. In [24,25], an efficient authentication and group authentication protocol based on chaotic mapping was designed for the Internet of Vehicles. In [26], a three-factor authentication scheme based on the chaotic map was designed for mobile devices, which can meet the corresponding security evaluation criteria. However, the above schemes do not conform to the architecture and message transmission mode of the AMI and cannot be directly applied to the advanced metering infrastructure.

1.1. Motivation

In [27], the important role of authentication and key agreement mechanism in smart grid environment, especially in AMI system, is expounded, which can effectively protect entities from adversary attacks and threats of unauthorized illegal entities and ensure the reliable operation of the whole system. In [28], the potential risks in the AMI system are evaluated by the OCTAVE Allegro method. According to [10,28], the key agreement scheme designed for the AMI system needs to be able to resist impersonation, man-in-the-middle, replay and other attacks in addition to mutual authentication, ensuring session key security, providing anonymity and forward confidentiality. These are the main requirements of smart grid security. At the same time, because the smart meter equipment has very limited resources, such as computing, communication and power supply, the scheme also needs to be as lightweight as possible to adapt to the increasing traffic in the AMI system.

Through the above analysis of the existing key agreement schemes in AMI or smart grid scenarios, it can be found that most of the existing schemes have been proven to have some security problems and cannot meet the security requirements well. Secondly, the existing key agreement schemes in AMI are basically based on cryptosystems with high computational complexity, such as bilinear pairings, elliptic curves, etc., which require high energy overheads, while ultra-lightweight hash operations cannot provide good security. Last but not least, most of the above schemes do not take into account the message transmission mode in the AMI and cannot adapt well to the actual AMI system. Therefore, in order to ensure secure communication between legitimate entities in the AMI system, the designed scheme needs to establish an appropriate balance between security and efficiency. Based on the premise of satisfying the required security, the overhead should be reduced as much as possible to adapt to the equipment with limited resources, and the architecture and message transmission mode of the AMI system should be fully considered.

1.2. Contribution

The main contributions of this article are as follows.

(1)

In order to ensure the secure communication between entities in AMI, a lightweight authentication and key agreement scheme based on Chebyshev chaotic map is proposed.

(2)

The chaotic map with a short key length, low memory occupation and a high secret strength is used to replace the time-consuming bilinear pairing and elliptic curve point multiplication operation, without additional storage certificate and key escrow, which saves the computation and communication overheads based on the premise of realizing the establishment of secure channel.

(3)

According to the AMI architecture and message transmission mode, the authentication and key agreement mechanism between entities is designed, which establishes a secure channel for message transmission between entities. In addition, in order to solve the problem of the repeated transmission of data and repeated occupation of bandwidth, we also design a multicast key generation mechanism.

(4)

The security analysis results show that the proposed scheme satisfies the security characteristics such as anonymity and forward secrecy and can resist common attacks such as replay, impersonation and man-in-the-middle. The performance analysis results show that compared with the related schemes, the proposed scheme requires lower computation and communication costs and allows more entities to participate in the same hardware and software environment. The proposed scheme is more suitable for the AMI with limited resources.

1.3. Organization

In Section 2, the concept of Chebyshev chaotic map and the hypothesis of its difficult problem are given. Section 3 introduces the AMI architecture. Section 4 introduces the algorithm design of the proposed scheme in detail. Section 5 presents a formal and informal analysis of the proposed scheme and compares it with related representative schemes. Section 6 compares and summarizes the proposed scheme and related work from the perspective of calculation cost and communication cost. Section 7 discusses the limitations of the proposed scheme and the prospect of future work. Finally, Section 8 summarizes the article and puts forward the future research directions.

2. Preliminaries

2.1. Chebyshev Polynomial

For integer n, variable $x\in [-1,+1]$, a large prime $P$, Chebyshev polynomial $T_n\left(x\right):[-1,+1]\to [-1,+1]$ of degree $n$ is defined as follows:

$$T_n\left(x\right)=\left\{\begin{array}{l}\mathit{cos}\left(n·{\mathit{arccos}}^{-1}\left(x\right)\right),x\in \left[-1,1\right]\\ \mathit{cos}\left(n\theta \right),x=\mathit{cos}\theta ,\theta \in \left[0,\mathsf{\pi }\right]\end{array}\right.$$

(1)

The recursive formula is as follows:

$$T_n\left(x\right)=\left\{\begin{array}{l}\hspace{1em}1\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\left(n=0\right)\\ \hspace{1em}x\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\left(n=1\right)\\ 2x{T}_{n-1}\left(x\right)-T_{n-2}\left(x\right),\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\left(n\ge 2\right)\end{array}\right.$$

(2)

Semigroup nature:

$$T_n\left(x\right)=\left(2x{T}_{n-1}\left(x\right)-T_{n-2}\left(x\right)\right)\left(\mathit{mod} P\right)$$

(3)

where $n\ge 2, x\in (-\infty ,+\infty )$.

$$T_p\left(T_q\left(x\right)\right)=T_{\mathit{pq}}\left(x\right)=T_q\left(T_p\left(x\right)\right)$$

(4)

where $p, q\in Z^{+}$.

2.2. Chaotic Maps Mathematical Hard Problems

Definition 1.

CMDLP (Chaotic Map-Based Discrete Logarithm Problem). Discrete logarithm problem on $T_n\left(x\right)$: given a large prime number $P$ and two large integers $x$ and $y$, find an integer $e$, such that

$$T_e\left(x\right) \mathit{mod} P \equiv y$$

(5)

Definition 2.

CMDHP (Chaotic Map-Based Diffie-Hellman Problem). Diffie–Hellman problem on extended $T_n\left(x\right)$: given a large prime number $P$, $T_p\left(x\right) \mathit{mod} P$ and $T_q\left(x\right) \mathit{mod} P$, find an integer $z$, such that

$$T_z\left(x\right)=T_{\mathit{pq}}\left(x\right) \mathit{mod} P$$

(6)

It is difficult to solve CMDL and CMDH problems in probabilistic polynomial time.

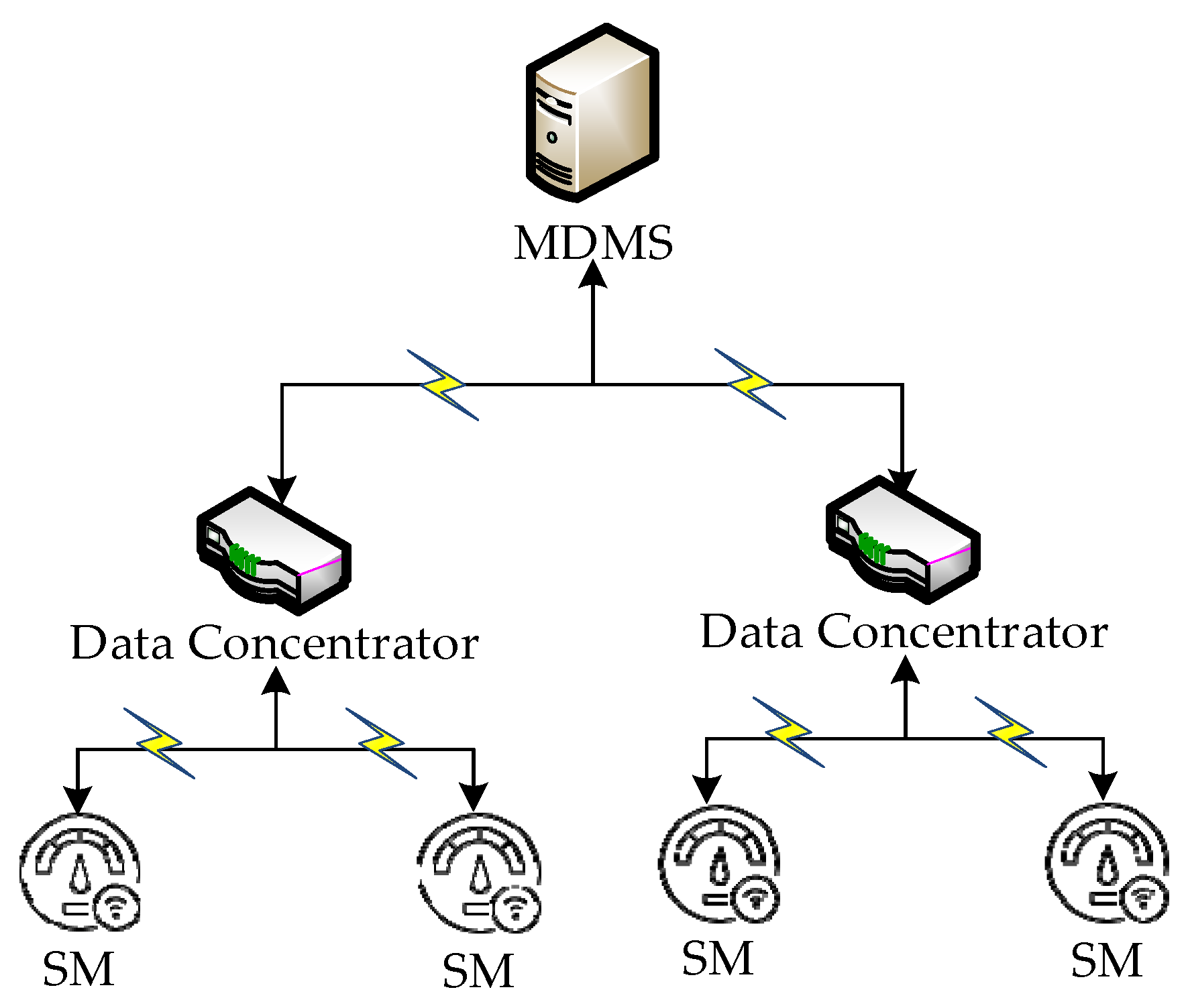
3. AMI System Model

In the AMI, the smart meter is located at the user side, and the collected measurement, illegal power consumption, fault and other data are uploaded to the data concentrator through RS485, PLC and other communication media. It is an intelligent instrument with a microprocessor as the core, and its memory and computing power are relatively limited. The data concentrator is generally installed in the substation, which processes and packages the collected data and forwards it to the measurement data management system through optical fibers, GPRS and other communication media. The measurement data management system is located in the power grid company to store, analyze and use all the data recorded by the smart meter. The communication mode in the uplink network is generally unicast communication, such as smart meter sending measurement data to a data concentrator. In the downlink network, there is also a multicast message transmission method, such as the measurement data management system sending the electricity price information to multiple smart meters simultaneously through the data concentrator. The architecture of the AMI system is shown in Figure 1.

The AMI has terminal access to a large number of smart meters, which record the power consumption information of each user in real time and upload the power consumption data to the measurement data management system regularly. Once the data are eavesdropped on and tampered with by adversaries, this will lead to the leakage of the user’s privacy information and affect the normal charging of the power company, which will cause conflicts and disputes between the supply and demand sides. The measurement data management system remotely controls the smart meter by transmitting control instructions, such as determining whether to cut off the power according to the user’s electricity bill balance, configuring parameters during the installation of the smart meter, and rewriting the electricity price parameter. Once the control instruction is issued wrongly, it will cause disorders in the power system and affect people’s normal life. In addition, attackers can impersonate legitimate entities and inject false messages into the channel to disrupt the normal operation of the system and even control the entire AMI system.

To sum up, in order to enable entities in AMI to transmit data and exchange information through a secure channel, a lightweight key agreement scheme based on chaotic map is designed in this article. Each entity generates a common session key through authentication and key agreement mechanisms and transmits information through encrypted channels to achieve secure data transmission, preventing unauthenticated devices from obtaining effective information. We also designed the generation of multicast keys to address the characteristics of multicast message transmission in AMI. In addition, the identity information of smart meters bound to users will not be leaked during the interaction process.

4. Proposed Scheme

Due to the use of the same key agreement scheme between MDMS and DC, as well as between DC and SM, for the convenience of description, this section describes the proposed scheme in detail by taking the interaction between DC and SM as an example.

We provide a preliminary explanation of the symbols and their meanings used in our scheme, as shown in Nomenclature part.

4.1. Initialization

The data concentrator is installed by the power company in the substation/distribution station, which is considered reliable. In order to achieve authentication and key agreement with the smart meter in the area under its jurisdiction, the data concentrator ${\mathit{DC}}_j$ performs the following initialization process:

${\mathit{DC}}_j$ selects a Chebyshev polynomial function $T_n\left(x\right)$ with seeds $x\in (-\infty ,+\infty )$, a large prime number $p$, selects collision-resistant hash functions $H(\cdot )\left(\mathit{SHA}\text{-}160\right)$ and $H_0(\cdot )\left(\mathit{SHA}\text{-}320\right)$, and sets a time threshold $\mathsf{\Delta }T$ to confirm the timeliness of the message. ${\mathit{DC}}_j$ selects a random number $s\in Z_P^{\ast }$ and calculates $S=T_s\left(x\right)$, where $s$ is the private key and $S$ is the public key.

${\mathit{DC}}_j$ publishes the system parameters $\left\{T_s\right(x),x, H\left(\cdot \right),H_0(\cdot )\}$.

4.2. Registration

Smart meters within the jurisdiction of the data concentrator ${\mathit{DC}}_j$ receive public parameters. The smart meter ${\mathit{SM}}_i$ selects a random number $k\in Z_P^{\ast }$ as its private key, calculates the public key $K=T_k\left(x\right)$ and publishes it. ${\mathit{SM}}_i$ then computes the ${\mathit{XID}}_i={\mathit{ID}}_i{T}_k\left(S\right) \mathit{mod} p$ and sends $\{{\mathit{XID}}_i,t_0\}$ to ${\mathit{DC}}_j$, where $t_0$ is the timestamp and ${\mathit{ID}}_i$ is the unique identification of the smart meter, which is bound to the user’s identity, corresponding to their home address, bank account and IP of the smart meter, relating to absolute privacy.

Upon receiving $\{{\mathit{XID}}_i,t_0\}$, ${\mathit{DC}}_j$ first verifies the timeliness of the message, and if $|t_{\mathit{current}}-t_0|\le \mathsf{\Delta }T$, it then proceeds to the next step of calculation: ${\mathit{ID}}_i={\mathit{XID}}_i/T_s\left(T_k\right(x\left)\right)$. After obtaining the ${\mathit{ID}}_i$, ${\mathit{DC}}_j$ selects the random number $e_i,r_i\in Z_P^{\ast }$ and computes

$${\mathit{PID}}_i=H\left({\mathit{ID}}_i\left|\right|e_i\right)$$

(7)

$$E_i=H\left({\mathit{ID}}_i\left|\right|s\left|\right|r_i\left|\right|{\mathit{PID}}_i\right)$$

(8)

where ${\mathit{PID}}_i$ is the pseudo identity of the smart meter ${\mathit{SM}}_i$, and ${\mathit{DC}}_j$ sends $\{{\mathit{PID}}_i,E_i\}$ to ${\mathit{SM}}_i$ and saves $\{{\mathit{ID}}_i,r_i\}$.

4.3. Mutual Authentication and Session Key Agreement

${\mathit{SM}}_i$ and ${\mathit{DC}}_j$ authenticate and negotiate to establish each other’s session key SK.

(1) The smart meter ${\mathit{SM}}_i$ selects a random number $u\in Z_P^{\ast }$ and a current timestamp $t_1$, and calculates

$$M_1=T_u\left(x\right)$$

(9)

$$M_2=T_u\left(T_s\left(x\right)\right)$$

(10)

$$M_3=\left({\mathit{ID}}_i\left|\right|E_i\right)⨁H_0\left(M_2\right)$$

(11)

$$M_4=H\left({\mathit{ID}}_i\left|\right|{\mathit{PID}}_i\left|\right|E_i\left|\right|M_2\left|\right|M_3\right)$$

(12)

Then, ${\mathit{SM}}_i$ sends $\{{\mathit{PID}}_i,M_1,M_3,M_4,t_1\}$ to ${\mathit{DC}}_j$.

(2) After receiving $\{{\mathit{PID}}_i,M_1,M_3,M_4,t_1\}$, ${\mathit{DC}}_j$ first verifies the timeliness of the message. If $|t_{\mathit{current}}-t_1|\le \mathsf{\Delta }T$, ${\mathit{DC}}_j$ performs the next operation. Otherwise, ${\mathit{DC}}_j$ terminates the session.

① After the message’s timeliness is verified, ${\mathit{DC}}_j$ calculates

$$M_2=T_s\left(M_1\right)$$

(13)

$$\left({\mathit{ID}}_i^{\prime }\left|\right|E_i^{\prime }\right)=M_3⨁H_0\left(M_2\right)$$

(14)

${\mathit{DC}}_j$ retrieves $\{{\mathit{ID}}_i,r_i\}$, and performs the following steps after successful retrieval; otherwise, ${\mathit{DC}}_j$ terminates the session.

②${ \mathit{DC}}_j$ performs the following calculation:

$$E_i=H\left({\mathit{ID}}_i\left|\right|s\left|\right|r_i\left|\right|{\mathit{PID}}_i\right)$$

(15)

and checks whether the equations $M_4=H\left({\mathit{ID}}_i\left|\right|{\mathit{PID}}_i\left|\right|E_i\left|\right|M_2\left|\right|M_3\right)$ and $E_i^{\prime }=E_i$ are established. After successful verification, ${\mathit{DC}}_j$ performs the next operation; otherwise, the session will be terminated.

③${ \mathit{DC}}_j$ selects $e_i^{\mathit{new}}\in Z_P^{\ast }$ and calculates:

$${\mathit{PID}}_i^{\mathit{new}}=H\left({\mathit{ID}}_i\left|\right|e_i^{\mathit{new}}\right)$$

(16)

$$E_i^{\mathit{new}}=H\left({\mathit{ID}}_i\left|\right|s\left|\right|r_i\left|\right|{\mathit{PID}}_i^{\mathit{new}}\right)$$

(17)

④${\mathit{DC}}_j$ selects $v\in Z_P^{\ast }$ and a current timestamp $t_2$, then computes:

$$M_5=T_v\left(x\right)$$

(18)

$$M_6=T_v\left(M_1\right)$$

(19)

$$M_7=\left({\mathit{PID}}_i^{\mathit{new}}\left|\right|E_i^{\mathit{new}}\right)⨁H_0\left(M_6\left|\right|E_i\right)$$

(20)

$${\mathit{SK}}_{\mathit{ji} }=H\left({\mathit{ID}}_i\left|\right|{\mathit{PID}}_i\left|\right|E_i\left|\right|E_i^{\mathit{new}}\left|\right|M_2\left|\right|M_6\right)$$

(21)

$$M_8=H\left({\mathit{ID}}_i\left|\right|{\mathit{PID}}_i\left|\right|E_i\left|\right|M_2\left|\right|M_5\right|\left|{\mathit{SK}}_{\mathit{ji} }\right)$$

(22)

⑤ ${\mathit{DC}}_j$ sends $\{M_5,M_7,M_8,t_2\}$ to ${\mathit{SM}}_i$.

(3) After receiving $\{M_5,M_7,M_8,t_2\}$, ${SM}_i$ first verifies the timeliness of the message. If $|t_{\mathit{current}}-t_2|\le \mathsf{\Delta }T$, ${\mathit{SM}}_i$ performs the next step. Otherwise, the session will be terminated.

① After the message timeliness is verified, ${\mathit{SM}}_i$ calculates:

$$M_6=T_u\left(M_5\right)$$

(23)

$$\left({\mathit{PID}}_i^{\mathit{new}}\left|\right|E_i^{\mathit{new}}\right)=M_7⨁H_0\left(M_6\left|\right|E_i\right)$$

(24)

$${\mathit{SK}}_{\mathit{ij}}=H\left({\mathit{ID}}_i\left|\right|{\mathit{PID}}_i\left|\right|E_i\left|\right|E_i^{\mathit{new}}\left|\right|M_2\right|\left|M_6\right)$$

(25)

② In order to prevent potential attacks, ${\mathit{SM}}_i$ checks whether the equation $M_8=H\left({\mathit{ID}}_i\left|\right|{\mathit{PID}}_i\left|\right|E_i\left|\right|M_2\left|\right|M_5\left|\right|{\mathit{SK}}_{\mathit{ji}}\right)$ is established. After successful verification, ${\mathit{SM}}_i$ and ${\mathit{DC}}_j$ share the session key $\mathit{SK}={\mathit{SK}}_{\mathit{ij}}={\mathit{SK}}_{\mathit{ji}}$; otherwise, the session will be terminated.

③${\mathit{SM}}_i$ updates $\{{\mathit{PID}}_i,E_i\}$ to $\{{\mathit{PID}}_i^{\mathit{new}},E_i^{\mathit{new}}\}$ for periodic key updates.

(4) After mutual authentication, the smart meter $\mathit{SM}$ and data concentrator $\mathit{DC}$ use the common session key $\mathit{SK}$ for encrypted communication. DC and MDMS negotiate to establish a secure channel through the same steps. The message transmitted in the communication needs to meet the communication protocol. The information frame in the AMI generally contains seven parts, and each part contains several bytes. The format is shown in Figure 2, where the data domain part is the main body of the communication content that needs to be encrypted.

The data concentrator receives control instructions from the MDMS through the secure channel, such as tripping and closing, and then transmits them to the corresponding smart meter through the secure channel. The information frame format transmitted in this process is shown in Figure 3, where the address field contains the address of DC and SM, $\mathit{PA}=98H$ stands for the secret level, and the data field $N_1~N_m$ will be filled with ciphertext.

4.4. Multicast Key Generation

In the downlink communication network, according to the communication protocol, one or more bytes of the address domain can be replaced by $\mathit{AAH}$, so as to achieve the effect that the current bytes are multicast addresses and realize the function of broadcasting a message to all eligible smart meters. In order to better adapt to the AMI message transmission mode, the multicast key agreement process is also designed after authentication and unicast key agreement. There are multiple smart meters within the jurisdiction of ${\mathit{DC}}_j$, and the multicast key agreement process will be described by using the interaction between ${\mathit{DC}}_j$, and ${\mathit{SM}}_i$ as an example.

① After realizing the unicast key agreement, ${DC}_j$ selects a current timestamp $t_3$ and performs the following calculations:

$$Y_i=T_v\left(M_1\right)$$

(26)

$$\mathit{GK}=H(Y_1{Y}_2\dots Y_i\dots Y_n)$$

(27)

$${\mathit{GK}}_i=\mathit{GK}/Y_i$$

(28)

$$M_9=H\left({\mathit{ID}}_i\left|\right|{\mathit{PID}}_i\left|\right|Y_i\left|\right|\mathit{GK}\right)$$

(29)

$${\mathit{EM}}_i={\mathit{Enc}}_{\mathit{SK}}\left({\mathit{GK}}_i\left|\right|M_9\left|\right|t_3\right)$$

(30)

where ${\mathit{EM}}_i$ is the encrypted ciphertext using the key $\mathit{SK}$ between ${\mathit{DC}}_j$ and ${\mathit{SM}}_i$. ${\mathit{DC}}_j$ sends ${\mathit{EM}}_i$ to ${\mathit{SM}}_i$.

② After receiving the ciphertext, ${\mathit{SM}}_i$ decrypts $M_i={\mathit{Dec}}_{\mathit{SK}}\left({\mathit{EM}}_i\right)$ with the session key to obtain $\{{\mathit{GK}}_i,M_9,t_3\}$, and then verifies the timeliness of the message. If $|t_{\mathit{current}}\text{-}{t}_3|\le \mathsf{\Delta }T$, ${\mathit{SM}}_i$ performs the following calculation; otherwise, it terminates the session.

$$Y_i=T_u\left(M_5\right)$$

(31)

$$\mathit{GK}=H\left({\mathit{GK}}_i{Y}_i\right)$$

(32)

③ ${\mathit{SM}}_i$ verifies whether the equation $M_9=H\left({\mathit{ID}}_i\left|\right|{\mathit{PID}}_i\left|\right|Y_i\left|\right|\mathit{GK}\right)$ is established. If successful, ${\mathit{DC}}_j$ encrypts the instruction information using the group key $\mathit{GK}$ and sends it to multiple smart meters. ${\mathit{SM}}_i$ decrypts and performs the corresponding operation using the group key $\mathit{GK}$; otherwise, ${\mathit{SM}}_i$ will terminate the session. The MDMS and DC implement multicast key agreement through the same steps as above.

5. Security Analysis and Comparison

In this section, we prove that the proposed scheme can meet the security requirements and can resist common attacks.

5.1. Adversary Model

In the AMI, entities often communicate and transmit data through insecure channels, which are vulnerable to various attacks. In this paper, we choose the well-known and widely accepted CK adversarial model, which defines the adversary A that can completely control the channel during the entire communication process. Its attack capabilities include listening, modifying, deleting and injecting messages. In addition, the adversary can further obtain the private secret value of the entity. In order to prove the security of this scheme under the CK model, we establish the following definition:

$\mathit{Participants}$: The scheme includes two entities, SM and DC. Any other entity is recorded as $I$.

Queries: Opponent A can query participants to achieve the interaction between the two. The following queries are used to simulate the attack ability of A.

$\mathit{Execute}({\mathit{SM}}_i$,${\mathit{DC}}_j)$: A can obtain all communication records between ${\mathit{SM}}_i$ and ${\mathit{DC}}_j$ through the query, which simulates passive attacks (such as an eavesdropping attack).

$\mathit{Send}(I,m)$: A carries out an active attack through the query. Adversary A sends a forged message $m$ to entity $I$, and $I$ responds to A, where $m$ can be obtained by means of interception.

$\mathit{Reveal}\left(I\right)$: A can obtain the session key owned by I through the query.

$\mathit{Corrupt}\left(I\right)$: Through the query, A requests $I$ and obtains its long-term secret value.

$\mathit{Test}\left(I\right)$: This query measures the semantic security of the session key. The adversary A sends a single test query to the oracle, and the oracle begins to toss a coin $b\in \{0,1\}$ after receiving the query. If b is 0, a random key of the same size as SK is returned to A. If b is 1, the real SK is passed to A.

$h\left(m\right)$: After receiving the query from A, I sends the hash value of the message $m$ replaced by the random number as a response to A.

Partnering: Entities ${\mathit{SM}}_i$ and ${\mathit{DC}}_j$ are partners, when they verify each other and negotiate a consistent key.

Freshness: For a session $S$ held by participant I, if the session $S$ has generated a session key, and A does not issue a $\mathit{Reveal}\left(I\right)$ query, and at most one $\mathit{Corrupt}\left(I\right)$ query is performed, the session $S$ is fresh.

5.2. Formal Security Proof

According to [2], we rigorously test the security of the proposed scheme via formal security analysis under the widely accepted random oracle model, and prove that the proposed scheme can effectively resist the adversary A defined in the adversarial model.

Definition 3.

We use ${\mathit{Game}}^{\mathit{AKA}}(I, A)$ to simulate the security of the scheme. Though the game, A can send multiple queries to participant I, but A can perform $\mathit{Test}\left(I\right)$ query at most once, and I returns $b^{\prime }\in \{0,1\}$. The goal of A is to correctly guess the value of b in the $\mathit{Test}\left(I\right)$ session. The probability that A wins in ${\mathit{Game}}^{\mathit{AKA}}(I, A)$ is defined as $\mathit{Pr}\left[\mathit{Succ}\right(A\left)\right]$. The advantage that A destroys the semantic security of the proposed scheme in polynomial time is defined as:

$${\mathit{Adv}}_p^{\mathit{AKA}}\left(A\right)=\left|2\mathit{Pr}\left[\mathit{Succ}\left(A\right)\right]\text{-}1\right|=\left|2\mathit{Pr}\left[b^{\prime }=b\right]\text{-}1\right|$$

(33)

This scheme is secure if adversary A’s advantage of destroying semantic security ${\mathit{Adv}}_p^{\mathit{AKA}}\left(A\right)$ can be ignored.

Lemma 1.

Suppose that $E_1, E_2, \mathit{and} F$ are events defined in a probability distribution, and assume that $E_1\wedge -F⟺E_2\wedge -F$. This means that $\left|\mathit{Pr}\left[E_1\right]-\mathit{Pr}\left[E_2\right]\right|\le \mathit{Pr}\left[F\right]$.

Theorem 1.

Assuming that A can perform at most $q_h$ $\mathit{hash}$ queries, $q_e \mathit{Execute}$ queries, and $q_s$ $\mathit{Send}$ queries, then the advantage of A is

$${\mathit{Adv}}_p^{\mathit{AKA}}\left(A\right)\le \frac{\left(q_s+{2q}_h^2\right)}{2^l}+\frac{2{\left(q_s+q_e\right)}^2}{p}+2q_h{\mathit{Adv}}_{\mathit{CMCDH}}\left(A\right)$$

(34)

where $l$ is the length of the hash value.

Proof. 

The proof consists of the game order ${\mathit{GM}}_i\left(i=0,1,2,3,4,5\right)$. For each game, A wins the game when A guesses the value of $b$ successfully. □

${\mathit{GM}}_0$: The game simulates attacks which are carried out under the standard model, therefore

$${\mathit{Adv}}_p^{\mathit{AKA}}\left(A\right)=\left|2\mathit{Pr}\left[{\mathit{GM}}_0\right]-1\right|$$

(35)

${\mathit{GM}}_1$: Through the query of $\mathit{Execute}({\mathit{SM}}_i,{\mathit{DC}}_j)$, A can obtain all the messages $\{{\mathit{PID}}_i,M_1,M_3,M_4\}$ and $\{M_5,M_7,M_8\}$ exchanged between ${\mathit{SM}}_i$ and ${\mathit{DC}}_j$. A can verify whether the calculated key SK is real by executing the query. It can be seen that the security of the key cannot be disclosed from the exchanged information. Therefore

$$\left|\mathit{Pr}\left[{\mathit{GM}}_1\right]-\mathit{Pr}\left[{\mathit{GM}}_0\right]\right|=0$$

(36)

${\mathit{GM}}_2$: The game simulates all types of queries, and as in ${\mathit{GM}}_1$, the game is suspended when the following two situations occur: (1) Hash queries conflict in output, and (2) $\{{\mathit{PID}}_i,M_1,M_3,M_4\}$ and $\{M_5,M_7,M_8\}$ are not uniformly distributed. From the birthday paradox, therefore,

$$\left|\mathit{Pr}\left[{\mathit{GM}}_2\right]-\mathit{Pr}\left[{\mathit{GM}}_1\right]\right|\le \frac{q_h^2}{2^{l+1}}+\frac{{\left(q_s+q_e\right)}^2}{2p}$$

(37)

${\mathit{GM}}_3$: When A successfully guesses $M_4$ and $M_8$ without querying the participants, the game will be suspended, which is different from other games. Therefore,

$$\left|\mathit{Pr}\left[{\mathit{GM}}_3\right]-\mathit{Pr}\left[{\mathit{GM}}_2\right]\right|\le \frac{q_s}{2^l}$$

(38)

${\mathit{GM}}_4$: In this game, the key SK can be guessed without querying for the corresponding random oracle. The game is no different from the above games, except that A performs a hash query on the random oracle on the $\left({\mathit{ID}}_i\left|\right|{\mathit{CID}}_i\left|\right|E_i\left|\right|E_i^{\mathit{new}}\left|\right|C_2\left|\right|K\right)$, where $K=\mathit{CMDH}(C_1,C_5)=T_{\mathit{uv}}\left(x\right)$. Therefore,

$$\left|\mathit{Pr}\left[{\mathit{GM}}_4\right]-\mathit{Pr}\left[{\mathit{GM}}_3\right]\right|\le q_h{\mathit{Adv}}_{\mathit{CMCDH}}\left(A\right)+\frac{q_s}{2^l}$$

(39)

where A queries the random tuple $〈T_{\theta }\left(x\right),T_{\mathsf{\phi }}\left(x\right)〉$ from the $h$ oracle to calculate $\mathit{CMCDH}\left(T_{\theta }\right(x),T_{\mathsf{\phi }}(x\left)\right)$, where $\theta , \mathsf{\phi }\in Z_p^{\ast }$.

${\mathit{GM}}_5$: A executes the $\mathit{Test}$ query in this game, which is different from the above game. If A performs a hash query on $\left({\mathit{ID}}_i\left|\right|{\mathit{CID}}_i\left|\right|E_i\left|\right|E_i^{\mathit{new}}\left|\right|C_2\left|\right|T_{\mathit{uv}}\right(x\left)\right)$, the probability that A can obtain SK does not exceed $q_h^2/2^{l+1}$. If A executes the $\mathit{Corrupt}$ query, it can be inferred from the definition of freshness that the probability of A obtaining $K$ does not exceed ${\left(q_s+q_e\right)}^2/2p$. Therefore,

$$\left|\mathit{Pr}\left[{\mathit{GM}}_5\right]-\mathit{Pr}\left[{\mathit{GM}}_4\right]\right|\le \frac{q_h^2}{2^{l+1}}+\frac{{\left(q_s+q_e\right)}^2}{2p}$$

(40)

Due to A’s inability to distinguish between a real and random session key without using the correct input to perform $h$ queries,

$$\mathit{Pr}\left[{\mathit{GM}}_5\right]=1/2$$

(41)

According to the game ${\mathit{GM}}_0–{\mathit{GM}}_5$ and Lemma 1, Theorem 1 can be verified. □

The above proof process means that the probability of attacker A winning in the game is negligible, so the proposed scheme is safe under the random oracle model. This protocol can guarantee the security of the session key in the process of authenticated key exchange when communicating between entities in AMI.

5.3. Informal Security Analysis

5.3.1. Mutual Authentication

In the proposed scheme, ${\mathit{DC}}_j$ authenticates ${\mathit{SM}}_i$ by confirming whether the equation $M_4^{\ast }=M_4$ is established, and ${\mathit{SM}}_i$ authenticates ${\mathit{DC}}_j$ by confirming whether the equation $M_8^{\ast }=M_8$ is established. After mutual authentication, SM and DC negotiate the session key $\mathit{SK}$ to build a secure channel.

5.3.2. Anonymity and Un-Traceability

In the proposed scheme, if the adversary obtains $\{{\mathit{PID}}_i,M_1,M_3,M_4\}$ and $\{M_5,M_7,M_8\}$ in the interaction process of ${\mathit{DC}}_j$ and ${\mathit{SM}}_i$ by means of eavesdropping, the ${\mathit{PID}}_i$ is generated by a one-way hash function and updated periodically. $M_2$ is generated by random numbers, $M_3=\left({\mathit{ID}}_i\left|\right|E_i\right)⨁H_0\left(M_2\right)$ is constantly changing with $M_2$, and $M_4=H\left({\mathit{ID}}_i\left|\right|{\mathit{PID}}_i\left|\right|E_i\left|\right|M_2\left|\right|M_3\right)$ is also variable. The adversary cannot derive or track the real ${\mathit{ID}}_i$, so the scheme provides anonymity and non-traceability for users.

5.3.3. Forward Secrecy

Even if all secret values of smart meters and data concentrators are obtained by the adversary, all previous session keys must remain secure. If $\{{\mathit{PID}}_i,M_1,M_3,M_4\}$ and $\{M_5,M_7,M_8\}$ are obtained by means of eavesdropping, the adversary $A$ can calculate $M_2=T_s\left(M_1\right)$ and $\left({\mathit{ID}}_i^{\prime }\left|\right|E_i^{\prime }\right)=C_3⨁H_0\left(M_2\right)$, but $A$ must obtain $M_6=T_u\left(M_5\right)=T_v\left(M_1\right)$ to calculate the previous key $\mathit{SK}=H\left({\mathit{ID}}_i\left|\right|{\mathit{PID}}_i\left|\right|E_i\left|\right|E_i^{\mathit{new}}\left|\right|M_2\left|\right|M_6\right)$. Due to the computational difficulties of CMDL and CMDH problems, it is not feasible for $A$ to obtain random numbers $u$ and $v$ from $M_1$ and $M_5$. So, $A$ cannot successfully calculate $\mathit{SK}$, and the scheme achieves forward secrecy.

5.3.4. SM Impersonation Attack Resistance

Adversary $A$ needs to obtain the value of $E_i$ to forge message $M_4$ in order to impersonate a legitimate smart meter. $E_i$ can be calculated by two means: (1) the legitimate smart meter can compute it; and (2) the data concentrator knows $\{r_i,s\}$ and can calculate it. It is computationally impossible for $A$ to compute these parameters, so $A$ does not have the ability to impersonate smart meters within the scope of $\mathit{DC}$. So, the scheme can effectively resist smart meter impersonation attack.

5.3.5. DC Impersonation Attack Resistance

In order to impersonate a legitimate data concentrator, adversary $A$ must compute a valid $\{M_5,M_7,M_8\}$.$M_7=({\mathit{PID}}_i^{\mathit{new}}\left|\right|E_i^{\mathit{new}})⨁H_0(M_6\left|\right|E_i)$ and $M_8=H\left({\mathit{ID}}_i\left|\right|{\mathit{PID}}_i\left|\right|E_i\left|\right|M_2\left|\right|M_5\left|\right|{\mathit{SK}}_{\mathit{ji}}\right)$ are calculated by $\{{\mathit{ID}}_i,{\mathit{PID}}_i,{\mathit{PID}}_i^{\mathit{new}},E_i,E_i^{\mathit{new}}\}$ and computed by the hash function. Therefore, $A$ cannot directly obtain these parameters and cannot guess the values successfully in polynomial time. In order to calculate the above parameters, $A$ must obtain $\{{\mathit{ID}}_i,s,r_i\}$, but it is impossible to obtain the private values $\{s,r_i\}$ in polynomial time, and because of the anonymity and un-traceability of the scheme, $A$ cannot obtain ${\mathit{ID}}_i$. Therefore, $A$ cannot calculate a valid response message, so the scheme can effectively resist data concentrator impersonation attack.

5.3.6. Replay Attack Resistance

In the proposed scheme, messages $\{{\mathit{PID}}_i,M_1,M_3,M_4,t_1\}$ and $\{M_5,M_7,M_8,t_2\}$ transmitted between entities all contain timestamps. In addition, before each interaction, the entity checks the timeliness of the received message, and only messages that arrive within the specified time will be received. Therefore, the scheme can effectively resist replay attack.

5.3.7. Man-in-the-Middle Attack Resistance

Suppose that $A$ intercepts the request message $\{{\mathit{PID}}_i,M_1,M_3,M_4\}$ and response message $\{M_5,M_7,M_8\}$; in order for the attack to succeed, the new information flow $\{{\mathit{PID}}_i^{\ast },M_1^{\ast },M_3^{\ast },M_4^{\ast }\}$ and $\{M_5^{\ast },M_7^{\ast },M_8^{\ast }\}$ need to be forged by A, or the previous information flows need to be replayed. As mentioned above, the scheme can resist replay attack and impersonation attack, so $A$ cannot authenticate through both smart meters and data concentrators simultaneously. Therefore, the scheme can resist man-in-the-middle attack.

5.3.8. ESL (Ephemeral Secret Leakage) Attack Resistance

Assuming that the secret value $u, v, \mathit{or}{ e}_i$ is obtained by the adversary $A$, $A$ can calculate $M_2$ and $M_6$. In order to obtain $\mathit{SK}$, $A$ must be able to calculate $\{E_i,E_i^{\mathit{new}}\}$ and the real ${\mathit{ID}}_i$. However, $A$ cannot calculate the correct $\{E_i,E_i^{\mathit{new}}\}$ that needs to be calculated using the long-term secret value $s$ in polynomial time. Therefore, the scheme can resist the ESL attack.

5.3.9. De-Synchronization Attack Resistance

Even if the first message flow is intercepted by the adversary during the key agreement phase, DC does not need to update the parameters in the database, which will not affect the consistency of the next communication. Even if the second message flow is intercepted by the adversary, it still cannot affect the consistency of communication between SM and DC. Only when $M_8^{\ast }=M_8$ is established will the communication parties update the data. Therefore, the scheme can resist de-synchronization attack.

5.3.10. DDoS (Distributed Denial of Service) Attack Resistance

DDoS attacks include replay, false data injection, de-synchronization, flooding, jamming, etc. The above security analysis shows that this scheme can achieve mutual authentication and session key security. Therefore, the proposed scheme can resist false message injection attacks, which are mainly against unauthenticated and unencrypted communication processes.

The above analysis shows that the proposed scheme can also resist the desynchronization attack. At each step, the entity verifies the validity of the received message, which ensures the consistency of the messages between the two sides of the communication. Consistency verification can also resist the jamming attack.

After receiving the authentication request, the data concentrator first checks the timeliness of the message, and directly discards the messages that do not meet the timeliness requirement, thus resisting the DoS attack by replaying the old message. Next, the data concentrator authenticates the smart meter. The verification of the authentication request only involves the Chebyshev polynomial and the hash operation with low computational overheads, which requires very few computing resources, and discards the packets that fail to verify and terminate the session at the same time, which can alleviate the impact of the flooding attack. A further defense scheme against DDoS attack is given in Section 7. Therefore, the proposed scheme can resist or mitigate the above DDoS attacks.

5.3.11. Key-Compromise Impersonation Resistance

Even if the secret value stored in the SM is obtained by the adversary, since the session key of different smart meters is different, it will only cause the session key leakage between ${\mathit{SM}}_i$ and ${\mathit{DC}}_j$ in this period, and will not cause the session key leakage between ${\mathit{SM}}_i^{\prime }$ and ${\mathit{DC}}_j^{\prime }$. So, the scheme can resist key-compromise impersonation attack.

We compared the proposed scheme with relevant representative schemes (i.e., Hu et al. [2], Abbasinezhad-mood et al. [13], Chaudhry et al. [17], Baghestani et al. [18], and Park et al. [20]) in terms of security, and the comparison results can be seen in

Table 1. Comparison of security features.

Security Features 1	Ref. [2]	Ref. [13]	Ref. [17]	Ref. [18]	Ref. [20]	Ours
S1
S2
S3
S4
S5
S6
S7
S8
S9
S10

¹ S1: Mutual authentication; S2: anonymity and un-traceability; S3: forward secrecy; S4: impersonation attack resistance; S5: replay attack resistance; S6: man-in-the-middle attack resistance; S7: ESL attack resistance; S8: de-synchronization attack resistance; S9: DDoS attack resistance; S10: key-compromise impersonation resistance.

. The symbol “” represents that the scheme has this security feature, and “” indicates that the scheme does not meet or does not mention this security feature. From Table 1, it can be seen that the proposed scheme provides higher security and is more suitable for AMI scenarios.

6. Performance Evaluation

In this section, the performance of the proposed scheme is analyzed in terms of computation cost, communication cost and energy consumption, where the cost mainly depends on the authentication and key agreement phases. This section also compares the proposed scheme with related representative schemes (i.e., Hu et al. [2], Abbasinezhad-mood et al. [13], Chaudhry et al. [17], Baghestani et al. [18], and Park et al. [20]) to evaluate the performance of our scheme.

6.1. Computation Cost

In order to measure the computational overheads of the proposed scheme in the key agreement process, according to [25,26], we conducted experiments on different encryption primitives using the big data computing library to measure their execution time. Our experimental environment was set as follows: (1) hardware environment: Inter Core I5-12500H processor (Intel, Santa Clara, America) with clock frequency of 2.50 GHz, 16 GB RAM Memory; (2) software configuration: Windows 10 operating system, Visual C++ 2017 Software, MIRACL (Multiprecision Integer and Rational Arithmetic C/C++ Library) big data library computing. We took the average value of one hundred operations as the execution time of the related operations to reduce the error. According to the migration experiment in [29], the time cost required for smart meters equipped with microprocessor R5F212B8SDFP (Renesas, Tokyo, Japan) to perform corresponding operations can be obtained by migration experiments. The time cost corresponding to different operations is shown in

Table 2. Execution time.

Operation	Description	DC Execution Time (ms)	SM Execution Time (ms)
$T_m$	Time of elliptic curve point multiplication	≈ $2.234$	≈ $53.616$
$T_a$	Time of elliptic curve point addition	≈ $0.245$	≈ $5.88$
$T_C$	Time of Chebyshev chaotic map	≈ $0.642$	≈ $15.408$
$T_H$	Time of a hash function	≈ $0.023$	≈ $0.552$
$T_s$	Time of symmetric encryption/decryption	≈ $0.068$	≈ $1.632$

, and

Table 3. Comparison of computation cost and communication cost.

Scheme	SM Execution Time (ms)	DC Execution Time (ms)	Communication Cost (Bits)
Ref. [13]	$4T_m+2T_a+4T_H$	$4{\mathit{nT}}_m+2{\mathit{nT}}_a+4{\mathit{nT}}_H$	$896+896=1792$
Ref. [2]	$3T_m+T_a+4T_H$	$3{\mathit{nT}}_m+{\mathit{nT}}_a+4n{T}_H$	$736+736=1472$
Ref. [17]	$3T_m+2T_s+4T_H$	$4n{T}_m+2n{T}_s+6n{T}_H$	$768+768=1536$
Ref. [20]	$2T_m+7T_H$	$2n{T}_m+4n{T}_H$	$704+672=1376$
Ref. [18]	$2T_m+5T_H$	$2n{T}_m+11n{T}_H$	$864+832=1696$
Ours	$3T_C+10T_H$	$3n{T}_C+8n{T}_H$	$560+496=1056$

lists the computational costs required for the proposed scheme compared to other representative schemes. The computation costs for XOR and string concatenation operations can be ignored compared to the operations in Table 2, so they were omitted.

Figure 4 shows the computation cost of the smart meter in different schemes, indicating that the computation cost of our scheme on the smart meter side is the lowest, which is mainly due to the time-consuming bilinear pairing and elliptic curve point multiplication operation replaced by the Chebyshev chaotic map. The overhead of the smart meter side was reduced by 77.35%, 69.37%, 68.89%, 53.42%, and 52.96%, respectively.

Figure 5 shows the time required for this scheme and the comparison scheme to complete the key agreement when the number of smart meters is 100, 200, 300, 400 and 500, respectively. The time required of our scheme is much smaller than that of the comparison scheme, and the overhead is only about 1.1 s when the number of smart meters reaches 500, which accounts for only 22% of the message transmission time threshold (5 s) in AMI. Our scheme is better than the existing lightweight schemes. With the increase in the number of smart meters and the limited computing resources of the AMI network infrastructure, our scheme has the slowest growth rate in time overhead. It means that in the same hardware and software environment, this scheme allows more smart meters to access. Compared with other schemes, our scheme has better scalability.

6.2. Communication Cost

In our scheme, the size of a smart meter identity ID, a Chebyshev polynomial, a random number, a hash output, a timestamp, and a ciphertext in the symmetric encryption and decryption algorithm is assumed to be 64, 160, 64, 160, 16, 128 bits, respectively. In the process of key agreement, only two information interactions are carried out. Firstly, the smart meter sends $\{{\mathit{PID}}_i,M_1,M_3,M_4,t_1\}$ to the data concentrator, with the communication cost of (64 + 160 + 160 + 160 + 16) = 560 bits; secondly, the data concentrator sends $\{M_5,M_7,M_8,t_2\}$ to the smart meter, with the communication cost of (160 + 160 + 160 + 16) = 496 bits. The total communication cost in the key agreement process of the proposed scheme is 1056 bits.

The communication costs between the scheme and other representative schemes are shown in Table 3. Figure 6 shows the comparison of communication costs among different schemes, indicating that the proposed scheme has the lowest communication cost.

6.3. Energy Consumption

Since the smart meter resources in the AMI are very limited and usually rely on limited power supply to operate, energy consumption is also the key to performance analysis. Here, we analyze the energy consumption of smart meters in sending/receiving messages. According to [15], the energy consumed by the smart meter to send and receive 1 bit of data is $0.72 \mathsf{\mu }\mathrm{J}$ and $0.81 \mathsf{\mu }\mathrm{J}$, respectively, so the energy consumption of the proposed scheme is about $804.96 \mathsf{\mu }\mathrm{J}$. Through the above analysis of computing and communication overheads, it can be seen that this scheme also has advantages in energy consumption. Combined with Table 3, it is easy to calculate the corresponding energy consumption. Figure 7 shows the comparison of the proposed scheme with other related schemes in terms of energy consumption.

In summary, the proposed scheme achieves communication security of AMI with the minimum computation, communication cost and energy consumption, greatly improving performance and reducing the burden on smart meters. The improvement of performance means that the scheme can accommodate more access to smart meters, thereby reducing the cost of software and hardware iteration, which is of great significance in practical applications.

7. Discussion

In this article, our scheme relies on the reliability of DC, which may lead to the single-point failure problem. With the development of blockchain technology, the cost of hardware and software is gradually reduced, and the access volume of smart meters in AMI system is also increasing year by year. The average technical cost per user is also getting lower and lower. We are designing new solutions to solve the potential single-point failure problem by introducing decentralized blockchain into AMI.

In the traditional centralized structure, the resources of a single device are limited and the ability to resist attacks is weak, which may affect the entire network in the event of failure or in the face of new security threats. The introduction of blockchain can not only solve the problem of single point of failure, but also enhance the flexibility and anti-attack ability of the scheme, such as enhancing the system’s ability to resist flooding attacks. With the increase in the number of blockchain nodes, the total computing power is also growing, and the entire AMI network will become more and more difficult to be submerged or even paralyzed. In addition, the dynamic addition and revocation of devices are also allowed.

In our scheme, different entities of AMIs adopt the same cryptosystem. However, in the actual AMI system, due to the complexity of the communication network and the differences in resource capacity, different entities may adopt different cryptosystems. This provides ideas for our further research. In future research, we will consider the design and application of heterogeneous cryptosystems in the AMI to enhance the applicability of the AMI with different configurations.

In addition, we will further conduct testing on larger AMI networks to better evaluate the effectiveness of the proposed scheme, which will help us to identify actual security challenges and compatibility issues and make corresponding adjustments.

8. Conclusions

The AMI is an important part of the smart grid. In this article, a lightweight key agreement scheme based on chaotic map is designed for the AMI. The proposed scheme realizes mutual authentication, key agreement and multicast key generation between entities, so that secure data transmission can be carried out between entities. Security analysis shows that the proposed scheme can meet the security requirements of the AMI and can resist commonly known attacks. The performance analysis result shows that compared with the existing schemes, our scheme requires the lowest computation and communication cost. Designing a secure and efficient key agreement protocol has always been the focus of the field of information security in the smart grid environment. The proposed scheme fully considers the message transmission mode of the AMI system and the limitations of resource constraints, and minimizes the overhead caused by security measures. Compared with the existing schemes, the proposed scheme is more suitable for the AMI scenario.