Dynamic Flow and Heat Transfer Characteristics of Uncracked Hydrocarbon Fuel under Super-Critical Pressure in the Cooling Channel of a Regeneratively Cooled Scramjet
Abstract
1. Introduction
2. Numerical Model and Calculation Scheme
2.1. Governing Equation
2.2. Thermo-Physical Property Calculation Model
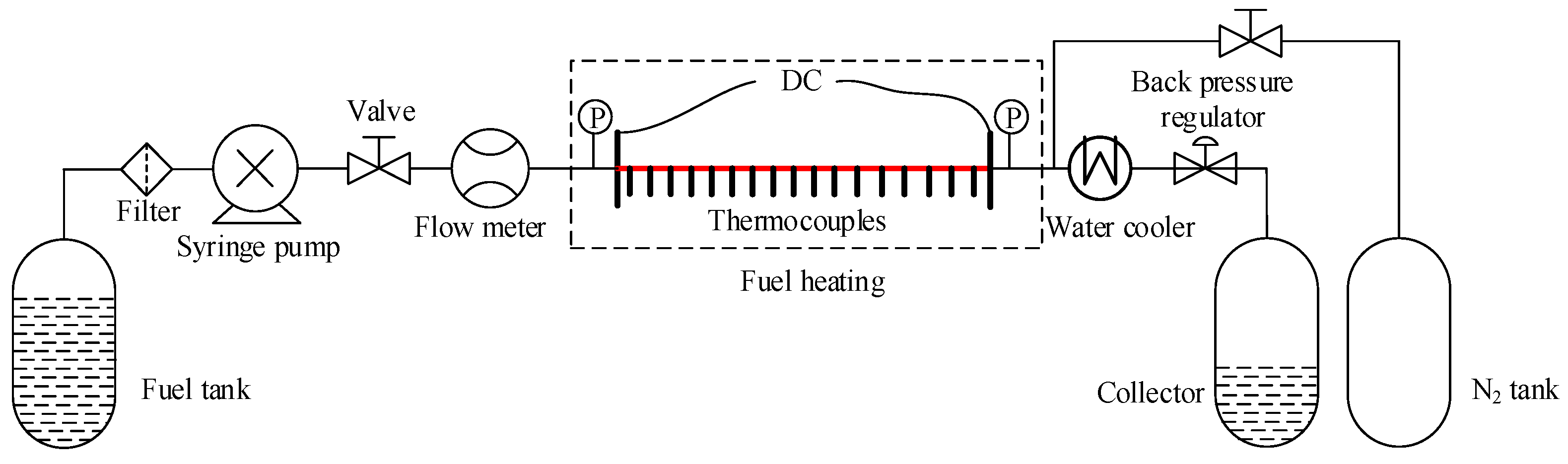
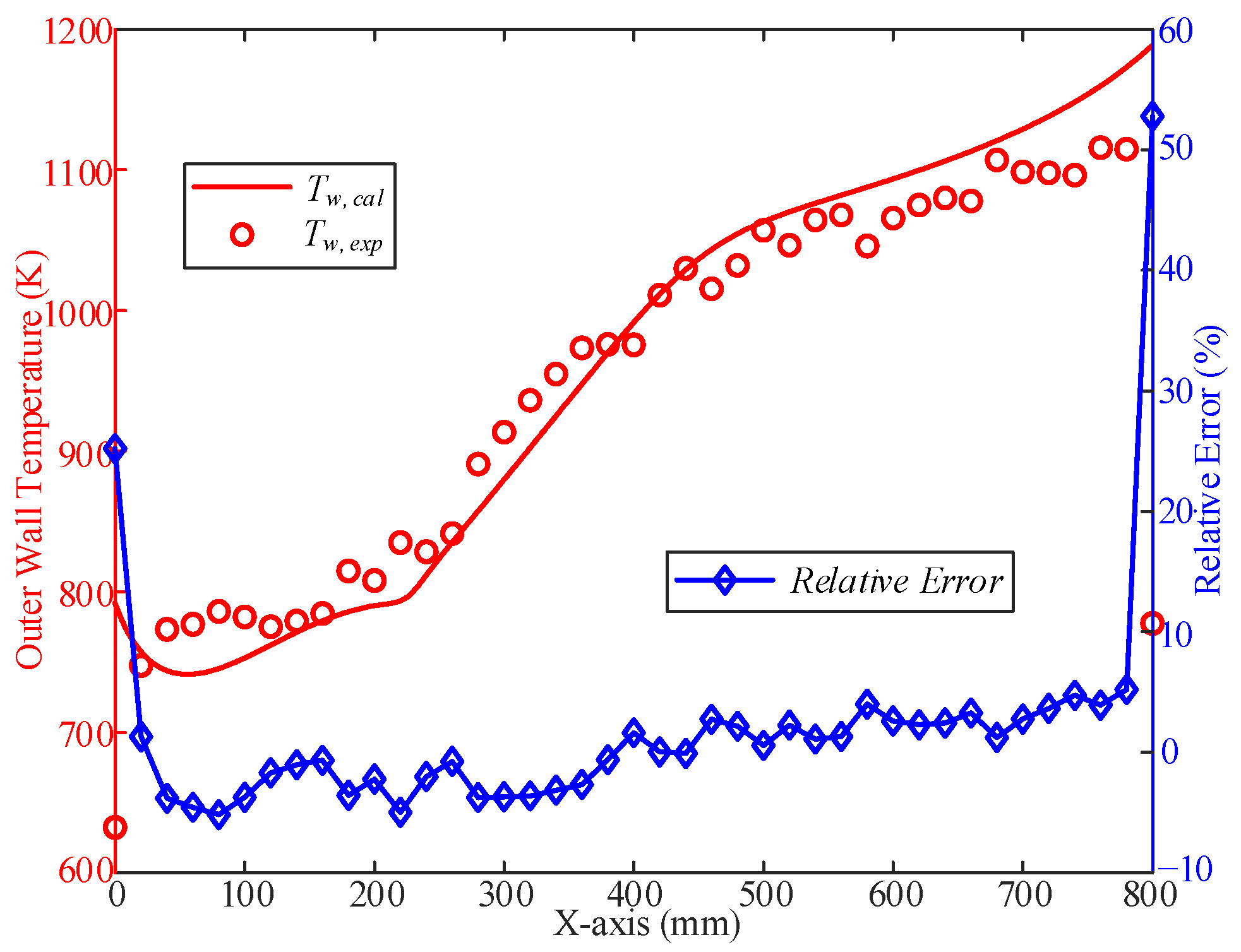
2.3. Model Validation
3. Results and Discussion
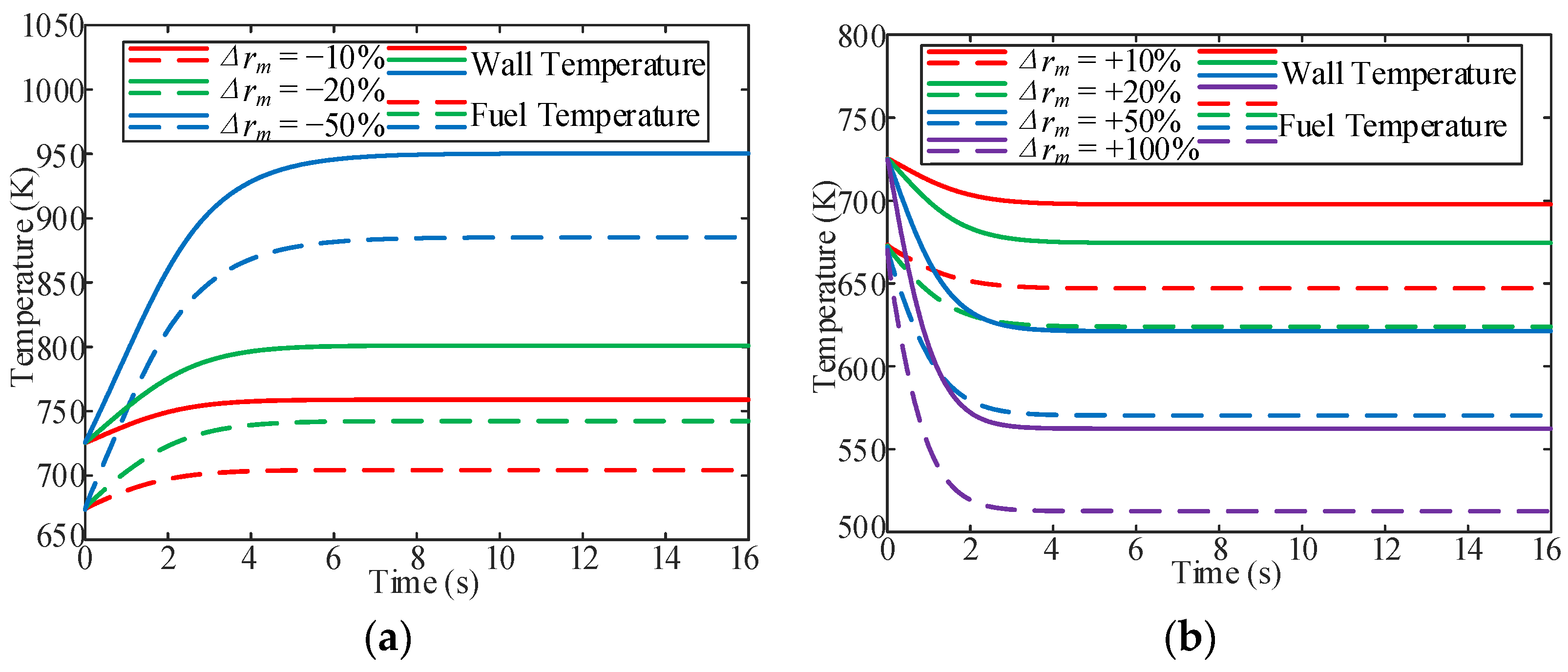
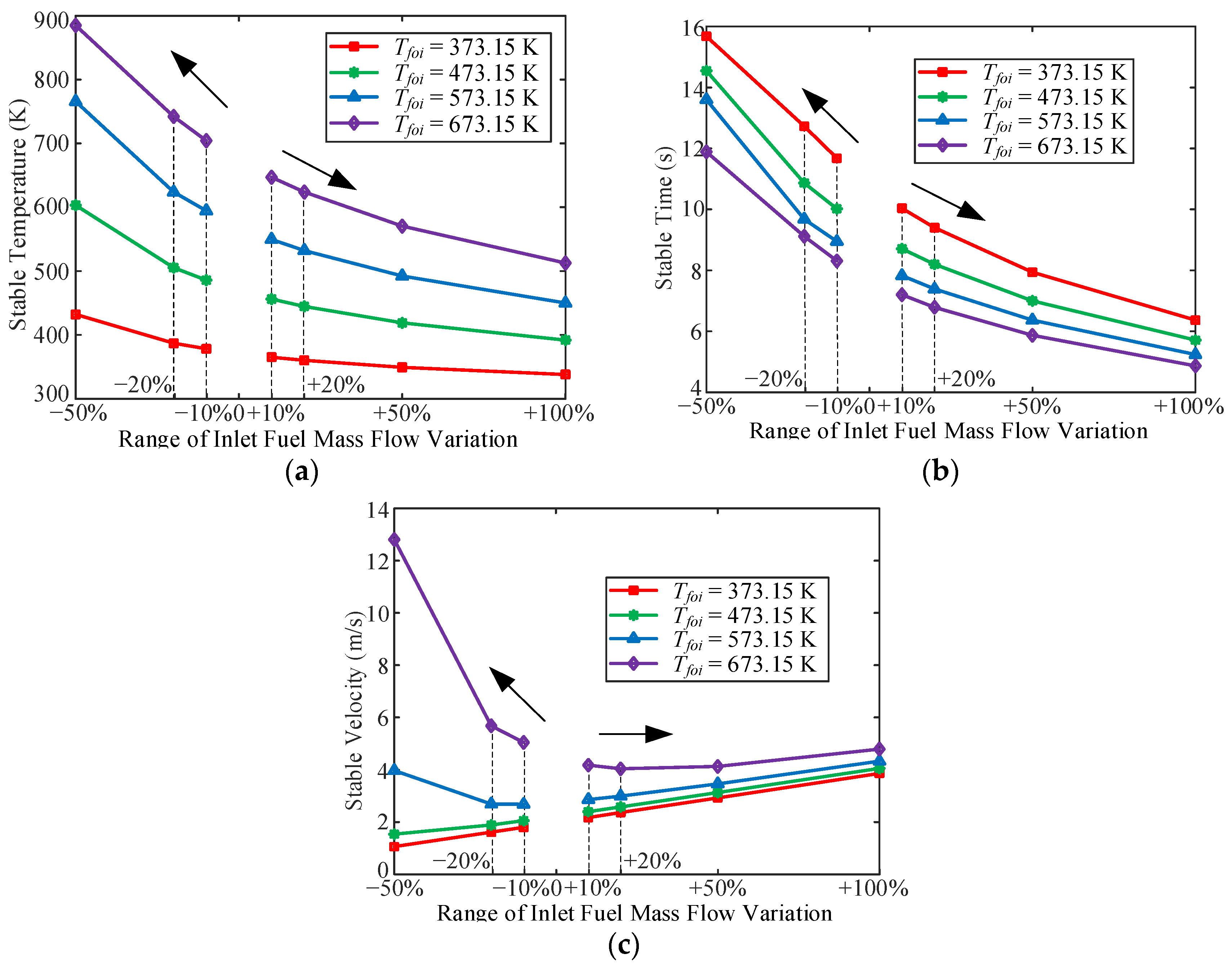
3.1. Influence of Inlet Fuel Mass Flow
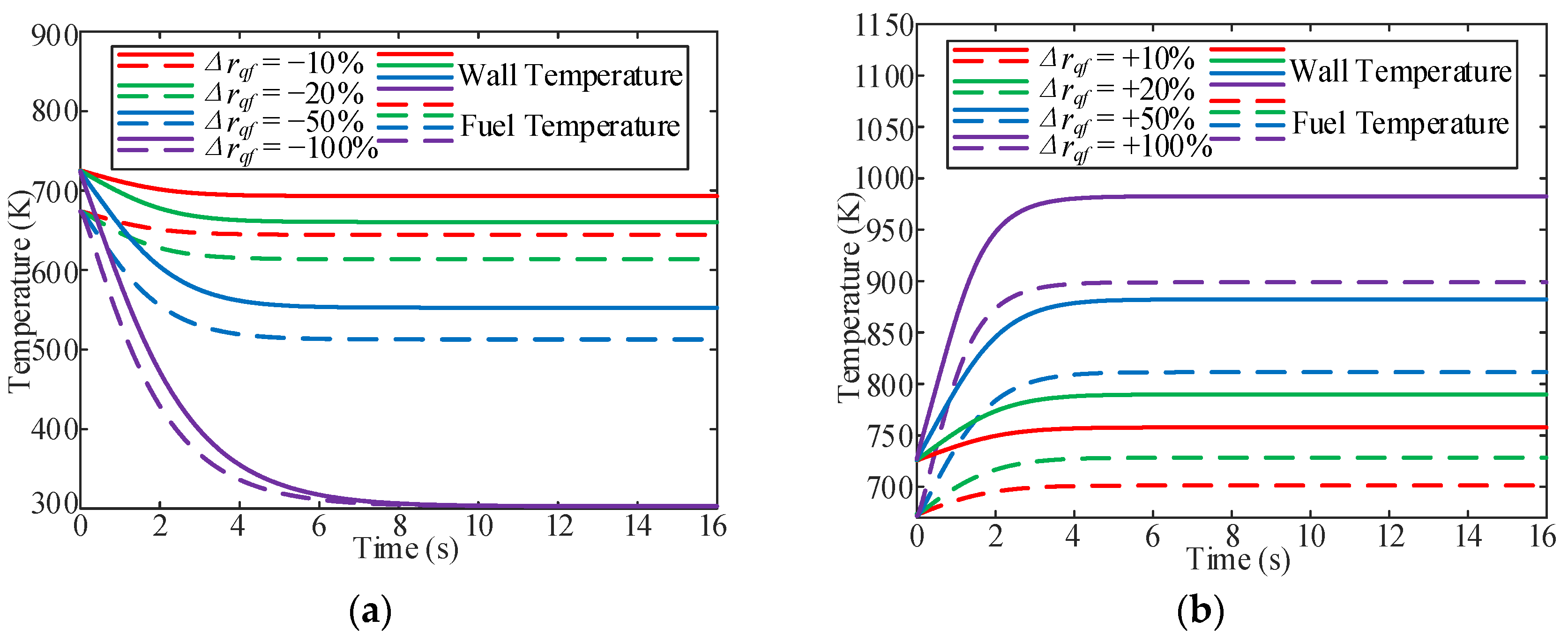
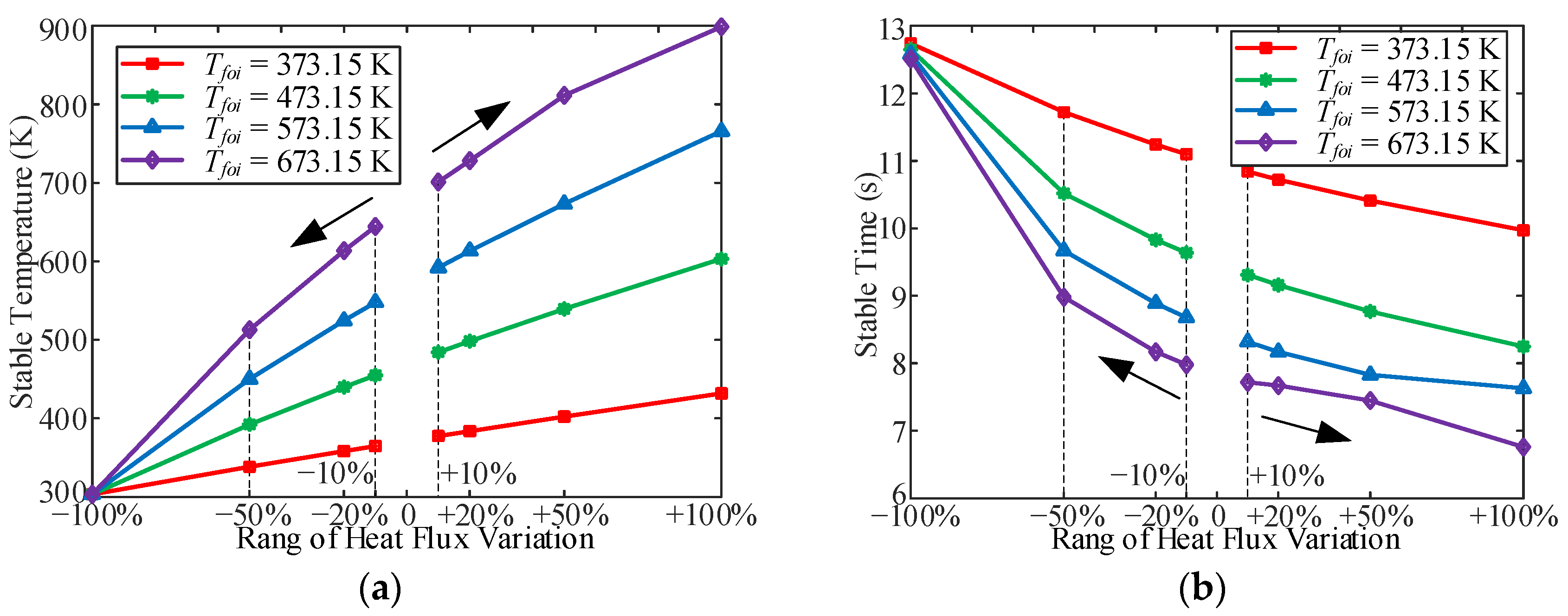
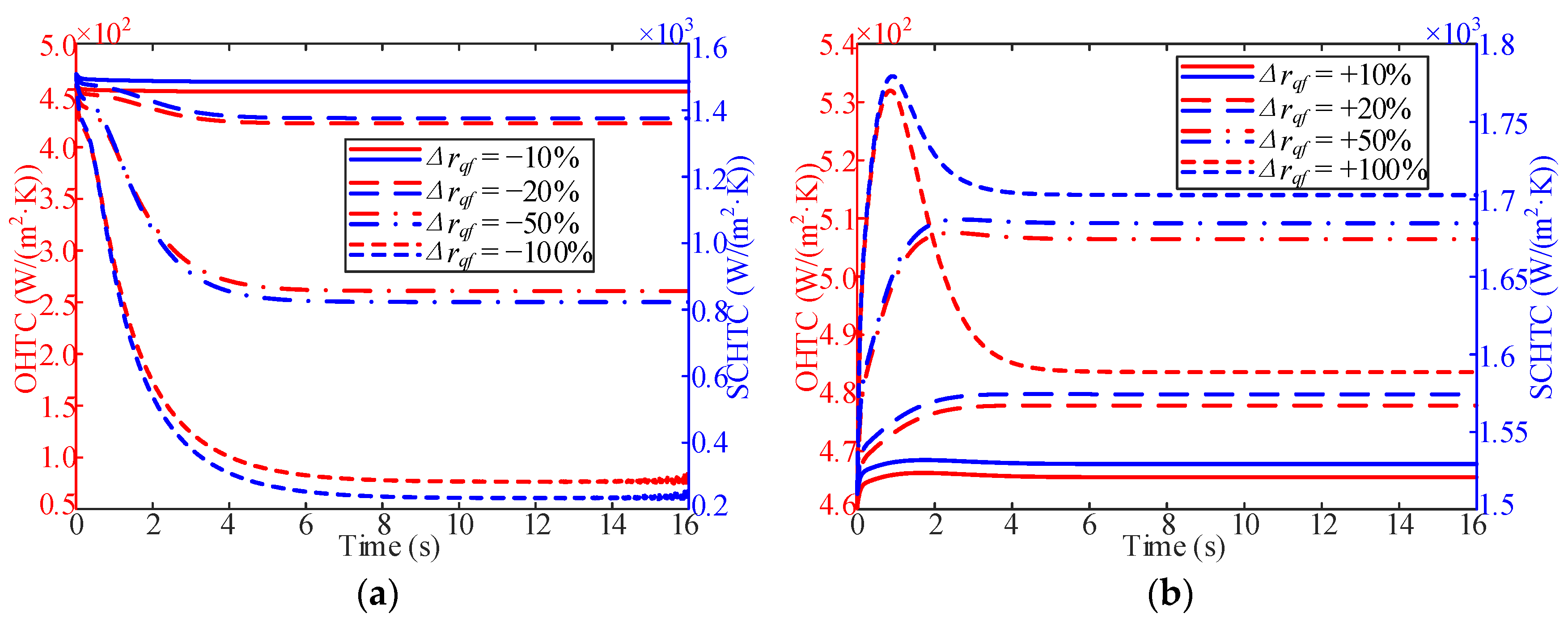
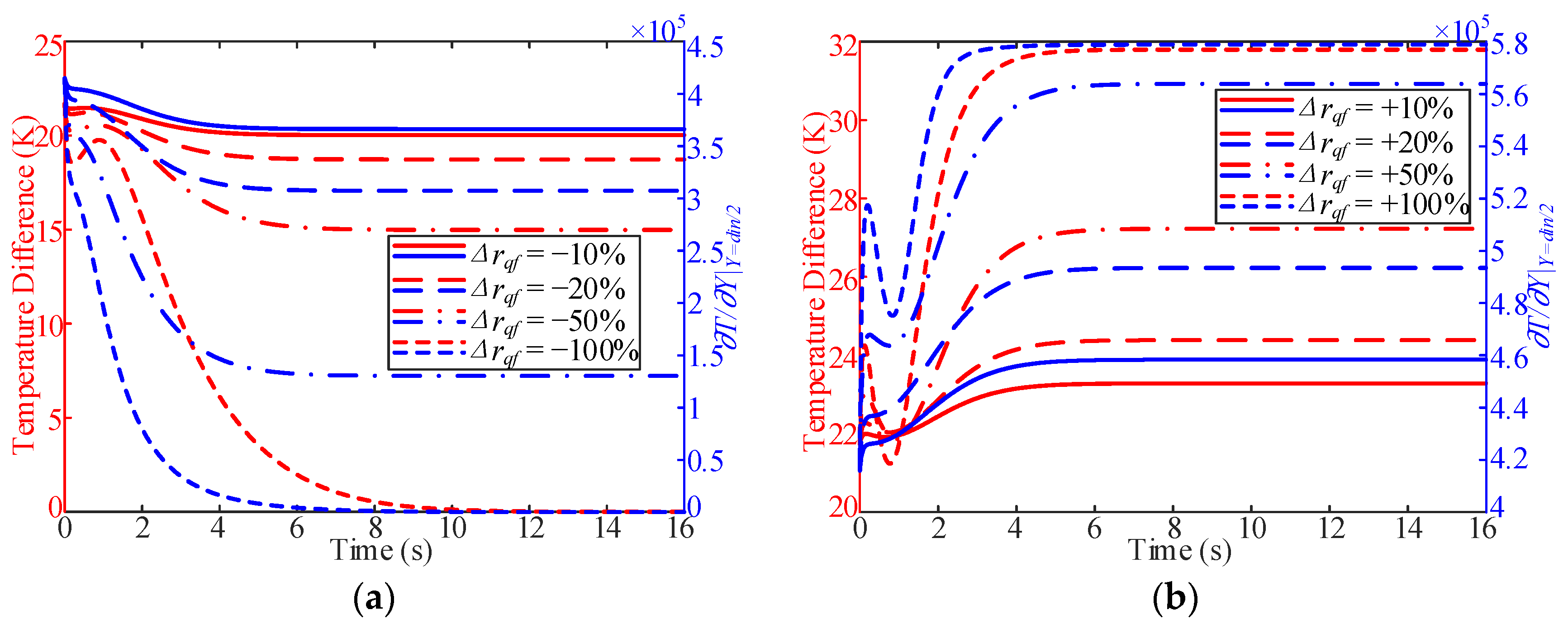
3.2. Influence of Heat Flux
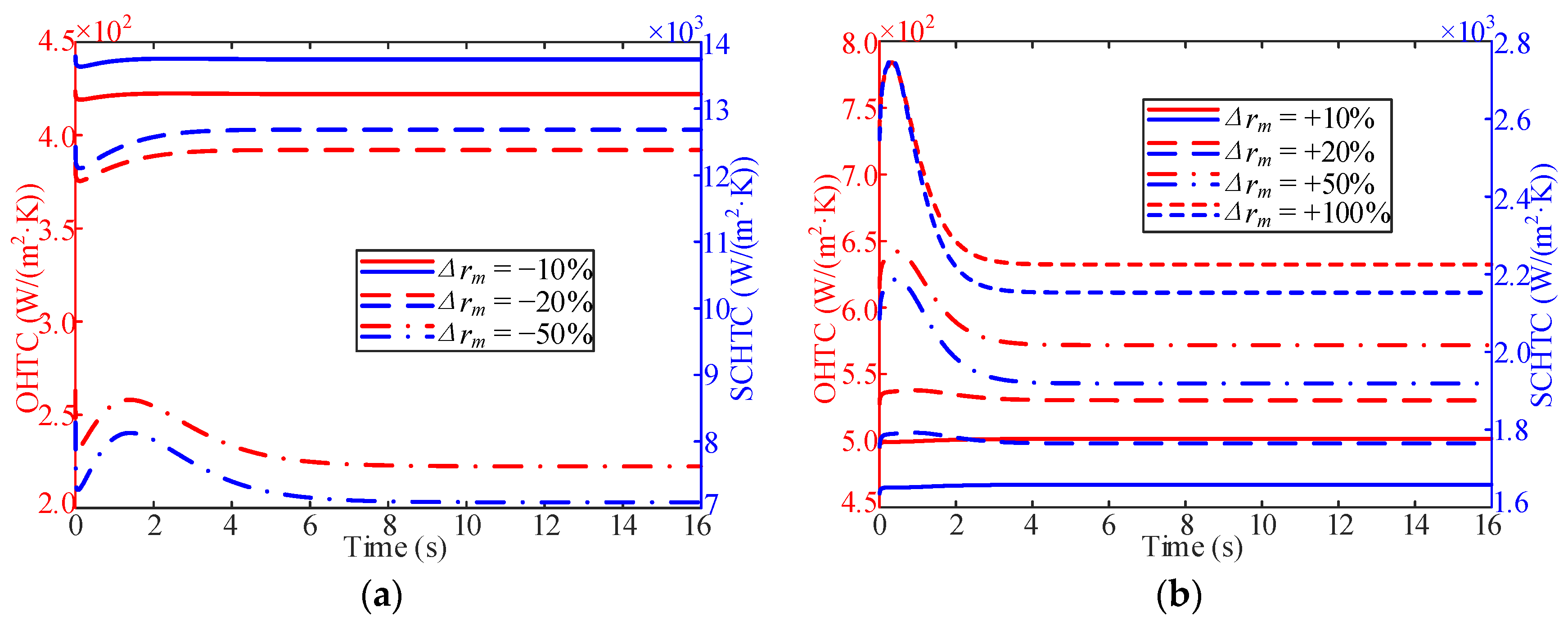
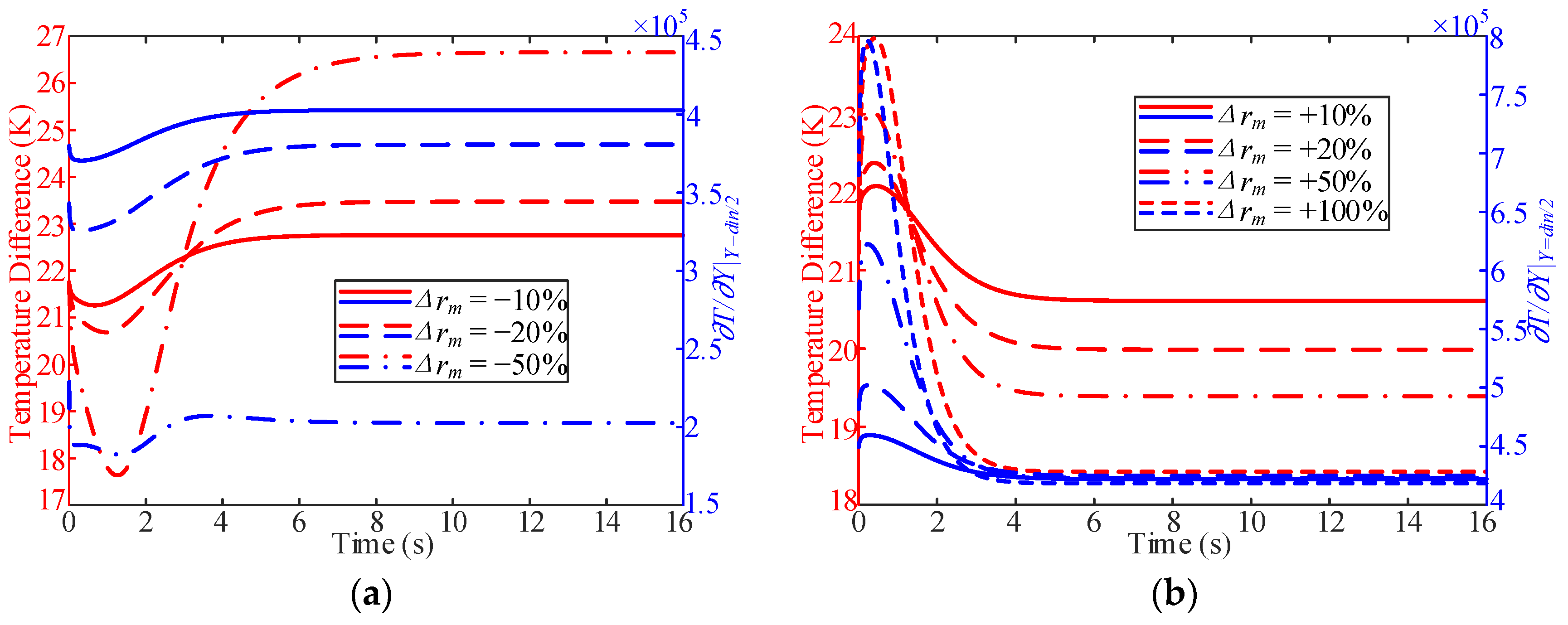
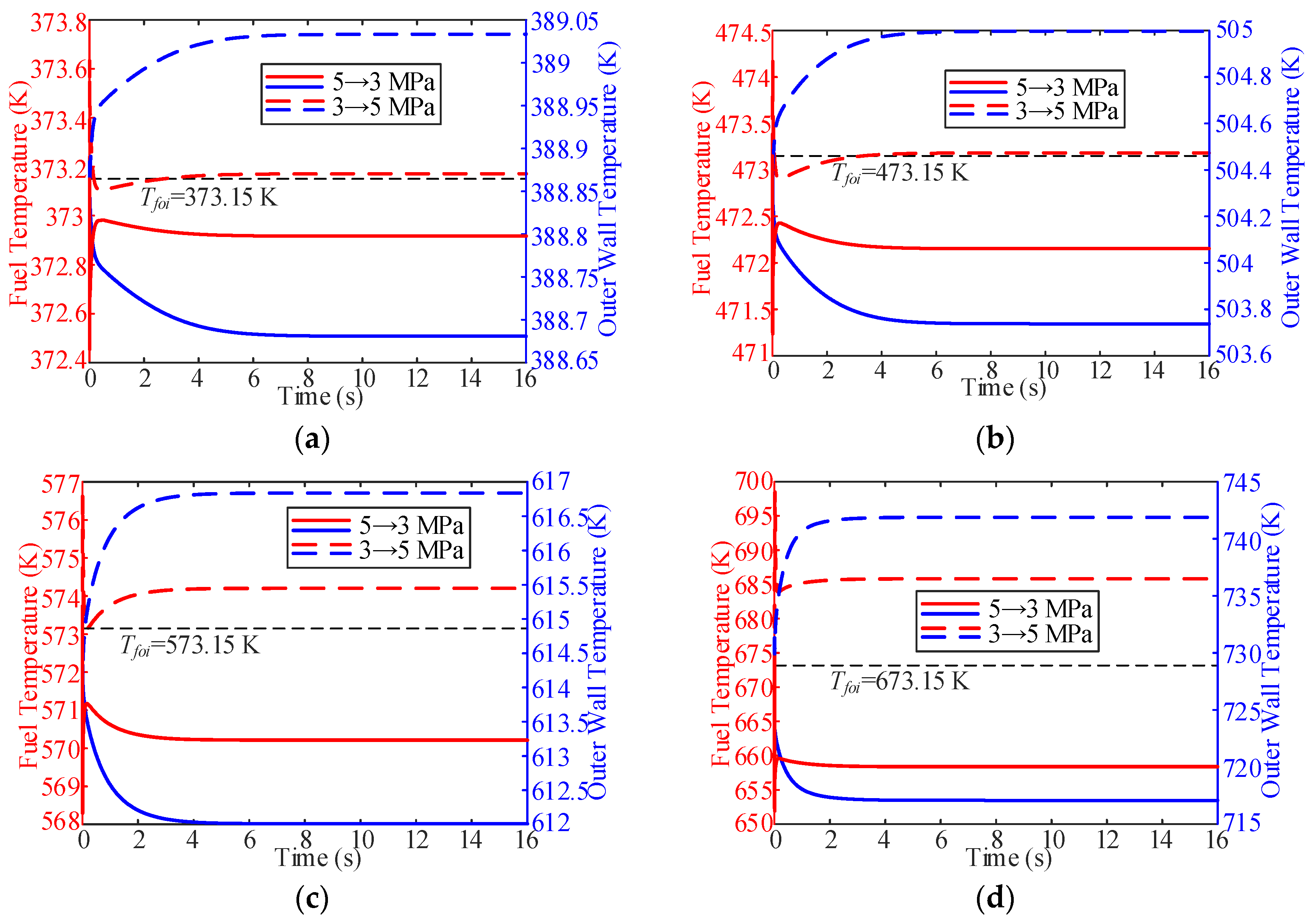
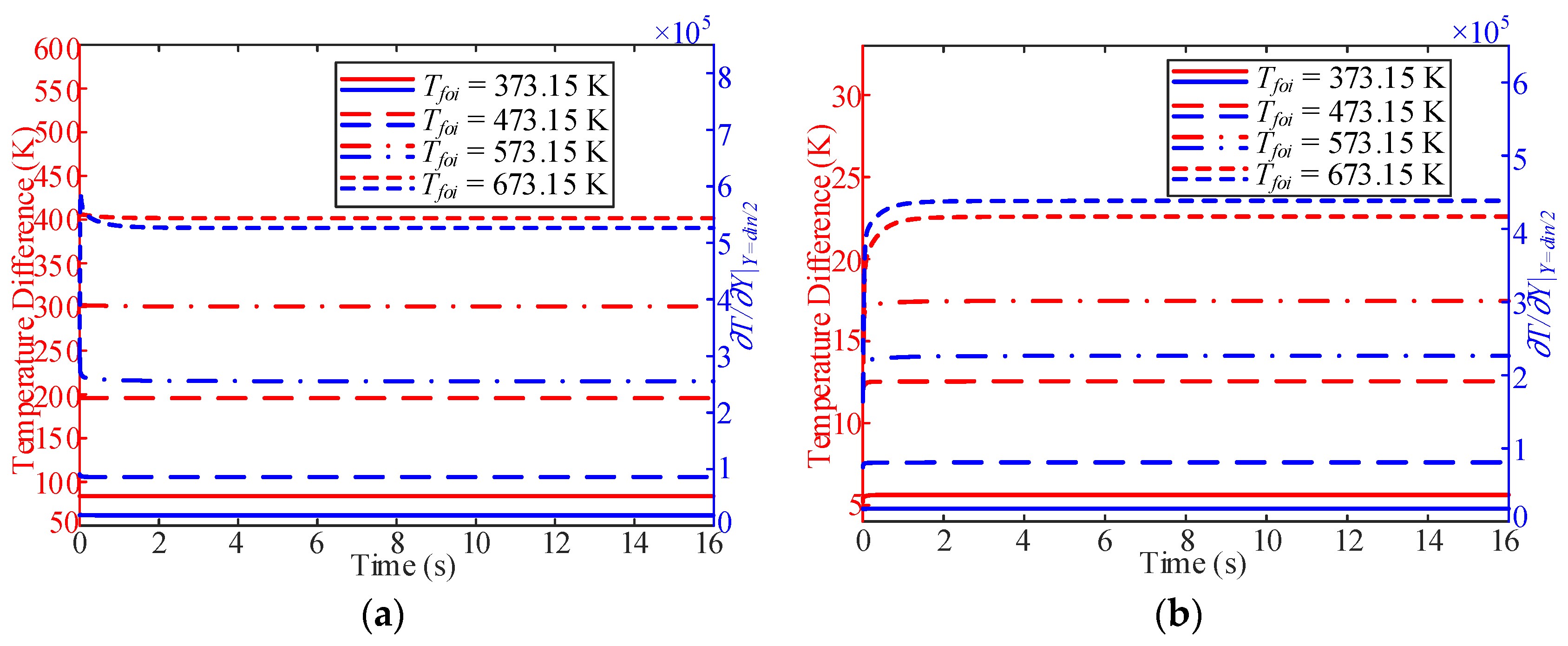
3.3. Influence of Working Pressure
4. Conclusions
- (1)
- Three dynamic working conditions for the cooling channel were proposed, considering the real working process of a scramjet. The modified overall heat transfer coefficient was adopted to characterize the dynamic flow and heat transfer process as precisely as possible, which helps in analyzing the heat transfer enhancement under dynamic working conditions.
- (2)
- In the variable inlet mass flow process, the stable time for the fuel temperature increased with a decrease in the inlet mass flow. In addition, near the quasi-critical temperature zone, the outlet velocity increased with a decrease in the inlet mass flow. It can be observed that there is an overshoot of the OHTC at the beginning of the fuel mass flow increasing the working conditions, which implies that the increase in fuel mass flow can enhance heat transfer in the cooling channel.
- (3)
- In the variable heat flux process, the stable time for the fuel temperature increased with a decrease in the heat flux. In addition, without heating, the stable time required for the outlet fuel temperature to decrease to room temperature at different Tfoi values is almost the same (approximately 12.5 s). There is also an overshoot of the OHTC at the beginning of the heat-flux-increasing working conditions because of the thermal acceleration of the fuel bought by the heat flux in the cooling channel.
- (4)
- In the process of variable working pressure, the fuel temperature was more sensitive to changes in the working pressure than to the wall temperature. In addition, with a change in pressure, the trend of the overall heat transfer coefficient changed slightly and only fluctuated at the initial stage of the response.
- (5)
- The dynamic flow and heat transfer processes of hydrocarbon fuels in cooling channels were also studied. The heat transfer characteristics were discussed using a modified heat transfer coefficient calculation method. Based on this, a suitable heat transfer correlation for the dynamic flow and heat transfer process was determined, which may provide a better understanding of the dynamic heat transfer process.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| A | pre-exponential factor, s−1 |
| a | measurement error coefficient |
| c | specific heat capacity, J/(kg·K) |
| C | diffusion term |
| d | diameter, mm |
| e | specific internal energy, J/kg |
| E | activation energy, kJ/mol |
| h | surface convective heat transfer coefficient, W/(m2·K) |
| I | turbulent intensity, % |
| i | number of fluid radial stratification |
| k | turbulent kinetic energy, m2/s2 overall heat coefficient, W/(m2·K) |
| l | micro-channel length, m |
| m | inlet fuel mass flow, g/s |
| Mw | molar mass, kg/mol |
| n | number of solid domains |
| Nu | Nusselt number |
| OHTC | overall heat coefficient, W/(m2·K) |
| p | pressure, Pa |
| P | production term |
| Pr | Prandtl number |
| q | heat flux, W/m2 |
| Re | Reynolds number |
| Ru | universal gas constant, J/(mol·K) |
| S | source term |
| SCHTC | surface convective heat transfer coefficient, W/(m2·K) |
| T | temperature, K |
| che | chemical |
| E | energy, J |
| f | Fluid |
| i | number of fluid radial stratification species i |
| in | Inner |
| j | number of fluid axis stratification |
| bulk temperature, K | |
| t | time, s |
| u | species diffusion rate, m/s |
| U | velocity vector, m/s |
| V | critical volume, cm3/mol |
| X | X-axis, mm |
| Y | Y-axis, mm species mass fraction |
| Greek symbols | |
| α, β, β*, δ | parameters in the k–ω model |
| δ | relative error, % |
| Δr | rate of change, % |
| internal heat source, W/m3 | |
| λ | thermal conductivity, W/(m·K) |
| ω | specific dissipation rate, 1/s chemical reaction rate, mol/(m3·s) |
| μ | dynamic viscosity at high pressure, μP |
| μ* | dynamic viscosity at low pressure, μP |
| ∇ | Hamiltonian |
| ρ | density, kg/m3 |
| τ | stress, Pa |
| σ | measurement error |
| Subscripts | |
| adj | adjacent |
| c | critical |
| cal | calculated |
| k | turbulent kinetic energy |
| l | laminar |
| M | momentum |
| m | mass flow |
| out | outer |
| p | pressure |
| qf | heat flux |
| t | turbulent |
| w | wall |
| foi | initial time outlet fluid |
| eff | effective |
| exp | experimental |
References
- Wu, X.; Wei, Z. Comparison of Dual-Combustion Ramjet and Scramjet Performances Considering Combustion Efficiency. Appl. Sci. 2023, 13, 480. [Google Scholar] [CrossRef]
- Davis, M.; White, J. Flight-test-determined aerodynamic force and moment characteristics of the X-43A at Mach 7.0. AIAA Pap. 2006, 45, 472–484. [Google Scholar]
- Zhang, S.; Li, X.; Zuo, J.; Qin, J.; Cheng, K.; Feng, Y.; Bao, W. Research progress on active thermal protection for hypersonic vehicles. Prog. Aerosp. Sci. 2020, 119, 100646. [Google Scholar] [CrossRef]
- Landsberg, W.; Vanyai, T.; Mcintyre, T.; Veeraragavan, A. Experimental scramjet combustion models of hydrocarbon mixtures at Mach 8 flight conditions. AIAA J. 2020, 58, 5117–5122. [Google Scholar] [CrossRef]
- Li, X.; Zhang, Y.; Zhang, S.; Qin, J.; Bao, W. Effects of pyrolysis on heat transfer enhancement for hydrocarbon fuel flow in unilateral heated channels with dimples. Appl. Therm. Eng. 2022, 218, 119301. [Google Scholar] [CrossRef]
- Marshall, L.; Bahm, C.; Corpening, G.; Sherrill, R. Overview with results and lessons learned of the X-43A Mach 10 flight. In Proceedings of the AIAA/CIRA 13th International Space Planes and Hypersonics Systems and Technologies Conference, Capua, Italy, 16–20 May 2005. [Google Scholar]
- Hank, J.; Murphy, J.; Mutzman, R. The X-51A scramjet engine flight demonstration program. In Proceedings of the 15th AIAA International Space Planes and Hypersonic Systems and Technologies Conference, Dayton, OH, USA, 28 April–1 May 2008. [Google Scholar]
- Feng, Y.; Cao, J.; Li, X.; Feng, Y.; Zhang, S.; Qin, J.; Rao, Y. Flow and heat transfer characteristics of supercritical hydrocarbon fuel in mini channels with dimples. J. Heat Transf. 2017, 139, 122401. [Google Scholar] [CrossRef]
- Dinda, S.; Vuchuru, K.; Konda, S.; Uttaravalli, A. Heat management in supersonic/hypersonic vehicles using endothermic fuel: Perspective and challenges. ACS Omega 2021, 6, 26741–26755. [Google Scholar] [CrossRef] [PubMed]
- Cheng, Y.; Wang, Y.; Jiang, P.; Zhu, Y. Oxidative and pyrolytic coking characteristics of supercritical-pressure n-decane and its influence mechanism on heat transfer. Fuel 2024, 362, 130874. [Google Scholar] [CrossRef]
- Feng, Y.; Zhang, S.; Wu, K.; Jiang, Q.; Yong, C.; Huang, H. Numerical investigation of distribution of reaction rate during convective heat transfer with endothermic chemical reaction. Int. Commun. Heat Mass Transf. 2017, 83, 1–7. [Google Scholar] [CrossRef]
- Sun, F.; Li, Y.; Sunden, B.; Xie, G. The behavior of turbulent heat transfer deterioration in supercritical hydrocarbon fuel flow considering thermal resistance distribution. Int. J. Therm. Sci. 2019, 141, 19–32. [Google Scholar] [CrossRef]
- Fu, Y.; Zhi, T.; Xu, G.; Deng, H.; Jia, Z. Experimental study of flow distribution for aviation kerosene in parallel helical tubes under supercritical pressure. Appl. Therm. Eng. 2015, 90, 102–109. [Google Scholar] [CrossRef]
- Zhu, Y.; Zhao, R.; Wang, Y.; Jiang, P. Investigation of flow and heat transfer instabilities and oscillation inhibition of n-decane at supercritical pressure in vertical pipe. Appl. Therm. Eng. 2019, 161, 114143. [Google Scholar] [CrossRef]
- Li, H.; Qin, J.; Jiang, Y.; Zhou, W.; Bao, W.; Huang, H. Experimental study on the thermodynamic characteristics of the high temperature hydrocarbon fuel in the cooling channel of the hypersonic vehicle. Acta Astronaut. 2019, 155, 63–79. [Google Scholar] [CrossRef]
- Cheng, X.; Feng, S.; Bi, Q. Surface coke deposition influences on flow and heat transfer of hydrocarbon fuel in circular tubes with twisted-tape inserts. Int. Commun. Heat Mass Transf. 2021, 122, 105125. [Google Scholar] [CrossRef]
- Liu, Z.; Bi, Q.; Cuo, Y.; Yang, Z. Convective heat transfer and pressure drop characteristics of near-critical-pressure hydrocarbon fuel in a minichannel. Appl. Therm. Eng. 2013, 51, 1047–1054. [Google Scholar] [CrossRef]
- Dong, M.; Huang, H. Hydrocarbon Fuel Flow and Heat Transfer Investigation in Rotating Channels. Energies 2023, 16, 5020. [Google Scholar] [CrossRef]
- Zhang, Y.; Cao, Y.; Feng, Y.; Zhang, D.; Qin, J. Investigation into effect of residence time on cooling characteristics of RP-3. J. Thermophys. Heat Transf. 2022, 37, 435–447. [Google Scholar] [CrossRef]
- Jiang, X.; Liu, M.; Wu, H.; Zheng, Y.; Zhuang, J. Numerical study on low-temperature region as heat sink and its heat dissipation capacity for hypersonic vehicle. Aerospace 2021, 8, 238. [Google Scholar] [CrossRef]
- Zhang, L.; Zhang, R.; Xiao, S.; Jiang, J.; Le, J. Experimental investigation on heat transfer correlations of n-decane under supercritical pressure. Int. J. Heat Mass Transf. 2013, 64, 393–400. [Google Scholar] [CrossRef]
- Jiao, S.; Li, S.; Pu, H.; Dong, M.; Shang, Y. Investigation of pressure effect on thermal cracking of n-decane at supercritical pressures. Energy Fuels 2018, 32, 4040–4048. [Google Scholar] [CrossRef]
- Li, X.; Zhang, S.; Bao, W.; Qin, J.; Haidn, O. Flow resistance characteristics of hydrocarbon fuel at supercritical pressure under various heat fluxes in regenerative cooling channel with micro-ribs. Aerosp. Sci. Technol. 2022, 131, 107999. [Google Scholar] [CrossRef]
- Gatski, T.; Rumsey, C. Linear and Nonlinear Eddy Viscosity Models; Cambridge University Press: London, UK, 2002. [Google Scholar]
- Kim, S.; Choi, H.; Kim, Y. Thermo-physical modeling based on a generalized cubic equation of state for kerosene/LOx rocket combustion. Combust. Flame 2012, 159, 1351–1365. [Google Scholar] [CrossRef]
- Li, X.; Qin, J.; Zhang, S.L.; Cui, N.; Bao, W. Effects of micro-ribs on the thermal behavior of transcritical n-decane in asymmetric heated rectangular mini-channels under near critical pressure. J. Heat Transf.-Trans. ASME 2018, 140, 122402. [Google Scholar] [CrossRef]
- Li, X.; Zhang, S.; Qin, J.; Bao, W. Parametric analysis on the thermal behavior of cracking hydrocarbon fuel flow inside asymmetry heated cooling channels with micro-ribs. Int. J. Heat Mass Transf. 2020, 160, 120154. [Google Scholar] [CrossRef]
- Li, Y.; Xie, G.N.; Sunden, B. Flow and thermal performance of supercritical n-decane in double-layer channels for regenerative cooling of a scramjet combustor. Appl. Therm. Eng. 2020, 180, 115695. [Google Scholar] [CrossRef]
- Poling, E.; Prausnitz, J.; Paul, O. The Properties of Gases and Liquids; McGraw-Hill: New York, NY, USA, 2001. [Google Scholar]
- Li, H.; Lin, G.; Xu, Q.; Fang, X.; Xian, S. Overall heat transfer coefficient evaluation method for uncracked hydrocarbon fuel in a regeneratively-cooled heat exchanger of a scramjet. Appl. Sci. 2022, 12, 6590. [Google Scholar] [CrossRef]

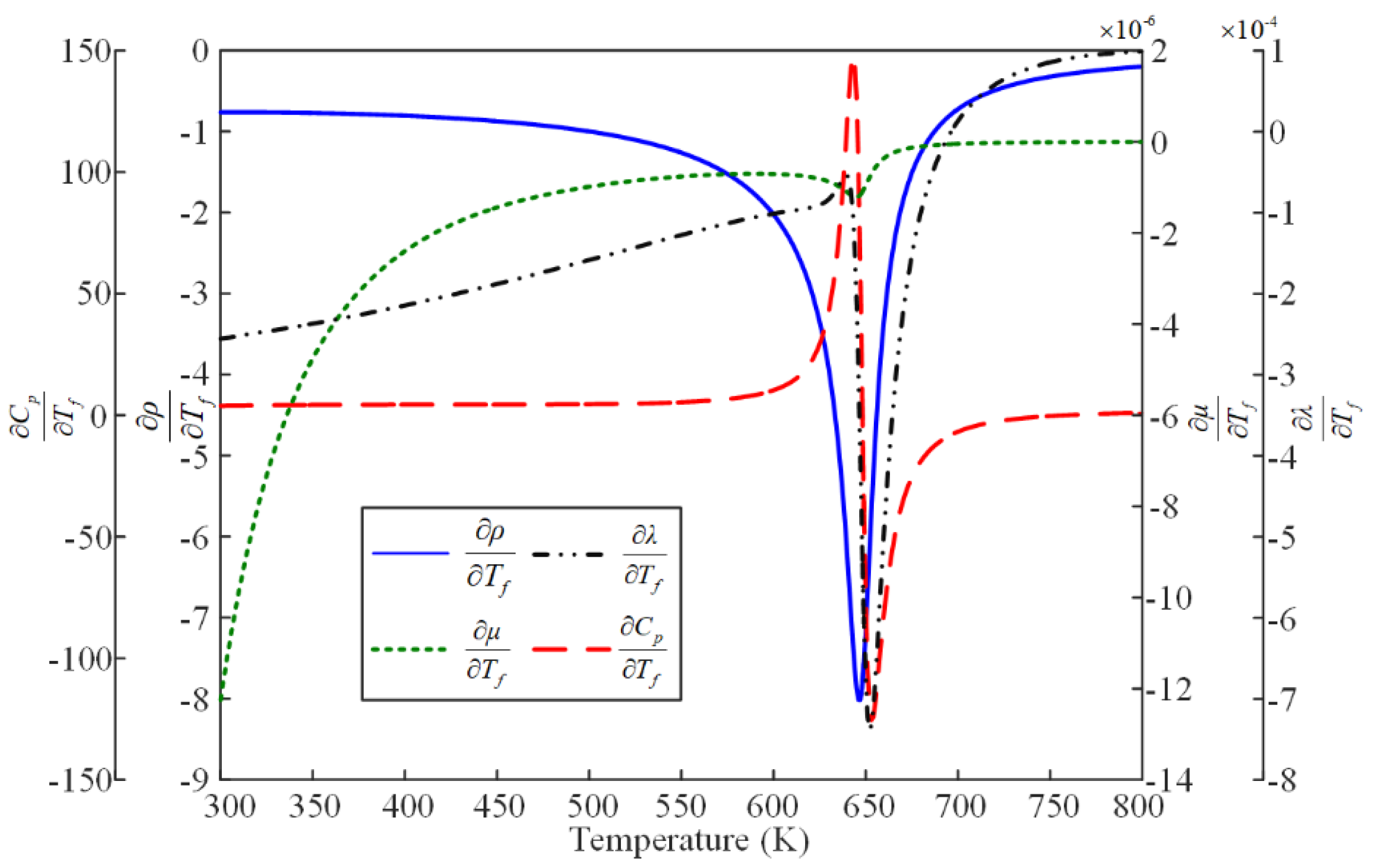
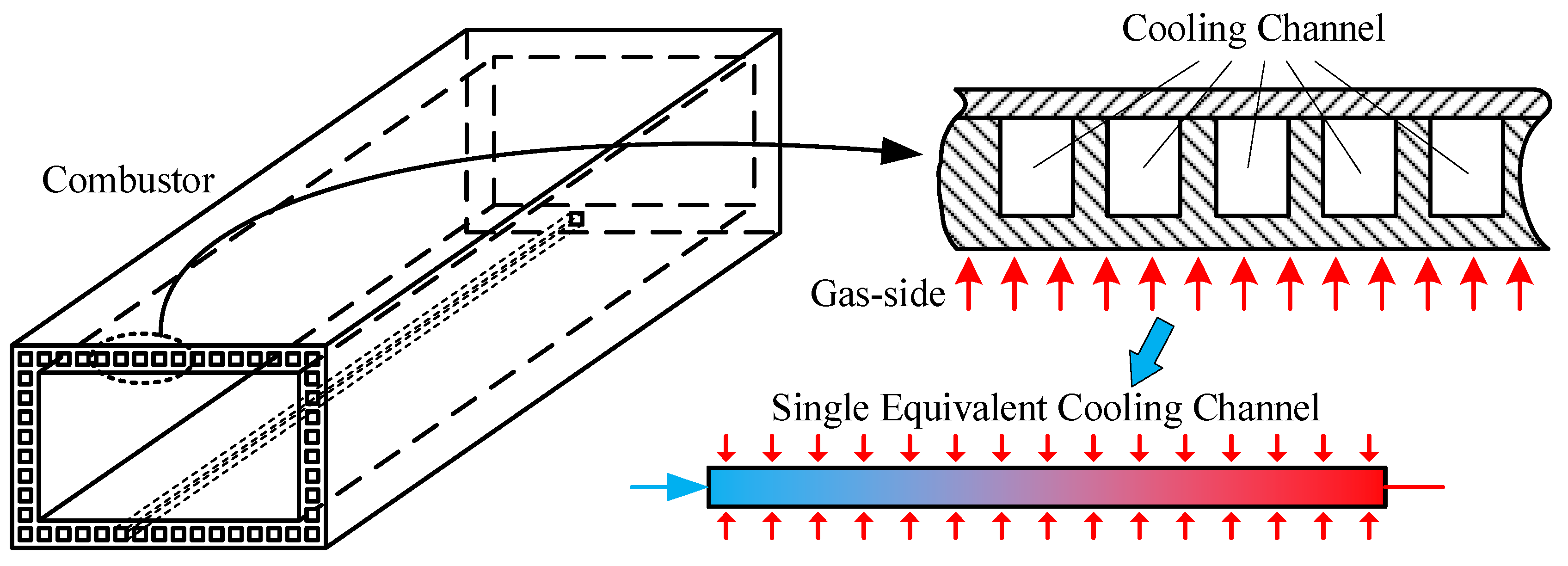
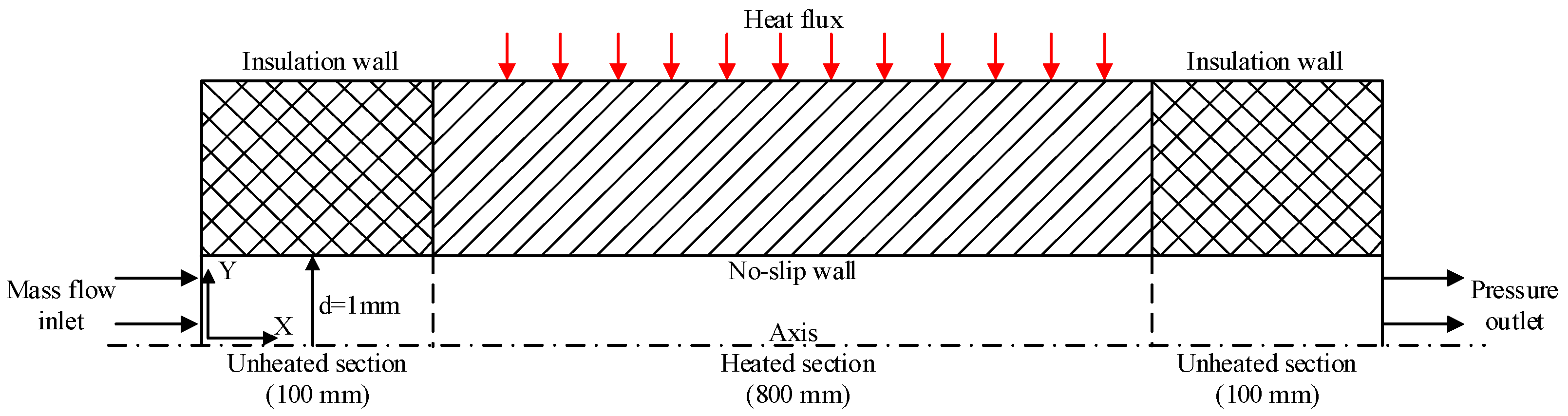
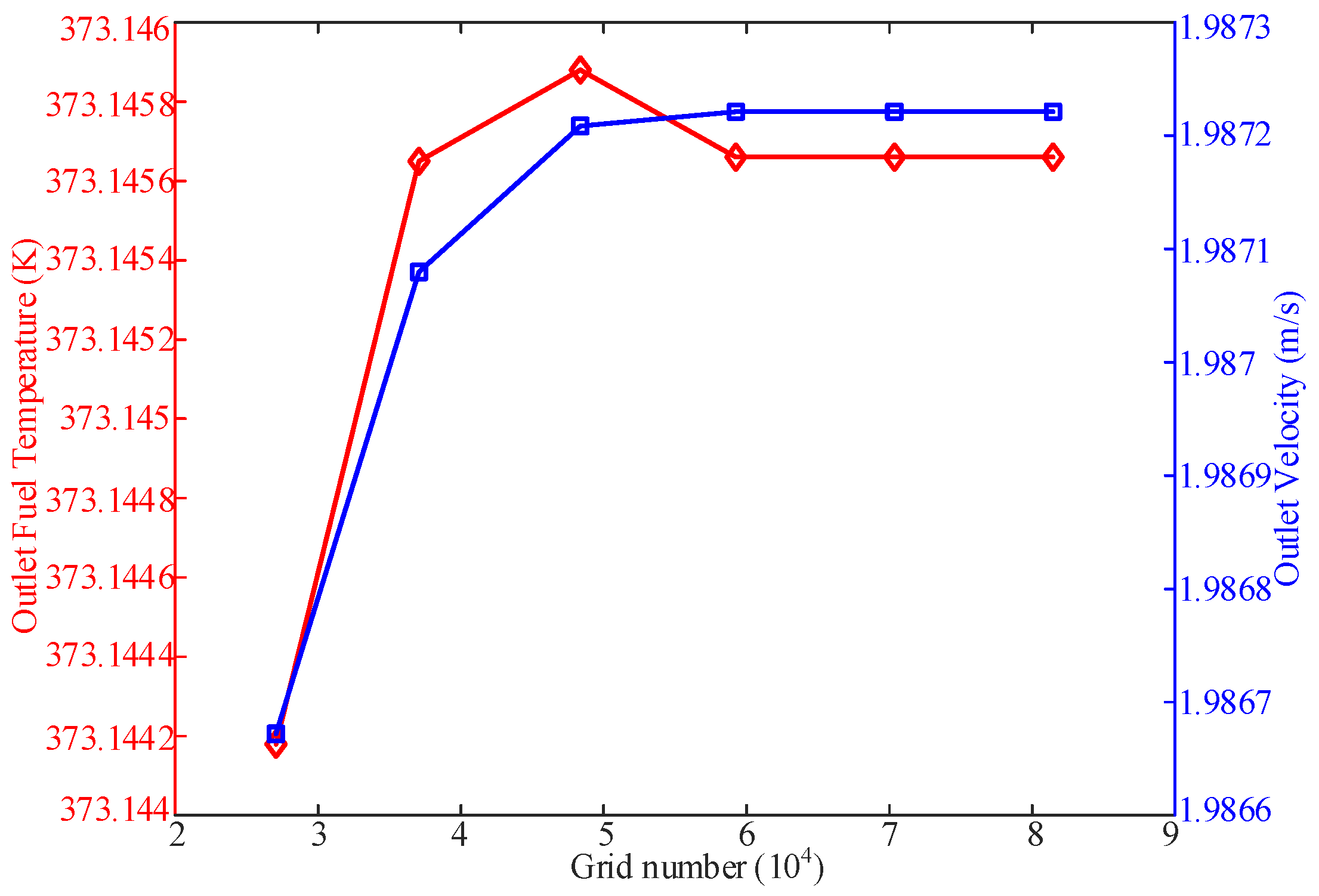


| T (K) | 273.15 | 473.15 | 573.15 | 673.15 | 773.15 | 873.15 | 973.15 | 1073.15 |
|---|---|---|---|---|---|---|---|---|
| cpw (J/(kg·K)) | 113.91 | 120.21 | 127.47 | 137.36 | 142.20 | 152.84 | 154.48 | 159.54 |
| λw (W/(m·K)) | 11.30 | 12.56 | 14.24 | 15.49 | 16.75 | 18.42 | 19.68 | 21.35 |
| Working Pressure (MPa) | Outlet Fuel Temperature (K) | Required Heat Flux (W/m2) |
|---|---|---|
| 5 | 373.15 | 20,855 |
| 473.15 | 55,735 | |
| 573.15 | 96,793 | |
| 673.15 | 145,355 | |
| 3 | 373.15 | 20,895 |
| 473.15 | 55,930 | |
| 573.15 | 97,695 | |
| 673.15 | 152,760 |
| Equipment | Type | Accuracy |
|---|---|---|
| Pump | SP1020 Type High-Pressure Double Plunger Pump | ≤±1% |
| Heating Power | DC Power | 0.5% |
| Temperature Sensor | K Type Thermocouple | 0.4% |
| Pressure Difference Sensor | ROSEMOUNT 3051CD Type Differential Pressure Transmitter | 0.25% |
| Mass Flow Meter | Micro Motion Elite Type Coriolis CMF010 Mass Flow Meter | 0.1% |
| Data Acquisition System | NI cRIO-9205 | ≤±0.1‰ |
| Temperature: NI 9205 | ≤±0.12‰ | |
| Pressure, pressure difference: NI 9264 | ≤±0.15‰ |
| Measurement | Measurement Error Expression | Uncertainty |
|---|---|---|
| Mass flow | ±1.01% | |
| Temperature | ±0.2% | |
| Pressure | ±0.125% | |
| Heat flux | ±0.32% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, Q.; Lin, G.; Li, H.; Feng, Y. Dynamic Flow and Heat Transfer Characteristics of Uncracked Hydrocarbon Fuel under Super-Critical Pressure in the Cooling Channel of a Regeneratively Cooled Scramjet. Appl. Sci. 2024, 14, 2508. https://doi.org/10.3390/app14062508
Xu Q, Lin G, Li H, Feng Y. Dynamic Flow and Heat Transfer Characteristics of Uncracked Hydrocarbon Fuel under Super-Critical Pressure in the Cooling Channel of a Regeneratively Cooled Scramjet. Applied Sciences. 2024; 14(6):2508. https://doi.org/10.3390/app14062508
Chicago/Turabian StyleXu, Qing, Guowei Lin, Haowei Li, and Yaoxun Feng. 2024. "Dynamic Flow and Heat Transfer Characteristics of Uncracked Hydrocarbon Fuel under Super-Critical Pressure in the Cooling Channel of a Regeneratively Cooled Scramjet" Applied Sciences 14, no. 6: 2508. https://doi.org/10.3390/app14062508
APA StyleXu, Q., Lin, G., Li, H., & Feng, Y. (2024). Dynamic Flow and Heat Transfer Characteristics of Uncracked Hydrocarbon Fuel under Super-Critical Pressure in the Cooling Channel of a Regeneratively Cooled Scramjet. Applied Sciences, 14(6), 2508. https://doi.org/10.3390/app14062508





