Abstract
Tunnel construction projects are a classic type of repetitive project, and hold a crucial position in the construction industry. The linear scheduling method (LSM) has been in the spotlight in scheduling optimization for repetitive construction projects since it was first proposed. However, the possibility of changing the construction sequence during application is very often overlooked, which is not in line with actual engineering practices. Incorporating soft logic into LSM and considering the characteristics of tunnel construction, we propose an optimization method for the tunnel construction schedule to shorten the duration by opening up an additional working surface. A mixed-integer programming (MIP) model is developed, which considers various constraints, such as construction sequence and work continuity. The exact algorithm and genetic algorithm (GA) are designed via Python, and the validity is verified through practical cases. A comparative analysis was conducted between the two algorithms and their outcomes demonstrates that the method can satisfy the restrictive constraints of tunnel construction projects. In addition, improvement strategies for tunnel construction management are recommended.
1. Introduction
With population growth and increasing traffic congestion, the development of tunnel engineering has become inevitable. By the end of 2022, China had constructed 24,850 road tunnels. At present, the technique and management of tunnel construction have achieved maturity, but there is still the unavoidable issue of work stopping due to environmental changes. This seriously affects the duration of construction projects and leads to a waste of labor, materials, and machinery resources. Tunnel construction is significantly characterized as involving repetitive construction projects, which consist of multiple repetitive units. The same activities are repeated in each unit, and construction resources are transferred from one unit to the next in a well-timed manner [1,2]. The scheduling of projects is an essential part of project management [3]. The resource-constrained project scheduling problem is a classic issue in project scheduling, where the purpose is to allocate finite resources to activities in the construction project, as well as to establish a schedule of construction project activities [4]. In recent years, the optimal problem of scheduling repetitive construction projects has attracted considerable attention from researchers [5]. Duration is regarded as one of the most important objectives for construction companies, and tunnel construction can be accelerated by increasing the number of working surfaces. However, a large portion of existing tunnel construction schedules are formulated based on manual experience and lack efficient and scientific calculation methods. Under the developing trend of construction management refinement, there is an urgent demand to explore the optimization of the tunnel construction schedule to provide a practical and scientific method for tunnel construction management.
Given the accessibility of computational programs and commercial software packages, traditional Gantt charts and network planning techniques, such as planning review techniques and the critical path method (CPM) [6], are extensively applied to construction projects for planning and scheduling. Nevertheless, these methods have a restricted degree of adaptability to repetitive construction projects and do not allow for efficient planning for them [7]. As a result, linear scheduling methods (LSMs) for repetitive projects have been gradually applied in the field of construction engineering [8]. The most representative methods are the line-of-balance (LOB) [9] and linear scheduling method (LSM) [10,11]. The LSM has been proven to have significant advantages as an approach to the scheduling of repetitive construction projects [12]. Most of the studies related to the LSM assume that the logical relationships are fixed, meaning that the construction of the whole project is carried out in a fixed sequence [13]. Such assumptions differ from the actual conditions. The project may be accomplished by multiple construction teams and the construction sequence may be subject to shifts due to environmental changes [14]. The same activities in different units and different activities in the same unit are linked by logical relationships, which can be “fixed” and “soft” [15]. In contrast to fixed logic, the implementation order of the construction units in soft logic relationships is changed. An increasing number of scholars have focused their studies on the optimization of construction schedules considering soft logic.
The scheduling optimization of repetitive construction projects has been extensively studied in recent years. However, there are still research gaps regarding aspects related to the optimization of the tunnel construction schedule, especially the lack of consideration of the situations in which the construction sequence can be changed. To address these issues, an optimization model for the tunnel construction schedule is developed by combining LSM and soft logic relationships.
The study is aimed at the optimization of the tunnel construction schedule, and the major contributions are as follows:
- (1)
- By introducing soft logic relationships into the field of tunnel construction management, this study takes sufficient account of the changes in the construction sequence compared to the traditional fixed sequence in order to optimize the tunnel construction schedule.
- (2)
- A mixed-integer programming (MIP) model for tunnel construction schedule is proposed based on LSM and soft logic relationships, which intuitively represents the constraint relationships related to logic, continuity, time, space, and construction team scheduling.
- (3)
- The optimization issue is addressed using both the exact algorithm and genetic algorithm (GA), followed by a comparative analysis of the outcomes generated by these two methods. The objective is to address the issue being studied to the optimal extent.
2. Literature Review
2.1. Scheduling Optimization for Repetitive Construction Projects
The distinction between the scheduling of repetitive and non-repetitive construction projects is mainly due to labor and machinery allocation strategies, as well as work continuity requirements, such as construction sequence constraints, labor allocation constraints, and work continuity constraints [16]. The existing studies can be categorized into two types based on whether construction interruptions are permitted: (1) activities are required to maintain continuity [9]; (2) partial interruptions of activities are permitted [17]. The objectives of scheduling optimization for repetitive construction projects are primarily work continuity and resource continuity to minimize the duration and project cost [18]. Generally, enforcing requirements for work continuity may result in longer durations [19,20]. If a suitable schedule is formulated that allows for work interruptions at appropriate times, the duration can be shortened to a certain extent [21].
Scholars have employed a variety of methods to solve the scheduling optimization issues in repetitive construction projects, mainly mathematical planning methods, constrained planning techniques, and heuristic methods. Shafahi et al. [22] and Zhentao et al. [23] proposed a linear programming model for small-scale instances and optimized the calculation. Tang et al. [24] used constraint planning techniques to solve the schedule control issue in repetitive construction projects. Tran et al. [25] and Eid et al. [11] used genetic algorithms (GAs) to solve these kinds of issues. Ze et al. employed the gray wolf optimization algorithm to provide insights into the issue [26]. In the practical construction process, heuristic methods have been extensively applied to the scheduling optimization of repetitive construction projects, in which the application of GAs is particularly significant [27,28,29].
2.2. Scheduling Optimization for Repetitive Construction Projects Based on LSM
LSM was first proposed in 1981 in the construction field and was initially employed to solve project management issues such as highway projects. It employs a Cartesian coordinate system to describe the construction schedule, with the horizontal axis representing the spatial location and the vertical axis representing the temporal progress [30]. It can represent the spatial progress of each activity per unit of time, namely, the construction speed, and thus can be considered as continuous and oriented to the construction progress. According to the duration and complexity of the activities, LSM categorizes the activities of repetitive construction projects into three types, linear, strip, and block [31], with certain temporal and spatial buffers between the activities. The LSM can characterize the attributes of the activities and the logical relationships within them.
LSM has unique superiority compared to traditional construction scheduling methods for the scheduling optimization of repetitive construction projects [32]. Traditional construction scheduling methods, such as CPM and network scheduling techniques, are not very suitable for scheduling the optimization of repetitive construction projects because they overlook construction continuity and labor scheduling strategies during their application [33]. Yamín et al. [34] compared LSM and CPM in detail and concluded that LSM is superior when dealing with the very specific issues of projects, but further, more in-depth research is necessary. Both LSM and LOB are linear scheduling techniques and are strongly related [35]. While LOB is event-centered [33], LSM is schedule-centered. LSM has more significant engineering characteristics and is extensively applied in the scheduling of repetitive construction projects [36].
2.3. Scheduling Optimization for Repetitive Construction Projects Based on Soft Logic
The concept of soft logic was first mentioned by Tammi et al. [37] in 1988, and it was utilized to update network schedule diagrams caused by unexpected events. El-Sersy et al. classified soft logic into three types, soft, or, and exclusive-or, and activities with soft logic relationships can change the sequence of occurrences or take place simultaneously on different units. Soft logic relationships are essential for flexibility when facing scheduling optimization issues in repetitive construction projects.
Numerous scholars have incorporated soft logic relationships with the scheduling optimization of repetitive construction projects. Fan et al. [38] integrated soft logic with RSM, focusing on the soft logic relationships for the simultaneous construction of multiple units. Tao et al. addressed schedule optimization with or without resource constraints in conjunction with soft logic [29]. Zhang et al. focused on the soft logic issue of interchangeable unit sequences of construction, and successively achieved the scheduling optimization of repetitive construction projects by inserting the concept of resource transfer cost [28], reducing the number of construction teams [39], and maximizing the work continuity [15].
2.4. Knowledge Gaps
Work continuity is a critical factor influencing the duration of studies on the scheduling optimization of repetitive construction projects. Currently, there are fewer studies on the optimization of tunnel construction schedules, and their specific constraints still need to be further investigated. The exact algorithms and GAs have been extensively applied in the scheduling optimization of repetitive construction projects. Nevertheless, the optimization models that are more in line with the characteristics of tunnel construction projects remain to be explored.
LSM is frequently applied to the scheduling optimization of repetitive construction projects, which usually assumes that there are only fixed logical relationships between activities and neglects variations in the construction sequence. Therefore, it is necessary to associate LSM with other theories or methods in order to solve the issues of logical relationships between construction activities and to develop a more efficient and feasible schedule.
Soft logic relationships can be referenced for the scheduling optimization of repetitive construction projects, but they typically involve subjective judgments and ambiguous concepts that require that explicit constraints are determined. Moreover, the scheduling optimization of repetitive construction projects with soft logic relationships could result in an increasing number of feasible solutions, which puts higher demands on the models and algorithms.
3. Method
Given the current research limitations, LSM and soft logic are combined to discuss the optimization problem of tunnel construction schedules. Specifically, we construct an optimization model of tunnel construction schedule (TSMOM) and design the exact algorithm and GA accordingly.
3.1. Problem Description
Tunnel construction involves complex optimization issues, including the scheduling of labor, materials, and machinery resources, among others. The optimization of tunnel construction schedule aims to increase the working surfaces by scheduling construction teams in a manner that satisfies all basic and reasonable constraints. On the one hand, this improves the efficiency of construction, thus shortening the project’s duration; on the other hand, it largely prevents personnel or equipment idle time, thereby reducing construction costs and the waste of resources. The exact algorithm and GA are used to optimize the scheduling problem of tunnel construction.
Following an on-site investigation, a scenario was formulated in relation to the situation at a particular tunnel site. The details are as follows.
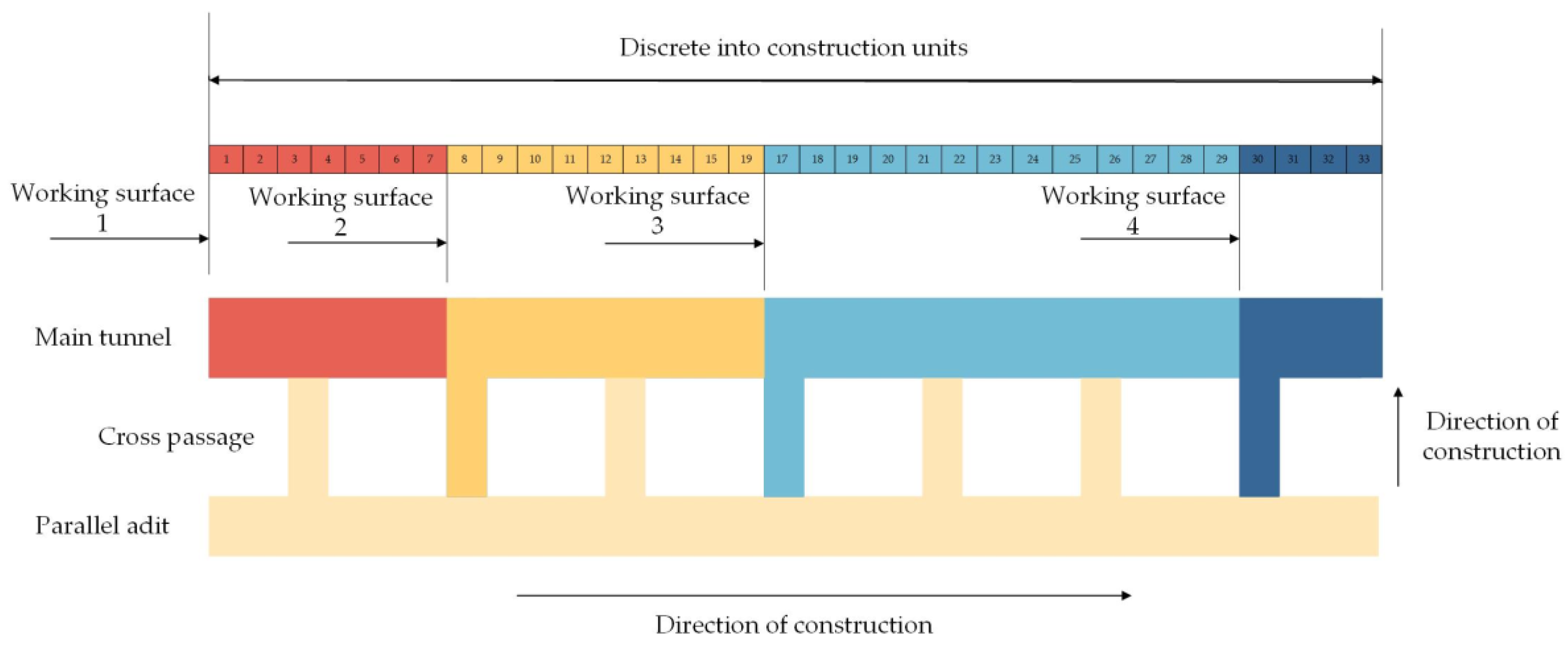
In tunnel construction, additional working surfaces are often created through auxiliary tunnels to accelerate the construction progress. Figure 1 shows a schematic diagram of the optimization of the tunnel construction schedule. Tunnel projects are usually well-stocked to ensure the successful completion of construction, so the limited resources are mainly considered constraints for the construction teams. The number of construction teams and the direction of construction are fixed. Each activity within each construction unit can only be carried out by one construction team, which can continue to the next part of the work after the corresponding part of the construction team has finished their work. Each construction team needs to work continuously over a certain distance due to the construction continuity requirement, so there is a certain distance constraint between two adjacent working surfaces. The proposed cost is mainly calculated based on project quantities, so this model does not consider the variation in costs.
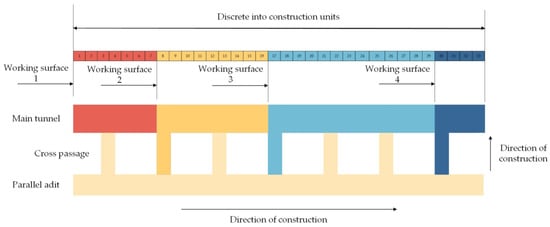
Figure 1.
Tunnel construction schedule optimization.
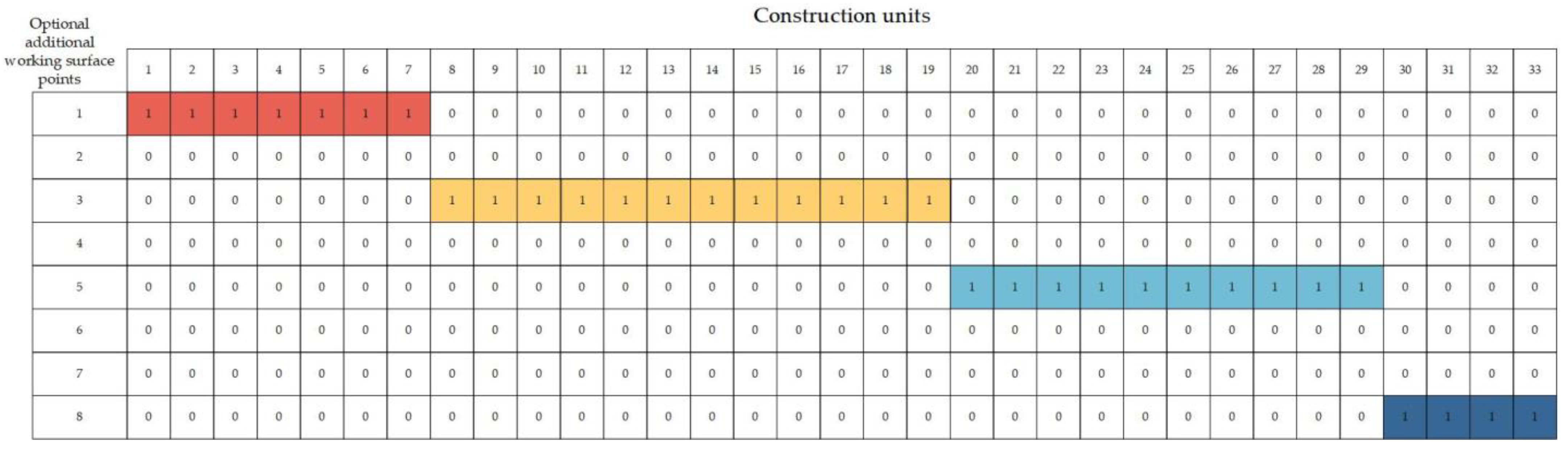
Combining the LSM and soft logic, the relationships between construction units and working surfaces are analyzed and determined according to the characteristics of the tunnel construction projects, as shown in Figure 2. As a result, information such as the location and start time of the additional working surfaces can be determined, thus optimizing the objective function.
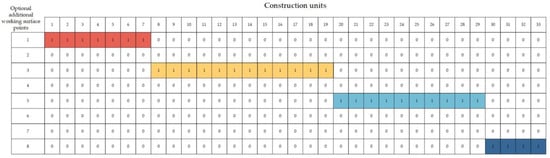
Figure 2.
Relationships between working surfaces and construction units.
3.2. Mathematical Model
3.2.1. Parameters
To facilitate the construction of the model, the relevant parameters are defined as shown in Table 1, Table 2 and Table 3:

Table 1.
Index of TSMOM.

Table 2.
Variables of the TSMOM.

Table 3.
Constants of the TSMOM.
3.2.2. Objective Function
LSM requires that a coordinate system is established in which the start time of activities without any predecessors in repetitive construction projects is assumed to be 0. This start time is regarded as the beginning of the entire construction schedule, as shown in Equation (1).
Duration is the latest completion date for all activities, as shown in Equation (2).
3.2.3. Constraints
- (1)
- Logical constraints
This type of constraint is responsible for the prioritization and backwardness of each activity. Typically, there are four types of logical relationships between construction activities, as follows: start-to-start (S-S), finish-to-start (F-S), start-to-finish (S-F), and finish-to-finish (F-F). If activity is a predecessor of activity , the logical relationships can be expressed by the following equations:
- S-S relationship
The latter activity can only begin after the previous one has started, as shown in Equation (3).
- 2.
- F-S relationship
The previous activity is completed before the subsequent activity can begin, as shown in Equation (4).
- 3.
- S-F relationship
The latter activity cannot be completed until the previous activity has begun, as shown in Equation (5).
- 4.
- F-F relationship
The previous activity will not be completed until the subsequent activity is completed, as shown in Equation (6).
- (2)
- Work continuity constraints
Work interruptions affect the proficiency of the construction team, which is not conducive to learning and advancement [40]. There are additional costs associated with idle construction teams and transfers to other construction sites [15]. In practice, in order to shorten the interruption of activities and minimize the transfer of construction teams, the minimum time of continuous work or the shortest continuous working distance of the construction teams is usually constrained.
In each activity, the working surface can only be accessed and carried out using one additional working surface optional point, and there is no situation where a construction team can work on the same working surface from multiple optional additional working surface points, as shown in Equation (7).
The construction team may perform activities on multiple units using an additional working surface, but these units must be continuous, as shown in Equations (8)–(10).
Construction team switching is only allowed when the work continuity constraints are met. A certain distance constraint must be met between the original and the new working surface before the new construction team is allowed to work on the new working surface, as shown in Equations (11) and (12).
The end time of the additional working surface from unit j is shown in Equation (13).
- (3)
- Temporal constraints
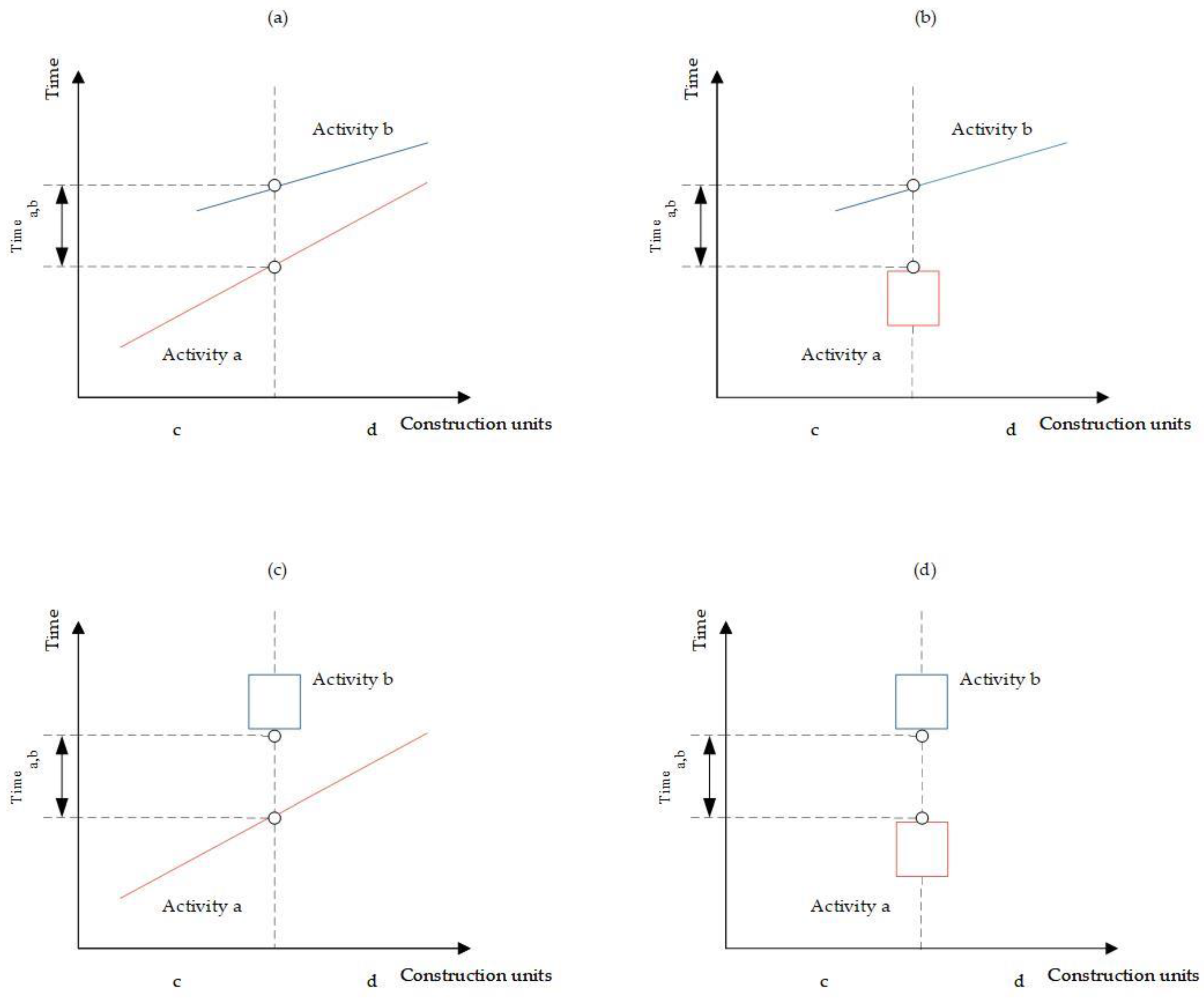
The specific temporal constraints are mainly based on the type of unit and activity. The directions of the activities discussed in this paper are all fixed. Strip activities can be viewed as block activities with a unit span of 0, so they can be discussed as a class of activities. Assume that activity a is the predecessor activity to b, and unit c is the preceding unit to d. Taking the constraint at the junction of unit c and d as an example, the relationship between activity a and b is shown in Figure 3.
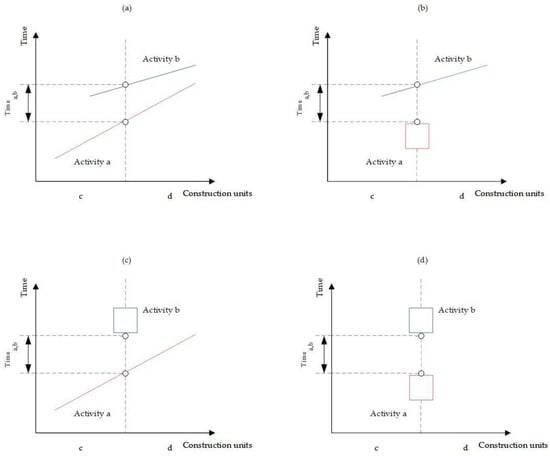
Figure 3.
The time constraint relationships between activities: (a)
a
and
b
are both linear activities; (b)
a
is a strip or block activity and
b
is a linear activity; (c)
a
is a linear activity and
b
is a strip or block activity; (d)
a
and
b
are both strip or block activities.
- The relationships when both activities a and b are linear, or when one of them is linear, are shown in Equations (14) and (15).
- 2.
- When both activities a and b are strip or block activities, the relationships are shown in Equations (16) and (17).
The maximum end time for all activities is less than or equal to the expected project completion time, as shown in Equation (18).
- (4)
- Spatial constraints
Spatial resources are a type of resource that is required for a series of activities and remain occupied during the activities. Activities will be subject to spatial constraints due to the construction techniques and operational requirements. For instance, during tunnel construction, the lining construction should not fall behind the excavation face by more than 80 m. Spatial constraints are related to the speed and time of the work, and they can be mutually translated while considering temporal constraints. Thus, the spatial constraints will not be explained too much here.
- (5)
- Construction team constraints
If the additional working surface is selected to begin at unit j, there must be a construction team to carry out activities at j, as shown in Equation (19).
The summary of the work carried out by the construction team on each working surface is equal to the total quantity of the project, as shown in Equation (20).
In addition, the number of construction teams conducting activities at the same time should not exceed the total number of construction teams.
4. Algorithm Design and Model Verification
4.1. Exact Algorithm
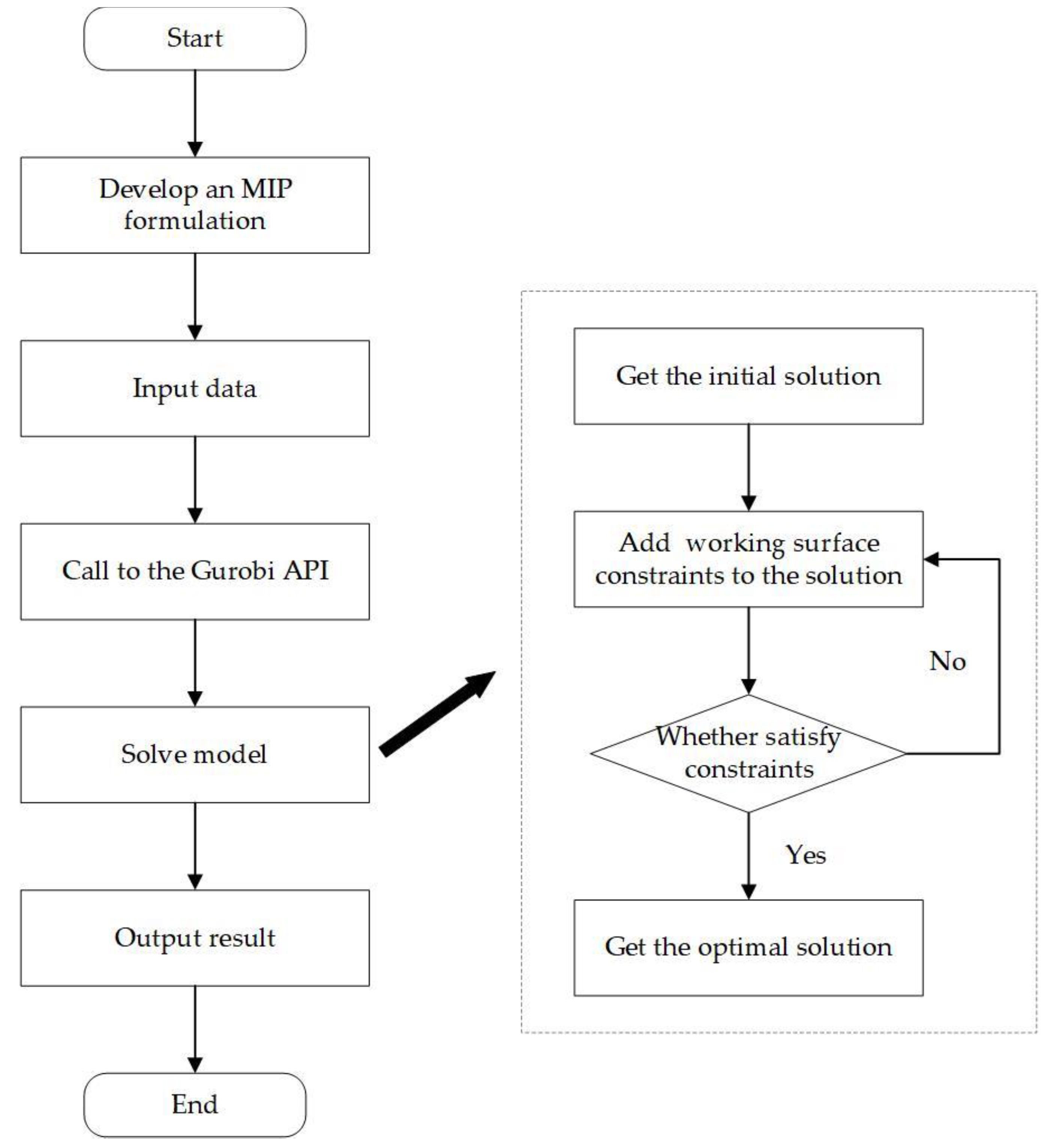
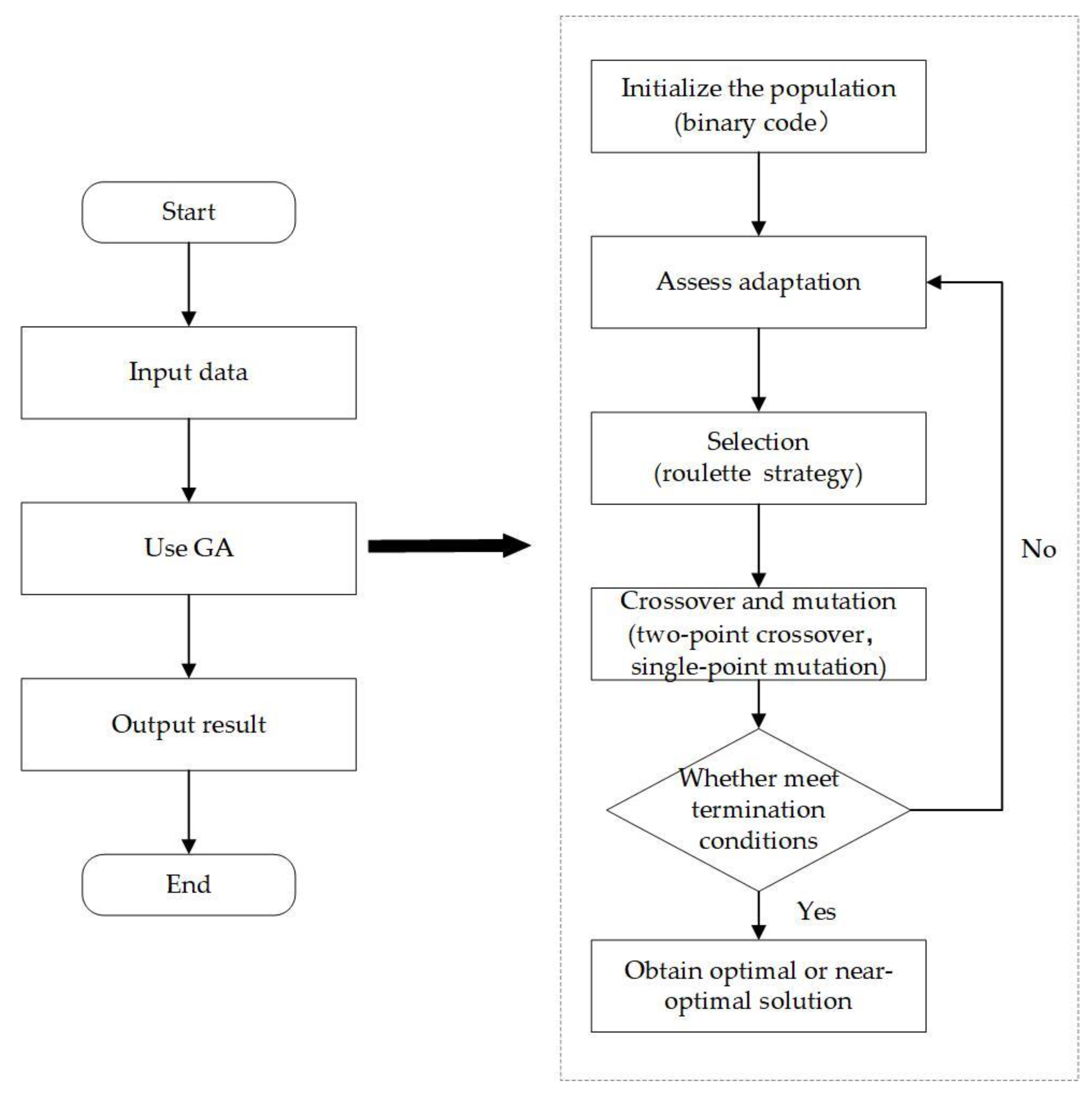
An exact algorithm is an algorithm that solves the problem in an optimal way. For hard combinatorial optimization problems, the exact algorithm can find the optimal solution within an acceptable time frame when the problem is small. The exact algorithm solution slows down when the problem is large, but can provide a feasible solution to the problem. It can also provide initial solutions for heuristic algorithms in order to improve the search efficiency and find better solutions. The Gurobi solver was chosen to solve the above MIP formulation, and the relevant solution program was developed by Python 3.7.0. The main steps of the solution procedure are represented in Figure 4.
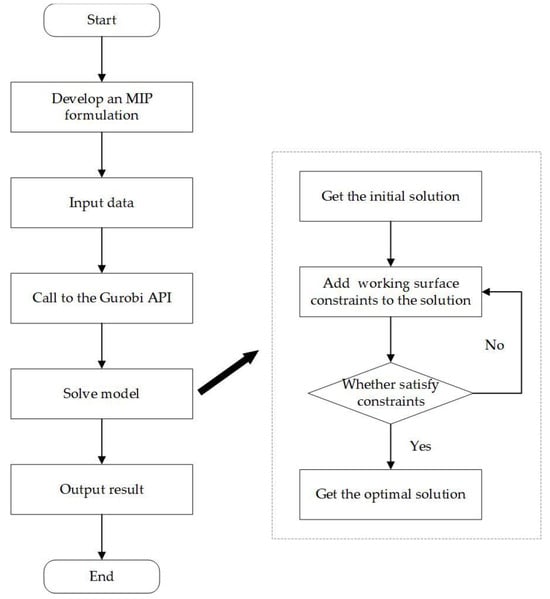
Figure 4.
TSMOM optimization process using an exact algorithm.
Considering the limitations on the number of construction teams and work continuity, the actual start time of the construction team needs to be compared with the end time of all the ongoing teams when adding a new working surface that meets the distance constraints. This cannot be directly represented in the mathematical model, so the cutting plane method is used for optimization.
- (1)
- The optimization of the model with linear constraints leads to an initial solution.
- (2)
- Add the cutting plane constraint for working surface switching and continue the solution. When the initial construction team completes a job task and moves on to work on an additional working surface, the start time of the new working surface must be greater than or equal to the completion time of the previous working surface.
- (3)
- Repeat the above steps until an optimal solution is found.
4.2. Genetic Algorithm
The basic principle of GA is to simulate the process of natural selection and the evolution of organisms [41]. Random individuals are taken to form an initial population and then a new generation is generated through selection, crossover, and mutation. After multiple iterations, the optimal solution to the problem is found.
Currently, GA is widely applied to multi-objective optimization problems in engineering management because it has the following advantages: (1) it can be executed on multiple processing units or computing nodes at the same time, accelerating the search process, and is able to provide a feasible solution in an acceptable time; (2) it is capable of handling discrete, continuous, and mixed variables, and is applicable to various types of engineering management problems, including resource allocation, project scheduling, path planning, etc.; (3) it does not require information about the gradient of the objective function to be solved, and can cope with problems that are nonlinear, nonconvex, and have no explicit mathematical expression; (4) it generates new solutions through crossover and mutation operations, which can maintain diversity in the population and prevent the local optimal solutions from being used. The optimization model calculations are implemented via Python version 3.7.0 and the main execution steps are shown in Figure 5.
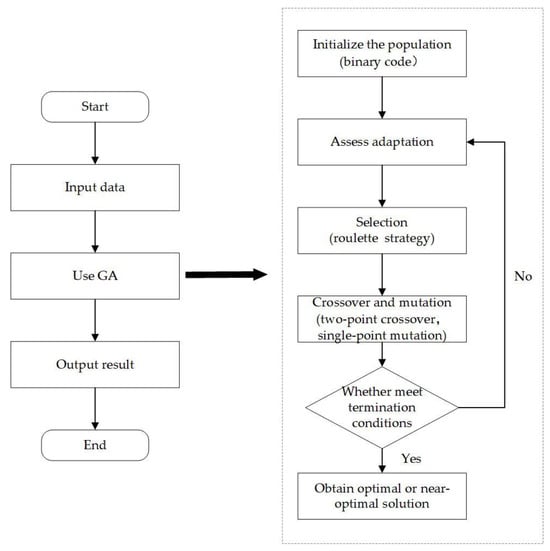
Figure 5.
TSMOM solution flow using GA.
4.2.1. Initialize the Population
A binary code is used to indicate whether a new working surface is added at the optional additional working surface point, as shown in
Figure 6.

Figure 6.
Coding method.
Chromosomes are randomly generated, with values within a custom domain, and the initial population is formed after repeating the “pop” times. Here, “pop” is the population size. The quality of the initial population has a large impact on the solution results, so the validity of the initial population needs to be judged. If the initial population does not satisfy the duration constraints, the initial population is regenerated.
4.2.2. Fitness Function
In populations, individuals with higher fitness values are superior. The fitness function takes the inverse of the duration and makes the fitness value sufficiently small for individuals that violate the constraints.
4.2.3. Selection
The selection strategy is based on the roulette wheel selection method, where the probability of selection for each candidate is proportional to its fitness.
4.2.4. Crossover and Mutation
The selected crossover was a random selection of crossover points, achieved by crossing two of them, and the mutation that was used was a single point variation.
4.3. Model Verification
Combining the actual situation of a completed tunnel construction project with the above reasonable assumptions, the example data used in the paper are as follows.
The total length of both the main tunnel and the parallel adit is 7095 m, with a total of 14 cross-passages of approximately 40 m in length. The main tunnel and parallel adit start and end at the same horizontal position. The first cross-passage is 270 m from the starting point of the main tunnel, and thereafter cross-passages occur at intervals of 500 m. There were three construction teams, one for the construction of the parallel adit and two others for the main tunnel and the cross-passages in shifts. The work continuity distance constraint R between working surfaces is 1000 m. The original duration was 2028 days. The initial optimized program was to enter the main tunnel from cross-passages 4, 7, and 11 to carry out the working surface operations for working surface selection points 5, 8, and 12, respectively. The construction speeds of the main tunnel, the parallel adit, and the cross passages are shown in Table 4.

Table 4.
Average construction speeds for each part of the tunnel project.
The above-mentioned MIP model was solved using the Gurobi solver and the GA was employed to solve the given instance, which ultimately results in an optimal or near-optimal solution, respectively. Comparing the optimization results from both sources reveals a perfect concordance, indicating that the solution process and outcome of the GA applied to the given issue are reliable and capable of providing a satisfactory solution. In addition, the average computation time for optimization by Python 3.7.0, using two methods 10 times, can be obtained: the exact algorithm took 379.5 milliseconds and the GA took 273.8 milliseconds. The average time taken to obtain the same result using the GA is 105.7 milliseconds shorter than the exact algorithm, suggesting that the GA has a clear advantage.
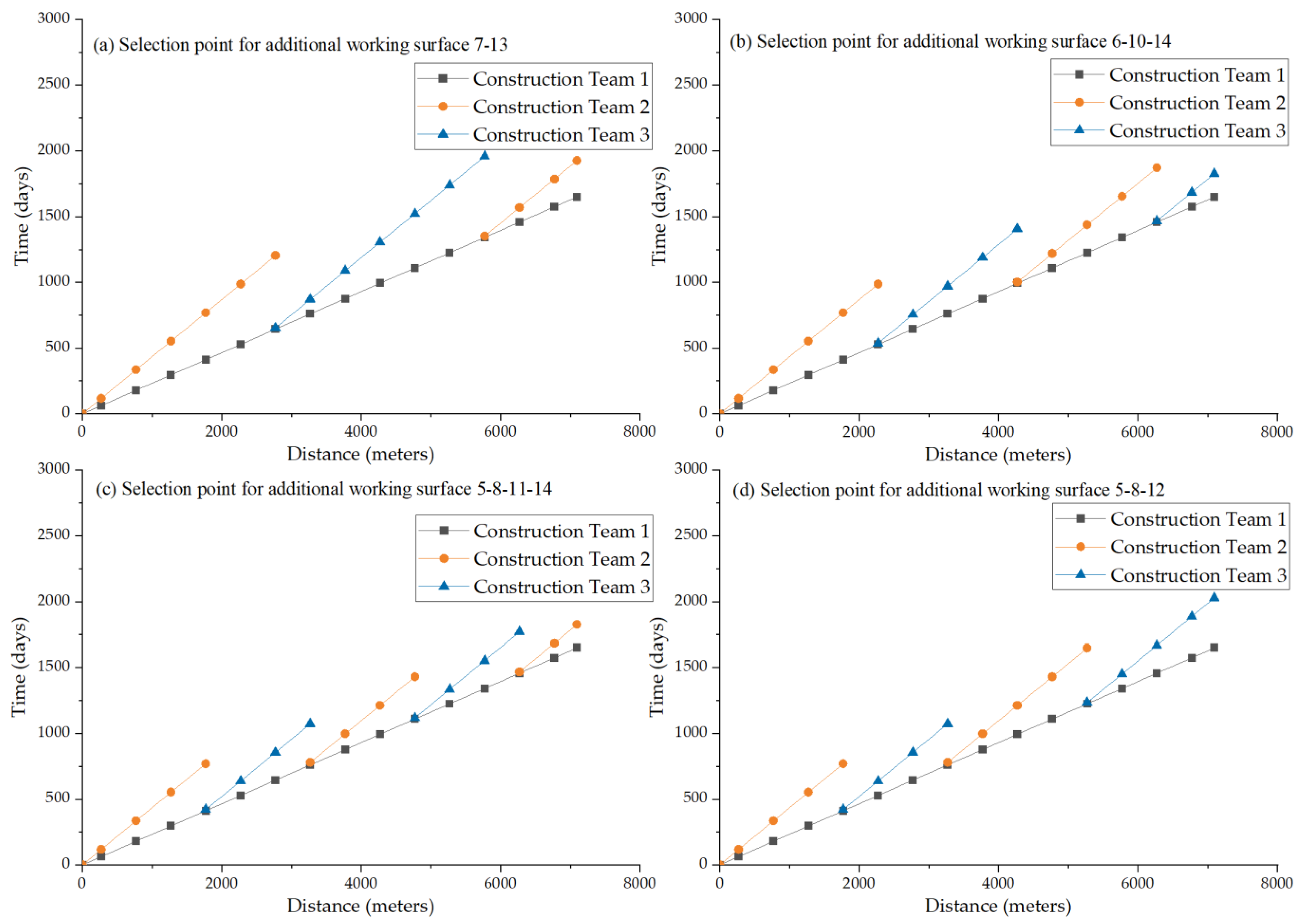
Although there is almost no significant difference between the distance constraints of 1000 and 999 m in practical construction, the computer would regard the 999 m as violating the constraints, which could lead to a part of the better-quality solution being lost. Furthermore, if an appropriate relaxation of the work continuity constraints is allowed, the effect of different distance constraints on the duration could be explored. Therefore, the optimization outcome is compared with the actual situation, and a sensitivity analysis of the distance constraints is performed. The optimization solution of the tunnel construction schedule was obtained, as illustrated in Table 5 and Figure 7.

Table 5.
Optimization of tunnel construction schedule.
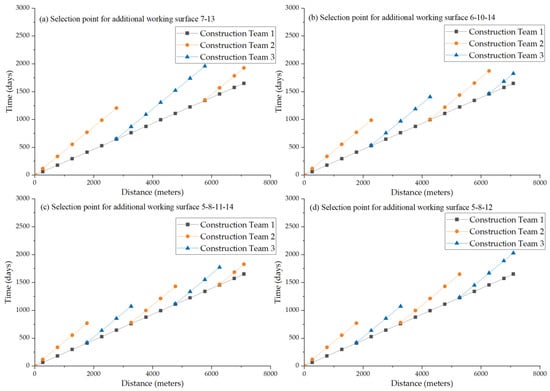
Figure 7.
Tunnel construction schedule optimization schematic.
Evidently, the construction team selected the additional working surface from the 7th and 13th points with a total duration of 1958 days, which is 70 days shorter in comparison with the original optimization schedule, subject to the strict requirement of fixed working continuity distance constraints of 1000 m. Additionally, it has been calculated that the practical construction program that selected additional working surfaces on selection points 5, 8, and 12 would not meet the 1000 m work continuity distance constraints.
With the appropriate relaxation of the work continuity distance constraint, such as a constraint of 800 m, the total duration of the construction project is 1872 days, which is a reduction of 156 days compared to the original duration. When the distance constraint is decreased to 600 m, the total duration of the project is 1826 days, with a saving of 202 days versus the original duration.
5. Practical Case Study
5.1. Case Description
Based on the data sources table provided by the tunnel construction site, the total length of the main tunnel and parallel adit of the study area is 7079 m, and the cross-passage is approximately 33.3 m. There are, in total, 14 cross-passages, the first of which is 54 m from the beginning of main tunnel, with subsequent cross-passages at intervals of 500 m. Three construction teams are involved, with Construction Team 3 responsible for the construction of the parallel adit, while two others were assigned to alternating shifts for the construction of the main tunnel and the cross-passage. The construction speeds for the main tunnel and parallel adit vary according to the tunnel rock mass rating, as displayed in Table 6 and Table A1. The original duration is 3033 days and the work continuity distance constraint is limited to 500 m.

Table 6.
Speed of tunnel construction.
5.2. Results and Analysis
As seen in Table 7, four optimization programs can be generated from the calculation, which are Optimization Program 1, with additional working surface switching points of 6-11-13-15, Optimization Program 2, with additional working surface switching points of 7-11-13-15, Optimization Program 3, with additional working surface switching points of 8-12-15, and Optimization Program 4, with additional working surface switching points of 8-13-15. The optimized durations of the programs are all 2387 days, which is a reduction of 646 days compared to the original duration. In the above-mentioned programs, the idle time of the construction teams was 741, 597, 502, and 459 days, respectively. It can be deduced that the construction team has the minimum waiting time in Optimization Program 4. However, the distance between the 13th and 15th additional working surface switching points is too short; therefore, Optimization Program 4 cannot fulfill the 500 m work continuity constraints. Thus, Optimization Program 3 can be regarded as the optimal tunnel construction schedule plan, in consideration of the duration, construction team idle time, and work continuity distance constraints.

Table 7.
Optimization of tunnel construction schedule.
Through the optimization program presented above, it can be seen that the final additional working surface switching points are all found at position 15, and the last construction activities are located on the working surface that opened in that position; hence, it can be concluded that the position of the final additional working surface switching point is critical to determine the duration. Furthermore, the gap between the construction speeds of the parallel adits and the main tunnel is not sufficiently large, leading to a long idle time for the construction team, which also seriously affects the duration. Therefore, the duration of the project can be shortened by speeding up the parallel adits in a way that creates more additional working surfaces.
By utilizing the TSMOM model and its corresponding algorithms, the tunnel construction schedule can be optimized, leading to the formulation of practical strategies to effectively shorten the duration. Through the methods mentioned above, we can effectively address the limitations of various conditions, such as logical, work continuity, temporal, and spatial constraints, ensuring that the construction meets all relevant requirements. It can also better coordinate the allocation of labor, materials, and machinery resources to reduce idleness and construction stoppages, thereby improving efficiency. In addition, by formulating appropriate strategies tailored to the specific conditions of tunnel construction, it is possible to maximize the utilization of existing resources and mitigate resource wastage and redundant investment. Finally, optimizing tunnel construction scheduling through the above-mentioned methods can enhance the construction’s resilience to uncertainties and improve its risk management capabilities, thereby reducing the likelihood of delays.
6. Conclusions
In summary, the focus of the study is on the optimization of the tunnel construction schedule under soft logic relationships, and the following contributions are presented:
- (1)
- In tunnel construction management, combining soft logic relationships with LSM allows for scenarios where the construction sequence can be changed. In this situation, with work continuity and other conditions as constraints, the duration can be optimized by the creation of additional working surfaces. This could offer a new means of optimizing the tunnel construction schedule.
- (2)
- An MIP model that is applicable to tunnel construction is constructed, which intuitively represents the linear and nonlinear relationships between various construction activities. This provides a reference for the application of the mathematical planning in the optimization of tunnel construction schedules.
- (3)
- Both the exact algorithm and GA are utilized to solve the above-mentioned MIP model using Python 3.7.0, and the obtained results are subsequently analyzed. With the same degree of accuracy, optimization results can be obtained more quickly via GA, which sufficiently demonstrates the superiority of using GA for the optimization of tunnel construction schedules.
- (4)
- The paper carries on the analysis of the actual construction project case, and puts forward improvement strategies with significant practical value. Through the implementation of the TSMOM model and related algorithms, managers can not only optimize resource utilization and enhance construction efficiency, but they also reduce the risk of delays while meeting project requirements. This is conducive to the development of tunnel construction management.
Nevertheless, this study is still characterized by certain limitations. It only focuses on the construction schedule of tunnel projects and does not deal with the optimization of other objectives, such as the cost, the construction quality, and the resource balancing. However, considering the limitations of mathematical planning, the model may not be implemented if more sophisticated constraints and a large number of activities are involved. Therefore, this study is mainly concerned with the optimization of the duration. Moreover, it does not consider factors such as construction modes and the construction directions of activities, and there is still a certain gap with the actual situation in the field. Upcoming research will continue to address the above-mentioned issues, thereby advancing the development of tunnel construction management.
Author Contributions
Conceptualization, J.W. and Y.L.; methodology, J.W. and X.L.; validation, J.W., X.L., Y.F. and Y.W.; formal analysis, J.W. and Y.L.; data curation, J.W.; writing-original draft preparation, J.W.; writing-review and editing, J.W.; visualization, J.W.; supervision, J.W.; project administration, J.W.; funding acquisition, J.W. and Y.L. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the State Key Laboratory for Track Technology of High-speed Railway (grant number 2021YJ111), the Beijing Social Science Foundation (grant numbers 23JCC111), and the Fundamental Research Funds for Central Universities (grant number 2022YJS050).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A

Table A1.
The construction speeds of the parallel adit.
Table A1.
The construction speeds of the parallel adit.
| Distance (Meter) | Construction Speed (Meter/Month) | Duration (Day) |
|---|---|---|
| 0 | — | — |
| 94 | 70 | 37 |
| 294 | 130 | 46 |
| 379 | 70 | 36 |
| 1124 | 130 | 172 |
| 1371 | 70 | 106 |
| 1471 | 30 | 100 |
| 1509 | 70 | 17 |
| 1689 | 130 | 42 |
| 1964 | 190 | 44 |
| 2124 | 130 | 37 |
| 2354 | 190 | 36 |
| 3004 | 130 | 150 |
| 3064 | 30 | 60 |
| 3244 | 70 | 78 |
| 3434 | 130 | 44 |
| 3524 | 65 | 42 |
| 3654 | 30 | 130 |
| 3714 | 70 | 26 |
| 4704 | 130 | 229 |
| 5169 | 70 | 199 |
| 5969 | 130 | 185 |
| 6069 | 70 | 43 |
| 6169 | 30 | 100 |
| 6284 | 70 | 49 |
| 6949 | 130 | 184 |
| 7079 | 30 | 130 |
References
- Zou, X.; Zhang, L.; Zhang, Q. Time-Cost Optimization in Repetitive Project Scheduling with Limited Resources. Eng. Constr. Archit. Manag. 2022, 29, 669–701. [Google Scholar] [CrossRef]
- Monghasemi, S.; Abdallah, M. Linear Optimization Model to Minimize Total Cost of Repetitive Construction Projects and Identify Order of Units. J. Manag. Eng. 2021, 37, 04021036. [Google Scholar] [CrossRef]
- Ding, H.; Zhuang, C.; Liu, J. Extensions of the Resource-Constrained Project Scheduling Problem. Autom. Constr. 2023, 153, 104958. [Google Scholar] [CrossRef]
- Kamandanipour, K.; Tavakkoli-Moghaddam, R.; Haji Yakhchali, S. A Discrete Time/Resource Trade-off Problem with a Critical Chain Method under Uncertainty: A Hybrid Meta-Heuristic Algorithm. Soft Comput. 2023, 27, 17867–17885. [Google Scholar] [CrossRef]
- Altuwaim, A.; El-Rayes, K. Multiobjective Optimization Model for Planning Repetitive Construction Projects. J. Constr. Eng. Manag. 2021, 147, 04021072. [Google Scholar] [CrossRef]
- Tomczak, M.; Jaśkowski, P. Harmonizing Construction Processes in Repetitive Construction Projects with Multiple Buildings. Autom. Constr. 2022, 139, 104266. [Google Scholar] [CrossRef]
- Hegazy, T.; Mostafa, K.; Ojulari, S. Tetris-Inspired Approach for Generating Tightly-Packed Repetitive Schedules. Autom. Constr. 2021, 124, 103601. [Google Scholar] [CrossRef]
- Yogesh, G.; Hanumanth Rao, C. A Study on Linear Scheduling Methods in Road Construction Projects. Mater. Today Proc. 2021, 47, 5475–5478. [Google Scholar] [CrossRef]
- Tang, Y.; Liu, R.; Wang, F.; Sun, Q.; Kandil, A.A. Scheduling Optimization of Linear Schedule with Constraint Programming. Comput. Aided Civ. Infrastruct. Eng. 2018, 33, 124–151. [Google Scholar] [CrossRef]
- Wang, Z.; Hu, Z.; Tang, Y. Float-Based Resource Leveling Optimization of Linear Projects. IEEE Access 2020, 8, 176997–177020. [Google Scholar] [CrossRef]
- Eid, M.S.; Elbeltagi, E.E.; El-Adaway, I.H. Simultaneous Multi-Criteria Optimization for Scheduling Linear Infrastructure Projects. Int. J. Constr. Manag. 2021, 21, 41–55. [Google Scholar] [CrossRef]
- García-Nieves, J.D.; Ponz-Tienda, J.L.; Ospina-Alvarado, A.; Bonilla-Palacios, M. Multipurpose Linear Programming Optimization Model for Repetitive Activities Scheduling in Construction Projects. Autom. Constr. 2019, 105, 102799. [Google Scholar] [CrossRef]
- Liu, S.-S.; Budiwirawan, A.; Arifin, M.F.A. Non-Sequential Linear Construction Project Scheduling Model for Minimizing Idle Equipment Using Constraint Programming (CP). Mathematics 2021, 9, 2492. [Google Scholar] [CrossRef]
- Hegazy, T.; Kamarah, E. Schedule Optimization for Scattered Repetitive Projects. Autom. Constr. 2022, 133, 104042. [Google Scholar] [CrossRef]
- Zou, X.; Wu, G.; Zhang, Q. Work Continuity Constraints in Repetitive Project Scheduling Considering Soft Logic. Eng. Constr. Archit. Manag. 2021, 28, 1713–1738. [Google Scholar] [CrossRef]
- Hegazy, T.; Saad, D.A.; Mostafa, K. Enhanced Repetitive-Scheduling Computation and Visualization. J. Constr. Eng. Manag. 2020, 146, 04020118. [Google Scholar] [CrossRef]
- Hu, Z.; Wang, F.; Tang, Y. Scenario-oriented Repetitive Project Scheduling Optimization. Comput. Aided Civ. Infrastruct. Eng. 2023, 38, 1239–1273. [Google Scholar] [CrossRef]
- Salama, T.; Moselhi, O. Multi-Objective Optimization for Repetitive Scheduling under Uncertainty. Eng. Constr. Archit. Manag. 2019, 26, 1294–1320. [Google Scholar] [CrossRef]
- Altuwaim, A.; El-Rayes, K. Minimizing Duration and Crew Work Interruptions of Repetitive Construction Projects. Autom. Constr. 2018, 88, 59–72. [Google Scholar] [CrossRef]
- Hassan, A.; El-Rayes, K.; Attalla, M. Optimizing the Scheduling of Crew Deployments in Repetitive Construction Projects under Uncertainty. Eng. Constr. Archit. Manag. 2021, 28, 1615–1634. [Google Scholar] [CrossRef]
- Altuwaim, A.; El-Rayes, K. Optimizing the Scheduling of Repetitive Construction to Minimize Interruption Cost. J. Constr. Eng. Manag. 2018, 144, 04018051. [Google Scholar] [CrossRef]
- Shafahi, A.; Haghani, A. Project Selection and Scheduling for Phase-Able Projects with Interdependencies among Phases. Autom. Constr. 2018, 93, 47–62. [Google Scholar] [CrossRef]
- Zhentao, H.; Nanfang, C.; Xuejun, H.; Edgar Mahaffey, M.A. Time- and Resource-Based Robust Scheduling Algorithms for Multi-Skilled Projects. Autom. Constr. 2023, 153, 104948. [Google Scholar] [CrossRef]
- Tang, Y.; Liu, R.; Sun, Q. Two-Stage Scheduling Model for Resource Leveling of Linear Projects. J. Constr. Eng. Manag. 2014, 140, 04014022. [Google Scholar] [CrossRef]
- Tran, D.-H.; Chou, J.-S.; Luong, D.-L. Optimizing Non-Unit Repetitive Project Resource and Scheduling by Evolutionary Algorithms. Oper. Res. Int. J. 2022, 22, 77–103. [Google Scholar] [CrossRef]
- Yu, Z.; Wang, C.; Zhao, Y.; Hu, Z.; Tang, Y. Linear Project-Scheduling Optimization Considering a Reverse Construction Scenario. Appl. Sci. 2023, 13, 9407. [Google Scholar] [CrossRef]
- Gupta, R.; Trivedi, M.K. AEHO: Apriori-Based Optimized Model for Building Construction to Time-Cost Tradeoff Modeling. IEEE Access 2022, 10, 103852–103871. [Google Scholar] [CrossRef]
- Huang, Y.; Zou, X.; Zhang, L. Genetic Algorithm–Based Method for the Deadline Problem in Repetitive Construction Projects Considering Soft Logic. J. Manag. Eng. 2016, 32, 04016002. [Google Scholar] [CrossRef]
- Tao, S.; Wu, C.; Sheng, Z.; Wang, X. Space-Time Repetitive Project Scheduling Considering Location and Congestion. J. Comput. Civ. Eng. 2018, 32, 04018017. [Google Scholar] [CrossRef]
- Su, Y.; Lucko, G. Linear Scheduling with Multiple Crews Based on Line-of-Balance and Productivity Scheduling Method with Singularity Functions. Autom. Constr. 2016, 70, 38–50. [Google Scholar] [CrossRef]
- Hegazy, T.; Abdel-Monem, M.; Atef Saad, D. Framework for Enhanced Progress Tracking and Control of Linear Projects. Eng. Constr. Archit. Manag. 2014, 21, 94–110. [Google Scholar] [CrossRef]
- Tang, Y.; Liu, R.; Sun, Q. Schedule Control Model for Linear Projects Based on Linear Scheduling Method and Constraint Programming. Autom. Constr. 2014, 37, 22–37. [Google Scholar] [CrossRef]
- Tang, Y.; Sun, Q.; Liu, R.; Wang, F. Resource Leveling Based on Line of Balance and Constraint Programming. Comput. Aided Civ. Infrastruct. Eng. 2018, 33, 864–884. [Google Scholar] [CrossRef]
- Yamín, R.A.; Harmelink, D.J. Comparison of Linear Scheduling Model (LSM) and Critical Path Method (CPM). J. Constr. Eng. Manag. 2001, 127, 374–381. [Google Scholar] [CrossRef]
- García-Nieves, J.D.; Ponz-Tienda, J.L.; Salcedo-Bernal, A.; Pellicer, E. The Multimode Resource-Constrained Project Scheduling Problem for Repetitive Activities in Construction Projects. Comput. Aided Civ. Infrastruct. Eng. 2018, 33, 655–671. [Google Scholar] [CrossRef]
- Lucko, G.; Alves, T.D.C.L.; Angelim, V.L. Challenges and Opportunities for Productivity Improvement Studies in Linear, Repetitive, and Location-Based Scheduling. Constr. Manag. Econ. 2014, 32, 575–594. [Google Scholar] [CrossRef]
- Tamimi, S.; Diekmann, J. Soft Logic in Network Analysis. J. Comput. Civ. Eng. 1988, 2, 289–300. [Google Scholar] [CrossRef]
- Fan, S.-L.; Tserng, H.P.; Wang, M.-T. Development of an Object-Oriented Scheduling Model for Construction Projects. Autom. Constr. 2003, 12, 283–302. [Google Scholar] [CrossRef]
- Zou, X.; Zhang, L. A Constraint Programming Approach for Scheduling Repetitive Projects with Atypical Activities Considering Soft Logic. Autom. Constr. 2020, 109, 102990. [Google Scholar] [CrossRef]
- Pan, X.; Zhao, X.; Shen, H. The Concept, Influence, and Mechanism of Human Work Interruptions Based on the Grounded Theory. Front. Psychol. 2023, 14, 1044233. [Google Scholar] [CrossRef]
- Peiris, A.; Hui, F.K.P.; Duffield, C.; Ngo, T. Production Scheduling in Modular Construction: Metaheuristics and Future Directions. Autom. Constr. 2023, 150, 104851. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).