A Tube Linear Model Predictive Control Approach for Autonomous Vehicles Subjected to Disturbances
Abstract
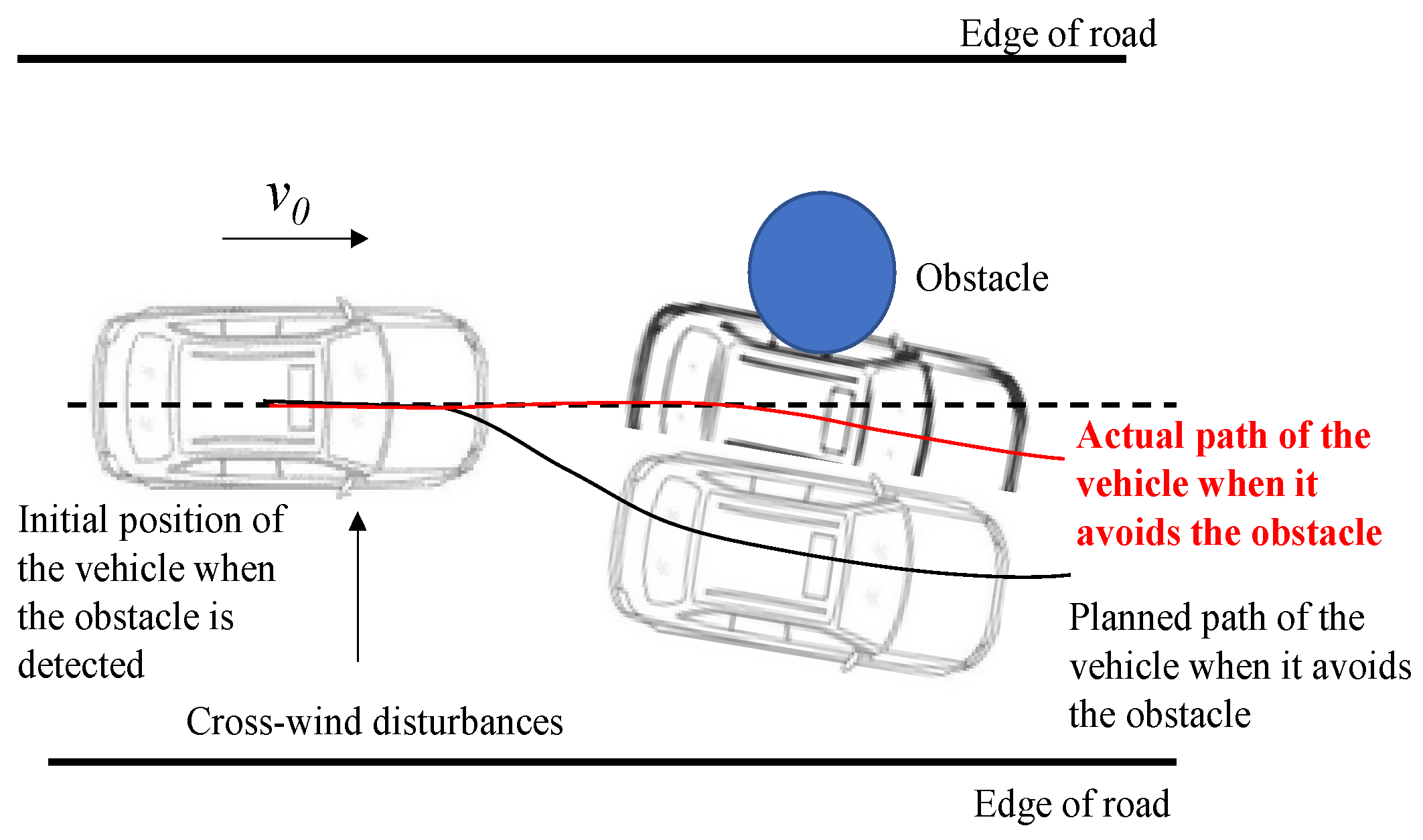
1. Introduction
2. Tube Linear MPC Methodology
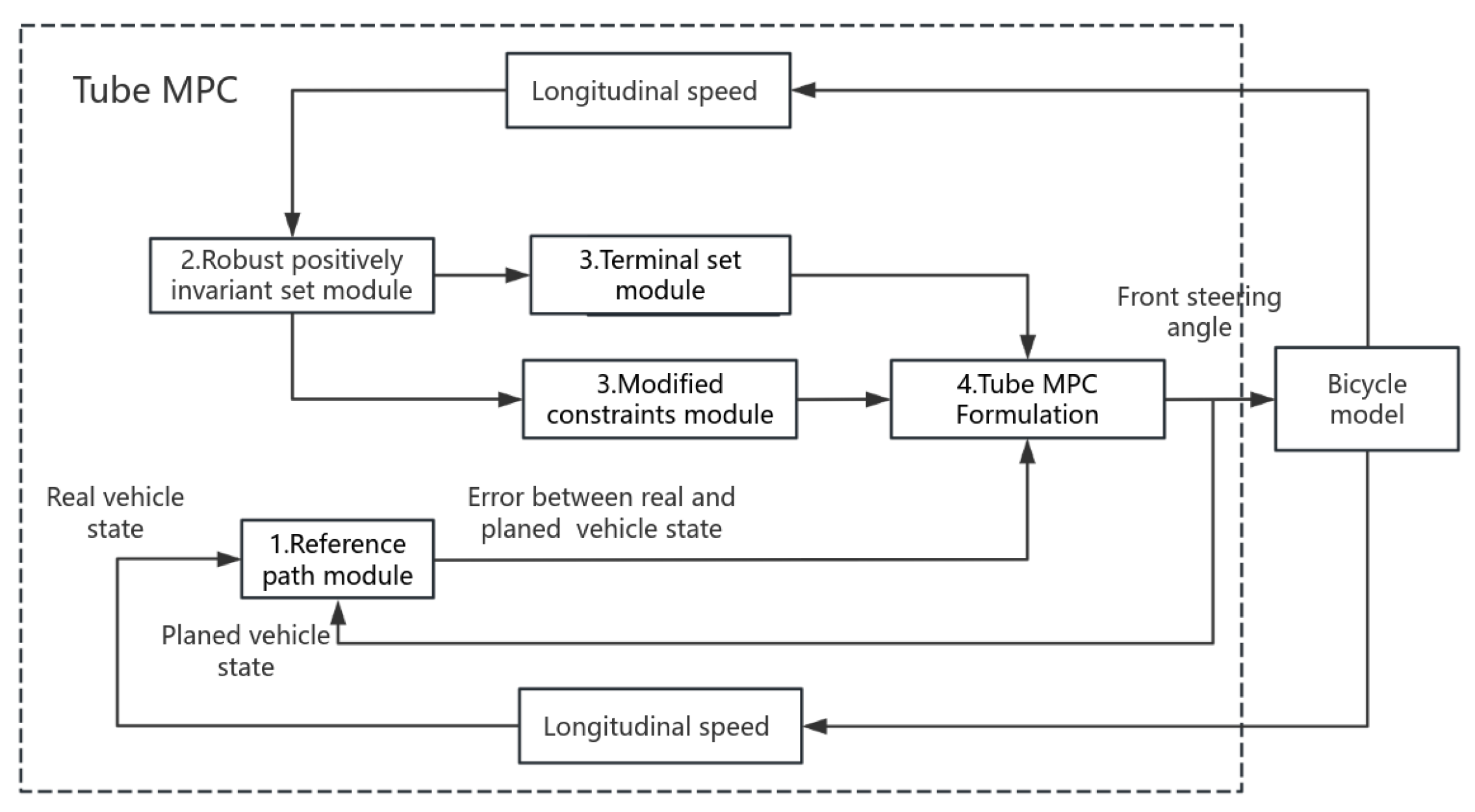
2.1. Control Architecture of Tube MPC
2.2. Set Invariance Theory
2.3. Tube MPC Theory
2.4. Computation of the Approximate Invariant Set
| Algorithm 1. Computation of the minimal robust positively invariant set |
| 1: Input |
| 2: |
| 3: Repeat |
| 4: Compute with Equation (16) |
| 5: Compute with Equation (17) |
| 6: |
| 7: Until |
| 8: Compute with Equation (14) and |
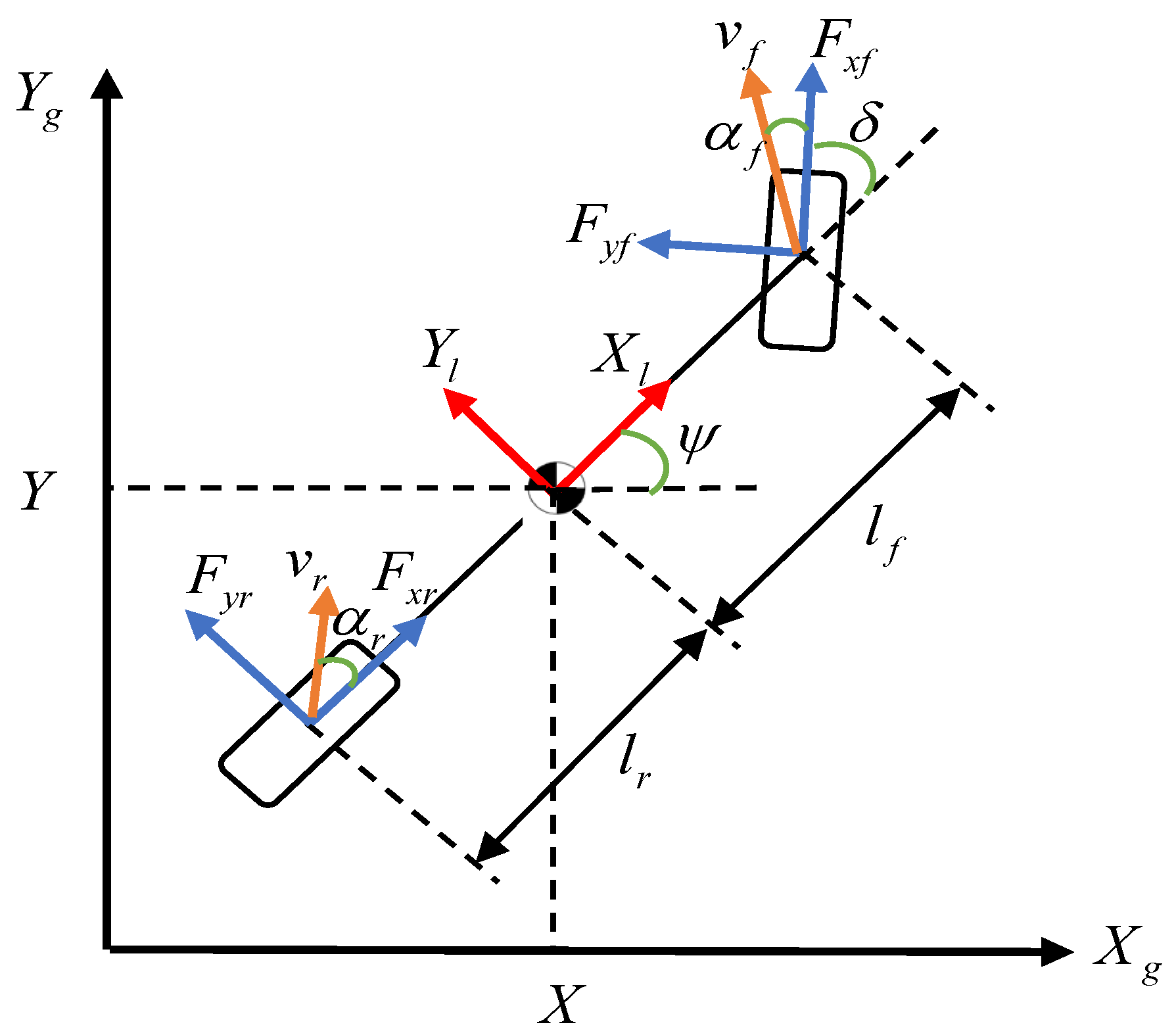
3. Vehicle Dynamics Model
3.1. Lateral Dynamics and Tracking Error Model
3.2. The Zero Steady-State Model
4. Collision Avoidance Constraints
5. The Tube MPC Optimization Problem
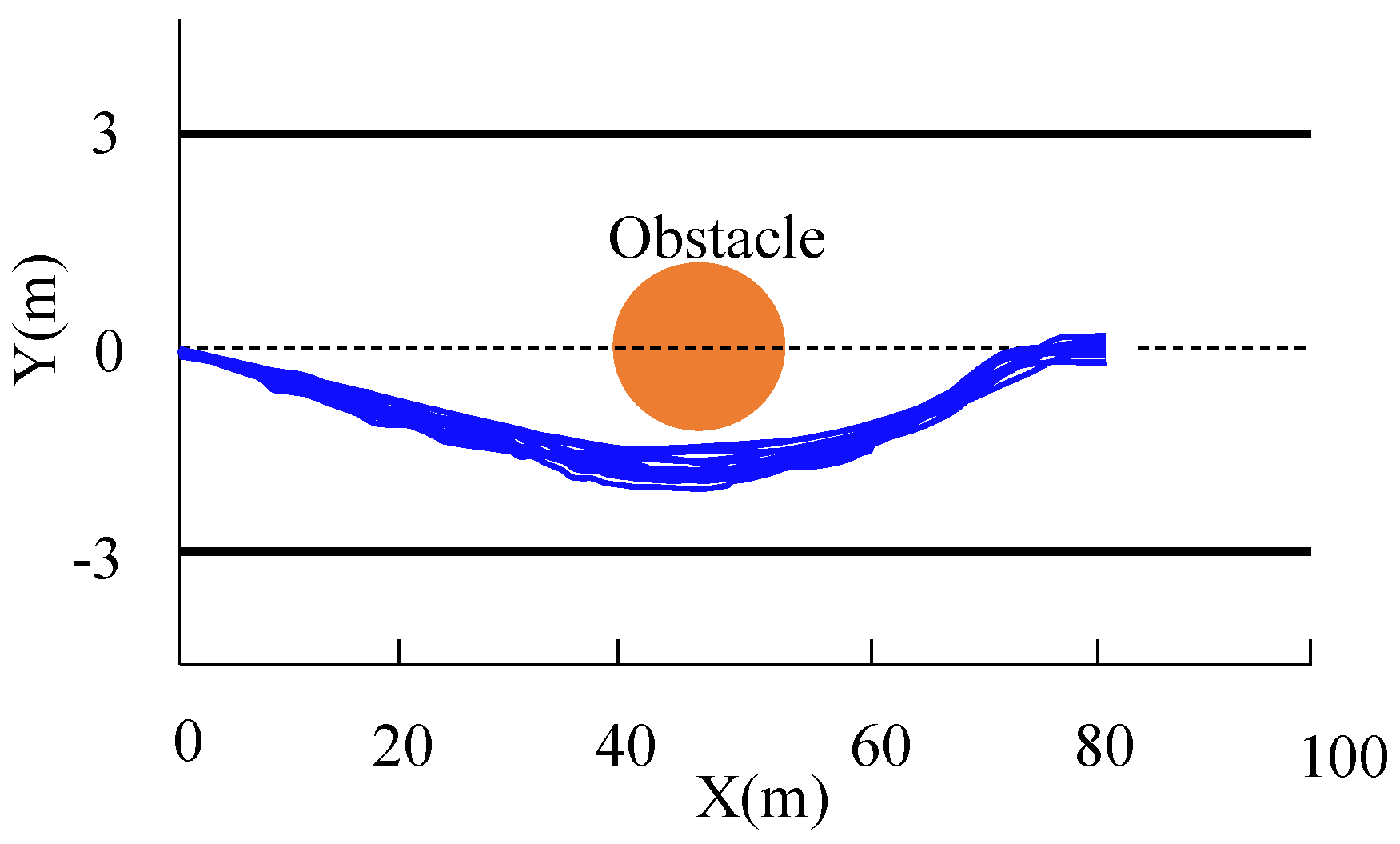
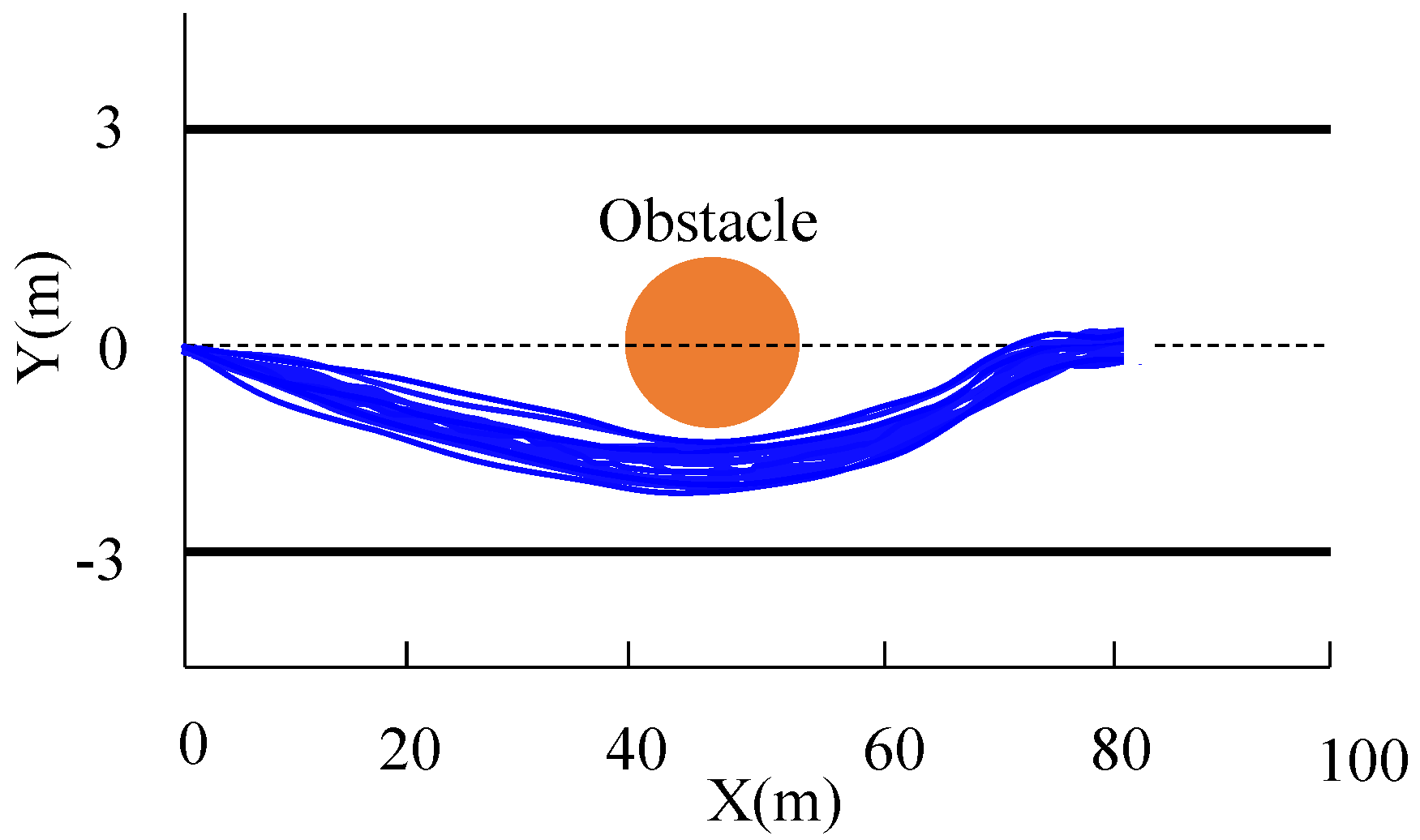
6. Simulation Results and Discussion
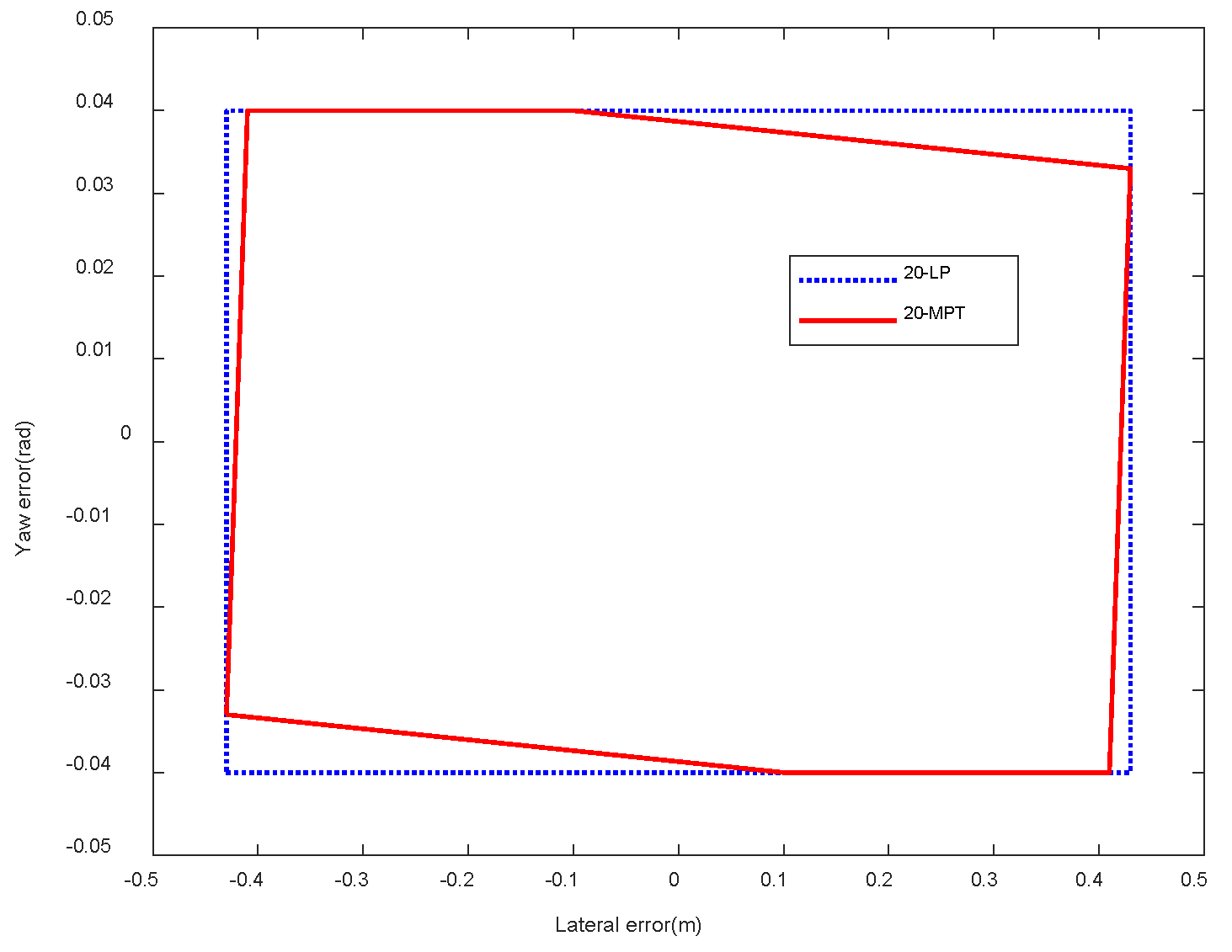
6.1. Comparison of the Robust Invariant Set by the MPT and LP Method
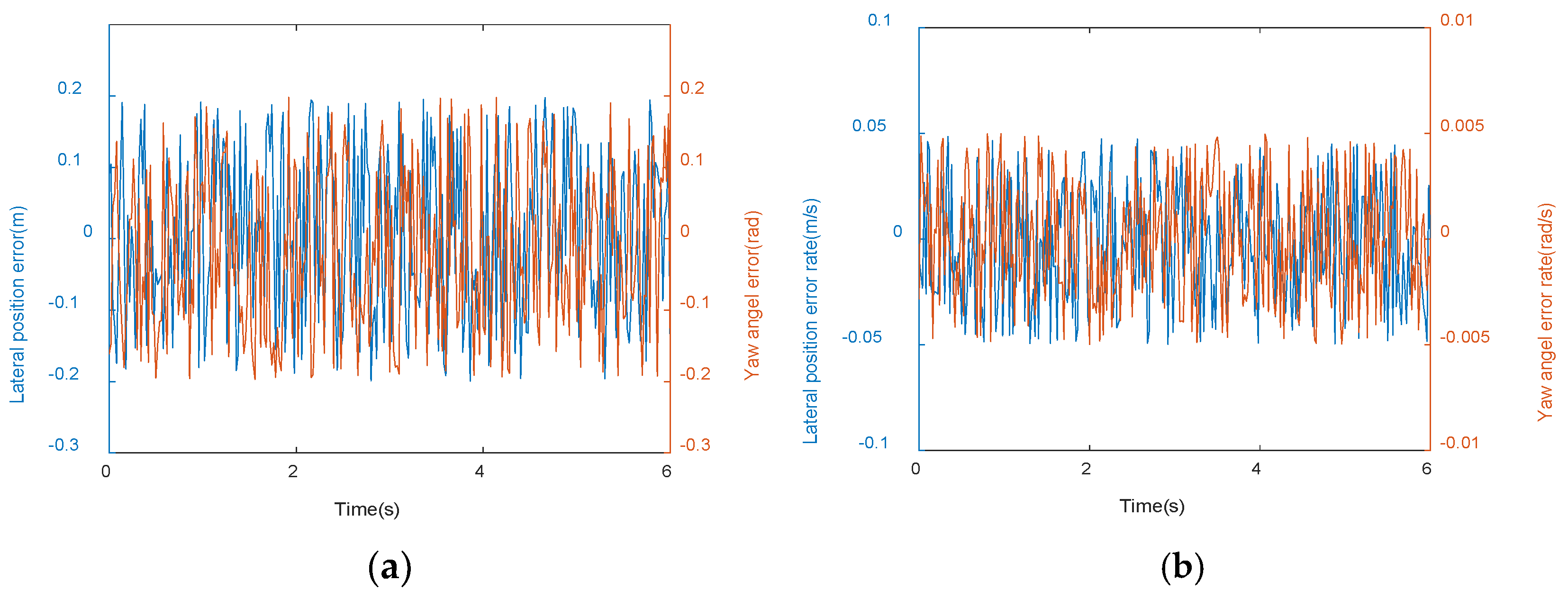
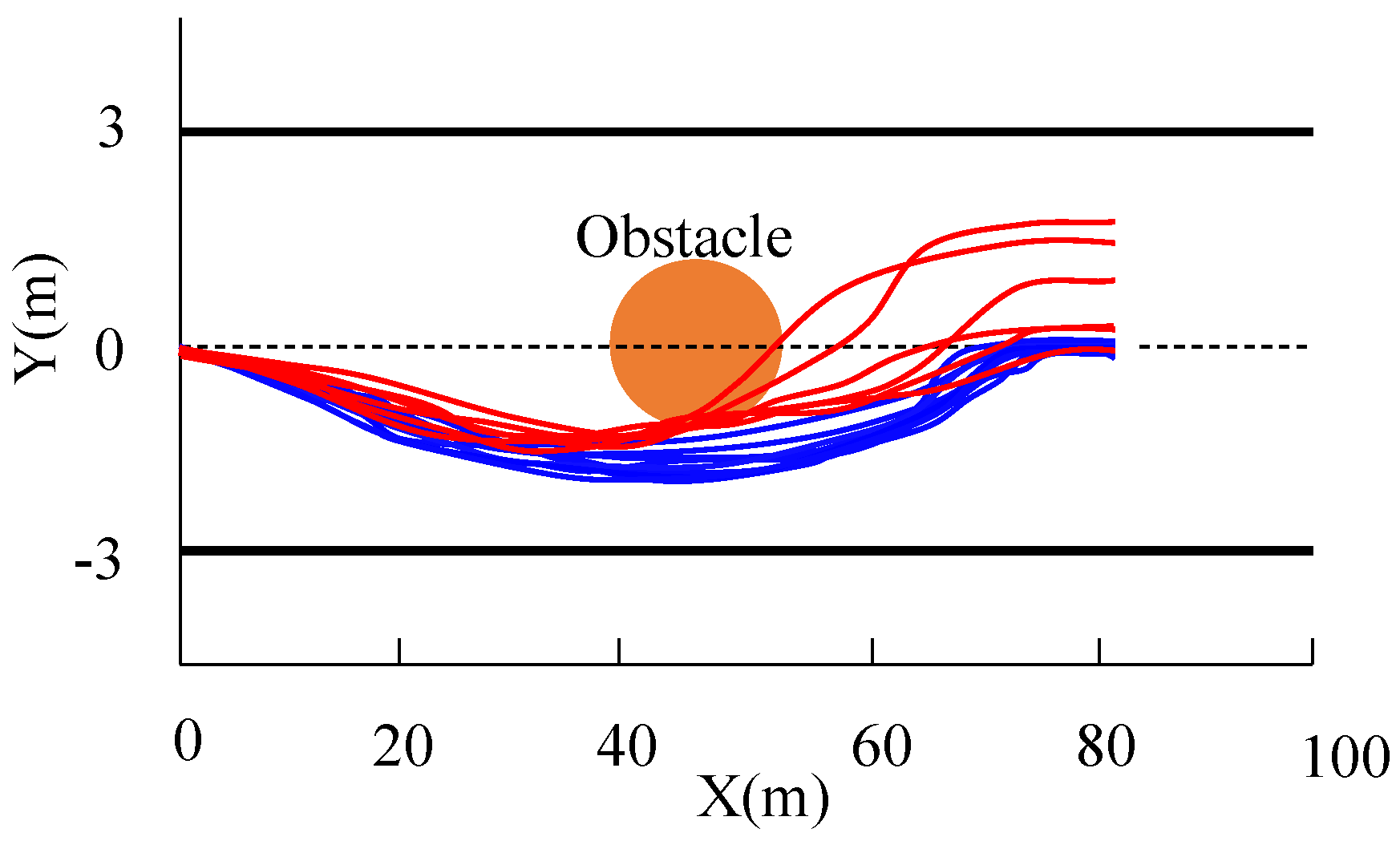
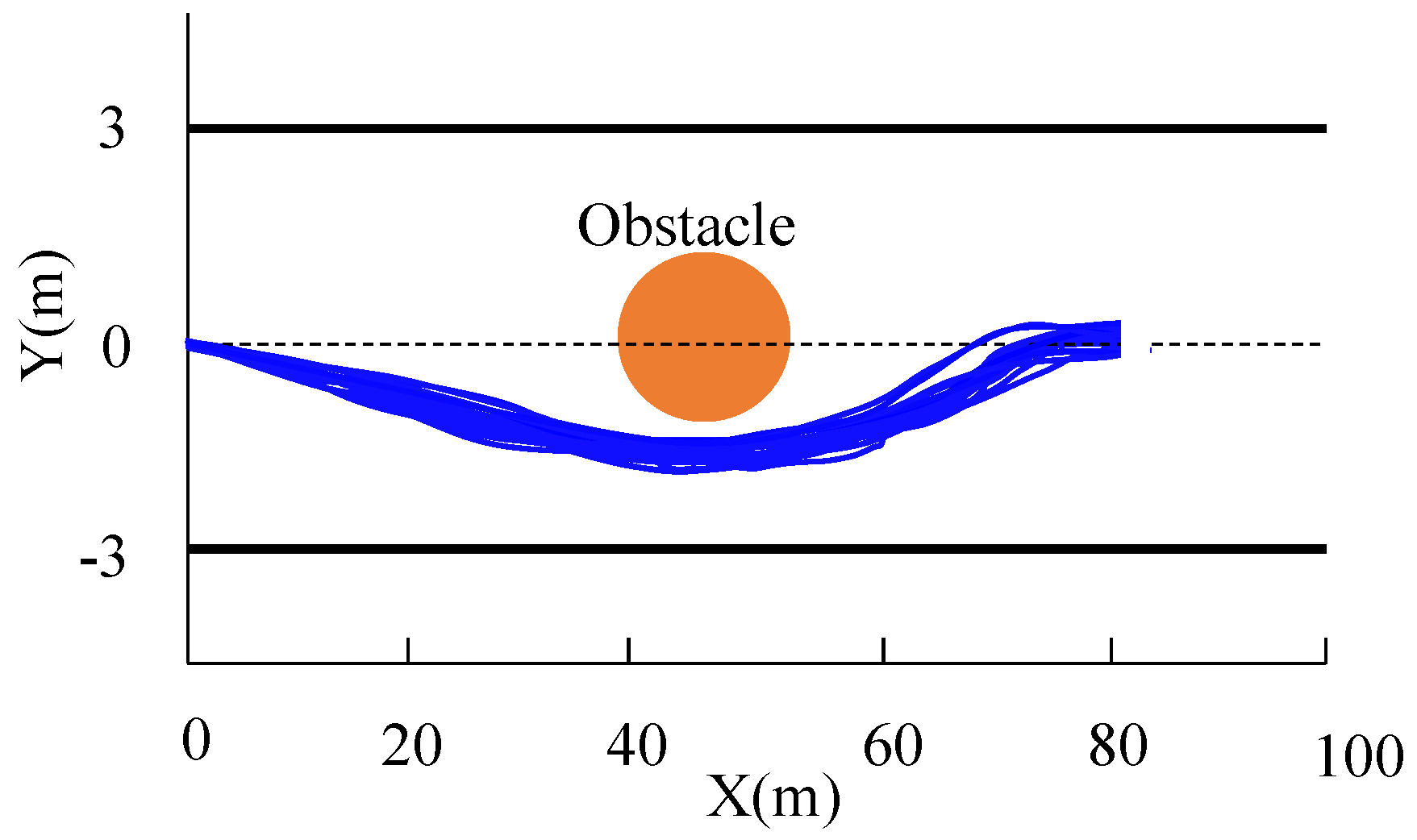
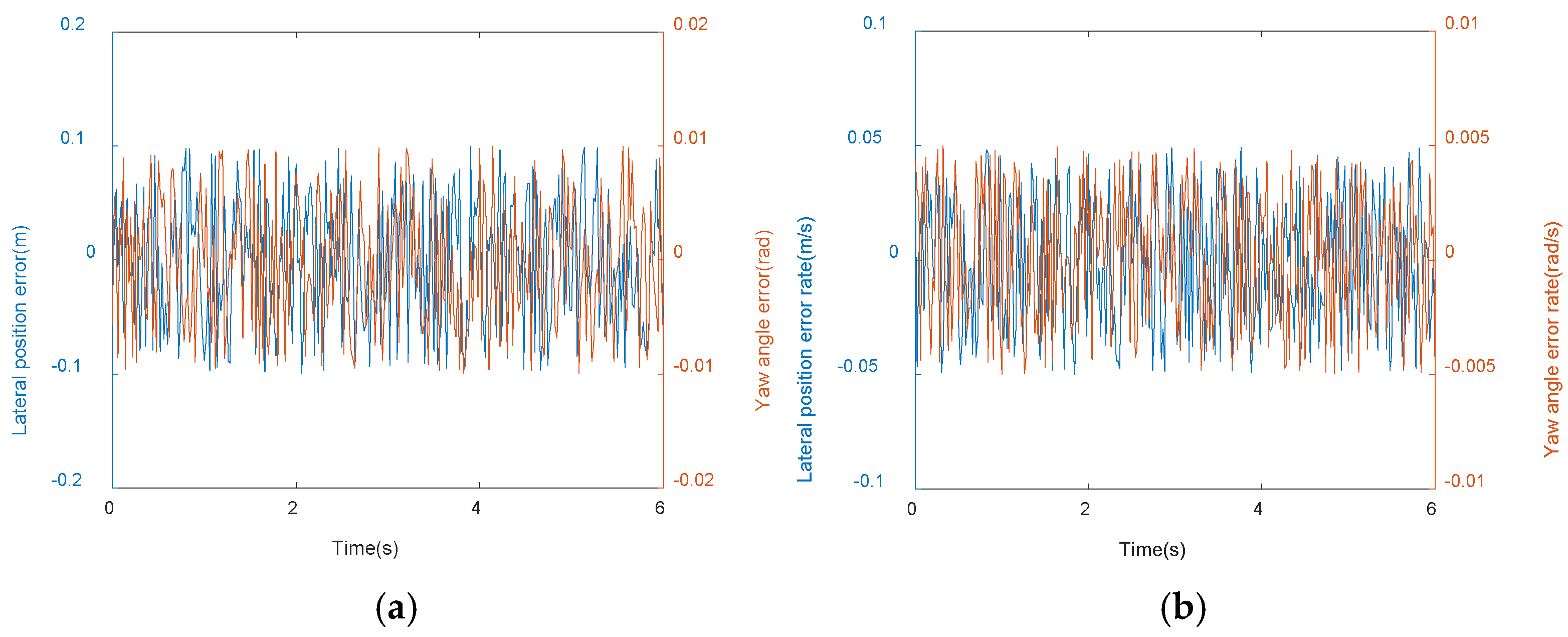
6.2. Performance with State Disturbances
6.3. Performance with Uncertain Tire Road Friction Coefficients
6.4. Performance with Cross-Wind Disturbances
6.5. The Performance with Both Uncertain Wind Disturbance and Friction Coefficients
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Li, Z.; Cui, G.; Li, S.; Zhang, N.; Tian, Y.; Shang, X. Lane Keeping Control Based on Model Predictive Control Under Region of Interest Prediction Considering Vehicle Motion States. Int. J. Automot. Technol. 2020, 21, 1001–1011. [Google Scholar] [CrossRef]
- Liu, Y.; Jiang, J. Optimum path-tracking control for inverse problem of vehicle handling dynamics. J. Mech. Sci. Technol. 2016, 30, 3433–3440. [Google Scholar] [CrossRef]
- Liu, Z.; Yuan, Q.; Nie, G.; Tian, Y. A Multi-Objective Model Predictive Control for Vehicle Adaptive Cruise Control System Based on a New Safe Distance Model. Int. J. Automot. Technol. 2021, 22, 475–487. [Google Scholar] [CrossRef]
- Pyun, B.; Seo, M.; Kim, S.; Choi, H. Development of an Autonomous Driving Controller for Articulated Bus Using Model Predictive Control Algorithm with Inner Model. Int. J. Automot. Technol. 2022, 23, 357–366. [Google Scholar] [CrossRef]
- Yin, J.; Fu, W. Framework of integrating trajectory replanning with tracking for self-driving cars. J. Mech. Sci. Technol. 2021, 35, 5655–5663. [Google Scholar] [CrossRef]
- Song, Y.; Huh, K. Driving and steering collision avoidance system of autonomous vehicle with model predictive control based on non-convex optimization. Adv. Mech. Eng. 2021, 13, 16878140211027669. [Google Scholar] [CrossRef]
- Seo, J.H.; Kwon, S.K.; Kim, K.D. A discrete-time linear model predictive control for motion planning of an autonomous vehicle with adaptive cruise control and obstacle overtaking. Adv. Mech. Eng. 2022, 14, 16878132221119899. [Google Scholar] [CrossRef]
- Calzolari, D.; Schürmann, B.; Althoff, M. Comparison of trajectory tracking controllers for autonomous vehicles. In Proceedings of the 2017 IEEE 20th International Conference on Intelligent Transportation Systems (ITSC), Yokohama, Japan, 16–19 October 2017. [Google Scholar]
- Cao, J.; Song, C.; Peng, S.; Song, S.; Zhang, X.; Xiao, F. Trajectory tracking control algorithm for autonomous vehicle considering cornering characteristics. IEEE Access 2020, 8, 59470–59484. [Google Scholar] [CrossRef]
- Qian, Y.; Feng, S.; Hu, W.; Wang, W. Obstacle avoidance planning of autonomous vehicles using deep reinforcement learning. Adv. Mech. Eng. 2022, 14, 16878132221139661. [Google Scholar] [CrossRef]
- Liu, H.; Yao, Y.; Wang, J.; Qin, Y.; Li, T. A control architecture to coordinate energy management with trajectory tracking control for fuel cell/battery hybrid unmanned aerial vehicles. Int. J. Hydrog. Energy 2022, 47, 15236–15253. [Google Scholar] [CrossRef]
- He, W.; Tang, X.; Wang, T.; Liu, Z. Trajectory tracking control for a three-dimensional flexible wing. IEEE Trans. Control Syst. Technol. 2022, 30, 2243–2250. [Google Scholar] [CrossRef]
- Zhai, L.; Wang, C.; Hou, Y.; Liu, C. MPC-based integrated control of trajectory tracking and handling stability for intelligent driving vehicle driven by four hub motor. IEEE Trans. Veh. Technol. 2022, 71, 2668–2680. [Google Scholar] [CrossRef]
- Rovira-Más, F.; Zhang, Q. Fuzzy logic control of an electrohydraulic valve for auto-steering off-road vehicles. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2008, 222, 917–934. [Google Scholar] [CrossRef]
- Nam, K.; Oh, S.; Fujimoto, H.; Hori, Y. Robust yaw stability control for electric vehicles based on active front steering control through a steer-by-wire system. Int. J. Automot. Technol. 2012, 13, 1169–1186. [Google Scholar] [CrossRef]
- Guo, J.; Luo, Y.; Li, K. Adaptive coordinated collision avoidance control of autonomous ground vehicles. Proc. Inst. Mech. Eng. Part I J. Syst. Control Eng. 2018, 232, 1120–1133. [Google Scholar] [CrossRef]
- Norouzi, A.; Kazemi, R.; Azadi, S. Vehicle lateral control in the presence of uncertainty for lane change maneuver using adaptive sliding mode control with fuzzy boundary layer. Proc. Inst. Mech. Eng. Part I J. Syst. Control Eng. 2018, 232, 12–28. [Google Scholar] [CrossRef]
- Li, S.; Li, Z.; Yu, Z.; Zhang, B.; Zhang, N. Dynamic trajectory planning and tracking for autonomous vehicle with obstacle avoidance based on model predictive control. IEEE Access 2019, 7, 132074–132086. [Google Scholar] [CrossRef]
- Naus, G.; Van Den Bleek, R.; Ploeg, J.; Scheepers, B.; van de Molengraft, R.; Steinbuch, M. Explicit MPC design and performance evaluation of an ACC Stop-&-Go. In Proceedings of the 2008 American Control Conference, Washington, DC, USA, 11–13 June 2008; IEEE: Piscataway, NJ, USA, 2008; pp. 224–229. [Google Scholar]
- Sename, O.; Gaspar, P.; Bokor, J. (Eds.) Robust Control and Linear Parameter Varying Approaches: Application to Vehicle Dynamics; Springer: Berlin/Heidelberg, Germany, 2013; Volume 437. [Google Scholar]
- Tuchner, A.; Haddad, J. Vehicle platoon formation using interpolating control: A laboratory experimental analysis. Transp. Res. Part C Emerg. Technol. 2017, 84, 21–47. [Google Scholar] [CrossRef]
- Li, S.E.; Jia, Z.; Li, K.; Cheng, B. Fast online computation of a model predictive controller and its application to fuel economy–oriented adaptive cruise control. IEEE Trans. Intell. Transp. Syst. 2014, 16, 1199–1209. [Google Scholar] [CrossRef]
- Hoffmann, C.; Werner, H. A survey of linear parameter-varying control applications validated by experiments or high-fidelity simulations. IEEE Trans. Control Syst. Technol. 2014, 23, 416–433. [Google Scholar] [CrossRef]
- Liniger, A.; Zhang, X.; Aeschbach, P.; Georghiou, A.; Lygeros, J. Racing miniature cars: Enhancing performance using stochastic MPC and disturbance feedback. In Proceedings of the 2017 American Control Conference (ACC), Washington, DC, USA, 24–26 May 2017; IEEE: Piscataway, NJ, USA, 2017. [Google Scholar]
- Mayne, D.Q.; Seron, M.M.; Raković, S.V. Robust model predictive control of constrained linear systems with bounded disturbances. Automatica 2005, 41, 219–224. [Google Scholar] [CrossRef]
- Gao, Y.; Gray, A.; Tseng, H.E.; Borrelli, F. A tube-based robust nonlinear predictive control approach to semiautonomous ground vehicles. Veh. Syst. Dyn. 2014, 52, 802–823. [Google Scholar] [CrossRef]
- Seo, J.; Yi, K. Robust Mode Predictive Control for Lane Change of Automated Driving Vehicles; SAE Technical Paper; SAE: Warrendale, PA, USA, 2015. [Google Scholar]
- Wischnewski, A.; Euler, M.; Gümüs, S.; Lohmann, B. Tube model predictive control for an autonomous race car. Veh. Syst. Dyn. 2022, 60, 3151–3173. [Google Scholar] [CrossRef]
- Wischnewski, A.; Herrmann, T.; Werner, F.; Lohmann, B. A tube-MPC approach to autonomous multi-vehicle racing on high-speed ovals. IEEE Trans. Intell. Veh. 2022, 8, 368–378. [Google Scholar] [CrossRef]
- Yu, J.; Guo, X.; Pei, X.; Chen, Z.; Zhou, W.; Zhu, M.; Wu, C. Path tracking control based on tube MPC and time delay motion prediction. Intell. Transp. Syst. 2020, 14, 1–12. [Google Scholar] [CrossRef]
- Rakovic, S.V.; Kerrigan, E.C.; Kouramas, K.I.; Mayne, D.Q. Invariant approximations of the minimal robust positively invariant set. IEEE Trans. Autom. Control 2005, 50, 406–410. [Google Scholar] [CrossRef]
- Chen, J.; Tian, G.; Fu, Y. A novel multi-objective tuning strategy for model predictive control in trajectory tracking. J. Mech. Sci. Technol. 2023, 37, 6657–6667. [Google Scholar] [CrossRef]
- Rajamani, R. Vehicle Dynamics and Control; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Kvasnica, M.; Grieder, P.; Baotić, M.; Morari, M. Multi-parametric toolbox (MPT). In Proceedings of the Hybrid Systems: Computation and Control: 7th International Workshop, HSCC 2004, Philadelphia, PA, USA, 25–27 March 2004; Proceedings 7. Springer: Berlin/Heidelberg, Germany, 27 March 2004; pp. 448–462. [Google Scholar]
- Hosseinzadeh, M.; Sinopoli, B.; Kolmanovsky, I.; Baruah, S. Robust to early termination model predictive control. IEEE Trans. Autom. Control 2023. [Google Scholar] [CrossRef]
- Feller, C.; Ebenbauer, C. Sparsity-exploiting anytime algorithms for model predictive control: A relaxed barrier approach. IEEE Trans. Control Syst. Technol. 2018, 28, 425–435. [Google Scholar] [CrossRef]




| Mass | 1723 kg |
| Inertia moment | 2175 kg/m2 |
| Distance between the front axle and center mass | 1.232 m |
| Distance between the rear axle and center mass | 1.468 m |
| The cornering stiffness of the front tire | 66,900 N/Rad |
| The cornering stiffness of the rear tire | 62,700 N/Rad |
| The initial speed | 50 km/h |
| Friction coefficients | 0.5 |
| Predictive horizon | 20 |
| Control horizon | 10 |
| Sample time | 0.02 s |
| State disturbance | |
| Q | [1, 1; 0, 5] |
| R | [1] |
| P | [1, 1; 1, 1] |
| H | 10,000 |
| Limited slip angle of vehicle | |
| Limited slip angle of the front and rear tires | 0.25 |
| LP | MPT | |
|---|---|---|
| The 20-step robust invariant set | 0.03 s | 9.6 s |
| Proposed Tube MPC Method | Traditional MPC Method | |
|---|---|---|
| Number of trajectories | 20 | 14 |
| Proposed Tube MPC Method | Traditional MPC Method | |
|---|---|---|
| Number of trajectories | 20 | 16 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, J.; Tian, G. A Tube Linear Model Predictive Control Approach for Autonomous Vehicles Subjected to Disturbances. Appl. Sci. 2024, 14, 2793. https://doi.org/10.3390/app14072793
Chen J, Tian G. A Tube Linear Model Predictive Control Approach for Autonomous Vehicles Subjected to Disturbances. Applied Sciences. 2024; 14(7):2793. https://doi.org/10.3390/app14072793
Chicago/Turabian StyleChen, Jianqiao, and Guofu Tian. 2024. "A Tube Linear Model Predictive Control Approach for Autonomous Vehicles Subjected to Disturbances" Applied Sciences 14, no. 7: 2793. https://doi.org/10.3390/app14072793
APA StyleChen, J., & Tian, G. (2024). A Tube Linear Model Predictive Control Approach for Autonomous Vehicles Subjected to Disturbances. Applied Sciences, 14(7), 2793. https://doi.org/10.3390/app14072793






