Experimental and Theoretical Investigations of the Mechanical Behavior of Column-Free Quasi-Rectangular Segmental Tunnel Linings
Abstract
Featured Application
Abstract
1. Introduction
2. Prototype Experiment
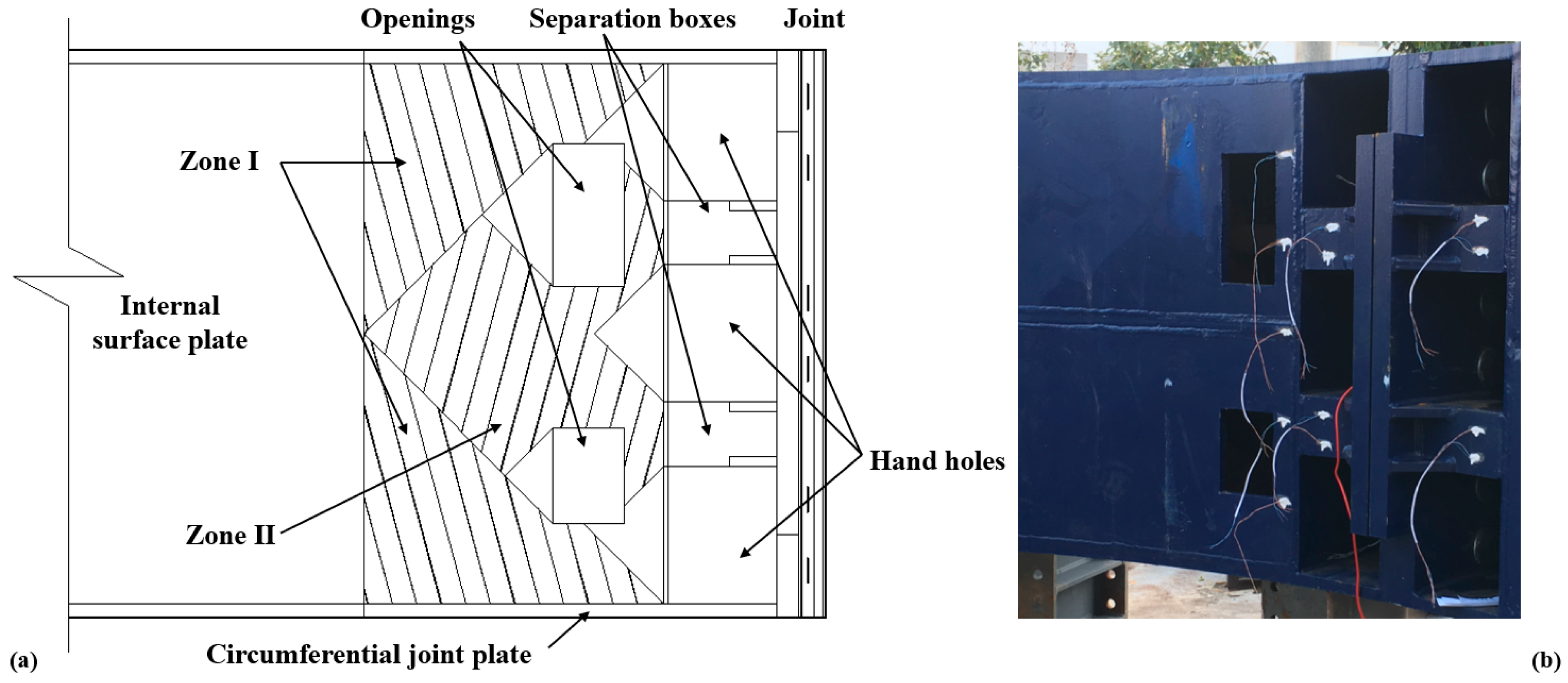
2.1. Project Background and Test Specimen
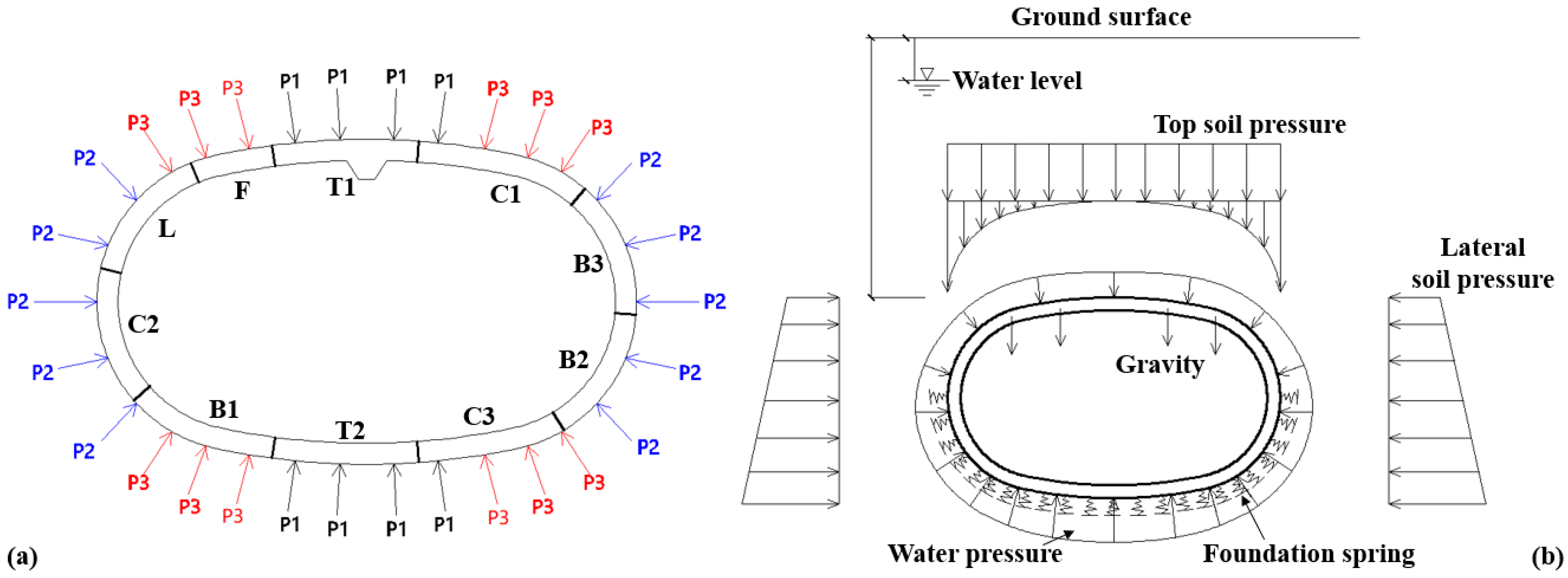
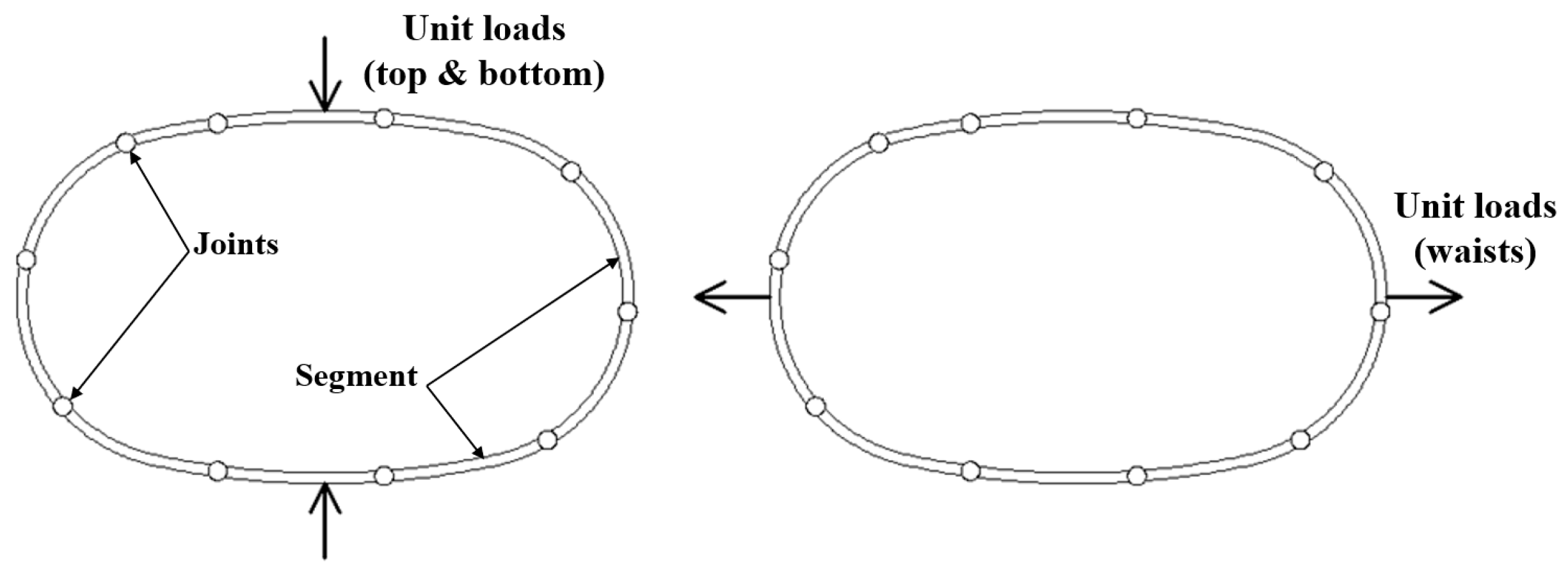
2.2. Test Setup
- All test loads must fulfill a self-balancing condition [33] to ensure the safety and stability of the prototype test platform during the test loading process. If the design of the test load is unbalanced, it will cause unexpected relative motion between the centers of the specimen and the counterforce frame, thereby affecting the stability of the platform;
- It is necessary to ensure that the deviation of target structural responses (deformation or internal force) between the design loading state and the test loading state remains within an acceptable range. Considering that the design of segments and joints is mainly governed by bending moment, greater emphasis should be placed on bending moment rather than axial force and shear force when determining the test loads.
- Structural deformation;
- Joint deformation and bolt axial force.
2.3. Experimental Results
2.3.1. Structural Deformation
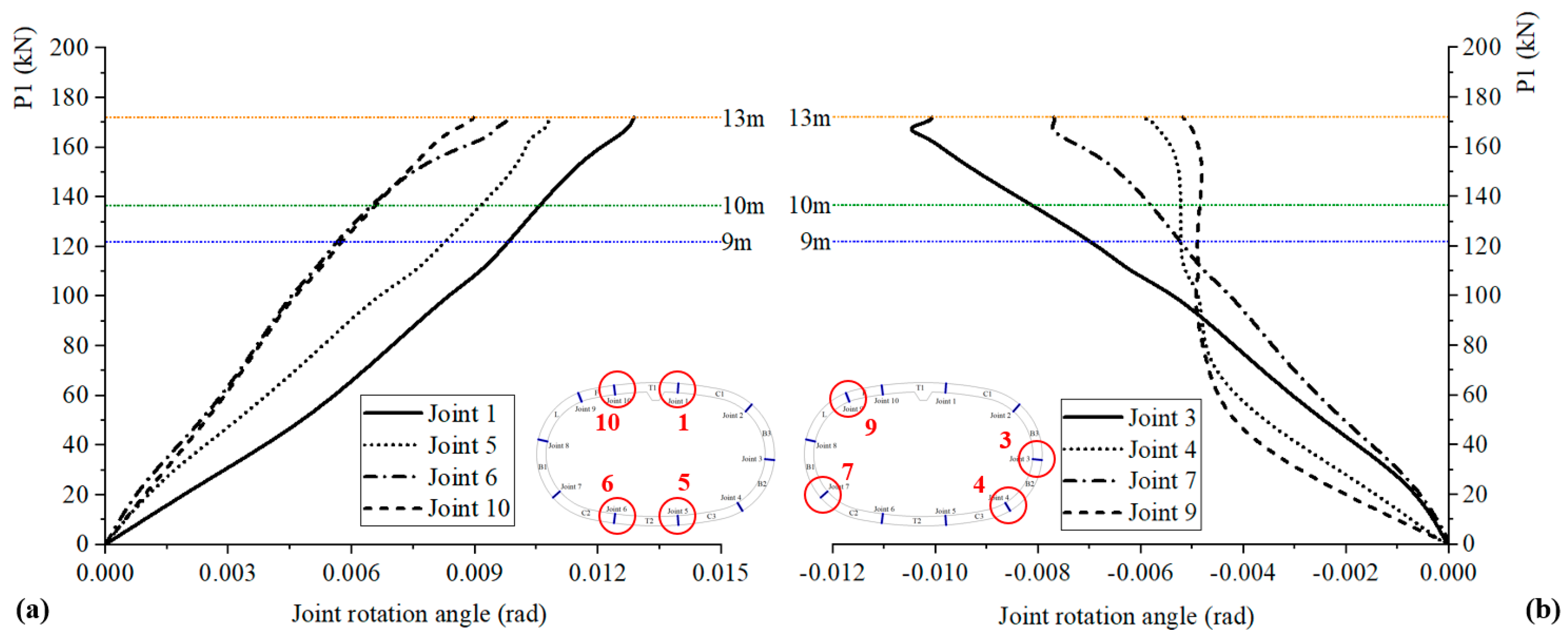
2.3.2. Joint Response
2.4. Analysis of Structural Behavior
- (1)
- The structural convergence deformation along the short axis at the top and bottom is relatively larger than that along the long axis at the waists. This phenomenon is attributed to the higher vertical load levels compared to the horizontal load levels. Moreover, the span of the structure primarily extends along the long axis, resulting in greater deformations in the vertical direction, corresponding to the structural convergence deformation along the short axis.
- (2)
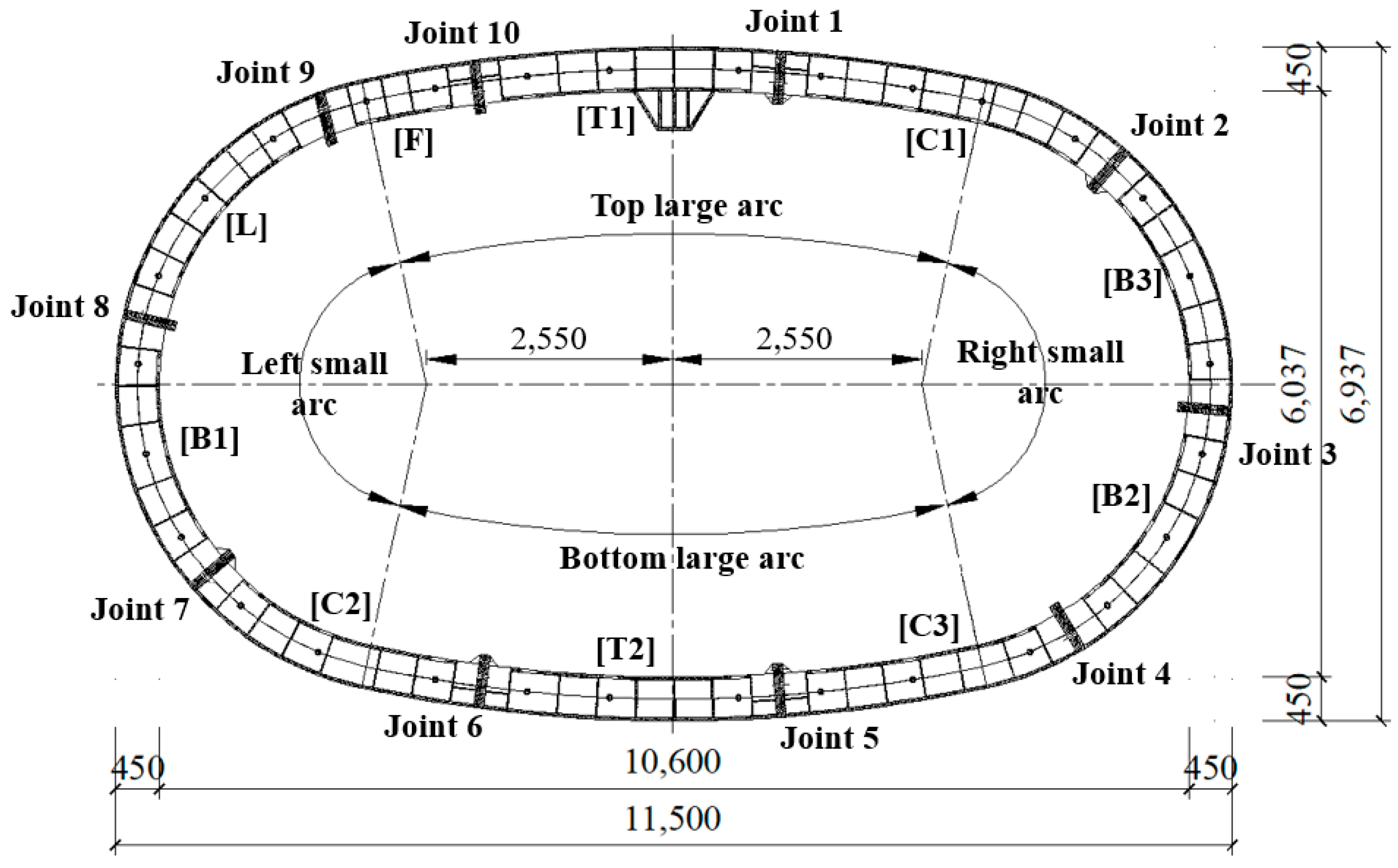
- Asymmetry in structural deformation. Considering that longitudinal joints represent the most significant characteristic of segmental tunnel linings, the asymmetry in the structure mainly originated from the distribution of joints. Specifically, Joints 1 and 5 are closer to the short axis, while Joints 3 and 8 are closer to the long axis, causing local deformations at four positions (top, bottom, left waist, and right waist) shifting towards these joint positions. According to the given distribution of joints, the deformations at the top and bottom exhibit axial symmetry with respect to the long axis of the structure, while the deformations at the waists exhibit central symmetry with respect to the center of the structure. These deformation characteristics are also consistent with the experimental results of joint responses.
3. Simulation and Analysis of Structural Behavior
3.1. Input Parameters for Models
3.1.1. ESHR Model
3.1.2. BS Model
3.1.3. MBS Model
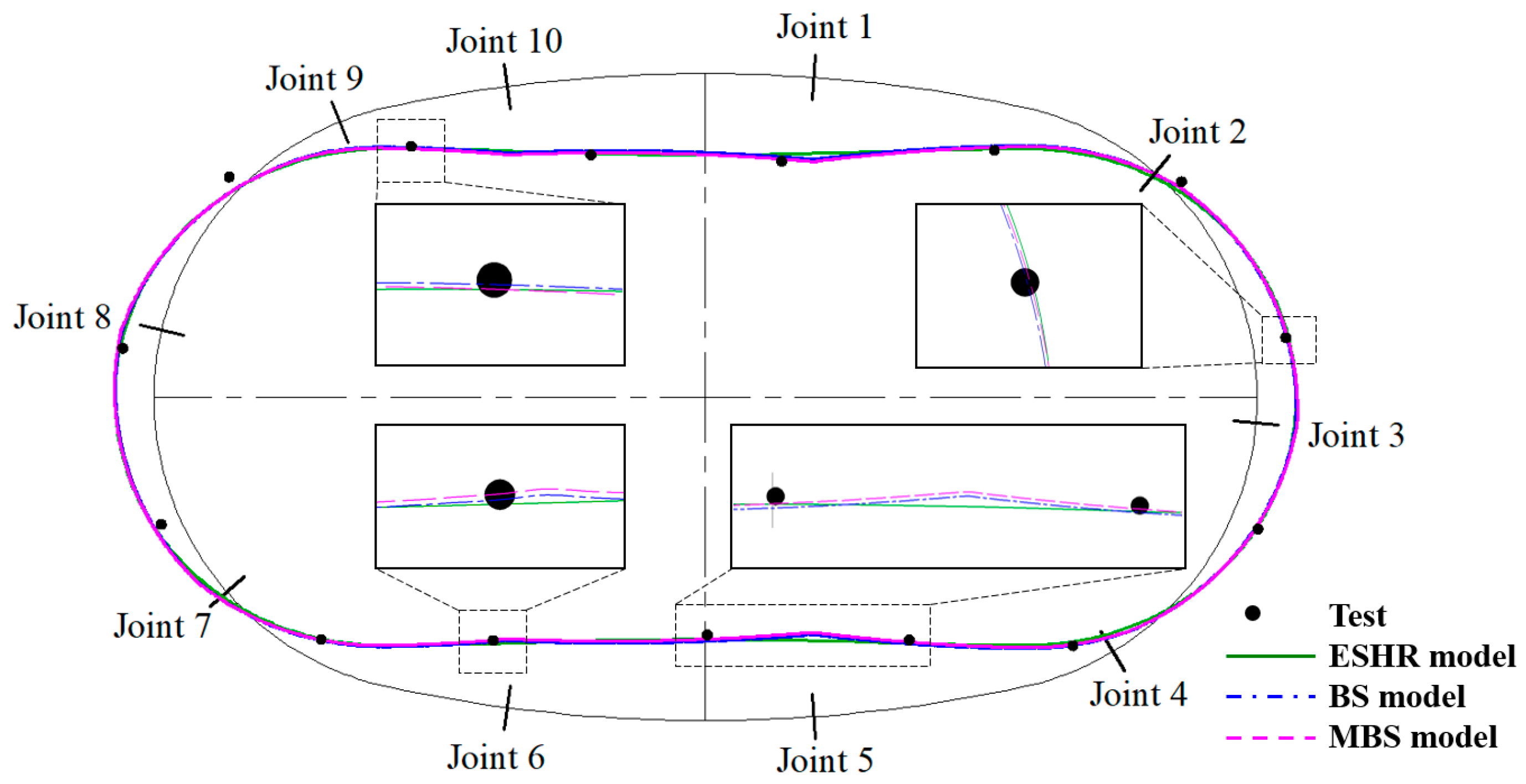
3.2. Simulation Process and Results
3.3. Deformation Mechanism
4. Structural Design
4.1. Structural Design during the Construction Process
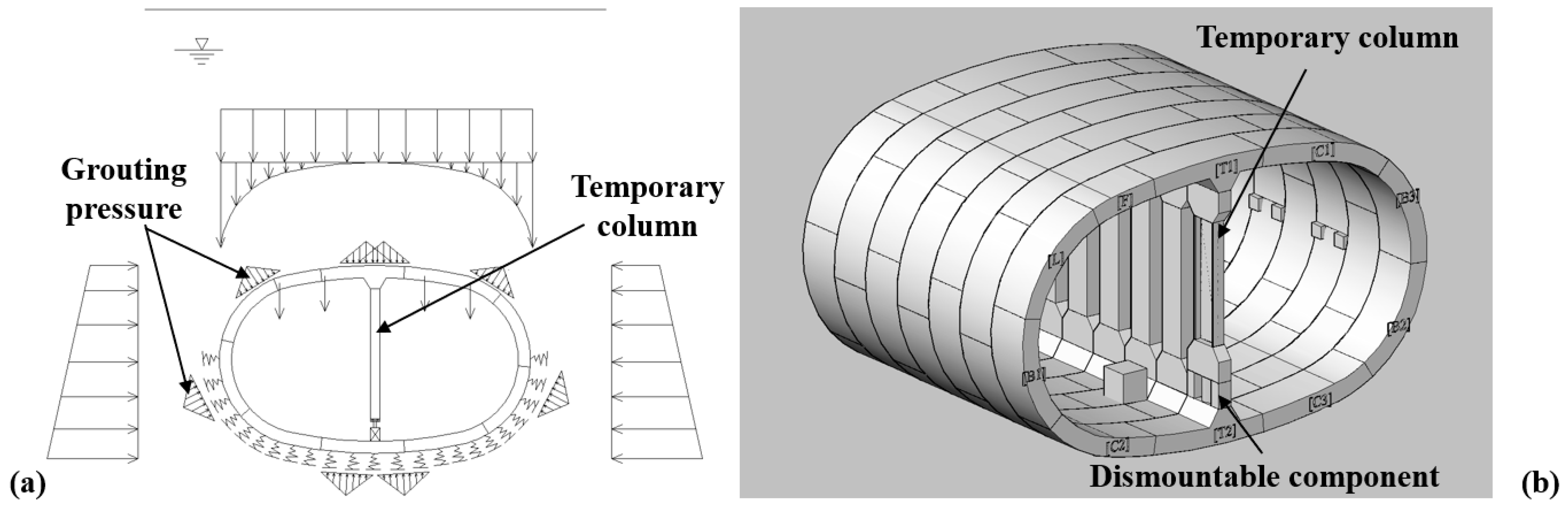
- Synchronous grouting condition. After the tunnel structure comes out from the shield tail, the external soil–water pressure and grouting pressure are resisted by the column-free QRST structure and the temporary support, the load-bearing state of which is similar to that of the typical QRST structure, as shown in Figure 15.
- Stable load condition. As the grouting pressure gradually dissipates and the external load stabilizes, the structure undergoes an unloading process while the structural form remains unchanged.
- Column removal condition. Subsequently, the temporary column is removed slowly to ignore the dynamic structural response. During this process, soil–structure interaction is simulated by a set of foundation springs surrounding the tunnel structure. The final state of the structure is the same as that depicted in Figure 6b.
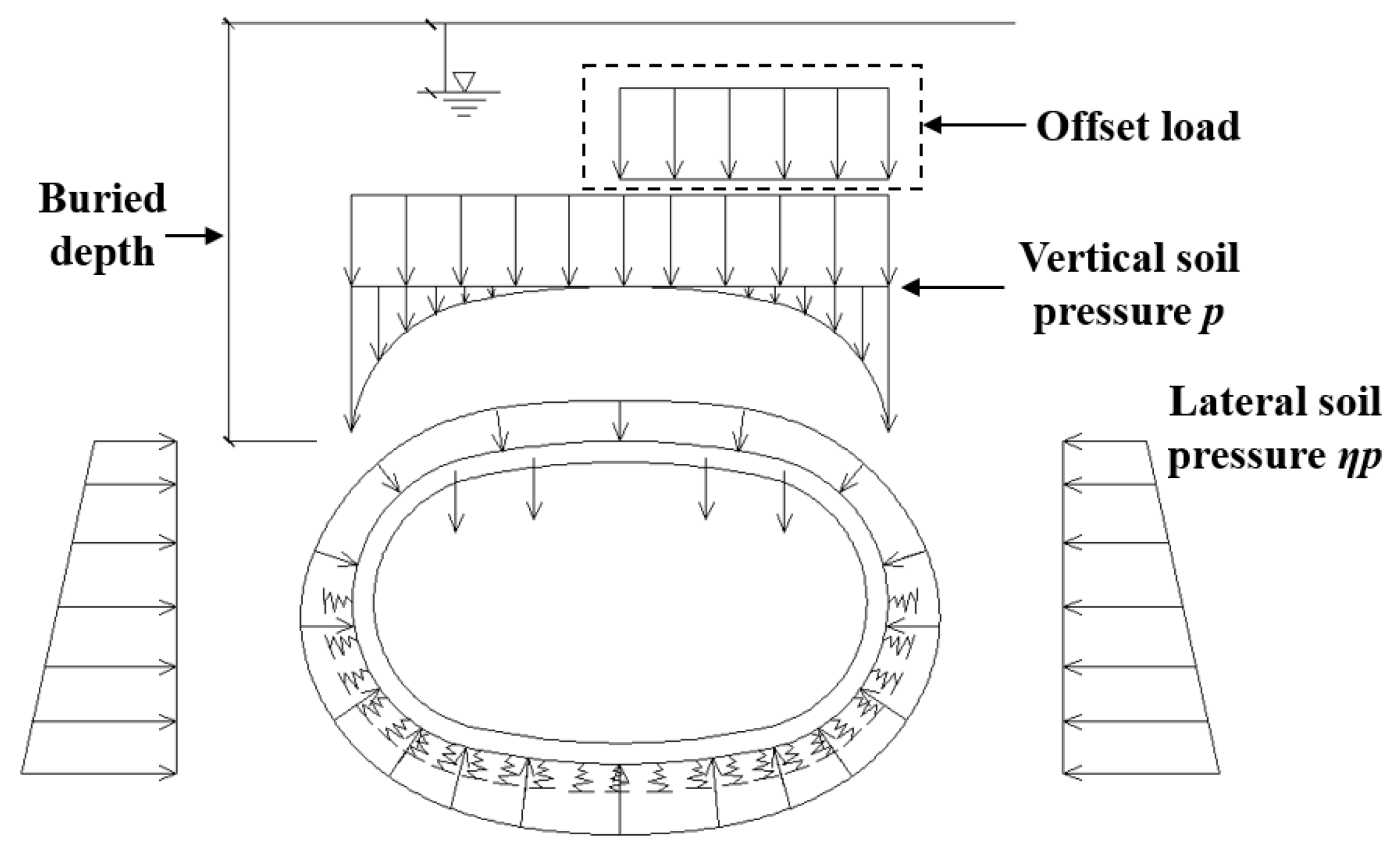
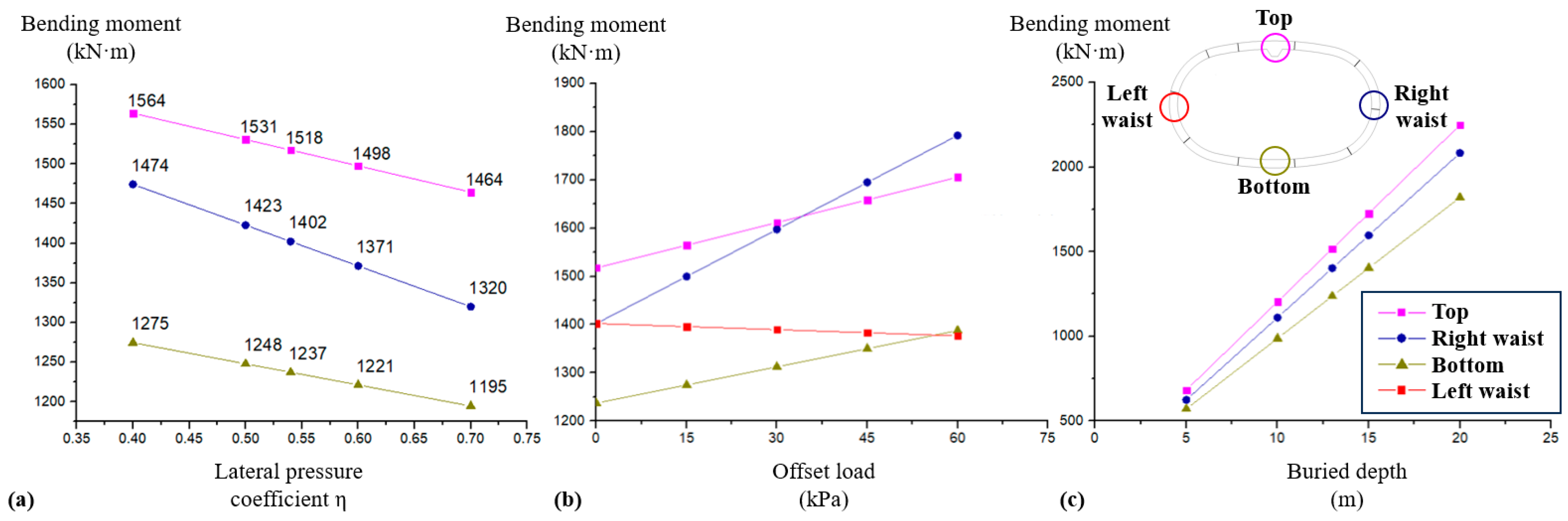
4.2. Sensitivity Analysis of Key Load Parameters
4.3. Engineering Recommendations
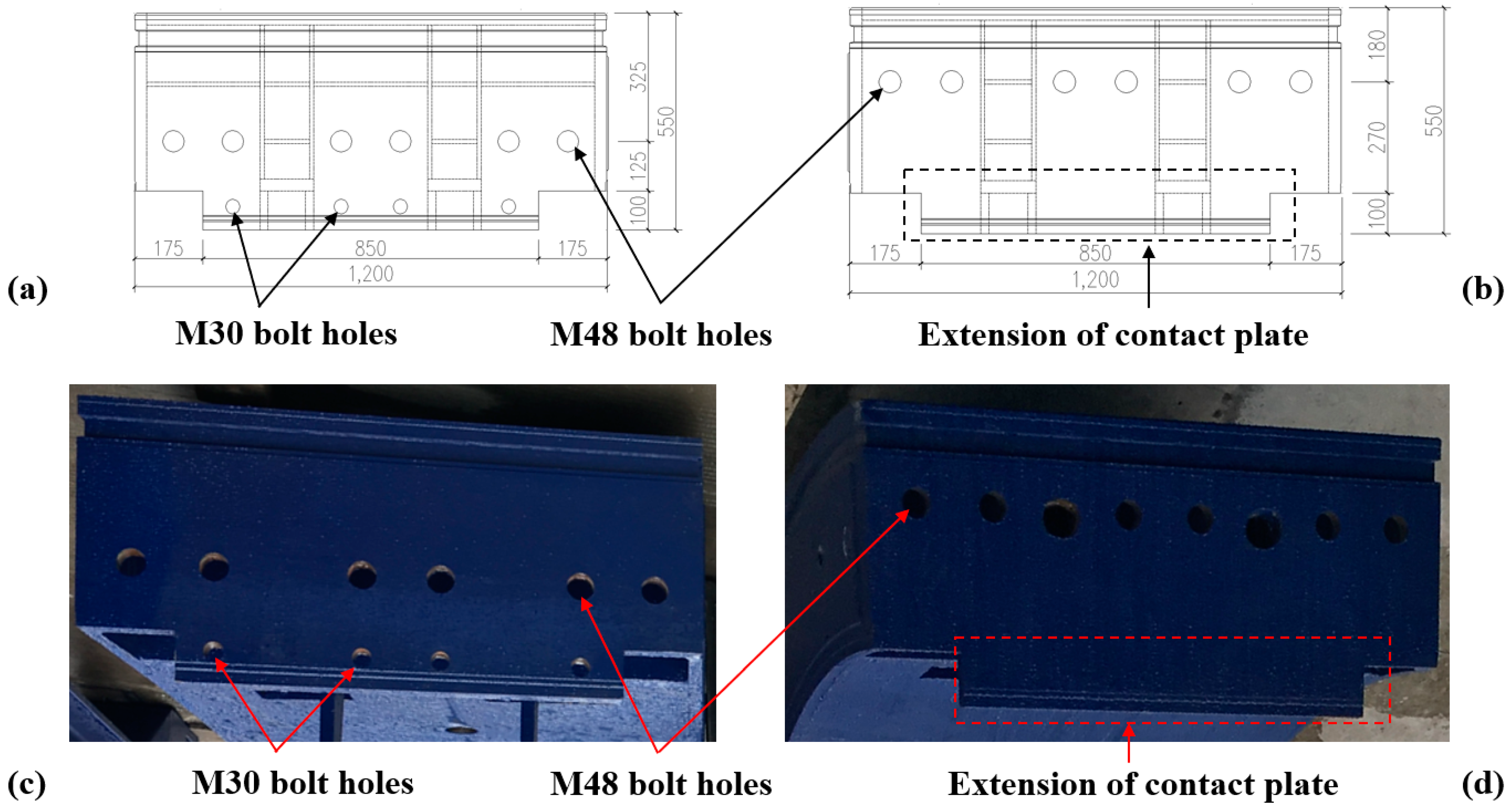
- Joints: All joint contact plates can be fully extended with a width of 1200 mm. For positive moment joints, change the positions of M48 bolts and M30 bolts to fully exploit the load-bearing capacity of M48 bolts. For negative moment joints with waterproofing permitted, the position of bolts is suggested to be fully moved toward the external surface direction.
- Temporary support: Considering the additional loads during the construction stage beyond the loads considered in the service stage, it is suggested that temporary support be employed to ensure structural safety.
- Segmentation and joint positions: After canceling interior columns, the joints are now situated at relatively unfavorable positions compared to typical QRSTs with interior columns. It is recommended that larger segments be used at the top, bottom, and waists to mitigate the joints’ exposure to high bending moments, thereby further reducing overall structural deformation.
- Ring-to-ring interaction: The experiments and simulations conducted are focused on single-ring structures and do not account for the interaction effects between rings in real tunnels. In practice, QRSTs are assembled in a staggered fashion. With the help of circumferential joints, structural deformation can be reduced. It is suggested that tongue-and-groove or shear keys be used to ensure the overall integrity of the tunnel system.
5. Conclusions
- At the service stage with a designed buried depth of 13 m, the inward vertical convergence deformation along the short axis of the structure is 108.64 mm, while the outward horizontal convergence deformation along the long axis is 49.03 mm. The column-free QRST structure predominantly experiences inward deformation;
- The development of joint deformations and bolt axial forces indicates that as the load level increases, among the positive moment joints, deformations and internal forces of Joints 1 and 5 develop faster than those of Joints 6 and 10. For negative moment joints, Joints 3 and 8 exhibit faster development compared to Joints 2 and 7, with Joints 4 and 9 exhibiting only rapid initial development. Based on the experimental results, it is recommended that the bolt dimension and bolt position for negative moment joints be optimized, and the rows of M48 and M30 bolts be repositioned for positive moment joints, with the help of sophisticated finite element models;
- The experimental results indicate that the deformation and internal force distribution of the structure are mainly determined by the shape of the tunnel cross-section and joint distribution. The span of the structure in the horizontal direction results in significant convergence deformation along the short axis at the top and bottom. Based on the given distribution of the joints, the structural deformations at the top and bottom exhibit an axis symmetricity with respect to the long axis of the structure, while those at the waists exhibit a central symmetry with respect to the center of the structure;
- The ESHR model, BS model, and MBS model are capable of reflecting the mechanical performance of column-free QRST structures. The BS and MBS models exhibit better simulation effects, particularly for local deformations near joints, while the ESHR model can serve as a design model for structures with appropriate calculation parameters;
- The deformations contributed by joints in column-free QRST structures account for approximately 65–70%, indicating optimization potentials for joints;
- When using the ESHR model to design column-free QRST structures subjected to the construction process, the results calculated by the three-stage calculation method are more reliable. For ease of engineering applications, structural responses calculated by the direct calculation method, with the response magnified by 10%, is sufficient to ensure structural safety;
- The influence of structural buried depth on structural response is generally proportional. In cases of changes in offset load and lateral pressure coefficient, the negative bending moment regions at the waists of the structure are more sensitive. Considering unexpected conditions such as ground surface surcharge or adjacent construction activities during the service period, special attention should be paid to the structural safety reserves of the negative bending moment regions at the waists.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Broere, W. Urban underground space: Solving the problems of today’s cities. Tunn. Undergr. Sp. Technol. 2016, 55, 245–248. [Google Scholar] [CrossRef]
- Latif, K.; Sharafat, A.; Seo, J. Digital twin-driven framework for TBM performance prediction, visualization, and monitoring through machine learning. Appl. Sci. 2023, 13, 11435. [Google Scholar] [CrossRef]
- Sharafat, A.; Latif, K.; Seo, J. Risk analysis of TBM tunneling projects based on generic bow-tie risk analysis approach in difficult ground conditions. Tunn. Undergr. Sp. Technol. 2021, 111, 103860. [Google Scholar] [CrossRef]
- Wasantha, P.; Guerrieri, M.; Xu, T. Effects of tunnel fires on the mechanical behaviour of rocks in the vicinity–A review. Tunn. Undergr. Sp. Technol. 2021, 108, 103667. [Google Scholar] [CrossRef]
- Yu, C.; Zhou, A.; Chen, J.; Arulrajah, A.; Horpibulsuk, S. Analysis of a tunnel failure caused by leakage of the shield tail seal system. Undergr. Space 2020, 5, 105–114. [Google Scholar] [CrossRef]
- Ye, G.-L.; Hashimoto, T.; Shen, S.-L.; Zhu, H.-H.; Bai, T.-H. Lessons learnt from unusual ground settlement during Double-O-Tube tunnelling in soft ground. Tunn. Undergr. Sp. Technol. 2015, 49, 79–91. [Google Scholar] [CrossRef]
- Liu, X.; Liu, Z.; Yuan, Y.; Zhu, Y. Quasi-Rectangular Shield Tunneling Technology in the Ningbo Rail Transit Project. In High Tech Concrete: Where Technology and Engineering Meet, Proceedings of the 2017 Fib Symposium, Maastricht, The Netherlands, 12–14 June 2017; Springer International Publishing: Berlin/Heidelberg, Germany, 2018; pp. 2765–2773. [Google Scholar]
- Zhang, W.; De Corte, W.; Liu, X.; Taerwe, L. Optimization Study on Longitudinal Joints in Quasi-Rectangular Shield Tunnels. Appl. Sci. 2021, 11, 573. [Google Scholar] [CrossRef]
- Liu, X.; Liu, Z.; Ye, Y.; Bai, Y.; Zhu, Y. Mechanical behavior of quasi-rectangular segmental tunnel linings: Further insights from full-scale ring tests. Tunn. Undergr. Sp. Technol. 2018, 79, 304–318. [Google Scholar] [CrossRef]
- Chow, B. Double-O-tube shield tunneling technology in the Shanghai Rail Transit Project. Tunn. Undergr. Sp. Technol. 2006, 21, 594–601. [Google Scholar] [CrossRef]
- Liu, X.; Hu, X.; Guan, L.; Sun, W. The ultimate bearing capacity of rectangular tunnel lining assembled by composite segments: An experimental investigation. Steel Compos. Struct. 2017, 24, 481–497. [Google Scholar] [CrossRef]
- Zhu, Y.; Zhang, Z.; Huang, X.; Zhu, Y.; Wang, S. Exploring the progressive failure characteristics of a large special-shaped shield tunnel lining based on ‘standing’prototype loading tests. Tunn. Undergr. Sp. Technol. 2019, 93, 103107. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhu, Y.; Huang, X.; Zhu, Y.; Liu, W. ‘Standing’full-scale loading tests on the mechanical behavior of a special-shape shield lining under shallowly-buried conditions. Tunn. Undergr. Sp. Technol. 2019, 86, 34–50. [Google Scholar] [CrossRef]
- Nakamura, H.; Kubota, T.; Furukawa, M.; Nakao, T. Unified construction of running track tunnel and crossover tunnel for subway by rectangular shape double track cross-section shield machine. Tunn. Undergr. Sp. Technol. 2003, 18, 253–262. [Google Scholar] [CrossRef]
- Du, D.; Dias, D.; Do, N. Lining performance optimization of sub-rectangular tunnels using the Hyperstatic Reaction Method. Comput. Geotech. 2020, 117, 103279. [Google Scholar] [CrossRef]
- Zhang, W.; De Corte, W.; Liu, X.; Taerwe, L. Influence of rotational stiffness modeling on the joint behavior of quasi-rectangular shield tunnel linings. Appl. Sci. 2020, 10, 8396. [Google Scholar] [CrossRef]
- Zhang, L.; Feng, K.; He, C.; Yang, W.; Zhang, J.; Xiao, M. Numerical investigation of the compression–bending stiffness of segmental joints with different types of joint surfaces. Tunn. Undergr. Sp. Technol. 2023, 132, 104898. [Google Scholar] [CrossRef]
- Hu, X.; Zhang, Z.; Teng, L. An analytical method for internal forces in DOT shield-driven tunnel. Tunn. Undergr. Sp. Technol. 2009, 24, 675–688. [Google Scholar] [CrossRef]
- Shen, S.-L.; Horpibulsuk, S.; Liao, S.-M.; Peng, F.-L. Analysis of the behavior of DOT tunnel lining caused by rolling correction operation. Tunn. Undergr. Sp. Technol. 2009, 24, 84–90. [Google Scholar] [CrossRef]
- Shen, S.-L.; Du, Y.-J.; Luo, C.-Y. Evaluation of the effect of rolling correction of double-o-tunnel shields via one-side loading. Can. Geotech. J. 2010, 47, 1060–1070. [Google Scholar] [CrossRef]
- Huang, X.; Zhu, Y.; Zhang, Z.; Zhu, Y.; Wang, S.; Zhuang, Q. Mechanical behaviour of segmental lining of a sub-rectangular shield tunnel under self-weight. Tunn. Undergr. Sp. Technol. 2018, 74, 131–144. [Google Scholar] [CrossRef]
- Hefny, A.M.; Chua, H.C. An investigation into the behaviour of jointed tunnel lining. Tunn. Undergr. Sp. Technol. 2006, 21, 428. [Google Scholar] [CrossRef]
- Ding, Z.; Zhang, X.; He, S.-H.; Qi, Y.-J.; Lin, C.-G. Experimental and theoretical study on longitudinal deformation and internal force of shield tunnel under surcharge. Tunn. Undergr. Sp. Technol. 2024, 144, 105506. [Google Scholar] [CrossRef]
- Zhang, J.-Z.; Huang, H.-W.; Zhang, D.-M.; Phoon, K.K. Experimental study of the coupling effect on segmental shield tunnel lining under surcharge loading and excavation unloading. Tunn. Undergr. Sp. Technol. 2023, 140, 105199. [Google Scholar] [CrossRef]
- Shi, C.; Cao, C.; Lei, M.; Peng, L.; Ai, H. Effects of lateral unloading on the mechanical and deformation performance of shield tunnel segment joints. Tunn. Undergr. Sp. Technol. 2016, 51, 175–188. [Google Scholar] [CrossRef]
- Wu, H.N.; Chen, S.; Chen, R.P.; Cheng, H.Z.; Feng, D.L. Deformation behaviors and failure mechanism of segmental RC lining under unloading condition. Tunn. Undergr. Sp. Technol. 2022, 130, 104687. [Google Scholar] [CrossRef]
- Liang, R.; Kang, C.; Xiang, L.; Li, Z.; Lin, C.; Gao, K.; Guo, Y. Responses of in-service shield tunnel to overcrossing tunnelling in soft ground. Environ. Earth Sci. 2021, 80, 183. [Google Scholar] [CrossRef]
- Liang, R.; Wu, W.; Yu, F.; Jiang, G.; Liu, J. Simplified method for evaluating shield tunnel deformation due to adjacent excavation. Tunn. Undergr. Sp. Technol. 2018, 71, 94–105. [Google Scholar] [CrossRef]
- Schreyer, J.; Winselmann, D. Suitability tests for the lining for the 4th Elbe tunnel tube–Results of large-scale tests. Tunnel 2000, 1, 34–44. [Google Scholar]
- Lu, L.; Lu, X.; Fan, P. Full-ring experimental study of the lining structure of Shanghai Changjiang tunnel. J. Civ. Eng. Archit. 2011, 5, 300–305. [Google Scholar]
- Zhu, Y.; Zhu, Y.; Wang, Q.; Zhang, Z.; Huang, X.; Liu, W. Prototype Loading Tests on the Mechanical behaviors of the Shield Lining Structure of a Water Storage and Sewage Tunnel. In Proceedings of the WTC 2020, Kuala Lumpur, Malaysia, 15–21 May 2020; pp. 2314–2516. [Google Scholar]
- Liu, X.; Ye, Y.; Liu, Z.; Huang, D. Mechanical behavior of Quasi-rectangular segmental tunnel linings: First results from full-scale ring tests. Tunn. Undergr. Sp. Technol. 2018, 71, 440–453. [Google Scholar] [CrossRef]
- Huang, X.; Liu, W.; Zhang, Z.; Wang, Q.; Wang, S.; Zhuang, Q.; Zhu, Y.; Zhang, C. Exploring the three-dimensional response of a water storage and sewage tunnel based on full-scale loading tests. Tunn. Undergr. Sp. Technol. 2019, 88, 156–168. [Google Scholar] [CrossRef]
- Li, X.J.; Yan, Z.G.; Wang, Z.; Zhu, H.H. Experimental and analytical study on longitudinal joint opening of concrete segmental lining. Tunn. Undergr. Sp. Technol. 2015, 46, 52–63. [Google Scholar] [CrossRef]
- Tsiampousi, A.; Yu, J.; Standing, J.; Vollum, R.; Potts, D. Behaviour of bolted cast iron joints. Tunn. Undergr. Sp. Technol. 2017, 68, 113–129. [Google Scholar] [CrossRef]
- Yu, J.; Standing, J.; Vollum, R.; Potts, D.; Burland, J. Experimental investigations of bolted segmental grey cast iron lining behaviour. Tunn. Undergr. Sp. Technol. 2017, 61, 161–178. [Google Scholar] [CrossRef]
- Fukuchi, G. The present and future of mechanized tunnel works in soft ground. Tunn. Undergr. Sp. Technol. 1991, 6, 175–183. [Google Scholar] [CrossRef]
- Uchida, K. Design and engineering of large bore slurry shield tunnel lining system for Trans-Tokyo Bay Highway. Civ. Eng. Jpn. 1992, 30, 54–67. [Google Scholar]
- Lee, K.; Hou, X.; Ge, X.; Tang, Y. An analytical solution for a jointed shield-driven tunnel lining. Int. J. Numer. Anal. Methods Geomech. 2001, 25, 365–390. [Google Scholar] [CrossRef]
- Madenci, E.; Guven, I. The Finite Element Method and Applications in Engineering Using ANSYS®; Springer: New York, NY, USA, 2015. [Google Scholar]
- Ding, W.; Peng, Y.; Yan, Z.; Shen, B.; Zhu, H.; Wei, X. Full-scale testing and modeling of the mechanical behavior of shield TBM tunnel joints. Struct. Eng. Mech. Int. J. 2013, 45, 337–354. [Google Scholar] [CrossRef]
- Tvede-Jensen, B.; Faurschou, M.; Kasper, T. A modelling approach for joint rotations of segmental concrete tunnel linings. Tunn. Undergr. Sp. Technol. 2017, 67, 61–67. [Google Scholar] [CrossRef]
- Blom, C.B.M. Design Philosophy of Concrete Linings for Tunnels in Soft Soils. Ph.D. Thesis, Technische Universiteit Delft, Delft, The Netherlands, 2004. [Google Scholar]
- Ding, W.; Duan, C.; Zhu, Y.; Zhao, T.; Huang, D.; Li, P. The behavior of synchronous grouting in a quasi-rectangular shield tunnel based on a large visualized model test. Tunn. Undergr. Sp. Technol. 2019, 83, 409–424. [Google Scholar] [CrossRef]
- Zhou, Z.; Zhao, J.; Tan, Z.; Zhou, X. Mechanical responses in the construction process of super-large cross-section tunnel: A case study of Gongbei tunnel. Tunn. Undergr. Sp. Technol. 2021, 115, 104044. [Google Scholar] [CrossRef]
- Liu, X.; Gao, Y.; Zhang, J.; Zhu, Y. Structural response of main tunnel linings during construction of connecting aisle by means of mechanized drilling. Chin. J. Geotech. Eng. 2020, 42, 951–960. [Google Scholar]
- Liang, R.; Xia, T.; Huang, M.; Lin, C. Simplified analytical method for evaluating the effects of adjacent excavation on shield tunnel considering the shearing effect. Comput. Geotech. 2017, 81, 167–187. [Google Scholar] [CrossRef]
- Zhang, Q.; Xia, T.; Ding, Z.; Huang, X.; Lin, C. Effect of nearby undercrossing tunneling on the deformation of existing metro tunnel and construction control. Rock Soil Mech. 2016, 37, 3561–3568. [Google Scholar]

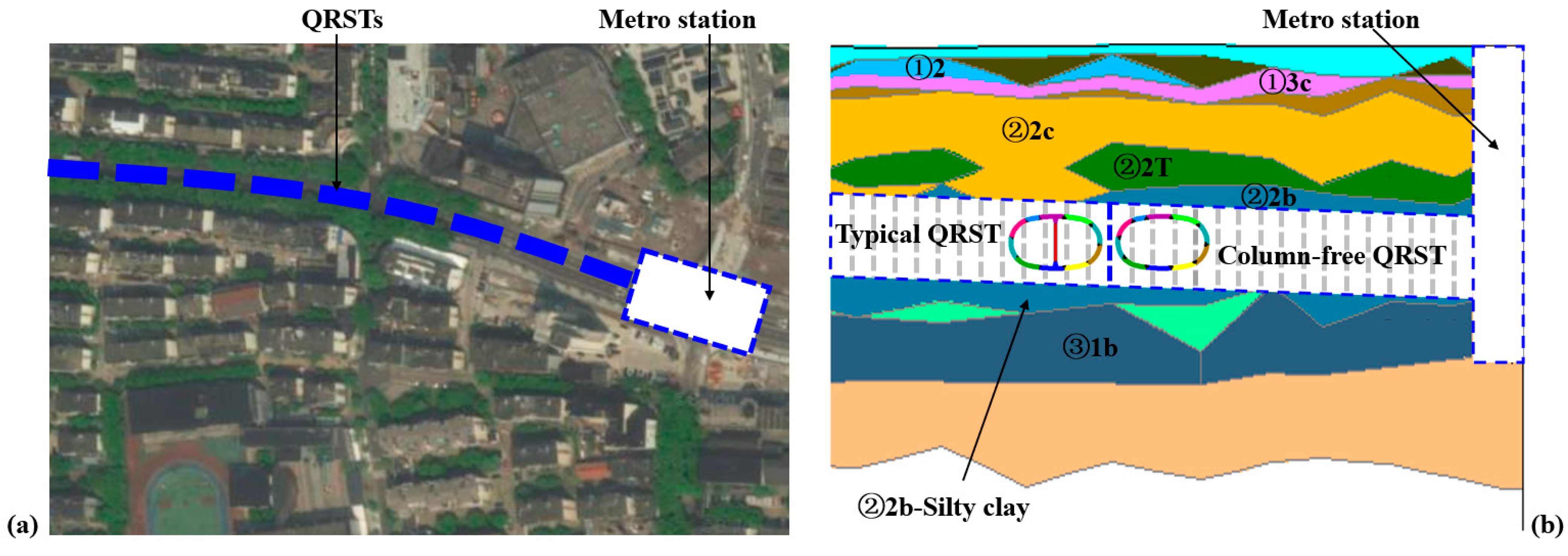





| Soil Layer | Layer Thickness (m) | Water Content (%) | Unit Weight (kN/m3) | Internal Friction Angle (°) | Cohesion (kPa) |
|---|---|---|---|---|---|
| ① 2-Clay | 0.6~3.4 | 27.9 | 19.3 | 18.9 | 28.7 |
| ① 3c-Silty clay | 0.5~4.4 | 38.0 | 18.0 | 19.5 | 7.2 |
| ② 2c-Silty clay | 1.0~6.6 | 39.7 | 17.7 | 21.8 | 5.5 |
| ② 2b-Silty clay | 15.1~20.0 | 47.9 | 16.9 | 13.4 | 12.5 |
| ② 2T-Silt sand | 0.6~4.5 | 28 | 19.0 | 18.9 | 28.7 |
| ③ 1b-Silt sand | 4.0~8.7 | 22.4 | 19.6 | 19.5 | 7.2 |
| Loading Step | P1 (kN) | P2 (kN) | P3 (kN) |
|---|---|---|---|
| 1 | 25 | 23 | 22 |
| 2 | 49 | 46 | 44 |
| 3 | 74 | 70 | 67 |
| 4 | 86 | 81 | 78 |
| 5 | 98 | 93 | 89 |
| 6 | 105 | 99 | 94 |
| 7 | 111 | 104 | 100 |
| 8 | 117 | 110 | 105 |
| 9 (9 m service stage) | 123 | 116 | 111 |
| 10 | 130 | 122 | 137 |
| 11 (10 m service stage) | 137 | 129 | 164 |
| 12 | 141 | 114 | 144 |
| 13 | 146 | 100 | 125 |
| 14 | 150 | 85 | 106 |
| 15 | 157 | 110 | 119 |
| 16 | 165 | 134 | 132 |
| 17 (13 m service stage) | 172 | 159 | 145 |
| Parameter | Unit | Value |
|---|---|---|
| Segment | ||
| Thickness | mm | 450 |
| Width | mm | 1200 |
| Thickness of internal and external steel plates | mm | 30 |
| Total thickness of web plates | mm | 90 |
| Area of the segment A0 | m2 | 1.071 × 10−1 |
| Moment of inertia of the segment I0 | m4 | 3.625 × 10−3 |
| Material properties of steel | ||
| Young’s modulus E | GPa | 206 |
| Poisson ratio ν | / | 0.31 |
| Stiffness of segment | ||
| Axial compressive stiffness EA0 | N | 2.206 × 1010 |
| Bending stiffness EI0 | N·m2 | 7.468 × 108 |
| Location | Experimental Results | ESHR Model | BS Model | MBS Model |
|---|---|---|---|---|
| Short axis | −108.64 | −108.69 (0.04%) | −105.55 (−2.84%) | −108.72 (0.07%) |
| Long axis | 49.03 | 52.17 (6.4%) | 51.56 (5.15%) | 53.13 (8.36%) |
| Left short axis | −104.67 | −106.99 (2.22%) | −102.26 (−2.31%) | −105.34 (0.64%) |
| Right short axis | −110.82 | −106.99 (−3.45%) | −108 (−2.54%) | −111.25 (0.38%) |
| Condition | Deformation of Short Axis (mm) | |
|---|---|---|
| Analysis Total (Joint Contribution) | Test | |
| 9 m service stage | 79.73 (52.74) | 72.00 |
| 10 m service stage | 95.59 (66.35) | 94.88 |
| 13 m service stage | 111.31 (74.49) | 108.64 |
| Position | Direct Calculation Method | Three-Stage Calculation Method | ||
|---|---|---|---|---|
| Bending Moment (kN·m) | Axial Force (kN) | Bending Moment (Kn·M) | Axial Force (kN) | |
| Top | 1764 | −982 | 1772 (+0.5%) | −992 |
| Right waist | −1861 | −2066 | −1890 (+1.6%) | −2089 |
| Bottom | 1629 | −1480 | 1759 (+8.0%) | −1492 |
| Left waist | −1660 | −1950 | −1688 (+1.7%) | −1972 |
| Load Parameter | Unit | Design Value | Values for Sensitivity Analysis |
|---|---|---|---|
| Lateral pressure coefficient η | / | 0.54 | 0.4, 0.5, 0.54, 0.6, 0.7 |
| Offset load | kPa | 30 | 0, 15, 30, 45, 60 |
| Buried depth | m | 13 | 5, 10, 13, 15, 20 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Z.; Chen, Y.; Wu, Y.; Liu, X. Experimental and Theoretical Investigations of the Mechanical Behavior of Column-Free Quasi-Rectangular Segmental Tunnel Linings. Appl. Sci. 2024, 14, 2896. https://doi.org/10.3390/app14072896
Liu Z, Chen Y, Wu Y, Liu X. Experimental and Theoretical Investigations of the Mechanical Behavior of Column-Free Quasi-Rectangular Segmental Tunnel Linings. Applied Sciences. 2024; 14(7):2896. https://doi.org/10.3390/app14072896
Chicago/Turabian StyleLiu, Zhen, Yizheng Chen, Yuebin Wu, and Xian Liu. 2024. "Experimental and Theoretical Investigations of the Mechanical Behavior of Column-Free Quasi-Rectangular Segmental Tunnel Linings" Applied Sciences 14, no. 7: 2896. https://doi.org/10.3390/app14072896
APA StyleLiu, Z., Chen, Y., Wu, Y., & Liu, X. (2024). Experimental and Theoretical Investigations of the Mechanical Behavior of Column-Free Quasi-Rectangular Segmental Tunnel Linings. Applied Sciences, 14(7), 2896. https://doi.org/10.3390/app14072896






