Multi-Material Optimization for Lattice Materials Based on Nash Equilibrium
Abstract
:1. Introduction
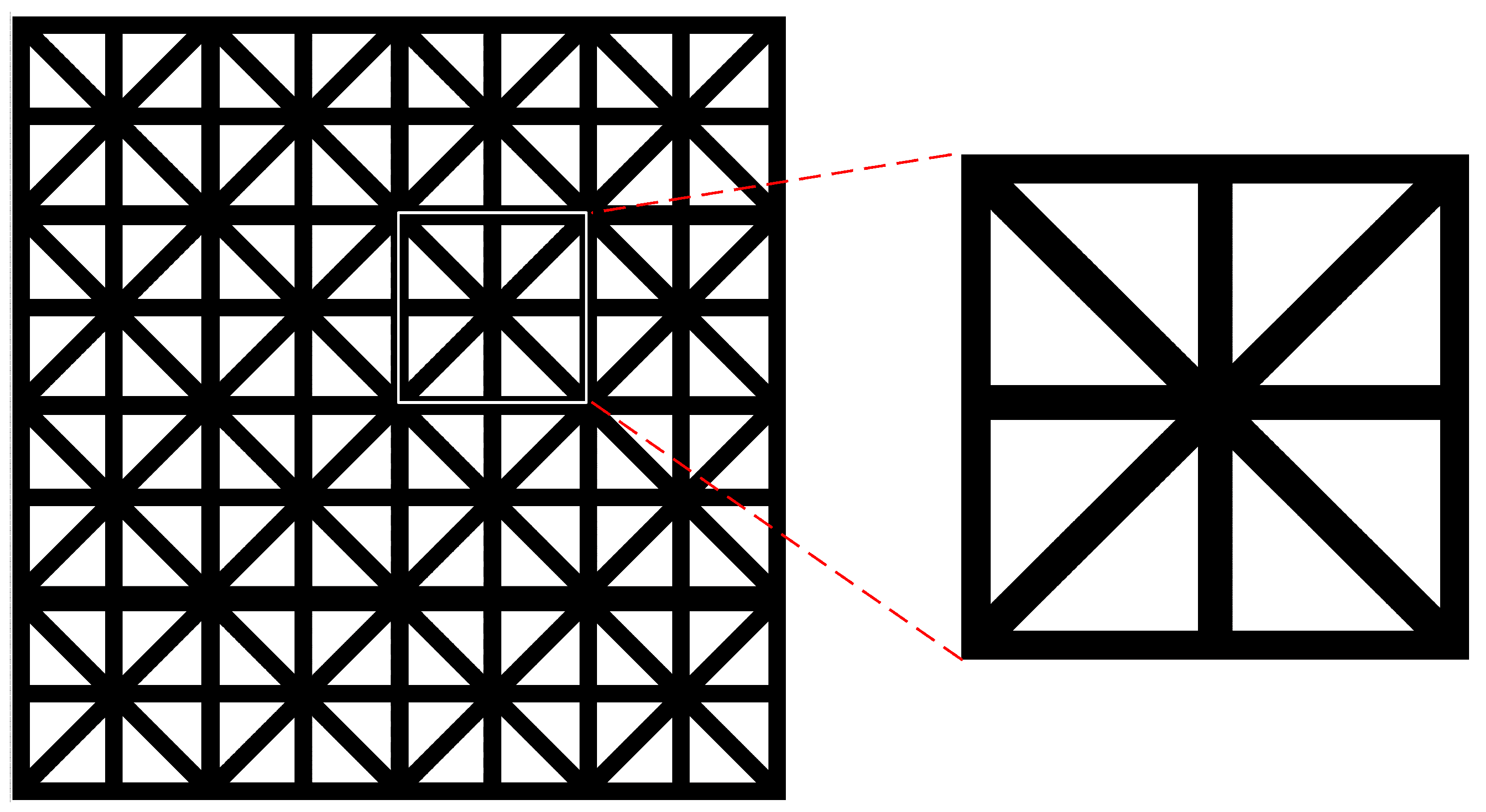
2. Analysis of Equivalent Mechanical Properties of Lattice Materials
2.1. Solution of Base Function
2.2. Solution of Equivalent Stiffness Matrix
3. Multi-Material Optimization Formulations Based on Nash Equilibrium
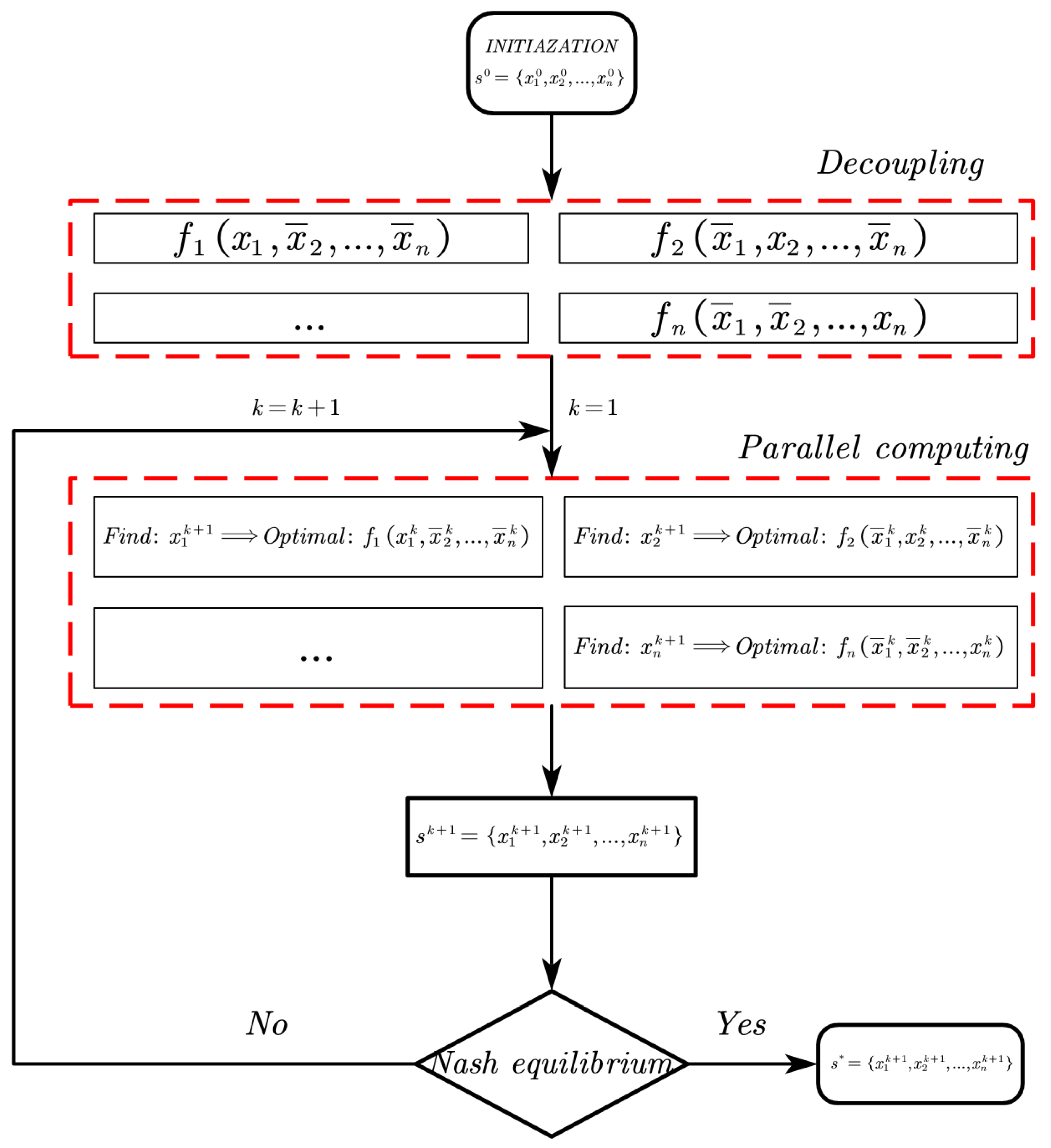
3.1. Nash Equilibrium Theory
3.2. Multi-Material Optimization Formulations
3.3. Optimization Subproblem Formulations
3.4. Material Overlap Phenomenon And Solution
- After each iteration, search for overlapped elements in the entire design domain. The set of these supersaturated elements is:where is the threshold value. When the design variable within a design domain exceeds a threshold, it is considered an overlapped element.
- Calculate the equivalent stiffness of each material within the overlapped elements.
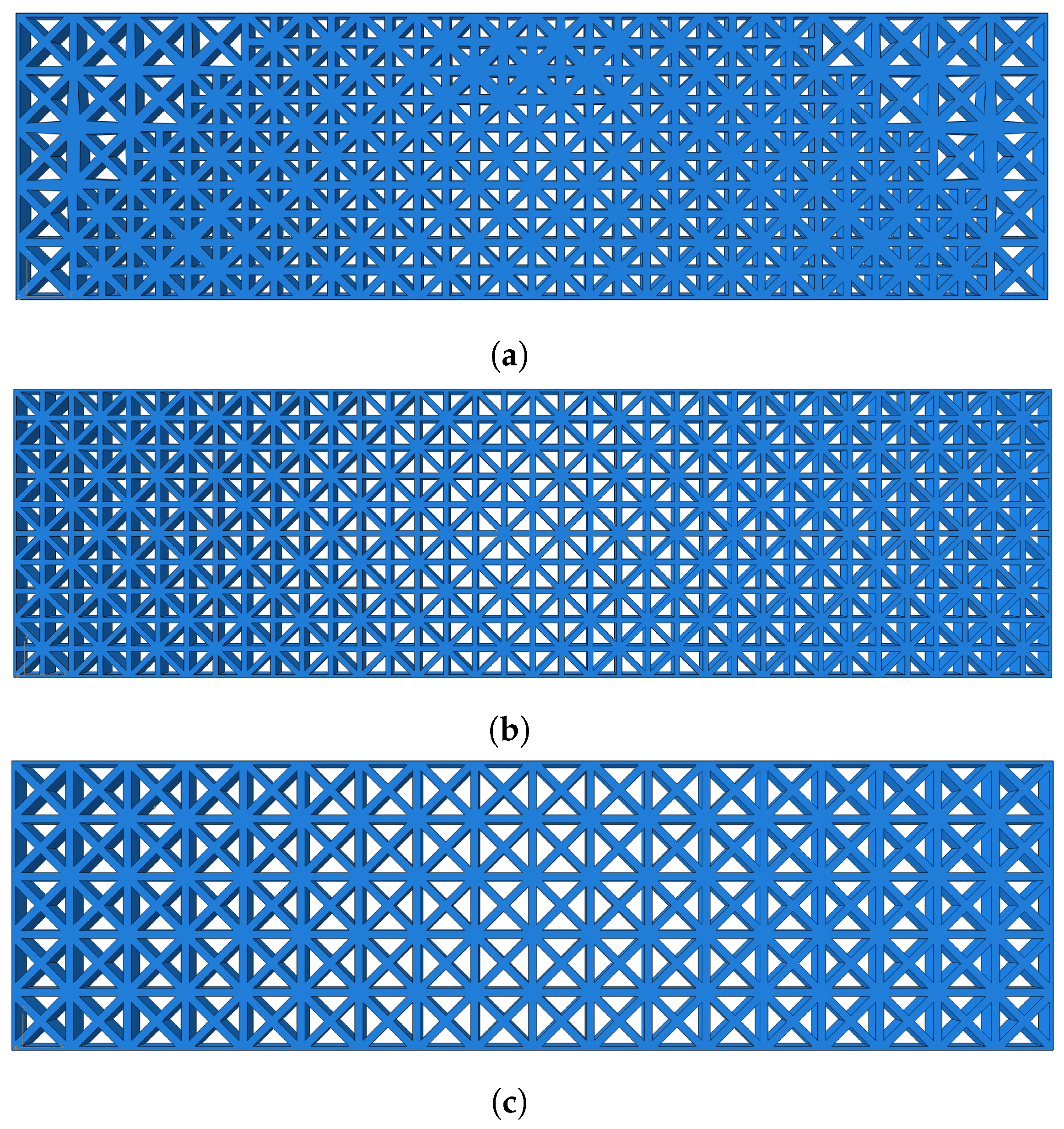
- Compare the equivalent stiffness of each material within the overlapped elements, keep the design variable of material with the largest equivalent stiffness unchanged, and then restrict the design variables of other materials as follows:where is the penalty coefficient, which is generally taken as 0.5 based on engineering experience. The optimization results after adding suppression methods are shown in Figure 5, which can verify the effectiveness of the method.
4. Numerical Examples and Tests
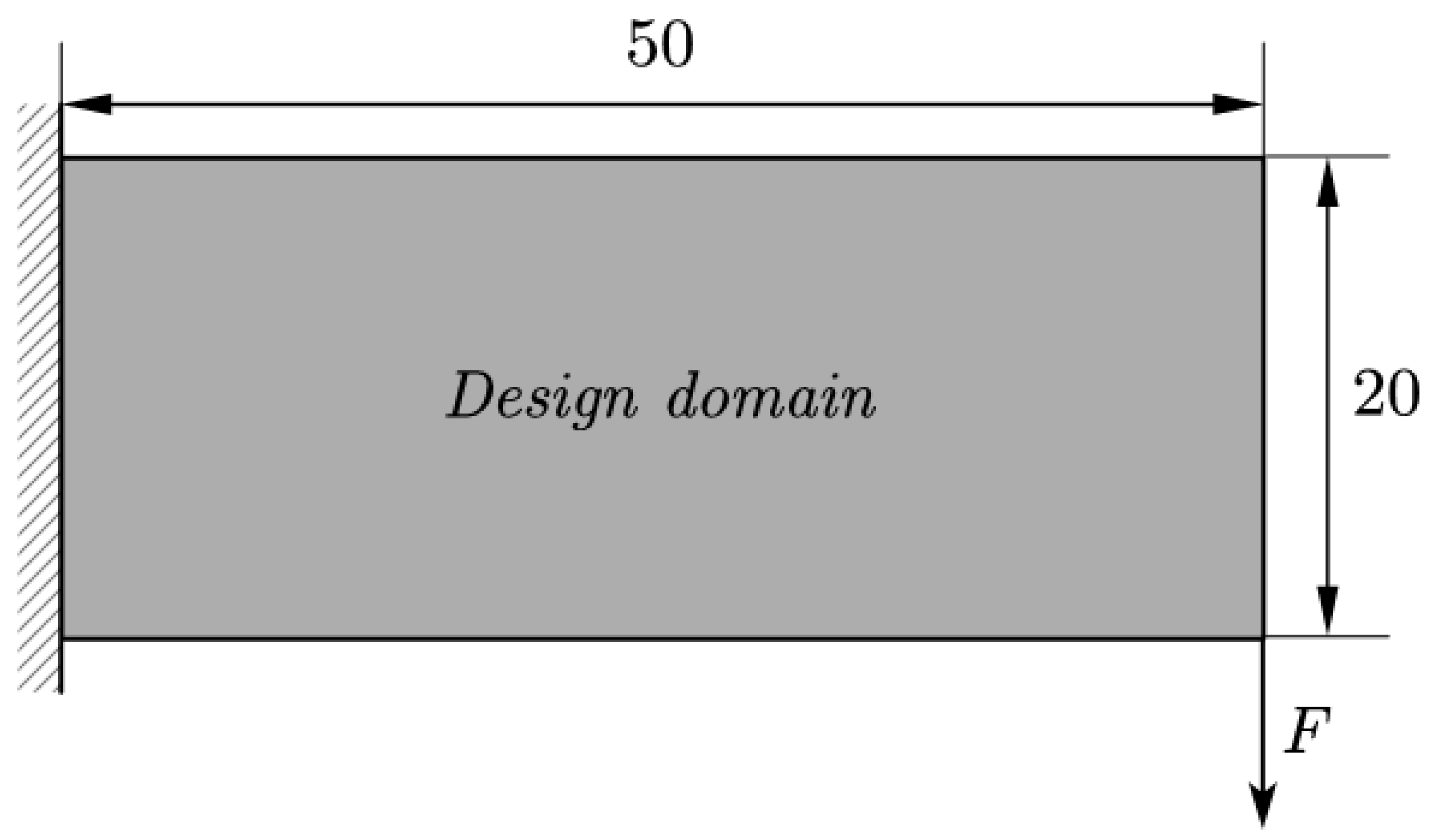
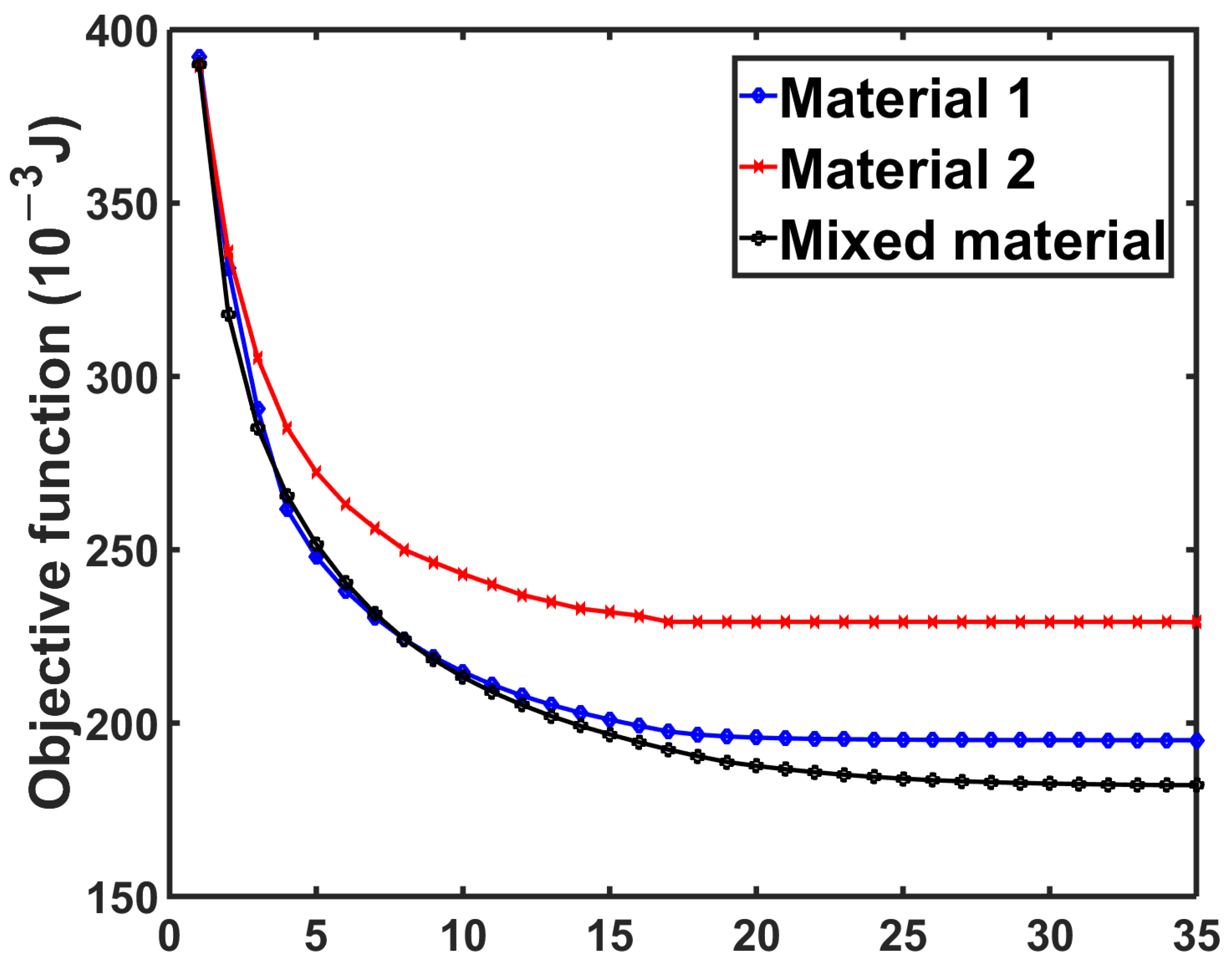
4.1. Cantilever Beam
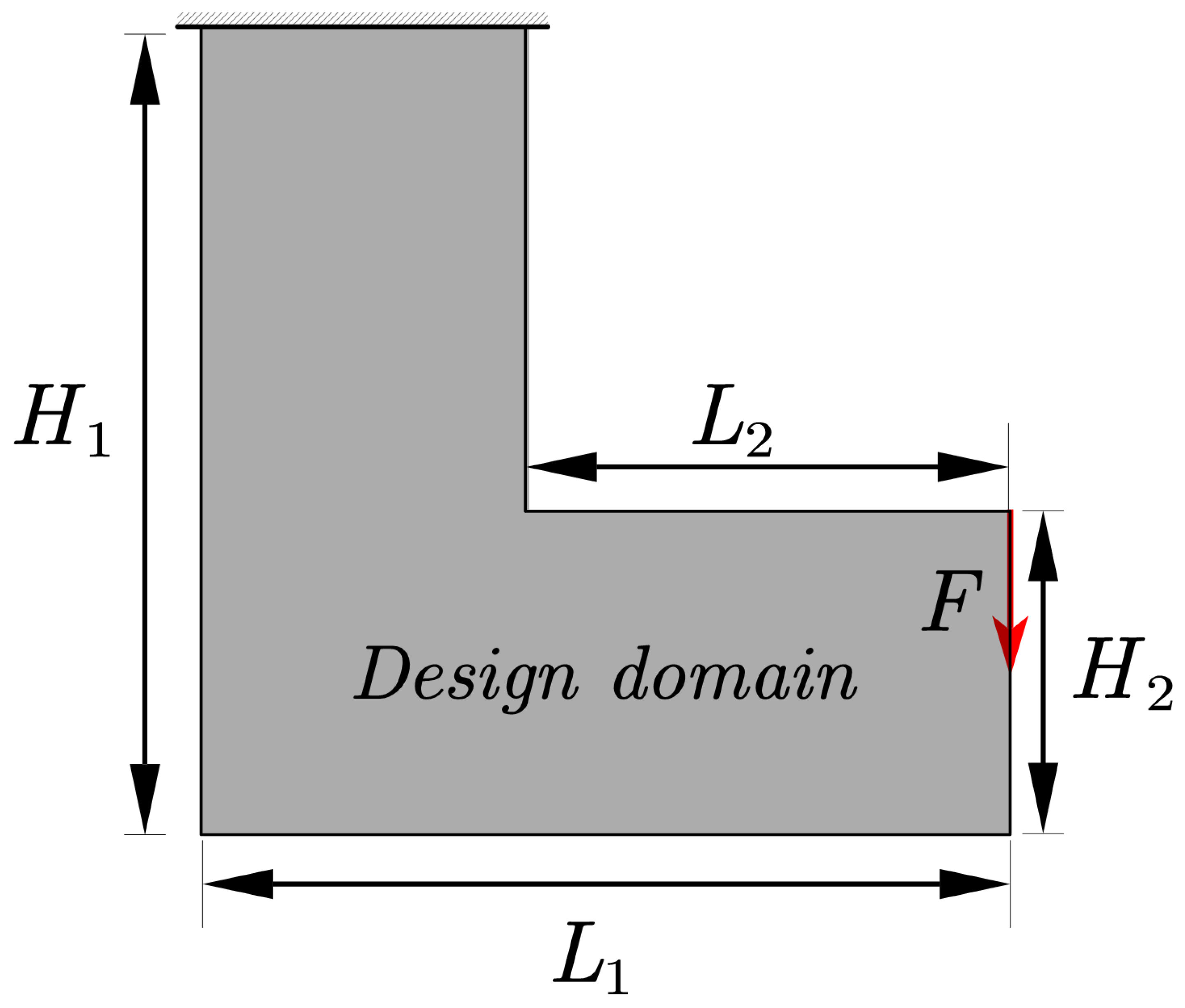
4.2. L-Shaped Beam
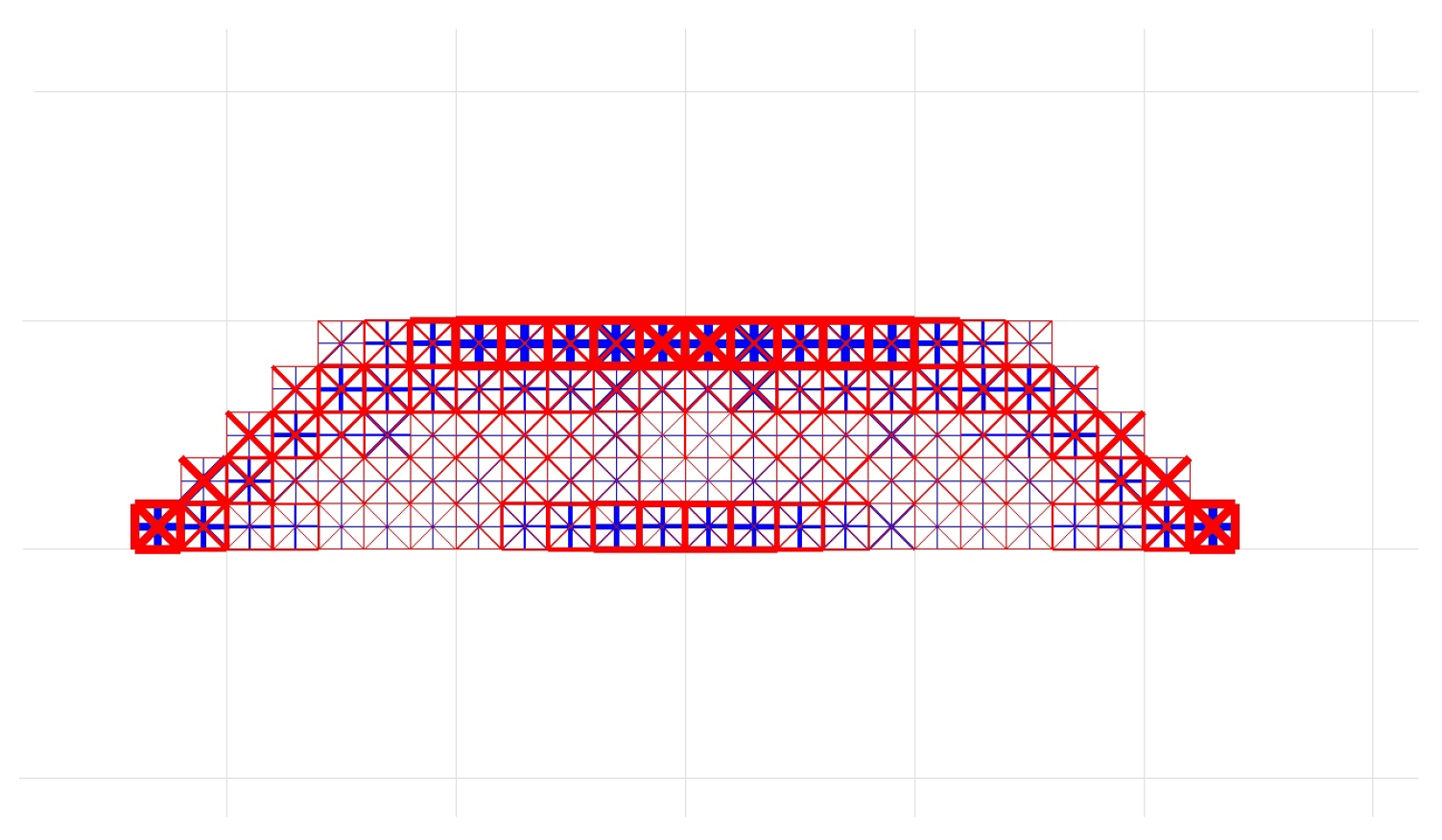
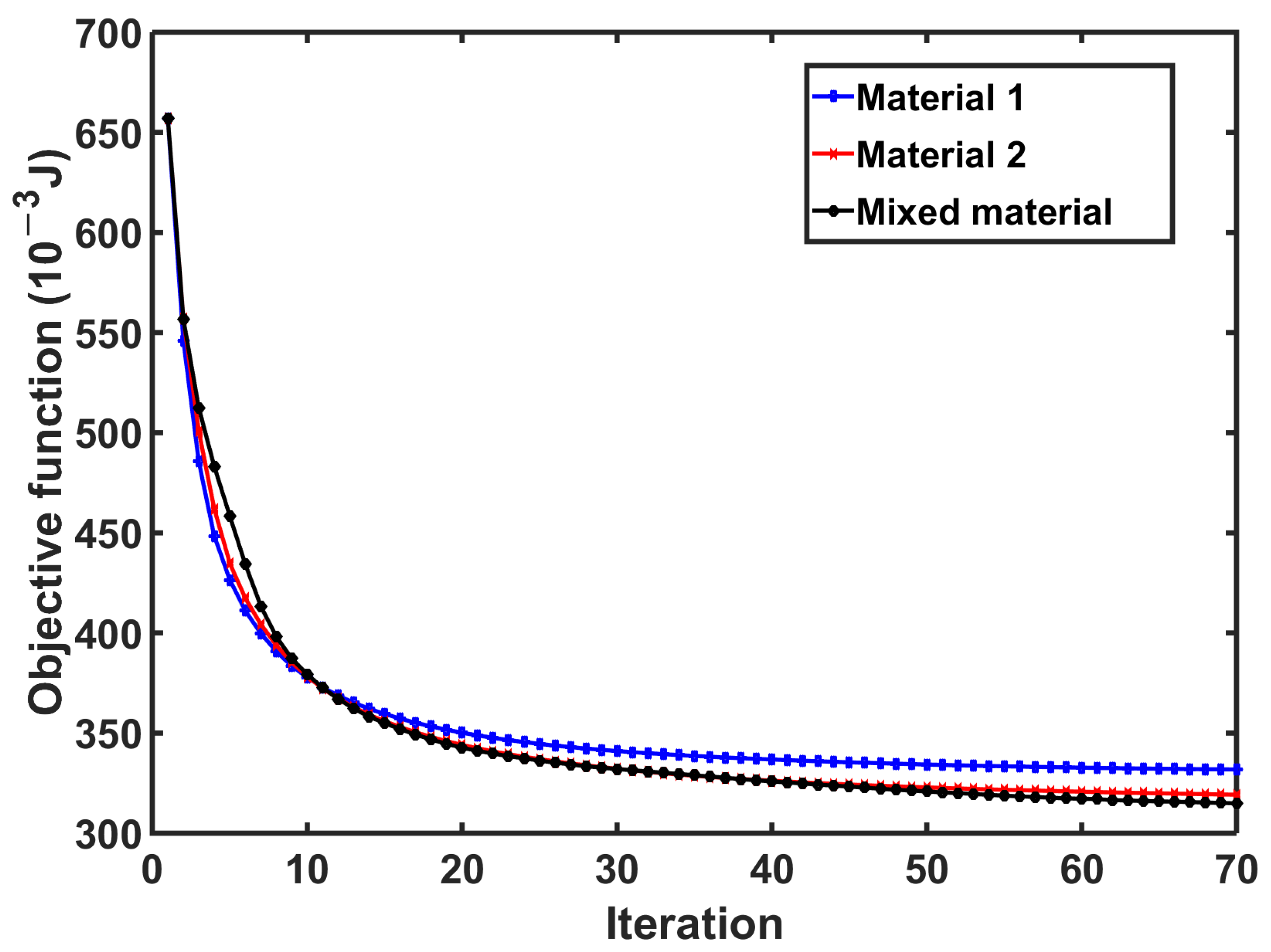
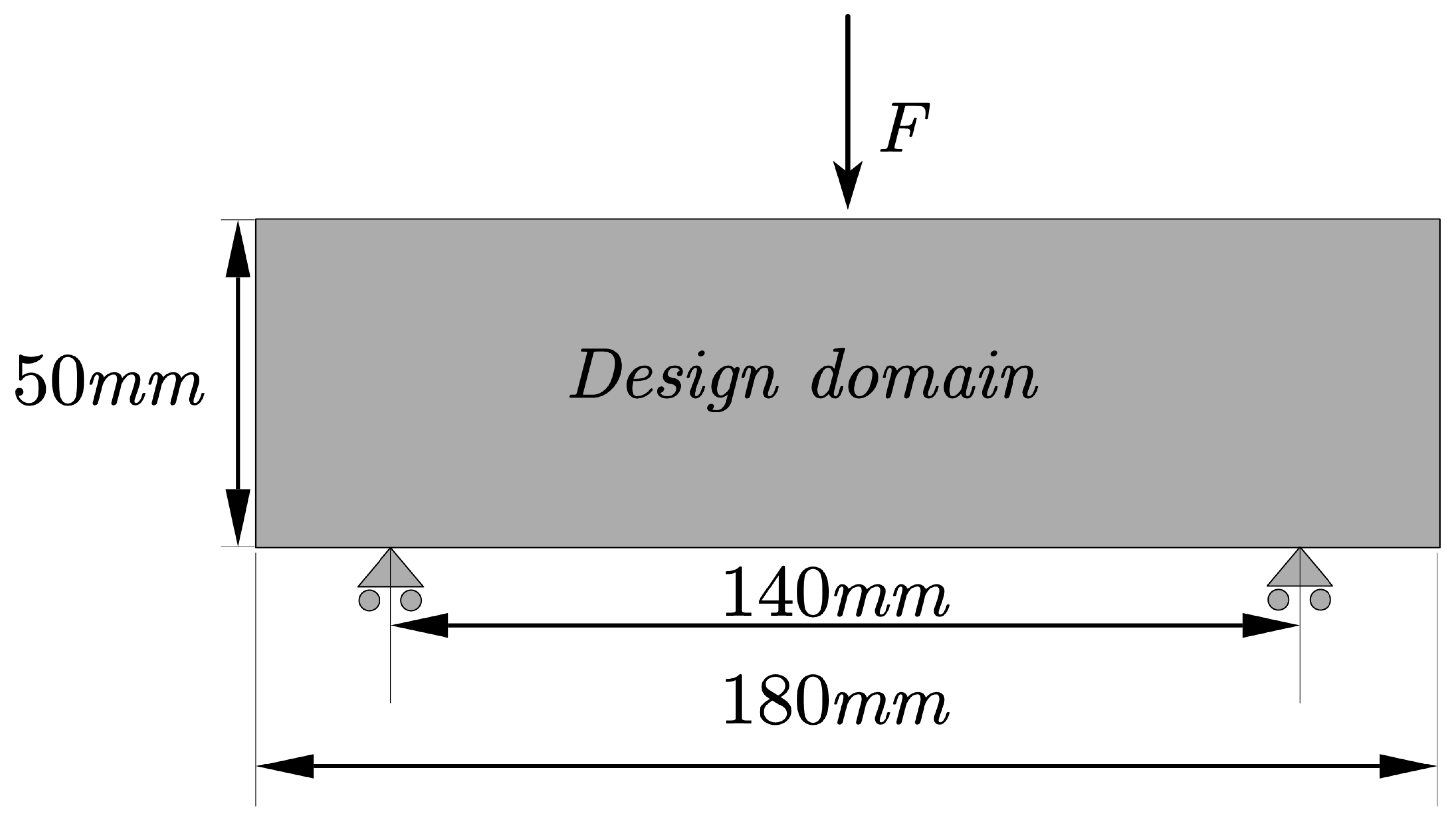
4.3. Three-Point Bending Test
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Xiong, J.; Mines, R.; Ghosh, R.; Vaziri, A.; Ma, L.; Ohrndorf, A.; Christ, H.J.; Wu, L. Advanced Micro-Lattice Materials. Adv. Eng. Mater. 2015, 17, 1253–1264. [Google Scholar] [CrossRef]
- Surjadi, J.U.; Gao, L.; Du, H.; Li, X.; Xiong, X.; Fang, N.X.; Lu, Y. Mechanical Metamaterials and Their Engineering Applications. Adv. Eng. Mater. 2019, 21, 1800864. [Google Scholar] [CrossRef]
- Han, S.C.; Lee, J.W.; Kang, K. A New Type of Low Density Material: Shellular. Adv. Mater. 2015, 27, 5506–5511. [Google Scholar] [CrossRef]
- Sun, Z.; Guo, Y.; Shim, V. Deformation and energy absorption characteristics of additively-manufactured polymeric lattice structures—Effects of cell topology and material anisotropy. Thin-Walled Struct. 2021, 169, 108420. [Google Scholar] [CrossRef]
- Sajjad, U.; ur Rehman, T.; Ali, M.; Park, C.W.; Yan, W.M. Manufacturing and potential applications of lattice structures in thermal systems: A comprehensive review of recent advances. Int. J. Heat Mass Transf. 2022, 198, 123352. [Google Scholar] [CrossRef]
- Fawaz, A.; Hua, Y.; Le Corre, S.; Fan, Y.; Luo, L. Topology optimization of heat exchangers: A review. Energy 2022, 252, 124053. [Google Scholar] [CrossRef]
- Aslan, B.; Yıldız, A.R. Optimum design of automobile components using lattice structures for additive manufacturing. Mater. Test. 2020, 62, 633–639. [Google Scholar] [CrossRef]
- Wang, C.; Zhu, J.; Wu, M.; Hou, J.; Zhou, H.; Meng, L.; Li, C.; Zhang, W. Multi-scale design and optimization for solid-lattice hybrid structures and their application to aerospace vehicle components. Chin. J. Aeronaut. 2021, 34, 386–398. [Google Scholar] [CrossRef]
- Zhu, J.H.; Zhang, W.H.; Xia, L. Topology Optimization in Aircraft and Aerospace Structures Design. Arch. Comput. Methods Eng. 2016, 23, 595–622. [Google Scholar] [CrossRef]
- Hulme, J.; Sakhaei, A.H.; Shafiee, M. Mechanical analysis and additive manufacturing of 3D-printed lattice materials for bone scaffolds. Mater. Today Proc. 2023. [Google Scholar] [CrossRef]
- Uribe-Lam, E.; Treviño-Quintanilla, C.D.; Cuan-Urquizo, E.; Olvera-Silva, O. Use of additive manufacturing for the fabrication of cellular and lattice materials: A review. Mater. Manuf. Process. 2021, 36, 257–280. [Google Scholar] [CrossRef]
- Wallach, J.; Gibson, L. Mechanical behavior of a three-dimensional truss material. Int. J. Solids Struct. 2001, 38, 7181–7196. [Google Scholar] [CrossRef]
- Quintana-Alonso, I.; Fleck, N.A. Fracture of Brittle Lattice Materials: A Review. Major Accomplishments in Composite Materials and Sandwich Structures; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Willis, J.R. Variational and Related Methods for the Overall Properties of Composites. Adv. Appl. Mech. 1981, 21, 1–78. [Google Scholar]
- Bendsoe, M.P.; Sigmund, O. Material interpolation schemes in topology optimization. Arch. Appl. Mech. 1999, 69, 635–654. [Google Scholar] [CrossRef]
- Yan, J. Preddicion of equivalent elastic properties of truss materials with periodic microstructure and the scale effects. Acta Mech. Solida Sin. 2005, 26, 421. [Google Scholar]
- Zhang, H.W.; Wu, J.K.; Lv, J.; Fu, Z.D. Extended multiscale finite element method for mechanical analysis of heterogeneous materials. Acta Mech. Solida Sin. 2010, 26, 899–920. [Google Scholar] [CrossRef]
- Berinskii, I. Elastic networks to model auxetic properties of cellular materials. Int. J. Mech. Sci. 2016, 115–116, 481–488. [Google Scholar] [CrossRef]
- Safina, L.; Baimova, J.; Krylova, K.; Murzaev, R.; Mulyukov, R. Simulation of metal-graphene composites by molecular dynamics: A review. Lett. Mater. 2020, 10, 351–360. [Google Scholar] [CrossRef]
- Liu, T.; Guessasma, S.; Zhu, J.; Zhang, W. Designing Cellular Structures for Additive Manufacturing Using Voronoi–Monte Carlo Approach. Polymers 2019, 11, 1158. [Google Scholar] [CrossRef]
- Bendsøe, M.P.; Kikuchi, N. Generating optimal topologies in structural design using a homogenization method. Comput. Methods Appl. Mech. Eng. 1988, 71, 197–224. [Google Scholar] [CrossRef]
- Bendsoe, M.P.; Sigmund, O. Topology Optimization: Theory, Methods, and Applications; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2003. [Google Scholar]
- Allaire, G.; Jouve, F. Structural Optimization by the Level-Set Method; Birkhäuser: Basel, Switzerland, 2003. [Google Scholar]
- Sigmund, O.; Maute, K. Topology optimization approaches. Struct. Multidiscip. Optim. 2013, 48, 1031–1055. [Google Scholar] [CrossRef]
- Sigmund, O. Design of multiphysics actuators using topology optimization—Part II: Two-material structures. Comput. Methods Appl. Mech. Eng. 2001, 190, 6605–6627. [Google Scholar] [CrossRef]
- Stegmann, J.; Lund, E. Discrete material optimization of general composite shell structures. Int. J. Numer. Methods Eng. 2007, 62, 2009–2027. [Google Scholar] [CrossRef]
- Zhou, S.; Wang, M.Y. Multimaterial structural topology optimization with a generalized Cahn–Hilliard model of multiphase transition. Struct. Multidiscip. Optim. 2007, 33, 89–111. [Google Scholar] [CrossRef]
- Hvejsel, C.F.; Lund, E. Material interpolation schemes for unified topology and multi-material optimization. Struct. Multidiscip. Optim. 2011, 43, 811–825. [Google Scholar] [CrossRef]
- Tajs-Zielińska, K.; Bochenek, B. Cellular Automata Approach to Topology Optimization of Graded Multi-Material Structures. Appl. Sci. 2023, 13, 2929. [Google Scholar] [CrossRef]
- Zheng, R.; Yi, B.; Peng, X.; Yoon, G.H. An Efficient Code for the Multi-Material Topology Optimization of 2D/3D Continuum Structures Written in Matlab. Appl. Sci. 2024, 14, 657. [Google Scholar] [CrossRef]
- Andreassen, E.; Clausen, A.; Schevenels, M.; Lazarov, B.S.; Sigmund, O. Efficient topology optimization in MATLAB using 88 lines of code. Struct. Multidiscip. Optim. 2011, 43, 1–16. [Google Scholar] [CrossRef]
- Sohrabi, M.K.; Azgomi, H. A Survey on the Combined Use of Optimization Methods and Game Theory. Arch. Comput. Methods Eng. 2020, 27, 59–80. [Google Scholar] [CrossRef]
- Greiner, D.; Periaux, J.; Emperador, J.M.; Galván, B.; Winter, G. Game Theory Based Evolutionary Algorithms: A Review with Nash Applications in Structural Engineering Optimization Problems. Arch. Comput. Methods Eng. 2017, 24, 703–750. [Google Scholar] [CrossRef]
- Louis, A.K. Feature reconstruction in inverse problems. Inverse Probl. 2011, 27, 065010. [Google Scholar] [CrossRef]
- Maxwell, J.C. I.—On Reciprocal Figures, Frames, and Diagrams of Forces. Trans. R. Soc. Edinb. 1870, 26, 1–40. [Google Scholar] [CrossRef]
- Greiner, D.; Emperador, J.M.; Winter, G. Single and multiobjective frame optimization by evolutionary algorithms and the auto-adaptive rebirth operator. Comput. Methods Appl. Mech. Eng. 2004, 193, 3711–3743. [Google Scholar] [CrossRef]
- Holmberg, E.; Thore, C.J.; Klarbring, A. Game theory approach to robust topology optimization with uncertain loading. Struct. Multidiscip. Optim. 2017, 55, 1383–1397. [Google Scholar] [CrossRef]
- Habbal, A.; Petersson, J.; Thellner, M. Multidisciplinary topology optimization solved as a Nash game. Int. J. Numer. Methods Eng. 2010, 61, 949–963. [Google Scholar] [CrossRef]
- Périaux, J.; Chen, H.Q.; Mantel, B.; Sefrioui, M.; Sui, H.T. Combining game theory and genetic algorithms with application to DDM-nozzle optimization problems. Finite Elem. Anal. Des. 2001, 37, 417–429. [Google Scholar] [CrossRef]
- Desideri, J.A. Platform for Prioritized Multi-Objective Optimization by Metamodel-Assisted Nash Games; Inria Sophia Antipolis: Valbonne, France, 2019. [Google Scholar]
- Nash, J.F. Equilibrium Points in N-Person Games. Proc. Natl. Acad. Sci. USA 1950, 36, 48–49. [Google Scholar] [CrossRef]
- Dhatt, G.; Lefrançois, E.; Touzot, G. Finite Element Method; John Wiley & Sons: Hoboken, NJ, USA, 2012. [Google Scholar]
- Wu, T.; Li, S. An efficient multiscale optimization method for conformal lattice materials. Struct. Multidiscip. Optim. 2021, 63, 1063–1083. [Google Scholar] [CrossRef]
- Chuang, W.; Hong, Z.J.; Hong, Z.W.; Ying, L.S.; Jie, K. Concurrent topology optimization design of structures and non-uniform parameterized lattice microstructures. Struct. Multidiscip. Optim. 2018, 58, 35–50. [Google Scholar]
- Mohamed, O.A.; Masood, S.H.; Bhowmik, J.L. Optimization of fused deposition modeling process parameters:a review of current research and future prospects. Adv. Manuf. 2015, 3, 42–53. [Google Scholar] [CrossRef]
- Liao, Z. Graded-density Lattice Structure Optimization Design Based on Topology Optimization. J. Mech. Eng. 2019, 55, 65. [Google Scholar] [CrossRef]











Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xiao, Y.; Hu, W.; Li, S. Multi-Material Optimization for Lattice Materials Based on Nash Equilibrium. Appl. Sci. 2024, 14, 2934. https://doi.org/10.3390/app14072934
Xiao Y, Hu W, Li S. Multi-Material Optimization for Lattice Materials Based on Nash Equilibrium. Applied Sciences. 2024; 14(7):2934. https://doi.org/10.3390/app14072934
Chicago/Turabian StyleXiao, Yangyang, Wei Hu, and Shu Li. 2024. "Multi-Material Optimization for Lattice Materials Based on Nash Equilibrium" Applied Sciences 14, no. 7: 2934. https://doi.org/10.3390/app14072934
APA StyleXiao, Y., Hu, W., & Li, S. (2024). Multi-Material Optimization for Lattice Materials Based on Nash Equilibrium. Applied Sciences, 14(7), 2934. https://doi.org/10.3390/app14072934




