Influence of Site Effects on Scaling Relation Between Rotational and Translational Signals Produced by Anthropogenic Seismicity
Abstract
:1. Introduction
- Investigated the possibility of estimating the site effect parameters of rotational motion using the rewritten horizontal-to-vertical spectral ratio method and comparing the obtained results to the translational motion.
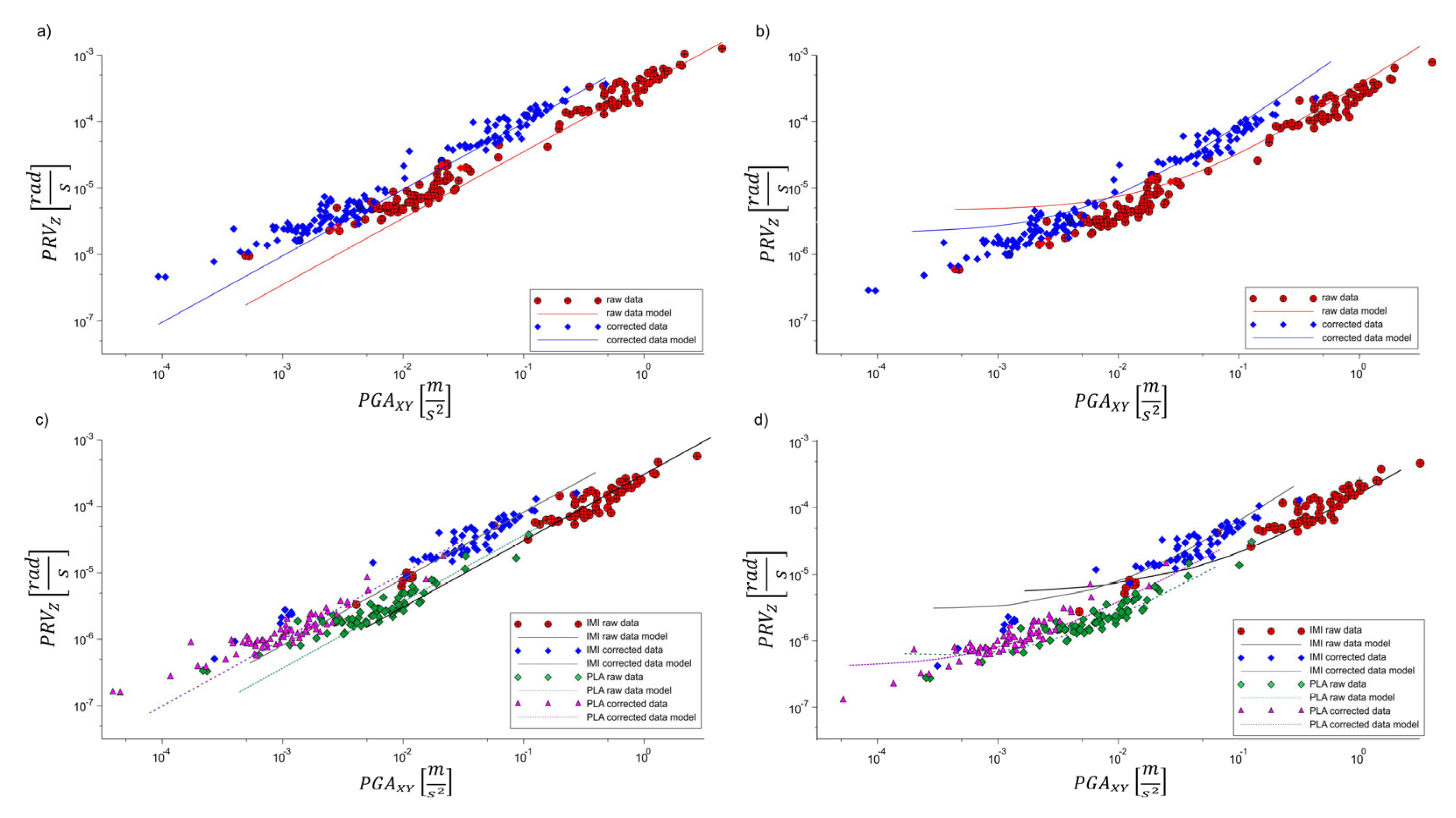
- Estimated the scaling relation between the maximum peak values of horizontal ground acceleration (PGA) and vertical rotational velocity (PRV) for two models, y = ax and y = ax + b, checking whether the intercept b is significant and what physical meaning it may have.
- Analyzed the influence of amplification on the scaling relation function by re-estimating the models for amplification factor-corrected data sets.
2. Materials and Methods
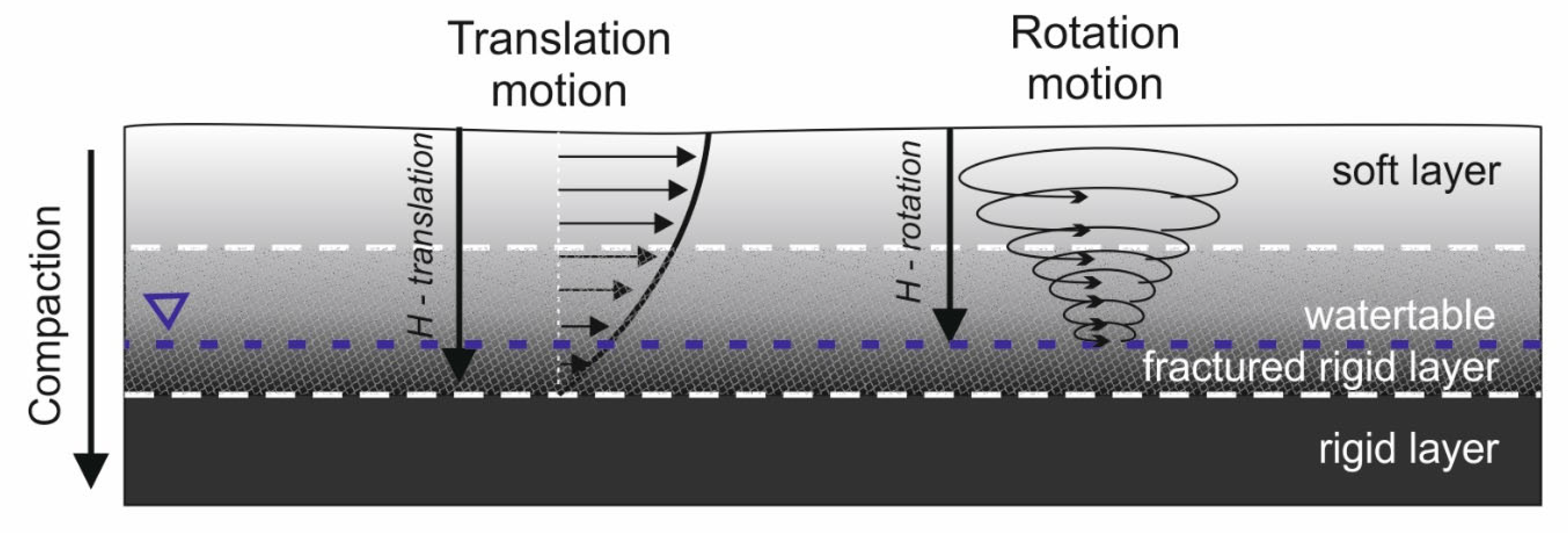
2.1. Site Conditions
2.2. Data and Sensors
2.3. Site Effect
2.3.1. Theoretical HVSR
2.3.2. Empirical HVSR
2.4. Scaling Relation
3. Results
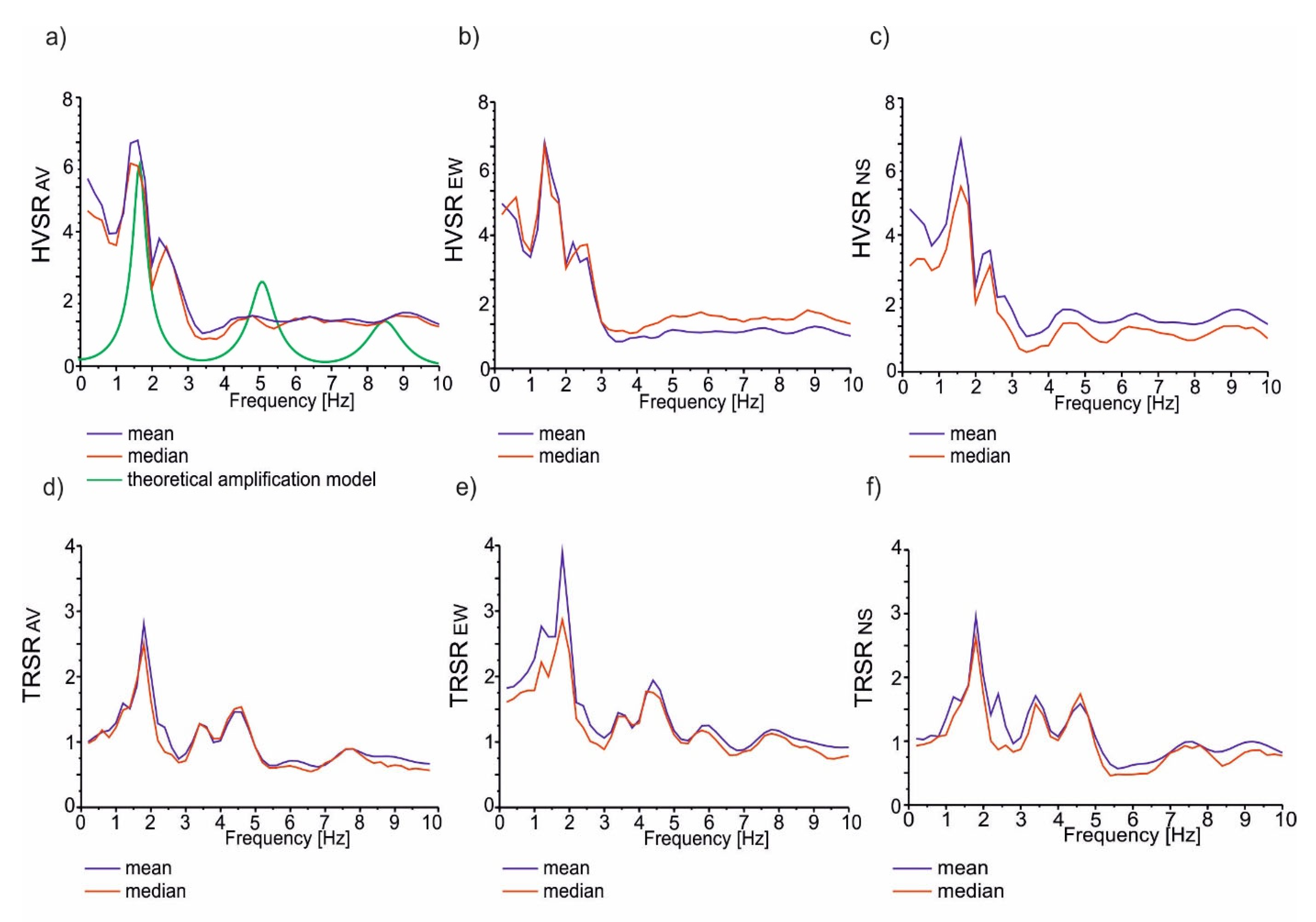
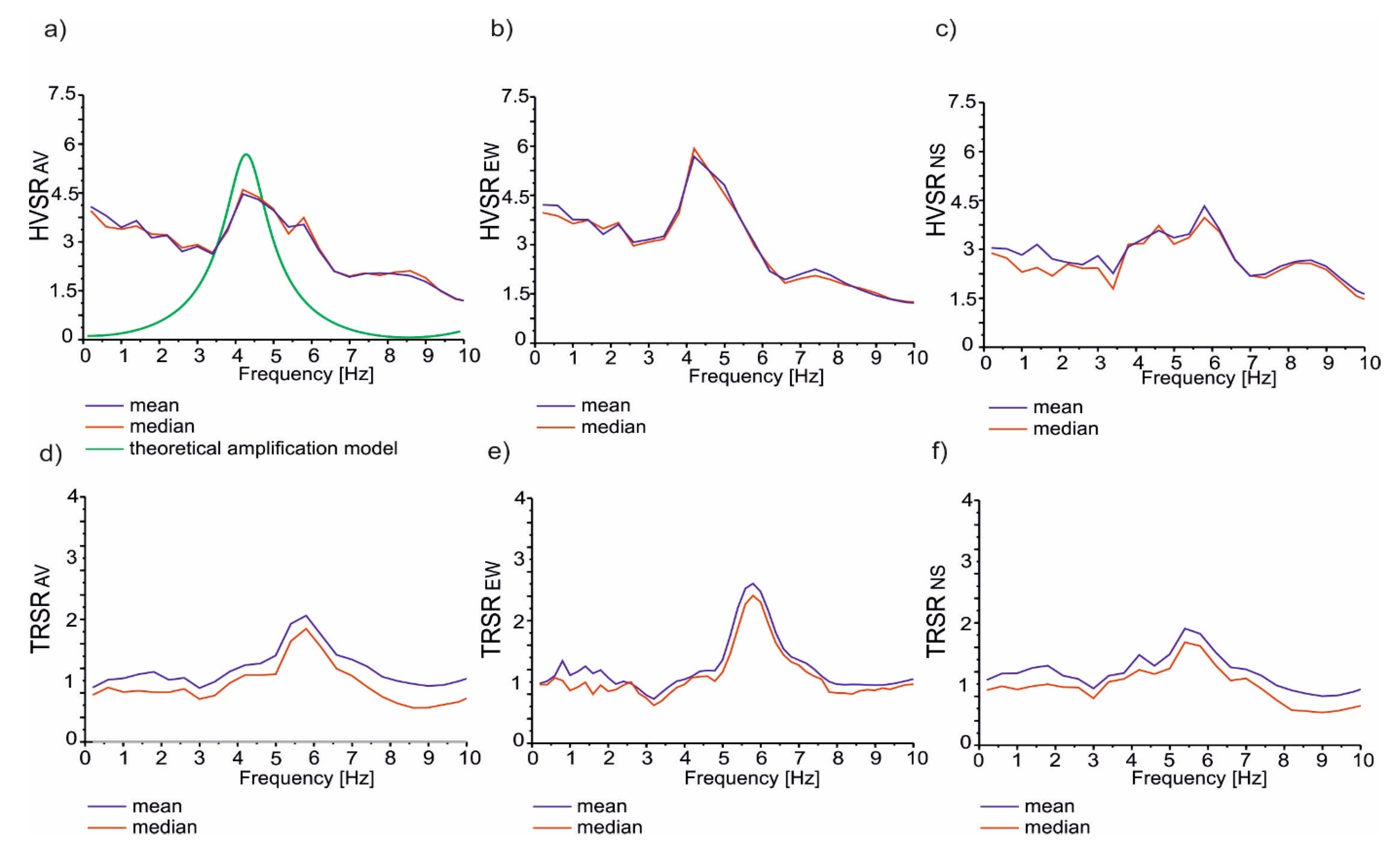
3.1. Site Effect Curves of the Translational and Rotational Motion
3.2. Peak Rotation and Translation Scaling Relations
4. Discussion
4.1. Site Effect Differences
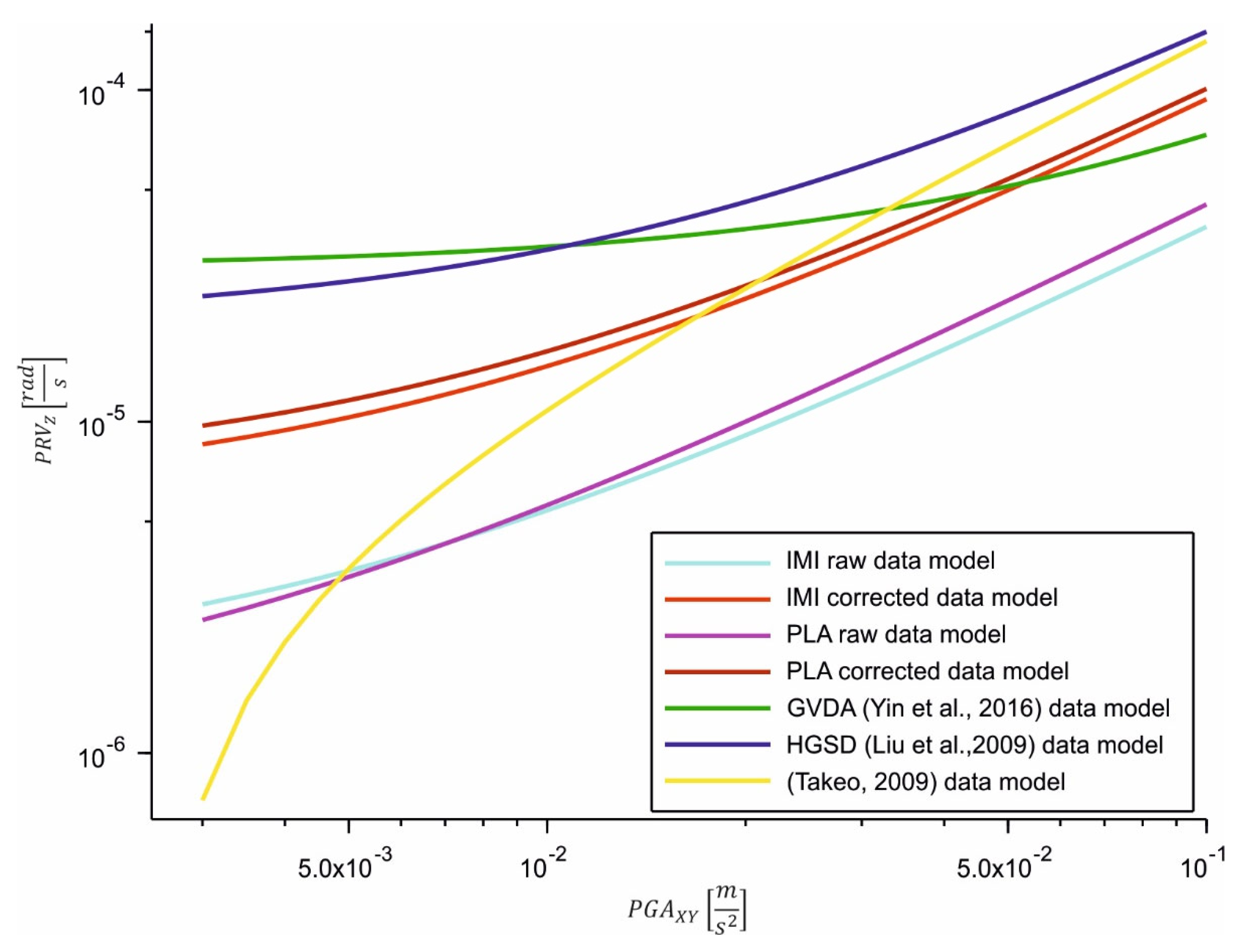
4.2. Scaling Relation
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zembaty, Z. Deriving seismic surface rotations for engineering purposes. In Earthquake Source Asymmetry, Structural Media and Rotation Effects; Teisseyre, R., Majewski, E., Takeo, M., Eds.; Springer: Berlin/Heidelberg, Germany, 2006; pp. 549–568. [Google Scholar]
- Igel, H.; Cochard, A.; Wassermann, J.; Schreiber, U.; Velikoseltsev, A.; Pham, N.D. Broadband observations of rotational ground motions. Geophys. J. Int. 2007, 168, 182–197. [Google Scholar] [CrossRef]
- Lee, V.W.; Liang, L. Rotational components of strong motion earthquakes. In Proceedings of the 14th World Conference on Earthquake Engineering, Beijing, China, 12–17 October 2008. [Google Scholar]
- Lee, W.H.K.; Huang, B.S.; Langston, C.A.; Lin, C.J.; Liu, C.C.; Shin, T.C.; Teng, T.L.; Wu, C.F. Review: Progress in rotational ground motion observations from explosions and local earthquakes in Taiwan. Bull. Seismol. Soc. Am. 2009, 99, 958–967. [Google Scholar] [CrossRef]
- Liu, C.C.; Huang, B.S.; Lee, W.H.K.; Lin, C.J. Observing rotational and translational ground motions at the HGSD station in Taiwan from 2007 to 2008. Bull. Seismol. Soc. Am. 2009, 99, 1228–1236. [Google Scholar] [CrossRef]
- Stupazzini, M.; de la Puente, J.; Smerzini, C.; Käser, M.; Igel, H.; Castellani, A. Study of Rotational Ground Motion in the Near-Field Region. Bull. Seismol. Soc. Am. 2009, 99, 1271–1286. [Google Scholar] [CrossRef]
- Kalab, Z.; Knejzlik, J.; Lednicka, M. Application of newly developed rotational sensor for monitoring of mining-induced seismic events in the Karvina region. Acta Geodyn. Geomater. 2012, 2, 197–205. [Google Scholar] [CrossRef]
- Zembaty, Z.; Mutke, G.; Nawrocki, D.; Bobra, P. Rotational ground-motion records from induced seismic events. Seismol. Res. Lett. 2017, 88, 13–22. [Google Scholar] [CrossRef]
- Mutke, G.; Lurka, A.; Zembaty, Z. Prediction of rotational ground motion for mining-induced seismicity—Case study from Upper Silesian Coal Basin, Poland. Eng. Geol. 2020, 276, 105767. [Google Scholar] [CrossRef]
- Sarokolayi, L.K.; Beitollahi, A.; Abdollahzadeh, G.; Amreie, S.T.T.; Kutanaei, S.S. Modeling of ground motion rotational components for near-fault and far-fault earthquake according to soil type. Arab. J. Geosci. 2015, 8, 3785–3797. [Google Scholar] [CrossRef]
- Sbaa, S.; Hollender, F.; Perron, V.; Imtiaz, A.; Bard, P.-Y.; Mariscal, A.; Cochard, A.; Dujardin, A. Analysis of rotation sensor data from the SINAPS@ Kefalonia (Greece) post-seismic experiment—Link to surface geology and wavefield characteristics. Earth Planets Space 2017, 69, 124. [Google Scholar] [CrossRef]
- Wang, H.; Igel, H.; Gallovič, F.; Cochard, A. Source and Basin Effects on Rotational Ground Motions: Comparison with Translations. Bull. Seismol. Soc. Am. 2009, 99, 1162–1173. [Google Scholar] [CrossRef]
- Pham, N.D.; Igel, H.; Puente, J.; Käser, M.; Schoenberg, M. Rotational motions in homogeneous anisotropic elastic media. Geophysics 2010, 75, 47–56. [Google Scholar] [CrossRef]
- Trifunac, M.D. The role of strong motion rotations in the response of structures near earthquake faults. Soil Dyn. Earthq. Eng. 2009, 29, 382–393. [Google Scholar] [CrossRef]
- Basu, D.; Whittaker, A.S.; Constantinou, M.C. Characterizing rotational components of earthquake ground motion using a surface distribution method and response of sample structures. J. Eng. Struct. 2015, 99, 685–707. [Google Scholar] [CrossRef]
- Falamarz-Sheikhabadi, M.R.; Ghafory-Ashtiany, M. Rotational components in structural loading. Soil Dyn. Earthq. Eng. 2015, 75, 220–233. [Google Scholar] [CrossRef]
- Bońkowski, P.A.; Zembaty, Z.; Minch, M.Y. Engineering analysis of strong ground rocking and its effect on tall structures. Soil Dyn. Earthq. Eng. 2019, 116, 358–370. [Google Scholar] [CrossRef]
- Huang, M.; Fan, X.; Wang, H. Three-dimensional upper bound stability analysis of slopes with weak interlayer based on rotational-translational mechanisms. Eng. Geol. 2017, 223, 82–91. [Google Scholar] [CrossRef]
- Jiren, X.; Uchimura, T.; Wang, G.; Selvarajah, H.; Maqsood, Z.; Shen, Q.; Mei, G.; Qiao, S. Predicting the sliding behaviour of rotational landslides based on the tilting measurement of the slope surface. Eng. Geol. 2020, 269, 105554. [Google Scholar] [CrossRef]
- Nakamura, Y. A method for dynamic characteristics estimation of subsurface using microtremor on the ground surface. Q. Rep. RTRI 1989, 130, 25–33. [Google Scholar]
- Ringler, A.; Anthony, R.; Holland, A.; Wilson, D.; Lin, C.J. Observations of Rotational Motions from Local Earthquakes Using Two Temporary Portable Sensors in Waynoka, Oklahoma. Bull. Seismol. Soc. Am. 2018, 108, 3562–3575. [Google Scholar] [CrossRef]
- Nawrocki, D.; Mendecki, M.; Teper, L. Estimation of site resonance frequency using HVSR method for rotational and translational signals: Result comparison from Fourier and response spectrum methods. In Proceedings of the 3rd European Conference on Earthquake Engineering and Seismology, Bucharest, Romania, 4–9 September 2022. [Google Scholar]
- Nawrocki, D.; Mendecki, M.; Teper, L. Estimation of the resonance frequency of rotational and translational signals evoked by mining-induced seismicity. Front. Earth Sci. 2024, 12, 1403043. [Google Scholar] [CrossRef]
- Nawrocki, D.; Mendecki, M.; Teper, L. The effects of component rotation on H/V spectra: A comparison of rotational and translational data. Geol. Geophys. Environ. 2024, 50, 145–154. [Google Scholar]
- Igel, H.; Schreiber, U.; Flaws, A.; Schuberth, B.; Velikoseltsev, A.; Cochard, A. Rotational motions induced by the M8.1 Tokachi-oki earthquake, September 25, 2003. Geophys. Res. Lett. 2005, 32, L08309. [Google Scholar] [CrossRef]
- Takeo, M. Rotational motions observed during an earthquake swarm in April 1998 offshore Ito, Japan. Bull. Seismol. Soc. Am. 2009, 99, 1457–1467. [Google Scholar] [CrossRef]
- Sagan, G.; Teper, L.; Zuberek, W.M. Tectonic analysis of mine tremor mechanisms from the Upper Silesian Coal Basin. Pure Appl. Geophys. 1996, 147, 217–238. [Google Scholar] [CrossRef]
- Buła, Z.; Kotas, A. (Eds.) Geological Atlas of the Upper Silesian Coal Basin, Part III. Structural-Geological Maps 1:100 000; Państwowy Instytut Geologiczny: Warszawa, Poland, 1994. [Google Scholar]
- Teper, L. Geometry of fold arrays in the Silesian-Cracovian region of southern Poland. Geol. Soc. Spec. Publ. Lond. 2000, 169, 167–179. [Google Scholar] [CrossRef]
- Mendecki, M.J.; Szczygieł, J.; Lizurek, G.; Teper, L. Mining-triggered seismicity governed by a fold hinge zone: The Upper Silesian Coal Basin, Poland. Eng. Geol. 2020, 274, 105728. [Google Scholar] [CrossRef]
- Jureczka, J.; Aust, J.; Buła, Z.; Dopita, M.; Zdanowski, A. Geological Map of the Upper Silesian Coal Basin (Carboniferous Subcrop) 1:200 000; Państwowy Instytut Geologiczny: Warszawa, Poland, 1995. [Google Scholar]
- Stec, K. Characteristics of seismic activity of the Upper Silesian Coal Basin in Poland. Geophys. J. Int. 2006, 168, 757–768. [Google Scholar] [CrossRef]
- eentec. Instruction Manual, Model R-1, St. Louis, Missouri. 2008. 8p. Available online: http://www.eentec.com/ (accessed on 1 July 2020).
- Bernauer, F.; Wassermann, J.; Igel, H. Rotational sensors—A comparison of different sensor types. J. Seismol. 2012, 16, 595–602. [Google Scholar] [CrossRef]
- Mutke, G.; Kotyrba, A.; Lurka, A.; Olszewska, D.; Dykowski, P.; Borkowski, A.; Araszkiewicz, A.; Barański, A. Upper Silesian Geophysical Observation System—A unit of the EPOS project. J. Sustain. Min. 2019, 18, 198–207. [Google Scholar] [CrossRef]
- Bard, P.Y.; SESAME Participants. The SESAME project: An overview and main results. In Proceedings of the 13th World Conference on Earthquake Engineering, Paper 2207, Vancouver, BC, Canada, 1–6 August 2004. [Google Scholar]
- Stephenson, W.J.; Hartzell, S.; Frankel, A.; Asten, M.; Carver, D.; Kim, W. Site characterization for urban seismic hazards in lower Manhattan, New York City, from microtremor array analysis. Geophys. Res. Lett. 2009, 36, L03301. [Google Scholar] [CrossRef]
- Pastén, C.; Sáez, M.; Ruiz, S.; Leyton, F.; Salomón, J.; Poli, P. Deep Characterization of the Santiago Basin using HVSR and Cross-correlation of Ambient Seismic Noise. Eng. Geol. 2015, 201, 57–66. [Google Scholar] [CrossRef]
- Stanko, D.; Markušić, S.; Strelec, S.; Gazdek, M. HVSR analysis of seismic site effects and soil-structure resonance in Varaždin city (North Croatia). Soil. Dynam Earthq. Eng. 2017, 92, 666–677. [Google Scholar] [CrossRef]
- Stanko, D.; Markušić, S. An empirical relationship between resonance frequency, bedrock depth and VS30 for Croatia based on HVSR forward modelling. Nat. Hazards 2020, 103, 3715–3743. [Google Scholar] [CrossRef]
- Szczygieł, J.; Wróblewski, W.; Mendecki, M.J.; Hercman, H.; Bosák, P. Soft-sediment deformation structures in cave deposits and their possible causes (Kalacka Cave, Tatra Mts., Poland). J. Struct. Geol. 2020, 140, 104161. [Google Scholar] [CrossRef]
- Kawase, H. Site effects on strong ground motions. In International Handbook of Earthquake and Engineering Seismology; Lee, W.H., Jennings, P., Kisslinger, C., Kanamori, H., Eds.; 81B; Academic Press: Cambridge, MA, USA, 2002; pp. 1013–1030. [Google Scholar]
- Rong, M.; Fu, L.Y.; Wang, Z.; Li, X.; Carpenter, N.S.; Woolery, E.W.; Lyu, Y. On the amplitude discrepancy of HVSR and site amplification from strong-motion observations. Bull. Seismol. Soc. Am. 2017, 107, 2873–2884. [Google Scholar] [CrossRef]
- Zhu, C.; Cotton, F.; Pilz, M. Detecting Site Resonant Frequency Using HVSR: Fourier versus Response Spectrum and the First versus the Highest Peak Frequency. Bull. Seismol. Soc. Am. 2020, 110, 427–440. [Google Scholar] [CrossRef]
- Yin, J.; Nigbor, R.L.; Chen, Q.; Steidl, J. Engineering analysis of measured rotational ground motions at GVDA. Soil. Dyn. Earthq. Eng. 2016, 87, 125–137. [Google Scholar] [CrossRef]
- Konno, K.; Ohmachi, T. Ground-Motion Characteristics Estimated from Spectral Ratio between Horizontal and Vertical Components of Microtremor. Bull. Seismol. Soc. Am. 1998, 88, 228–241. [Google Scholar] [CrossRef]
- Suryanto, W. Rotational Motions in Seismology: Theory and Application. Ph.D. Dissertation, Ludwig-Maximilians University München, Faculty of Geosciences, München, Germany, 2006. [Google Scholar]
- Schön, J. Physical Properties of Rocks: A Workbook; Elsevier: Oxford, UK, 2011; Volume 8. [Google Scholar]
- Singh, S.; Capdeville, Y.; Igel, H. Correcting wavefield gradients for the effects of local small-scale heterogeneities. Geophys. J. Int. 2020, 220, 996–1011. [Google Scholar] [CrossRef]
- Okamoto, S. Introduction to Earthquake Engineering; University of Tokyo Press: Tokyo, Japan, 1984. [Google Scholar]
- Pischiutta, M.; Rovelli, A.; Salvini, F.; Fletcher, J.B.; Savage, M.K. Directional Amplification at Rock Sites in Fault Damage Zones. Appl. Sci. 2023, 13, 6060. [Google Scholar] [CrossRef]
- Pischiutta, M.; Savage, M.K.; Holt, R.A.; Salvini, F. Fracture-related wavefield polarization and seismic anisotropy across the Greendale Fault. J. Geophys. Res. Solid Earth 2015, 120, 7048–7067. [Google Scholar] [CrossRef]
- Moriya, T.; Teisseyre, R. Design of rotation seismometer and non-linear behavior of rotation components of earthquakes. In Earthquake Source Asymmetry, Structural Media and Rotation Effects; Teisseyre, R., Majewski, E., Takeo, M., Eds.; Springer: Berlin/Heidelberg, Germany, 2006; pp. 439–450. [Google Scholar]
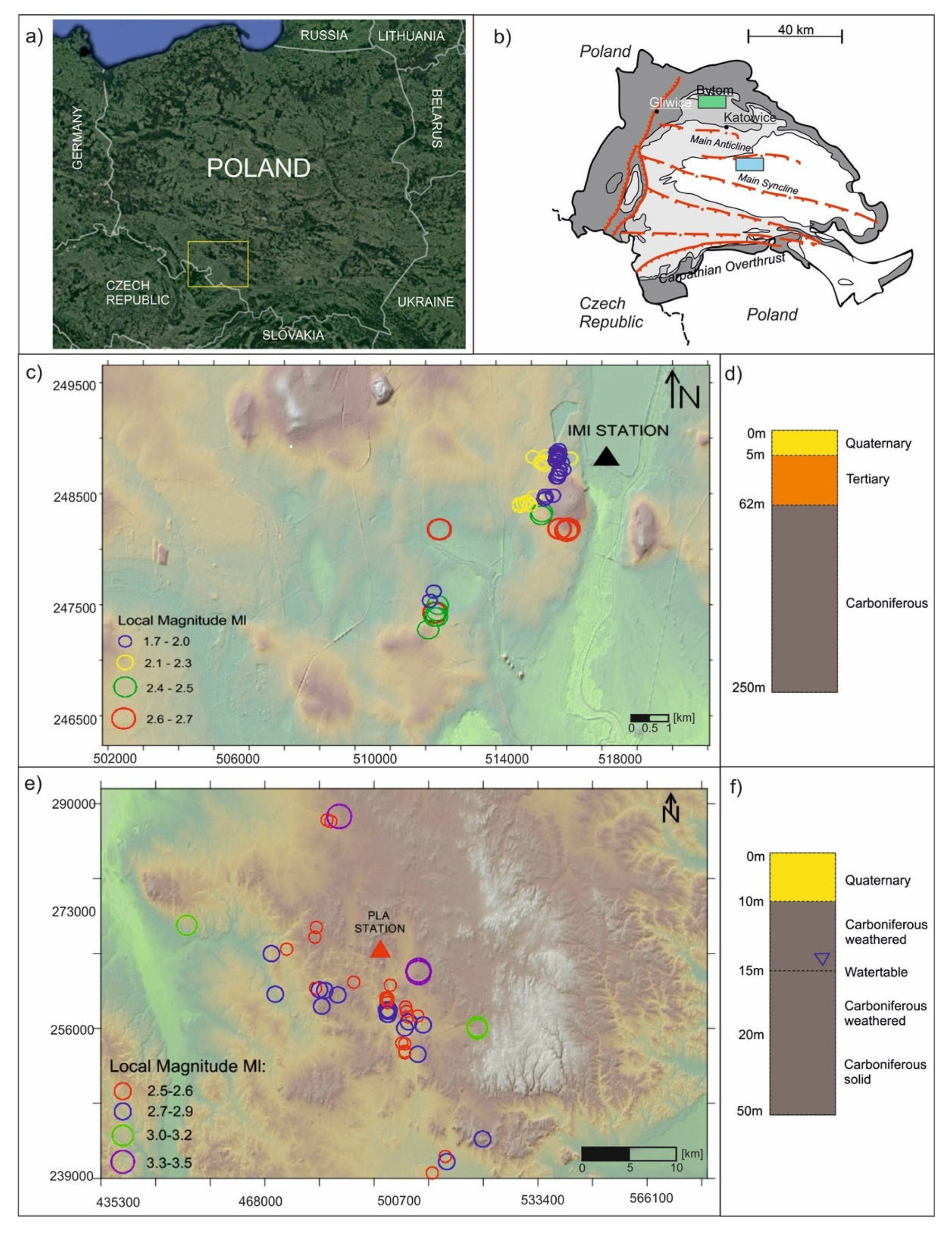
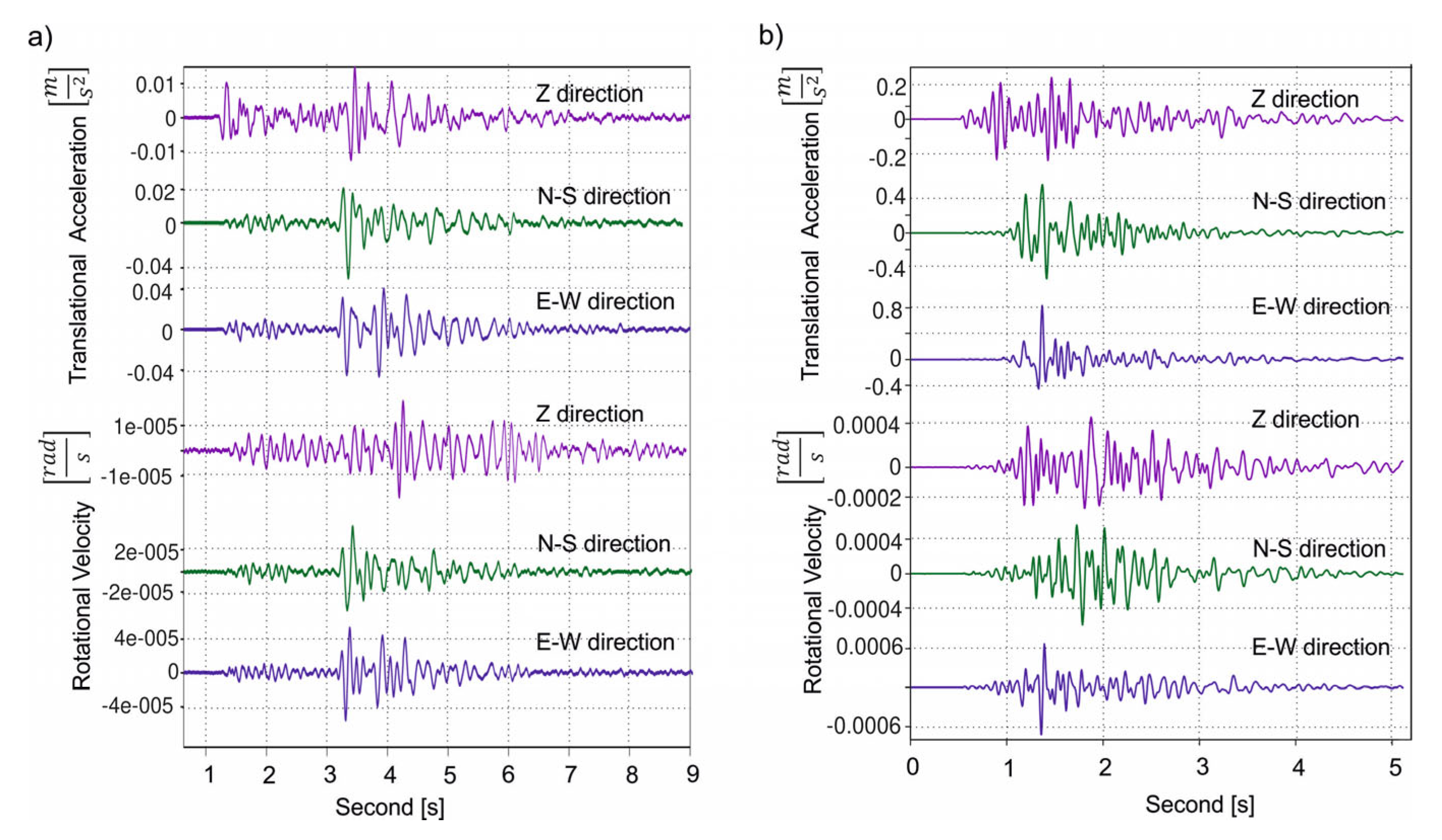

| Energy [J] | ML | IMI STATION | PLA STATION | ||
|---|---|---|---|---|---|
| Number | Epicentral Distance for the Energy Range [km] | Number | Epicentral Distance for the Energy Range [km] | ||
| 1.0 × 105–5.0 × 105 | 1.7–2.0 | 35 | 0.75–5.13 | 0 | - |
| 6.0 × 105–9.9 × 105 | 2.1–2.3 | 13 | 0.65–1.42 | 0 | - |
| 1.0 × 106–5.0 × 106 | 2.4–2.5 | 7 | 1.17–5.52 | 22 | 5.68–18.99 |
| 6.0 × 106–8.5 × 106 | 2.6–2.7 | 5 | 1.34–4.20 | 28 | 5.63–18.32 |
| 1.3 × 107–2.4 × 107 | 2.8–2.9 | - | - | 12 | 5.67–20.43 |
| 3.2 × 107–7.6 × 107 | 3.0–3.2 | - | - | 5 | 5.91–12.38 |
| 1.2 × 108–2.8 × 108 | 3.3–3.5 | - | - | 3 | 8.20–9.70 |
| Station | Vs Basement [m/s] | Vs Resonant [m/s] | Density Basement [g/cm3] | Density Resonant [g/cm3] | Attenuation Factor | Thickness [m] | Max (H/V) | f0 [Hz] |
|---|---|---|---|---|---|---|---|---|
| IMI | 3800 | 400 | 2.5 | 1.8 | 0.05 | 62.0 | 6.4 | 1.65 |
| PLA | 2200 | 340 | 2.1 | 1.8 | 0.05 | 20.0 | 4.7 | 4.25 |
| Type of Motion | Component | IMI Station | PLA Station | ||||
|---|---|---|---|---|---|---|---|
| Maximum I | Maximum II | Maximum | |||||
| f0 [Hz] | Amplification Peak Value | f0 [Hz] | Amplification Peak Value | f0 [Hz] | Amplification Peak Value | ||
| Translation | AV HVSR PGA | 1.6 | 6.8 | 2.2 | 3.9 | 4.2 | 4.7 |
| EW PGA | 1.6 | 6.7 | 2.4 | 3.4 | 5.8 | 4.3 | |
| NS PGA | 1.4 | 7.1 | 2.2 | 4.1 | 4.2 | 5.6 | |
| Rotation | AV TRSR PRV | 1.8 | 2.5 | 4.4 | 1.6 | 5.6 | 1.9 |
| EW PRV | 1.8 | 3.1 | 4.6 | 1.7 | 5.8 | 2.7 | |
| NS PRV | 1.8 | 3.7 | 4.4 | 1.7 | 5.4 | 1.8 | |
| Station | Type of Data | Model Without Intercept | Model Intercept | |||||
|---|---|---|---|---|---|---|---|---|
| a ± Δa | R2 | SEE | a ± Δa | B ± Δb | R2 | SEE | ||
| Total | Raw data | (46.2 ± 0.6) × 10−5 | 0.93 | 1.6× 10−5 | (40.7 ± 1.2) × 10−5 | (5.1 ± 1.4) × 10−6 | 0.92 | 1.6 × 10−5 |
| Corrected data | (129.0 ± 1.3) × 10−5 | 0.93 | 5.5 × 10−6 | (93.7 ± 2.1) × 10−5 | (1.8 ± 0.4) × 10−6 | 0.93 | 5.7 × 10−6 | |
| IMI | Raw data | (45.4 ± 1.3) × 10−5 | 0.91 | 2.1× 10−5 | (37.3 ± 1.4) × 10−5 | (1.7 ± 0.6) × 10−6 | 0.89 | 2.3 × 10−5 |
| Corrected data | (100.8 ± 2.4) × 10−5 | 0.93 | 8.7 × 10−6 | (87.4 ± 3.1) × 10−5 | (5.4 ± 1.2) × 10−6 | 0.88 | 7.9 × 10−6 | |
| PLA | Raw data | (50.8 ± 1.5) × 10−5 | 0.92 | 1.8 × 10−6 | (42.0 ± 1.9) × 10−5 | (1.2 ± 0.5) × 10−6 | 0.89 | 1.6 × 10−6 |
| Corrected data | (129.0 ± 3.5) × 10−5 | 0.92 | 9.6× 10−7 | (94.7 ± 3.8) × 10−5 | (6.8 ± 1.2) × 10−6 | 0.89 | 8.6 × 10−7 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nawrocki, D.; Mendecki, M.J.; Mutke, G.; Teper, L. Influence of Site Effects on Scaling Relation Between Rotational and Translational Signals Produced by Anthropogenic Seismicity. Appl. Sci. 2025, 15, 102. https://doi.org/10.3390/app15010102
Nawrocki D, Mendecki MJ, Mutke G, Teper L. Influence of Site Effects on Scaling Relation Between Rotational and Translational Signals Produced by Anthropogenic Seismicity. Applied Sciences. 2025; 15(1):102. https://doi.org/10.3390/app15010102
Chicago/Turabian StyleNawrocki, Dariusz, Maciej J. Mendecki, Grzegorz Mutke, and Lesław Teper. 2025. "Influence of Site Effects on Scaling Relation Between Rotational and Translational Signals Produced by Anthropogenic Seismicity" Applied Sciences 15, no. 1: 102. https://doi.org/10.3390/app15010102
APA StyleNawrocki, D., Mendecki, M. J., Mutke, G., & Teper, L. (2025). Influence of Site Effects on Scaling Relation Between Rotational and Translational Signals Produced by Anthropogenic Seismicity. Applied Sciences, 15(1), 102. https://doi.org/10.3390/app15010102






