Prediction of GNSS Velocity Accuracies Using Machine Learning Algorithms for Active Fault Slip Rate Determination and Earthquake Hazard Assessment

Abstract

GNSS technology utilizes satellite signals to determine the position of a point on Earth. Using this location information, the GNSS velocities of the points can be calculated. GNSS velocity accuracies are crucial for studies requiring high precision, as fault slip rates typically range within a few millimeters per year. This study employs machine learning (ML) algorithms to predict GNSS velocity accuracies for fault slip rate estimation and earthquake hazard analysis. GNSS data from four CORS stations collected over 1-, 2-, and 3-year intervals with observation durations of 2, 4, 6, 8, and 12 h, were analyzed to generate velocity estimates. Position accuracies, observation intervals, and corresponding velocity accuracies formed two datasets for the East and North components. ML models, including Support Vector Machine, Random Forest, K-Nearest Neighbors, and Multiple Linear Regression, were used to model the relationship between position and velocity accuracies. The findings reveal that the Random Forest, which makes more accurate and reliable predictions by evaluating many decision trees together, achieved over 90% accuracy for both components. Velocity accuracies of ±1.3 mm/year were obtained for 1-year interval data, while accuracies of ±0.6 mm/year were achieved for the 2- and 3-year intervals. Three campaigns were deemed sufficient for Holocene faults with higher slip rates. However, for Quaternary faults with lower slip rates, longer observation periods or additional campaigns are necessary to ensure reliable velocity estimates. This highlights the need for GNSS observation planning based on fault activity.

1. Introduction

Tectonic movements are fundamental processes that shape the dynamic structure of the Earth’s crust, involving the movement of tectonic plates [1]. In tectonically active regions, these plate movements can trigger catastrophic earthquakes [2]. As such, modeling tectonic motions is crucial for understanding the Earth’s crust dynamics and predicting natural disasters resulting from these movements [3,4,5]. Accurately determining the rate of energy accumulation along faults and forecasting how this accumulated energy will be released over time is essential for assessing earthquake risk.

The Global Navigation Satellite System (GNSS) technique that offers high location accuracy is widely used for modeling tectonic movements [3,4,6,7,8,9,10]. GNSS-based velocity measurements, geodetic observations, and artificial intelligence-assisted prediction methods have made great advances in modeling tectonic movements. Especially in regions such as Turkey, which is located at the intersection of multiple plate boundaries, such models both reveal new scientific knowledge and help the society to be prepared against natural disasters. The estimation of accurate geodetic velocity has, therefore, great importance in geosciences [11].

The modeling of tectonic movements with the GNSS technique consists of three stages. The first is to establish a GNSS network near the fault that is to be modeled with a geometry representing the fault. At this stage, factors such as the distribution of the stations to be included in the network, their location with respect to the fault and each other (proximity, distance, angle, etc.), and the type of ground on which the station will be established (e.g., rocky) are determined. The second one is where stations in the GNSS network are measured. At this stage, at least three campaigns of GNSS measures are performed (usually one year apart) at stations in the network. In the third and final, the GNSS data are evaluated with suitable software (GAMIT/GLBOK, Bernese, Gipsy X, etc.), and the location and velocity information of each station are obtained. By analyzing the velocity data that are obtained, the fault is modeled by using information that includes fault kinematics, slip rate, and strain rate, and an earthquake hazard analysis is performed with this information [2,10].

All stages mentioned above are important for modeling tectonic movements. To realize a better model, the velocities of the stations in the GNSS network must be determined with high accuracy. When it is considered that the slip velocities of the faults are within an accuracy of a few mm/year, it can be seen that the velocity accuracies to be obtained should be lower than the fault slip velocities. If this is not the case, it will not be possible to determine the fault slip rates with the velocity data to be obtained. On the other hand, the velocity accuracies are directly related to the position accuracies as a result of the measurements in each campaign, regardless of the displacement. High position accuracy is required for high velocity accuracy. To achieve high position accuracy, various models are employed during the data evaluation phase [12]. High accuracy in positioning with the GNSS depends on factors, including measurement time, facility type, and the GNSS data evaluation strategy. In addition, the time elapsed between campaigns is also important in determining velocity accuracy [13]. Thus, it is important to model the position accuracies in each campaign and the elapsed time between campaigns in determining GNSS velocities in order to produce a higher level of accuracy in deformation and tectonic modeling studies with GNSS.

It is possible to calculate the positions and velocities of continuous GNSS stations with high accuracy (provided sufficient data is available). This is because these stations do not include effects such as leveling error or antenna height measurement error, and they provide uninterrupted data. However, the installation of these stations is quite costly. Considering the need for GNSS stations for modeling tectonic movements, it is not possible to install, operate, and manage dozens of stations for each fault. Instead, periodic campaign-type GNSS measurements are preferred. In this way, larger areas can be modeled tectonically with less cost and effort thanks to GNSS measurements performed once or several times a year.

The determination of GNSS velocity has been investigated in various studies [9,10,13,14,15,16,17]. A velocity field obtained from GNSS observations offers essential insights into earthquake hazards, including the moment accumulation rate and strain rate [18]. Velocity data have been extensively utilized by numerous researchers in studies related to crustal motion, plate boundary dynamics, seismic site analysis, and deformation kinematics [3,4,5,9,10,19,20].

Ref. [11] analyzed two distinct Artificial Neural Network (ANN) models, namely, the Back-Propagation Artificial Neural Network and the Radial Basis Function Neural Network, to estimate the velocities of 125 GPS sites in Turkey, and they revealed that the Back-Propagation Artificial Neural Network is an alternative tool to conventional methods for geodetic station velocity estimation. Ref. [21] conducted a comparative assessment of three distinct Artificial Neural Network (ANN) models to estimate the geodetic velocities of 238 sites in Turkey, identifying the generalized regression neural network as the most suitable model. Ref. [22] investigated the applicability of four different deep learning (DL) methods for estimating GPS-derived geodetic velocities at 42 GNSS stations in northwestern Iran. The findings indicate that the CNN method exhibits a lower goodness of fit and higher root mean square error (RMSE). In the most recent study conducted by [17], ML algorithms were used to estimate horizontal GNSS velocities in active tectonic regions. In the study where cluster analysis was used, a velocity accuracy lower than 0.4 mm/year was estimated.

Machine learning constitutes a sub-branch of artificial intelligence that processes raw data by using mathematical and statistical methods and gains learning skills by detecting the relationship between data. With the success of machine learning techniques in revealing hidden patterns and complex relationships between data, they have been successfully applied in various fields such as pattern recognition, computer vision, and finance. The purpose of this discipline is to process large amounts of raw data and to create models that enable predictions to be made from this data. Machine learning techniques are grouped under three main headings: supervised learning, unsupervised learning, and reinforcement learning [23,24].

In this study, the GNSS data from four different CORS stations between 2011 and 2017 were divided into different measurement times and evaluated with GAMIT/GLOBK, the position accuracies of each campaign were obtained, and the velocity was produced by creating 375 combinations for each station. The results for the four stations (1500 rows of data) were evaluated with four different supervised machine learning estimation algorithms—(Support Vector Machine (SVM), Multiple Linear Regression (MLR), Random Forest (RF), and K-Nearest Neighbor (KNN))—and the effect of the time between campaigns and position accuracy in each campaign on velocity accuracy was modeled. In this way, we aimed to estimate the velocity accuracy by considering the accuracy achieved since the first campaign in studies where GNSS velocities were used.

2. Materials and Methods

2.1. Preparation of the Dataset

The dataset to be used in machine learning applications is of great importance for the success and accuracy of the model. Having a dataset that has been tested and approved in different studies in the literature saves time before the application. However, not having a ready dataset can complicate the pre-application process, but it also provides in-depth information during the data collection and preparation phase. Creating our own dataset for the application to be made using ML methods included collecting the specific data needed, cleaning these data, and labeling them appropriately. These stages are very important for obtaining accurate and reliable results, but they can also be time-consuming. The quality of the data directly affects the performance of the machine learning model; therefore, creating a good dataset by allocating enough time and resources is important for obtaining a more successful model in the long run.

In the literature, there is no ready dataset that includes the location, velocity accuracies, and year intervals of GNSS stations that can be used with machine learning algorithms. Therefore, the development of the machine learning (ML) model required the creation of a new dataset. To create this data set, four GNSS stations (BALK, BILE, ESKS, and HARC) belonging to the Turkish National Permanent GNSS Network Active (TUSAGA-Active, also known as CORS-TR) network in Turkey were selected considering their time series and whether each station had data on the same day of the years 2011–2017 (Figure 1 and Figure 2). During this period, no significant earthquakes occurred near the stations that would have caused any translational movement. The 24-h GNSS data from the selected stations were downloaded from the TUSAGA-Active website and were divided into 2-, 4-, 6-, 8-, and 12-h periods with Translation, Editing, and Quality Check (TEQC) software (February 2019 version). The precise Earth Orientation Parameters (EOPs), satellite orbits, and clocks [25] needed for the process were obtained from the IERS Bulletin EOP [26], while the antenna phase center models were obtained from the International GNSS Service (IGS). Noise stochasticity and offsets can significantly impact the accuracy of GNSS-derived velocity time series [27]. However, the GAMIT/GLOBK v10.71 software, employed for GNSS data processing, utilizes stochastic modeling, Kalman filtering, and statistical analysis of residuals to enhance the accuracy and reliability of velocity estimates [28]. Detailed information on this issue can be found in [28].

Following the processing of the GNSS data, a total of 1500 velocities were calculated in the Eurasian-fixed ITRF14 reference frame, with 375 velocities per station across four stations, to evaluate the effect of positional accuracy on velocity accuracy for each campaign. These velocities were calculated by considering all possible combinations of position data derived from GNSS observations conducted for 2, 4, 6, 8, and 12 h in each campaign, ensuring that only one observation duration was selected from each year. Following the processing of GNSS data and the velocity generation stage, the relevant data from the files, including the position and velocity accuracies produced by the GAMIT/GLOBK software [28], were extracted by writing small Python scripts, which were saved as a Comma Separated Values (CSV) file. In the dataset, there are seven independent variables (year interval, Se1, Sn1, Se2, Sn2, Se3, Sn3) and two dependent variables (Sve, Svn). Afterwards, velocity accuracies and position accuracies were separated on the basis of components, and two separate datasets were created. Detailed information about the datasets is given in

Table 1. Properties of variables and dataset.

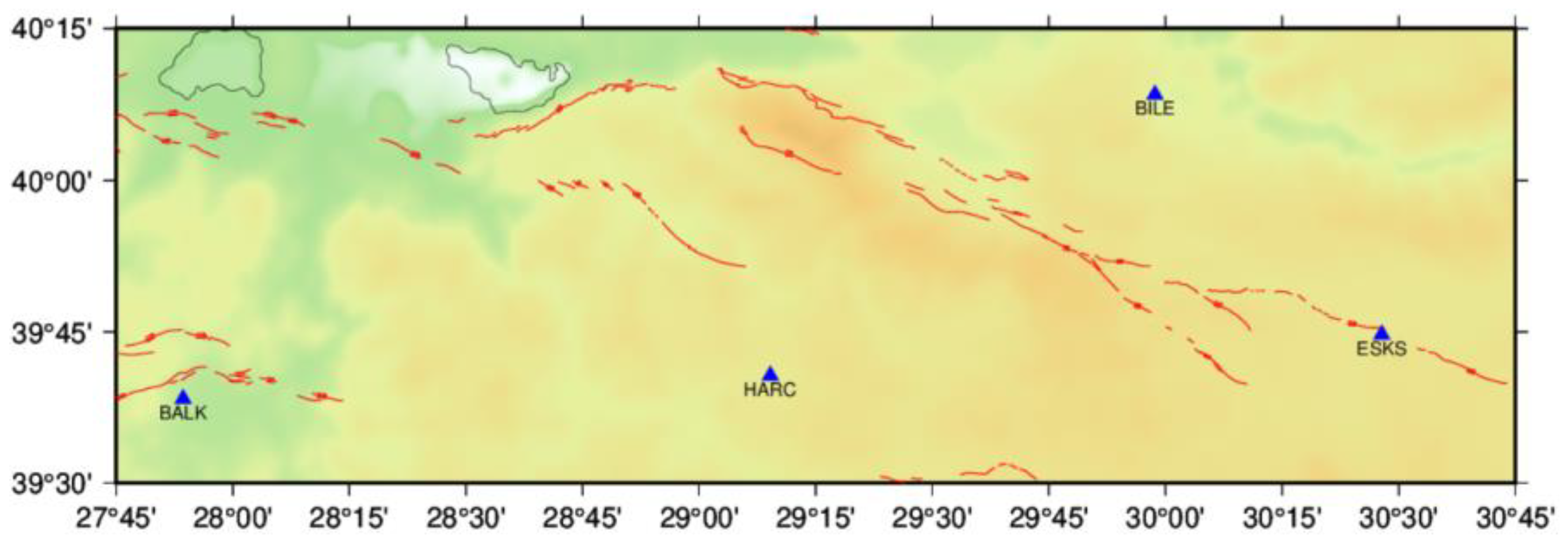
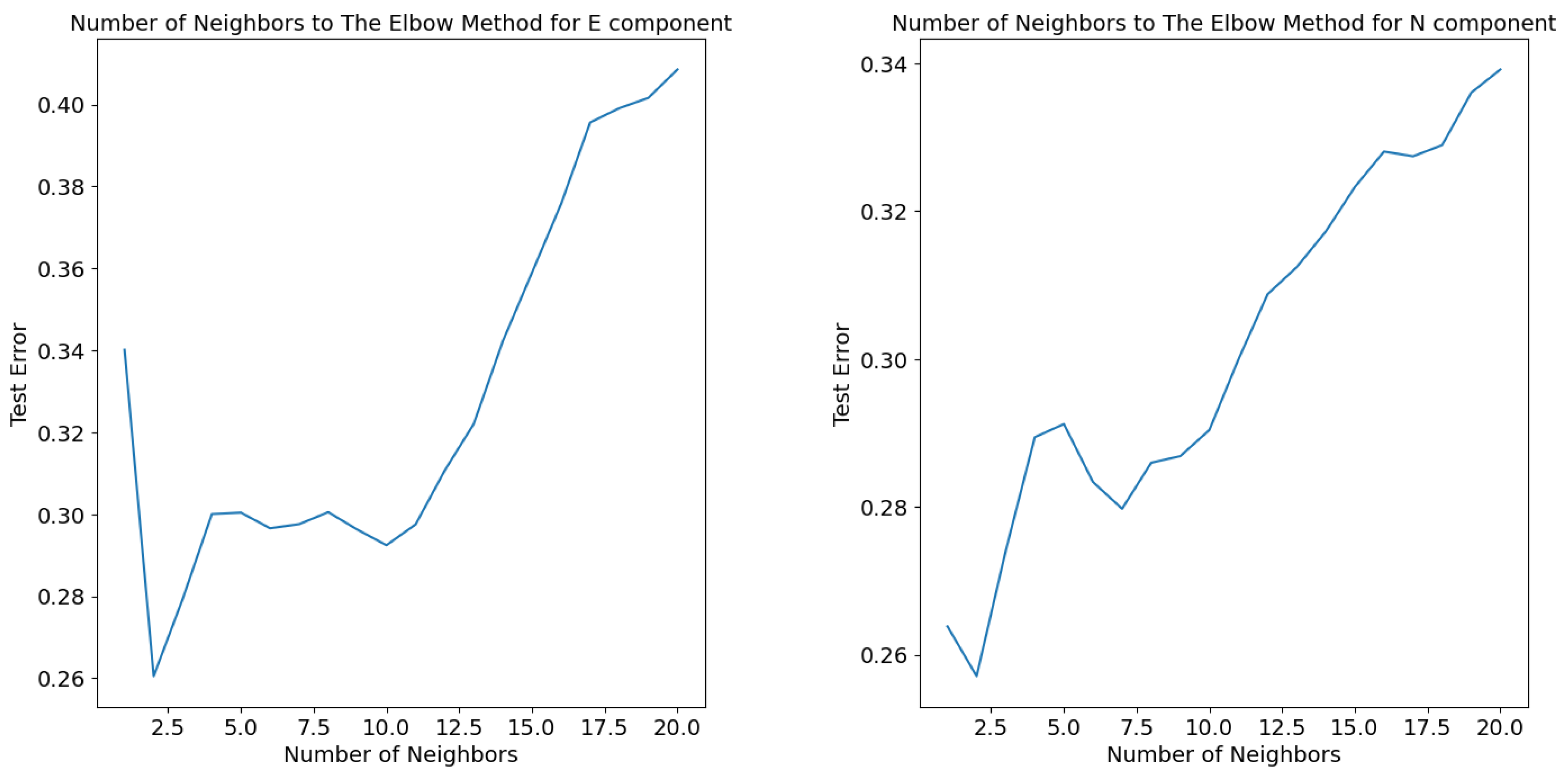
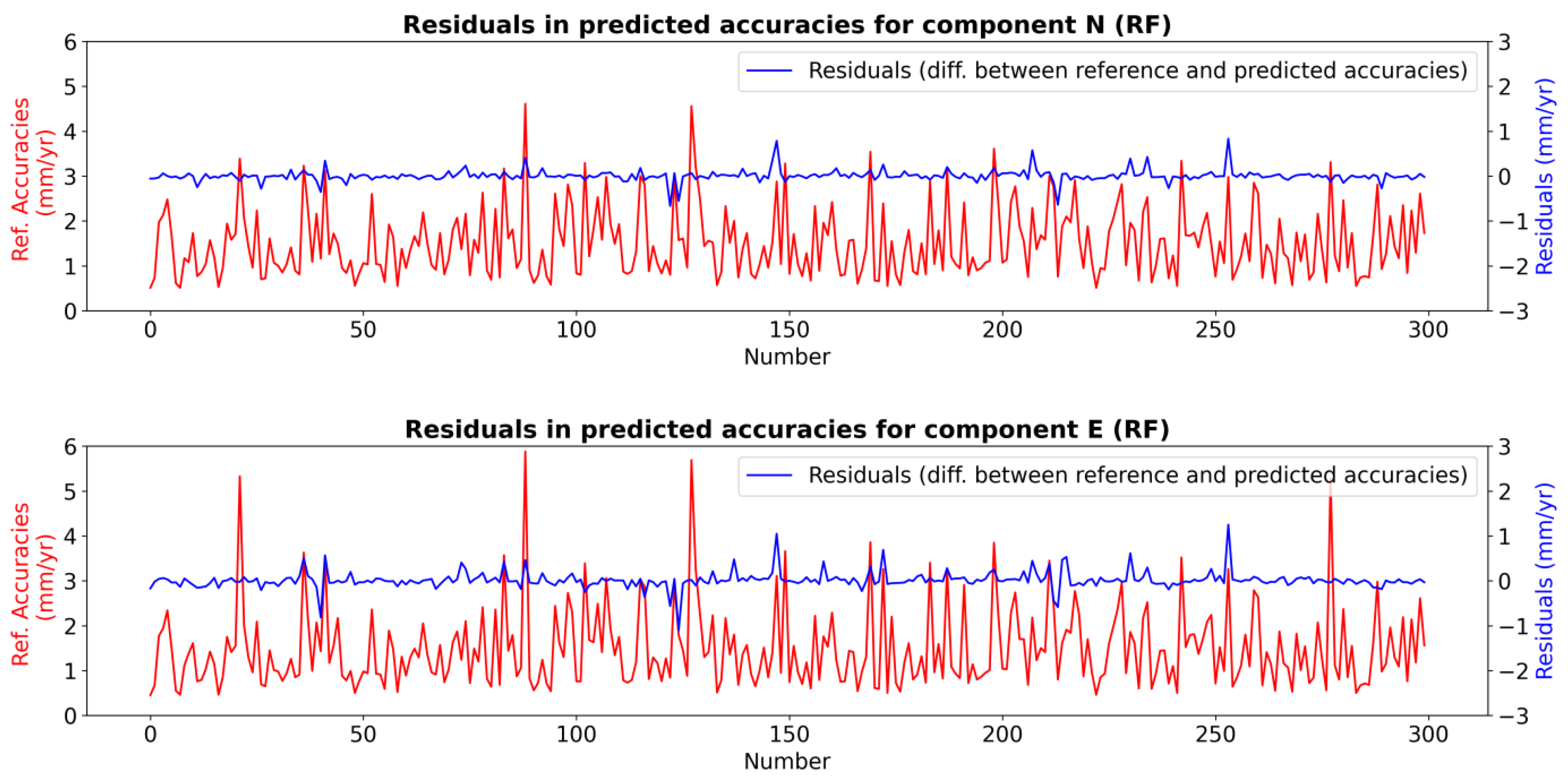
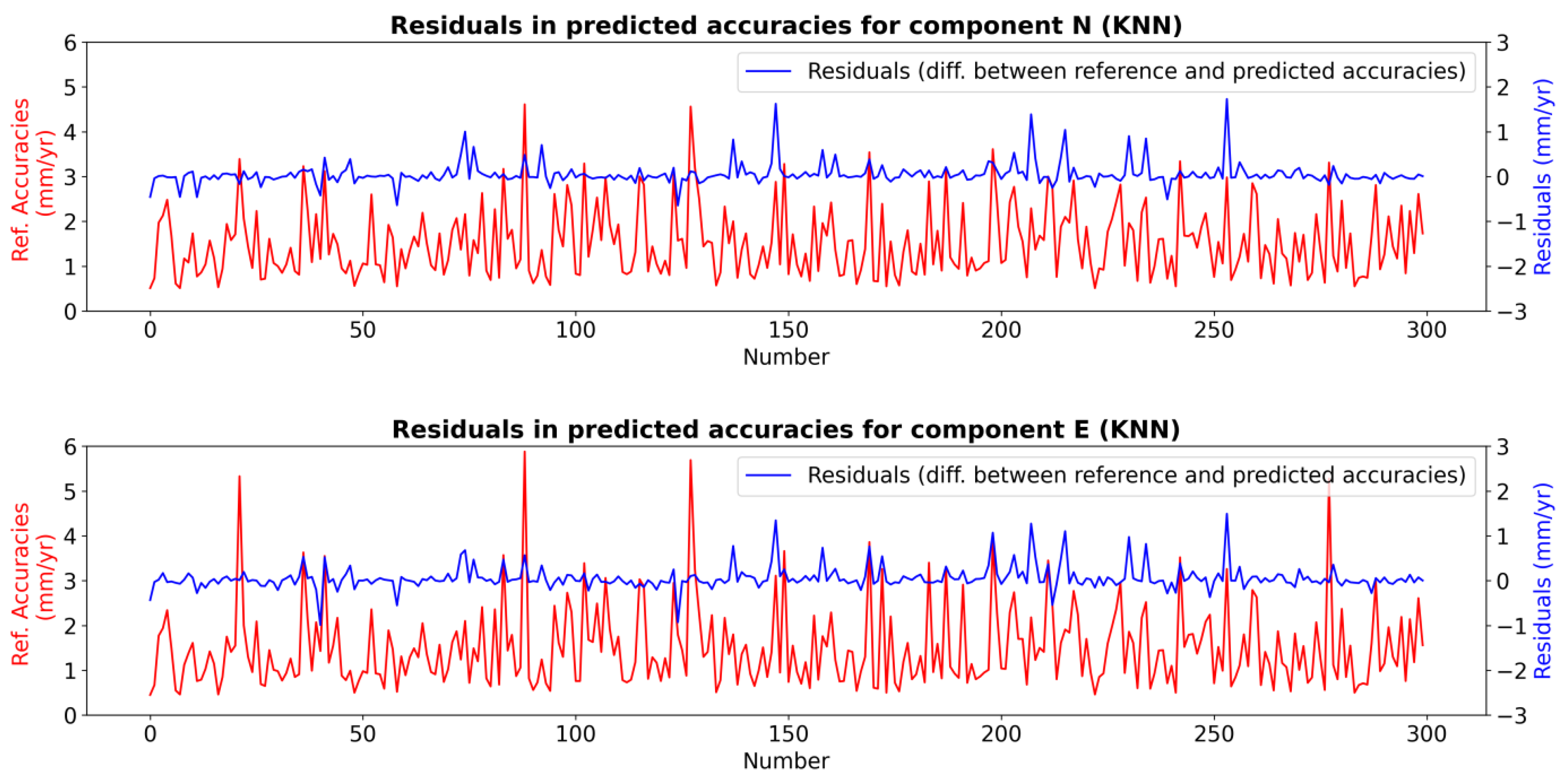
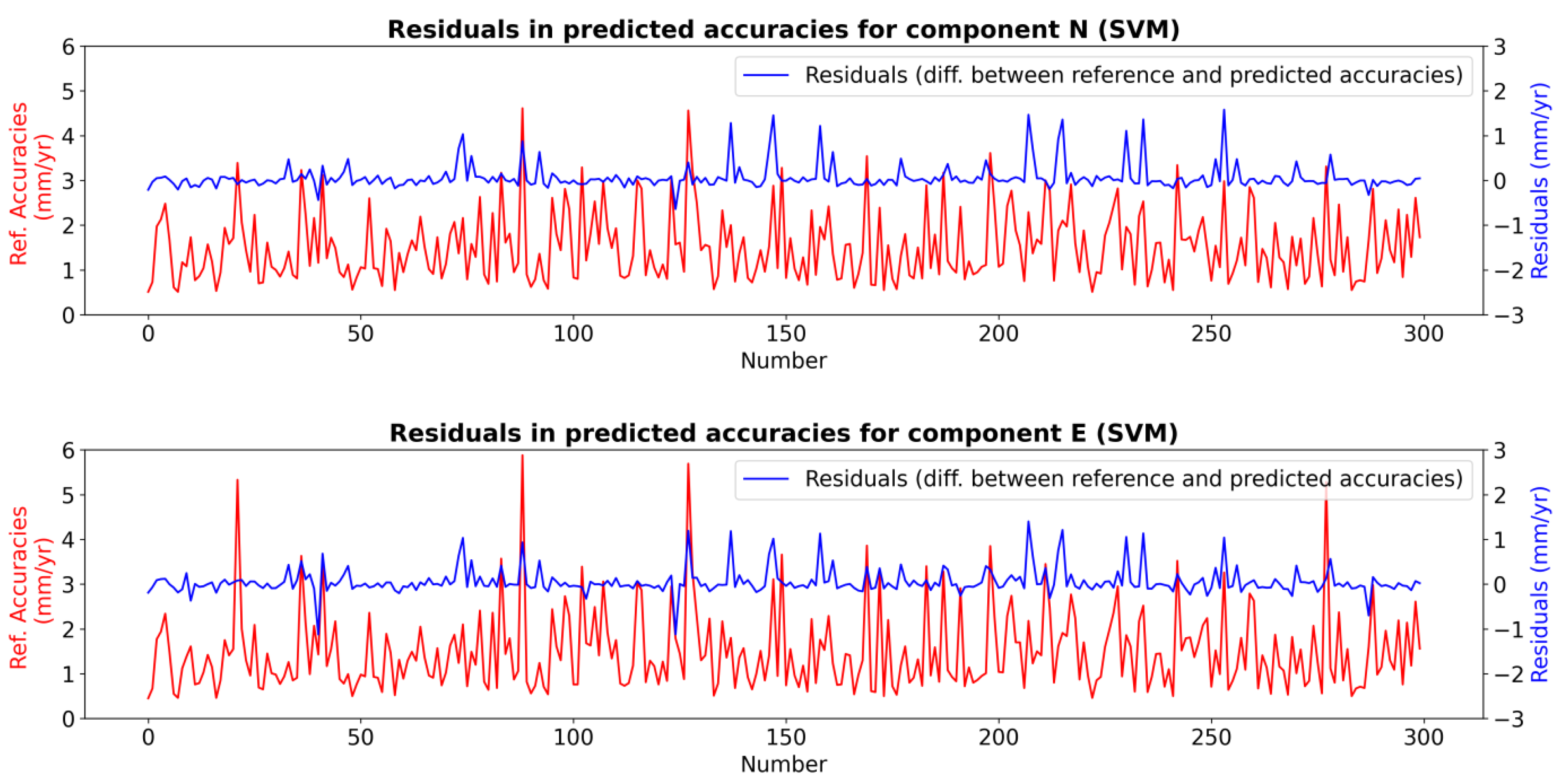
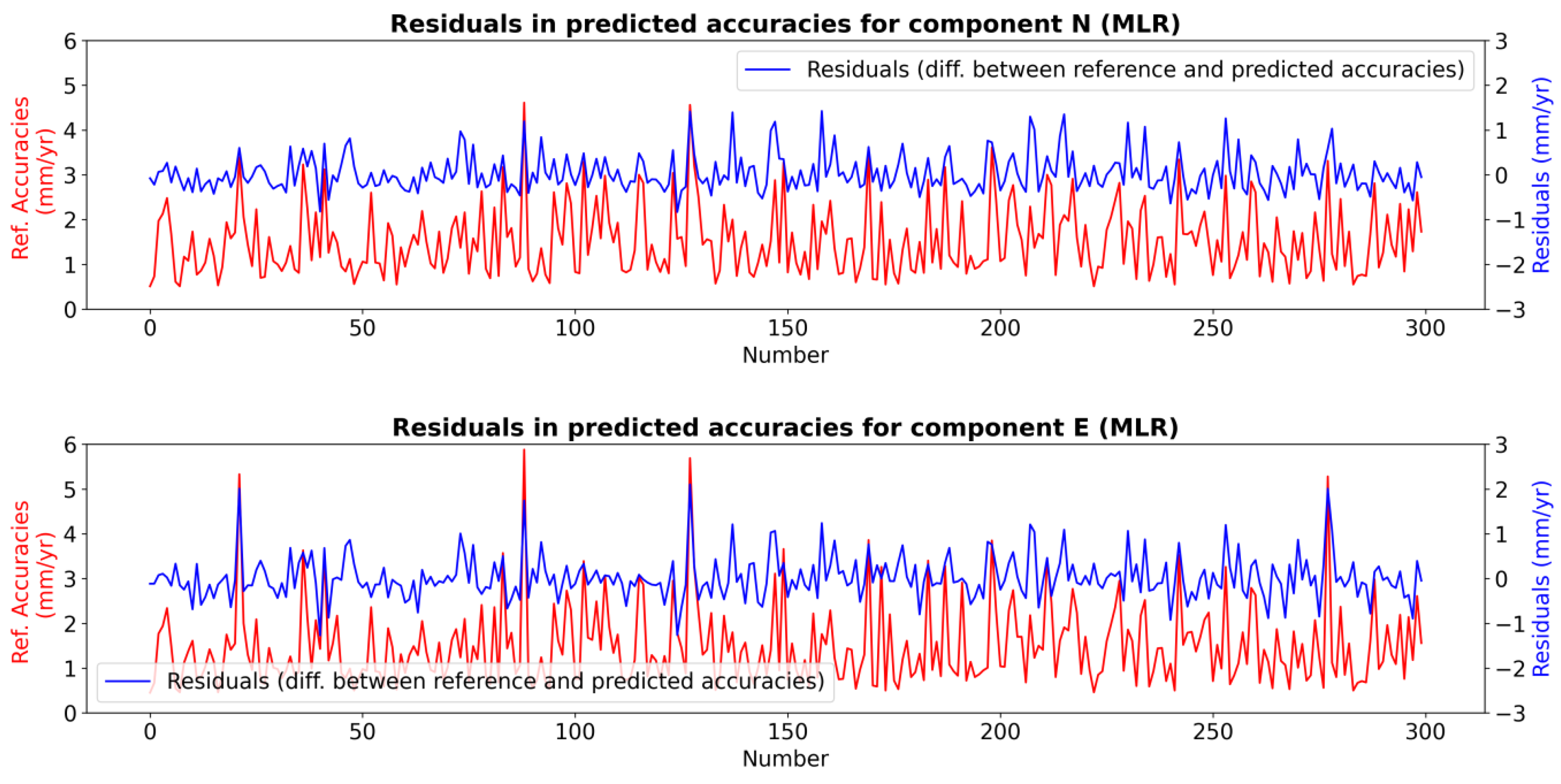
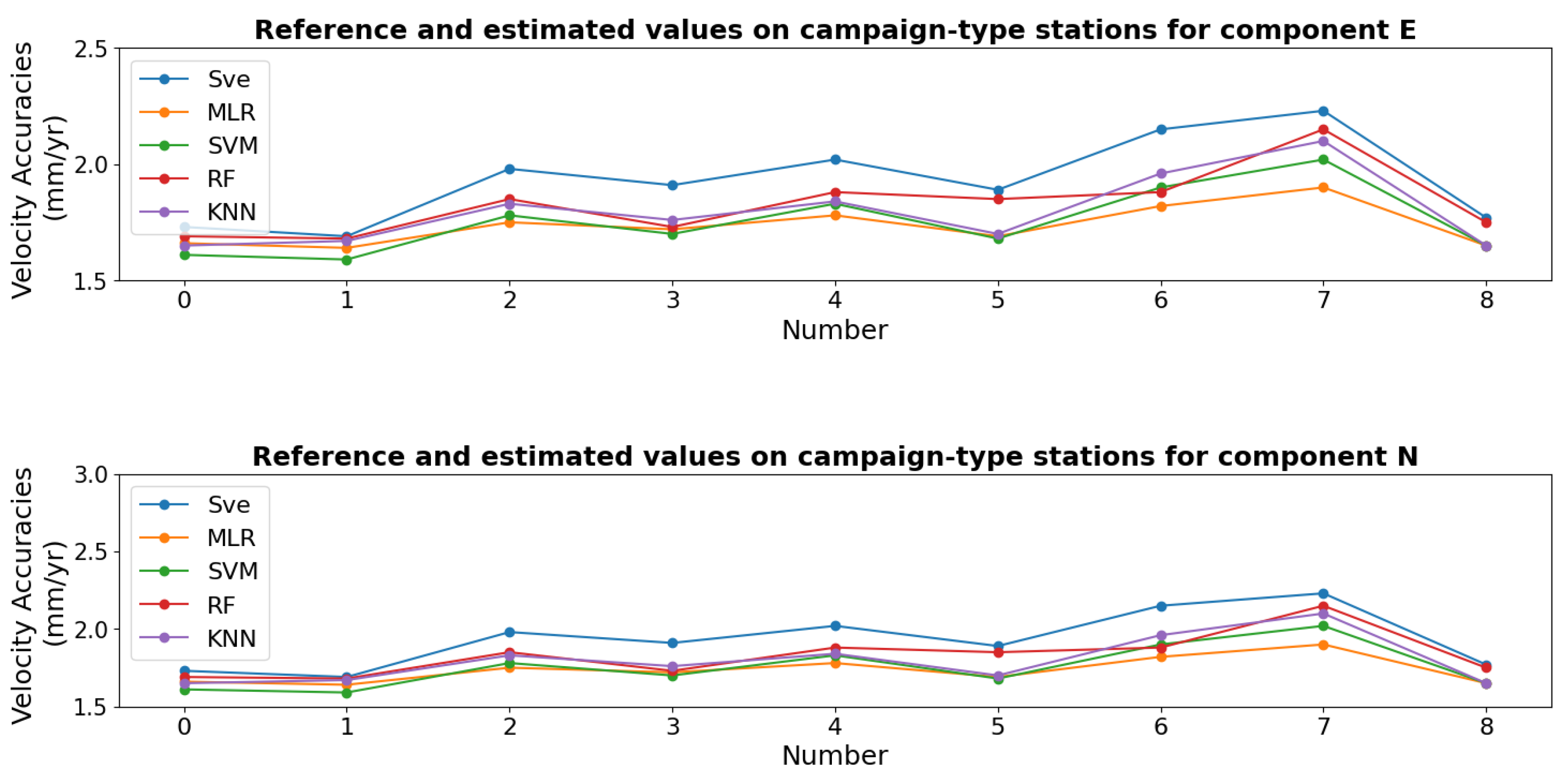
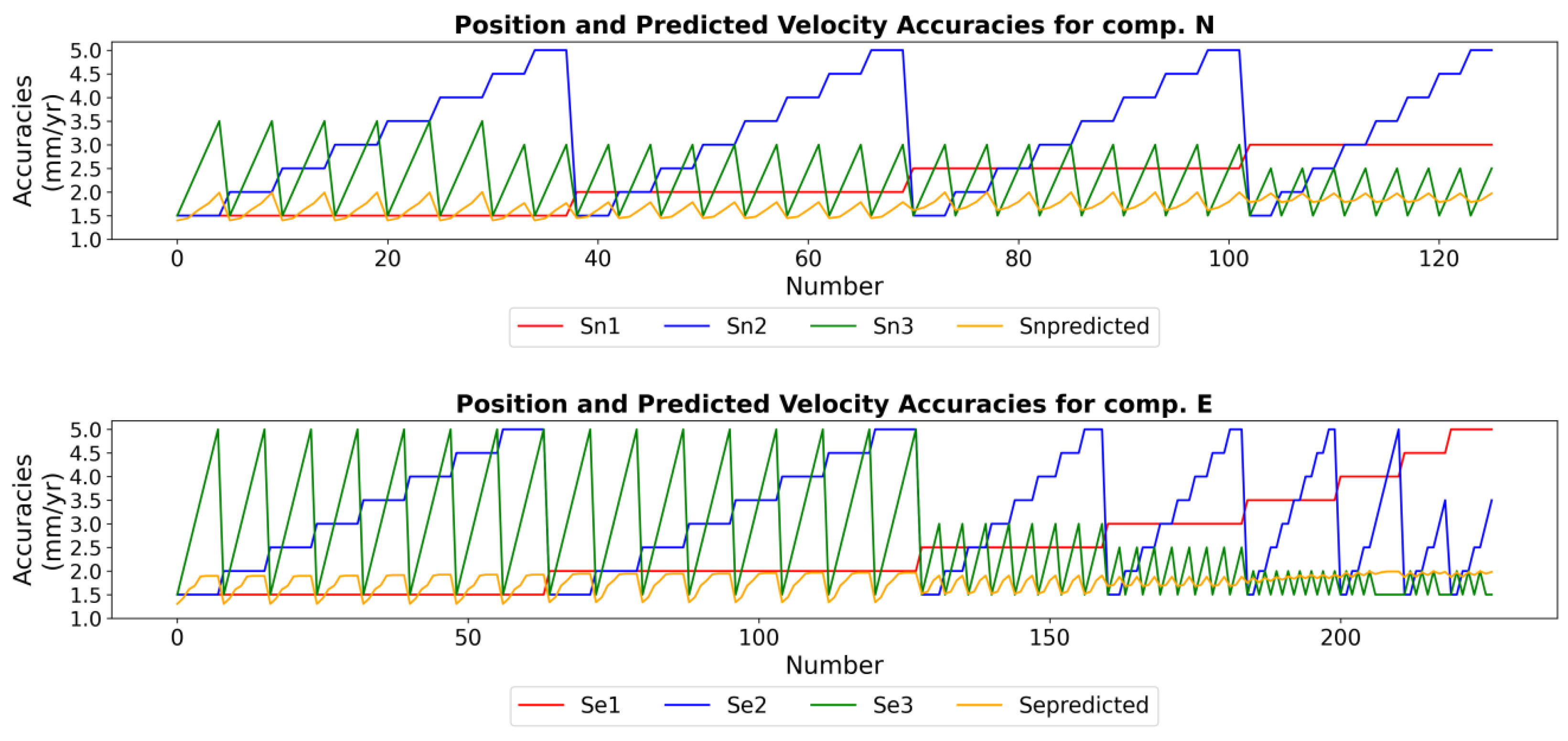
Variable Name	Variable Type	Dataset No	Value Type	Details
Year Interval	Input	1 and 2	Integer	Number of years between measurements
Se1	Input	1	Decimal	Position accuracy for the E component of the first measurement, independent of the measurement time
Se2	Input	1		Position accuracy for the E component of the second measurement, independent of the measurement time
Se3	Input	1		Position accuracy for the E component of the third measurement, independent of the measurement time
Sve	Output	1		Velocity accuracy for the E component
Sn1	Input	2		Position accuracy for the N component of the first measurement, independent of the measurement time
Sn2	Input	2		Position accuracy for the N component of the second measurement, independent of the measurement time
Sn3	Input	2		Position accuracy for the N component of the third measurement, independent of the measurement time
Svn	Output	2		Velocity accuracy for the N component

and

Table 2. Dataset summary.

Variable	Count	Mean	std	min.	25%	50%	75%	max.
year interval	1500	2	0.816769	1	1	2	3	3
Se1	1500	3.8	2.347546	1.63	2.19	2.79	4.07	8.37
Sn1	1500	3.45438	1.476844	1.73	2.43	3.07	4.06	6.49
Se2	1500	4.257367	2.965279	1.59	2.36	2.85	3.86	11.2
Sn2	1500	3.8696	1.86619	1.7	2.51	3.21	4.45	8.55
Se3	1500	3.411333	1.982387	1.59	2.0875	2.5	3.5225	7.93
Sn3	1500	3.279	1.329525	1.7	2.2875	2.765	3.7525	6.78
SVe	1500	1.52856	0.985174	0.45	0.8475	1.27	1.91	6.83
SVn	1500	1.514887	0.79991	0.51	0.9	1.3	1.96	4.83

.

2.2. Machine Learning

Machine learning is a sub-branch of artificial intelligence that works on numerical, text, and visual data to imitate the way humans learn, and it enables computers to learn with different algorithms and mathematical models with a focus on increasing accuracy. In other words, it is the use of statistical methods to determine the correlation between data in a certain data group, to detect complex patterns that humans cannot distinguish, and to give the computer the ability to decide [29]. In this context, regression algorithms from machine learning algorithms, including SVM, MLR, RF, and KNN, were used while analyzing the dataset.

2.2.1. Multiple Linear Regression

Multiple Linear Regression (MLR) is a statistical method used to model the linear relationship between a dependent variable (y) and multiple independent variables (x₁, x₂, x₃, …). This technique enables the estimation of the overall impact on the dependent variable by simultaneously analyzing the contributions of multiple factors [30,31]. For example, the multiple linear regression model for p independent and 1 dependent variable is given in Equation (1).

$$\mathrm{y}\mathrm{i}={\mathsf{\beta }}_{\mathrm{o}}+{\mathsf{\beta }}_1{\mathrm{x}}_{\mathrm{i}}+\cdots +{\mathsf{\beta }}_{\mathrm{p}}{\mathrm{x}}_{\mathrm{p}\mathrm{i}}+{\mathsf{ϵ}}_{\mathrm{i}},\mathrm{i}=1,$$

(1)

From this point of view, the multivariate regression equation in Equation (2) is obtained.

$$\mathrm{y}\mathrm{i}={\mathsf{\beta }}_{\mathrm{o}}+{\sum }_{\mathrm{j}=1}^{\mathrm{p}}{\mathrm{X}}_{\mathrm{i}\mathrm{j}}{\mathsf{\beta }}_{\mathrm{i}\mathrm{j}}+{\mathsf{ϵ}}_{\mathrm{i}}$$

(2)

This algorithm models the linear relationship between the dependent variable, velocity, and the independent variables, which include coordinates and their corresponding sigma values. The model was trained using the Ordinary Least Squares (OLS) method.

2.2.2. Support Vector Machines

Support Vector Machines (SVMs) constitute a supervised machine learning algorithm that can be used for classification or regression problems. The basic idea of the SVM regression method is to find the linear discriminant function that reflects the characteristics of the available training data as closely as possible and that fits the statistical learning theory. Similar to classification, kernel functions are used in regression to handle nonlinear cases. Two situations that can be encountered in SVMs are that the data are in a structure that can be separated linearly or in a structure that cannot be separated linearly. In case the samples can be separated linearly, the aim is to find the most suitable separator plane dividing both classes equidistantly [32].

$$\left({\mathrm{x}}_{\mathrm{i}},{\mathrm{y}}_{\mathrm{i}}\right),{\mathrm{x}}_{\mathrm{i}}\in {\mathrm{R}}^{\mathrm{n}},{\mathrm{y}}_{\mathrm{i}}\in \left\{1,-1\right\},\mathrm{i}=1,\dots ,1$$

(3)

The SVM model for Equation (3) is given in Equation (4).

$${\mathrm{m}\mathrm{i}\mathrm{n}}_{\mathrm{w},\mathrm{b}}{\displaystyle \frac{1}{2}}{\mathrm{w}}^{\mathrm{t}}\mathrm{w}+\mathrm{C}{\sum }_{\mathrm{i}=1}^1\mathsf{\delta }\left(\mathrm{w},\mathrm{b};{\mathrm{x}}_{\mathrm{i}},{\mathrm{y}}_{\mathrm{i}}\right)$$

(4)

$\mathsf{\delta }\left(\mathrm{w},\mathrm{b};{\mathrm{x}}_{\mathrm{i}},{\mathrm{y}}_{\mathrm{i}}\right)$ is the loss function, and $\mathrm{C}\ge 0$ is the penalty parameter for the training error. Two loss functions that are widely used are given in Equations (5) and (6).

$$\mathrm{m}\mathrm{a}\mathrm{x}(1-{\mathrm{y}}_{\mathrm{i}}\left({\mathrm{w}}^{\mathrm{T}}\mathsf{\sigma }\left({\mathrm{x}}_{\mathrm{i}}\right)+\mathrm{b}\right),0)$$

(5)

$${\mathrm{m}\mathrm{a}\mathrm{x}(1-{\mathrm{y}}_{\mathrm{i}}\left({\mathrm{w}}^{\mathrm{T}}\mathsf{\sigma }\left({\mathrm{x}}_{\mathrm{i}}\right)+\mathrm{b}\right),0)}^2$$

(6)

Here, $\mathsf{\sigma }$ represents the function used to move the training data to a higher dimensional space. The decision function for each x test data is given in Equation (7).

$$\mathrm{f}\left(\mathrm{x}\right)=\mathrm{s}\mathrm{g}\mathrm{n}\left({\mathrm{w}}^{\mathrm{T}}\mathsf{\sigma }\left(\mathrm{x}\right)+\mathrm{b}\right)$$

(7)

For SVM training, the RBF kernel function was used, which gives better results than linear, polynomial, and RBF (Radial Basis Function) functions. The formula is given in Equation (8):

$$\mathrm{K}\left({\mathrm{x}}_{\mathrm{i}},{\mathrm{x}}_{\mathrm{j}}\right)=\exp \left(-\mathsf{\gamma }{\left|\left|{\mathrm{x}}_{\mathrm{i}}-{\mathrm{x}}_{\mathrm{j}}\right|\right|}^2,\mathsf{\gamma }\right)>0$$

(8)

$$\mathsf{\gamma }={\displaystyle \frac{1}{2{\mathsf{\sigma }}^2}}$$

(9)

In the equation, ${\left|\left|{\mathrm{x}}_{\mathrm{i}}-{\mathrm{x}}_{\mathrm{j}}\right|\right|}^2$ shows vectorial distance. The $\mathsf{\gamma }$ parameter is a free variable, and it determines the width of function. As its value increases, the width of the bell-shaped function becomes narrower, and, as its value decreases, the width increases [33].

The Support Vector Machine (SVM) algorithm predicts outcomes by identifying the optimal hyperplane that separates data points. During model training, k-fold cross-validation was employed to optimize the C and ϵ hyperparameters, ensuring improved model performance.

2.2.3. Random Forest

Random Forest (RF) is a regression technique that combines the performance of multiple Decision Tree (DT) algorithms to classify or predict the value of a variable [34,35,36,37]. That is, when RF receives an (x) input vector made up of the values of the different evidential features analyzed for a given training area, RF builds a number K of regression trees and averages the results. After K, such trees ${\left\{\mathrm{T}\right(\mathrm{x}\left)\right\}}_1^{\mathrm{K}}$ are grown, and the RF regression predictor is as seen in Formula (10) [38]:

$${\widehat{\mathrm{f}}}_{\mathrm{r}\mathrm{f}}^{\mathrm{K}}(\mathrm{x})={\displaystyle \frac{1}{\mathrm{K}}}{\sum }_{\mathrm{k}=1}^{\mathrm{K}}\mathrm{T}\left(\mathrm{x}\right).$$

(10)

Even though it is expected to obtain a higher model performance when more trees are derived in the random forest regression algorithm, it can be stated that the increase in the number of trees does not always guarantee higher performance with regard to the type and size of the dataset. For this reason, it is recommended that model performances be compared by deriving different numbers of trees. One of the disadvantages of the model is that it is not possible to visually present the result with the tree structure via a single decision tree. Another one is that due to the complexity of the model, it does not allow the processing steps of the evaluation of many decision trees to be seen [38].

The RF algorithm is an ensemble method that combines multiple decision trees to make predictions. During model training, hyperparameters such as the number of trees (nestimators = 100) and the maximum depth (max_depth = 7) of the trees are optimized to enhance model accuracy.

2.2.4. K-Nearest Neighbor Regression (KNN)

K-nearest neighbor (K-NN) regression is a nonparametric regression method where the information derived from the observed data is applied to forecast the amount of predicted variables in real time without defining a predetermined parametric relation between the predictor and predicted variables. The basis of this method is calculating the similarity (neighborhood) of the real time amount of predictors ${\mathrm{X}}_{\mathrm{r}}=\left\{{\mathrm{x}}_{1\mathrm{r}},{\mathrm{x}}_{2\mathrm{r}},\dots ,{\mathrm{x}}_{\mathrm{m}\mathrm{r}}\right\}$ (with unknown forecast streamflow) with the amount of predictors for each of the historical observations ${\mathrm{X}}_{\mathrm{t}}=\left\{{\mathrm{x}}_{1\mathrm{t}},{\mathrm{x}}_{2\mathrm{t}},\dots ,{\mathrm{x}}_{\mathrm{m}\mathrm{t}}\right\}$ via the Euclidean distance function (${\mathrm{D}}_{\mathrm{r}\mathrm{t}}$) as seen in Formula (11) below [31].

$${\mathrm{D}}_{\mathrm{r}\mathrm{t}}=\sqrt{{{\sum }_{\mathrm{i}=1}^{\mathrm{m}}{\mathrm{w}}_{\mathrm{i}}\left({\mathrm{x}}_{\mathrm{i}\mathrm{r}}-{\mathrm{x}}_{\mathrm{i}\mathrm{t}}\right)}^2,}\mathrm{t}=\mathrm{1,2},\dots ,$$

(11)

Here, ${\mathsf{\omega }}_{\mathrm{i}}(\mathrm{i}=\mathrm{1,2},\dots ,\mathrm{m})$ are the weights of the predictors, and their sum is equal to 1. The estimated streamflow (${\mathrm{Y}}_{\mathrm{r}}$) is calculated using the following probabilistic function of the observed streamflows $\left({\mathrm{T}}_{\mathrm{j}}\right)$:

$${\mathrm{Y}}_{\mathrm{r}}={\sum }_{\mathrm{j}=1}^{\mathrm{K}}\mathrm{f}\left({\mathrm{D}}_{\mathrm{r}\mathrm{j}}\right)\mathrm{x}{\mathrm{T}}_{\mathrm{j}}$$

(12)

Here, $\mathrm{f}\left({\mathrm{D}}_{\mathrm{r}\mathrm{j}}\right)$ is the kernel function of the K-nearest neighbors (K observed data with the lowest distance from the real time predictor), which is calculated based on distance amounts (${\mathrm{D}}_{\mathrm{r}\mathrm{t}}$) as follows:

$$\mathrm{f}\left({\mathrm{D}}_{\mathrm{r}\mathrm{j}}\right)={\displaystyle \frac{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{${\mathrm{D}}_{\mathrm{r}\mathrm{j}}$}\right.}{{\sum }_{\mathrm{j}=1}^{\mathrm{K}}\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{${\mathrm{D}}_{\mathrm{r}\mathrm{j}}$}\right.}}$$

(13)

In the K-nearest neighbor algorithm, the amount of predictor weights ($\mathsf{\omega }$ in Equation (11)) and number of neighbors (K) affect the final results; therefore, their optimum amounts should be calculated to achieve the most appropriate results [39]. The K-Nearest Neighbors (KNNs) algorithm makes predictions by averaging the values of the (k) nearest neighbors to a given data point. During model training, the value of (k) (the number of neighbors) is optimized using k-fold cross-validation to improve model accuracy.

In this study, GNSS measurement data will be analyzed using the selected algorithms to estimate velocity accuracy. The dataset, divided into training and test subsets, will be utilized to assess model performance. This approach aims to predict the sigma value of velocity based on the sigma values of coordinates derived from each measurement.

2.3. Training, Testing, and Results of the ML Model

This study investigates the impact of position accuracy and the temporal intervals between campaigns on GNSS velocity accuracies for each component using machine learning techniques. The dataset is partitioned into two groups, corresponding to the East (E) and North (N) velocity components. For the E component, the independent variables (features) are Se1, Se2, and Se3, representing year intervals, while the dependent variable (target) is Sve. Similarly, for the N component, the independent variables are Sn1, Sn2, and Sn3, with Svn as the dependent variable. Both datasets are complete and contain no missing values (Table 1).

The data were partitioned into training (80%) and testing (20%) subsets. Four regression models—SVM, MLR, RF, and KNN—were implemented using the Scikit-Learn library in Python 3.10.0. The Elbow method was utilized to determine the optimal number of neighbors for the KNN algorithm, yielding values of 10 and 7 for the E and N components, respectively (Figure 3). During model training, k-fold (k = 5) cross-validation was employed [40]. Model performance, including training and testing scores, along with key evaluation metrics, is summarized in

Table 3. Training–test results for ML algorithms.

ML Algorithms	Train and Test Results
	MLR		SVM		RF		KNN
Components	E	N	E	N	E	N	E	N
Train Score (%)	72	76	92	91	97	98	94	94
Test Score (%)	71	72	90	86	95	97	91	89
Avg. Train RMSE (mm/year)	0.5	0.4	0.3	0.2	0.2	0.1	0.2	0.2
Avg. Test RMSE (mm/year)	0.5	0.4	0.3	0.3	0.2	0.1	0.3	0.3

. Additional performance metrics that are commonly used in the literature were also evaluated, yielding comparable results [41].

The results presented in Table 2 indicate that the RF algorithm delivered the most accurate performance for both the E and N components. The training and testing scores for both components exceeded 95%, with an average RMSE of approximately ±0.1 mm/year. Additionally, k-fold cross-validation results for the RF algorithm demonstrated training and testing scores above 90%, suggesting robust generalization and reliable performance on real-world data. In comparison, the SVM and KNN algorithms achieved training scores above 91% for both components, with test scores ranging from 86% to 91%. However, the average RMSE values for these algorithms were higher at approximately ±0.3 mm/year. Notably, their k-fold cross-validation scores, which fall below 79%, reveal a discrepancy between the training/testing performance and generalization capability. This indicates that the optimistic results observed during training and testing might not hold consistently for unseen data, highlighting the potential for greater error in real-world applications. The MLR algorithm, which performed the weakest among all methods, achieved training and testing scores between 72% and 76% for both components, with its average RMSE values ranging from ±0.4 to ±0.5 mm/year. The k-fold cross-validation results for MLR align closely with its training and testing scores, falling within the 70–75% range. This consistency suggests that while MLR exhibited lower predictive accuracy, its performance was stable across datasets.

To evaluate the performance of all algorithms on the test data, the residuals (differences between the reference values and the predicted values) were calculated. The reference values (velocity accuracies) and residuals for each algorithm were visualized using dual vertical axes to enhance resolution and clarity (Figure 4, Figure 5, Figure 6 and Figure 7). The visualizations were created using Python’s Matplotlib library.

The RF algorithm demonstrated a balanced predictive behavior, underestimating 53.7% and overestimating 46.3% of the 300 test samples for the E component (Figure 4). For the N component, these percentages were 52.3% and 47.7%, respectively, indicating no systematic bias in the model’s predictions. For the E component, 3.7% of the residuals exceeded ±0.5 mm/year, with 1.3% categorized as underestimations (minimum residual: −1.1 mm/year) and 2.4% as overestimations (maximum residual: 1.25 mm/year). For the N component, 2% of the residuals exceeded ±0.5 mm/year, with 1% representing underpredictions (minimum residual: −0.67 mm/year) and 1% representing overpredictions (maximum residual: 0.83 mm/year). Outlier analysis did not reveal any evidence of systematic error within the dataset. In addition, no correlation was observed between the reference velocity accuracies and the predicted velocity accuracies (Figure 4).

The residual distribution showed that 89.3% of predictions for the E component and 93.7% for the N component fell within a ±0.2 mm/year residual margin. This high proportion of small residuals reflects the RF model’s strong predictive performance and low generalization error, indicating that the model effectively mapped the feature space to the target variable with minimal deviation.

According to the performance metrics, the KNN algorithm ranks as the second most successful model after the RF algorithm (Figure 5). Considering that the training performance for the KNN algorithm was 94% for both the E and N components, and the test performance was 91% and 89%, respectively, it can be concluded that the model provides very high accuracy (Figure 5). Residuals greater than ±0.5 mm/year account for 7.3% of the predictions for the E component and 5% for the N component. The residual values are predominantly concentrated around small negative and positive values, although larger positive residuals are observed at the extremes. For example, the highest residual is 1.73 mm/year, while the lowest is −0.99 mm/year. Despite the generally small residuals (82.7% for comp. E and 86.3% for comp. N at less than ±0.2 mm/year), a few outliers with high residuals suggest that the model occasionally makes larger errors. This aligns with the model’s 90% performance on the test data, indicating that while the model predicts correctly most of the time, it occasionally produces larger errors in some cases.

Similar to the RF and KNN models, the distribution of positive and negative residuals is balanced, with no indication of systematic bias. For the E and N components, the algorithm produced residuals larger than ±0.5 mm/year in 8% and 6.3% of the predictions, respectively. These residuals were predominantly positive (indicating overestimation), with the largest residuals being 1.40 mm/year for the E component and 1.58 mm/year for the N component. Additionally, the proportion of errors exceeding ±1 mm/year was 4% for the E component and 3% for the N component. These larger residuals have the potential to influence the results in the studies that require high-accuracy GNSS velocity estimates.

The MLR algorithm, which exhibited the lowest prediction accuracy in this study, achieved training and test scores of 72% and 71% for the E component and 76% and 72% for the N component, respectively (Table 3). These scores indicate that while MLR can reasonably explain the dependent variable, its predictive power is limited. The model produced residuals larger than ±0.5 mm/year in 21% of the predictions for the E component and 16% for the N component (Figure 7). Additionally, the largest residual observed across all models, 2.1 mm/year, was generated by MLR. In contrast, for residuals smaller than ±0.2 mm/year, the model performed relatively better, with 47.7% of predictions for the E component and 41.3% for the N component falling within this range. A notable limitation of the MLR model is its reduced performance when actual velocity accuracy values exceed ±5 mm/year. This suggests that MLR struggles to generalize effectively in scenarios with high-accuracy requirements or when the target variable exhibits significant variability.

Although the models trained with ML algorithms showed high performance in the test data, they can contain high errors in real data outside the dataset. For this reason, the four ML algorithms used in the study were tested with nine GNSS data from stations other than the dataset (Figure 8). These data had a campaign type measure and were measured at one-year intervals.

Table 4. Test results of the developed models on campaign-based external GNSS datasets.

		Position Accuracies (mm)			Velocity Accuracy (mm/yr)	Predicted Velocity Accuracy (mm/yr)
	Station Number	Se1	Se2	Se3	Sv	MLR	SVM	RF	KNN
East Component	1	2.97	1.82	1.82	1.73	1.66	1.61	1.69	1.65
	2	3.14	1.36	1.71	1.69	1.64	1.59	1.68	1.67
	3	2.97	1.82	2.43	1.98	1.75	1.78	1.85	1.83
	4	3.14	1.36	2.19	1.91	1.72	1.70	1.73	1.76
	5	2.97	2.05	2.53	2.02	1.78	1.83	1.88	1.84
	6	2.81	1.53	2.34	1.89	1.69	1.68	1.85	1.70
	7	3.1	1.65	2.75	2.15	1.82	1.90	1.88	1.96
	8	3.48	2.08	2.64	2.23	1.90	2.02	2.15	2.10
	9	2.3	2.05	2.53	1.77	1.65	1.65	1.75	1.65
North Component	1	3.72	2.18	2.05	2.06	1.97	1.97	2.08	2.10
	2	3.98	1.65	1.91	2.01	1.97	1.93	2.07	2.11
	3	3.72	2.18	3.02	2.45	2.12	2.32	2.42	2.29
	4	3.98	1.65	2.65	2.36	2.09	2.17	2.31	2.22
	5	3.25	2.43	2.79	2.22	2.00	2.10	2.11	2.08
	6	3.57	1.76	2.88	2.35	2.04	2.16	2.37	2.18
	7	4.05	1.98	3.06	2.58	2.19	2.41	2.51	2.36
	8	4.36	2.43	3.2	2.74	2.30	2.64	2.54	2.46
	9	2.51	2.43	2.79	1.93	1.84	1.84	1.94	1.90

and Figure 8 demonstrate that the RF, KNN, and SVM models delivered the most accurate predictions across all sites for both the E and N components. The residuals for these three models in all components remained below 0.3 mm/year. In contrast, the MLR model achieved high accuracy (residuals < 0.2 mm/year) when predicting reference values below 2 mm/year in both components but struggled to maintain accuracy for higher values, indicating its limitations in handling larger target ranges.

Using the developed machine learning model, velocity accuracies were predicted for varying position accuracies and temporal intervals between observations, which were tailored for tectonic-focused GNSS studies (Figure 9). Given that fault slip rates in many tectonic zones are on the order of a few millimeters per year, the prediction range for position accuracies was constrained between ±1.5 mm and ±5 mm. The lower limit corresponds to the highest position accuracy observed in the dataset, while the upper limit reflects a realistic threshold for tectonic applications. Notably, the model remains applicable for position accuracies exceeding ±5 mm, although such cases were not explicitly included in the training data.

3. Conclusions

Lower positional accuracy directly affects the accuracy of station velocity predictions, which in turn hampers the accurate calculation of fault slip velocities. This limitation is particularly critical for faults with low slip rates (e.g., 1–2 mm/year), as the calculated slip velocities may fall within or below the sigma value, obscuring or entirely masking the fault’s actual movement.

The key findings derived from the analysis in the presented study are summarized below:

• East (E) Component: For 1-year interval GNSS data, achieving ±1.5 mm position accuracy per epoch resulted in a velocity accuracy greater than ±1 mm/year, with the best observed accuracy being ±1.3 mm/year. However, for 2- and 3-year interval datasets, submillimeter velocity accuracies could be achieved. Specifically, the best velocity accuracies were ±0.6 mm/year for 3-year intervals and ±0.7 mm/year for 2-year intervals.
• North (N) Component: Similarly, for 1-year interval GNSS data with ±1.5 mm position accuracy per epoch, the maximum attainable velocity accuracy was ±1.4 mm/year. For 2- and 3-year interval data, the best achievable velocity accuracies improved to ±0.6 mm/year for 3-year intervals and ±0.8 mm/year for 2-year intervals.
• Overall Observations: For GNSS campaigns conducted at 2- or 3-year intervals, velocity accuracies within ±1.5 mm/year are achievable for both components, provided the position accuracies remain below ±5 mm per epoch.
• The position accuracies of campaigns 1 and 3 had a more pronounced impact on velocity accuracy. However, as the positional accuracy of campaign 1 deteriorated, the influence of campaign 2’s positional accuracy became increasingly significant.

The findings indicate that conducting three campaigns (one epoch per year) with 1-year interval GNSS data is sufficient to achieve a velocity accuracy of less than ±2 mm/year, which is considered the reference threshold for fault slip rate determination studies. However, under the tested conditions, it was not feasible to obtain a velocity accuracy lower than ±1 mm/year with only three campaigns of 1-year interval data. This highlights the importance of developing a tailored observation plan based on fault activity, particularly in newly established seismogeodetic networks. Specifically, three campaigns with a 1-year interval are adequate for Holocene faults with relatively higher slip velocities. In contrast, for Quaternary faults, which generally exhibit lower slip rates, GNSS observations at 2- to 3-year intervals or the inclusion of four or more GNSS observations are necessary to achieve the required accuracy.

The developed ML model enables the analysis of the relationship between position accuracies and velocity accuracies in a unique dataset of 1500 lines produced specifically for the study. With these results obtained for the first time, when establishing a new seismogeodetic network or planning GNSS observations around faults that have experienced destructive earthquakes and completed their post-seismic period, the velocity accuracy can be predicted, and GNSS observation intervals can be optimized based on the required position accuracies, as outlined by [13] or [42]. This allows for more efficient planning of field studies for tectonic-focused GNSS observations, such as extending the measurement period, adding a fourth campaign, or increasing the time between campaigns. Consequently, this approach can help achieve velocity accuracies that enhance the precision of earthquake hazard analysis, ultimately leading to more reliable risk assessments.