Light-Weighting of Planetary Gearbox Based on Multi-Strategy Optimization Sparrow Search Algorithm
Abstract
:1. Introduction
- A new multi-strategy optimized algorithm is proposed;
- The approach to the light-weighting problem of wind yaw gearboxes is improved;
- The light-weighting result is given and compared to the original result;
- The process and results of the MSOSSA are compared to other algorithms.
2. Light-Weighting Problem
2.1. Transmission Ratio Problem
2.1.1. Objective Function and Variables
2.1.2. Constraints
- The total transmission ratio deviation shall not exceed 1.5%. It can be represented by Equation (9).
- The distribution of the transmission ratios should be uniform and reasonable. According to the literature [22], the transmission ratio of the low-speed stage should be between 4 and 5.6; the transmission ratio of the high-speed stage should be between 3.15 and 9; and the transmission ratio range of the intermediate stage should be between 5 and 8. It can be represented by Equations (10)–(12).
- As a rule of thumb, the radial diameter difference between two adjacent stages of transmission should not exceed 1.5 times. It can be represented by Equation (13).
2.2. Main Parameters Problem
2.2.1. Objective Function and Variables
2.2.2. Constraints
- It should be ensured that the number of gear teeth is selected to achieve the given transmission ratio. It can be expressed by Equation (22).
- The sum of the number of teeth of the internal gear and the sun gear must be an integral multiple of the number of teeth of the planetary gear. It can be expressed by Equation (23).
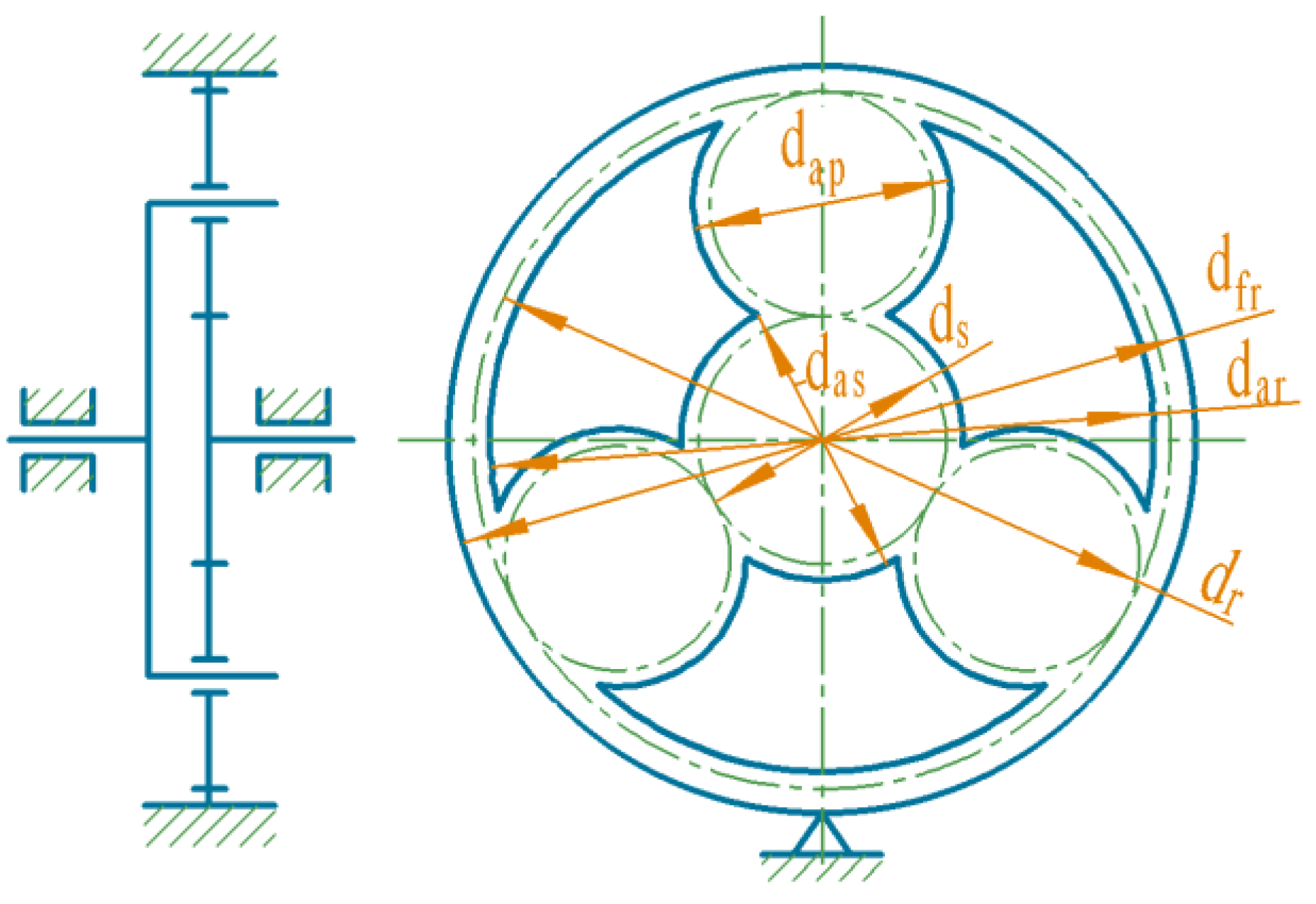
- To ensure that the individual planetary wheels do not collide, it is necessary to keep a distance between the tops of their teeth at all times. Therefore, the sum of the radii of the tooth top circles of two adjacent planetary gears is less than their center distance. It can be expressed by Equation (24).
- To ensure that the rotation axes of sun gear, planet gear, and inner gear coincide, Equation (25) needs to be satisfied.
- The tooth breakage strength is met. It can be expressed by Equation (26).
- The tooth contact strength is met. It can be expressed by Equation (27).
- The gear is not undercut. It can be expressed by Equation (28).
- According to experience, the module of the gear should be within an appropriate range. It can be expressed by Equation (29).
- According to experience, the ratio of tooth width to module should be within an appropriate range. It can be expressed by Equation (30).
3. Methodology
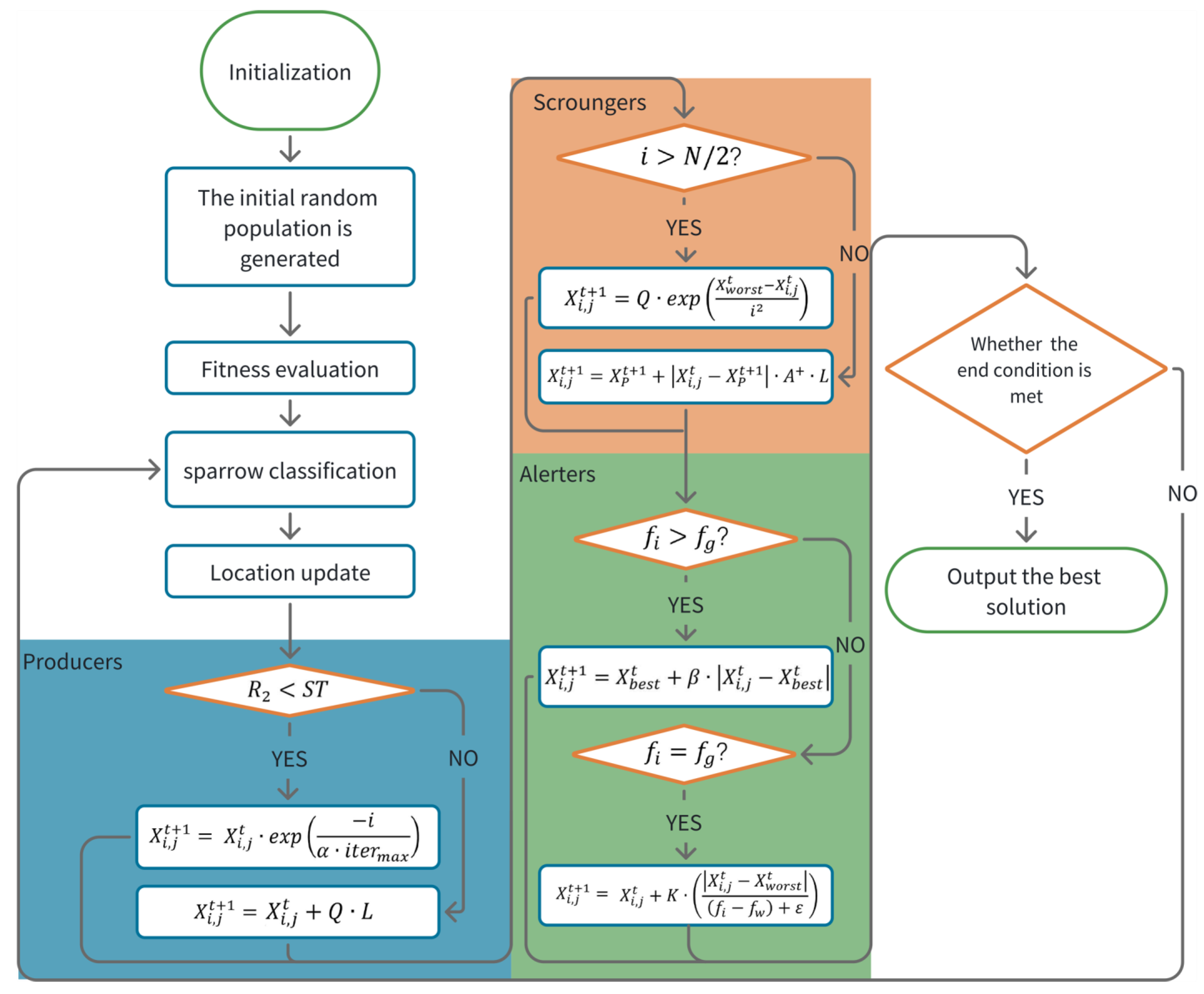
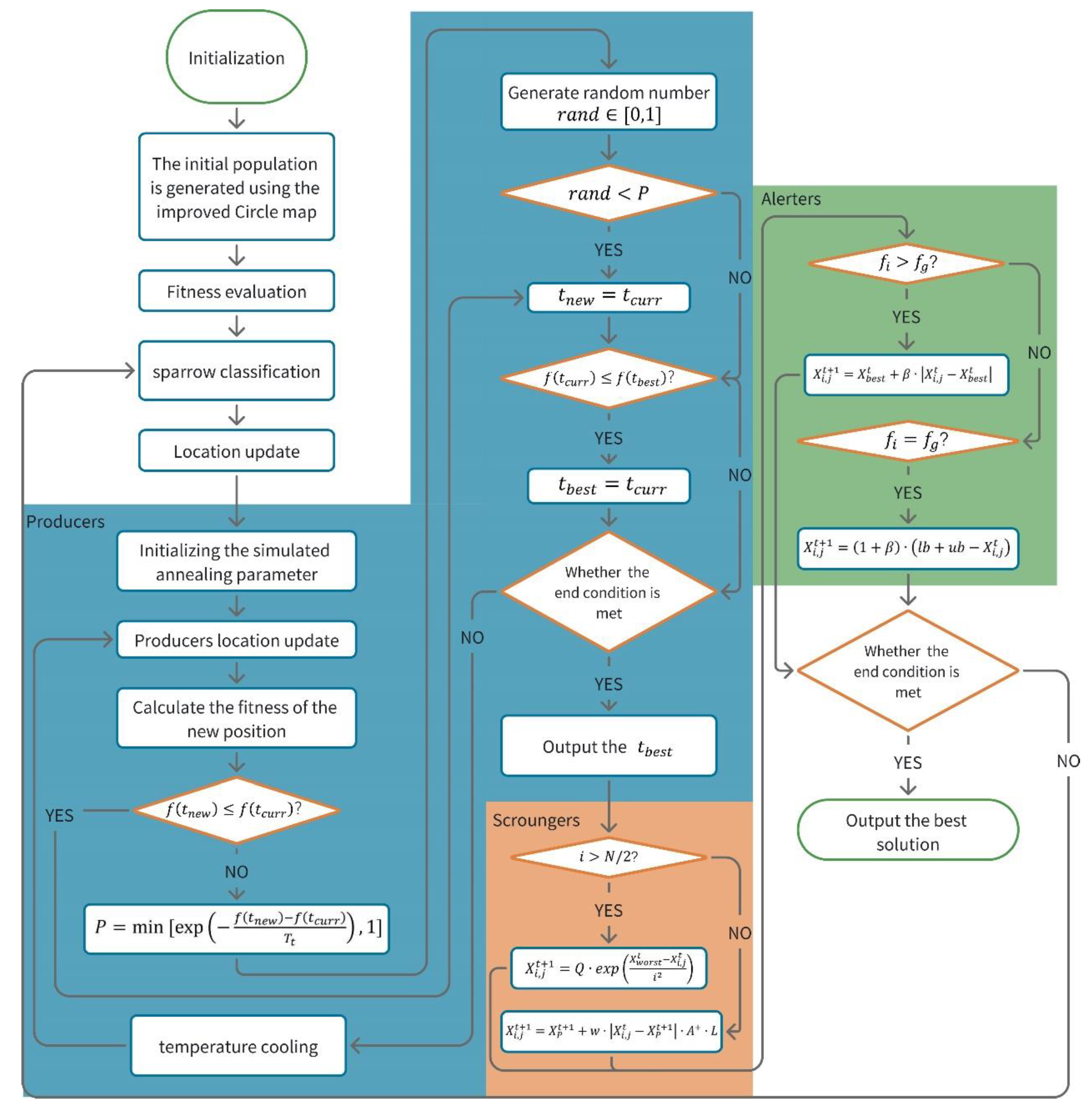
3.1. Sparrow Search Algorithm
3.2. Multi-Strategy Optimized Sparrow Search Algorithm
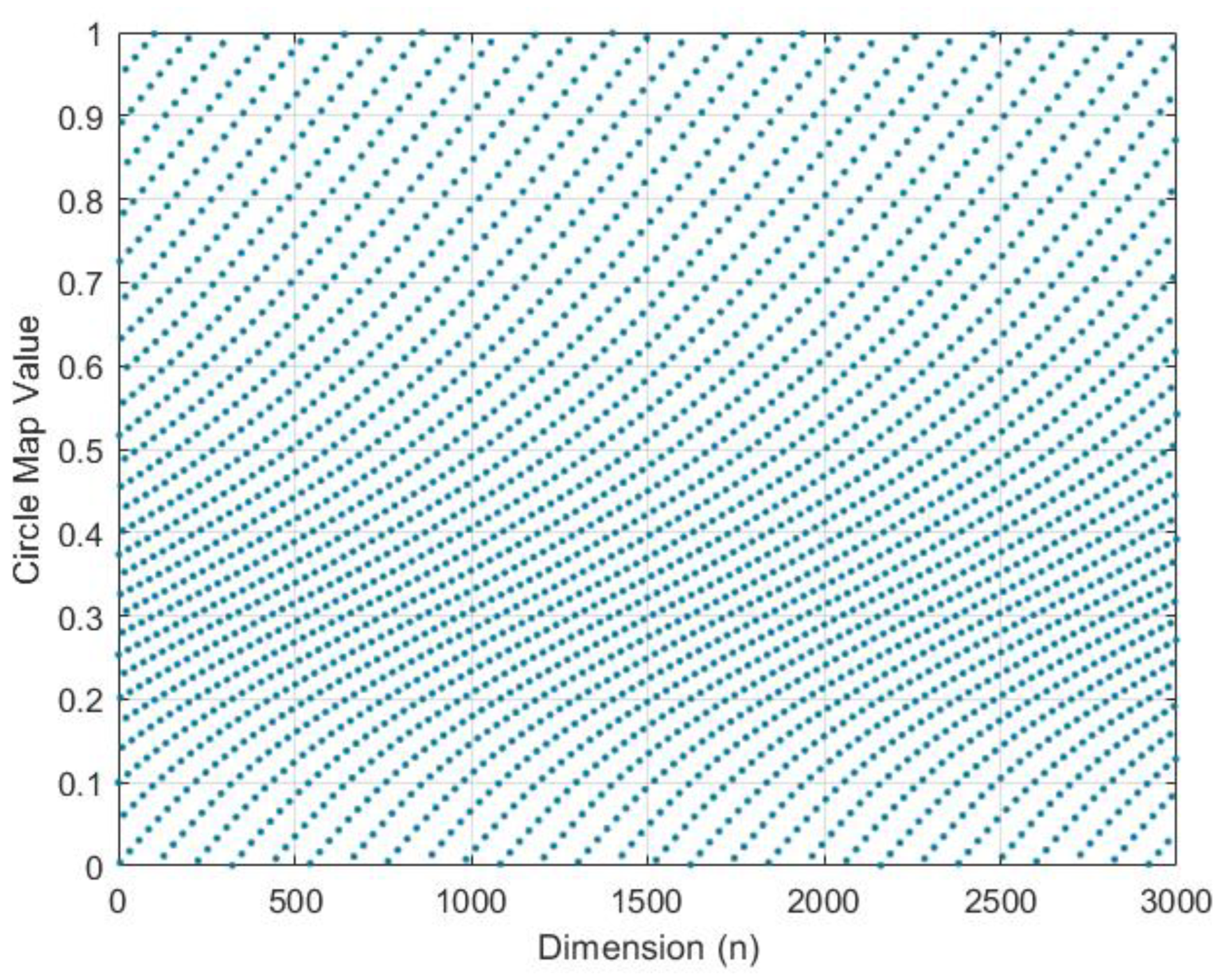
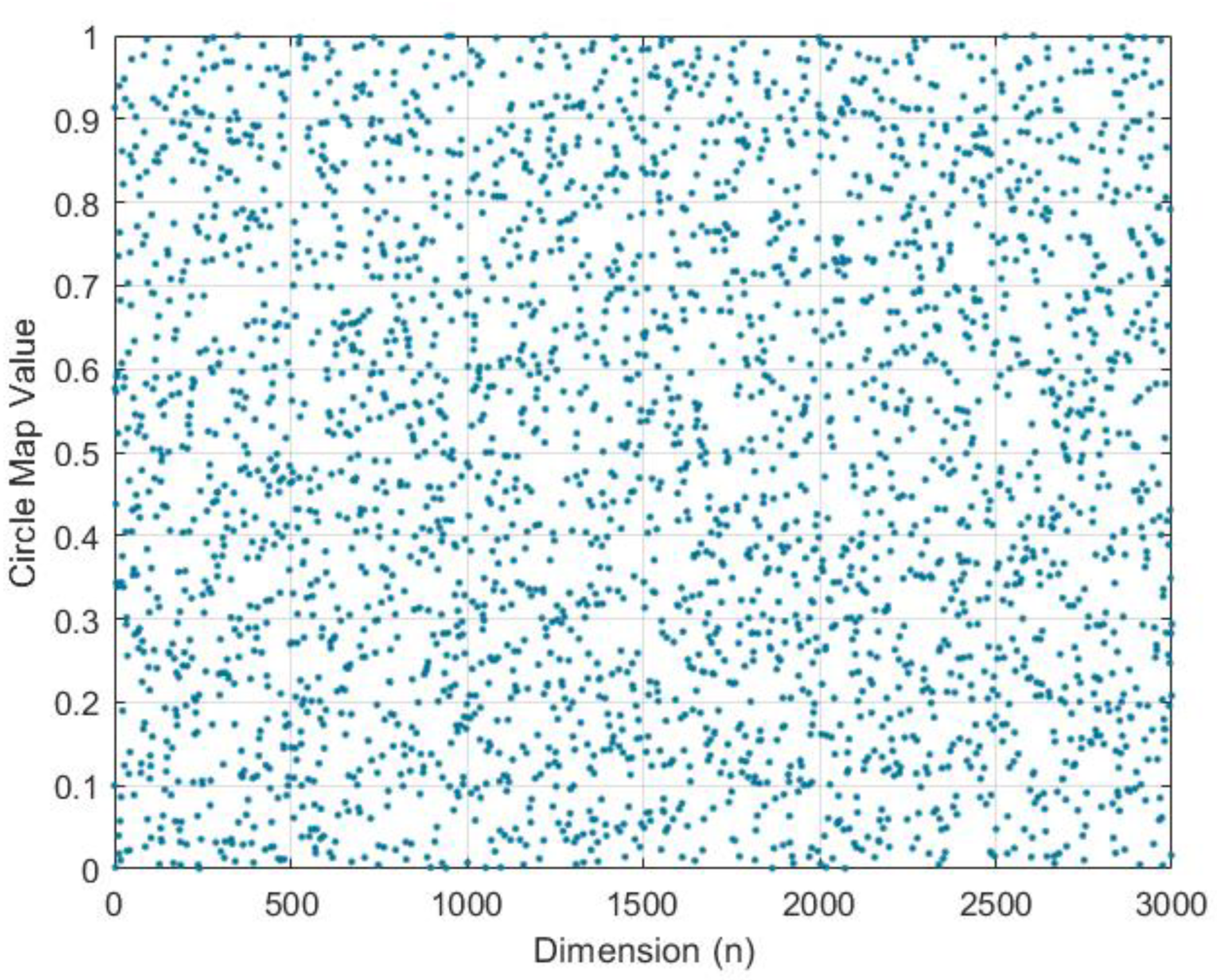
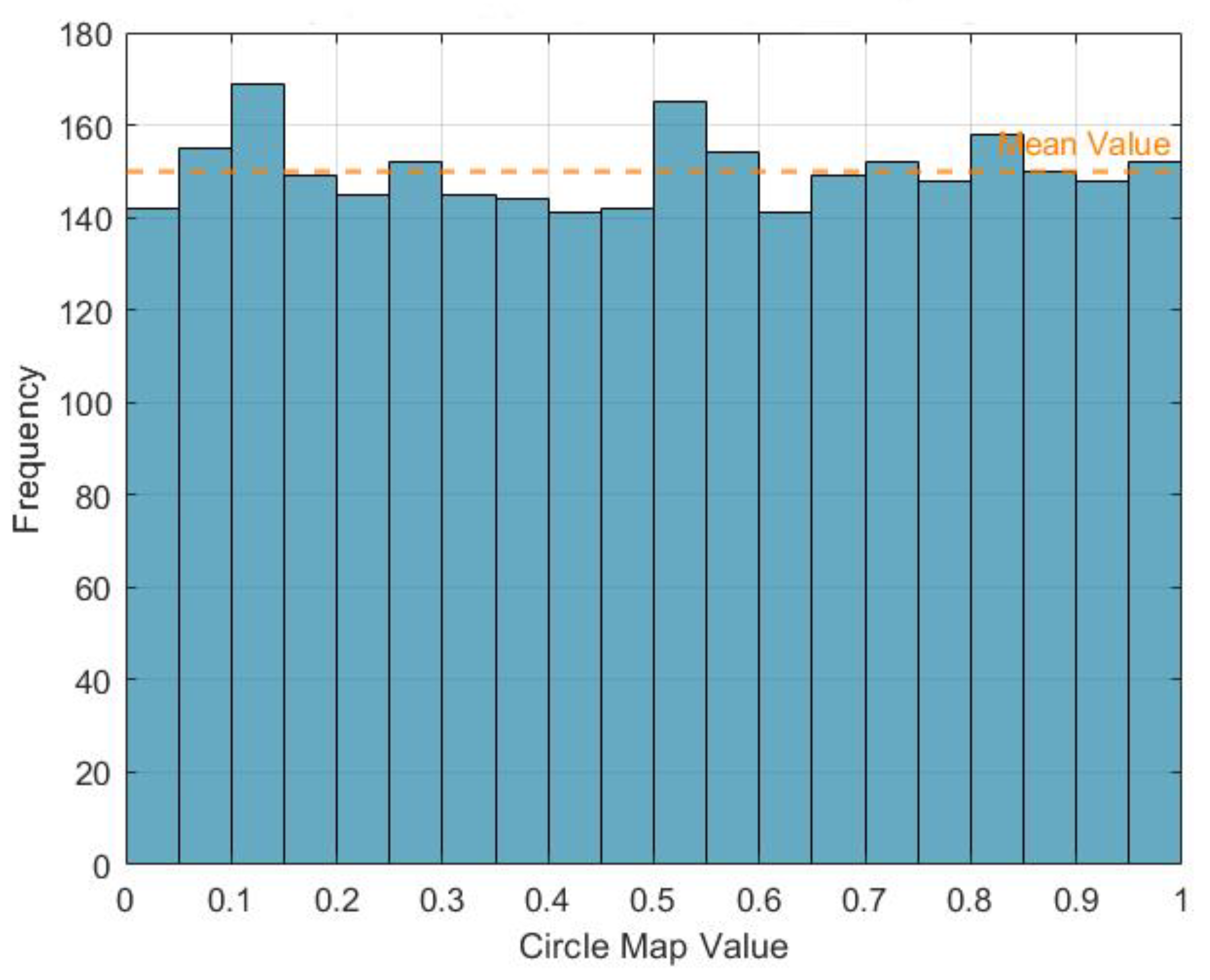
3.2.1. Improved Circle Mapping Optimization Strategy
3.2.2. Simulated Annealing Optimization Strategy
3.2.3. Nonlinear Weight Factor Optimization Strategy
3.2.4. Native Alerters Behavior Optimization Strategy
3.2.5. Magnification Penalty Function Optimization Strategy
4. Application, Results, and Discussion
4.1. Application
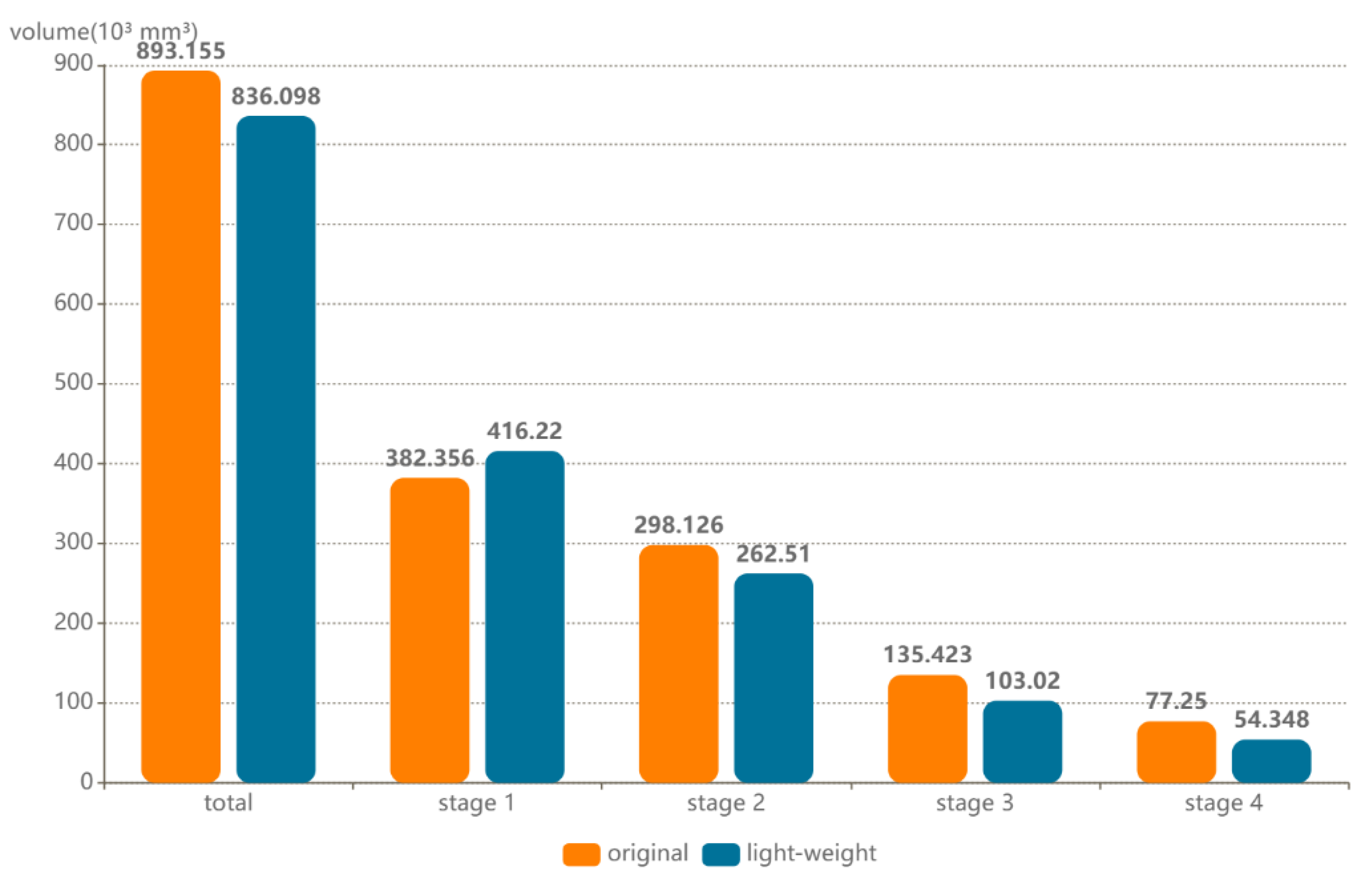
4.2. Application Result
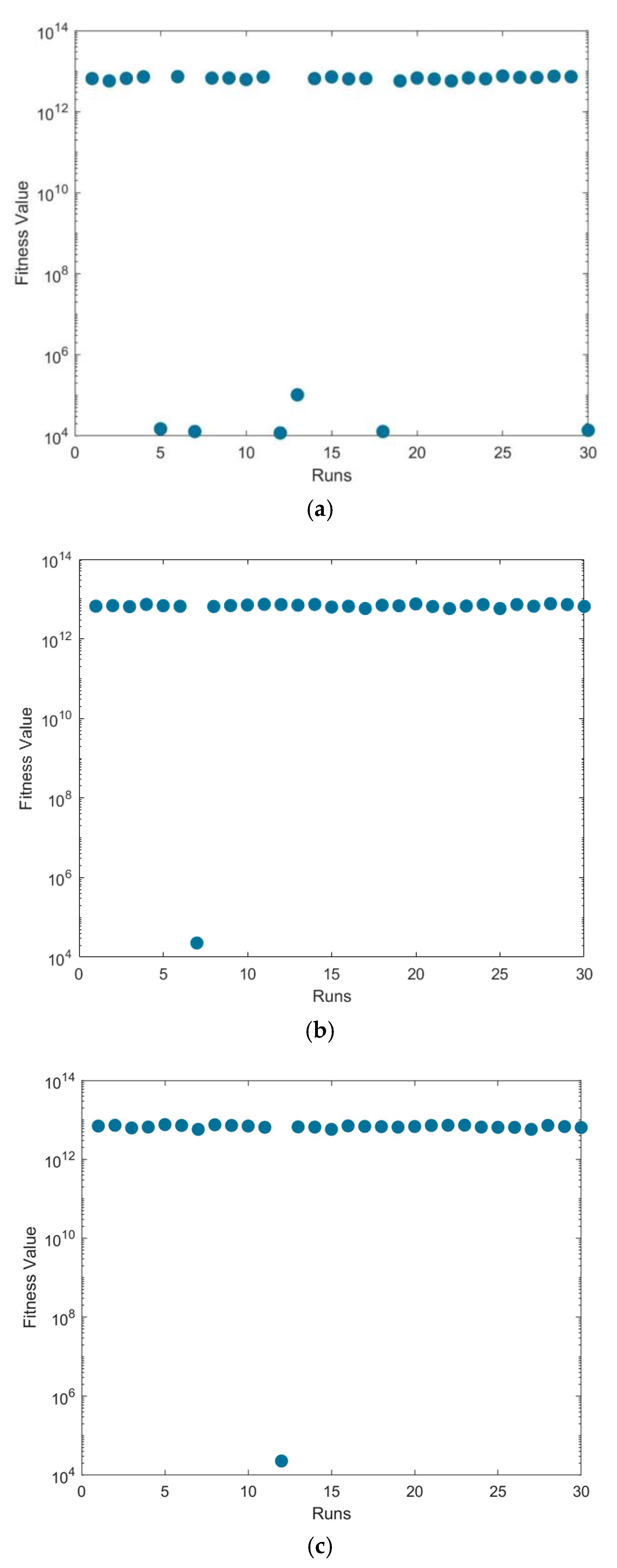
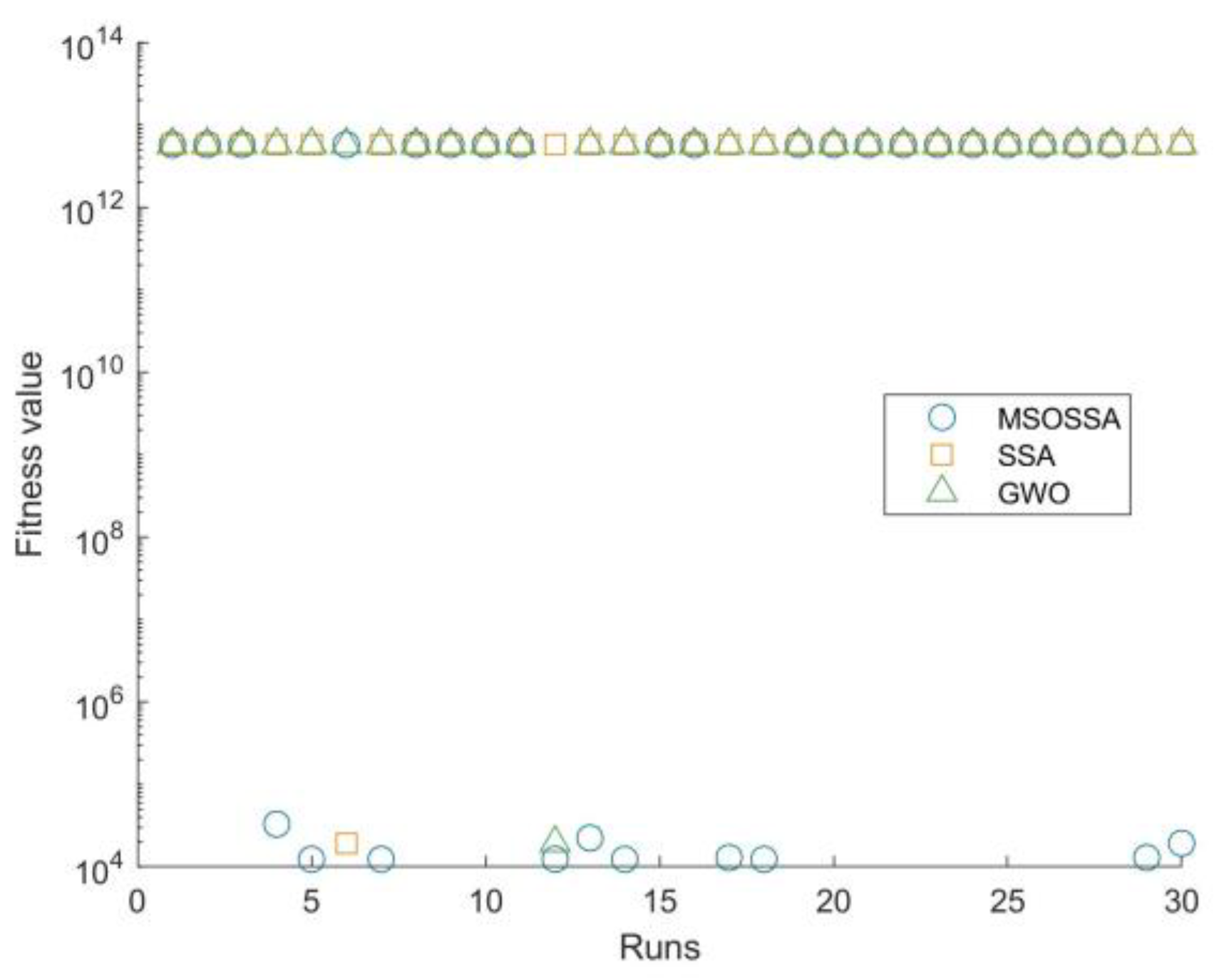
4.3. Comparative Analysis and Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Nutakor, C.; Klodowski, A.; Sopanen, J.; Mikkola, A.; Pedrero, J.I. Planetary gear sets power loss modeling: Application to wind turbines. Tribol. Int. 2017, 105, 42–54. [Google Scholar] [CrossRef]
- Xu, X.; Chen, J.; Lin, Z.; Qiao, Y.; Chen, X.; Zhang, Y.; Xu, Y.; Li, Y. Optimization design for the planetary gear train of an electric vehicle under uncertainties. Actuators 2022, 11, 49. [Google Scholar] [CrossRef]
- Huseyin Filiz, i.; Olguner, S.; Evyapan, E. A Study on Optimization of Planetary Gear Trains. Acta Phys. Pol. A 2017, 132, 728–733. [Google Scholar] [CrossRef]
- Rosic, B.; Radenovic, S.; Jankovic, L.; Milojevic, M. Optimisation of planetary gear train using multiobjective genetic algorithm. J. Balk. Tribol. Assoc. 2011, 17, 462–475. [Google Scholar]
- Sedak, M.; Rosic, B. Multi-Objective Optimization of Planetary Gearbox with Adaptive Hybrid Particle Swarm Differential Evolution Algorithm. Appl. Sci. 2021, 11, 1107. [Google Scholar] [CrossRef]
- Jiao, W.; Li, J. Equal Strength Optimal Design of Planetary Gear Transmission. J. Phys. Conf. Ser. 2023, 2557, 012024. [Google Scholar] [CrossRef]
- Yaw, M.W. Optimize Volume for Planetary Gear Train by using Algorithm Based Artificial Immune System. Int. J. Adv. Trends Comput. Sci. Eng. 2020, 9, 3757–3762. [Google Scholar] [CrossRef]
- Parmar, A.; Ramkumar, P.; Shankar, K. Macro geometry multi-objective optimization of planetary gearbox considering scuffing constraint. Mech. Mach. Theory 2020, 154, 104045. [Google Scholar] [CrossRef]
- Sedak, M.; Rosic, M. Hybrid Butterfly Optimization and Particle Swarm Optimization Algorithm-Based Constrained Multi-Objective Nonlinear Planetary Gearbox Optimization. Appl. Sci. 2023, 13, 11682. [Google Scholar] [CrossRef]
- Prayoonrat, S.; Walton, D. Practical approach to optimum gear train design. Comput. Aided Des 1988, 20, 83–92. [Google Scholar] [CrossRef]
- Yokota, T.; Taguchi, T.; Gen, M. A solution method for optimal weight design problem of the gear using genetic algorithms. Comput. Ind. Eng. 1998, 35, 523–526. [Google Scholar] [CrossRef]
- Chong, T.H.; Bae, I.; Park, G.J. A new and generalized methodology to design multi-stage gear drives by integrating the dimensional and the configuration design process. Mech. Mach. Theory 2002, 37, 295–310. [Google Scholar] [CrossRef]
- Maputi, E.S.; Arora, R. Multi-objective optimization of a 2-stage spur gearbox using NSGA-II and decision-making methods. J. Braz. Soc. Mech. Sci. Eng. 2020, 42, 477. [Google Scholar] [CrossRef]
- Hoseiniasl, M.; Fesharaki, J.J. 3D Optimization of Gear Train Layout Using Particle Swarm Optimization Algorithm. J. Appl. Comput. Mech. 2020, 6, 823–840. [Google Scholar]
- Tran, H.D.; Le, X.H.; Nguyen, T.T.N.; Hoang, X.T.; Trieu, Q.H.; Vu, N.P. Application of the Taguchi Method and Grey Relational Analysis for Multi-Objective Optimization of a Two-Stage Bevel Helical Gearbox. Machines 2023, 11, 716. [Google Scholar] [CrossRef]
- Top, N.; Dorterler, M.; Sahin, I. Optimization of planetary gearbox using nature inspired meta-heuristic optimizers. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2024, 238, 3338–3347. [Google Scholar] [CrossRef]
- Yue, Y.; Cao, L.; Lu, D.; Hu, Z.; Xu, M.; Wang, S.; Li, B.; Ding, H. Review and empirical analysis of sparrow search algorithm. Artif. Intell. Rev. 2023, 56, 10867–10919. [Google Scholar] [CrossRef]
- Wang, Z.; Qin, J.; Hu, Z.; He, J.; Tang, D. Multi-Objective Antenna Design Based on BP Neural Network Surrogate Model Optimized by Improved Sparrow Search Algorithm. Appl. Sci. 2022, 12, 12543. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, L.; Liang, J.; Chen, J.; Ke, C.; He, D. Application of a Multi-Strategy Improved Sparrow Search Algorithm in Bridge Crane PID Control Systems. Appl. Sci. 2024, 14, 5165. [Google Scholar] [CrossRef]
- Cheng, D. (Ed.) Mechanical Design Manual, 6th ed.; Chemical Industry Press: Beijing, China, 2017. [Google Scholar]
- Ye, K. Gear Manual; China Machine Press: Beijing, China, 1990; pp. 870–871. [Google Scholar]
- Yan, S. Design and Manufacture of Involute Gear Planetary Transmission; China Machine Press: Beijing, China, 2002. [Google Scholar]
- Xue, J.; Shen, B. A novel swarm intelligence optimization approach: Sparrow search algorithm. Syst. Sci. Control Eng. 2020, 8, 22–34. [Google Scholar] [CrossRef]

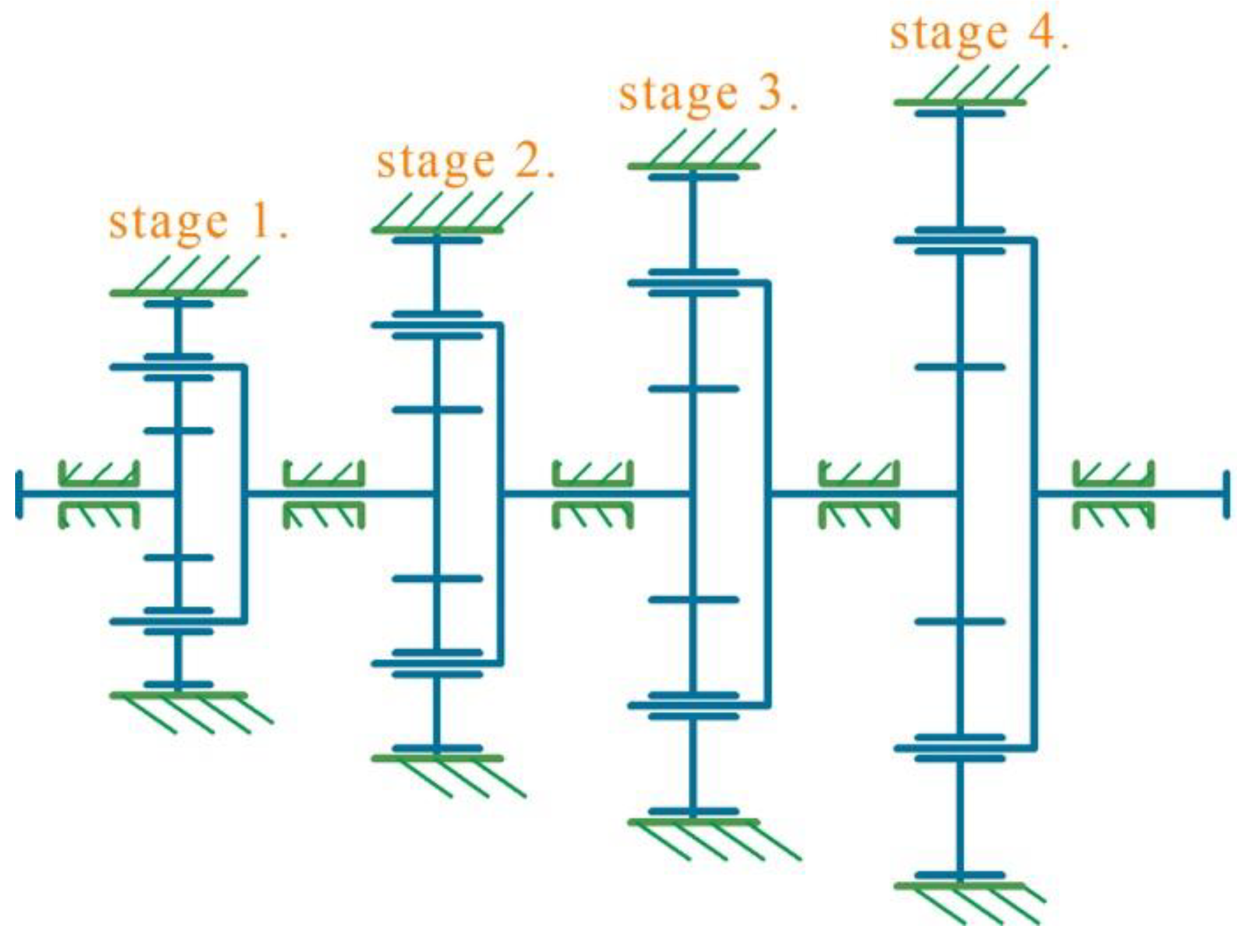

| stage | 1 | 2 | 3 | 4 |
| optimal solution | 9 | 6.8 | 5.6 | 4.6 |
| stage 1 | 18 | 63 | 144 | 1.5 | 20 |
| stage 2 | 20 | 49 | 118 | 1.5 | 20 |
| stage 3 | 17 | 31 | 79 | 1.5 | 20 |
| stage 4 | 17 | 22 | 61 | 1.5 | 20 |
| Algorithm | Main Parameters |
| MSOSSA | N = 400, n1:n2:n3 = 7:1:2; Max iter = 6 |
| SSA | N = 400, n1:n2:n3 = 7:1:2; Max iter = 6 |
| GWO | N = 400; Max iter = 6 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lin, S.; Zhang, Z.; Ma, Y.; Li, H. Light-Weighting of Planetary Gearbox Based on Multi-Strategy Optimization Sparrow Search Algorithm. Appl. Sci. 2025, 15, 122. https://doi.org/10.3390/app15010122
Lin S, Zhang Z, Ma Y, Li H. Light-Weighting of Planetary Gearbox Based on Multi-Strategy Optimization Sparrow Search Algorithm. Applied Sciences. 2025; 15(1):122. https://doi.org/10.3390/app15010122
Chicago/Turabian StyleLin, Shuting, Zhirong Zhang, Yinghao Ma, and Hua Li. 2025. "Light-Weighting of Planetary Gearbox Based on Multi-Strategy Optimization Sparrow Search Algorithm" Applied Sciences 15, no. 1: 122. https://doi.org/10.3390/app15010122
APA StyleLin, S., Zhang, Z., Ma, Y., & Li, H. (2025). Light-Weighting of Planetary Gearbox Based on Multi-Strategy Optimization Sparrow Search Algorithm. Applied Sciences, 15(1), 122. https://doi.org/10.3390/app15010122





