A Novel Optimization Method Using the Box–Behnken Design Integrated with a Back Propagation Neural Network–Genetic Algorithm for Hydrogen Purification
Abstract
1. Introduction
2. Materials and Methods
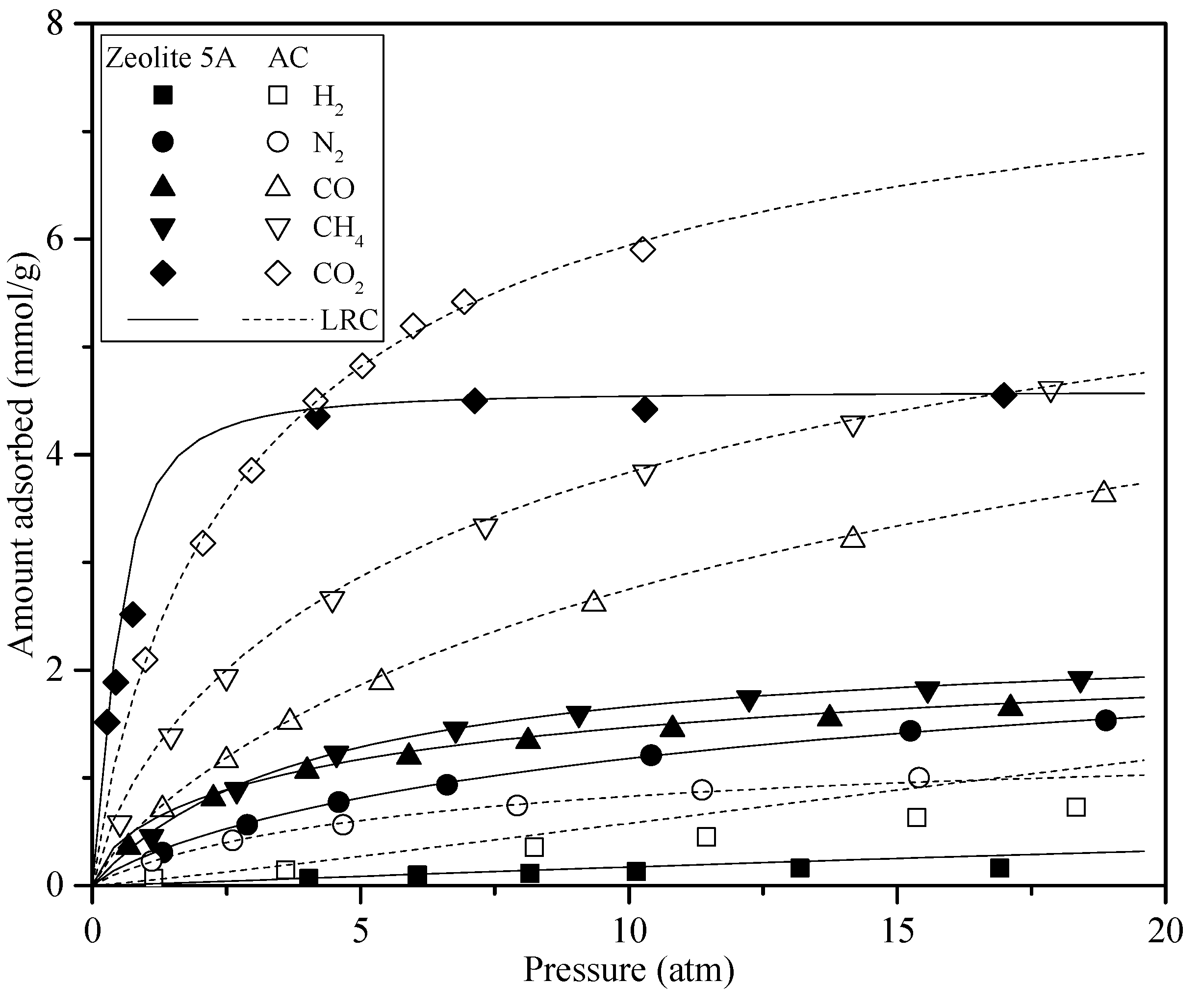
2.1. Mathematical Model for PSA Process
2.2. BBD Method for PSA Process
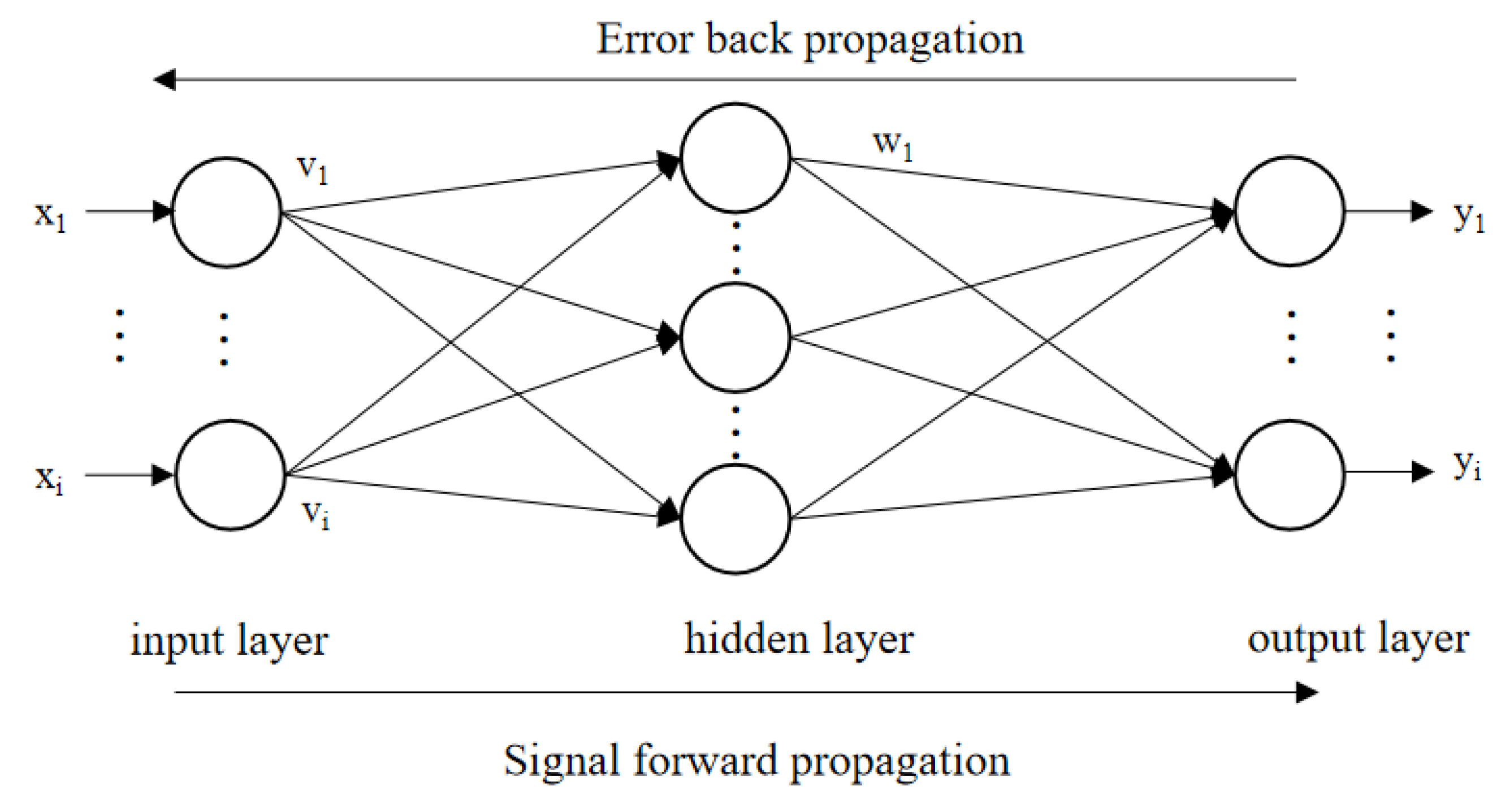
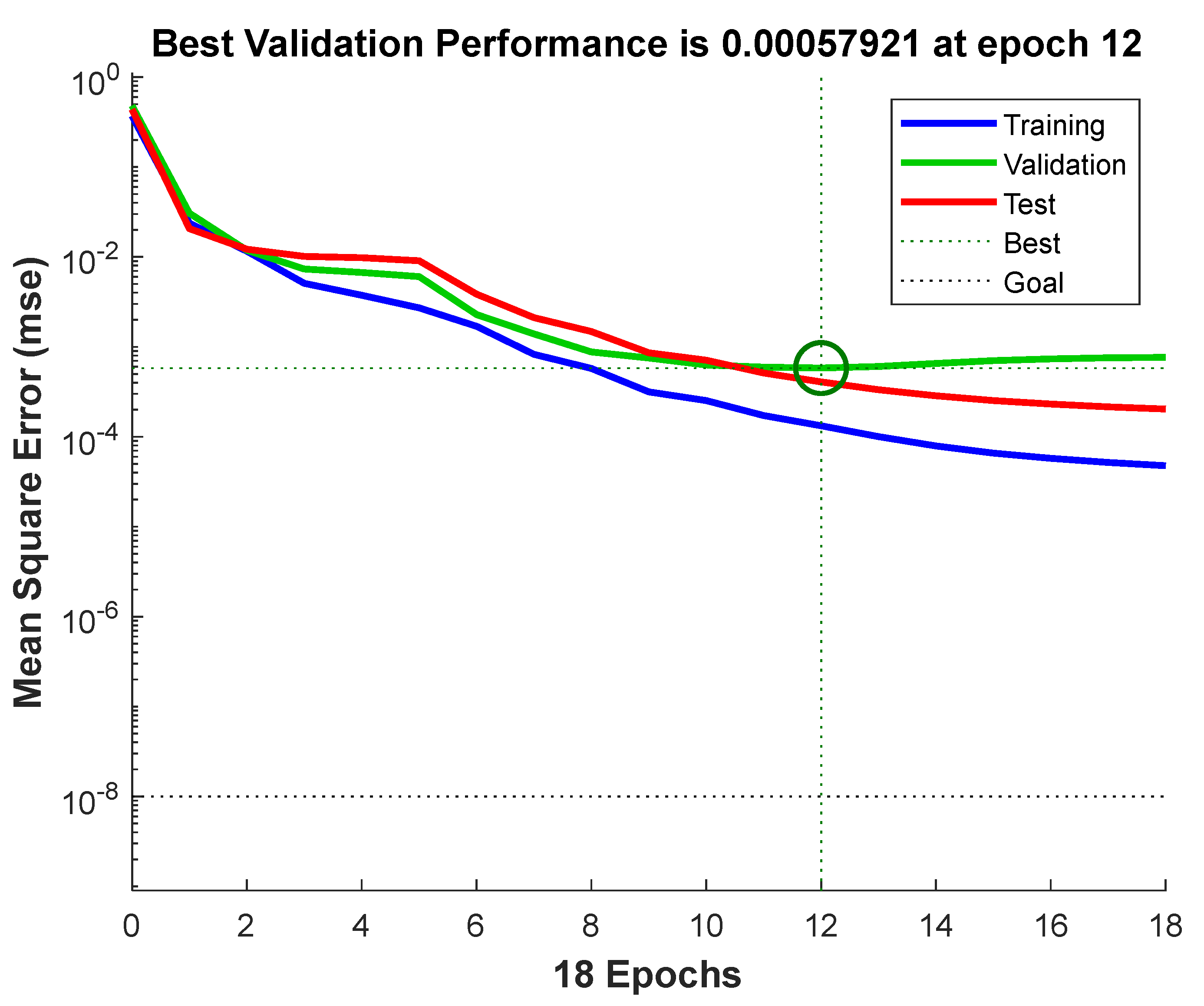
2.3. BPNN–GA for Optimization
3. Results
3.1. Simulation PSA Process
3.2. Prediction by BBD Method
3.3. Prediction by BPNN–GA Model
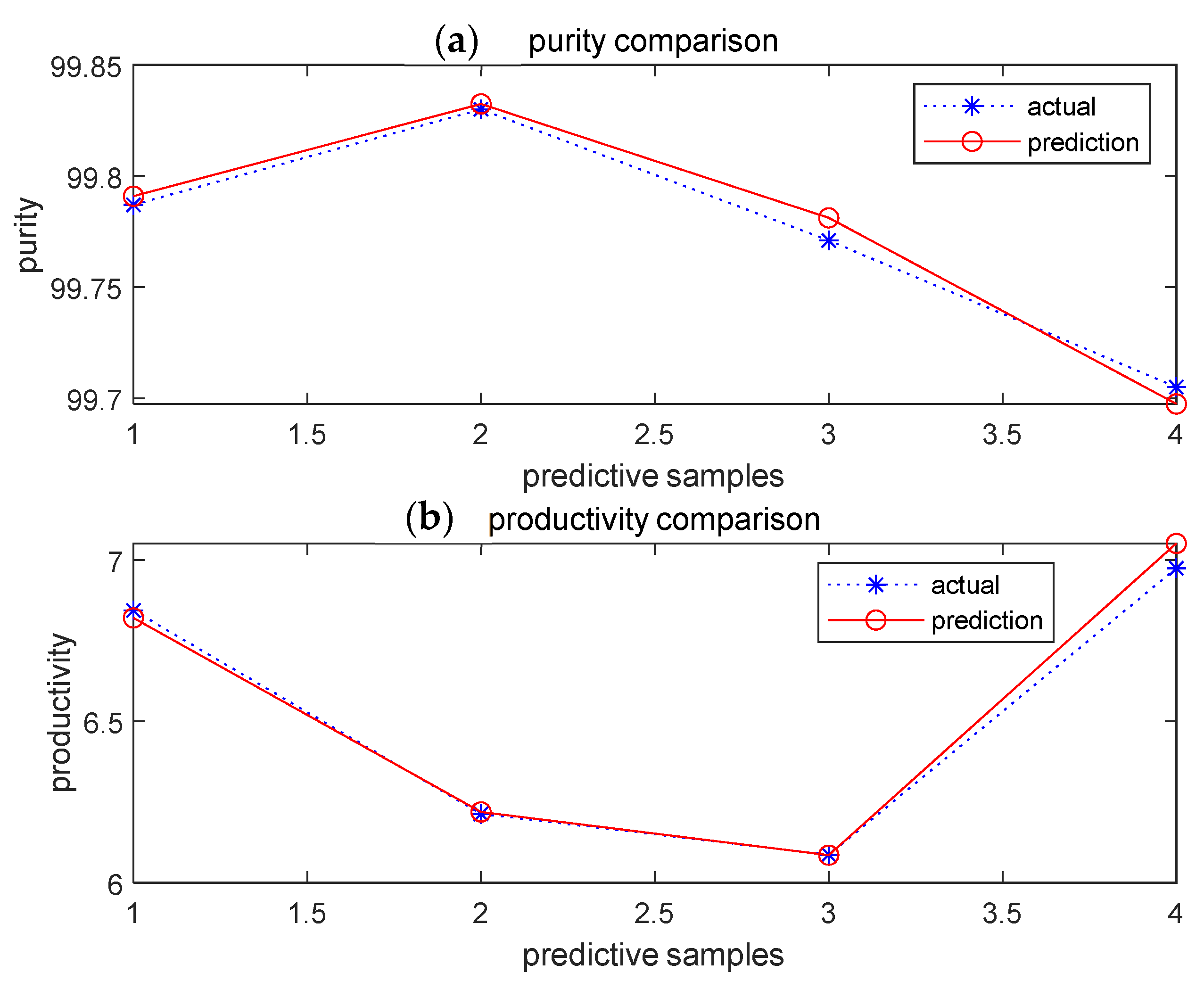
3.4. Prediction by BBD–BPNN–GA Model
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Xie, X.Y.; Awad, O.I.; Xie, L.L.; Ge, Z.Y. Purification of hydrogen as green energy with pressure-vacuum swing adsorption (PVSA) with a two-layers adsorption bed using activated carbon and zeolite as adsorbent. Chemosphere 2023, 338, 139347. [Google Scholar] [CrossRef] [PubMed]
- Golmakani, A.; Fatemi, S.; Tamnanloo, J. Investigating PSA, VSA, and TSA methods in SMR unit of refineries for hydrogen production with fuel cell specification. Sep. Purif. Technol. 2017, 176, 73–91. [Google Scholar] [CrossRef]
- Kumar, A.; Muthukumar, P. Experimental investigation on hydrogen transfer in coupled metal hydride reactors for multistage hydrogen purification application. Appl. Energy 2024, 363, 123076. [Google Scholar] [CrossRef]
- Achomo, M.A.; Kumar, A.; Muthukumar, P.; Peela, N.R. Experimental studies on hydrogen production from steam reforming of methanol integrated with metal hydride-based hydrogen purification system. Int. J. Hydrog. Energy 2024, 76, 28–43. [Google Scholar] [CrossRef]
- Zhang, H.T.; Yang, D.F.; Guan, M.J.; Li, Q. Study of supramolecular organic frameworks for purification of hydrogen through molecular dynamics simulations. Sep. Purif. Technol. 2024, 335, 126106. [Google Scholar] [CrossRef]
- Ganley, J. Pressure swing adsorption in the unit operations laboratory. Chem. Eng. Educ. 2018, 52, 44–51. [Google Scholar] [CrossRef]
- Bahrun, M.H.V.; Bono, A.; Othman, N.; Zaini, M.A.A. Carbon dioxide removal from biogas through pressure swing adsorption—A review. Chem. Eng. Res. Des. 2022, 183, 285–306. [Google Scholar] [CrossRef]
- Abd, A.A.; Othman, M.R.; Helwani, Z.; Kim, J. An overview of biogas upgrading via pressure swing adsorption: Navigating through bibliometric insights towards a conceptual framework and future research pathways. Energy Convers. Manag. 2024, 306, 118268. [Google Scholar] [CrossRef]
- Freund, D.; Güngör, A.; Atakan, B. Hydrogen production and separation in fuel-rich operated HCCI engine polygeneration systems: Exergoeconomic analysis and comparison between pressure swing adsorption and palladium membrane separation. Appl. Energy Combust. Sci. 2023, 13, 100108. [Google Scholar] [CrossRef]
- Milad, Y.; Habib, E.; Falamaki, C. Competitive adsorption equilibrium isotherms of CO, CO2, CH4, and H2 on activated carbon and zeolite 5A for hydrogen purification. J. Chem. Eng. 2016, 61, 3420–3427. [Google Scholar]
- Kacem, M.; Pellerano, M.; Delebarre, A. Pressure swing adsorption for CO2/N2 and CO2/CH4 separation: Comparison between activated carbons and zeolites performances. Fuel Process. Technol. 2015, 138, 271–283. [Google Scholar] [CrossRef]
- Lopes, F.V.S.; Grande, C.A.; Ribeiro, A.M. Adsorption of H2, CO2, CH4, CO, N2 and H2O in activated carbon and zeolite for hydrogen production. Sep. Purif. Technol. 2009, 44, 1045–1073. [Google Scholar]
- Zhang, N.N.; Xiao, J.S.; Bénard, P.; Chahine, R. Single-and double-bed pressure swing adsorption processes for H2/CO syngas separation. Int. J. Hydrog. Energy 2019, 44, 26405–26418. [Google Scholar] [CrossRef]
- Ribeiro, A.M.; Grande, C.A.; Lopes, F.V.S. Four beds pressure swing adsorption for hydrogen purification: Case of humid feed and activated carbon beds. AIChE 2009, 55, 2292–2302. [Google Scholar] [CrossRef]
- Rebello, C.M.; Martins, M.A.F.; Rodrigues, A.E.; Loureiro, J.M. A novel standpoint of pressure swing adsorption processes multi-objective optimization: An approach based on feasible operation region mapping. Chem. Eng. Res. Des. 2022, 178, 590–601. [Google Scholar] [CrossRef]
- Subraveti, S.G.; Pai, K.N.; Rajagopalan, A.K.; Wilkins, N.S. Cycle design and optimization of pressure swing adsorption cycles for pre-combustion CO2 capture. Appl. Energy 2019, 254, 113624. [Google Scholar] [CrossRef]
- Wang, Y.J.; Zheng, M.Y.; Liu, G.L.; Zhang, D.; Zhang, Q. Graphical method for simultaneous optimization of the hydrogen recovery and purification feed. Int. J. Hydrog. Energy 2016, 41, 2631–2648. [Google Scholar] [CrossRef]
- Tang, Y.Y.; Long, W.Q.; Wang, Y.; Xiao, G.; Wang, Y.J.; Lu, M.F. Multi-objective optimization of methanol reforming reactor performance based on response surface methodology and multi-objective particle swarm optimization coupling algorithm for on-line hydrogen production. Energy Convers. Manag. 2024, 307, 118377. [Google Scholar] [CrossRef]
- Zhang, N.N.; Bénard, P.; Chahine, R.; Yang, T.Q.; Xiao, J.S. Optimization of pressure swing adsorption for hydrogen purification based on Box-Behnken design method. Int. J. Hydrog. Energy 2021, 46, 5403–5417. [Google Scholar] [CrossRef]
- Karimifard, S.; Alavi, M.M.R. Application of response surface methodology in physicochemical removal of dyes from wastewater: A critical review. Sci. Total Environ. 2018, 640, 772–797. [Google Scholar] [CrossRef]
- Tahir, F.; Arshad, M.Y.; Saeed, M.A.; Ali, U. Integrated process for simulation of gasification and chemical looping hydrogen production using Artificial Neural Network and machine learning validation. Energy Convers. Manag. 2023, 296, 117702. [Google Scholar] [CrossRef]
- Yu, X.X.; Shen, Y.H.; Guan, Z.B.; Zhang, D.H.; Tang, Z.L.; Li, W.B. Multi-objective optimization of ANN-based PSA model for hydrogen purification from steam-methane reforming gas. Int. J. Hydrog. Energy 2021, 46, 11740–11755. [Google Scholar] [CrossRef]
- Streb, A.; Mazzotti, M. Performance limits of neural networks for optimizing an adsorption process for hydrogen purification and CO2 capture. Comput. Chem. Eng. 2022, 166, 107974. [Google Scholar] [CrossRef]
- Kani, G.T.; Ghahremani, A. Optimal design of heat pipes for city gate station heaters by applying genetic and Bayesian optimization algorithms to an artificial neural network model. Case Stud. Therm. Eng. 2024, 55, 104203. [Google Scholar] [CrossRef]
- Ahn, H.; Yang, J.; Lee, C.H. Effects of feed composition of coke oven gas on a layered bed H2 PSA process. Adsorption 2001, 7, 339–356. [Google Scholar] [CrossRef]
- Silva, F.; Silva, J.; Rodrigues, A. A general package for the simulation of cyclic adsorption processes. Adsorption 1999, 5, 229–244. [Google Scholar] [CrossRef]
- Sereno, C.; Rodrigues, A. Can steady-state momentum equations be used in modeling pressurization of adsorption beds? Gas. Sep. Purif. 1993, 7, 167–174. [Google Scholar] [CrossRef]
- Srivastava, A.; Aghilesh, K.; Nair, A.; Ram, S. Response surface methodology and artificial neural network modelling for the performance evaluation of pilot-scale hybrid nanofiltration (NF) & reverse osmosis (RO) membrane system for the treatment of brackish ground water. J. Environ. Manag. 2021, 278, 111497. [Google Scholar]
- Jang, H.; Lee, C.S.; Kim, J.H.; Kim, J.H. Optimization of photocatalytic ceramic membrane filtration by response surface methodology: Effects of hydrodynamic conditions on organic fouling and removal efficiency. Chemosphere 2024, 356, 141885. [Google Scholar] [CrossRef]
- Saberimoghaddam, A.; Nozari, A. An experimental and statistical model of a cyclic pressure swing adsorption column for hydrogen purification. Korean J. Chem. Eng. 2017, 34, 822–828. [Google Scholar] [CrossRef]
- Jee, J.G.; Kim, M.B.; Lee, C.H. Adsorption characteristics of hydrogen mixtures in a layered bed: Binary, ternary, and five-component mixtures. Ind. Eng. Chem. Res. 2001, 40, 868–878. [Google Scholar] [CrossRef]
- Yang, J.; Lee, C.H. Adsorption dynamics of a layered bed PSA for H2 recovery from coke oven gas. AIChE 2010, 44, 1325–1334. [Google Scholar] [CrossRef]
- Ahn, S.; You, Y.W.; Lee, D.G. Layered two- and four-bed PSA processes for H2 recovery from coal gas. Chem. Eng. Sci. 2012, 68, 413–423. [Google Scholar] [CrossRef]
- Cavenati, S.; Grande, C.A.; Rodrigues, A.E. Layered pressure swing adsorption for methane recovery from CH4/CO2/N2 streams. Adsorption 2005, 11, 549–554. [Google Scholar] [CrossRef]
- Yang, S.I.; Choi, D.Y.; Jang, S.C. Hydrogen separation by multi-bed pressure swing adsorption of synthesis gas. Adsorption 2008, 14, 583–590. [Google Scholar] [CrossRef]
- Park, J.; Kang, R.H.; Lee, J.W. Efficient pressure swing adsorption for improving H2 recovery in precombustion CO2 capture. Korean J. Chem. Eng. 2017, 34, 1763–1773. [Google Scholar] [CrossRef]
- Kundu, P.; Paul, V.; Kumar, V. Formulation development, modeling and optimization of emulsification process using evolving RSM coupled hybrid ANN-GA framework. Chem. Eng. Res. Des. 2015, 104, 773–790. [Google Scholar] [CrossRef]

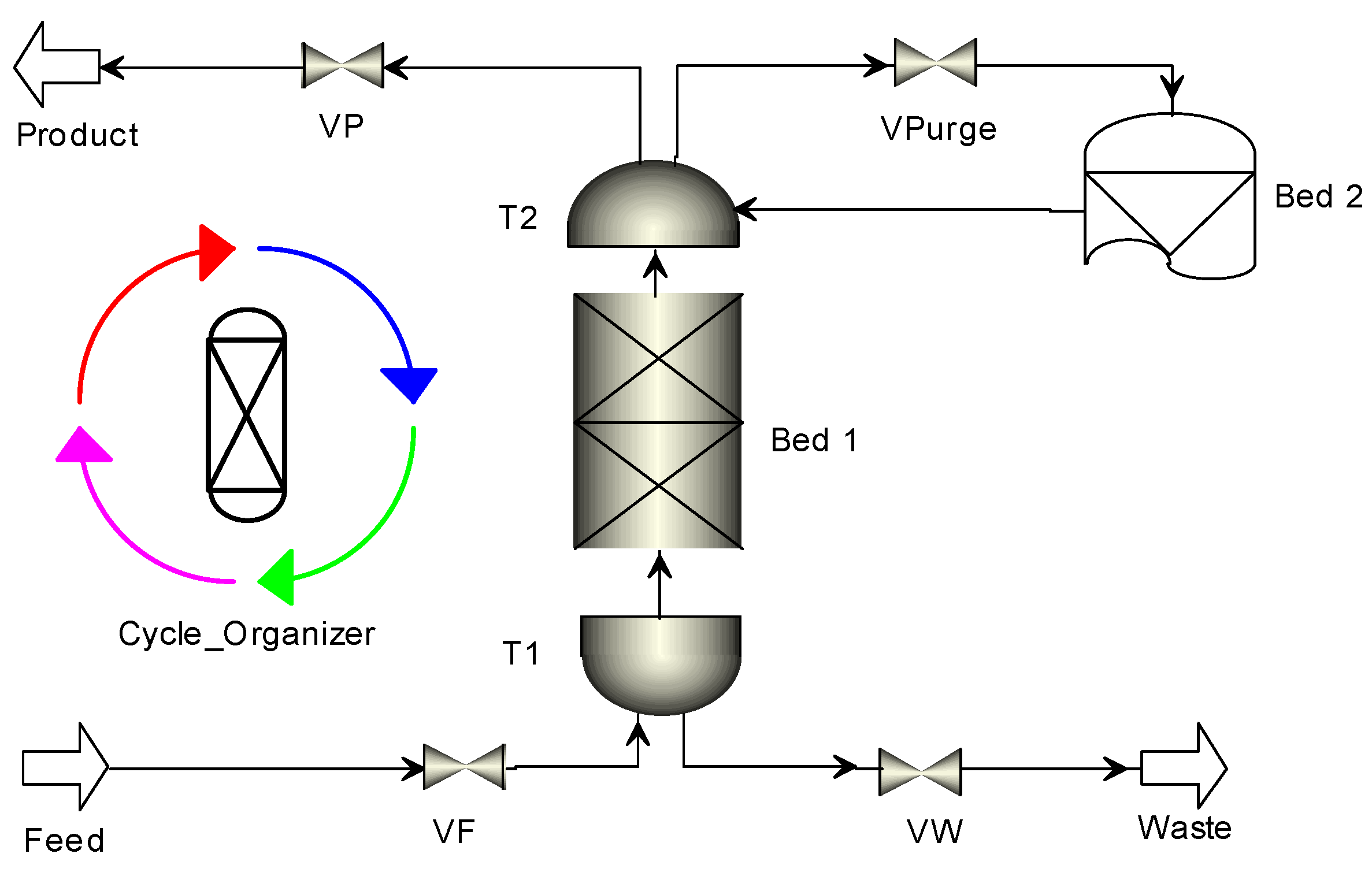







| Step | I | II | III | IV | V | VI |
|---|---|---|---|---|---|---|
| Schematic diagram of adsorption bed | 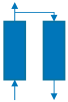 |  | 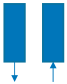 |  |  |  |
| Bed 1 | AD | DPE | DP | PG | PPE | FP |
| Bed 2 | PG | PPE | FP | AD | DPE | DP |
| Time (s) | 180 | 20 | 8 | 180 | 20 | 8 |
| Factors | Variables and Ranges | ||
|---|---|---|---|
| Adsorption Time (s) | Pressure Equalization Time (s) | Feed Flow Rate (L/min) | |
| –1 | 160 | 10 | 6 |
| 0 | 180 | 20 | 8 |
| +1 | 200 | 30 | 10 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, N.; Hu, S.; Xin, Q. A Novel Optimization Method Using the Box–Behnken Design Integrated with a Back Propagation Neural Network–Genetic Algorithm for Hydrogen Purification. Appl. Sci. 2025, 15, 140. https://doi.org/10.3390/app15010140
Zhang N, Hu S, Xin Q. A Novel Optimization Method Using the Box–Behnken Design Integrated with a Back Propagation Neural Network–Genetic Algorithm for Hydrogen Purification. Applied Sciences. 2025; 15(1):140. https://doi.org/10.3390/app15010140
Chicago/Turabian StyleZhang, Nannan, Sumeng Hu, and Qianqian Xin. 2025. "A Novel Optimization Method Using the Box–Behnken Design Integrated with a Back Propagation Neural Network–Genetic Algorithm for Hydrogen Purification" Applied Sciences 15, no. 1: 140. https://doi.org/10.3390/app15010140
APA StyleZhang, N., Hu, S., & Xin, Q. (2025). A Novel Optimization Method Using the Box–Behnken Design Integrated with a Back Propagation Neural Network–Genetic Algorithm for Hydrogen Purification. Applied Sciences, 15(1), 140. https://doi.org/10.3390/app15010140





