A Novel Traffic Analysis Zone Division Methodology Based on Individual Travel Data
Abstract
1. Introduction
2. Data Preprocessing
2.1. Data Cleaning
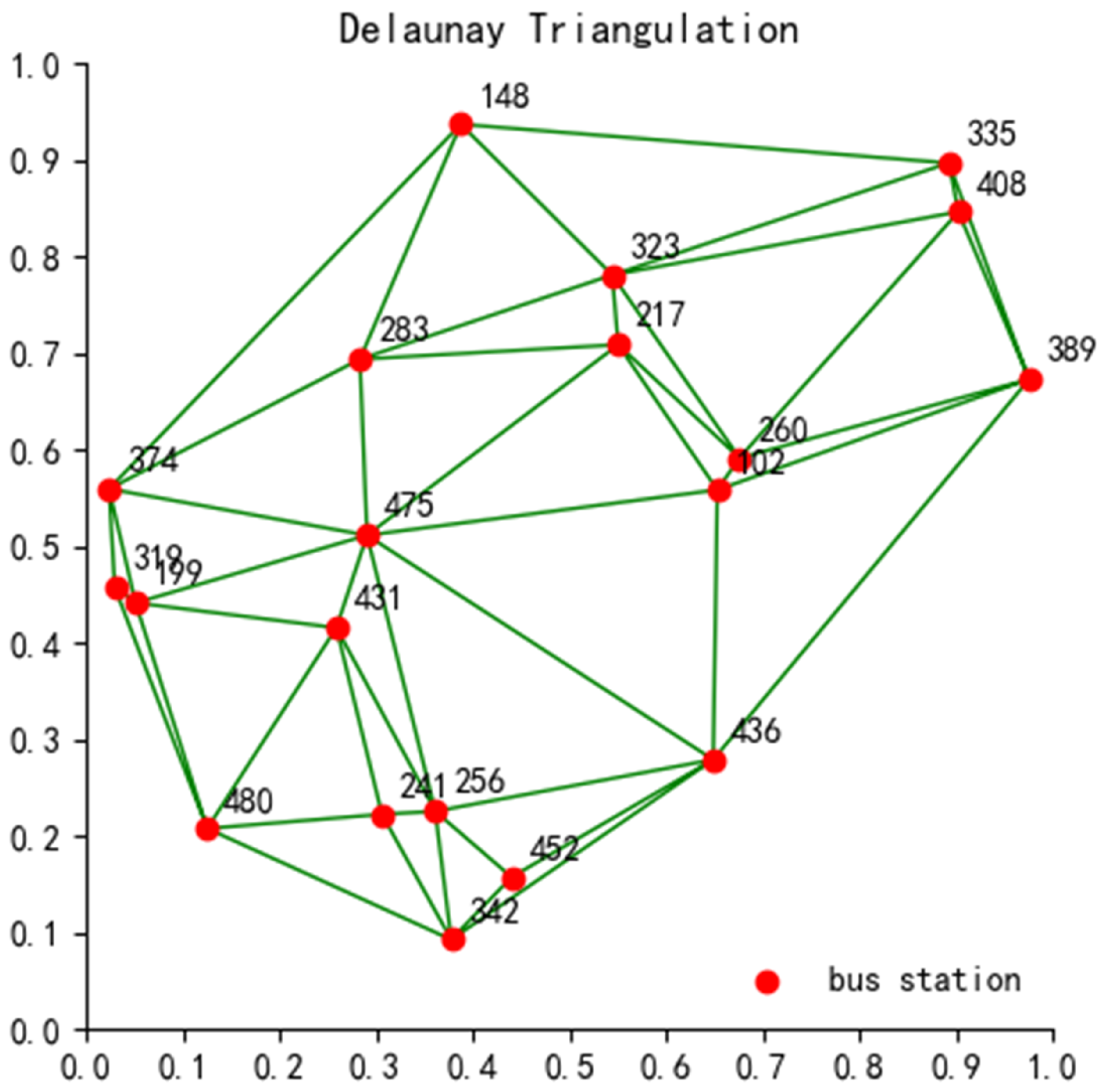
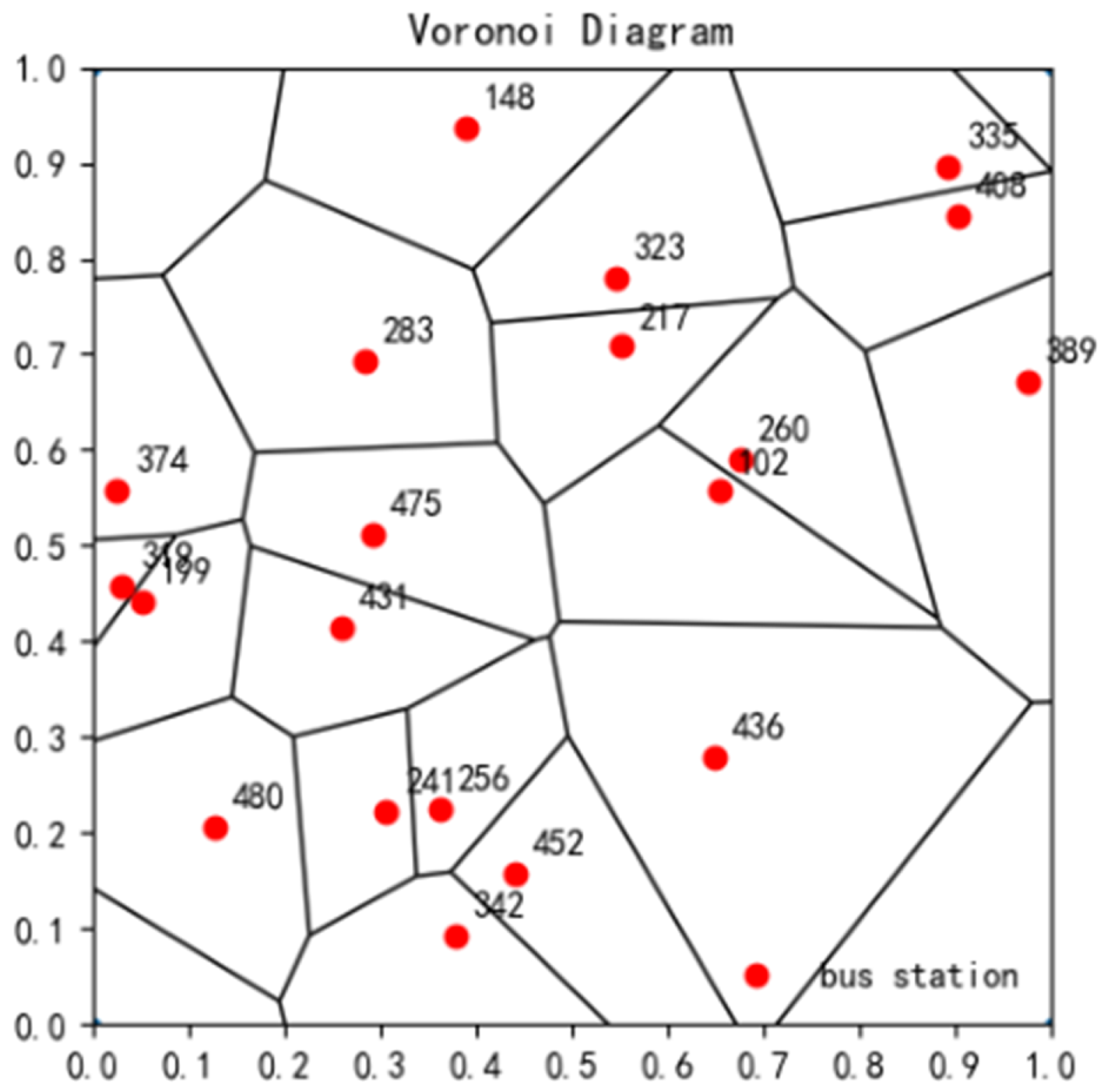
2.2. Space–Time Mapping and Discretization
2.3. Basic Data Construction
3. Traffic Subdivision Methods
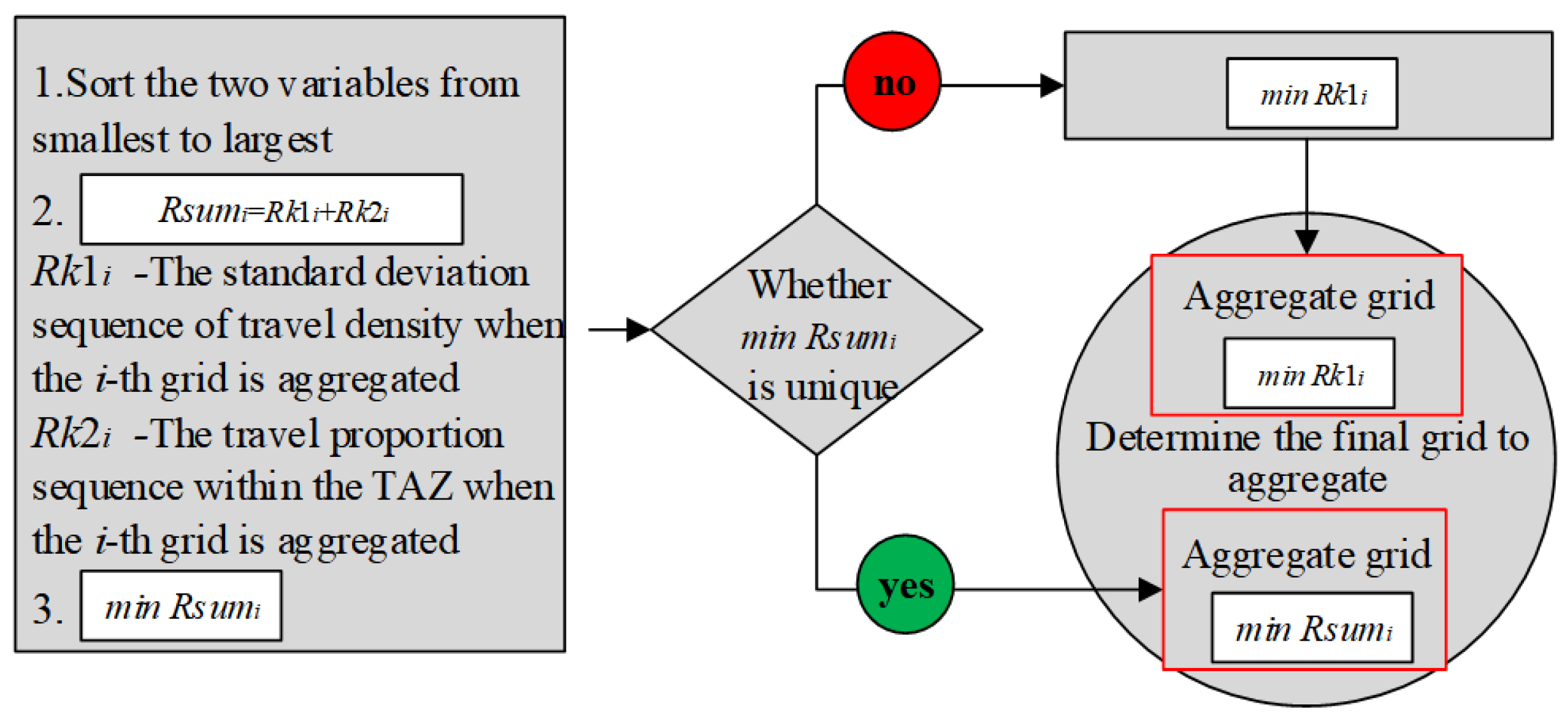
3.1. Preliminary Screening Conditions of Polymerization Unit
3.2. Optimal Modeling of Traffic Cell Segmentation
3.3. Evaluation of Optimization Effect
3.4. Solving Traffic Cell Segmentation Model

| Algorithm 1: TAZ division scheme and evaluation process. |
 |
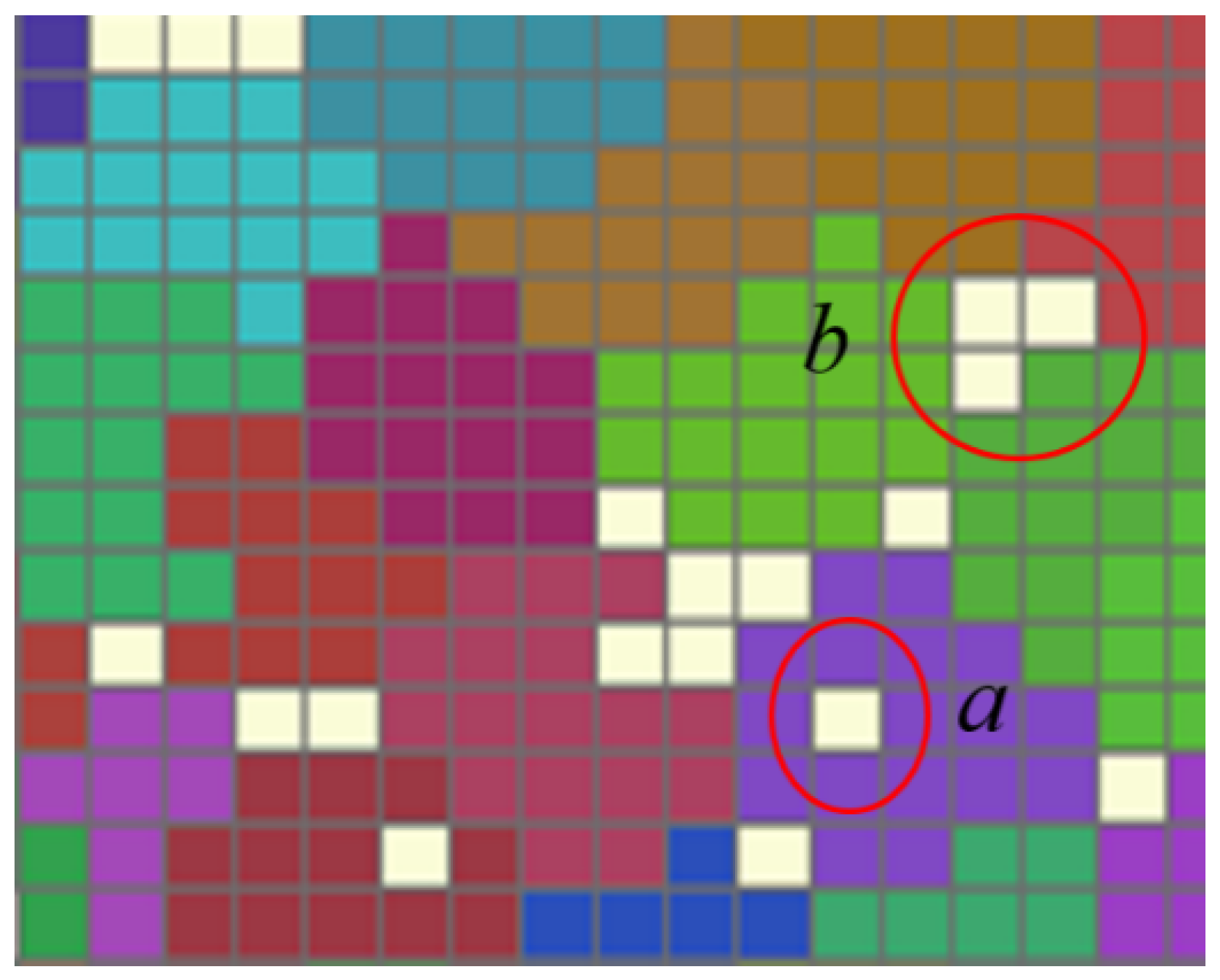
3.5. Programmatic Refinements
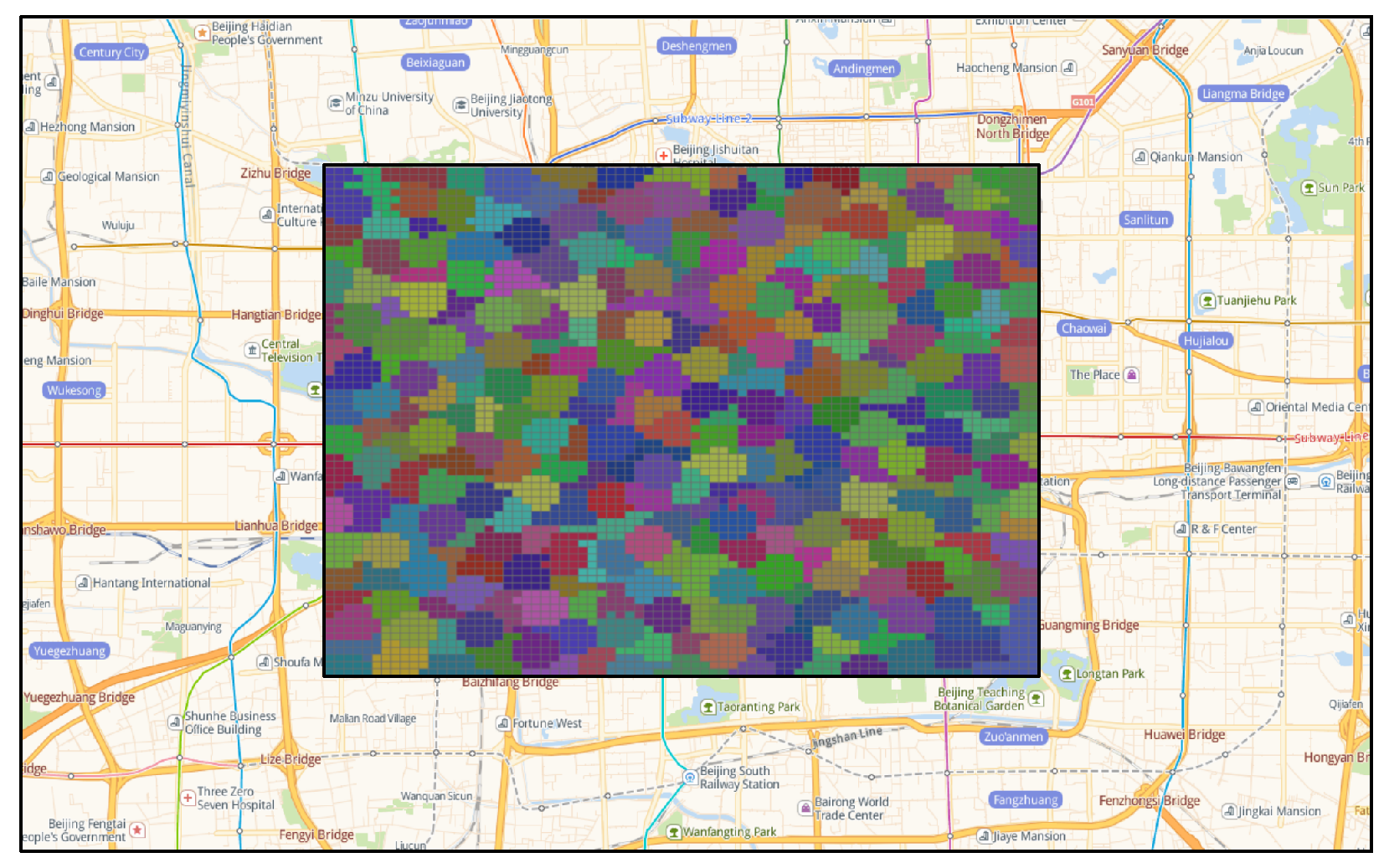
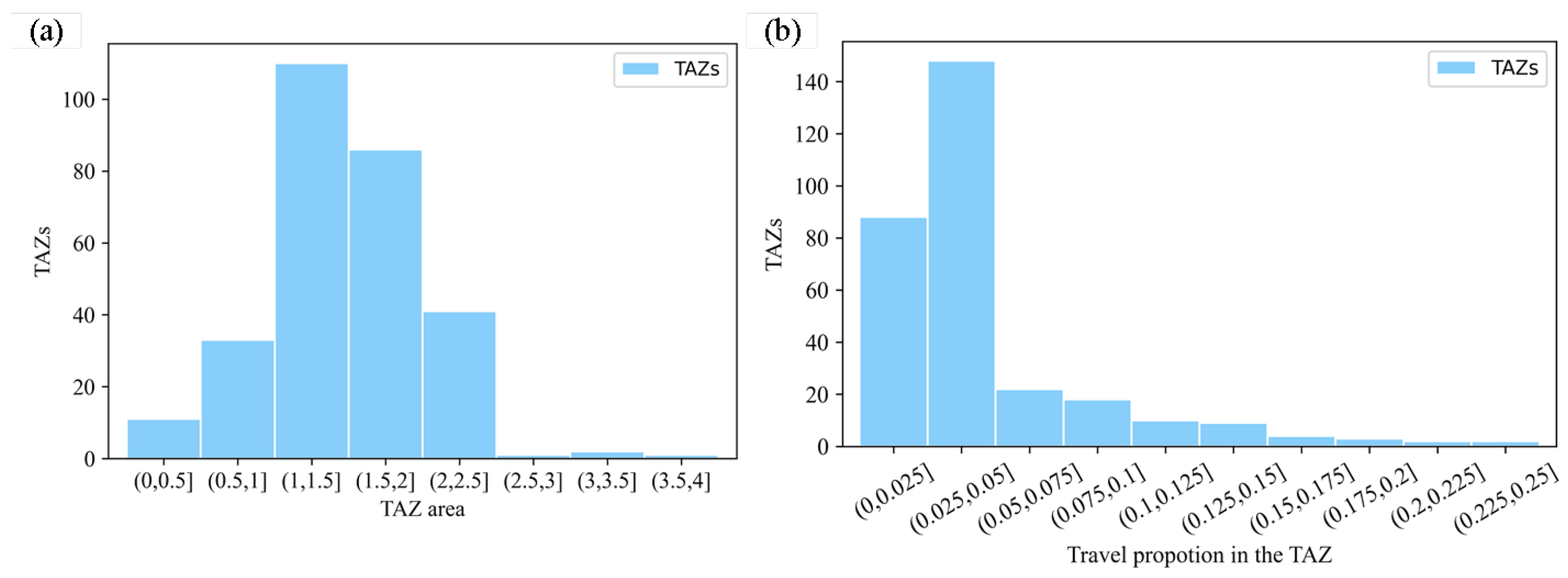
4. Case Validation and Analysis
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ghadiri, M.; Rassafi, A.A.; Mirbaha, B. The effects of traffic zoning with regular geometric shapes on the precision of trip production models. J. Transp. Geogr. 2019, 78, 150–159. [Google Scholar] [CrossRef]
- Hosseinzadeh, A.; Algomaiah, M.; Kluger, R.; Li, Z. Spatial analysis of shared e-scooter trips. J. Transp. Geogr. 2021, 92, 103016. [Google Scholar] [CrossRef]
- Mirzahossein, H.; Bakhtiari, A.R.; Kalantari, N.T.; Jin, X. Investigating mandatory and non-mandatory trip patterns based on socioeconomic characteristics and traffic analysis zone features using deep neural networks. Comput. Urban Sci. 2022, 2, 35. [Google Scholar] [CrossRef]
- Li, H.; Wu, D.; Zhang, Z.; Zhang, Y. Safety impacts of the discrepancies and accesses between adjacent traffic analysis zones. J. Transp. Saf. Secur. 2020, 14, 359–381. [Google Scholar] [CrossRef]
- Briz-Redón, A.; Martínez-Ruiz, F.; Montes, F. Investigation of the consequences of the modifiable areal unit problem in macroscopic traffic safety analysis: A case study accounting for scale and zoning. Accid. Anal. Prev. 2019, 132, 105276. [Google Scholar] [CrossRef] [PubMed]
- Guo, C. Suggestions on the Optimization and Application of Traffic District Division Scheme of National Railway Transportation Network; Research on Railway Economy: Beijing, China, 2019; pp. 1–5. [Google Scholar]
- Yang, B.; Tian, Y.; Wang, J.; Hu, X.; An, S. How to improve urban transportation planning in big data era? A practice in the study of traffic analysis zone delineation. Transp. Policy 2022, 127, 1–14. [Google Scholar] [CrossRef]
- Rahman, M.S.; Abdel-Aty, M.; Hasan, S.; Cai, Q. Applying machine learning approaches to analyze the vulnerable road-users’ crashes at statewide traffic analysis zones. J. Saf. Res. 2019, 70, 275–288. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Zhou, Q.; Yang, J.; You, S.; Song, Y.; Xue, M. Macro-level traffic safety analysis in Shanghai, China. Accid. Anal. Prev. 2019, 125, 249–256. [Google Scholar] [CrossRef]
- Sahu, P.K.; Aitichya Chandra, A.P.; Majumdar, B.B. Designing freight traffic analysis zones for metropolitan areas: Identification of optimal scale for macro-level freight travel analysis. Transp. Plan. Technol. 2020, 43, 620–637. [Google Scholar] [CrossRef]
- Moghaddam, S.; Ameli, M.; Rao, K.R.; Tiwari, G. Delineation of Traffic Analysis Zone for Public Transportation OD Matrix Estimation Based on Socio-spatial Practices. In Proceedings of the 4th Symposium on Management of Future Motorway and Urban Traffic Systems 2022 (MFTS2022), Dresden, Germany, 30 November–2 December 2022; pp. 205–2016. [Google Scholar] [CrossRef]
- Zhao, H.; Zhou, Y. Traffic Analysis Zones: How Do We Move Forward? In Applying Census Data for Transportation; TRB: Washington, DC, USA, 2017; p. 67. [Google Scholar]
- Miller, E. Traffic Analysis Zone Definition: Issues & Guidance; Travel Modeling Group, Transport Research Institute, University of Toronto: Toronto, ON, Canada, 2021. [Google Scholar]
- Lian, J.; Li, Y.; Huang, S.L.; Zhang, L. Mining mobility patterns with trip-based traffic analysis zones: A deep feature embedding approach. In Proceedings of the 2019 IEEE Intelligent Transportation Systems Conference (ITSC), Auckland, New Zealand, 27–30 October 2019; pp. 1650–1657. [Google Scholar]
- Castiglione, M.; Nigro, M.; Sacco, N. Multi-source Data-driven Procedure for Traffic Analysis Zones Definition. In Proceedings of the 2023 8th International Conference on Models and Technologies for Intelligent Transportation Systems (MT-ITS), Nice, France, 14–16 June 2023; pp. 1–6. [Google Scholar]
- Zhang, X.; Zhang, N. Dynamic OD extraction method of motor vehicles in traffic zones based on LPR and POI data. Integr. Transp. 2023, 45, 96–101. [Google Scholar]
- Gao, Y.; Liao, Y. Urban Tourism Traffic Analysis Zone Division Based on Floating Car Data. Promet-Traffic Transp. 2023, 35, 395–406. [Google Scholar] [CrossRef]
- Wang, X.Q.; Zhao, C.F.; Yin, C.Y.; Dong, C.J. Research on car ownership behavior considering the correlation of traffic zones. Transp. Syst. Eng. Inf. 2019, 19, 28–32+71. [Google Scholar] [CrossRef]
- Wu, D.; Ma, L.; Yan, X. Applying and Evaluating Data-Driven Fine Grid Partitioning Methods for Traffic Analysis Zones. J. Urban Plan. Dev. 2024, 150, 04024004. [Google Scholar] [CrossRef]
- Obelheiro, M.R.; da Silva, A.R.; Nodari, C.T.; Cybis, H.B.B.; Lindau, L.A. A new zone system to analyze the spatial relationships between the built environment and traffic safety. J. Transp. Geogr. 2020, 84, 102699. [Google Scholar] [CrossRef]
- Yao, H.; Chen, D. Comparison of apportionment methods for assigning trip data to rezoned traffic analysis zones: A case study of Toronto, Canada. Can. Geogr. Géographe Can. 2021, 65, 321–332. [Google Scholar] [CrossRef]
- Song, L.J.; Zhu, J.Z.; Liu, X.J.; Chen, J.; Xian, K. Optimization Method of Traffic Analysis Zones Division in Public Transit Corridor. J. Transp. Syst. Eng. Inf. Technol. 2020, 20, 34. [Google Scholar]
- Wang, J.; Gao, J.J. Urban traffic zone division based on DBSCAN algorithm. Smart City 2023, 9, 80–82. [Google Scholar] [CrossRef]
- Beijing Transportation Development & Research Center. The Fifth Comprehensive Traffic Survey Report of Beijing; Beijing Transportation Development & Research Center: Beijing, China, 2016. [Google Scholar]
- Yang, B.Y. Research on Traffic Zone Division Method Based on Multi-Source Data. Master’s Thesis, Harbin Polytechnic Institute, Harbin, China, 2020. [Google Scholar]
- Zhou, X.; Sun, C.; Niu, X.; Shi, C. The modifiable areal unit problem in the relationship between jobs–housing balance and commuting distance through big and traditional data. Travel Behav. Soc. 2022, 26, 270–278. [Google Scholar] [CrossRef]
- Amoh-Gyimah, R.; Saberi, M.; Sarvi, M. The effect of variations in spatial units on unobserved heterogeneity in macroscopic crash models. Anal. Methods Accid. Res. 2017, 13, 28–51. [Google Scholar] [CrossRef]
- Yue, Z.H. Optimization of Transfer Station Between Urban Rail Transit and Conventional Bus Based on Credit Card Data. Master’s Thesis, Beijing Jiaotong University, Beijing, China, 2017. [Google Scholar]
- Hwang, C.L.; Yoon, K. Multiple Attribute Decision Making: Methods and Applications—A State-of-the-Art Survey; Lecture Notes in Economics and Mathematical Systems; CRC Press: Boca Raton, FL, USA, 1981. [Google Scholar]


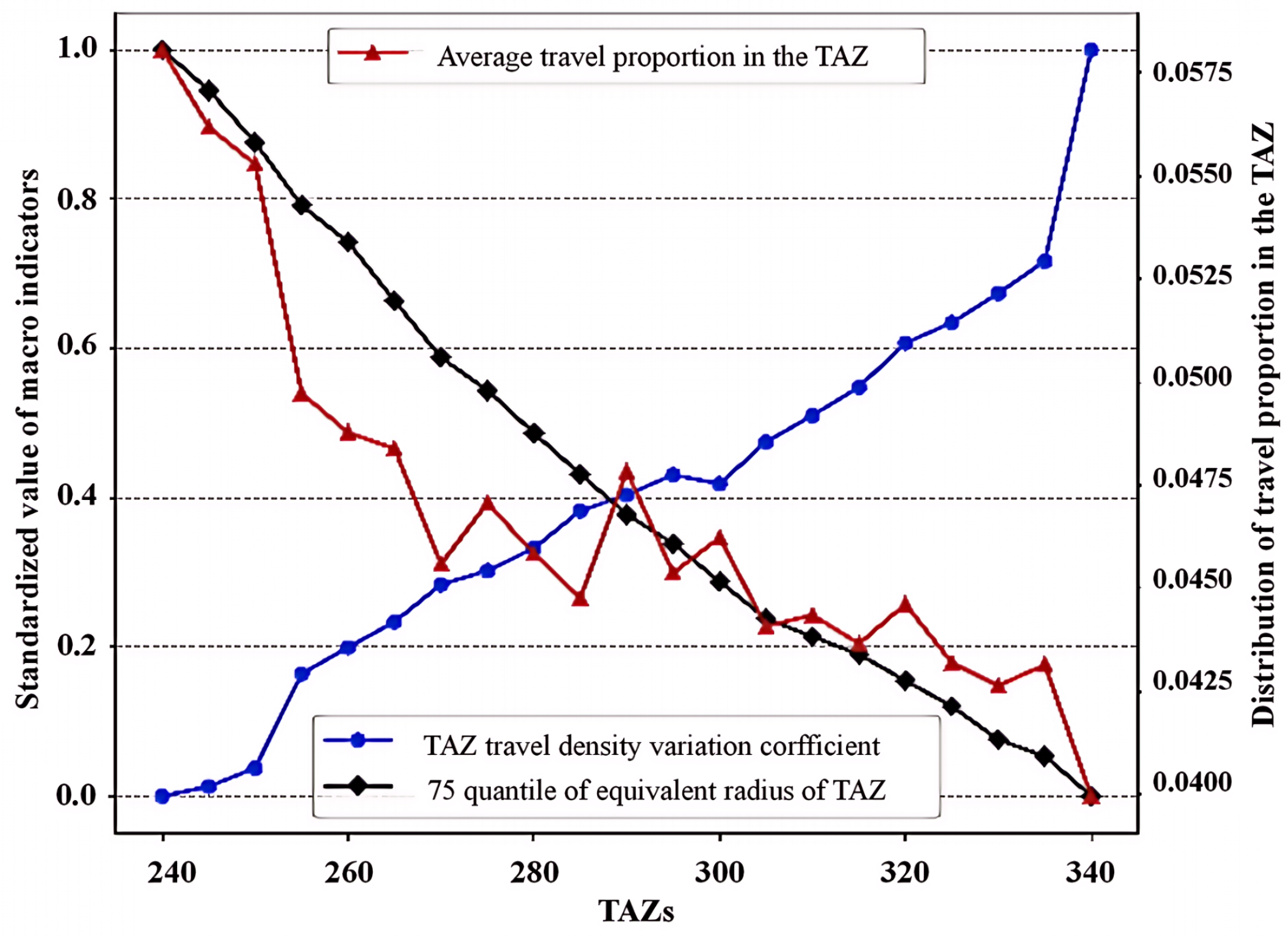
| Number of TAZ Division Schemes | Travel Density Variation Coefficient | Average Area | Average Travel Proportion in the TAZ |
|---|---|---|---|
| 240 | 0.0380 | 0.0552 | 0.0590 |
| 245 | 0.0381 | 0.0545 | 0.0571 |
| 250 | 0.0385 | 0.0535 | 0.0562 |
| 255 | 0.0432 | 0.0524 | 0.0506 |
| 260 | 0.0441 | 0.0517 | 0.0496 |
| 265 | 0.0446 | 0.0507 | 0.0492 |
| 270 | 0.0458 | 0.0497 | 0.0464 |
| 275 | 0.0460 | 0.0491 | 0.0479 |
| 280 | 0.0465 | 0.0483 | 0.0466 |
| 285 | 0.0477 | 0.0476 | 0.0438 |
| 290 | 0.0478 | 0.0469 | 0.0487 |
| 295 | 0.0483 | 0.0463 | 0.0462 |
| 300 | 0.0472 | 0.0457 | 0.0470 |
| 305 | 0.0486 | 0.0450 | 0.0448 |
| 310 | 0.0495 | 0.0447 | 0.0451 |
| 315 | 0.0505 | 0.0444 | 0.0444 |
| 320 | 0.0521 | 0.0439 | 0.0454 |
| 325 | 0.0526 | 0.0434 | 0.0439 |
| 330 | 0.0532 | 0.0428 | 0.0434 |
| 335 | 0.0544 | 0.0425 | 0.0439 |
| 340 | 0.0632 | 0.0418 | 0.0407 |
| Number of TAZ Division Schemes | Closeness | Number of TAZ Division Schemes | Closeness |
|---|---|---|---|
| 285 | 0.6624 | 260 | 0.5945 |
| 305 | 0.6598 | 325 | 0.5938 |
| 300 | 0.6535 | 330 | 0.5907 |
| 280 | 0.6420 | 255 | 0.5975 |
| 270 | 0.6409 | 320 | 0.5819 |
| 310 | 0.6369 | 335 | 0.5649 |
| 295 | 0.6327 | 250 | 0.5607 |
| 315 | 0.6251 | 245 | 0.5477 |
| 275 | 0.6222 | 240 | 0.5252 |
| 265 | 0.6053 | 340 | 0.4748 |
| 290 | 0.5989 | - | - |
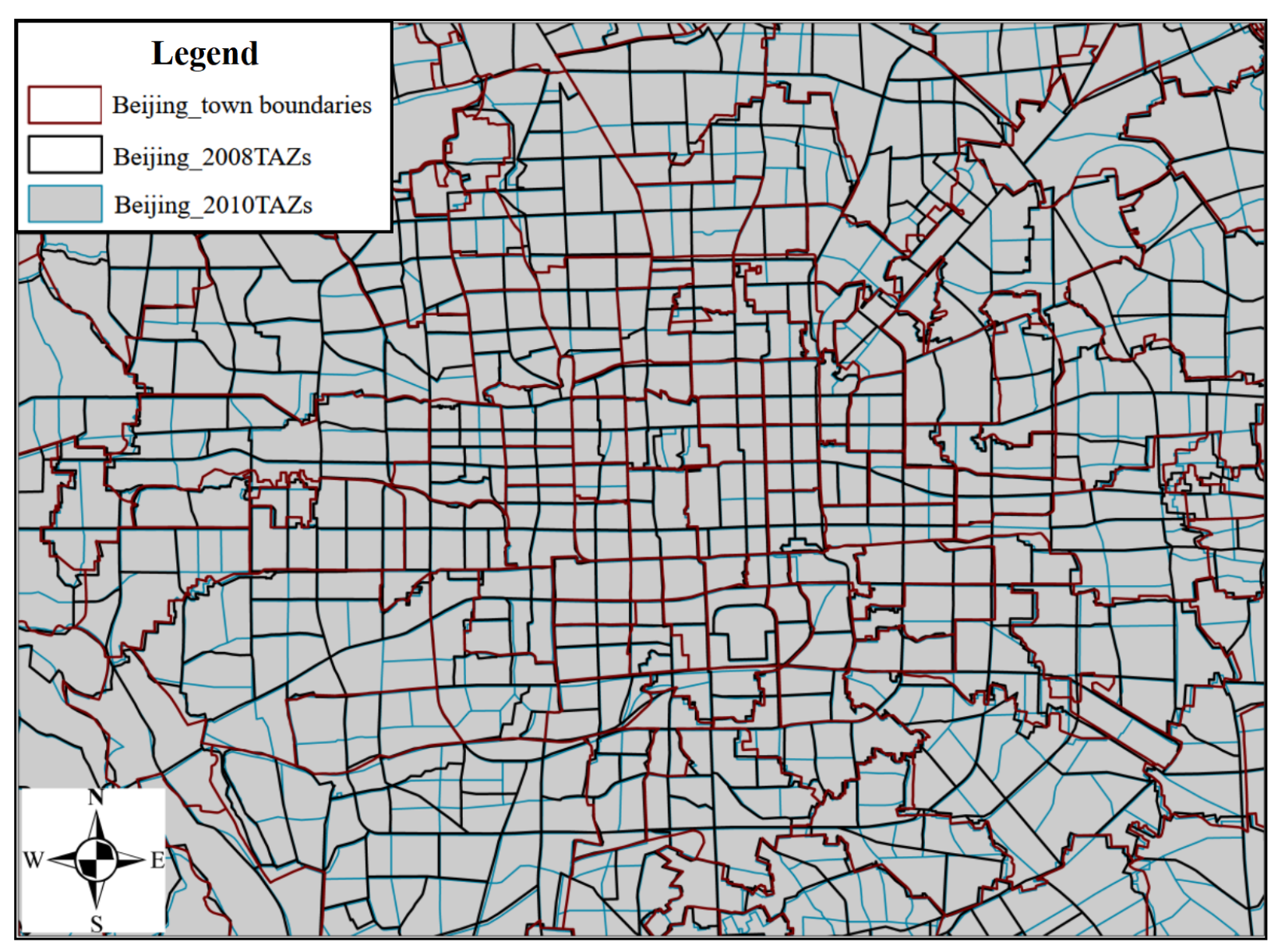
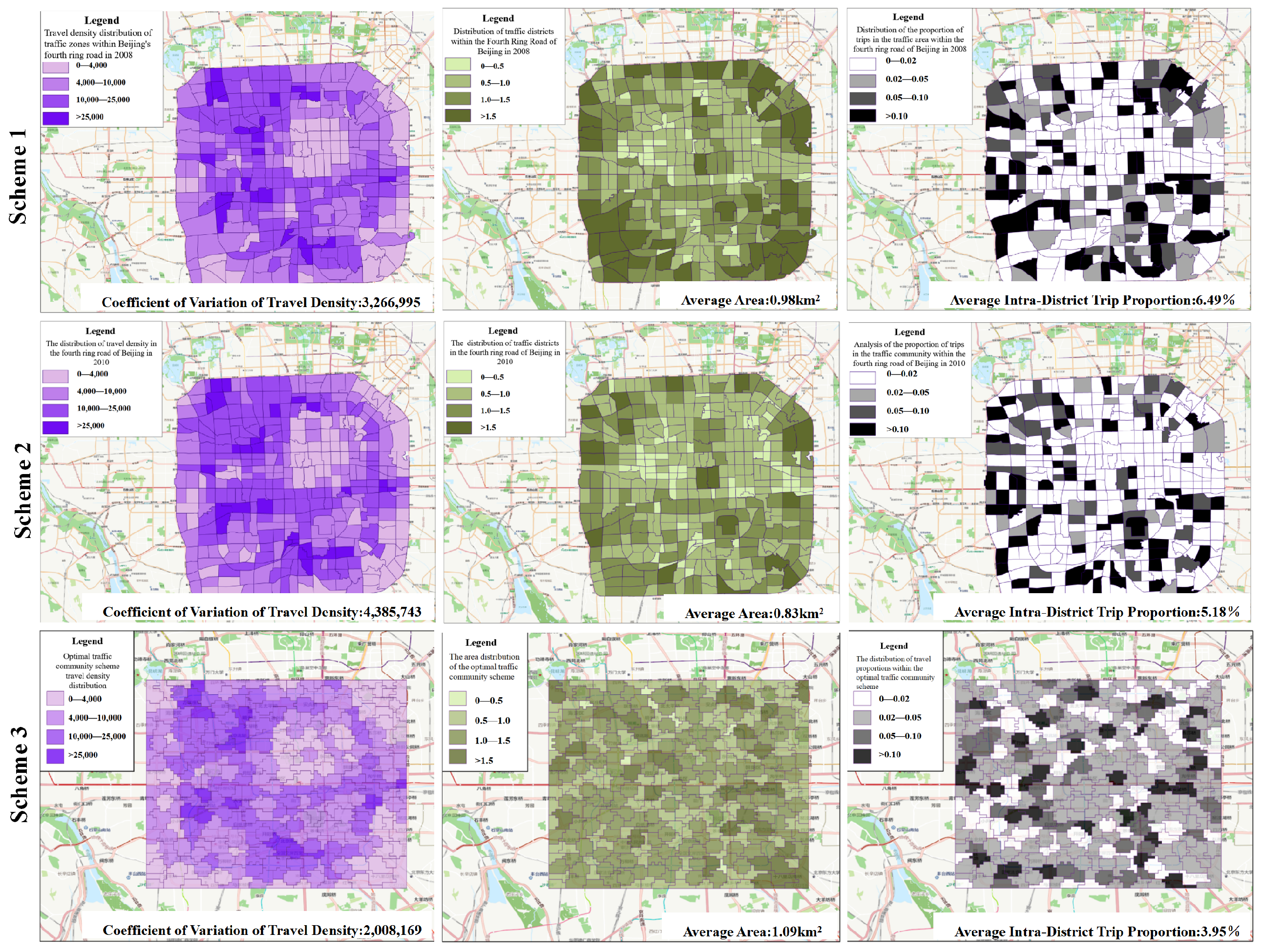
| Indicator | Optimal TAZ Division Scheme (285 TAZs) | TAZ Division Scheme in 2008 (304 TAZs) | TAZ Division Scheme in 2010 (364 TAZs) |
|---|---|---|---|
| Travel density variation coefficient | 2,008,169 | 3,266,995 | 4,385,743 |
| Average travel proportion in the TAZ | 3.95% | 6.49% | 5.18% |
| Average area | 1.09 km2 | 0.98 km2 | 0.83 km2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Du, K.; Song, J.; Chen, D.; Li, M.; Zhu, Y. A Novel Traffic Analysis Zone Division Methodology Based on Individual Travel Data. Appl. Sci. 2025, 15, 156. https://doi.org/10.3390/app15010156
Du K, Song J, Chen D, Li M, Zhu Y. A Novel Traffic Analysis Zone Division Methodology Based on Individual Travel Data. Applied Sciences. 2025; 15(1):156. https://doi.org/10.3390/app15010156
Chicago/Turabian StyleDu, Kai, Jingni Song, Dan Chen, Ming Li, and Yadi Zhu. 2025. "A Novel Traffic Analysis Zone Division Methodology Based on Individual Travel Data" Applied Sciences 15, no. 1: 156. https://doi.org/10.3390/app15010156
APA StyleDu, K., Song, J., Chen, D., Li, M., & Zhu, Y. (2025). A Novel Traffic Analysis Zone Division Methodology Based on Individual Travel Data. Applied Sciences, 15(1), 156. https://doi.org/10.3390/app15010156






