Research Progress and Engineering Applications of Viscous Fluid Mechanics
Abstract
:1. Introduction
2. Advances in the Study of the State of Motion of Viscous Fluids
2.1. Experimentation and Research
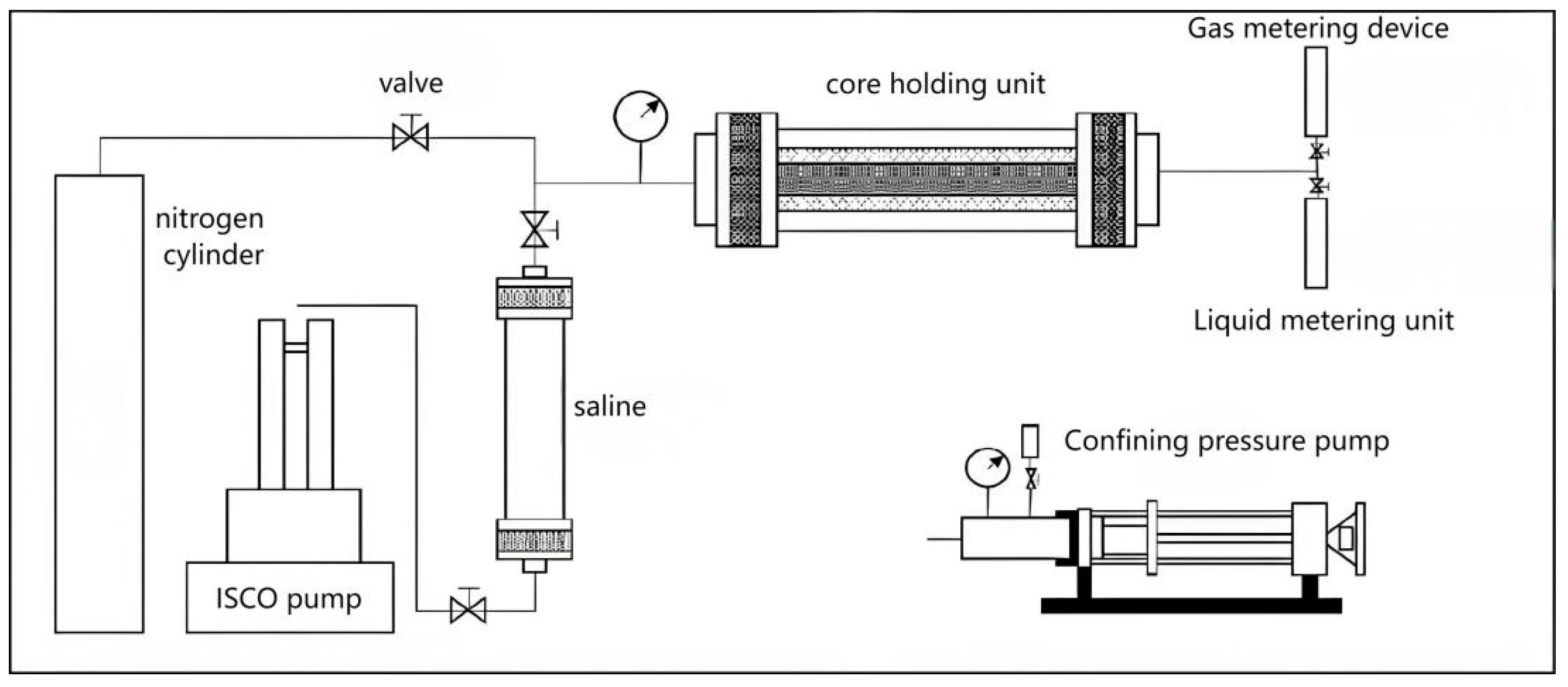
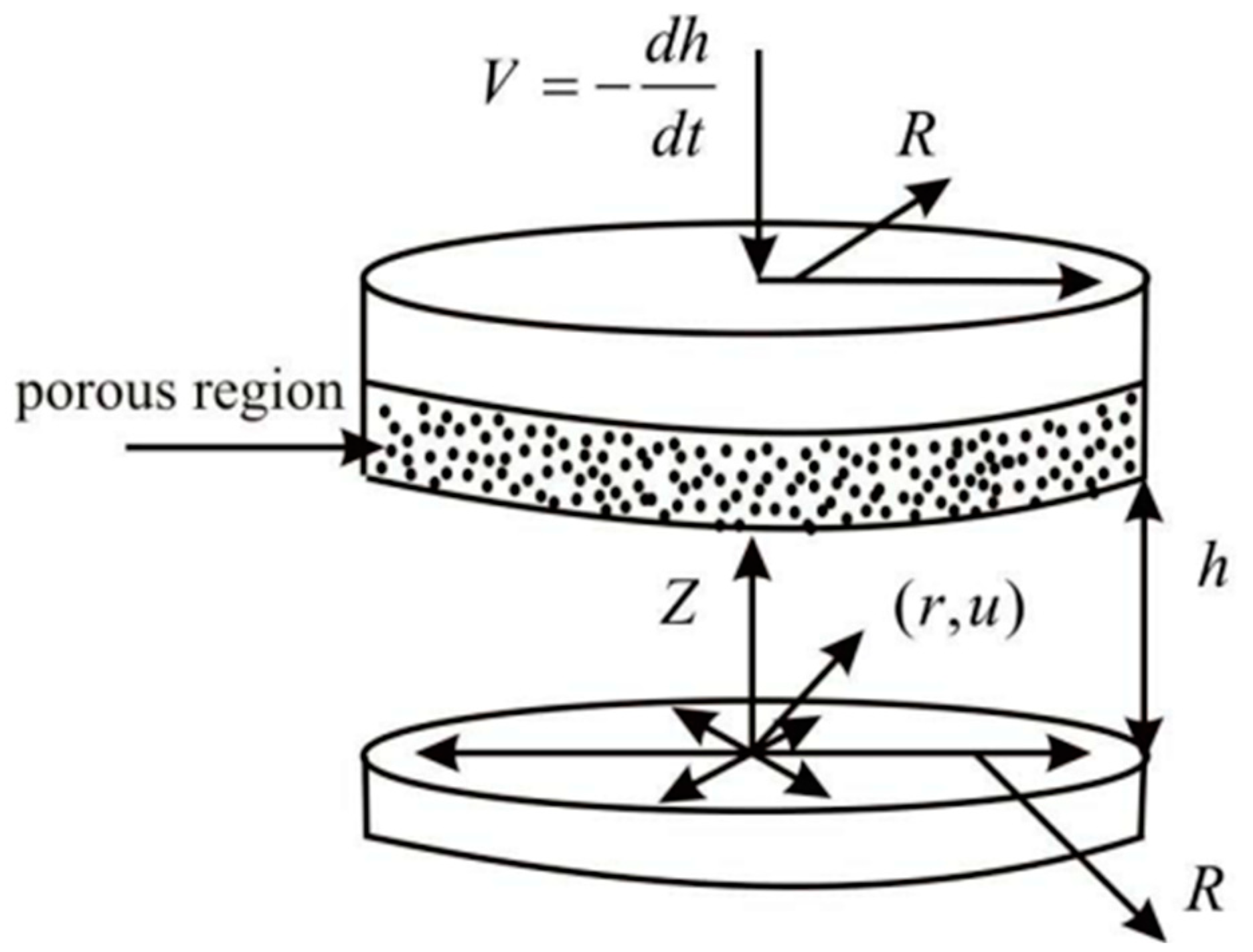
2.1.1. Experiments and Studies on the Permeability of Media to Viscous Fluids
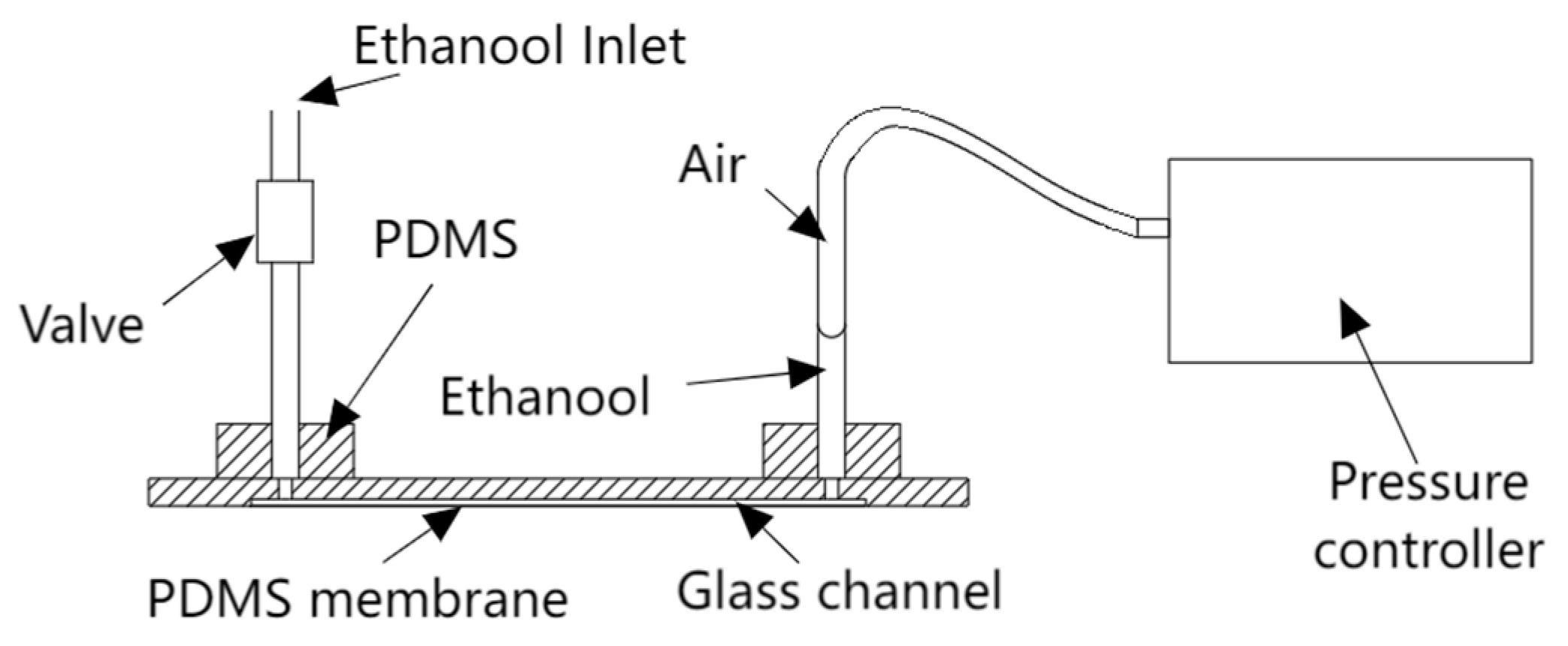
2.1.2. Experiments and Studies on Droplet Impacts in Viscous Fluids
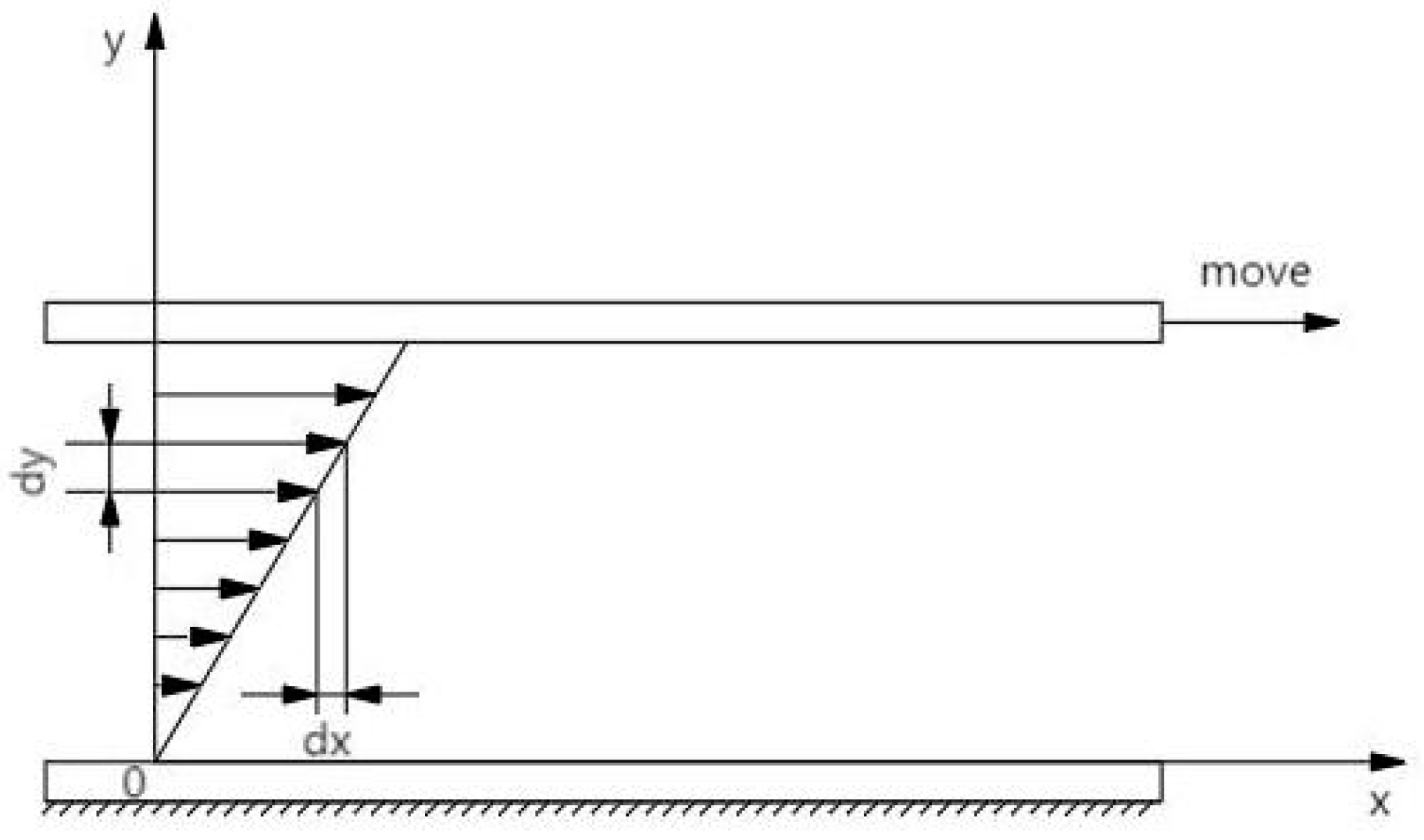
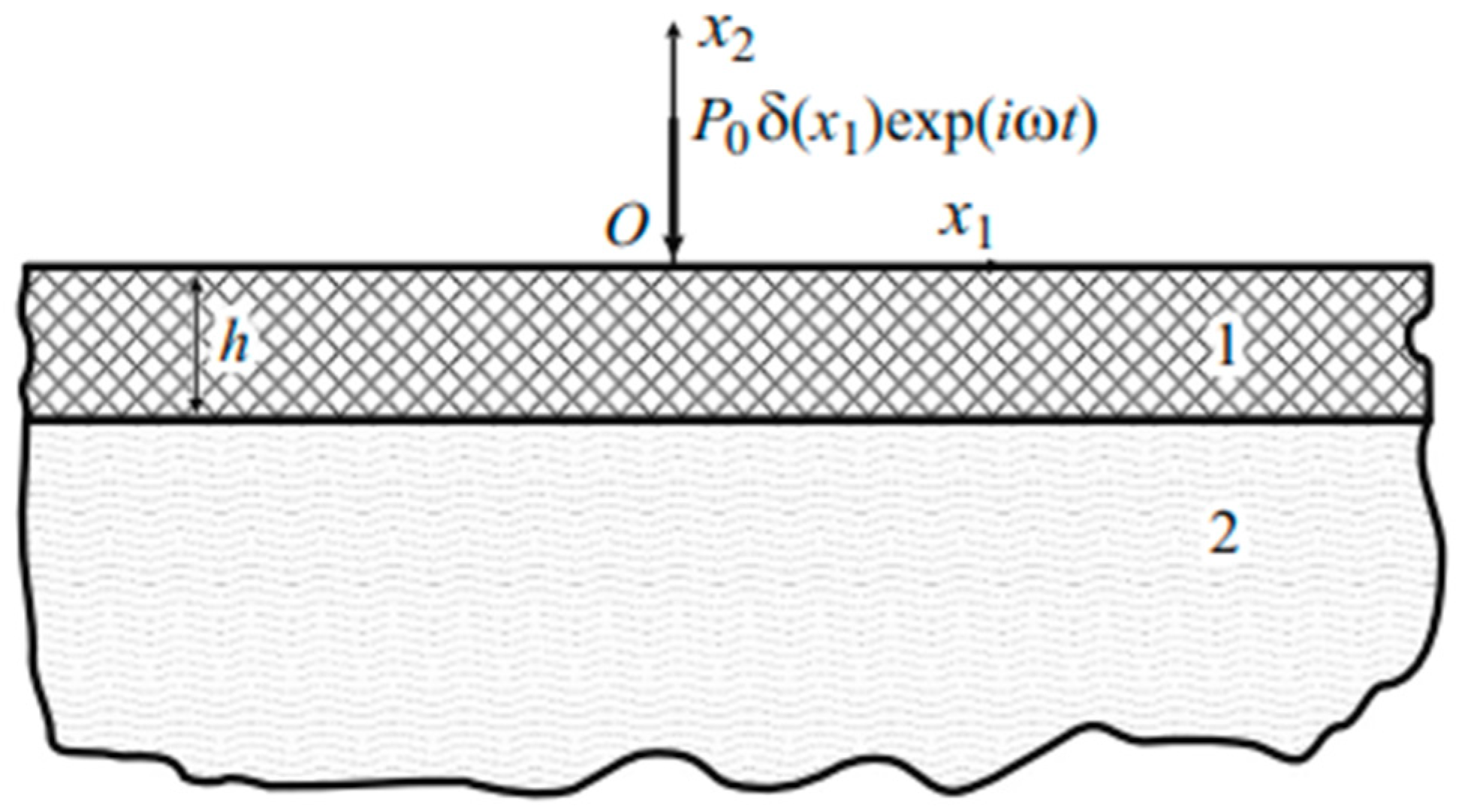
2.1.3. Experiments and Studies on the Flat-Plate Gap Method
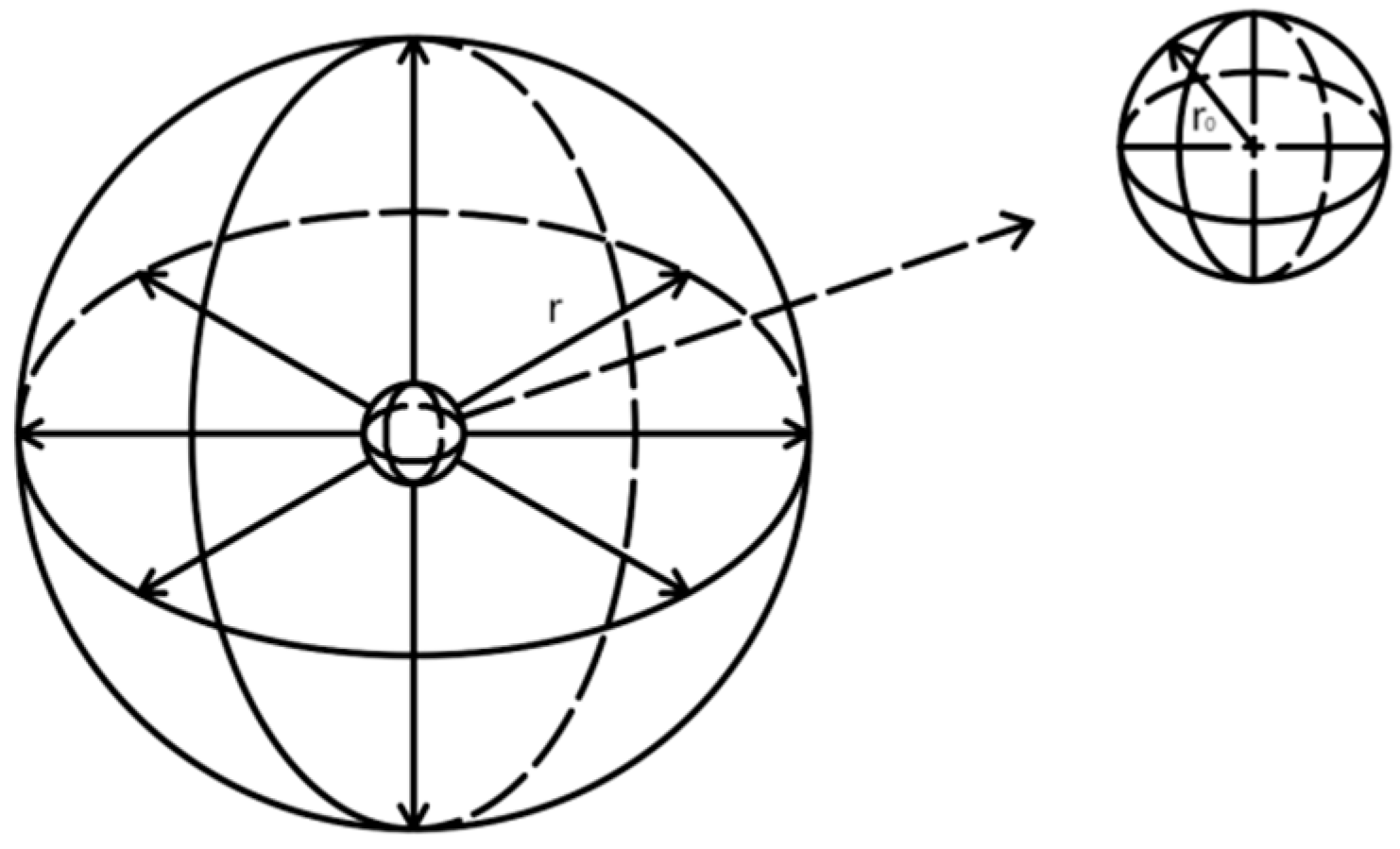
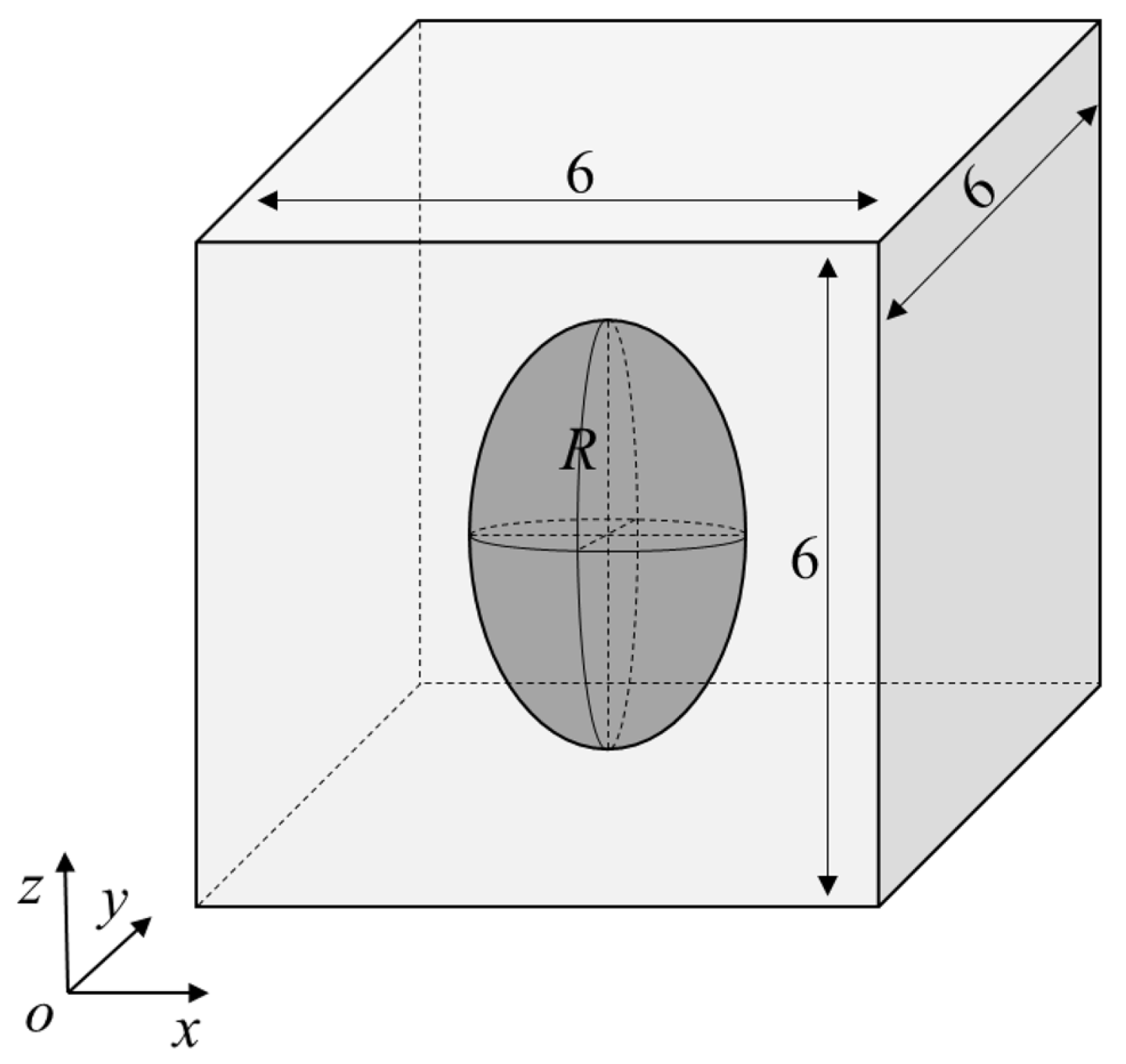
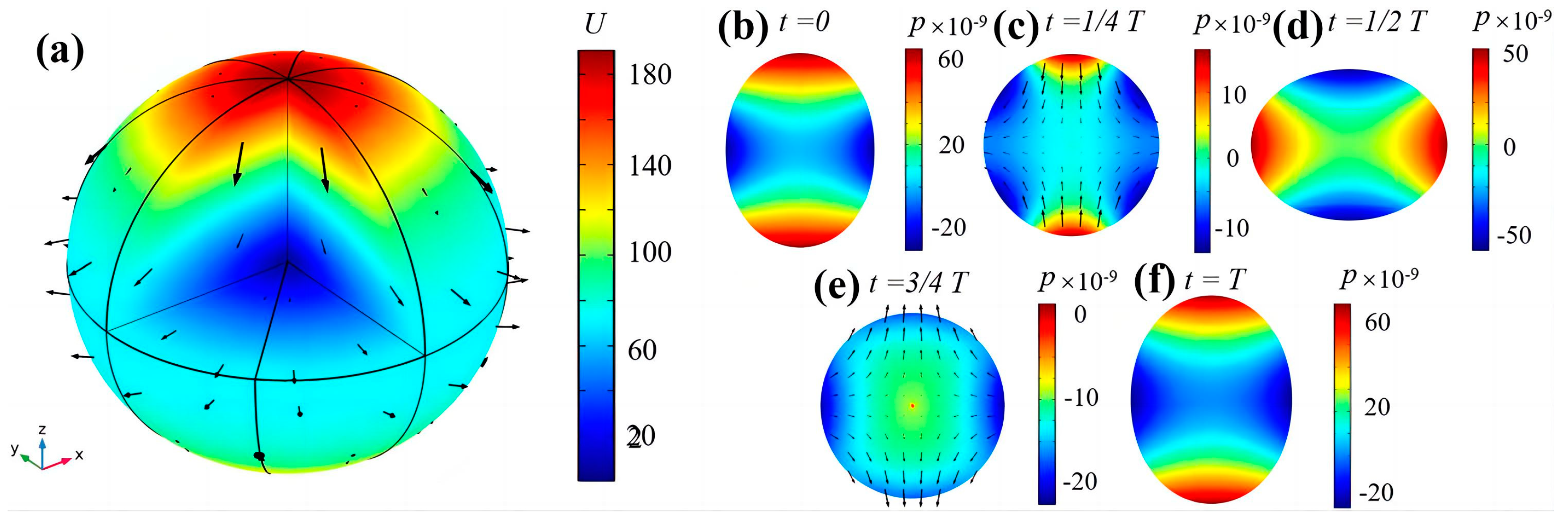
2.1.4. Experiments and Studies on the Oscillation Method
2.2. An Investigation of the Simulation of the State of Motion of Viscous Fluids by Modern Computer Technology
2.2.1. Computerized Algorithmic Solution of Viscous Fluids
2.2.2. Simulation of Viscous Fluid Motion by Computer Techniques
3. Application Areas of Engineering
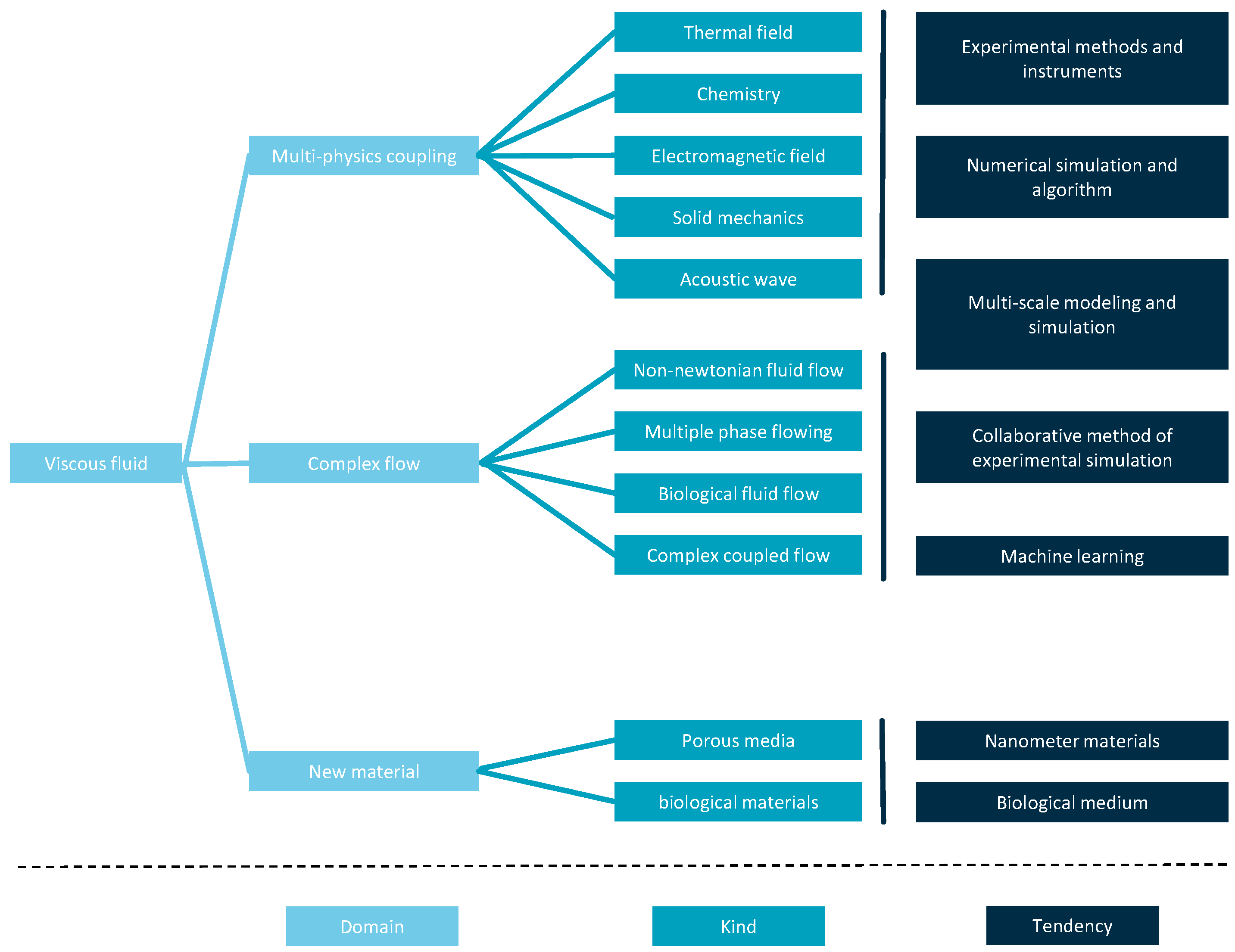
4. Future Trends and Directions
- (1)
- Future research in viscous fluid mechanics will pay more attention to the coupling of multiple physical fields. The physical fields and their effects that need attention include the following: (1) Thermal field: Temperature changes can significantly affect the viscosity of the fluid; usually, a temperature increase will lead to a decrease in the viscosity of the fluid, while a decrease in temperature will increase the viscosity. This coupling is particularly important in high-temperature lubrication and polymer fluid handling. (2) Chemical reactions: Chemical reactions can change the composition of a fluid and thus affect its viscosity. For example, cross-linking reactions in polymer fluids can lead to nonlinear changes in viscosity, which is critical for the processing and control of viscoelastic materials. (3) Electromagnetic fields: Magnetic fluids can produce morphological changes and controlled flow behavior under an applied magnetic field, such as electromagnetically driven fluids in liquid metals. This coupling can have applications in liquid metal metallurgy, aerospace technology, and biomedical sensors. (4) Solid mechanics: in fluids in contact with solid walls, the morphology and roughness of the solid surface can significantly affect the friction and adhesion behavior of the fluid.(5)Acoustic effects: Acoustic fields can affect the viscoelasticity and flow properties of fluids, for example, in the ultrasonic acoustic field for microfluidic manipulation and in biomedical imaging. This coupling helps to control the mixing and stirring process of microfluidics; not only limited to the above physical fields, or even using two or more kinds of physical fields coupled together, numerical simulation or complex experimental methods can be used in studies and analysis in order to add a comprehensive, in-depth understanding of complex engineering phenomena and natural phenomena. This multiphysical field coupling research method is expected to provide new ideas and solutions for innovations in the fields of energy conversion, environmental protection, and biomedicine. I believe that the optimization trends in this area are as follows: (1) for complex systems and phenomena, such as biofluids, multiphase flows, and non-Newtonian fluids, multiscale modeling and simulation methods should be improved to capture the details in different spatial and temporal scales; (2) for numerical simulation, new numerical simulation techniques and algorithms such as mixed-element methods, implicit-coupling methods, and adaptive mesh techniques should be improved to facilitate the numerical modeling and analysis of complex fluid systems;(3)experimental techniques, such as microfluidic experimental platforms and advanced imaging techniques, should be improved to further improve the precision of experimental device components and optimize real-time sensing techniques, which can more accurately validate theoretical models and numerical predictions.
- (2)
- One of the future research priorities will be the in-depth understanding and control of complex flow phenomena. Viscous fluid complex flow phenomena include the following: (1) non-Newtonian fluid flow: non-Newtonian fluid flow is not only affected by the velocity gradient but may also be affected by the non-uniformity and time-dependence of the flow field, resulting in complex flow behaviors, such as shear thinning and shear thickening phenomena; (2) multiphase flow: this refers to the simultaneous presence of two or more substances (e.g., gases, liquids, or solid particles) of the flow system, with a focus on gas–liquid, liquid–liquid, solid–liquid, and other combinations of flow, such as foam flow, bubble flow, the movement of particles in suspension, etc.; (3) biological fluid flow: the flow mechanism of blood flow in living organisms and fluid exchange across the walls between cells is very complex, and in the future, it may be possible to simulate blood flow, intercellular fluid exchange, and other biophysical fluid dynamics phenomena, which will aid in the diagnosis of diseases, the research and development of new drugs, and bioengineering; and (4) complex coupled flow: complex coupled flow mainly refers to those flow phenomena that are not only affected by the flow characteristics of the fluid itself but are also affected by the interaction between the fluid and the solid, the fluid and the electric field or magnetic field, etc., for example, electromagnetic fluids (such as plasma), magnetic fluids (such as magnetorheological fluids), and complex fluid systems that interact with particles. I think there are several optimization trends in this area: (1) data-driven method: using machine learning and data mining techniques to process a large amount of experimental data and numerical simulation data, such as the bird flocking algorithm and the whale algorithm in machine learning, to discover the patterns and laws in the flow and optimize the parameters and boundary conditions of the numerical model to improve the accuracy and efficiency of the simulation results; (2) experimental simulation synergistic method: comparing and verifying the experimental data with the numerical simulation results and continuously improving the numerical model to enhance its applicability and realism in complex flow systems; In addition to this, we can also can deepen the research on microscale flow, boundary layer control, wake phenomena, etc. By deepening the understanding and control of these complex flow phenomena, we can provide strong support for the innovation and development of related fields.
- (3)
- The development of viscous fluid mechanics will also be closely related to the application of new materials. This area currently has significant trends in the following areas: (1) Porous and complex media: with the deepening of the study of fluid mechanics in porous media, new porous materials (such as 3D printed structures) and complex media (such as nanomaterials) could be developed, and these materials may exhibit nonlinear, non-Newtonian flow properties, requiring new numerical simulation and experimental techniques to understand their flow behavior, for example, the permeability of the material, the surface tension and viscosity of liquid nanomaterials, etc. (2) Biomaterials: The field of biofluid dynamics has an increasing demand for research on biomaterials (e.g., soft tissues, cell membranes, etc.), and the characteristics of these materials may lead to complex flow behaviors, which need to be combined with experimental and simulation methods to conduct an in-depth study. In this regard, I’m more optimistic about the potential of nanotechnology in the study of viscous fluids, and we need to actively explore how to utilize new technologies such as nanotechnology to change the viscosity and surface tension of fluids and develop new fluid control and regulation technologies to meet different engineering needs and challenges.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Romatschke, P. New developments in relativistic viscous hydrodynamics. Int. J. Mod. Phys. E 2010, 19, 1–53. [Google Scholar] [CrossRef]
- Phillips, T.N.; Roberts, G.W. Lattice Boltzmann models for non-Newtonian flows. IMA J. Appl. Math. 2011, 76, 790–816. [Google Scholar] [CrossRef]
- Aharonov, E.; Rothman, D.H. Non-Newtonian flow (through porous media): A lattice-Boltzmann method. Geophys. Res. Lett. 1993, 20, 679–682. [Google Scholar] [CrossRef]
- Hu, H.; Zhang, G.; Zhao, T. Overview of computational fluid dynamics and discrete element coupling methods. In Proceedings of the 5th China Symposium on Hydraulic and Hydropower Geotechnical Mechanics and Engineering, Yichang, China, 17–21 September 2014; p. 4. [Google Scholar]
- Liu, Y.-Z. Overview of dynamic research methods for liquid-filled rigid bodies. Mech. Pract. 2015, 37, 397–400. [Google Scholar]
- Silva, D.P.; Coelho, R.C.; Pagonabarraga, I.; Succi, S.; da Gama, M.M.T.; Araújo, N.A. Lattice Boltzmann simulation of deformable fluid-filled bodies: Progress and perspectives. Soft Matter 2024, 20, 2419–2441. [Google Scholar] [CrossRef] [PubMed]
- Coussot, P. Yield stress fluid flows: A review of experimental data. J. Non-Newton. Fluid Mech. 2014, 211, 31–49. [Google Scholar] [CrossRef]
- Tatsumi, T. Fluid Mechanics in the turn of the century. Fluid Dyn. Res. 1999, 24, 315–319. [Google Scholar] [CrossRef]
- Rozenman, G.G.; Ullinger, F.; Zimmermann, M.; Efremov, M.A.; Shemer, L.; Schleich, W.P.; Arie, A. Observation of a phase space horizon with surface gravity water waves. Commun. Phys. 2024, 7, 165. [Google Scholar] [CrossRef]
- Otaru, A. Review on processing and fluid transport in porous metals with a focus on bottleneck structures. Met. Mater. Int. 2020, 26, 510–525. [Google Scholar] [CrossRef]
- Crespí-Llorens, D.; Vicente, P.; Viedma, A. Generalized Reynolds number and viscosity definitions for non-Newtonian fluid flow in ducts of non-uniform cross-section. Exp. Therm. Fluid Sci. 2015, 64, 125–133. [Google Scholar] [CrossRef]
- Delplace, F.; Leuliet, J. Generalized Reynolds number for the flow of power law fluids in cylindrical ducts of arbitrary cross-section. Chem. Eng. J. Biochem. Eng. J. 1995, 56, 33–37. [Google Scholar] [CrossRef]
- Abell, M.; Ames, W. Symmetry reduction of Reynolds equation and applications to film lubrication. J. Appl. Mech. 1992, 59, 206–210. [Google Scholar] [CrossRef]
- Metzner, A.; Reed, J. Flow of non-newtonian fluids—Correlation of the laminar, transition, and turbulent-flow regions. Aiche J. 1955, 1, 434–440. [Google Scholar] [CrossRef]
- Chhabra, R.P.; Richardson, J.F. Non-Newtonian Flow and Applied Rheology: Engineering Applications; Butterworth-Heinemann: Oxford, UK, 2011. [Google Scholar]
- Garcia, A.; Vicente, P.G.; Viedma, A. Experimental study of heat transfer enhancement with wire coil inserts in laminar-transition-turbulent regimes at different Prandtl numbers. Int. J. Heat Mass Transf. 2005, 48, 4640–4651. [Google Scholar] [CrossRef]
- Ni, H.; Zhang, L.; Xiong, X.; Mao, Z.; Wang, J. Supercritical fluids at subduction zones: Evidence, formation condition, and physicochemical properties. Earth-Sci. Rev. 2017, 167, 62–71. [Google Scholar] [CrossRef]
- Adam, J.; Locmelis, M.; Afonso, J.C.; Rushmer, T.; Fiorentini, M.L. The capacity of hydrous fluids to transport and fractionate incompatible elements and metals within the Earth’s mantle. Geochem. Geophys. Geosystems 2014, 15, 2241–2253. [Google Scholar] [CrossRef]
- Bai, J.; Wang, T.; Zou, L.; Li, P. Large Eddy Simulation of compressible multi-media viscous Fluid and Turbulence. Explos. Shock. Waves 2010, 30, 262–268. [Google Scholar]
- Khan, Z.A.; Ishaq, M.; Ghani, U.; Ullah, R.; Iqbal, S. Analysis of magnetohydrodynamics flow of a generalized viscous fluid through a porous medium with Prabhakar-like fractional model with generalized thermal transport. Adv. Mech. Eng. 2022, 14, 16878132221132949. [Google Scholar] [CrossRef]
- Elnaqeeb, T.; Shah, N.A.; Mirza, I.A. Natural convection flows of carbon nanotubes nanofluids with Prabhakar-like thermal transport. Math. Methods Appl. Sci. 2020, early view. [CrossRef]
- Hemalatha, R.; Kameswaran, P.K.; Murthy, P. Effect of nanoparticle shape on the mixed convective transport over a vertical cylinder in a non-Darcy porous medium. Int. Commun. Heat Mass Transf. 2022, 133, 105962. [Google Scholar] [CrossRef]
- Makris, N.; Dargush, G.; Constantinou, M. Dynamic analysis of generalized viscoelastic fluids. J. Eng. Mech. 1993, 119, 1663–1679. [Google Scholar] [CrossRef]
- Awasthi, M.; Tamsir, M. Viscous Corrections for the Viscous Potential Flow Analysis of Magneto-Hydrodynamic Kelvin-Helmholtz Instability through Porous Media. J. Porous Media 2013, 16, 663–676. [Google Scholar] [CrossRef]
- Craster, R.V.; Matar, O.K. Dynamics and stability of thin liquid films. Rev. Mod. Phys. 2009, 81, 1131–1198. [Google Scholar] [CrossRef]
- Pérez-Ràfols, F.; Wall, P.; Almqvist, A. On compressible and piezo-viscous flow in thin porous media. Proc. R. Soc. A Math. Phys. Eng. Sci. 2018, 474, 20170601. [Google Scholar] [CrossRef]
- Jegatheeswaran, S.; Ein-Mozaffari, F.; Wu, J. Laminar mixing of non-Newtonian fluids in static mixers: Process intensification perspective. Rev. Chem. Eng. 2020, 36, 423–436. [Google Scholar] [CrossRef]
- Song, R.; Stone, H.A.; Jensen, K.H.; Lee, J. Pressure-driven flow across a hyperelastic porous membrane. J. Fluid Mech. 2019, 871, 742–754. [Google Scholar] [CrossRef]
- Stafie, N.; Stamatialis, D.; Wessling, M. Effect of PDMS cross-linking degree on the permeation performance of PAN/PDMS composite nanofiltration membranes. Sep. Purif. Technol. 2005, 45, 220–231. [Google Scholar] [CrossRef]
- Delli, M.L.; Grozic, J.L. Experimental determination of permeability of porous media in the presence of gas hydrates. J. Pet. Sci. Eng. 2014, 120, 1–9. [Google Scholar] [CrossRef]
- Wang, S.; Wu, T.; Xia, K. Fractal permeability model of spherical porous media. J. Cent. China Norm. Univ. (Nat. Sci. Ed.) 2020, 54, 45–49. [Google Scholar] [CrossRef]
- Wang, M.; Li, X.; Yang, X.; Liu, H.; Zhang, Z.; Xu, D.; Liu, Z.-J. Experimental study on the influence of different fluids and clay minerals on rock permeability. Prog. Geophys. 2022, 37, 275–283. [Google Scholar]
- Sun, W.; Xiong, F.; Cao, H.; Yang, Z.; Lu, M. Complex fluid model and its applicability analysis in tight reservoir. Geophys. Prospect. Pet. 2021, 60, 136–148. [Google Scholar]
- Ding, L.; Ma, J.; Wang, J. Experimental study on permeability characteristics of sintered porous media. Q. J. Mech. 2012, 33, 375–381. [Google Scholar] [CrossRef]
- Kowal, K.N. Viscous banding instabilities: Non-porous viscous fingering. J. Fluid Mech. 2021, 926, A4. [Google Scholar] [CrossRef]
- Graeber, G.; Martin Kieliger, O.B.; Schutzius, T.M.; Poulikakos, D. 3D-printed surface architecture enhancing superhydrophobicity and viscous droplet repellency. ACS Appl. Mater. Interfaces 2018, 10, 43275–43281. [Google Scholar] [CrossRef]
- Bartolo, D.; Josserand, C.; Bonn, D. Retraction dynamics of aqueous drops upon impact on non-wetting surfaces. J. Fluid Mech. 2005, 545, 329–338. [Google Scholar] [CrossRef]
- Bird, J.C.; Dhiman, R.; Kwon, H.-M.; Varanasi, K.K. Reducing the contact time of a bouncing drop. Nature 2013, 503, 385–388. [Google Scholar] [CrossRef]
- Hao, C.; Zhou, Y.; Zhou, X.; Che, L.; Chu, B.; Wang, Z. Dynamic control of droplet jumping by tailoring nanoparticle concentrations. Appl. Phys. Lett. 2016, 109, 021601. [Google Scholar] [CrossRef]
- Bartolo, D.; Boudaoud, A.; Narcy, G.; Bonn, D. Dynamics of non-Newtonian droplets. Phys. Rev. Lett. 2007, 99, 174502. [Google Scholar] [CrossRef]
- Aksoy, Y.T.; Eneren, P.; Koos, E.; Vetrano, M.R. Spreading of a droplet impacting on a smooth flat surface: How liquid viscosity influences the maximum spreading time and spreading ratio. Phys. Fluids 2022, 34, 042106. [Google Scholar] [CrossRef]
- Eckert, M. Ludwig Prandtl and the growth of fluid mechanics in Germany. Comptes Rendus Mécanique 2017, 345, 467–476. [Google Scholar] [CrossRef]
- Bartram, E.; Goldsmith, H.; Mason, S. Particle motions in non-newtonian media: III. Furth. Obs. Elasticoviscous Fluids. Rheol. Acta 1975, 14, 776–782. [Google Scholar] [CrossRef]
- Patil, A. Laminar flow heat transfer and pressure drop characteristics of power-law fluids inside tubes with varying width twisted tape inserts. J. Heat Transf. 2000, 122, 143–149. [Google Scholar] [CrossRef]
- Carillo, S.; Jordan, P.M. On the structure of isothermal acoustic shocks under classical and artificial viscosity laws: Selected case studies. Meccanica 2023, 58, 1121–1139. [Google Scholar] [CrossRef]
- Finotello, G.; De, S.; Vrouwenvelder, J.C.; Padding, J.T.; Buist, K.A.; Jongsma, A.; Innings, F.; Kuipers, J. Experimental investigation of non-Newtonian droplet collisions: The role of extensional viscosity. Exp. Fluids 2018, 59, 113. [Google Scholar] [CrossRef]
- Lin, M.; Vo, Q.; Mitra, S.; Tran, T. Viscous droplet impingement on soft substrates. Soft Matter 2022, 18, 5474–5482. [Google Scholar] [CrossRef]
- Yang, L.; Liu, X.; Wang, J.; Zhang, P. An Experimental Study on Complete Droplet Rebound from Soft Surfaces: Critical Weber Numbers, Maximum Spreading, and Contact Time. Langmuir 2024, 40, 2165–2173. [Google Scholar] [CrossRef] [PubMed]
- Chang, T.-B.; Chen, R.-H. Experimental investigation into deposition/splashing behavior of droplets impacting vibrating surface. Adv. Mech. Eng. 2017, 9, 1687814017730004. [Google Scholar] [CrossRef]
- Liu, H.; Wang, J.; Shen, X.; Zheng, N.; Wang, J. Experiment and simulation of viscous fluid droplet impacting singular jet on superhydrophobic wall. Chin. Surf. Eng. 2023, 36, 124–134. [Google Scholar]
- Li, J.; Zhao, C.; Wang, C. Experimental study on the dynamics of droplet impacting on solid surface. Microfluid. Nanofluidics 2023, 27, 69. [Google Scholar] [CrossRef]
- Qian, W.W. Experimental Research and Numerical Simulation of Viscous Liquid and Dense Particle Jet Collision Process. Master’s Thesis, East China University of Science and Technology, Shanghai, China, 2016. [Google Scholar]
- Xing, L.; Zhang, J.; Jiang, M.; Zhao, L.; Guan, S. Experimental study on collision coalescence process of unequal large droplets on different wettability walls. Chem. Eng. 2024, 52, 43–48. [Google Scholar]
- Zong, S.; Xu, L.; Hao, J. Experimental study on droplet impact of viscous Newtonian fluid on dry or pre-wet mesh. Chin. J. Mech. Mech. 2024, 56, 101–111. [Google Scholar]
- Xing, L.; Li, J.; Jiang, M.; Zhao, L. Experimental study of droplet collision with different wettability inclined plate. J. Eng. Thermophys. 2024, 45, 2001–2011. [Google Scholar]
- Jung, S.; Hoath, S.D.; Hutchings, I.M. The role of viscoelasticity in drop impact and spreading for inkjet printing of polymer solution on a wettable surface. Microfluid. Nanofluidics 2013, 14, 163–169. [Google Scholar] [CrossRef]
- Jung, S.; Hoath, S.D.; Martin, G.D.; Hutchings, I.M. Experimental study of atomization patterns produced by the oblique collision of two viscoelastic liquid jets. J. Non-Newton. Fluid Mech. 2011, 166, 297–306. [Google Scholar] [CrossRef]
- Fürst, J.; Straka, P.; Příhoda, J.; Šimurda, D. Comparison of several models of the laminar/turbulent transition. EPJ Web Conf. 2013, 45, 01032. [Google Scholar] [CrossRef]
- Langtry, R.B.; Menter, F.R. Correlation-based transition modeling for unstructured parallelized computational fluid dynamics codes. AIAA J. 2009, 47, 2894–2906. [Google Scholar] [CrossRef]
- Mehendale, S.; Jacobi, A.; Shah, R. Fluid flow and heat transfer at micro-and meso-scales with application to heat exchanger design. Appl. Mech. Rev. 2000, 53, 175–193. [Google Scholar] [CrossRef]
- Hou, G.; Wang, J.; Layton, A. Numerical methods for fluid-structure interaction—A review. Commun. Comput. Phys. 2012, 12, 337–377. [Google Scholar] [CrossRef]
- Dowell, E.H.; Hall, K.C. Modeling of fluid-structure interaction. Annu. Rev. Fluid Mech. 2001, 33, 445–490. [Google Scholar] [CrossRef]
- Pihler-Puzović, D.; Illien, P.; Heil, M.; Juel, A. Suppression of Complex Fingerlike Patterns at the Interface between Air and a Viscous Fluid by Elastic Membranes. Phys. Rev. Lett. 2012, 108, 074502. [Google Scholar] [CrossRef]
- Naduvinamani, N.; Hiremath, P.; Gurubasavaraj, G. Effect of surface roughness on the couple-stress squeeze film between a sphere and a flat plate. Tribol. Int. 2005, 38, 451–458. [Google Scholar] [CrossRef]
- Lopes Filho, M.C.; Nussenzveig Lopes, H.J.; Titi, E.S.; Zang, A. Approximation of 2D Euler equations by the second-grade fluid equations with Dirichlet boundary conditions. J. Math. Fluid Mech. 2015, 17, 327–340. [Google Scholar] [CrossRef]
- Chae, D.; Constantin, P.; Wu, J. Inviscid models generalizing the two-dimensional Euler and the surface quasi-geostrophic equations. Arch. Ration. Mech. Anal. 2011, 202, 35–62. [Google Scholar] [CrossRef]
- Prausová, H.; Bublík, O.; Vimmr, J.; Luxa, M.; Hála, J. Clearance gap flow: Simulations by discontinuous Galerkin method and experiments. EPJ Web Conf. 2015, 92, 02073. [Google Scholar] [CrossRef]
- Christensen, A.H.; Jensen, K.H. Viscous flow in a slit between two elastic plates. Phys. Rev. Fluids 2020, 5, 044101. [Google Scholar] [CrossRef]
- Lin, J.-R.; Chu, L.-M.; Li, W.-L.; Lu, R.-F. Combined effects of piezo-viscous dependency and non-Newtonian couple stresses in wide parallel-plate squeeze-film characteristics. Tribol. Int. 2011, 44, 1598–1602. [Google Scholar] [CrossRef]
- Vijayakumar, B.; Kesavan, S. Effects of pressure distribution on parallel circular porous plates with combined effect of piezo-viscous dependency and non-Newtonian couple stress fluid. J. Phys. Conf. Ser. 2018, 1000, 012021. [Google Scholar] [CrossRef]
- Box, F.; Neufeld, J.A.; Woods, A.W. On the dynamics of a thin viscous film spreading between a permeable horizontal plate and an elastic sheet. J. Fluid Mech. 2018, 841, 989–1011. [Google Scholar] [CrossRef]
- Zamanov, A.; Ismailov, M.; Akbarov, S. The Effect of Viscosity of a Fluid on the Frequency Response of a Viscoelastic Plate Loaded by This Fluid. Mech. Compos. Mater. 2018, 54, 41–52. [Google Scholar] [CrossRef]
- Aureli, M.; Basaran, M.; Porfiri, M. Nonlinear finite amplitude vibrations of sharp-edged beams in viscous fluids. J. Sound Vib. 2012, 331, 1624–1654. [Google Scholar] [CrossRef]
- Aureli, M.; Porfiri, M. Low frequency and large amplitude oscillations of cantilevers in viscous fluids. Appl. Phys. Lett. 2010, 96, 164102. [Google Scholar] [CrossRef]
- Justesen, P. A numerical study of oscillating flow around a circular cylinder. J. Fluid Mech. 1991, 222, 157–196. [Google Scholar] [CrossRef]
- Apfel, R.E.; Tian, Y.; Jankovsky, J.; Shi, T.; Chen, X.; Holt, R.G.; Trinh, E.; Croonquist, A.; Thornton, K.C.; Sacco Jr, A. Free oscillations and surfactant studies of superdeformed drops in microgravity. Phys. Rev. Lett. 1997, 78, 1912. [Google Scholar] [CrossRef]
- Kitahata, H.; Tanaka, R.; Koyano, Y.; Matsumoto, S.; Nishinari, K.; Watanabe, T.; Hasegawa, K.; Kanagawa, T.; Kaneko, A.; Abe, Y. Oscillation of a rotating levitated droplet: Analysis with a mechanical model. Phys. Rev. E 2015, 92, 062904. [Google Scholar] [CrossRef] [PubMed]
- Trinh, E.; Zwern, A.; Wang, T. An experimental study of small-amplitude drop oscillations in immiscible liquid systems. J. Fluid Mech. 1982, 115, 453–474. [Google Scholar] [CrossRef]
- Nuriev, A.N.; Egorov, A.G.; Kamalutdinov, A.M. Hydrodynamic forces acting on the elliptic cylinder performing high-frequency low-amplitude multi-harmonic oscillations in a viscous fluid. J. Fluid Mech. 2021, 913, A40. [Google Scholar] [CrossRef]
- Kremer, J.; Kilzer, A.; Petermann, M. Simultaneous measurement of surface tension and viscosity using freely decaying oscillations of acoustically levitated droplets. Rev. Sci. Instrum. 2018, 89, 015109. [Google Scholar] [CrossRef] [PubMed]
- Brenn, G.; Teichtmeister, S. Linear shape oscillations and polymeric time scales of viscoelastic drops. J. Fluid Mech. 2013, 733, 504–527. [Google Scholar] [CrossRef]
- Feng, L.; Shi, W.-Y. Viscous Effect on the Frequency Shift of an Oscillating-Rotating Droplet. Microgravity Sci. Technol. 2023, 35, 27. [Google Scholar] [CrossRef]
- Ghaffari, A.; Hashemabadi, S.H.; Ashtiani, M. A review on the simulation and modeling of magnetorheological fluids. J. Intell. Mater. Syst. Struct. 2015, 26, 881–904. [Google Scholar] [CrossRef]
- Chae, D. On the a priori estimates for the Euler, the Navier-Stokes and the quasi-geostrophic equations. arXiv 2007, arXiv:0711.3403. [Google Scholar] [CrossRef]
- Chowdhury, M.; Fester, V.G. Modeling pressure losses for Newtonian and non-Newtonian laminar and turbulent flow in long square edged orifices. Chem. Eng. Res. Des. 2012, 90, 863–869. [Google Scholar] [CrossRef]
- Rahman, M.; Tachie, M. Effects of Reynolds number on turbulent characteristics of surface jet. In Proceedings of the Fluids Engineering Division Summer Meeting, Washington, DC, USA, 10–14 July 2016. V01BT20A002. [Google Scholar]
- Wang, F.Z.; Animasaun, I.; Muhammad, T.; Okoya, S. Recent advancements in fluid dynamics: Drag reduction, lift generation, computational fluid dynamics, turbulence modelling, and multiphase flow. Arab. J. Sci. Eng. 2024, 49, 10237–10249. [Google Scholar] [CrossRef]
- Bakhtyar, R.; Razmi, A.M.; Barry, D.A.; Yeganeh-Bakhtiary, A.; Zou, Q.-P. Air–water two-phase flow modeling of turbulent surf and swash zone wave motions. Adv. Water Resour. 2010, 33, 1560–1574. [Google Scholar] [CrossRef]
- Guerrero, J.; Sanguineti, M.; Wittkowski, K. CFD study of the impact of variable cant angle winglets on total drag reduction. Aerospace 2018, 5, 126. [Google Scholar] [CrossRef]
- Jeon, J.; Lee, J.; Vinuesa, R.; Kim, S.J. Residual-based physics-informed transfer learning: A hybrid method for accelerating long-term cfd simulations via deep learning. Int. J. Heat Mass Transf. 2024, 220, 124900. [Google Scholar] [CrossRef]
- Kadivar, M.; Tormey, D.; McGranaghan, G. A comparison of RANS Models used for CFD prediction of turbulent flow and heat transfer in rough and smooth channels. Int. J. Thermofluids 2023, 20, 100399. [Google Scholar] [CrossRef]
- Van Hirtum, A.; Grandchamp, X.; Cisonni, J. Reynolds number dependence of near field vortex motion downstream from an asymmetrical nozzle. Mech. Res. Commun. 2012, 44, 47–50. [Google Scholar] [CrossRef]
- Wang, Z.; Mao, B.; Zhu, R.; Bai, X.; Han, X. Study on oscillating flow model of fractional Maxwell viscoelastic colloidal damper. J. Ordnance Eng. 2020, 41, 984–995. [Google Scholar]
- Lee, Y.K.; Ahn, K.H. A novel lattice Boltzmann method for the dynamics of rigid particles suspended in a viscoelastic medium. J. Non-Newton. Fluid Mech. 2017, 244, 75–84. [Google Scholar] [CrossRef]
- Zhu, L.; Wang, Q.; Qian, J.; Xue, Z. Mechanical characteristics of particle migration with viscoelastic fluid in a square tube. Light Ind. Mach. 2019, 37, 39–44. [Google Scholar]
- Li, H.; Li, Y.; Zhou, W.J.; He, L. Lattice Boltzmann simulation analysis of particle settlement in viscoelastic fluid expansion and contraction flow. Q. J. Mech. 2020, 41, 319–328. [Google Scholar] [CrossRef]
- Tsepelev, I. Iterative algorithm for solving the retrospective problem of thermal convection in a viscous fluid. Fluid Dyn. 2011, 46, 835–842. [Google Scholar] [CrossRef]
- Xu, X.; Deng, X.-L. An improved weakly compressible SPH method for simulating free surface flows of viscous and viscoelastic fluids. Comput. Phys. Commun. 2016, 201, 43–62. [Google Scholar] [CrossRef]
- Moulinec, C.; Violeau, D.; Laurence, D.; Lee, E.; Stansby, P.; Xu, R. Comparisons of Weakly Compressible and Truly Incompressible Algorithms for the SPH Mesh Free Simulation with Polyhedral Meshes. J. Comput. Phys. 2008, 227, 8417–8436. [Google Scholar]
- Li, G.; Ma, X.; Zhang, B.; Xu, H. An integrated smoothed particle hydrodynamics method for numerical simulation of the droplet impacting with heat transfer. Eng. Anal. Bound. Elem. 2021, 124, 1–13. [Google Scholar] [CrossRef]
- Saintillan, D. Rheology of active fluids. Annu. Rev. Fluid Mech. 2018, 50, 563–592. [Google Scholar] [CrossRef]
- Pudasaini, S.P.; Mergili, M. A multi-phase mass flow model. J. Geophys. Res. Earth Surf. 2019, 124, 2920–2942. [Google Scholar] [CrossRef]
- Tian, F.-B.; Dai, H.; Luo, H.; Doyle, J.F.; Rousseau, B. Fluid–structure interaction involving large deformations: 3D simulations and applications to biological systems. J. Comput. Phys. 2014, 258, 451–469. [Google Scholar] [CrossRef]
- Sun, P.-N.; Le Touze, D.; Oger, G.; Zhang, A.-M. An accurate FSI-SPH modeling of challenging fluid-structure interaction problems in two and three dimensions. Ocean Eng. 2021, 221, 108552. [Google Scholar] [CrossRef]
- Atangana, A.; Baleanu, D. New fractional derivatives with nonlocal and non-singular kernel: Theory and application to heat transfer model. arXiv 2016, arXiv:1602.03408. [Google Scholar] [CrossRef]
- Balduzzi, F.; Bianchini, A.; Maleci, R.; Ferrara, G.; Ferrari, L. Critical issues in the CFD simulation of Darrieus wind turbines. Renew. Energy 2016, 85, 419–435. [Google Scholar] [CrossRef]
- Khayyer, A.; Gotoh, H.; Falahaty, H.; Shimizu, Y. An enhanced ISPH–SPH coupled method for simulation of incompressible fluid–elastic structure interactions. Comput. Phys. Commun. 2018, 232, 139–164. [Google Scholar] [CrossRef]
- Xu, B.; Liu, B.; Liu, Y.; Tan, S.; Du, Y.; Liu, C. Numerical simulation of distributed mixing under the action of different staggered angular triangular rotors. J. Chem. Eng. 2020, 71, 3545–3555. [Google Scholar]
- Liang, Y.-f. Numerical Simulation of Viscoelastic Fluid turbulence drag Reduction. Master’s Thesis, Guangzhou University, Guangdong, China, 2022. [Google Scholar]
- Shi, K.; Zhu, R.; Xu, D. A spectral coupled boundary element method for the simulation of nonlinear surface gravity waves. J. Ocean. Eng. Sci. 2023, in press. [Google Scholar] [CrossRef]
- Zhu, Y. Visual Analysis and Application of viscous liquid mutual diffusion. Master’s Thesis, North China University of Science and Technology, Tangshan, China, 2021. [Google Scholar]
- Shen, Y.; Wang, Q.; Liu, T.-J. Effect of shear thinning rheological properties on particle migration in microchannels. Appl. Math. Mech. 2024, 45, 637–650. [Google Scholar]
- Qiu, L.-C. Numerical simulation of deformation process of viscous liquid drop based on the incompressible smoothed particle hydrodynamics. Acta Phys. Sin. 2013, 62, 124702. [Google Scholar]
- Frezzotti, M.L.; Ferrando, S. The chemical behavior of fluids released during deep subduction based on fluid inclusions. Am. Mineral. 2015, 100, 352–377. [Google Scholar] [CrossRef]
- Buttazzo, G.; Frediani, A.; Frediani, A.; Montanari, G. Best wing system: An exact solution of the Prandtl’s problem. In Variational Analysis and Aerospace Engineering; Springer: New York, NY, USA, 2009; pp. 183–211. [Google Scholar]
- Eckert, M. Theory from wind tunnels: Empirical roots of twentieth century fluid dynamics. Centaurus 2008, 50, 233–253. [Google Scholar] [CrossRef]
- Sekundov, A. On the boundary conditions for differential turbulence models. Fluid Dyn. 2012, 47, 20–25. [Google Scholar] [CrossRef]
- Singla, A.; Ray, B. Effects of surface topography on low Reynolds number droplet/bubble flow through a constricted passage. Phys. Fluids 2021, 33, 011301. [Google Scholar] [CrossRef]
- Eskandari, A.; Ahmadi Arpanahi, R.; Daneh-Dezfuli, A.; Mohammadi, B.; Hosseini Hashemi, S. Investigation of vibration of the nano rotating blade coupled with viscous fluid medium by considering the nonlocal elastic theory. J. Low Freq. Noise Vib. Act. Control. 2024, 43, 863–879. [Google Scholar] [CrossRef]
- Zhang, D.; Zheng, W.; Ma, Q.; Yang, P. Numerical simulation of viscous flow around rowing based on FLUENT. In Proceedings of the 2009 ISECS International Colloquium on Computing, Communication, Control, and Management, Sanya, China, 8–9 August 2009; pp. 429–433. [Google Scholar]
- Yang, H.-y.; Pan, M. Engineering research in fluid power: A review. J. Zhejiang Univ. Sci. A 2015, 16, 427–442. [Google Scholar] [CrossRef]
- Zhang, Z.-r.; Li, B.-q.; Zhao, F. The comparison of turbulence models applied to viscous ship flow computation. J. Hydrodyn. 2004, 19, 637–642. [Google Scholar]
- Nadeem, S.; Waqar, H.; Akhtar, S.; Zidan, A.M.; Almutairi, S.; Ghazwani, H.A.S.; Kbiri Alaoui, M.; Tarek El-Waked, M. Mathematical assessment of convection and diffusion analysis for a non-circular duct flow with viscous dissipation: Application of physiology. Symmetry 2022, 14, 1536. [Google Scholar] [CrossRef]
- Li, X.-L.; Fu, D.-X.; Ma, Y.-W.; Liang, X. Direct numerical simulation of compressible turbulent flows. Acta Mech. Sin. 2010, 26, 795–806. [Google Scholar] [CrossRef]
- Sharp, N.S.; Neuscamman, S.; Warhaft, Z. Effects of large-scale free stream turbulence on a turbulent boundary layer. Phys. Fluids 2009, 21, 095105. [Google Scholar] [CrossRef]
- Bhatti, M.; Ellahi, R.; Zeeshan, A. Study of variable magnetic field on the peristaltic flow of Jeffrey fluid in a non-uniform rectangular duct having compliant walls. J. Mol. Liq. 2016, 222, 101–108. [Google Scholar] [CrossRef]
- Elbaz, S.; Gat, A. Dynamics of viscous liquid within a closed elastic cylinder subject to external forces with application to soft robotics. J. Fluid Mech. 2014, 758, 221–237. [Google Scholar] [CrossRef]
- Tchomeni, B.X.; Alugongo, A. Modelling and numerical simulation of vibrations induced by mixed faults of a rotor system immersed in an incompressible viscous fluid. Adv. Mech. Eng. 2018, 10, 1687814018819341. [Google Scholar] [CrossRef]
- Gushchin, V.; Matyushin, P. Classification of the stratified fluid flows regimes around a square cylinder. AIP Conf. Proc. 2015, 1684, 100002. [Google Scholar]
- Belotserkovskii, O.M.; Gushchin, V.A.E.; Kon’shin, V.N. The splitting method for investigating flows of a stratified liquid with a free surface. USSR Comput. Math. Math. Phys. 1987, 27, 181–191. [Google Scholar] [CrossRef]
- Amouroux, S.C.; Heider, D.; Gillespie, J.W., Jr. Permeability estimation of nano-porous membranes for nonwetting fluids. J. Porous Media 2010, 13, 319–329. [Google Scholar] [CrossRef]
- Raupp, S.M.; Schmitt, M.; Walz, A.-L.; Diehm, R.; Hummel, H.; Scharfer, P.; Schabel, W. Slot die stripe coating of low viscous fluids. J. Coat. Technol. Res. 2018, 15, 899–911. [Google Scholar] [CrossRef]
- Stone, H.A. Interfaces: In fluid mechanics and across disciplines. J. Fluid Mech. 2010, 645, 1–25. [Google Scholar] [CrossRef]
- Ajdari, A.; Bocquet, L. Giant Amplification of Interfacially Driven Transport by Hydrodynamic Slip:Diffusio-Osmosis and Beyond. Phys. Rev. Lett. 2006, 96, 186102. [Google Scholar] [CrossRef] [PubMed]



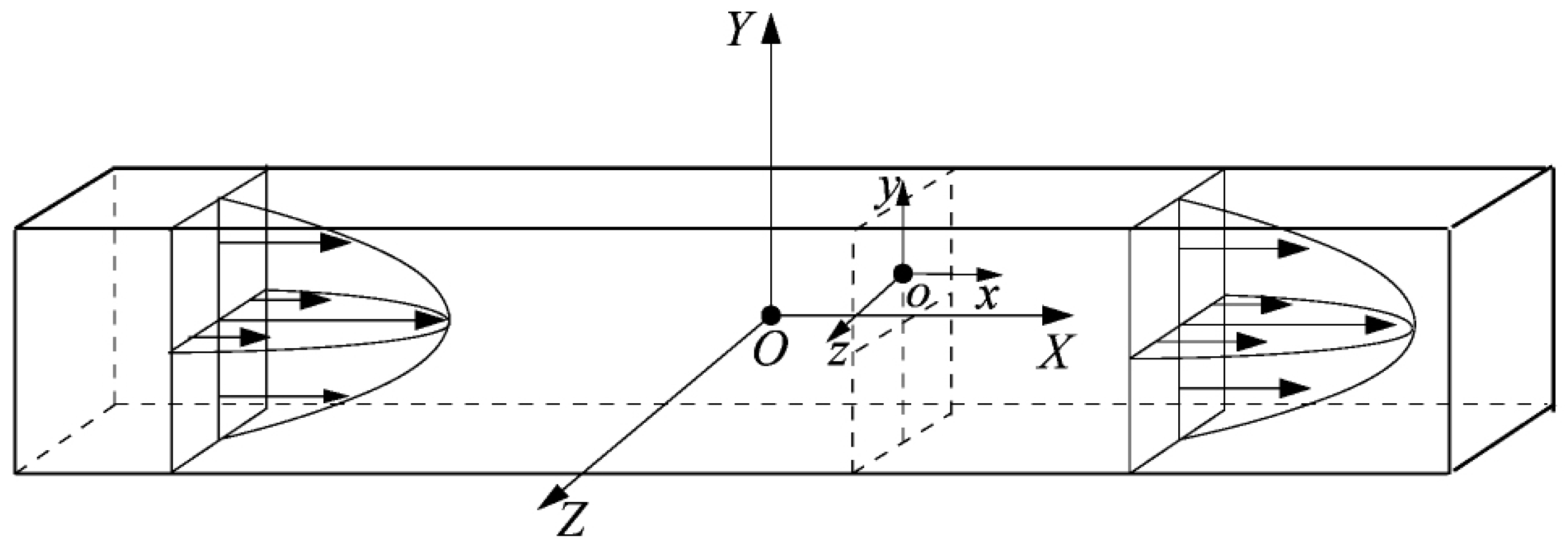

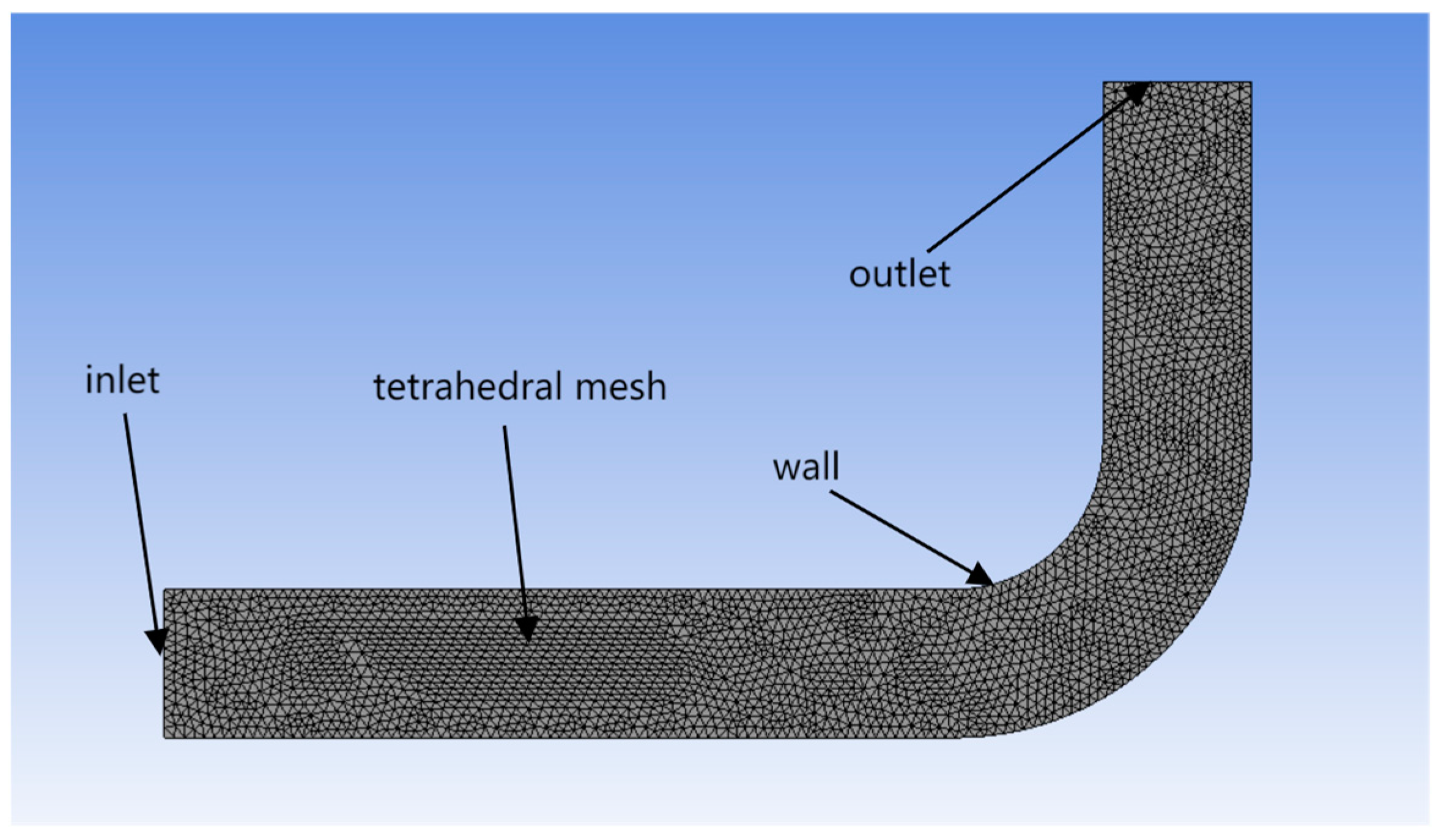
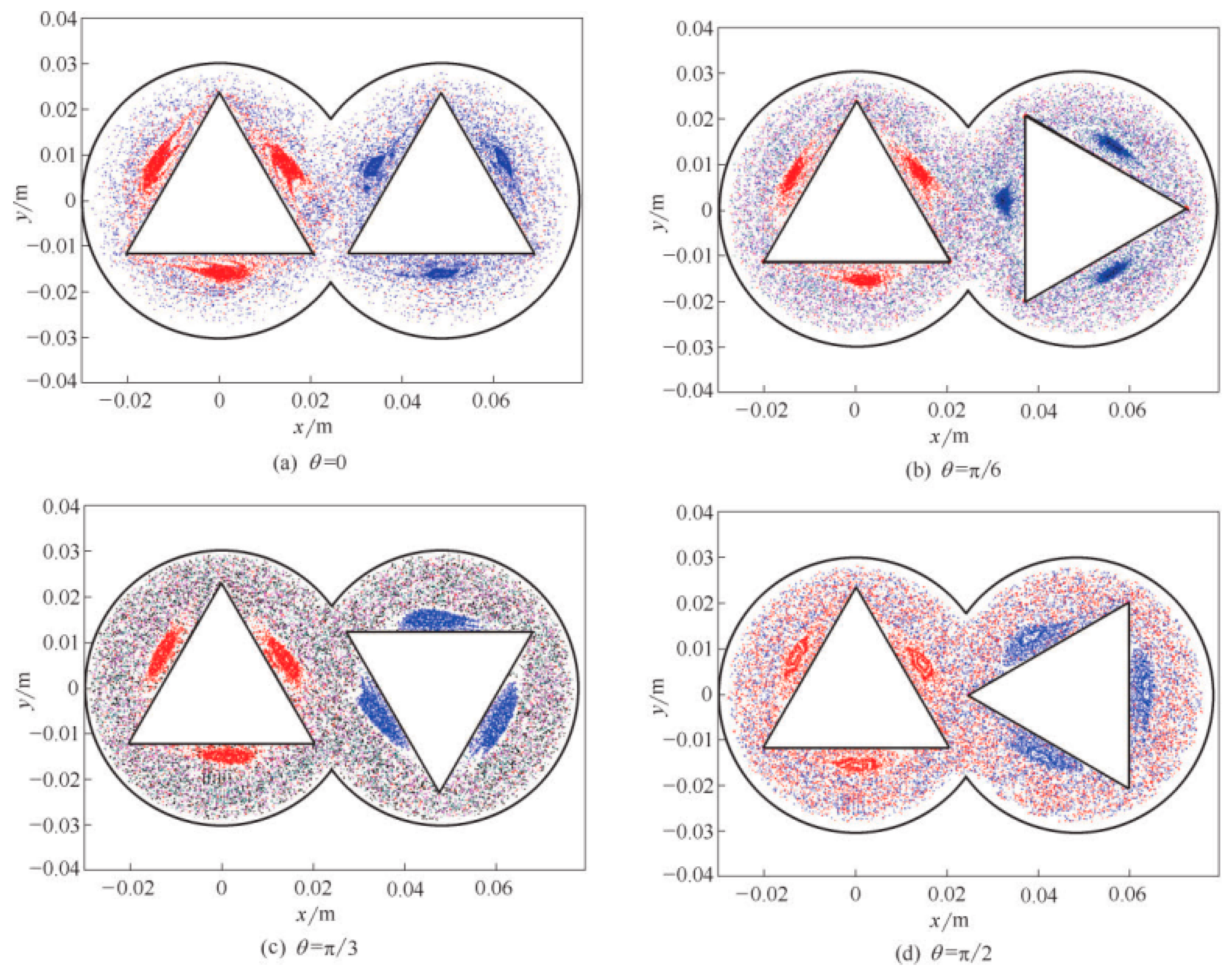


| Method | Cost | Accuracy | Time Consumption | Future Development Potential |
|---|---|---|---|---|
| Conventional contact shock method | High | Relatively low | High | Low |
| Non-contact oscillation method | High | Moderate | High | Relatively low |
| Digital simulation method | Low | High | Low | High |
| Method | Precision of Mathematical Results | Visualization | Time Cost | Complexity Adaptability |
|---|---|---|---|---|
| Arithmetic | High | Mediocre | Relatively low | Low |
| Emulate | Relatively low | First-rate | High | High |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Peng, J.; Feng, R.; Xue, M.; Zhou, E.; Wang, J.; Zhong, Z.; Ku, X. Research Progress and Engineering Applications of Viscous Fluid Mechanics. Appl. Sci. 2025, 15, 357. https://doi.org/10.3390/app15010357
Peng J, Feng R, Xue M, Zhou E, Wang J, Zhong Z, Ku X. Research Progress and Engineering Applications of Viscous Fluid Mechanics. Applied Sciences. 2025; 15(1):357. https://doi.org/10.3390/app15010357
Chicago/Turabian StylePeng, Jianjun, Run Feng, Meng Xue, Erhao Zhou, Junhua Wang, Zhidan Zhong, and Xiangchen Ku. 2025. "Research Progress and Engineering Applications of Viscous Fluid Mechanics" Applied Sciences 15, no. 1: 357. https://doi.org/10.3390/app15010357
APA StylePeng, J., Feng, R., Xue, M., Zhou, E., Wang, J., Zhong, Z., & Ku, X. (2025). Research Progress and Engineering Applications of Viscous Fluid Mechanics. Applied Sciences, 15(1), 357. https://doi.org/10.3390/app15010357







