Efficiency Optimization of the Main Operating Points of an EV Traction Motor
Abstract
1. Introduction
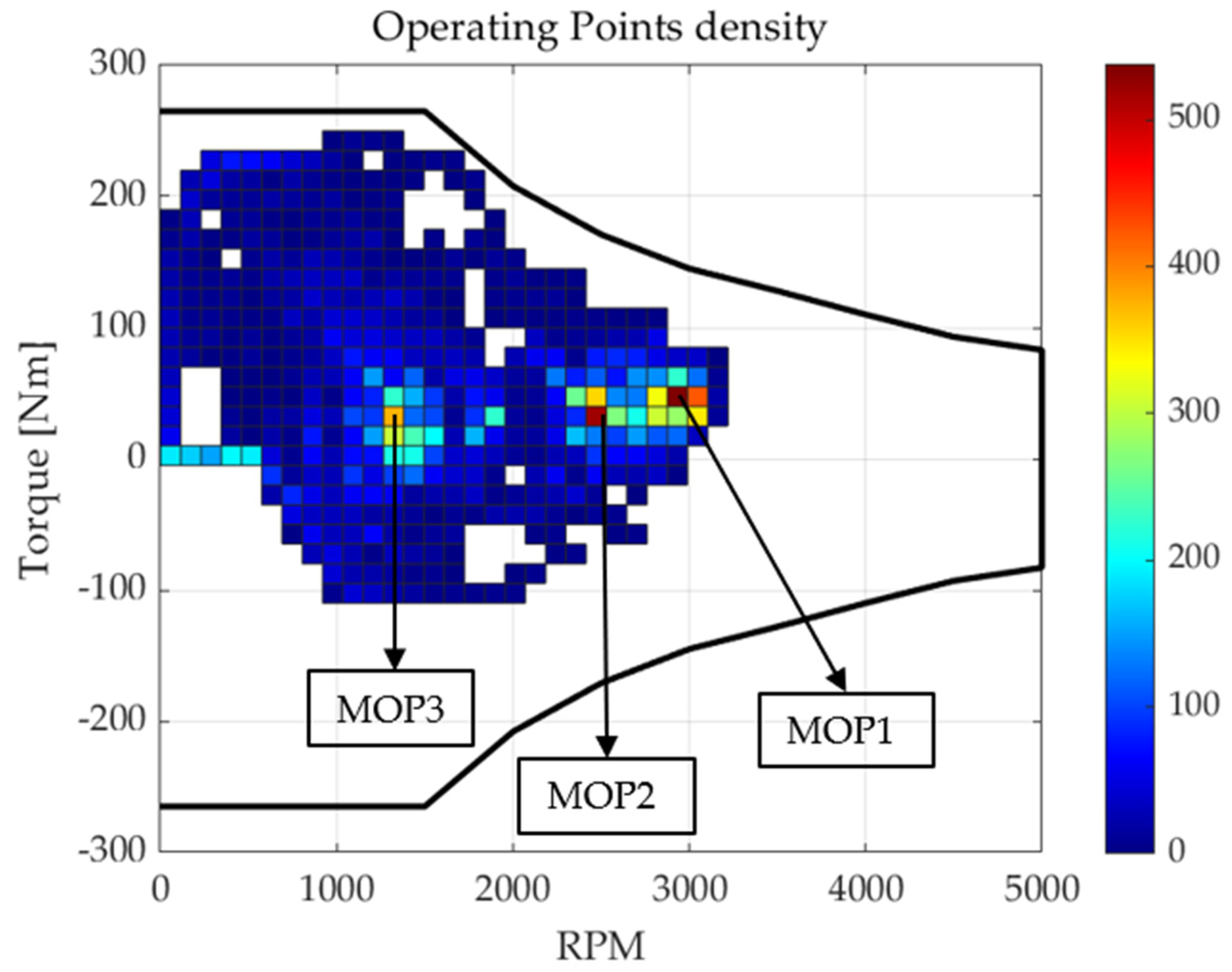
2. Selection of Main Operating Points
2.1. Model Specifications
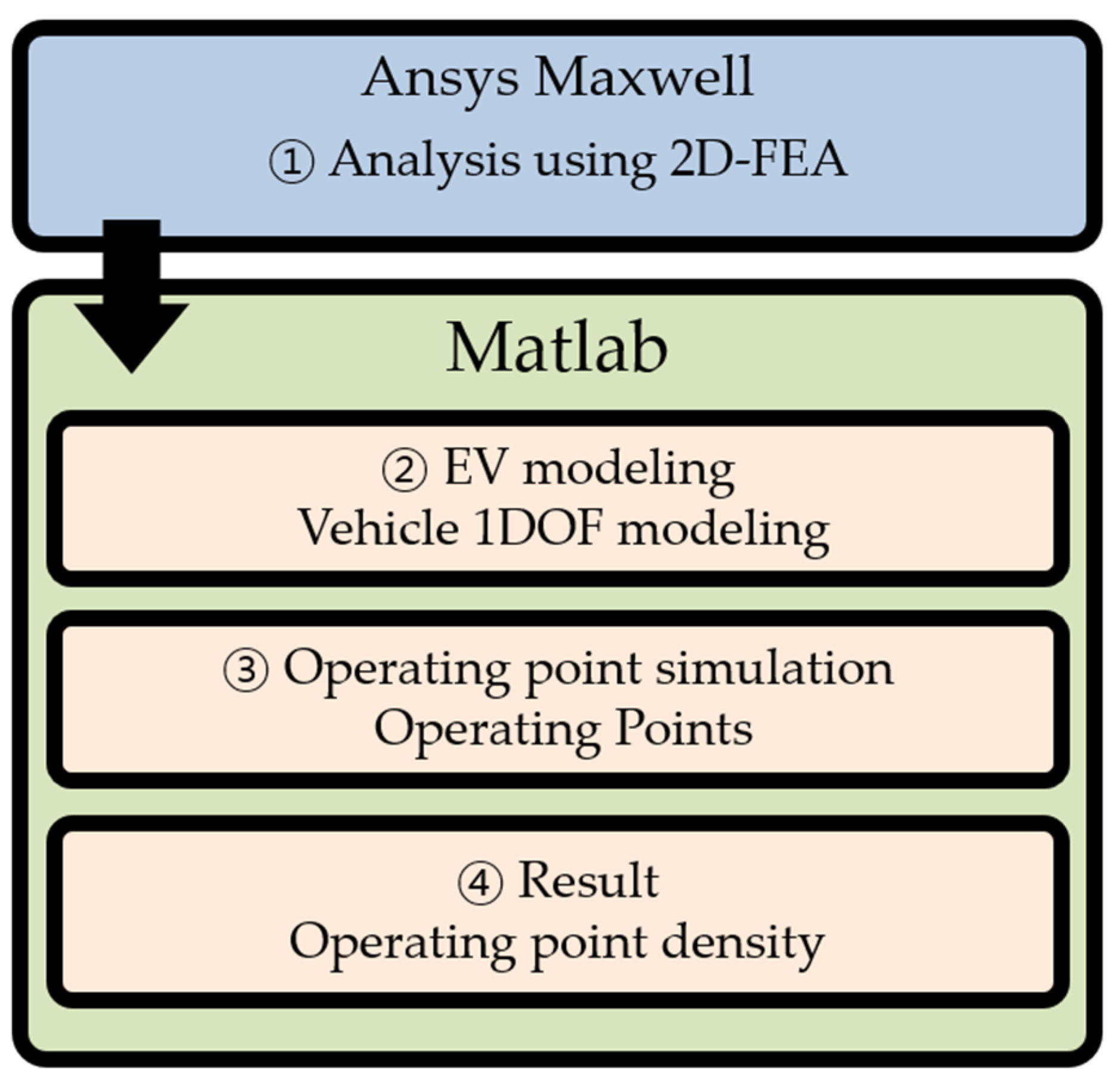
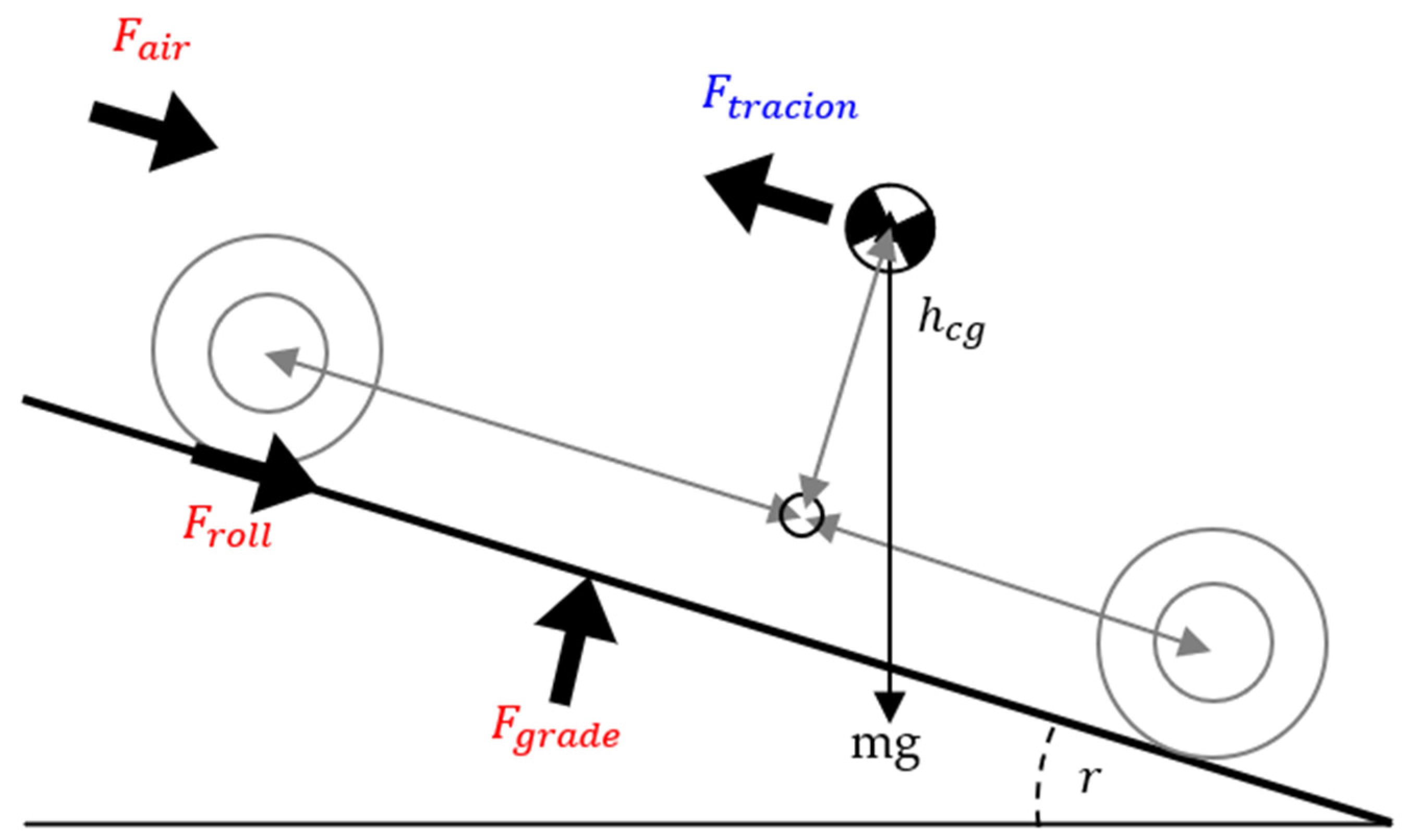
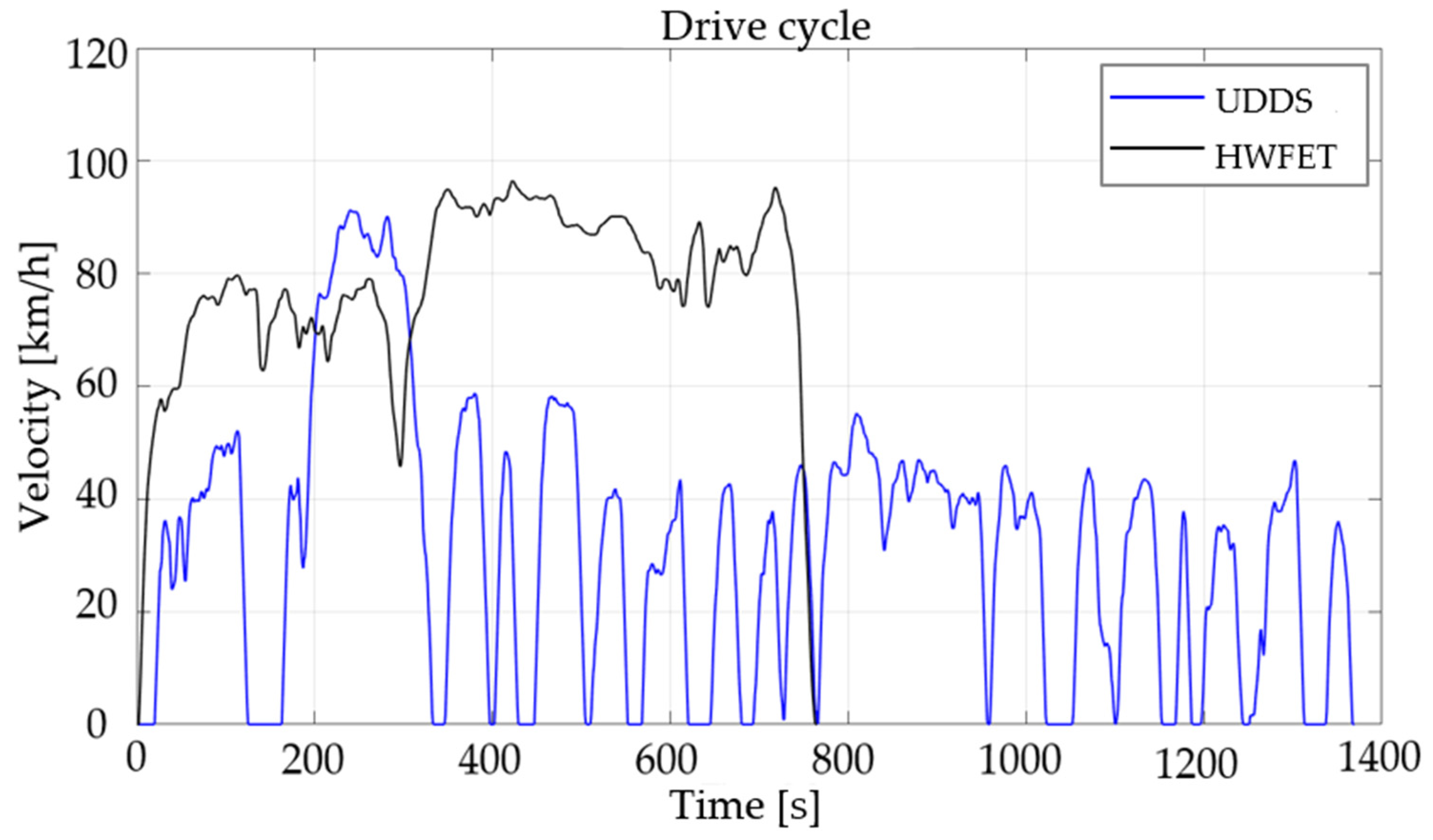
2.2. EV Simulation for Operating Point Analysis
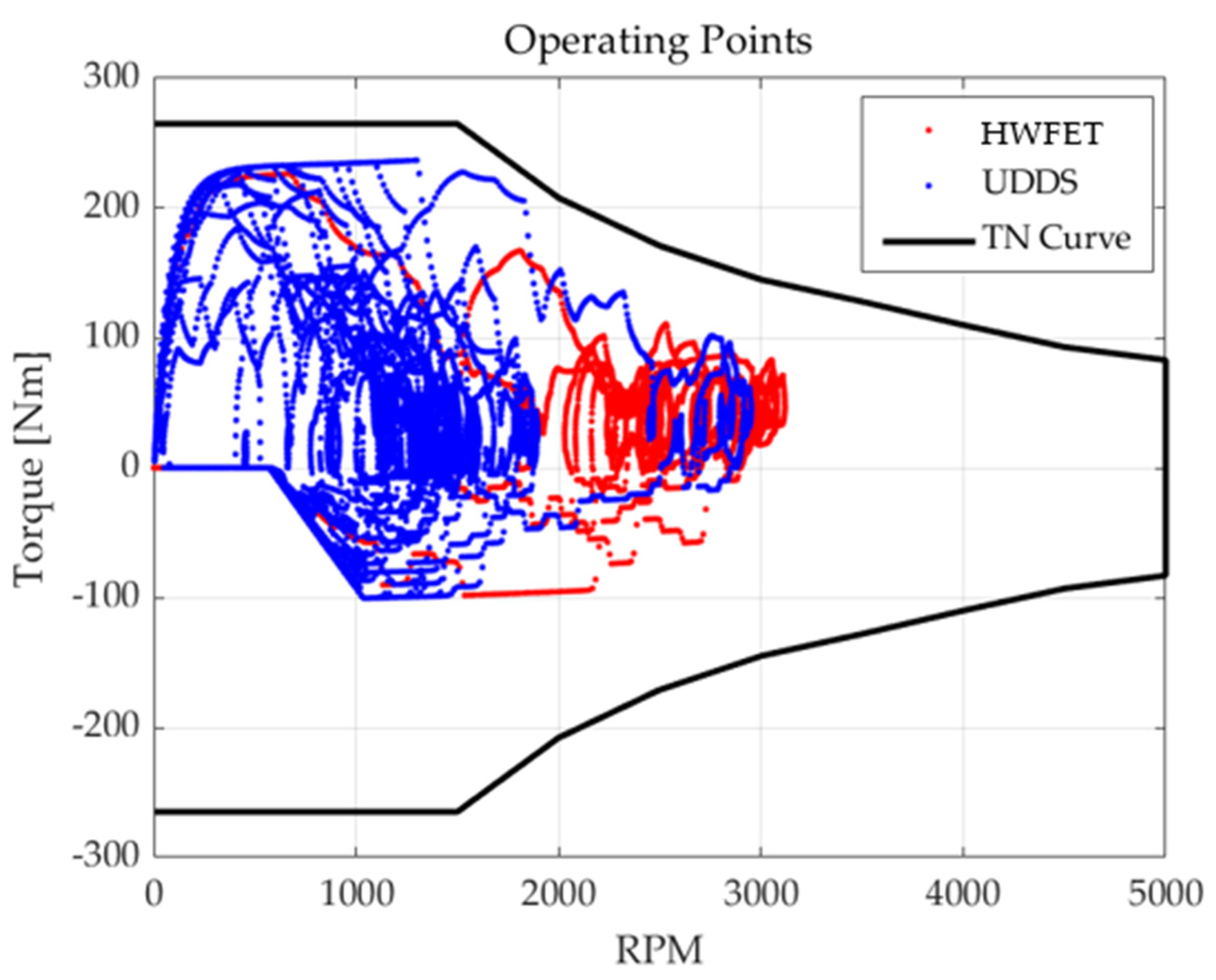
2.3. Operating Point Analysis
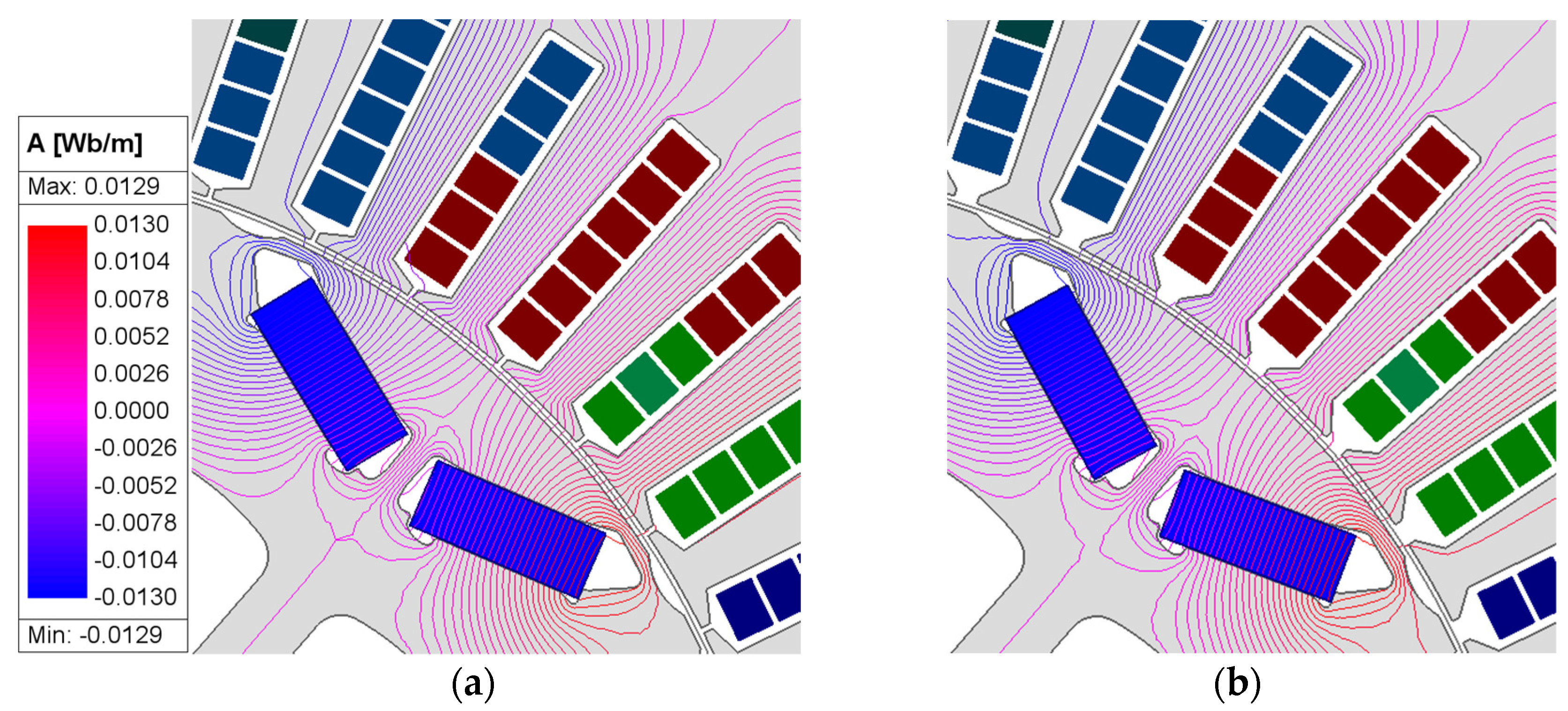
3. Optimal Design
3.1. Design Problem Formulation
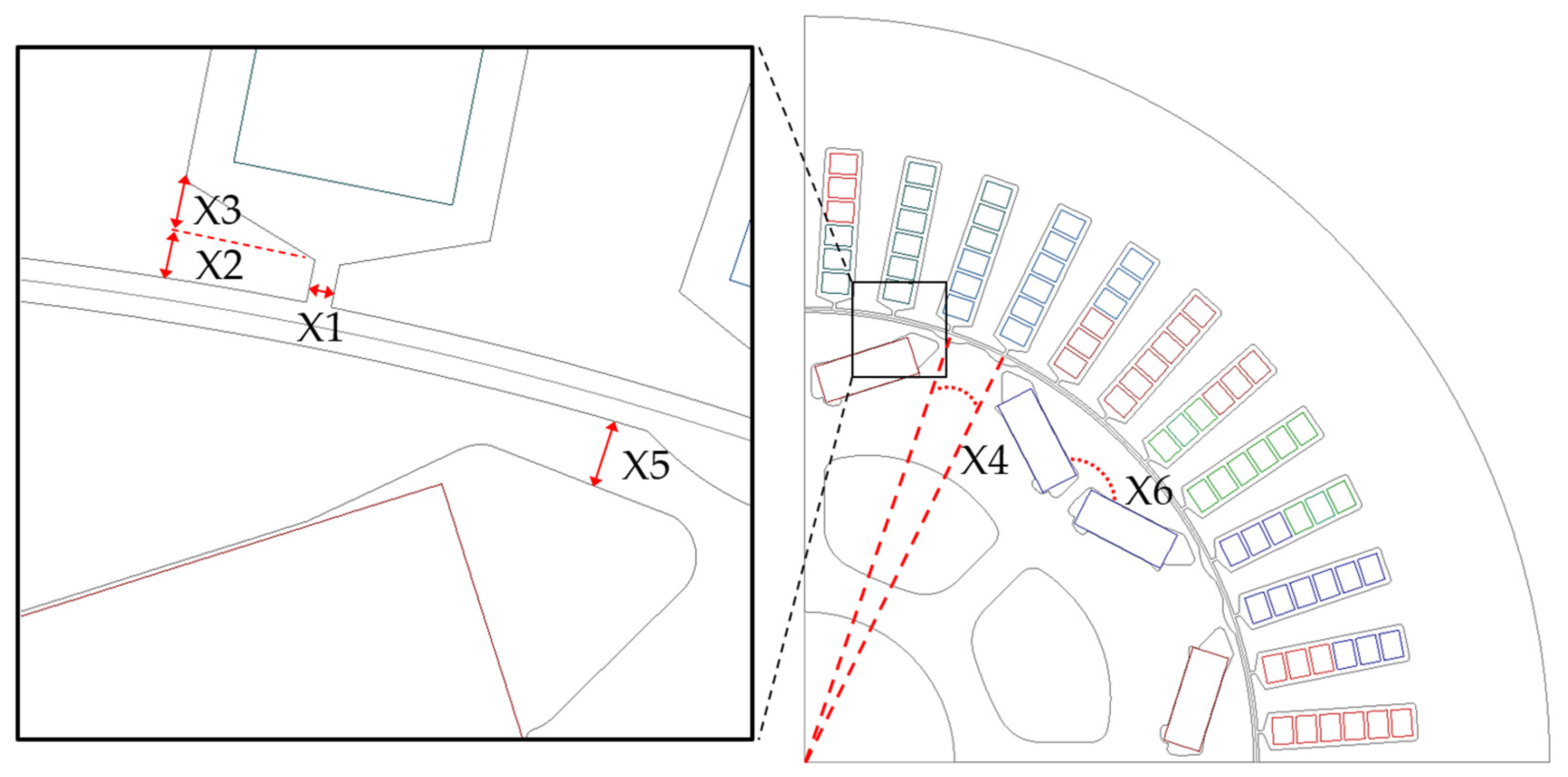
3.2. Sensitivity Analysis
3.3. Metamodeling
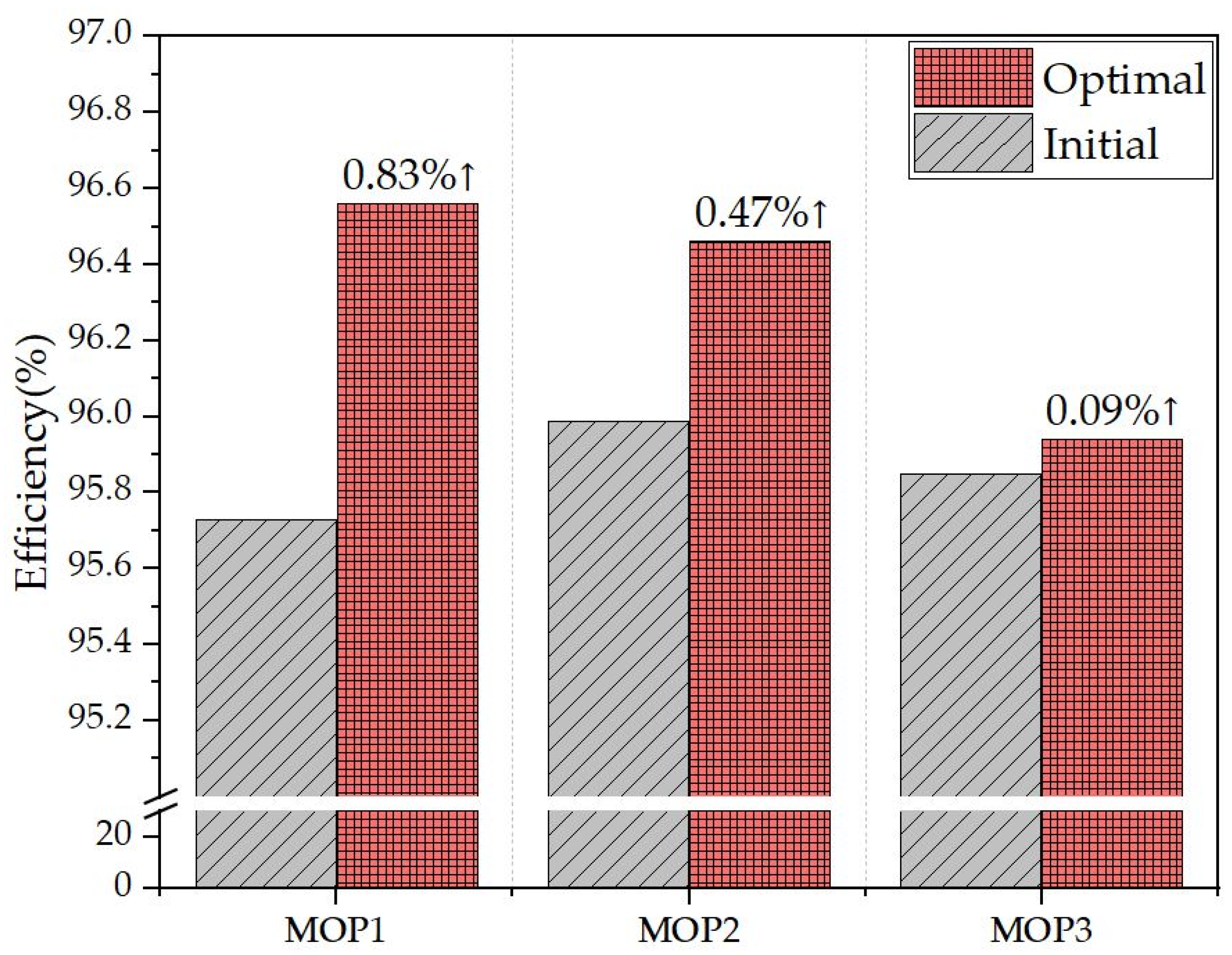
3.4. Optimal Design Results
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Abas, A.E.P.; Yong, J.; Mahlia, T.M.I.; Hannan, M.A. Techno-Economic Analysis and Environmental Impact of Electric Vehicle. IEEE Access 2019, 7, 98565–98578. [Google Scholar] [CrossRef]
- Heffner, R.R.; Kurani, K.S.; Turrentine, T.S. Symbolism in California’s early market for hybrid electric vehicles. Transp. Res. Part D Transp. Environ. 2007, 12, 396–413. [Google Scholar] [CrossRef]
- Karvonen, M.; Klemola, K.; Ranaei, S.; Kässi, T. Predicting the technological paths in automotive industry and the environmental impacts of electrification of automotive industry in selected OECD countries. In Proceedings of the 2015 Portland International Conference on Management of Engineering and Technology (PICMET), Portland, OR, USA, 2–6 August 2015; pp. 1247–1259. [Google Scholar] [CrossRef]
- Bilgin, B.; Magne, P.; Malysz, P.; Yang, Y.; Pantelic, V.; Preindl, M.; Korobkine, A.; Jiang, W.; Lawford, M.; Emadi, A. Making the Case for Electrified Transportation. IEEE Trans. Transp. Electrif. 2015, 1, 4–17. [Google Scholar] [CrossRef]
- Bianchi, N.; Bolognani, S. Interior PM synchronous motor for high performance applications. In Proceedings of the Power Conversion Conference-Osaka 2002 (Cat. No.02TH8579), Osaka, Japan, 2–5 April 2002; Volume 1, pp. 148–153. [Google Scholar] [CrossRef]
- Yang, Y.; Castano, S.M.; Yang, R.; Kasprzak, M.; Bilgin, B.; Sathyan, A.; Dadkhah, H.; Emadi, A. Design and Comparison of Interior Permanent Magnet Motor Topologies for Traction Applications. IEEE Trans. Transp. Electrif. 2017, 3, 86–97. [Google Scholar] [CrossRef]
- Popescu, M.; Goss, J.; Staton, D.A.; Hawkins, D.; Chong, Y.C.; Boglietti, A. Electrical Vehicles—Practical Solutions for Power Traction Motor Systems. IEEE Trans. Ind. Appl. 2018, 54, 2751–2762. [Google Scholar] [CrossRef]
- Park, H.-J.; Lim, M.-S. Design of High Power Density and High Efficiency Wound-Field Synchronous Motor for Electric Vehicle Traction. IEEE Access 2019, 7, 46677–46685. [Google Scholar] [CrossRef]
- Kim, C.-M.; Kim, K.-C. A Study on the Winding Method and Skew Effect Electromagnetic Field Characteristics of Hairpin Winding for High Power Density Motor Design. J. Korea Contents Assoc. 2023, 23, 17–25. [Google Scholar] [CrossRef]
- Shams Ghahfarokhi, P.; Podgornovs, A.; Cardoso, A.J.M.; Kallaste, A.; Belahcen, A.; Vaimann, T. Hairpin Windings for Electric Vehicle Motors: Modeling and Investigation of AC Loss-Mitigating Approaches. Machines 2022, 10, 1029. [Google Scholar] [CrossRef]
- Jun, S.-B.; Kim, D.-W.; Kim, J.-S.; Ko, Y.-Y.; Kim, Y.-J.; Jung, S.-Y. Comparison on the Charateristics of AC Copper Loss on IPMSM for EV Traction according to the Number of Conductors. J. Inst. Inf. Telecommun. Facil. Eng. 2019, 15, 6–11. [Google Scholar]
- Ju, X.; Cheng, Y.; Du, B.; Yang, M.; Yang, D.; Cui, S. AC Loss Analysis and Measurement of a Hybrid Transposed Hairpin Winding for EV Traction Machines. IEEE Trans. Ind. Electron. 2023, 70, 3525–3536. [Google Scholar] [CrossRef]
- Chin, J.-W.; Cha, K.-S.; Park, M.-R.; Park, S.-H.; Lee, E.-C.; Lim, M.-S. High Efficiency PMSM With High Slot Fill Factor Coil for Heavy-Duty EV Traction Considering AC Resistance. IEEE Trans. Energy Convers. 2021, 36, 883–894. [Google Scholar] [CrossRef]
- Hebala, A.; Nuzzo, S.; Connor, P.H.; Volpe, G.; Gerada, C.; Galea, M. Mitigation of AC Winding Losses for Aircraft Propulsion Motors. In Proceedings of the IECON 2022—48th Annual Conference of the IEEE Industrial Electronics Society, Brussels, Belgium, 17–20 October 2022; pp. 1–6. [Google Scholar] [CrossRef]
- Carraro, E.; Morandin, M.; Bianchi, N. Traction PMASR Motor Optimization According to a Given Driving Cycle. IEEE Trans. Ind. Appl. 2016, 52, 209–216. [Google Scholar] [CrossRef]
- Salameh, M.; Brown, I.P.; Krishnamurthy, M. Fundamental Evaluation of Data Clustering Approaches for Driving Cycle-Based Machine Design Optimization. IEEE Trans. Transp. Electrif. 2019, 5, 1395–1405. [Google Scholar] [CrossRef]
- Chen, L.; Wang, J.; Lazari, P.; Chen, X. Optimizations of a permanent magnet machine targeting different driving cycles for electric vehicles. In Proceedings of the 2013 International Electric Machines & Drives Conference, Chicago, IL, USA, 12–15 May 2013; pp. 855–862. [Google Scholar] [CrossRef]
- Ahn, K.; Bayrak, A.E.; Papalambros, P.Y. Electric Vehicle Design Optimization: Integration of a High-Fidelity Interior-Permanent-Magnet Motor Model. IEEE Trans. Veh. Technol. 2015, 64, 3870–3877. [Google Scholar] [CrossRef]
- Yoon, K.-Y.; Hwang, K.-Y. Optimal Design of Spoke-Type IPM Motor Allowing Irreversible Demagnetization to Minimize PM Weight. IEEE Access 2021, 9, 65721–65729. [Google Scholar] [CrossRef]
- Li, Y.; Song, B.; Mao, Z.; Tian, W. Analysis and Optimization of the Electromagnetic Performance of a Novel Stator Modular Ring Drive Thruster Motor. Energies 2018, 11, 1598. [Google Scholar] [CrossRef]
- Ahn, J.-M.; Baek, M.-K.; Park, S.-H.; Lim, D.-K. Optimal Design of IPMSM for EV Using Subdivided Kriging Multi-Objective Optimization. Processes 2021, 9, 1490. [Google Scholar] [CrossRef]
- Cho, S.-K.; Jung, K.-H.; Choi, J.-Y. Design Optimization of Interior Permanent Magnet Synchronous Motor for Electric Compressors of Air-Conditioning Systems Mounted on EVs and HEVs. IEEE Trans. Magn. 2018, 54, 8204705. [Google Scholar] [CrossRef]
- Bae, J.-N. Permanent Magnet Synchronous Machine Design Through an Automatic Selection of the Specific Loadings. Doctoral Dissertation, Hanyang University, Seoul, Republic of Korea, 2010. [Google Scholar]
- Kacker, R.N.; Lagergren, E.S.; Filliben, J.J. Taguchi’s Orthogonal Arrays Are Classical Designs of Experiments. J. Res. Natl. Inst. Stand. Technol. 1991, 96, 577–591. [Google Scholar] [CrossRef]
- Brenneman, M.T.; Morton, Y.T.; Zhou, Q. GPS Multipath Detection with ANOVA for Adaptive Arrays. IEEE Trans. Aerosp. Electron. Syst. 2010, 46, 1171–1184. [Google Scholar] [CrossRef]
- Patil, N.S.; Yaligar, M.F. Analysis of linear relation between P-value and co relational value using R programming. In Proceedings of the 2017 International Conference on Advances in Computing, Communications and Informatics (ICACCI), Udupi, India, 13–16 September 2017; pp. 983–987. [Google Scholar] [CrossRef]
- Hodson, T.O. Root-mean-square error (RMSE) or mean absolute error (MAE): When to use them or not. Geosci. Model Dev. 2022, 15, 5481–5487. [Google Scholar] [CrossRef]
- Mienye, D.; Jere, N. A Survey of Decision Trees: Concepts, Algorithms, and Applications. IEEE Access 2024, 12, 86716–86727. [Google Scholar] [CrossRef]
- Lebensztajn, L.; Marretto, C.A.R.; Costa, M.C.; Coulomb, J.L. Kriging: A useful tool for electromagnetic device optimization. IEEE Trans. Magn. 2004, 40, 1196–1199. [Google Scholar] [CrossRef]
- Al Bataineh, A.; Kaur, D.; Jalali, S.M.J. Multi-Layer Perceptron Training Optimization Using Nature Inspired Computing. IEEE Access 2022, 10, 36963–36977. [Google Scholar] [CrossRef]
- Hakim, M.; Choukri, S. Polynomial Metamodelling of Computer Simulation for UAV Design. In Proceedings of the 2024 4th International Conference on Innovative Research in Applied Science, Engineering and Technology (IRASET), FEZ, Morocco, 16–17 May 2024; pp. 1–5. [Google Scholar] [CrossRef]
- Lei, Y.; Ding, L.; Zhang, W. Generalization Performance of Radial Basis Function Networks. IEEE Trans. Neural Netw. Learn. Syst. 2015, 26, 551–564. [Google Scholar] [CrossRef]
- Chakravarty, S.; Mittra, R.; Williams, N.R. Application of a microgenetic algorithm (MGA) to the design of broadband microwave absorbers using multiple frequency selective surface screens buried in dielectrics. IEEE Trans. Antennas Propag. 2002, 50, 284–296. [Google Scholar] [CrossRef]
- Akimoto, Y.; Hansen, N. Diagonal Acceleration for Covariance Matrix Adaptation Evolution Strategies. Evol. Comput. 2020, 28, 405–435. [Google Scholar] [CrossRef]
- Yahagi, H.; Shimizu, S.; Ogata, T.; Hara, T.; Ota, J. Simulation-Based Rule Generation Considering Readability. Int. Sch. Res. Not. 2015, 2015, 159289. [Google Scholar] [CrossRef][Green Version]
- Lü, Z.; Glover, F.; Hao, J.-K. A hybrid metaheuristic approach to solving the UBQP problem. Eur. J. Oper. Res. 2010, 207, 1254–1262. [Google Scholar] [CrossRef]


| Items | Unit | Value | |
|---|---|---|---|
| Poles/Slots | - | 8/48 | |
| Rated speed | rpm | 1575 | |
| Maximum speed | rpm | 5000 | |
| Line-to-line voltage | 380 | ||
| Continuous current | 120 | ||
| Material | Electrical steel | - | N45SH |
| Permanent magnet | - | 35JN440 | |
| Items | Unit | Value |
|---|---|---|
| Curb weight | kg | 1721 |
| Frontal area | 2.27 | |
| Front axle distance | m | 1.015 |
| Rear axle distance | m | 1.495 |
| Axle height | 0.5 | |
| Drag coefficient | - | 0.7 |
| Wheel radius | m | 0.327 |
| Gear ratio | - | 5.16 |
| Gravitational acceleration | 9.81 | |
| Rolling resistance coefficient | - | 0.014 |
| Air density | 1.225 |
| Main Operating Points (MOP) | Speed (RPM) | Torque (Nm) | Percentage |
|---|---|---|---|
| MOP1 | 2900~3000 (2950) | 40~55 (42.5) | 537 (2.25%) |
| MOP2 | 2400~2500 (2450) | 25~40 (32.5) | 519 (2.17%) |
| MOT3 | 1265~1380 (1320) | 25~40 (32.5) | 374 (1.56%) |
| Design Variables | Unit | Lower | Initial | Upper |
|---|---|---|---|---|
| X1 (Slot open) | mm | 0.4 | 0.41 | 3.6 |
| X2 (Shoe thickness) | mm | 0.5 | 0.7 | 2 |
| X3 (Shoe angle) | mm | 0 | 0.85 | 2 |
| X4 (Notch angle) | ° | 5.2 | 7.21 | 7.5 |
| X5 (Rib thickness) | mm | 0.9 | 0.9 | 2 |
| X6 (Magnet angle) | ° | 135 | 145 | 155 |
| Items | X1 | X2 | X3 | X4 | X5 | X6 |
|---|---|---|---|---|---|---|
| MOP1 | 0 | 0.485 | 0.185 | 0.636 | 0 | 0.975 |
| MOP2 | 0.028 | 0.02 | 0.001 | 0.828 | 0 | 0.18 |
| MOP3 | 0.016 | 0 | 0 | 0.927 | 0 | 0.362 |
| 0 | 0.053 | 0.062 | 0.04 | 0.001 | 0 | |
| 0 | 0.405 | 0.05 | 0.129 | 0 | 0.132 | |
| 0 | 0 | 0.092 | 0.022 | 0 | 0.474 | |
| 0 | 0 | 0 | 0.006 | 0.006 | 0.003 | |
| 0.039 | 0.967 | 0.849 | 0.89 | 0.043 | 0.219 |
| Items | X1 | X2 | X3 | X4 | X5 | X6 |
|---|---|---|---|---|---|---|
| MOP1 | 52.4 | 1.26 | 3.18 | 0.84 | 42.31 | 0.04 |
| MOP2 | 7.63 | 10.45 | 21.42 | 0.37 | 56.52 | 3.6 |
| MOP3 | 7.39 | 22.89 | 34.96 | 0.12 | 33.06 | 1.58 |
| 58.57 | 2.02 | 1.86 | 2.19 | 12.52 | 22.84 | |
| 11.36 | 1 | 3.5 | 2.39 | 79.41 | 2.34 | |
| 72.31 | 9.74 | 2.61 | 4.44 | 10.12 | 0.79 | |
| 50.02 | 20.98 | 17.54 | 3.69 | 3.27 | 4.5 | |
| 41.6 | 0.36 | 1.84 | 1.26 | 37.87 | 17.06 |
| Items | EDT | KRG | MLP | PRG (BS) | PRG (FS) | PRG (FQ) | PRG (LR) | PRG (SC) | PRG (SQ) | RBF (Int) | RBF (Reg) |
|---|---|---|---|---|---|---|---|---|---|---|---|
| MOP1 | 0.0155 | 0.0129 | 0.0559 | 18.9496 | 0.0471 | 0.0479 | 0.0675 | 0.0479 | 0.0772 | 0.0608 | 0.0519 |
| MOP2 | 0.0608 | 0.0287 | 0.153 | 0.0361 | 0.0361 | 0.0436 | 0.0714 | 0.0436 | 0.0889 | 0.0648 | 0.0708 |
| MOP3 | 0.0549 | 0.0335 | 0.0643 | 0.0428 | 0.0418 | 0.048 | 0.0682 | 0.048 | 0.0775 | 0.0596 | 0.0418 |
| 0.2932 | 0.3955 | 0.5494 | 0.837 | 0.7324 | 1.075 | 1.8461 | 1.075 | 1.5921 | 0.6765 | 1.0536 | |
| 3.4306 | 3.3266 | 1.9608 | 2.3048 | 2.3048 | 1.9746 | 5.1139 | 1.9746 | 2.877 | 1.0895 | 2.2645 | |
| 6.1921 | 3.3484 | 3.9955 | 9.6987 | 8.932 | 9.73 | 8.5624 | 9.73 | 9.3322 | 15.3482 | 9.0585 | |
| 4.8343 | 4.9383 | 3.0527 | 6.1588 | 5.5731 | 5.0595 | 9.315 | 5.0595 | 6.9336 | 3.6986 | 3.4286 | |
| 0.0202 | 0.0275 | 0.0168 | 0.0273 | 0.0324 | 0.0243 | 0.0474 | 0.0243 | 0.0414 | 0.0268 | 0.0246 |
| Items | Unit | Initial | MGA | CMA-ES | PADO | HMA | |
|---|---|---|---|---|---|---|---|
| Objective Function | MOP3 | % | 95.85 | 95.94 | 95.93 | 95.99 | 95.93 |
| MOP2 | % | 95.99 | 96.46 | 96.03 | 96.06 | 96.03 | |
| MOP1 | % | 96.45 | 96.56 | 96.52 | 96.55 | 96.52 | |
| Constraints | % | 8.01 | 6.88 | 7.4 | 6.89 | 7.4 | |
| Nm | 250.6 | 247.7 | 248.3 | 247 | 248.5 | ||
| Nm | 76.48 | 83.17 | 90.49 | 83.19 | 83.79 | ||
| V | 362.4 | 360 | 358.95 | 365.1 | 363.5 | ||
| V | 8.74 | 8.83 | 9.21 | 6.12 | 8.92 | ||
| Items | Unit | Initial | Optimal (Metamodel) | Optimal (FEA) | |
| Design Variables | X1 | mm | 0.41 | 1.71 | |
| X2 | mm | 0.7 | 0.54 | ||
| X3 | mm | 0.85 | 1.5 | ||
| X4 | mm | 0.9 | 1.24 | ||
| X5 | ° | 145 | 140 | ||
| Objective Function | MOP1 | % | 95.73 | 96.52 | 96.56 |
| MOP2 | % | 95.99 | 96.32 | 96.46 | |
| MOP3 | % | 95.85 | 95.86 | 95.94 | |
| Constraints | % | 8.01 | 6.49 | 6.88 | |
| Nm | 250.55 | 248.82 | 247.73 | ||
| Nm | 76.48 | 83.16 | 83.17 | ||
| V | 362.37 | 357.93 | 360 | ||
| % | 8.74 | 8.88 | 8.93 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, G.-h.; You, Y.-m. Efficiency Optimization of the Main Operating Points of an EV Traction Motor. Appl. Sci. 2025, 15, 368. https://doi.org/10.3390/app15010368
Lee G-h, You Y-m. Efficiency Optimization of the Main Operating Points of an EV Traction Motor. Applied Sciences. 2025; 15(1):368. https://doi.org/10.3390/app15010368
Chicago/Turabian StyleLee, Gi-haeng, and Yong-min You. 2025. "Efficiency Optimization of the Main Operating Points of an EV Traction Motor" Applied Sciences 15, no. 1: 368. https://doi.org/10.3390/app15010368
APA StyleLee, G.-h., & You, Y.-m. (2025). Efficiency Optimization of the Main Operating Points of an EV Traction Motor. Applied Sciences, 15(1), 368. https://doi.org/10.3390/app15010368






