Co-Simulation Model for Determination of Optimal Active Power Filters Settings in Low-Voltage Network
Abstract
:1. Introduction
2. Literature Overview
| Test System | Reference | Variable Load/Variable Harmonic Level | Nonlinearity in Bus |
|---|---|---|---|
| IEEE 5 | [16] | No | 1 bus |
| [20] | No | 2 bus | |
| IEEE 16 | [34] | No | 5 bus |
| IEEE 17 | [22] | No | 8 bus |
| IEEE 18 | [35] | No | 3 bus |
| [36] | Two cases | 5 bus | |
| [36] | Three test cases | 3 NLL *1 | |
| [37] | Three test cases | 5 + 2 NLL *1 | |
| [38] | Three test cases | 6 bus | |
| [17] | No | 3 bus | |
| [39] | No | 3 bus | |
| IEEE 33 | [11] | Three test cases | max 5 bus |
| [40] | No | 5 bus with PV | |
| [39] | No | 3 bus | |
| IEEE 69 | [32] | YES | 8 bus (ends of RDS *2) |
| [34] | No | 19 bus | |
| RDS 5 | [16] | No | 3 NLL *1 |
| RDS 13 | [18] | No | 6 bus |
| RDS 17 | [12] | Yes (three cases) | 7 bus |
| [41] | No | 7 bus | |
| [42] | Three cases | 3 type of NLL *1 | |
| RDS 20 | [15] | No | 4 bus |
| RDS 33 | [20] | No | 4 bus (ends of RDS *2) |
| Lab. setup 7. Buses | [43] | No | 3 NLL *1 |
| Industrial plant | [44,45] | No | not specified |
| [23] | Percentage increase in the share of RES *3 | different types—34% of the load | |
| Ski station | [4] | No | 20 bus |
| Mine | [33] | No | different types of NLL *1 |
| 3-phase 415 V AC system | [46] | Yes (six test cases) | different types of NLL *1 |
Applied Optimization Objective Functions with Constraints in APF Allocation
- The effective values of the APF currents must be greater than the lower limit () and less than the upper limit () that the filter can provide.
- The effective values of the successive current harmonics of the APF are limited according to the physical limits of the APF.
- Commercially available sizes of APFs can be considered by introducing the size of the basic unit of the APF.
- The values of THDV and/or THDI at all buses must be lower than the specified prescribed values based on the standards and regulations that the authors refer to.
- The individual values of voltage and/or current harmonics at all buses must be lower than the specified prescribed values, depending on the standards and regulations referenced by the authors.
- Developing a co-simulation optimization model to determine the parameters and optimal settings of the parallel APF in an unbalanced low-voltage network.
- Optimal allocation of APFs with variability of harmonic spectra of different load types.
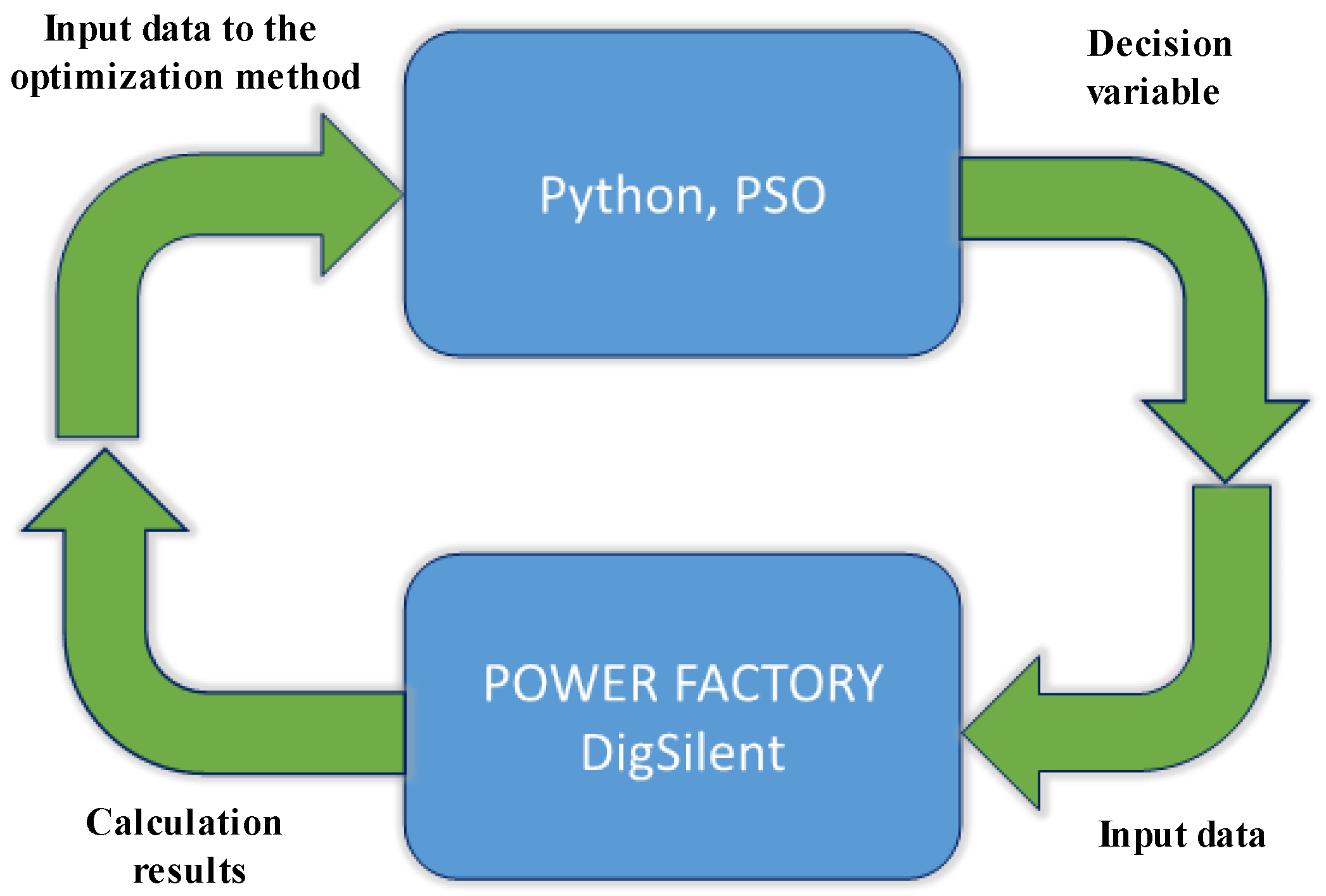
3. Optimization Framework
4. Problem Formulation
4.1. Optimization Problem Formulation
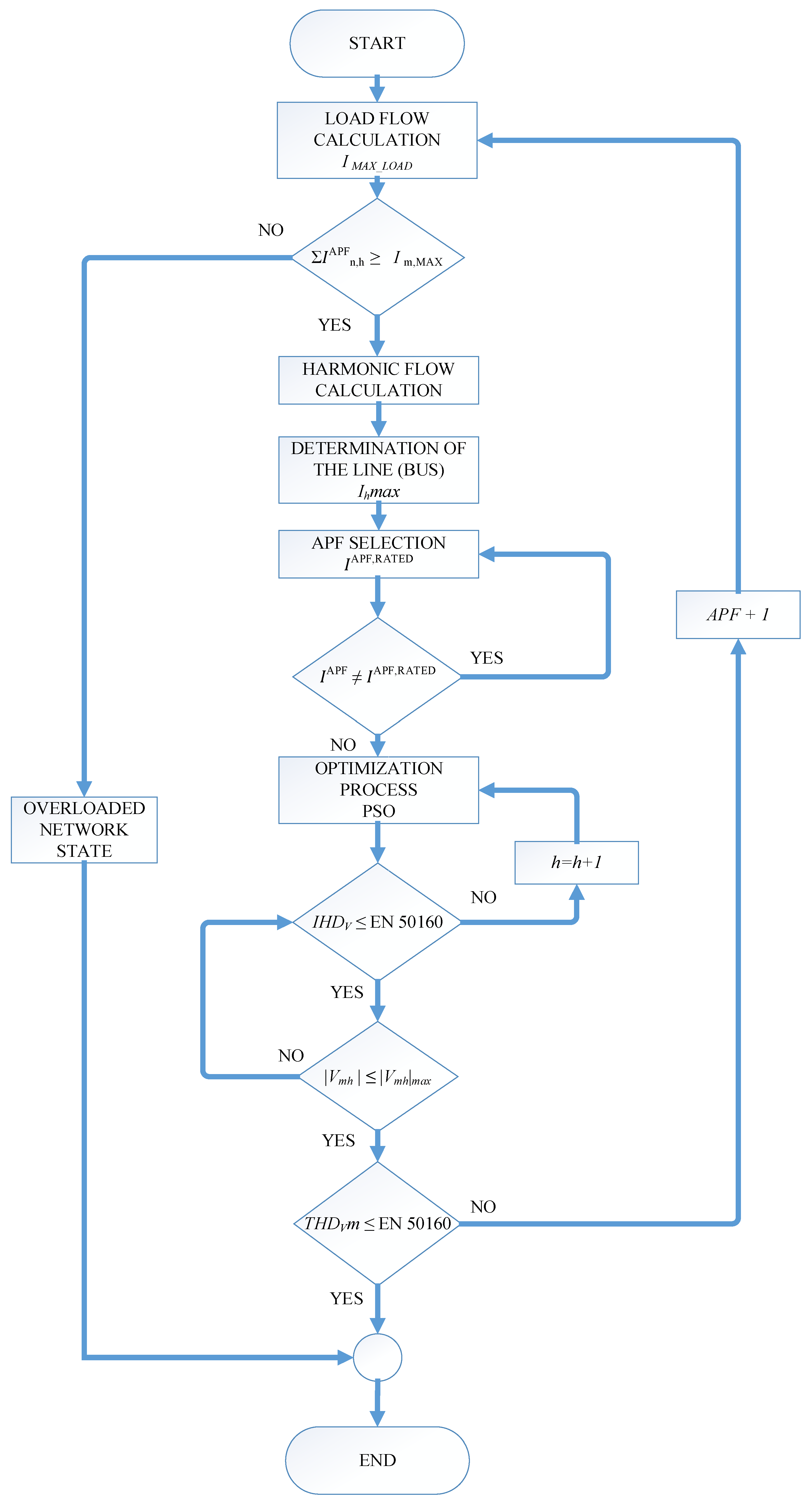
4.2. Algorithm for Determining Optimal Settings for APF
- Underloaded state of the test network
- 2.
- Additional underloaded state of network
- 3.
- Normal state of the test network
- 4.
- Additional normal state of network
- 5.
- Overloaded state of the test network
5. Evaluation of the Optimization Method for Determining Parameters and Optimal APF Settings in the Test Network
5.1. Test Network Model
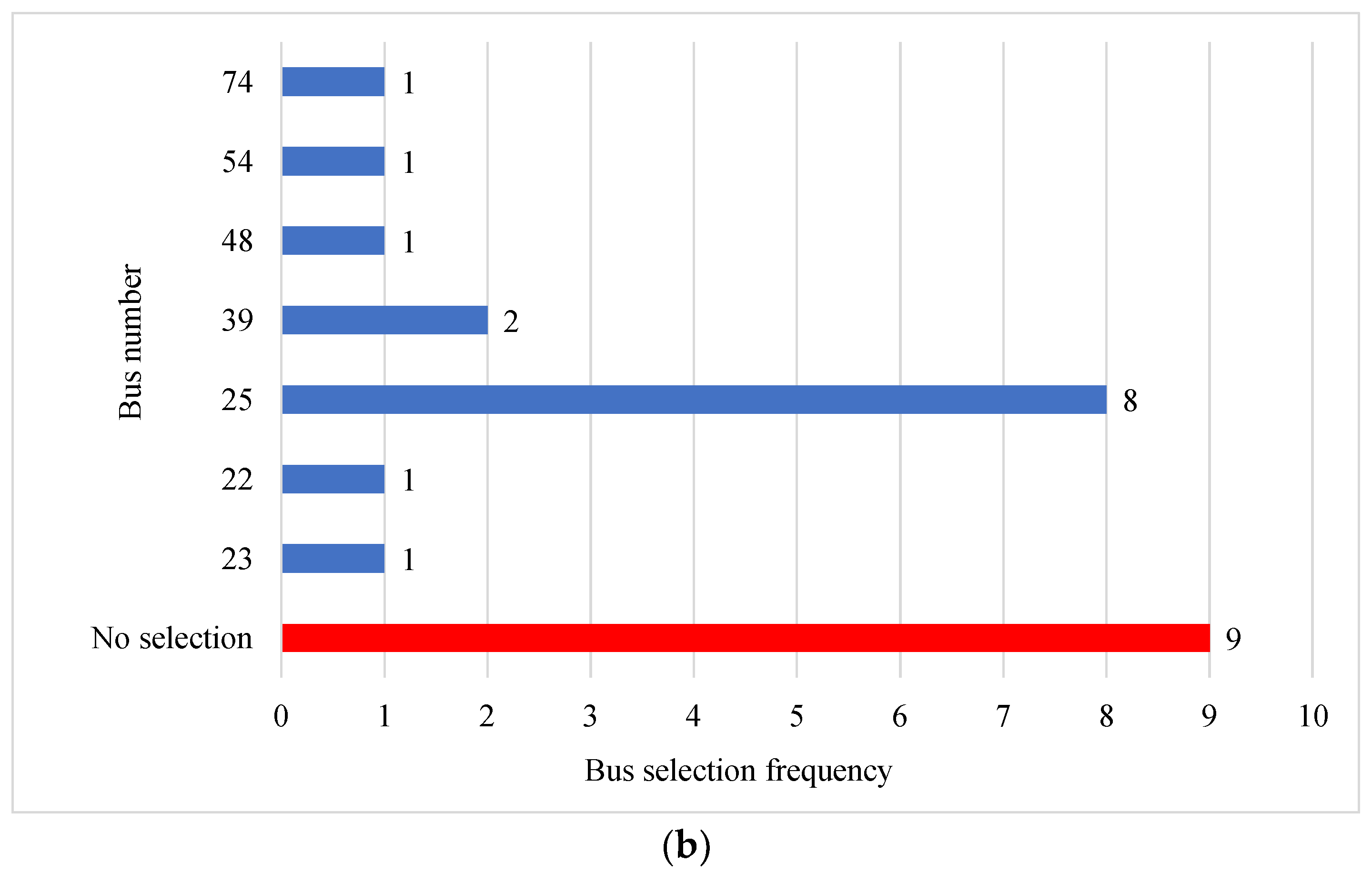
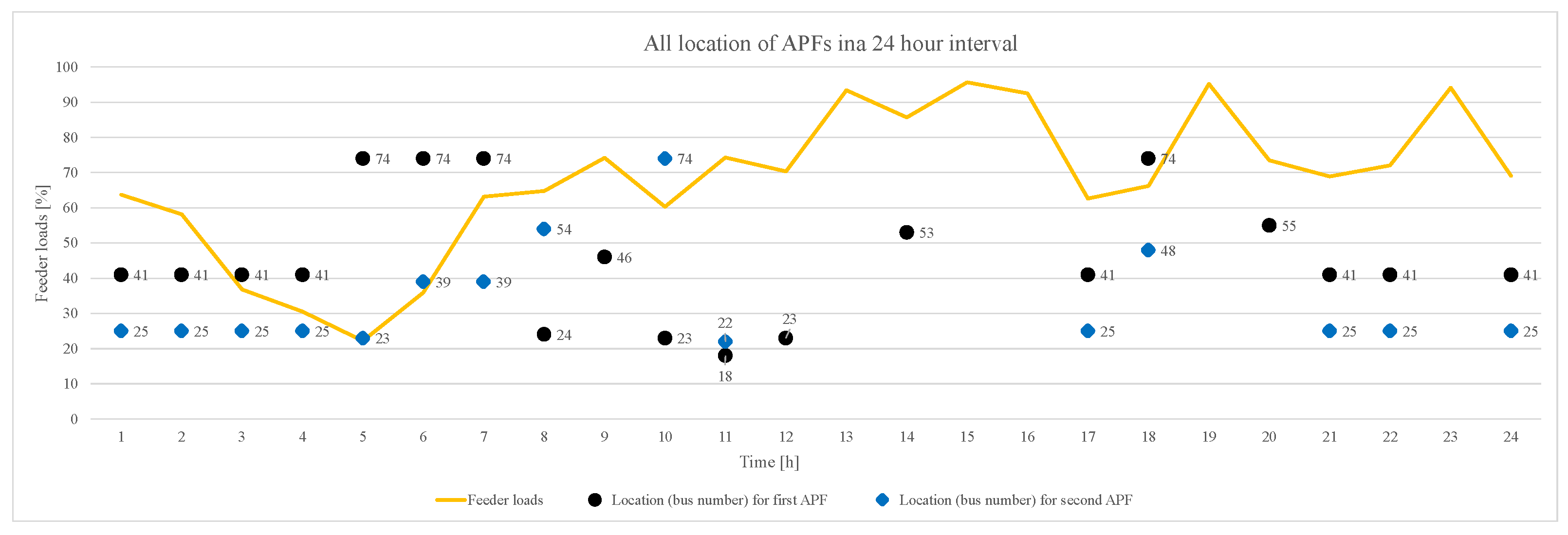
5.2. Algorithm Results over 24 H
- First state of test network (24:00 p.m.–4:00 a.m.)
- Second state of test network (4:00 a.m.–7:00 a.m.)
- Third state of test network (at 7:00 a.m., 8:00 a.m., 10:00 a.m., 11:00 a.m., 5:00 p.m., 6:00 p.m., 9:00 p.m., and 10:00 p.m.)
- Fourth state of test network (9:00 a.m., 12:00 a.m., 2:00 p.m., and 8:00 p.m.)
- Fifth state of test network (1:00 p.m., 3:00 p.m., 4:00 p.m., 7:00 p.m. and 11:00 p.m.)
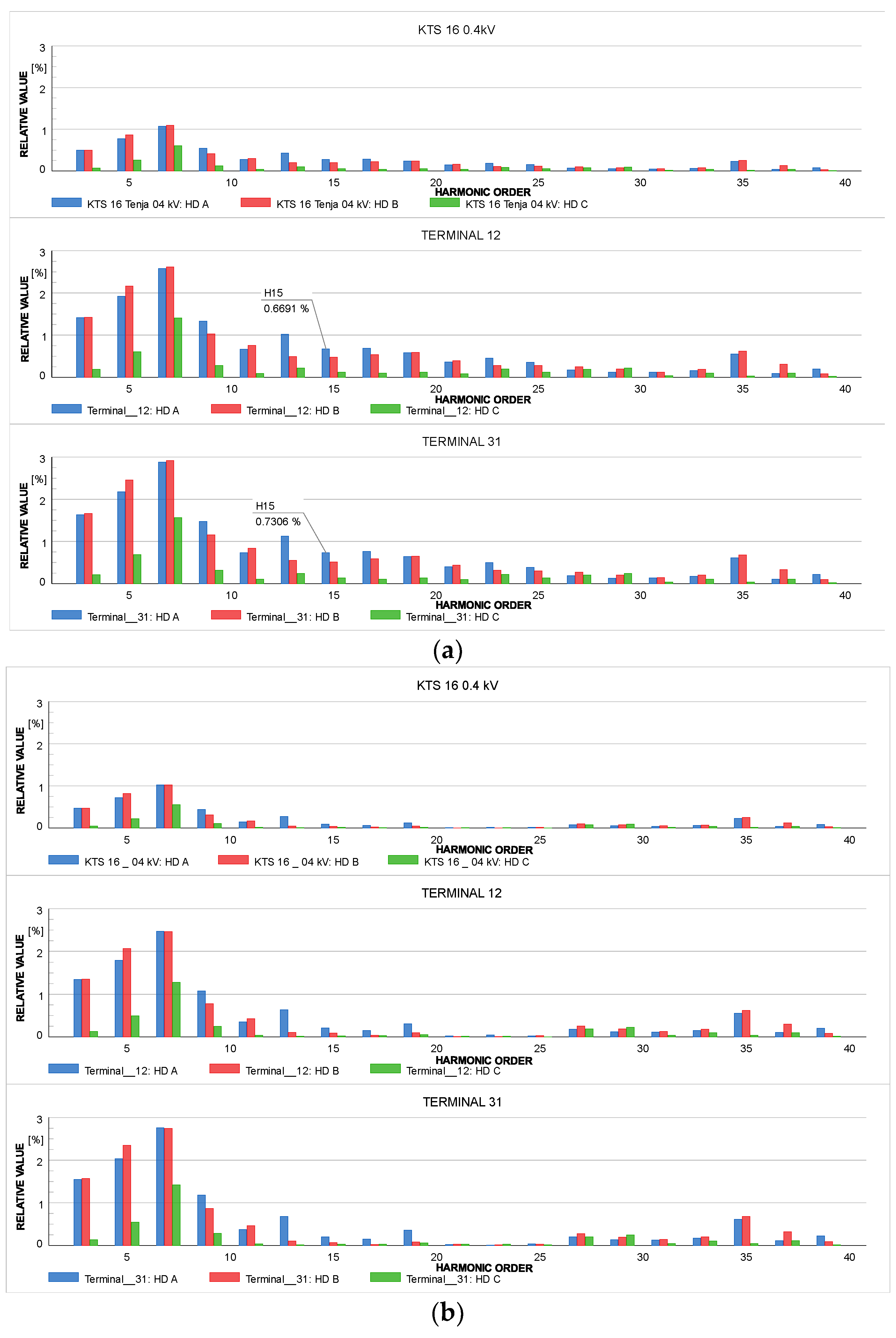
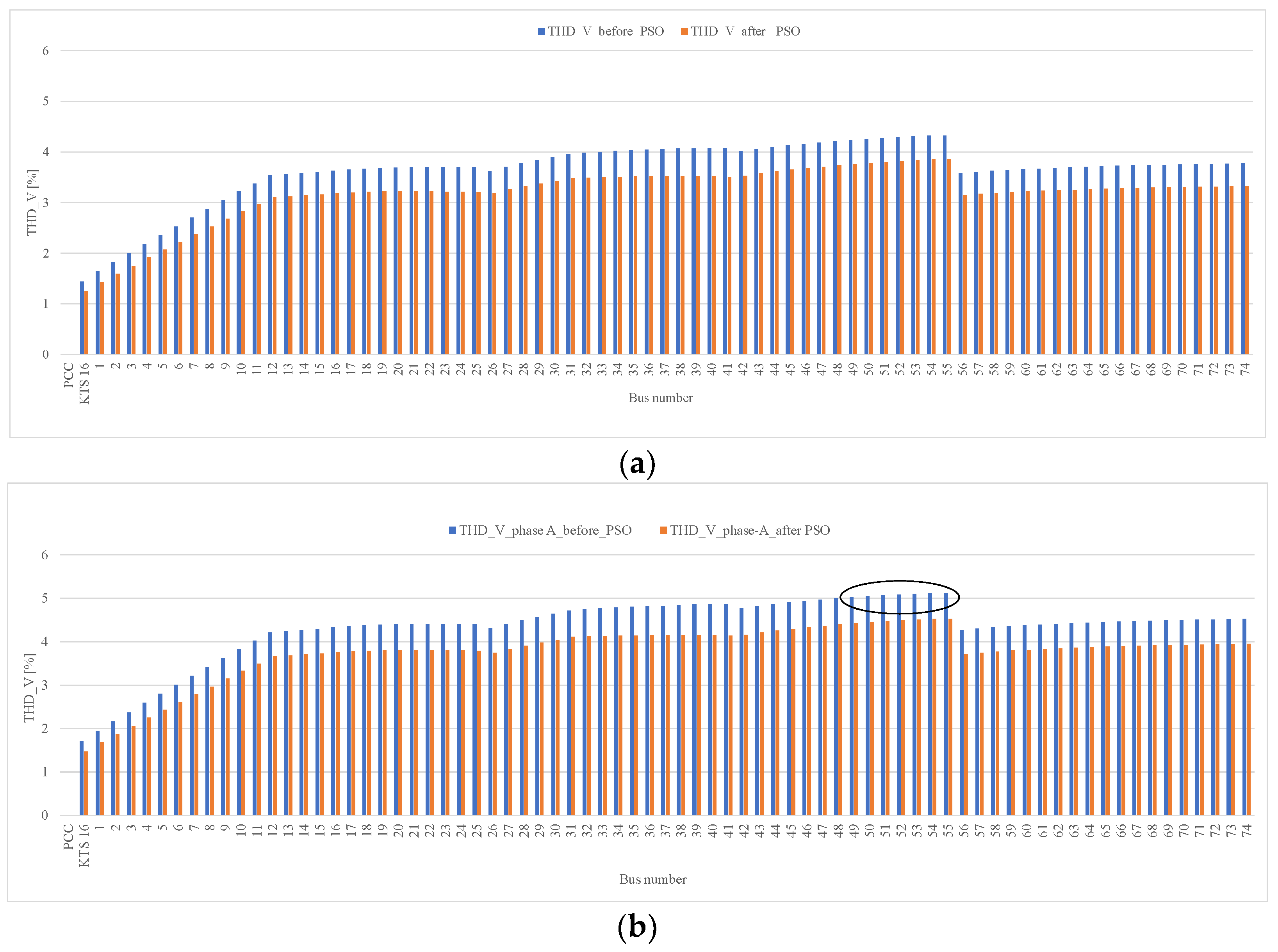
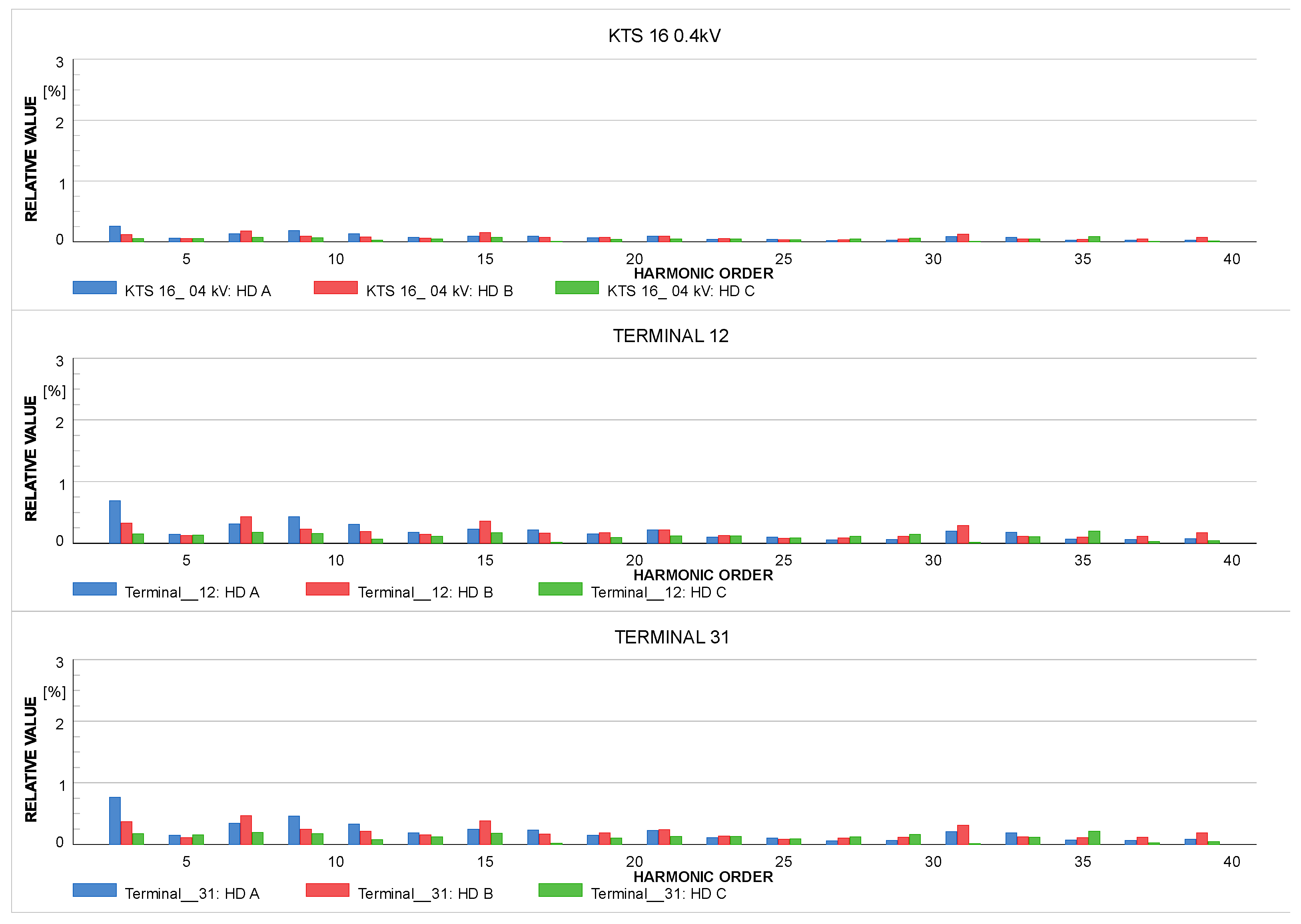
6. Discussion
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Antić, T.; Thurner, L.; Capuder, T.; Pavić, I. Modeling and open source implementation of balanced and unbalanced harmonic analysis in radial distribution networks. Electr. Power Syst. Res. 2022, 209, 107935. [Google Scholar] [CrossRef]
- EN 50160:2010; Voltage Characteristics of Electricity Supplied by Public Electricity Networks. European Standard: Brussels, Belgium, 2010.
- 519-2022; IEEE Standard for Harmonic Control in Electric Power Systems. IEEE: Piscataway, NJ, USA, 2022. Available online: https://ieeexplore.ieee.org/servlet/opac?punumber=9848438 (accessed on 20 April 2024). [CrossRef]
- Klimas, M.; Grabowski, D.; Buła, D. Application of decision trees for optimal allocation of harmonic filters in medium-voltage networks. Energies 2021, 14, 1173. [Google Scholar] [CrossRef]
- Jain, S. Control strategies of shunt active power filter. In Modeling and Control of Power Electronics Converter System for Power Quality Improvements; Elsevier: Amsterdam, The Netherlands, 2018; pp. 31–84. [Google Scholar] [CrossRef]
- Maciążek, M. Active Power Filters and Power Quality. Energies 2022, 15, 8483. [Google Scholar] [CrossRef]
- Fuchs Ewald, F.; Masoum Mohammad, A.S. Power Quality in Power Systems, Electrical Machines, and Power-Electronic Drives, 3rd ed.; Third. Elsevier Inc.: Amsterdam, The Netherlands, 2023. [Google Scholar] [CrossRef]
- Mrežna Pravila Distribucijskog Sustava. [Online]. Available online: https://narodne-novine.nn.hr/clanci/sluzbeni/2018_08_74_1539.html (accessed on 20 April 2024).
- Buła, D.; Grabowski, D.; Maciążek, M. A Review on Optimization of Active Power Filter Placement and Sizing Methods. Energies 2022, 15, 1175. [Google Scholar] [CrossRef]
- Hermina, A.; Alan, A.; Angelo, B. Handbook of Power Quality, 1st ed.; John Wiley & Sons Ltd.: Chichester, UK, 2008; Volume 1. [Google Scholar]
- Brahmachary, R.; Bhattacharya, A.; Ahmed, I. Allocation of Active Power Filter in Distribution Network Considering Nonlinear Loads. In Proceedings of the 2021 IEEE 2nd International Conference on Smart Technologies for Power, Energy and Control, STPEC 2021, Bilaspur, India, 19–22 December 2021; Institute of Electrical and Electronics Engineers Inc.: New York, NY, USA, 2021. [Google Scholar] [CrossRef]
- Carpinelli, G.; Proto, D.; Russo, A. Optimal Planning of Active Power Filters in a Distribution System Using Trade-off/Risk Method. IEEE Trans. Power Deliv. 2017, 32, 841–851. [Google Scholar] [CrossRef]
- Guo, M.; Jin, Q.; Yao, Z. Implementation of Adaptive Step-Size Algorithm in Distribution Network for Optimal Location and Sizing of SAPFs. In Proceedings of the 2020 IEEE/IAS Industrial and Commercial Power System Asia, I and CPS Asia 2020, Weihai, China, 13–16 July 2020; pp. 1562–1566. [Google Scholar] [CrossRef]
- Revuelta, P.S.; Litrán, S.P.; Thomas, J.P. Active Power Line Conditioners: Design, Simulation and Implementation for Improving Power Quality; Academic Press: Cambridge, MA, USA, 2015; pp. 1–421. [Google Scholar] [CrossRef]
- Wang, Y.S.; Hua, S.; Liu, X.M.; Jun, L.; Gou, S.B. Optimal allocation of the active filters based on the Tabu algorithm in distribution network. In Proceedings of the International Conference on Electrical and Control Engineering, ICECE 2010, Wuhan, China, 25–27 June 2010; pp. 1418–1421. [Google Scholar] [CrossRef]
- Moradifar, A.; Soleymanpour, H.R. A fuzzy based solution for allocation and sizing of multiple active power filters. J. Power Electron. 2012, 12, 830–841. [Google Scholar] [CrossRef]
- Shivaie, M.; Salemnia, A.; Ameli, M.T. A multi-objective approach to optimal placement and sizing of multiple active power filters using a music-inspired algorithm. Appl. Soft Comput. J. 2014, 22, 189–204. [Google Scholar] [CrossRef]
- Alhaddad, F.M.; El-Hawary, M. Optimal filter placement and sizing using ant colony optimization in electrical distribution system. In Proceedings of the 2014 Electrical Power and Energy Conference, EPEC 2014, Calgary, AB, Canada, 12–14 November 2014; Institute of Electrical and Electronics Engineers Inc.: New York, NY, USA, 2014; pp. 128–133. [Google Scholar] [CrossRef]
- Rosyadi, A.; Penangsang, O.; Soeprijanto, A. Optimal filter placement and sizing in Radial Distribution System using whale optimization algorithm. In Proceedings of the 2017 International Seminar on Intelligent Technology and Its Application: Strengthening the Link Between University Research and Industry to Support ASEAN Energy Sector, ISITIA 2017—Proceeding, Surabaya, Indonesia, 28–29 August 2017; pp. 87–92. [Google Scholar] [CrossRef]
- Lakum, A.; Mahajan, V. Optimal placement and sizing of multiple active power filters in radial distribution system using grey wolf optimizer in presence of nonlinear distributed generation. Electr. Power Syst. Res. 2019, 173, 281–290. [Google Scholar] [CrossRef]
- Sindhu, M.R.; Jisma, M.; Maya, P.; Krishnapriya, P.; Mohan, M.V. Optimal Placement and Sizing of Harmonic and Reactive Compensators in Interconnected Systems. In Proceedings of the 2018 15th IEEE India Council International Conference (INDICON), Coimbatore, India, 16–18 December 2018. [Google Scholar] [CrossRef]
- MacIazek, M.; Grabowski, D.; Pasko, M. Genetic and combinatorial algorithms for optimal sizing and placement of active power filters. Int. J. Appl. Math. Comput. Sci. 2015, 25, 269–279. [Google Scholar] [CrossRef]
- Ahmed, M.; Al Masood, N.; Aziz, T. An approach of incorporating harmonic mitigation units in an industrial distribution network with renewable penetration. Energy Rep. 2021, 7, 6273–6291. [Google Scholar] [CrossRef]
- Ziari, I.; Jalilian, A. Optimal placement and sizing of multiple APLCs using a modified discrete PSO. Int. J. Electr. Power Energy Syst. 2012, 43, 630–639. [Google Scholar] [CrossRef]
- Houran, M.A.; Sabzevari, K.; Hassan, A.; Oubelaid, A.; Tostado-Véliz, M.; Khosravi, N. Active power filter module function to improve power quality conditions using GWO and PSO techniques for solar photovoltaic arrays and battery energy storage systems. J. Energy Storage 2023, 72, 108552. [Google Scholar] [CrossRef]
- Samet, H.; Hashemi, F.; Ghanbari, T. Minimum non detection zone for islanding detection using an optimal Arti fi cial Neural Network algorithm based on PSO. Renew. Sustain. Energy Rev. 2015, 52, 1–18. [Google Scholar] [CrossRef]
- Krama, A.; Zellouma, L.; Benaissa, A.; Rabhi, B.; Bouzidi, M.; Benkhoris, M.F. Design and Experimental Investigation of Predictive Direct Power Control of Three-Phase Shunt Active Filter with Space Vector Modulation using Anti-windup PI Controller Optimized by PSO. Arab. J. Sci. Eng. 2019, 44, 6741–6755. [Google Scholar] [CrossRef]
- El-Arwash, H.M.; Azmy, A.M.; Rashad, E.M. A GA-Based Initialization of PSO for Optimal APFs Allocation in Water Desalination Plant. In Proceedings of the 2017 Nineteenth International Middle East Power Systems Conference (MEPCON), Cairo, Egypt, 19–21 December 2017. [Google Scholar] [CrossRef]
- Gad, A.G. Particle Swarm Optimization Algorithm and Its Applications: A Systematic Review. Arch. Comput. Methods Eng. 2022, 29, 2531–2561. [Google Scholar] [CrossRef]
- Al-Shetwi, A.Q.; Sujod, M.Z.; Hannan, M.A.; Abdullahd, M.A.; Al-Ogaili, A.S.; Jern, K.P. Impact of Inverter Controller-Based Grid-Connected PV System in the Power Quality. Int. J. Electr. Electron. Eng. Telecommun. 2020, 9, 462–469. [Google Scholar] [CrossRef]
- Ikic, M.; Colic, B.; Mikulovic, J.; Jokic, S. Impact assessment of irradiance and temperature variation on PV system current harmonics injection. In Proceedings of the 2022 21st International Symposium Infoteh-Jahorina, Infoteh 2022—Proceedings, East Sarajevo, Bosnia and Herzegovina, 16–18 March 2022; Institute of Electrical and Electronics Engineers Inc.: New York, NY, USA, 2022. [Google Scholar] [CrossRef]
- Lakum, A.; Mahajan, V. A novel approach for optimal placement and sizing of active power filters in radial distribution system with nonlinear distributed generation using adaptive grey wolf optimizer. Eng. Sci. Technol. Int. J. 2021, 24, 911–924. [Google Scholar] [CrossRef]
- Buła, D.; Grabowski, D.; Lewandowski, M.; Maciażek, M.; Piwowar, A. Software solution for modeling, sizing, and allocation of active power filters in distribution networks. Energies 2021, 14, 133. [Google Scholar] [CrossRef]
- Farhoodnea, M.; Mohamed, A.; Shareef, H.; Zayandehroodi, H. Optimum placement of active power conditioner in distribution systems using improved discrete firefly algorithm for power quality enhancement. Appl. Soft Comput. 2014, 23, 249–258. [Google Scholar] [CrossRef]
- Keypour, R.; Seifi, H.; Yazdian-Varjani, A. Genetic based algorithm for active power filter allocation and sizing. Electr. Power Syst. Res. 2004, 71, 41–49. [Google Scholar] [CrossRef]
- Ziari, I.; Jalilian, A. A new approach for allocation and sizing of multiple active power-line conditioners. IEEE Trans. Power Deliv. 2010, 25, 1026–1035. [Google Scholar] [CrossRef]
- Chicco, G.; Postolache, P.; Toader, C. Triplen harmonics: Myths and reality. Electr. Power Syst. Res. 2011, 81, 1541–1549. [Google Scholar] [CrossRef]
- Yang, Z.; Zhuo, F.; Tao, R.; Zhang, Z.; Yi, H.; Wang, M.; Zhu, C. Implementation of Multi-objective Particle Swarm Optimization in Distribution Network for Highefficiency Allocation and Sizing of SAPFs. In Proceedings of the 22nd International Conference on Electrical Machines and Systems (ICEMS), Harbin, China, 11–14 August 2019. [Google Scholar] [CrossRef]
- Far, A.M.; Foroud, A.A. Cost-effective optimal allocation and sizing of active power filters using a new fuzzy-MABICA method. IETE J. Res. 2016, 62, 307–322. [Google Scholar] [CrossRef]
- Guo, W.; Xu, W. Research on optimization strategy of harmonic suppression and reactive power compensation of photovoltaic multifunctional grid connected inverter. Int. J. Electr. Power Energy Syst. 2023, 145, 108649. [Google Scholar] [CrossRef]
- Guido, C.; Angela, R.; Pietro, V. Active filters: A multi-objective approach for the optimal allocation and sizing in distribution networks. In Proceedings of the 2014 International Symposium on Power Electronics, Ischia, Italy, 18–20 June 2014. [Google Scholar] [CrossRef]
- Carpinelli, G.; Mottola, F.; Proto, D.; Russo, A. A Decision Theory Approach for the Multi-objective Optimal Allocation of Active Filters in Smart Grids. In Proceedings of the International Conference on Harmonics and Quality of Power, ICHQP, Naples, Italy, 29 May–1 June 2022; IEEE Computer Society: Washington, DC, USA, 2022. [Google Scholar] [CrossRef]
- Zhai, H.; Zhuo, F.; Zhu, C.; Yi, H.; Wang, Z.; Tao, R.; Wei, T. An Optimal Compensation Method of Shunt Active Power Filters for System-Wide Voltage Quality Improvement. IEEE Trans. Ind. Electron. 2020, 67, 1270–1281. [Google Scholar] [CrossRef]
- Biswas, P.P.; Suganthan, P.N.; Amaratunga, G.A.J. Minimizing harmonic distortion in power system with optimal design of hybrid active power filter using differential evolution. Appl. Soft Comput. J. 2017, 61, 486–496. [Google Scholar] [CrossRef]
- Zobaa, A.F. Optimal multiobjective design of hybrid active power filters considering a distorted environment. IEEE Trans. Ind. Electron. 2014, 61, 107–114. [Google Scholar] [CrossRef]
- Mahaboob, S.; Ajithan, S.K.; Jayaraman, S. Optimal design of shunt active power filter for power quality enhancement using predator-prey based firefly optimization. Swarm Evol. Comput. 2019, 44, 522–533. [Google Scholar] [CrossRef]
- Chang, W.K.; Empros, S.; Park, B. Minimizing Harmonic Voltage Distortion with Multiple Current-Constrained Active Power Line Conditioners. IEEE Trans. Power Deliv. 1997, 12, 837–843. [Google Scholar] [CrossRef]
- Devassy, S.; Singh, B. Implementation of Solar Photovoltaic System with Universal Active Filtering Capability. In IEEE Transactions on Industry Applications; Institute of Electrical and Electronics Engineers Inc.: New York, NY, USA, 2019; pp. 3926–3934. [Google Scholar] [CrossRef]
- Kumar, V.; Yadav, S.M. A State-of-the-Art Review of Heuristic and Metaheuristic Optimization Techniques for the Management of Water Resources; IWA Publishing: London UK, 2022. [Google Scholar] [CrossRef]
- Klaić, Z. Kvaliteta Električne Energije—Harmonici, Predavanja; FERIT: Osijek, Croatia, 2023. [Google Scholar]
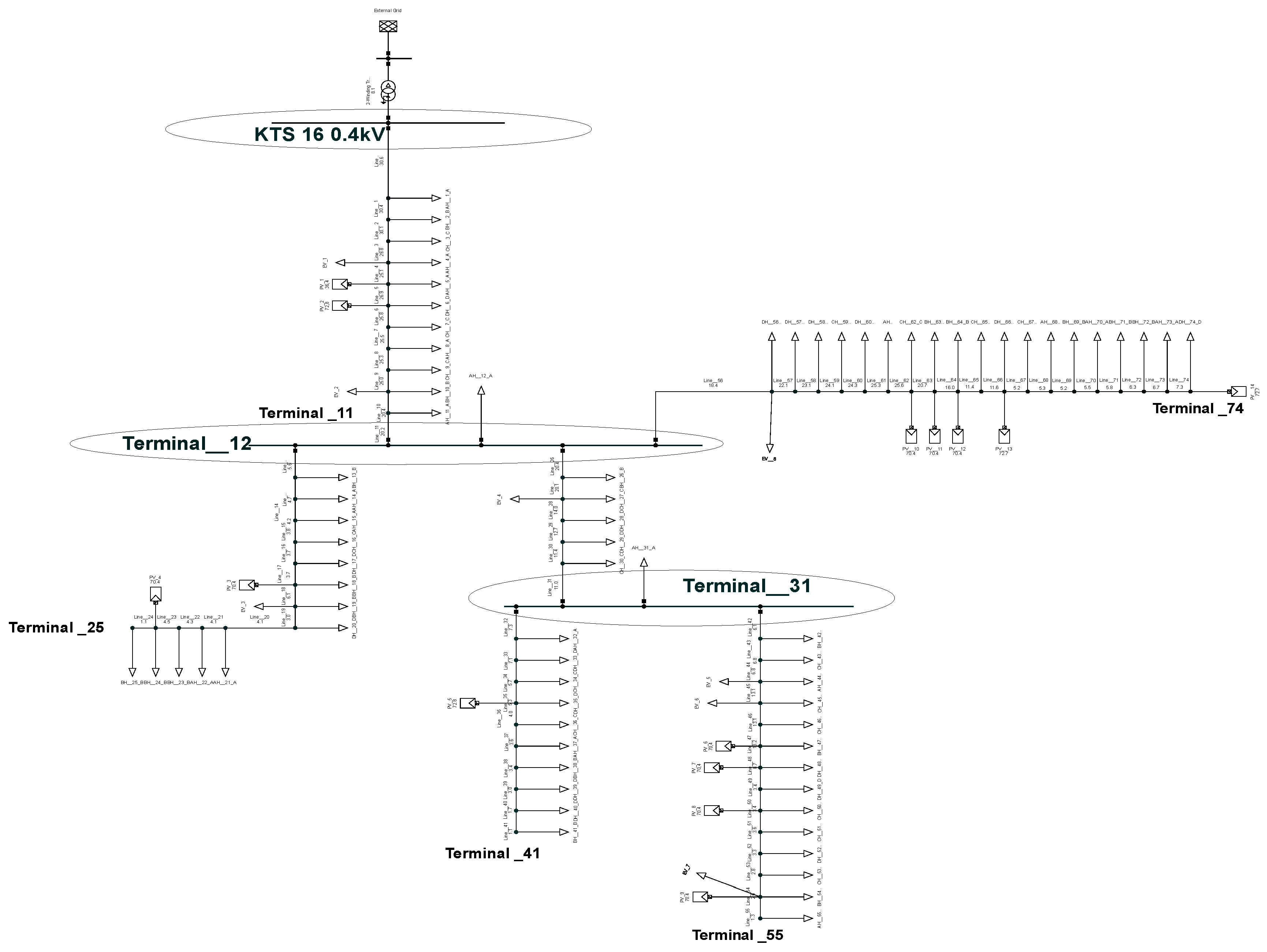

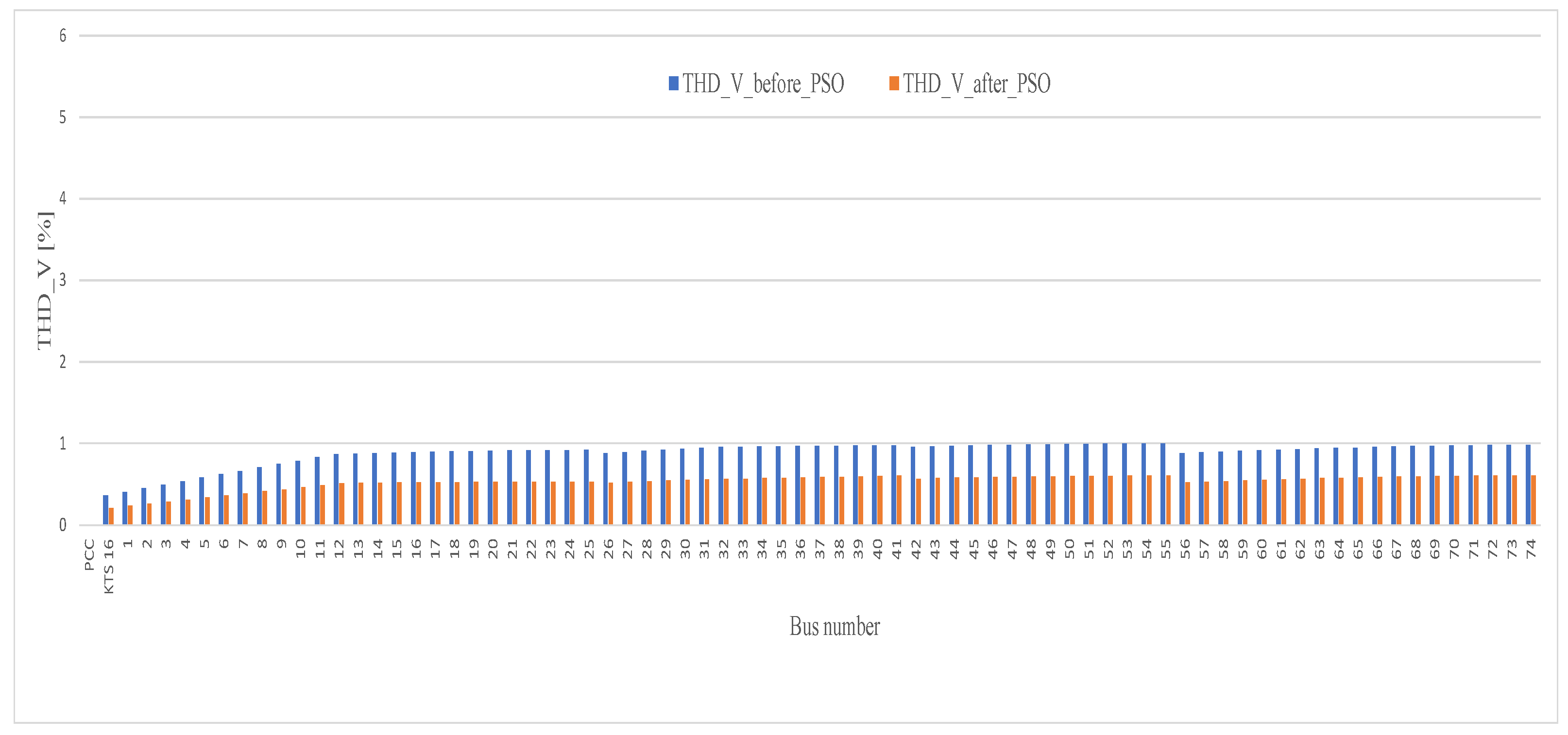
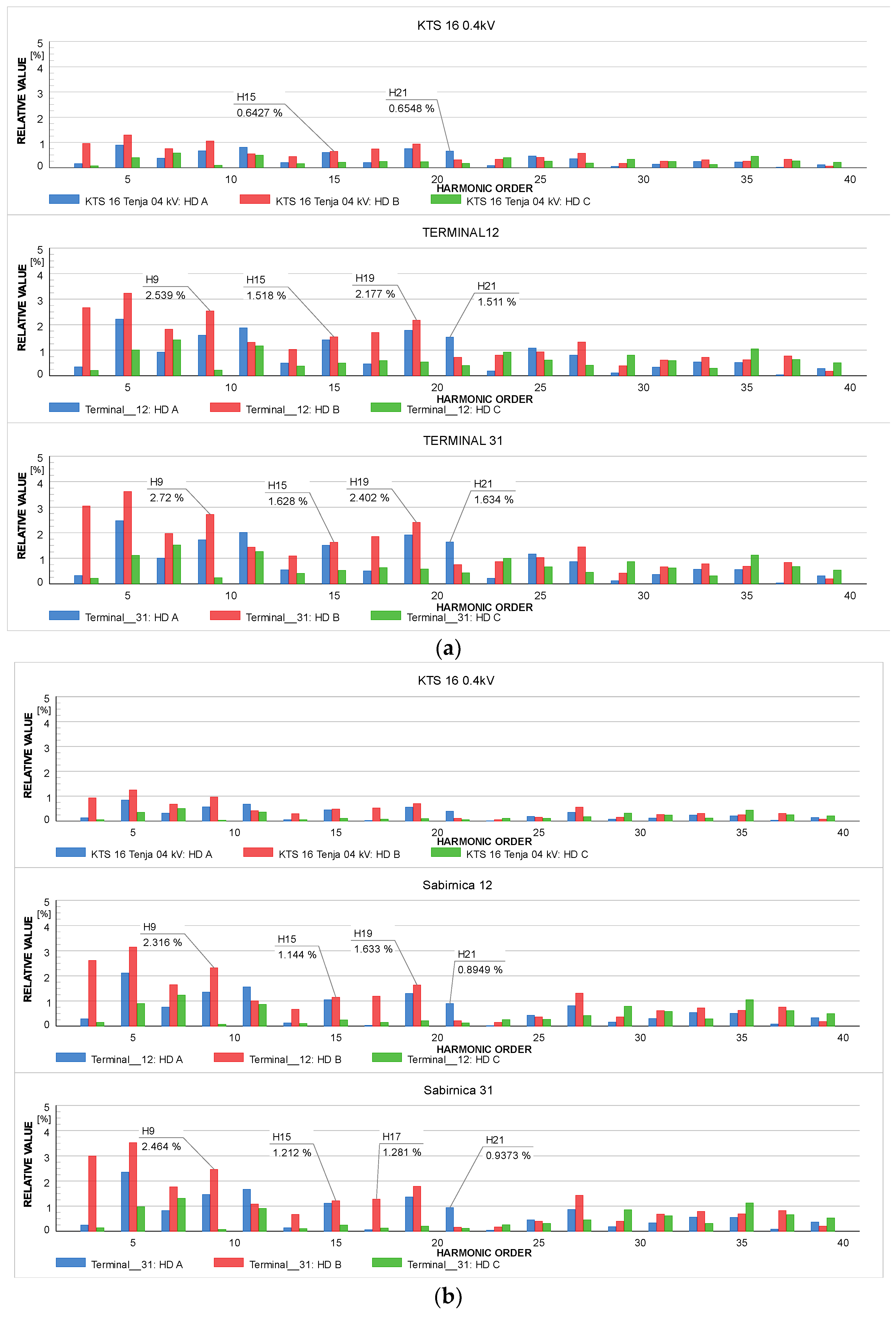

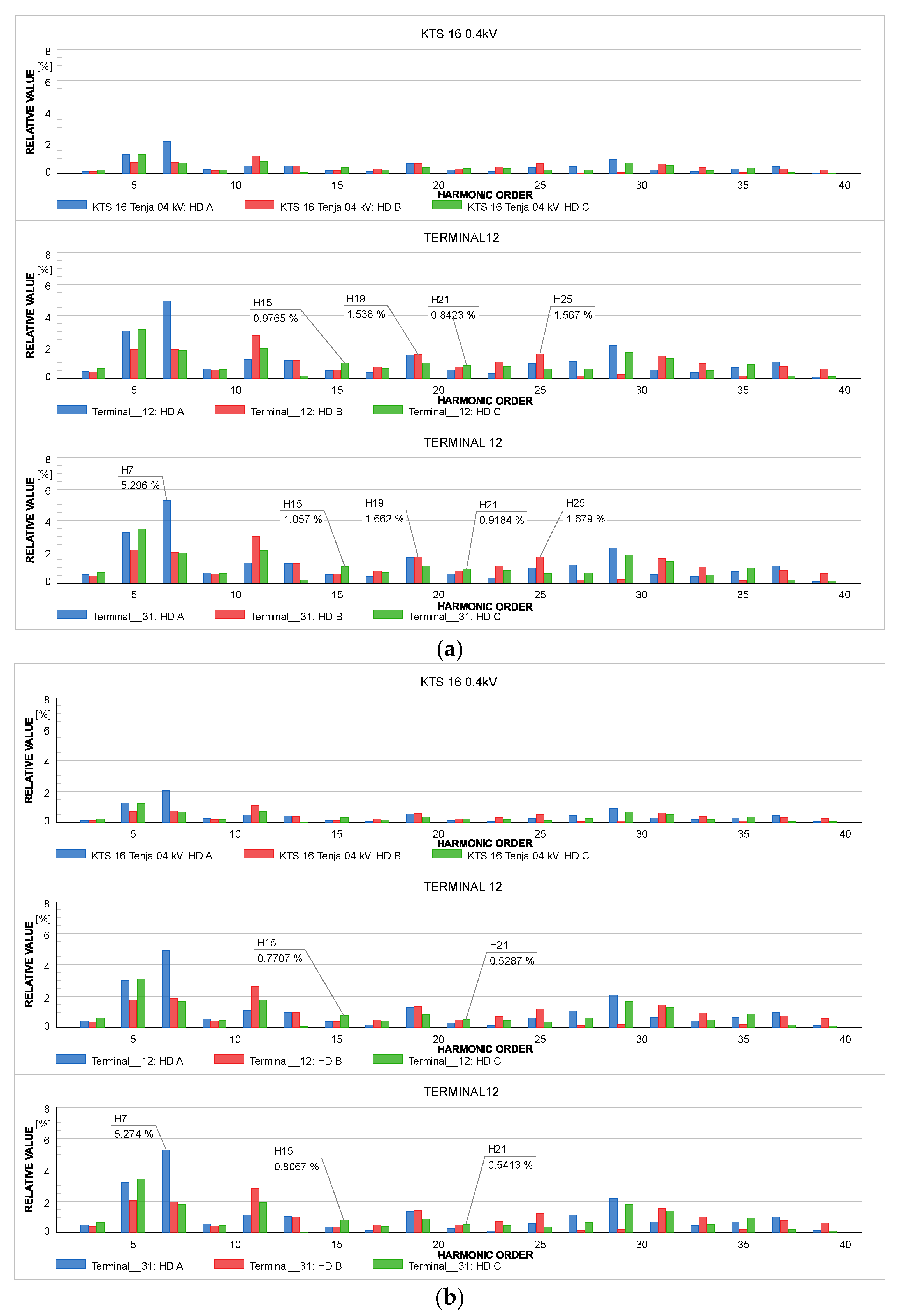

| Model | Type | Quantity | Bus Number |
|---|---|---|---|
| Uncontrollable load model | Single phase | 18 | 6, 17, 20, 28, 29, 33, 35, 39, 40, 48, 49, 52, 56, 57, 58, 60, 66, 74 |
| Three phase | 56 | All others | |
| Controllable load model | Single phase | 2 | 45, 56 |
| Three phase | 6 | 4, 10, 19, 27, 44, 54 | |
| PV system model | Single phase | 4 | 6, 35, 66, 74 |
| Three phase | 10 | 5, 18, 24, 47, 48, 50, 54, 62, 63, 64 |
| Time | PCC Loads Before Optimization | Location (Bus Number) for First APF | Location (Bus Number) for Second APF | PCC Load After Optimization |
|---|---|---|---|---|
| 1:00 a.m. | 63.7 | 41 | 25 | 96.80 |
| 2:00 a.m. | 58.2 | 41 | 25 | 97.10 |
| 3:00 a.m. | 36.8 | 41 | 25 | 85.20 |
| 4:00 a.m. | 30.5 | 41 | 25 | 83.50 |
| 5:00 a.m. | 22.2 | 74 | 23 | 76.80 |
| 6:00 a.m. | 35.9 | 74 | 39 | 86.70 |
| 7:00 a.m. | 63.2 | 74 | 39 | 96.60 |
| 8:00 a.m. | 64.8 | 24 | 54 | 98.90 |
| 9:00 a.m. | 74.2 | 46 | OL | 98.50 |
| 10:00 a.m. | 60.3 | 23 | 74 | 97.00 |
| 11:00 a.m. | 74.3 | 18 | 22 | 97.00 |
| 22:00 a.m. | 70.4 | 23 | OL | 95.00 |
| 13:00 p.m. | 93.4 | OL | OL | 93.40 |
| 14:00 p.m. | 85.7 | 53 | OL | 95.60 |
| 15:00 p.m. | 95.7 | OL | OL | 95.70 |
| 16:00 p.m. | 92.5 | OL | OL | 92.50 |
| 17:00 p.m. | 62.6 | 41 | 25 | 96.60 |
| 18:00 p.m. | 66.2 | 74 | 48 | 96.30 |
| 19:00 p.m. | 95.2 | OL | OL | 95.20 |
| 20:00 p.m. | 73.5 | 55 | OL | 96.80 |
| 21:00 p.m. | 68.9 | 41 | 25 | 95.30 |
| 22:00 p.m. | 72.1 | 41 | 25 | 97.70 |
| 23:00 p.m. | 94.1 | OL | OL | 94.10 |
| 24:00 p.m. | 69.1 | 41 | 25 | 97.80 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Primorac, M.; Klaić, Z.; Adrić, H.; Žnidarec, M. Co-Simulation Model for Determination of Optimal Active Power Filters Settings in Low-Voltage Network. Appl. Sci. 2025, 15, 469. https://doi.org/10.3390/app15010469
Primorac M, Klaić Z, Adrić H, Žnidarec M. Co-Simulation Model for Determination of Optimal Active Power Filters Settings in Low-Voltage Network. Applied Sciences. 2025; 15(1):469. https://doi.org/10.3390/app15010469
Chicago/Turabian StylePrimorac, Mario, Zvonimir Klaić, Heidi Adrić, and Matej Žnidarec. 2025. "Co-Simulation Model for Determination of Optimal Active Power Filters Settings in Low-Voltage Network" Applied Sciences 15, no. 1: 469. https://doi.org/10.3390/app15010469
APA StylePrimorac, M., Klaić, Z., Adrić, H., & Žnidarec, M. (2025). Co-Simulation Model for Determination of Optimal Active Power Filters Settings in Low-Voltage Network. Applied Sciences, 15(1), 469. https://doi.org/10.3390/app15010469







