SRB-ELL: A Vector-Friendly Sparse Matrix Format for SpMV on Scratchpad-Augmented Architectures
Abstract
1. Introduction
2. Related Works
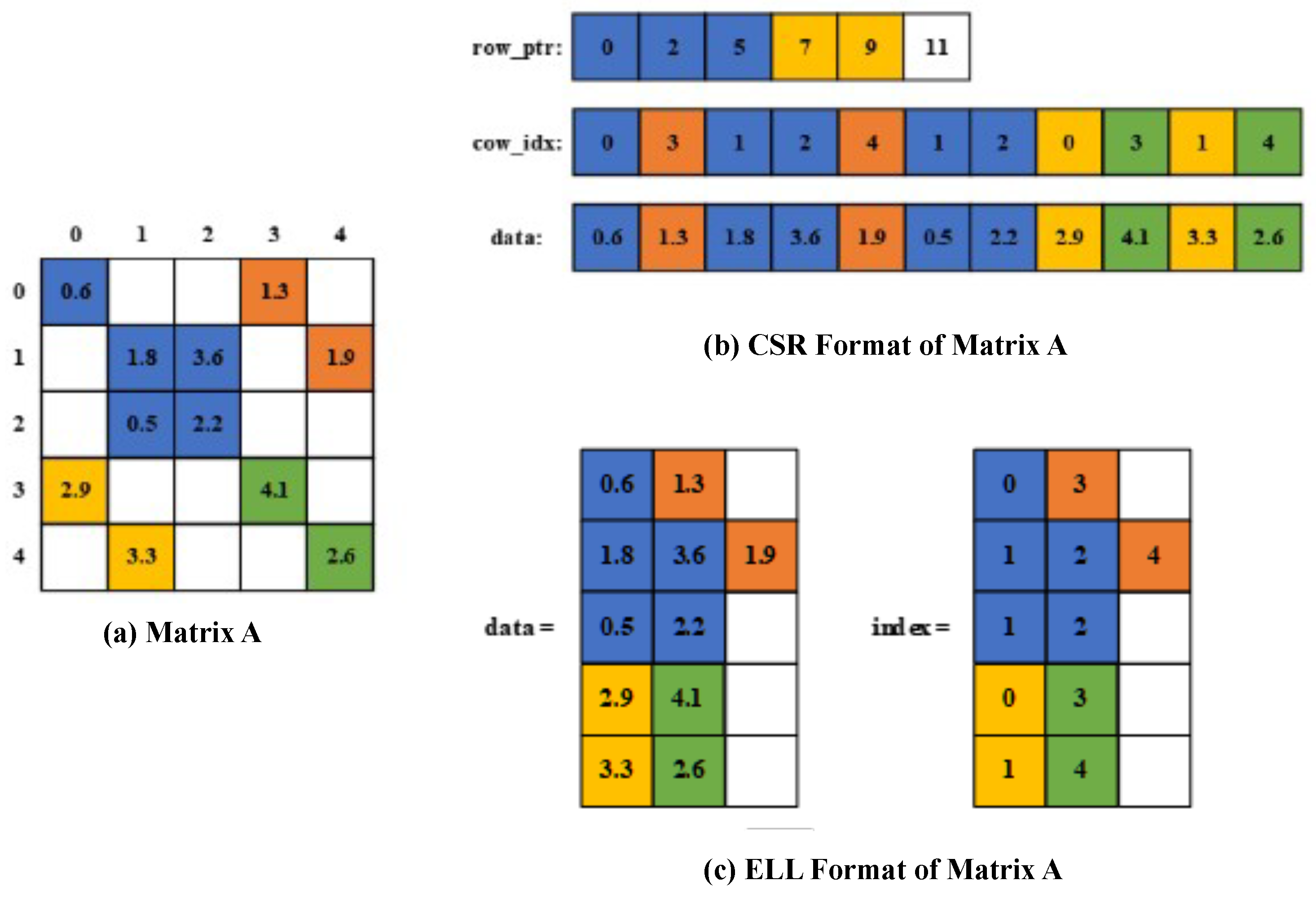
2.1. Sparse Matrix Compressed Formats
| Algorithm 1 CSR-Based SpMV Implementation. |
|
| Algorithm 2 ELL-Based SpMV Implementation. |
|
2.2. SpMV Vectorization Bottlenecks
3. Design and Implementation
3.1. SRB-ELL Design and Vectorized Algorithm
- dividing the matrix into row blocks;
- storing each block independently;
- sorting blocks by increasing row length;
- removing blocks with zero-length rows.
| Algorithm 3 SVE Vectorized SRB-ELL SpMV Implementation. |
|
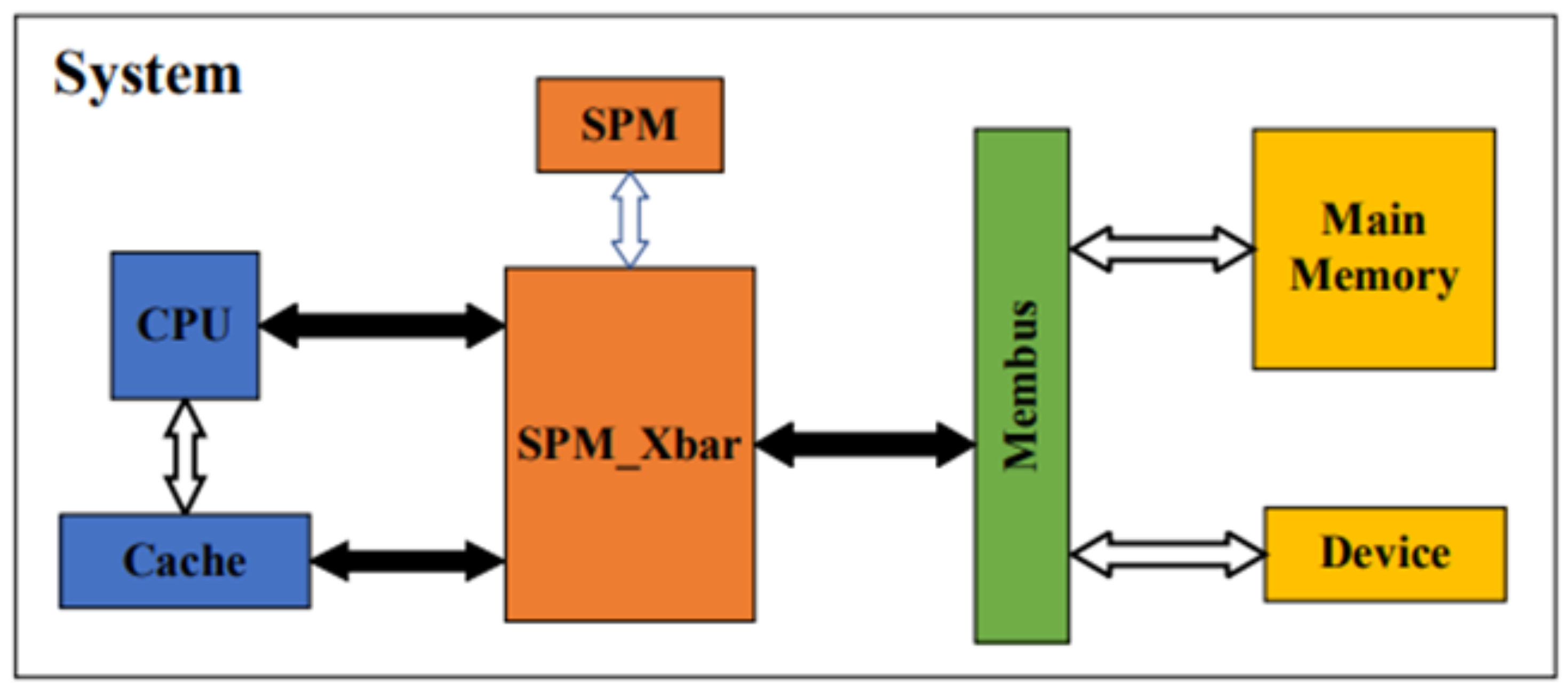
3.2. Scratchpad Memory Implementation in gem5
4. Results
4.1. Full-System Simulation Infrastructure
4.2. Real-World Data Sets
4.3. Experimental Results
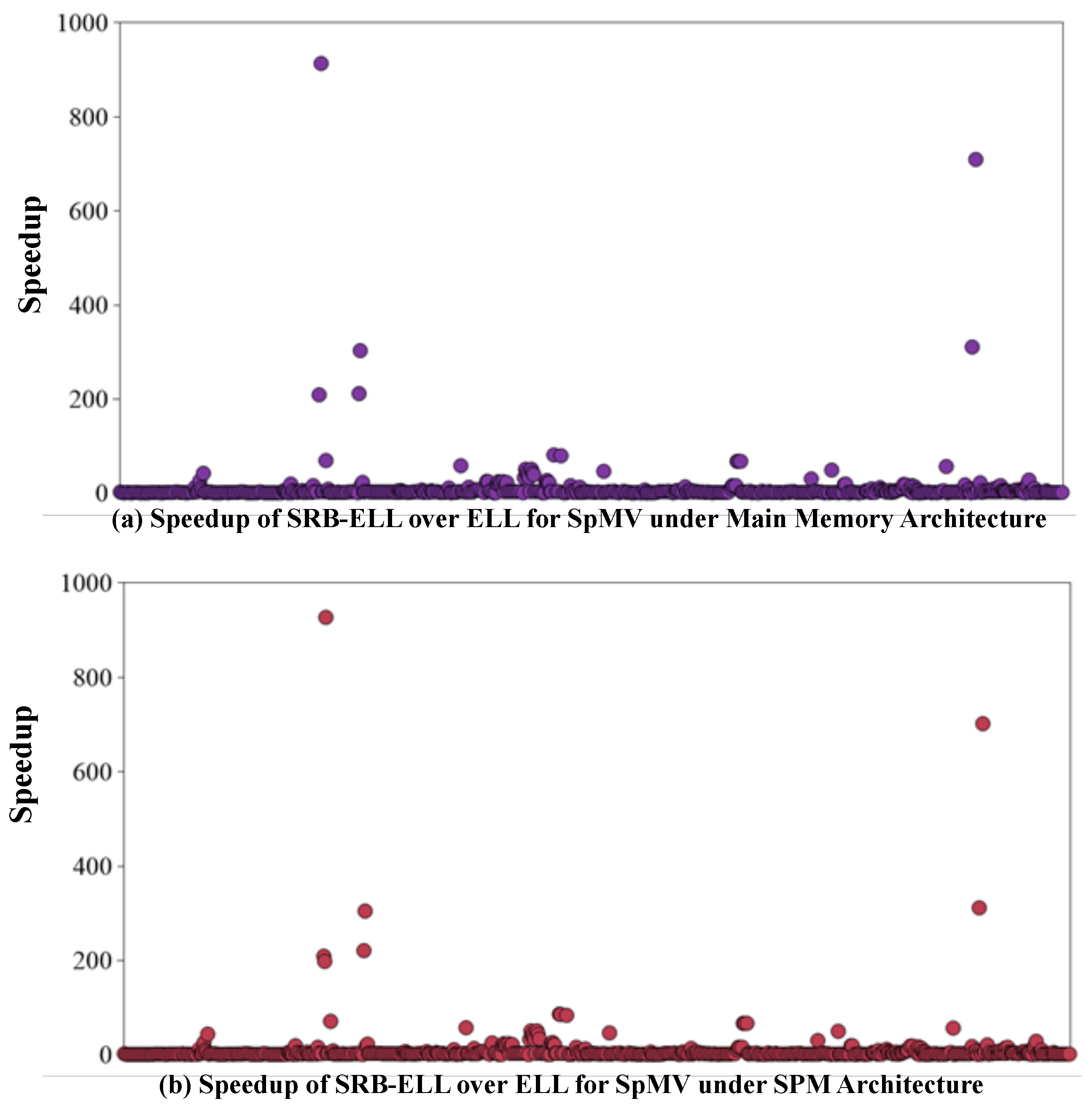
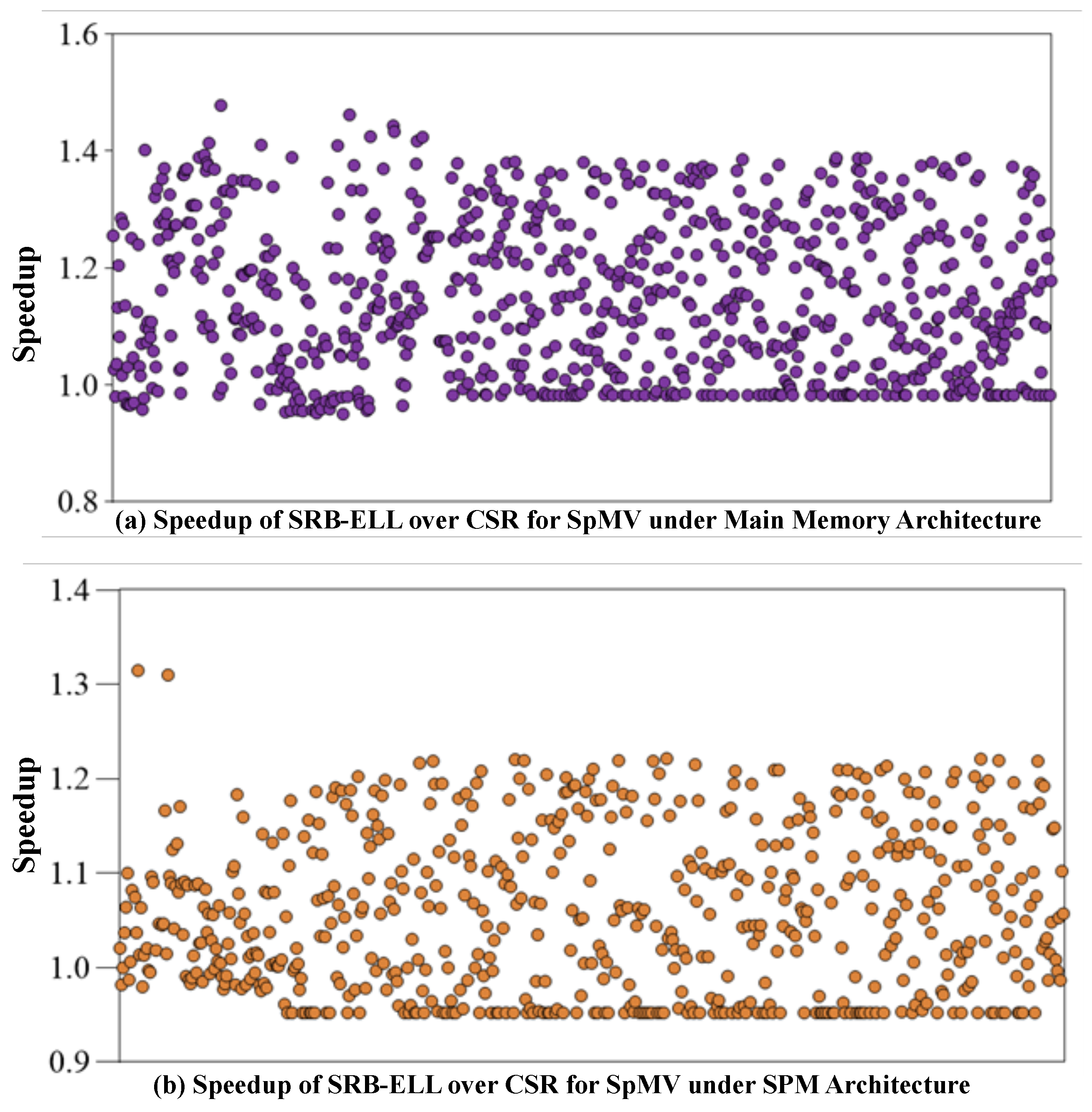
4.3.1. Storage Overhead
4.3.2. SpMV Performance Analysis
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| SpMV | Sparse Matrix–Vector Multiplication |
| HPC | High-performance computing |
| AI | Artificial intelligence |
| DLP | Data-level parallelism |
| SIMD | Single Instruction Multiple Data |
| SPM | Scratchpad Memory |
| CPU | Center Processor Unit |
| HPCG | High-Performance Conjugate Gradient |
| SVM | Support Vector Machine |
| CSR | Compressed Sparse Row |
| ELL | ELLPACK |
| SVE | Scalable Vector Extension |
| SRB-ELL | Sorted-Row-Block ELLPACK |
| MSHR | Miss Status Holding Register |
| SSE | Stream SIMD Extension |
References
- Asanović, K. Vector Microprocessors. Ph.D. Dissertation, University of California, Berkeley, CA, USA, 1998. [Google Scholar]
- Espasa, R.; Valero, M.; Smith, J.E. Vector Architectures: Past, Present and Future. In Proceedings of the 12th International Conference on Supercomputing (ICS), Melbourne, Australia, 13–17 July 1998; pp. 425–432. Available online: https://dl.acm.org/doi/10.1145/277830.277935 (accessed on 31 August 2025).
- AMD Corporation. AMD64 Architecture Programmer’s Manual Volume 4: 128-Bit and 256-Bit Media Instructions; AMD: Sunnyvale, CA, USA, 2019. [Google Scholar]
- Intel Corporation. Intel 64 and IA-32 Architectures Software Developer’s Manual Volume 2A: Instruction Set Reference; Intel: Santa Clara, CA, USA, 2015. [Google Scholar]
- Hennessy, J.L.; Patterson, D.A. Computer Architecture, Sixth Edition: A Quantitative Approach, 6th ed.; Morgan Kaufmann Publishers Inc.: San Francisco, CA, USA, 2017. [Google Scholar]
- Satish, N.; Kim, C.; Chhugani, J.; Saito, H.; Krishnaiyer, R.; Smelyanskiy, M.; Girkar, M.; Dubey, P. Can Traditional Programming Bridge the Ninja Performance Gap for Parallel Computing Applications? In Proceedings of the 39th Annual International Symposium on Computer Architecture (ISCA), Portland, OR, USA, 9–13 June 2012; pp. 440–451. Available online: http://dl.acm.org.recursos.biblioteca.upc.edu/citation.cfm?id=2337159.2337210 (accessed on 31 August 2025).
- Bramas, B.; Kus, P. Computing the Sparse Matrix Vector Product Using Block-Based Kernels without Zero Padding on Processors with AVX-512 Instructions. arXiv 2018, arXiv:1801.01134. Available online: http://arxiv.org/abs/1801.01134 (accessed on 31 August 2025). [CrossRef] [PubMed]
- D’Azevedo, E.F.; Fahey, M.R.; Mills, R.T. Vectorized Sparse Matrix Multiply for Compressed Row Storage Format. In Computational Science–ICCS 2005; Sunderam, V.S., van Albada, G.D., Sloot, P.M.A., Dongarra, J.J., Eds.; Springer: Berlin/Heidelberg, Germany, 2005; pp. 99–106. [Google Scholar]
- Gilbert, J.R.; Reinhardt, S.; Shah, V.B. High-Performance Graph Algorithms from Parallel Sparse Matrices. In International Workshop on Applied Parallel Computing; Springer: Berlin/Heidelberg, Germany, 2006; pp. 260–269. [Google Scholar]
- Greathouse, J.L.; Daga, M. Efficient Sparse Matrix-Vector Multiplication on GPUs Using the CSR Storage Format. In Proceedings of the SC’14: Proceedings of the International Conference for High Performance Computing, Networking, Storage and Analysis, New Orleans, LA, USA, 16–21 November 2014; IEEE: Piscataway, NJ, USA, 2014; pp. 769–780. [Google Scholar]
- Kepner, J.; Alford, S.; Gadepally, V.; Jones, M.; Milechin, L.; Robinett, R.; Samsi, S. Sparse Deep Neural Network Graph Challenge. In Proceedings of the 2019 IEEE High Performance Extreme Computing Conference (HPEC), Waltham, MA, USA, 24–26 September 2019; pp. 1–7. [Google Scholar]
- Parashar, A.; Rhu, M.; Mukkara, A.; Puglielli, A.; Venkatesan, R.; Khailany, B.; Emer, J.; Keckler, S.; Dally, W. SCNN: An Accelerator for Compressed-Sparse Convolutional Neural Networks. In Proceedings of the 44th Annual International Symposium on Computer Architecture (ISCA), Toronto, ON, Canada, 24–28 June 2017; pp. 27–40. [Google Scholar]
- Yuan, F.; Yang, X.; Li, S.; Dong, D.; Huang, C.; Wang, Z. Optimizing Multi-Grid Preconditioned Conjugate Gradient Method on Multi-Cores. IEEE Trans. Parallel Distrib. Syst. 2024, 35, 768–779. [Google Scholar] [CrossRef]
- Fu, X.; Su, X.; Dong, D.Z.; Qian, C.D. Dense Linear Solver on Many-Core CPUs: Characterization and Optimization. Comput. Eng. Sci. 2024, 46, 984. [Google Scholar]
- Dongarra, J.J.; Luszczek, P.; Petitet, A. The LINPACK Benchmark: Past, Present and Future. Concurr. Comput. Pract. Exp. 2003, 15, 803–820. [Google Scholar] [CrossRef]
- Dongarra, J.; Heroux, M.A. Toward a New Metric for Ranking High Performance Computing Systems; Sandia Report SAND2013-4744; Sandia National Laboratories: Albuquerque, Mexico, 2013; pp. 150–168. [Google Scholar]
- Evgeniou, T.; Pontil, M. Support Vector Machines: Theory and Applications. In Advanced Course on Artificial Intelligence; Springer: Berlin/Heidelberg, Germany, 1999; pp. 249–257. [Google Scholar]
- Kepner, J.; Aaltonen, P.; Bader, D.; Buluç, A.; Franchetti, F.; Gilbert, J.; Hutchison, D.; Kumar, M.; Lumsdaine, A.; Meyerhenke, H.; et al. Mathematical Foundations of the GraphBLAS. In Proceedings of the 2016 IEEE High Performance Extreme Computing Conference (HPEC), Waltham, MA, USA, 13–15 September 2016; pp. 1–9. [Google Scholar]
- Leskovec, J.; Krevl, A. SNAP Datasets: Stanford Large Network Dataset Collection. Available online: http://snap.stanford.edu/data (accessed on 31 August 2025).
- Liu, W.; Vinter, B. CSR5: An Efficient Storage Format for Cross-Platform Sparse Matrix-Vector Multiplication. In Proceedings of the 29th ACM International Conference on Supercomputing (ICS), Newport Beach, CA, USA, 8–11 June 2015; pp. 339–350. [Google Scholar]
- Kourtis, K.; Karakasis, V.; Goumas, G.; Koziris, N. CSX: An Extended Compression Format for SpMV on Shared Memory Systems. ACM SIGPLAN Not. 2011, 46, 247–256. [Google Scholar] [CrossRef]
- Yan, S.; Li, C.; Zhang, Y.; Zhou, H. yaSpMV: Yet Another SpMV Framework on GPUs. ACM SIGPLAN Not. 2014, 49, 107–118. [Google Scholar] [CrossRef]
- Cao, W.; Yao, L.; Li, Z.; Wang, Y.; Wang, Z. Implementing Sparse Matrix-Vector Multiplication Using CUDA Based on a Hybrid Sparse Matrix Format. In Proceedings of the 2010 International Conference on Computer Application and System Modeling (ICCASM), Taiyuan, China, 22–24 October 2010; Volume 11, pp. V11-161–V11-165. [Google Scholar]
- Buluç, A.; Fineman, J.T.; Frigo, M.; Gilbert, J.R.; Leiserson, C.E. Parallel Sparse Matrix-Vector and Matrix-Transpose-Vector Multiplication Using Compressed Sparse Blocks. In Proceedings of the Twenty-First Annual Symposium on Parallelism in Algorithms and Architectures (SPAA), Calgary, AB, Canada, 11–13 August 2009; pp. 233–244. [Google Scholar]
- Eigen. The Matrix Class, Dense Matrix and Array Manipulation. Available online: https://www.eigen.tuxfamily.org/dox/group__TutorialMatrixClass.html (accessed on 31 August 2025).
- Kjolstad, F.; Chou, S.; Lugato, D.; Kamil, S.; Amarasinghe, S. TACO: A Tool to Generate Tensor Algebra Kernels. In Proceedings of the 2017 32nd IEEE/ACM International Conference on Automated Software Engineering (ASE), Urbana, IL, USA, 30 October–3 November 2017; pp. 943–948. [Google Scholar]
- Pavon, J.; Valdivieso, I.V.; Barredo, A.; Ramasubramanian, N.; Hernandez, R.; Badia, R.M.; Ayguadé, E.; Labarta, J. VIA: A Smart Scratchpad for Vector Units with Application to Sparse Matrix Computations. In Proceedings of the 2021 IEEE International Symposium on High-Performance Computer Architecture (HPCA), Seoul, Republic of Korea, 27 February–3 March 2021; pp. 921–934. [Google Scholar]
- Lowe-Power, J.; Ahmad, A.M.; Akram, A.; Alian, M.; Amslinger, R.; Andreozzi, M.; Arvanitis, A.; Bates, S.; Bewick, G.; Black, G.; et al. The gem5 Simulator: Version 20.0+. arXiv 2020, arXiv:2007.03152. Available online: https://arxiv.org/abs/2007.03152 (accessed on 31 August 2025).
- Arm. Arm Compiler for Linux: Scalable Vector Extension (SVE) Intrinsics Reference Guide. Available online: https://developer.arm.com/documentation/dht0002/ (accessed on 31 August 2025).
- Arm. Arm Architecture Reference Manual: Armv8, for Armv8-A Architecture Profile. Available online: https://developer.arm.com/documentation/102476/latest/ (accessed on 31 August 2025).
- Stephens, N.; Biles, S.; Boettcher, M.; Eapen, J.; Eyole, M.; Gabrielli, G.; Horsnell, M.; Magklis, G.; Martinez, A.; Premillieu, N.; et al. The ARM Scalable Vector Extension. IEEE Micro 2017, 37, 26–39. [Google Scholar] [CrossRef]
- Arm. Arm Architecture Reference Manual Supplement, the Scalable Vector Extension (SVE), for Armv8-A; Version Beta. Available online: https://developer.arm.com/documentation/ddi0584/ag/ (accessed on 31 August 2025).
- Tang, W.T.; Zhao, R.; Lu, M.; Liang, Y.; Huynh, P.H.; Li, X.; Goh, R.S.M. Optimizing and Autotuning Sparse Matrix-Vector Multiplication on Intel Xeon Phi. In Proceedings of the 13th IEEE/ACM International Symposium on Code Generation and Optimization (CGO), San Francisco, CA, USA, 7–11 February 2015; IEEE Computer Society: Washington, DC, USA, 2015; pp. 136–145. [Google Scholar]
- Liu, X.; Smelyanskiy, M.; Chow, E.; Dubey, P. Efficient Sparse Matrix-Vector Multiplication on x86-based Manycore Processors. In Proceedings of the 27th ACM International Conference on Supercomputing (ICS), Eugene, OR, USA, 10–14 June 2013; ACM: New York, NY, USA, 2013. [Google Scholar]
- Kreutzer, M.; Hager, G.; Wellein, G.; Fehske, H.; Bishop, A.R. A Unified Sparse Matrix Data Format for Modern Processors with Wide SIMD Units. arXiv 2013, arXiv:1307.6209. Available online: http://arxiv.org/abs/1307.6209 (accessed on 31 August 2025).
- Anzt, H.; Tomov, S.; Dongarra, J. Implementing a Sparse Matrix Vector Product for the SELL-C/SELL-C-σ Formats on NVIDIA GPUs; Technical Report ut-eecs-14-727; University of Tennessee: Knoxville, TN, USA, 2014. [Google Scholar]
- Chen, L.; Jiang, P.; Agrawal, G. Exploiting Recent SIMD Architectural Advances for Irregular Applications. In Proceedings of the 14th International Symposium on Code Generation and Optimization (CGO), Barcelona, Spain, 12–18 March 2016; ACM: New York, NY, USA, 2016; pp. 47–58. [Google Scholar]
- Xie, B.; Zhan, J.; Liu, X.; Gao, W.; Jia, Z.; He, X.; Zhang, L. CVR: Efficient Vectorization of SpMV on x86 Processors. In Proceedings of the 2018 International Symposium on Code Generation and Optimization (CGO), Vienna, Austria, 24–28 February 2018; IEEE: San Francisco, CA, USA, 2018; pp. 149–162. [Google Scholar]
- Pinar, A.; Heath, M.T. Improving Performance of Sparse Matrix-Vector Multiplication. In Proceedings of the 1999 ACM/IEEE Conference on Supercomputing, Portland, OR, USA, 14–19 November 1999; p. 30. [Google Scholar]
- Vuduc, R.W.; Moon, H.J. Fast Sparse Matrix-Vector Multiplication by Exploiting Variable Block Structure. In Proceedings of the International Conference on High Performance Computing and Communications; Springer: Berlin/Heidelberg, Germany, 2005; pp. 807–816. [Google Scholar]
- Cuthill, E.; McKee, J. Reducing the Bandwidth of Sparse Symmetric Matrices. In Proceedings of the 1969 24th National Conference, New York, NY, USA, 26–28 August 1969; ACM: New York, NY, USA, 1969; pp. 157–172. [Google Scholar]
- SuiteSparse Matrix Collection. Available online: https://sparse.tamu.edu/ (accessed on 31 August 2025).
- Davis, T.A.; Hu, Y. The University of Florida Sparse Matrix Collection. ACM Trans. Math. Softw. 2011, 38, 1–25. [Google Scholar] [CrossRef]




| Component | Configuration |
|---|---|
| CPU | 1 GHz; ARMv8; in-order core |
| L1 Data Cache | 32 KB; 2-way assoc; 2 cycles; 64B line; 4 MSHRs; |
| L1 Instruction Cache | 32 KB; 2-way assoc; 2 cycles; 64B line; 4 MSHRs; |
| L2 Cache | 1 MB; 8-way assoc; 20 cycles; 64B line; 20 MSHRs; |
| DRAM | 4 GB DDR4 |
| Scratchpad Memory | 128 KB; 2 cycles; 512 GB/s |
| Matrix Feature | Max | Min | Avg |
|---|---|---|---|
| Num_Of_Rows | 16,384 | 18 | 5320 |
| Sparsity (%) | 100.00 | 0.00017 | 1.17 |
| NNZ (Non-Zeros) | 18,068,388 | 24 | 58,990 |
| NNZ_Per_Row | 14,231 | 0 | 11 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, S.; Bai, W.; Zhang, Z.; Xie, X.; Tang, X. SRB-ELL: A Vector-Friendly Sparse Matrix Format for SpMV on Scratchpad-Augmented Architectures. Appl. Sci. 2025, 15, 9811. https://doi.org/10.3390/app15179811
Zhang S, Bai W, Zhang Z, Xie X, Tang X. SRB-ELL: A Vector-Friendly Sparse Matrix Format for SpMV on Scratchpad-Augmented Architectures. Applied Sciences. 2025; 15(17):9811. https://doi.org/10.3390/app15179811
Chicago/Turabian StyleZhang, Sheng, Wuqiang Bai, Zongmao Zhang, Xuchao Xie, and Xuebin Tang. 2025. "SRB-ELL: A Vector-Friendly Sparse Matrix Format for SpMV on Scratchpad-Augmented Architectures" Applied Sciences 15, no. 17: 9811. https://doi.org/10.3390/app15179811
APA StyleZhang, S., Bai, W., Zhang, Z., Xie, X., & Tang, X. (2025). SRB-ELL: A Vector-Friendly Sparse Matrix Format for SpMV on Scratchpad-Augmented Architectures. Applied Sciences, 15(17), 9811. https://doi.org/10.3390/app15179811





