Uncertainty Propagation for Vibrometry-Based Acoustic Predictions Using Gaussian Process Regression
Abstract
1. Introduction
2. Methodology
2.1. Interpolation Based on Gaussian Process Regression
2.2. Sound Power Estimates
2.3. Confidence of the Sound Power Prediction
2.4. Approximation of the Expected Value and Variance to Describe the Sound Power
2.5. Adaptive Refinement Procedure
3. Application
3.1. Exact Gaussian Process Regression
3.2. Stochastic Variational Gaussian Process Regression
4. Hypotheses
5. Results
5.1. Computational Performance Improvement
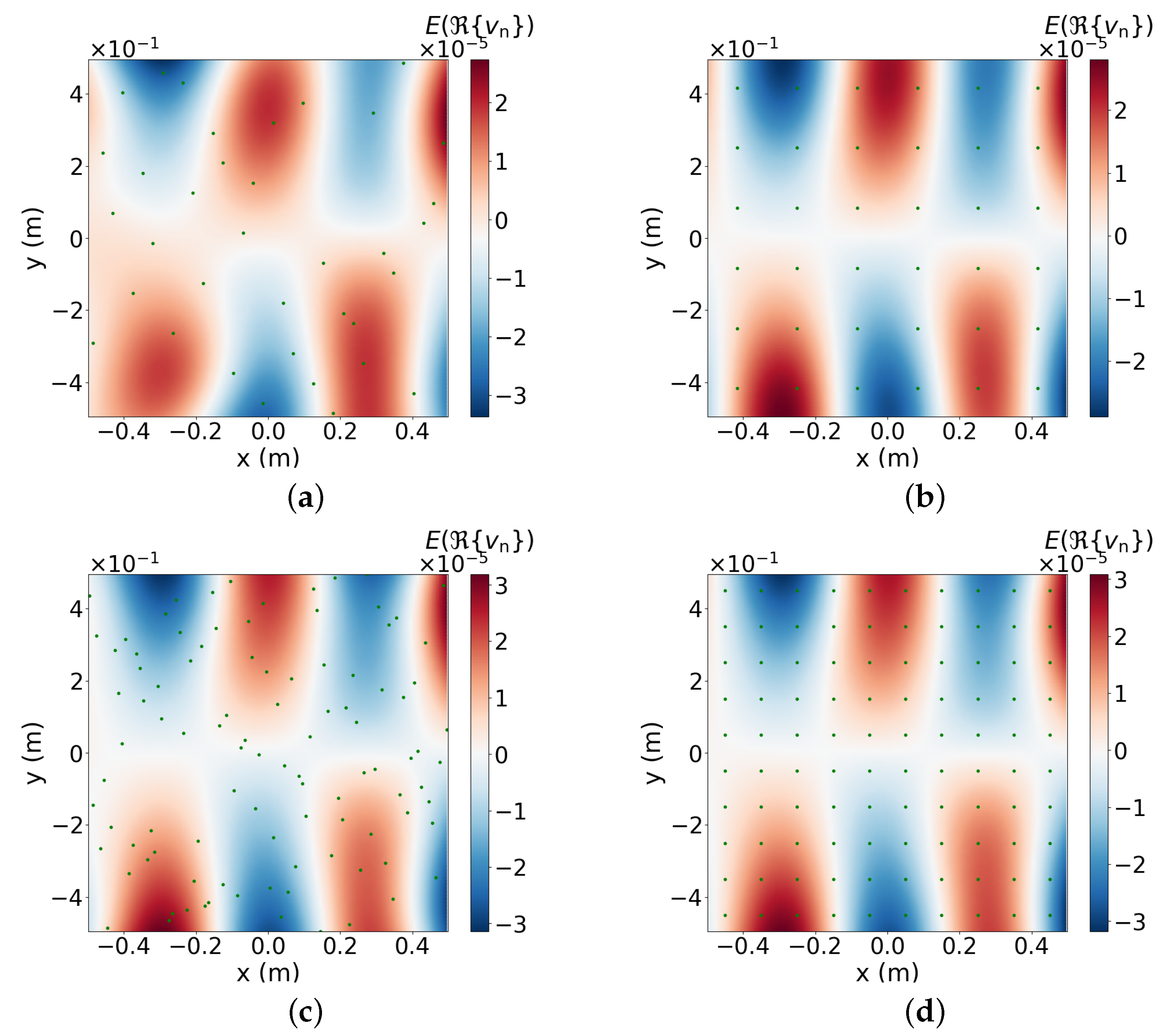
5.2. Expected Value and Variance of the Sound Power
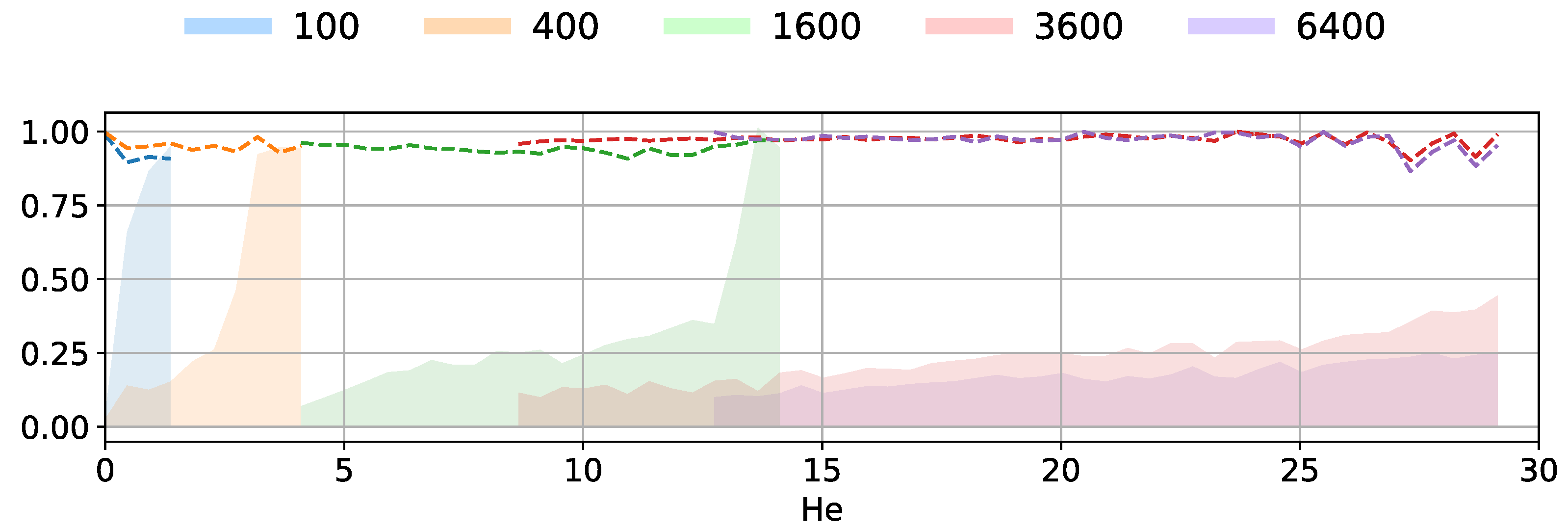
5.3. Correlation Between Sound Power Error and Predicted Uncertainty
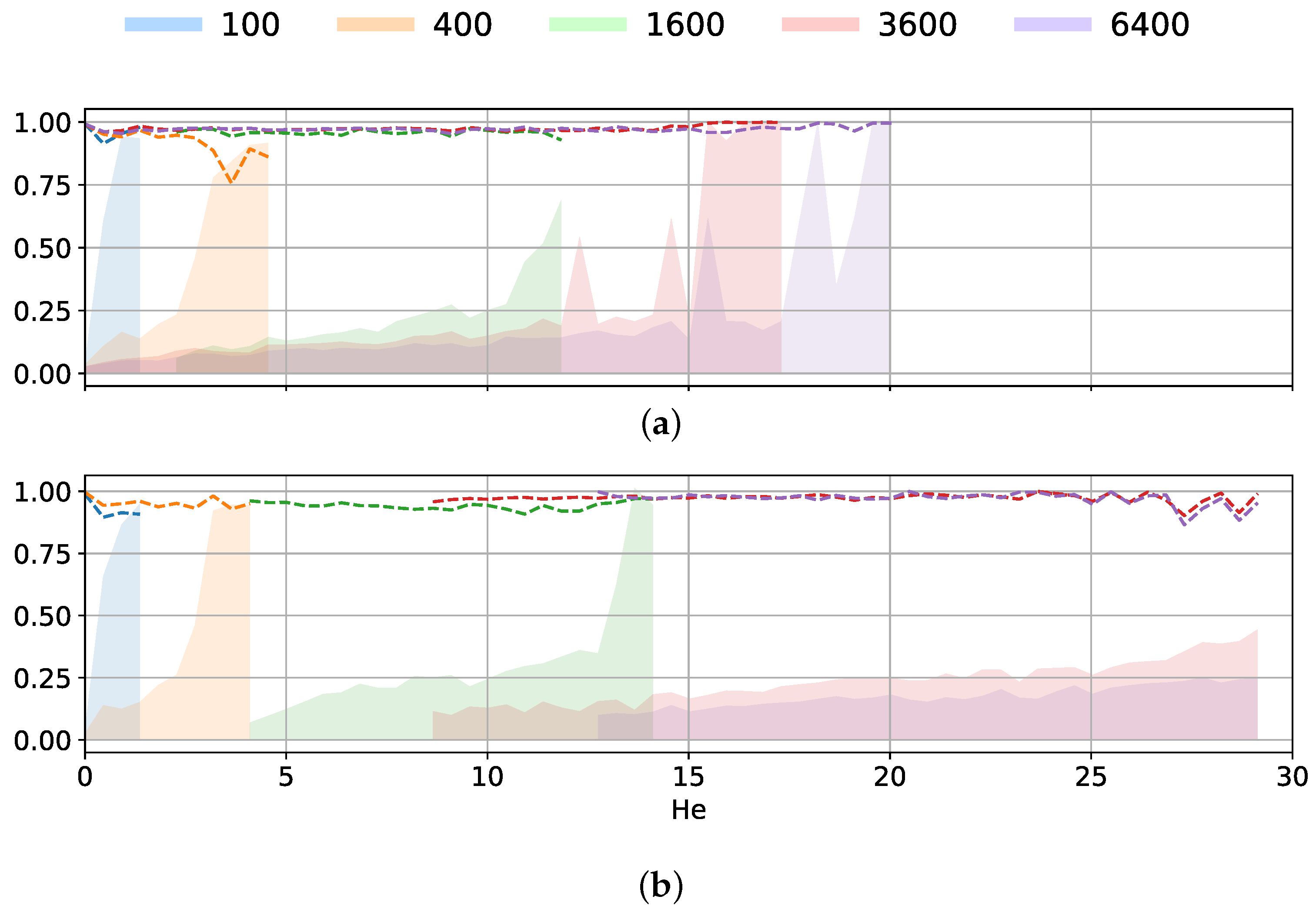
5.4. Uniform Sampling Versus Latin-Hypercube Sampling for the Surface Velocity
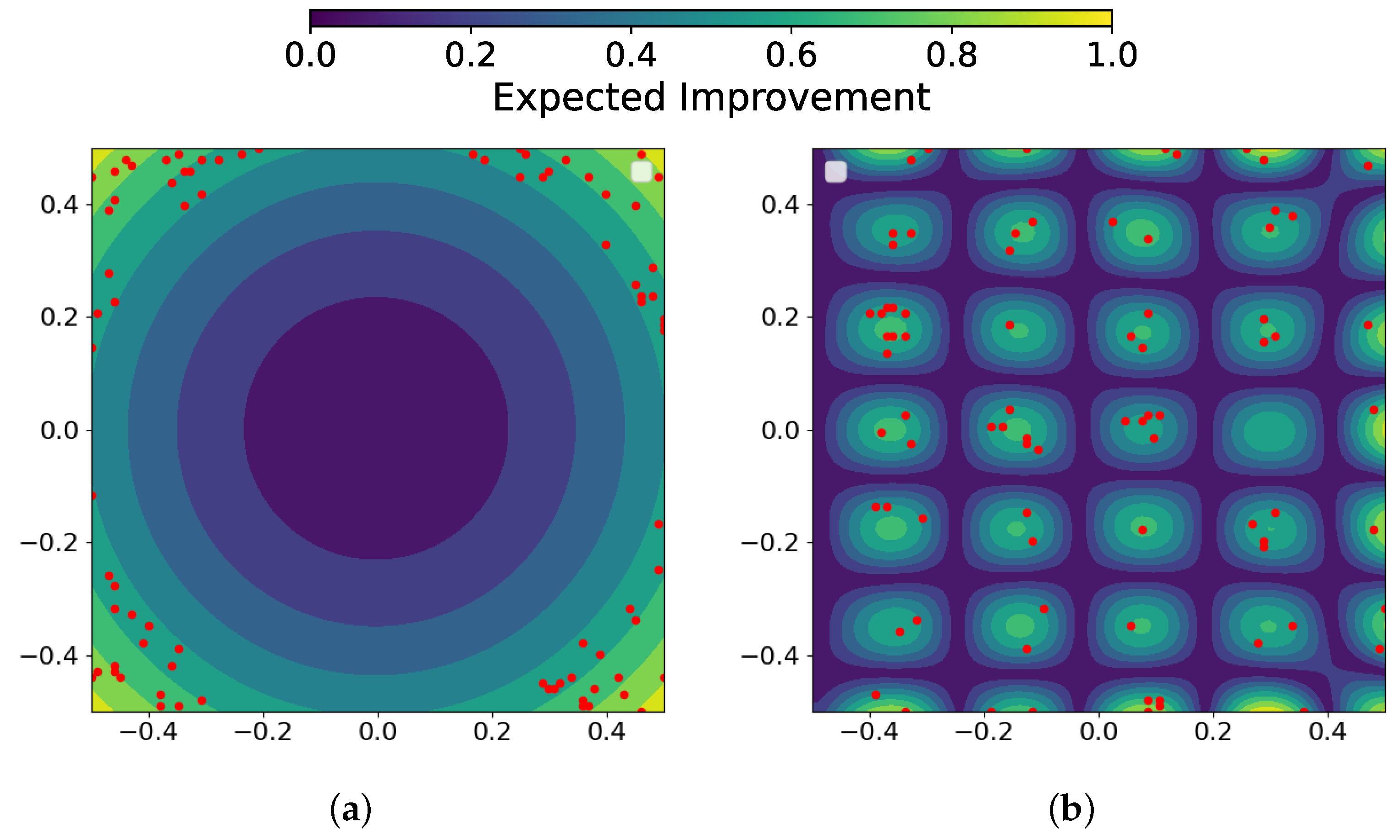
5.5. Design of Experiement Using Adaptive Refinement
5.6. Detailed Comparison of Sound Power Estimates
5.7. Computational Performance Using Pre-Trained Models
5.8. Influence of Measurement Noise
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kumar, S.; Forster, H.M.; Bailey, P.; Griffiths, T.D. Mapping Unpleasantness of Sounds to Their Auditory Representation. J. Acoust. Soc. Am. 2008, 124, 3810–3817. [Google Scholar] [CrossRef]
- Marburg, S. Boundary Element Method for Time-Harmonic Acoustic Problems. In Computational Acoustics; Kaltenbacher, M., Ed.; CISM International Centre for Mechanical Sciences; Springer International Publishing: Cham, Switzerland, 2018; pp. 69–158. [Google Scholar] [CrossRef]
- Vachálek, J.; Bartalskỳ, L.; Rovnỳ, O.; Šišmišová, D.; Morháč, M.; Lokšík, M. The digital twin of an industrial production line within the industry 4.0 concept. In Proceedings of the 2017 21st International Conference on Process Control (PC), Štrbské Pleso, Slovakia, 6–9 June 2017; pp. 258–262. [Google Scholar]
- Klippel, W. End-of-line testing. In Assembly Line-Theory and Practice; Grzechca, W., Ed.; Books on Demand: Norderstedt, Germany, 2011; pp. 181–206. [Google Scholar]
- Wurzinger, A.; Kraxberger, F.; Maurerlehner, P.; Mayr-Mittermüller, B.; Rucz, P.; Sima, H.; Kaltenbacher, M.; Schoder, S. Experimental Prediction Method of Free-Field Sound Emissions Using the Boundary Element Method and Laser Scanning Vibrometry. Acoustics 2024, 6, 65–82. [Google Scholar] [CrossRef]
- Rasmussen, C.E. Gaussian processes in machine learning. In Summer School on Machine Learning; Springer: Berlin/Heidelberg, Germany, 2003; pp. 63–71. [Google Scholar]
- Wurzinger, A.; Kraxberger, F.; Mayr-Mittermüller, B.; Rucz, P.; Sima, H.; Kaltenbacher, M.; Schoder, S. Assessment of vibro-acoustic sound emissions based on structural dynamics. In Proceedings of the Proceedings of DAGA 2024, Hannover, Germany, 18–21 March 2024. [Google Scholar]
- Li, J.; Wang, H. Gaussian Processes Regression for Uncertainty Quantification: An Introductory Tutorial. arXiv 2025, arXiv:2502.03090. [Google Scholar] [CrossRef]
- Schulz, E.; Speekenbrink, M.; Krause, A. A Tutorial on Gaussian Process Regression: Modelling, Exploring, and Exploiting Functions. J. Math. Psychol. 2018, 85, 1–16. [Google Scholar] [CrossRef]
- Tuo, R.; Wang, W. Uncertainty quantification for Bayesian optimization. In Proceedings of the International Conference on Artificial Intelligence and Statistics, Virtual, 28–30 March 2022; pp. 2862–2884. [Google Scholar]
- Bect, J.; Bachoc, F.; Ginsbourger, D. A Supermartingale Approach to Gaussian Process Based Sequential Design of Experiments. Bernoulli 2019, 25, 2883–2919. [Google Scholar] [CrossRef]
- Jault, D.; Gillet, N.; Schaeffer, N.; Mandéa, M. Local Estimation of Quasi-Geostrophic Flows in Earth’s Core. Geophys. J. Int. 2023, 234, 494–511. [Google Scholar] [CrossRef]
- Xia, G.; Han, Z.; Zhao, B.; Wang, X. Unmanned Surface Vehicle Collision Avoidance Trajectory Planning in an Uncertain Environment. IEEE Access 2020, 8, 207844–207857. [Google Scholar] [CrossRef]
- Kocev, B.; Hahn, H.K.; Linsen, L.; Wells, W.M.; Kikinis, R. Uncertainty-Aware Asynchronous Scattered Motion Interpolation Using Gaussian Process Regression. Comput. Med. Imaging Graph. 2019, 72, 1–12. [Google Scholar] [CrossRef]
- Jahanandish, M.H.; Fey, N.P.; Hoyt, K. Lower Limb Motion Estimation Using Ultrasound Imaging: A Framework for Assistive Device Control. IEEE J. Biomed. Health Inform. 2019, 23, 2505–2514. [Google Scholar] [CrossRef]
- Omainska, M. Visual Pursuit With Switched Motion Estimation and Rigid Body Gaussian Processes. Trans. Inst. Syst. Control Inf. Eng. 2023, 36, 327–335. [Google Scholar] [CrossRef]
- Binois, M.; Huang, J.; Gramacy, R.B.; Ludkovski, M. Replication or Exploration? Sequential Design for Stochastic Simulation Experiments. Technometrics 2018, 61, 7–23. [Google Scholar] [CrossRef]
- Gardner, J.; Pleiss, G.; Weinberger, K.Q.; Bindel, D.; Wilson, A.G. Gpytorch: Blackbox matrix-matrix gaussian process inference with gpu acceleration. Adv. Neural Inf. Process. Syst. 2018, 31. [Google Scholar]
- Raychaudhuri, S. Introduction to monte carlo simulation. In Proceedings of the 2008 Winter Simulation Conference, Miami, FL, USA, 7–10 December 2008; pp. 91–100. [Google Scholar]
- Wurzinger, A.; Heidegger, P.; Kraxberger, F.; Mayr-Mittermüller, B.; Sima, H.; Kaltenbacher, M.; Schoder, S. Prediction of vibro-acoustic sound emissions based on mapped structural dynamics. In Proceedings of the INTER-NOISE and NOISE-CON Congress and Conference Proceedings, Nantes, France, 25–29 August 2024; Volume 270, pp. 8251–8260. [Google Scholar] [CrossRef]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-Learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Bilionis, I.; Zabaras, N. Multi-Output Local Gaussian Process Regression: Applications to Uncertainty Quantification. J. Comput. Phys. 2012, 231, 5718–5746. [Google Scholar] [CrossRef]
- Mones, L.; Bernstein, N.; Csányi, G. Exploration, Sampling, And Reconstruction of Free Energy Surfaces with Gaussian Process Regression. J. Chem. Theory Comput. 2016, 12, 5100–5110. [Google Scholar] [CrossRef]
- Titsias, M. Variational learning of inducing variables in sparse Gaussian processes. In Proceedings of the Artificial Intelligence and Statistics, Clearwater Beach, FL, USA, 16–18 April 2009; pp. 567–574. [Google Scholar]
- Maddox, W.J.; Stanton, S.; Wilson, A.G. Conditioning Sparse Variational Gaussian Processes for Online Decision-making. In Proceedings of the Advances in Neural Information Processing Systems; Ranzato, M., Beygelzimer, A., Dauphin, Y., Liang, P., Vaughan, J.W., Eds.; Curran Associates, Inc.: New York, NY, USA, 2021; Volume 34, pp. 6365–6379. [Google Scholar]
- Bauer, M.; Van der Wilk, M.; Rasmussen, C.E. Understanding probabilistic sparse Gaussian process approximations. Adv. Neural Inf. Process. Syst. 2016, 29. [Google Scholar]
- Williams, C.; Rasmussen, C. Gaussian processes for regression. Adv. Neural Inf. Process. Syst. 1995, 8. [Google Scholar]
- Rasmussen, C.E.; Williams, C.K.I. Gaussian Processes for Machine Learning, 3rd ed.; Adaptive Computation and Machine Learning; MIT Press: Cambridge, MA, USA, 2008. [Google Scholar]
- Fiala, P.; Rucz, P. NiHu: An Open Source C++ BEM Library. Adv. Eng. Softw. 2014, 75, 101–112. [Google Scholar] [CrossRef]
- Burton, A.J.; Miller, G.F. The Application of Integral Equation Methods to the Numerical Solution of Some Exterior Boundary-Value Problems. Proc. R. Soc. Lond. 1971, 323, 201–210. [Google Scholar] [CrossRef]
- Luegmair, M.; Münch, H. Advanced Equivalent Radiated Power (ERP) Calculation for Early Vibro-acoustic Product Optimization. In Proceedings of the The 22nd International Congress on Sound and Vibration, Florence, Italy, 12–16 July 2015. [Google Scholar]
- Fritze, D.; Marburg, S.; Hardtke, H.J. Estimation of radiated sound power: A case study on common approximation methods. Acta Acust. United Acust. 2009, 95, 833–842. [Google Scholar] [CrossRef]
- Cremer, L.; Heckl, M.; Petersson, B. Sound Radiation from Structures. In Structure-Borne Sound: Structural Vibrations and Sound Radiation at Audio Frequencies; Springer: Berlin/Heidelberg, Germany, 2005; pp. 449–535. [Google Scholar] [CrossRef]
- Kvist, K.; Sorokin, S.V.; Larsen, J.B. Radiation Efficiency Varying Equivalent Radiated Power. J. Acoust. Soc. Am. 2025, 157, 169–177. [Google Scholar] [CrossRef] [PubMed]
- Das, A.; Geisler, W.S. Methods to integrate multinormals and compute classification measures. arXiv 2020, arXiv:2012.14331. [Google Scholar]
- Schoder, S.; Roppert, K. openCFS: Open Source Finite Element Software for Coupled Field Simulation—Part Acoustics. arXiv 2022, arXiv:2207.04443. [Google Scholar] [CrossRef]
- Langer, P.; Maeder, M.; Guist, C.; Krause, M.; Marburg, S. More Than Six Elements Per Wavelength: The Practical Use of Structural Finite Element Models and Their Accuracy in Comparison with Experimental Results. J. Comput. Acoust. 2017, 25, 1750025. [Google Scholar] [CrossRef]
- Schoder, S.; Roppert, K.; Weitz, M.; Junger, C.; Kaltenbacher, M. Aeroacoustic source term computation based on radial basis functions. Int. J. Numer. Methods Eng. 2020, 121, 2051–2067. [Google Scholar] [CrossRef]
- Hensman, J.; Matthews, A.; Ghahramani, Z. Scalable Variational Gaussian Process Classification. arXiv 2014, arXiv:1411.2005. [Google Scholar] [CrossRef]
- Blei, D.M.; Kucukelbir, A.; McAuliffe, J.D. Variational Inference: A Review for Statisticians. J. Am. Stat. Assoc. 2017, 112, 859–877. [Google Scholar] [CrossRef]
- Kullback, S.; Leibler, R.A. On information and sufficiency. Ann. Math. Stat. 1951, 22, 79–86. [Google Scholar] [CrossRef]
- Snelson, E.; Ghahramani, Z. Sparse Gaussian processes using pseudo-inputs. Adv. Neural Inf. Process. Syst. 2005, 18. [Google Scholar]
- Hensman, J.; Fusi, N.; Lawrence, N.D. Gaussian Processes for Big Data. arXiv 2013, arXiv:1309.6835. [Google Scholar] [CrossRef]
- Dai, Z.; Damianou, A.; Hensman, J.; Lawrence, N. Gaussian Process Models with Parallelization and GPU acceleration. arXiv 2014, arXiv:1410.4984. [Google Scholar] [CrossRef]
- Gal, Y.; van der Wilk, M.; Rasmussen, C.E. Distributed Variational Inference in Sparse Gaussian Process Regression and Latent Variable Models. In Proceedings of the Advances in Neural Information Processing Systems; Ghahramani, Z., Welling, M., Cortes, C., Lawrence, N., Weinberger, K., Eds.; Curran Associates, Inc.: New York, NY, USA, 2014; Volume 27. [Google Scholar]
- Paszke, A.; Gross, S.; Massa, F.; Lerer, A.; Bradbury, J.; Chanan, G.; Killeen, T.; Lin, Z.; Gimelshein, N.; Antiga, L.; et al. PyTorch: An Imperative Style, High-Performance Deep Learning Library. In Advances in Neural Information Processing Systems 32; Curran Associates, Inc.: New York, NY, USA, 2019; pp. 8024–8035. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Krause, A.; Singh, A.; Guestrin, C. Near-optimal sensor placements in Gaussian processes: Theory, efficient algorithms and empirical studies. J. Mach. Learn. Res. 2008, 9, 235–284. [Google Scholar]
- Jones, D.R.; Schonlau, M.; Welch, W.J. Efficient global optimization of expensive black-box functions. J. Glob. Optim. 1998, 13, 455–492. [Google Scholar] [CrossRef]
- Lázaro-Gredilla, M.; Titsias, M.K. Variational Heteroscedastic Gaussian Process Regression. In Proceedings of the ICML, Washington, DC, USA, 28 June–2 July 2011; pp. 841–848. [Google Scholar]
- Ghosh, S.; Kristensen, J.; Zhang, Y.; Subber, W.; Wang, L. A Strategy for Adaptive Sampling of Multi-Fidelity Gaussian Processes to Reduce Predictive Uncertainty; American Society of Mechanical Engineers: New York, NY, USA, 2019. [Google Scholar] [CrossRef]






| Task of Sound Prediction | BEM | ERP | ||||
|---|---|---|---|---|---|---|
| (Monte Carlo) | ( -EV-Based) | ( ) | ||||
| Exact GPR [20] | scikit-learn | |||||
| Training (L-BFGS) | 535.0 | |||||
| Variational GPR | GPyTorch | |||||
| Training (L-BFGS) | 9.93 | |||||
| Training (Adam) | 7.96 | |||||
| Draw samples | 0.20 | - | - | |||
| Evaluate radiated power distribution | 5.49 | 0.004 | 3.15 | 0.04 | ||
| Total time (Adam) | 13.65 | 8.16 | 10.11 | 8.00 | ||
| Run | ||||
|---|---|---|---|---|
| 100, uni | 2.626 | 0.428 | 2.589 | 0.256 |
| 400, uni | 4.380 | 4.951 | 4.288 | 2.764 |
| 1600, uni | 43.244 | 7.982 | 45.849 | 9.108 |
| 3600, uni | - | 28.952 | - | 38.339 |
| 6400, uni | - | 68.506 | - | 58.513 |
| Run | Training Epochs | Pre-Trained Model Used | ||
|---|---|---|---|---|
| 1600, uni | 5.57 | 1.94 | 1500 | no |
| 1600, uni | 3.59 | 0.91 | 1500 | yes |
| 1600, uni | 2.23 | 0.09 | 150 | yes |
| 1600, uni | 1.14 | 0.12 | 75 | yes |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wurzinger, A.; Schoder, S. Uncertainty Propagation for Vibrometry-Based Acoustic Predictions Using Gaussian Process Regression. Appl. Sci. 2025, 15, 10652. https://doi.org/10.3390/app151910652
Wurzinger A, Schoder S. Uncertainty Propagation for Vibrometry-Based Acoustic Predictions Using Gaussian Process Regression. Applied Sciences. 2025; 15(19):10652. https://doi.org/10.3390/app151910652
Chicago/Turabian StyleWurzinger, Andreas, and Stefan Schoder. 2025. "Uncertainty Propagation for Vibrometry-Based Acoustic Predictions Using Gaussian Process Regression" Applied Sciences 15, no. 19: 10652. https://doi.org/10.3390/app151910652
APA StyleWurzinger, A., & Schoder, S. (2025). Uncertainty Propagation for Vibrometry-Based Acoustic Predictions Using Gaussian Process Regression. Applied Sciences, 15(19), 10652. https://doi.org/10.3390/app151910652







