Research and Application of Foam Filling Material in Soft Rock Roadways

Abstract

Due to the soft mechanical properties of soft rock strata, roof fall accidents are frequent, causing great hazards to production. In order to eliminate hazards in the actual mining process, a new type of bag-filling scheme was designed by analyzing the mechanisms of roof falls in soft rock strata. By testing the filling material, the optimal ratio of foam filling material was determined, and the corresponding filling process was formulated. Through the field verification of this filling process, better support was achieved in the roof fall area, providing useful guidance and support for mines with similar conditions.

1. Introduction

Gold was one of the earliest metals discovered and exploited by human beings and it plays an important role in ensuring national economic security. The risk of roof falls and sloughing seriously threatens the safety of mine production and the life and health of operators. Therefore, production safety has become a long-standing theme of mining enterprises, and the management of safety hazards has also been emphasized by both the state and enterprises [1]. The nature of the failure deformation of roadway-surrounding rock is the plastic failure of the surrounding rock, and the range of the plastic zone determines the height of roof falls [2]. Large-deformation roadways located near a tectonic belt are generally in an environment with a non-uniform stress field, leading to obvious non-uniform deformation of the roadway-surrounding rock; consequently, traditional theories are basically unable to guide practical applications [3].

Many scholars have conducted in-depth research on supporting soft rock roadways. Dowon Park et al. [4] analyzed tunnel roof stability in geomaterial with a tension cutoff, and the level of support stress required to assure stability was derived. He Manchao et al. [5,6] pointed out that the roof fall accidents of soft rock roadways were mainly due to the mechanical characteristics of the soft rock itself and its softening and disintegration after encountering water, which resulted in the accelerated development of the softening of roadway-surrounding rock. Based on the physical and mechanical properties of soft rock roadways, Yiouta-Mitra et al. [7,8,9] show that an arched roof can support a much greater load than a horizontal beam. By presenting a unique numerical model that more completely represents in situ roof conditions, it was determined which parameters are most critical for roof stability. Wadslin Frenelus et al. [10] consider the seepage conditions, stresses, displacements, and plastic zone radius, as well as the Mogi–Coulomb strength criterion and the elasticity–plasticity theory. They propose analytical solutions for stresses, displacements, and the radius of soft rock under seepage conditions by using nonlinear elastoplastic approaches. Eren Komurlu et al. [11] investigated the effect of rock material strength on the RMR value and tunnel support designs using analytical research and numerical analyses. It was found that rock material strength has quite a limited effect in the RMR method when determining a rock mass class accurately in order to design tunnel support. Ivan Sakhno et al. [12] achieved stability by performing numerical simulations in the finite element analysis software system Ansys (https://www.ansys.com/, accessed on 2 January 2025) and reinforcing an inverted arch-shaped floor. A reliable relationship was established between the modulus of elasticity of the rock in the reinforced area and the ratio of the modulus of elasticity of the surrounding rock with the bulge of the reinforced rock. Qin Dongdong et al. [13,14] studied the load-carrying structure distribution characteristics of the surrounding rock in soft rock roadways through theoretical analysis and numerical simulation, analyzing the influence of active and passive supports on roadway stability and proposing a combined support method that includes shielding, floor pressure relief, and grouting. By analyzing numerous engineering examples, Kang Hongpu et al. [15] identified the reasons for the failure of rock bolts (cable anchors) in supporting systems, emphasizing the influence of track ropes with large shear stress on the stability control of surrounding rock; they concluded that the larger the range of the track rope, the stronger the load-carrying capacity. Liu Hongtao et al. [16,17] classified roof fall problems by establishing a mechanical model, identifying four types of entry that have a high risk of roof falls. The soft rock roadway supporting optimization theory, proposed by MA Nianjie et al. [18], asserts that the stability of soft rock roadways should be effectively controlled, transforming the “compound type” into a “single type”, and that there should be an effort to produce a plastic ring of reasonable thickness in a controlled manner, thereby releasing the deformation energy of the surrounding rock to the greatest extent. M.A. Millán et al. [8] efficiently reproduce the nonlinear behavior of rock for every configuration of their model with an artificial neural network. Their approach gives highly accurate results with minimum costs. Yoonsung Lee et al. [19] suggested using artificial neural networks (ANNs) to replace strain inversion in order to determine five elastic constants of TI rocks with a strip load test method, and this significantly reduced the computing time required for strain inversion by numerical modeling. Ambrosios-Antonios Savvides et al. [20] utilized a computational tool provided by a neural network to accurately evaluate the material properties of materials with limited data.

To date, many research results have been obtained regarding the support of soft rock roadways, providing a valuable theoretical basis for this study. Taking the soft rock roadway of the Songxian Shanjin Gold Mine as an example, and based on determining the roof falls mechanism, an innovative bag-filling method is proposed, which mainly includes high-quality waterproof canvas bags and a self-developed foam filling material. The optimal ratio of the foam filling material was determined by testing the viscosity, setting time, swellability, and foam loss percentage of the filling material. After application in the field, the bag-filling process was developed and improved through an analysis of construction efficiency, the filling effect, and the economic benefits, effectively solving the local roof falls problem at the Songxian Shanjin Gold Mine.

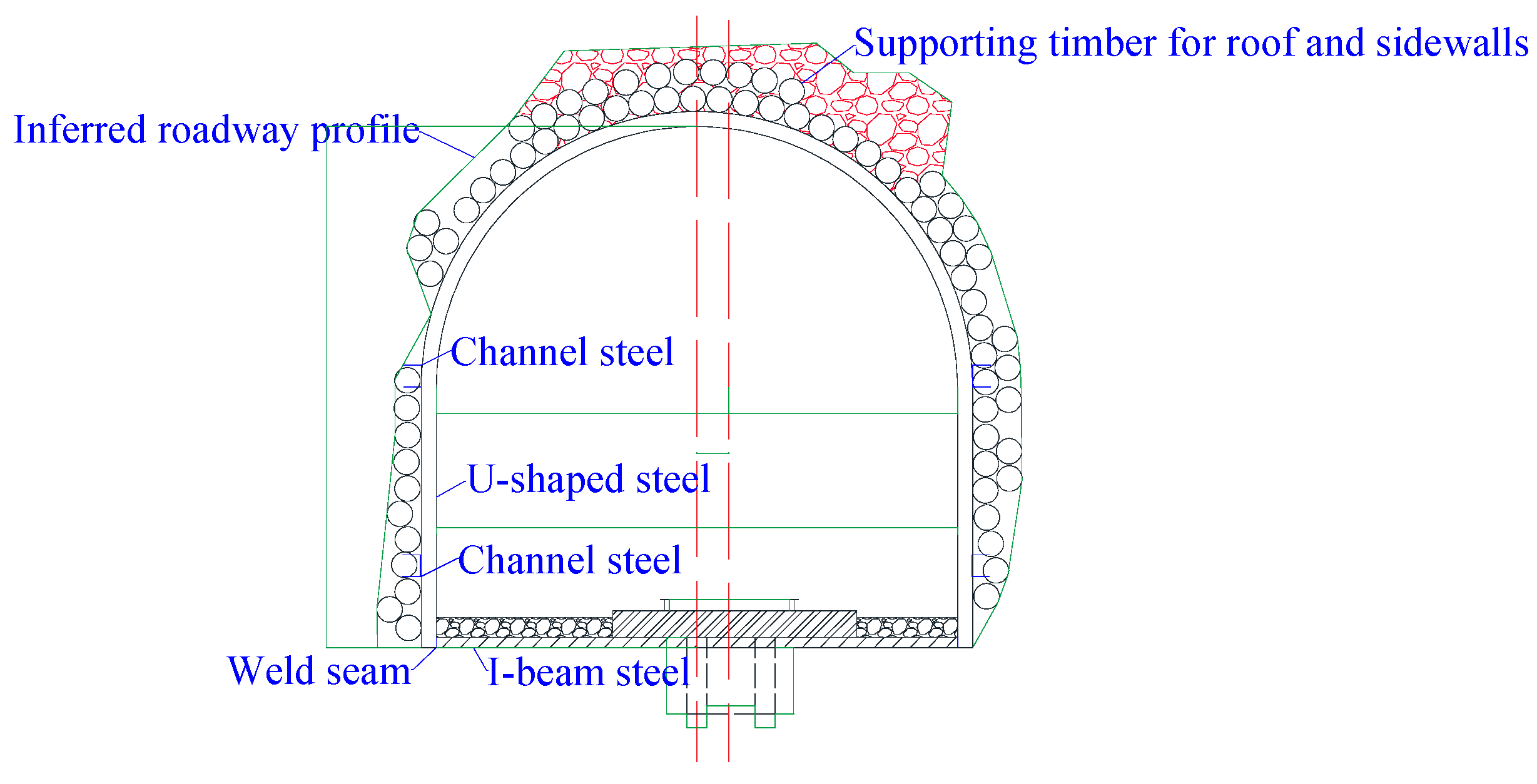
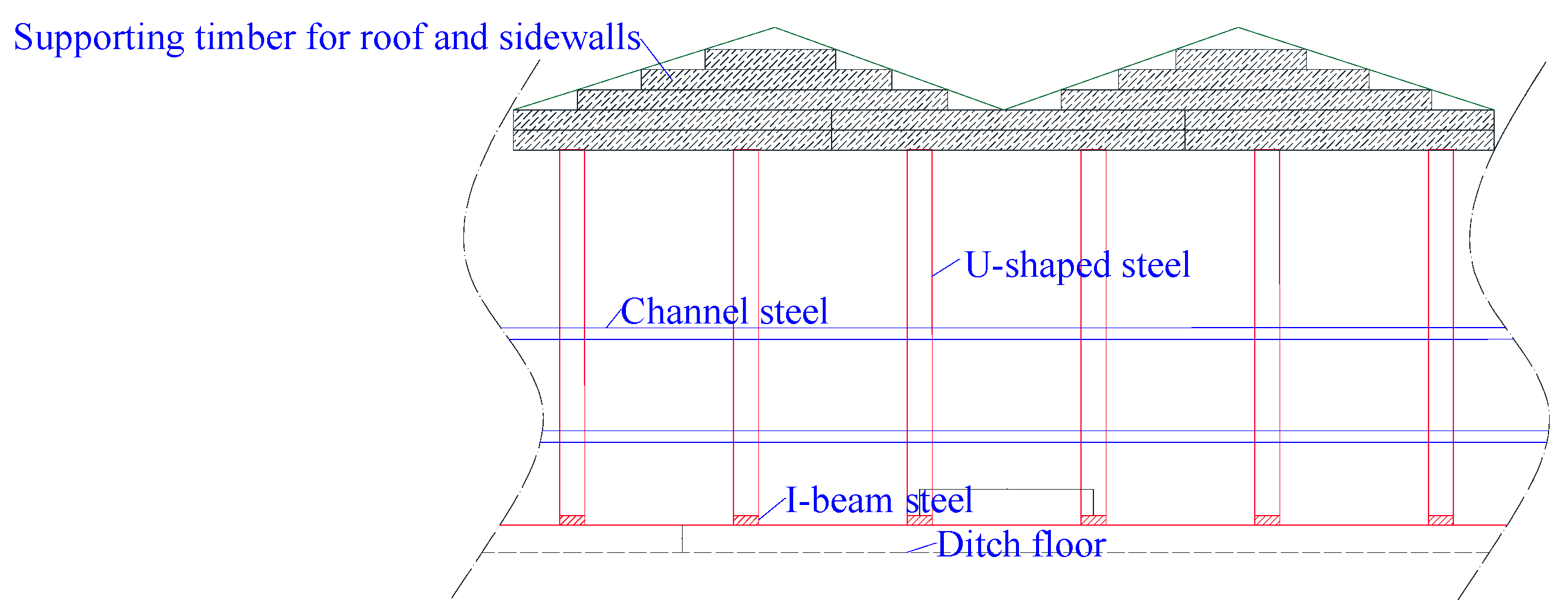
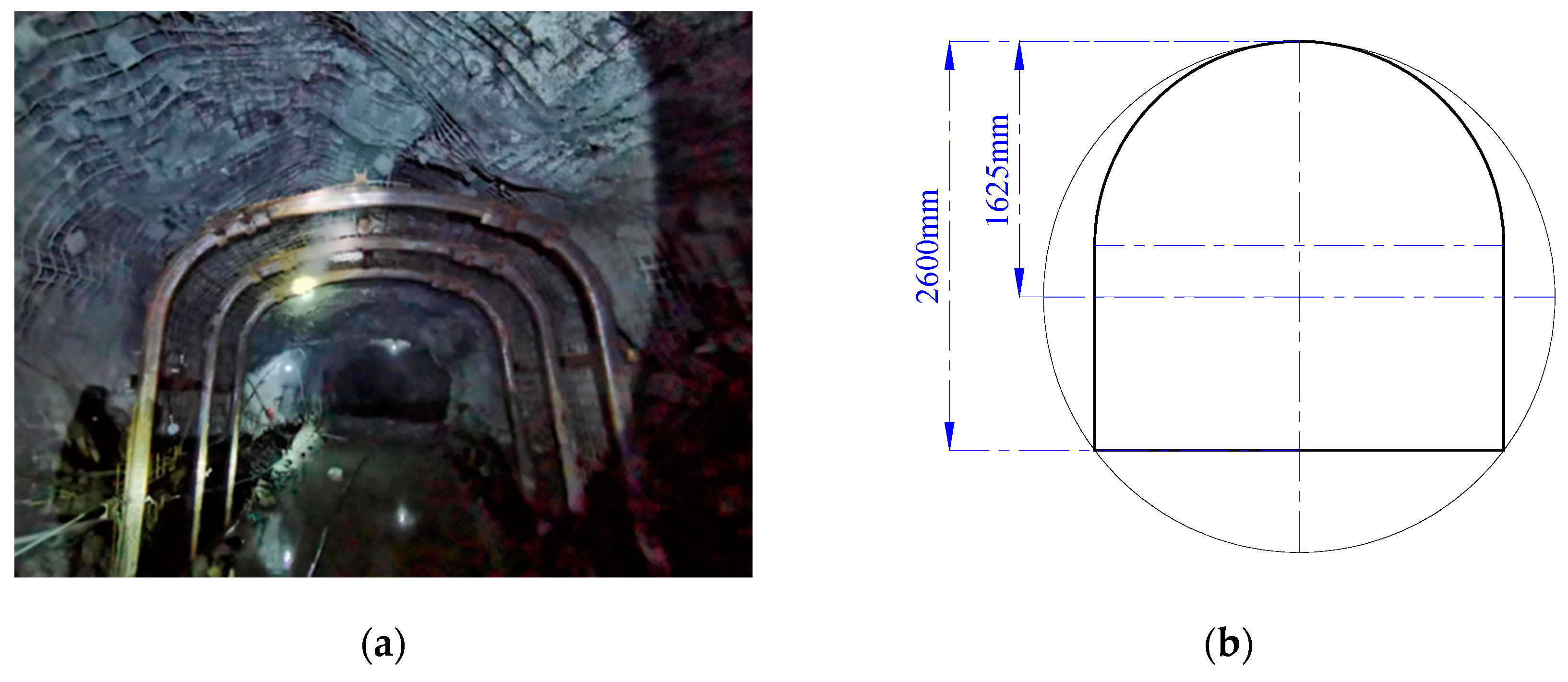
2. Project Overview

With increases in mining depth and scale, the situation regarding mine safety is becoming increasingly severe. Roof falls are the most frequent type of accident affecting mining safety. The overall mining conditions of the deposit are favorable; however, roadway stability is poor and is affected by geological origin and structure, making the roadway more prone to partial roof falls.

The Songxian Shanjin Gold Mine is located in the Xuanger Mountain gold mineralization concentration area on the southern margin of the North China Block. The region is characterized by strong tectonic activity and magmatic events, which provide a favorable metallogenic geological background. The main ore body is strictly controlled by fault fracture zones, and is mostly hosted within these fault zones and alteration zones. The fault structures provide excellent mineral-guiding and mineral-hosting conditions for the ore body, and these are predominantly found at the structural turning points. The overall mining conditions of the deposit are favorable, but the stability of the tunnels is poor. Due to the influence of geological formations and structures, roof collapses are more likely to occur during the blasting and mining process. Correctly selecting the roof collapse treatment technologies and methods plays a crucial role in the production of the mine.

Based on field investigation, the basic conditions of roof falls and the specific situation of top slope collapses at the Songxian Shanjin Gold Mine site are as follows: In the pressure area, varying degrees of sidewall and top slope collapse occurred. The collapse contour is shown in Figure 1 and Figure 2. The width of the sidewall collapse is approximately 0.5–1 m, with a length of about 3 m. The width of the top slope collapse is 2–3 m, and the height ranges from 0.5 to 2 m.

Currently, the Songxian Shanjin Gold Mine roadway primarily employs roofing and filling technology, as shown in Figure 3. This method not only results in high labor intensity for workers and significant safety risks, but is also costly and inefficient and does not meet the latest national standards. Wood decay reduces the strength of the support, which leads to collapse. Due to the low strength of wood and its susceptibility to corrosion, more scholars are studying integrated support systems. Yuyang Wang et al. [21] designed a high-resistance combined support scheme. It mainly includes “floor grouting + transverse steel beams + shallow base anchor injection” combined with U-shaped steel supports and prefabricated small deflection reverse arches. This design effectively reduces harmful deformation. However, wooden supports remain in use due to their low cost. To balance economic efficiency, they are still applied in practice. It is urgent to study a new filling technology for steel supporting roof joints in order to achieve safe and efficient construction.

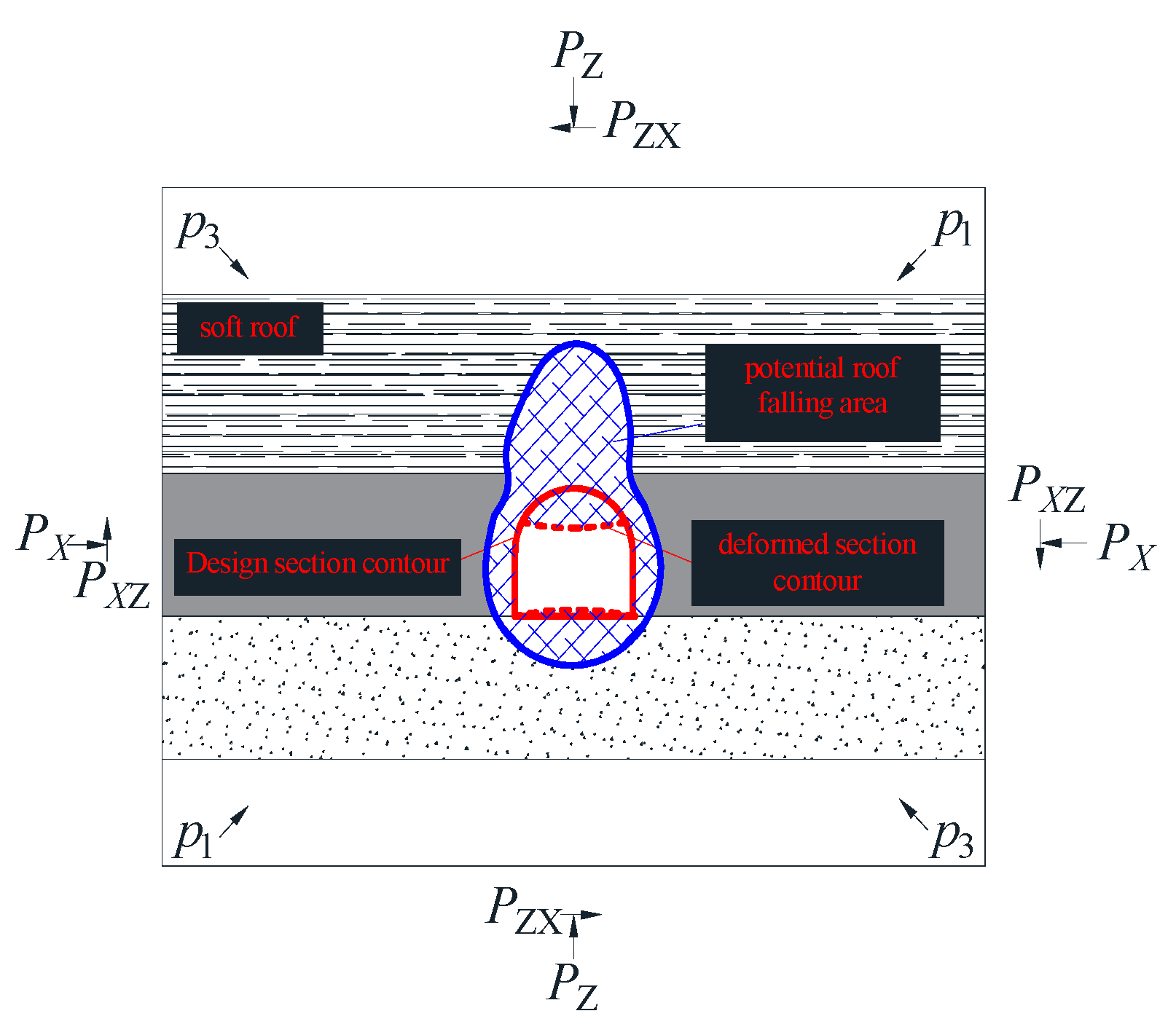
3. Analysis of Roof Falls Mechanism in Soft Rock Roadways

3.1. Basic Species of Plastic Zone of Roadway-Surrounding Rock

The section of the Songxian Shanjinyan Gold Mine roadway under study is a straight-wall semi-circular arch, as shown in Figure 4. Working according to relevant research results, the basic elastoplastic constitutive equation based on strain space, which was derived by Hongjian Liao et al. [22], is adopted. This is shown in Equation (1):

$$dq=3G\left[1-{\displaystyle \frac{2Gq}{2Gq+\frac{\partial k}{\partial {\epsilon }_s^p}}}\right]d{\epsilon }_s$$

(1)

where q is the deviatoric stress and k is the hardening parameter of the shear yield surface. In this paper, we take the function of plastic shear strain, k = k(${\epsilon }_s^p$).

The morphological evolution law of the surrounding rock stress field and plastic zone in circular roadways has universal applicability, and it is still applicable to non-circular roadways. Therefore, the semi-circular arch section of the straight wall can be simplified into a circular section for subsequent analysis.

Under the condition of a non-uniform stress field and a given rock lithology, the species of plastic zones in roadway-surrounding rocks are mainly divided into three shapes: circular, oval, and butterfly. According to the shape characteristics of the plastic zone boundaries, we can define them as follows:

• Circular plastic zone: under the condition of bidirectional isobaric stress, the boundary of the plastic zone appears circular.
• Oval plastic zone: The oval plastic zone under non-isobaric conditions is illustrated in Figure 5. In this case, the maximum radius of the plastic zone boundary is on the vertical axis, while the minimum radius is on the horizontal axis.

3.

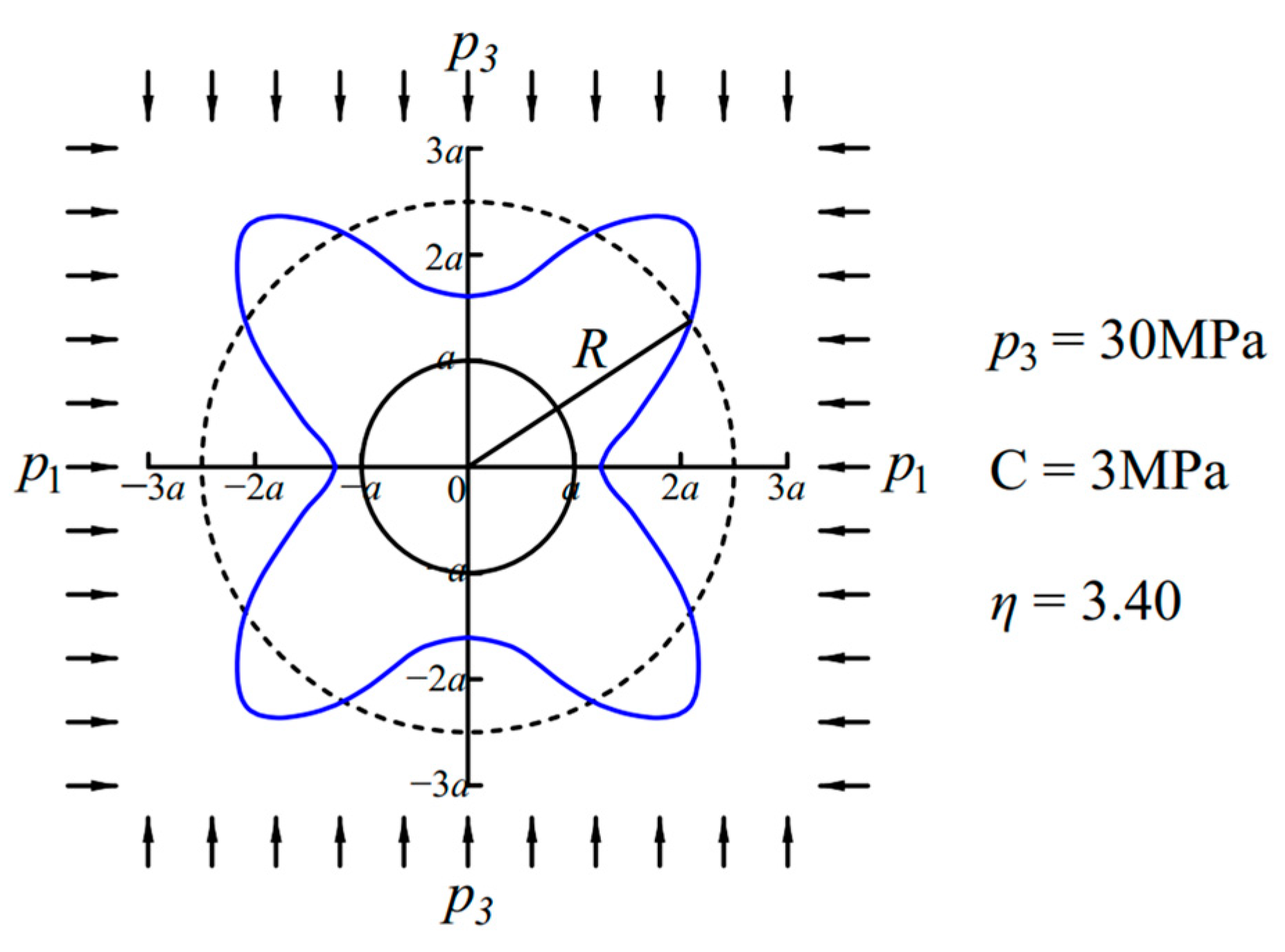
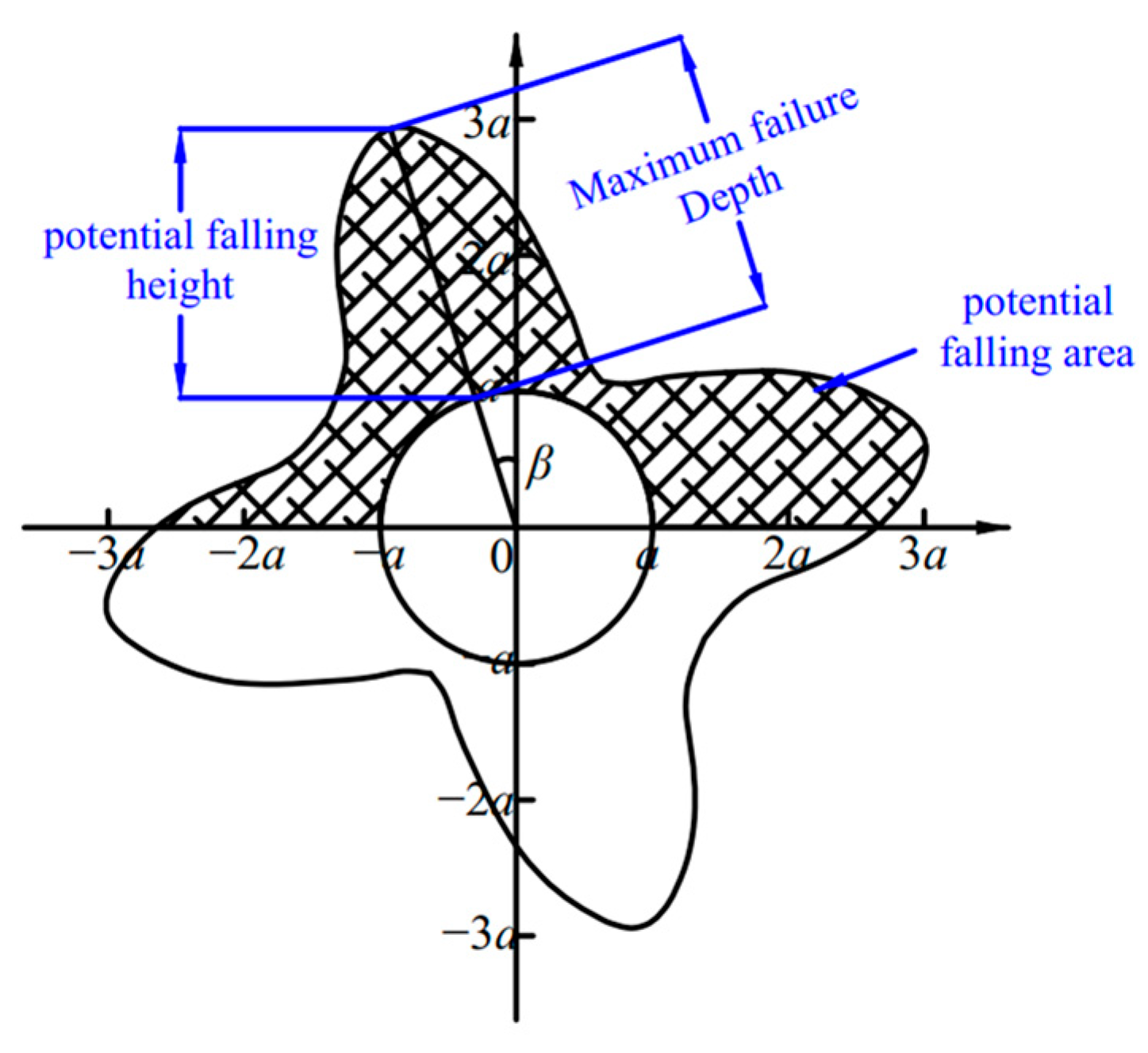
Butterfly plastic zone: The butterfly plastic zone under non-isobaric conditions is shown in Figure 6, where the minimum radius of the plastic zone boundary is located on the horizontal axis, while the maximum radius is distributed across four quadrants. These boundary outlines take on a butterfly-like shape, with dips along the axes and prominent features in the quadrants.

Because of the complex nature of rock strata, in practice, there are far more than just these three basic forms.

This form can be obtained by rotating, superimposing, and combining these three basic forms. Among the three basic forms of the plastic zone, the butterfly plastic zone is the most common.

The butterfly plastic zone is regarded as a more advanced extension form, evolving from the circular and oval plastic zone. When butterfly plastic zone failure occurs in the roadway-surrounding rock, significant deformation and failure of the surrounding rock often follow, bringing new problems in ensuring the stability of the roadway-surrounding rock. However, after an in-depth study of the butterfly plastic zone and reaching an understanding of its expansion behavior, the range distribution law of the butterfly plastic zone can be clarified, providing a critical positioning standard for the stability analysis of roadway-surrounding rock. This helps to better address the challenges associated with the stability of roadway-surrounding rock.

3.2. Roof Falls Mechanism of Butterfly Plastic Zone of Roadway-Surrounding Rock

In the actual production process, the direction of the butterfly leaf in the butterfly plastic zone changes with the direction of the maximum principal stress. As can be seen from Figure 7, in the cross-section of the roadway, we can define the range of the plastic zone in the vertical direction as the potential roof fall area, while the distance related to the horizontal failure depth at the top of the roadway can be referred to as the possible roof fall height.

As shown in Figure 8, when the stress conditions are determined, if the principal stress directions of the butterfly plastic zone are different, the maximum failure depth of the surrounding rock and the range of the potential roof fall zone will also differ. The characteristics of the butterfly plastic zone are such that the surrounding rock within the range of the butterfly leaves will experience strong damage. When the weight of the surrounding rock exceeds the load-carrying capacity of the rock bolts or cable anchors, this leads to the occurrence of butterfly roof falls.

As shown in Figure 8, once the roadway-surrounding rock forms a butterfly plastic zone, it will significantly impact the stability of the roadway. Its failure range is wide, its distribution is irregular, and it is easily affected by stress changes. When butterfly failure occurs, it aggravates the failure of the roadway. When the load in the direction of maximum or minimum confining pressure is removed, the extent of the failure zone may increase, which will raise the requirements for the supporting range and affect the completed support structure. This situation increases the difficulty of controlling the stability of the surrounding rock and greatly elevates the risk of roof falls.

4. Foam Filling Material Performance Index Test

Regarding the unique properties of the filling materials used in rock cracks, these materials must possess certain swellability characteristics to effectively fill the voids. Bing Chen et al. [23] divided inorganic foaming materials into two groups, A and B. The base material for Group A was a sulfoaluminate cement clinker, while the base material for Group B was lime and gypsum. They also added water reducers, thickeners, quick-setting agents, foaming agents, fibers, and other additives. Through extensive experimental research, they concluded that the optimal effect was achieved when the contents of quick-setting agent, fiber, and foaming agent in the inorganic foaming material were 1.6%, 0.8%, and 0.3%, respectively. This solution addressed the roof collapse problem in the studied mining area. To increase the volume of the filling materials during the solidification process, a chemical foaming method was employed in the test. The parameters tested included the viscosity, setting time, swellability, foam loss percentage, and mechanical strength of the filling materials.

4.1. Determination of Material Foam

The main raw materials for the filling material are portland cement, a foaming agent, a stabilizer, and water. Although most foam filling materials are low in toxicity, some chemical additives may still impact the environment, especially in underground environments where they are in prolonged contact. However, no additional additives are used in this study. If the foam lacks good stability, it might decompose or leak during the filling process, leading to environmental contamination, particularly if it permeates water sources or soil. However, using foam filling materials ensures even distribution in the mine, reducing disturbances to the underground ecosystem. Foam filling materials are lightweight and elastic, providing sufficient support to maintain the stability of the mine and reduce the risk of collapse or subsidence. This helps to maintain long-term environmental stability in mining areas.

Adding an appropriate amount of cement can adjust the consistency, viscosity, and plasticity of the slurry. It has high strength, significant hydration heat, good frost resistance, low dry shrinkage, good wear resistance, good carbonation resistance, poor corrosion resistance, and poor high-temperature resistance. Portland cement is mixed with water at a ratio of 1:3 to prepare a prefabricated slurry. The composition and physical properties parameter of portland cement are shown in

Table 1. Composition table of portland cement.

Chemical Composition	CaO	SiO2	Fe2O	Al2O3	MgO	Na2O
content	50–70	15–30	2–4	4–6	0.006–0.01	0.5–1

and

Table 2. Physical properties parameter table of portland cement.

Density	Strength Level	Setting Time/min		Rupture Strength		Compressive Strength
		Initial Setting	Final Setting	3 d	28 d	3 d	28 d
3.11	42.5	97	160	4.9	8.1	26.1	42.8

.

4.2. Material Slurry Viscosity Test

Using the ZNN-D6B electric six-speed rotary viscometer, the pre-configured slurry is first poured into a 500 mL measuring cup at a temperature of 18 to 22 °C. It is necessary to select the appropriate rotor and install it on the instrument. Then, one must slowly lower the rotor into the measuring cup and adjust the specific rotor number and speed. After the experiment begins, the viscosity of the slurry is recorded at 1 min intervals.

As shown in Figure 9, the viscosity of the material slurry decreases as the ratio of material to water decreases. This occurs because a lower ratio increases the water content in the slurry, resulting in greater distances between microscopic molecules, weakening the molecular interaction. The viscosity of the slurry is primarily influenced by intermolecular force, leading to a decrease in viscosity with a decreasing material-to-water ratio.

According to the test results, when the ratio of material to water reaches A3, the effect of increasing the material-to-water ratio on slurry viscosity becomes less significant. This is because, with a higher proportion of water in the slurry, the swelling performance of the material may be compromised, reducing its ability to resist damage; therefore, the optimal ratio of material to water is 1:2.

4.3. Material Setting Time Test

Working according to the test standard “Test methods for water requirement of normal consistency, setting time and soundness of the portland cement” [24], a method for determining the setting time of the slurry was designed. We used a Φ1.1 × 50 mm Vika test needle and a Φ65 × Φ75 × 40 mm cone die. First, we placed the test equipment and materials into the standard curing box. Then, we started the machine and waited for 10 min. We selected a fixed time interval of 1 min to remove the test mold, and then placed it on the cement consistency meter. We adjusted the position of the test needle and fixed it when it was at the same height as the slurry surface. We allowed the test needle to fall freely, recording the indication number at 30 s or when the pointer was at rest. We set the time interval when the pointer fell for the first time so that it did not exceed 4 ± 1 mm as the initial setting time of the test slurry.

According to the test results of the setting times of the material slurry, shown in

Table 3. Test results of material slurry setting time.

Water–Solid Ratio	Foam Content/%(C)	Initial Setting Time/min	Final Setting Time/min
1:1	1.5	6	14
	2	7	15
	2.5	8	18
	3	9	18
	3.5	9	19
1.5:1	1.5	10	16
	2	10	18
	2.5	11	20
	3	11	22
2:1	1.5	12	19
	2	12	20
	2.5	14	22
	3	16	24
	3.5	16	25
2.5:1	1.5	28	32
	2	29	34
	2.5	31	37
	3	32	40
	3.5	33	40
3:1	1.5	37	53
	2	38	55
	2.5	42	57
	3	44	58
	3.5	47	60

, we observed that the initial setting time was between 6 and 47 min, while final setting time occurred between 14 and 60 min. When the ratio of water to solid was less than or equal to 2.0:1, the changes in initial and final setting time times were not significant. However, when the ratio of water to solid exceeded 2.0:1, both the initial and final setting time times were noticeably increased.

In fact, in filling operations, particularly using the bag-filling method for roadway roofs, the mixed grout needs to have a flow time. To ensure that the mixture slurry is fully and evenly combined with the foam, and considering that the transport pipe length is not less than 10 m, a flow time of approximately 15 min is usually required. Therefore, based on the selected ratio, we sought to ensure that the initial setting time of the material exceeded 15 min.

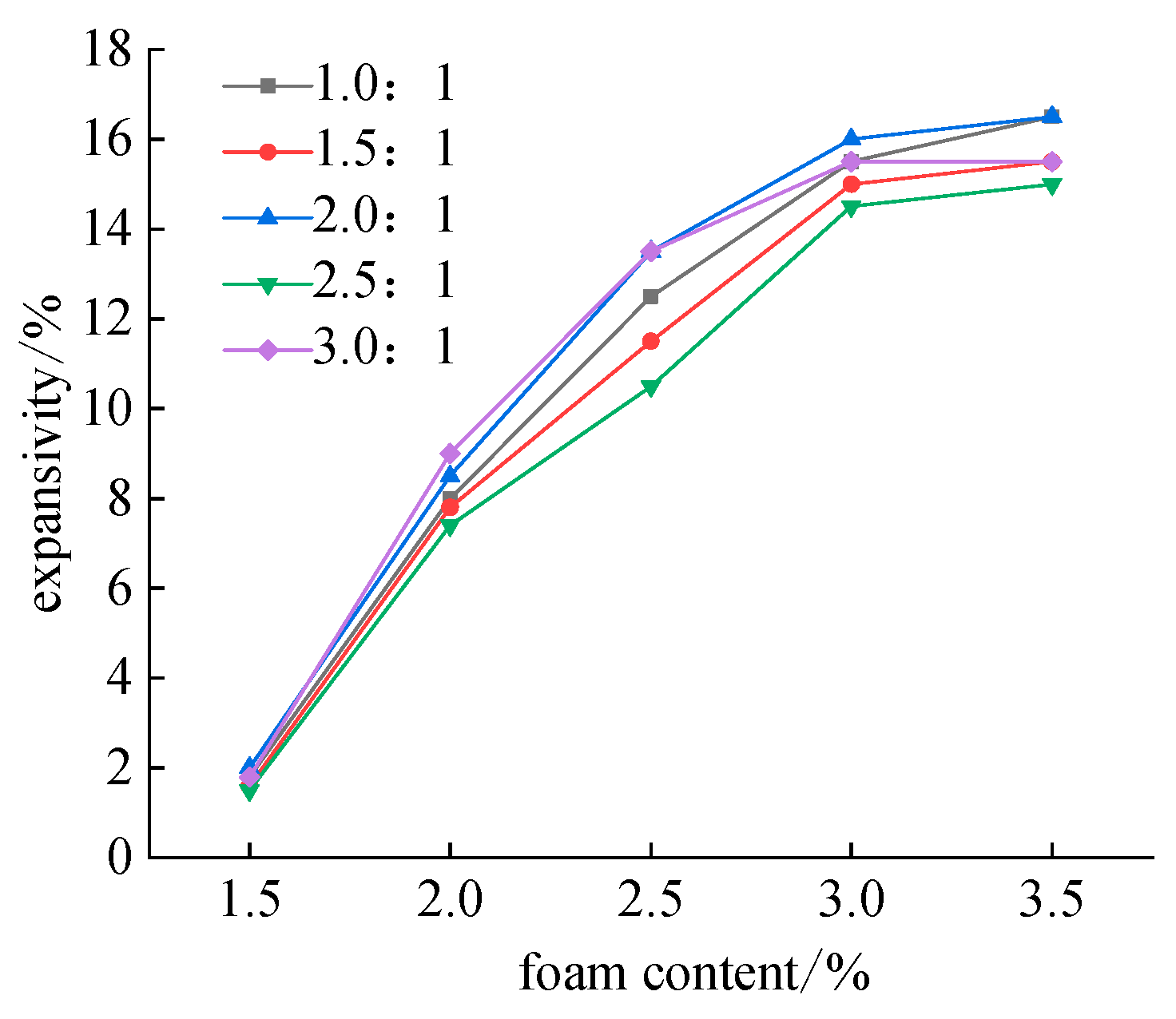
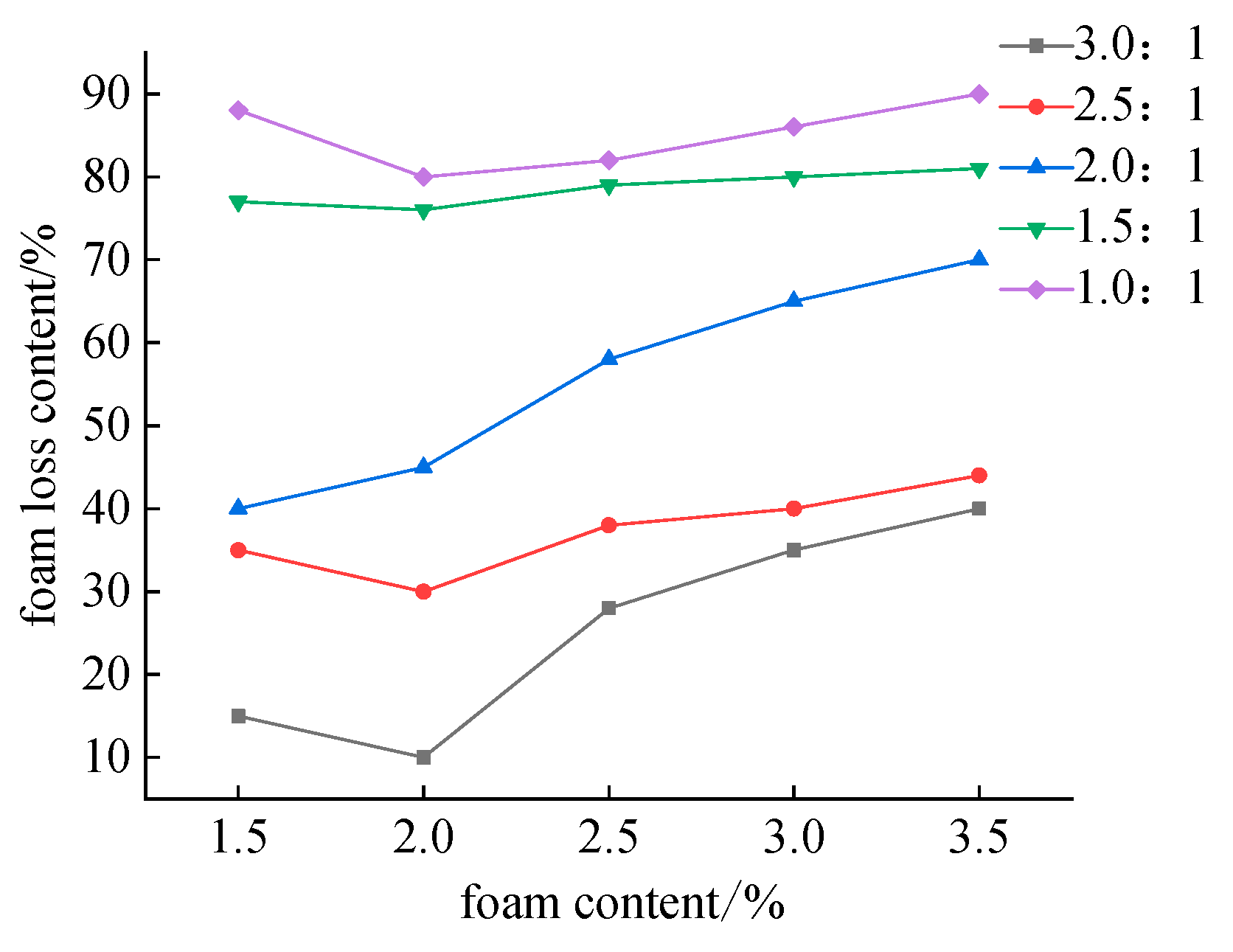
4.4. Material Swellability and Foam Loss Percentage Test

If the selected filling material decreases in volume after solidification, this may cause the filling material to detach from the surface of the filling bag, leading to the formation of unfilled spaces. Therefore, to ensure the effective sealing of the filling bag, the filling material must have volume swellability capability.

The formula for calculating the swellability percentage of foaming material slurry is given in Equation (2).

$$V_{\mathrm{s}}={\displaystyle \frac{V_2-V_1}{V_1}}$$

(2)

where V_s is the volume swellability percentage of the material; V₁ is the initial slurry volume; and V₂ is the volume after mixing and solidifying with foam.

The formula for calculating the foam loss percentage is provided in Equation (3).

$$\eta ={\displaystyle \frac{V_{\mathrm{f}}+V_1-V_2}{V_{\mathrm{f}}}}$$

(3)

where η is the foam loss percentage of high-water and high-foaming material, and V_f is the volume of added foam.

Based on the cement ratio, water–solid ratio, foam content, and fly ash content, 25 sets of orthogonal experiments were designed and carried out to evaluate the swellability percentage of the material slurry. According to the results shown in Figure 10, it can be observed that the swellability percentage of the foaming material increases with the foaming content, while the growth rate of the swellability percentage gradually decreases. When the content of the foaming agent reaches 3.5%, the slope of the curve approaches 0. This is due to excessive foam content, which makes the foam more likely to break. Therefore, considering all factors, it is advisable for the foaming content to not exceed 3%.

The test results of the foam loss percentage of material slurry are shown in Figure 11. When the water–solid ratio is 1.0:1 and 1.5:1, the foam loss percentages are between 80 and 90% and 70 and 80%, indicating relatively high foam loss. This can be attributed to the lower moisture content, which leads to a higher particle concentration in the slurry. The increased “extrusion” between particles makes it more likely for the foam to break.

From the tests, it can be seen that at the water–solid ratios of 2.0:1, 2.5:1, and 3.0:1, when the foaming agent content is 1.5%, the foam loss percentages are 40%, 78.6%, and 89%. These percentages are significantly lower compared to those at a water–solid ratio greater than 1.5:1. This analysis indicates that as the water content in the slurry increases, the concentration of particles decreases, reducing the impact of “extrusion” and allowing the foam to be better preserved. Additionally, when the water–solid ratio is between 2.5:1 and 3.0:1, the foam loss percentages remain below 44%.

4.5. Mechanical Strength Test of Materials

It is only with effective resistance to failure that filling materials can play a protective role after being applied, ensuring the normal progress of filling tasks and achieving the expected filling effect. According to SL237-1999 Geotechnical Test Regulations, the well-matched grout was injected into a cuboid model with a side length of 7 cm, removed after 24 h, and then placed under specific environmental conditions for 7 days of maintenance. The environmental conditions were set at a room temperature of 18–22 °C and a relative humidity of 45–55%. After 7 days of maintenance, the RMT-150B electro-hydraulic servo testing machine was used to test the samples. Each group was tested three times, and the average value was used as the test result.

The test results are shown in

Table 4. Uniaxial compressive strength test table.

Water–Solid Ratio	Foam Content/wt%(C)	Uniaxial Compressive Strength/MPa
		1 d	7 d	28 d
1:1	1.5	3.28	4.28	4.98
	2	2.77	4.11	4.81
	2.5	2.46	4.04	4.78
	3	1.92	3.92	4.56
	3.5	1.78	3.72	4.49
1.5:1	1.5	1.88	2.98	3.89
	2	1.78	2.72	3.42
	2.5	1.63	2.36	3.19
	3	1.59	2.38	2.99
	3.5	1.52	2.21	2.84
2:1	1.5	1.56	1.83	2.09
	2	1.37	1.78	1.99
	2.5	1.25	1.36	1.86
	3	1.19	1.27	1.76
	3.5	1.09	1.19	1.49
2.5:1	1.5	1.29	1.59	1.89
	2	1.18	1.49	1.62
	2.5	1.09	1.36	1.44
	3	0.98	1.29	1.23
	3.5	0.87	1.14	1.02

. According to the findings, for the test cube, the sample with a side length of 70.7 mm exhibited a certain mechanical strength when removed from the model after 1 day, showing a 100% increase compared to the strength measured 7 h after removal. After 7 days and beyond, the strength increased steadily. For foaming test cubes with water–solid ratios of 2:1 and 2.5:1, the final strength was not significantly enhanced compared to the strength measured 1 day after removal. In contrast, for foaming materials with water–solid ratios of 1.5:1 and 1:1, the final strength increased by approximately 47.7% compared to the strength measured one day after removal.

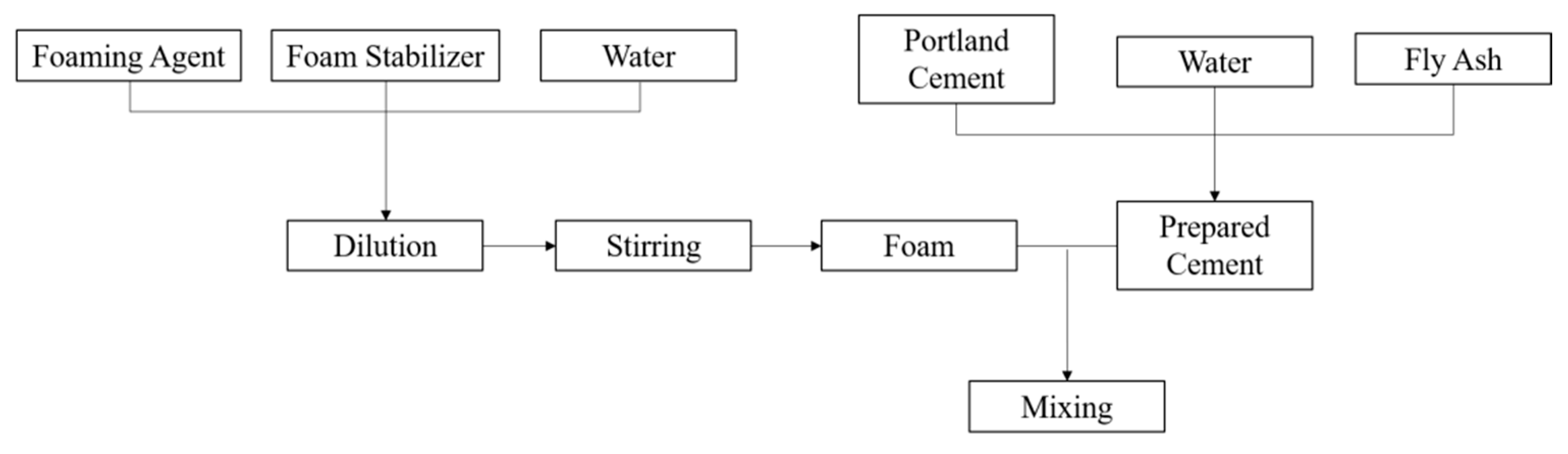
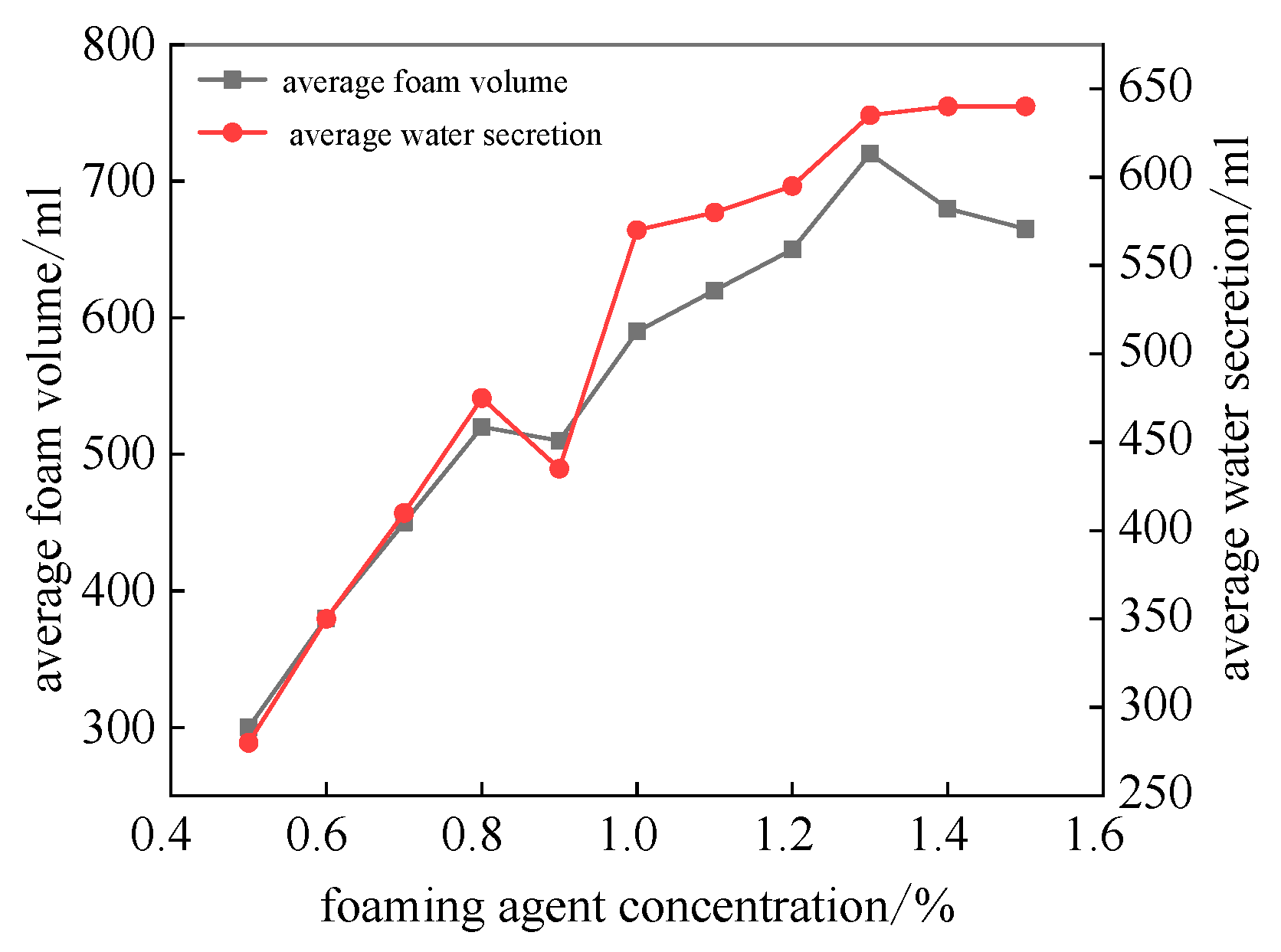
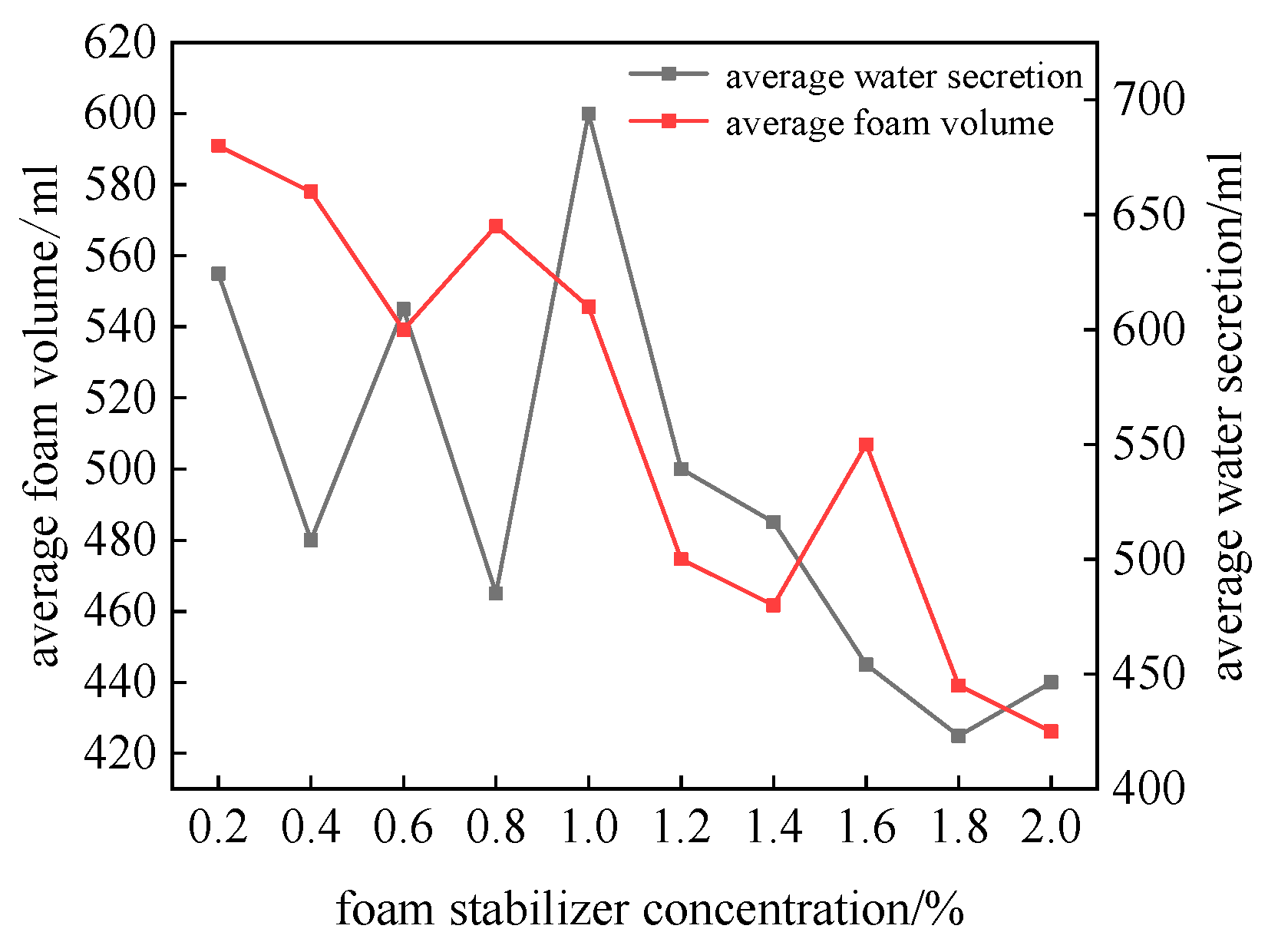
5. Preparation of Filling Material and Determination of Foam Stabilizer Concentration

The preparation process flow chart for the foaming material is shown in Figure 12. First, the foaming agent and foam stabilizer are mixed in proportion with water. They are then diluted and stirred to form a soaking system. Next, the mud to be prepared is created by mixing Portland cement, quick-setting cement, fly ash, and water in proportion to one another.

To determine the concentration of the foaming agent, as shown in Figure 13, foaming agents with mass fractions of 0.5%, 0.6%, 0.7%, 0.8%, 0.9%, 1.0%, 1.1%, 1.2%, 1.3%, 1.4%, and 1.5% were fully stirred in 100 mL of water using a high-speed stirring method in order to measure the foam volume. As illustrated in Figure 14, the 5 min water secretion (the volume of foaming agent aqueous solution produced after foam destruction) was recorded. Five groups of experiments were conducted for each foaming agent, and the average value was calculated.

The experimental results are shown in Figure 15. From the perspective of water secretion, the difference between foam volume and water secretion gradually increases with the concentration. When the concentration of the foaming agent reaches 1.3%, the difference between the two is the largest.

A single foaming agent often cannot meet the preparation requirements of foaming cement, and so a foam stabilizer is usually required at an appropriate concentration to enhance foam stability. Foam stabilizers with concentrations of 0.2%, 0.4%, 0.6%, 0.8%, 1.0%, 1.2%, 1.4%, 1.6%, 1.8%, and 2.0% were selected, and the above test was repeated; the experimental results are shown in Figure 16.

In the foaming system, as the concentration of the foam stabilizer increases, the five-minute water secretion fluctuates downward. When the concentration of the foam stabilizer is less than 0.6%, the five-minute water secretion of the foaming system changes little. However, when the concentration is in the range of 0.6% to 1.4%, water secretion begins to drop sharply. As the concentration of the foam stabilizer increases further, the five-minute water secretion of the foaming system does not decrease significantly.

The concentration of foam stabilizer reaches a peak at 1.0%, with concentrations of 0.2% to 1.0% and 1.2% to 2.0% both showing a downward trend, indicating that 1.0% is the optimal concentration.

6. Bag-Filling Scheme and Field Application

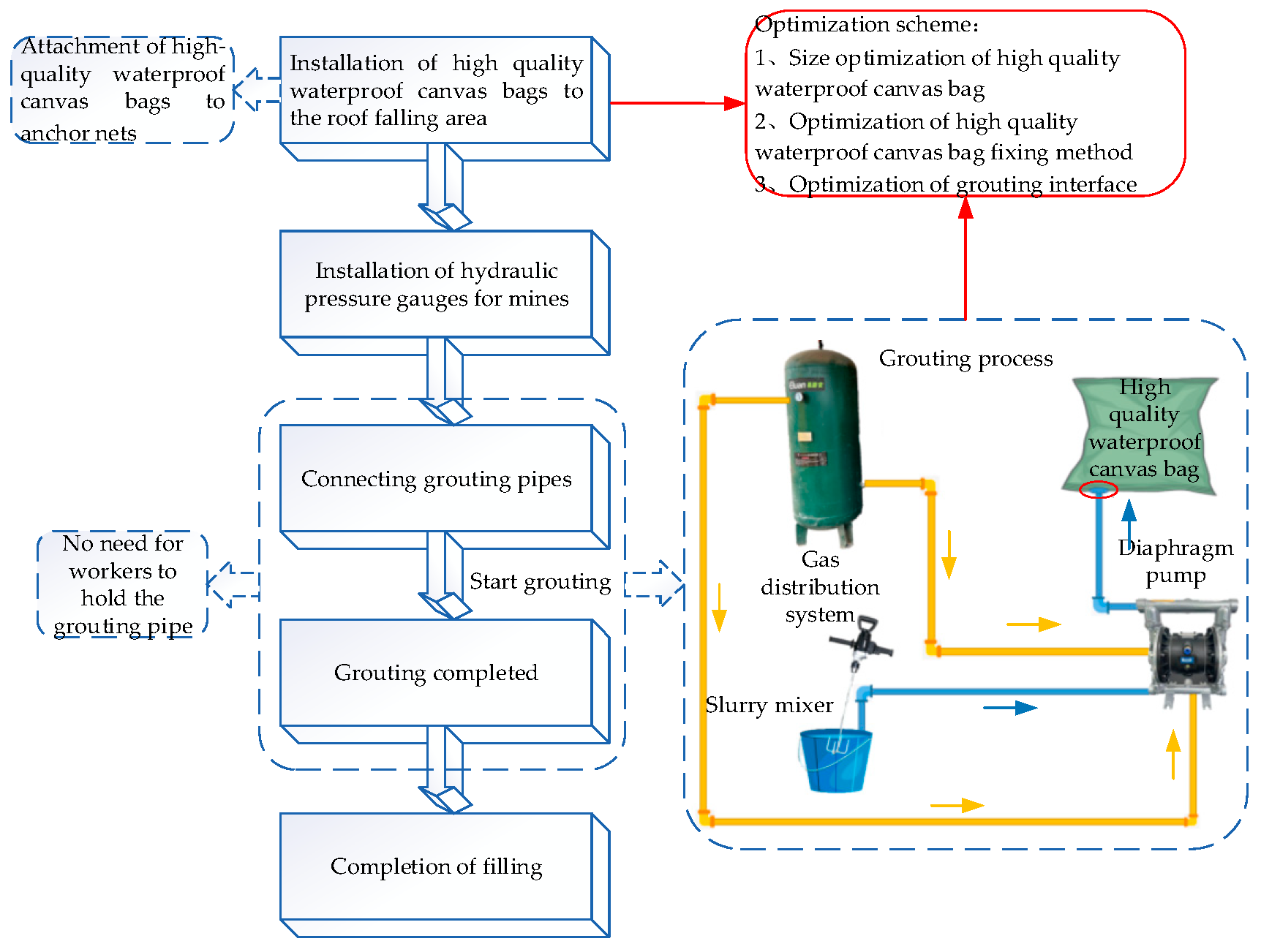
6.1. Bag-Filling Scheme

Based on field research, theoretical analysis, and laboratory tests, and considering factors such as underground environment, material properties, instrument usage, and filling effects, the preliminary filling scheme was formulated as follows. The field application is shown in Figure 17.

• Install a high-quality waterproof canvas bag in the roof falls area: The high-quality waterproof canvas bag is made of tear-resistant, high-strength cloth. The material is soft, has a longer service life, and provides strong waterproof capabilities, effectively preventing slurry seepage.
• Install the mine hydraulic pressure gauge in the specified position: this paper selects the YH-45-type mine hydraulic pressure gauge and the pointer MCZ rock bolt (cable anchor) dynamometer as the monitoring instruments for rock pressure in mines.
• Connect the grouting pipe and start grouting: the grouting process is continuously optimized through laboratory tests, with the final grouting process illustrated in Figure 18.
• After grouting is completed, check the sealing of the grouting bag.
• Complete the filling.

6.2. Field Application Effect

Compared to traditional wooden crib filling, the bag-filling scheme achieved significant safety and economic benefits after its application in the Songxian Shanjin Gold Mine, as shown in Figure 19. One day after the filling, the filling body was inspected, and it was observed that the filling body closely adhered to the roof without any voids, demonstrating a better filling effect. Following the filling, the displacement of the roof was monitored for three months. During this period, the structure of the filling body remained stable, and there was no significant sinking of the roof.

Previously, the roof fall area of the Songxian Shanjin Gold Mine often employed treatments such as scaffolds and wooden cribbing, which required about four workers, with a filling cost of approximately 800 CNY/m³ (CNY means Renminbi—¥). As shown in

Table 5. Comparison of filling costs.

	Labor Cost	Economic Cost
		Materials	Unit Price	Filling Cost
Log pack	4 people	Pit timber	800 CNY/m3	800 CNY/m3
Material filling	2 people	Foam filling material	2000 CNY/t	500 CNY/m3	545 CNY/m3
		High-quality waterproof canvas bag	300 CNY/per piece	45 CNY/m3

, the foaming material filling method only requires two workers, which reduced the filling cost to 545 CNY/m³. This approach effectively decreases labor costs by 50% and overall filling costs by about 32%, while also improving construction safety and efficiency.

Currently, the steel supporting roof at Songxian Shanjin Gold Mine is approximately 1200 m³ per year. The foaming material filling technology is expected to save about CNY 300,000 in support costs and reduce labor costs by around 50% annually. Additionally, the original wooden filling method is prone to fire hazards, secondary collapses, and other accidents. The new filling material not only ensures safety but also reduces the costs associated with secondary maintenance.

7. Conclusions

This paper addresses the issues of roof falls in the soft rock roadway of Songxian Shanjin Gold Mine, as well as the inefficacy of traditional support methods. It proposes a bag-filling scheme that effectively mitigates the risk of roof falls through the independent research and development of foaming materials and bag-filling techniques, accompanied by mechanical analysis, laboratory tests, and field trials. The following conclusions are drawn:

• In the soft rock roadway of Songxian Shanjin, due to its relatively low physical and mechanical properties, the natural fractures in the rock may collapse during the blasting and mining process. The existing timber fill support methods cannot meet the required support strength. The self-developed foam material overcomes the problems of timber fill not being able to fully contact the roof, as well as the issues of wooden structures being prone to corrosion and strength reduction, effectively preventing roof collapse accidents.
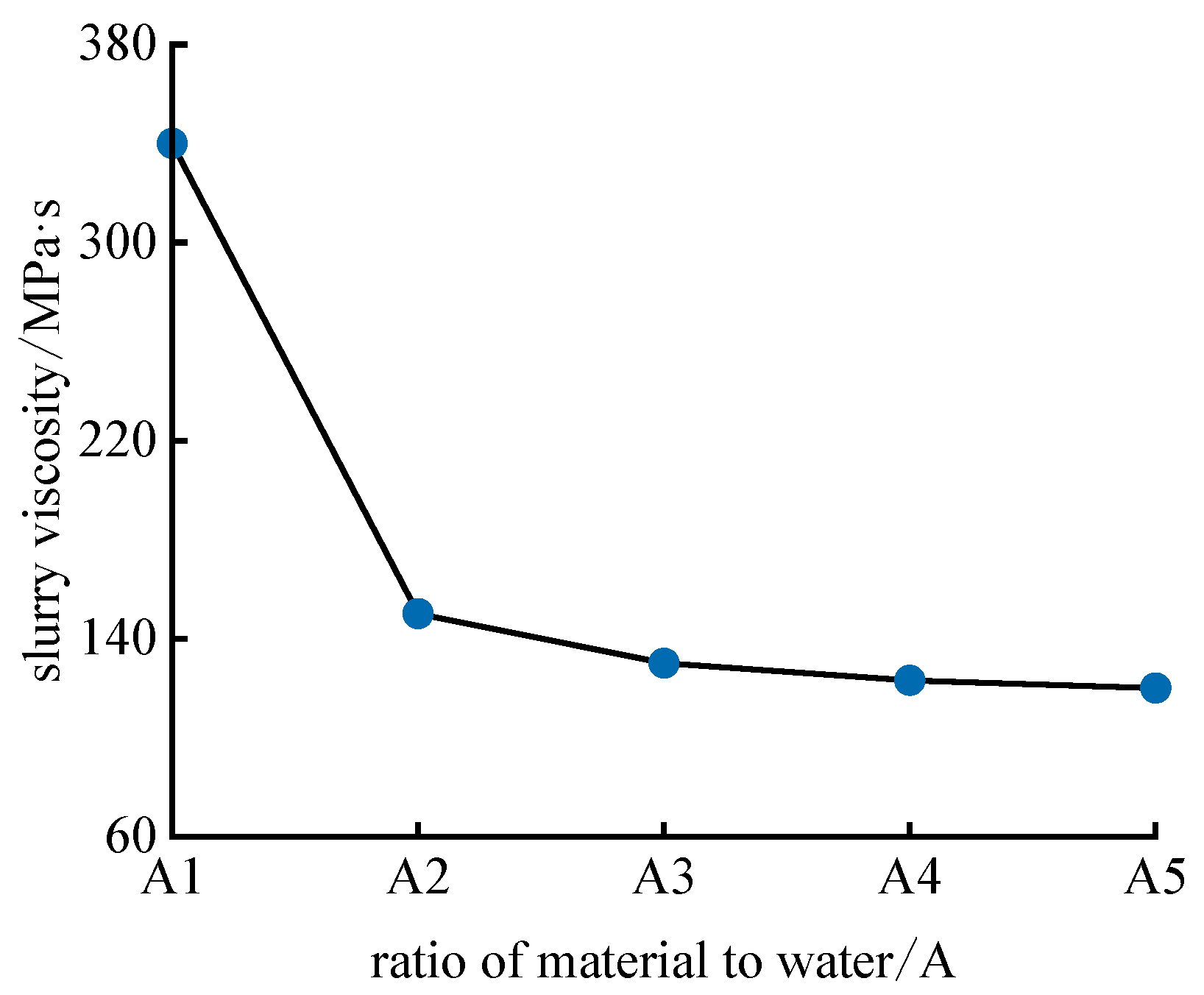
• When the solid–water ratio of the foaming material exceeds the A3 level, the change in slurry viscosity is minimal, occurring at a ratio of 1:2. During the actual filling process, the mixed slurry requires a flow time of about 15 min, meaning the initial setting time of the material should exceed this duration, leading to a minimum water–solid ratio of 2.5:1. When seeking to incorporate more foam, maintaining a water–solid ratio between 2.5:1 and 3.0:1 results in a foam loss percentage of less than 44%. The final strength of the foaming material with water–solid ratio of 1.5:1 and 1:1 increases by approximately 47.7% compared to the strength at 1 day. Additionally, when the concentration of the foam stabilizer is at 1.0%, it reaches a peak effectiveness, indicating that this concentration is optimal. Based on practical requirements, a ratio of 1:3 for portland cement to water was selected, with a foam stabilizer concentration of 1%. This ensures sufficient flow time while meeting the strength requirements for filling support.
• Using high-quality waterproof canvas bags and self-developed foaming materials, a new bag-filling process was proposed. The filling cost was reduced from 800 CNY/m³ to 545 CNY/m³, a decrease of approximately 32%. The required workforce was reduced from 4 workers to 2, cutting labor costs by 50%. It is estimated that annual support costs can be reduced by about CNY 300,000. The bag-filling scheme was used to fill and reinforce the roof falls area in the roadway. This improved the support strength of the filling material, fundamentally eliminating the conditions for fire hazards and reducing the likelihood of secondary collapse accidents. Roof displacement was monitored continuously for three months, showing no significant subsidence. This effectively ensured the safety of the roadway roof surrounding rock.