Super Typhoons Simulation: A Comparison of WRF and Empirical Parameterized Models for High Wind Speeds
Abstract
:1. Introduction
2. Model and Data Description
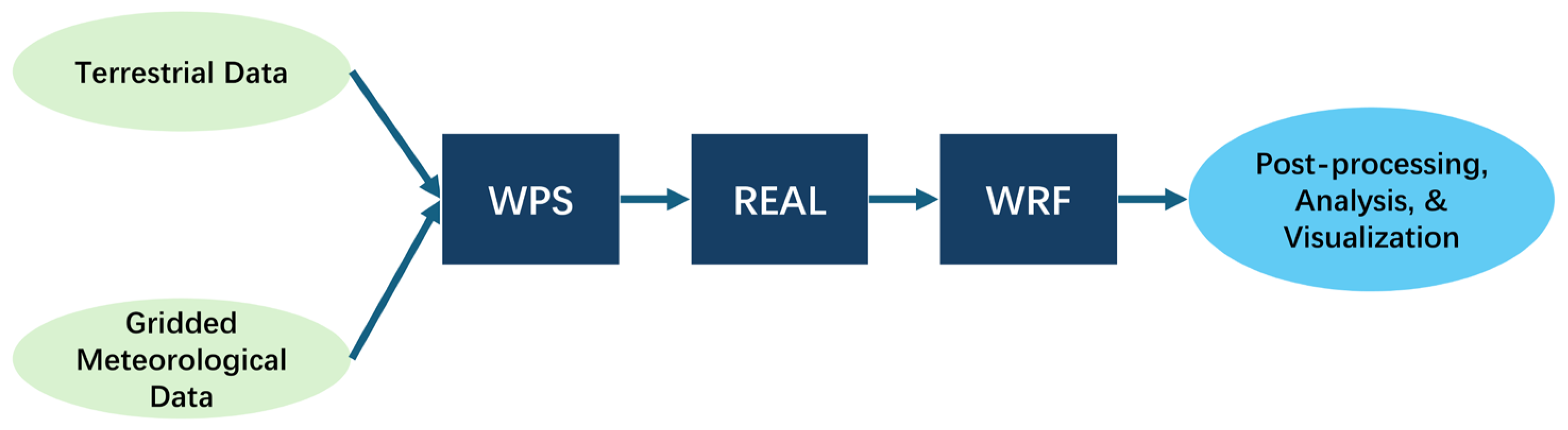
2.1. WRF Model
2.2. Empirical Parametric Typhoon Models
2.3. SWAN Model
2.4. Data Description
3. Simulation Scheme Description
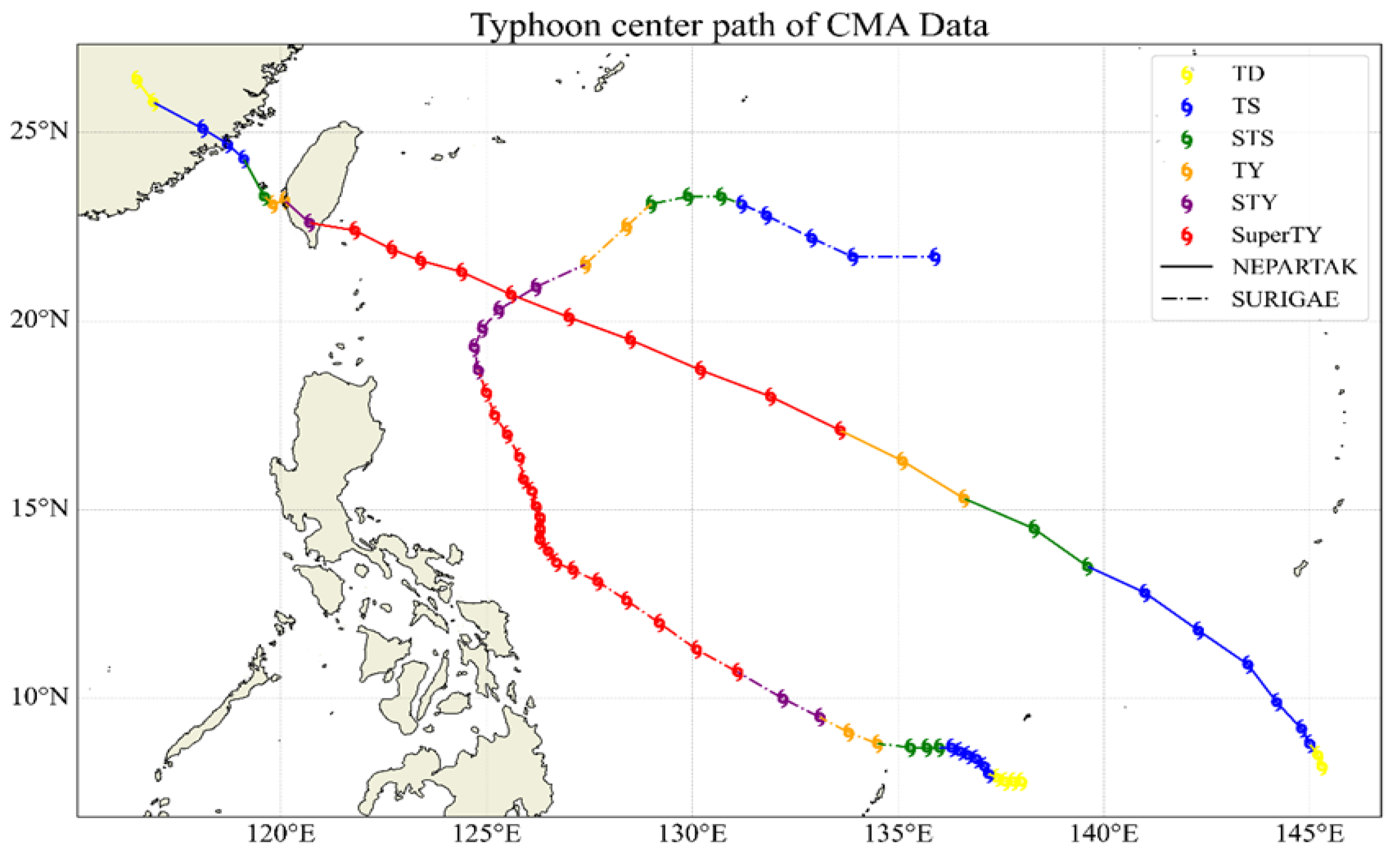
3.1. Typhoon Description
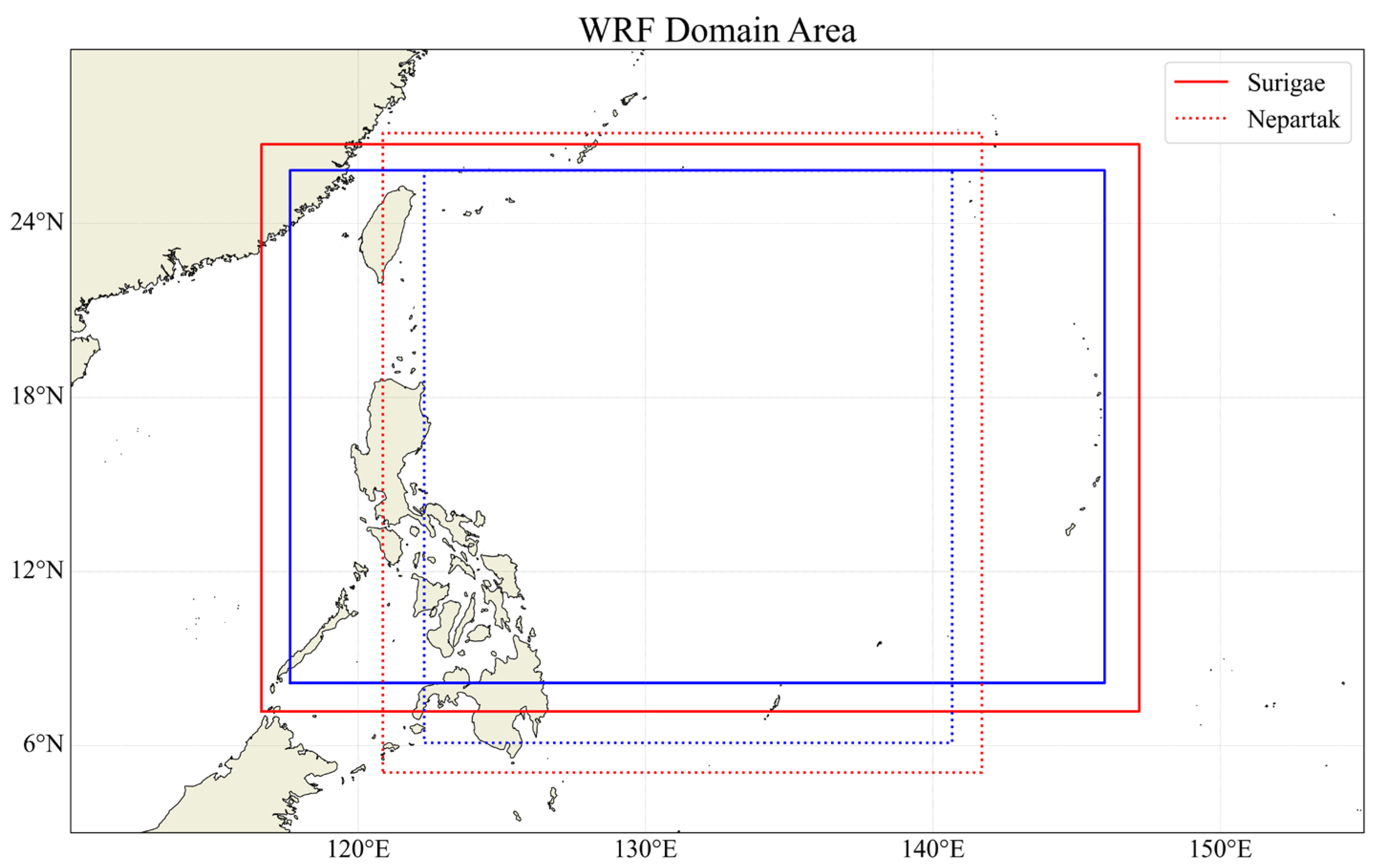
3.2. WRF Scheme Description
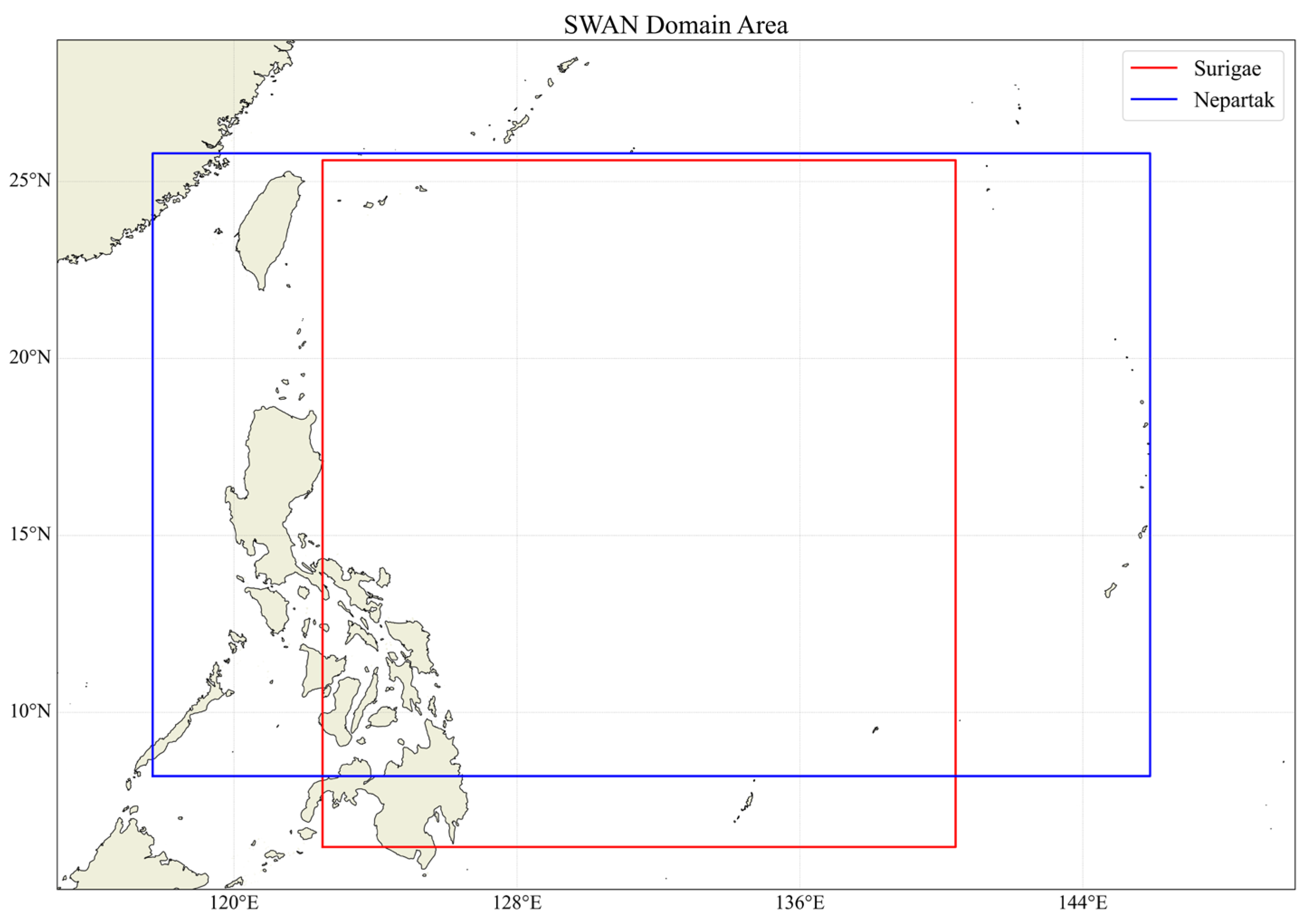
3.3. Description of the SWAN Scheme
4. Results
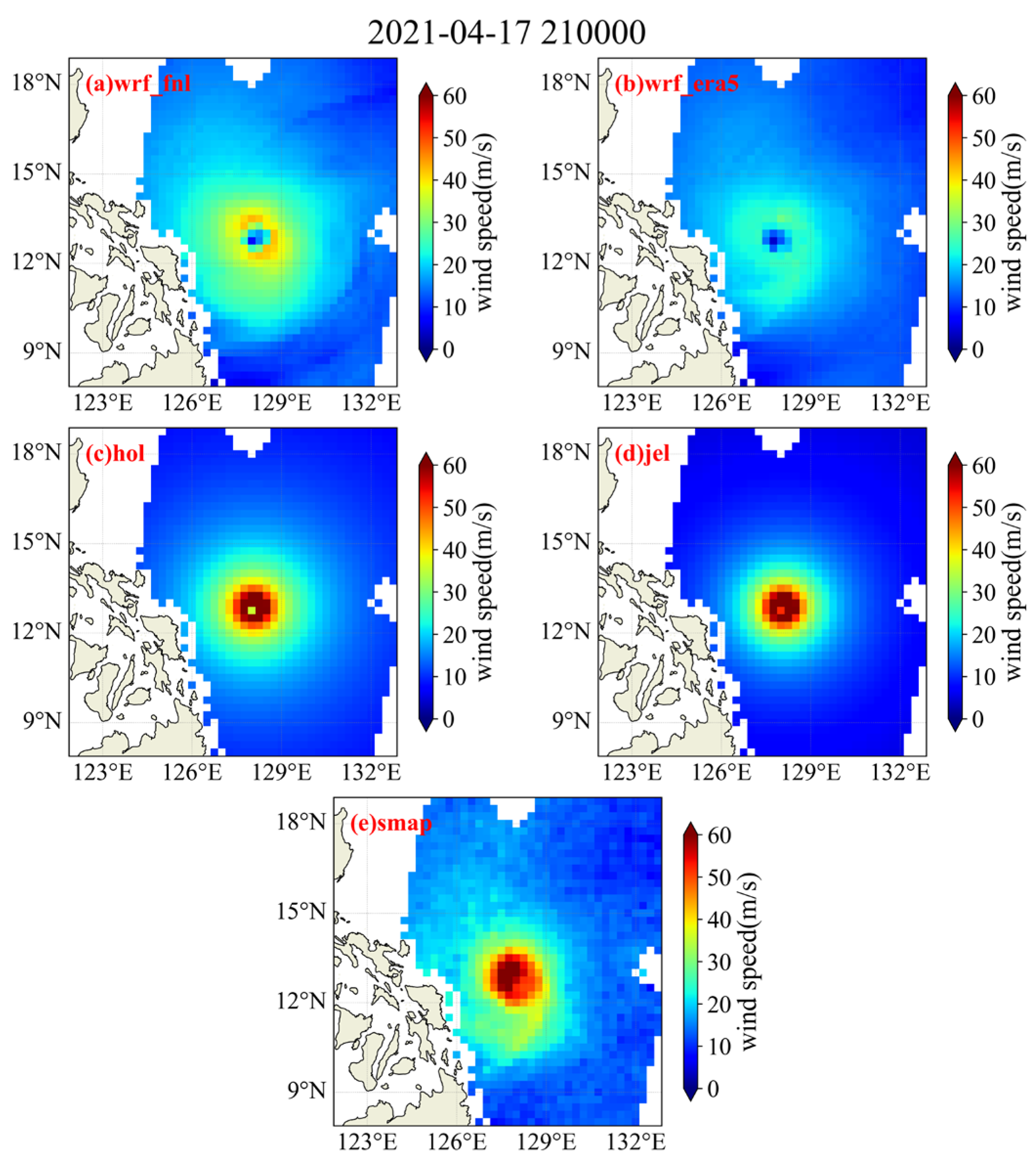
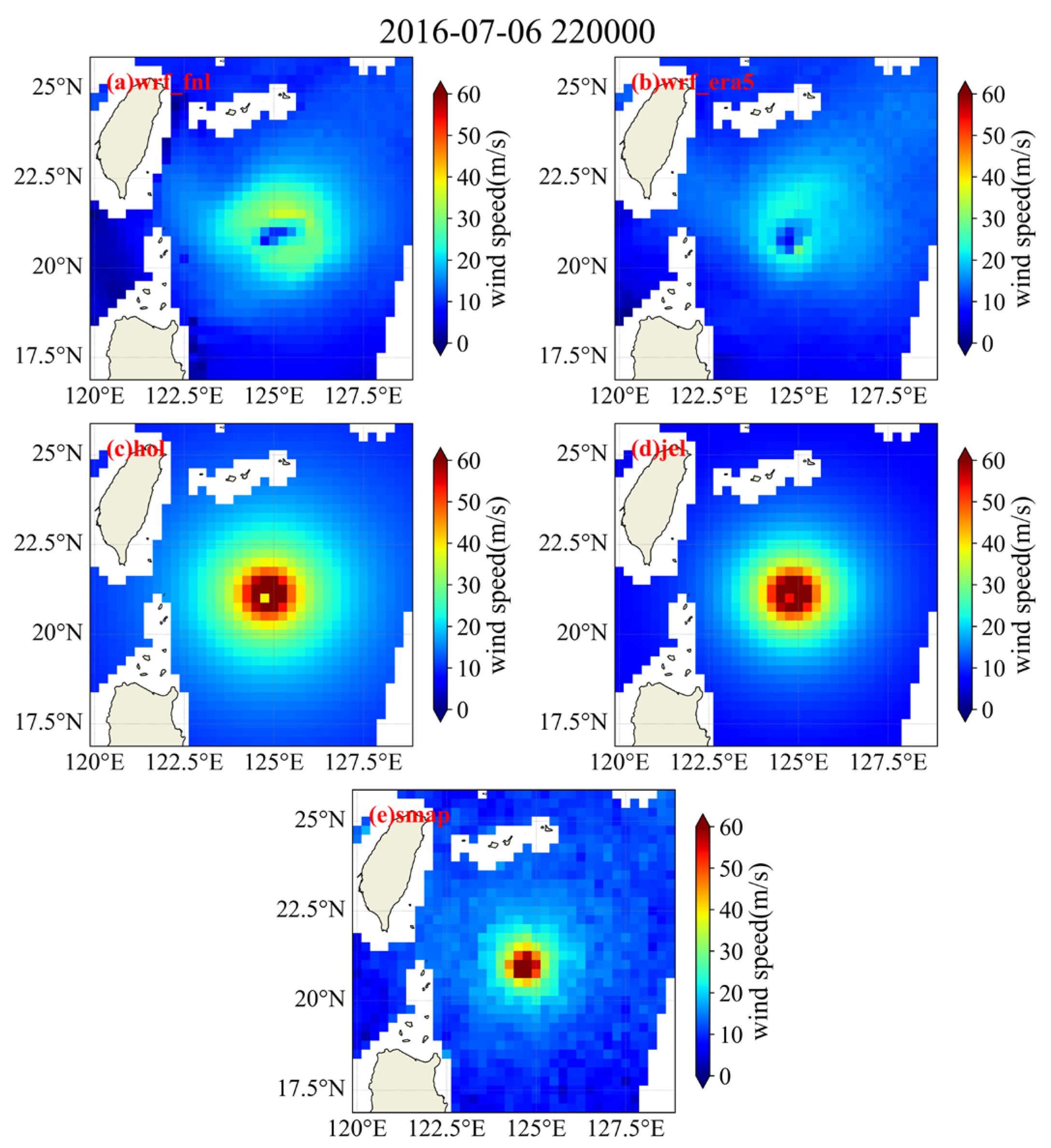
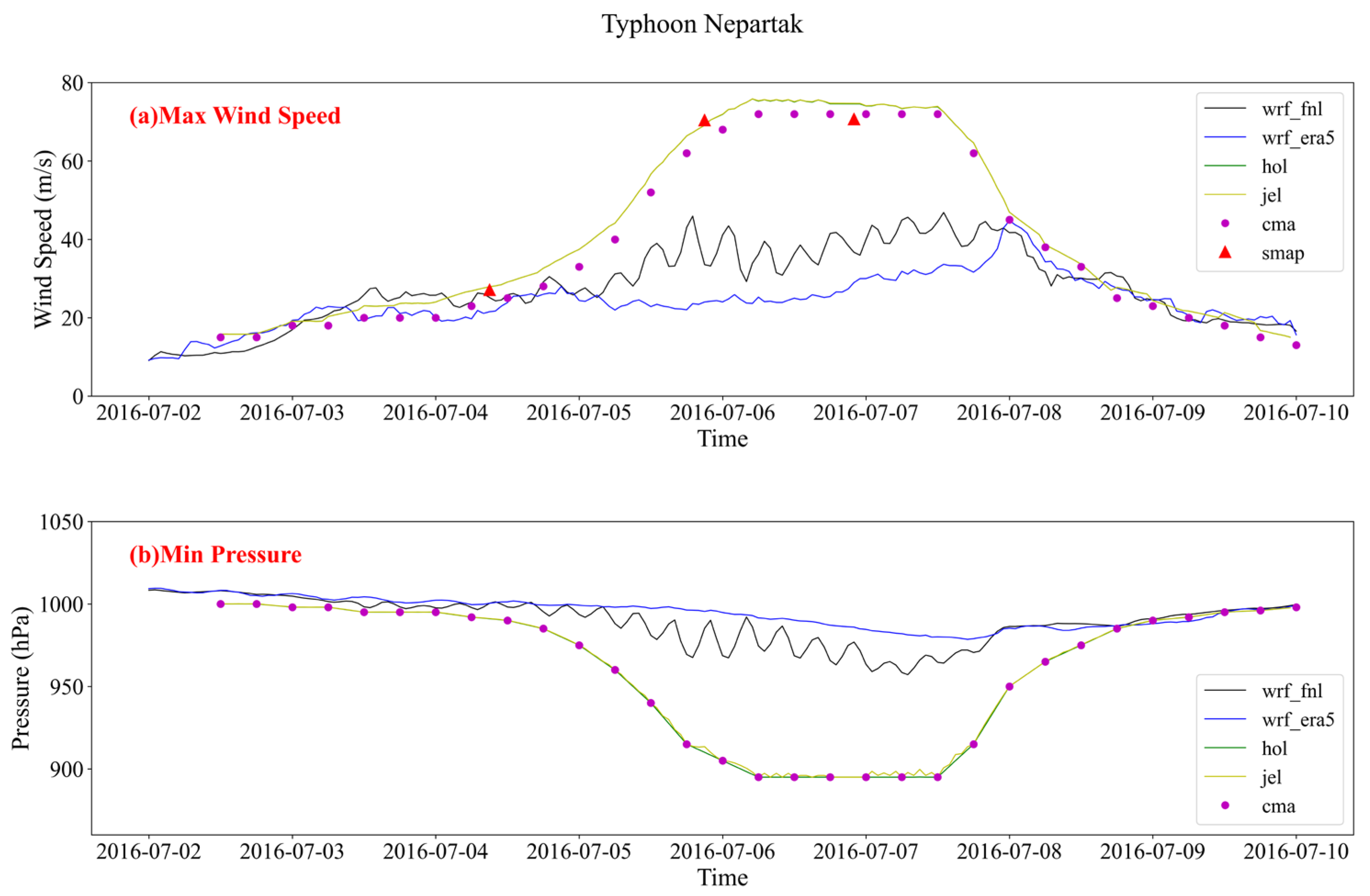
4.1. Evaluation of Simulated Typhoon Wind Speed
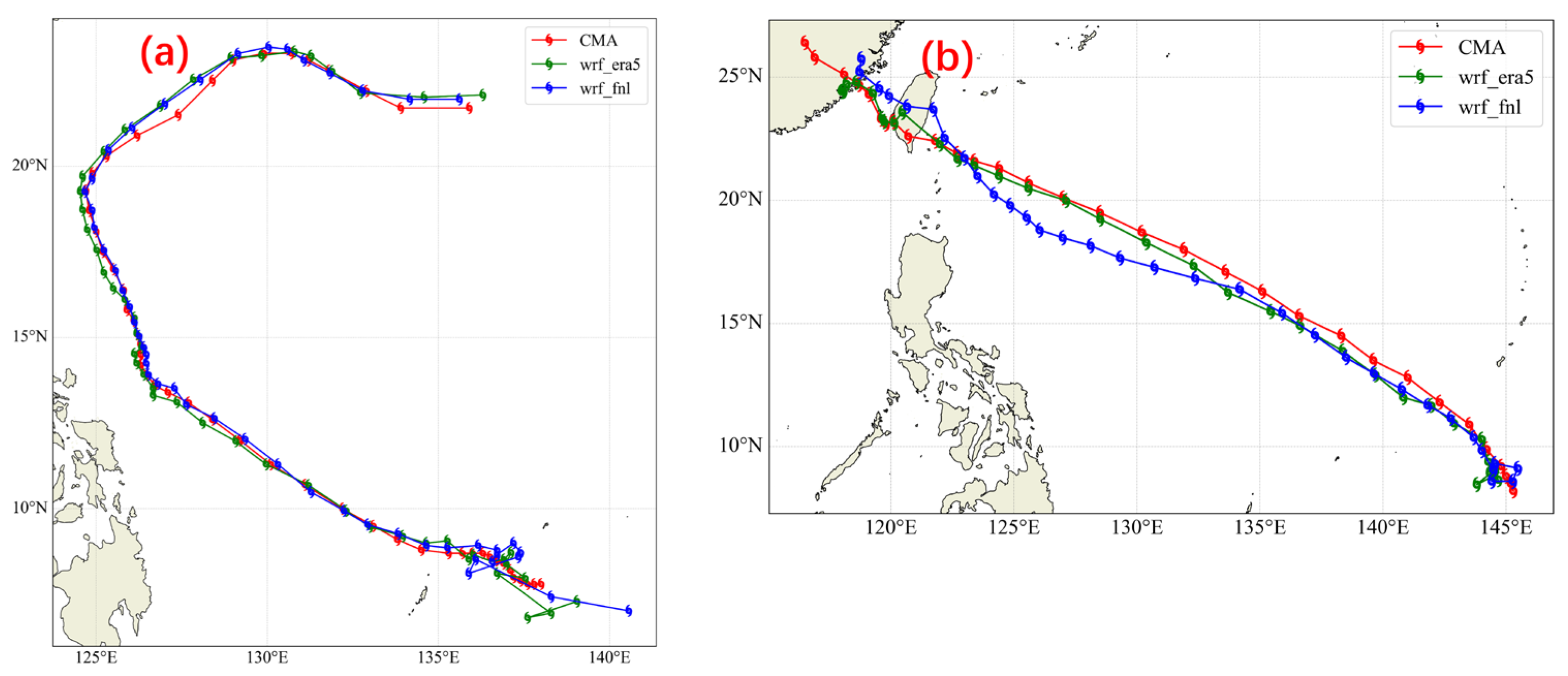
4.2. Typhoon Center Path Compare
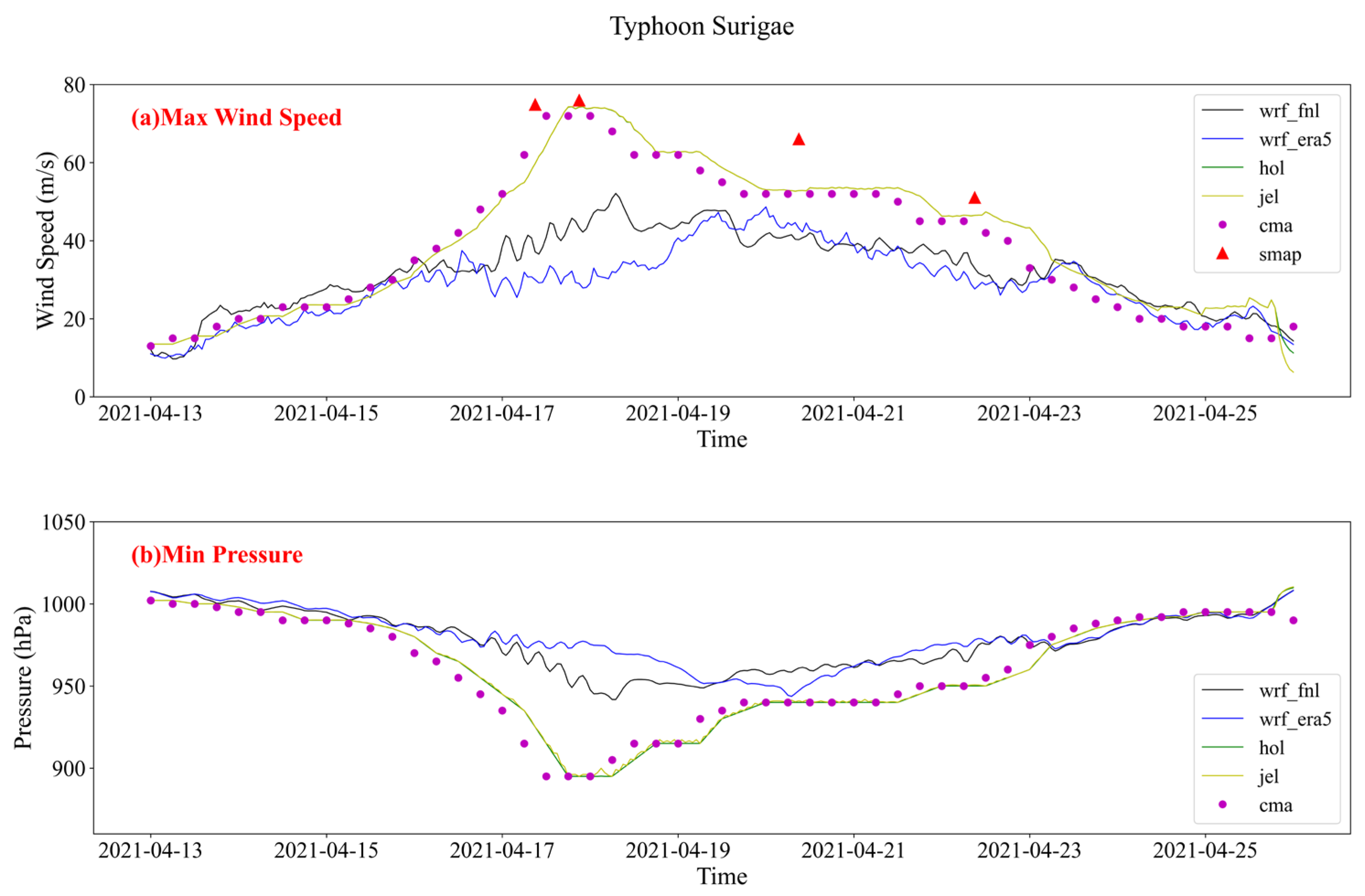
4.3. Comparison of Typhoon Intensity Simulations
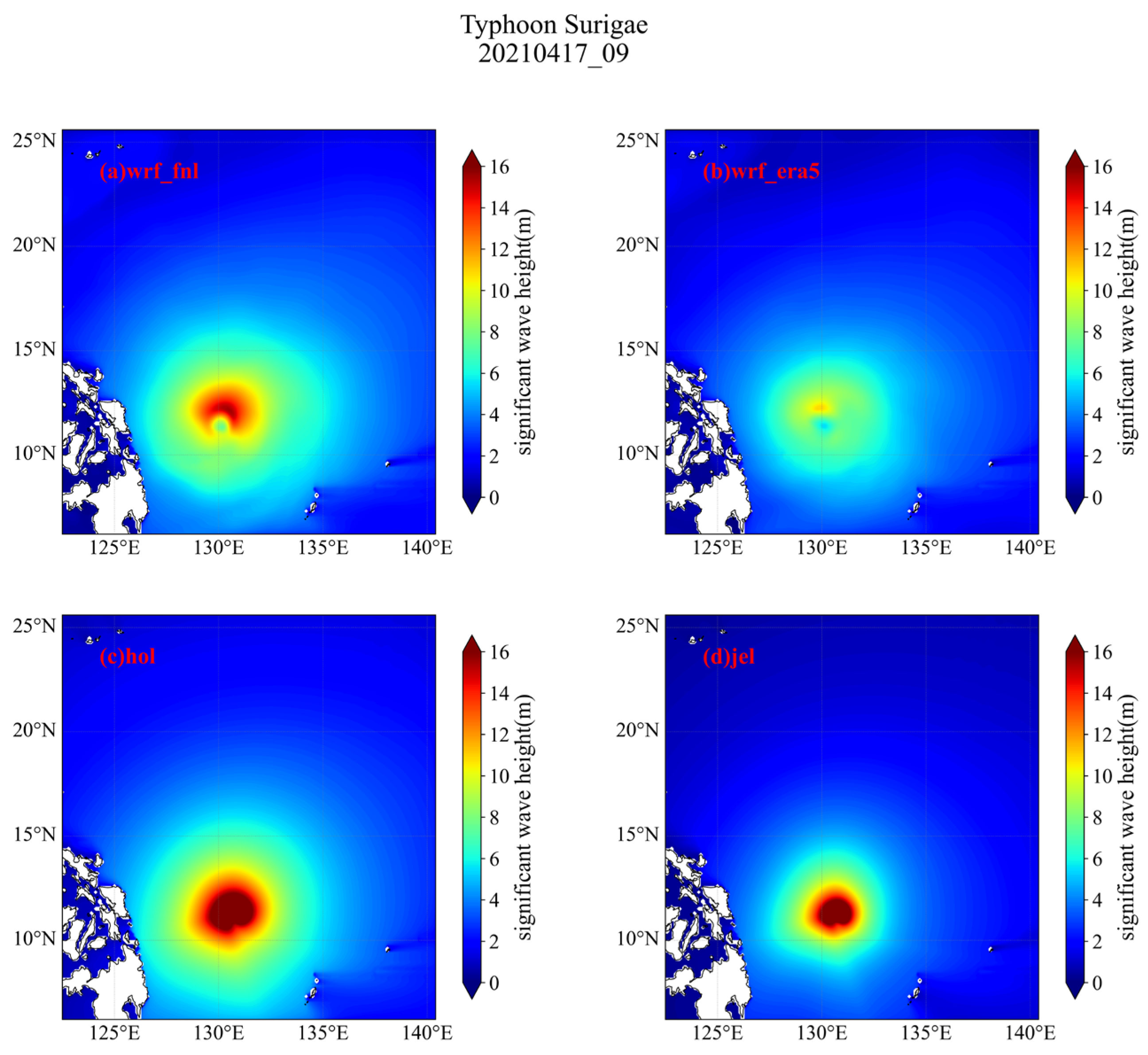
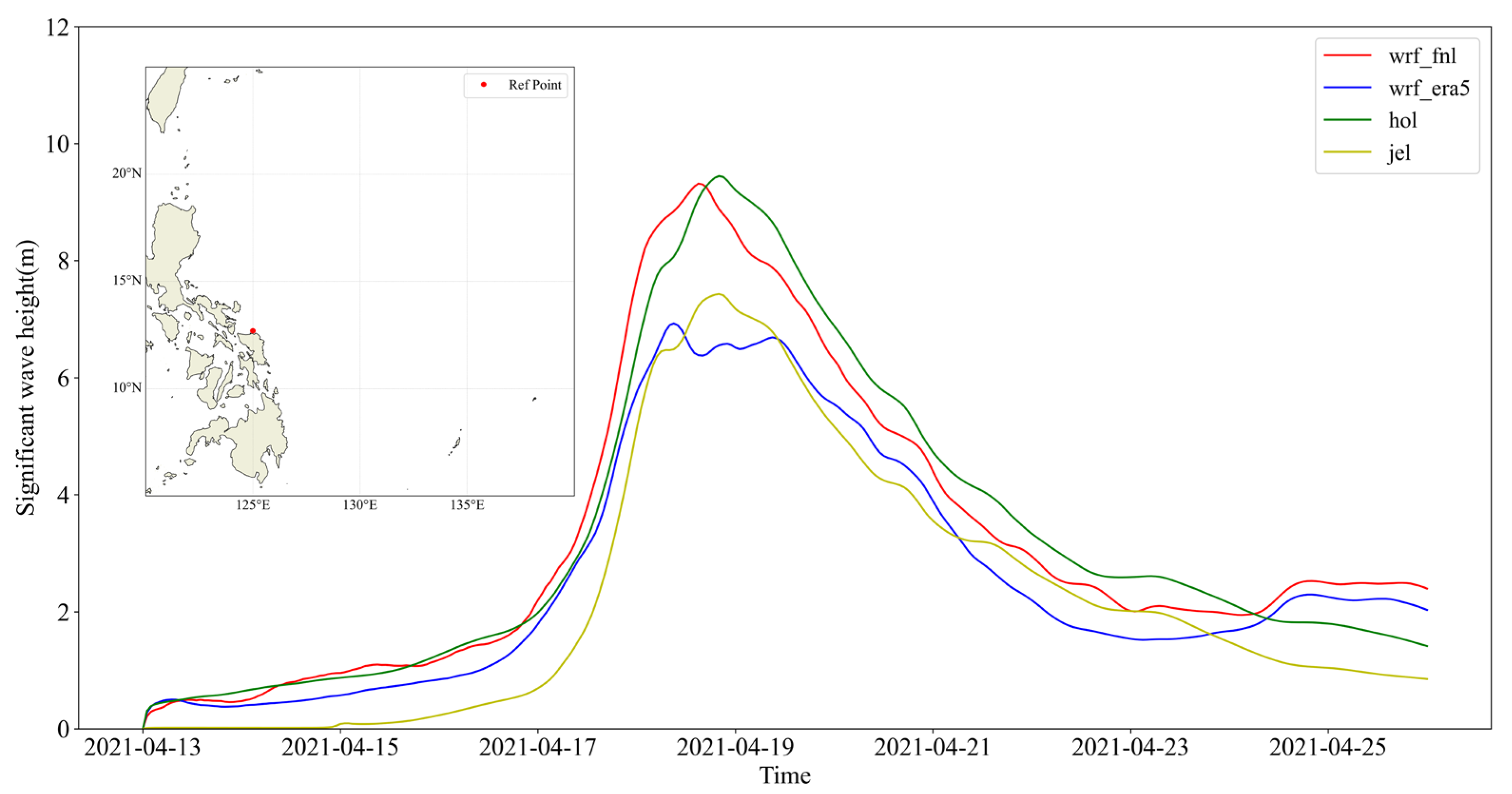
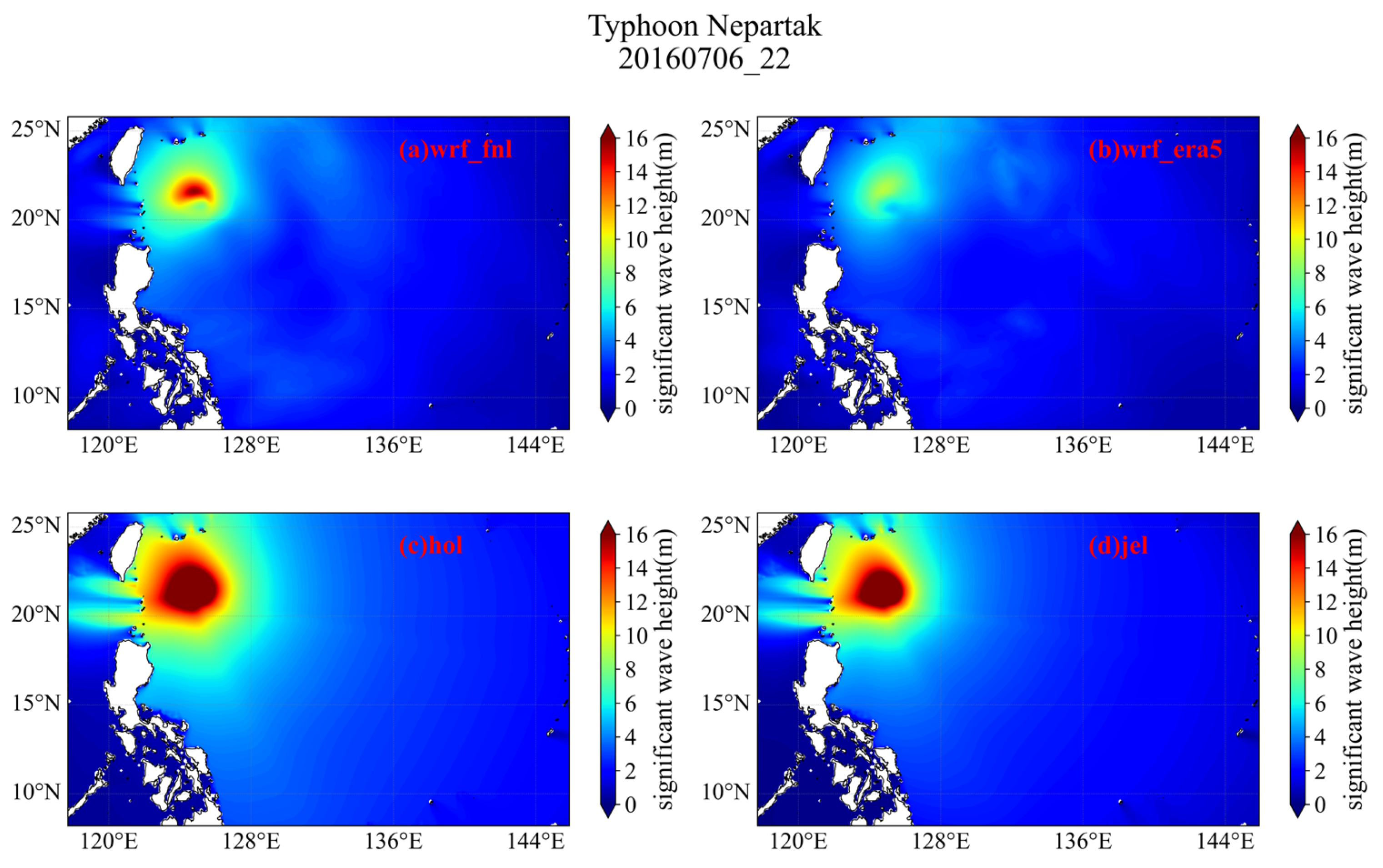
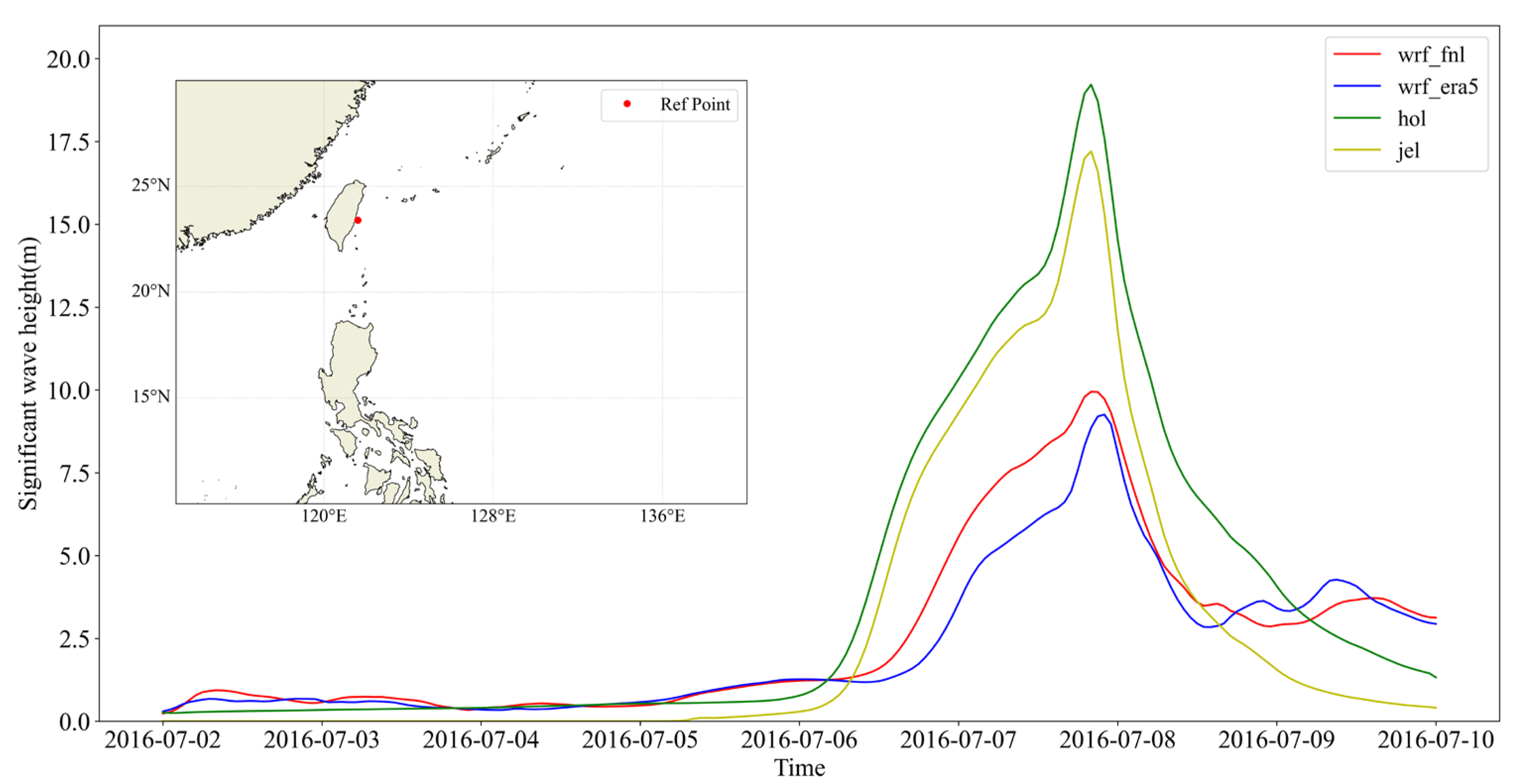
4.4. Significant Wave Height Results from SWAN
5. Discussion and Conclusions
5.1. Discussion
5.2. Conclusions
- (1).
- The Holland and Jelesnianski models simulate extreme wind speeds (above 50 m/s) better than the WRF model driven by FNL and ERA5 data.
- (2).
- WRF simulations driven by FNL data perform better in simulating high wind speeds than those driven by ERA5. Additionally, WRF simulates the wind field in the outer regions of the typhoon more accurately than the empirical models.
- (3).
- The maximum wind radius range simulated by the Holland empirical parameterized typhoon model tends to be overestimated, resulting in higher wind speed and significant wave height simulations at locations closer to the typhoon’s central path. Therefore, parameters such as the maximum wind radius require careful consideration and refinement.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Li, X.; Han, G.; Yang, J.; Wang, C. Remote Sensing Analysis of Typhoon-Induced Storm Surges and Sea Surface Cooling in Chinese Coastal Waters. Remote Sens. 2023, 15, 1844. [Google Scholar] [CrossRef]
- Tang, R.; Shen, F.; Ge, J.; Yang, S.; Gao, W. Investigating typhoon impact on SSC through hourly satellite and real-time field observations: A case study of the Yangtze Estuary. Cont. Shelf Res. 2021, 224, 104475. [Google Scholar] [CrossRef]
- Yang, C.; Shi, B.; Min, J. The Combination Application of FY-4 Satellite Products on Typhoon Saola Forecast on the Sea. Remote Sens. 2024, 16, 4105. [Google Scholar] [CrossRef]
- Chen, X.-Z.; Ma, Y.-L.; Lin, C.-Q.; Fan, L.-L. Assessment of Typhoon Precipitation Forecasts Based on Topographic Factors. Atmosphere 2023, 14, 1607. [Google Scholar] [CrossRef]
- Zeng, Z.-h.; Chen, L.; Wang, Y.-q. A numerical simulation study of super Typhoon Saomei (2006) intensity and structure changes. Acta Meteorol. Sin. 2009, 67, 750–763. [Google Scholar]
- Chen, Y.Z.; Zhan, J.M.; Luo, Y.Y.; Wai, O.W.H.; Tang, L. Responses of thermal structure and vertical dynamic structure of South China Sea to Typhoon Chanchu. J. Hydrodyn. 2014, 26, 458–466. [Google Scholar] [CrossRef]
- Potty, J.; Oo, S.; Raju, P.; Mohanty, U. Performance of nested WRF model in typhoon simulations over West Pacific and South China Sea. Nat. Hazards 2012, 63, 1451–1470. [Google Scholar] [CrossRef]
- Sunce, L.; Mingfeng, H.; Wenjuan, L.; Wei, L.; Zhibin, X. Numerical simulation of a urban wind field under the influence of typhoon “Mangkhut”. Acta Aerodyn. Sin. 2021, 39, 107–116. [Google Scholar]
- Wu, Z.; Jiang, C.; Deng, B.; Chen, J.; Liu, X. Sensitivity of WRF simulated typhoon track and intensity over the South China Sea to horizontal and vertical resolutions. Acta Meteorol. Sin. 2019, 38, 74–83. [Google Scholar] [CrossRef]
- Yang, M.J.; Ching, L. A modeling study of Typhoon Toraji (2001): Physical parameterization sensitivity and topographic effect. Terr. Atmos. Ocean. Sci. 2005, 16, 177–213. [Google Scholar] [CrossRef]
- Deppermann, C.E. Notes on the origin and structure of Philippine typhoons. Bull. Am. Meteorol. Soc. 1947, 28, 399–404. [Google Scholar] [CrossRef]
- Holland, G.J. An Analytic Model of the Wind and Pressure Profiles in Hurricanes. Mon. Weather Rev. 1980, 108, 1212–1218. [Google Scholar] [CrossRef]
- Jelesnianski, C.P. Numerical computations of storm surges without bottom stress. Mon. Weather Rev. 1966, 94, 379–394. [Google Scholar] [CrossRef]
- Myers, V.A. Characteristics of United States Hurricanes Pertinent to Levee Design for Lake Okeechobee, Florida; US Government Printing Office: Washington, DC, USA, 1954; Volume 30.
- Wang, L.; Zhang, Z.; Liang, B.; Lee, D.; Luo, S. An efficient method for simulating typhoon waves based on a modified Holland vortex model. J. Mar. Sci. Eng. 2020, 8, 177. [Google Scholar] [CrossRef]
- Xu, Y.; Wang, Z.F. Response of Surface Ocean Conditions to Typhoon Rammasun (2014). J. Coast. Res. 2017, 80, 92–97. [Google Scholar] [CrossRef]
- Zhong, X.; Wei, K.; Shang, D.M. An improved azimuth-dependent Holland model for typhoons along the Zhejiang coast prior to landfall based on WRF-ARW simulations. Nat. Hazards 2023, 117, 2325–2346. [Google Scholar] [CrossRef]
- Wen, Y.F.; Liu, Y.D.; Tan, W.C.; Peng, K.M.; Chen, H.F. The Impact of Horizontal Resolution on the Intensity and Microstructure of Super Typhoon Usagi. J. Trop. Meteorol. 2019, 25, 24–33. [Google Scholar] [CrossRef]
- Ruan, Z.X.; Li, J.N.; Li, F.Z.; Lin, W.S. Effects of local and non-local closure PBL schemes on the simulation of Super Typhoon Mangkhut (2018). Front. Earth Sci. 2022, 16, 277–290. [Google Scholar] [CrossRef]
- Xue, G.; Zhang, J.; Chen, H.; Yu, H. Analysis on causes of strengthening of super strong typhoon Saomai (0608) and numerical experiments of the impact of SST on its intensity. Quat. Sci. 2007, 27, 311–321. [Google Scholar]
- Xu, H.X. A Numerical Study on Impact of Taiwan Island Surface Heat Flux on Super Typhoon Haitang (2005). Adv. Meteorol. 2015, 2015, 710348. [Google Scholar] [CrossRef]
- Zhang, W.Q.; Zhang, J.L.; Guan, C.L.; Sun, J. Impacts of Surface Exchange Coefficients on Simulations of Super Typhoon Megi (2010) Using a Coupled Ocean-Atmosphere-Wave Model. J. Ocean Univ. China 2023, 22, 587–600. [Google Scholar] [CrossRef]
- Ou, S.H.; Liau, J.M.; Hsu, T.W.; Tzang, S.Y. Simulating typhoon waves by SWAN wave model in coastal waters of Taiwan. Ocean Eng. 2002, 29, 947–971. [Google Scholar] [CrossRef]
- Sheng, Y.X.; Shao, W.Z.; Li, S.Q.; Zhang, Y.M.; Yang, H.W.; Zuo, J.C. Evaluation of Typhoon Waves Simulated by WaveWatch-III Model in Shallow Waters Around Zhoushan Islands. J. Ocean Univ. China 2019, 18, 365–375. [Google Scholar] [CrossRef]
- Shi, Q.; Tang, J.; Shen, Y.M.; Ma, Y.X. Numerical investigation of ocean waves generated by three typhoons in offshore China. Acta Oceanol. Sin. 2021, 40, 125–134. [Google Scholar] [CrossRef]
- Wu, Y.; Dou, S.T.; Fan, Y.S.; Yu, S.B.; Dai, W.Q. Research on the influential characteristics of asymmetric wind fields on typhoon waves. Front. Mar. Sci. 2023, 10, 1113494. [Google Scholar] [CrossRef]
- Wang, L.; Wei, X.; Sun, Y.; Jiang, M.; Li, Q. The Wave Numeric Simulation of 0920 Super Typhoon Lupit. Adv. Mar. Sci. 2015, 2, 94–101. [Google Scholar]
- Wu, Z.; Jiang, C.; Deng, B.; Chen, J.; Cao, Y.; Li, L. Evaluation of numerical wave model for typhoon wave simulation in South China Sea. Water Sci. Eng. 2018, 11, 229–235. [Google Scholar] [CrossRef]
- Hsiao, S.C.; Chen, H.E.; Wu, H.L.; Chen, W.B.; Chang, C.H.; Guo, W.D.; Chen, Y.M.; Lin, L.Y. Numerical Simulation of Large Wave Heights from Super Typhoon Nepartak (2016) in the Eastern Waters of Taiwan. J. Mar. Sci. Eng. 2020, 8, 217. [Google Scholar] [CrossRef]
- Mazyak, A.R.; Shafieefar, M. Development of a hybrid wind field for modeling the tropical cyclone wave field. Cont. Shelf Res. 2022, 245, 104788. [Google Scholar] [CrossRef]
- Sebastian, M.; Behera, M.R.; Prakash, K.R.; Murty, P.L.N. Performance of various wind models for storm surge and wave prediction in the Bay of Bengal: A case study of Cyclone Hudhud. Ocean Eng. 2024, 297, 117113. [Google Scholar] [CrossRef]
- Shashank, V.; Sriram, V.; Sannasiraj, S. Improvements in wind field hindcast for storm surge predictions in the Bay of Bengal: A case study for the tropical cyclone Varadah. Appl. Ocean Res. 2022, 127, 103324. [Google Scholar] [CrossRef]
- Skamarock, W.C.; Klemp, J.B.; Dudhia, J.; Gill, D.O.; Liu, Z.; Berner, J.; Wang, W.; Powers, J.G.; Duda, M.G.; Barker, D.M. A Description of the Advanced Research WRF Version 4; NCAR Technical Notes NCAR/TN-556+STR; National Center for Atmospheric Research: Boulder, CO, USA, 2019; Volume 145. [Google Scholar]
- Dewen, C. Research on the Typhoon Sea Surface Wind Field and Its Modeling in the Sea Areas around Taiwan Island; Xiamen University: Xiamen, China, 2006. [Google Scholar]
- Willoughby, H.E.; Darling, R.; Rahn, M. Parametric representation of the primary hurricane vortex. Part II: A new family of sectionally continuous profiles. Mon. Weather Rev. 2006, 134, 1102–1120. [Google Scholar] [CrossRef]
- Jakobsen, F.; Madsen, H. Comparison and further development of parametric tropical cyclone models for storm surge modelling. J. Wind Eng. Ind. Aerodyn. 2004, 92, 375–391. [Google Scholar] [CrossRef]
- Jelesnianski, C.P. A Numerical Calculation of Storm Tides Induced by a Tropical Storm Impinging on a Continental Shelf. Mon. Weather Rev. 1965, 93, 343–358. [Google Scholar] [CrossRef]
- Team, S. SWAN: Scientific and Technical Documentation (SWAN Cycle III Version 41.31 A); Delft University of Technology: Delft, The Netherlands, 2020; Available online: https://swanmodel.sourceforge.net/download/zip/swantech.pdf (accessed on 22 November 2022).
- Department of Commerce. NCEP FNL Operational Model Global Tropospheric Analyses, Continuing from July 1999; The National Center for Atmospheric Research, Computational and Information Systems Laboratory: Boulder, CO, USA, 2000. [Google Scholar]
- Hersbach, H.; Bell, B.; Berrisford, P.; Hirahara, S.; Horányi, A.; Muñoz-Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Schepers, D.; et al. The ERA5 global reanalysis. Q. J. R. Meteorol. Soc. 2020, 146, 1999–2049. [Google Scholar] [CrossRef]
- Meissner, T.; Ricciardulli, L.; Wentz, F. Remote Sensing Systems SMAP Daily Sea Surface Winds Speeds on 0.25 Deg Grid, Version 01.0. [NRT or FINAL]; Remote Sensing Systems: Santa Rosa, CA, USA, 2018. [Google Scholar]
- Ying, M.; Zhang, W.; Yu, H.; Lu, X.Q.; Feng, J.X.; Fan, Y.X.; Zhu, Y.T.; Chen, D.Q. An Overview of the China Meteorological Administration Tropical Cyclone Database. J. Atmos. Ocean. Technol. 2014, 31, 287–301. [Google Scholar] [CrossRef]
- Lu, X.Q.; Yu, H.; Ying, M.; Zhao, B.K.; Zhang, S.; Lin, L.M.; Bai, L.N.; Wan, R.J. Western North Pacific Tropical Cyclone Database Created by the China Meteorological Administration. Adv. Atmos. Sci. 2021, 38, 690–699. [Google Scholar] [CrossRef]


| Dataset Name | Usage | Description |
|---|---|---|
| FNL | The dataset used to drive the WRF model | FNL data are on 1-degree by 1-degree grids prepared operationally every six hours, and can be downloaded from https://rda.ucar.edu/datasets/d083002/ (accessed on 1 October 2024) [39]. |
| ERA5 | The dataset used to drive the WRF model | ERA5 data are on 0.25-degree by 0.25-degree grids prepared operationally every hour and can be downloaded from https://cds.climate.copernicus.eu/datasets (accessed on 1 October 2024) [40]. |
| SMAP | Actual observational dataset | Each SMAP file consists of two 0.25° gridded daily maps of wind speeds, the wind speed data at a 10 m height above the sea surface is obtained through the L-band radiometer onboard the SMAP satellite and can be downloaded from https://remss.com/missions/SMAP/winds/ (accessed on 1 October 2024) [41]. |
| CMA | Actual observational dataset | CMA dataset provides the position and intensity of tropical cyclones in the Northwest Pacific (including the South China Sea, north of the equator, and west of 180°E) every 6 h since 1949, can be downloaded from https://tcdata.typhoon.org.cn/zjljsjj.html (accessed on 1 October 2024) [42,43]. |
| Namelist Parameter | Setting Codes | Description |
|---|---|---|
| mp_physics | 24, 24 | WSM7 |
| ra_lw_physics | 1, 1 | RRTM |
| ra_sw_physics | 1, 1 | Dudhia |
| sf_sfclay_physics | 1, 1 | revised MM5 Monin–Obukhov |
| sf_surface_physics | 2, 2 | unified Noah |
| bl_pbl_physics | 1, 1 | YSU |
| cu_physics | 1, 1 | Kain–Fritsch (new Eta) |
| sf_ocean_physics | 1 | simple ocean mixed layer (oml) model |
| isftcflx | 1 | Donelan Cd + constant Z0q for Ck |
| Abbreviation | Description |
|---|---|
| wrf_fnl | The WRF simulation results driven by FNL data |
| wrf_era5 | The WRF simulation results driven by ERA5 data |
| hol | The simulation results of the Holland model |
| jel | The simulation results of the Jelesnianski model |
| smap | The SMAP wind field data |
| CMA | The CMA tropical cyclone’s best track data |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fu, H.; Wang, Y.; Xie, Y.; Luo, C.; Shang, S.; He, Z.; Wei, G. Super Typhoons Simulation: A Comparison of WRF and Empirical Parameterized Models for High Wind Speeds. Appl. Sci. 2025, 15, 776. https://doi.org/10.3390/app15020776
Fu H, Wang Y, Xie Y, Luo C, Shang S, He Z, Wei G. Super Typhoons Simulation: A Comparison of WRF and Empirical Parameterized Models for High Wind Speeds. Applied Sciences. 2025; 15(2):776. https://doi.org/10.3390/app15020776
Chicago/Turabian StyleFu, Haihua, Yan Wang, Yanshuang Xie, Chenghan Luo, Shaoping Shang, Zhigang He, and Guomei Wei. 2025. "Super Typhoons Simulation: A Comparison of WRF and Empirical Parameterized Models for High Wind Speeds" Applied Sciences 15, no. 2: 776. https://doi.org/10.3390/app15020776
APA StyleFu, H., Wang, Y., Xie, Y., Luo, C., Shang, S., He, Z., & Wei, G. (2025). Super Typhoons Simulation: A Comparison of WRF and Empirical Parameterized Models for High Wind Speeds. Applied Sciences, 15(2), 776. https://doi.org/10.3390/app15020776






