Influence of the Radial Gap on the External Gear Pump Performance
Abstract
:1. Introduction and Motivation
2. Design Features and CFD Model
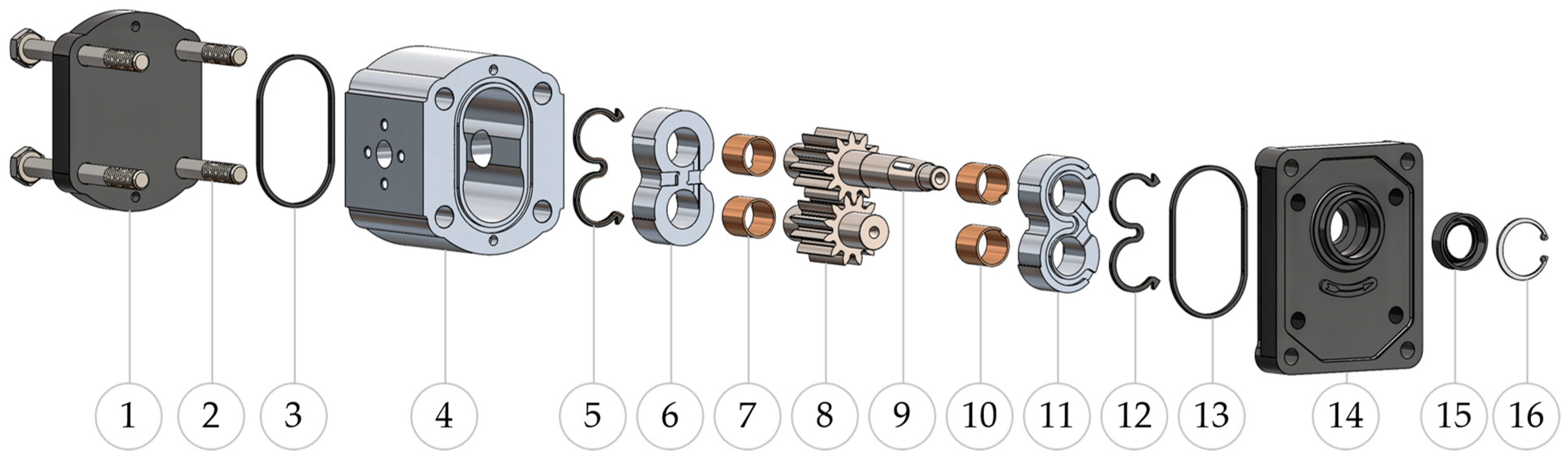
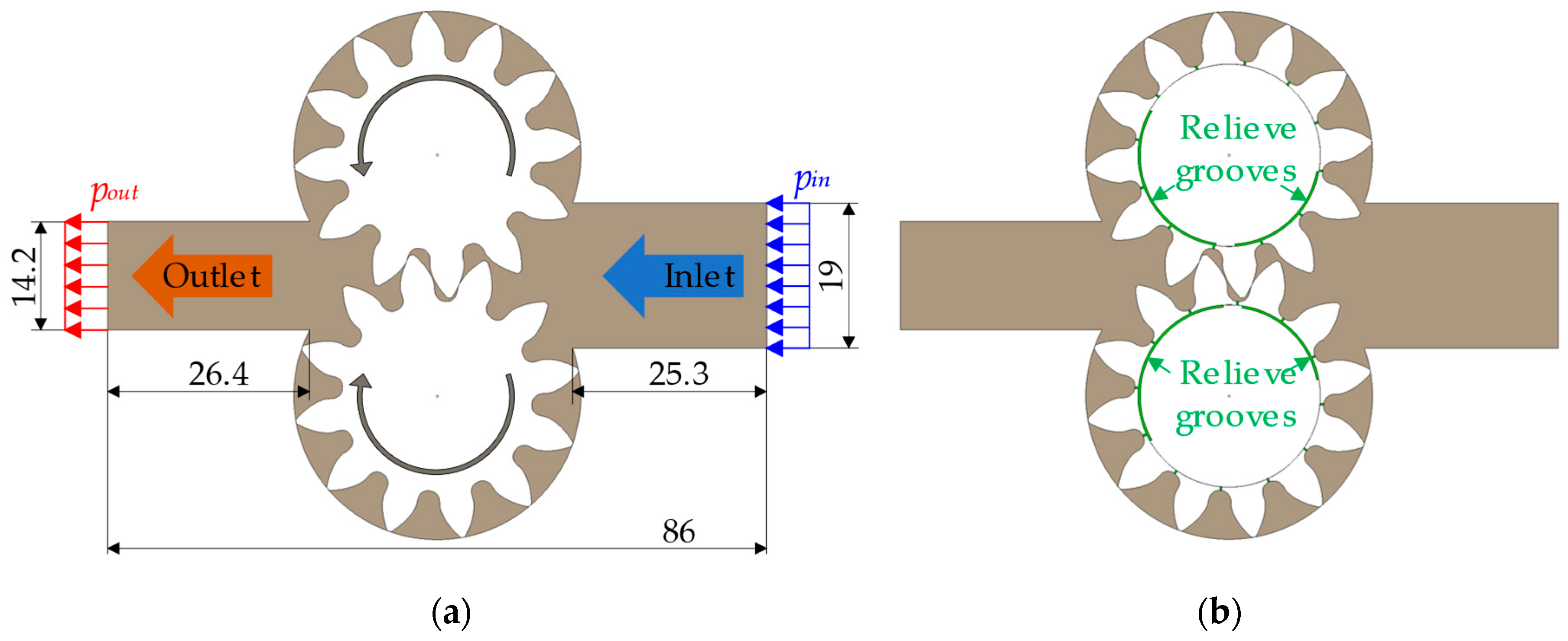
2.1. Design Features and Geometric Model of the Pump
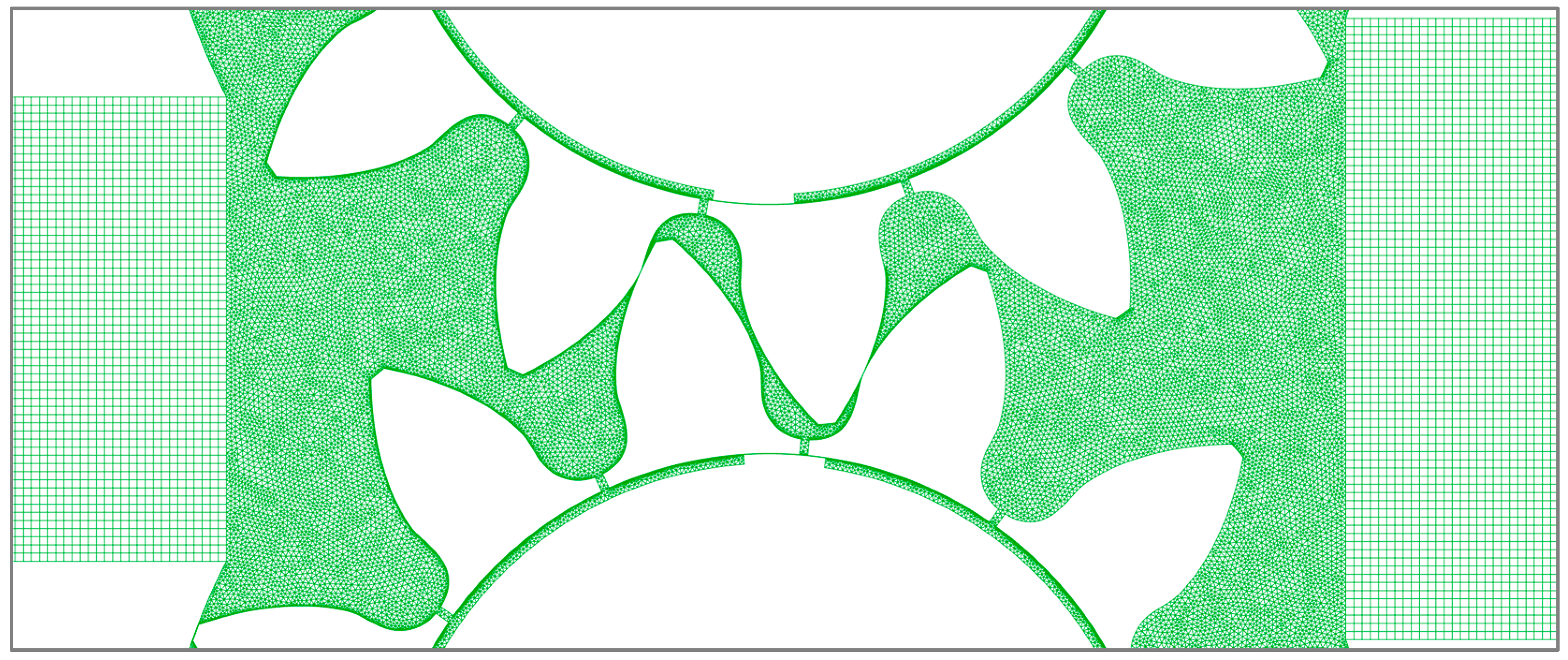
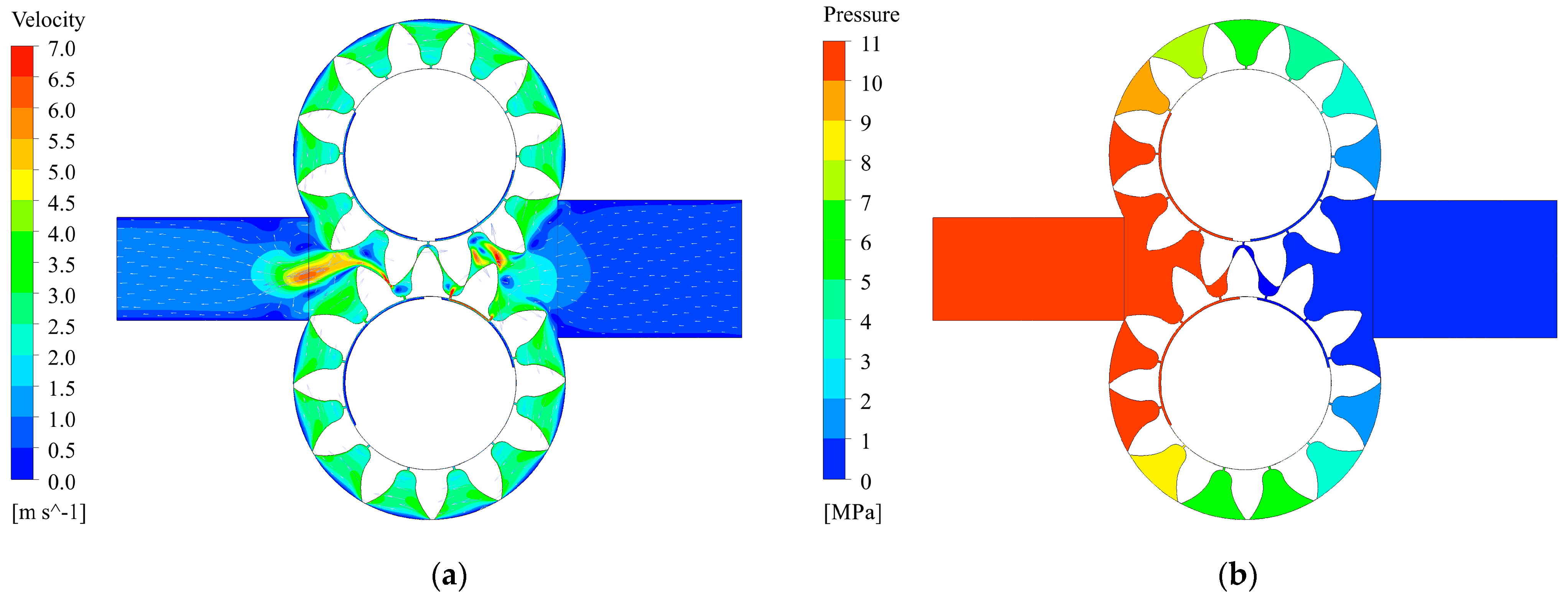
2.2. CFD Model
3. Pump Performance at Different Values of the Radial Gap
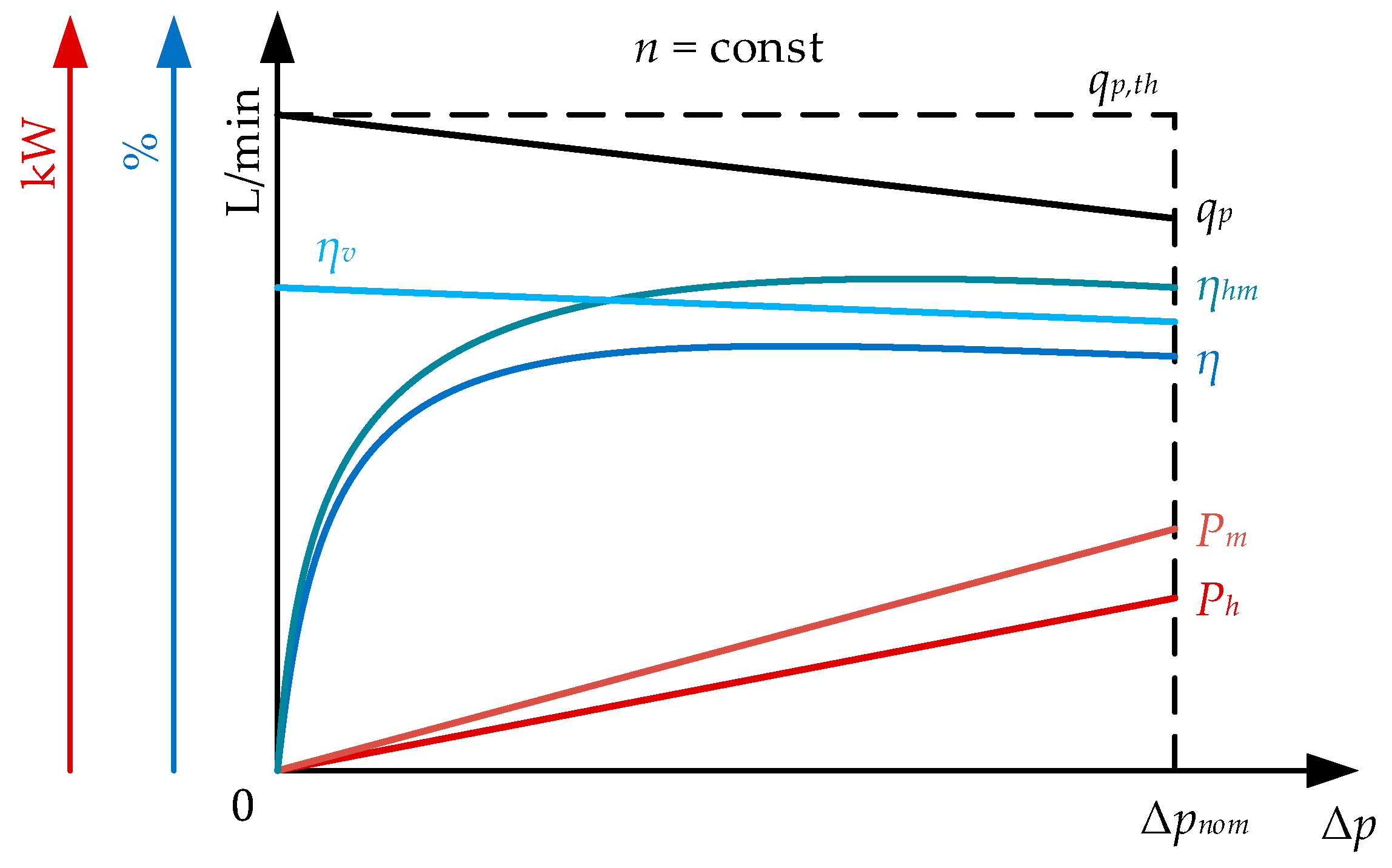
3.1. Theoretical Background
3.2. Methodology for Pump Efficiency Determination at Different Radial Gap Sizes
4. CFD Results and Verification
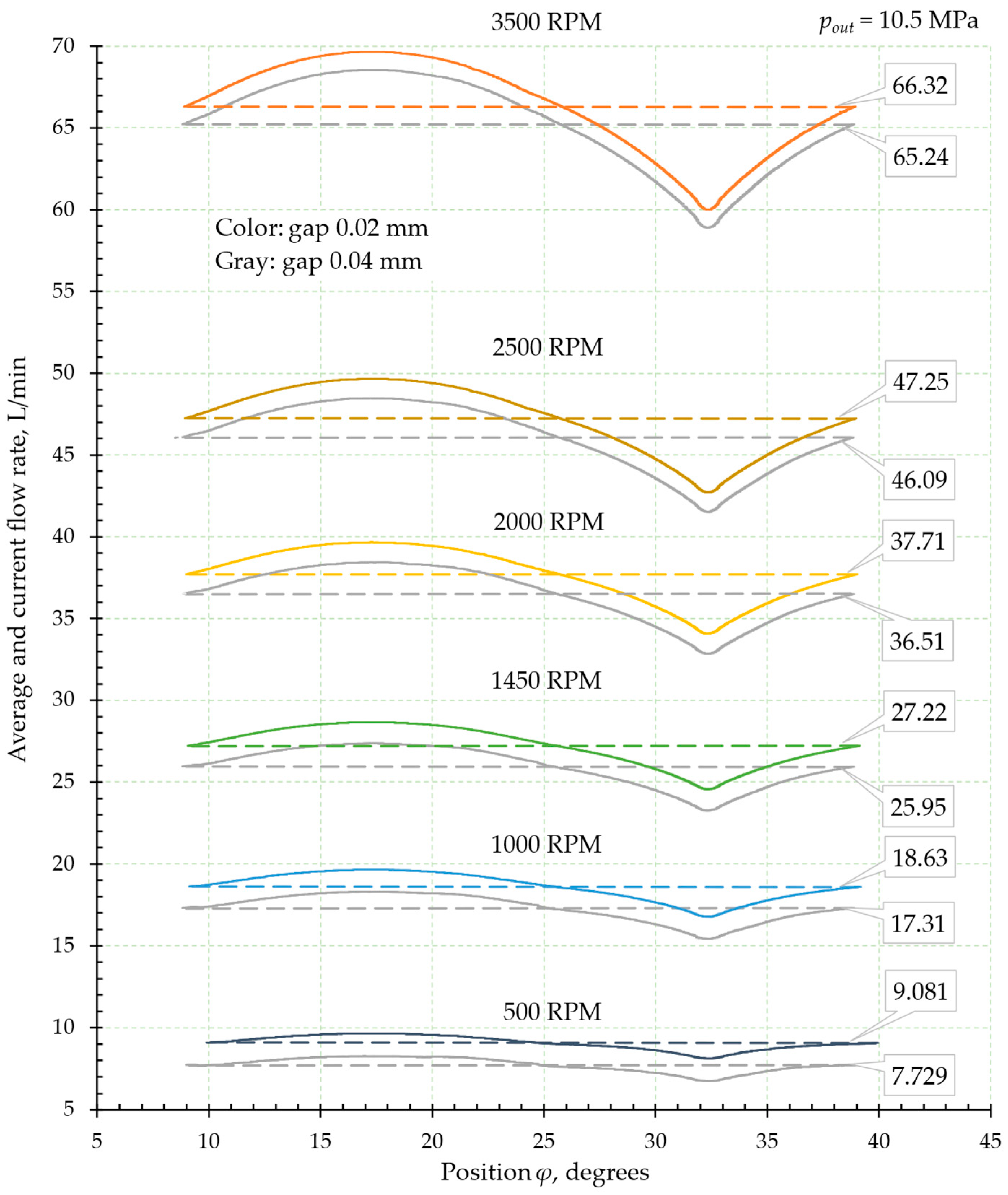
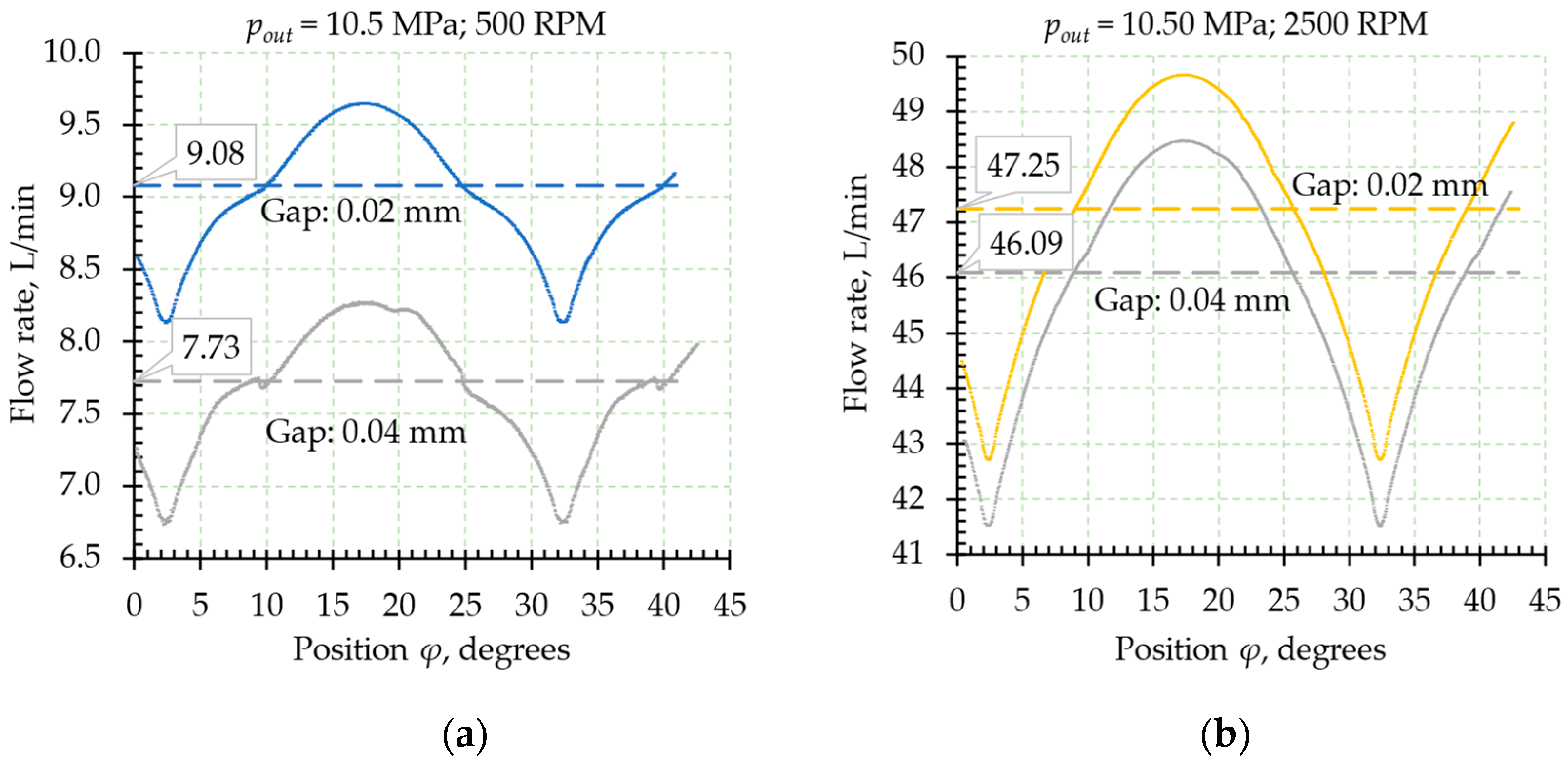
4.1. Average and Current Values of the Flow Rate
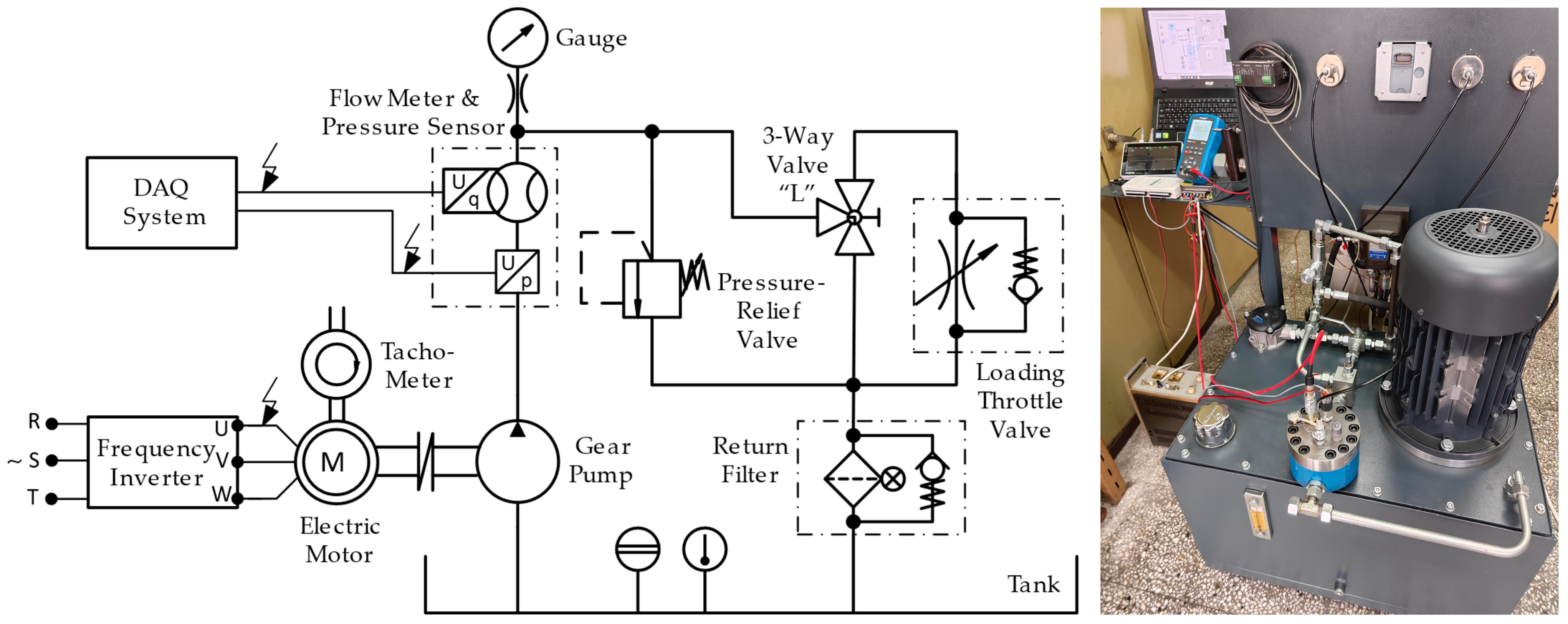
4.2. Experimental Verification of the CFD Results
4.3. Verification of the CFD Results with Manufacturer Data
5. Radial Gap Size Influence on the Volumetric Flow Rate
6. Pump Efficiency Estimation at Different Radial Gap Sizes
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Findeisen, D.; Helduser, S. Ölhydraulik; Springer: Berlin/Heidelberg, Germany, 2015. [Google Scholar]
- ISO 3662:1976; Hydraulic Fluid Power—Pumps and Motors—Geometric Displacements. International Organization for Standardization: Geneva, Switzerland, 1976.
- Ivantysyn, J.; Ivantysynova, M. Hydrostatic Pumps and Motors: Principles, Design, Performance, Modelling, Analysis, Control and Testing; Academia Books International: New Delhi, India, 2001. [Google Scholar]
- Beacham, T.E. High-Pressure Gear Pumps. Proc. Inst. Mech. Eng. 1946, 155, 417–452. [Google Scholar] [CrossRef]
- Frosina, E.; Senatore, A.; Rigosi, M. Study of a high-pressure external gear pump with a computational fluid dynamic modeling approach. Energies 2017, 10, 1113. [Google Scholar] [CrossRef]
- Marinaro, G.; Frosina, E.; Senatore, A. A Numerical Analysis of an Innovative Flow Ripple Reduction Method for External Gear Pumps. Energies 2021, 14, 471. [Google Scholar] [CrossRef]
- Egbe, E.A.P. Design Analysis and Testing of a Gear Pump. Int. J. Eng. Sci. 2013, 3, 1–7. [Google Scholar]
- Mali, P.S.; Joshi, G.S.; Patil, I.A. Performance improvement of external gear pump through CFD analysis. Int. Res. J. Eng. Technol. 2018, 5, 430–433. [Google Scholar]
- Yanada, H.; Ichikawa, T.; Itsuji, Y. Study of the trapping of fluid in a gear pump. Proc. Inst. Mech. Eng. Part A Power Process Eng. 1987, 201, 39–45. [Google Scholar] [CrossRef]
- Nagamura, K.; Ikejo, K.; Tutulan, F.G. Design and performance of gear pumps with a non-involute tooth profile. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2004, 218, 699–712. [Google Scholar] [CrossRef]
- Cieślicki, R.; Karpenko, M. An investigation of the impact of pump deformations on circumferential gap height as a factor influencing volumetric efficiency of external gear pumps. Transport 2022, 37, 373–382. [Google Scholar] [CrossRef]
- Szwemin, P.; Fiebig, W. The Influence of Radial and Axial Gaps on Volumetric Efficiency of External Gear Pumps. Energies 2021, 14, 4468. [Google Scholar] [CrossRef]
- Peng, Z.; Wei, L.; Liu, R.; Liang, M.; Qiang, Y. Flow Field Modeling and Simulation of High-Speed Gear Pump Considering Optimal Radial and End Clearance. IEEE Access 2023, 11, 64725–64737. [Google Scholar] [CrossRef]
- Corvaglia, A.; Rundo, M.; Bonati, S.; Rigosi, M. Simulation and experimental activity for the evaluation of the filling capability in external gear pumps. Fluids 2023, 8, 251. [Google Scholar] [CrossRef]
- Borghi, M.; Zardin, B.; Specchia, E. External Gear Pump Volumetric Efficiency: Numerical and Experimental Analysis; SAE Technical Paper; SAE: Warrendale, PA, USA, 2009. [Google Scholar]
- Choudhuri, K.; Biswas, N.; Mandal, S.K.; Mitra, C.; Biswas, S. A numerical study of an external gear pump operating under different conditions. Mater. Today Proc. 2022, in press. [Google Scholar] [CrossRef]
- Mucchi, E.; Dalpiaz, G.; Rivola, A. Dynamic behavior of gear pumps: Effect of variations in operational and design parameters. Meccanica 2011, 46, 1191–1212. [Google Scholar] [CrossRef]
- Del Campo, D.; Castilla, R.; Raush, G.A.; Gamez Montero, P.J.; Codina, E. Numerical analysis of external gear pumps including cavitation. J. Fluids Eng. Trans. ASME 2012, 134, 081105. [Google Scholar] [CrossRef]
- Del Campo, D. Analysis of the Suction Chamber of External Gear Pumps and Their Influence on Cavitation and Volumetric Efficiency. Ph.D. Thesis, Universitat Politècnica de Catalunya, Barcelona, Spain, 2012. [Google Scholar]
- Ouyang, T.; Mo, X.; Lu, Y.; Wang, J. CFD-vibration coupled model for predicting cavitation in gear transmissions. Int. J. Mech. Sci. 2022, 225, 107377. [Google Scholar] [CrossRef]
- Killedar, J.S. CFD Analysis of Gear Pump. Master’s Thesis, Youngstown State University, Youngstown, OH, USA, 2005. [Google Scholar]
- Lee, J.-H.; Lee, S.-W. Numerical Simulations of Cavitation Flow in Volumetric Gear Pump. J. Korean Soc. Vis. 2011, 9, 28–34. [Google Scholar]
- Muzzioli, G.; Montorsi, L.; Polito, A.; Lucchi, A.; Sassi, A.; Milani, M. About the Influence of Eco-Friendly Fluids on the Performance of an External Gear Pump. Energies 2021, 14, 799. [Google Scholar] [CrossRef]
- Martorana, P.; Bayer, I.S.; Steele, A.; Loth, E. Effect of graphite and carbon nanofiber additives on the performance efficiency of a gear pump driven hydraulic circuit using ethanol. Ind. Eng. Chem. Res. 2010, 49, 11363–11368. [Google Scholar] [CrossRef]
- Novaković, B.; Radovanović, L.; Zuber, N.; Radosav, D.; Đorđević, L.; Kavalić, M. Analysis of the influence of hydraulic fluid quality on external gear pump performance. Eksploat. I Niezawodn. 2022, 24, 260–268. [Google Scholar] [CrossRef]
- Maccioni, L.; Concli, F. Computational fluid dynamics applied to lubricated mechanical components: Review of the approaches to simulate gears, bearings, and pumps. Appl. Sci. 2020, 10, 8810. [Google Scholar] [CrossRef]
- Dalla Lana, E.; De Negri, V.J. A New Evaluation Method for Hydraulic Gear Pump Efficiency Through Temperature Measurement; SAE Technical Papers; SAE: Warrendale, PA, USA, 2006. [Google Scholar]
- Battarra, M.; Mucchi, E. On the assessment of lumped parameter models for gear pump performance prediction. Simul. Model. Pract. Theory 2020, 99, 102008. [Google Scholar] [CrossRef]
- Yoon, Y.; Park, B.-H.; Shim, J.; Han, Y.-O.; Hong, B.-J.; Yun, S.-H. Numerical simulation of three-dimensional external gear pump using immersed solid method. Appl. Therm. Eng. 2017, 118, 539–550. [Google Scholar] [CrossRef]
- Zeleny, Z.; Vodicka, V.; Novotny, V.; Mascuch, J. Gear pump for low power output ORC—An efficiency analysis. Energy Procedia 2017, 129, 1002–1009. [Google Scholar] [CrossRef]
- Abdellah El-Hadj, A. Optimization of an External Gear Pump using Response Surface Method. J. Mech. 2020, 36, 567–575. [Google Scholar] [CrossRef]
- Casoli, P.; Vacca, A.; Berta, G.L. Optimization of relevant design parameters of external gear pumps. In Proceedings of the 7th International Symposium on Fluid Power JFPS, Toyama, Japan, 15–18 September 2008. [Google Scholar]
- Zardin, B.; Natali, E.; Borghi, M. Evaluation of the Hydro—Mechanical Efficiency of External Gear Pumps. Energies 2019, 12, 2468. [Google Scholar] [CrossRef]
- Kollek, W.; Radziwanowska, U. Energetic efficiency of gear micropumps. Arch. Civ. Mech. Eng. 2015, 15, 109–115. [Google Scholar] [CrossRef]
- McKelvey, J.M. Performance of gear pumps in polymer processing. Polym. Eng. Sci. 1984, 24, 398–402. [Google Scholar] [CrossRef]
- Michael, P.; Khalid, H.; Wanke, T. An Investigation of External Gear Pump Efficiency and Stribeck Values; SAE Technical Papers; SAE: Warrendale, PA, USA, 2012. [Google Scholar]
- Torrent, M.; Gamez-Montero, P.J.; Codina, E. Parameterization, Modeling, and Validation in Real Conditions of an External Gear Pump. Sustainability 2021, 13, 3089. [Google Scholar] [CrossRef]
- Wang, S.; Sakurai, H.; Kasarekar, A. The optimal design in external gear pumps and motors. IEEE/ASME Trans. Mechatron. 2011, 16, 945–952. [Google Scholar] [CrossRef]
- Manring, N.D.; Kasaragadda, S.B. The theoretical flow ripple of an external gear pump. J. Dyn. Syst. Meas. Control. Trans. ASME 2003, 125, 396–404. [Google Scholar] [CrossRef]
- Adake, D.G.; Dhote, N.D.; Khond, M.P. Experimentation and 2D Fluid Flow Simulation over an External Gear Pump. J. Phys. Conf. Ser. 2023, 2601, 012029. [Google Scholar] [CrossRef]
- Mitov, A.; Nikolov, N.; Nedelchev, K.; Kralov, I. CFD Modeling and Experimental Validation of the Flow Processes of an External Gear Pump. Processes 2024, 12, 261. [Google Scholar] [CrossRef]
- Castilla, R.; Gamez-Montero, P.J.; Del Campo, D.; Raush, G.; Garcia-Vilchez, M.; Codina, E. Three-dimensional numerical simulation of an external gear pump with decompression slot and meshing contact point. J. Fluids Eng. Trans. ASME 2015, 137, 041105. [Google Scholar] [CrossRef]
- Rundo, M. Models for Flow Rate Simulation in Gear Pumps: A Review. Energies 2017, 10, 1261. [Google Scholar] [CrossRef]
- Nikolov, N.; Mitov, A.; Kralov, I. Advanced 2D Computational Fluid Dynamics Model of an External Gear Pump Considering Relief Grooves. Appl. Sci. 2024, 14, 4299. [Google Scholar] [CrossRef]
- ISO 4413:2010; Hydraulic Fluid Power—General Rules and Safety Requirements for Systems and Their Components. International Organization for Standardization: Geneva, Switzerland, 2010.
- Bashta, T.M. Engineering Hydraulics: Handbook; Mashinostroenie: Moscow, Russia, 1963. [Google Scholar]
- Xu, W.; Wang, Z.; Zhou, Z.; Sun, C.; Zhang, J.; Yan, R.; Chen, X. An advanced pressure pulsation model for external gear pump. Mech. Syst. Signal Process. 2023, 187, 109943. [Google Scholar] [CrossRef]
- Cengel, Y.A.; Cimbala, J.M. Fluid Mechanics: Fundamental and Applications; McGraw-Hill: New York, NY, USA, 2013. [Google Scholar]
- Ansys Fluent. 12.0 Theory Guide; Ansys Inc.: Canonsburg, PA, USA, 2009. [Google Scholar]
- Linsingen, I. Fundamentos de Sistemas Hidráulicos; UFSC Ed.: Florianópolis, Brazil, 2008. [Google Scholar]
- VDI 3279:1971-12; Characteristic Quantities of Oil-Hydraulic Devices; Hydraulic Pumps (Including Flight Hydraulics). Verein Deutscher Ingenieure (VDI): Düsseldorf, Germany, 1971.
- ISO 4391:1983; Hydraulic Fluid Power—Pumps, Motors and Integral Transmissions—Parameter Definitions and Letter Symbols. International Organization for Standardization: Geneva, Switzerland, 1983.
- ISO 4409:2019; Hydraulic Fluid Power—Positive-Displacement Pumps, Motors and Integral Transmissions—Methods of Testing and Presenting Basic Steady State Performance. International Organization for Standardization: Geneva, Switzerland, 2019.
- Hydravlika Kazanlak DSO, Kombinat “Hydravlika”. Technical Data Sheet H2-1-01, Machinoexport, Bulgaria, 1985.
- Lakshmanan, K.; Tessicini, F.; Gil, A.J.; Auricchio, F. A fault prognosis strategy for an external gear pump using Machine Learning algorithms and synthetic data generation methods. Appl. Math. Model. 2023, 123, 348–372. [Google Scholar] [CrossRef]
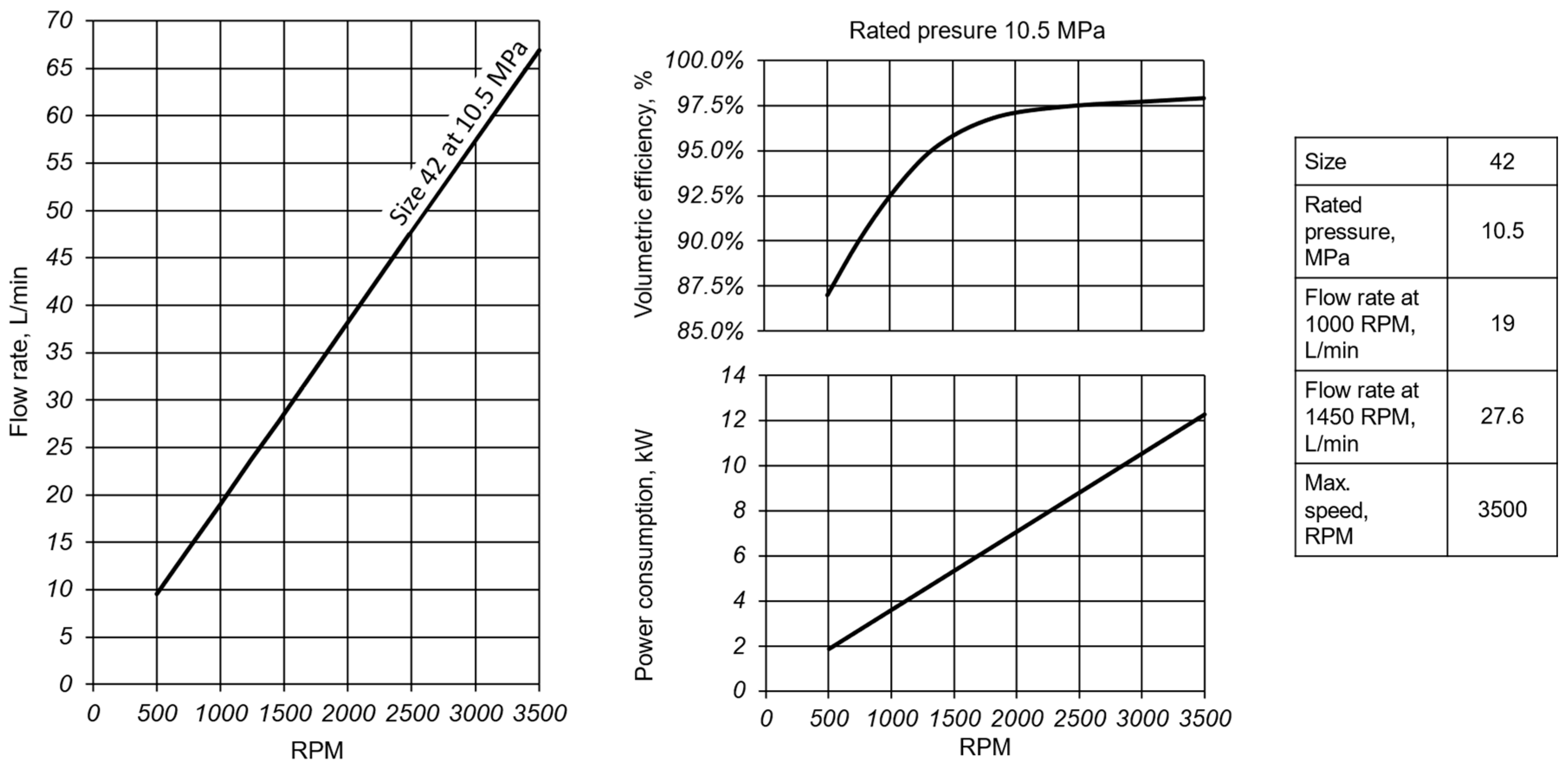
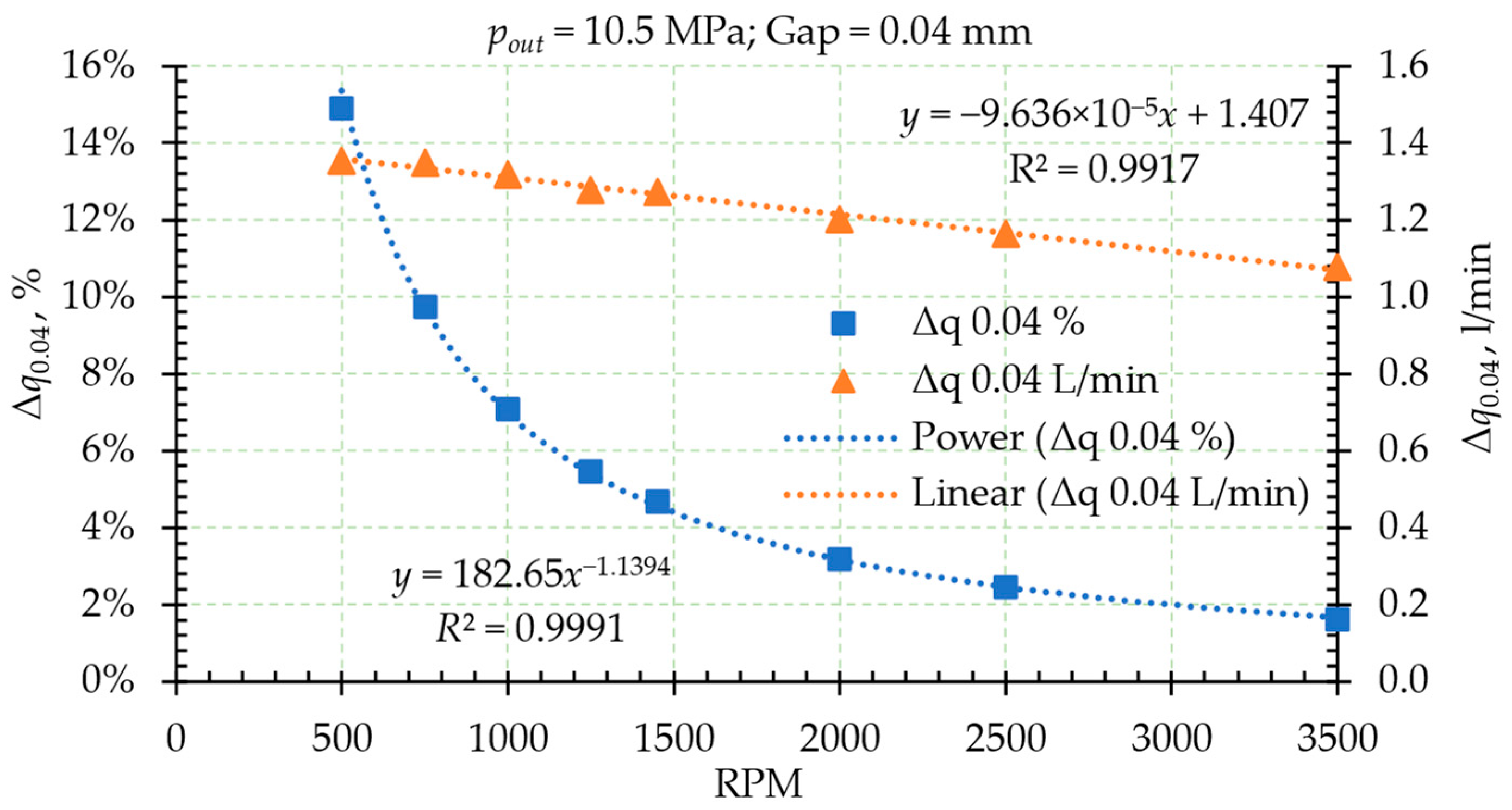

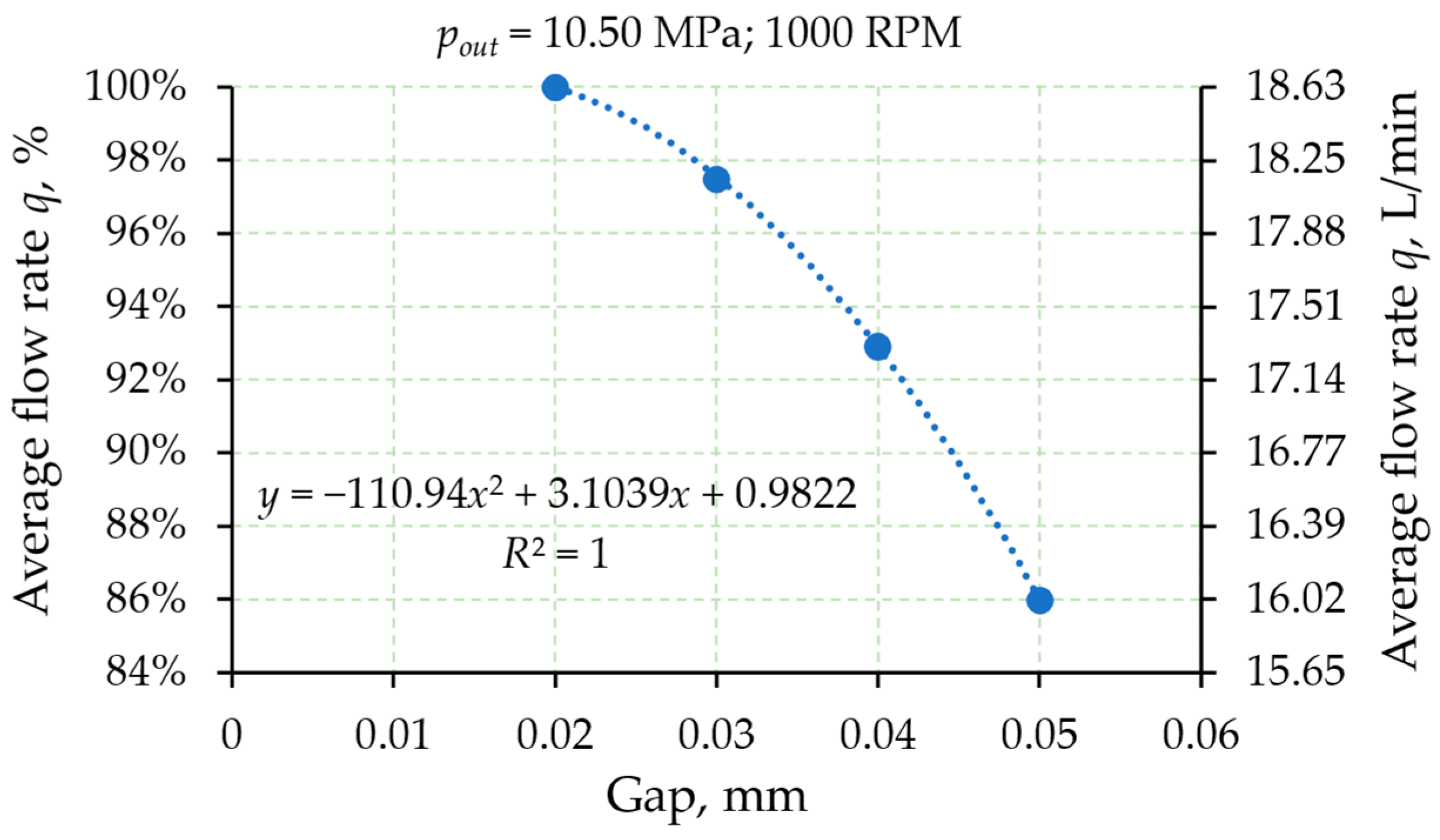

| CFD | Experiment | Tech Data | CFD/Exp | CFD/Tech | Exp/Tech | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| RPM | MPa | L/min | min−1 | MPa | L/min | L/min | kW | % | % | % | ||
| 500 | 10.5 | 9.08 | 498 | 10.41 | 8.94 | 9.56 | 1.88 | 1.58% | −4.96% | −6.44% | ||
| 750 | 10.5 | 13.85 | 749 | 10.38 | 13.46 | 14.33 | 2.60 | 2.88% | −3.38% | −6.09% | ||
| 1000 | 10.5 | 18.63 | 1002 | 10.20 | 18.24 | 19.00 | 3.47 | 2.14% | −1.96% | −4.02% | ||
| 1250 | 10.5 | 23.40 | 1250 | 10.47 | 22.89 | 23.89 | 4.33 | 2.21% | −2.05% | −4.17% | ||
| 1450 | 10.5 | 27.22 | 1450 | 10.46 | 26.56 | 27.60 | 5.03 | 2.48% | −1.37% | −3.76% | ||
| 2000 | 10.5 | 37.71 | - | - | 36.78 | 38.22 | 6.93 | - | −1.33% | −3.76% | ||
| 2500 | 10.5 | 47.25 | - | - | 46.07 | 47.78 | 8.67 | - | −1.11% | −3.57% | ||
| 3500 | 10.5 | 66.32 | - | - | 64.65 | 66.89 | 12.27 | - | −0.86% | −3.35% | ||
| Gap | 0.02 mm | 0.04 mm | |||
|---|---|---|---|---|---|
| RPM | L/min | L/min | L/min | % | |
| 500 | 9.08 | 7.73 | 1.35 | 14.89% | |
| 750 | 13.85 | 12.50 | 1.35 | 9.73% | |
| 1000 | 18.63 | 17.31 | 1.32 | 7.08% | |
| 1250 | 23.40 | 22.12 | 1.28 | 5.46% | |
| 1450 | 27.22 | 25.95 | 1.27 | 4.67% | |
| 2000 | 37.71 | 36.51 | 1.20 | 3.19% | |
| 2500 | 47.25 | 46.09 | 1.16 | 2.46% | |
| 3500 | 66.32 | 65.24 | 1.08 | 1.62% | |
| Gap | q | Q |
|---|---|---|
| mm | L/min | % |
| 0.02 | 18.628 | 100.00 |
| 0.03 | 18.162 | 97.50 |
| 0.04 | 17.309 | 92.92 |
| 0.05 | 16.017 | 85.99 |
| Gap | 0.02 mm | 0.04 mm | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| RPM | ||||||||||||
| L/min | L/min | % | % | % | % | % | L/min | % | % | % | ||
| 500 | 9.08 | 9.50 | 95.6% | 87.0% | 91.0% | 82.7% | 95.1% | 7.73 | 81.4% | 74.0% | 70.4% | |
| 750 | 13.85 | 14.25 | 97.2% | 90.0% | 92.6% | 89.6% | 99.5% | 12.50 | 87.7% | 81.2% | 80.9% | |
| 1000 | 18.63 | 19.00 | 98.0% | 92.5% | 94.3% | 89.4% | 96.7% | 17.31 | 91.1% | 86.0% | 83.1% | |
| 1250 | 23.40 | 23.75 | 98.5% | 94.5% | 95.9% | 92.2% | 97.6% | 22.12 | 93.1% | 89.3% | 87.2% | |
| 1450 | 27.22 | 27.55 | 98.8% | 95.6% | 96.8% | 92.1% | 96.3% | 25.95 | 94.2% | 91.1% | 87.8% | |
| 2000 | 37.71 | 38.00 | 99.2% | 97.1% | 97.8% | 92.9% | 95.6% | 36.51 | 96.1% | 94.0% | 89.9% | |
| 2500 | 47.25 | 47.50 | 99.5% | 97.5% | 98.0% | 93.0% | 95.4% | 46.09 | 97.0% | 95.1% | 90.8% | |
| 3500 | 66.32 | 66.50 | 99.7% | 97.9% | 98.2% | 92.2% | 94.2% | 65.24 | 98.1% | 96.3% | 90.7% | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mitov, A.; Nikolov, N.; Kralov, I. Influence of the Radial Gap on the External Gear Pump Performance. Appl. Sci. 2025, 15, 907. https://doi.org/10.3390/app15020907
Mitov A, Nikolov N, Kralov I. Influence of the Radial Gap on the External Gear Pump Performance. Applied Sciences. 2025; 15(2):907. https://doi.org/10.3390/app15020907
Chicago/Turabian StyleMitov, Alexander, Nikolay Nikolov, and Ivan Kralov. 2025. "Influence of the Radial Gap on the External Gear Pump Performance" Applied Sciences 15, no. 2: 907. https://doi.org/10.3390/app15020907
APA StyleMitov, A., Nikolov, N., & Kralov, I. (2025). Influence of the Radial Gap on the External Gear Pump Performance. Applied Sciences, 15(2), 907. https://doi.org/10.3390/app15020907






