Abstract
High-speed rail (HSR) environments present unique challenges due to their high mobility and dense passenger traffic, resulting in dynamic and unpredictable task generation patterns. Mobile Edge Computing (MEC) has emerged as a transformative paradigm to address these challenges by deploying computation resources closer to end-users. However, the limited resources of MEC servers necessitate efficient task partitioning, wherein a single task is divided into multiple sub-tasks for parallel processing across MEC servers. In the context of HSR environments, the task partitioning ratio is pivotal in ensuring quality of service (QoS) and optimizing resource utilization, particularly under dynamic and high-demand conditions. This paper proposes a deep reinforcement learning (DRL)-based task partitioning mechanism using Twin Delayed Deep Deterministic Policy Gradient (TD3) for HSR environments with MEC servers (MECSs). The proposed method dynamically adjusts task partitioning ratios by leveraging real-time information about task characteristics and server load conditions. The experimental results show that when the task arrival rate is 20, the delay is improved by about 5% compared to random and about 13% compared to no_partition. When it is 50, there is no significant difference from random and about 2% improvement compared to no_partition. The task throughput is almost the same when it is 20. However, when it is 50, random is much better. We also looked at the performance change according to the number of serving MECSs. In this process, we can also note the research direction of finding an appropriate number of serving MECSs K. The results highlight the efficacy of DRL-based approaches in dynamically adapting to the unique characteristics of HSR environments, achieving optimal resource allocation and maintaining high QoS. This paper contributes to advancing task partitioning strategies for HSR systems and lays the groundwork for future research in MEC-based HSR systems.
1. Introduction
Over the past two decades, Intelligent Transport Systems (ITSs) have emerged as a critical technology for enhancing the efficiency and performance of transportation systems. High-speed railway (HSR) has garnered significant attention as a fast, eco-friendly, and sustainable means of transport, driving the innovation of modern transportation systems [1,2]. HSR offers distinct advantages, including substantially lower greenhouse gas emissions compared to air and road transportation, while ensuring comfort, safety, and high punctuality for passengers. These attributes have positioned HSR as an efficient and reliable transportation option worldwide, with China’s HSR network expected to expand to 18,000 km by 2020 [3].
Despite these advantages, HSR systems present unique challenges due to their operational characteristics. High speeds of approximately 100 m/s lead to frequent handovers and interference issues. Additionally, channel characteristics are difficult to model accurately as they are influenced by diverse environmental factors. High-speed trains (HSTs) operating on HSR lines also face challenges in optimizing the quality of service (QoS) for various applications, including passenger services [4].
High-Performance Computing (HPC) technologies are emerging as promising solutions to address these challenges. By supporting stable and efficient communication, HPC can be applied in areas such as fault diagnosis, management systems, and simulations [5]. When combined with artificial intelligence (AI) techniques like machine learning and reinforcement learning, HPC can significantly enhance the performance of HSR systems. HPC techniques, such as parallel processing, distributed computing, and mobile cloud computing, enable advanced capabilities.
In the HSR environment, characterized by high mobility, existing mobile cloud computing (MCC) approaches [6] face limitations in minimizing task execution delays and network load. Mobile Edge Computing (MEC) technology has, thus, emerged as a viable alternative by placing servers closer to the network edge to perform computational tasks [7]. MEC servers (MECSs) offer significant advantages, including reduced task execution delays, real-time services, and improved user experience. They also support mobility and rapid response times, enabling stable and efficient data processing in HSR environments. However, the limited computational resources of MECSs, such as CPU, memory, and bandwidth, necessitate efficient task distribution and processing strategies.
Advances in technology have also heightened passenger demands for high-spec services such as real-time streaming, online gaming, and remote work. These services impose stringent processing constraints, including large-scale data handling and low-latency requirements. Task offloading and partitioning have become essential mechanisms for meeting these demands. Task offloading involves transferring tasks from user devices to nearby MECSs, thereby reducing computational burdens and minimizing execution delays. Task partitioning, on the other hand, involves dividing a task into subtasks for parallel processing across multiple MECSs, achieving load balancing and enhancing system performance [8].
Existing research has explored various techniques for optimizing MEC systems, including reducing delay and improving energy efficiency [9]. For instance, ref. [10] utilized binary particle swarm optimization (BPSO) to dynamically allocate tasks in vehicular networks, though their approach is limited to static network states. Similarly, ref. [11] employed support vector machines (SVMs) for task offloading decisions based on network state and resource availability, but their method struggles to adapt to real-time changes. Ref. [12] proposed a game-theoretic approach to allocate MEC resources efficiently, managing delays and network loads. While these techniques leverage metaheuristics, machine learning, and game theory, they fall short of processing large volumes of tasks in highly dynamic, real-time environments.
In such unpredictable and dynamic scenarios, deep reinforcement learning (DRL) has emerged as a promising alternative [13]. Unlike model-based methods, DRL employs a model-free approach, enabling agents to learn optimal actions through interactions with the environment without prior knowledge. This capability is particularly valuable in HSR MEC environments, where task occurrences and MECS load states are inherently uncertain. Furthermore, DRL optimizes long-term rewards, ensuring continuous improvement even under heavy task loads [14]. By learning complex and nonlinear patterns of task occurrence, DRL enhances resource management policies, maximizing the efficient utilization of MEC resources while maintaining QoS.
Ref. [15] addressed complex resource optimization problems in vehicular environments by utilizing the Deep Deterministic Policy Gradient (DDPG) algorithm, a technique within the deep reinforcement learning (DRL) paradigm. Their study focused on optimizing the allocation of spectrum, computing, and storage resources to meet the quality of service (QoS) requirements of various vehicular applications. However, a notable limitation of their centralized approach is the significant increase in computational complexity as the number of vehicles or system scale grows. Similarly, ref. [16] proposed a DDPG-based method for optimizing task offloading decisions, with the objective of minimizing delay and optimizing computational resource usage. This centralized method also faced challenges in scalability and computational overhead in environments with a large number of vehicles or dynamic conditions.
In contrast, ref. [17] adopted the Twin Delayed Deep Deterministic Policy Gradient (TD3) algorithm to enable optimal task offloading in a dynamic vehicular environment where mobility and communication conditions change over time. By leveraging a distributed approach, their study effectively allocated resources to minimize delay and energy consumption. Unlike centralized approaches, distributed strategies allow for local data processing, which significantly reduces delay times and enhances scalability by distributing computational demands across multiple MEC servers (MECSs).
In the context of task offloading, centralized approaches offer advantages such as global optimization and simplified management; however, they are less suitable for real-time applications due to inherent delays caused by central server communication. Furthermore, performance can degrade in large-scale networks where centralized processing becomes a bottleneck. Distributed approaches, on the other hand, process tasks locally, enabling faster response times and greater scalability, as resource allocation occurs independently at each MECS.
The HSR-MEC environment presents additional challenges compared to conventional MEC-based vehicular systems due to the significantly higher speeds of high-speed trains (HSTs), which exacerbate issues such as frequent handovers and Doppler effects. Additionally, the high passenger density in HSR environments leads to increased demand for communication and computational resources. Ref. [18] explored task migration to maintain uninterrupted services in high-mobility HSR scenarios. Their work, which used DDPG for task offloading and resource allocation, focused on optimizing the task success rate but was limited by a singular optimization goal. Ref. [19] proposed a solution to optimize task execution delays by integrating a caching framework that enhances computational resource stability and network performance. Furthermore, ref. [20] combined Deep Double Q-learning (DDQN) and DDPG to improve both energy consumption and delay, employing two DRL methods to determine task offloading ratios and resource allocation decisions.
This paper addresses a scenario where multiple HSTs traverse the HSR network, creating highly dynamic and complex environments. Managing all HSTs through a centralized approach is impractical due to the system’s scale and variability. To overcome this limitation, we propose a distributed multi-agent DRL-based method for determining task partitioning ratios. Unlike prior techniques that primarily focused on deciding whether to offload tasks or balancing between local execution and a single MECS, our approach considers task partitioning across multiple MECSs simultaneously. This enables the optimization of both throughput and delay, akin to existing HSR-MEC studies. Additionally, to reduce the dimensionality of the DRL action space, the proposed algorithm is designed with a two-part structure, further enhancing its computational efficiency and applicability.
This paper is organized as follows: Section 2 presents the proposed system model, and Section 3 introduces the proposed algorithm. Section 4 also evaluates the performance of the proposed technique through experimental results. Finally, Section 5 concludes the paper and outlines future research directions.
2. System Model
This section presents the architecture of the MEC system designed for the HSR environment. It describes the system components, their interactions, the network scenario, and the models for communication and computation resources.
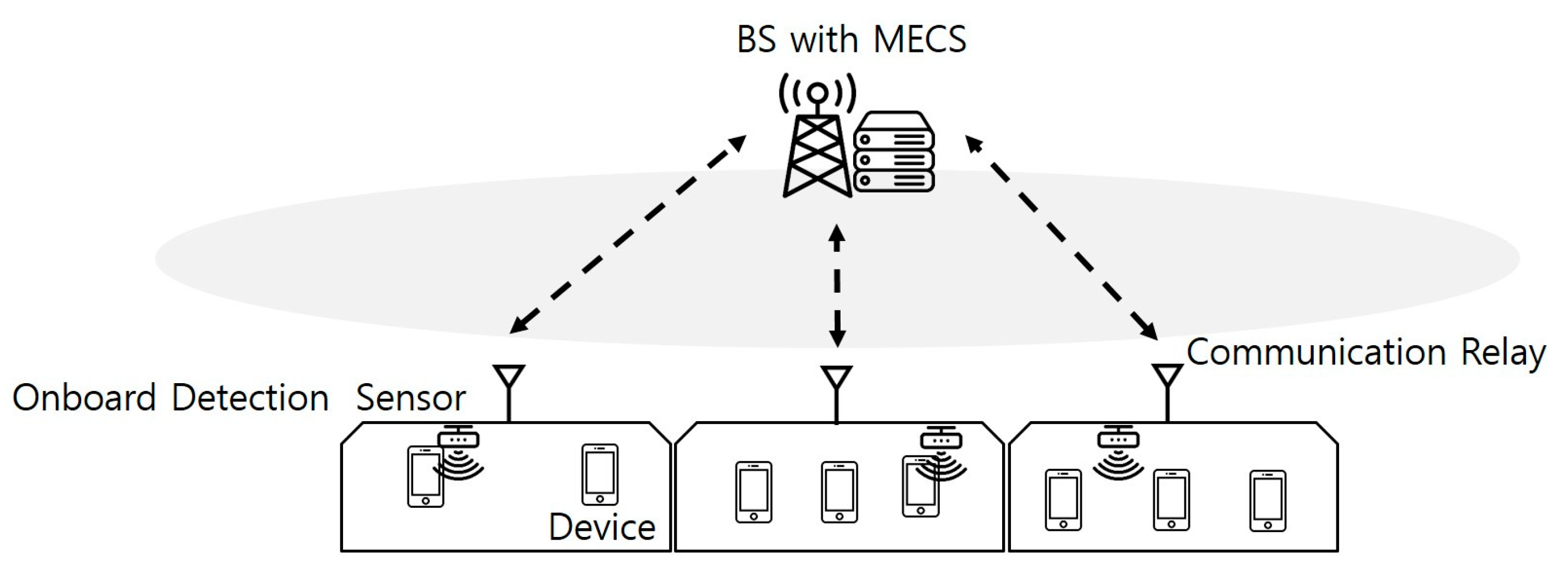
The proposed HSR MEC system integrates communication relays installed on HSTs to facilitate task communication with Base Stations (BSs) [21]. As illustrated in Figure 1, each HST is equipped with a device-detection sensor that identifies devices generating tasks. These tasks are transmitted to the BS via communication relays. The model assumes an environment characterized by the presence of multiple HSTs near a station. It further considers that the number of HSTs, the volume of tasks, and the locations of the HSTs dynamically evolve over time. Based on these assumptions, we propose a simplified and idealized environment to address the problem effectively, recognizing that this model serves as an initial framework and a basis for future, more detailed investigations.
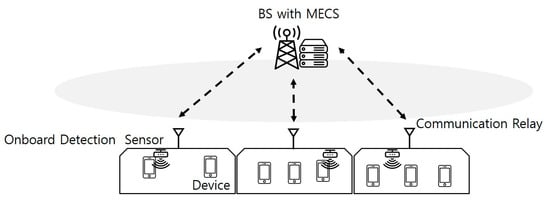
Figure 1.
The HSR system structure with the MECS.
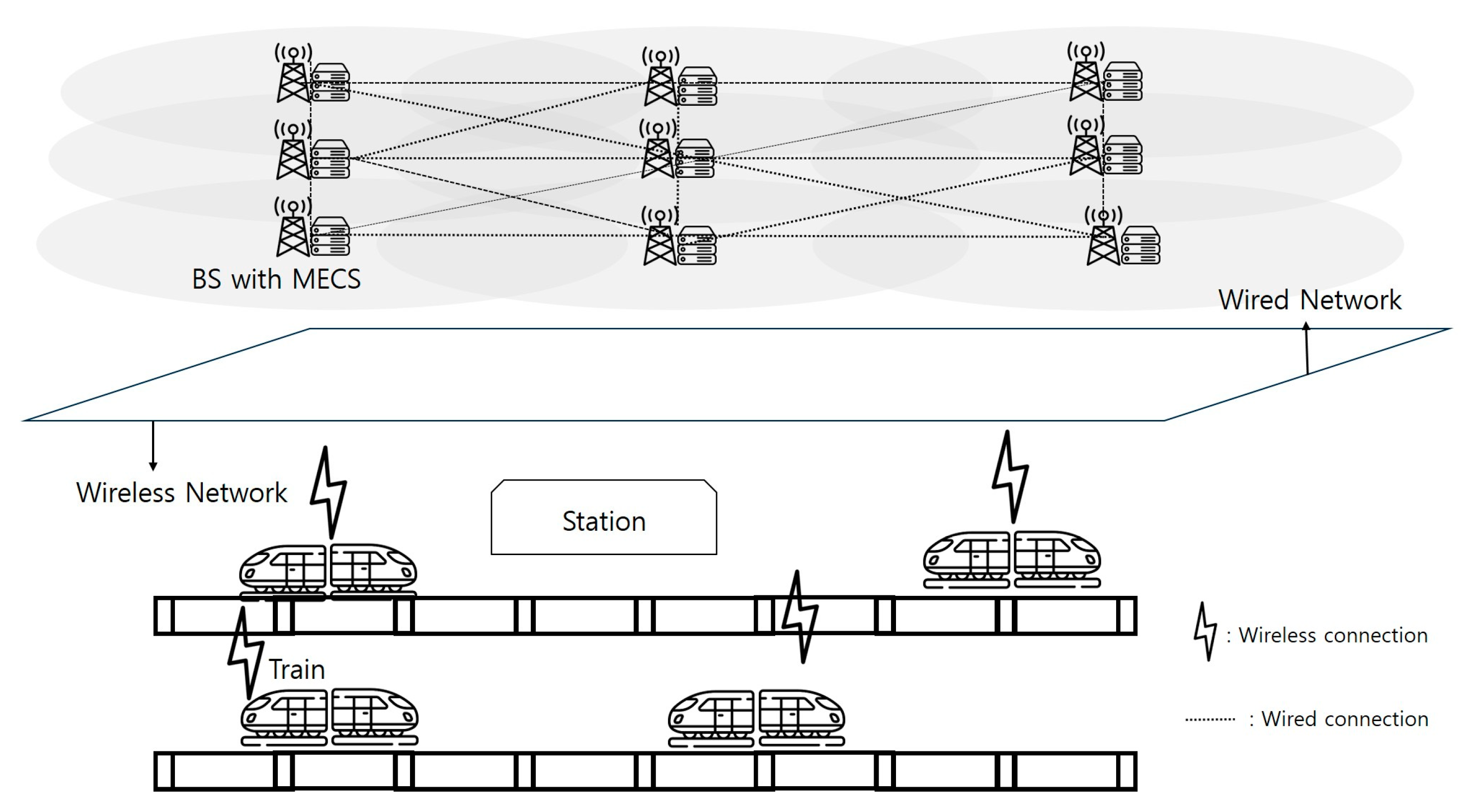
Unlike traditional vehicular MEC environments, the HSR-MEC system forms communication cells along railway tracks using BSs equipped with MECSs. As shown in Figure 2, the proposed system model largely consists of M MECSs () and N HSTs (), and it processes tasks using wireless and wired networks. Each BS is co-located with an MECS and interconnected with other MECSs through a wired network. This architecture enables task handoffs and load balancing across MECSs, preventing overload on any single server. Tasks generated in HSTs are first transmitted to the nearest BS and subsequently offloaded to MECSs for processing. The interconnected MECSs ensure cooperative task handling and optimal resource utilization.
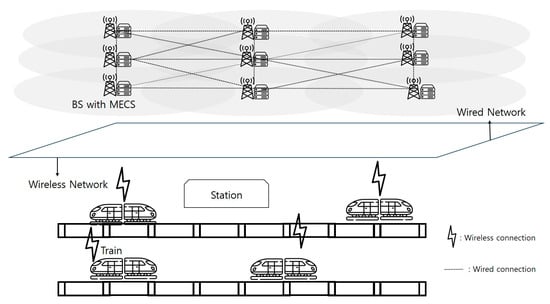
Figure 2.
The proposed overall environment based on the HSR system with the MECS.
In the proposed HSR system, where MECSs are employed, the task that occurs from each HST is conducted on the MECSs. Information regarding the state and task of each HST is transmitted to the nearest MECS. Due to the interconnected nature of the MECSs, seamless information sharing between MECSs is enabled, facilitating coordinated decision-making. The system selects a fixed number (K) of MECSs among a number of MECSs and then performs task partitioning considering only the K MECSs. The K servers selected in this way are defined as a set of serving MECSs (). Since the MECSs are connected to each other, they exchange information. In this process, if multiple tasks occur by multiple passengers in an HST, the generated tasks are transmitted to the BS through the communication relay as one super-task. Then, it is decided at what ratio the tasks will be divided and sent to the serving MECSs.
Based on this system model, this paper proposes a technique to dynamically adjust the task partitioning ratio between MECSs to maximize the processing throughput of tasks and minimize the processing delay occurring in tasks in HSTs. This technique aims to effectively process a large number of tasks and improve real-time QoS by considering the HSR environment. In this study, HSTs generate tasks at each time slot t, and the tasks generated are offloaded to the MECSs by determining the optimal task partitioning ratio. In this way, the task generated in each HST n at time t is composed of . represents the data size, and represents the number of cycles per bit, i.e., the workload of the task. represents the delay constraint for guaranteeing QoS. The delay time required to process the task is calculated as follows:
Here, is the waiting delay to process . In order to process a task on an MECS, tasks waiting in the MECS queue that were offloaded during the previous time slot (t − 1) must be processed before the task generated at the current time slot (t) is processed. The waiting delay is calculated as follows:
In Equation (2), is the task processing capacity of MECS k. And is the total workload of tasks waiting in the queue of MEC server k at time t. In this paper, the optimal task partitioning ratio of task to K MECSs among the total M MECSs is determined. The generated tasks are always divided according to the determined partitioning ratio considering the state of K MECSs. In this process, the optimal ratio is calculated by considering the current load status of each MECS and the task status generated from HSTs.
When task is assigned to K MECS, each MECS forms a queue to process the task assigned to it. At this time, in order to evaluate the waiting delay of task that occurred in the current time slot t, the longest waiting delay among the K MECSs is considered. That is, the total waiting delay of task is calculated based on the longest value among the waiting delay of the queues from the K MECSs. In Equation (1), is the delay to execute at time slot t. The calculation equation is as follows:
In Equation (3), is the partition ratio of task to be executed to MECS k. Therefore, must be a value between 0 and 1, and Equation (4) must be satisfied. If is 0, it indicates that task is not processed to MECS k, and if is 1, it means that task is processed only on MECS k. In addition, since the sub-tasks are executed simultaneously on MECSs, the execution delay of tasks processed on each MECS may be different. In this case, the subtask with the longest execution delay among the sub-tasks is selected as the final execution delay. Therefore, the value of is an important factor that determines the efficiency in task execution. In Equation (5), is the transmission delay to send to the MECS closest to the HST that generated task at time slot t. Since the result value after processing the task on the MECS is very small, the downlink transmission delay is not considered separately. The calculation formula for is as follows:
In Equation (6), is the uplink transmission rate at which HST n transmits a task to MECS m, and the calculation formula is as follows:
represents the network bandwidth between HST n and MECS m, and represents the signal-to-noise ratio (SNR) between HST n and MECS m.
In Equation (7), is the transmission power of HST n toward MECS m, represents the noise power, and is the path loss between HST n and MECS m. Task throughput means the cumulative sum of the number of cycles when a task is completed.
The research we propose aims to minimize the throughput and execution delay time of tasks generated in HST by optimizing the resources of the MEC system in the HSR environment. The objective function for this can be defined as Equation (8) by integrating the optimization of two objectives using the weight (. The cost function in Equation (8) is designed as a linear form (). This is chosen to balance throughput and latency efficiently while maintaining simplicity in optimization. The weight represents the hyper-parameter for adjusting the contribution between two objectives. The range of weight value is [0,1]. The larger the value, the more emphasis is placed on the task throughput .
Equation (8) expresses the objective of maximizing task throughput and minimizing task execution time . Equations (8a)–(8d) ensure that task execution adheres to system limitations, such as delay thresholds and valid task partitioning among MEC servers. Equation (8a) means that the time taken to process a task occurring in HST n at time t must be within the delay threshold (). Equation (8b) represents the proportion of a task assigned to serving MECSs for processing. In other words, represents the proportion of task assigned to MECS k. Therefore, they must sum to 1, as in Equation (8c). And they must have values between 0 and 1, as in Equation (8d).
3. Proposed Algorithm
In this paper, we aim to maximize task throughput and minimize processing delay by considering the occurrence of tasks that are difficult to predict at train stations with dense user traffic and the characteristics of HSTs that are different from existing vehicles. To achieve this, we need to determine the optimal ratio when tasks are processed by multiple MECSs. The optimized partitioning ratio contributes to the efficient processing of tasks and plays an important role in improving the performance of the entire system. In the dynamic HSR environment, the number of HSTs and the passenger density aboard each HST vary over time. Passenger density is closely related to the task size, as a higher number of passengers increases the likelihood of task generation, thereby leading to larger task sizes that need to be processed by the MEC servers (MECSs). When task generation is minimal, a single MECS can handle the task without being overloaded. However, during peak passenger density, efficient task partitioning becomes crucial to prevent MECS overload and ensure QoS. Additionally, the dynamic changes in the number of HSTs influence the task partitioning decisions among the MECSs. For instance, if an HST allocates a significant proportion of its tasks to a specific MECS, and another HST similarly allocates a large proportion to the same MECS, this increases the likelihood of overloading that MECS. Furthermore, MECSs do not only process tasks received from HSTs, but the overhead of MECSs must also be considered. Therefore, determining the optimal task partitioning ratio is critical for achieving load balancing across MECSs, reducing both overloaded and underutilized MECSs. This dynamic and adaptive partitioning mechanism ensures efficient resource utilization and maintains QoS in the constantly changing HSR environment.
The proposed algorithm optimizes the task partitioning ratio in HSR environments through a two-step process. In the first step, a set of serving MECSs, , is selected to support the divided subtasks. This selection is based on the MECS selection probability ), which is defined as follows for each MECS :
where represents the load of MECS at time t, such as the size of its current task queue. This probability ensures that MECSs with higher loads have a lower likelihood of being selected, thereby balancing the load across the available MECSs and reducing the risk of overloading any specific MECS. By selecting a subset of serving MECSs, rather than considering the entire set of MECSs for each decision, the algorithm effectively reduces the action space for decision-making. This dimensionality reduction simplifies the optimization process while maintaining an efficient task distribution among MECSs.
In the second step, the task partitioning ratio is dynamically determined for the k selected serving MECSs by utilizing the TD3 algorithm. The problem is that the existing static partitioning research has limitations in producing optimal results due to the dynamic environment that cannot be predicted at every time slot and the large number of tasks generated by the dense users. In such a complex environment, the task partitioning ratio becomes more important, so we intend to determine the optimal partitioning ratio through deep reinforcement learning (DRL). First of all, among the DRL methods, Deep Q-Network (DQN) [22] and Deep Deterministic Policy Gradient (DDPG) [23] are widely used. However, DQN is not suitable for continuous action decisions such as task partitioning ratio decisions. And DDPG is suitable for continuous action decisions, but it can cause unstable learning due to the overestimation bias and the accumulating error problem in the TD update process. Therefore, TD3, which has improved this, was selected. There are three main features to solve the aforementioned problems.
The first one is Clipped Double Q-learning. TD3 alleviates the overestimation problem of Q function by estimating the value of state-action pairs using two Q functions . First, to update the neural network, randomly sample a mini-batch of B transactions from the replay buffer. The main critic network is updated using the sampled mini-batch. The main critic network updates by calculating the mean square of the TD error of the current Q value () and the target Q value (). This can be found through Equation (10). The target Q value can be calculated using Equation (11).
Here, represents the reward of the current state, represents the discount factor, s′ represents the next state, and is the action of s′ obtained through the target actor network. This is performed by obtaining the Q values for the next state (s′) and the next action () through two target critic networks, and then using a small Q value to avoid overestimation.
The second is Delayed policy updates. TD3 delays policy updates so that the policy network learns based on a stable Q-function estimation. This delayed update reduces the instability of learning and maintains a balance between policy exploration and exploitation even in dynamic environments such as HSR environments.
Equation (12) shows that the parameter of the main actor network is updated by using the deterministic policy gradient. The actor network updates using one of the two critic networks, being the first main critic network. represents the main actor network.
Here, is the parameter of the actor network, and is the parameter of the critic network. is the parameter of the target actor network, and is the parameter of the target critic network. After updating the actor network through Equation (12), the target network parameters () are updated through Equation (13). In the process of updating, TD3 proposed a method of updating the main actor network and the target network slower than the main critic network for stable update in the process of updating.
The third is Target policy smoothing regularization. It induces changes in the action space to prevent the actor from being overly dependent on a specific action and plays a role in increasing the stability of the Target Q-value. As shown in Equation (14), TD3 adds Gaussian noise () to the actions of the target policy and clips it. This prevents the Q function from learning excessively rapid changes. This increases the stability of the Q-function learning and supports smooth and generalized policy learning.
The proposed algorithm is designed based on the TD3 algorithm. The proposed algorithm can be seen in Algorithm 1. It basically follows the structure of TD3, but some structures are changed as follows to solve the requirements of the task partitioning ratio decision problem in the HSR environment with MECSs.
| Algorithm 1 TD3-based task partitioning ratio decision algorithm | |
| 1 | |
| 3 | |
| 4 | |
| 5 | Initialize HSR environment |
| 6 | for e = 1 to E do |
| 7 | for t = 1 to T do |
| 8 | for n = 1 to N do |
| 9 | |
| 10 | |
| 11 | , and observe reward r and new state s′ |
| 12 | |
| 13 | |
| 14 | |
| 15 | |
| 16 | |
| 17 | if t mod d then |
| 18 | by deterministic policy gradient: |
| 19 | |
| 20 | Update target network parameters: |
| 21 | |
| 22 | |
| 23 | end if |
| 24 | end for |
| 25 | end for |
| 26 | end for |
First, regarding the Actor network activation function of lines 11 and 14 of Algorithm 1, the existing TD3 limited the network output to the Tanh (Hyperbolic Tangent) function, so the action range was set to [−1, 1]. However, the problem of this paper is a ratio determination problem, so the action range should be 0 to 1 and the total sum of the actions should be 1. Therefore, the Dirichlet distribution was used instead of the Tanh activation function. First, the Dirichlet distribution is a probability distribution that generates a multidimensional probability vector. The result sampled from this distribution is a probability vector, and each element has a value between 0 and 1, and the sum of the vectors is always 1. The input parameter is used in the Dirichlet distribution to sample the output value, which is the action. Since this sampling is random, various output values can be obtained even with the same input parameter. This change contributes to solving the problem in a differentiated way from the basic structure of TD3 by reflecting uncertainty and dynamic task requirements in a MECS-based HSR environment.
Deep reinforcement learning (DRL) is a methodology in which an agent learns an optimal action policy while interacting with the environment, and it is based on the Markov Decision Process (MDP). The MDP generally refers to the process of probabilistically controlling states and actions at discrete time steps, which provides the mathematical basis for reinforcement learning. MDP formally defines the dynamic characteristics of the environment and the decision-making process of the agent. The agent can select the optimal action using it. The main components of MDP are S, which represents a state set, and A, which represents an action set. r represents a reward function, and P represents the state transition probability which is unknown in our proposed problem. It is usually expressed in the form of a tuple such as (S, A, P, r).
In this paper, the MDP that determines the optimal task partitioning ratio that maximizes the throughput of tasks and minimizes the delay time in an HSR environment with an MECS. MDP modeling is critical for performance optimization in dynamic environments. In the proposed environment, the number of HSTs and the density of users aboard the HST vary over time, resulting in fluctuations in the amount of tasks generated. Consequently, the load on the MECS also changes dynamically. The algorithm addresses these changes by adjusting the task partitioning ratio in real time, which directly impacts task throughput and latency. Task latency is influenced by waiting time, which is, in turn, affected by the MEC server load. When MECSs become overloaded, tasks may exceed the latency constraints due to prolonged waiting times, making it difficult to ensure QoS. To address this, the proposed algorithm determines the task partitioning ratio based on the dynamically changing MEC load and the size of the generated tasks. The optimal task partitioning ratio calculated by the algorithm allocates fewer tasks to heavily loaded MECSs and more tasks to lightly loaded MECSs. This approach improves overall system efficiency by maximizing task throughput and maintaining QoS through reduced waiting times. Additionally, the algorithm minimizes delay time by distributing tasks effectively across MEC servers, achieving load balancing and optimizing resource utilization. Based on this proposed environment, we define MDP as follows:
- Agent: All HSRs are agents. , which observes the state of the HSR environment with MECSs, chooses actions according to the policy, receives rewards, and updates the environment. By repeating this, they learn the optimal action strategy to maximize the cumulative reward.
- State: The state consists of the information () of the task generated in HST n and the information () of the currently considered serving MECSs . consists of the data size, workload, and delay constraint of the task, and represents the load states of k serving MECSs considered by HST n. This provides environmental information for task partitioning ratio decisions.
- Action: defines as the task partitioning ratio to be processed among the K serving MECSs considered by HST .
- Reward: In Equation (15), is defined based on the task throughput and the delay . The reward function is designed to minimize delay while maximizing task throughput . Here, task throughput refers to the resources of a task that succeeds within the delay constraint, while delay represents the time consumed when processing a task. These two objectives are conflicting, as one seeks to minimize delay and the other seeks to maximize the throughput. To address this, the reward function penalizes task execution delay () by applying it as a penalty term, while task throughput (), whose goal is to maximize, is applied as a reward term. In addition, the weights in the reward function that constitutes this multi-objective sum to 1 and represent values between 0 and 1. This indicates importance. If greater emphasis on the task throughput is desired, the weight assigned to the task throughput can be increased accordingly:
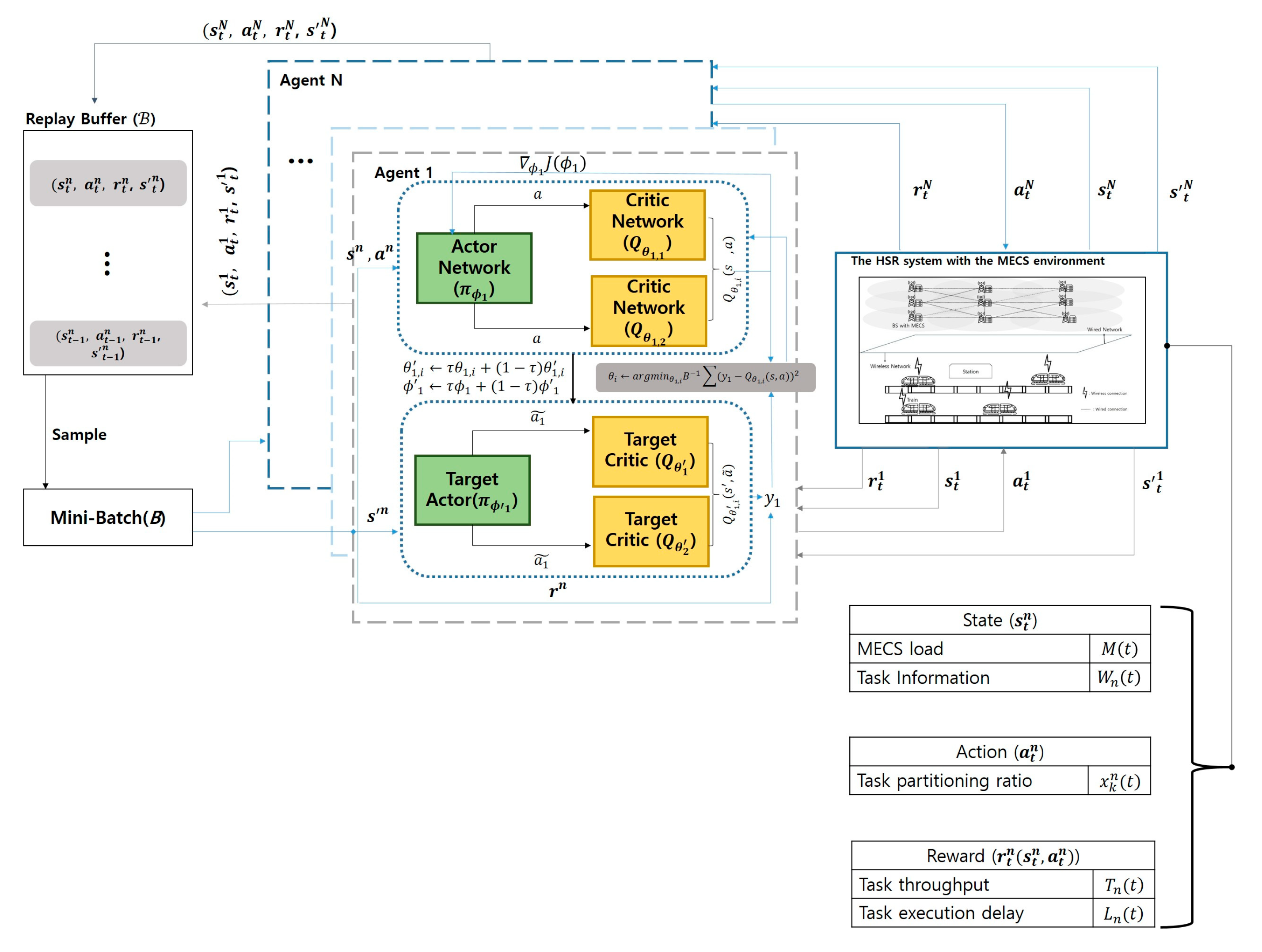
Figure 3 illustrates a simplified flowchart for determining the task partitioning ratio in the proposed system. The flowchart depicted in Figure 3 represents the TD3 learning process at time slot t. Based on the MDP defined above, it demonstrates the operation of the TD3 algorithm within the HSR environment. In this setup, multiple agents represent HSTs, which operate independently without sharing a common environment. The process begins with each agent observing the current state () and selecting an action () based on the Actor network’s policy. The environment then provides a reward () and the next state (), which are stored as transitions () in the replay buffer. During the learning process, a mini-batch of transitions is sampled to update the Critic networks using the TD3 loss function. Finally, the Actor network is updated based on the deterministic policy gradient. Each agent learns by sampling B transitions randomly from a replay buffer. These transitions are used to update the agent’s policy and value networks. The reward is generated based on the actions taken by the agents, which are determined from the information observed in the environment. The proposed environment is dynamically changing at every time slot, and it has the characteristics of generating large-scale tasks due to user density. By utilizing the characteristics of TD3 described above, this study aims to effectively solve the problem of determining task partitioning ratio in an HSR environment. In particular, the approach ensures stable and efficient task partitioning ratio decisions, even in environments characterized by dynamic MECS loads, varying numbers of HSTs, and high task generation rates caused by dense user traffic.
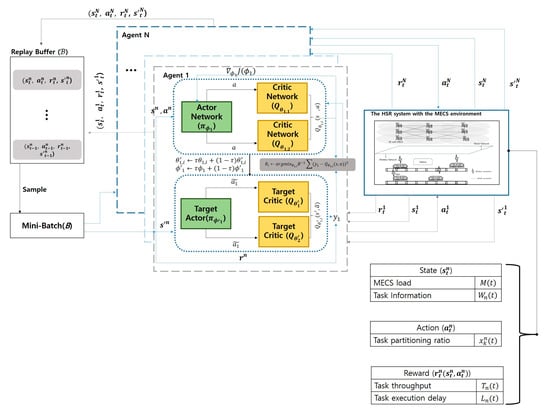
Figure 3.
Task partition ratio decision algorithm flowchart using TD3.
4. Simulation Results
This section presents the experimental results conducted to evaluate the performance of the proposed algorithm in an HSR environment with MECSs. The experimental environment was built based on python 3.9 and pytorch 2.4.1+cu118. The experimental environment consists of HSTs moving along HSRs track and BSs with MECSs. The BS was placed along the railway. The experiment was conducted in a scenario including multiple HSTs and MECSs. Multiple passengers were set to create tasks through UEs inside the HST, and the number of HSTs was designed to change dynamically over time. In addition, the movement information of the HST was conducted using SUMO (Simulation of Urban MObility) [24].
The proposed model for the simulation is an initial scenario model for subsequent studies. In the experimental environment, the speed of HSR was set to 0~100 m/s, and the service radius of BS was configured to 200 m. The task occurrence was modeled by forming a distribution based on the Poisson Process, and the performance of the proposed algorithm was evaluated in various network and task and HST environments. The experimental parameters in HSR are referred to in [20]. The specific experimental parameters are specified in Table 1.

Table 1.
The parameters setting of the HSR.
The network structure used in this paper is designed based on the TD3 algorithm. The actor network receives a state as input and generates continuous actions, and the structure consists of a fully connected layer of [256, 256]. The first hidden layer is mapped from the state space size to 256 units, and the second hidden layer maintains 256 units. The last layer is mapped from 256 units to the action space size, and the output value is converted to the parameters of the Dirichlet distribution through the Softplus activation function. Through this, the action sampled from the Dirichlet distribution is output so that it can solve continuous and probabilistic ratio-based problems.
The Critic network consists of two independent Q-networks (), which take state and action as input and output Q values. Each Q-network consists of a fully connected layer of [256, 256], where the first hidden layer maps 256 units from the input of the state space size and the action space size, and the second hidden layer also maintains 256 units. The last layer outputs a single scalar value from the 256 units to generate the Q value. Both hidden layers used the ReLU activation function, and the two Q-networks were trained independently to ensure the stability of Clipped Double Q-Learning. The specific hyper-parameter values used in TD3 are specified in Table 2.

Table 2.
The hyper parameter of the proposed algorithm.
In order to evaluate the proposed algorithm in this paper, the performance was compared with the following three different types of schemes.
- Random: This method randomly selects the task partitioning ratio, without considering the task characteristics or MECS status. This is used as a reference point to check how much the structured decision-making method improves performance.
- No Partition: This method processes all tasks on the initially selected MECS without performing task partitioning. This is used to compare the impact of task partitioning on resource utilization and performance.
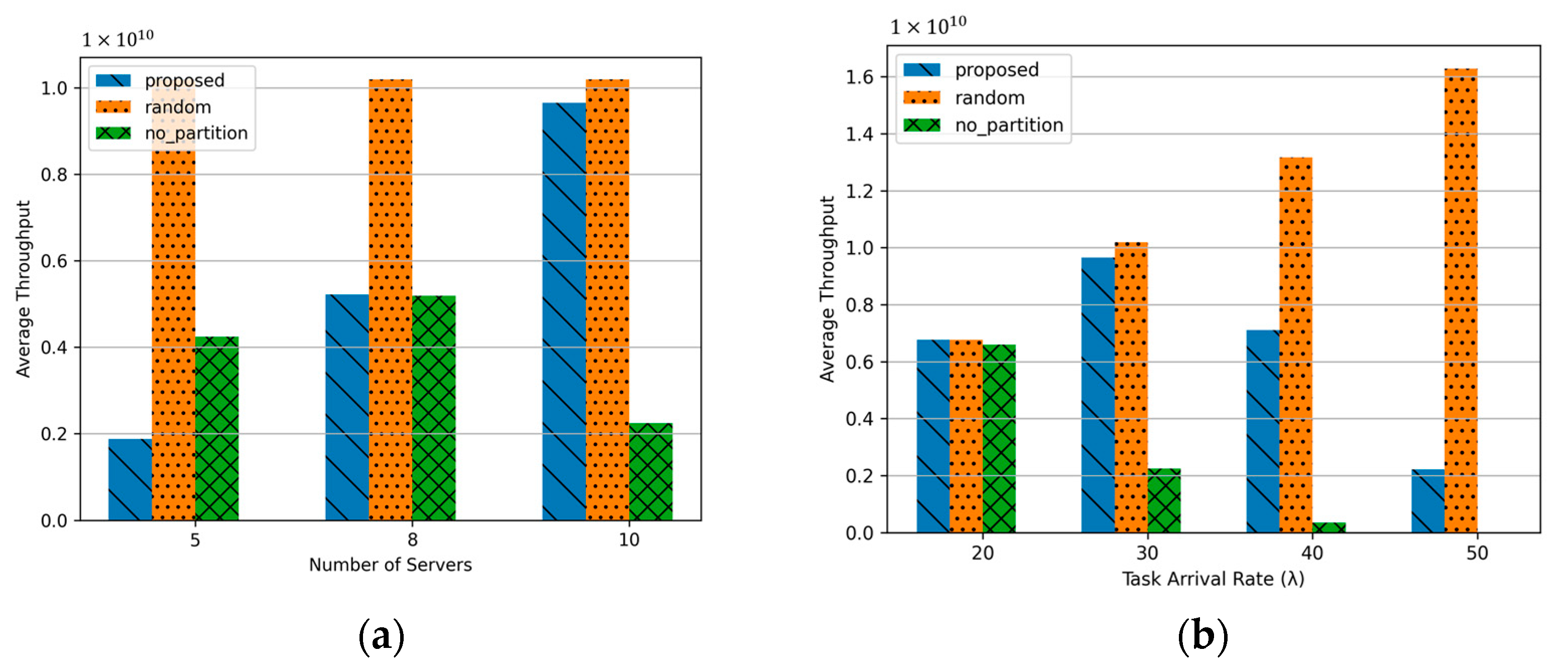
Figure 4a illustrates the performance showing task throughput as the number of serving MECSs increases. The proposed algorithm demonstrates improved throughput with an increasing number of serving MECSs. This improvement is attributed to the ability to partition tasks across a larger number of MECSs, enabling parallel processing. Consequently, the system can handle a higher volume of tasks within the delay constraints, resulting in increased throughput. Random scheme achieves the highest throughput among the compared methods. This result stems from the uniform distribution of tasks across the MECSs, which, despite lacking server load awareness or partitioning strategies, effectively balances the load. In contrast, the No Partition scheme records the lowest throughput when the number of serving MECSs reaches 10. This is because tasks are always assigned to the nearest MECS, increasing the likelihood of exceeding the processing delay threshold, which negatively impacts performance. Unlike the proposed algorithm, the throughput of the No Partition scheme is inconsistent regardless of the number of serving MECSs. This inconsistency is influenced by the movement patterns of HSTs. Interestingly, the proposed algorithm achieves its highest throughput when the number of serving MECSs is 8. This result can be attributed to the even distribution of HSTs, which ensures that tasks are uniformly allocated to MECSs, maximizing processing efficiency and throughput under this configuration.
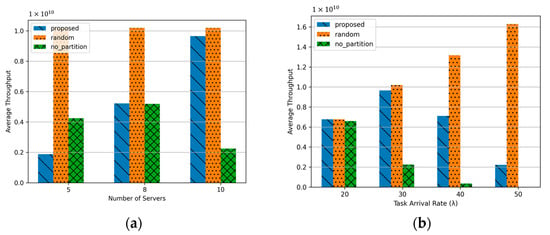
Figure 4.
Average throughput about number of server and task arrival rate: (a) Number of serving MECSs (K) (5, 8, 10); (b) Task arrival rate in a HST (20, 30, 40, 50).
Figure 4b illustrates the performance of throughput as the task arrival rate increases. For this experiment, the number of serving MEC servers was fixed at 10 to evaluate the effectiveness of task distribution across servers. In the case of No Partition, the throughput significantly decreases as the task arrival rate increases. This is because, as more tasks are generated, the size of tasks sent to a single MEC server increases, which leads to fewer tasks being processed within the required delay constraints. Notably, at a task arrival rate of 50, no tasks are successfully processed, resulting in a throughput of zero, as indicated by the absence of the corresponding bar in the graph. On the other hand, Random achieves higher throughput as the task arrival rate increases, owing to its ability to distribute tasks evenly across servers. However, the Proposed Method demonstrates the highest throughput at a task arrival rate of 30. This is because, while the proposed method effectively manages task partitioning, the higher task arrival rate leads to an increased number of tasks to be processed, which limits its performance beyond a certain threshold.
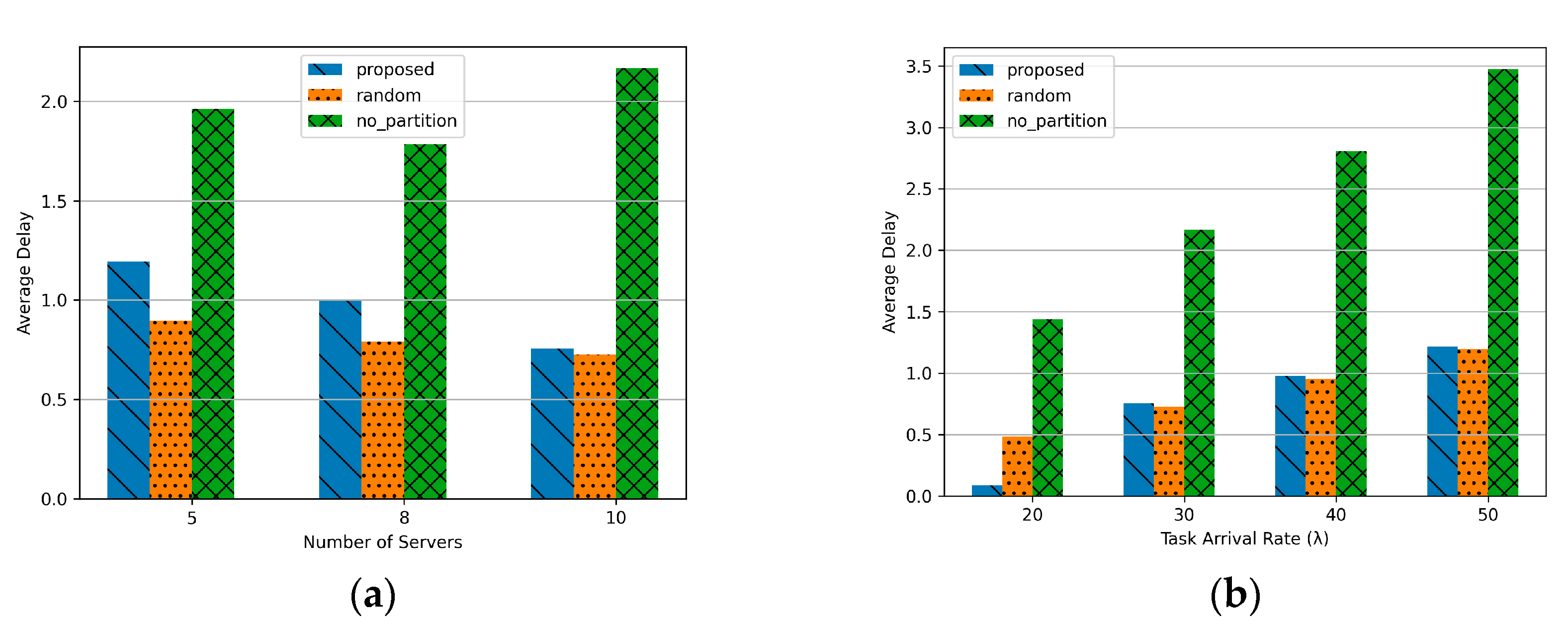
Figure 5 illustrates the performance of average delay under varying task arrival rates and the number of servers. Figure 5a demonstrates that the average delay decreases as the number of servers increases. This improvement can be attributed to the increased availability of serving MEC servers, enabling tasks to be partitioned and processed in parallel. For the No partition approach, tasks are not divided among servers, resulting in significant delays due to the high dependency on the movement of high-speed trains (HSTs). While there is a slight improvement in delay when the number of servers increases from 5 to 8, the overall delay remains the highest compared to other methods since tasks are processed on a single MEC server. In contrast, both the proposed method and the Random approach leverage task partitioning, leading to progressively reduced delays as the number of MEC servers increases. However, the Random method outperforms the proposed method in terms of delay. This is because Random evenly distributes tasks across the MEC servers, preventing overloading on a single server, thereby achieving the lowest delay among the methods analyzed.
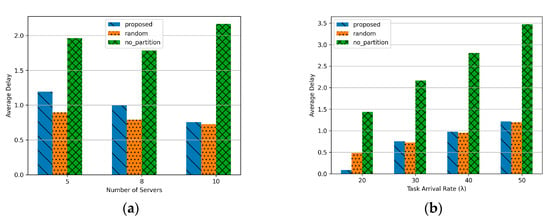
Figure 5.
Average delay about number of server and task arrival rate: (a) Number of serving MECSs (K) (5, 8, 10); (b) Task arrival rate in a HST (20, 30, 40, 50).
Figure 5b illustrates the average delay as a function of task arrival rates. As the task arrival rate increases, the average delay shows an overall upward trend due to the higher task load. In particular, the No partition method exhibits the worst delay performance because tasks are concentrated on a single MEC server without partitioning. As a result, it becomes highly inefficient in managing increasing task loads. Moreover, as mentioned in Figure 5a, the Random approach achieves better delay performance compared to the proposed method. This improvement is attributed to the uniform distribution of tasks across the available MEC servers, which prevents server overload and reduces processing bottlenecks. Consequently, the Random approach demonstrates a significant advantage in minimizing delay under high task arrival rates.
In conclusion, task partitioning proves to be advantageous in scenarios involving high task loads. The proposed method demonstrates its best performance when the task arrival rate is at a moderate level. While the Random approach achieves superior throughput performance, it exhibits negligible differences in delay compared to the proposed method. Future research will aim to enhance the proposed policy by incorporating certain advantages of the Random approach, thereby addressing its current limitations and further improving performance. Also, the proposed paper shows that the performance varies depending on how the serving MECS K is determined. It shows that the smaller K is, the worse the performance is. The reason is that the more MECS are considered, the more the number of tasks to be divided increases, which reduces the delay and increases the throughput. However, if many serving MECSs are simply considered, the computational complexity will increase significantly. Determining the appropriate K even in dynamic environment can be another research topic.
5. Conclusions
This paper addresses the task partitioning decision in HSR environments with MECSs. The proposed DRL-based task partitioning mechanism dynamically adjusts the task partitioning ratio in response to a real-time environment in which the number of HSTs changes every time slot, the density of passengers inside the HST, the server load of the MECS, and the data size of generated tasks change. The experimental results show that when the task occurrence rate is 20, the delay time is improved by about 5% compared to random and about 13% compared to no_partition. When it is 50, there is no significant difference from random and about 2% improvement compared to no_partition. There is almost no difference in task processing when it is 20. However, when it is 50, random is much better. Future research will focus on integrating resource optimization and task partitioning mechanisms to develop a unified framework capable of dynamically adapting to HSR environments. This study supports uninterrupted services for passengers by ensuring stable task processing and QoS even during high-speed movement in the HSR system. Furthermore, by adjusting the task partitioning ratio to balance the load among MECSs, the approach increases the utilization of MEC system resources, reduces task execution delay, and enhances task throughput. This study also contributes to the development of scalable and intelligent transportation systems. It supports the implementation of scalable operations while maintaining QoS in environments characterized by high density and high-speed mobility. These contributions have far-reaching implications for the realization of smart cities and advancements in high-speed transportation technologies. Future research will focus on developing an integrated framework that dynamically adapts to HSR environments by combining resource optimization and task partitioning mechanisms. Given the high-speed nature of HSR environments, managing interference is critical. To address this challenge effectively, future work will also explore power resource allocation optimization, aiming to further enhance system performance under the unique constraints of HSR scenarios.
Author Contributions
Conceptualization, S.K. and Y.L.; methodology, S.K. and Y.L; software, S.K.; writing—original draft preparation, S.K.; writing—review and editing, S.K.; visualization, S.K.; supervision, Y.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors on request.
Acknowledgments
This work was supported by the IITP (Institute of Information & Communications Technology Planning & Evaluation)-ICAN(ICT Challenge and Advanced Network of HRD) grant funded by the Korea government(Ministry of Science and ICT)(IITP-2025-RS-2022-00156299).
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Ai, B.; Guan, K.; Rupp, M.; Kürner, T.; Cheng, X.; Yin, X.; Wang, Q.; Ma, G.; Li, Y.; Xiong, L. Future Railway Services-Oriented Mobile Communications Network. IEEE Commun. Mag. 2015, 53, 78–85. [Google Scholar] [CrossRef]
- Ai, B.; Molisch, A.F.; Rupp, M.; Zhong, Z. 5G Key Technologies for Smart Railways. Proc. IEEE 2020, 108, 856–893. [Google Scholar] [CrossRef]
- Gheth, W.; Rabie, K.M.; Adebisi, B.; Ijaz, M.; Harris, G. Communication Systems of High-Speed Railway: A Survey. Trans. Emerg. Telecommun. Technol. 2021, 32, e4189. [Google Scholar] [CrossRef]
- Xu, S.; Zhu, G.; Ai, B.; Zhong, Z. A Survey on High-Speed Railway Communications: A Radio Resource Management Perspective. Comput. Commun. 2016, 86, 12–28. [Google Scholar] [CrossRef]
- Ren, S.; Li, Y. A Review of High-Performance Computing Applications in High-Speed Rail Systems. High-Speed Railw. 2023, 1, 92–96. [Google Scholar] [CrossRef]
- Mao, Y.; You, C.; Zhang, J.; Huang, K.; Letaief, K.B. A Survey on Mobile Edge Computing: The Communication Perspective. IEEE Commun. Surv. Tutor. 2017, 19, 2322–2358. [Google Scholar] [CrossRef]
- Jiang, C.; Cheng, X.; Gao, H.; Zhou, X.; Wan, J. Toward Computation Offloading in Edge Computing: A Survey. IEEE Access 2019, 7, 131543–131558. [Google Scholar] [CrossRef]
- Liu, J.; Zhang, Q. Offloading Schemes in Mobile Edge Computing for Ultra-Reliable Low Latency Communications. IEEE Access 2018, 6, 12825–12837. [Google Scholar] [CrossRef]
- De Souza, A.B.; Rego, P.A.L.; Carneiro, T.; Rodrigues, J.D.C.; Filho, P.P.R.; De Souza, J.N.; Chamola, V.; De Albuquerque, V.H.C.; Sikdar, B. Computation Offloading for Vehicular Environments: A Survey. IEEE Access 2020, 8, 198214–198243. [Google Scholar] [CrossRef]
- Zhu, C.; Tao, J.; Pastor, G.; Xiao, Y.; Ji, Y.; Zhou, Q.; Li, Y.; Ylä-Jääski, A. Folo: Latency and Quality Optimized Task Allocation in Vehicular Fog Computing. IEEE Internet Things J. 2019, 6, 4150–4161. [Google Scholar] [CrossRef]
- Wu, S.; Xia, W.; Cui, W.; Chao, Q.; Lan, Z.; Yan, F.; Shen, L. An Efficient Offloading Algorithm Based on Support Vector Machine for Mobile Edge Computing in Vehicular Networks. In Proceedings of the 2018 10th International Conference on Wireless Communications and Signal Processing (WCSP), Hangzhou, China, 18–20 October 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Wang, Y.; Lang, P.; Tian, D.; Zhou, J.; Duan, X.; Cao, Y.; Zhao, D. A Game-Based Computation Offloading Method in Vehicular Multiaccess Edge Computing Networks. IEEE Internet Things J. 2020, 7, 4987–4996. [Google Scholar] [CrossRef]
- Liu, J.; Ahmed, M.; Mirza, M.A.; Khan, W.U.; Xu, D.; Li, J.; Aziz, A.; Han, Z. RL/DRL Meets Vehicular Task Offloading Using Edge and Vehicular Cloudlet: A Survey. IEEE Internet Things J. 2022, 9, 8315–8338. [Google Scholar] [CrossRef]
- Arulkumaran, K.; Deisenroth, M.P.; Brundage, M.; Bharath, A.A. Deep Reinforcement Learning: A Brief Survey. IEEE Signal Process. Mag. 2017, 34, 26–38. [Google Scholar] [CrossRef]
- Peng, H.; Shen, X. Deep Reinforcement Learning Based Resource Management for Multi-Access Edge Computing in Vehicular Networks. IEEE Trans. Netw. Sci. Eng. 2020, 7, 2416–2428. [Google Scholar] [CrossRef]
- Ren, Y.; Yu, X.; Chen, X.; Guo, S.; Qiu, X. Vehicular Network Edge Intelligent Management: A Deep Deterministic Policy Gradient Approach for Service Offloading Decision. In Proceedings of the 2020 International Wireless Communications and Mobile Computing (IWCMC), Limassol, Cyprus, 15–19 June 2020; pp. 905–910. [Google Scholar] [CrossRef]
- Yao, L.; Xu, X.; Bilal, M.; Wang, H. Dynamic Edge Computation Offloading for Internet of Vehicles with Deep Reinforcement Learning. IEEE Trans. Intell. Transp. Syst. 2023, 24, 12991–12999. [Google Scholar] [CrossRef]
- Chen, Y.; Wu, H. Resource Allocation for Edge Collaboration with Deep Deterministic Policy Gradient in Smart Railway. In Proceedings of the 2021 IEEE 4th International Conference on Electronics Technology (ICET), Chengdu, China, 8–12 May 2021; pp. 1163–1167. [Google Scholar] [CrossRef]
- Zhao, J.; He, L.; Zhang, D.; Gao, X. A TP-DDPG Algorithm Based on Cache Assistance for Task Offloading in Urban Rail Transit. IEEE Trans. Veh. Technol. 2023, 72, 10671–10681. [Google Scholar] [CrossRef]
- Xu, J.; Ai, B.; Chen, L.; Cui, Y.; Wang, N. Deep Reinforcement Learning for Computation and Communication Resource Allocation in Multiaccess MEC-Assisted Railway IoT Networks. IEEE Trans. Intell. Transp. Syst. 2022, 23, 23797–23808. [Google Scholar] [CrossRef]
- Guo, Q.; Xu, Z.; Yuan, J.; Wei, Y. Computation Offloading Strategy for Detection Task in Railway IoT with Integrated Sensing, Storage, and Computing. Electronics 2024, 13, 2982. [Google Scholar] [CrossRef]
- Mnih, V.; Kavukcuoglu, K.; Silver, D.; Rusu, A.A.; Veness, J.; Bellemare, M.G.; Graves, A.; Riedmiller, M.; Fidjeland, A.K.; Ostrovski, G.; et al. Playing Atari with Deep Reinforcement Learning. arXiv 2013, arXiv:1312.5602. [Google Scholar]
- Lillicrap, T.P.; Hunt, J.J.; Pritzel, A.; Heess, N.; Erez, T.; Tassa, Y.; Silver, D.; Wierstra, D. Continuous Control with Deep Reinforcement Learning. arXiv 2015, arXiv:1509.02971. [Google Scholar]
- Lopez, P.A.; Behrisch, M.; Bieker-Walz, L.; Erdmann, J.; Flötteröd, Y.-P.; Hilbrich, R.; Lücken, L.; Rummel, J.; Wagner, P.; Wiessner, E. Microscopic Traffic Simulation Using SUMO. In Proceedings of the 2018 21st International Conference on Intelligent Transportation Systems (ITSC), Maui, HI, USA, 4–7 November 2018; pp. 2575–2582. [Google Scholar] [CrossRef]
- Zhang, W.; Yao, D.; Yang, M. Implementation of LTE-R Transceiver and the Performance with WINNER D2a Channel Model. In Proceedings of the 2013 5th IEEE International Symposium on Microwave, Antenna, Propagation and EMC Technologies for Wireless Communications (MAPE), Chengdu, China, 29–31 October 2013; pp. 704–708. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).