Research on Damage Detection Methods for Concrete Beams Based on Ground Penetrating Radar and Convolutional Neural Networks
Abstract
1. Introduction
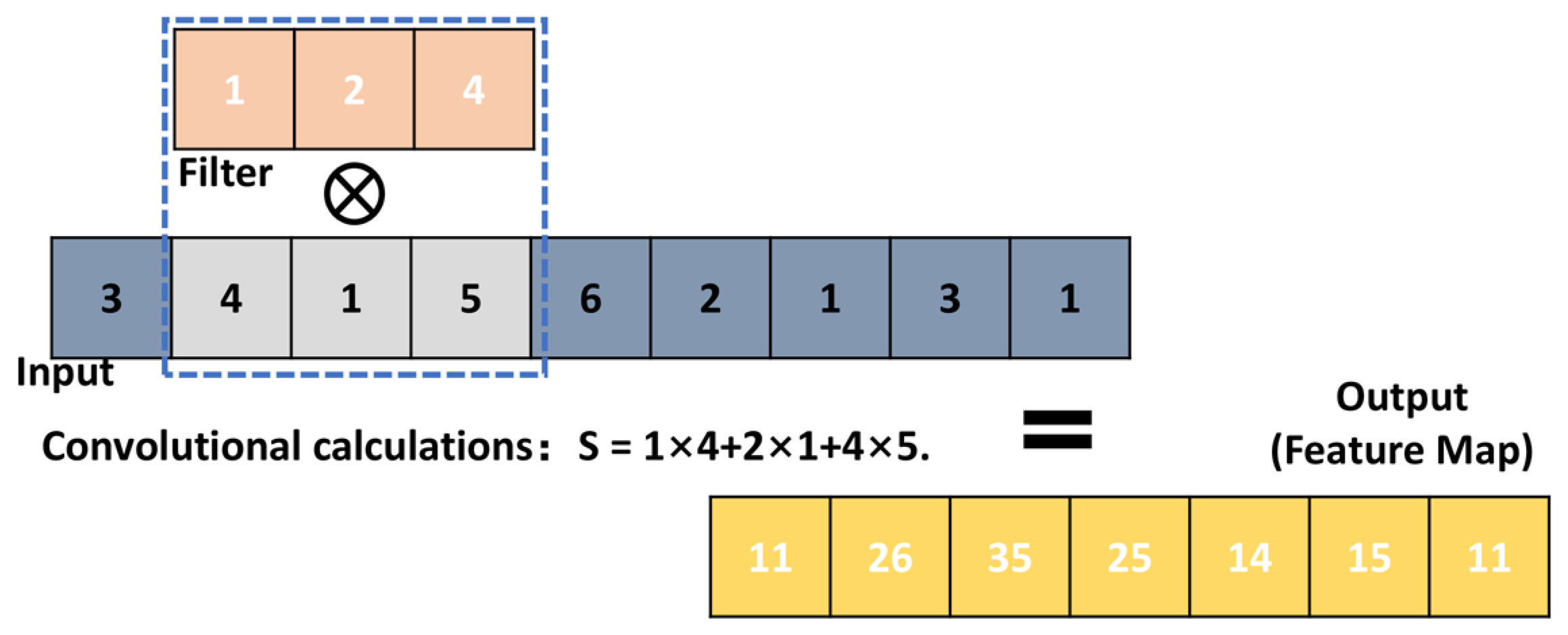
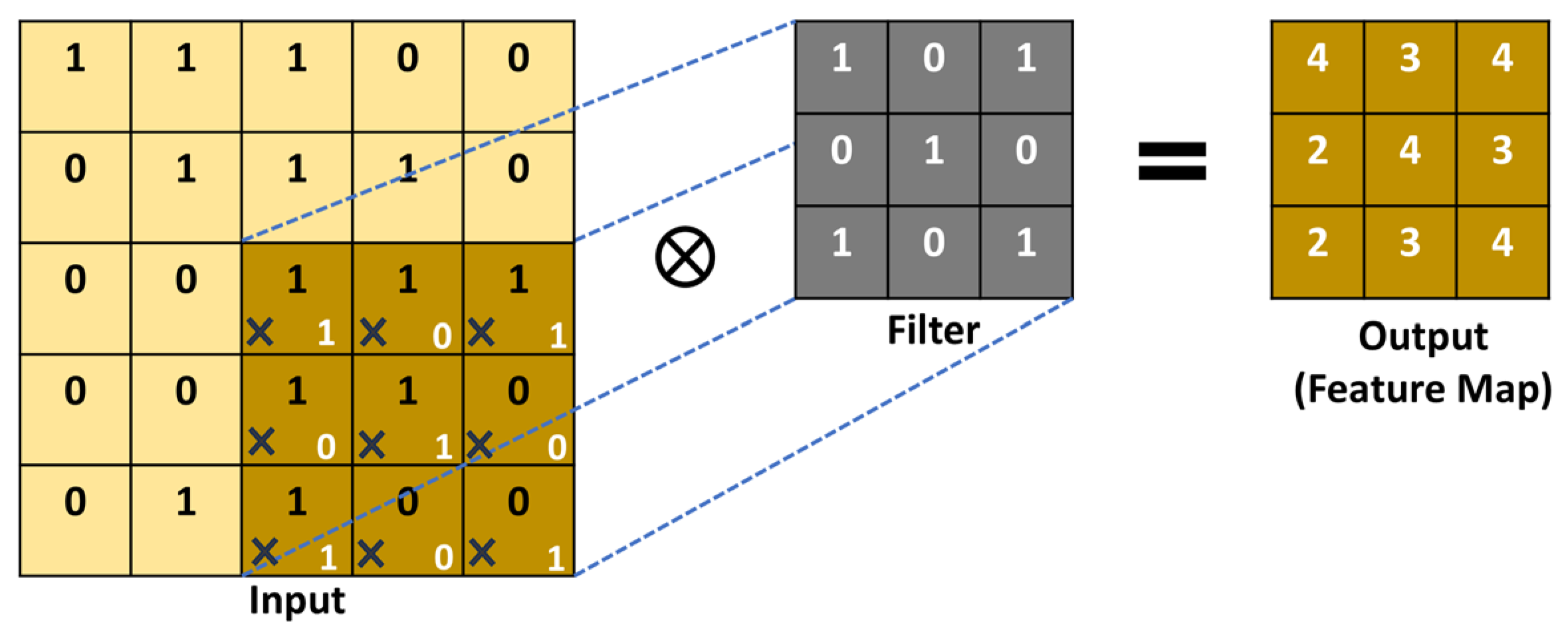
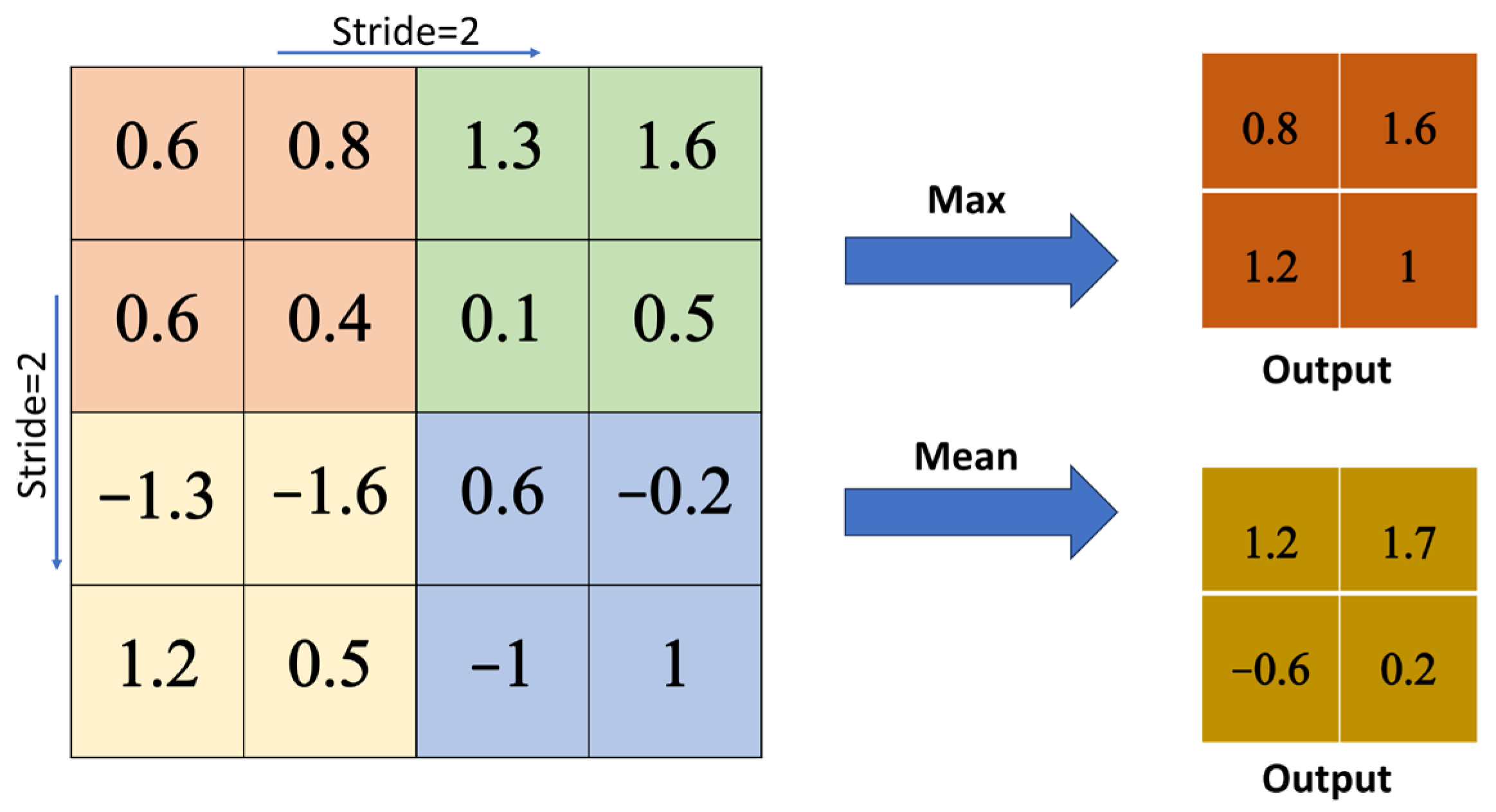
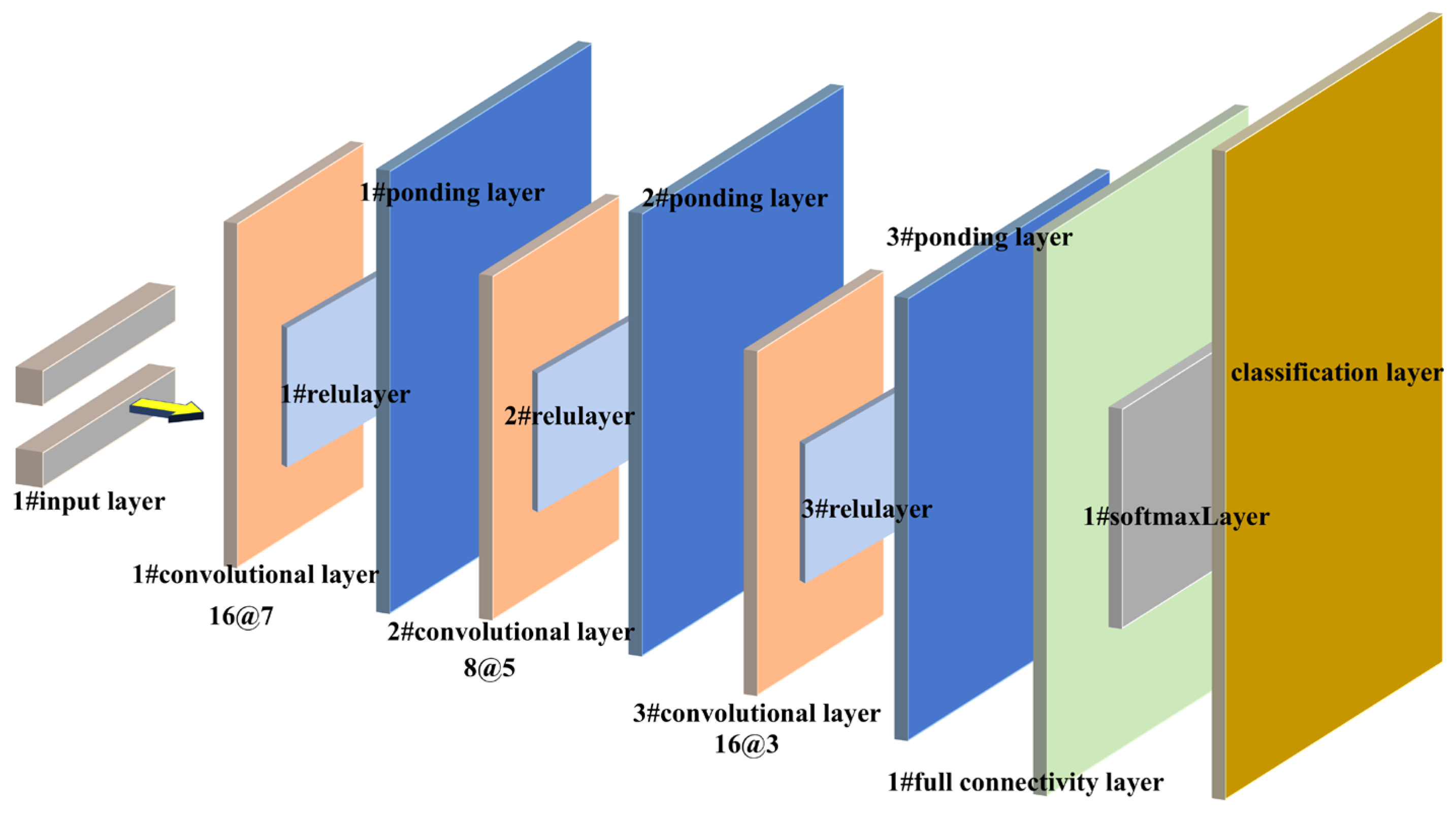
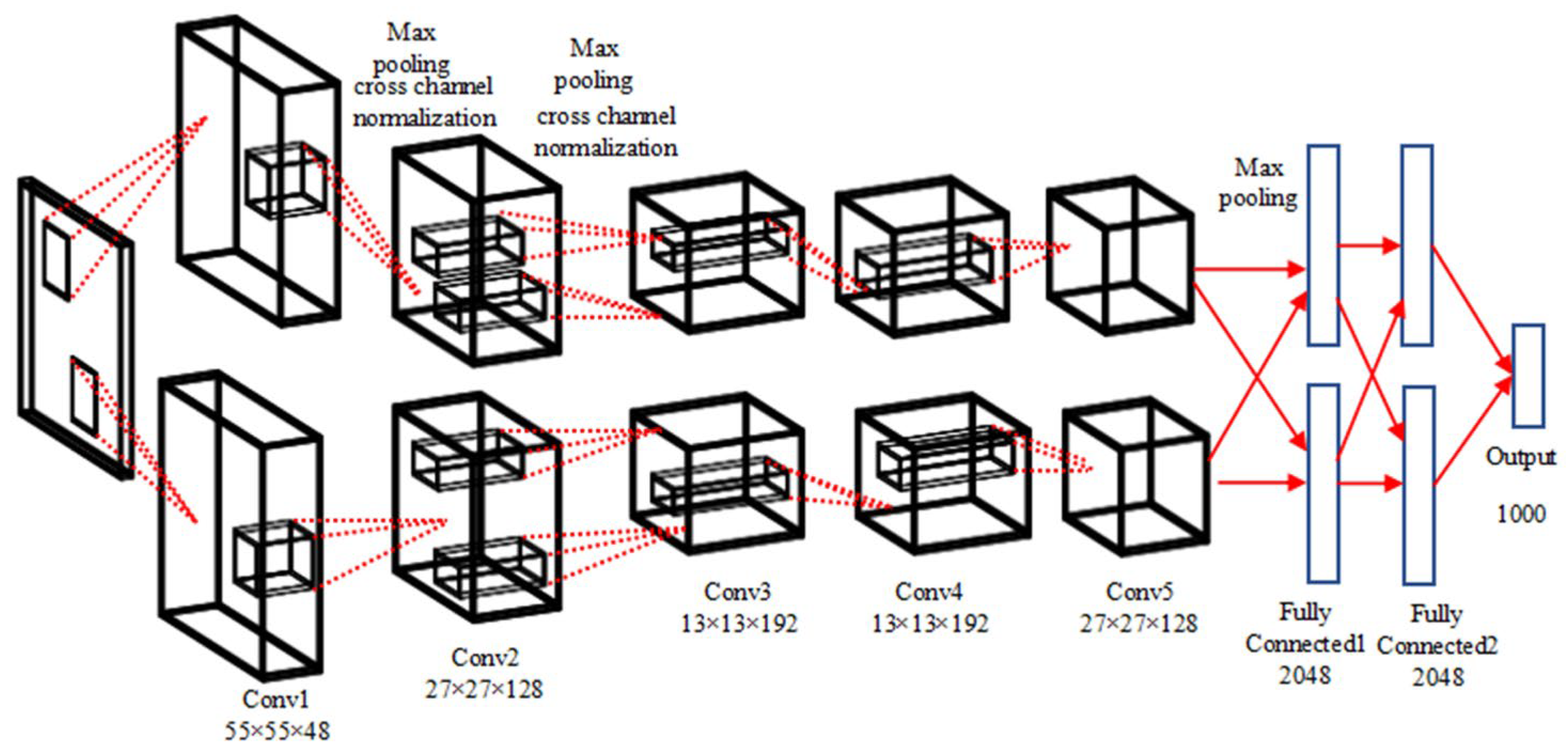
2. Architecture of the CNNs
3. Numerical Simulation and Laboratory Testing
3.1. Design of Concrete Beams with Defects
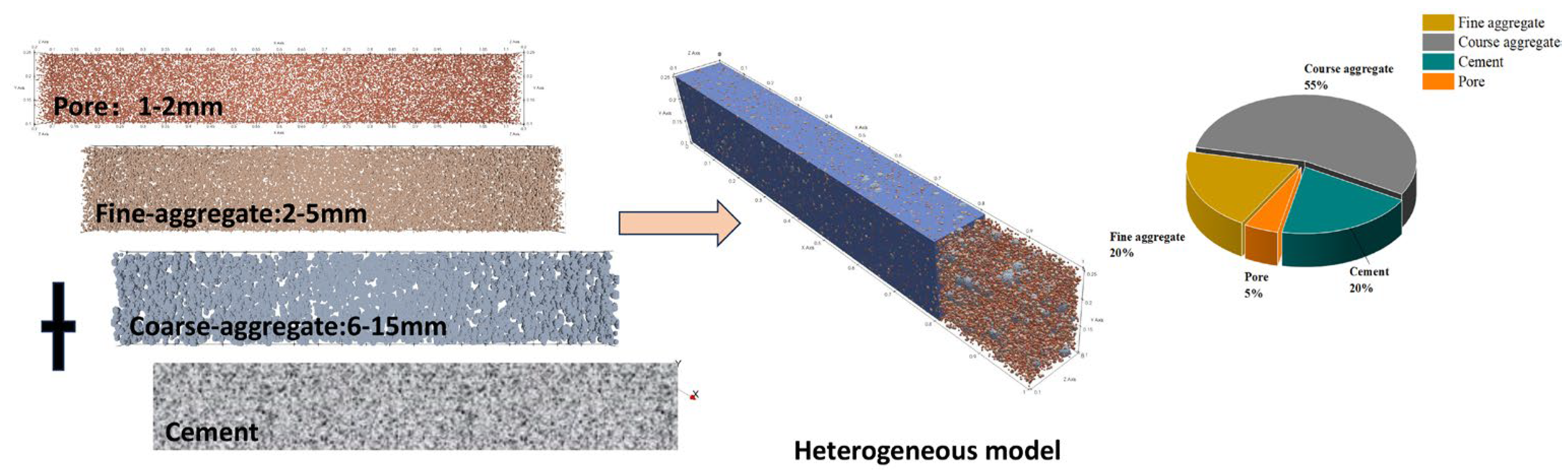
3.2. Numerical Simulation
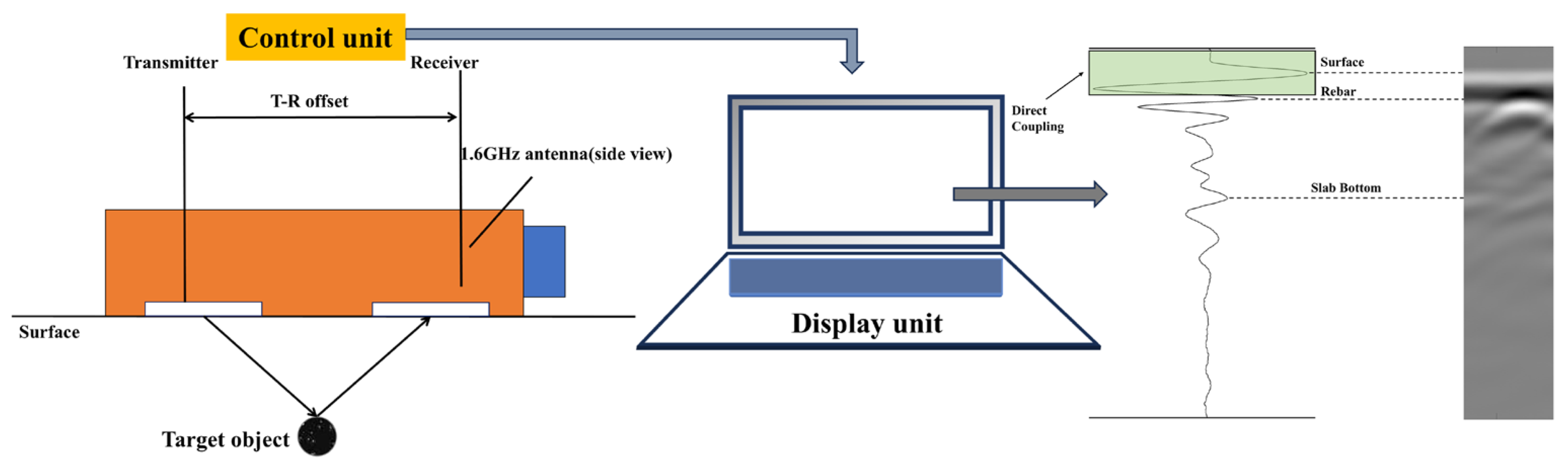
3.3. Laboratory Testing
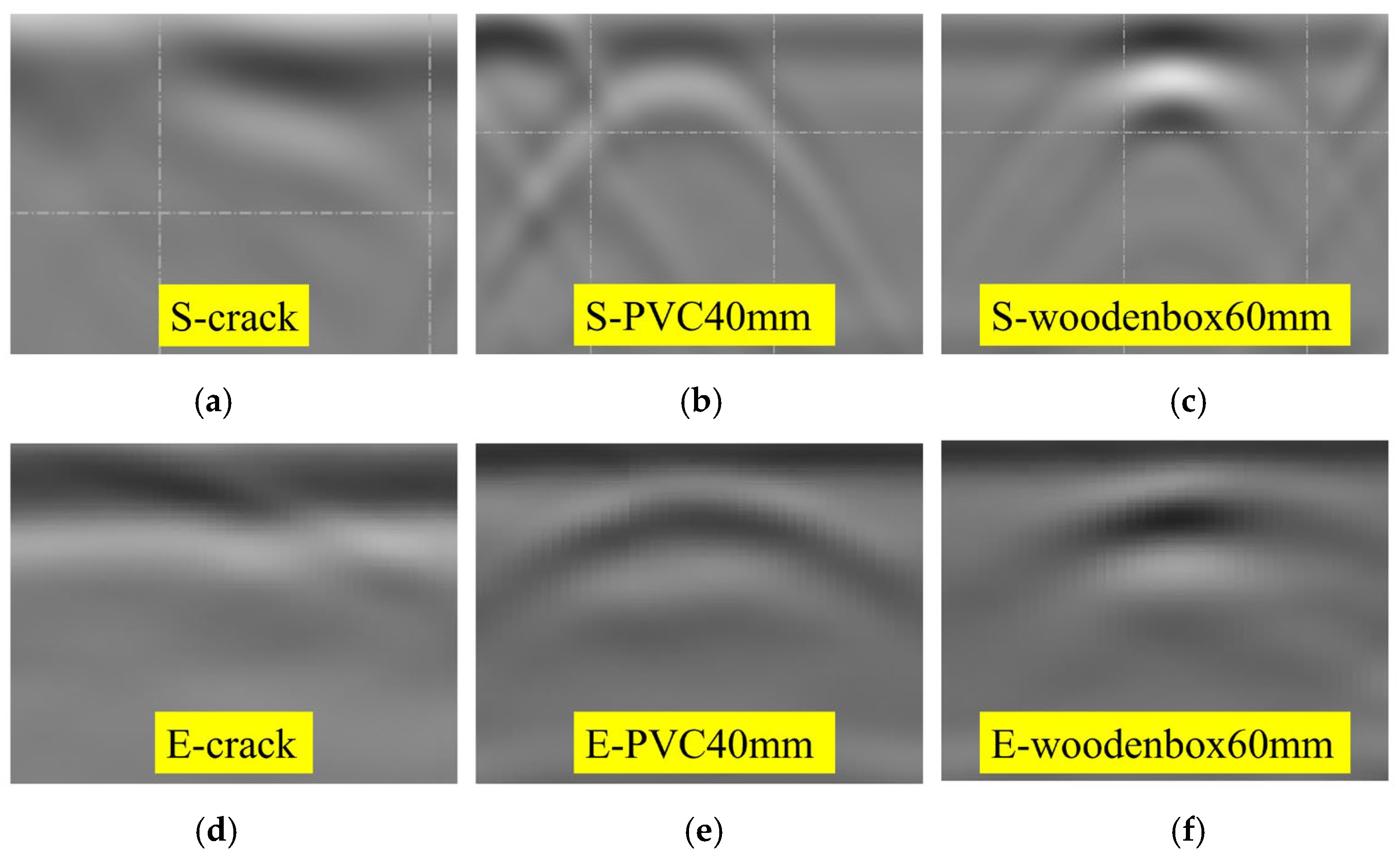
3.4. Results of Experiments and Simulations
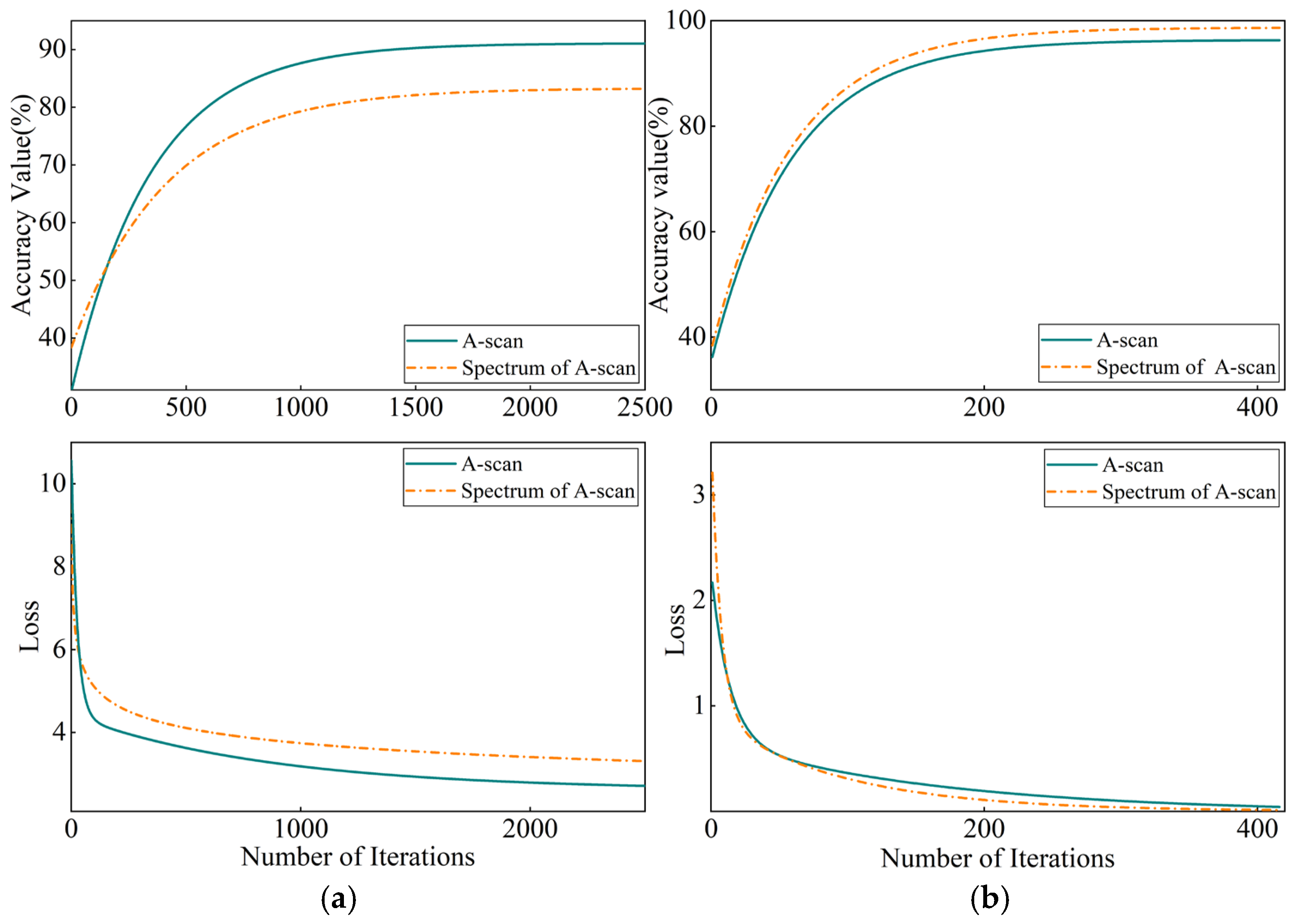
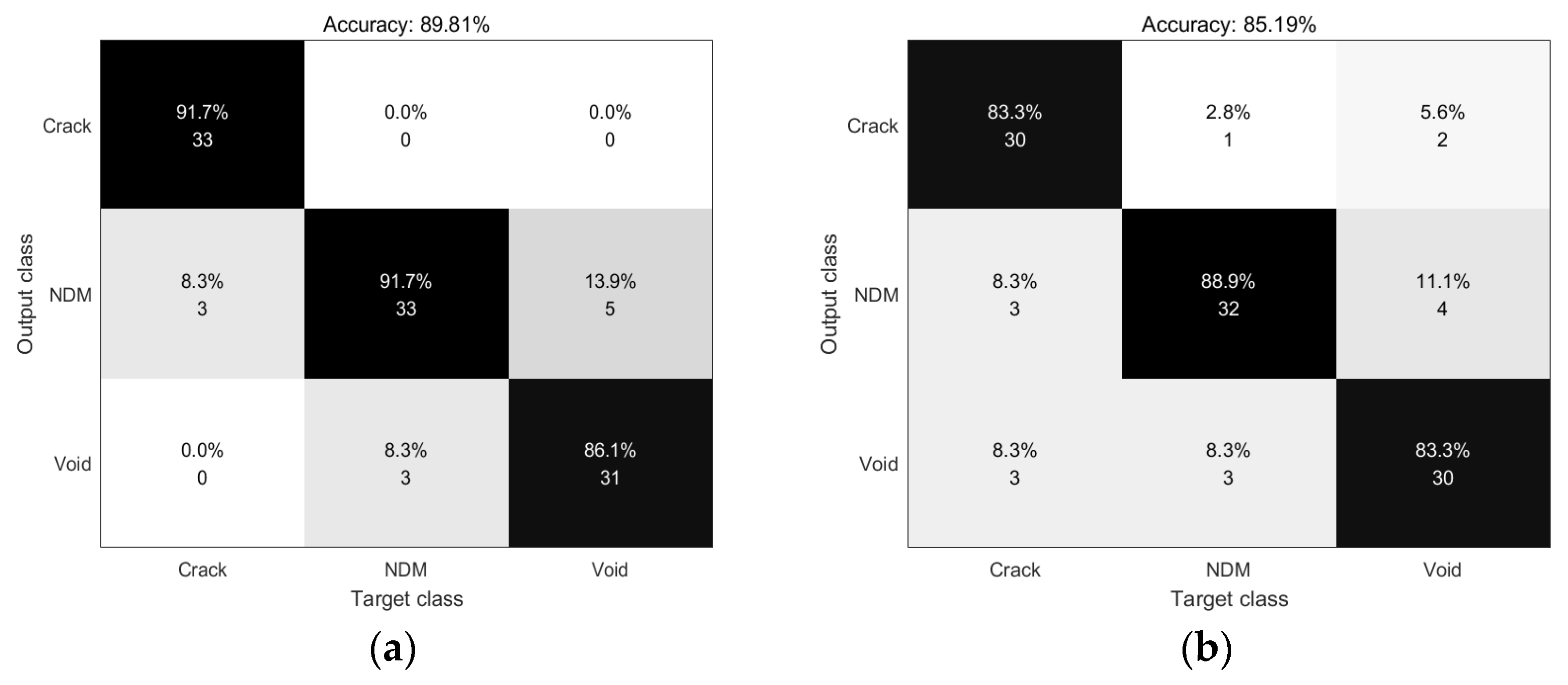
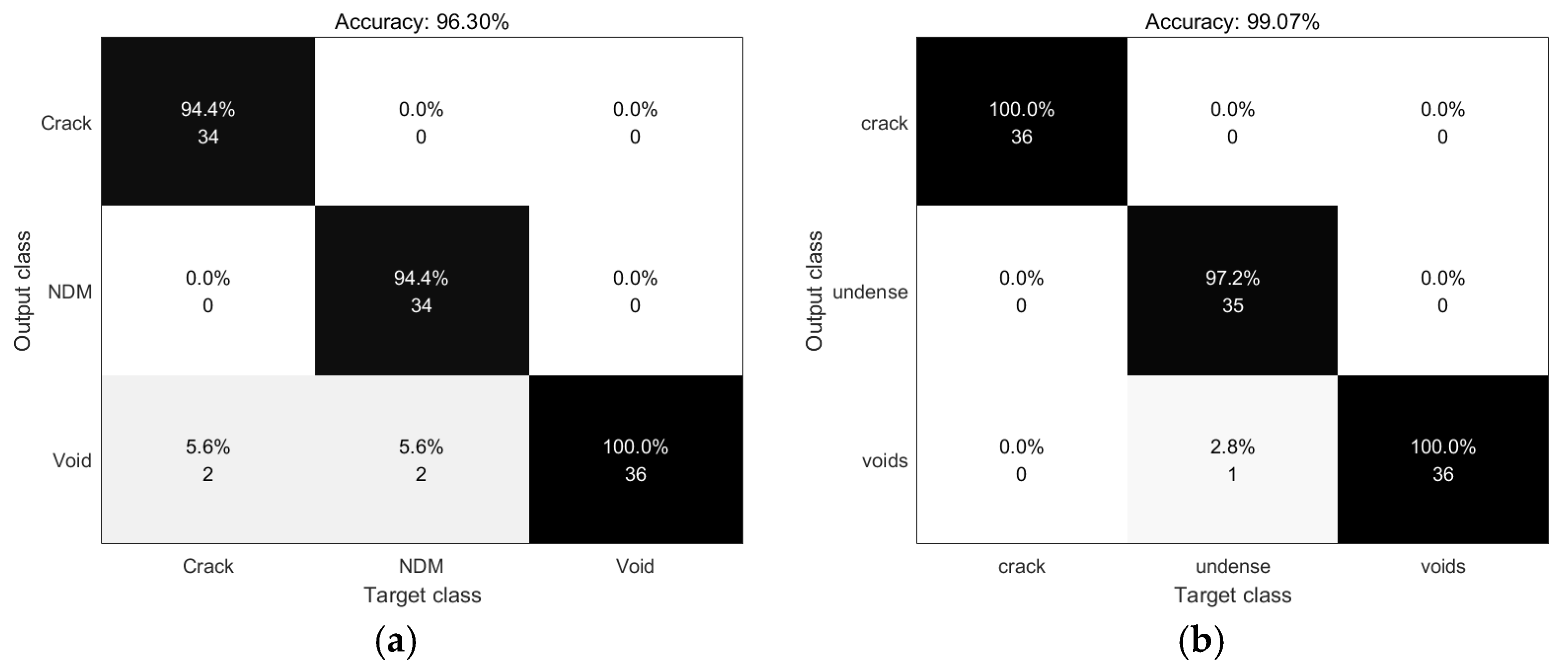
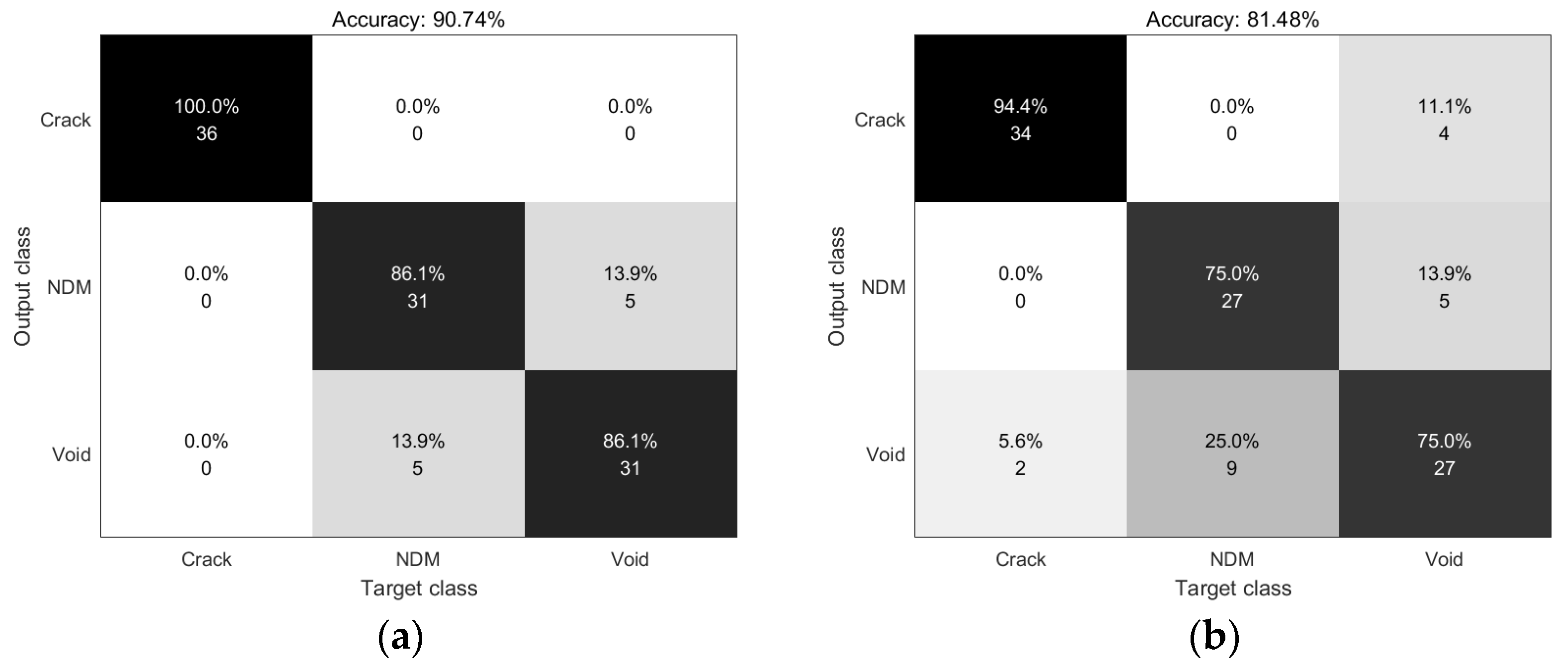
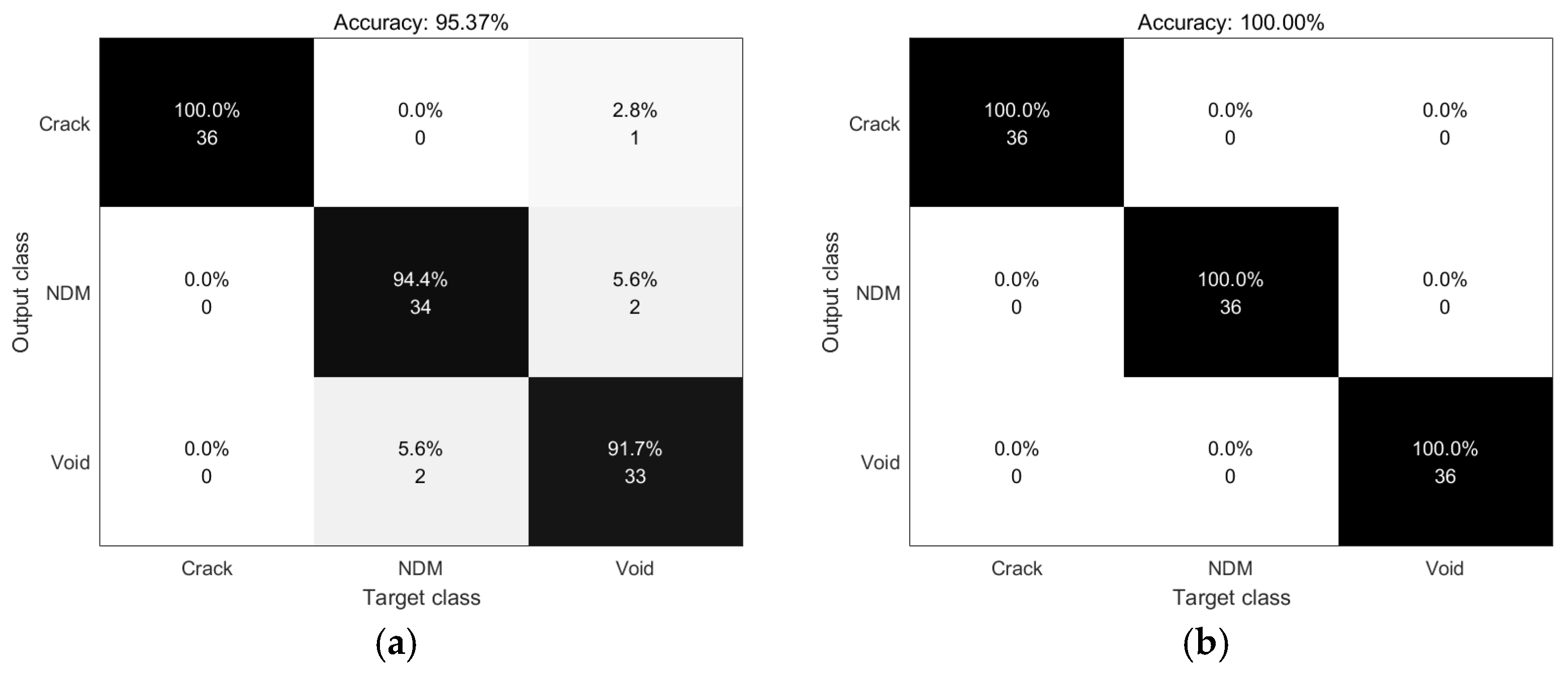
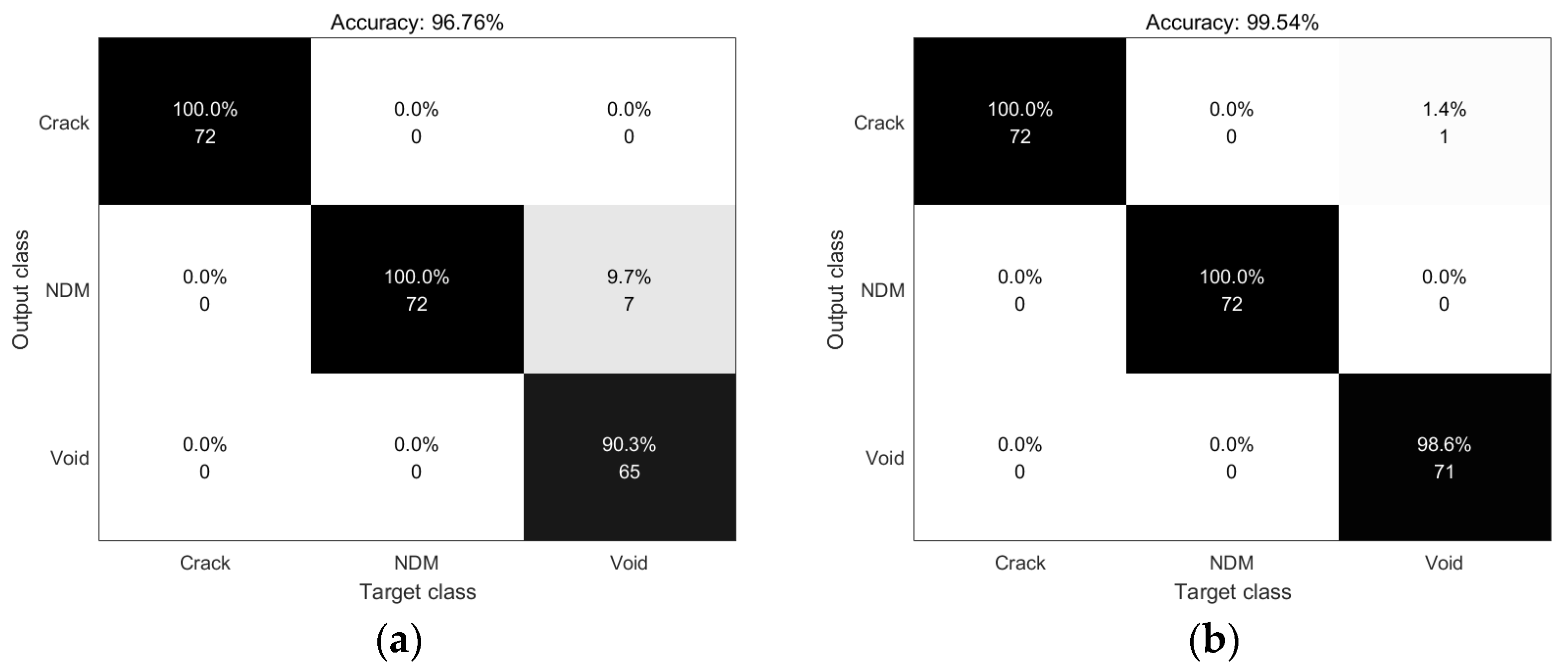
4. Training Process and Results
5. Conclusions and Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Worden, K.; Farrar, C.R.; Manson, G.; Park, G. The fundamental axioms of structural health monitoring. Proc. R. Soc. A Math. Phys. Eng. Sci. 2007, 463, 1639–1664. [Google Scholar] [CrossRef]
- Durmus, A.; Ozturk, H.T.; Durmus, A. A reliable approach for determining concrete strength in structures by using cores. Comput. Concr. 2013, 11, 463–473. [Google Scholar] [CrossRef]
- Patil, S.; Banerjee, S.; Tallur, S. Smart structural health monitoring (SHM) system for on-board localization of defects in pipes using torsional ultrasonic guided waves. Sci. Rep. 2024, 14, 24455. [Google Scholar] [CrossRef]
- Liu, Z.; Gu, X.; Wu, C.; Ren, H.; Zhou, Z.; Tang, S. Studies on the validity of strain sensors for pavement monitoring: A case study for a fiber Bragg grating sensor and resistive sensor. Constr. Build. Mater. 2022, 321, 126085. [Google Scholar] [CrossRef]
- Benedetto, A.; Tosti, F.; Bianchini Ciampoli, L.; D’Amico, F. An overview of ground-penetrating radar signal processing techniques for road inspections. Signal Process 2017, 132, 201–209. [Google Scholar] [CrossRef]
- Farahani, R.V.; Penumadu, D. Damage identification of a full-scale five-girder bridge using time-series analysis of vibration data. Eng. Struct. 2016, 115, 129–139. [Google Scholar] [CrossRef]
- Tosti, F.; Ferrante, C. Using Ground Penetrating Radar Methods to Investigate Reinforced Concrete Structures. Surv. Geophys. 2019, 41, 485–530. [Google Scholar] [CrossRef]
- Dinh, K.; Gucunski, N. Factors affecting the detectability of concrete delamination in GPR images. Constr. Build. Mater. 2021, 274, 121837. [Google Scholar] [CrossRef]
- Liu, X.; Hao, P.; Wang, A.; Zhang, L.; Gu, B.; Lu, X. Non-destructive detection of highway hidden layer defects using a ground-penetrating radar and adaptive particle swarm support vector machine. Peerj Comput. Sci. 2021, 7, e417. [Google Scholar] [CrossRef]
- Gucunski, N.; Kim, J.; Duong, T.H. Understanding depth-amplitude effects in assessment of GPR data from concrete bridge decks. NdtE Int. 2016, 83, 48–58. [Google Scholar] [CrossRef]
- Hong, S.; Mo, G.; Song, S.; Li, D.; Huang, Z.; Hou, D.; Chen, H.; Mao, X.; Lou, X.; Dong, B. Research on reinforcement corrosion detection method based on the numerical simulation of ground-penetrating radar. J. Build. Eng. 2024, 85, 108760. [Google Scholar] [CrossRef]
- Tesic, K.; Baricevic, A.; Serdar, M.; Gucunski, N. Characterization of ground penetrating radar signal during simulated corrosion of concrete reinforcement. Autom. Constr. 2022, 143, 104548. [Google Scholar] [CrossRef]
- Zhang, W.; Sun, K.; Lei, C.; Zhang, Y.; Li, H.; Spencer, B.F. Fuzzy Analytic Hierarchy Process Synthetic Evaluation Models for the Health Monitoring of Shield Tunnels. Comput.-Aided Civ. Inf. 2014, 29, 676–688. [Google Scholar] [CrossRef]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. ImageNet Classification with Deep Convolutional Neural Networks. Commun. ACM 2017, 60, 84–90. [Google Scholar] [CrossRef]
- Bao, Y.; Tang, Z.; Li, H.; Zhang, Y. Computer vision and deep learning–based data anomaly detection method for structural health monitoring. Struct. Health Monit. 2018, 18, 401–421. [Google Scholar] [CrossRef]
- Travassos, X.L.; Avila, S.L.; Ida, N. Artificial Neural Networks and Machine Learning techniques applied to Ground Penetrating Radar: A review. Appl. Comput. Inf. 2020, 17, 296–308. [Google Scholar] [CrossRef]
- Abdeljaber, O.; Avci, O.; Kiranyaz, M.S.; Boashash, B.; Sodano, H.; Inman, D.J. 1-D CNNs for structural damage detection: Verification on a structural health monitoring benchmark data. Neurocomputing 2018, 275, 1308–1317. [Google Scholar] [CrossRef]
- Xue, Y.; Li, Y. A Fast Detection Method via Region-Based Fully Convolutional Neural Networks for Shield Tunnel Lining Defects. Comput.-Aided Civ. Inf. 2018, 33, 638–654. [Google Scholar] [CrossRef]
- Zhou, Z.; Zhang, J.; Gong, C. Automatic detection method of tunnel lining multi-defects via an enhanced You Only Look Once network. Comput.-Aided Civ. Inf. 2022, 37, 762–780. [Google Scholar] [CrossRef]
- Guo, S.; Yang, T.; Gao, W.; Zhang, C. A Novel Fault Diagnosis Method for Rotating Machinery Based on a Convolutional Neural Network. Sensors 2018, 18, 1429. [Google Scholar] [CrossRef]
- Zhang, Y.; Miyamori, Y.; Mikami, S.; Saito, T. Vibration-based structural state identification by a 1-dimensional convolutional neural network. Comput.-Aided Civ. Inf. 2019, 34, 822–839. [Google Scholar] [CrossRef]
- Abdeljaber, O.; Avci, O.; Kiranyaz, S.; Gabbouj, M.; Inman, D.J. Real-time vibration-based structural damage detection using one-dimensional convolutional neural networks. J. Sound Vib. 2017, 388, 154–170. [Google Scholar] [CrossRef]
- Mao, G.; Zhang, Z.; Qiao, B.; Li, Y. Fusion Domain-Adaptation CNN Driven by Images and Vibration Signals for Fault Diagnosis of Gearbox Cross-Working Conditions. Entropy 2022, 24, 119. [Google Scholar] [CrossRef]
- Kim, N.; Kim, S.; An, Y.-K.; Lee, J.-J. A novel 3D GPR image arrangement for deep learning-based underground object classification. Int. J. Pavement. Eng. 2019, 22, 740–751. [Google Scholar] [CrossRef]
- Liu, W.; Luo, R.; Xiao, M.; Chen, Y. Intelligent detection of hidden distresses in asphalt pavement based on GPR and deep learning algorithm. Constr. Build. Mater. 2024, 416, 135089. [Google Scholar] [CrossRef]
- Zhang, J.; Yang, X.; Li, W.; Zhang, S.; Jia, Y. Automatic detection of moisture damages in asphalt pavements from GPR data with deep CNN and IRS method. Autom. Constr. 2020, 113, 103119. [Google Scholar] [CrossRef]
- Gao, J.; Yuan, D.; Tong, Z.; Yang, J.; Yu, D. Autonomous pavement distress detection using ground penetrating radar and region-based deep learning. Measurement 2020, 164, 108077. [Google Scholar] [CrossRef]
- Jazayeri, S.; Saghafi, A.; Esmaeili, S.; Tsokos, C.P. Automatic object detection using dynamic time warping on ground penetrating radar signals. Expert. Syst. Appl. 2019, 122, 102–107. [Google Scholar] [CrossRef]
- Xu, J.; Zhang, J.; Sun, W. Recognition of the Typical Distress in Concrete Pavement Based on GPR and one-dimensional. Remote Sens. 2021, 13, 2375. [Google Scholar] [CrossRef]
- Li, X.; Liu, H.; Zhou, F.; Chen, Z.; Giannakis, I.; Slob, E. Deep learning–based nondestructive evaluation of reinforcement bars using ground-penetrating radar and electromagnetic induction data. Comput.-Aided Civ. Infrastruct. Eng. 2022, 37, 1834–1853. [Google Scholar] [CrossRef]
- He, R.; Lu, N. Unveiling the dielectric property change of concrete during hardening process by ground penetrating radar with the antenna frequency of 1.6 GHz and 2.6 GHz. Cem. Concr. Comp. 2023, 144, 105279. [Google Scholar] [CrossRef]
- Zhong, Y.; Wang, Y.; Zhang, B. Research on correlation between dielectric properties and compressive strength of concrete based on aggregate particle size. J. Build. Eng. 2024, 97, 110844. [Google Scholar] [CrossRef]
- Lachowicz, J.; Rucka, M. A novel heterogeneous model of concrete for numerical modelling of ground penetrating radar. Constr. Build. Mater. 2019, 227, 116703. [Google Scholar] [CrossRef]
- Warren, C.; Giannopoulos, A.; Giannakis, I. gprMax: Open source software to simulate electromagnetic wave propagation for Ground Penetrating Radar. Comput. Phys. Commun. 2016, 209, 163–170. [Google Scholar] [CrossRef]
- Warren, C.; Giannopoulos, A.; Gray, A.; Giannakis, I.; Patterson, A.; Wetter, L.; Hamrah, A. A CUDA-based GPU engine for gprMax: Open source FDTD electromagnetic simulation software. Comput. Phys. Commun. 2019, 237, 208–218. [Google Scholar] [CrossRef]
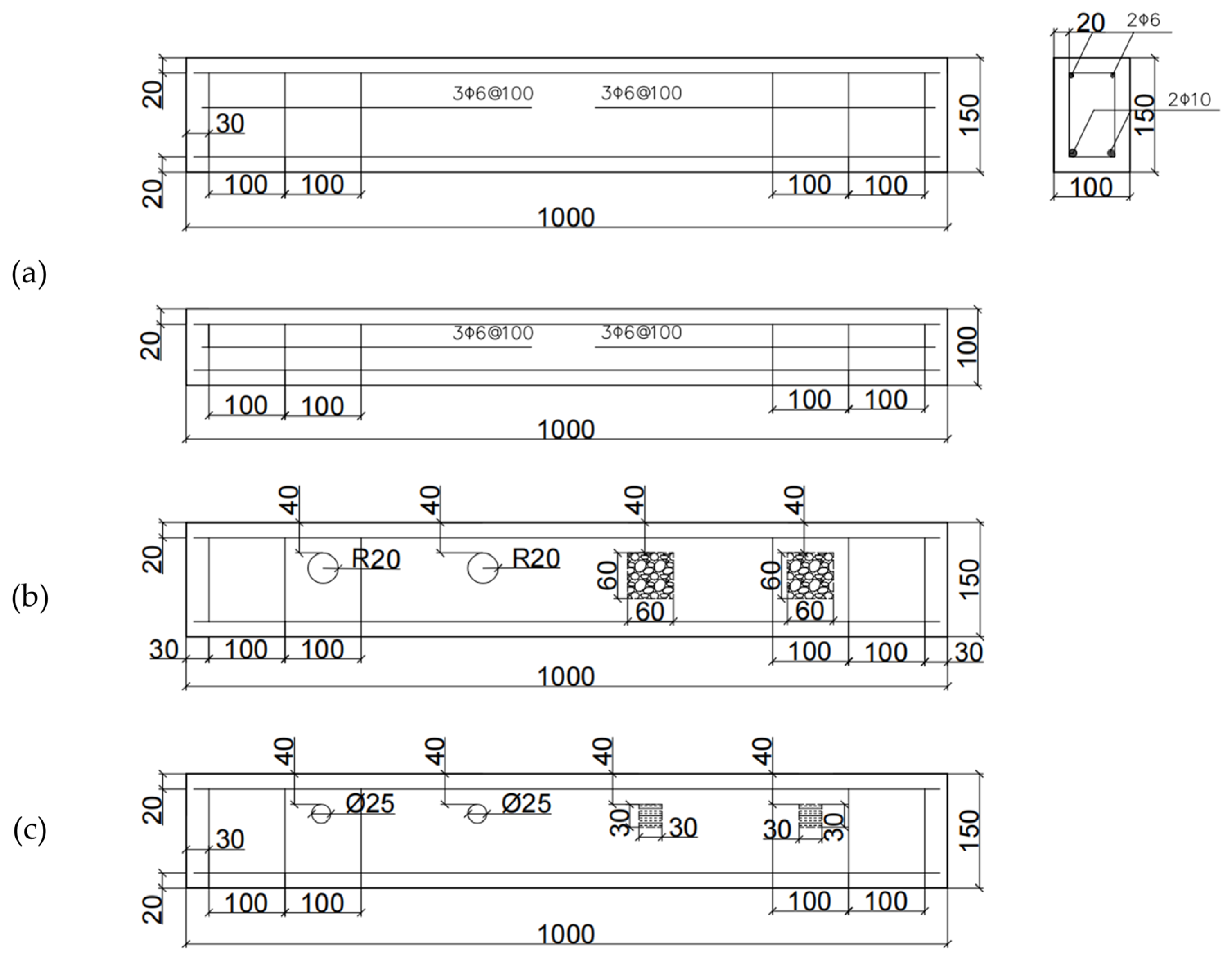
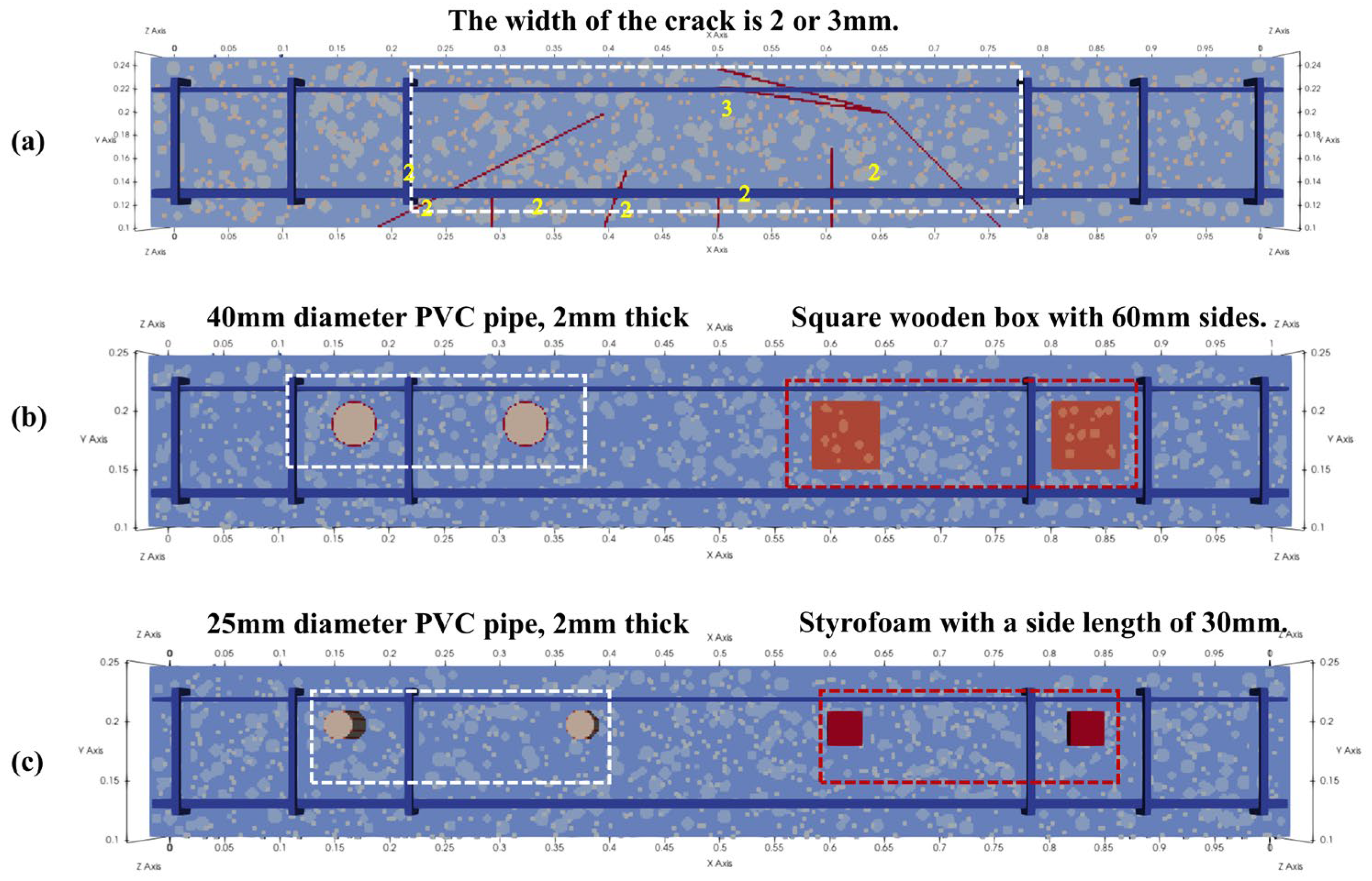





| Information | Number | Defective Layout | Measurement Method | Strength & Dimensions |
|---|---|---|---|---|
| (a) | H_B0 | - | scan after loading | Strength: C30 Dimensions: 1000 × 150 × 100 mm |
| (b) | H_BF1 | PVC, Wooden box | Direct scan | |
| (c) | H_BF2 | PVC, Styrofoam | Direct scan |
| Materials | Dielectric Constant | Electric Conductivity | Relative Permeability | Magnetic Loss | Volume Proportion | Particle Size (mm) |
|---|---|---|---|---|---|---|
| Coarse aggregate | 7.0 | 0 | 1.0 | 0 | 55% | 6–20 |
| Fine aggregate | 6.0 | 0 | 1.0 | 0 | 20% | 2–5 |
| Cement | 6.5 | 0 | 1.0 | 0 | 20% | - |
| Air | 1.0 | 0 | 1.0 | 0 | 5% | 2 |
| Defective Material | Dielectric Constant | Size |
|---|---|---|
| PVC | 4 | Diameter size: 40 mm, 25 mm |
| Wooden box | 2.5 | Length: 60 mm |
| Crushed stone | 7 | - |
| Styrofoam | 3 | Length: 30 mm |
| Parameters | Specified Value |
|---|---|
| domain | 1.000 0.150 0.100 |
| dx_dy_dz | 0.002 |
| time_window | 5 × 10−9 |
| waveform | Ricker, 1.6 GHz |
| hertzian_dipole | 0.056 0.250 0.050 |
| rx | 0.114 0.250 0.050 |
| steps | 0.004 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, N.; Ge, Y.; Bai, X.; Zhang, Z.; Shangguan, Y.; Li, Y. Research on Damage Detection Methods for Concrete Beams Based on Ground Penetrating Radar and Convolutional Neural Networks. Appl. Sci. 2025, 15, 1882. https://doi.org/10.3390/app15041882
Liu N, Ge Y, Bai X, Zhang Z, Shangguan Y, Li Y. Research on Damage Detection Methods for Concrete Beams Based on Ground Penetrating Radar and Convolutional Neural Networks. Applied Sciences. 2025; 15(4):1882. https://doi.org/10.3390/app15041882
Chicago/Turabian StyleLiu, Ning, Ya Ge, Xin Bai, Zi Zhang, Yuhao Shangguan, and Yan Li. 2025. "Research on Damage Detection Methods for Concrete Beams Based on Ground Penetrating Radar and Convolutional Neural Networks" Applied Sciences 15, no. 4: 1882. https://doi.org/10.3390/app15041882
APA StyleLiu, N., Ge, Y., Bai, X., Zhang, Z., Shangguan, Y., & Li, Y. (2025). Research on Damage Detection Methods for Concrete Beams Based on Ground Penetrating Radar and Convolutional Neural Networks. Applied Sciences, 15(4), 1882. https://doi.org/10.3390/app15041882






