Investigation of the Layered Effect on the Tensile Fracture Characteristics of Sandstone Using Intact and Pre-Cracked Brazilian Disk Specimens

Abstract

To investigate the stratification effect on rock splitting and Mode I fracture characteristics, standard Brazilian splitting disk specimens and straight-crack disk specimens were subjected to splitting loading tests, and a high-speed camera system and acoustic emission (AE) system were used to study the rocks’ mechanical properties, fracture parameters, and AE characteristics. The results demonstrate the following: (1) The tensile strength and fracture toughness of the layered rock exhibit significant stratification effects, gradually decreasing with the increase in the number of layers and the layer angle. (2) The different angles of the stratification planes lead to the diversity of failure modes in the disk specimens. (3) The S-value and the cumulative AE count curve of specimens without prefabricated cracks show two types of pattern during loading: fluctuating increase mode, and “gentle–steep” increase mode. (4) Layered rock specimens exhibit a low ratio of rise time to voltage amplitude (RA) value and high average frequency (AF) characteristics during fracture, and the shear failure mainly occurs during the stable propagation phase after the initiation of macroscopic cracks. (5) The fracture process zone (FPZ)’s length at the peak point of the specimens decreases exponentially with the increase in the number of layers, but this reduction does not go on indefinitely, and there exists a minimum value. Within the range of 0° to 60°, the FPZ length decreases linearly with increasing stratification angle.

1. Introduction

In many engineering fields, the safety and stability of rock engineering are significantly influenced by layered jointed rock masses. The tensile failure characteristics of layered rock masses play a decisive role in the success of engineering projects. Currently, more than two-thirds of the Earth’s land surface is covered by rocks with layered structures, and in China, this proportion exceeds 77%. These rocks are characterized by numerous weak structural planes, such as stratification, foliation, and fractures [1,2,3], which impart varying degrees of anisotropy to their mechanical properties and significantly affect their overall mechanical behavior and failure modes.

Currently, the study of the splitting characteristics of layered rocks primarily employs the Brazilian splitting test method [4,5,6,7]. For example, Khanlari et al. [8] measured the tensile strength of shales from different regions using splitting tests, concluding that the tensile strength of rocks might follow a linear relationship with the stratification angle. Tavallali [9,10] and Khanlari [11] observed that, at different inclinations, the tensile strength of layered sandstone decreases non-linearly with an increasing stratification angle. Basu [12] and Jie [13] summarized Brazilian splitting test results for various typical layered rocks, finding a non-linear decrease in tensile strength with increasing stratification angle, and developed corresponding failure mode diagrams. Many studies [14,15,16] have conducted tensile tests on shale, slate, gneiss, and chlorite schist, discovering that the tensile strength of layered rocks initially increases and then decreases with increasing stratification dip angle, and that the deformation characteristics of layered rocks also exhibit complex changes with varying stratification dip angles. This complexity is mainly due to differences in the forces experienced by the stratification planes at different stratification dip angles. Tan et al. [17] carried out a multi-angle loading of layered gneiss specimens and found that, when the loading direction is parallel to the stratification plane (90°), the failure mode is primarily tensile failure between weak layers and within the mineral matrix. When the stratification dip angle is less than 90°, due to the anisotropy and heterogeneity of the gneiss, the failure mode becomes a complex tensile–shear composite failure. Zhang et al. [18] combined Brazilian tests and AE technology to investigate the mechanical properties and fracture modes of shale under different loading directions. The changes in AE counts revealed the fracture response of shale at different stratification angles, particularly at low stratification angles, where internal fissures and pores were not significantly compacted, resulting in the accumulation of less AE activity. These above studies, through tensile tests on layered rocks, have deeply explored the impact of stratification direction on the tensile strength and failure modes of layered rock masses.

In addition to splitting characteristics, the fracture characteristics of rocks allow for a more in-depth study of the formation and propagation of internal cracks. In engineering practice, tensile (Mode I) failure is the predominant fracture mode in rocks. Currently, beyond the four recommended methods and specimen configurations proposed by the ISRM for measuring Mode I fracture toughness [19,20,21], the centrally cracked Brazilian disk (CSTBD) specimen [22] has garnered substantial attention due to its straightforward configuration and ease of preparation. For example, Xie et al. [23] conducted fracture tests on CSTBD specimens at different loading rates. Mishaan Lilienthal et al. [24] and Yang et al. [25] analyzed the relationship between rock fracture toughness and specimen size and crack size. Lee et al. [26] investigated the effect of stratification angles on the Mode I fracture toughness of shale. Chen et al. [27] and Ke et al. [28] investigated the composite fracture properties of layered granite using HCCD and CSTBD specimens, finding that the stratification angle significantly affects the fracture behavior of layered granite. Liu et al. [29] focused on the microscopic characteristics of Mode I cracks in shale and constructed a computational framework to assess the Mode I fracture toughness of shale. Zhang et al. [30] examined the tensile fracture characteristics and crack propagation behavior of weakly layered carbonaceous slate from the Muzhailing Tunnel, demonstrating that the slate exhibits notable anisotropy in its mechanical properties and complex crack propagation patterns contingent upon different stratification angles.

Current research on the anisotropy of layered rocks predominantly focuses on variations in stratification angles and typically considers only a single joint plane. However, in practical engineering applications, such as slopes or underground chambers, layered rocks often exhibit multiple joint planes. In these scenarios, both the anisotropy of the rock and the number of stratification planes become critical factors influencing deformation and failure processes. This study addresses this gap by using dolomitic glue to simulate weak stratification planes and preparing layered rock specimens for Brazilian splitting tests. By integrating high-speed imaging and acoustic emission (AE) techniques, this research analyzes and explores the effects of the stratification angle and the number of stratification planes on the tensile failure characteristics and strength properties of layered rocks. Additionally, this study examines the impact of stratification on Mode I fracture behavior in rocks, thereby providing theoretical support for engineering applications involving layered rock masses.

2. Materials and Methods

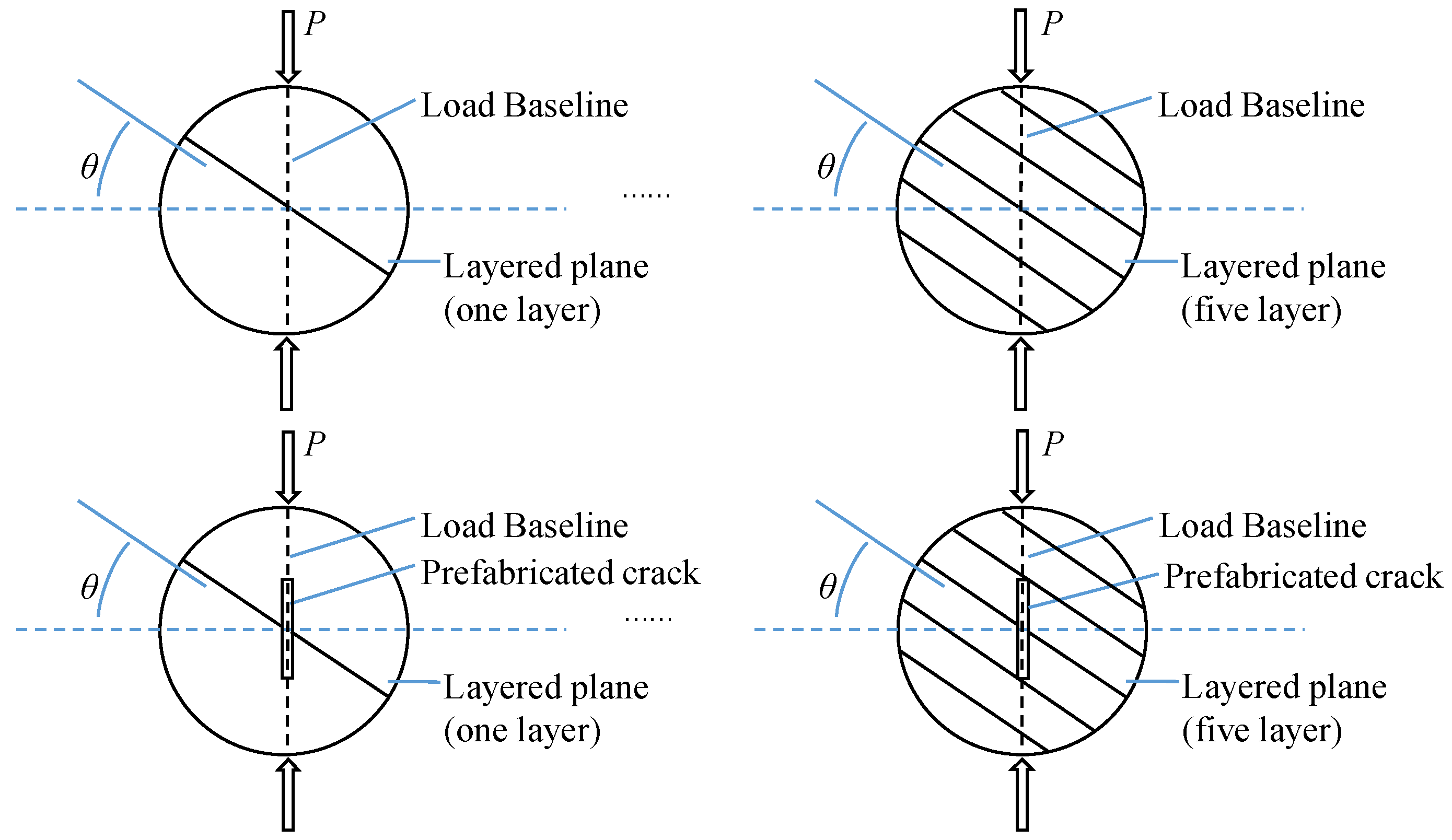
2.1. Specimen Preparation

To determine the mechanical properties of the uniformly green sandstone bedrock, uniaxial compression and Brazilian splitting tests were conducted on cylindrical specimens with a diameter of 50 mm and height-to-diameter ratios of 2 and 0.5, respectively. The results indicated a compressive strength of 72.31 MPa, tensile strength of 5.83 MPa, elastic modulus of 19.3 GPa, and Poisson’s ratio of 0.15. Currently, dolomitic glue is commonly utilized for fabricating layered composite rocks [25,31]. Experimental results demonstrate that, under standard curing conditions, the vertical tensile bond strength of dolomitic glue can reach 2.1 MPa after 48 h, which is lower than the tensile strength of green sandstone. Given this characteristic, dolomitic glue serves effectively as an adhesive for bonding sandstone, thereby simulating the bonding properties of natural layered rocks.

The specimens were drilled from larger blocks of this uniformly green sandstone using a diamond core drill to ensure uniformity and precision in sample preparation. The drilling process was carried out under controlled conditions to maintain the integrity of the rock and avoid introducing any fractures or defects. In the preliminary stage of the experiment, a rock-cutting machine and a rock-grinding machine were used to cut and polish the sandstone into thin, cuboid slices of specific thickness. According to the experimental design, rock slices of different sizes and quantities were prepared, with the specific parameters listed in

Table 1. Size and number of rock cube flakes.

Rock Type	Specimen Size/mm	Quantities
Green sandstone	250 × 240 × 30	20
	250 × 240 × 18	2
	250 × 240 × 12.5	4
	250 × 240 × 10	6
	250 × 240 × 8.5	8

. Subsequently, the glue and curing agent were mixed evenly at a certain ratio, and the mixed adhesive was uniformly applied to the surfaces of the stone to be bonded. By gently pressing, we ensured that the glue was fully distributed and tightly adhered, maintaining appropriate pressure until the glue began to cure. After the rock specimens were prepared and underwent 48 h of standard curing, they were cored, cut, and polished into standard Brazilian disk specimens with a diameter of 50 mm and a thickness of 25 mm [32]. The specimen preparation process was as shown in Figure 1. To study the stratification effects of rock fracture characteristics, a 0.4 mm wide initial crack was cut in the center of the Brazilian disk specimens using a diamond wire under water-cooled conditions to prevent the formation of additional cracks during the process. The crack length was uniformly set at 20 mm.

2.2. Testing Procedure for Intact and Pre-Cracked Brazilian Disk Specimens

The experimental setup and loading schematic are shown in Figure 2. The tensile tests on the layered rock were performed using the WHY-300/10 microcomputer-controlled loading system (Shanghai Hualong Testing Instrument Co., Ltd., Shanghai, China). This apparatus features a dual-channel, dual-sensor configuration, with a test force capacity of 300 kN in the primary channel and 10 kN in the secondary channel, maintaining a relative error within 1%. To comprehensively capture the entire process of crack initiation and propagation, the loading rate for the specimens was set at a low rate of 0.12 mm/min. The PCI-2 AE monitoring system produced by the PAC company was used to collect AE signals during the rock fracture process (Physical Acoustics Corporation, Princeton, NJ, USA). Two MINI-30 AE sensors (each with a diameter and height of 9 mm) were symmetrically fixed on both sides of the loading direction (Physical Acoustics Corporation, Princeton, NJ, USA). These sensors have a detection frequency range of 125~750 kHz and a resonant frequency of 300 (±10%) kHz, which can better collect the AE signals of granite’s fracture process. The pre-amplifier gain and threshold value of the AE system were set to 40 dB, with a sampling rate of 10 Msps and a sampling length of 5 kb. The waveform definition parameters for PDT, HDT, and HLT were set to 50 µs, 200 µs, and 300 µs, respectively [33]. During the experiment, the sensors were attached to both sides of the specimen in the loading direction. To ensure good contact between the sensors and the loading boards, petroleum jelly was applied to the contact areas. Additionally, to obtain the displacement and strain fields around the initial crack tip region, a high-definition camera was used to capture scatter images of the rock specimens’ surface, with an image resolution of 4090 × 3000 and a sampling rate of 6 Hz.

To study the stratification effects in layered rocks during the Brazilian splitting test, the tests were conducted at different stratification loading angles of 0°, 30°, 45°, 60°, and 90°, with the number of layers being 1, 2, 3, 4, and 5. The loading schematic is shown in Figure 3. Three replicates were selected for each group of specimens, and the sandstone specimens were set as the control group. Each specimen without prefabricated cracks was named “stratification number-loading angle-1/2/3”, and each specimen with prefabricated cracks was named “Y stratification number-loading angle-1/2/3”. For the 90° inclination angle, the loading of layered disk specimens without prefabricated cracks was conducted in two forms: through the stratification plane, and not through the stratification plane, so only one-layer and four-layer specimens were selected as typical specimens for the 90° inclination angle.

3. Results and Discussion

3.1. The Stratification Effects of Rock’s Splitting Characteristics

3.1.1. Tensile Strength and Failure Mode Analysis

The tensile strength of the specimen can be expressed as follows:

$${\mathsf{\sigma }}_{\mathrm{t}}={\displaystyle \frac{2P_{\max }}{\pi DB}}$$

(1)

where σ_t represents the tensile strength of the rock, B represents the specimen length(thickness), D represents the diameter, and P_max represents the failure load.

The experimental results, as shown in Figure 4, indicate that the number of stratification planes and the stratification angle significantly affect the tensile strength of the rock. Specifically, the tensile strength of layered rocks decreases with an increasing number of stratification planes. This is mainly because the weaker the stratification planes, the higher the probability of failure along these planes, leading to a gradual decrease in tensile strength. As the stratification angle increases, the failure mode of the rock transitions from internal matrix fracture to shear splitting along the stratification planes. The shear failure along the stratification planes mainly relies on the bonding strength of the dolomitic glue in the rock, which is relatively low. Therefore, with an increasing stratification angle, failure along the stratification planes becomes easier, resulting in a reduction in overall tensile strength.

Table 2. Failure patterns of rock specimens with different stratification numbers and stratification angles.

Angle Type	0°	30°	45°	60°	90°
One stratification
Two stratifications
Three stratifications
Four stratifications
Five stratifications

shows the final failure modes of the layered rock specimens. It can be seen that the number of stratification planes has a relatively minor impact on the failure mode of the disks. The diversity in failure modes is mainly caused by the different angles of the stratification planes. The interactions between particles within the rock and the bonding strength between layers vary with the angle of the stratification planes relative to the loading direction, resulting in different failure behaviors.

Based on the stress state, deformation characteristics, and crack morphology, the failure modes of layered rock can be categorized into four types: stratification tensile, stratification tensile–shear, matrix tensile, and matrix tensile–shear.

a. Stratification Tensile Type (θ = 90°):

When θ = 90°, the specimen typically splits along the central stratification plane into two halves. The opening of the stratification plane provides space for lateral deformation, resulting in the lowest tensile strength.

b. Stratification Tensile–Shear Type (θ = 45°, 60°):

When θ is 45°or 60°, the failure mode of the rock changes. The rock does not fully crack along the stratification plane, nor does it form continuous cracks through the upper and lower loading points. Instead, it splits by a crack at a certain angle to the stratification plane, but the angle of this crack is not fixed, with noticeable peeling of the stratification plane within the crack. The tensile strength slowly decreases as θ increases within this range.

c. Matrix Tensile Type (θ = 0°):

When θ = 0°, the rock first experiences local crushing near the loading point. Subsequently, cracks extend down to a specific stratification plane, where the shear stress exceeds the cohesion between layers, causing local failure. Due to the large area of the stratification planes intersected by the crack tip, the cohesion between layers exceeds the shear stress, causing the crack to propagate along the stratification planes layer by layer through the sandstone matrix until complete penetration.

d. Matrix Tensile–Shear Type (θ = 30°):

At θ = 30°, the loading direction is approximately perpendicular to the stratification direction. During loading, the ends of the specimen undergo local crushing, and a crack perpendicular to the stratification direction forms at the center of the specimen. This crack extends along the stratification direction, eventually causing the specimen to fail. This failure mode is classified as matrix tensile–shear failure.

Based on the previous discussion, when θ is 0°, loading causes the rock to split layer by layer, while at θ between 45° and 90°, the rock splits along the stratification plane. This indicates that when θ is between 30° and 45°, layered rocks undergo a transition from matrix tensile–shear failure to stratification tensile–shear failure. During this transition, the loading force breaks down into smaller shear stresses in the direction of the stratification plane and larger positive stresses in the direction normal to the stratification plane. This makes it harder for the crack to propagate along the stratification plane, causing it to develop from the tips of pre-existing microcracks toward the direction of maximum compressive stress. As the crack continues to extend along the direction of maximum compressive stress and the stratification plane, the rock is eventually fractured.

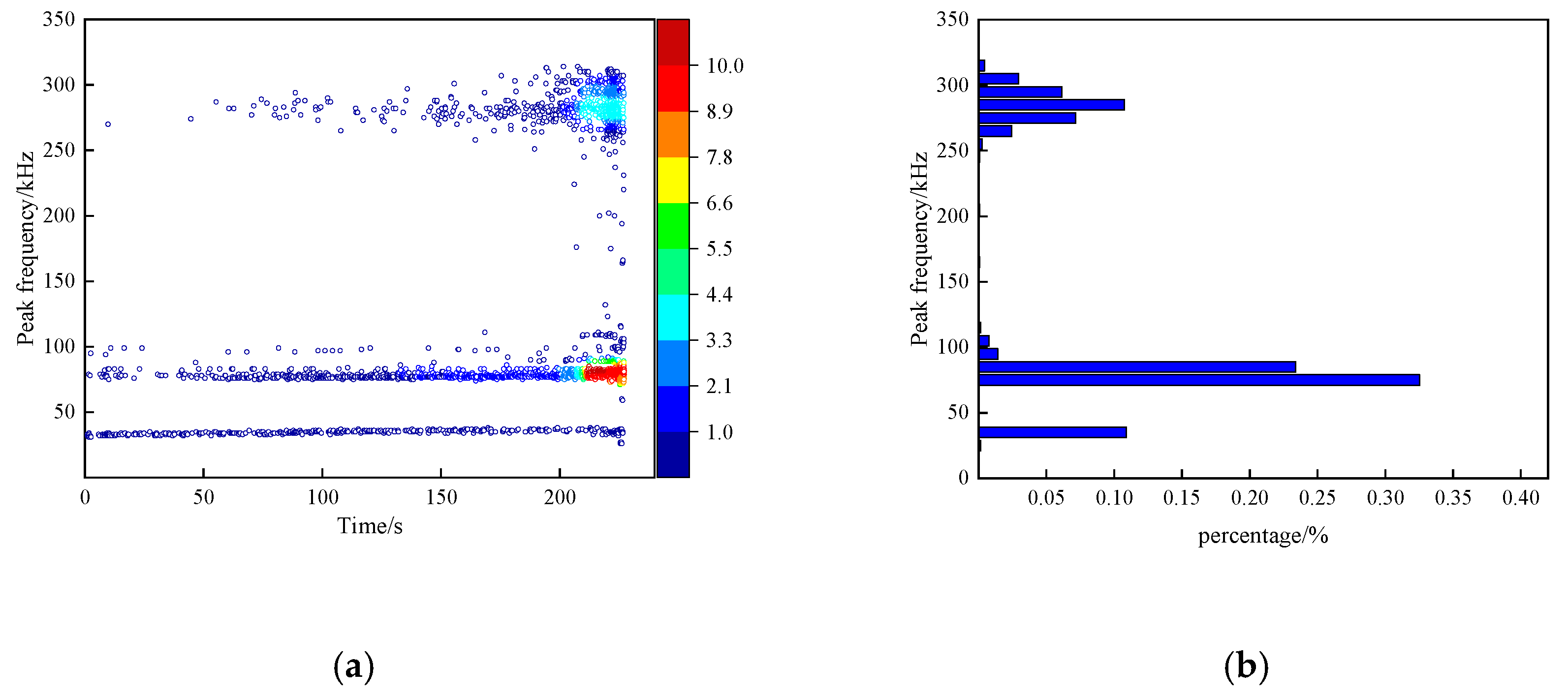
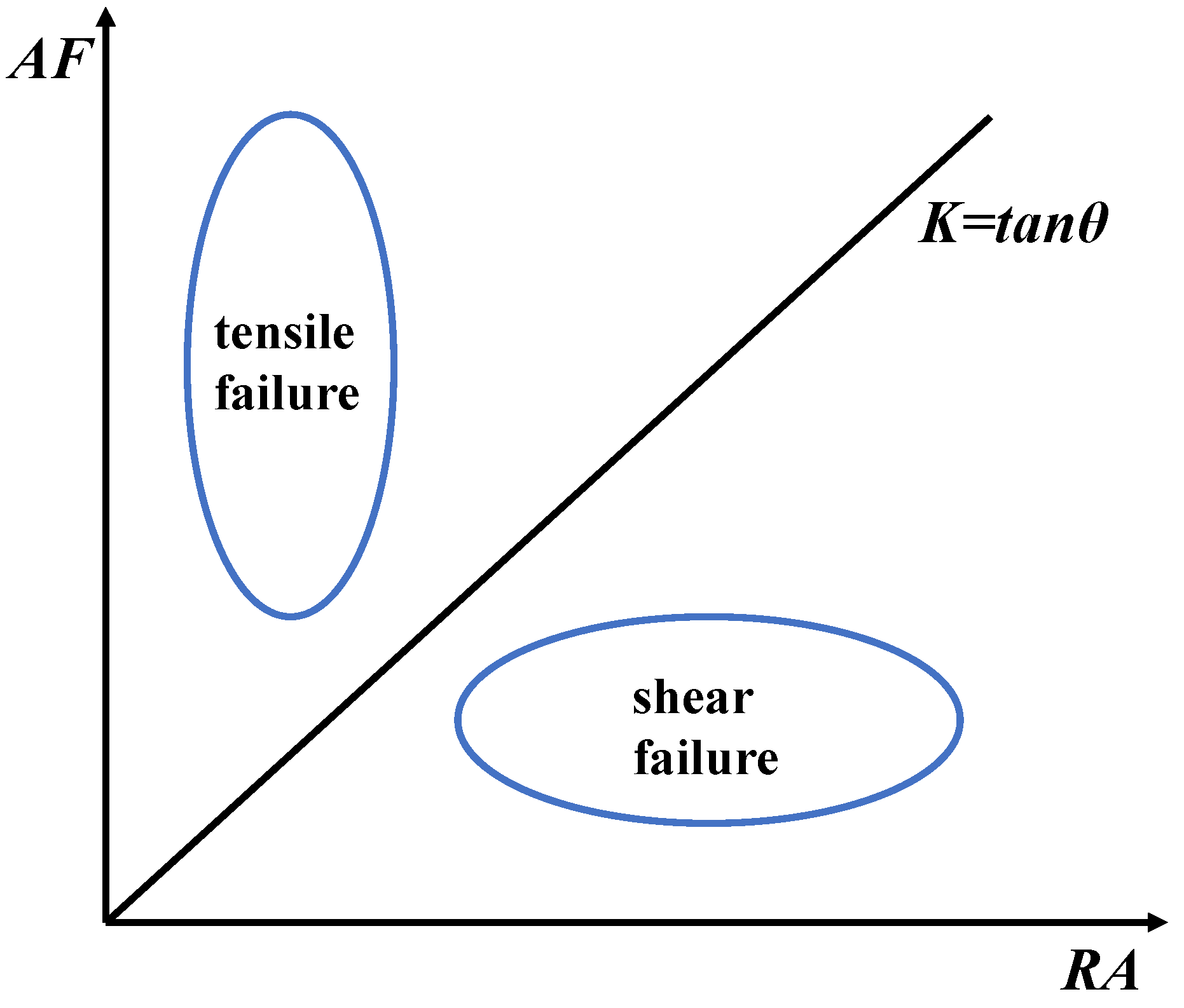
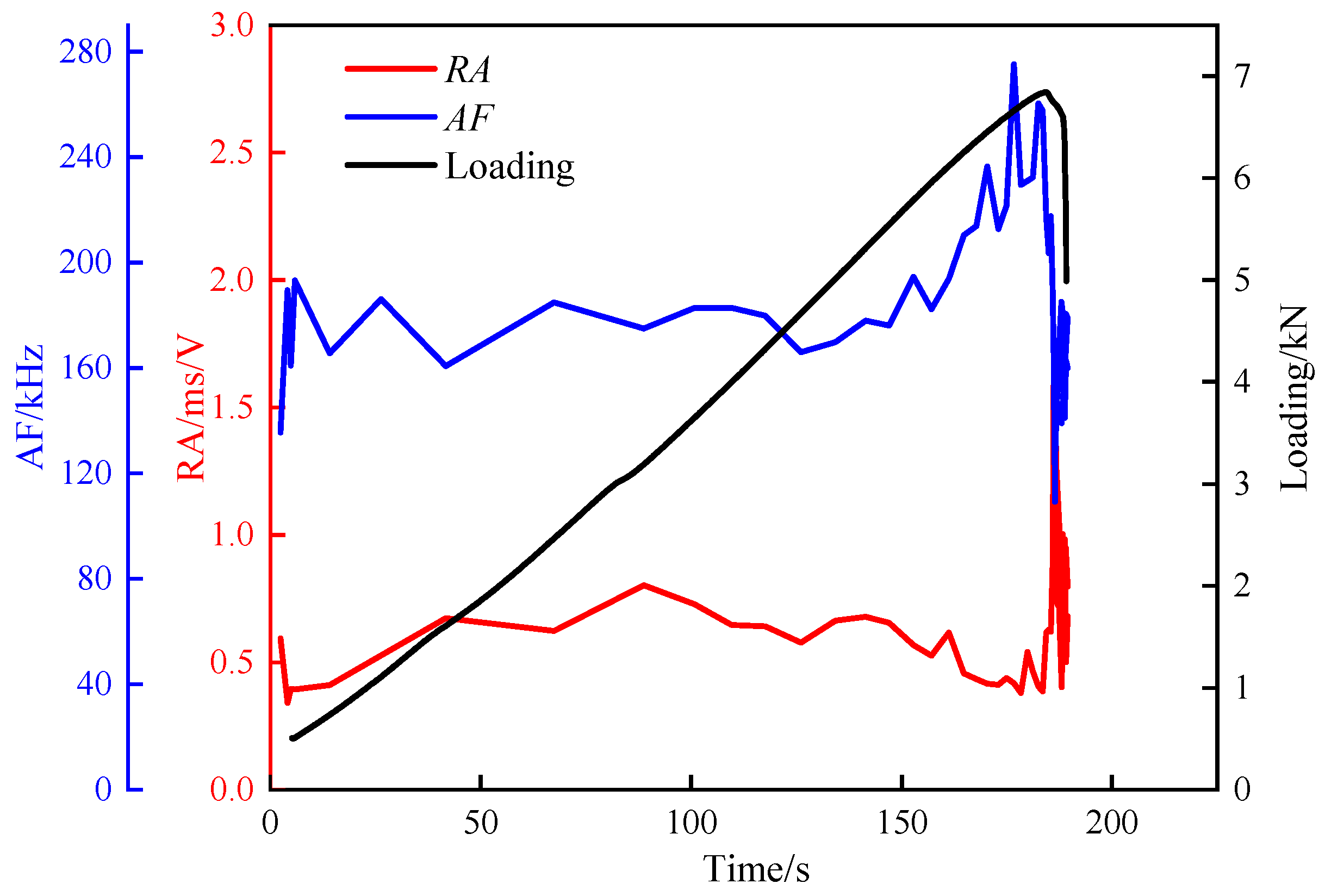
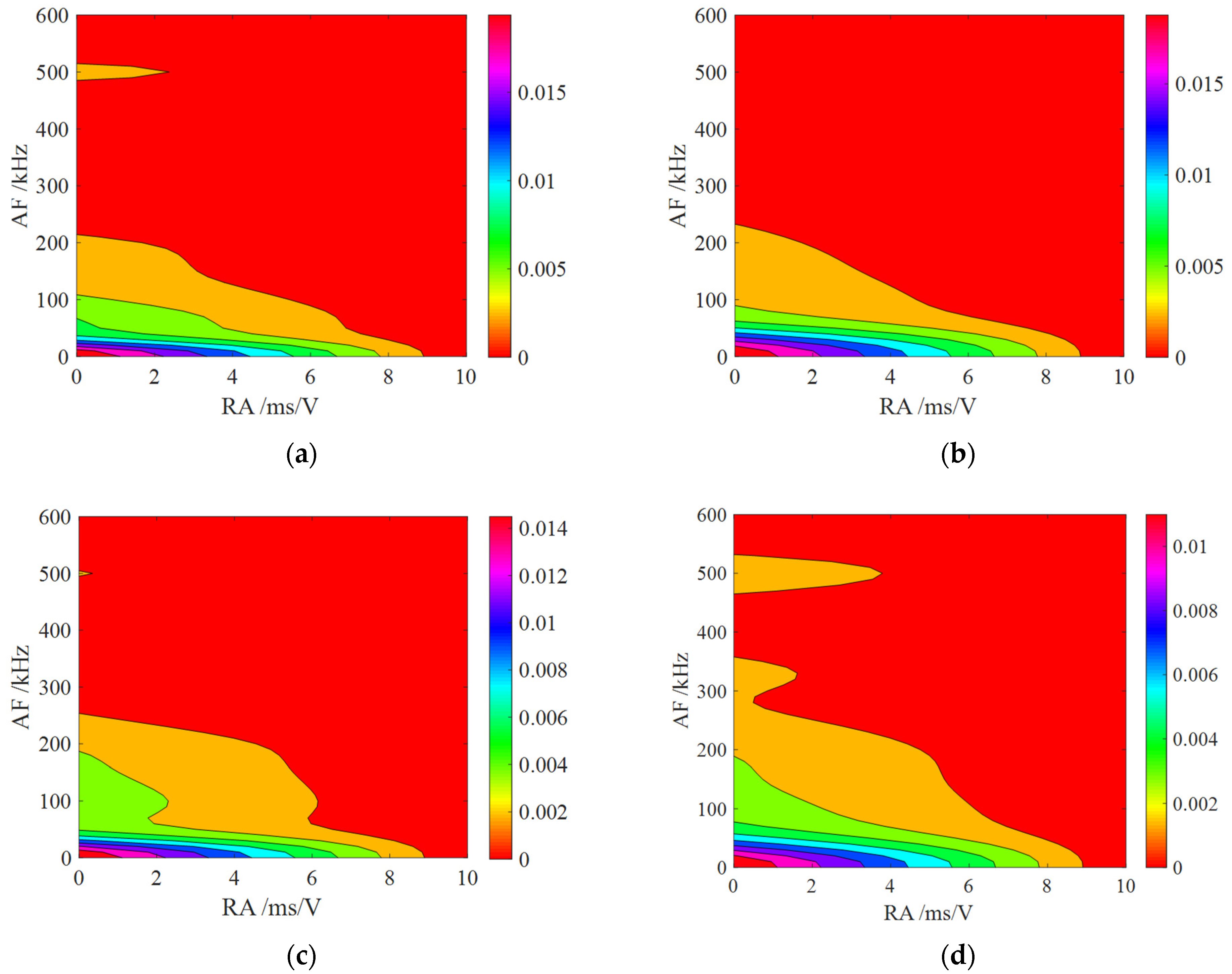
3.1.2. Contribution of AE Characteristic Parameters

The frequency characteristics of acoustic emission (AE) signals are crucial parameters for describing the rock rupture process. These characteristics are directly correlated with the fracture mechanisms of the seismic source. Ruptures of varying scales produce different peak frequencies: large-scale fractures generate signals with prominent low-frequency components, whereas small-scale fractures yield signals with dominant high-frequency components [34,35,36]. Additionally, the peak frequency is associated with the speed of crack propagation: a higher propagation speed results in a higher peak frequency, while a slower propagation speed results in a lower peak frequency. Consequently, peak frequency characteristics provide insights into the dynamic properties and mechanisms of crack propagation [29].

Figure 5 illustrates the temporal variation and distribution of AE peak frequency signals. For specimen 1-0-2, the peak frequency signals exhibit a distinct strip-like pattern, with a low-frequency concentration at 75–95 kHz and a high-frequency band at 260–310 kHz. Low-frequency signals predominate over high-frequency signals. High-frequency signals predominantly emerge during the later stages of loading. During the pre-loading phase, stress accumulates, crack propagation is slower, and energy release is more dispersed, resulting in a predominance of low-frequency signals. High-frequency signals, on the other hand, become more apparent in the later stages, when cracks rapidly propagate and extend.

Based on the peak frequency distribution, high-frequency signals are significantly lower than low-frequency signals across the five different numbers of stratification layers. To further analyze the relationship between the stratification number and the proportion of high-frequency signals, the average proportion of high-frequency signals was calculated for 0–5 stratification layers at a stratification angle of 0°, as shown in Figure 6. The proportion of high-frequency signals decreases exponentially with an increase in the number of stratification layers. This is mainly because of the high density and uniformity of intact sandstone, which facilitate small-scale fractures, resulting in a higher proportion of high-frequency signals. As the number of weak stratification planes increases, the number of large pores in the specimen also increases, leading to a higher probability of large-scale cracks. Additionally, under vertical loading, the crack propagation process is hindered by the stratification planes, and the high-frequency signals decrease, resulting in an increased proportion of low-frequency signals and decreasing the proportion of high-frequency signals.

The variation in the proportion of high-frequency AE signals with the stratification angle is shown in Figure 7. As the stratification angle increases, the proportion of high-frequency AE signals initially rises and subsequently declines. Specifically, the proportion of high-frequency AE signals increases for stratification angles of 30°, 45°, and 60°, with the average proportions reaching 34.52%, 38.165%, and 42.97%, respectively. When the angle between the loading direction and the bedding direction is small, crack propagation primarily follows the bedding direction. The rock exhibits strong structural coherence, limiting the initiation and expansion of cracks, resulting in lower-frequency acoustic emission (AE) signals. During this process, the deformation of the rock material is mainly dominated by shear and slow crack propagation, with fewer high-frequency components generated. As the angle increases to a certain range, the loading direction is no longer fully aligned with the bedding direction, causing greater resistance to crack propagation between the bedding planes, which induces new microcracks. Under these conditions, the interactions between cracks become more complex, and the crack propagation speed increases, producing a higher proportion of high-frequency AE signals, thus increasing the proportion of high-frequency signals. The frequency distribution characteristics of the AE signals further validate the crack propagation features of bedded rock samples under different loading angles, as well as the variations in tensile strength, as described in Section 3.1.1.

As previously discussed, the failure mode is significantly correlated with the stratification angle. However, there is no consensus regarding the relationship between the dominant frequency characteristics of AE signals and rock failure modes. Deng et al. [37] investigated the frequency characteristics of AE signals under three loading conditions: direct tension, Brazilian splitting, and uniaxial compression, finding that low-frequency AE signals originate from tensile fractures, while high-frequency signals stem from shear fractures. Bucheim [38] and Yuan [39] concluded from their AE tests that tensile rupture in rock specimens generates higher-frequency AE signals, whereas shear fractures produce lower-frequency signals. To more accurately analyze the failure mechanisms of seismic sources, we generally examine two key AE parameters: the AF and RA. As shown in Figure 8, high AF values and low RA values are typically associated with tensile failure, while low AF values and high RA values correspond to shear failure. By observing the changes in the RA and AF values of the AE signals over time during the fracture process of this specimen, the characteristics of microcrack evolution during shear and tensile failure at different load levels are revealed.

As shown in Figure 9, during the early elastic failure stage, both RA and AF values remain relatively stable, indicating that shear and tensile failures within the rock are relatively stable at this stage. Around 157 s, when the load level of the specimen approaches 90% of the maximum load (Pmax), the RA and AF values begin to change. Specifically, the RA value gradually decreases with fluctuations, while the AF value shows an upward trend. This indicates that, during the initiation and propagation of new cracks, a significant number of tensile cracks start to form. After the specimen reaches the peak load, the RA value rapidly increases, while the AF value quickly decreases. This phenomenon reflects that, during the fracture process, the coalescence of microcracks forms macrocracks. The uneven stress at the crack tip causes the macrocrack to change direction and propagate along the weak planes, resulting in the formation of a substantial number of shear cracks. Consequently, in the macroscopic failure stage, shear failures become more prevalent.

When the number of acoustic emission (AE) signals is large, it becomes challenging to effectively observe the data distribution. In recent years, kernel density estimation (KDE), a non-parametric estimation method, has frequently been employed for data density estimation research. The KDE algorithm can be utilized to identify the concentration regions of RA and AF values during the fracture process. Furthermore, the primary advantage of the KDE method lies in its enhanced capacity for data point visualization. The estimated value of the multivariate data density P(z) is calculated using the following formula [40]:

$$P(\mathrm{z})={\displaystyle \frac{1}{nh}}{\displaystyle \sum _{i=1}^{n}K(\frac{z-z_i}{h})}$$

(2)

Prior to performing the KDE calculation, the original AE data for different stratification numbers and angles were screened to exclude data points where both the RA and AF values were zero, as these points do not provide useful information for analyzing fracture modes. Through the kernel density cloud shown in Figure 10, it was observed that the most densely distributed RA-AF values were concentrated along the vertical axis. This indicates that most AE events exhibit low RA values and high AF characteristics, suggesting that tensile failure predominates over shear failure during the fracture process. This distribution characteristic was found to have little relationship with the number of stratification layers and was more influenced by the stratification angle.

Figure 10 presents the kernel density cloud plots for specimens with two stratification numbers as a function of the angle. The plots indicate that, as the stratification angle increases from 0°to 60°, the densest data region shifts downward along the vertical axis. This suggests that, with an increasing stratification angle, there is a higher occurrence of AE events characterized by high RA values and low AF values during the rock fracture process. Consequently, the fracture mode of layered rock transitions from tensile failure to shear failure as the stratification angle increases. This observation aligns with the changes in the fracture modes of layered rock discussed in Section 3.1.1 (Tensile Strength and Failure Mode Analysis).

3.2. The Stratification Effects of Mode I Fracture Characteristics

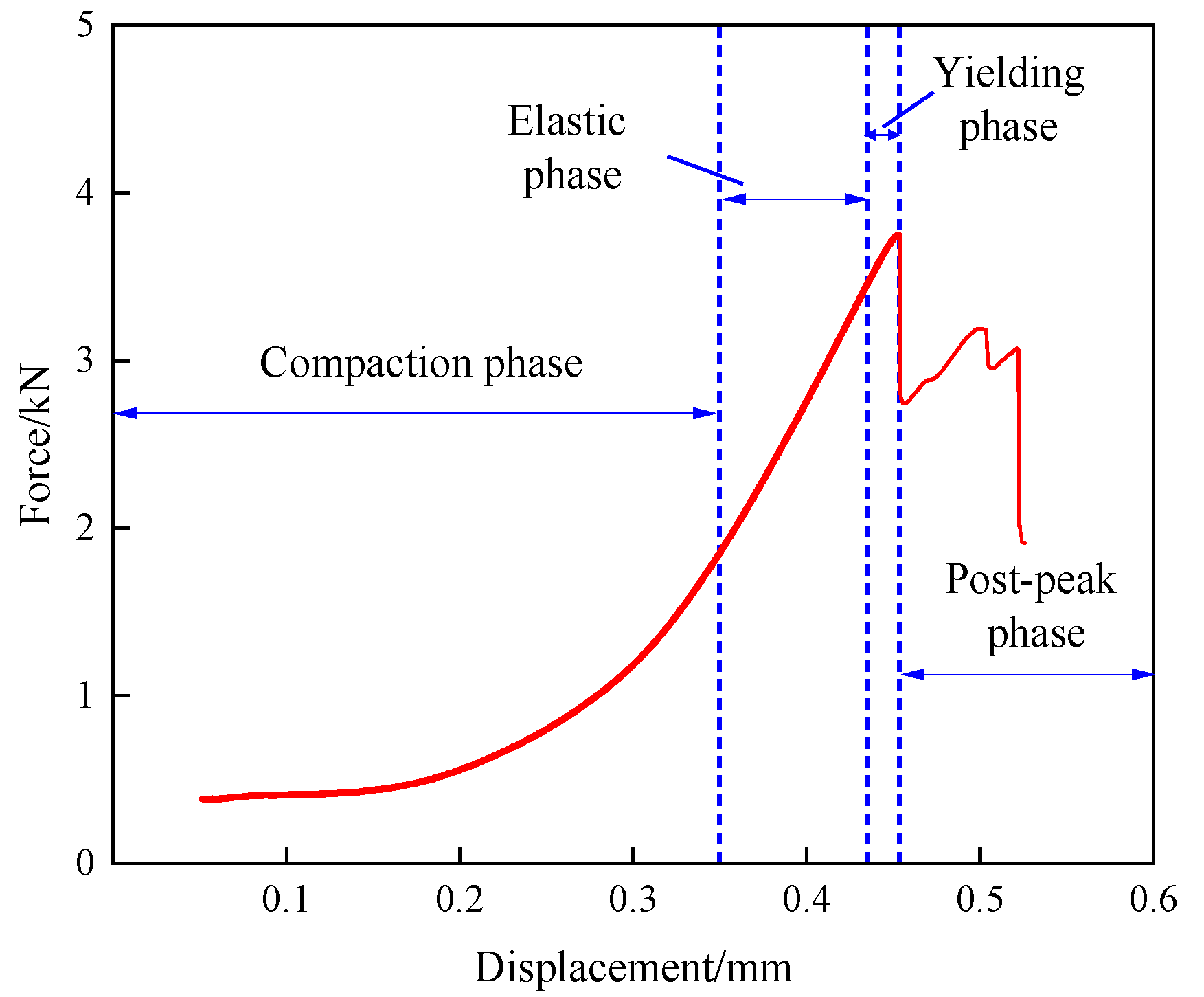
3.2.1. Load–Displacement Curves

By analyzing the load–displacement curves of CSTBD rock specimens, it is evident that the failure process of layered rock specimens generally involves four main stages: compaction, elastic, plastic yielding, and post-peak decline. Taking specimen Y1-45-3 as a representative example, as illustrated in Figure 11, during the initial stage of loading, pre-existing cracks in the specimen close under compression, resulting in an upward concave shape in the load–displacement curve and an increase in specimen density. This phase is referred to as the compaction stage. As the applied load increases, the specimen transitions into the elastic stage, characterized by a roughly linear relationship in the load–displacement curve due to lattice interactions. Prior to reaching peak stress, the specimen experiences a brief period of plastic yielding, during which the curve’s slope slightly decreases, the volumetric strain increases, and the rate of stress increment diminishes, indicating dilation and softening phenomena. This phase is marked by instability. Following peak stress, the specimen undergoes significant impact and instability, resulting in a rapid increase in strain.

3.2.2. Fracture Modes

Table 3. Fracture patterns of CSTBD specimens with different stratification numbers and stratification angles.

Angle Type	0°	30°	45°	60°	90°
One stratification
Two stratifications
Three stratifications
Four stratifications
Five stratifications

presents the failure patterns of CSTBD specimens subjected to varying numbers of stratification layers and stratification angles. As indicated in Table 3, the presence of a central straight crack, in contrast to specimens without pre-existing cracks, results in stress concentration at the crack tip. This reduces the local stress concentration along the stratification planes, thereby decreasing the likelihood of failure occurring along these planes. For CSTBD specimens, as the stratification angle increases, failures along the stratification planes become less frequent. However, at lower stratification angles (0° ≤ θ ≤ 30°), the final failure patterns typically feature cracks along the stratification planes. During the initial loading phase, tensile cracks develop along the direction of the applied load. As the external load gradually increases, these cracks expand until they traverse the entire specimen, forming a new free surface. This new free surface alleviates the deformation constraints originally imposed by the pre-existing crack plane. As shown in Figure 12, with the continuous increase in load, compressive deformation occurs in the free surface area at the crack center. Due to the uneven stress distribution perpendicular to the crack plane, tensile stress is generated in the region where the horizontal extension plane of the crack intersects with the specimen’s edge. Additionally, because the stratification planes inherently possess low tensile strength, the specimen is more prone to developing new tensile cracks along these stratification planes in this region.

3.2.3. Fracture Toughness

During the loading process, when the stress intensity factor around the crack tip increases to a particular critical value, the material can no longer withstand the stress state, resulting in rapid crack propagation. This critical value is referred to as the critical stress intensity factor, denoted as K_IC. The K_IC value characterizes the material’s resistance to crack growth, commonly known as its fracture toughness. The following formula is generally used to calculate the Mode I fracture toughness for CSTBD configuration specimens [41]:

$$K_{\mathrm{IC}}=Y{\displaystyle \frac{P_{\max }\sqrt{\pi a}}{\pi BR}}$$

(3)

$$Y=(1-0.5\mathsf{\alpha }+1.56{\mathsf{\alpha }}^2-3.18{\mathsf{\alpha }}^3+10.1{\mathsf{\alpha }}^4-20.78{\mathsf{\alpha }}^5+20.13{\mathsf{\alpha }}^6-7.51{\mathsf{\alpha }}^7)/\sqrt{1-\mathsf{\alpha }}$$

(4)

$$\mathsf{\alpha }=a/R$$

(5)

where a is the half-length of the crack in the disk, R is the radius of the disk, B is the thickness of the disk, P_max is the peak load, and Y is the dimensionless stress intensity factor.

Figure 13 illustrates the relationship between fracture toughness and stratification angles across different numbers of stratification layers. The data reveal a pronounced effect of stratification on the rock’s fracture toughness. Specifically, at a stratification angle of 0°, where cracks are perpendicular to the stratification planes, the rock demonstrates the highest fracture toughness due to significant resistance to crack propagation along these planes, along with the predominant constraint imposed by the higher tensile strength of the rock matrix. Conversely, as the stratification angle increases, the fracture toughness decreases linearly. This reduction can be attributed to the reduced obstructive effect of the stratification planes on crack propagation, with cracks more readily advancing along these inherently weaker surfaces. Consequently, the lower tensile strength of the stratification planes compared to the rock matrix results in diminished overall fracture toughness when cracks propagate along these planes. Additionally, experimental observations indicate that, with an increasing number of stratification layers, the fracture toughness continues to decrease. The linear fit’s slope becomes steeper with a greater number of stratification layers, highlighting a more pronounced reduction in fracture toughness with higher stratification angles. This suggests that a higher number of stratification layers exacerbates the influence of stratification angles on fracture toughness, as additional stratification planes create more potential paths for crack propagation, thereby further diminishing the rock’s overall fracture toughness.

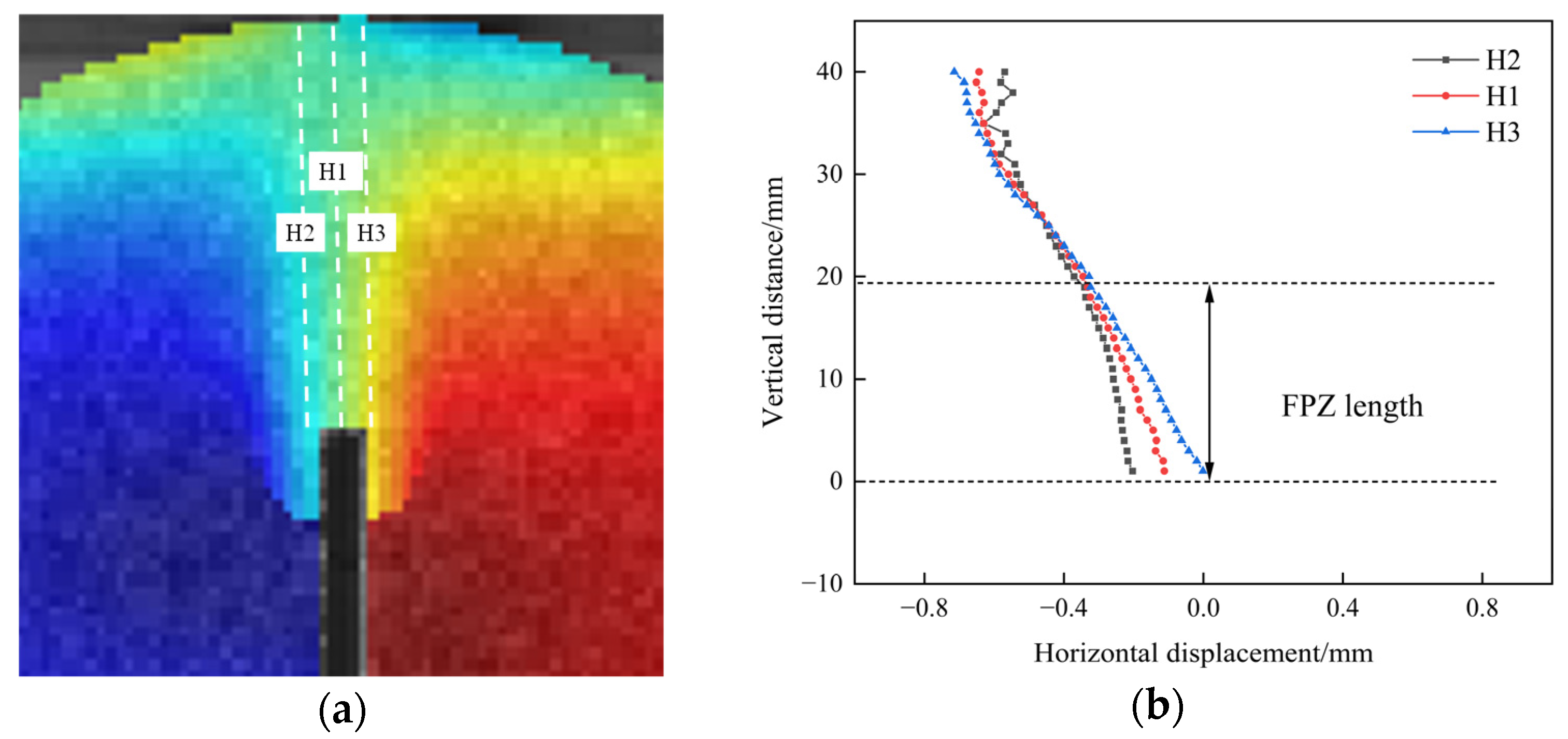
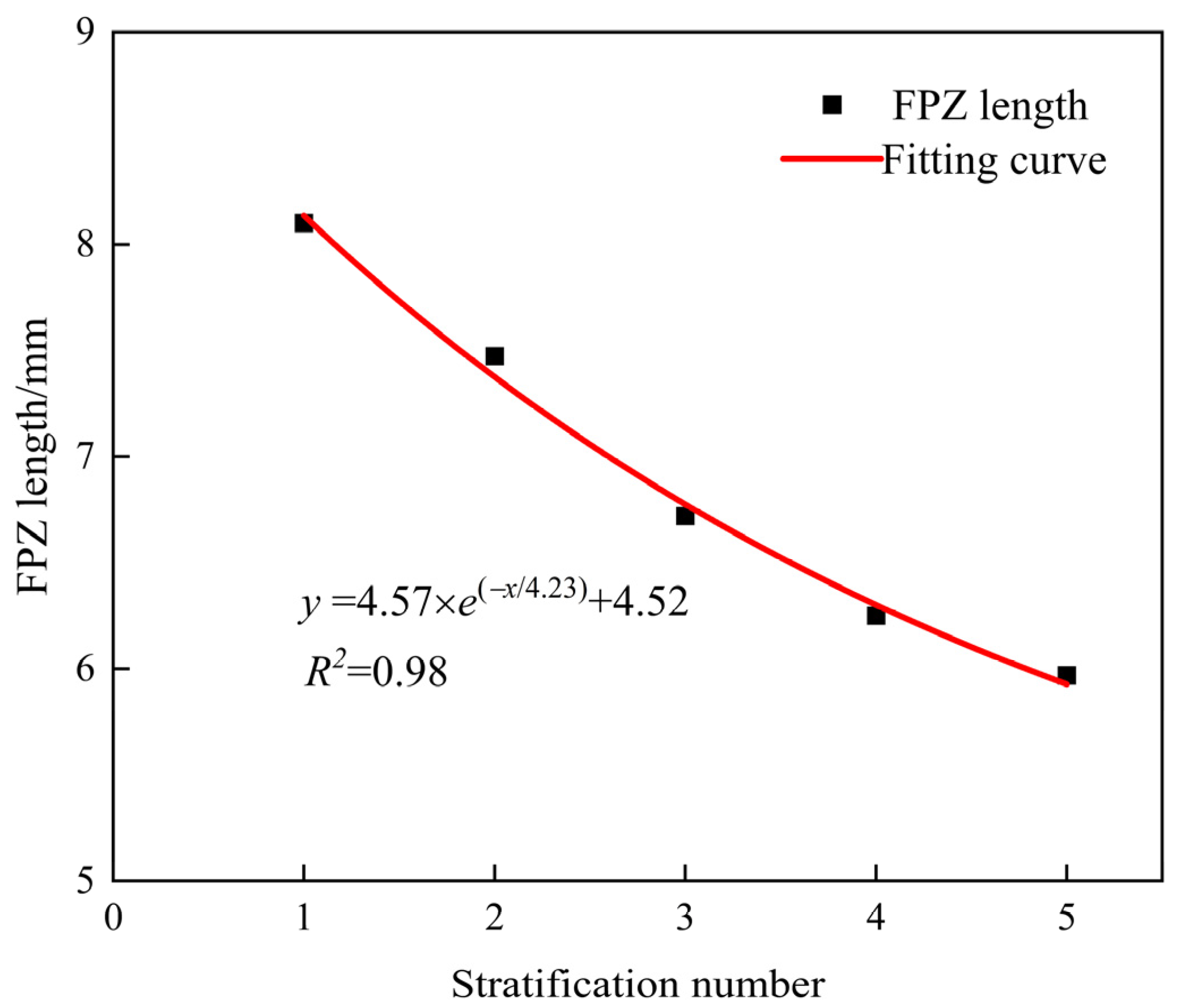
3.2.4. FPZ Length

The FPZ, which characterizes the local deformation and fracture region surrounding the crack tip, is essential for a comprehensive understanding of material fracture mechanisms. The extent of the FPZ is closely associated with fracture toughness, as materials exhibiting higher fracture toughness generally possess a larger FPZ. This correlation indicates that such materials are capable of absorbing and dissipating greater amounts of energy prior to crack propagation. Consequently, following a detailed examination of fracture toughness, the subsequent focus will be on analyzing the FPZ length to achieve a more thorough understanding of the mechanical response and underlying micro-mechanisms of materials during crack propagation.

The FPZ length is determined using the Digital Image Correlation (DIC) method, which digitizes deformation information on the specimen surface through advanced image processing techniques [42,43]. To analyze the characteristics of the FPZ under varying stratification angles and numbers of stratification layers, the first image captured during the experiment is used as the reference for evaluating the FPZ length at the crack tip during the peak load stage. The procedure for calculating the FPZ length is illustrated in Figure 14a. Initially, a vertical sampling line, denoted as H1, is positioned from the initial crack tip. Subsequently, additional sampling lines, H2 and H3, are placed at intervals of 0.02 mm on either side of H1, and the corresponding horizontal displacement values for these lines are extracted from the subset of the image, as depicted in Figure 14b. Significant differences in horizontal displacement values are observed at the initial crack tip. However, as the sampling lines extend toward the upper boundary of the specimen, the disparity between the displacement values gradually diminishes, and they eventually converge. The range from the starting position of the sampling lines to this convergence point is defined as the FPZ length.

To investigate the effect of stratification on the FPZ length in layered rocks, specimens with a stratification angle of θ = 0° and varying numbers of stratification layers were selected. The FPZ lengths were measured under peak load conditions for specimens with 1 to 5 layers. The average FPZ lengths for these specimens were 8.1 mm, 7.47 mm, 6.72 mm, 6.25 mm, and 5.97 mm, respectively, as shown in Figure 15. The data reveal a progressive decrease in FPZ length with an increasing number of stratification layers. This reduction can be attributed to the significantly lower strength of the stratification planes compared to the bedrock. As the number of stratification layers increases and the bedrock’s thickness decreases, cracks more readily propagate through these weaker stratification planes, resulting in shorter FPZ lengths and reduced fracture toughness. The observed decrease in FPZ length follows an exponential decay trend, suggesting that while additional stratification layers lead to a reduction in FPZ length, this decrease asymptotically approaches a minimum value rather than continuing indefinitely.

Figure 16 illustrates the effect of varying stratification angles on FPZ length, with the angle held constant and the FPZ length averaged across all specimens with different numbers of stratification layers. The data reveal a linear decrease in FPZ length as the stratification angle increases. This reduction can be attributed to the stratification planes facilitating crack propagation. Specifically, when the stratification planes are more aligned with the loading direction, cracks more readily slide and propagate along these weaker planes, resulting in shorter FPZ lengths. Conversely, when the stratification planes are more perpendicular to the loading direction, resistance to crack propagation is higher, leading to longer FPZ lengths and greater fracture toughness.

4. Conclusions

This study used sandstone as the base material to fabricate layered rock specimens with five variations in the number of layers. Brazilian splitting tests were conducted to examine the fracture characteristics of the layered rocks under different loading angles. The main conclusions are as follows:

(1)

The tensile strength of the layered rock exhibits a significant stratification effect, with tensile strength gradually decreasing as the number of stratification layers and the stratification angles increase. The number of stratification planes has a minimal impact on the specimen’s failure mode; instead, the diversity of failure modes of the disk specimens is mainly due to the different stratification angles.

(2)

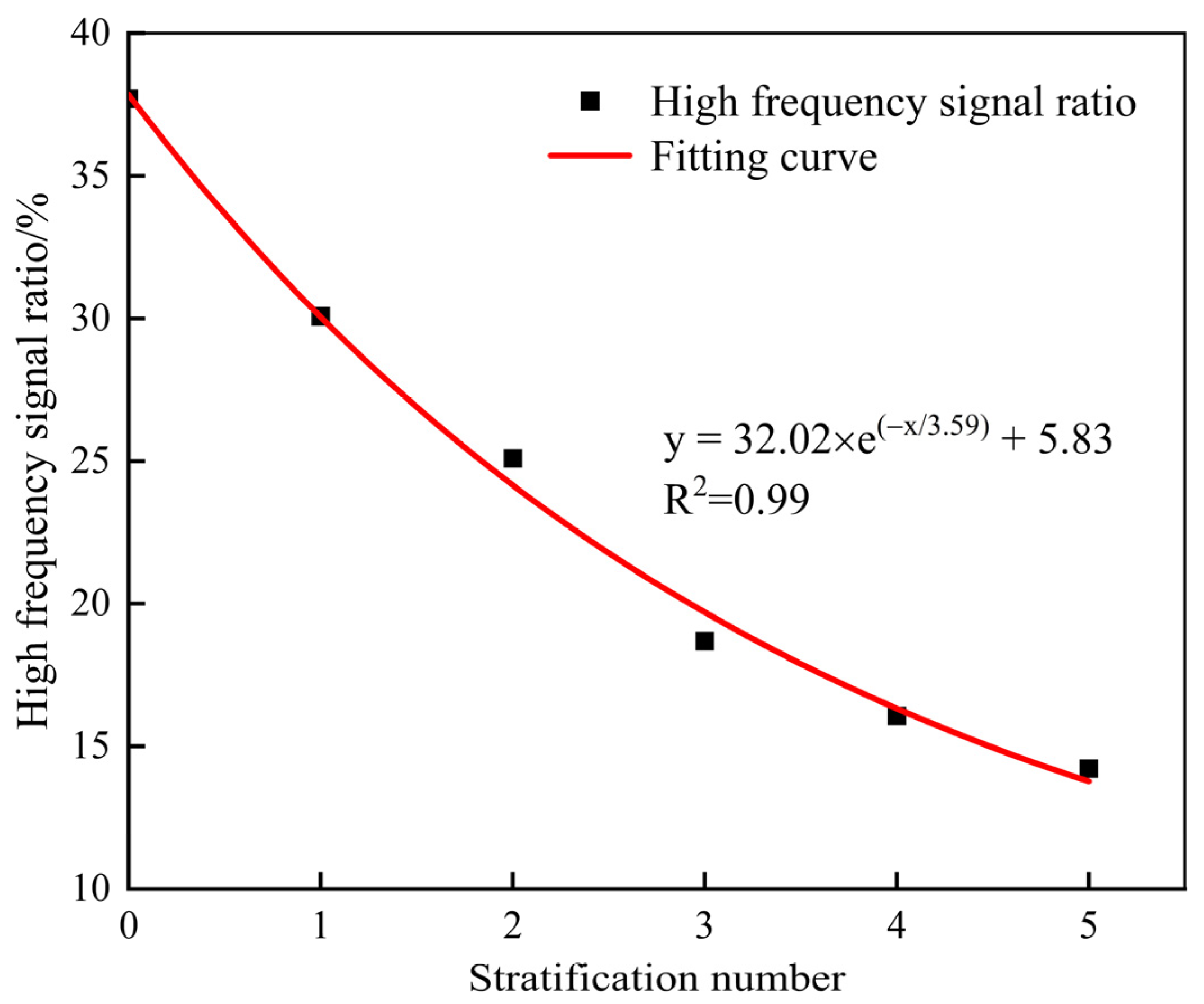
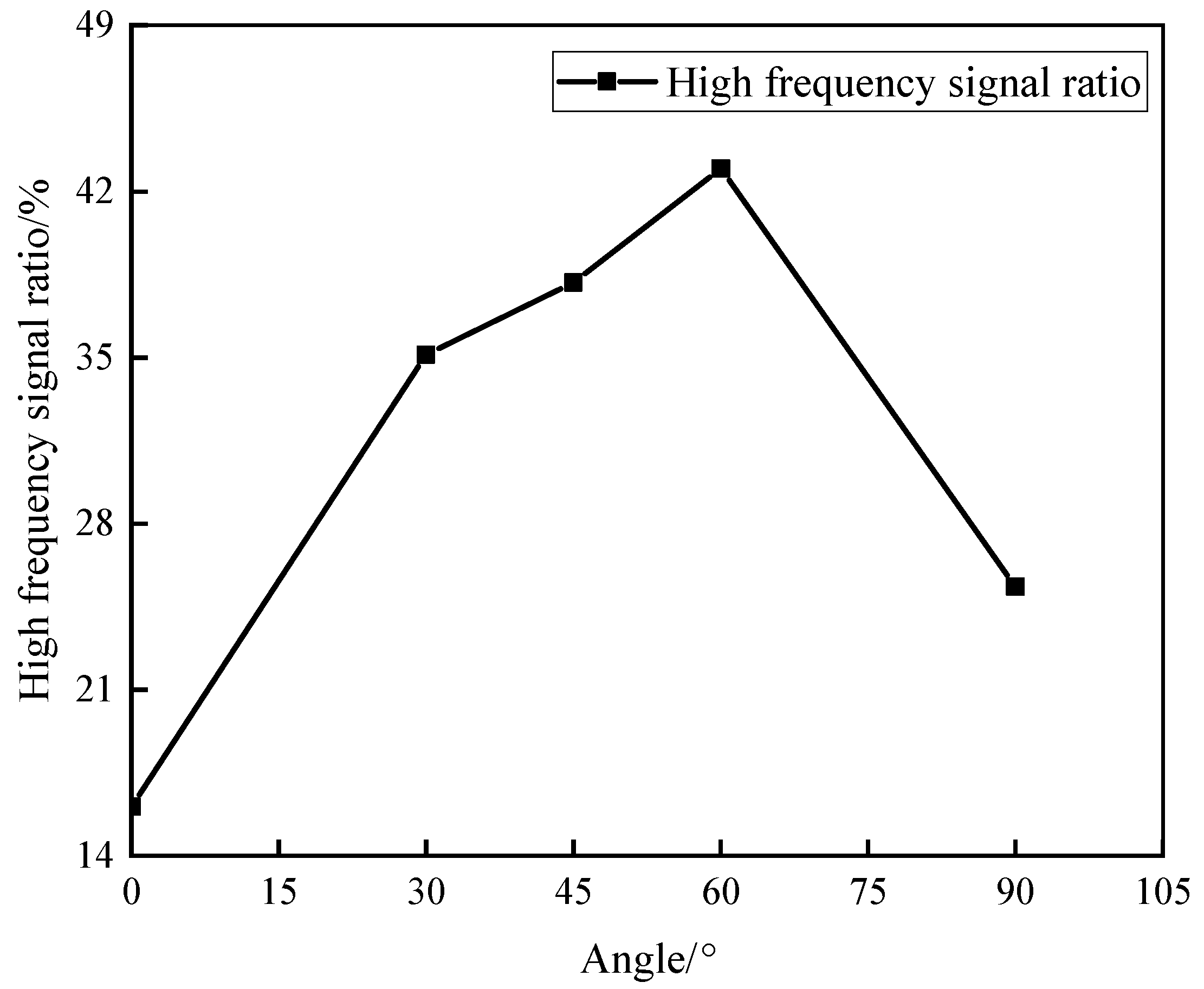
The S-value and cumulative AE count curves during the loading process of specimens without prefabricated cracks exhibit two types: a fluctuating upward mode, and a “gentle–steep increase” mode. For specimens with five different numbers of stratification planes, high-frequency signals are significantly lower than low-frequency signals, and the proportion of high-frequency signals gradually decreases as the number of stratification planes increases. As the stratification angle increases, the proportion of high-frequency signals shows a trend of first increasing and then decreasing. During the fracture process of layered rock specimens, they consistently exhibit low RA values and high AF characteristics. As the stratification angle increases from 0° to 60°, the failure mode gradually transitions from tensile failure to shear failure.

(3)

For Mode I fracture, the stratification effect on fracture toughness is significant. The effect of stratification angles on fracture toughness is amplified with an increasing number of stratification planes, resulting in a more pronounced decline in fracture toughness with greater stratification angles. Additionally, the FPZ length at peak load decreases exponentially as the number of stratification planes increases. Within the stratification angle range of 0° to 60°, the FPZ length decreases linearly with increasing stratification angle.