Influences of an Arrow’s Aerodynamic Pressure Center on Recurve Bow Shooting
Abstract
:1. Introduction
2. Materials and Methods
2.1. Calculation Method for the Center of Aerodynamic Pressure of an Arrow
2.1.1. Main Governing Equations and Turbulence Model
- (1)
- The mass conservation equation iswhere is the fluid density (kg/m3); denotes the velocity vector (m/s).
- (2)
- The momentum conservation equation iswhere p, I, F, and denote the pressure (Pa), momentum vector (N∙s), vector of body force (N), and dynamic viscosity (Pa∙s), respectively.
- (3)
- Relevant equations of the RANS k-ε turbulence model are as follows.
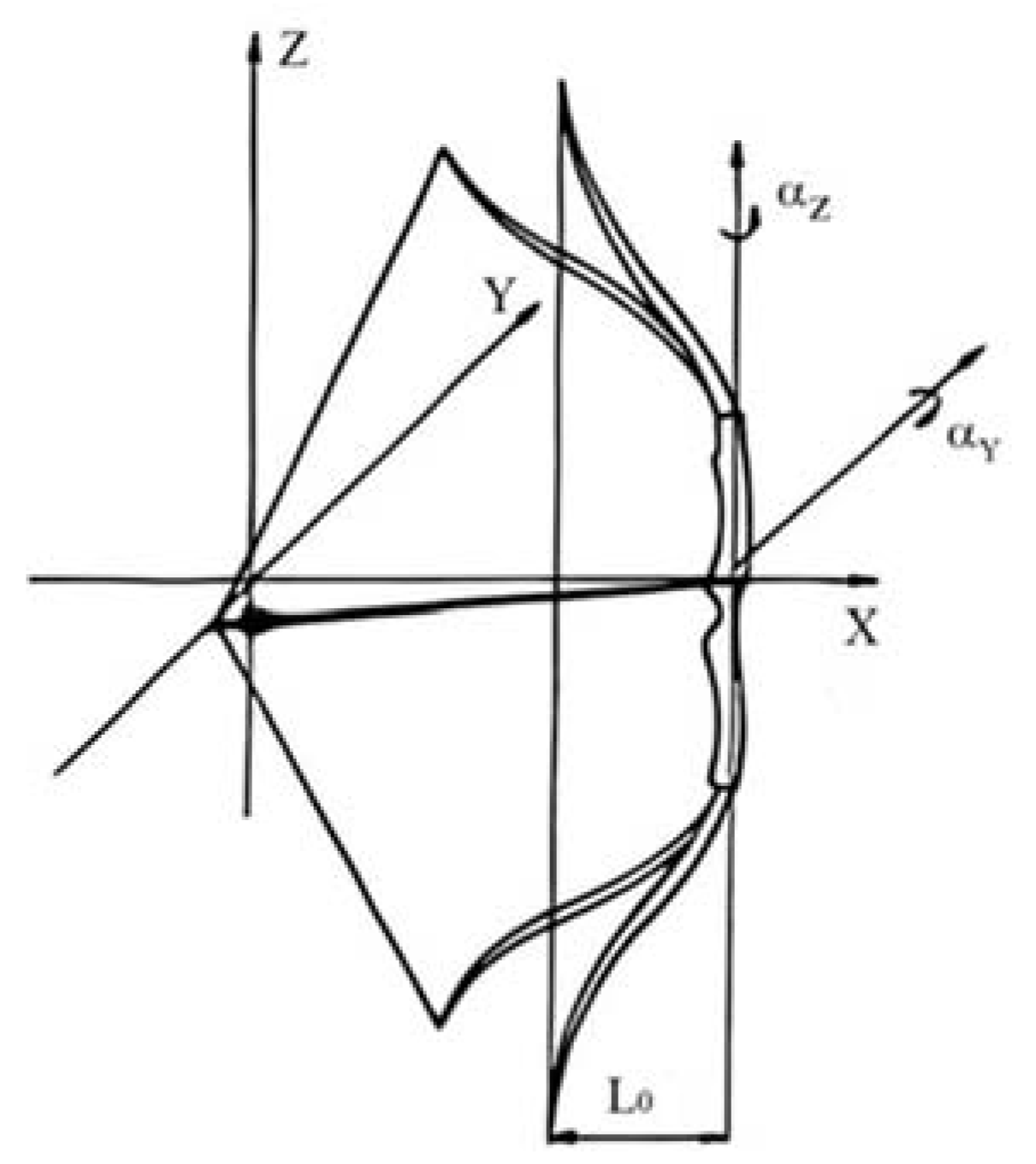
2.1.2. Geometric and Physical Model of an Arrow
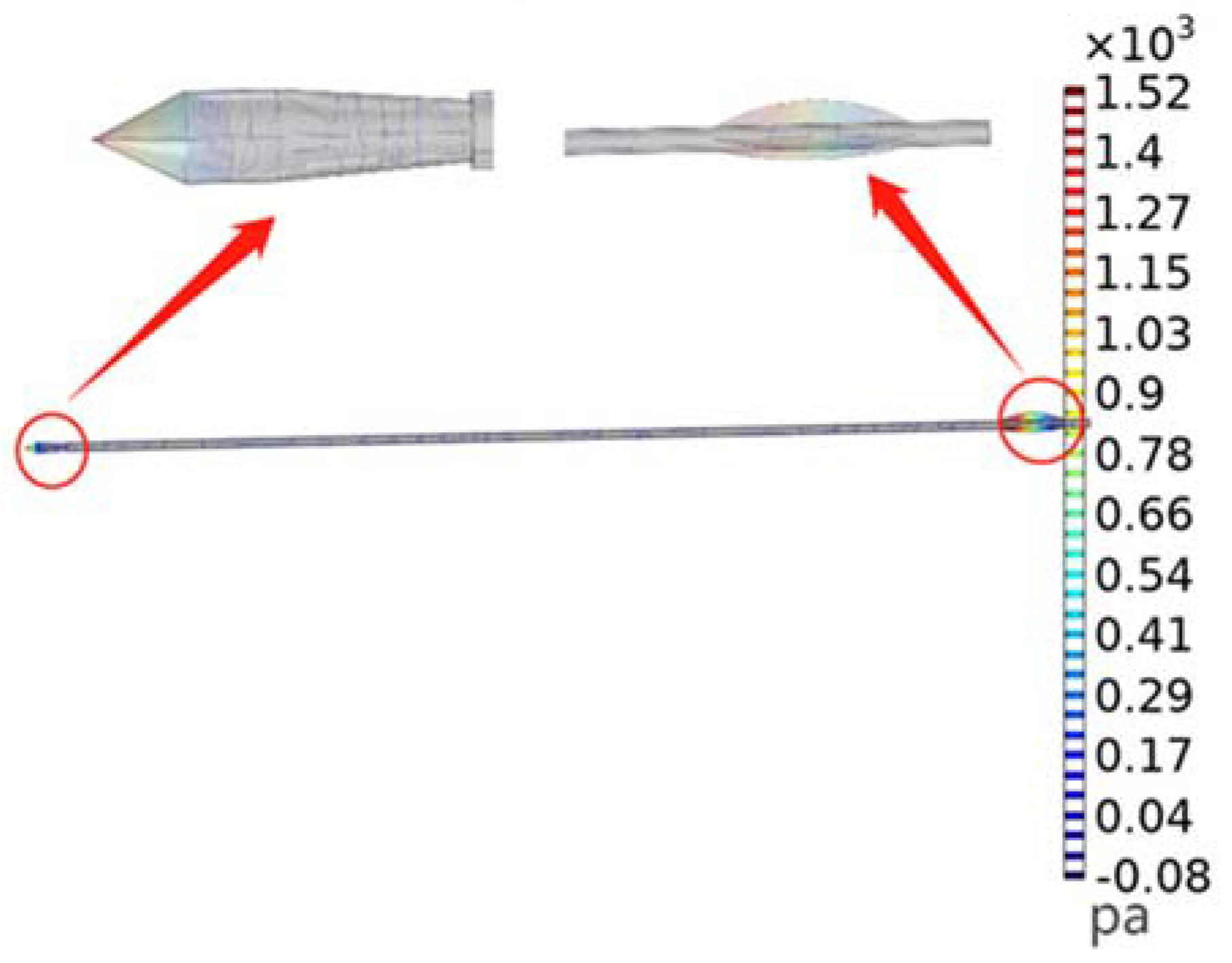
2.1.3. Boundary Conditions and Meshing
2.1.4. Verification of the Turbulence Model
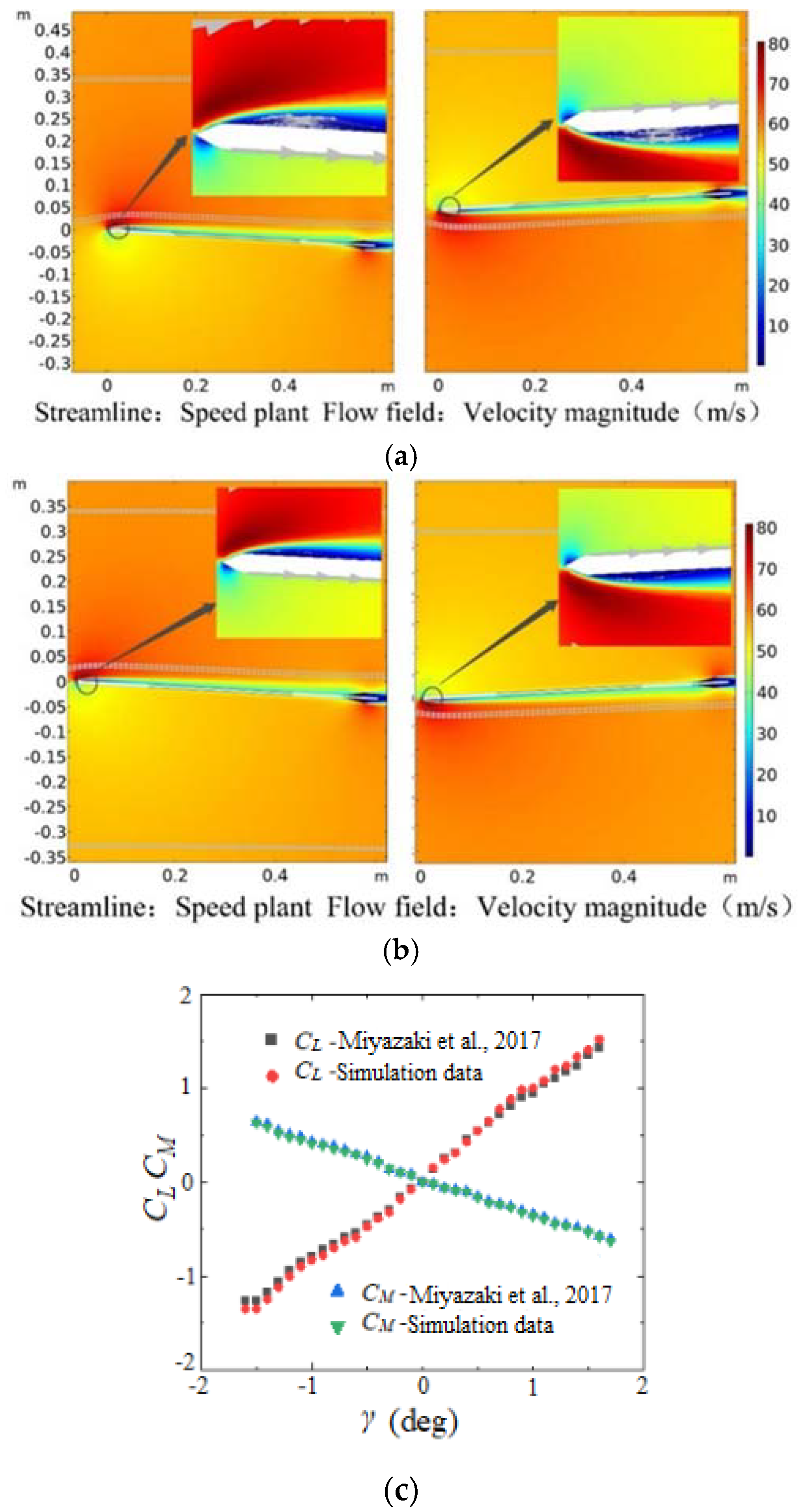
2.1.5. Processing of the Calculated Results
- (1)
- The pressure coefficient at a certain point on the arrow surface iswhere p is the static pressure at the point; pinf denotes the far-field air pressure; is the far-field air density, and Vinf is the far-field air velocity.
- (2)
- The pressure vector at a certain point on the arrow surface iswhere np = (npx, npy, npz) is the normal vector component at the point.
- (3)
- The Cp position iswhere A is the surface area of the arrow; dS refers to the element area on the material surface.
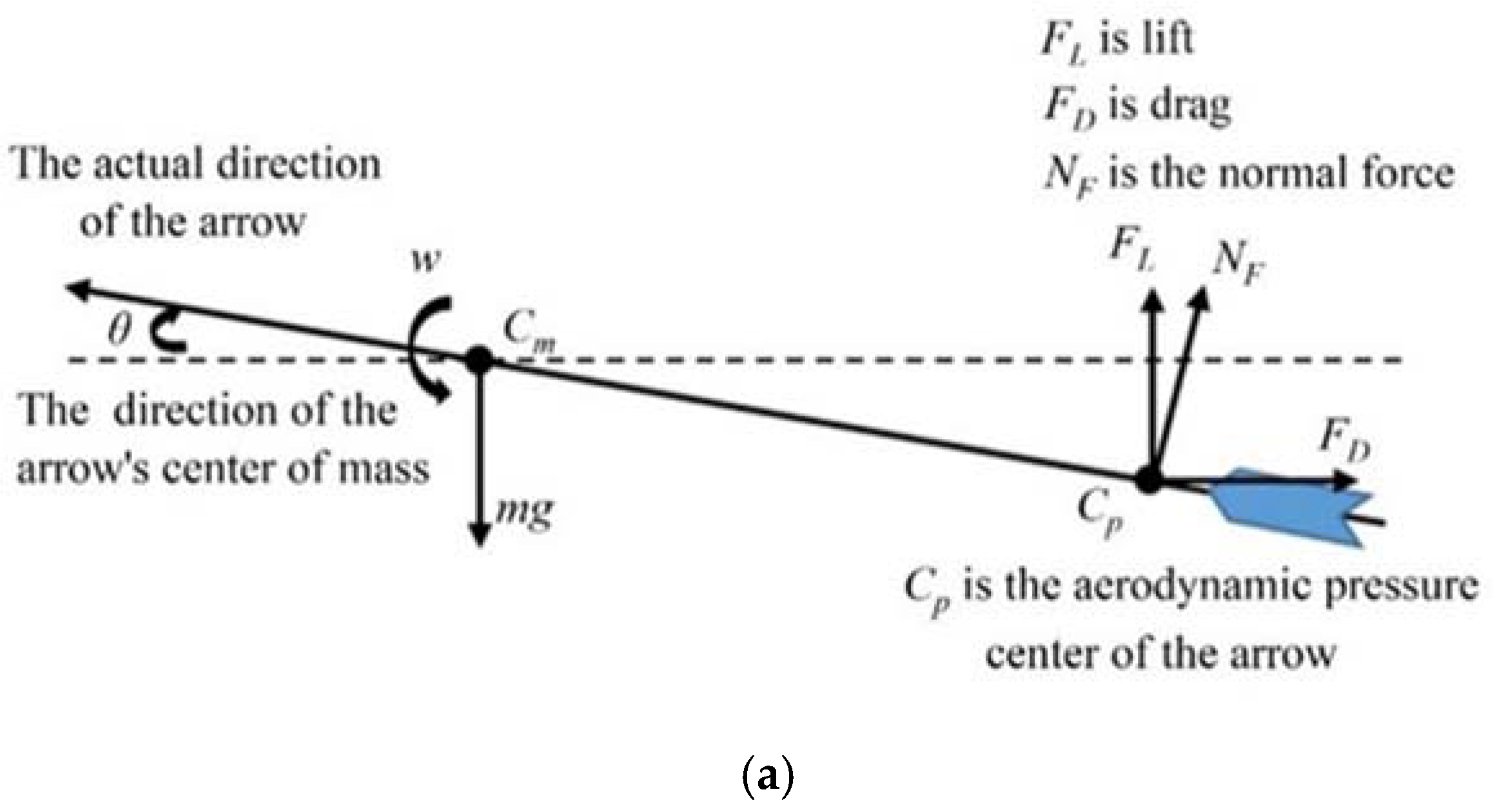
2.2. Aerodynamics Model
2.2.1. Aerodynamics Characteristics of the Arrow
2.2.2. Equations of Motion
2.2.3. Initial Conditions
2.2.4. Model Validation
3. Results
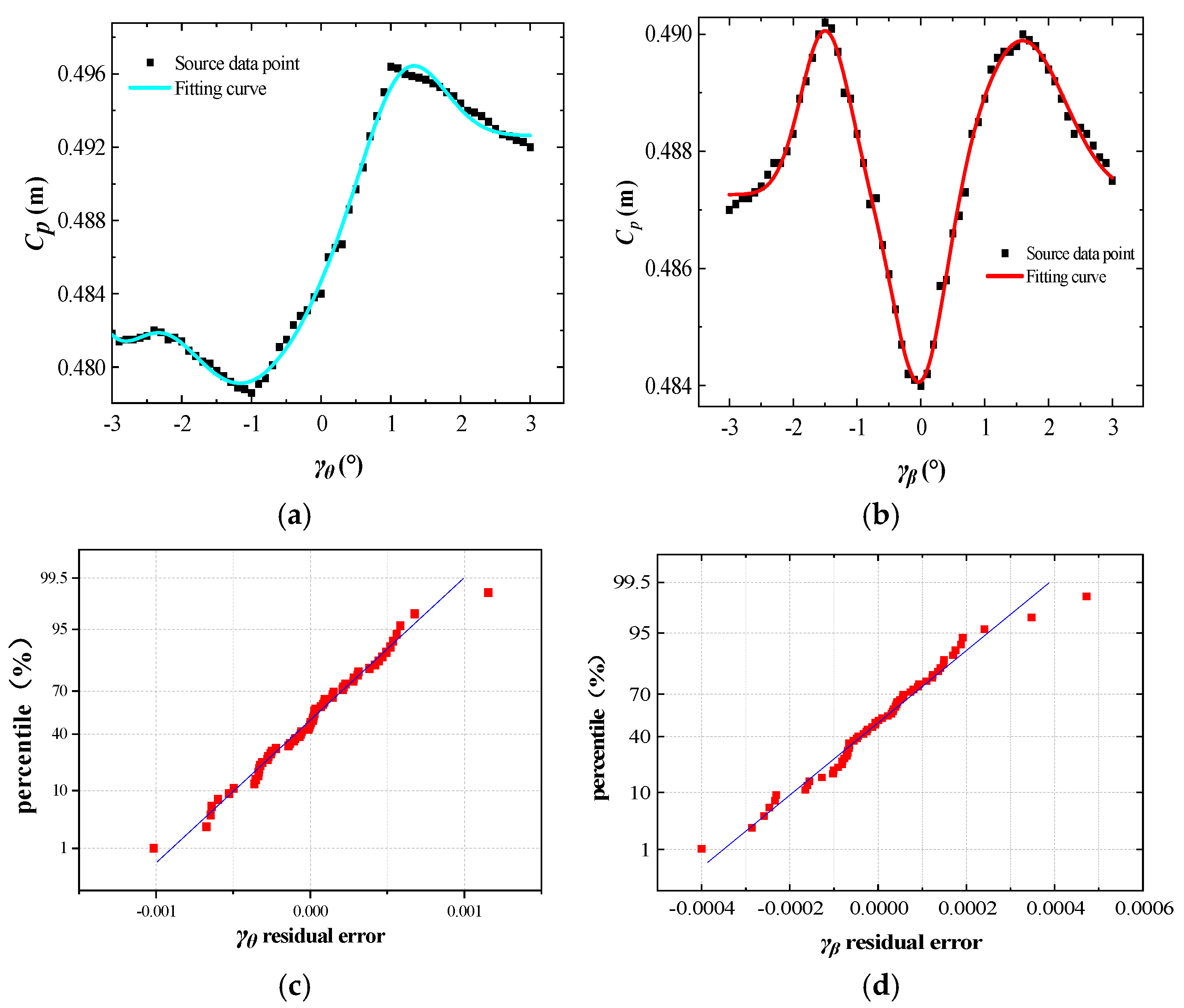
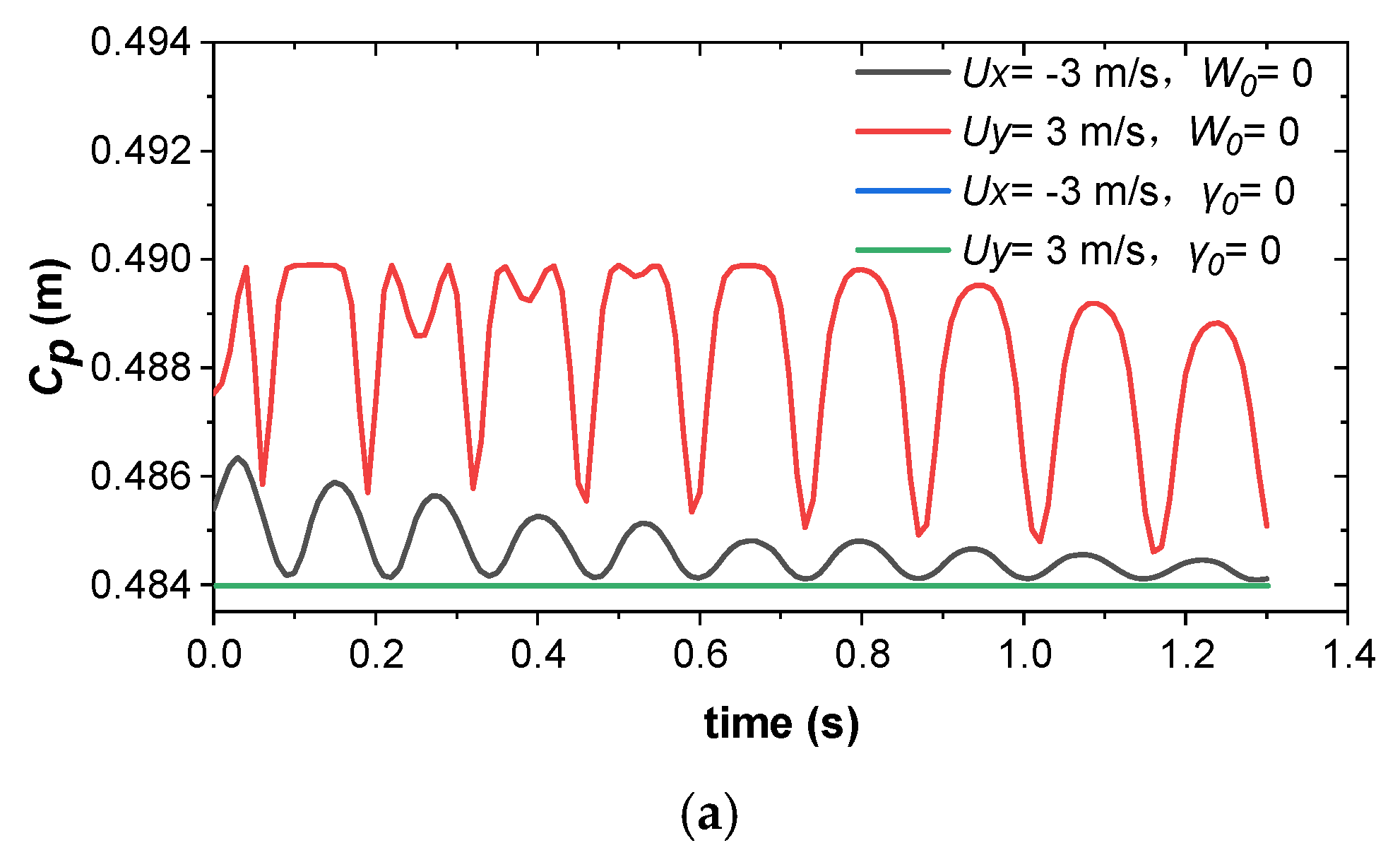
3.1. Influences of Changes in γ on CP
3.2. Arrow Behaviors Under Uniform Background Winds
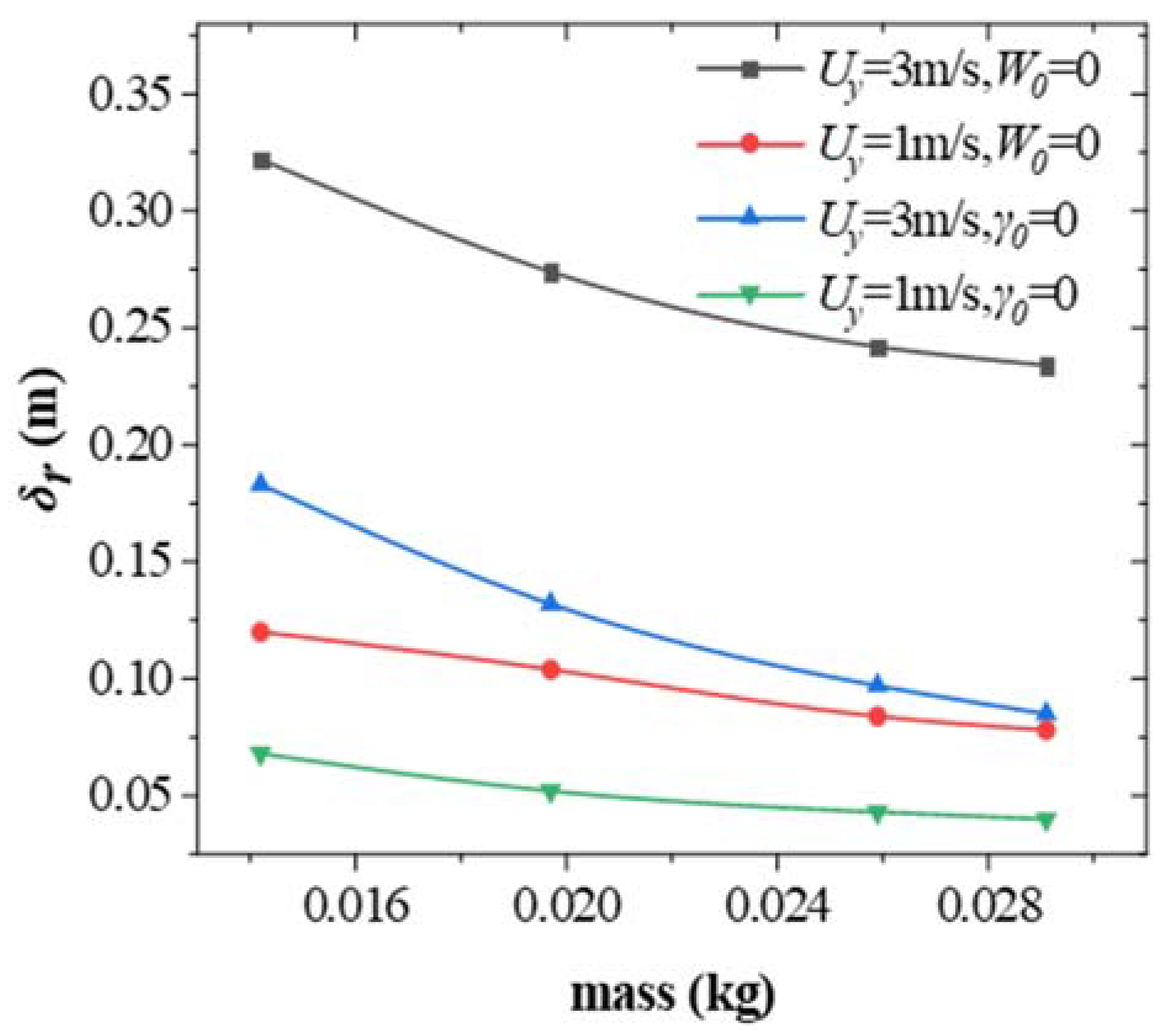
3.2.1. Influences of the Arrow Mass on the Shooting Accuracy
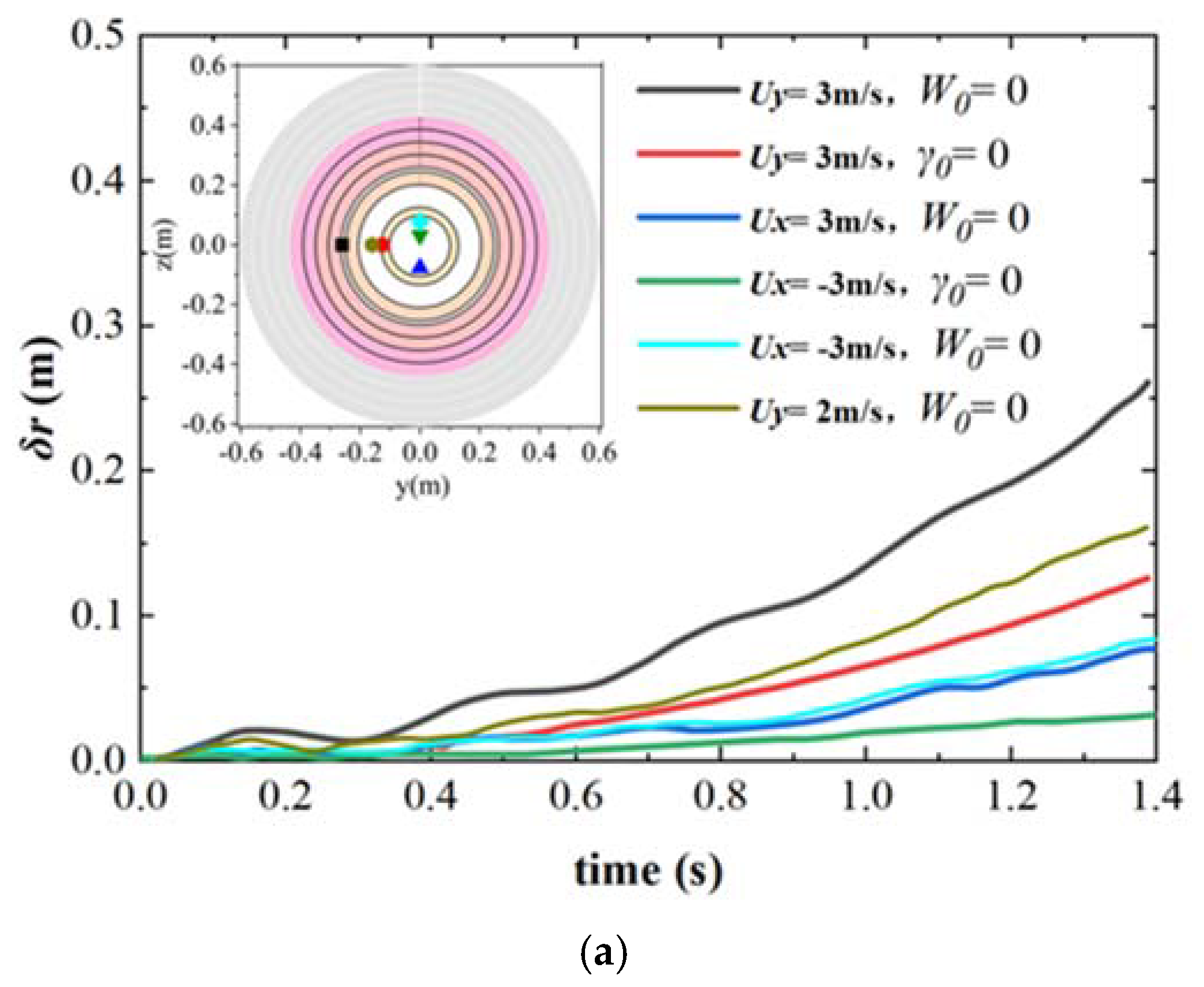
3.2.2. Changes in the Offset
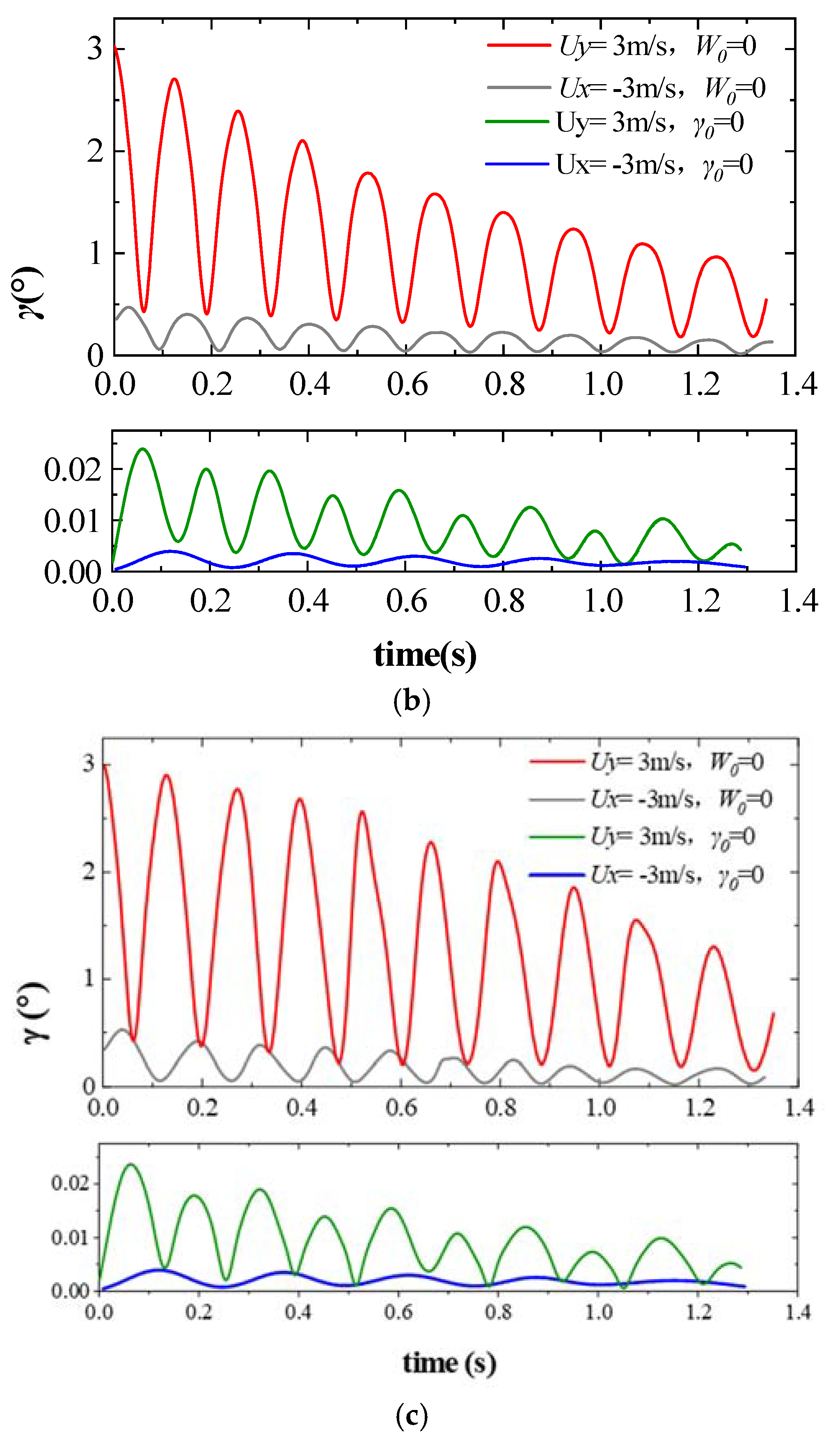
3.2.3. Changes in Cp and γ
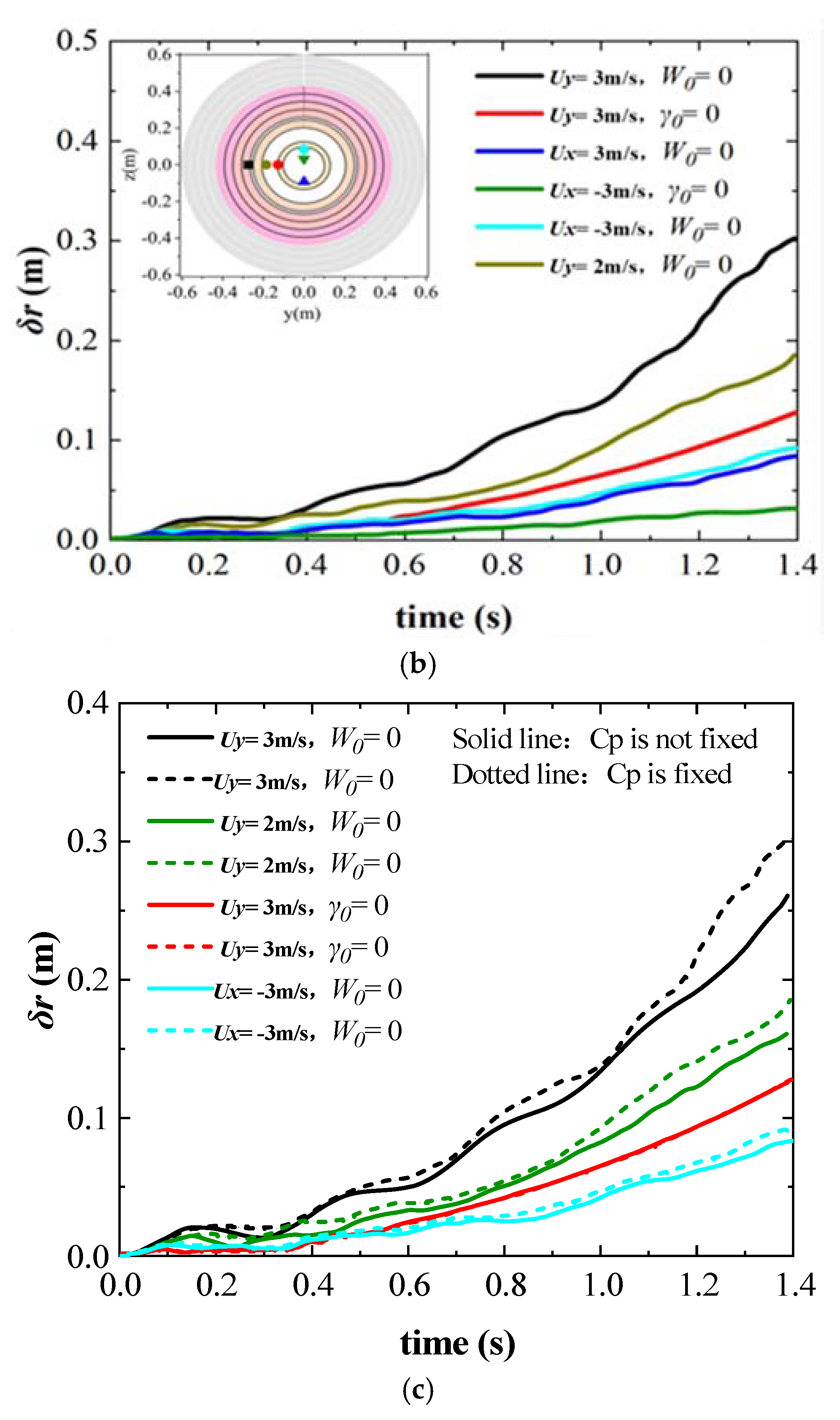
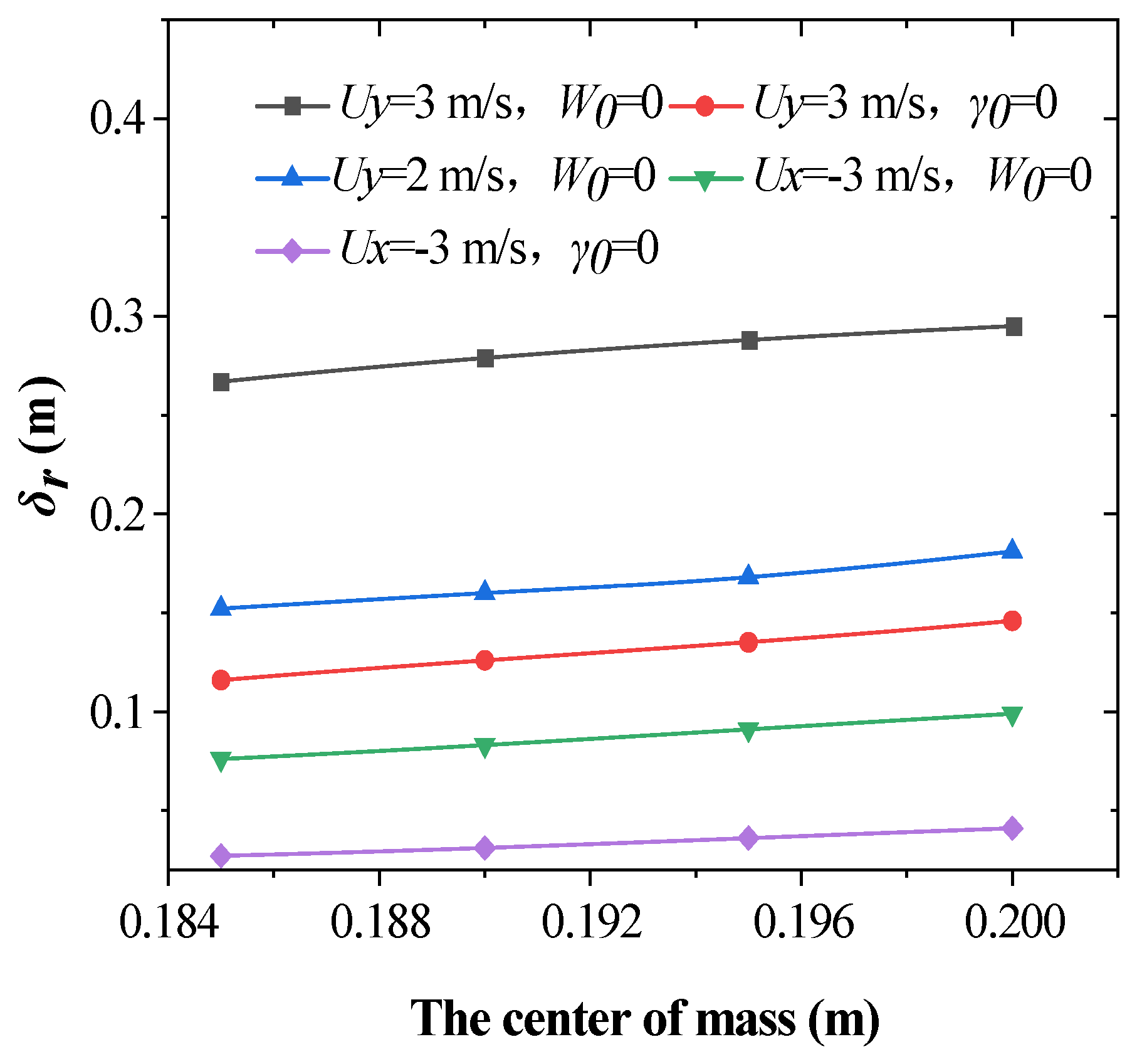
3.2.4. Influences of the Cm Position on Shooting Accuracy
3.3. Practical Performance and Adjustment Strategies for Athletes on the Archery Field
4. Conclusions
- (1)
- Cp is located towards the rear of the arrow and varies with the angle of attack (γ). Such variation manifests as increases or decreases of several millimeters, and it reaches a maximum of 0.496 m when γθ = 1°. Keeping Cp stable and backwards is key to reducing the offset.
- (2)
- A uniform crosswind affects an arrow more significantly than a uniform headwind or tailwind. Furthermore, within a specific range, either increasing the mass of the arrow or shifting its center of mass forward (while maintaining a constant arrow length and wind speed) can enhance the arrow’s resistance to wind deflection.
- (3)
- An improvement in the initial shooting conditions plays a significant role in reducing the offset. When the arrow is shot under zero γ, the Cp of the arrow can remain stable in flight, and the boundary layer remains laminar, thus improving the accuracy of the shot.
- (4)
- Compared to the model with a fixed Cp, the model introduced in this study has improved its accuracy by 15% under crosswind conditions and by 8% under headwind/tailwind conditions. The data from this research can help athletes more accurately predict arrow deviations and adjust their techniques accordingly.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| CFD | Computational fluid dynamics |
| Cp | Center of aerodynamic pressure |
| Cm | Center of mass |
| γ | Angle of attack |
| αy | The angles of a bow’s torsion around the y-axis |
| αz | The angles of a bow’s torsion around the z-axis |
| L0 | The length of an initial draw |
| Re | Reynolds number |
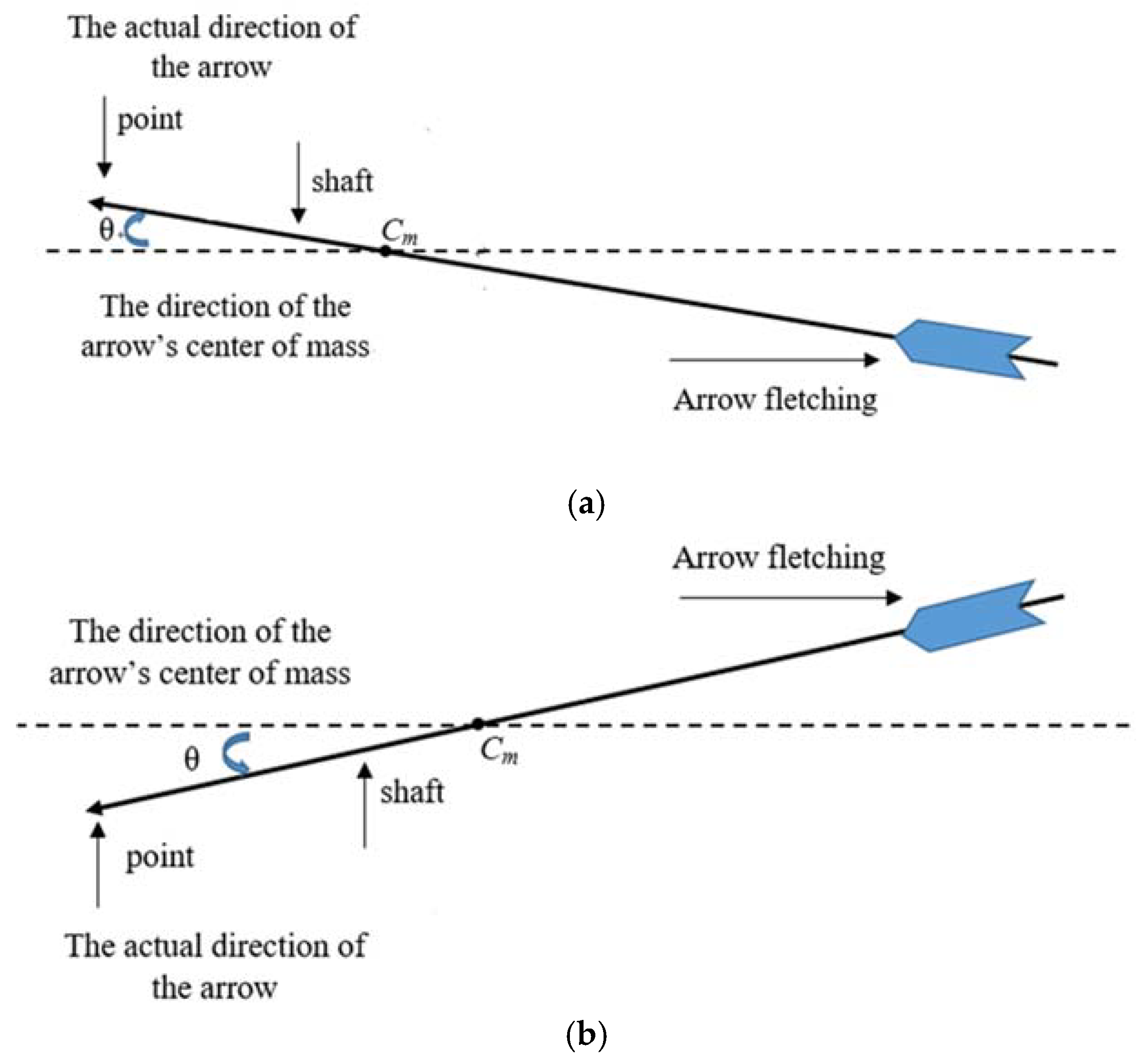
| γθ | The included angle between the arrow shaft and center of mass, Cm, velocity in the Z-direction |
| γβ | The included angle between the arrow shaft and Cm velocity in the Y-direction |
| ρ | Fluid density (kg/m3) |
| u | Fluid velocity (m/s) |
| p | Pressure (Pa) |
| F | Body force (N) |
| μ | Dynamic viscosity (Pa∙s) |
| k | Turbulence energy (m2/s2) |
| σK | Turbulent Prandtl number in k equation |
| ε | Dissipation rate (m2/s3) |
| σε | Turbulent Prandtl number in ε equation |
| μT | Turbulent viscosity coefficient |
| θ | The included angle between the velocity direction of the arrow and the arrow’s center of mass |
| CL | Lift coefficient |
| CM | Pitching moment coefficient |
| Pc | Pressure coefficient |
| pinf | The far-field air pressure (Pa) |
| ρinf | The far-field air density (kg/m3) |
| Vinf | the far-field air velocity (m/s) |
| Pvec | Pressure vector |
| A | The surface area of the arrow (m2) |
| Sp | Spin parameter |
| CD | Drag coefficient |
| I | Moment of inertia |
| FD | Drag force (N) |
| FL | Lift force (N) |
| δr | Offset (m) |
References
- Park, J.L. Arrow behavior in free flight. Proc. Inst. Mech. Eng. Part P J. Sports Eng. Technol. 2011, 225, 241–252. [Google Scholar]
- Ortiz, J.; Serino, A.; Hasegawa, T.; Onoguchi, T.; Maemukai, H.; Miyazaki, T.; Sugiura, H. Experimental and Computational Study of Archery Arrows Fletched with Straight Vanes. Proceedings 2020, 49, 56. [Google Scholar] [CrossRef]
- Kuch, A.; Debril, J.F.; Tizzoni, J.M.; Laguillaumie, P.; Monnet, T. A study of the influence of arrow mass on ballistics. Comput. Methods Biomech. Biomed. Eng. 2019, 22, S526–S528. [Google Scholar] [CrossRef]
- Hickman, C.N. The dynamics of a bow and arrow. J. Appl. Phys. 1937, 8, 404–409. [Google Scholar] [CrossRef]
- Klopsteg, P.E. Bows and Arrows: A Chapter in the Evolution of Archery in America; Smithsonian Institution: Washington, DC, USA, 1963. [Google Scholar]
- Pekalski, R. An improved archery simulator for objective dynamic tests of bows and arrows. J. Biomech. 1987, 20, 818. [Google Scholar] [CrossRef]
- Kooi, B.W.; Sparenberg, J.A. On the mechanics of the arrow: Archer’s Paradox. J. Eng. Math. 1997, 31, 285–303. [Google Scholar] [CrossRef]
- Park, J.L. Arrow behaviour in the lateral plane during and immediately following the power stroke of a recurve archery bow. Proc. Inst. Mech. Eng. Part P J. Sports Eng. Technol. 2013, 227, 172–183. [Google Scholar] [CrossRef]
- Pekalski, R. Experimental and theoretical research in archery. J. Sports Sci. 1990, 8, 259–279. [Google Scholar] [CrossRef]
- Kooi, B.W. On the mechanics of the modern working-recurve bow. Comput. Mech. 1991, 8, 291–304. [Google Scholar] [CrossRef]
- Goff, J.E. A review of recent research into aerodynamics of sport projectiles. Sports Eng. 2013, 16, 137–154. [Google Scholar] [CrossRef]
- Ertan, H. Exploratory spatial analysis of hit distribution in archery. Int. J. Acad. Res. 2013, 5, 112–118. [Google Scholar] [CrossRef]
- Kooi, B.W. Bow-arrow interaction in archery. J. Sports Sci. 1998, 16, 721–731. [Google Scholar] [CrossRef] [PubMed]
- Sawada, H.; Umezawa, K.; Yokozeki, T.; Watanabe, A.; Otsu, T. Wind tunnel test of Japanese arrows with the JAXA 60-cm magnetic suspension and balance system. Exp. Fluids 2012, 53, 451–466. [Google Scholar] [CrossRef]
- Zanevskyy, I. Mechanical and mathematical modeling of sport archery arrow ballistics. Int. J. Comput. Sci. Sport 2008, 7, 40–49. [Google Scholar]
- Liston, T.L. Physical Laws of Archery; Liston & Associates: Village, CA, USA, 1991. [Google Scholar]
- Park, J.L. The aerodynamic drag and axial rotation of an arrow. Proc. Inst. Mech. Eng. Part P J. Sports Eng. Technol. 2011, 225, 199–211. [Google Scholar] [CrossRef]
- Park, J.L.; Hodge, M.R.; Al-Mulla, S.; Sherry, M.; Sheridan, J. Air flow around the point of an arrow. Proc. Inst. Mech. Eng. Part P J. Sports Eng. Technol. 2013, 227, 64–69. [Google Scholar] [CrossRef]
- Okawa, K.; Komori, Y.; Miyazaki, T.; Taguchi, S.; Sugiura, H. Free flight and wind tunnel measurements of the drag exerted on an archery arrow. Procedia Eng. 2013, 60, 67–72. [Google Scholar] [CrossRef]
- Iftikhar, S.; Sherbaz, S.; Haider Sehole, H.A.; Maqsood, A.; Mustansar, Z. Large eddy simulation of the flow past a soccer ball. Math. Probl. Eng. 2022, 2022, 3455235. [Google Scholar] [CrossRef]
- Rasmussen, J.; Zee, M.D. A Simulation of the effects of badminton serve release height. Appl. Sci. 2021, 11, 2903. [Google Scholar] [CrossRef]
- Alam, F.; Chowdhury, H.; Theppadungporn, C.; Subic, A. Measurements of aerodynamic properties of badminton shuttlecocks. Procedia Eng. 2010, 2, 2487–2492. [Google Scholar] [CrossRef]
- Asai, T.; Kamemoto, K. Flow structure of knuckling effect in footballs. J. Fluids Struct. 2011, 27, 727–733. [Google Scholar] [CrossRef]
- Clanet, C. Sports ballistics. Annu. Rev. Fluid Mech. 2015, 47, 455–478. [Google Scholar] [CrossRef]
- Maheras, A. The Javelin: Basic Javelin Aerodynamics and Flight Characteristics (Part 1). Tech. Track Field Cross Ctry. 2013, 7, 30. [Google Scholar]
- Ocokoljic, G.J.; Rasuo, B.P.; Bengin, A.C. Aerodynamic shape optimization of guided missile based on wind tunnel testing and computational fluid dynamics simulation. Therm. Sci. 2017, 21, 1543–1554. [Google Scholar] [CrossRef]
- Zhang, W.; Wang, Y.; Liu, Y. Aerodynamic study of theater ballistic missile target. Aerosp. Sci. Technol. 2013, 24, 221–225. [Google Scholar] [CrossRef]
- Ortiz, J.; Ando, M.; Murayama, K.; Miyazaki, T.; Sugiura, H. Computation of the trajectory and attitude of arrows subject to background wind. Sports Eng. 2019, 22, 7. [Google Scholar] [CrossRef]
- Ortiz, J.; Ando, M.; Miyazaki, T. Numerical simulation of wind drift of arrows on the Olympic venue for Tokyo 2020. Athens J. Sports 2020, 7, 1–20. [Google Scholar] [CrossRef]
- Miyazaki, T.; Mukaiyama, K.; Komori, Y.; Okawa, K.; Taguchi, S.; Sugiura, H. Aerodynamic properties of an archery arrow. Sports Eng. 2013, 16, 43–54. [Google Scholar] [CrossRef]
- Miyazaki, T.; Matsumoto, T.; Ando, R.; Ortiz, J.; Sugiura, H. Indeterminacy of drag exerted on an arrow in free flight: Arrow attitude and laminar-turbulent transition. Eur. J. Phys. 2017, 38, 064001. [Google Scholar] [CrossRef]
- Kumar, G.; Natale, G. Settling dynamics of two spheres in a suspension of Brownian rods. Phys. Fluids 2019, 31, 073104. [Google Scholar] [CrossRef]
- Cai, S.G.; Mozaffari, S.; Jacob, J.; Sagaut, P. Application of immersed boundary based turbulence wall modeling to the Ahmed body aerodynamics. Phys. Fluids 2022, 34, 095106. [Google Scholar] [CrossRef]
- Passiatore, D.; Sciacovelli, L.; Cinnella, P.; Pascazio, G. Finite-rate chemistry effects in turbulent hypersonic boundary layers: A direct numerical simulation study. Phys. Rev. Fluids 2021, 6, 054604. [Google Scholar] [CrossRef]
- Kan, K.; Li, H.; Yang, Z. Large eddy simulation of turbulent wake flow around a marine propeller under the influence of incident waves. Phys. Fluids 2023, 35, 055124. [Google Scholar]


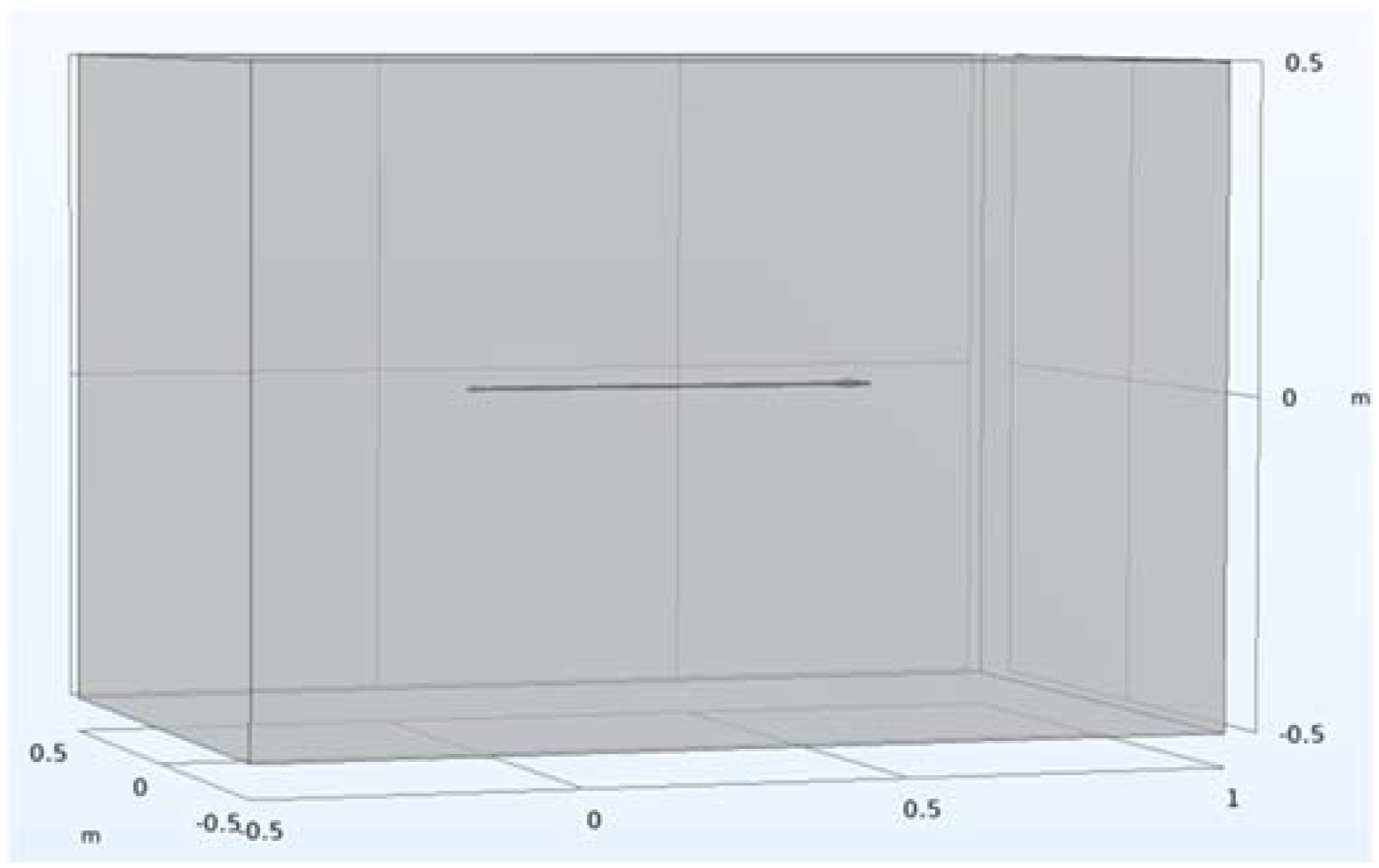
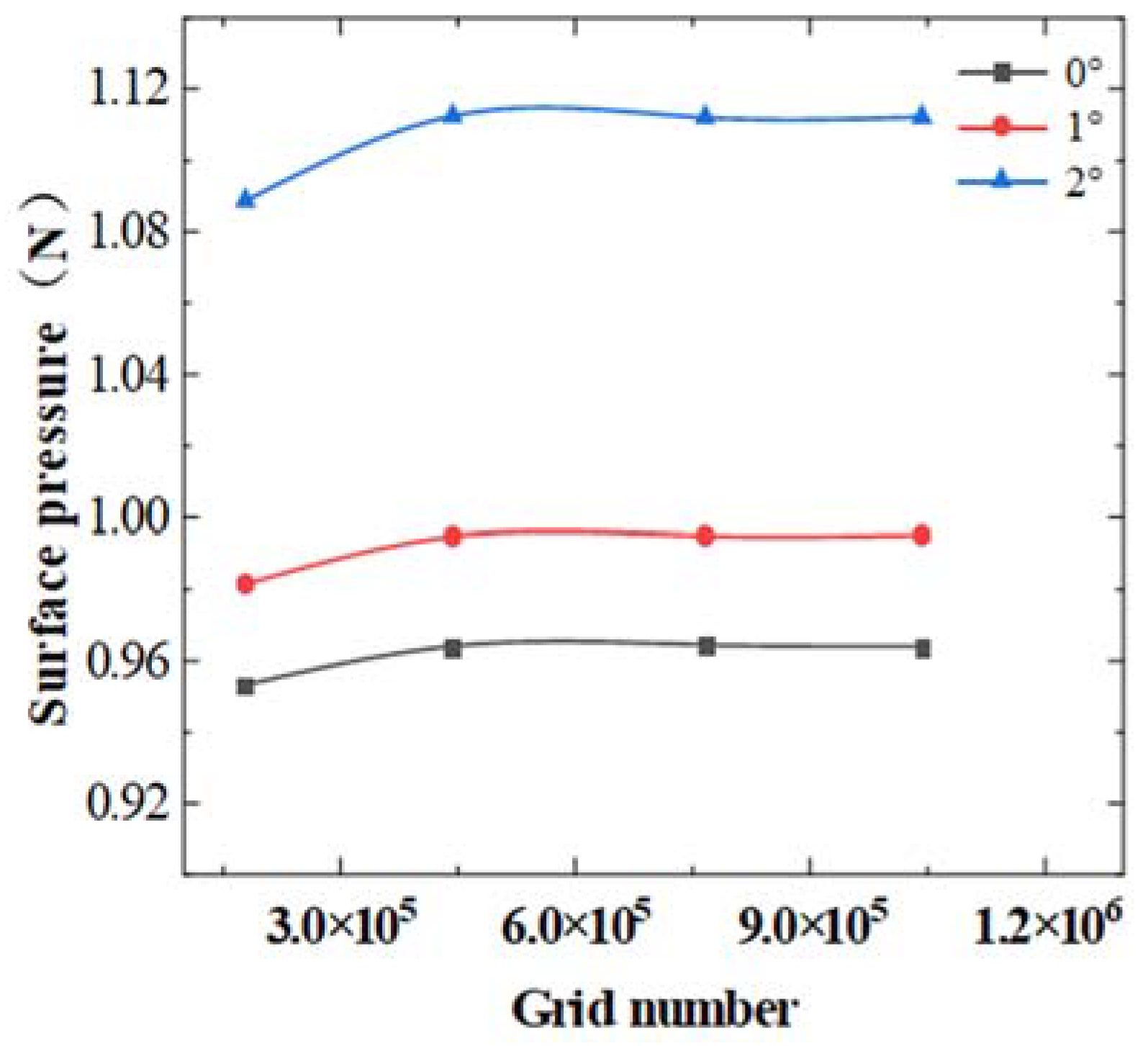
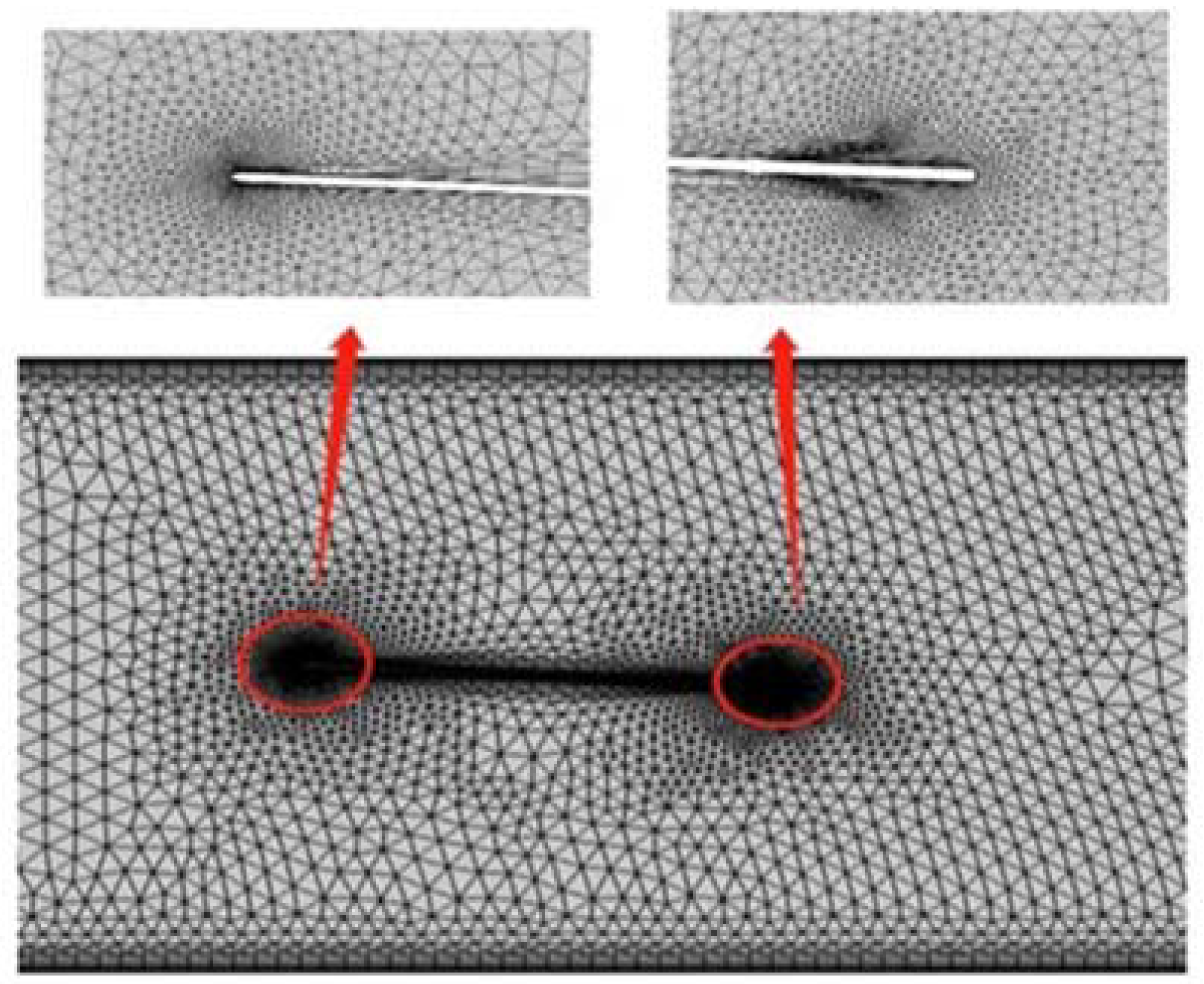

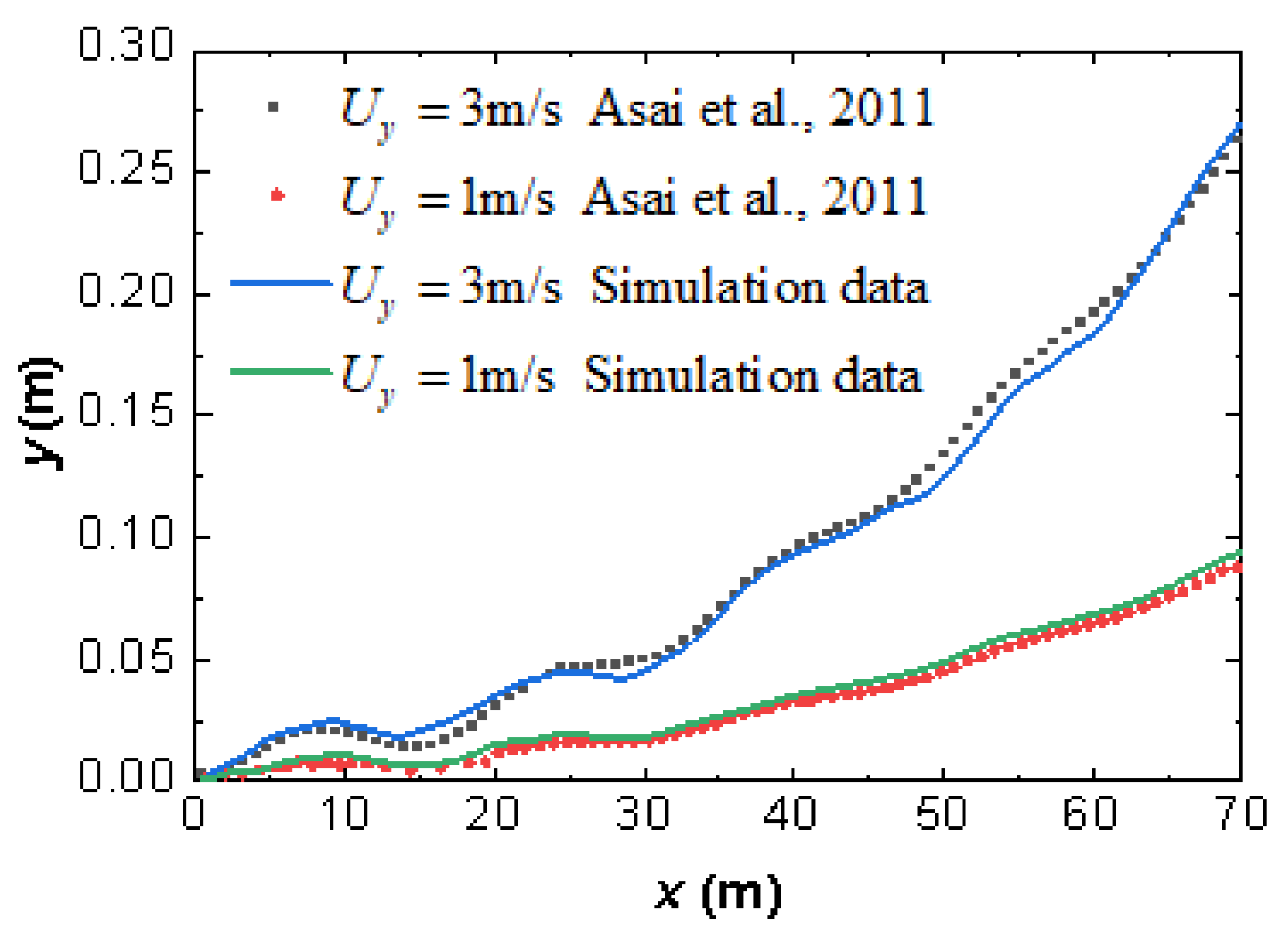





| Symbol | Characteristic | Parameter |
|---|---|---|
| M [kg] | Mass | 0.0197 |
| L [m] | Length | 0.625 |
| R [m] | Shaft radius | 2.4 × 10−3 |
| h [m] | Vane thickness | 1× 10−4 |
| Case | 0° | 1° | 2° |
|---|---|---|---|
| A | 178,767 | 180,213 | 182,236 |
| B | 443,473 | 449,813 | 435,662 |
| C | 765,932 | 769,542 | 776,529 |
| D | 1,042,675 | 1,022,884 | 1,041,078 |
| Symbol | Characteristic | Parameter |
|---|---|---|
| α [1/rad] | Alpha | 45.1 |
| β [1/rad] | Beta | 21.2 |
| Sp | Spin parameter | 0.0034 |
| CD (lam) | Drag coefficient | 1.63 |
| CD (turb) | Drag coefficient | 3.23 |
| V0 [m·s−1] | Initial velocity | 57 |
| c.g. [m] | Center of gravity | 0.19 |
| I3 [kg·m2] | Moment of inertia | 3.23 × 10−7 |
| I [kg·m2] | Moment of inertia | 8.79 × 10−4 |
| 1 | 2 | 3 | |
|---|---|---|---|
| C0 | 0.49266 | ||
| C1 | 0.48726 | ||
| −3.05668 | −1.1604 | 1.1752 | |
| 0.98994 | 2.43656 | 1.11593 | |
| −0.00819 | −0.04134 | 0.00793 | |
| −1.49773 | −0.01171 | 1.59082 | |
| 0.75978 | 0.786 | 1.3424 | |
| 0.00267 | −0.0033 | 0.00443 | |
| δr ( is Fixed) | δr ( is not Fixed) | Improvement of Accuracy | |
|---|---|---|---|
| Uy = 1 m/s | 0.103 m | 0.091 m | 13% |
| Uy = 2 m/s | 0.188 m | 0.161 m | 16% |
| Uy = 3 m/s | 0.302 m | 0.258 m | 17% |
| Ux = 1 m/s | 0.049 m | 0.046 m | 6% |
| Ux = 2 m/s | 0.066 m | 0.061 m | 8% |
| Ux = 3 m/s | 0.084 m | 0.078 m | 7% |
| Ux = −1 m/s | 0.053 m | 0.049 m | 8% |
| Ux = −2 m/s | 0.070 m | 0.064 m | 9% |
| Ux = −3 m/s | 0.092 m | 0.085 m | 8% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shen, W.; Hu, L.; Hu, J.; Xu, Y.; Xu, X.; Zheng, J. Influences of an Arrow’s Aerodynamic Pressure Center on Recurve Bow Shooting. Appl. Sci. 2025, 15, 2168. https://doi.org/10.3390/app15042168
Shen W, Hu L, Hu J, Xu Y, Xu X, Zheng J. Influences of an Arrow’s Aerodynamic Pressure Center on Recurve Bow Shooting. Applied Sciences. 2025; 15(4):2168. https://doi.org/10.3390/app15042168
Chicago/Turabian StyleShen, Wenfeng, Liang Hu, Jing Hu, Yiming Xu, Xixia Xu, and Jieqing Zheng. 2025. "Influences of an Arrow’s Aerodynamic Pressure Center on Recurve Bow Shooting" Applied Sciences 15, no. 4: 2168. https://doi.org/10.3390/app15042168
APA StyleShen, W., Hu, L., Hu, J., Xu, Y., Xu, X., & Zheng, J. (2025). Influences of an Arrow’s Aerodynamic Pressure Center on Recurve Bow Shooting. Applied Sciences, 15(4), 2168. https://doi.org/10.3390/app15042168






