Numerical Simulation for Impeller Structure Optimization for Vortex Pump Based on Orthogonal Design Method
Abstract
1. Introduction
2. Calculation Model
2.1. Model Structure
2.2. Theoretical Model
2.2.1. Control Equation
2.2.2. Main Performance
2.3. Simulation Model
2.4. Boundary Condition
3. Calculation Results and Analysis
3.1. Influence of Different Rotational Speeds on Internal Fluid Velocity
3.2. Influence of Different Rotational Speeds on Internal Fluid Pressure
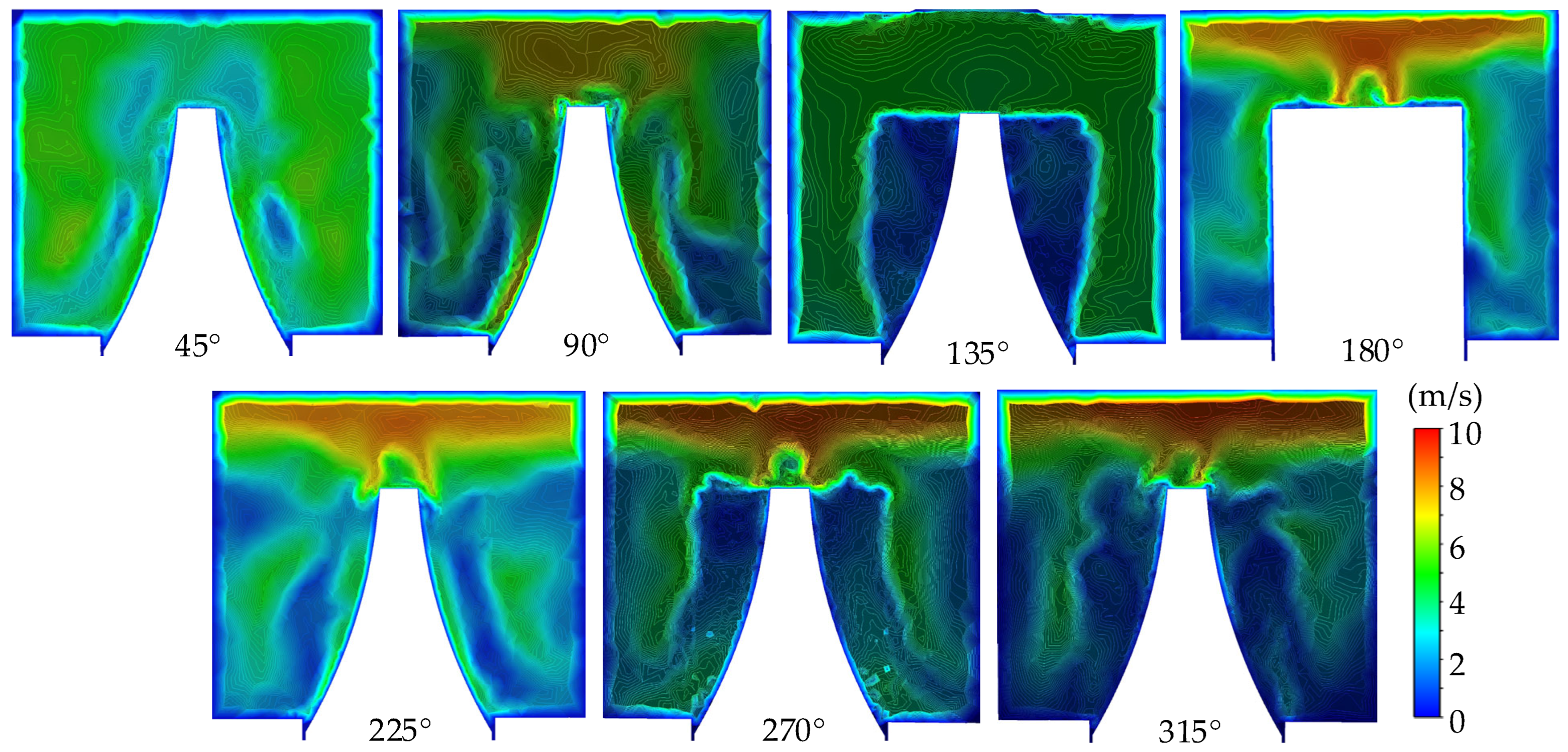
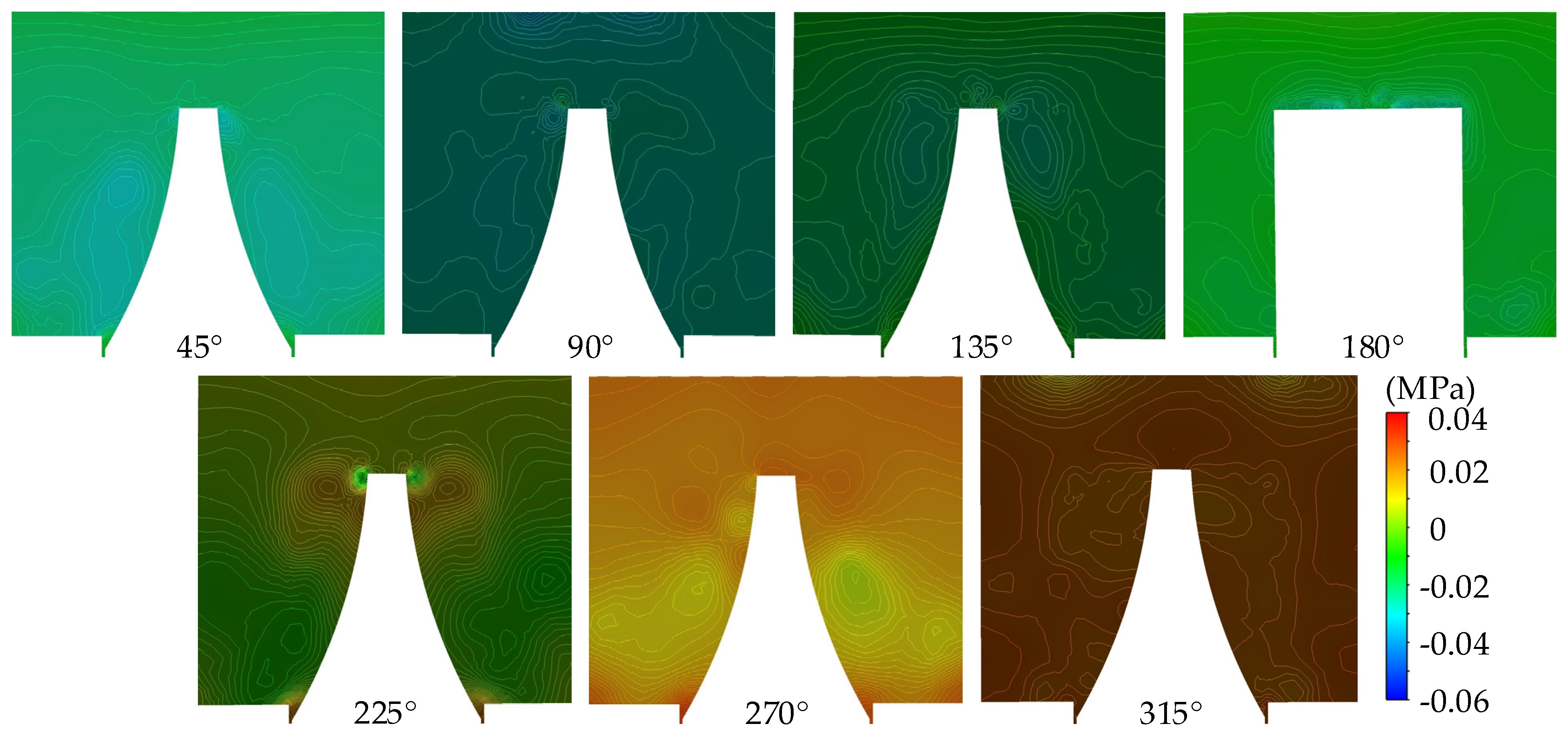
3.3. Characteristics of Fluid Velocity and Pressure Changes Under Different Circumferential Sections
3.4. Characteristics of Fluid Velocity Vector Variation Under Different Sections
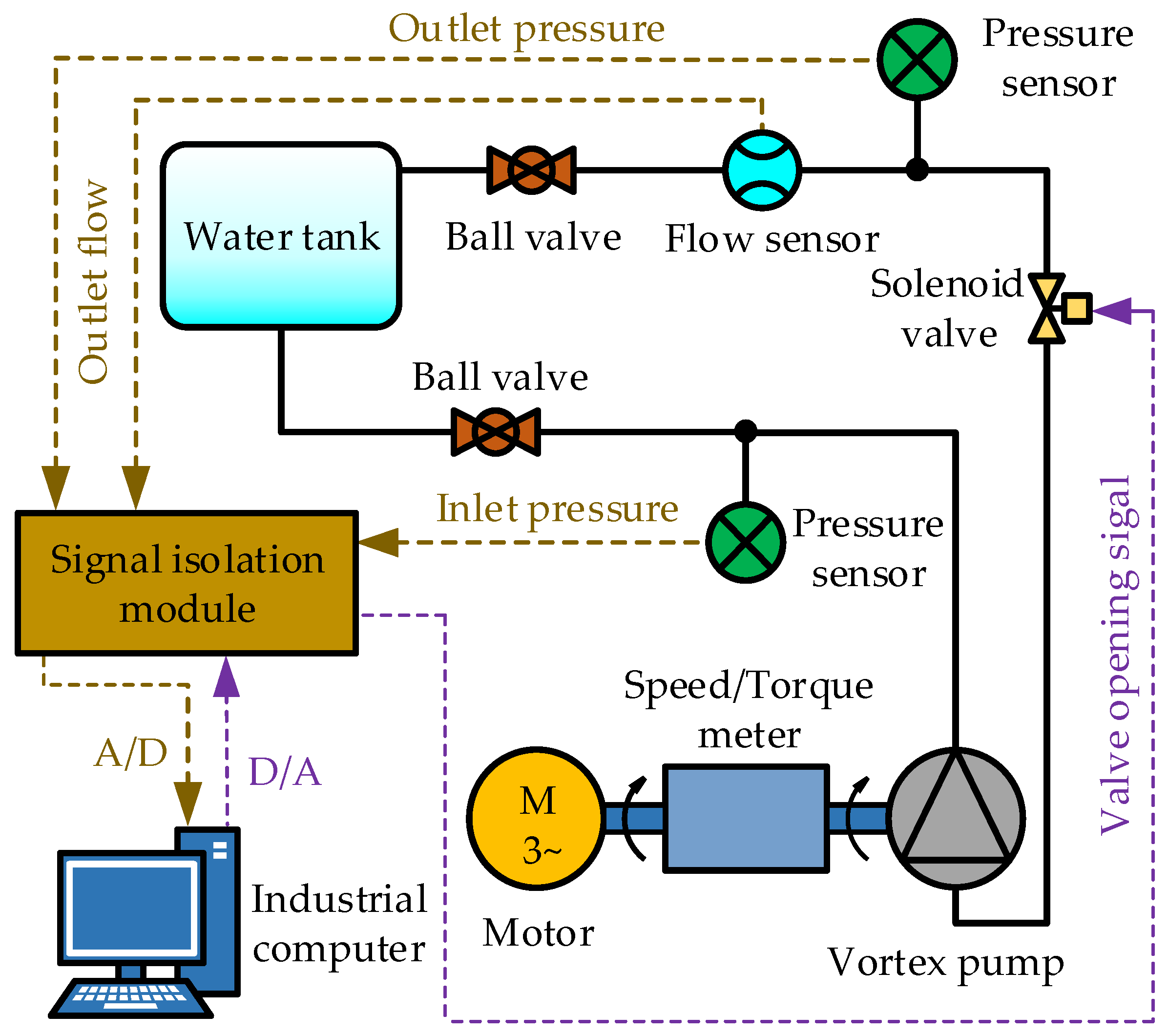
4. Experimental Verification
5. Structural Optimization of the Vortex Pump
5.1. Optimization Scheme
- Impeller diameter D2: The recommended design range of impeller diameter D2 is usually 40~50 mm. For closed vortex pumps, it is necessary to consider that the value range of the clearance δ2 between the impeller and the baffle tongue is usually 0.1~0.3 mm. Based on the basic parameter D2, which is 45.9 mm of the impeller diameter of the original model in Table 1, the corresponding value of δ2 is 0.1. Compared with the original model, the values of the slightly smaller 45.7 and 45.8, the final D2 is selected as 45.7, 45.8, and 45.9 as the three levels for D2.
- Blade groove radius r: The blade groove is the hub structure connecting the blade, and its radius plays a decisive role in the overall performance of the pump. If the radius of the blade groove is small, the tip of the groove can be sharp, which inhibits the formation of vortices and reduces the effective transfer of energy. In contrast, if the radius of the blade groove is large, the flow of fluid between the vanes is restricted, which prevents the smooth flow of fluid and leads to the decline in the overall performance of the pump. Therefore, based on the basic parameter r of the blade groove radius of 15 of the vortex pump for the original model in Table 1, the final r is 14.9, 15, and 15.1 as the three levels.
- Blade number Z: Through preliminary screening through single-factor simulation calculation, the overall performance of the vortex pump is poor when the number of blades is less than 27. When the number of blades is 27~33, the pump head can be increased. When the number of blades is greater than 33, the increase in head and efficiency growth slows down or even decreases in order to reduce the load per unit area of the blade and enhance the constraint of the fluid between the blades. Therefore, based on the basic parameter Z of the blade number, which is 30 of the vortex pump blades for the original model in Table 1, the final Z is selected as 28, 30, and 32 as three levels.
- Impeller width b: The axial clearance δ1 formed between the impeller and the shell is the key parameter that affects the flow rate and high head, and the value of δ1 is usually 0.04~0.25 mm. In order to reduce the volume loss of the vortex pump and meet the performance of the pump, the δ1 value corresponding to 5.15 of the impeller width b of the original model in Table 1 is 0.22. Considering that it is convenient to compare the performance differences between the two larger impeller widths and the original model impeller width, we selected the value 5.37, which lies midway between 5.15 and 5.51. Therefore, the value 5.37, which is larger than both 5.15 and 5.51, was chosen. Finally, 5.15, 5.37, and 5.51 are selected as the three levels for b.
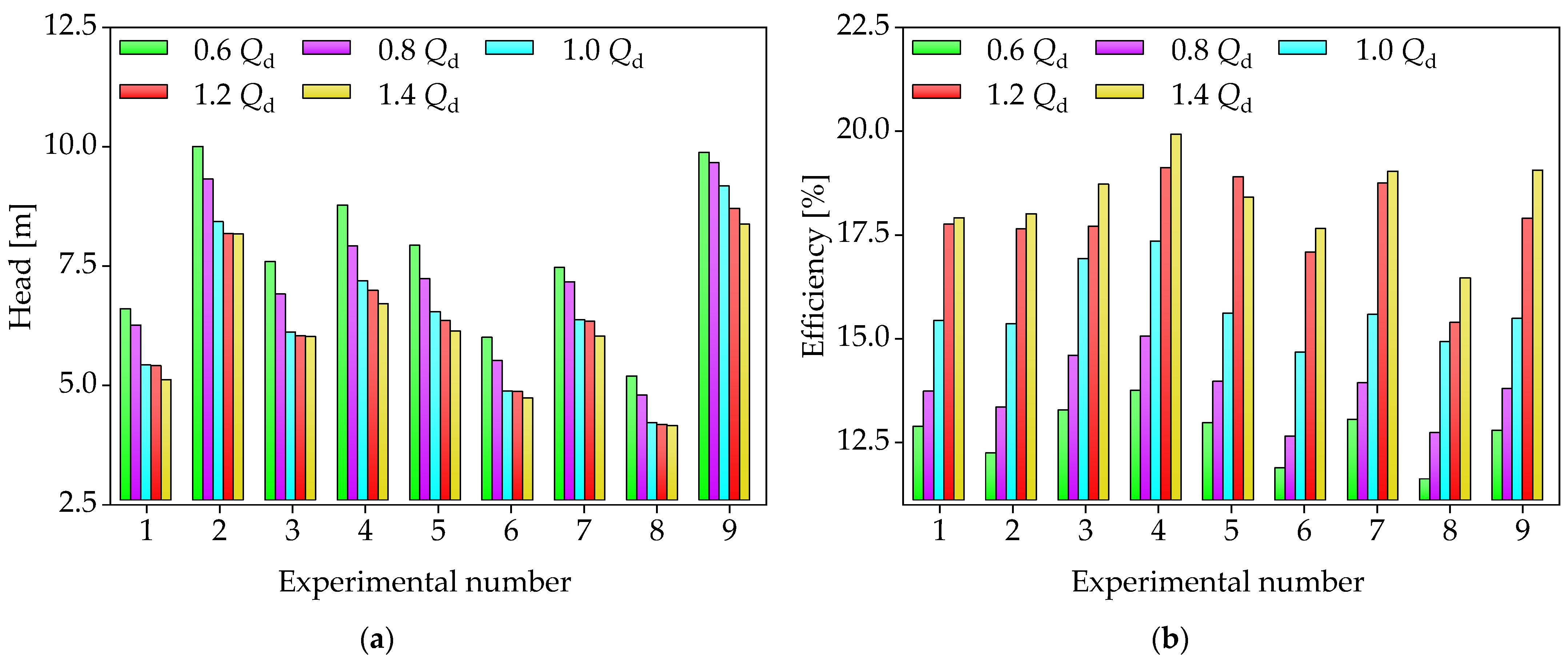
5.2. Optimal Results
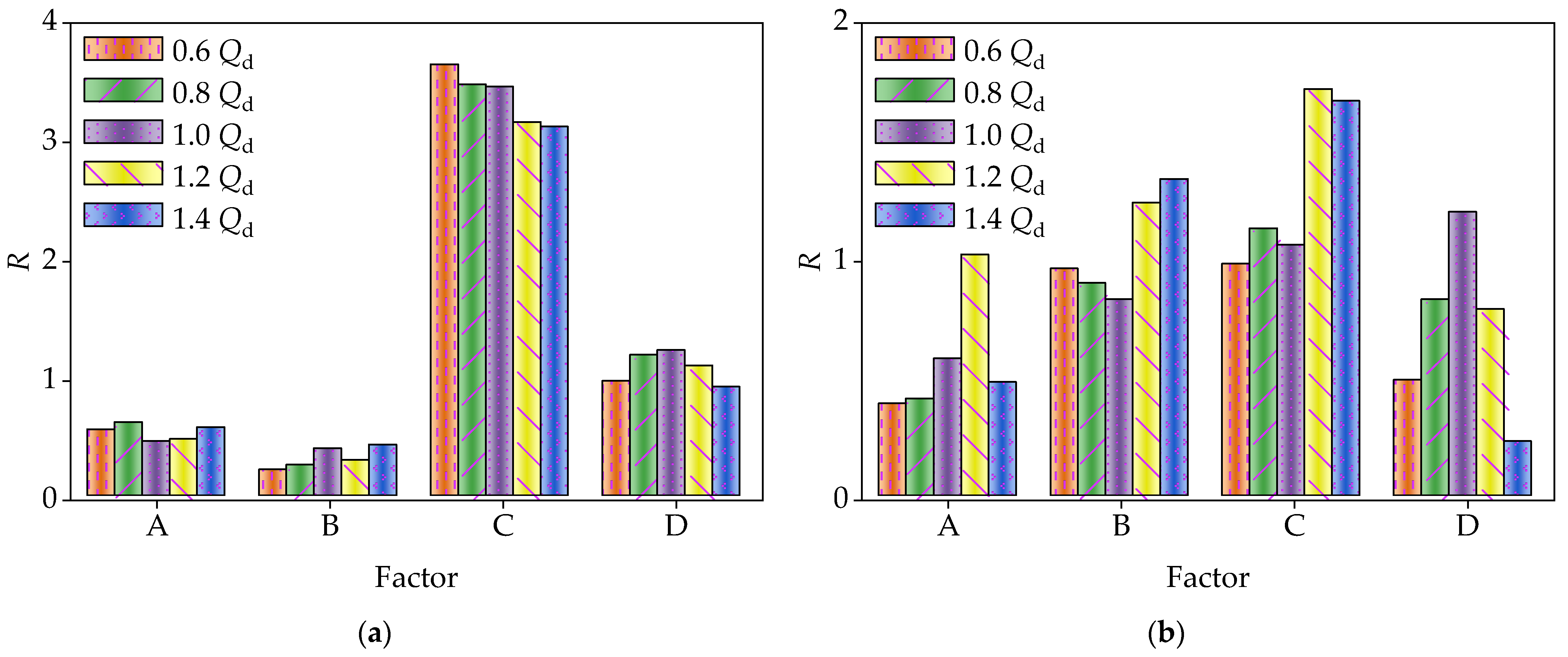
- Under the working condition of 0.6Qd~1.0Qd, the influence degree of each factor on the head H is C, D, A, and B from large to small.
- Under the condition of 0.6Qd~0.8Qd, the values of B and C are close, and the degree of influence of each factor on the efficiency η is C, B, D, and A in order from large to small. Under the working condition of 1.2Qd~1.4Qd, the influence degree of each factor on the efficiency η is C, B, A, and D in order from large to small. Under 1.0Qd condition, the values of B, C, and D are close, and the degree of influence of each factor on the efficiency η is D, C, B, and A in order from large to small. Since the design of the vortex pump model is more focused on the efficiency improvement of the rated working condition of 1.0Qd. Overall, in the working condition of 0.6Qd~1.4Qd, the influence degree of each factor on η is C, B, D, and A in order from large to small.
- In the working condition of 0.6Qd~1.4Qd, the value of C is far greater than the value of the other three factors, and C can be determined as the primary factor affecting the performance of the vortex pump.
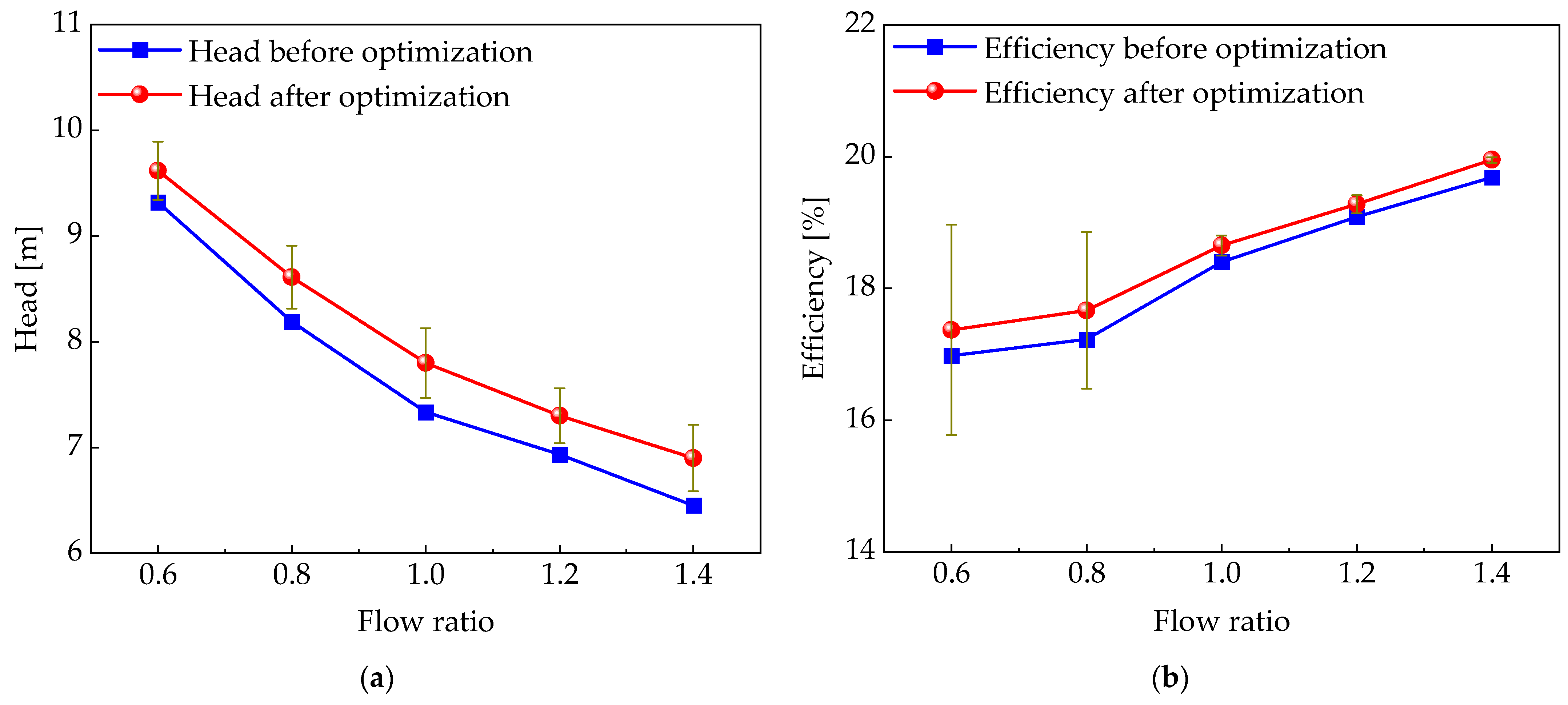
5.3. Comparison of External Characteristics
6. Conclusions
- The internal fluid velocity of the vortex pump is closely related to the speed of the pump. As the rotational speed increases, the fluid velocity gradually increases, especially in the outer edge area of the impeller. At the same time, the fluid pressure also increases, which promotes the formation of higher pressure at the outlet of the pump, thereby achieving high head.
- The flow field structure internal to the vortex pump is extremely complex, and the fluid generates longitudinal vortices in the blade root area, which are subsequently transformed into transverse vortices. The fluid in the flow channel forms circular longitudinal vortices, and the continuous formation and shedding of these vortices provide continuous energy output for the vortex pump, which improves the performance of the pump.
- The system performance of the vortex pump is optimized by applying the orthogonal design method. The range analysis method further determines the primary factors affecting pump performance, which are the number of blades, impeller width, impeller diameter, and blade groove radius. Through the optimization, the optimal combination of impeller structural parameters is determined as impeller diameter D2 of 45.7 mm, blade groove radius r of 14.9 mm, blade number Z of 32, and impeller width b of 5.15 mm. The optimization of these parameters significantly improved the overall performance of the vortex pump.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Quan, H.; Fu, B.H.; Li, R.N.; Zhang, T.; Han, W.; Li, J. Research stage and development tendency of vortex pump. Fluid Mach. 2016, 44, 36–40. [Google Scholar]
- Zhang, F.; Fleder, A.; Böhle, M.; Yuan, S.Q. Effect of suction side blade profile on the performance of a side channel pump. Proc. Inst. Mech. Eng. Part A J. Power Energy 2016, 230, 586–597. [Google Scholar] [CrossRef]
- Mihalic, T.; Guzovic, Z.; Predin, A. Performances and flow analysis in the centrifugal vortex pump. J. Fluids Eng. 2013, 135, 011107. [Google Scholar] [CrossRef]
- Liu, R.J.; Zheng, F.J.; Fu, P.D.; Wang, P. Orthogonal test and experimental study on fire floating pump. IOP Conf. Ser. Mater. Sci. Eng. 2013, 52, 032010. [Google Scholar] [CrossRef]
- Mosshammer, M.; Benigni, H.; Jaberg, H.; Konrad, J. Maximum Efficiency Despite Lowest Specific Speed-Simulation and Optimisation of a Side Channel Pump. Int. J. Turbomach. Propuls. Power 2019, 4, 6. [Google Scholar] [CrossRef]
- Zhang, B.W.; Cheng, L.; Zhu, M.H.; Jiao, W.X.; Zhang, D. Numerical simulation and analysis of the flow characteristics of the roof-attached vortex (RAV) in a closed pump sump. Machines 2022, 10, 209. [Google Scholar] [CrossRef]
- Wu, X.; Shao, C.; Tan, M.; Liu, H.; Hua, R.; Li, H. Unsteady flow and excitation characteristics in a vortex pump. Flow Meas. Instrum. 2024, 100, 102716. [Google Scholar] [CrossRef]
- Cheng, Y.; Li, W.; Ma, S.; Ji, L.; Xiao, C.; Li, Y. The Influence of Different Working Fluid Temperatures on the Hydraulic Performance of Magnetic Vortex Pumps. Water 2024, 16, 1601. [Google Scholar] [CrossRef]
- Zhao, K.; Tan, M.; Wu, X.; Shao, C.; Liu, H. Effect of impeller installation position on unsteady flow characteristics of a vortex pump. Eng. Comput. 2023, 40, 335–347. [Google Scholar] [CrossRef]
- Barrio, R.; Parrondo, J.; Blanco, E. Numerical analysis of the unsteady flow in the near-tongue region in a volute-type centrifugal pump for different operating points. Comput. Fluids 2010, 39, 859–870. [Google Scholar] [CrossRef]
- Jafarzadeha, B.; Hajari, A.; Alishahi, M.M.; Akbari, M.H. The flow simulation of a low-specific-speed high-speed centrifugal pump. Appl. Math. Model. 2011, 35, 242–249. [Google Scholar] [CrossRef]
- Gao, X.F.; Zhao, T.; Shi, W.D.; Zhang, D.S.; Shi, Y.; Zhou, L.; Chang, H. Numerical Investigation of an Open-Design Vortex Pump with Different Blade Wrap Angles of Impeller. Processes 2020, 8, 1601. [Google Scholar] [CrossRef]
- Dai, L.; Gu, L.; Wang, J.; Ao, X.; Zhu, X.B. The Effect of Impeller Indent Distance on the Performance of Vortex Pumps. Int. J. Fluid Mach. Syst. Int. J. Fluid Mach. Syst. 2020, 13, 42–54. [Google Scholar] [CrossRef]
- Quan, H.; Cheng, J.; Guo, Y.; Kang, L.; Peng, G.Y. Influence of Screw Centrifugal Inducer on Internal Flow Structure of Vortex Pump. J. Fluids Eng. 2020, 142, 091203. [Google Scholar] [CrossRef]
- Quan, H.; Li, Y.A.; Kang, L.; Yu, X.Y.; Song, K.; Wu, Y.K. Influence of Blade Type on the Flow Structure of a Vortex Pump for Solid-Liquid Two-Phase Flow. Machines 2021, 9, 353. [Google Scholar] [CrossRef]
- Quan, H.; Guo, Y.; Li, R.; Peng, G.; Su, Q.; Chai, Y. Optimization design and experimental study of vortex pump based on orthogonal test. Sci. Prog. 2019, 103, 0036850419881883. [Google Scholar] [CrossRef]
- Zhang, H.; Huang, S.H.; Zhou, J.P.; Song, M.; Song, W.B.; Ma, Y.M. Optimization Analysis of Head Cover Structure of High Head Pump Turbine. J. Phys. Conf. Ser. 2024, 2752, 012087. [Google Scholar]
- Sun, K.; Deng, H.S.; Zhang, S.W.; Hu, X.; Wang, C.; Wang, S.H.; Li, K.; Wang, L. A novel twisted rotor blade suitable for high-speed turbomolecular pumps: Numerical modelling and structural optimization. Heliyon 2024, 10, e26994. [Google Scholar] [CrossRef]
- Zhou, L.; Zhou, C.; Bai, L.; Agarwal, R. Numerical and Experimental Analysis of Vortex Pump with Various Axial Clearances. Water 2024, 16, 1602. [Google Scholar] [CrossRef]
- Tang, D.L.; Lu, Y.; Li, Q.Q.; Ge, J.; Miao, X.T. Numerical Investigation of Impeller Parameters on the Performance and Internal Flow Characteristics in Regenerative Flow Pumps. J. Phys. Conf. Ser. 2024, 2752, 012110. [Google Scholar] [CrossRef]
- Wang, C.; Luo, Y.; Li, Z.H.; Shen, Z.H.; Ye, D.X. Influence of Impeller Structure Parameters on the Hydraulic Performance and Casting Molding of Spiral Centrifugal Pumps. Water 2024, 16, 1598. [Google Scholar] [CrossRef]
- Liu, Q.; Zhuang, S.G.; Bao, H.F.; He, Z.F.; Wang, K.; Liu, H.L. The Optimization of a First-Stage Liquid-Sealing Impeller Structure for a Turbopump Based on Response Surface Methodology. Processes 2022, 10, 1999. [Google Scholar] [CrossRef]
- Chi, J.P. Optimization of vane pump structure based on modal characteristic analysis. Vibroeng. Procedia 2023, 52, 81–86. [Google Scholar] [CrossRef]
- Li, W.; Pu, W.; Ji, L.L.; Zhang, X.; He, X.R. Hydraulic structure optimization of centrifugal pump based on orthogonal test. J. Phys. Conf. Ser. 2024, 2707, 012056. [Google Scholar] [CrossRef]

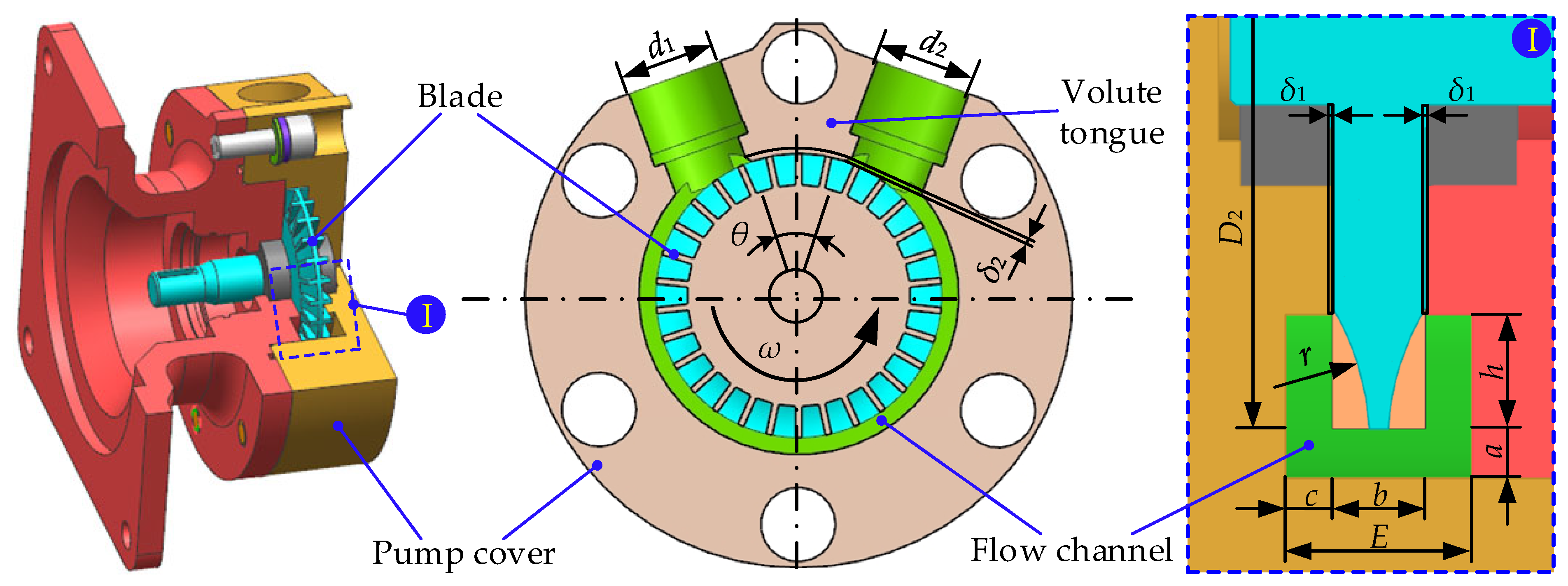




| Parameter | Value |
|---|---|
| Channel width, E (mm) | 10.32 |
| Impeller width, b (mm) | 5.15 |
| Inlet diameter, d1 (mm) | 15 |
| Outlet diameter, d2 (mm) | 15 |
| Tongue wrap angle, θ (°) | 60 |
| Blade groove radius, r (mm) | 15 |
| Impeller diameter, D2 (mm) | 45.9 |
| Number of blades, Z | 30 |
| Distance between the impeller outer diameter and the channel, a (mm) | 2.75 |
| Distance between the impeller end face and the channel, c (mm) | 2.36 |
| Blade height, h (mm) | 6.35 |
| Design head of the vortex pump, H (m) | 10 |
| Rated speed, n (r/min) | 3000 |
| Rated flow rate, Qd (L/min) | 10 |
| Total weight (kg) | 3 |
| Impeller materials | 2CrB-GJB2294-1995 |
| Level | Factor | |||
|---|---|---|---|---|
| A | B | C | D | |
| 1 | 45.7 | 14.9 | 28 | 5.15 |
| 2 | 45.8 | 15 | 30 | 5.37 |
| 3 | 45.9 | 15.1 | 32 | 5.51 |
| Experimental Number | Design Parameter | |||
|---|---|---|---|---|
| D2/mm | r/mm | Z/- | b/mm | |
| 1 | 45.7 | 14.9 | 28 | 5.15 |
| 2 | 45.7 | 15 | 32 | 5.37 |
| 3 | 45.7 | 15.1 | 30 | 5.51 |
| 4 | 45.8 | 14.9 | 32 | 5.51 |
| 5 | 45.8 | 15 | 30 | 5.15 |
| 6 | 45.8 | 15.1 | 28 | 5.37 |
| 7 | 45.9 | 14.9 | 30 | 5.37 |
| 8 | 45.9 | 15 | 28 | 5.51 |
| 9 | 45.9 | 15.1 | 32 | 5.15 |
| Parameter | H | η | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Index | R | R | |||||||
| 0.6Qd | A | 8.02 | 7.52 | 7.46 | 0.56 | 12.71 | 12.78 | 12.39 | 0.39 |
| B | 7.56 | 7.66 | 7.78 | 0.22 | 13.14 | 12.18 | 12.56 | 0.96 | |
| C | 5.87 | 7.62 | 9.52 | 3.65 | 12.03 | 13.01 | 12.83 | 0.98 | |
| D | 8.10 | 7.78 | 7.13 | 0.97 | 12.79 | 12.30 | 12.78 | 0.49 | |
| 0.8Qd | A | 7.45 | 6.83 | 7.16 | 0.62 | 13.81 | 13.80 | 13.40 | 0.41 |
| B | 7.05 | 7.06 | 7.31 | 0.26 | 14.16 | 13.26 | 13.59 | 0.90 | |
| C | 5.45 | 7.05 | 8.93 | 3.48 | 12.95 | 14.08 | 13.98 | 1.13 | |
| D | 7.67 | 7.28 | 6.48 | 1.19 | 13.75 | 13.22 | 14.05 | 0.83 | |
| 1.0Qd | A | 6.60 | 6.14 | 6.53 | 0.46 | 15.84 | 15.81 | 15.26 | 0.58 |
| B | 6.27 | 6.34 | 6.67 | 0.40 | 16.06 | 15.23 | 15.63 | 0.83 | |
| C | 4.76 | 6.28 | 8.22 | 3.46 | 14.94 | 15.98 | 16.00 | 1.06 | |
| D | 7.00 | 6.50 | 5.77 | 1.23 | 15.44 | 15.14 | 16.34 | 1.20 | |
| 1.2Qd | A | 6.49 | 6.01 | 6.35 | 0.48 | 17.65 | 18.32 | 17.30 | 1.02 |
| B | 6.19 | 6.18 | 6.48 | 0.30 | 18.50 | 17.26 | 17.51 | 1.24 | |
| C | 4.75 | 6.19 | 7.91 | 3.16 | 16.69 | 18.41 | 18.18 | 1.72 | |
| D | 6.77 | 6.41 | 5.67 | 1.10 | 18.14 | 17.78 | 17.35 | 0.79 | |
| 1.4Qd | A | 6.38 | 5.80 | 6.12 | 0.58 | 18.17 | 18.62 | 18.14 | 0.48 |
| B | 5.89 | 6.09 | 6.32 | 0.43 | 18.92 | 17.58 | 18.44 | 1.34 | |
| C | 4.59 | 6.00 | 7.71 | 3.12 | 17.29 | 18.68 | 18.96 | 1.67 | |
| D | 6.48 | 6.25 | 5.56 | 0.92 | 18.42 | 18.19 | 18.33 | 0.23 | |
| Parameter | 0.6Qd | 0.8Qd | 1.0Qd | 1.2Qd | 1.4Qd | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| A | B | C | D | A | B | C | D | A | B | C | D | A | B | C | D | A | B | C | D | |
| H | A1 | B3 | C3 | D1 | A1 | B3 | C3 | D1 | A1 | B3 | C3 | D1 | A1 | B3 | C3 | D1 | A1 | B3 | C3 | D1 |
| η | A2 | B1 | C2 | D1 | A1 | B1 | C2 | D3 | A1 | B1 | C3 | D3 | A2 | B1 | C2 | D1 | A2 | B1 | C3 | D1 |
| Index | Before Optimization | After Optimization | Improvement Rate |
|---|---|---|---|
| H | 7.64 m | 9.09 m | 18.90% |
| η | 11.79% | 13.16% | 11.60% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, J.; Li, X.; Cheng, D.; Ji, J.; Zhao, M.; Guo, W.; He, L. Numerical Simulation for Impeller Structure Optimization for Vortex Pump Based on Orthogonal Design Method. Appl. Sci. 2025, 15, 2265. https://doi.org/10.3390/app15052265
Yang J, Li X, Cheng D, Ji J, Zhao M, Guo W, He L. Numerical Simulation for Impeller Structure Optimization for Vortex Pump Based on Orthogonal Design Method. Applied Sciences. 2025; 15(5):2265. https://doi.org/10.3390/app15052265
Chicago/Turabian StyleYang, Jiahao, Xiangyang Li, Donghong Cheng, Jiangtao Ji, Mengwen Zhao, Wen Guo, and Lile He. 2025. "Numerical Simulation for Impeller Structure Optimization for Vortex Pump Based on Orthogonal Design Method" Applied Sciences 15, no. 5: 2265. https://doi.org/10.3390/app15052265
APA StyleYang, J., Li, X., Cheng, D., Ji, J., Zhao, M., Guo, W., & He, L. (2025). Numerical Simulation for Impeller Structure Optimization for Vortex Pump Based on Orthogonal Design Method. Applied Sciences, 15(5), 2265. https://doi.org/10.3390/app15052265





