A Comparison of the Application of Load Monitoring Metrics for Key Match Characteristics in Women’s Rugby Sevens
Abstract
Featured Application
Abstract
1. Introduction
2. Materials and Methods
2.1. Participant Information
2.2. Procedures
2.3. Statistical Analysis
3. Results
3.1. Workload Measures and Match Category
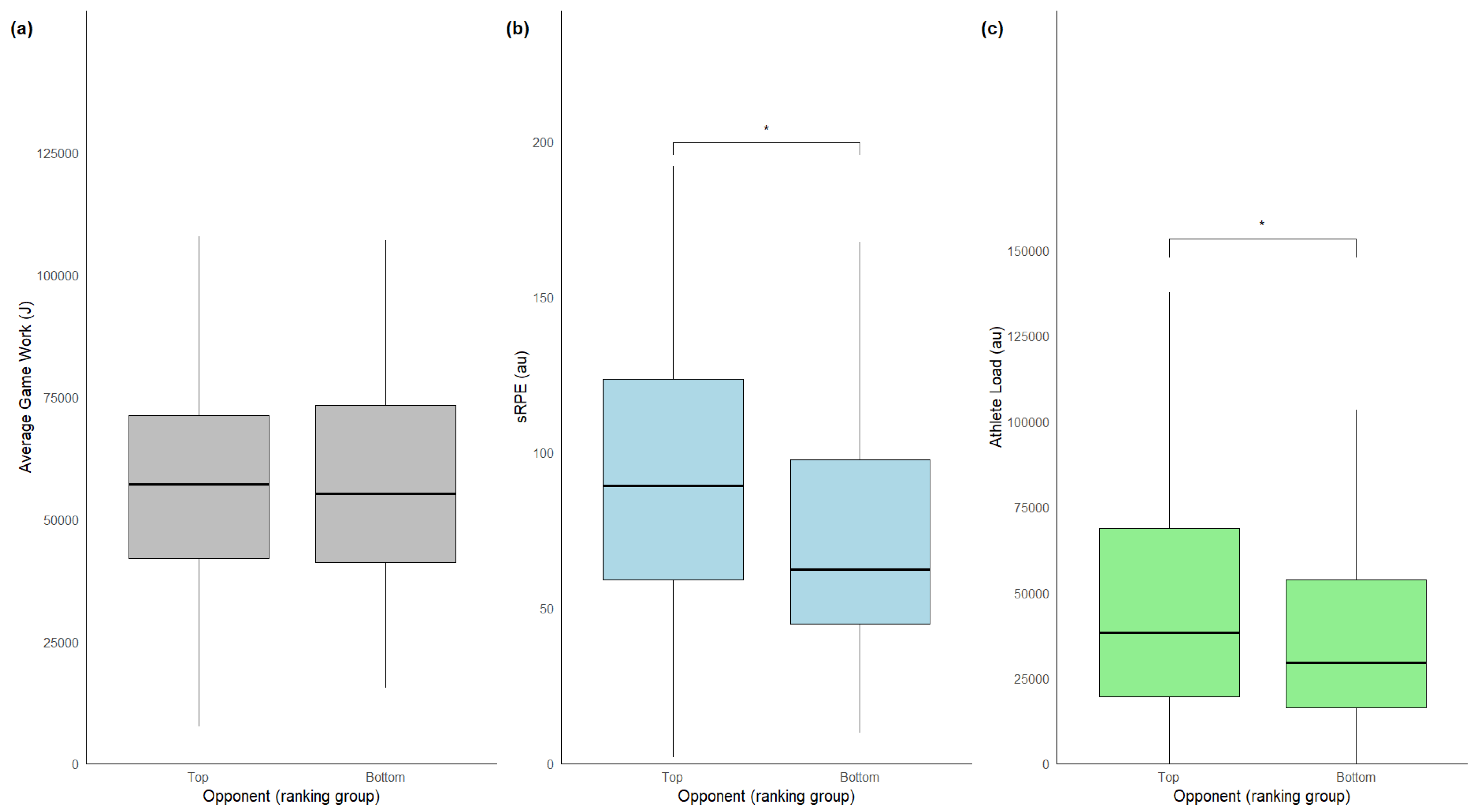
3.2. Workload Measures and Opponent
3.3. Workload Measures and Match Outcome
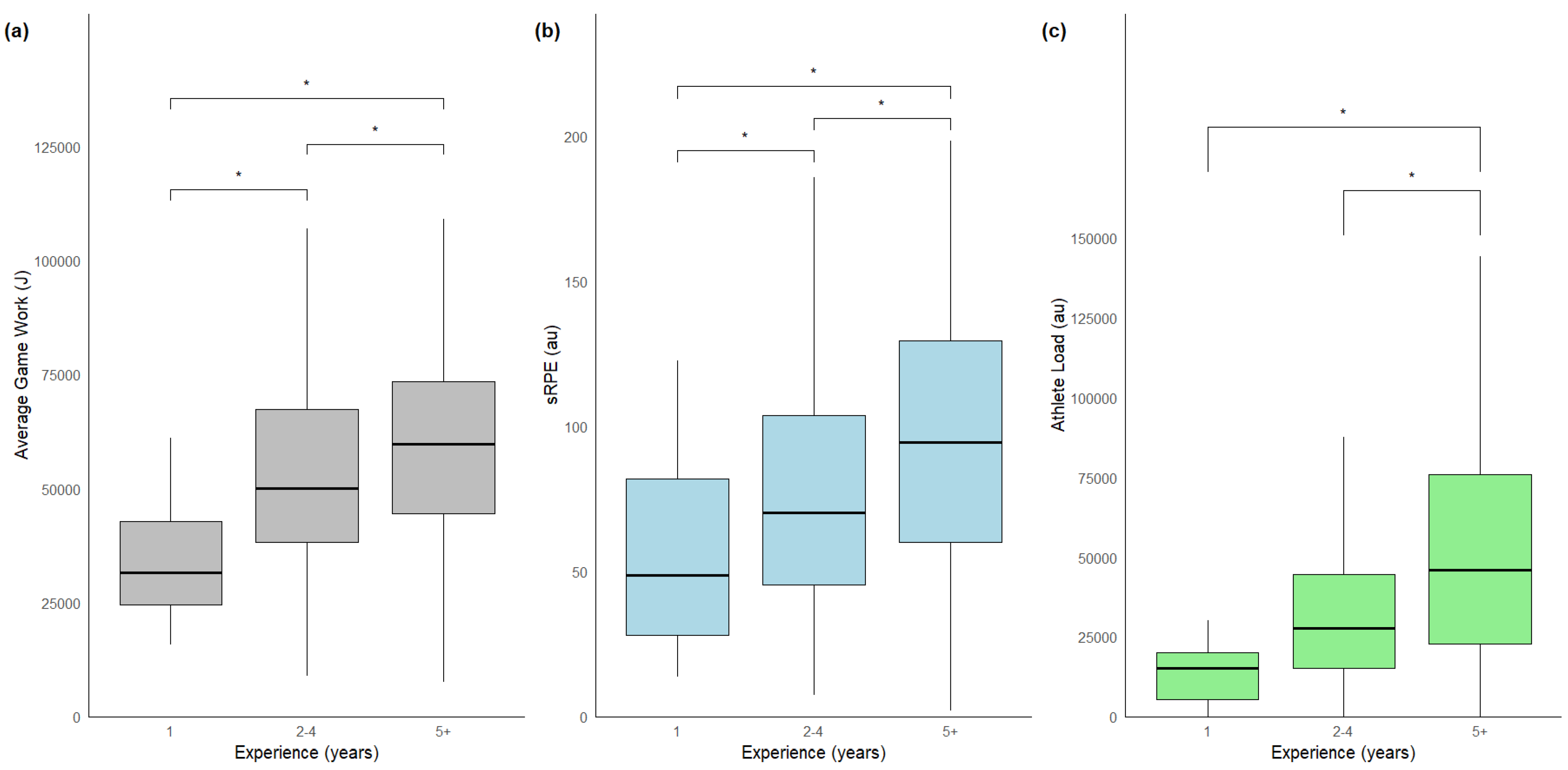
3.4. Workload Measures and Player Experience
4. Discussion
4.1. Workload Measures and Match Category
4.2. Workload Measures and Opponent
4.3. Workload Measures and Match Outcome
4.4. Workload Measures and Player Experience
4.5. Considerations for Use of Workload Measures
5. Limitations
6. Practical Implications
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Arjol-Serrano, J.L.; Lampre, M.; Díez, A.; Castillo, D.; Sanz-López, F.; Lozano, D. The influence of playing formation on physical demands and technical-tactical actions according to playing positions in an elite soccer team. Int. J. Environ. Res. Public Health 2021, 18, 4148. [Google Scholar] [CrossRef]
- Folgado, H.; Duarte, R.; Fernandes, O.; Sampaio, J. Competing with lower level opponents decreases intra-team movement synchronization and time-motion demands during pre-season soccer matches. PLoS ONE 2014, 9, e97145. [Google Scholar] [CrossRef] [PubMed]
- Oliveira, R.; Brito, J.M.; Loureiro, N.; Padinha, V.; Ferreira, B.; Mendes, B. Effects of match location, match result and the quality of opposition in training load on a two-matches week in a top-class elite European soccer team. Cuad. Psicol. Deporte 2021, 21, 183–197. [Google Scholar] [CrossRef]
- Gallo, T.; Cormack, S.; Gabbett, T.; Williams, M.; Lorenzen, C. Characteristics impacting on session rating of perceived exertion training load in Australian footballers. J. Sports Sci. 2014, 33, 467–475. [Google Scholar] [CrossRef]
- Bourdon, P.C.; Cardinale, M.; Murray, A.; Gastin, P.; Kellmann, M.; Varley, M.C.; Gabbett, T.J.; Coutts, A.J.; Burgess, D.J.; Gregson, W.; et al. Monitoring athlete training loads: Consensus statement. Int. J. Sport Physiol. 2017, 12, 161–170. [Google Scholar] [CrossRef] [PubMed]
- Gabbett, T.J. The training-injury prevention paradox: Should athletes be training smarter and harder? Br. J. Sports Med. 2016, 50, 273–280. [Google Scholar] [CrossRef] [PubMed]
- Haddad, M.; Stylianides, G.; Djaoui, L.; Dellal, A.; Chamari, K. Session-RPE method for training load monitoring: Validity, ecological usefulness, and influencing factors. Front. Neurosci. 2017, 11, 612. [Google Scholar] [CrossRef] [PubMed]
- Delaney, J.A.; Cummins, C.J.; Thornton, H.R.; Duthie, G.M. Importance, reliability, and usefulness of acceleration measures in team sports. J. Strength Cond. Res. 2018, 32, 3485–3493. [Google Scholar] [CrossRef]
- Mara, J.K.; Thompson, K.G.; Pumpa, K.L.; Morgan, S. The acceleration and deceleration profiles of elite female soccer players during competitive matches. J. Sci. Med. Sport 2017, 20, 867–872. [Google Scholar] [CrossRef] [PubMed]
- Staunton, C.A.; Abt, G.; Weaving, D.; Wundersitz, D.W.T. Misuse of the term ‘load’ in sport and exercise science. J. Sci. Med. Sport 2022, 25, 439–444. [Google Scholar] [CrossRef] [PubMed]
- Epp-Stobbe, A.; Tsai, M.C.; Klimstra, M. Work smarter not harder: Mechanical work as a measure of athlete workload. ISBS Proc. Arch. 2024, 42, 51. [Google Scholar]
- Bartlett, J.D.; O’Connor, F.; Pitchford, N.; Torres-Ronda, L.; Robertson, S.J. Relationships between internal and external training load in team-sport athletes: Evidence for an individualized approach. Int. J. Sports Physiol. Perform. 2017, 12, 230–234. [Google Scholar] [CrossRef] [PubMed]
- Epp-Stobbe, A.; Tsai, M.-C.; Klimstra, M.D. Predicting Athlete Workload in Women’s Rugby Sevens Using GNSS Sensor Data, Contact Count and Mass. Sensors 2024, 24, 6699. [Google Scholar] [CrossRef] [PubMed]
- Schuster, J.; Howells, D.; Robineau, J.; Couderc, A.; Natera, A.; Lumley, N.; Gabbett, T.J.; Winkelman, N. Physical-preparation recommendations for elite rugby sevens performance. Int. J. Sports Physiol. Perform. 2018, 13, 255–267. [Google Scholar] [CrossRef]
- Delaney, J.A.; Duthie, G.M.; Thornton, H.R.; Scott, T.J.; Gay, D.; Dascombe, B.J. Acceleration-based running intensities of professional rugby league match play. Int. J. Sports Physiol. Perform. 2016, 11, 802–809. [Google Scholar] [CrossRef] [PubMed]
- Epp-Stobbe, A.; Tsai, M.-C.; Klimstra, M. Comparison of Imputation Methods for Missing Rate of Perceived Exertion Data in Rugby. Mach. Learn. Knowl. Extr. 2022, 4, 827–838. [Google Scholar] [CrossRef]
- Ferioli, D.; Scanlan, A.T.; Conte, D.; Tibiletti, E.; Rampinini, E. The business end of the season: A comparison between playoff and regular-season workloads in professional basketball players. Int. J. Sports Physiol. Perform. 2021, 16, 655–662. [Google Scholar] [CrossRef] [PubMed]
- Schultz de Arruda, A.F.; Aoki, M.S.; Drago, G.; Moreira, A. Salivary testosterone concentration, anxiety, perceived performance and ratings of perceived exertion in basketball players during semi-final and final matches. Physiol. Behav. 2019, 198, 102–107. [Google Scholar] [CrossRef] [PubMed]
- Gabbett, T.J. Relationship Between Accelerometer Load, Collisions, and Repeated High-Intensity Effort Activity in Rugby League Players. J. Strength Cond. Res. 2015, 29, 3424–3431. [Google Scholar] [CrossRef]
- Cunniffe, B.; Proctor, W.; Baker, J.S.; Davies, B. An Evaluation of the Physiological Demands of Elite Rugby Union Using Global Positioning System Tracking Software. J. Strength Cond. Res. 2009, 23, 1195–1203. [Google Scholar] [CrossRef]
- Vescovi, J.D. Physical demands of regular season and playoff matches in professional women’s soccer: A pilot from the Female Athletes in Motion (FAiM) study. In International Research in Science and Soccer II; Reilly, T., Korkusuz, F., Eds.; Routledge: London, UK, 2015; p. 12. [Google Scholar]
- Barrett, S.; McLaren, S.; Spears, I.; Ward, P.; Weston, M. The influence of playing position and contextual factors on soccer players’ match differential ratings of perceived exertion: A preliminary investigation. Sports 2018, 6, 13. [Google Scholar] [CrossRef] [PubMed]
- Epp-Stobbe, A.; Tsai, M.C.; Morris, C.; Klimstra, M. The influence of physical contact on athlete load in international female rugby sevens. J. Strength Cond. Res. 2022, 37, 383–387. [Google Scholar] [CrossRef] [PubMed]
- Fessi, M.S.; Moalla, W. Postmatch perceived exertion, feeling, and wellness in professional soccer players. Int. J. Sports Physiol. Perform. 2018, 13, 631–637. [Google Scholar] [CrossRef] [PubMed]
- Gabbett, T.J. Influence of the opposing team on the physical demands of elite rugby league match play. J. Strength Cond. Res. 2013, 27, 1629–1635. [Google Scholar] [CrossRef]
- Hills, S.P.; Izri, E.; Howells, D.; Lonergan, B.; Kilduff, L.P.; Waldron, M. Assessing the locomotor demands of international men’s and women’s rugby sevens match-play according to passage of play. PLoS ONE 2024, 19, e0304186. [Google Scholar] [CrossRef]
- Becirovic, M.; Bischofberger, J.; Kornfeind, P.; Stifter, S.; Baca, A. Analysis of sprint-related performance indicators in professional youth soccer across age groups & positions. ISBS Proc. Arch. 2024, 42, 218. [Google Scholar]
- Griffin, A.; Kenny, I.C.; Comyns, T.M.; Purtill, H.; Tiernan, C.; O’Shaughnessy, E.; Lyons, M. Training load monitoring in team sports: A practical approach to addressing missing data. J. Sports Sci. 2021, 39, 2161–2171. [Google Scholar] [CrossRef] [PubMed]
- Guyon, J. Choose your opponent: A new knockout design for hybrid tournaments. J. Sports Anal. 2022, 8, 9–29. [Google Scholar] [CrossRef]
- Saw, A.E.; Main, L.C.; Gastin, P.B. Monitoring the athlete training response: Subjective self-reported measures trump commonly used objective measures: A systematic review. Br. J. Sports Med. 2016, 50, 281–291. [Google Scholar] [CrossRef]
- Coyne, J.O.C.; Haff, G.G.; Coutts, A.J.; Newton, R.U.; Nimphius, S. The current state of subjective training load monitoring—A practical perspective and call to action. Sports Med. Open 2018, 4, 58. [Google Scholar] [CrossRef]
- Gabbett, T.J.; Nassis, G.P.; Oetter, E.; Pretorius, J.; Johnston, N.; Medina, D.; Rodas, G.; Myslinski, T.; Howells, D.; Beard, A.; et al. The athlete monitoring cycle: A practical guide to interpreting and applying training monitoring data. Br. J. Sports Med. 2017, 51, 1451–1452. [Google Scholar] [CrossRef]
- West, S.W.; Clubb, J.; Torres-Ronda, L.; Howells, D.; Leng, E.; Vescovi, J.D.; Carmody, S.; Posthumus, M.; Dalen-Lorentsen, T.; Windt, J. More than a metric: How training load is used in elite sport for athlete management. Int. J. Sports Med. 2021, 42, 300–306. [Google Scholar] [CrossRef] [PubMed]


| Match Category | Operational Definition |
|---|---|
| Pool | Denotes games happening in the first phase of play (pool play) to determine a ranking within a small group of teams determined ahead of the tournament. |
| Cup Quarterfinal | First knockout stage of the tournament for teams, after pool play, whereby the team finished in top half of their respective pool and advanced in the tournament. |
| Cup Semifinal | Second knockout stage of the tournament, after the quarterfinal, whereby the team is guaranteed a top four finish in the tournament. |
| Cup Final | Final knockout stage of the tournament, after the medal semifinal, whereby the team plays for a final placing, with a win meaning either a bronze medal (third place) or gold medal (first place) in the tournament. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Epp-Stobbe, A.; Tsai, M.-C.; Klimstra, M. A Comparison of the Application of Load Monitoring Metrics for Key Match Characteristics in Women’s Rugby Sevens. Appl. Sci. 2025, 15, 2344. https://doi.org/10.3390/app15052344
Epp-Stobbe A, Tsai M-C, Klimstra M. A Comparison of the Application of Load Monitoring Metrics for Key Match Characteristics in Women’s Rugby Sevens. Applied Sciences. 2025; 15(5):2344. https://doi.org/10.3390/app15052344
Chicago/Turabian StyleEpp-Stobbe, Amarah, Ming-Chang Tsai, and Marc Klimstra. 2025. "A Comparison of the Application of Load Monitoring Metrics for Key Match Characteristics in Women’s Rugby Sevens" Applied Sciences 15, no. 5: 2344. https://doi.org/10.3390/app15052344
APA StyleEpp-Stobbe, A., Tsai, M.-C., & Klimstra, M. (2025). A Comparison of the Application of Load Monitoring Metrics for Key Match Characteristics in Women’s Rugby Sevens. Applied Sciences, 15(5), 2344. https://doi.org/10.3390/app15052344








