A Multiscale CNN-Based Intrinsic Permeability Prediction in Deformable Porous Media
Abstract
:1. Introduction
2. Macroscopic Saturated Porous Media Model
2.1. Homogenization, Volume Fractions, and Densities
2.2. Kinematics of Multi-Phase Continua
2.3. Local Balance Relations
- Non-polar constituents with symmetric stress tensor (). Thus, the angular momentum balance equation is always satisfied.
- A quasi-static biphasic model with negligible inertia terms, i.e., .
- Isothermal conditions, which eliminates the need for the energy balance equation.
- No mass production between the solid and the fluid phases, i.e., .
- Constituent mass balance:
- Constituent momentum balance:
2.4. Effective Stresses and Permeability Formulation
2.5. Governing Balance Equations
2.6. Porous Media Flow Models
2.6.1. Darcy Flow
2.6.2. Darcy–Brinkman Flow
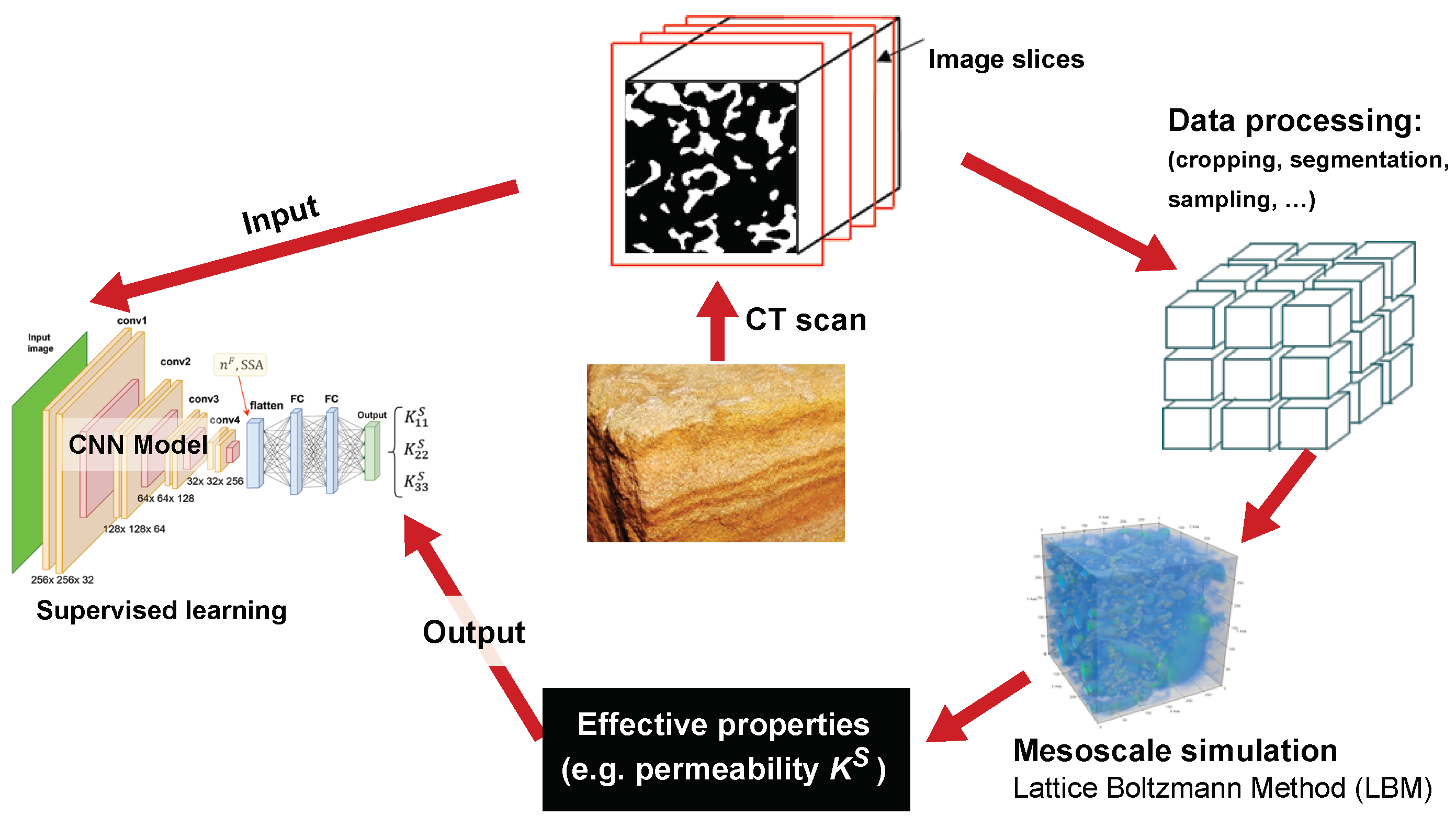
3. Database Generation
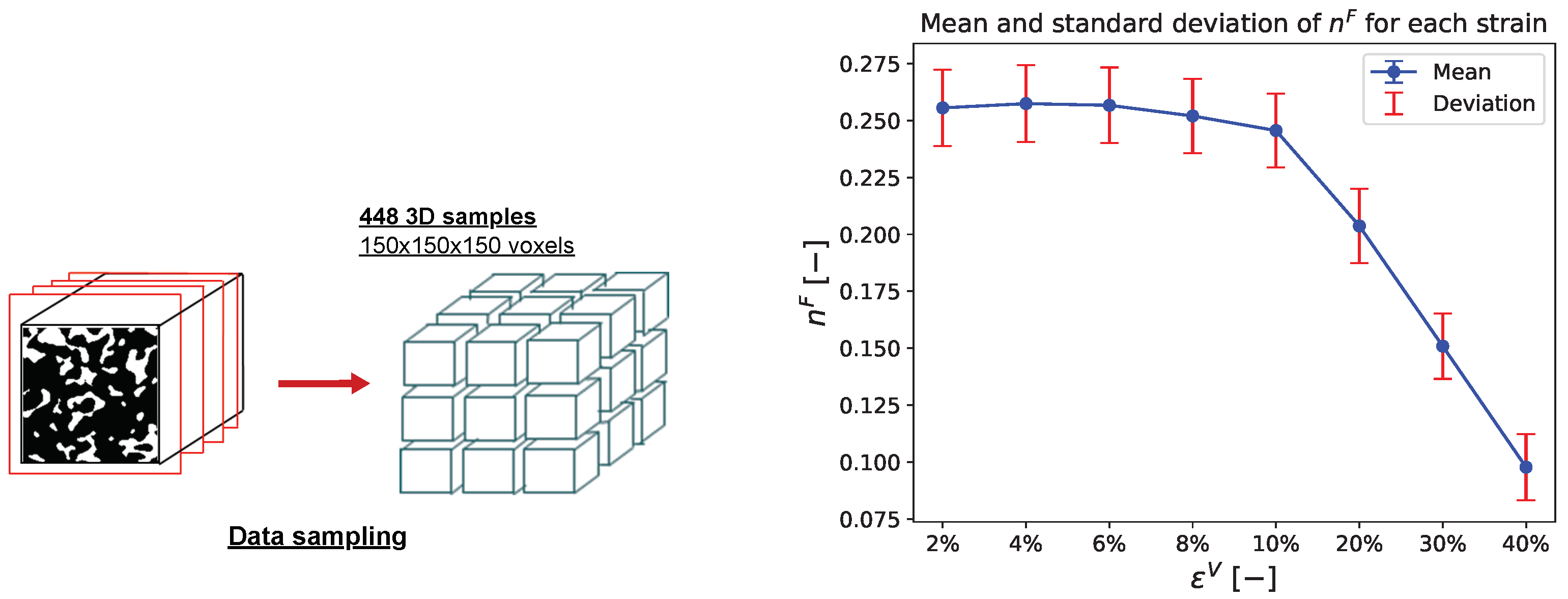
3.1. Image Processing
3.2. Lbm for Single-Phase Fluid Flow
3.3. Intrinsic Permeability Computation
4. Model (1): -CNN Model
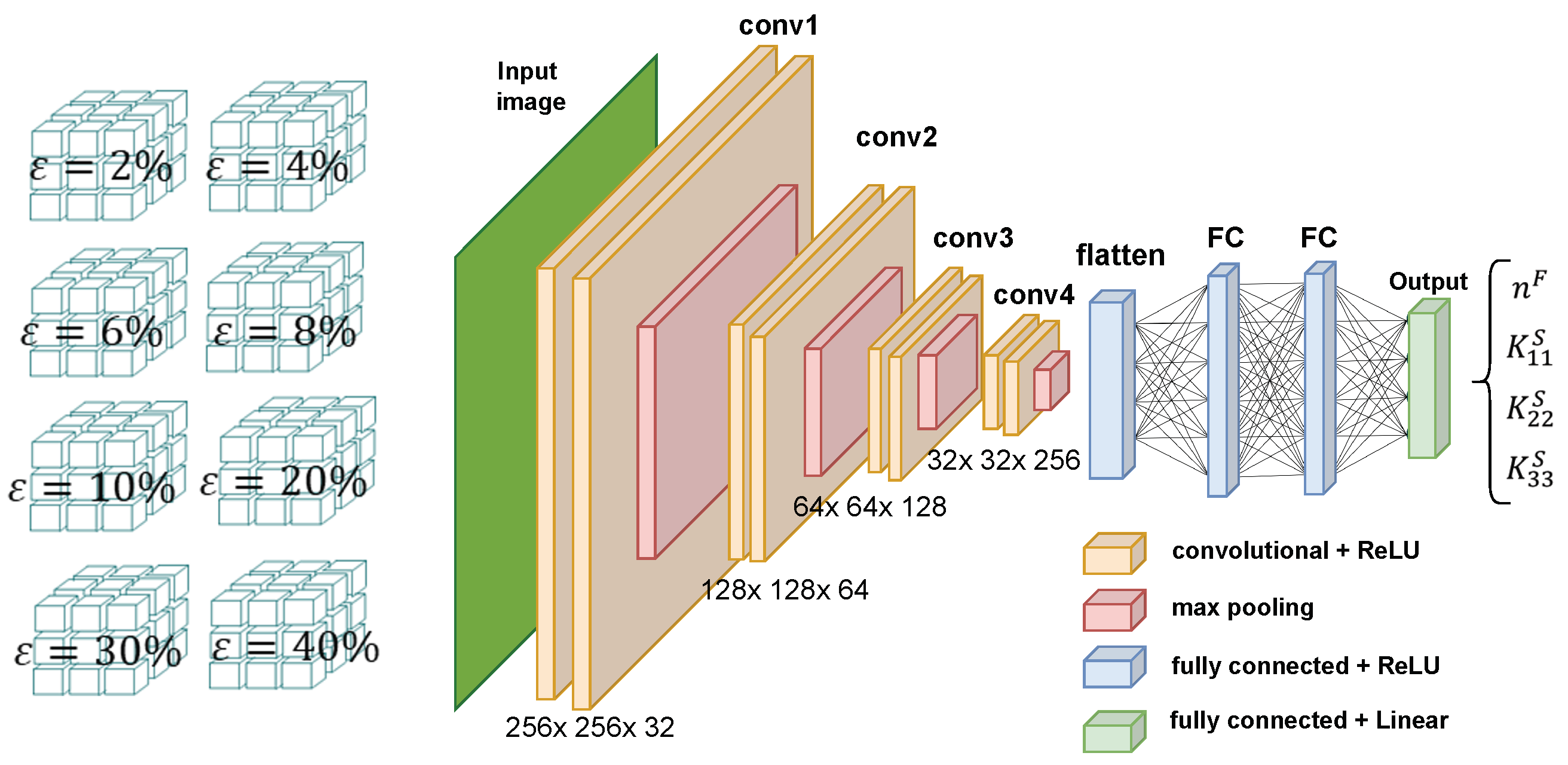
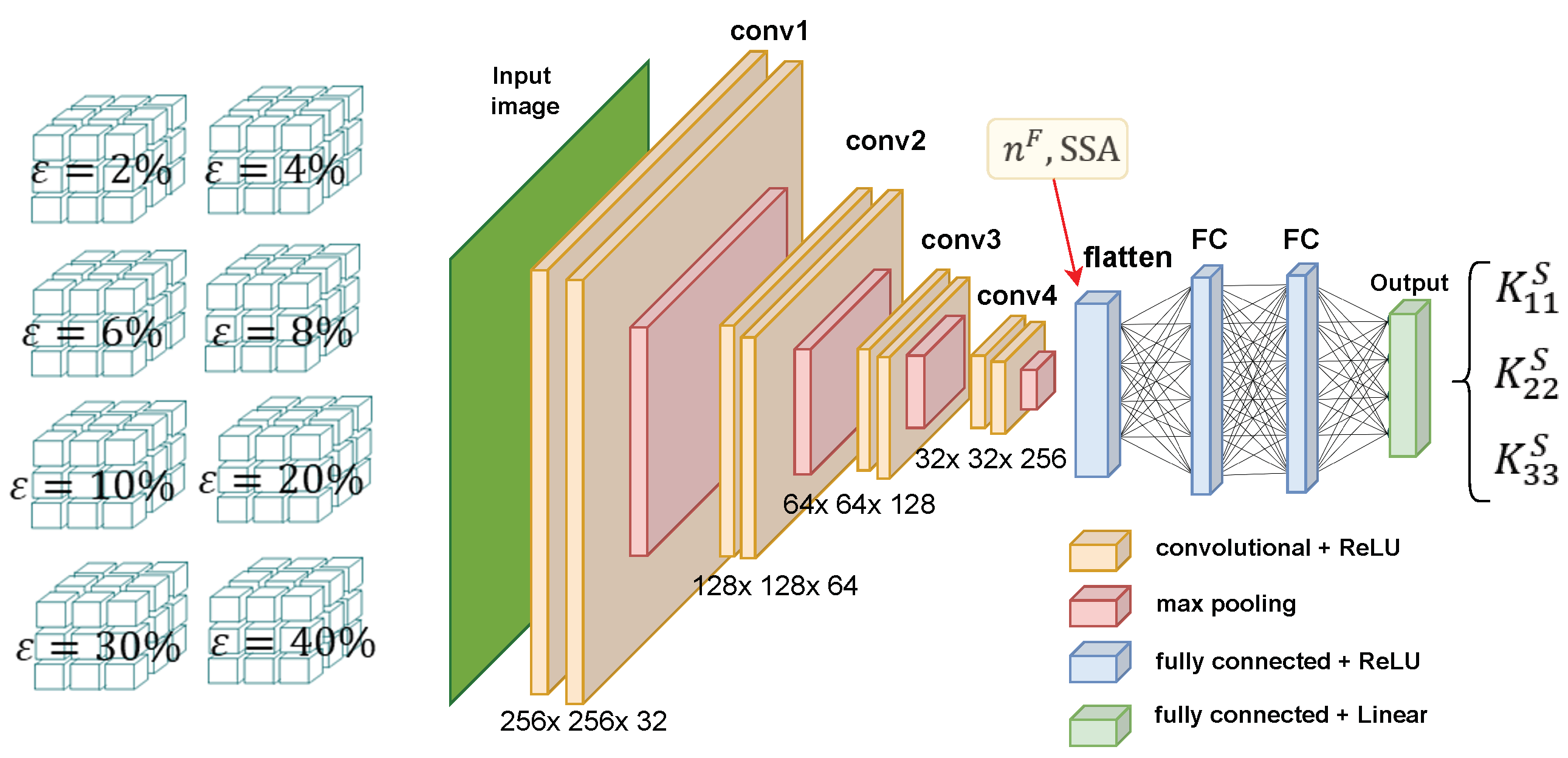
4.1. CNN Model Architecture and Hyperparameters
- Convolution Operation: This step involves the application of a 2D filter (also known as a kernel or feature detector) to the input data, resulting in the generation of a feature map. This process highlights important features within the CT images by detecting patterns and edges that are crucial for permeability and porosity predictions.
- Pooling Operation: After the convolution operation, a pooling layer is applied to the feature map. This process aims to down-sample the feature map by calculating, for instance, their maximum or average values and sending only the significant features to the next CNN layer.
- Multi-Layer Perceptron (MLP): The MLP consists of fully connected (dense) layers that take the pooled feature map as input and produce a 1D feature vector as output.
- Data preparation:
- ∘
- The image-related input data are transposed and reshaped to ensure compatibility with the 3D CNN model architecture.
- ∘
- Before splitting into training, validation, and test subsets, data indices are shuffled to randomize the samples.
- ∘
- After Splitting, the output data ( and ) are scaled using the MinMaxScaler, class of the sklearn.preprocessing toolkit [68], to normalize the values between 0 and 1, which is essential for stabilizing the training process.
- Model architecture:
- ∘
- The CNN model features four convolutional blocks, each comprising two 3D convolutional layers with increasing filter sizes (32, 64, 128, 256) and a kernel size progressively increasing from 3 × 3 × 3 to 7 × 7 7.
- ∘
- Each convolutional layer employs ReLU activation and same padding to maintain spatial dimensions.
- ∘
- Following each convolutional block, a MaxPooling3D layer with a pool size of 2 × 2 × 2 is incorporated to down-sample the spatial dimensions, reducing computational load and mitigating overfitting.
- Fully-connected (dense) layers:
- ∘
- Post convolutional and pooling operations, a Flatten layer transforms the 3D feature maps into a 1D feature vector.
- ∘
- This 1D vector is then fed into a series of fully connected (Dense) layers, configured with 64 and 32 units respectively, both employing ReLU activation and regularization to prevent overfitting.
- ∘
- The final Dense layer contains four units (related to and with ) with a “linear” activation function, suitable for regression tasks.
- Loss Function and Optimization:
- ∘
- The model is compiled using the mean squared error (MSE) loss function, i.e.,where n is the number of output data points and .
- ∘
- Optimization is managed by the Adam optimizer, configured with a learning rate of .
- Training and Callbacks:
- ∘
- The training process spans up to 500 epochs, i.e., 500 complete passes through the entire training dataset, with a batch size of 16, comprising validation data to monitor performance.
- ∘
- Callback mechanisms such as ReduceLROnPlateau, ModelCheckpoint, and EarlyStopping are implemented.
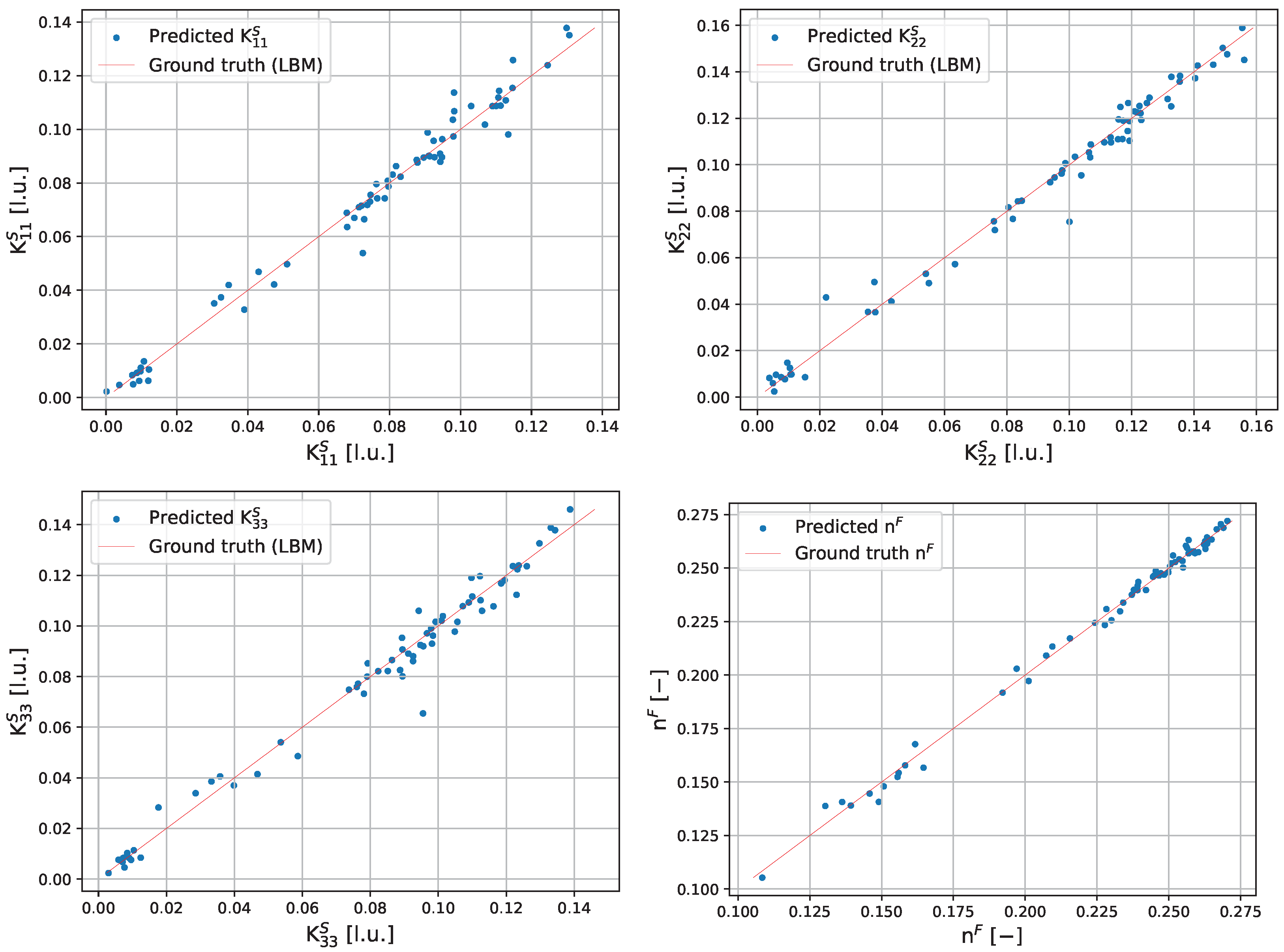
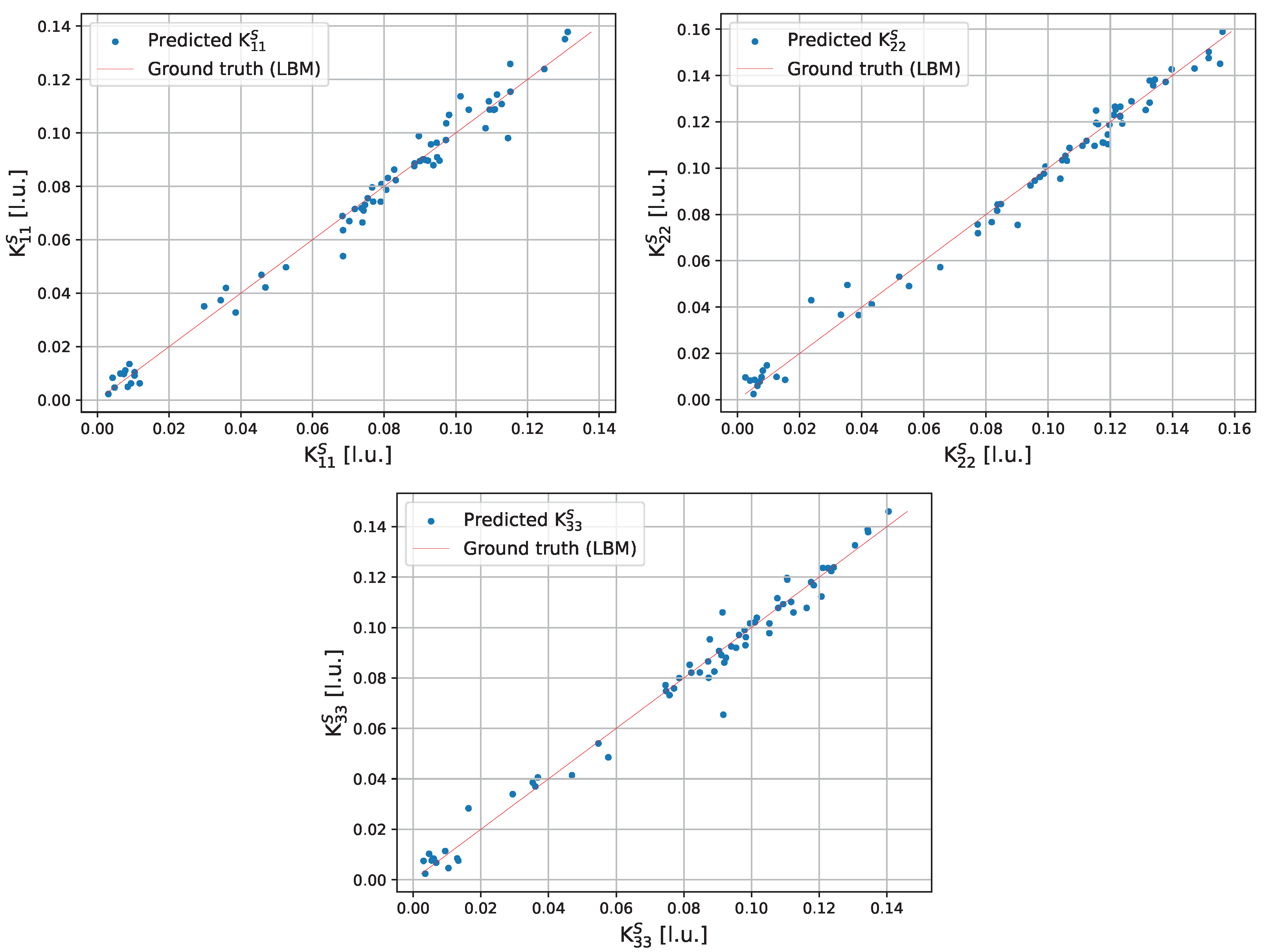
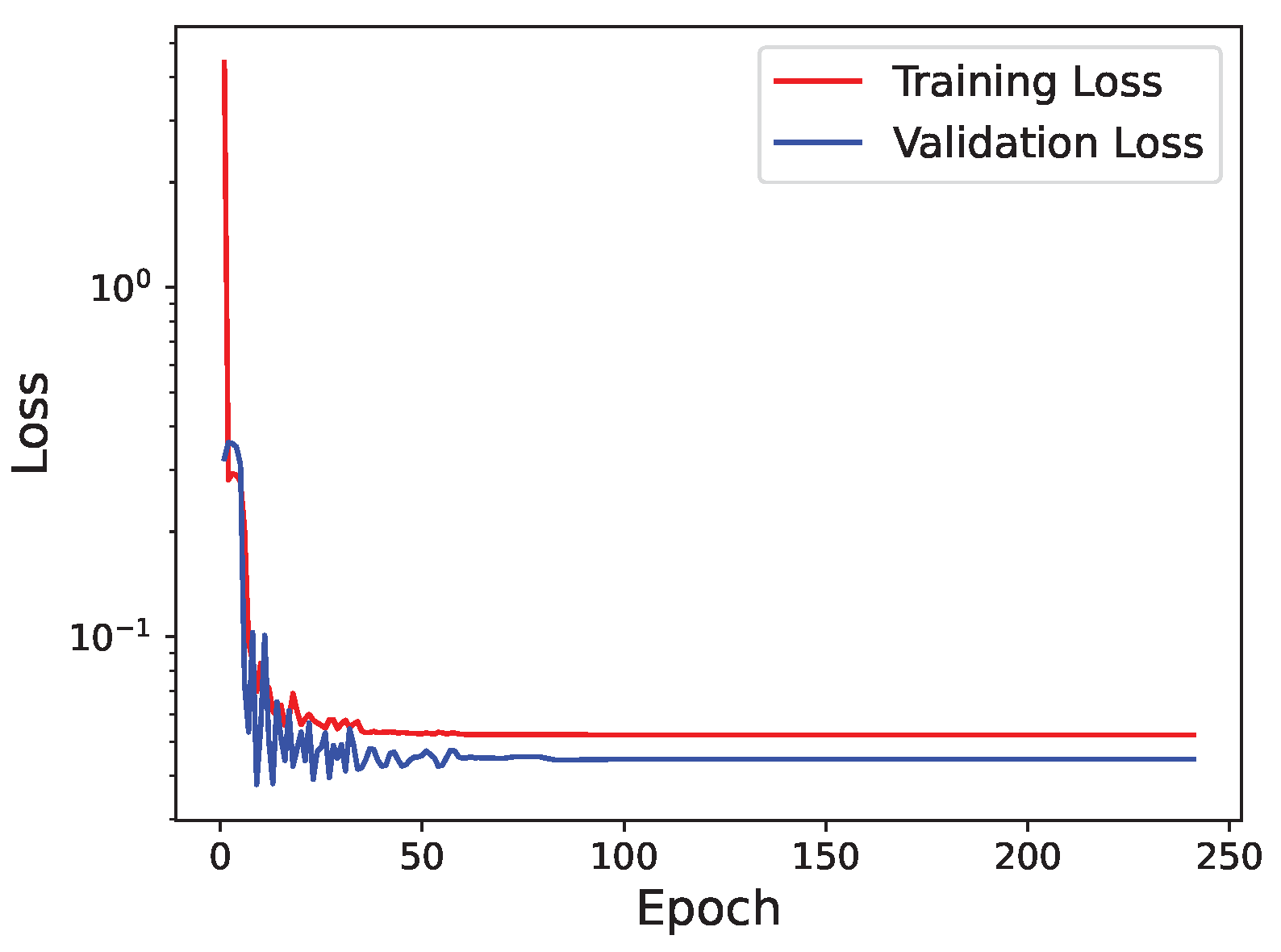
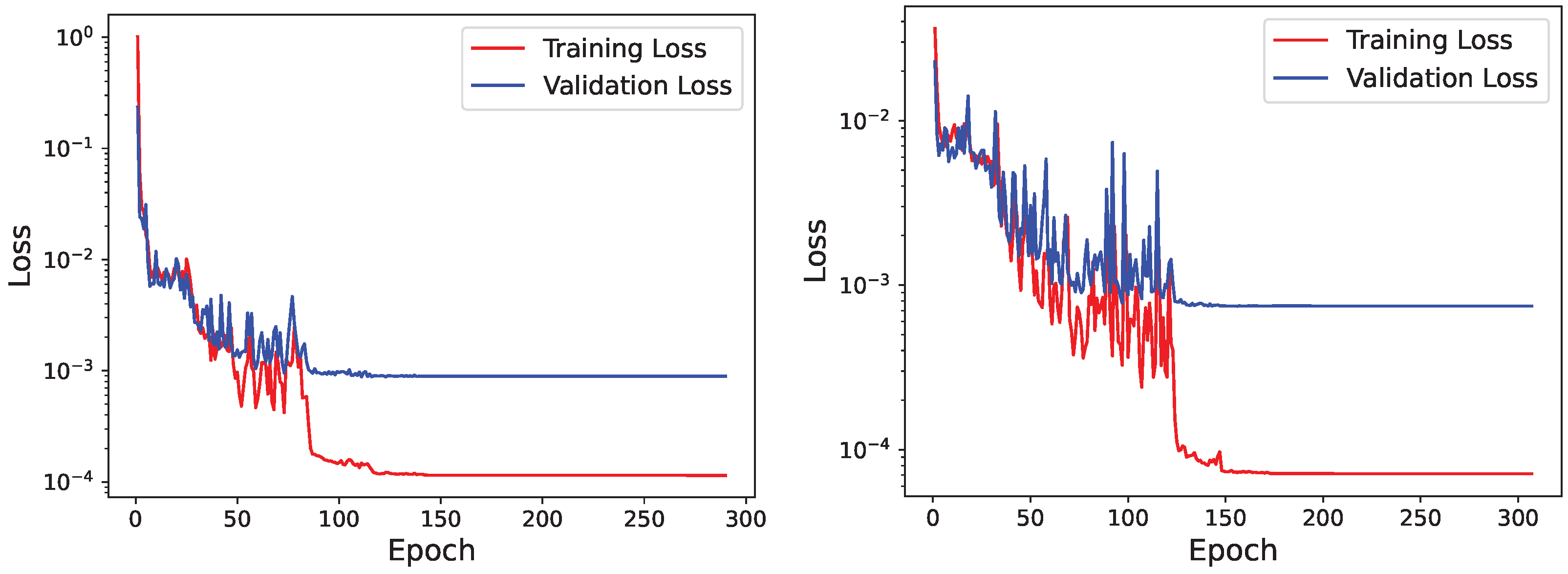
4.2. Training and Testing of Model (1)
5. Model (2): Informed -CNN Model
6. Model (3): Enriched -CNN Model
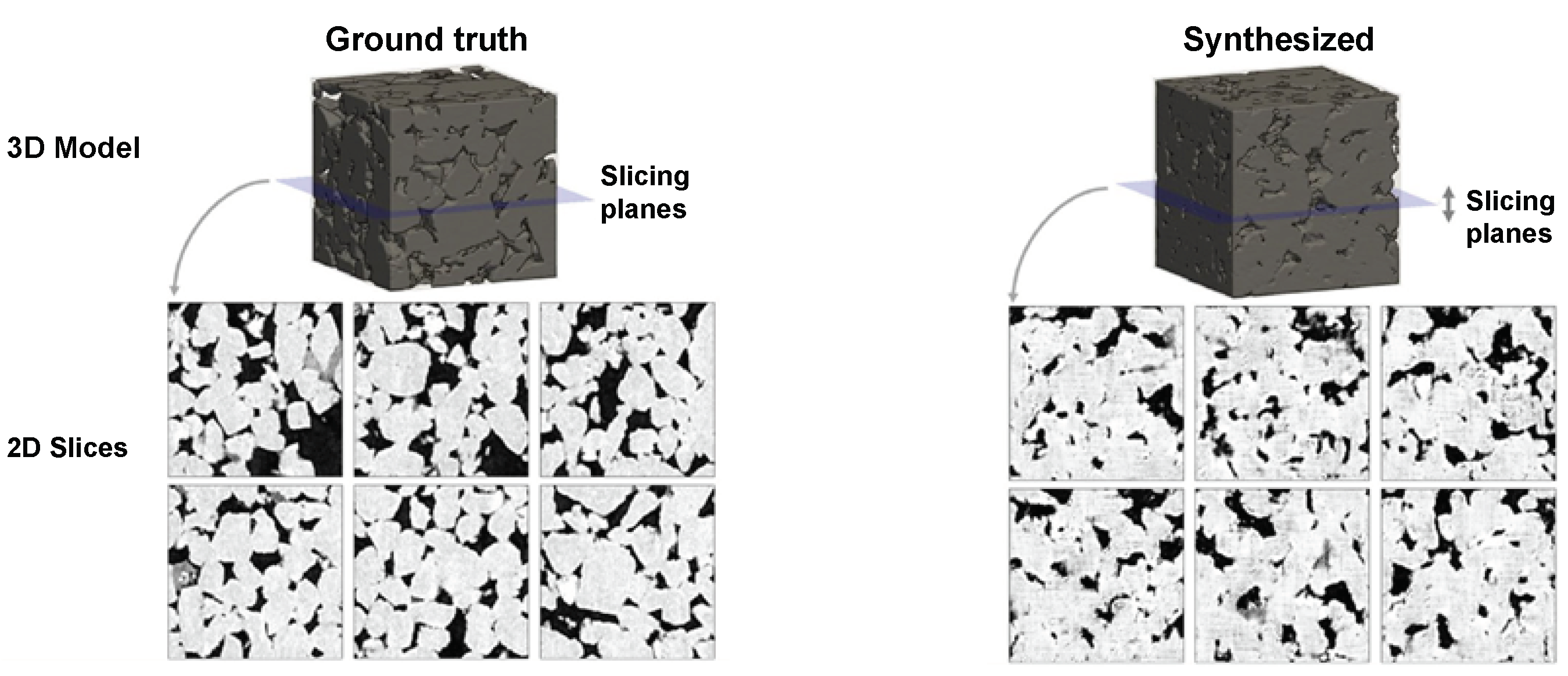
6.1. Training with the Synthetic Data
6.2. Transfer Learning Effect on the Model Learning
7. Discussion of the Approaches
8. Conclusions and Future Aspects
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| ANN | Artificial neural networks |
| CNN | Convolutional neural networks |
| CT | Computed tomography |
| RVE | Representative volume elements |
| LBM | Lattice Boltzmann method |
| TPM | Theory of porous media |
| SSA | Specific surface area |
| ML | Machine learning |
| BGK | Bhatnagar–Gross–Krook |
| DNN | Deep neural networks |
| GAN | Generative adversarial networks |
| PNM | Pore network model |
| RNN | Recurrent neural networks |
| FFNN | Feed-forward neural networks |
References
- Ehlers, W. Darcy, Forchheimer, Brinkman and Richards: Classical hydromechanical equations and their significance in the light of the TPM. Arch. Appl. Mech. 2022, 92, 619–639. [Google Scholar] [CrossRef]
- Ehlers, W.; Graf, T.; Ammann, M. Deformation and localization analysis of partially saturated soil. Comput. Methods Appl. Mech. Eng. 2004, 193, 2885–2910. [Google Scholar] [CrossRef]
- Mosthaf, K.; Baber, K.; Flemisch, B.; Helmig, R.; Leijnse, A.; Rybak, I.; Wohlmuth, B. A coupling concept for two-phase compositional porous-medium and single-phase compositional free flow. Water Resour. Res. 2011, 47, W10522. [Google Scholar] [CrossRef]
- Markert, B.; Heider, Y.; Ehlers, W. Comparison of monolithic and splitting solution schemes for dynamic porous media problem. Int. J. Numer. Meth. Eng. 2010, 82, 1341–1383. [Google Scholar] [CrossRef]
- Markert, B. A survey of selected coupled multifield problems in computational mechanics. J. Coupled. Syst. Multiscale Dyn. 2013, 27, 22–48. [Google Scholar] [CrossRef]
- Ehlers, W.; Wagner, A. Modelling and simulation methods applied to coupled problems in porous-media mechanics. Arch. Appl. Mech. 2019, 89, 609–628. [Google Scholar] [CrossRef]
- Heider, Y. A review on phase-field modeling of hydraulic fracturing. Eng. Fract. Mech. 2021, 253, 107881. [Google Scholar] [CrossRef]
- Peters, S.; Heider, Y.; Markert, B. Numerical simulation of miscible multiphase flow and fluid–fluid interaction in deformable porous media. PAMM 2023, 23, e202300209. [Google Scholar] [CrossRef]
- Miehe, C.; Mauthe, S. Phase field modeling of fracture in multi-physics problems. Part III. Crack driving forces in hydro-poro-elasticity and hydraulic fracturing of fluid-saturated porous media. Comput. Methods Appl. Mech. Eng. 2016, 304, 619–655. [Google Scholar] [CrossRef]
- Gawin, D.; Pesavento, F.; Koniorczyk, M.; Schrefler, B.A. Poro-mechanical model of strain hysteresis due to cyclic water freezing in partially saturated porous media. Int. J. Solids Struct. 2020, 206, 322–339. [Google Scholar] [CrossRef]
- Wang, K.; Sun, W. An updated Lagrangian LBM–DEM–FEM coupling model for dual-permeability fissured porous media with embedded discontinuities. Comput. Methods Appl. Mech. Eng. 2019, 344, 276–305. [Google Scholar] [CrossRef]
- Choo, J.; Borja, R.I. Stabilized mixed finite elements for deformable porous media with double porosity. Comput. Methods Appl. Mech. Eng. 2015, 293, 131–154. [Google Scholar] [CrossRef]
- Jenny, P.; Lee, S.H.; Tchelepi, H.A. Adaptive multiscale finite-volume method for multiphase flow and transport in porous media. Multiscale Model. Simul. 2005, 3, 50–64. [Google Scholar] [CrossRef]
- Heider, Y.; Wang, K.; Sun, W. SO (3)-invariance of informed-graph-based deep neural network for anisotropic elastoplastic materials. Comput. Methods Appl. Mech. Eng. 2020, 363, 112875. [Google Scholar] [CrossRef]
- Heider, Y.; Sun, W. Objectivity and accuracy enhancement within ANN-based multiscale material modeling. PAMM 2023, 22, e202200203. [Google Scholar] [CrossRef]
- Fuchs, A.; Heider, Y.; Wang, K.; Sun, W.; Kaliske, M. DNN2: A hyper-parameter reinforcement learning game for self-design of neural network based elasto-plastic constitutive descriptions. Comput. Struct. 2021, 249, 106505. [Google Scholar] [CrossRef]
- Tragoudas, A.; Alloisio, M.; Elsayed, E.S.; Gasser, T.C.; Aldakheel, F. An enhanced deep learning approach for vascular wall fracture analysis. Arch. Appl. Mech. 2024, 94, 2519–2532. [Google Scholar] [CrossRef]
- Aldakheel, F.; Satari, R.; Wriggers, P. Feed-forward neural networks for failure mechanics problems. Appl. Sci. 2021, 11, 6483. [Google Scholar] [CrossRef]
- Linden, L.; Klein, D.K.; Kalina, K.A.; Brummund, J.; Weeger, O.; Kästner, M. Neural networks meet hyperelasticity: A guide to enforcing physics. J. Mech. Phys. Solids 2023, 179, 105363. [Google Scholar] [CrossRef]
- Wessels, H.; Böhm, C.; Aldakheel, F.; Hüpgen, M.; Haist, M.; Lohaus, L.; Wriggers, P. Computational Homogenization Using Convolutional Neural Networks. In Current Trends and Open Problems in Computational Mechanics; Aldakheel, F., Hudobivnik, B., Soleimani, M., Wessels, H., Weißenfels, C., Marino, M., Eds.; Springer International Publishing: Cham, Switzerland, 2022; pp. 569–579. [Google Scholar] [CrossRef]
- Jin, H.; Zhang, E.; Espinosa, H.D. Recent Advances and Applications of Machine Learning in Experimental Solid Mechanics: A Review. Appl. Mech. Rev. 2023, 75, 061001. [Google Scholar] [CrossRef]
- Wang, K.; Sun, W. A multiscale multi-permeability poroplasticity model linked by recursive homogenizations and deep learning. Comput. Methods Appl. Mech. Eng. 2018, 334, 337–380. [Google Scholar] [CrossRef]
- Heider, Y.; Suh, H.S.; Sun, W. An offline multi-scale unsaturated poromechanics model enabled by self-designed/self-improved neural networks. Int. J. Numer. Anal. Methods Geomech. 2021, 45, 1212–1237. [Google Scholar] [CrossRef]
- Cai, C.; Vlassis, N.; Magee, L.; Ma, R.; Xiong, Z.; Bahmani, B.; Wong, T.F.; Wang, Y.; Sun, W. Equivariant Geometric Learning for Digital Rock Physics: Estimating Formation Factor and Effective Permeability Tensors from Morse Graph. Int. J. Multiscale Comput. Eng. 2023, 21, 1–24. [Google Scholar] [CrossRef]
- Chaaban, M.; Heider, Y.; Sun, W.; Markert, B. A machine-learning supported multi-scale LBM-TPM model of unsaturated, anisotropic, and deformable porous materials. Int. J. Numer. Anal. Methods Geomech. 2024, 4, 889–910. [Google Scholar] [CrossRef]
- Wu, J.; Yin, X.; Xiao, H. Seeing permeability from images: Fast prediction with convolutional neural networks. Sci. Bull. 2018, 63, 1215–1222. [Google Scholar] [CrossRef] [PubMed]
- Hong, J.; Liu, J. Rapid estimation of permeability from digital rock using 3D convolutional neural network. Comput. Geosci. 2020, 24, 1523–1739. [Google Scholar] [CrossRef]
- Bishara, D.; Xie, Y.; Liu, W.K.; Li, S. A State-of-the-Art Review on Machine Learning-Based Multiscale Modeling, Simulation, Homogenization and Design of Materials. Arch. Comput. Methods Eng. 2023, 30, 191–222. [Google Scholar] [CrossRef]
- Herrmann, L.; Kollmannsberger, S. Deep learning in computational mechanics: A review. Comput. Mech. 2024, 74, 281–331. [Google Scholar] [CrossRef]
- Nguyen, P.C.H.; Vlassis, N.N.; Bahmani, B.; Sun, W.; Udaykumar, H.S.; Baek, S.S. Synthesizing controlled microstructures of porous media using generative adversarial networks and reinforcement learning. Sci. Rep. 2022, 12, 9034. [Google Scholar] [CrossRef] [PubMed]
- Ehlers, W. Foundations of multiphasic and porous materials. In Porous Media: Theory, Experiments and Numerical Applications; Ehlers, W., Bluhm, J., Eds.; Springer: Berlin/Heidelberg, Germany, 2002; pp. 3–86. [Google Scholar]
- Markert, B. A constitutive approach to 3-d nonlinear fluid flow through finite deformable porous continua. Transp. Porous Media 2007, 70, 427. [Google Scholar] [CrossRef]
- Chaaban, M.; Heider, Y.; Markert, B. Upscaling LBM-TPM simulation approach of Darcy and non-Darcy fluid flow in deformable, heterogeneous porous media. Int. J. Heat Fluid Flow 2020, 83, 108566. [Google Scholar] [CrossRef]
- Markert, B. Advances in Extended and Multifield Theories for Continua; Springer Science & Business Media: Berlin, Germany, 2011; Volume 59. [Google Scholar]
- De Marchi, N.; Xotta, G.; Ferronato, M.; Salomoni, V. An efficient multi-field dynamic model for 3D wave propagation in saturated anisotropic porous media. J. Comput. Phys. 2024, 510, 113082. [Google Scholar] [CrossRef]
- Chaaban, M.; Heider, Y.; Markert, B. A multiscale LBM–TPM–PFM approach for modeling of multiphase fluid flow in fractured porous media. Int. J. Numer. Anal. Methods Geomech. 2022, 46, 2698–2724. [Google Scholar] [CrossRef]
- Phu, N.T.; Navrath, U.; Heider, Y.; Carmai, J.; Markert, B. Investigating the impact of deformation on foam permeability through CT scans and the Lattice-Boltzmann method. PAMM 2024, 24, e202300154. [Google Scholar] [CrossRef]
- Zhang, X.; Huang, T.; Ge, Z.; Man, T.; Huppert, H.E. Infiltration characteristics of slurries in porous media based on the coupled Lattice-Boltzmann discrete element method. Comput. Geotech. 2025, 177, 106865. [Google Scholar] [CrossRef]
- Yang, G.; Xu, R.; Tian, Y.; Guo, S.; Wu, J.; Chu, X. Data-driven methods for flow and transport in porous media: A review. Int. J. Heat Mass Transf. 2024, 235, 126149. [Google Scholar] [CrossRef]
- Jiao, S.; Li, W.; Li, Z.; Gai, J.; Zou, L.; Su, Y. Hybrid physics-machine learning models for predicting rate of penetration in the Halahatang oil field, Tarim Basin. Sci. Rep. 2024, 14, 5957. [Google Scholar] [CrossRef]
- Chen, J.; Gildin, E.; Killough, J.E. Transfer Learning-Based Physics-Informed Convolutional Neural Network for Simulating Flow in Porous Media with Time-Varying Controls. Mathematics 2024, 12, 3281. [Google Scholar] [CrossRef]
- Aldakheel, F.; Soyarslan, C.; Palanisamy, H.S.; Elsayed, E.S. Machine learning aided multiscale magnetostatics. Mech. Mater. 2023, 184, 104726. [Google Scholar] [CrossRef]
- Aldakheel, F.; Elsayed, E.; Zohdi, T.; Wriggers, P. Efficient multiscale modeling of heterogeneous materials using deep neural networks. Comput. Mech. 2023, 72, 155–171. [Google Scholar] [CrossRef]
- Bowen, R.M. Theory of Mixtures. In Continuum Physics; Eringen, A.C., Ed.; Academic Press: New York, NY, USA, 1976; Volume III, pp. 1–127. [Google Scholar]
- Haupt, P. Foundation of Continuum Mechanics. In Continuum Mechanics in Environmental Sciences and Geophysics; Hutter, K., Ed.; CISM Courses and Lectures No. 337; Springer: Berlin/Heidelberg, Germany, 1993; pp. 1–77. [Google Scholar]
- Heider, Y.; Markert, B. A phase-field modeling approach of hydraulic fracture in saturated porous media. Mech. Res. Commun. 2017, 80, 38–46. [Google Scholar] [CrossRef]
- Bishop, A.W. The effective stress principle. Tek. Ukebl. 1959, 39, 859–863. [Google Scholar]
- de Boer, R.; Ehlers, W. The development of the concept of effective stresses. Acta Mech. 1990, 83, 77–92. [Google Scholar] [CrossRef]
- Ehlers, W. Effective Stresses in Multiphasic Porous Media: A thermodynamic investigation of a fully non-linear model with compressible and incompressible constituents. Geomech. Energy Environ. 2018, 15, 35–46. [Google Scholar] [CrossRef]
- Brinkman, H. A calculation of the viscous force exerted by a flowing fluid on a dense swarm of particles. Appl. Sci. Res. A 1949, 1, 27–34. [Google Scholar] [CrossRef]
- Moon, C.; Andrew, M. Bentheimer Networks. 2019. Available online: http://www.digitalrocksportal.org/projects/223 (accessed on 1 September 2024). [CrossRef]
- Degruyter, W.; Burgisser, A.; Bachmann, O.; Malaspinas, O. Synchrotron X-ray microtomography and lattice Boltzmann simulations of gas flow through volcanic pumices. Geosphere 2010, 6, 470–481. [Google Scholar] [CrossRef]
- Latt, J.; Malaspinas, O.; Kontaxakis, D.; Parmigiani, A.; Lagrava, D.; Brogi, F.; Belgacem, M.B.; Thorimbert, Y.; Leclaire, S.; Li, S.; et al. Palabos: Parallel Lattice Boltzmann Solver. Comput. Math. Appl. 2020, 81, 334–350. [Google Scholar] [CrossRef]
- Chaaban, M.; Heider, Y.; Markert, B. A multiscale study of the retention behavior and hydraulic anisotropy in deformable porous media. PAMM 2023, 23, e202200129. [Google Scholar] [CrossRef]
- Boltzmann, L. Lectures on Gas Theory; Brush, S.G., Translator; Originally Published as Vorlesungen über Gastheorie in 1896–1898; Dover Publications: New York, NY, USA, 1964. [Google Scholar]
- Krüger, T.; Kusumaatmaja, H.; Kuzmin, A.; Shardt, O.; Silva, G.; Viggen, E.M. The Lattice BOltzmann Method; Springer International Publishing: Cham, Switzerland, 2017; Volume 10, pp. 4–15. [Google Scholar]
- He, X.; Luo, L.S. Theory of the lattice Boltzmann method: From the Boltzmann equation to the lattice Boltzmann equation. Phys. Rev. E 1997, 56, 6811–6817. [Google Scholar] [CrossRef]
- Bhatnagar, P.L.; Gross, E.P.; Krook, M. A Model for Collision Processes in Gases. I. Small Amplitude Processes in Charged and Neutral One-Component Systems. Phys. Rev. 1954, 94, 511–525. [Google Scholar] [CrossRef]
- Wolf-Gladrow, D.A. Lattice-Gas Cellular Automata and Lattice Boltzmann Models: An Introduction; Springer: Berlin/Heidelberg, Germany, 2004. [Google Scholar]
- Zou, Q.; He, X. On pressure and velocity boundary conditions for the lattice Boltzmann BGK model. Phys. Fluids 1997, 9, 1591–1598. [Google Scholar] [CrossRef]
- Kuhn, M.R.; Sun, W.; Wang, Q. Stress-induced anisotropy in granular materials: Fabric, stiffness, and permeability. Acta Geotech. 2015, 10, 399–419. [Google Scholar] [CrossRef]
- Gu, J.; Wang, Z.; Kuen, J.; Ma, L.; Shahroudy, A.; Shuai, B.; Liu, T.; Wang, X.; Wang, G.; Cai, J.; et al. Recent advances in convolutional neural networks. Pattern Recognit. 2018, 77, 354–377. [Google Scholar] [CrossRef]
- Eidel, B. Deep CNNs as universal predictors of elasticity tensors in homogenization. Comput. Methods Appl. Mech. Eng. 2023, 403, 115741. [Google Scholar] [CrossRef]
- Dhillon, A.; Verma, G. Convolutional neural network: A review of models, methodologies and applications to object detection. Prog. Artif. Intell. 2020, 9, 85–112. [Google Scholar] [CrossRef]
- Tandale, S.; Stoffel, M. Recurrent and convolutional neural networks in structural dynamics: A modified attention steered encoder–decoder architecture versus LSTM versus GRU versus TCN topologies to predict the response of shock wave-loaded plates. Comput. Mech. 2023, 72, 765–786. [Google Scholar] [CrossRef]
- Chollet, F. Keras. 2015. Available online: https://github.com/fchollet/keras (accessed on 1 April 2024).
- Abadi, M.; Agarwal, A.; Barham, P.; Brevdo, E.; Chen, Z.; Citro, C.; Corrado, G.S.; Davis, A.; Dean, J.; Devin, M.; et al. Tensorflow: Large-scale machine learning on heterogeneous distributed systems. arXiv 2016, arXiv:1603.04467. [Google Scholar]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Goodfellow, I.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.; Bengio, Y. Generative adversarial networks. Commun. Acm 2020, 63, 139–144. [Google Scholar] [CrossRef]
- Gostick, J.; Aghighi, M.; Hinebaugh, J.; Tranter, T.; Hoeh, M.A.; Day, H.; Spellacy, B.; Sharqawy, M.H.; Bazylak, A.; Burns, L.; et al. OpenPNM: A pore network modeling package. Comput. Sci. Eng. 2016, 18, 60–74. [Google Scholar] [CrossRef]



| Feature | Model (1): -CNN | Model (2): Informed -CNN | Model (3): Enriched -CNN |
|---|---|---|---|
| Input | -CT images | -CT images | -CT images |
| + physical parameters (, SSA) | (Real & synthetic) | ||
| Output | |||
| Loss function | Includes | Includes only | Includes |
| Complexity | Moderate | Higher (additional input branch | Highest (pre-training |
| & complicated CNN architecture) | & transfer learning) | ||
| Training | Some overfitting (≈ loss) | Similar overfitting (≈ loss) | Similar overfitting (≈ loss) |
| Final score | ≈0.985 | ≈0.983 | Similar to Model (1) (≈0.985) |
| Advantage | Simple & effective | Incorporates physical information | Faster training, |
| in the CNN architecture | good for small datasets |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Heider, Y.; Aldakheel, F.; Ehlers, W. A Multiscale CNN-Based Intrinsic Permeability Prediction in Deformable Porous Media. Appl. Sci. 2025, 15, 2589. https://doi.org/10.3390/app15052589
Heider Y, Aldakheel F, Ehlers W. A Multiscale CNN-Based Intrinsic Permeability Prediction in Deformable Porous Media. Applied Sciences. 2025; 15(5):2589. https://doi.org/10.3390/app15052589
Chicago/Turabian StyleHeider, Yousef, Fadi Aldakheel, and Wolfgang Ehlers. 2025. "A Multiscale CNN-Based Intrinsic Permeability Prediction in Deformable Porous Media" Applied Sciences 15, no. 5: 2589. https://doi.org/10.3390/app15052589
APA StyleHeider, Y., Aldakheel, F., & Ehlers, W. (2025). A Multiscale CNN-Based Intrinsic Permeability Prediction in Deformable Porous Media. Applied Sciences, 15(5), 2589. https://doi.org/10.3390/app15052589








