Assist-as-Needed Controller of a Rehabilitation Exoskeleton for Upper-Limb Natural Movements
Abstract
:1. Introduction
2. Materials and Methods
2.1. System Design
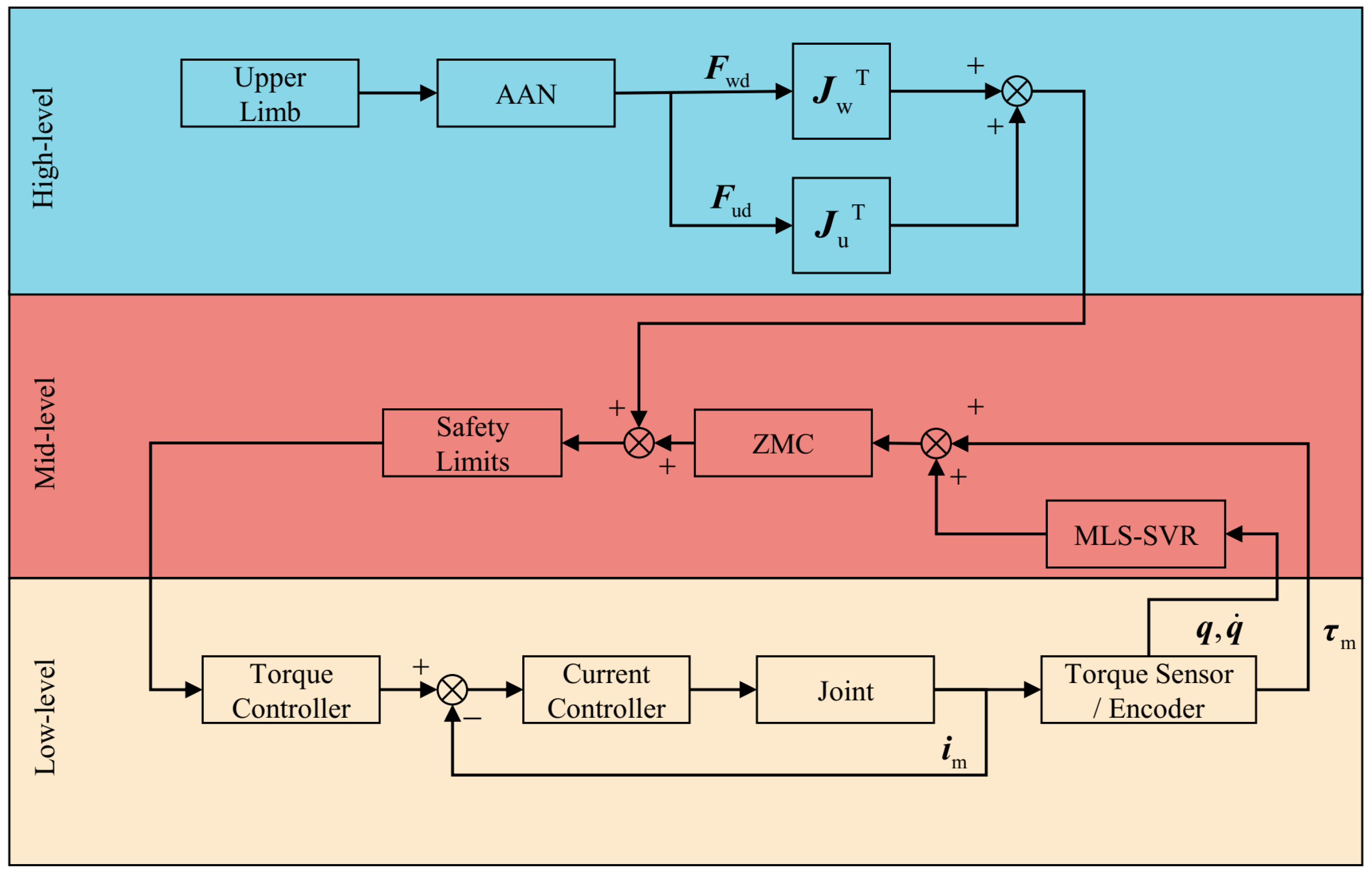
2.2. Zero Moment Control
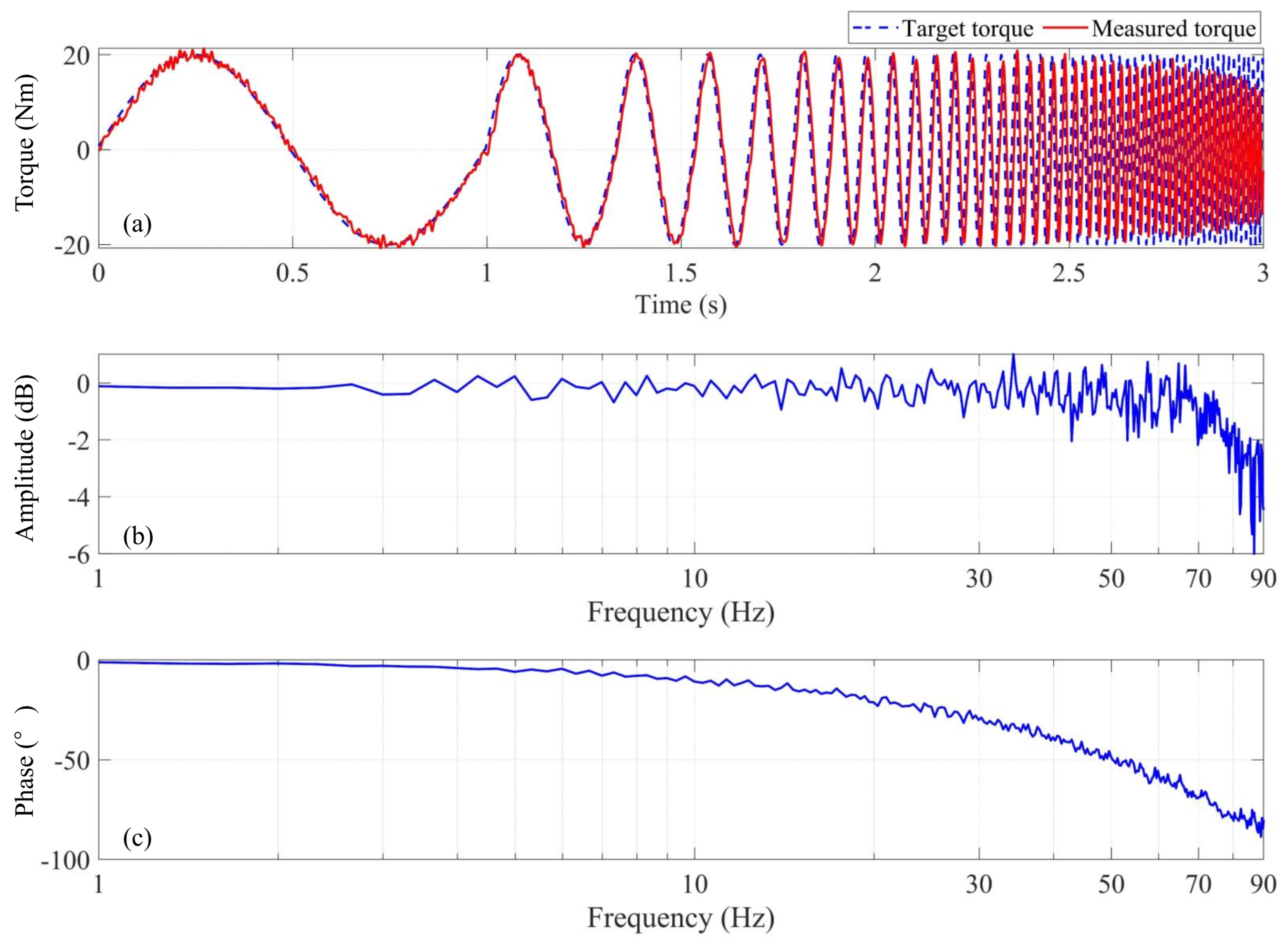
- Robot control based on dynamic models involves two types of feedback: measuring current and measuring torque. Current signal contains significant high-frequency noise, making it difficult to extract accurate raw signals. Additionally, the precision of calculating joint friction through current measurements is not ideal. Each joint of FREE is equipped with a torque sensor and can be used for the detection of torque applied to joint. The measured signals include inertial torque, centripetal torque, Coriolis torque, gravitational torque, frictional torque, and HRI torque. Therefore, ZMC must compensate for the influence of other torques and assist the user to achieve robot traction with minimal interaction force.
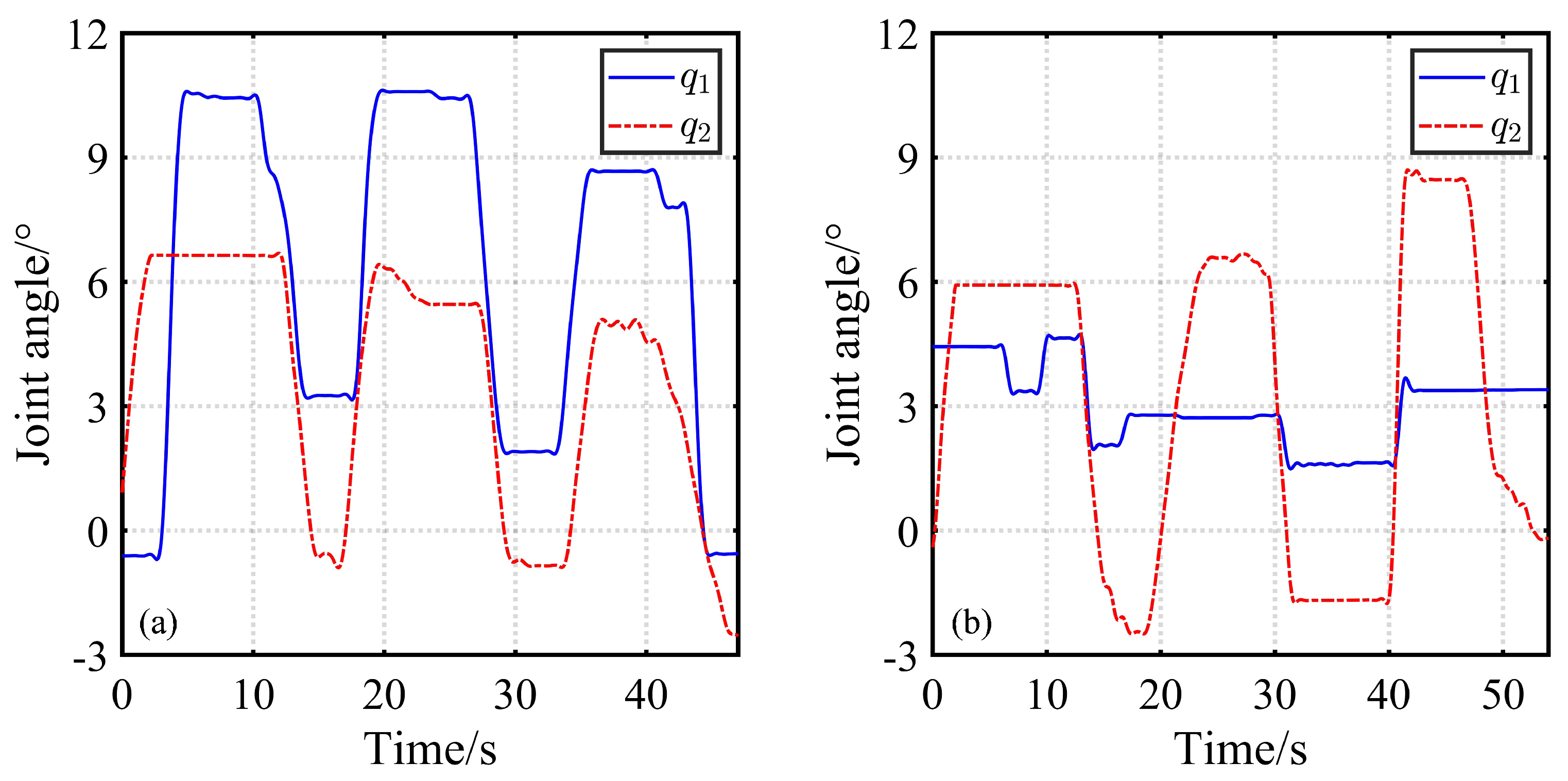
- After the user moves FREE to a desired pose, it is essential to ensure that FREE remains stationary under the influence of gravity. When the user does not apply any force to the exoskeleton, FREE is capable of compensating for its own weight and remaining stationary.
- FREE has comprehensive force sensing capabilities. Its force sensing area is not limited to the above two interaction points. FREE can detect interaction forces applied by the user at any point on itself and respond according to the user’s intent.
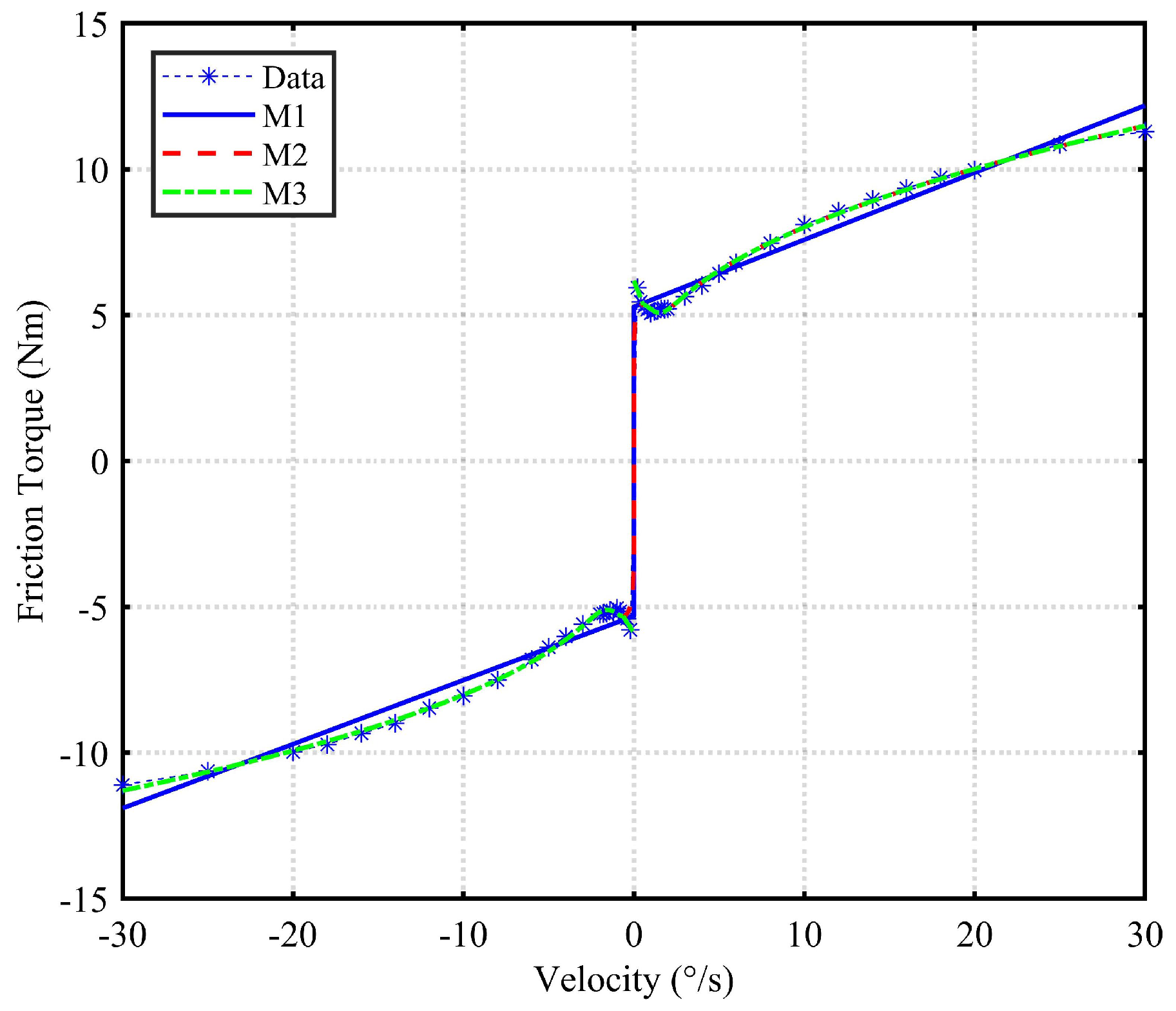
2.3. Friction Modeling
2.4. AAN Control Strategy
2.5. Stability Analysis
3. Experimental Result
3.1. Elbow Joint Torque Response
3.2. Parameter Identification of Friction Model
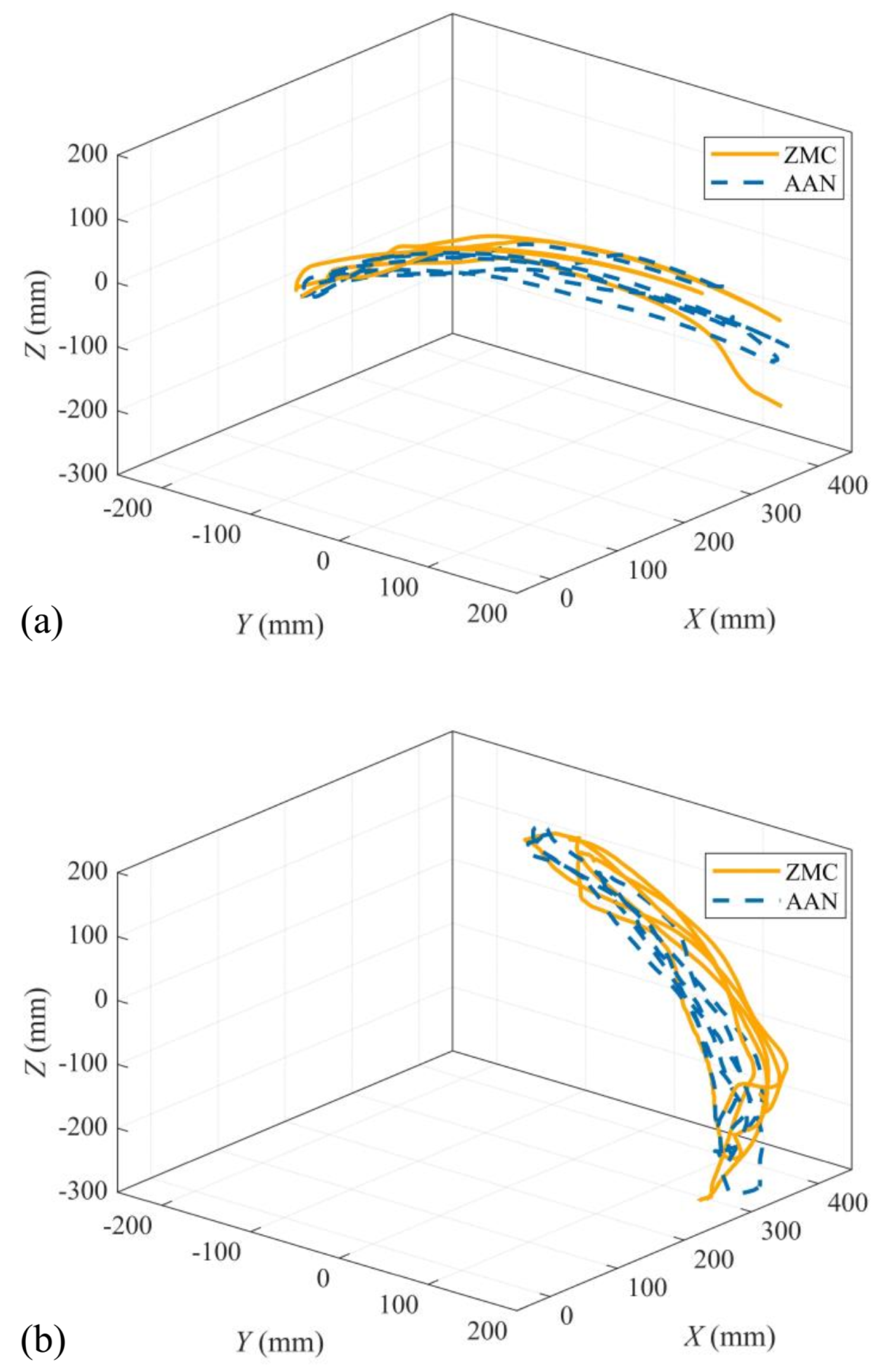
3.3. Evaluation of AAN Controller
4. Discussion
4.1. Control Characterization
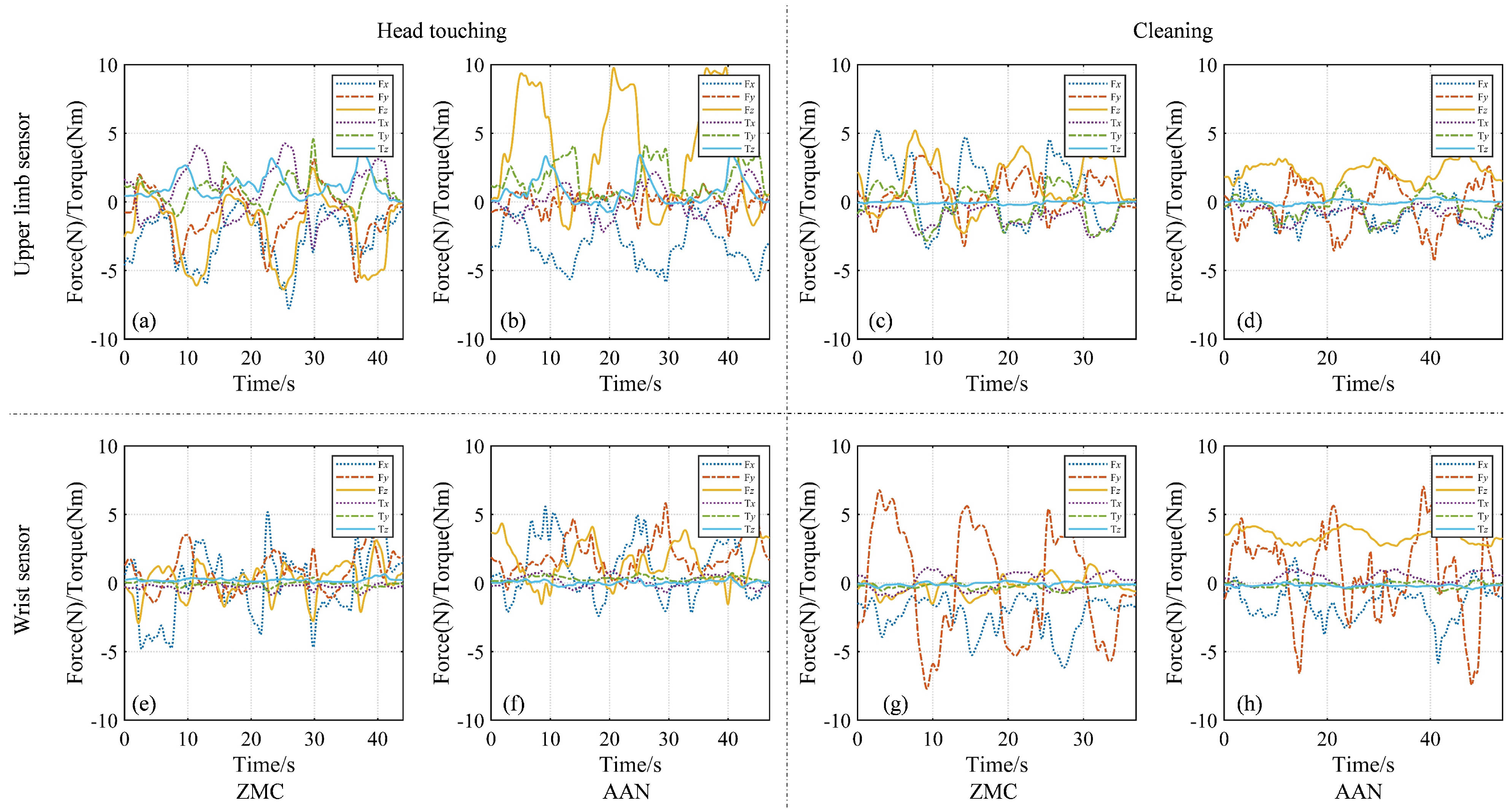
4.2. Rehabilitation Scenarios
4.3. Limitations and Future Works
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| Assist-as-needed | |
| Activities of daily living | |
| Degrees of freedom | |
| Electromyography | |
| Electroencephalography | |
| Multiple-input-multiple-output | |
| Range of motion | |
| Root mean square error | |
| Relative standard deviation | |
| Zero moment control |
References
- Adamson, J.; Beswick, A.; Ebrahim, S. Is stroke the most common cause of disability? J. Stroke Cerebrovasc. Dis. 2004, 13, 171–177. [Google Scholar] [CrossRef] [PubMed]
- Lindsay, M.P.; Norrving, B.; Sacco, R.L.; Brainin, M.; Hacke, W.; Martins, S.; Pandian, J.; Feigin, V. World Stroke Organization (WSO): Global stroke fact sheet 2019. Int. J. Stroke 2019, 14, 806–817. [Google Scholar] [CrossRef] [PubMed]
- Kwakkel, G.; Veerbeek, J.M.; van Wegen, E.E.; Wolf, S.L. Constraint-induced movement therapy after stroke. Lancet Neurol. 2015, 14, 224–234. [Google Scholar] [CrossRef] [PubMed]
- Sharma, B.; Phan, P.T.; Davies, J.; Hoang, T.T.; Nguyen, C.C.; Ji, A.; Zhu, K.; Nicotra, E.; Lovell, N.H.; Do, T.N. Soft Upper-Limb Wearable Robotic Devices: Technology and Applications. Adv. Intell. Syst. 2024, 6, 2400266. [Google Scholar] [CrossRef]
- Toedtheide, A.; Fortunic, E.P.; Kuhn, J.; Jensen, E.R.; Haddadin, S. A wearable force-sensitive and body-aware exoprosthesis for a transhumeral prosthesis socket. IEEE Trans. Robot. 2023, 39, 2203–2223. [Google Scholar] [CrossRef]
- Niu, B.; Yang, D.; Wang, P.; Yang, H.; Zhang, L.; Gu, Y.; Jiang, L. Virtual-force-guided intraoperative ultrasound scanning with online lesion location prediction: A phantom study. Int. J. Med. Robot. Comput. Assist. Surg. 2023, 19, e2491. [Google Scholar] [CrossRef]
- Liu, Y.; Liu, Y.; Han, R.; Zheng, K.; Yao, Y.; Zhong, M. Interactive Prompt-Guided Robotic Grasping for Arbitrary Objects Based on Promptable Segment Anything Model and Force-Closure Analysis. Adv. Intell. Syst. 2024, 2400404. [Google Scholar] [CrossRef]
- De Oliveira, A.C.; Sulzer, J.S.; Deshpande, A.D. Assessment of upper-extremity joint angles using harmony exoskeleton. IEEE Trans. Neural Syst. Rehabil. Eng. 2021, 29, 916–925. [Google Scholar] [CrossRef]
- Buccelli, S.; Tessari, F.; Fanin, F.; De Guglielmo, L.; Capitta, G.; Piezzo, C.; Bruschi, A.; Van Son, F.; Scarpetta, S.; Succi, A.; et al. A gravity-compensated upper-limb exoskeleton for functional rehabilitation of the shoulder complex. Appl. Sci. 2022, 12, 3364. [Google Scholar] [CrossRef]
- Song, R.; Tong, K.Y.; Hu, X.; Li, L. Assistive control system using continuous myoelectric signal in robot-aided arm training for patients after stroke. IEEE Trans. Neural Syst. Rehabil. Eng. 2008, 16, 371–379. [Google Scholar] [CrossRef]
- Yang, R.; Shen, Z.; Lyu, Y.; Zhuang, Y.; Li, L.; Song, R. Voluntary assist-as-needed controller for an ankle power-assist rehabilitation robot. IEEE Trans. Biomed. Eng. 2022, 70, 1795–1803. [Google Scholar] [CrossRef] [PubMed]
- Sedighi, P.; Li, X.; Tavakoli, M. Emg-based intention detection using deep learning for shared control in upper-limb assistive exoskeletons. IEEE Robot. Autom. Lett. 2023, 9, 41–48. [Google Scholar] [CrossRef]
- Shao, Q.; Bassett, D.N.; Manal, K.; Buchanan, T.S. An EMG-driven model to estimate muscle forces and joint moments in stroke patients. Comput. Biol. Med. 2009, 39, 1083–1088. [Google Scholar] [CrossRef] [PubMed]
- Bhagat, N.A.; Venkatakrishnan, A.; Abibullaev, B.; Artz, E.J.; Yozbatiran, N.; Blank, A.A.; French, J.; Karmonik, C.; Grossman, R.G.; O’Malley, M.K.; et al. Design and optimization of an EEG-based brain machine interface (BMI) to an upper-limb exoskeleton for stroke survivors. Front. Neurosci. 2016, 10, 122. [Google Scholar] [CrossRef]
- Nann, M.; Cordella, F.; Trigili, E.; Lauretti, C.; Bravi, M.; Miccinilli, S.; Catalan, J.M.; Badesa, F.J.; Crea, S.; Bressi, F.; et al. Restoring activities of daily living using an EEG/EOG-controlled semiautonomous and mobile whole-arm exoskeleton in chronic stroke. IEEE Syst. J. 2020, 15, 2314–2321. [Google Scholar] [CrossRef]
- Buerkle, A.; Eaton, W.; Lohse, N.; Bamber, T.; Ferreira, P. EEG based arm movement intention recognition towards enhanced safety in symbiotic human-robot collaboration. Robot. Comput. Integr. Manuf. 2021, 70, 102137. [Google Scholar] [CrossRef]
- Formaggio, E.; Masiero, S.; Bosco, A.; Izzi, F.; Piccione, F.; Del Felice, A. Quantitative EEG evaluation during robot-assisted foot movement. IEEE Trans. Neural Syst. Rehabil. Eng. 2016, 25, 1633–1640. [Google Scholar] [CrossRef]
- Li, X.; Liu, Y.H.; Yu, H. Iterative learning impedance control for rehabilitation robots driven by series elastic actuators. Automatica 2018, 90, 1–7. [Google Scholar] [CrossRef]
- Wu, Q.; Wang, X.; Chen, B.; Wu, H. Development of a minimal-intervention-based admittance control strategy for upper extremity rehabilitation exoskeleton. IEEE Trans. Syst. Man Cybern. Syst. 2017, 48, 1005–1016. [Google Scholar] [CrossRef]
- Zimmermann, Y.; Küçüktabak, E.B.; Farshidian, F.; Riener, R.; Hutter, M. Towards dynamic transparency: Robust interaction force tracking using multi-sensory control on an arm exoskeleton. In Proceedings of the 2020 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Las Vegas, NV, USA, 24 October 2020–24 January 2021; pp. 7417–7424. [Google Scholar]
- Naghavi, N.; Akbarzadeh, A.; Tahamipour-Z, S.M.; Kardan, I. Assist-As-Needed control of a hip exoskeleton based on a novel strength index. Robot. Auton. Syst. 2020, 134, 103667. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, S.; Nolan, K.J.; Zanotto, D. Reinforcement learning assist-as-needed control for robot assisted gait training. In Proceedings of the 2020 8th IEEE RAS/EMBS International Conference for Biomedical Robotics and Biomechatronics (BioRob), New York, NY, USA, 29 November–1 December 2020; pp. 785–790. [Google Scholar]
- Dos Santos, W.M.; Siqueira, A.A. Optimal impedance via model predictive control for robot-aided rehabilitation. Control Eng. Pract. 2019, 93, 104177. [Google Scholar] [CrossRef]
- Fang, X.K.; Han, B.; Wang, J.H.; Liu, D.Y. Adaptive velocity field control of upper-limb rehabilitation robot. In Proceedings of the 2016 Chinese Control and Decision Conference (CCDC), Yinchuan, China, 28–30 May 2016; pp. 5438–5443. [Google Scholar]
- Asl, H.J.; Yamashita, M.; Narikiyo, T.; Kawanishi, M. Field-based assist-as-needed control schemes for rehabilitation robots. IEEE/ASME Trans. Mechatron. 2020, 25, 2100–2111. [Google Scholar] [CrossRef]
- Zhang, L.; Guo, S.; Sun, Q. Development and assist-as-needed control of an end-effector upper limb rehabilitation robot. Appl. Sci. 2020, 10, 6684. [Google Scholar] [CrossRef]
- Guo, Y.; Tian, Y.; Wang, H.; Han, S. Adaptive hybrid-mode assist-as-needed control of upper limb exoskeleton for rehabilitation training. Mechatronics 2024, 100, 103188. [Google Scholar] [CrossRef]
- Pei, S.; Wang, J.; Yang, Y.; Dong, A.; Guo, B.; Guo, J.; Yao, Y. A Human-centered kinematics design optimization of upper limb rehabilitation exoskeleton based on configuration manifold. IEEE Open J. Comput. Soc. 2024, 6, 282–293. [Google Scholar] [CrossRef]
- Albu-Schäffer, A.; Ott, C.; Hirzinger, G. A unified passivity-based control framework for position, torque and impedance control of flexible joint robots. Int. J. Robot. Res. 2007, 26, 23–39. [Google Scholar] [CrossRef]
- Zarrin, R.S.; Zeiaee, A.; Langari, R.; Buchanan, J.J.; Robson, N. Towards autonomous ergonomic upper-limb exoskeletons: A computational approach for planning a human-like path. Robot. Auton. Syst. 2021, 145, 103843. [Google Scholar] [CrossRef]
- Pei, S.; Wang, J.; Guo, J.; Yin, H.; Yao, Y. A Human-like Inverse Kinematics Algorithm of an Upper Limb Rehabilitation Exoskeleton. Symmetry 2023, 15, 1657. [Google Scholar] [CrossRef]
- Ott, C.; Albu-Schaffer, A.; Kugi, A.; Hirzinger, G. On the passivity-based impedance control of flexible joint robots. IEEE Trans. Robot. 2008, 24, 416–429. [Google Scholar] [CrossRef]
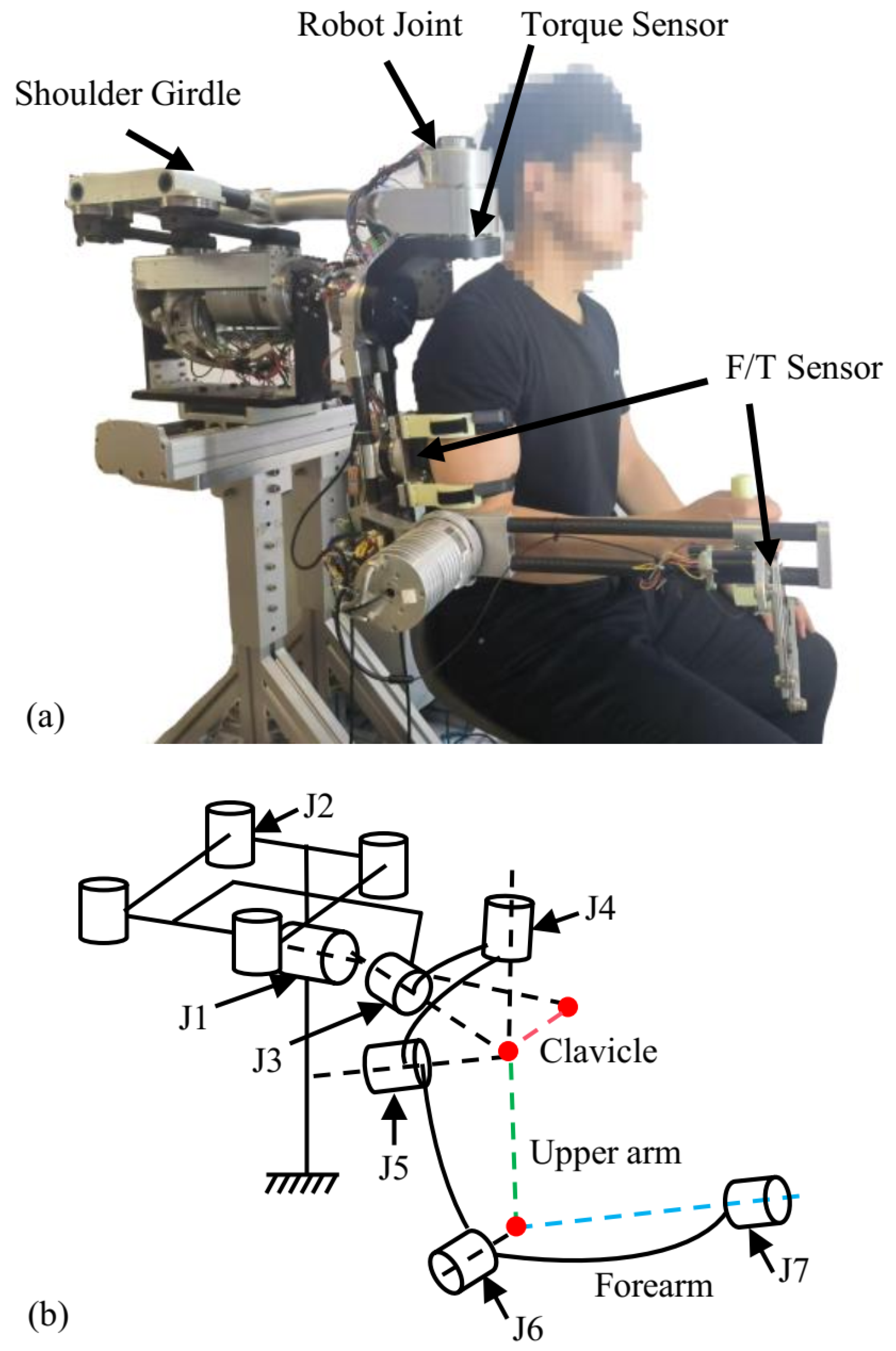
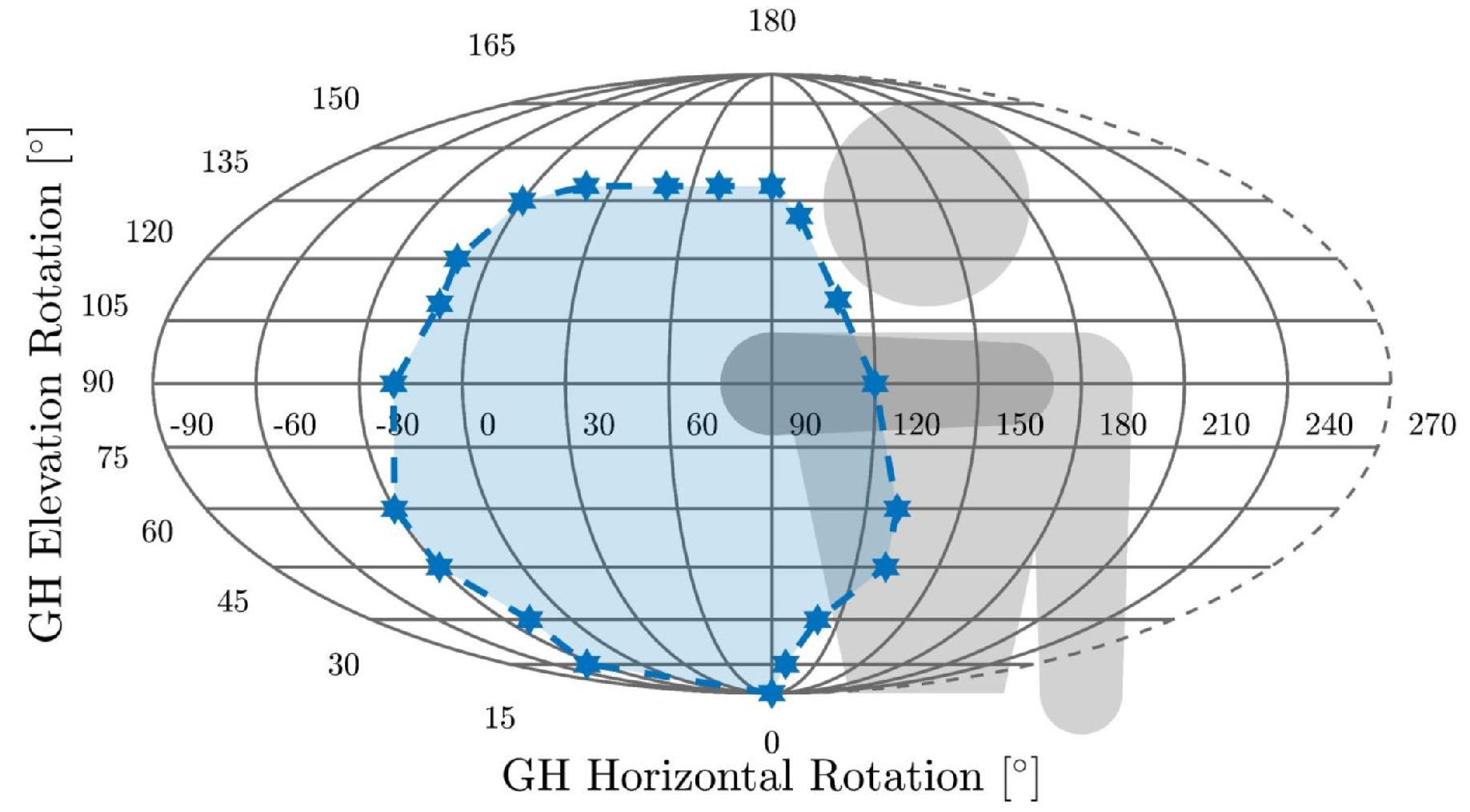

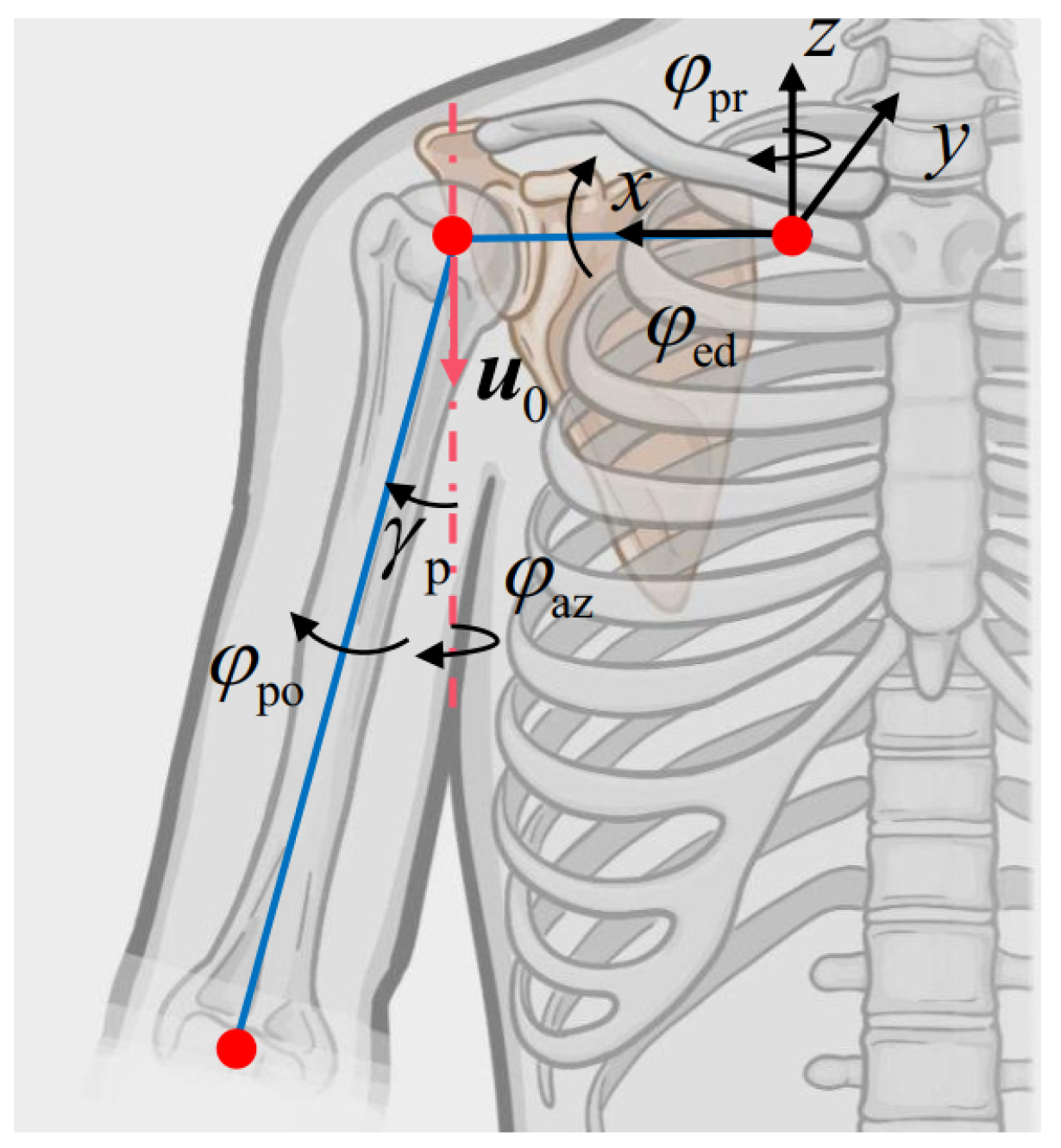
| J1 | J2 | J3 | J4 | J5/6 | J7 | |
|---|---|---|---|---|---|---|
| Reduction Ratio | 161:1 | 121:1 | 161:1 | 101:1 | 121:1 | 51:1 |
| Nominal Torque | 87 Nm | 65 Nm | 41 Nm | 35 Nm | 22 Nm | 5 Nm |
| Nominal Speed | /s | /s | /s | /s | /s | /s |
| Metrics | Model | J1 | J2 | J3 | J4 | J5 |
|---|---|---|---|---|---|---|
| M1_f | 0.9372 | 0.9713 | 0.9597 | 0.9892 | 0.9114 | |
| M2_f | 0.9933 | 0.9994 | 0.9906 | 0.9968 | 0.9517 | |
| M3_f | 0.9935 | 0.9994 | 0.9982 | 0.9967 | 0.9517 | |
| M1_r | 0.9199 | 0.9595 | 0.9553 | 0.9827 | 0.9201 | |
| M2_r | 0.9860 | 0.9974 | 0.9899 | 0.9981 | 0.9083 | |
| M3_r | 0.9914 | 0.9974 | 0.9976 | 0.9991 | 0.9084 | |
| M1_f | 1.9292 | 0.9357 | 2.4775 | 0.0592 | 1.0432 | |
| M2_f | 0.6311 | 0.1394 | 1.1752 | 0.0320 | 0.7704 | |
| M3_f | 0.6197 | 0.1390 | 0.5211 | 0.0329 | 0.7699 | |
| M1_r | 2.0902 | 1.1122 | 2.5684 | 0.0820 | 0.9546 | |
| M2_r | 0.8745 | 0.2819 | 1.2224 | 0.0273 | 1.0227 | |
| M3_r | 0.6829 | 0.2818 | 0.5945 | 0.0182 | 1.0218 | |
| M1_f | 7.5385 | 4.4991 | 5.4049 | 0.7564 | 19.2490 | |
| M2_f | 2.2334 | 0.5751 | 1.7412 | 0.3552 | 5.3526 | |
| M3_f | 2.1778 | 0.5681 | 1.1477 | 0.3794 | 5.2395 | |
| M1_r | 8.2486 | 5.4993 | 5.6672 | 1.0181 | 16.3971 | |
| M2_r | 2.0808 | 0.7506 | 1.8865 | 0.3089 | 6.7566 | |
| M3_r | 1.5845 | 0.7472 | 1.3080 | 0.2428 | 6.8118 |
| Task | Interaction Point | (N) | (N) | (N) | (Nm) | (Nm) | (Nm) |
|---|---|---|---|---|---|---|---|
| Head Touching | Upper Arm | 2.65 | 1.56 | 2.26 | 1.58 | 1.02 | 1.13 |
| Wrist | 1.92 | 1.13 | 1.80 | 1.02 | 1.08 | 0.08 | |
| Cleaning | Upper Arm | 2.03 | 1.25 | 0.98 | 0.30 | 0.13 | 0.21 |
| Wrist | 2.31 | 3.64 | 0.53 | 0.57 | 0.27 | 0.10 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pei, S.; Wang, J.; Tian, C.; Li, X.; Guo, B.; Guo, J.; Yao, Y. Assist-as-Needed Controller of a Rehabilitation Exoskeleton for Upper-Limb Natural Movements. Appl. Sci. 2025, 15, 2644. https://doi.org/10.3390/app15052644
Pei S, Wang J, Tian C, Li X, Guo B, Guo J, Yao Y. Assist-as-Needed Controller of a Rehabilitation Exoskeleton for Upper-Limb Natural Movements. Applied Sciences. 2025; 15(5):2644. https://doi.org/10.3390/app15052644
Chicago/Turabian StylePei, Shuo, Jiajia Wang, Chenghua Tian, Xibin Li, Bingqi Guo, Junlong Guo, and Yufeng Yao. 2025. "Assist-as-Needed Controller of a Rehabilitation Exoskeleton for Upper-Limb Natural Movements" Applied Sciences 15, no. 5: 2644. https://doi.org/10.3390/app15052644
APA StylePei, S., Wang, J., Tian, C., Li, X., Guo, B., Guo, J., & Yao, Y. (2025). Assist-as-Needed Controller of a Rehabilitation Exoskeleton for Upper-Limb Natural Movements. Applied Sciences, 15(5), 2644. https://doi.org/10.3390/app15052644







