Simulation and Experimental Research on Composite Diaphragm Hydraulic Force/Displacement Amplification Mechanism with Adjustable Initial Volume
Abstract
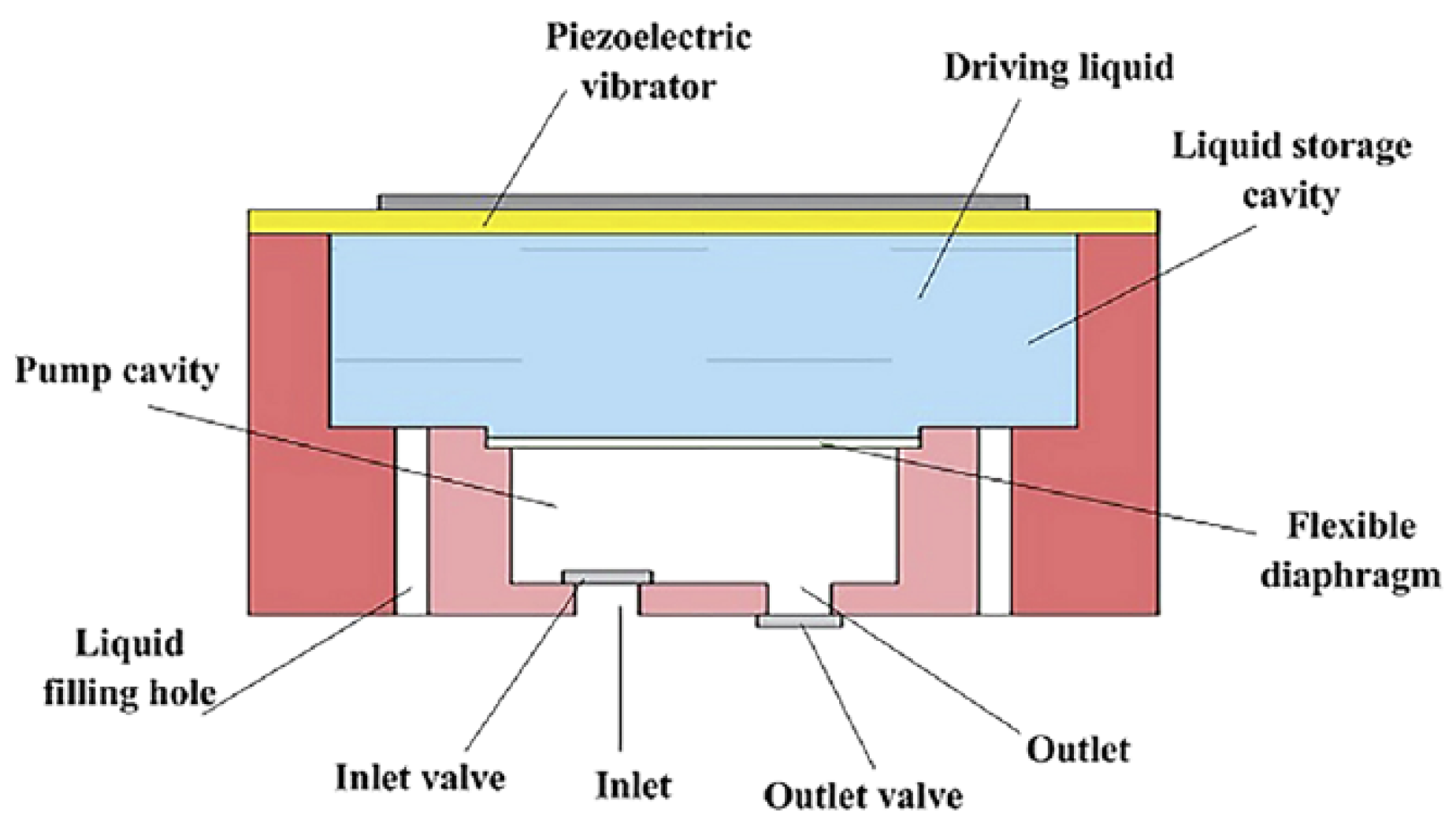
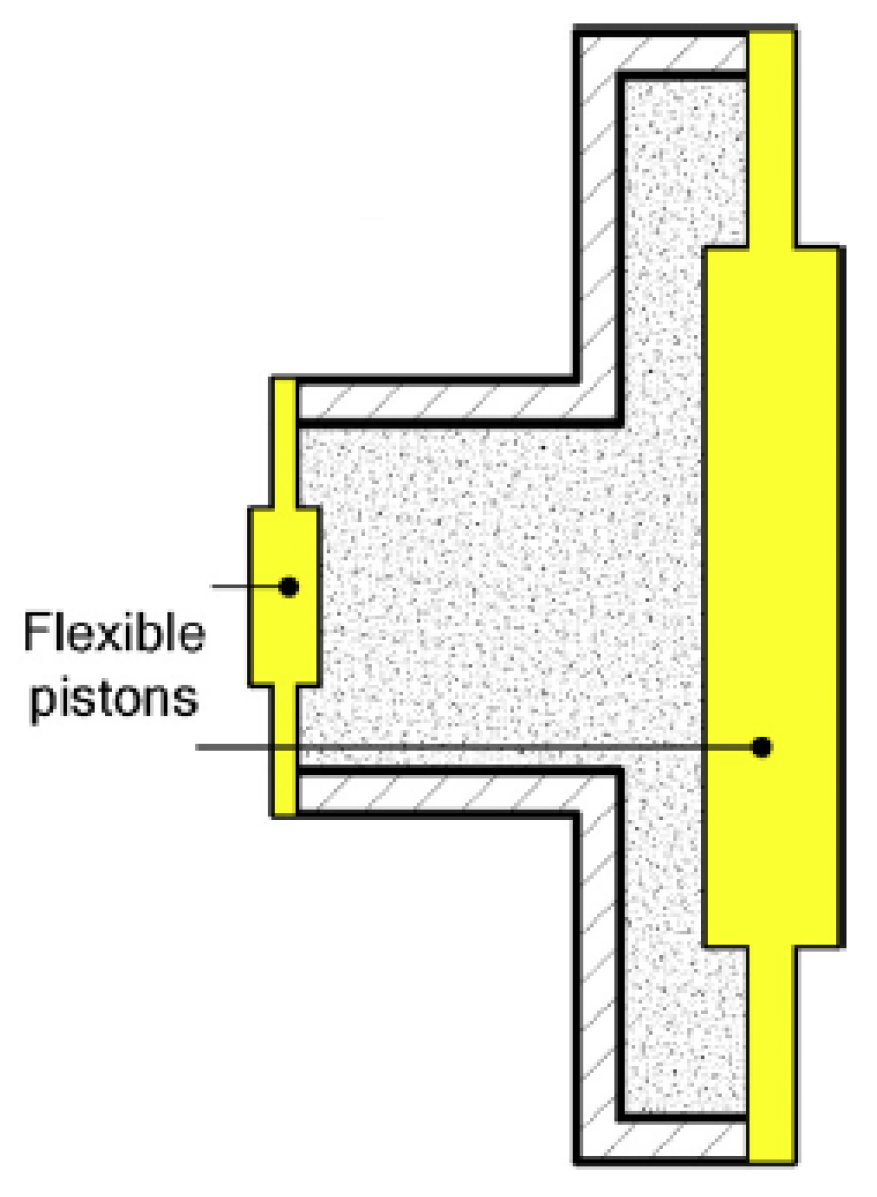
1. Introduction
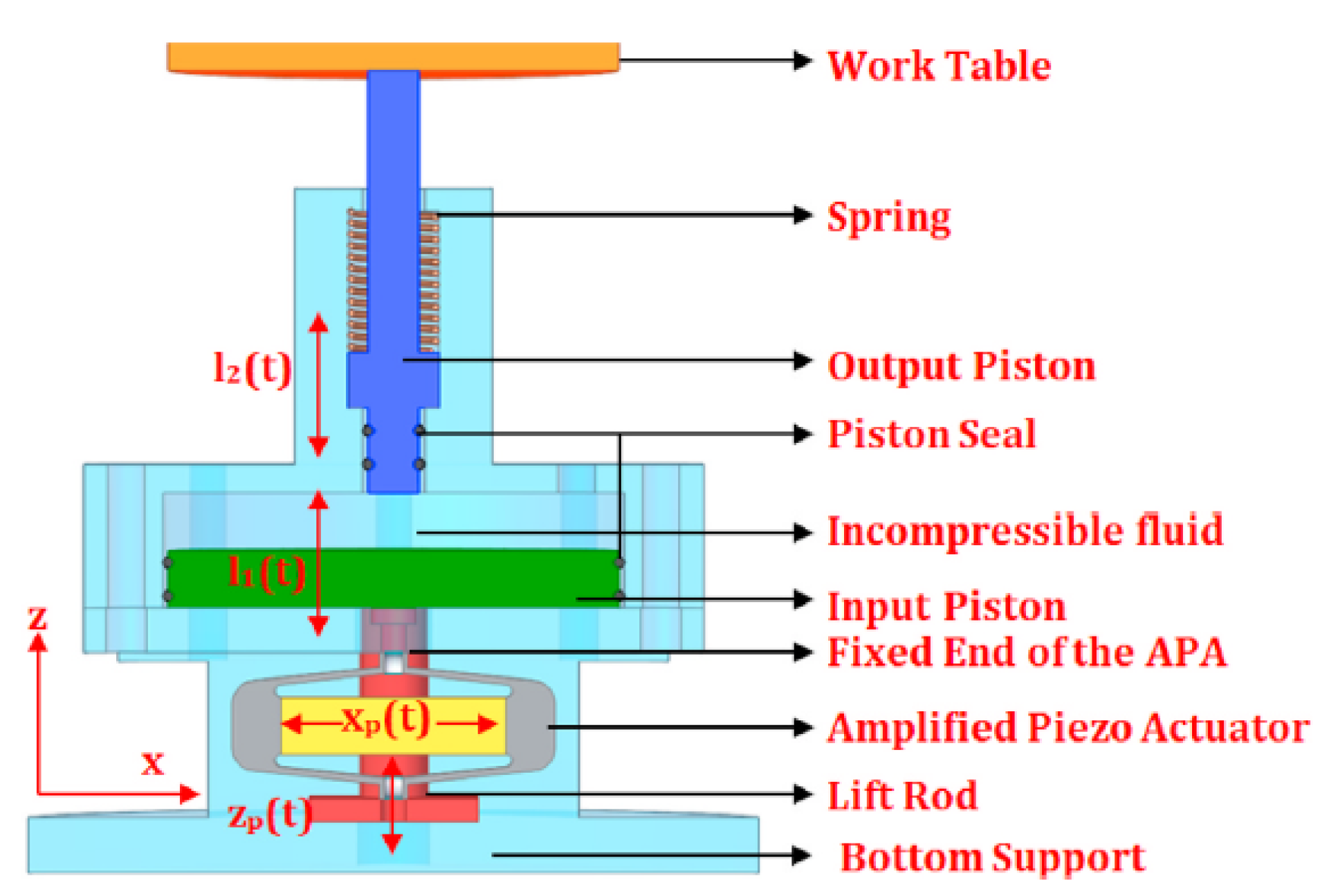
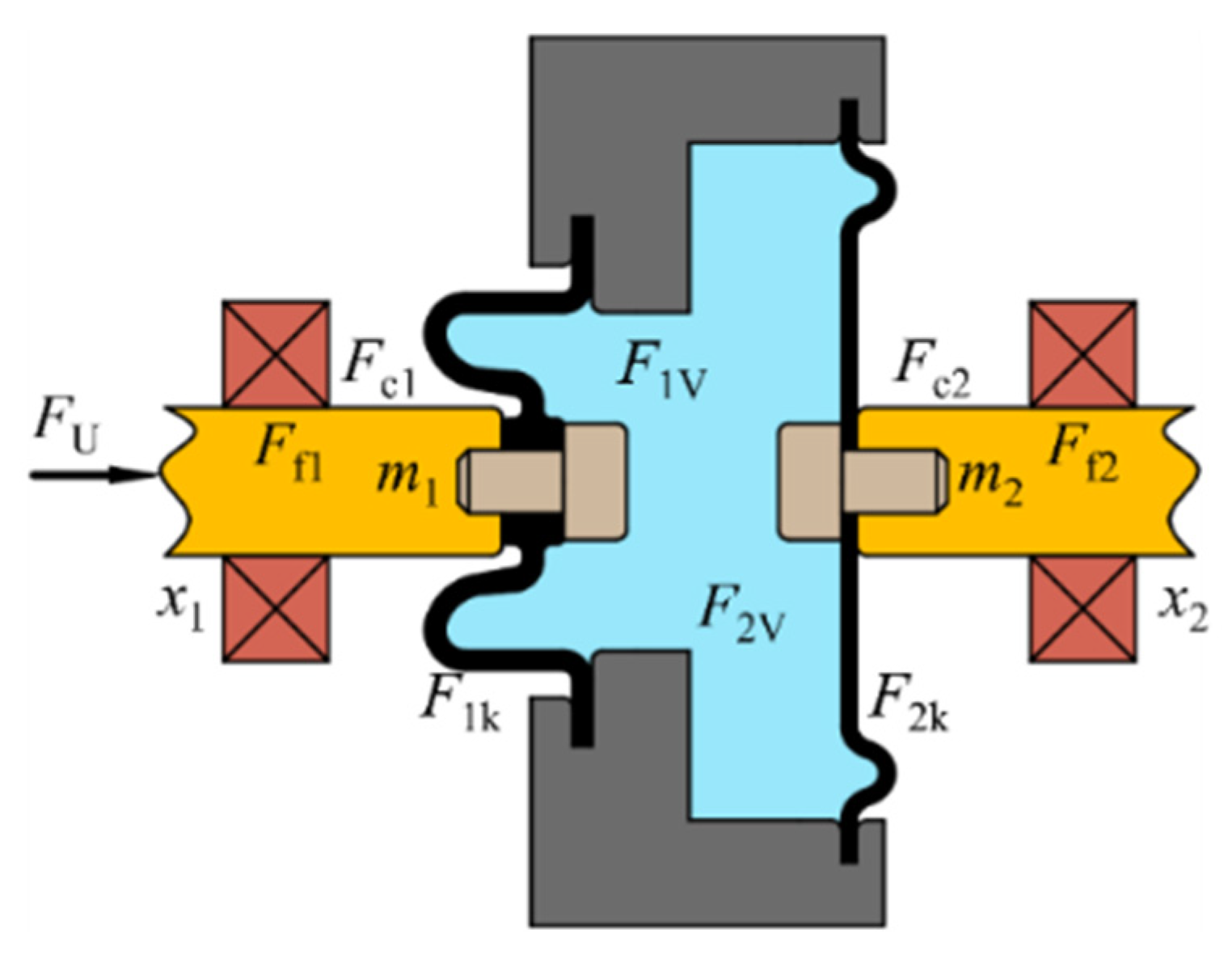
2. Working Principle and Modeling
2.1. Working Principle
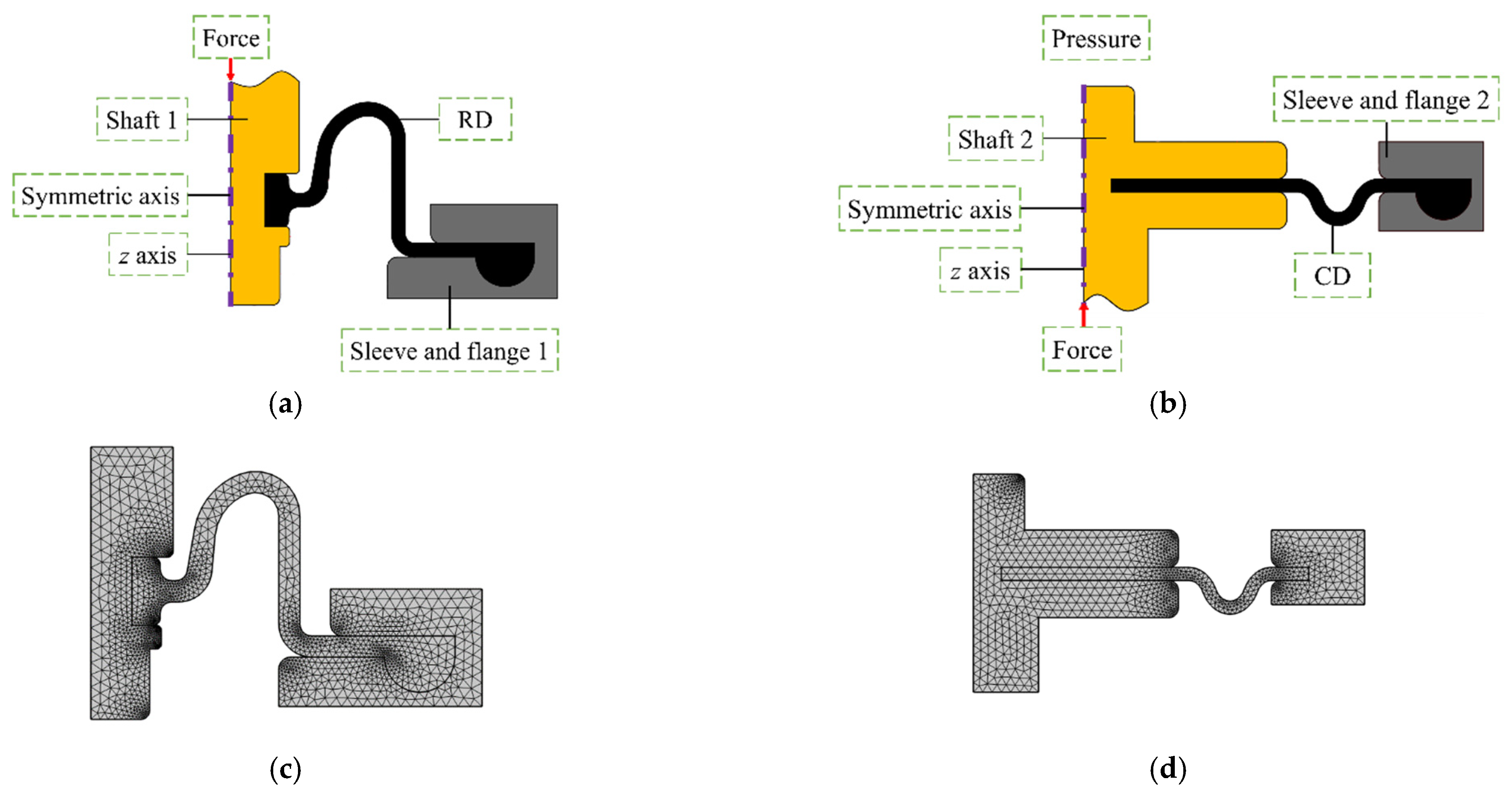
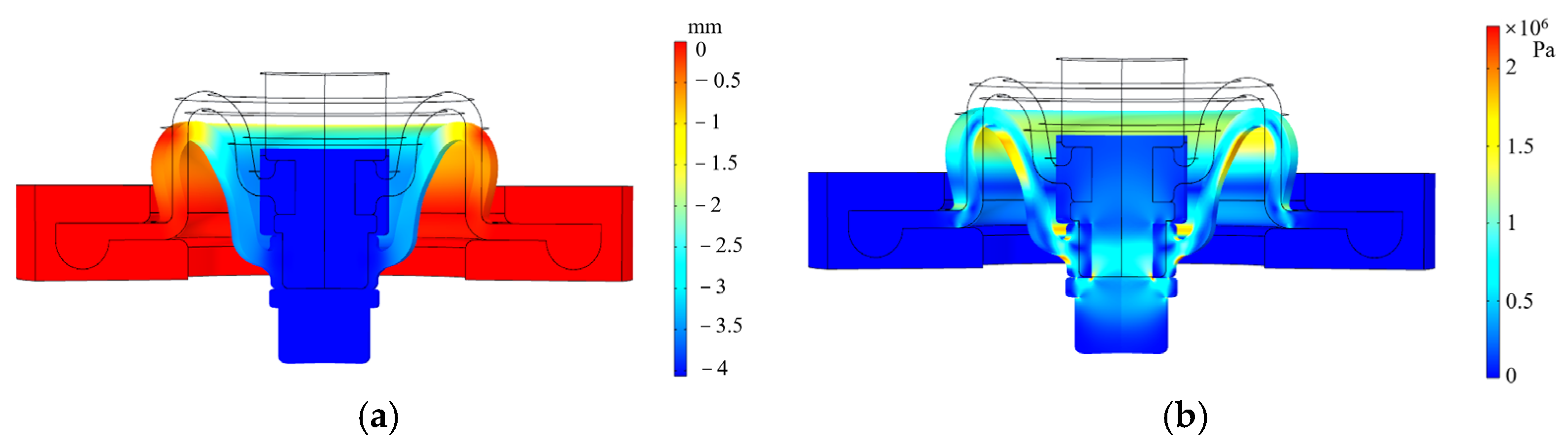
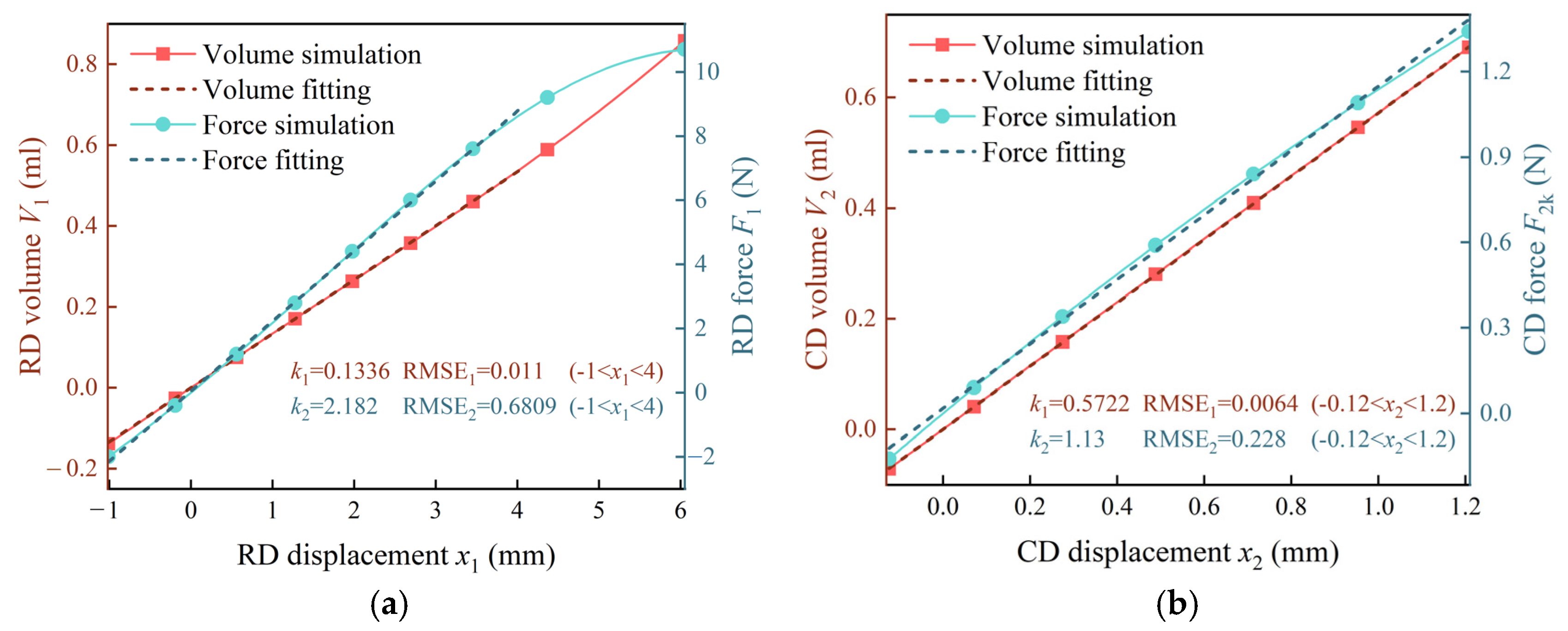
2.2. Mathematical Model
2.3. Diaphragm Mechanical Model
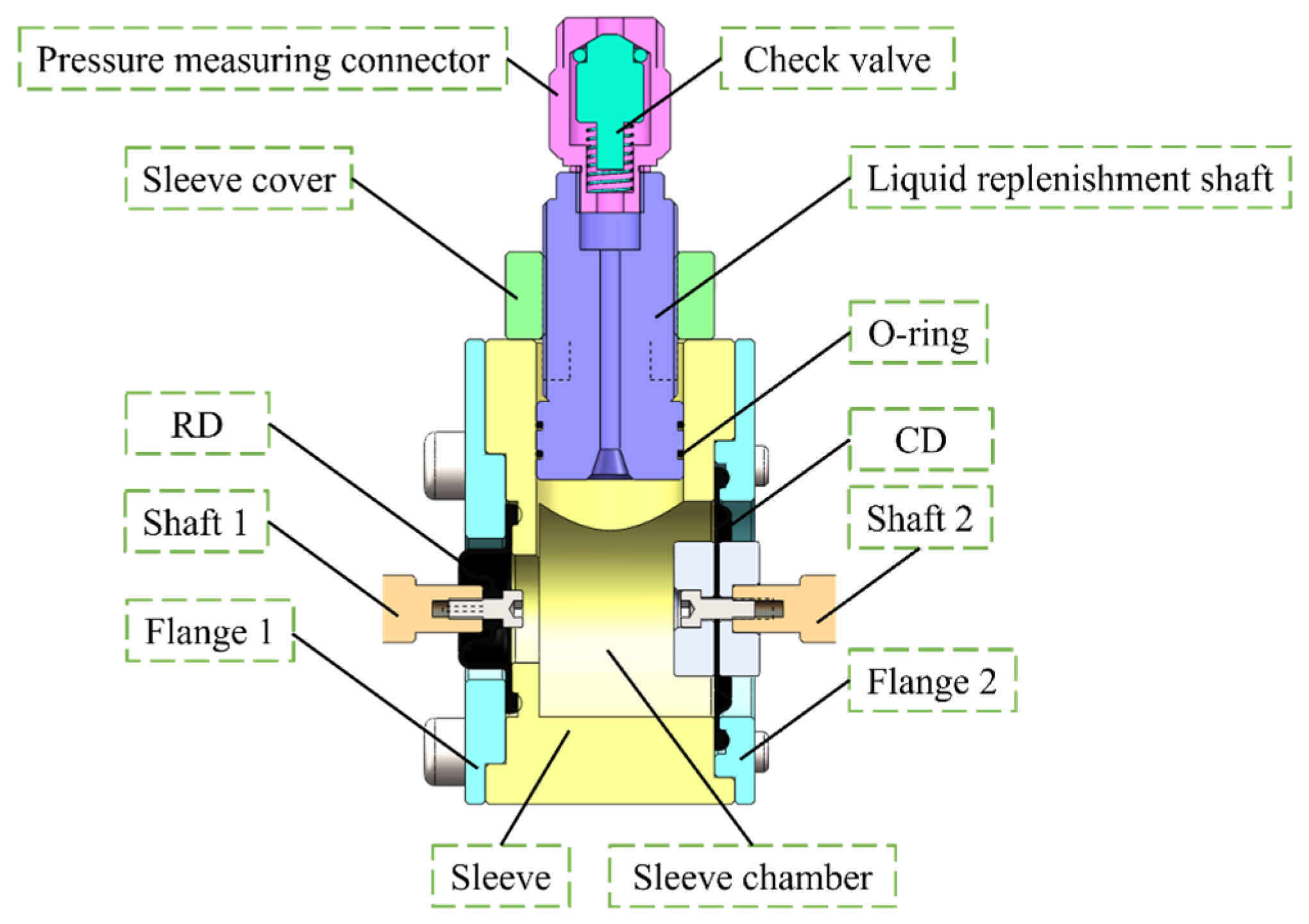
3. Experimental Research and Discussion
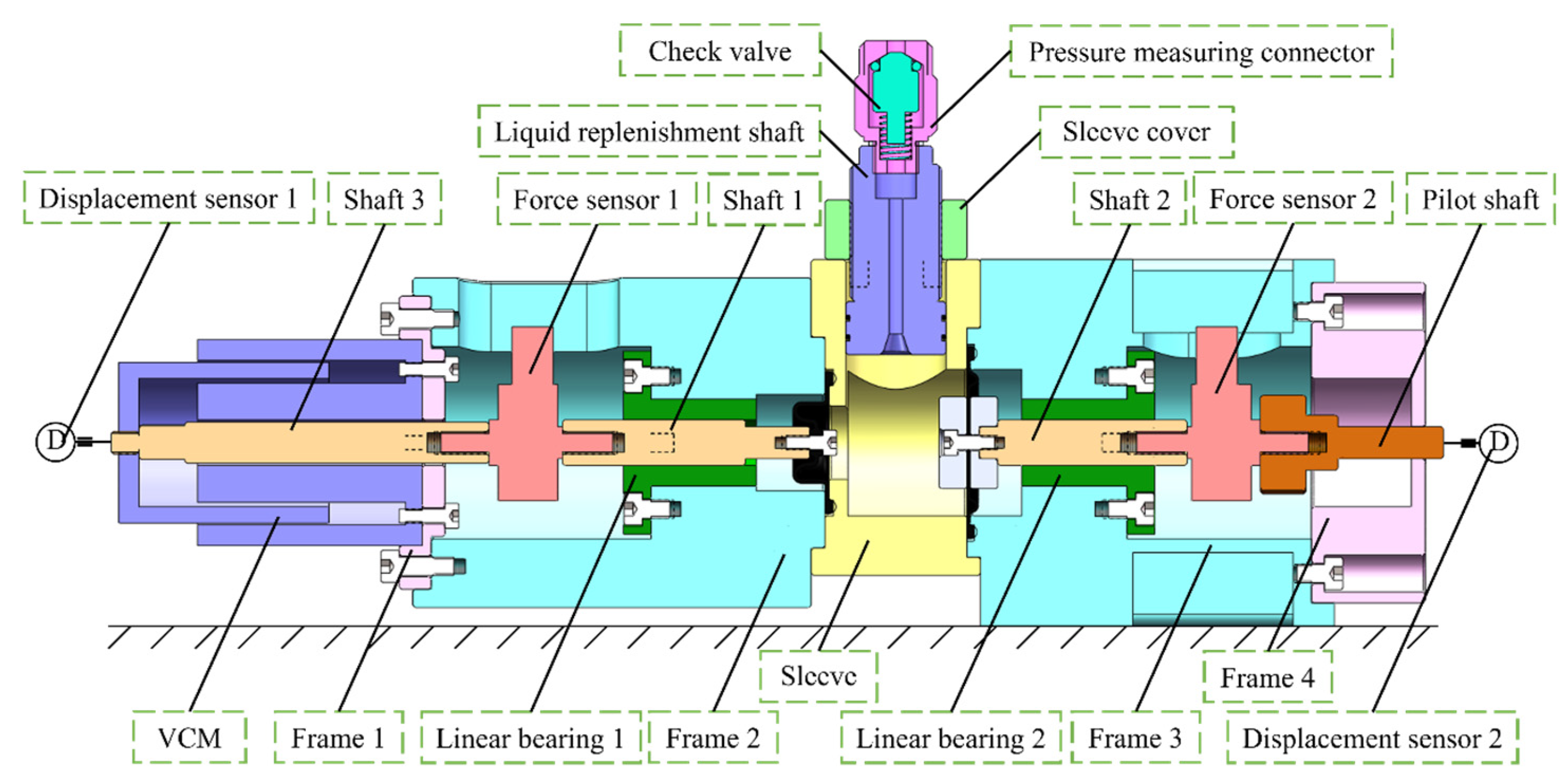
3.1. Experimental System
3.2. Results and Discussion
3.3. Static Characteristic
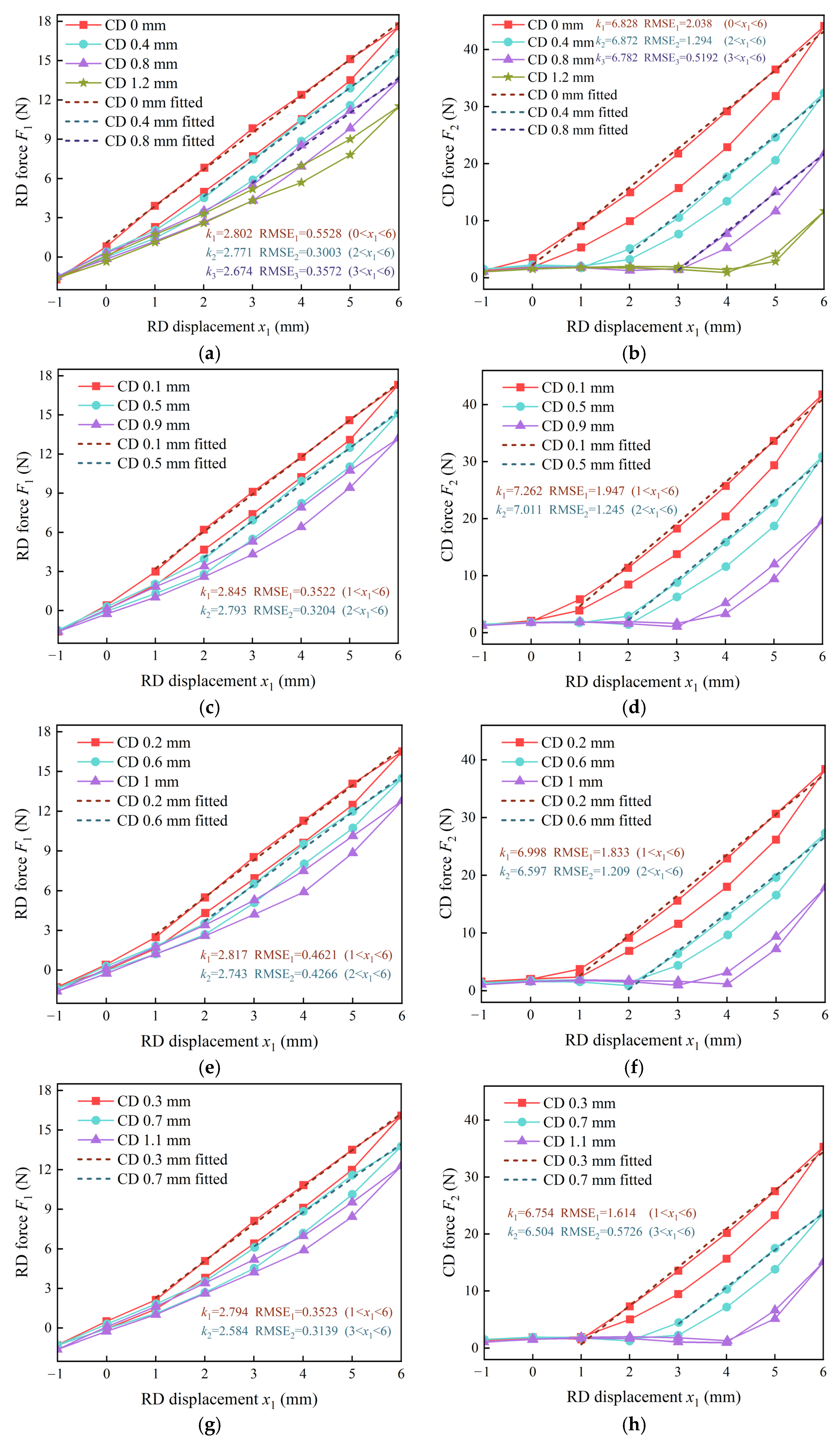
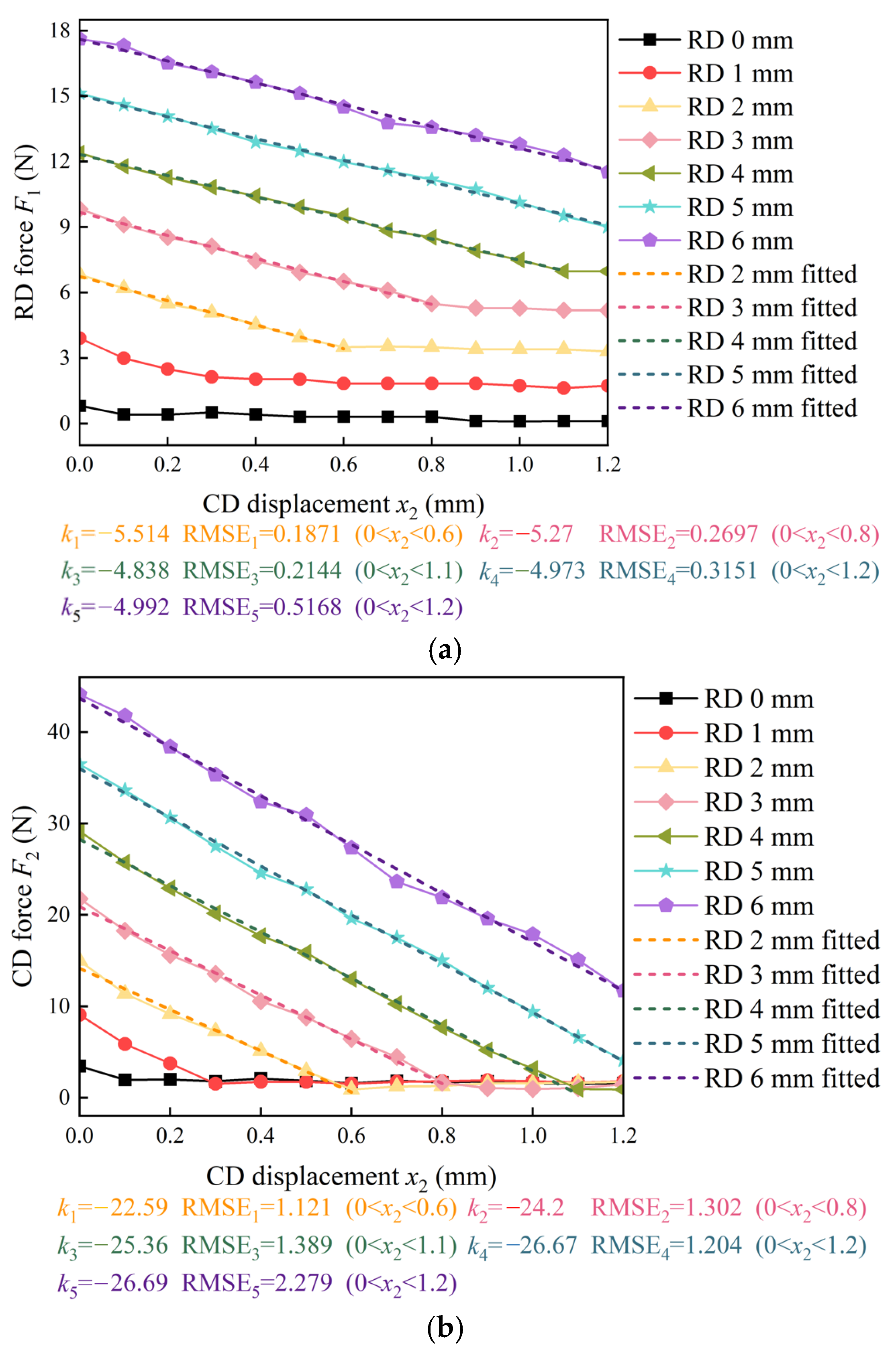
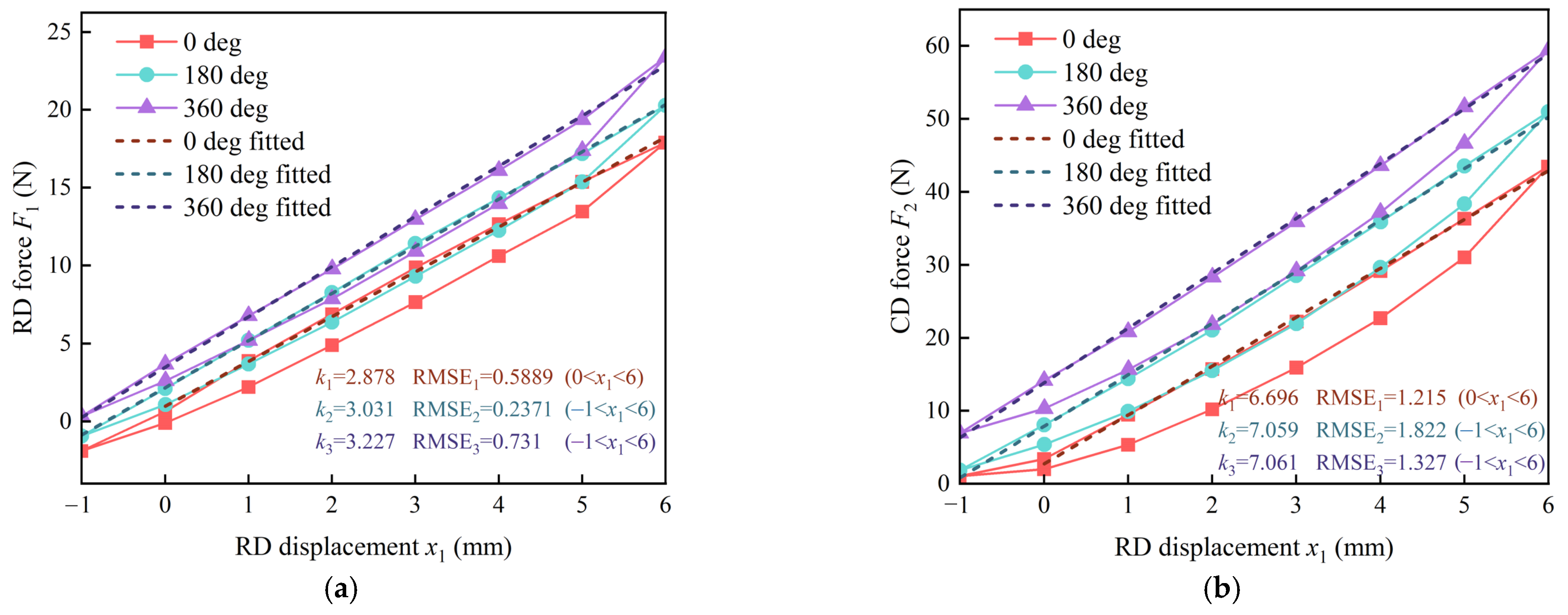
3.3.1. Influence of Different Diaphragm Displacements
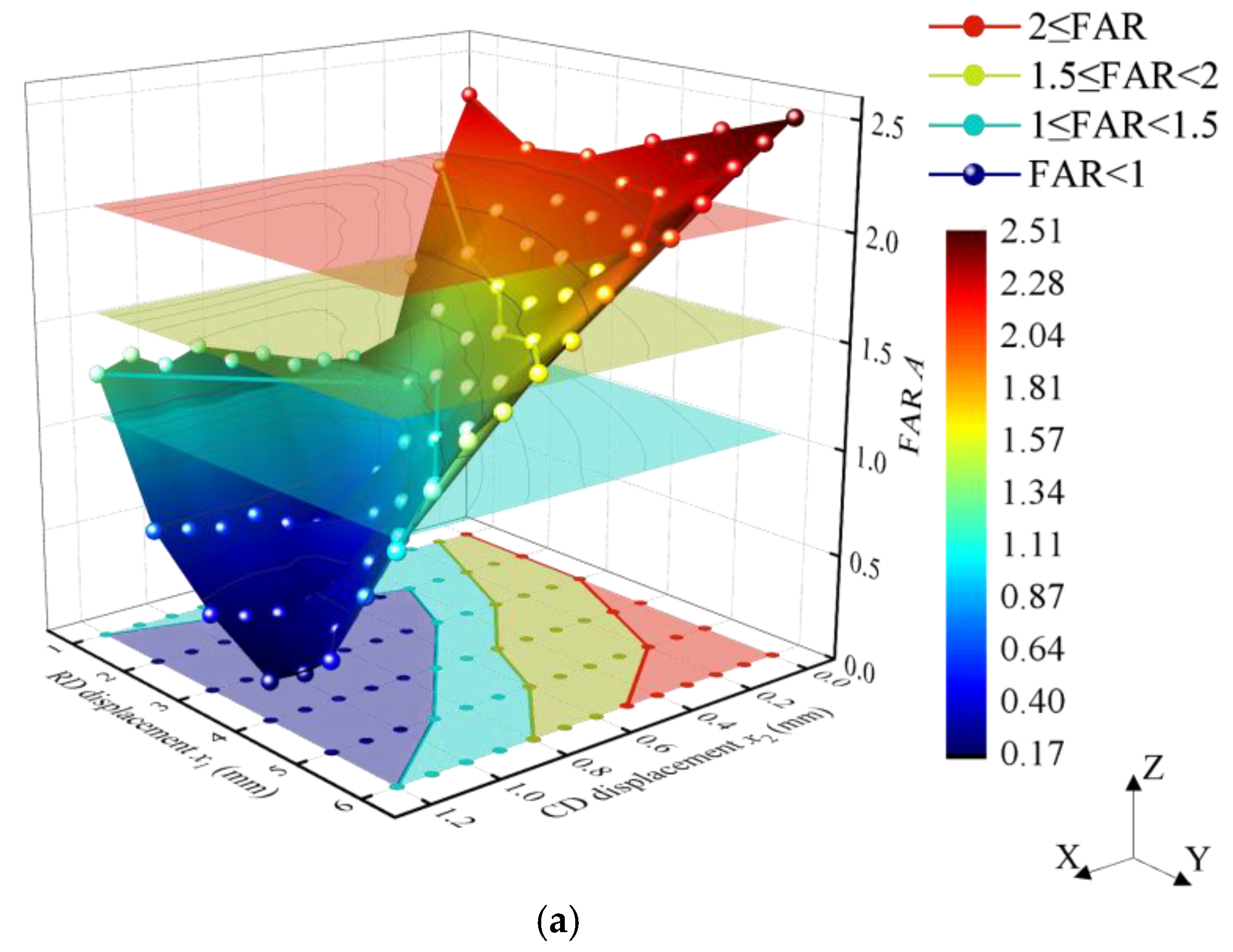
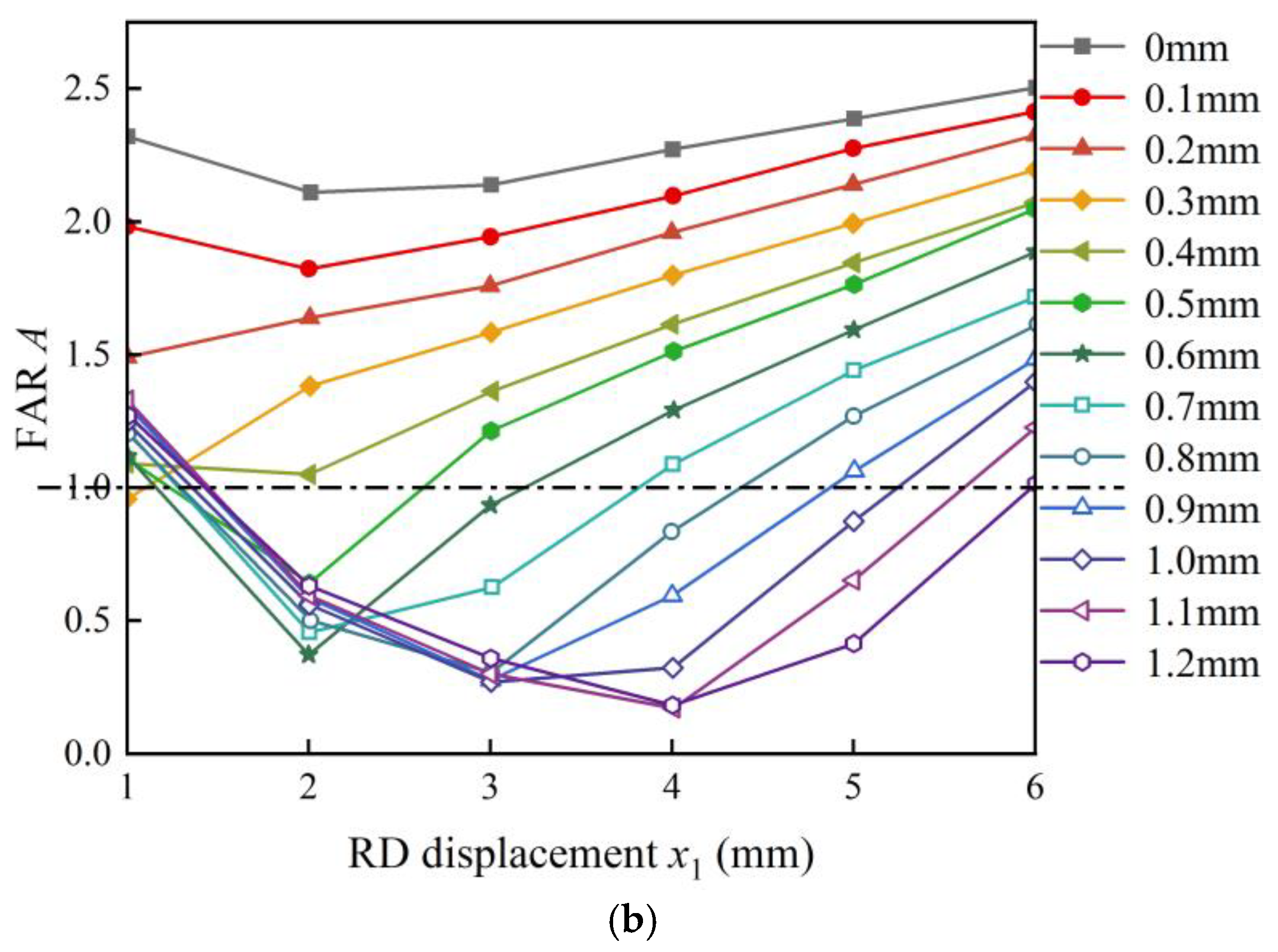
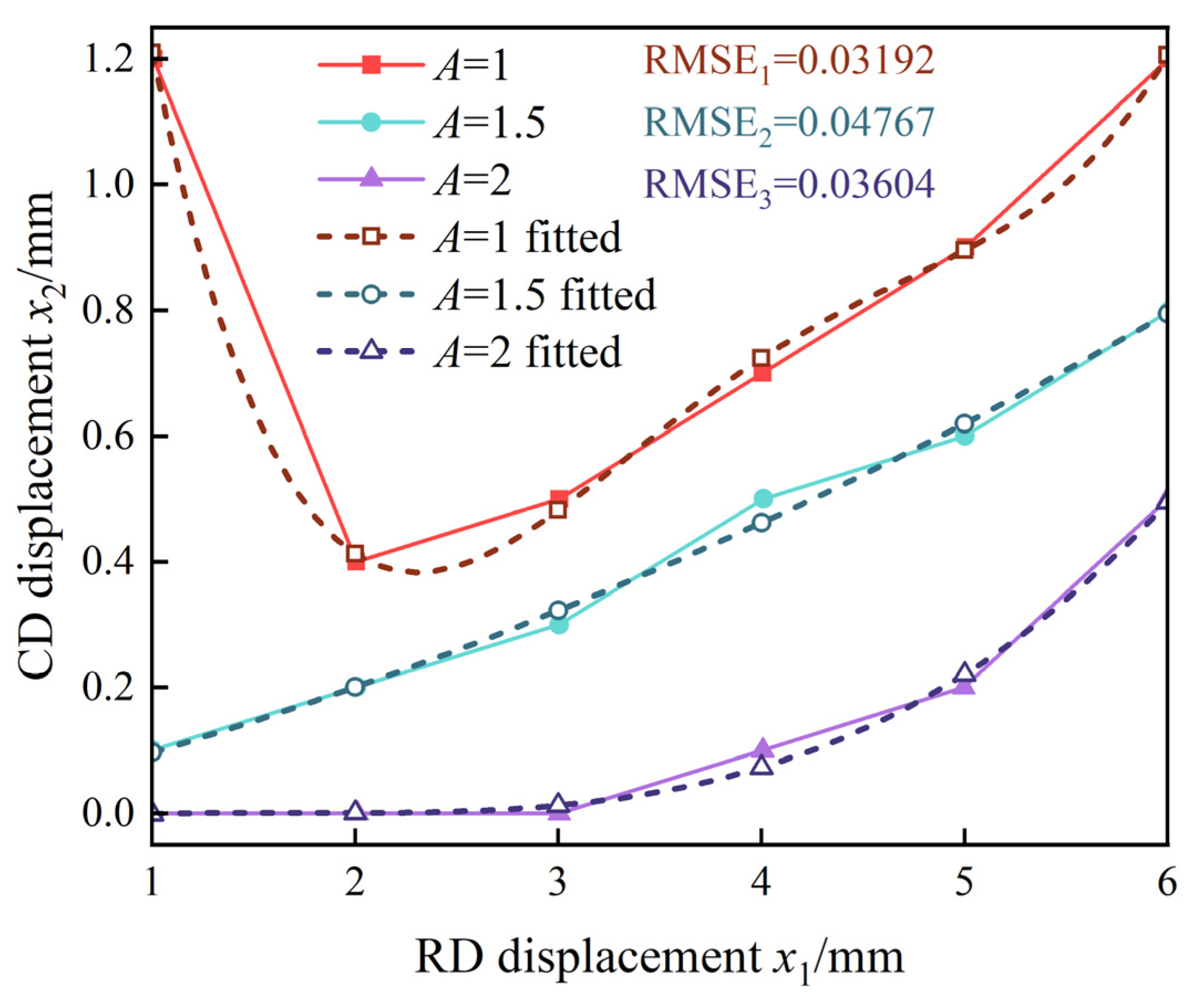
3.3.2. Experimental Analysis of FAR
3.3.3. Influence of Initial Volume
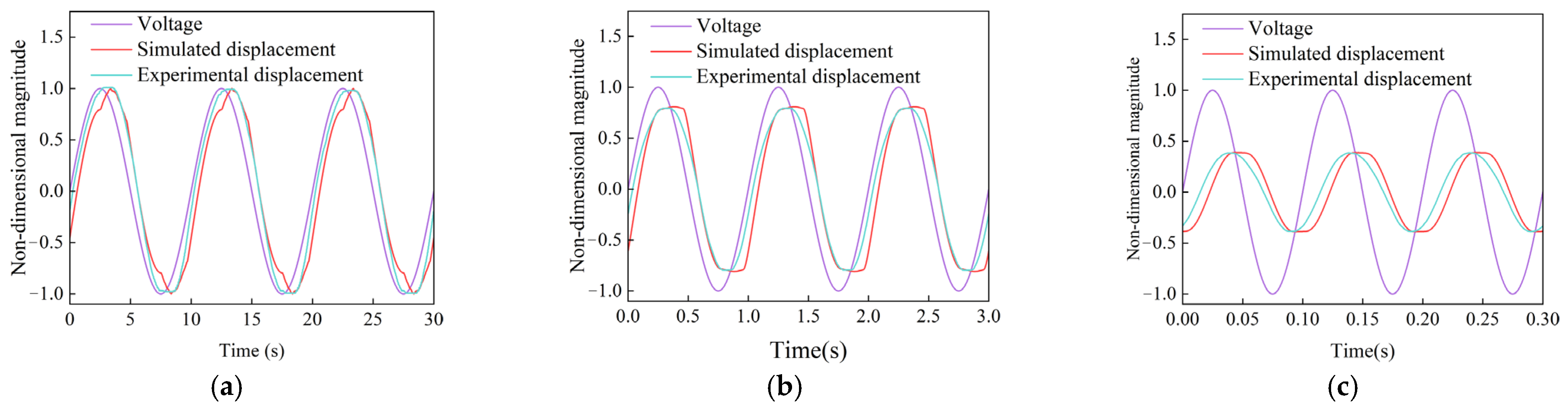
3.4. Dynamic Characteristic
4. Conclusions
- The experiments with different diaphragm displacements show that the forces of the diaphragms increase with the increase in the RD displacement and decrease with the increase in the CD displacement. There is hysteresis in the axial reciprocating motion of the diaphragm, and the hysteresis decreases with the increase in the CD displacement.
- The trend of the FARs with displacement shows that when the displacements of the RD exceed 2 mm, the FARs increase with the increase in the RD displacement but decrease with the increase in the CD displacement. The maximum FAR of the HFAM in the research is 2.5. Based on the FARs of 1, 1.5, and 2, the fitting expressions of the critical curves were obtained, and the displacement ranges of the RD and CD under different FAR ranges were determined.
- The experiments with different initial volumes show that when the displacements of the RD and the CD remain unchanged, the forces of the diaphragms increase with the increase in the initial volume. Furthermore, changing the initial volume does not affect the hysteresis of the diaphragms.
- Dynamic experiments show that when the frequency is less than 1 Hz, the maximum magnitude deviation between the simulation and the experiment is 0.35 dB, and the maximum phase deviation is 3.04 degrees. When the frequency is greater than 1 Hz, the maximum magnitude deviation between the simulation and the experiment is 1.14 dB, and the maximum phase deviation is 21.96 degrees. The accuracy of the established dynamic model was verified, and the model is helpful to the practical application of the HFAM.
- In subsequent research, factors such as temperature and pressure could be added to the model to further improve the accuracy of the model to adapt to different working conditions. And the influence of the diaphragm size parameters on the working effect of the HFAMs could be further studied. Based on the study results, the working effect of the HFAMs can be optimized by adjusting the diaphragms’ sizes when facing different working conditions and requirements.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Xu, B.; Shen, J.; Liu, S.; Su, Q.; Zhang, J. Research and development of electro-hydraulic control valves oriented to industry 4.0: A review. Chin. J. Mech. Eng. 2020, 33, 29. [Google Scholar] [CrossRef]
- Zhang, Y.; Yan, P.; Zhang, Z. High precision tracking control of a servo gantry with dynamic friction compensation. ISA Trans. 2016, 62, 349–356. [Google Scholar] [CrossRef]
- Xie, F.; Zhou, R.; Wang, D.; Ke, J.; Guo, X.; Nguyen, V.X. Simulation study on static and dynamic characteristics of electromagnet for electro-hydraulic proportional valve used in shock absorber. IEEE Access 2020, 8, 41870–41881. [Google Scholar] [CrossRef]
- Kim, H.J.; Yang, W.S. Effect of asymmetric piezoelectric multimorph ceramic on frequency response characteristics of piezoelectric acoustic actuator. In Proceedings of the 2013 Joint IEEE International Symposium on Applications of Ferroelectric and Workshop on Piezoresponse Force Microscopy (ISAF/PFM), Prague, Czech Republic, 21–25 July 2013; IEEE: Piscataway Township, NJ, USA, 2013; pp. 332–335. [Google Scholar]
- Gou, J.; Ma, T.; Liu, X.; Zhang, C.; Sun, L.; Sun, G.; Xia, W.; Ren, X. Large and sensitive magnetostriction in ferromagnetic composites with nanodispersive precipitates. NPG Asia Mater. 2021, 13, 6. [Google Scholar] [CrossRef]
- Mohith, S.; Rao, M.; Karanth, N.; Kulkarni, S.M.; Upadhya, A.R. Development and assessment of large stroke piezo-hydraulic actuator for micro positioning applications. Precis. Eng. 2021, 67, 324–338. [Google Scholar]
- Wang, B.; Xu, N.; Wu, P.; Yang, R. Simulation on an electro-hydrostatic actuator controlled by a high-pressure piezoelectric pump with a displacement amplifier. Assem. Autom. 2021, 41, 413–418. [Google Scholar] [CrossRef]
- Xiao, R.; Shao, S.; Xu, M.; Jing, Z. Design and analysis of a novel piezo-actuated XYθz micropositioning mechanism with large travel and kinematic decoupling. Adv. Mater. Sci. Eng. 2019, 2019, 5461725. [Google Scholar] [CrossRef]
- Song, E.Z.; Zhao, G.F.; Yao, C.; Ma, Z.K.; Ding, S.L.; Ma, X.Z. Study of nonlinear characteristics and model based control for proportional electromagnet. Math. Probl. Eng. 2018, 2018, 2549456. [Google Scholar] [CrossRef]
- Kim, J.Y.; Ahn, D. Analysis of high force voice coil motors for magnetic levitation. Actuators 2020, 9, 133. [Google Scholar] [CrossRef]
- Schmitt, P.; Hoffmann, M. Engineering a compliant mechanical amplifier for MEMS sensor applications. J. Microelectromech. Syst. 2020, 29, 214–227. [Google Scholar] [CrossRef]
- Pan, B.; Zhao, H.; Zhao, C.; Zhang, P.; Hu, H. Nonlinear characteristics of compliant bridge-type displacement amplification mechanisms. Precis. Eng. 2019, 60, 246–256. [Google Scholar] [CrossRef]
- Zhu, J.; Hao, G. Design and test of a compact compliant gripper using the Scott–Russell mechanism. Arch. Civ. Mech. Eng. 2020, 20, 81. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, D.; Chen, Y.; Zhang, B. Design of micro-displacement amplifier for the micro-channel cooling system in the micro-pump. Forsch. Im Ingenieurwesen Eng. Res. 2020, 84, 161–168. [Google Scholar] [CrossRef]
- Ling, M.; Wang, J.; Wu, M.; Cao, L.; Fu, B. Design and modeling of an improved bridge-type compliant mechanism with its application for hydraulic piezo-valves. Sens. Actuators A Phys. 2021, 324, 112687. [Google Scholar] [CrossRef]
- Tang, H.; Li, Y.; Xiao, X. Development and assessment of a novel hydraulic displacement amplifier for piezo-actuated large stroke precision positioning. In Proceedings of the 2013 IEEE International Conference on Robotics and Automation, Karlsruhe, Germany, 6–10 May 2013; IEEE: Piscataway Township, NJ, USA, 2013; pp. 1409–1414. [Google Scholar]
- Muralidhara; Rao, R. Displacement characteristics of a piezoactuator-based prototype microactuator with a hydraulic displacement amplification system. J. Mech. Sci. Technol. 2015, 29, 4817–4822. [Google Scholar] [CrossRef]
- Tian, X.C.; Wang, H.G.; Wang, H.; Wang, Z.C.; Sun, Y.Z.; Zhu, J.Z.; Zhao, J.; Zhang, S.; Yang, Z. Design and test of a piezoelectric micropump based on hydraulic amplification. AIP Adv. 2021, 11, 065230. [Google Scholar] [CrossRef]
- Yang, Z.; He, Z.; Li, D.; Cui, X.; Xue, G.; Zhao, Z. Dynamic analysis and application of a novel hydraulic displacement amplifier based on flexible pistons for micro stage actuator. Sens. Actuators A Phys. 2015, 236, 228–246. [Google Scholar] [CrossRef]
- Whitney, J.P.; Glisson, M.F.; Brockmeyer, E.L.; Hodgins, J.K. A low-friction passive fluid transmission and fluid-tendon soft actuator. In Proceedings of the 2014 IEEE/RSJ International Conference on Intelligent Robots and Systems, Chicago, IL, USA, 14–18 September 2014; IEEE: Piscataway Township, NJ, USA, 2014; pp. 2801–2808. [Google Scholar]
- Liu, B.; Zheng, G.; Wang, A.; Gui, C.; Yu, H.; Shan, M.; Zhong, Z. Optical fiber Fabry–Perot acoustic sensors based on corrugated silver diaphragms. IEEE Trans. Instrum. Meas. 2019, 69, 3874–3881. [Google Scholar] [CrossRef]
- Peng, X.; Han, L.; Li, L. A consistently compressible Mooney-Rivlin model for the vulcanized rubber based on the Penn’s experimental data. Polym. Eng. Sci. 2021, 61, 2287–2294. [Google Scholar] [CrossRef]
- Meththananda, I.M.; Parker, S.; Patel, M.P.; Braden, M. The relationship between Shore hardness of elastomeric dental materials and Young’s modulus. Dent. Mater. 2009, 25, 956–959. [Google Scholar] [CrossRef]
- Zhang, H.; Dong, J.; Cui, C.; Liu, S. Stress and strain analysis of spherical sealing cups of fluid-driven pipeline robot in dented oil and gas pipeline. Eng. Fail. Anal. 2020, 108, 104294. [Google Scholar] [CrossRef]



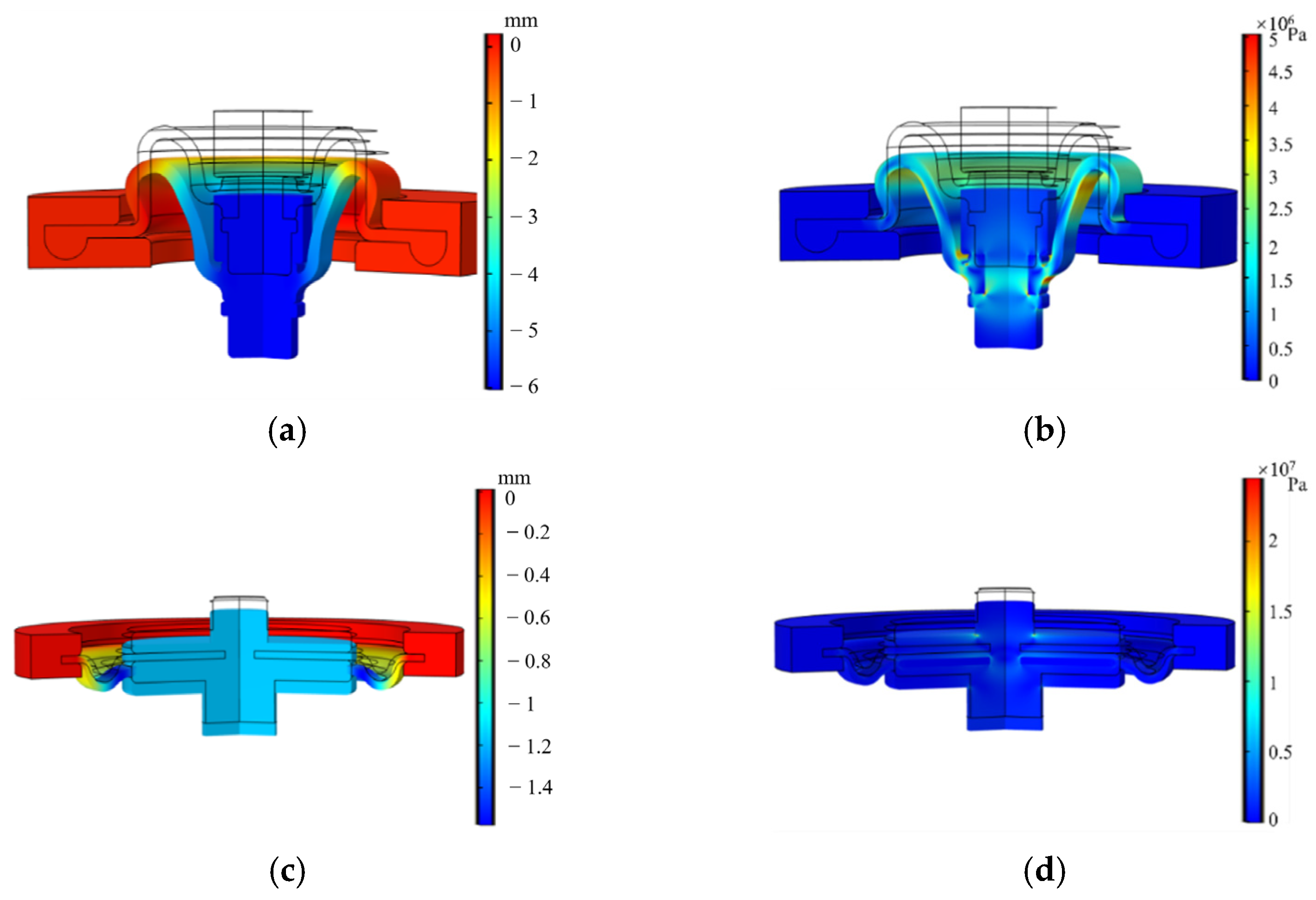



| Definition | Parameter | Value | Unit |
|---|---|---|---|
| Shore hardness | s | 70 | HA |
| Density | ρ | 1.3 | g/cm3 |
| Mechanical characteristic coefficient of the constitutive model | kr | 0.25 | - |
| Model parameter | C10 | 0.7388 | MPa |
| Model parameter | C01 | 0.1847 | MPa |
| Elastic modulus | E | 5.545 | MPa |
| Poisson’s ratio | μ | 0.5 | - |
| Grid Independence Test of the RD | ||||
|---|---|---|---|---|
| Number | Domain Unit | Edge Unit | Displacement | Deviation Rate Compared to the Next Grid |
| 1 | 4050 | 432 | 3.9572 mm | 2.48% |
| 2 | 6136 | 527 | 4.0552 mm | 2.14% |
| 3 | 12,437 | 796 | 4.1419 mm | 1.09% |
| 4 | 40,262 | 1414 | 4.1869 mm | - |
| Grid Independence Test of the CD | ||||
| Number | Domain Unit | Edge Unit | Displacement | Deviation Rate Compared to the Next Grid |
| 5 | 2633 | 347 | 1.1599 mm | 2.73% |
| 6 | 3954 | 421 | 1.1916 mm | 2.24% |
| 7 | 11,737 | 695 | 1.2183 mm | 0.84% |
| 8 | 41,785 | 1287 | 1.2285 mm | - |
| Definition | Parameter | Value | Unit |
|---|---|---|---|
| Force constant | Kf | 24.55 | N/A |
| Resistance | R | 6.8 | Ω |
| Inductance | L | 2.5 × 10−3 | H |
| Displacement range | s1 | 15 | mm |
| Peak force | Fp | 70 | N |
| Continuous force | Fcon | 27.5 | N |
| Sensor Type | Voltage Range | Measuring Range | Accuracy |
|---|---|---|---|
| Displacement sensor 1 | 0–5 V | 0–15 mm | 1‰ |
| Displacement sensor 2 | 0–10 V | 0–10 mm | 1‰ |
| Force sensor 1 | −10–10 V | −50–50 N | 1‰ |
| Force sensor 2 | −10–10 V | −100–100 N | 1‰ |
| Relationships Between RD Displacement x1 and CD Displacement x2 | FAR A Ranges |
|---|---|
| x2 ≥ 0.01885x14 − 0.3043x13 + 1.788x12 − 4.314x1 + 4.021 | A < 1 |
| 0.008885x12 + 0.07746x1 + 0.009964 ≤ x2 < 0.01885x14 − 0.3043x13 + 1.788x12 − 4.314x1 + 4.021 | 1 ≤ A < 1.5 |
| 0.006457x13 − 0.03382x12 + 0.0583x1 − 0.03243 ≤ x2 < 0.008885x12 + 0.07746x1 + 0.009964 | 1.5 ≤ A < 2 |
| x2 ≤ 0.006457x13 − 0.03382x12 + 0.0583x1 − 0.03243 | 2 ≤ A ≤ 2.5 |
| Definition | Parameter | Value | Unit |
|---|---|---|---|
| Force constant | Kf | 24.55 | N/A |
| Resistance | R | 6.8 | Ω |
| Inductance | L | 2.5 × 10−3 | H |
| Total mass of the RD end | m1 | 0.17189 | kg |
| Total mass of the CD end | m2 | 0.13383 | kg |
| Static friction force of the RD end | Ff1 | 2.5 | N |
| Static friction force of the CD end | Ff2 | 0.2 | N |
| RD elastic slope | k1 | 2.182 | N/mm |
| CD elastic slope | k2 | 1.13 | N/mm |
| Displacement proportional coefficient | kp1 | 4.2829 | - |
| Area proportional coefficient | kp2 | 0.25 | - |
| Viscous friction coefficient of the RD | cv1 | 55 | N·s/m |
| Viscous friction coefficient of the CD | cv2 | 27 | N·s/m |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, Y.; Geng, T.; Zhang, Z.; Hou, J.; Ning, D.; Gong, Y. Simulation and Experimental Research on Composite Diaphragm Hydraulic Force/Displacement Amplification Mechanism with Adjustable Initial Volume. Appl. Sci. 2025, 15, 2754. https://doi.org/10.3390/app15052754
Yang Y, Geng T, Zhang Z, Hou J, Ning D, Gong Y. Simulation and Experimental Research on Composite Diaphragm Hydraulic Force/Displacement Amplification Mechanism with Adjustable Initial Volume. Applied Sciences. 2025; 15(5):2754. https://doi.org/10.3390/app15052754
Chicago/Turabian StyleYang, Yong, Tingyu Geng, Zengmeng Zhang, Jiaoyi Hou, Dayong Ning, and Yongjun Gong. 2025. "Simulation and Experimental Research on Composite Diaphragm Hydraulic Force/Displacement Amplification Mechanism with Adjustable Initial Volume" Applied Sciences 15, no. 5: 2754. https://doi.org/10.3390/app15052754
APA StyleYang, Y., Geng, T., Zhang, Z., Hou, J., Ning, D., & Gong, Y. (2025). Simulation and Experimental Research on Composite Diaphragm Hydraulic Force/Displacement Amplification Mechanism with Adjustable Initial Volume. Applied Sciences, 15(5), 2754. https://doi.org/10.3390/app15052754






