Damping of Liquid Sloshing Using Hydrophobic Walls in the Off-Impulse Regime
Abstract
:1. Introduction
2. Experimental Procedure
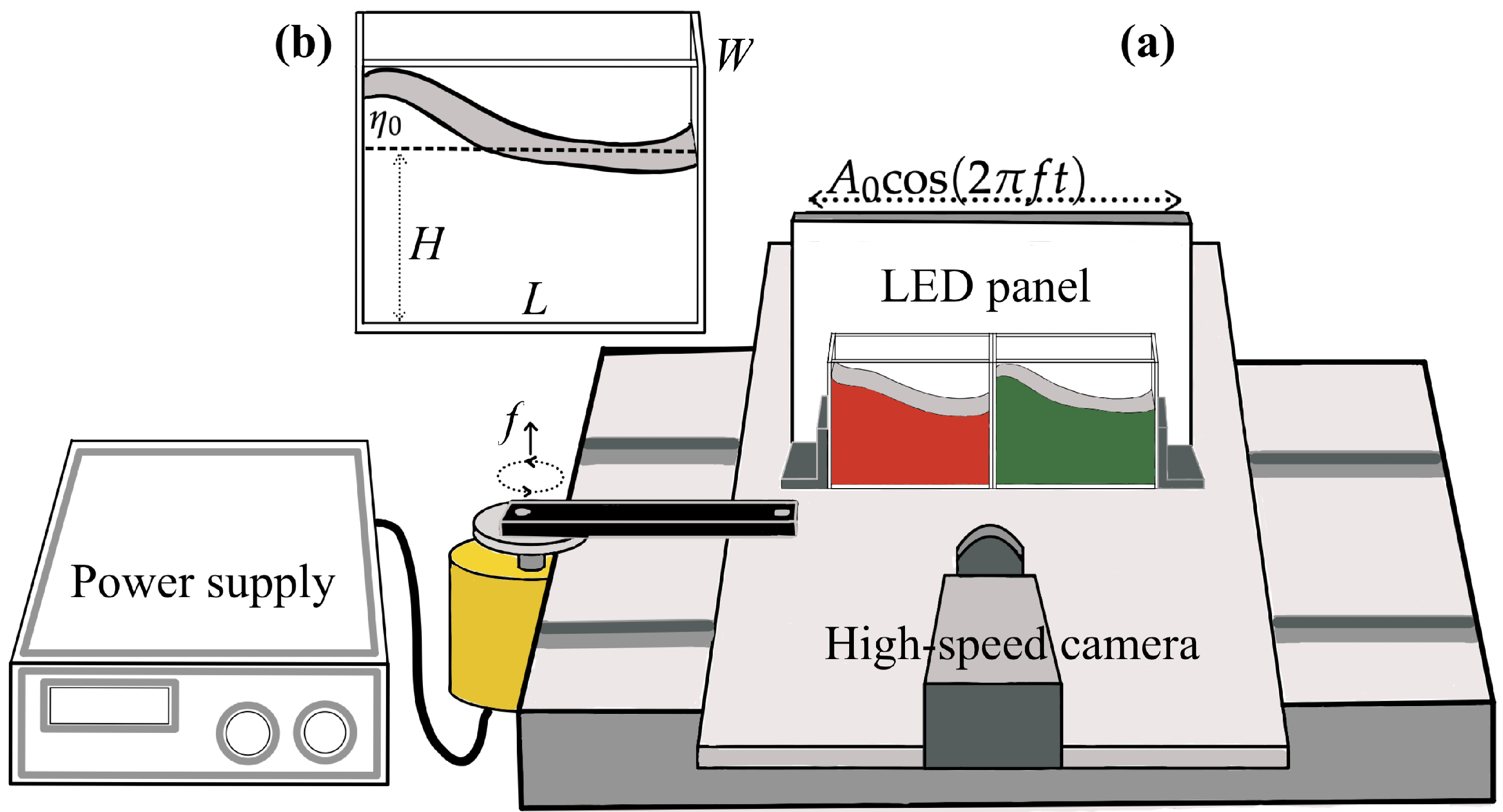
2.1. Experimental Setup
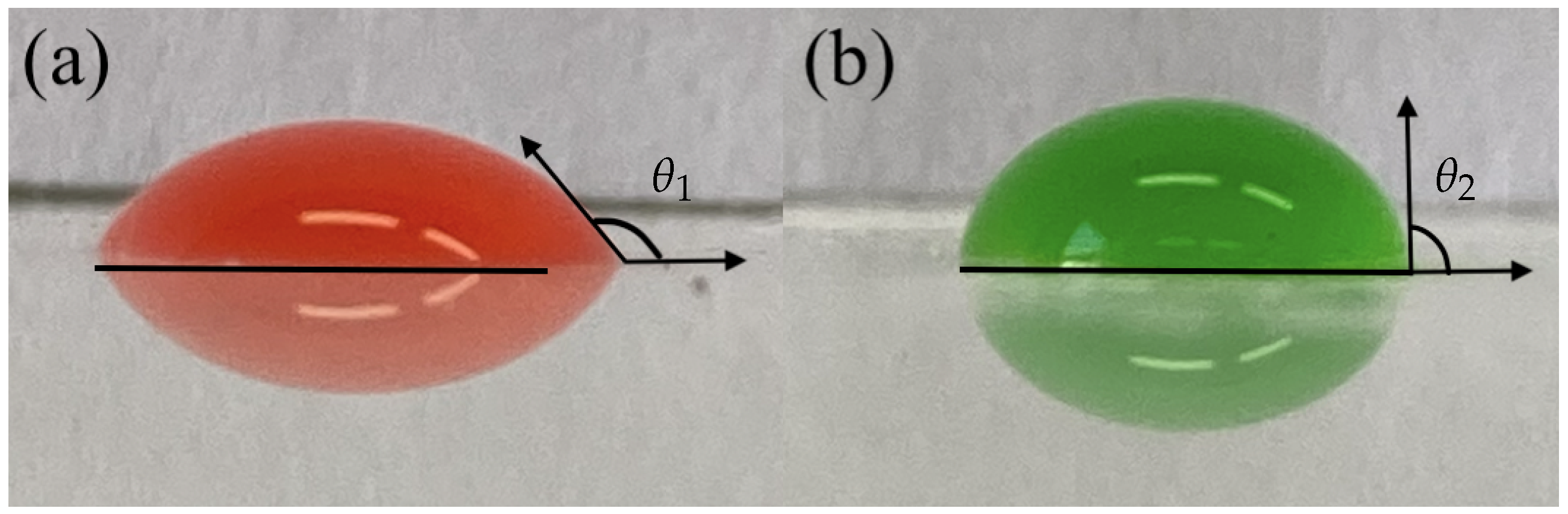
2.2. Video Processing: Wave Height Estimation Based on RGB Images and Data Extraction
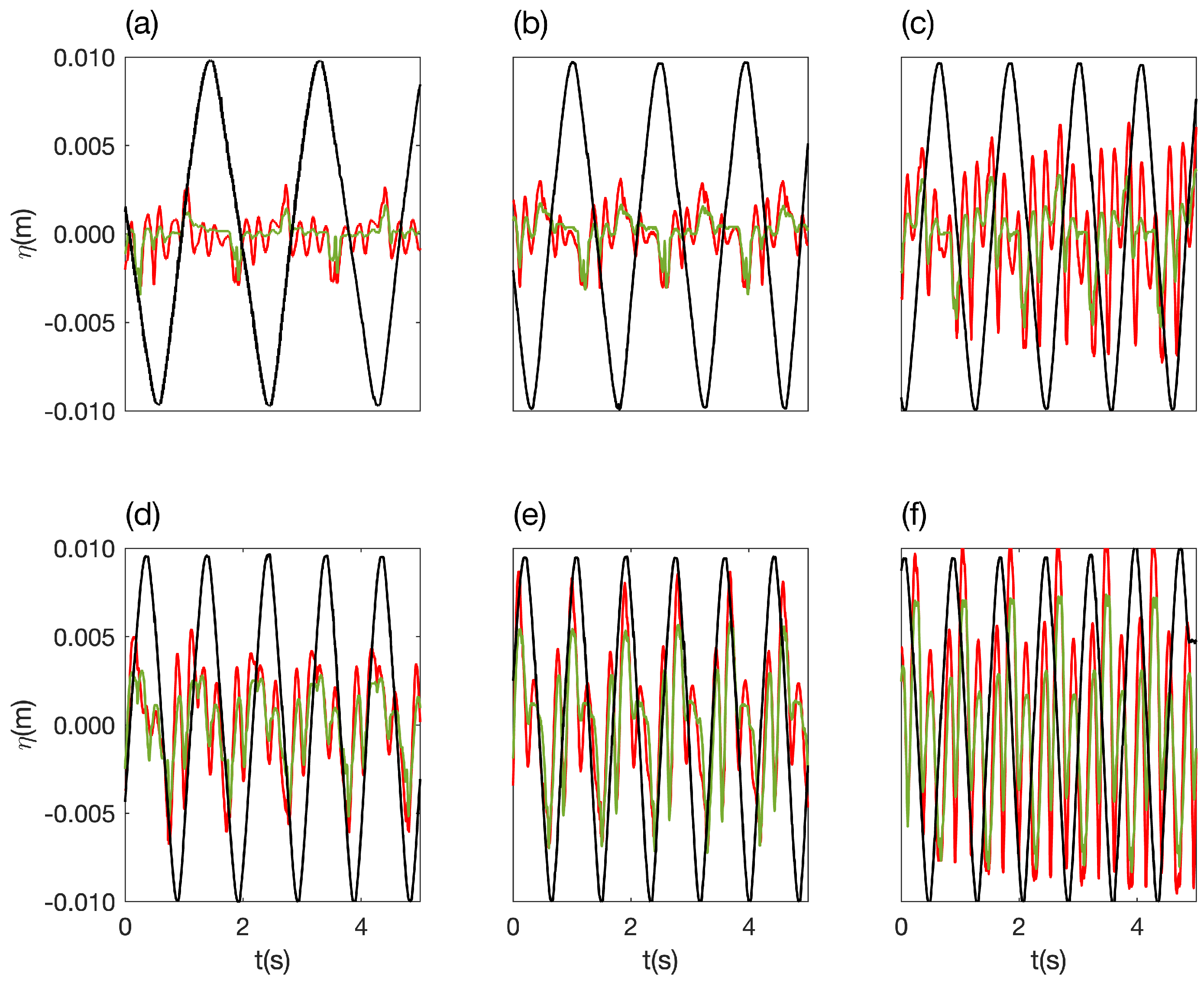
3. Forcing
4. Free Surface Damping
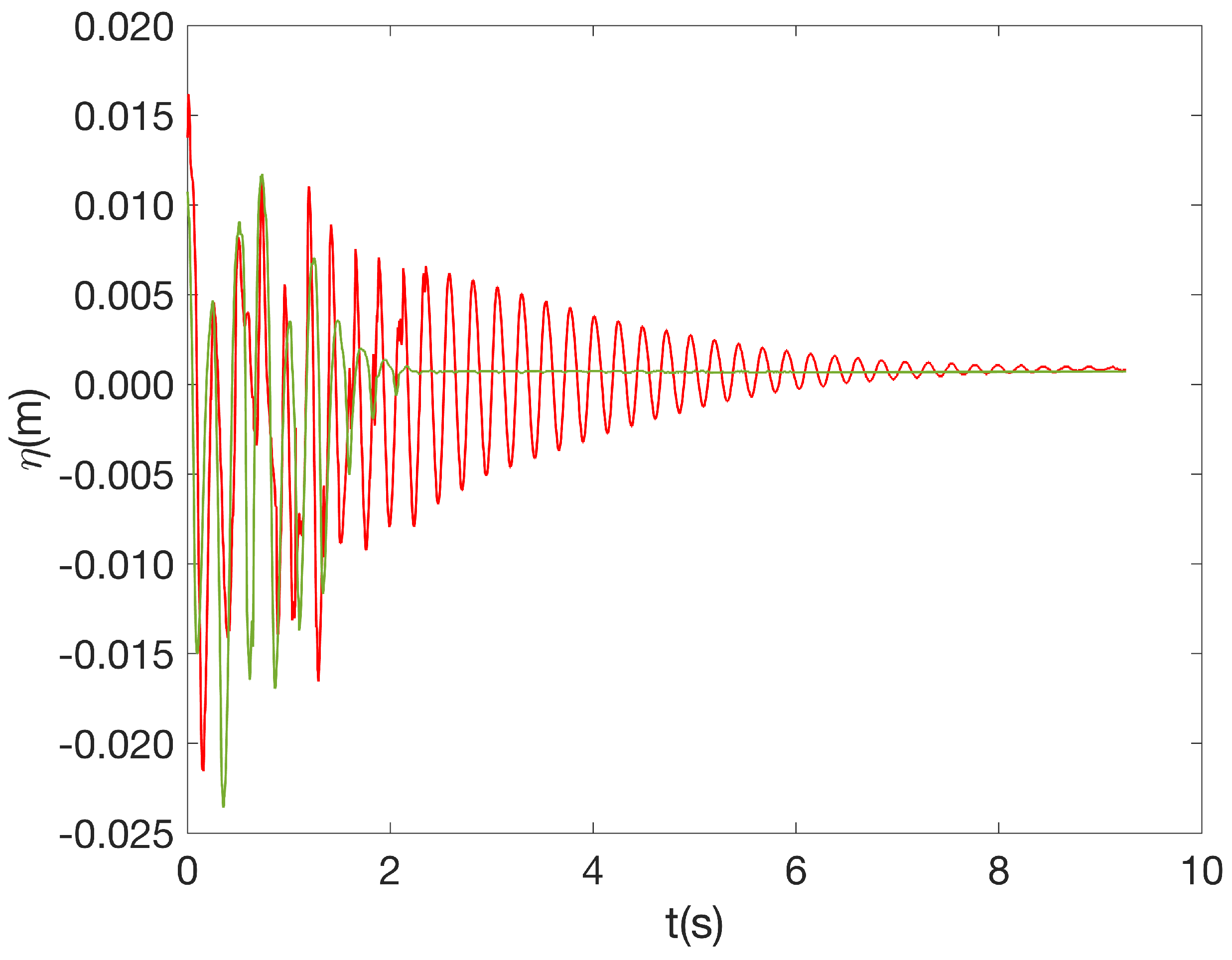
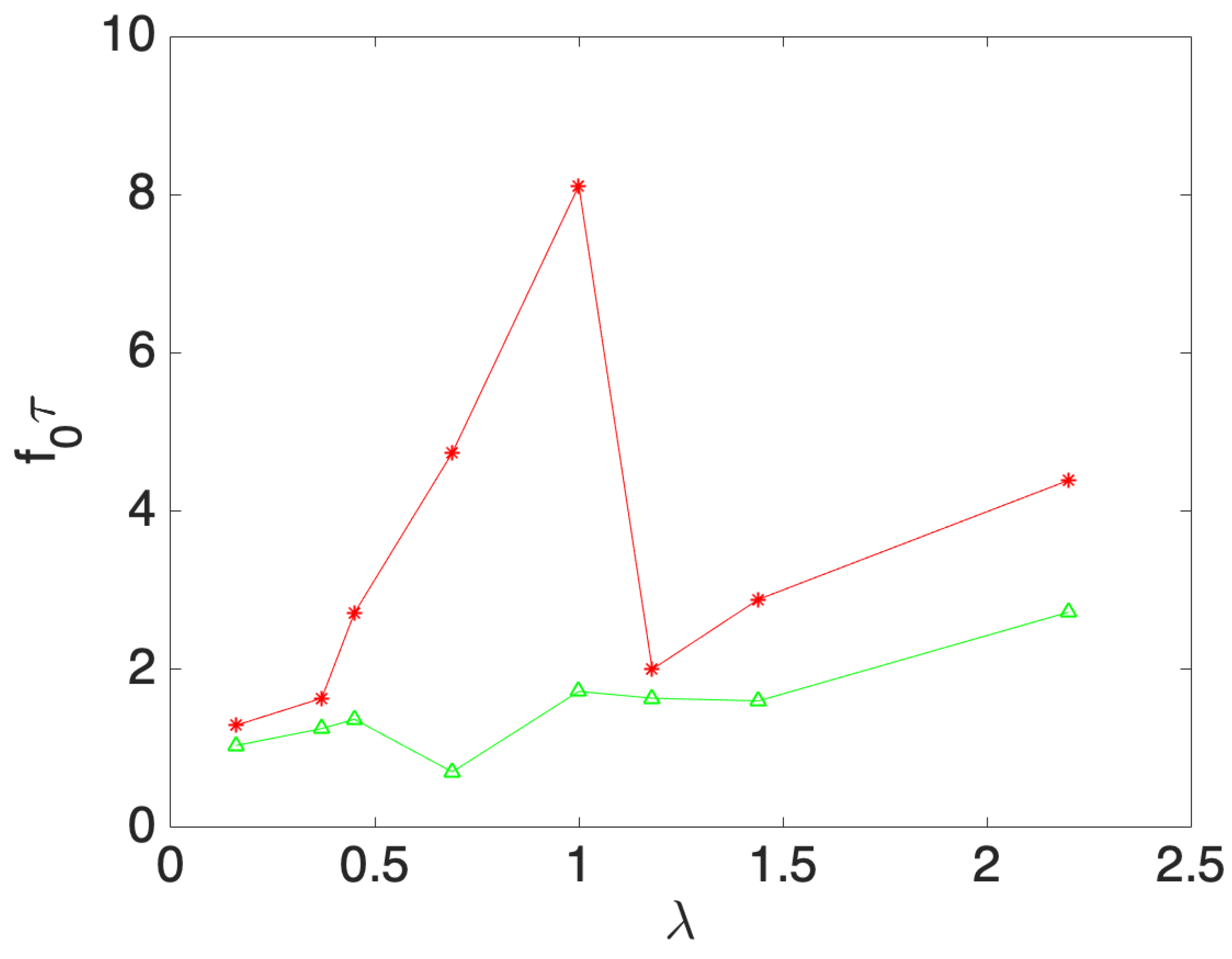
4.1. Damping Time
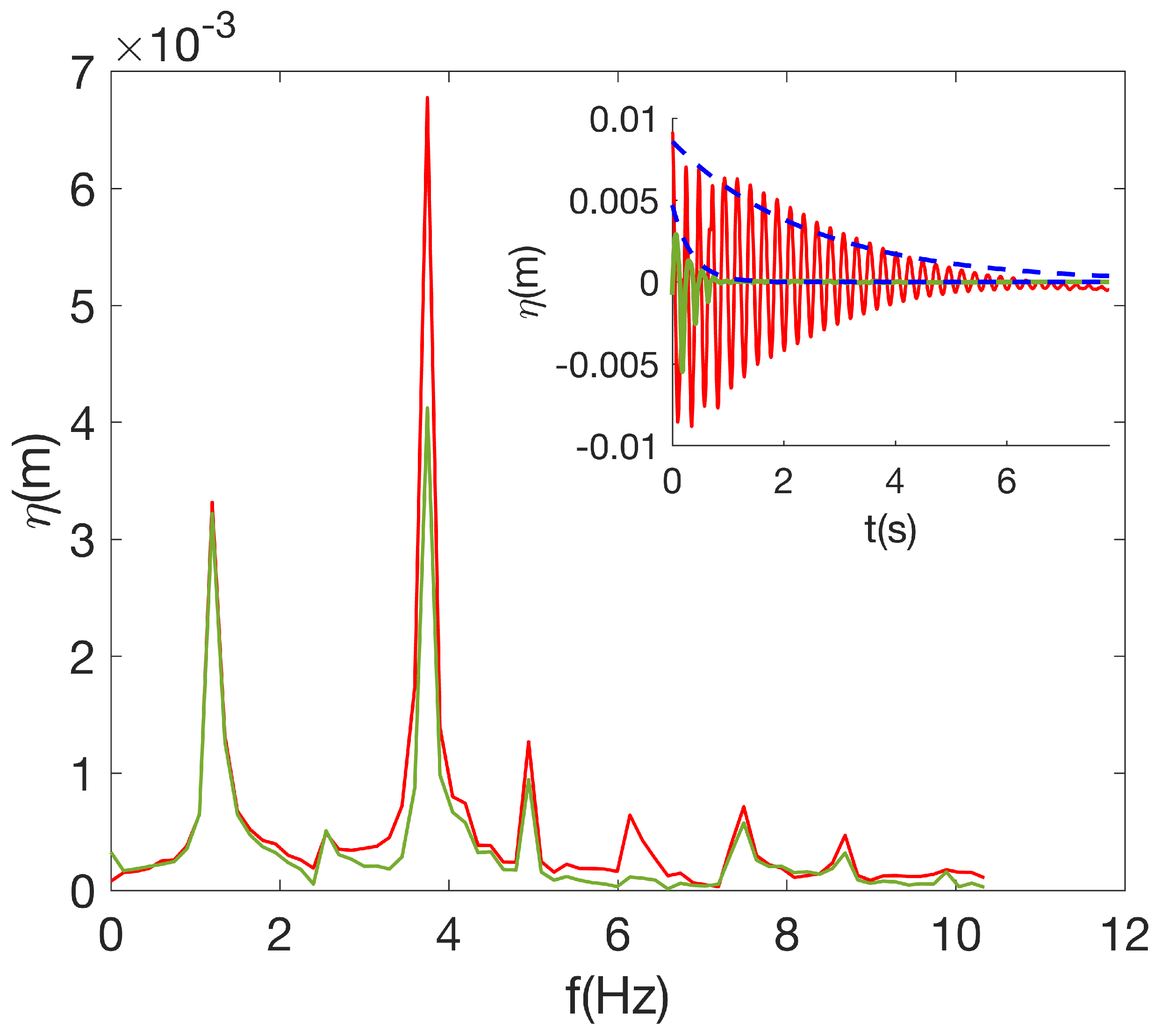
4.2. Waves Visualization
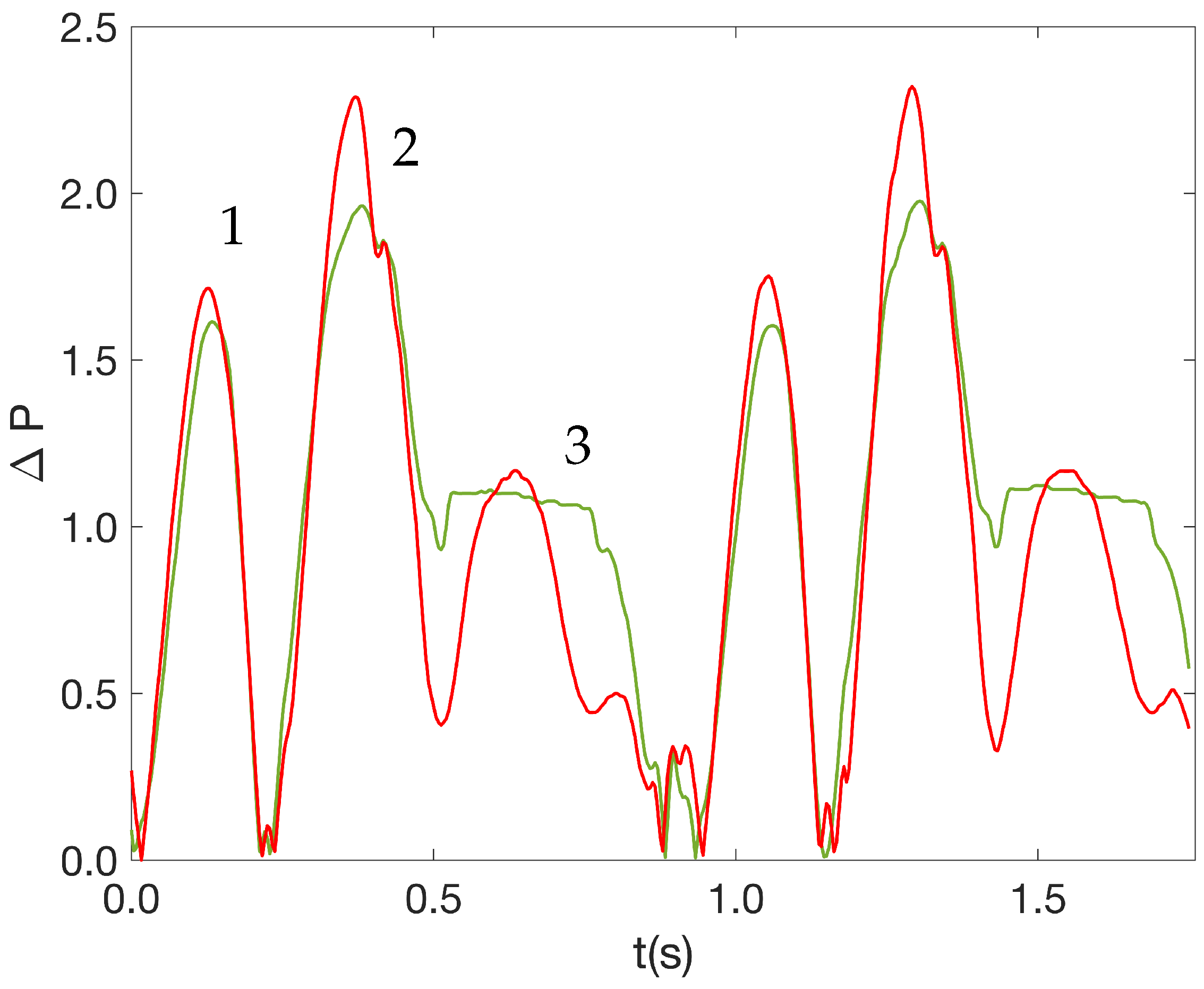
4.3. Pressure Load
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ibrahim, R.A. Liquid Sloshing Dynamics: Theory and Applications; Cambridge University Press: Cambridge, UK, 2005. [Google Scholar]
- Zou, C.F.; Wang, D.Y.; Cai, Z.H.; Li, Z. The effect of liquid viscosity on sloshing characteristics. Int. J. Nav. Archit. Ocean Eng. 2015, 7, 670–690. [Google Scholar] [CrossRef]
- Maleki, A.; Ziyaeifar, M. Sloshing damping in cylindrical liquid storage tanks with baffles. J. Sound Vib. 2007, 311, 372–385. [Google Scholar] [CrossRef]
- Zhang, C.; Su, P.; Ning, D. Hydrodynamic study of an anti-sloshing technique using floating foams. Ocean Eng. 2019, 175, 62–70. [Google Scholar] [CrossRef]
- Xue, M.A.; Zheng, J.; Lin, P.; Yuan, X. Experimental study on vertical baffles of different configurations in suppressing sloshing pressure. Ocean Eng. 2017, 136, 178–189. [Google Scholar] [CrossRef]
- Ma, C.; Xiong, C.; Ma, G. Numerical study on suppressing violent transient sloshing with single and double vertical baffles. Ocean Eng. 2021, 223, 108557. [Google Scholar] [CrossRef]
- Jin, H.; Liu, Y.; Li, H.J. Experimental study on sloshing in a tank with an inner horizontal perforated plate. Ocean Eng. 2014, 82, 75–84. [Google Scholar] [CrossRef]
- George, A.; Cho, I.H. Anti-slosh effect of a horizontal porous baffle in a swaying/rolling rectangular tank: Analytical and experimental approaches. Int. J. Nav. Archit. Ocean Eng. 2021, 13, 833–847. [Google Scholar] [CrossRef]
- Jin, X.; Lin, P. Viscous effects on liquid sloshing under external excitations. Ocean Eng. 2018, 171, 695–707. [Google Scholar] [CrossRef]
- Korkmaz, F.C. Damping of sloshing impact on bottom-layer fluid by adding a viscous top-layer fluid. Ocean Eng. 2022, 254, 111357. [Google Scholar] [CrossRef]
- Cappello, J.; Sauret, A.; Boulogne, F.; Dressaire, E.; Stone, H.A. Damping of liquid sloshing by foams: From everyday observations to liquid transport. J. Vis. 2015, 18, 269–271. [Google Scholar] [CrossRef]
- Sauret, A.; Boulogne, F.; Cappello, J.; Dressaire, E.; Stone, H.A. Damping of liquid sloshing by foams. Phys. Fluids 2015, 27, 022103. [Google Scholar] [CrossRef]
- Korkmaz, F.C.; Güzel, B. Insights from sloshing experiments in a rectangular hydrophobic tank. Exp. Therm. Fluid Sci. 2023, 146, 110920. [Google Scholar] [CrossRef]
- Wang, Z.; Elimelech, M.; Lin, S. Environmental Applications of Interfacial Materials with Special Wettability. Environ. Sci. Technol. 2016, 50, 2132–2150. [Google Scholar] [CrossRef] [PubMed]
- Battaglia, L.; Cruchaga, M.; Storti, M.; D’Elía, J.; Núñez-Aedo, J.; Reinoso, R. Numerical modelling of 3D sloshing experiments in rectangular tanks. Appl. Math. Model. 2018, 59, 357–378. [Google Scholar] [CrossRef]
- Zou, C.F.; Wang, D.Y.; Cai, Z.H. Effects of boundary layer and liquid viscosity and compressible air on sloshing characteristics. Int. J. Nav. Archit. Ocean Eng. 2015, 7, 670–690. [Google Scholar] [CrossRef]
- Tretheway, D.C.; Meinhart, C.D. Apparent fluid slip at hydrophobic microchannel walls. Phys. Fluids 2002, 3, L9–L12. [Google Scholar] [CrossRef]
- Hansson, P.M.; Claesson, P.M.; Swerin, A.; Briscoe, W.H.; Schoelkopf, J.; Gane, P.A.; Thormann, E. Frictional forces between hydrophilic and hydrophobic particle coated nanostructured surfaces. Phys. Chem. Chem. Phys. 2013, 15, 17893–17902. [Google Scholar] [CrossRef]
- Bronfort, A.; Caps, H. Faraday instability at foam-water interface. Phys. Rev. E 2012, 86, 066313. [Google Scholar] [CrossRef]
- Wang, J.; He, L.; Pan, A.; Zhao, Y. Hydrophobic and durable adhesive coatings fabricated from fluorinated glycidyl copolymers grafted on SiO2 nanoparticles. ACS Appl. Nano Mater. 2018, 2, 617–626. [Google Scholar] [CrossRef]
- Tan, D.; Meng, F.; Ni, Y.; Sun, W.; Liu, Q.; Wang, X.; Shi, Z.; Zhao, Q.; Lei, Y.; Luan, S.; et al. Robust and smart underwater adhesion of hydrophobic hydrogel by phase change. Chem. Eng. J. 2023, 471, 144625. [Google Scholar] [CrossRef]
- Souto-Iglesias, A.; Bulian, G.; Botia-Vera, E. A set of canonical problems in sloshing. Part 2: Influence of tank width on impact pressure statistics in regular forced angular motion. Ocean Eng. 2015, 105, 136–159. [Google Scholar] [CrossRef]



| W (cm) | L (cm) | H (cm) | (Hz) | |
|---|---|---|---|---|
| 0.16 | 2.50 | 15.0 | 6.0 | 2.3 |
| 0.37 | 4.70 | 12.7 | 8.0 | 2.5 |
| 0.45 | 4.30 | 9.50 | 2.5 | 2.9 |
| 0.69 | 7.60 | 11.0 | 6.0 | 2.7 |
| 1.00 | 4.30 | 4.30 | 6.0 | 4.3 |
| 1.18 | 15.0 | 12.7 | 3.0 | 2.5 |
| 1.44 | 11.0 | 7.60 | 4.5 | 3.2 |
| 2.20 | 9.50 | 4.30 | 2.5 | 4.3 |
| (Hz) | (Hz) | Relative Difference (%) | |
|---|---|---|---|
| 0.16 | 1.78 | 2.22 | 20 |
| 0.37 | 1.53 | 2.00 | 23 |
| 0.45 | 1.07 | 2.12 | 50 |
| 0.69 | 0.57 | 3.84 | 85 |
| 1.00 | 0.53 | 2.50 | 78 |
| 1.18 | 1.25 | 1.53 | 19 |
| 1.44 | 1.11 | 2.00 | 44 |
| 2.20 | 0.98 | 1.58 | 38 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cruz-Gómez, R.C.; Cros, A.; Monzón, C.O.; Capetillo-Peréz, L.E. Damping of Liquid Sloshing Using Hydrophobic Walls in the Off-Impulse Regime. Appl. Sci. 2025, 15, 2841. https://doi.org/10.3390/app15052841
Cruz-Gómez RC, Cros A, Monzón CO, Capetillo-Peréz LE. Damping of Liquid Sloshing Using Hydrophobic Walls in the Off-Impulse Regime. Applied Sciences. 2025; 15(5):2841. https://doi.org/10.3390/app15052841
Chicago/Turabian StyleCruz-Gómez, R. C., Anne Cros, C. O. Monzón, and L. E. Capetillo-Peréz. 2025. "Damping of Liquid Sloshing Using Hydrophobic Walls in the Off-Impulse Regime" Applied Sciences 15, no. 5: 2841. https://doi.org/10.3390/app15052841
APA StyleCruz-Gómez, R. C., Cros, A., Monzón, C. O., & Capetillo-Peréz, L. E. (2025). Damping of Liquid Sloshing Using Hydrophobic Walls in the Off-Impulse Regime. Applied Sciences, 15(5), 2841. https://doi.org/10.3390/app15052841






