Development of a Short-Range Multispectral Camera Calibration Method for Geometric Image Correction and Health Assessment of Baby Crops in Greenhouses
Abstract
1. Introduction
Related Work
2. Materials and Methods
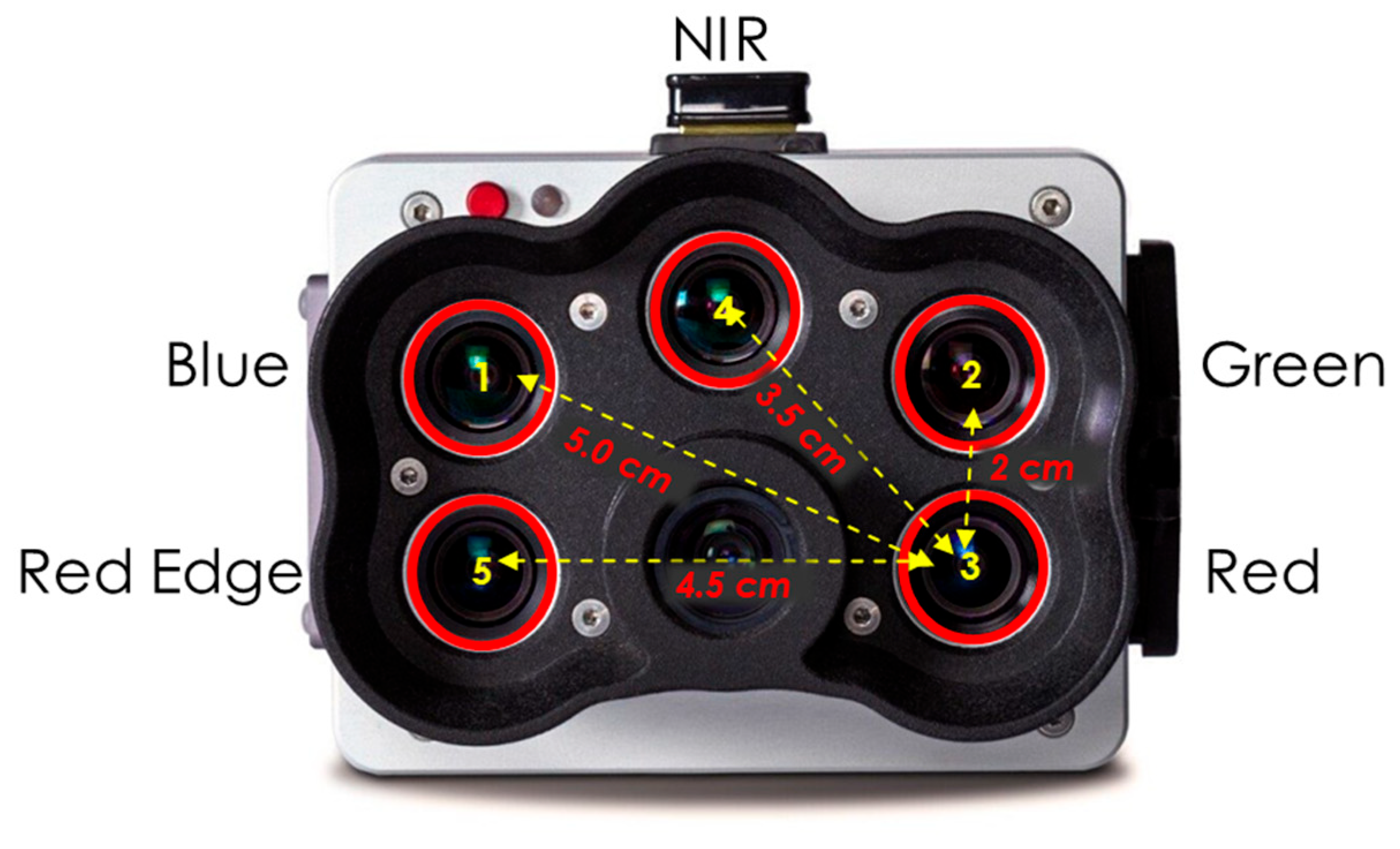
2.1. Stereo Camera Calibration
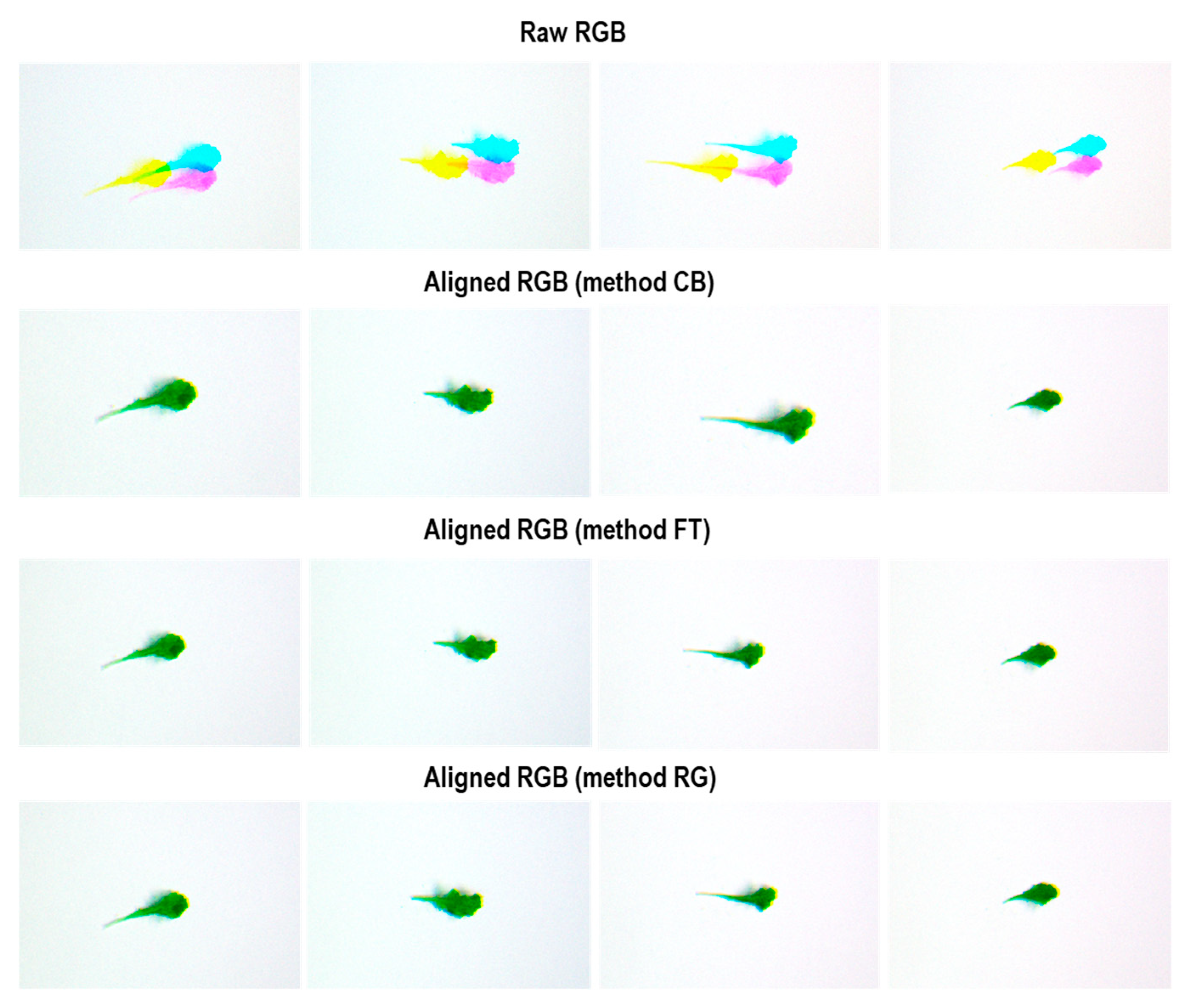
2.2. Image Registration
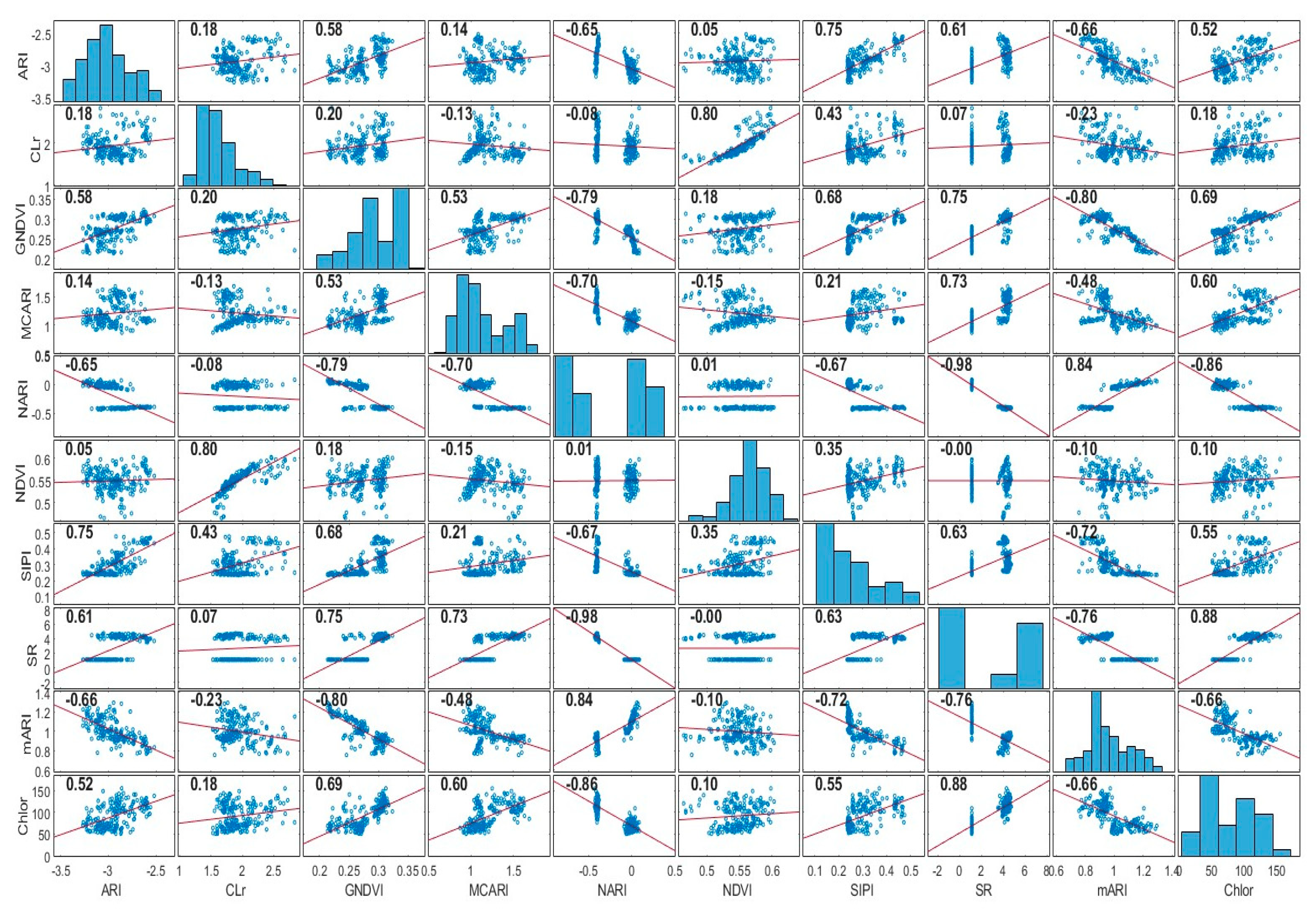
2.3. Crop Health Assessment
3. Results
3.1. Stereo Camera Calibration
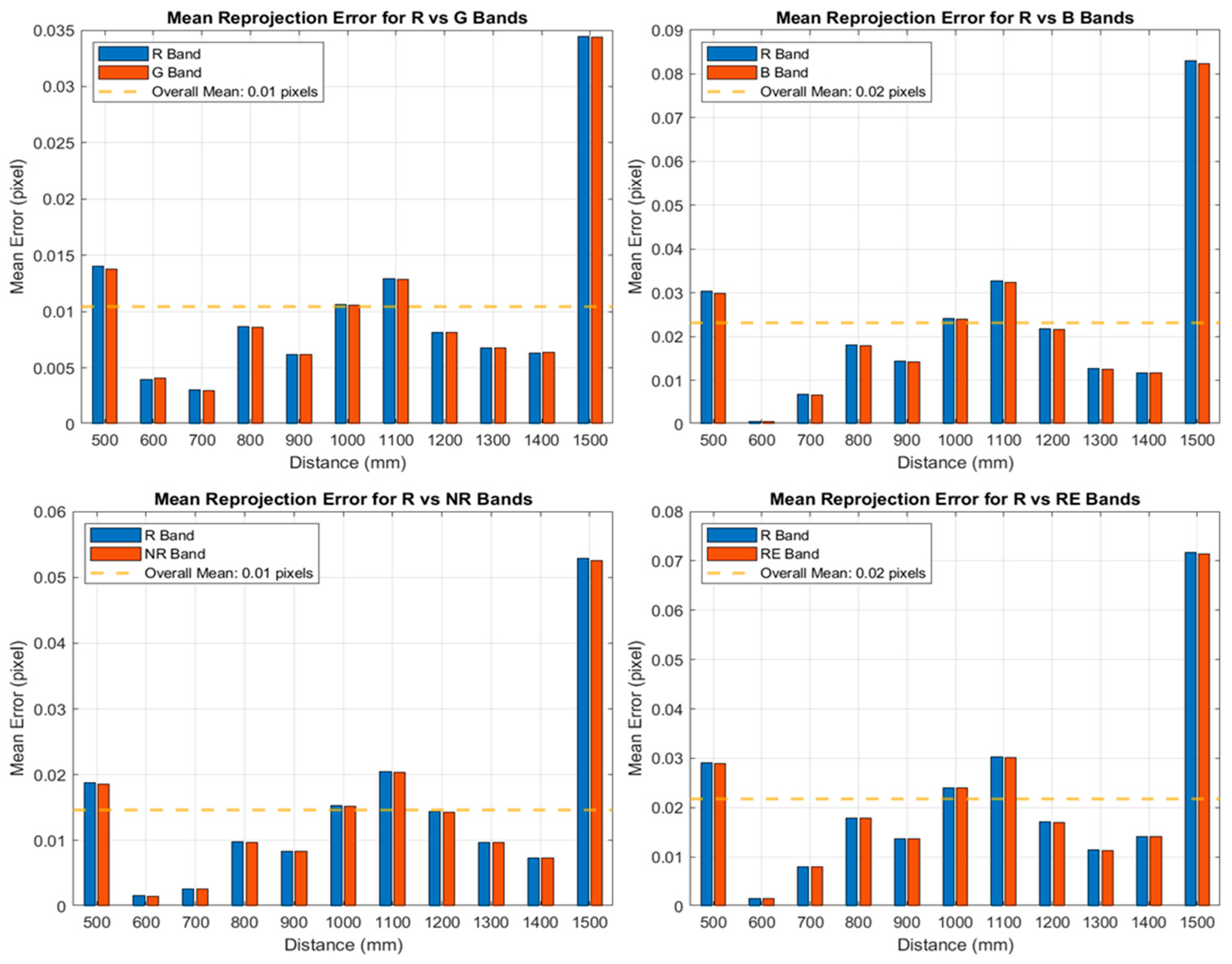
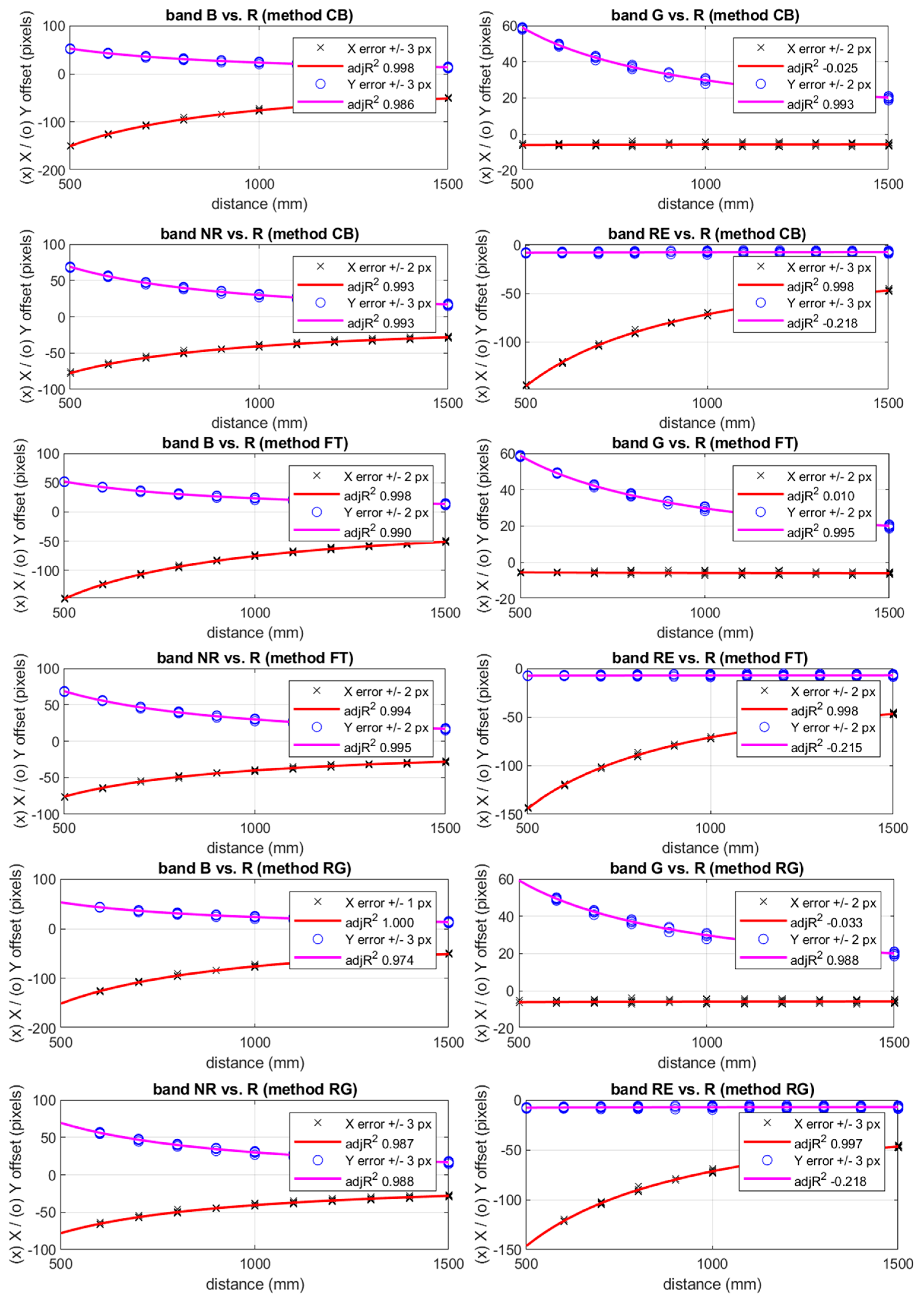
3.2. Image Registration Model
3.3. Crop Health Assessment
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Mishra, P.; Polder, G.; Vilfan, N. Close Range Spectral Imaging for Disease Detection in Plants Using Autonomous Platforms: A Review on Recent Studies. Curr. Robot. Rep. 2020, 1, 43–48. [Google Scholar] [CrossRef]
- Deng, L.; Mao, Z.; Li, X.; Hu, Z.; Duan, F.; Yan, Y. UAV-Based Multispectral Remote Sensing for Precision Agriculture: A Comparison between Different Cameras. ISPRS J. Photogramm. Remote Sens. 2018, 146, 124–136. [Google Scholar] [CrossRef]
- Mishra, P.; Asaari, M.S.M.; Herrero-Langreo, A.; Lohumi, S.; Diezma, B.; Scheunders, P. Close Range Hyperspectral Imaging of Plants: A Review. Biosyst. Eng. 2017, 164, 49–67. [Google Scholar] [CrossRef]
- Laveglia, S.; Altieri, G.; Genovese, F.; Matera, A.; Di Renzo, G.C. Advances in Sustainable Crop Management: Integrating Precision Agriculture and Proximal Sensing. AgriEngineering 2024, 6, 3084–3120. [Google Scholar] [CrossRef]
- Gang, M.S.; Kim, H.J.; Kim, D.W. Estimation of Greenhouse Lettuce Growth Indices Based on a Two-Stage CNN Using RGB-D Images. Sensors 2022, 22, 5499. [Google Scholar] [CrossRef]
- Thrash, T.; Lee, H.; Baker, R.L. A Low-Cost High-Throughput Phenotyping System for Automatically Quantifying Foliar Area and Greenness. Appl. Plant Sci. 2022, 10, e11502. [Google Scholar] [CrossRef]
- Singh, G.; Slonecki, T.; Wadl, P.; Flessner, M.; Sosnoskie, L.; Hatterman-Valenti, H.; Gage, K.; Cutulle, M. Implementing Digital Multispectral 3D Scanning Technology for Rapid Assessment of Hemp (Cannabis sativa L.) Weed Competitive Traits. Remote Sens. 2024, 16, 2375. [Google Scholar] [CrossRef]
- Tripodi, P.; Vincenzo, C.; Venezia, A.; Cocozza, A.; Pane, C. Precision Phenotyping of Wild Rocket (Diplotaxis tenuifolia) to Determine Morpho-Physiological Responses under Increasing Drought Stress Levels Using the PlantEye Multispectral 3D System. Horticulturae 2024, 10, 496. [Google Scholar] [CrossRef]
- Feng, X.; Zhan, Y.; Wang, Q.; Yang, X.; Yu, C.; Wang, H.; Tang, Z.Y.; Jiang, D.; Peng, C.; He, Y. Hyperspectral Imaging Combined with Machine Learning as a Tool to Obtain High-Throughput Plant Salt-Stress Phenotyping. Plant J. 2020, 101, 1448–1461. [Google Scholar] [CrossRef]
- Genangeli, A.; Avola, G.; Bindi, M.; Cantini, C.; Cellini, F.; Grillo, S.; Petrozza, A.; Riggi, E.; Ruggiero, A.; Summerer, S.; et al. Low-Cost Hyperspectral Imaging to Detect Drought Stress in High-Throughput Phenotyping. Plants 2023, 12, 1730. [Google Scholar] [CrossRef]
- Fan, X.; Zhang, H.; Zhou, L.; Bian, L.; Jin, X.; Tang, L.; Ge, Y. Evaluating Drought Stress Response of Poplar Seedlings Using a Proximal Sensing Platform via Multi-Parameter Phenotyping and Two-Stage Machine Learning. Comput. Electron. Agric. 2024, 225, 109261. [Google Scholar] [CrossRef]
- Malounas, I.; Paliouras, G.; Nikolopoulos, D.; Liakopoulos, G.; Bresta, P.; Londra, P.; Katsileros, A.; Fountas, S. Early Detection of Broccoli Drought Acclimation/Stress in Agricultural Environments Utilizing Proximal Hyperspectral Imaging and AutoML. Smart Agric. Technol. 2024, 8, 100463. [Google Scholar] [CrossRef]
- Cho, W.J.; Yang, M. High-Throughput Plant Phenotyping System Using a Low-Cost Camera Network for Plant Factory. Agriculture 2023, 13, 1874. [Google Scholar] [CrossRef]
- Scutelnic, D.; Muradore, R.; Daffara, C. A Multispectral Camera in the VIS–NIR Equipped with Thermal Imaging and Environmental Sensors for Non Invasive Analysis in Precision Agriculture. HardwareX 2024, 20, e00596. [Google Scholar] [CrossRef]
- Amitrano, C.; Junker, A.; D’Agostino, N.; De Pascale, S.; De Micco, V. Integration of High-Throughput Phenotyping with Anatomical Traits of Leaves to Help Understanding Lettuce Acclimation to a Changing Environment. Planta 2022, 256, 1–19. [Google Scholar] [CrossRef]
- Kohzuma, K.; Tamaki, M.; Hikosaka, K. Corrected Photochemical Reflectance Index (PRI) Is an Effective Tool for Detecting Environmental Stresses in Agricultural Crops under Light Conditions. J. Plant Res. 2021, 134, 683–694. [Google Scholar] [CrossRef] [PubMed]
- Polder, G.; Dieleman, J.A.; Hageraats, S.; Meinen, E. Imaging Spectroscopy for Monitoring the Crop Status of Tomato Plants. Comput. Electron. Agric. 2024, 216, 108504. [Google Scholar] [CrossRef]
- Susič, N.; Žibrat, U.; Širca, S.; Strajnar, P.; Razinger, J.; Knapič, M.; Vončina, A.; Urek, G.; Gerič Stare, B. Discrimination between Abiotic and Biotic Drought Stress in Tomatoes Using Hyperspectral Imaging. Sens Actuators B Chem. 2018, 273, 842–852. [Google Scholar] [CrossRef]
- Gitelson, A.A.; Merzlyak, M.N.; Chivkunova, O.B. Optical Properties and Nondestructive Estimation of Anthocyanin Content in Plant Leaves. Photochem. Photobiol. 2001, 74, 38. [Google Scholar] [CrossRef]
- Parry, C.; Blonquist, J.M.; Bugbee, B. In Situ Measurement of Leaf Chlorophyll Concentration: Analysis of the Optical/Absolute Relationship. Plant Cell Environ. 2014, 37, 2508–2520. [Google Scholar] [CrossRef]
- Qiao, L.; Tang, W.; Gao, D.; Zhao, R.; An, L.; Li, M.; Sun, H.; Song, D. UAV-Based Chlorophyll Content Estimation by Evaluating Vegetation Index Responses under Different Crop Coverages. Comput. Electron. Agric. 2022, 196, 106775. [Google Scholar] [CrossRef]
- Zubler, A.V.; Yoon, J.Y. Proximal Methods for Plant Stress Detection Using Optical Sensors and Machine Learning. Biosensors 2020, 10, 193. [Google Scholar] [CrossRef] [PubMed]
- Qin, J.; Monje, O.; Nugent, M.R.; Finn, J.R.; O’Rourke, A.E.; Wilson, K.D.; Fritsche, R.F.; Baek, I.; Chan, D.E.; Kim, M.S. A Hyperspectral Plant Health Monitoring System for Space Crop Production. Front. Plant. Sci. 2023, 14, 1133505. [Google Scholar] [CrossRef] [PubMed]
- Laveglia, S.; Altieri, G. A Method for Multispectral Images Alignment at Different Heights on the Crop. Lect. Notes Civ. Eng. 2024, 458, 401–419. [Google Scholar]
- Fernández, C.I.; Leblon, B.; Wang, J.; Haddadi, A.; Wang, K. Detecting Infected Cucumber Plants with Close-Range Multispectral Imagery. Remote Sens. 2021, 13, 2948. [Google Scholar] [CrossRef]
- Rana, S.; Gerbino, S.; Crimaldi, M.; Cirillo, V.; Carillo, P.; Sarghini, F.; Maggio, A. Comprehensive Evaluation of Multispectral Image Registration Strategies in Heterogenous Agriculture Environment. J. Imaging 2024, 10, 61. [Google Scholar] [CrossRef]
- Wasonga, D.O.; Yaw, A.; Kleemola, J.; Alakukku, L.; Mäkelä, P.S.A. Red-Green-Blue and Multispectral Imaging as Potential Tools for Estimating Growth and Nutritional Performance of Cassava under Deficit Irrigation and Potassium Fertigation. Remote Sens. 2021, 13, 598. [Google Scholar] [CrossRef]
- Lee, H.; He, Y.; Isaac, M.E. Close-Range Imaging for Green Roofs: Feature Detection, Band Matching, and Image Registration for Mixed Plant Communities. Geomatica 2024, 76, 100011. [Google Scholar] [CrossRef]
- Lowe, D.G. Distinctive Image Features from Scale-Invariant Keypoints. Int. J. Comput. Vis. 2004, 60, 91–110. [Google Scholar] [CrossRef]
- Mistry, D.; Banerjee, A. Comparison of Feature Detection and Matching Approaches: SIFT and SURF. Glob. Res. Dev. J. Eng. 2017, 2, 7–13. [Google Scholar]
- Tareen, S.A.K.; Saleem, Z. A Comparative Analysis of SIFT, SURF, KAZE, AKAZE, ORB, and BRISK. In Proceedings of the 2018 International Conference on Computing, Mathematics and Engineering Technologies: Invent, Innovate and Integrate for Socioeconomic Development, iCoMET 2018—Proceedings 2018, Sukkur, Pakistan, 1–10 January 2018. [Google Scholar] [CrossRef]
- Fernández, C.I.; Haddadi, A.; Leblon, B.; Wang, J.; Wang, K. Comparison between Three Registration Methods in the Case of Non-Georeferenced Close Range of Multispectral Images. Remote Sens. 2021, 13, 396. [Google Scholar] [CrossRef]
- Sturm, P. Pinhole Camera Model. In Computer Vision: A Reference Guide; Springer International Publishing: Cham, Switzerland, 2021; pp. 983–986. [Google Scholar] [CrossRef]
- Longuet-higgins, H.C. A Computer Algorithm for Reconstructing a Scene from Two Projections. Nature 1981, 293, 133–135. [Google Scholar] [CrossRef]
- Memon, Q.; Khan, S. Camera Calibration and Three-Dimensional World Reconstruction of Stereo-Vision Using Neural Networks. Int. J. Syst. Sci. 2001, 32, 1155–1159. [Google Scholar] [CrossRef]
- Heikkila, J.; Silven, O. Four-Step Camera Calibration Procedure with Implicit Image Correction. In Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition, San Juan, PR, USA, 17–19 June 1997; pp. 1106–1112. [Google Scholar] [CrossRef]
- Camera Calibration Toolbox for Matlab. Available online: https://data.caltech.edu/records/jx9cx-fdh55 (accessed on 26 January 2025).
- Zitová, B.; Flusser, J. Image Registration Methods: A Survey. Image Vis. Comput. 2003, 21, 977–1000. [Google Scholar] [CrossRef]
- Rouse, J.W., Jr.; Haas, R.H.; Schell, J.A.; Deering, D.W. Monitoring Vegetation Systems in the Great Plains with ERTS. NASA. Goddard Space Flight Center 3d ERTS-1 Symp., Volume 1, Sect. A, Paper A20, 1974; pp. 309–317. Available online: https://ntrs.nasa.gov/citations/19740022614 (accessed on 29 January 2025).
- Birth, G.S.; McVey, G.R. Measuring the Color of Growing Turf with a Reflectance Spectrophotometer 1. Agron J. 1968, 60, 640–643. [Google Scholar] [CrossRef]
- Gitelson, A.; Merzlyak, M.N. Quantitative Estimation of Chlorophyll-a Using Reflectance Spectra: Experiments with Autumn Chestnut and Maple Leaves. J. Photochem. Photobiol. B Biol. 1994, 22, 247–252. [Google Scholar] [CrossRef]
- Bayle, A.; Carlson, B.Z.; Thierion, V.; Isenmann, M.; Choler, P. Improved Mapping of Mountain Shrublands Using the Sentinel-2 Red-Edge Band. Remote Sens. 2019, 11, 2807. [Google Scholar] [CrossRef]
- Gitelson, A.A.; Merzlyak, M.N. Signature Analysis of Leaf Reflectance Spectra: Algorithm Development for Remote Sensing of Chlorophyll. J. Plant Physiol. 1996, 148, 494–500. [Google Scholar] [CrossRef]
- Penuelas, J.; Baret, F.; Filella, I. Semi-Empirical Indices to Assess Carotenoids/Chlorophyll a Ratio from Leaf Spectral Reflectance. Photosynthetica 1995, 31, 221–230. [Google Scholar]
- Wang, C.; Liu, S.; Wang, X.; Lan, X. Time Synchronization and Space Registration of Roadside LiDAR and Camera. Electronics 2023, 12, 537. [Google Scholar] [CrossRef]
- Kim, C.; van Iersel, M.W. Image-Based Phenotyping to Estimate Anthocyanin Concentrations in Lettuce. Front. Plant Sci. 2023, 14, 1155722. [Google Scholar] [CrossRef] [PubMed]
- Kurunc, A. Effects of Water and Salinity Stresses on Growth, Yield, and Water Use of Iceberg Lettuce. J. Sci. Food Agric. 2021, 101, 5688–5696. [Google Scholar] [CrossRef]
- Ihuoma, S.O.; Madramootoo, C.A. Recent Advances in Crop Water Stress Detection. Comput. Electron. Agric. 2017, 141, 267–275. [Google Scholar] [CrossRef]
- Ncama, K.; Sithole, N.J. The Effect of Nitrogen Fertilizer and Water Supply Levels on the Growth, Antioxidant Compounds, and Organic Acids of Baby Lettuce. Agronomy 2022, 12, 614. [Google Scholar] [CrossRef]
- Paim, B.T.; Crizel, R.L.; Tatiane, S.J.; Rodrigues, V.R.; Rombaldi, C.V.; Galli, V. Mild Drought Stress Has Potential to Improve Lettuce Yield and Quality. Sci. Hortic. 2020, 272, 109578. [Google Scholar] [CrossRef]
- Zelinsky, A. Learning OpenCV—Computer Vision with the OpenCV Library. IEEE Robot. Autom. Mag. 2009, 16, 100. [Google Scholar] [CrossRef]



| Vegetation Indices | Formula | References |
|---|---|---|
| NDVI (Normalized Difference Vegetation Index) | (NIR − RED)/(NIR + RED) | [39] |
| MCARI (Modified Chlorophyll Absorption in Reflectance Index) | [(RE − RED) − 0.2 × (RE−G)] × (RED/RE) | [39] |
| SR (Spectral Ratio) | RED/NIR | [40] |
| CLr (Chlorophyll Red Index) | (RED/NIR) − 1 | [41] |
| NARI (Normalized Anthocyanin Reflectance Index) | (1/G + 1/RED)/(1/G − 1/RED) | [42] |
| ARI (Anthocyanin Reflectance Index) | (1/G) − (1/RED) | [19] |
| mARI (Modified Anthocyanin Reflectance Index) | (1/G − 1/RE) × NIR | [19] |
| GNDVI (Green Normalized Difference Vegetation Index) | (NIR + G)/(NIR − G) | [43] |
| SIPI (Structural Independent Pigment Index) | (NIR + RED)/(NIR − B) | [44] |
| Depth Estimation (Z) Error, Band G vs. R | Depth Estimation (Z) Error, Band B vs. R | ||||||
|---|---|---|---|---|---|---|---|
| dist_mm | nPoints | Mean ± std | Err% | dist_mm | nPoints | Mean ± std | Err% |
| 800 | 1.49 × 105 | 653.11 ± 2.86 × 10−5 | 18.36 | 800 | 1.26 × 105 | 750.43 ± 3.13 × 10−5 | 6.20 |
| 1000 | 1.05 × 105 | 767.77 ± 2.58 × 10−5 | 23.22 | 1000 | 91,071 | 884.05 ± 3.19 × 10−5 | 11.60 |
| 1300 | 70,961 | 1054.60 ± 5.35 × 10−5 | 18.88 | 1300 | 55,859 | 1207.90 ± 4.45 × 10−5 | 7.08 |
| 1370 | 55,048 | 1077.90 ± 1.02 × 10−4 | 21.32 | 1370 | 45,625 | 1238.10 ± 8.46 × 10−5 | 9.63 |
| Depth Estimation (Z) Error, Band NR vs. R | Depth Estimation (Z) Error, Band RE vs. R | ||||||
| dist_mm | nPoints | Mean ± std | Err% | dist_mm | nPoints | Mean ± std | Err% |
| 800 | 1.37 × 105 | 729.23 ± 2.50 × 10−5 | 8.85 | 800 | 99,057 | 762.22 ± 3.23 × 10−5 | 4.72 |
| 1000 | 99,340 | 856.87 ± 2.85 × 10−5 | 14.31 | 1000 | 82,246 | 895.92 ± 3.38 × 10−5 | 10.41 |
| 1300 | 52,389 | 1173.40 ± 4.53 × 10−5 | 9.74 | 1300 | 48,286 | 1222.70 ± 4.19 × 10−5 | 5.95 |
| 1370 | 49,960 | 1195.80 ± 6.28 × 10−5 | 12.72 | 1370 | 55,965 | 1258.60 ± 8.57 × 10−5 | 8.13 |
| X Offset Model, Band B vs. R | Y Offset Model, Band B vs. R |
|---|---|
| General model: y(x) = a + b/x a = −1.266 (−2.457, −0.07416) b = −7.432 × 104 (−7.531× 104, −7.332 × 104) adjrsquare: 0.9977 rmse: 1.4953 | General model: y(x) = a + b/x a = −5.597 (−6.756, −4.437) b =2.897 × 104 (2.8 × 104, 2.994 × 104) adjrsquare: 0.9860 rmse: 1.4550 |
| X Offset Model, Band G vs. R | Y Offset Model, Band G vs. R |
| General model: y(x) = a + b/x a = −5.427 (−6.151, −4.703) b = −293.5 (−898, 311) adjrsquare: −0.0248 rmse: 0.9082 | General model: y(x) = a + b/x a = 0.7586 (−0.05633, 1.574) b = 2.909 × 104 (2.841 × 104, 2.977 × 104) adjrsquare: 0.9930 rmse: 1.0229 |
| X Offset Model, Band NR vs. R | Y Offset Model, Band NR vs. R |
| General model: y(x) = a + b/x a = −3.452 (−4.464, −2.439) b = −3.716 × 104 (−3.801 × 104, −3.632 × 104) adjrsquare: 0.9934 rmse: 1.2709 | General model: y(x) = a + b/x a = −8.98 (−10.04, −7.919) b = 3.897 × 104 (3.808 × 104, 3.985 × 104) adjrsquare: 0.9934 rmse: 1.3311 |
| X Offset Model, Band RE vs. R | Y Offset Model, Band RE vs. R |
| General model: y(x) = a + b/x a = 2.719 (1.645, 3.794) b = −7.421 × 104 (−7.51 × 104, −7.331× 104) adjrsquare: 0.9981 rmse: 1.3484 | General model: y(x) = a + b/x a = −6.818 (−7.848, −5.788) b = −409.5 (−1270, 451.2) adjrsquare: −0.2176 rmse: 1.2931 |
| X Offset Model, Band B vs. R | Y Offset Model, Band B vs. R |
|---|---|
| General model: y(x) = a + b/x a = −2.171 (−3.162, −1.18) b = −7.311 × 104 (−7.394 × 104, −7.229 × 104) adjrsquare: 0.9984 rmse: 1.2438 | General model: y(x) = a + b/x a = −5.471 (−6.427, −4.516) b = 2.873 × 104 (2.794 × 104, 2.953 × 104) adjrsquare: 0.9903 rmse: 1.1996 |
| X Offset Model, Band G vs. R | Y Offset Model, Band G vs. R |
| General model: y(x) = a + b/x a = −6.028 (−6.664, −5.392) b = 319.5 (−211.6, 850.6) adjrsquare: 0.0104 rmse: 0.7980 | General model: y(x) = a + b/x a = 0.83 (0.1613, 1.499) b = 2.898 × 104 (2.842 × 104, 2.954 × 104) adjrsquare: 0.9952 rmse: 0.8393 |
| X Offset Model, Band NR vs. R | Y Offset Model, Band NR vs. R |
| General model: y(x) = a + b/x a = −4.199 (−5.128, −3.271) b = −3.599 × 104 (−3.677 × 104, −3.521 × 104) adjrsquare: 0.9940 rmse: 1.1650 | General model: y(x) = a + b/x a = −8.899 (−9.784, −8.014) b = 3.877 × 104 (3.803 × 104, 3.951 × 104) adjrsquare: 0.9954 rmse: 1.1107 |
| X Offset Model, Band RE vs. R | Y Offset Model, Band RE vs. R |
| General model: y(x) = a + b/x a = 1.81 (0.8442, 2.775) b = −7.298 × 104 (−7.379 × 104, −7.218 × 104) adjrsquare: 0.9984 rmse: 1.2115 | General model: y(x) = a + b/x a = −6.91 (−7.78, −6.04) b = −304.6 (−1031, 422.1) adjrsquare: −0.2151 rmse: 1.0918 |
| X Offset Model, Band B vs. R | Y Offset Model, Band B vs. R |
|---|---|
| General model: y(x) = a + b/x a = −0.8794 (−1.293, −0.4655) b = −7.479 × 104 (−7.517 × 104, −7.441 × 104) adjrsquare: 0.9997 rmse: 0.4196 | General model: y(x) = a + b/x a = −6.139 (−7.659, −4.618) b = 2.956 × 104 (2.813 × 104, 3.099 × 104) adjrsquare: 0.9742 rmse: 1.4956 |
| X Offset Model, Band G vs. R | Y Offset Model, Band G vs. R |
| General model: y(x) = a + b/x a = −5.421 (−6.224, −4.619) b = −301.1 (−1004, 401.8) adjrsquare: −0.0333 rmse: 0.9353 | General model: y(x) = a + b/x a =0.4707 (−0.5691, 1.511) b = 2.939 × 104 (2.843 × 104, 3.036 × 104) adjrsquare: 0.9877 rmse: 1.0540 |
| X Offset Model, Band NR vs. R | Y Offset Model, Band NR vs. R |
| General model: y(x) = a + b/x a = −3.174 (−4.51, −1.837) b = −3.739 × 104 (−3.863 × 104, −3.615 × 104) adjrsquare: 0.9874 rmse: 1.3549 | General model: y(x) = a + b/x a = −9.352 (−10.73, −7.972) b = 3.936 × 104 (3.809 × 104, 4.064 × 104) adjrsquare: 0.9880 rmse: 1.3990 |
| X Offset Model, Band RE vs. R | Y Offset Model, Band RE vs. R |
| General model: y(x) = a + b/x a = 3.196 (1.836, 4.556) b = −7.472 × 104 (−7.598 × 104, −7.346 × 104) adjrsquare: 0.9967 rmse: 1.3787 | General model: y(x) = a + b/x a = −6.818 (−7.848, −5.788) b = −409.5 (−1270, 451.2) adjrsquare: −0.2176 rmse: 1.2931 |
| Distance (m) | b/x (Pixel) | y(x) = a + b/x (Pixel) | Relative Error (err%) |
|---|---|---|---|
| 1 | 28.970 | 23.373 | 517.91% |
| 10 | 2.897 | −2.700 | 51.77% |
| 20 | 1.449 | −4.148 | 25.88% |
| 30 | 0.966 | −4.631 | 17.26% |
| 50 | 0.579 | −5.018 | 10.34% |
| 100 | 0.290 | −5.307 | 5.18% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Laveglia, S.; Altieri, G.; Genovese, F.; Matera, A.; Scarano, L.; Di Renzo, G.C. Development of a Short-Range Multispectral Camera Calibration Method for Geometric Image Correction and Health Assessment of Baby Crops in Greenhouses. Appl. Sci. 2025, 15, 2893. https://doi.org/10.3390/app15062893
Laveglia S, Altieri G, Genovese F, Matera A, Scarano L, Di Renzo GC. Development of a Short-Range Multispectral Camera Calibration Method for Geometric Image Correction and Health Assessment of Baby Crops in Greenhouses. Applied Sciences. 2025; 15(6):2893. https://doi.org/10.3390/app15062893
Chicago/Turabian StyleLaveglia, Sabina, Giuseppe Altieri, Francesco Genovese, Attilio Matera, Luciano Scarano, and Giovanni Carlo Di Renzo. 2025. "Development of a Short-Range Multispectral Camera Calibration Method for Geometric Image Correction and Health Assessment of Baby Crops in Greenhouses" Applied Sciences 15, no. 6: 2893. https://doi.org/10.3390/app15062893
APA StyleLaveglia, S., Altieri, G., Genovese, F., Matera, A., Scarano, L., & Di Renzo, G. C. (2025). Development of a Short-Range Multispectral Camera Calibration Method for Geometric Image Correction and Health Assessment of Baby Crops in Greenhouses. Applied Sciences, 15(6), 2893. https://doi.org/10.3390/app15062893







