A Novel Multi-Criteria Decision-Making Framework of Vehicle Structural Factor Evaluation for Public Transportation Safety
Abstract
1. Introduction
- This study is the first to comprehensively identify and evaluate the structural factors contributing to vehicle malfunctions. A customized MCDM framework has been designed to explore all possible factors and rigorously analyze their interrelationships.
- Fault Tree Analysis (FTA) and the Interval-Valued Pythagorean Fuzzy Analytic Hierarchy Process (IVPF-AHP) evaluate the relative importance of structural factors as regards occurrence probability and severity. Additionally, the Interval-Valued Pythagorean Fuzzy Decision-Making Trial and Evaluation Laboratory (IVPF-DEMATEL) examines the cause–effect interrelationships between the crucial factors.
- This work conducts the practical case study for public transportation buses. The maintenance records reported at bus depots and expert judgements collected from professional staff are used as data sources. Based on the assessment results, this work provides actionable recommendations for maintenance management.
- The outputs of this work can further ensure roadworthiness, thereby ensuring more reliable public transportation services. The optimized maintenance strategies help to prevent minor issues from escalating into major failures and to avoid the spread of failures to other structure parts.
- The maintenance recommendations generated from this work can help to enhance operational efficiency and financial performance. Engineers can allocate manpower and material resources more effectively, concentrating efforts on addressing the most critical failure factors, thereby optimizing maintenance scheduling. Public transportation operators can reduce maintenance costs, achieve better inventory control, and minimize service disruptions.
2. Methodology
2.1. Framework of Methodology
2.2. Uncertainty Reduction by Interval-Valued Pythagorean Fuzzy Set
2.3. Occurrence Probability Analysis by Fault Tree Analysis
2.4. Severity Impact Analysis by Interval-Valued Pythagorean Fuzzy Analytic Hierarchy Process
- Establishment of the hierarchical structure.
- 2.
- Construction of the Interval-Valued Pythagorean pairwise comparison matrix .
- 3.
- The calculation of the difference matrix is as follows:
- 4.
- The calculation of the multiplicative matrix is as follows:
- 5.
- The calculation of the indeterminacy matrix matrix is as follows:
- 6.
- The calculation of the unnormalized weights is as follows:
- 7.
- The determination of the criterion weight for each factor is as follows:
2.5. Factor Ranking Using Results from Fault Tree Analysis and Interval-Valued Pythagorean Fuzzy Analytic Hierarchy Process
2.6. Cause–Effect Relationship Analysis by Interval-Valued Pythagorean Fuzzy Decision-Making Trial and Evaluation Laboratory
- Build of the Interval-Valued Pythagorean initial direct relation matrix .
- 2.
- Defuzzification of the Interval-Valued Pythagorean initial direct relation matrix for a crisp direct relation matrix is carried out according to Definition 6.
- 3.
- The normalization of the crisp direct relation matrix is as follows:where .
- 4.
- Computation of the total relation matrix is as follows:where is an identity matrix.
- 5.
- The influence degree, influenced degree, centrality degree, and cause degree are calculated.
- 6.
- Generation of the influential diagram.
3. Case Study: Structural Factor Analysis for Public Transportation Bus
3.1. Data Description
3.2. Preprocessing Work for Maintenance Records
3.3. Identification of Structural Factors for Public Transportation Bus
3.4. Selection of Critical Structural Factors
3.4.1. Factor Selection Considering Occurrence Probability by Fault Tree Analysis
3.4.2. Factor Selection Considering Severity Impact by Interval-Valued Pythagorean Fuzzy Analytic Hierarchy Process
3.4.3. Factor Selection Considering Both Occurrence Probability and Severity Impact
3.4.4. Cause–Effect Relationship Analysis by Interval-Valued Pythagorean Fuzzy Decision-Making Trial and Evaluation Laboratory
3.5. Result Analysis
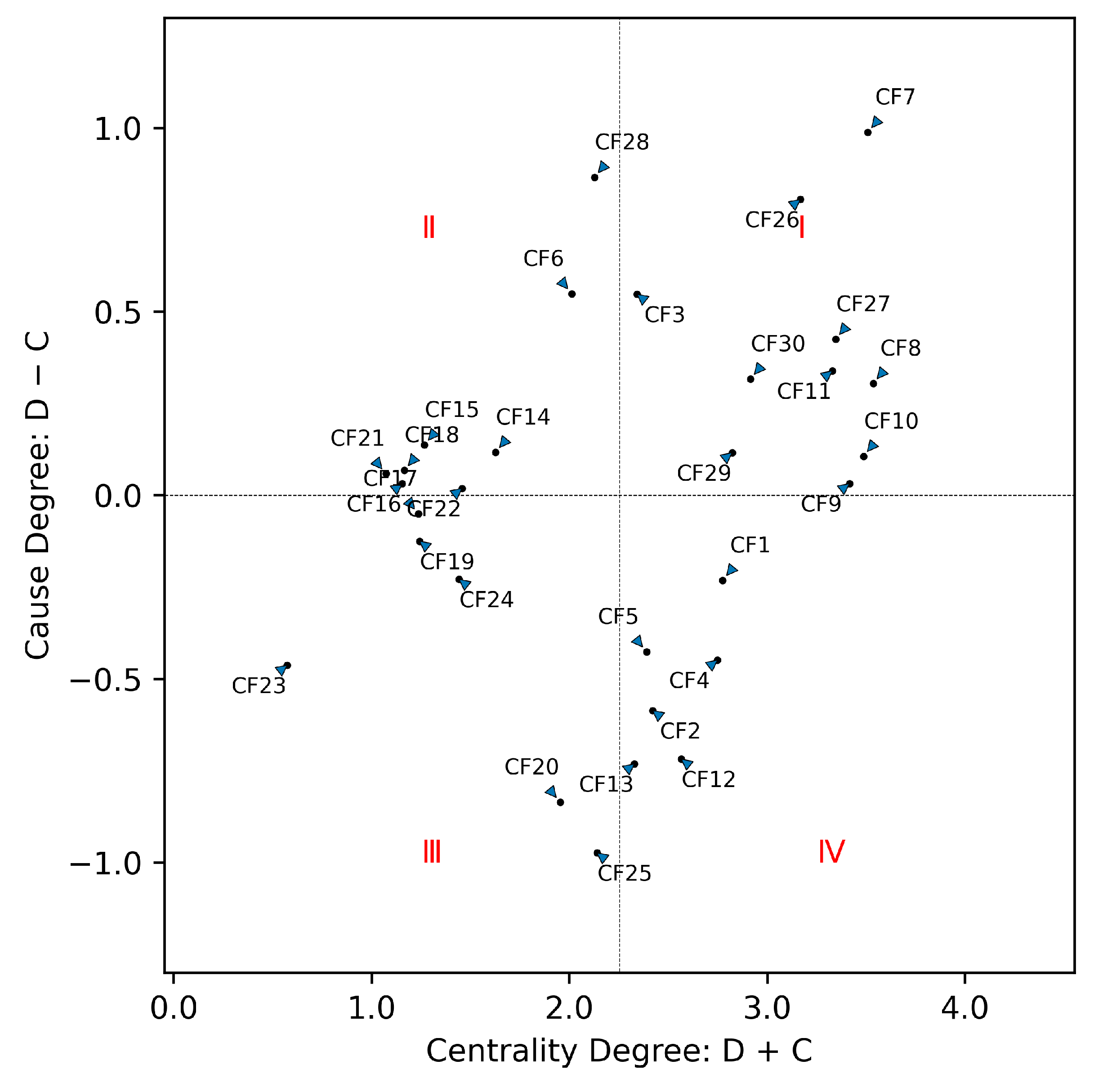
3.5.1. Cause Group Analysis
3.5.2. Effect Group Analysis
3.6. Discussion
3.6.1. Summary of Analysis Findings
3.6.2. Managerial Insights
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| AHP | Analytic Hierarchy Process |
| ANP | Analytic Network Process |
| BEs | Basic Events |
| BIM | Birnbaum Importance Measure |
| DEMATEL | Decision-Making Trial and Evaluation Laboratory |
| DMs | Decision-Makers |
| FMEA | Failure Modes and Effects Analysis |
| FST | Fuzzy Set Theory |
| FT | Fault Tree |
| FTA | Failure Tree Analysis |
| IFS | Intuitionistic Fuzzy Set |
| IVFS | Interval-Valued Fuzzy Set |
| IVPF-AHP | Interval-Valued Pythagorean Fuzzy Analytic Hierarchy Process |
| IVPF-DEMATEL | Interval-Valued Pythagorean Fuzzy Decision-Making Trial and Evaluation Laboratory |
| IVPFS | Interval-Valued Pythagorean Fuzzy Set |
| MCDM | Multi-Criteria Decision-Making |
| PFS | Pythagorean Fuzzy Set |
| PHM | Prognostic and Health Management |
| TE | Top Event |
References
- Hyder, A.A.; Hoe, C.; Hijar, M.; Peden, M. The political and social contexts of global road safety: Challenges for the next decade. Lancet 2022, 400, 127–136. [Google Scholar] [CrossRef] [PubMed]
- Lie, A.; Tingvall, C.; Michael, J.P.; Fell, J.C.; Dinh-Zarr, T.B. Vision Zero and impaired driving: Near and longer-term opportunities for preventing death and injuries. Accid. Anal. Prev. 2024, 194, 107344. [Google Scholar] [CrossRef] [PubMed]
- Monthly Traffic and Transport Digest. 2024. Available online: https://www.td.gov.hk/en/transport_in_hong_kong/transport_figures/monthly_traffic_and_transport_digest/2023/index.html (accessed on 7 April 2024).
- Se, C.; Champahom, T.; Jomnonkwao, S.; Chonsalasin, D.; Ratanavaraha, V. Modeling of single-vehicle and multi-vehicle truck-involved crashes injury severities: A comparative and temporal analysis in a developing country. Accid. Anal. Prev. 2024, 197, 107452. [Google Scholar] [CrossRef]
- Elvik, R. Risk factors as causes of accidents: Criterion of causality, logical structure of relationship to accidents and completeness of explanations. Accid. Anal. Prev. 2024, 197, 107469. [Google Scholar] [CrossRef]
- Assemi, B.; Hickman, M. Relationship between heavy vehicle periodic inspections, crash contributing factors and crash severity. Transp. Res. Part A Policy Pract. 2018, 113, 441–459. [Google Scholar] [CrossRef]
- White, P.; Dennis, N.; Tyler, N. Analysis of recent trends in bus and coach safety in Britain. Saf. Sci. 1995, 19, 99–107. [Google Scholar] [CrossRef]
- Li, Z.; Liao, H.; Tang, R.; Li, G.; Li, Y.; Xu, C. Mitigating the impact of outliers in traffic crash analysis: A robust Bayesian regression approach with application to tunnel crash data. Accid. Anal. Prev. 2023, 185, 107019. [Google Scholar] [CrossRef]
- Riccardi, M.R.; Augeri, M.G.; Galante, F.; Mauriello, F.; Nicolosi, V.; Montella, A. Safety Index for evaluation of urban roundabouts. Accid. Anal. Prev. 2022, 178, 106858. [Google Scholar] [CrossRef]
- Ali, Y.; Sharma, A.; Haque, M.M.; Zheng, Z.; Saifuzzaman, M. The impact of the connected environment on driving behavior and safety: A driving simulator study. Accid. Anal. Prev. 2020, 144, 105643. [Google Scholar] [CrossRef]
- Yau, K.K.; Lo, H.-P.; Fung, S.H. Multiple-vehicle traffic accidents in Hong Kong. Accid. Anal. Prev. 2006, 38, 1157–1161. [Google Scholar] [CrossRef]
- Shin, J.; Lee, I. Reliability-based vehicle safety assessment and design optimization of roadway radius and speed limit in windy environments. J. Mech. Des. 2014, 136, 081006. [Google Scholar] [CrossRef]
- Loo, B.P.; Fan, Z.; Lian, T.; Zhang, F. Using computer vision and machine learning to identify bus safety risk factors. Accid. Anal. Prev. 2023, 185, 107017. [Google Scholar] [CrossRef] [PubMed]
- Vujanović, D.; Momčilović, V.; Bojović, N.; Papić, V. Evaluation of vehicle fleet maintenance management indicators by application of DEMATEL and ANP. Expert Syst. Appl. 2012, 39, 10552–10563. [Google Scholar] [CrossRef]
- De Villiers, P.-R.H.; Jooste, J.L.; Lucke, D. Smart maintenance system for inner city public bus services. Procedia CIRP 2023, 120, 285–290. [Google Scholar] [CrossRef]
- James, A.T. Maintenance performance evaluation of bus fleet garages using a hybrid approach. Int. J. Ind. Syst. Eng. 2022, 41, 472–501. [Google Scholar] [CrossRef]
- Daimi, S.; Rebai, S. Sustainability performance assessment of Tunisian public transport companies: AHP and ANP approaches. Socio-Econ. Plan. Sci. 2023, 89, 101680. [Google Scholar] [CrossRef]
- Khosravi, F.; Izbirak, G. A framework of index system for gauging the sustainability of iranian provinces by fusing analytical hierarchy process (AHP) and rough set theory (RST). Socio-Econ. Plan. Sci. 2024, 95, 101975. [Google Scholar] [CrossRef]
- Gürler, H.E.; Özçalıcı, M.; Pamucar, D. Determining criteria weights with genetic algorithms for multi-criteria decision making methods: The case of logistics performance index rankings of European Union countries. Socio-Econ. Plan. Sci. 2024, 91, 101758. [Google Scholar] [CrossRef]
- Li, W.; Li, B.; Fang, R.; You, P.; Zou, Y.; Xu, Z.; Guo, S. Risk evaluation of electric power grid enterprise related to electricity transmission and distribution tariff regulation employing a hybrid MCDM model. Mathematics 2021, 9, 989. [Google Scholar] [CrossRef]
- Djenadic, S.; Tanasijevic, M.; Jovancic, P.; Ignjatovic, D.; Petrovic, D.; Bugaric, U. Risk evaluation: Brief review and innovation model based on fuzzy logic and MCDM. Mathematics 2022, 10, 811. [Google Scholar] [CrossRef]
- Andjelković, D.; Stojić, G.; Nikolić, N.; Das, D.K.; Subotić, M.; Stević, Ž. A Novel Data-Envelopment Analysis Interval-Valued Fuzzy-Rough-Number Multi-Criteria Decision-Making (DEA-IFRN MCDM) Model for Determining the Efficiency of Road Sections Based on Headway Analysis. Mathematics 2024, 12, 976. [Google Scholar] [CrossRef]
- Hagag, A.M.; Yousef, L.S.; Abdelmaguid, T.F. Multi-criteria decision-making for machine selection in manufacturing and construction: Recent trends. Mathematics 2023, 11, 631. [Google Scholar] [CrossRef]
- Xiong, Z.; Chen, S. A multi-fidelity approach for reliability-based risk assessment of single-vehicle crashes. Accid. Anal. Prev. 2024, 195, 107391. [Google Scholar] [CrossRef] [PubMed]
- Li, Q.; Wang, Z.; Li, M.; Yang, R.; Lin, P.-S.; Li, X. Development of crash modification factors for roadway illuminance: A matched case-control study. Accid. Anal. Prev. 2021, 159, 106279. [Google Scholar] [CrossRef]
- Ganji, S.S.; Rassafi, A.A.; Kordani, A.A. Vehicle safety analysis based on a hybrid approach integrating DEMATEL, ANP and ER. KSCE J. Civ. Eng. 2018, 22, 4580–4592. [Google Scholar] [CrossRef]
- Du, Z.; Zhou, J.; Yang, Z.; Bo, J. The research on operational reliability evaluation of straddle-type monorail vehicle. Syst. Sci. Control Eng. 2018, 6, 537–546. [Google Scholar] [CrossRef]
- Dong, S.; Yu, F.; Wang, K. Safety evaluation of rail transit vehicle system based on improved AHP-GA. PLoS ONE 2022, 17, e0273418. [Google Scholar] [CrossRef]
- Porcu, F.; Olivo, A.; Giulio, M.; Coni, M.; Michela, B.; Barabino, B. Assessing the risk of bus crashes in transit systems. Eur. Transp./Trasp. Eur. 2021, 81, 1–14. [Google Scholar] [CrossRef]
- Yuan, Q.; Dai, X.; Wang, W. Contributing factors and severity of serious single-passenger vehicle collisions in Beijing. Int. J. Crashworthiness 2016, 21, 32–40. [Google Scholar] [CrossRef]
- Renu, R.; Visotsky, D.; Knackstedt, S.; Mocko, G.; Summers, J.D.; Schulte, J. A knowledge based FMEA to support identification and management of vehicle flexible component issues. Procedia Cirp 2016, 44, 157–162. [Google Scholar] [CrossRef]
- Zadeh, L.A. Fuzzy sets. Inf. Control 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Zadeh, L.A. The concept of a linguistic variable and its application to approximate reasoning—III. Inf. Sci. 1975, 9, 43–80. [Google Scholar] [CrossRef]
- Zadeh, L.A. The concept of a linguistic variable and its application to approximate reasoning—II. Inf. Sci. 1975, 8, 301–357. [Google Scholar] [CrossRef]
- Zadeh, L.A. The concept of a linguistic variable and its application to approximate reasoning—I. Inf. Sci. 1975, 8, 199–249. [Google Scholar] [CrossRef]
- Guillaume, S. Designing fuzzy inference systems from data: An interpretability-oriented review. IEEE Trans. Fuzzy Syst. 2001, 9, 426–443. [Google Scholar] [CrossRef]
- Ojha, V.; Abraham, A.; Snášel, V. Heuristic design of fuzzy inference systems: A review of three decades of research. Eng. Appl. Artif. Intell. 2019, 85, 845–864. [Google Scholar] [CrossRef]
- Namgung, H.; Kim, J.-S. Collision risk inference system for maritime autonomous surface ships using COLREGs rules compliant collision avoidance. IEEE Access 2021, 9, 7823–7835. [Google Scholar] [CrossRef]
- Namgung, H. Local route planning for collision avoidance of maritime autonomous surface ships in compliance with COLREGs rules. Sustainability 2021, 14, 198. [Google Scholar] [CrossRef]
- Atanassov, K.T. Intuitionistic fuzzy sets. Fuzzy Sets Syst. 1986, 20, 87–96. [Google Scholar] [CrossRef]
- Castillo, O.; Melin, P. Towards interval type-3 intuitionistic fuzzy sets and systems. Mathematics 2022, 10, 4091. [Google Scholar] [CrossRef]
- Gorzalczany, M.B. A method of inference in approximate reasoning based on interval-valued fuzzy sets. Fuzzy Sets Syst. 1987, 21, 1–17. [Google Scholar] [CrossRef]
- Yager, R.R. Pythagorean Membership Grades in Multicriteria Decision Making. IEEE Trans. Fuzzy Syst. 2014, 22, 958–965. [Google Scholar] [CrossRef]
- Garg, H. Linguistic Interval-Valued Pythagorean Fuzzy Sets and Their Application to Multiple Attribute Group Decision-making Process. Cogn. Comput. 2020, 12, 1313–1337. [Google Scholar] [CrossRef]
- Wang, J. Chapter 11—Safety Analysis Methods for Train Control Systems. In Safety Theory and Control Technology of High-Speed Train Operation; Wang, J., Ed.; Academic Press: Cambridge, MA, USA, 2018; pp. 309–354. [Google Scholar]
- He, L.; Pan, R.; Wang, Y.; Gao, J.; Xu, T.; Zhang, N.; Wu, Y.; Zhang, X. A Case Study of Accident Analysis and Prevention for Coal Mining Transportation System Based on FTA-BN-PHA in the Context of Smart Mining Process. Mathematics 2024, 12, 1109. [Google Scholar] [CrossRef]
- Yazdi, M.; Nedjati, A.; Zarei, E.; Abbassi, R. A novel extension of DEMATEL approach for probabilistic safety analysis in process systems. Saf. Sci. 2020, 121, 119–136. [Google Scholar] [CrossRef]
- Saaty, T.L. The analytic hierarchy process (AHP). J. Oper. Res. Soc. 1980, 41, 1073–1076. [Google Scholar]
- Pant, S.; Kumar, A.; Ram, M.; Klochkov, Y.; Sharma, H.K. Consistency indices in analytic hierarchy process: A review. Mathematics 2022, 10, 1206. [Google Scholar] [CrossRef]
- Chan, H.K.; Sun, X.; Chung, S.-H. When should fuzzy analytic hierarchy process be used instead of analytic hierarchy process? Decis. Support Syst. 2019, 125, 113114. [Google Scholar] [CrossRef]
- Ayyildiz, E.; Yildiz, A.; Taskin, A.; Ozkan, C. An interval valued Pythagorean fuzzy AHP integrated quality function deployment methodology for hazelnut production in Turkey. Expert Syst. Appl. 2023, 231, 120708. [Google Scholar] [CrossRef]
- Gabus, A.; Fontela, E. World Problems, an Invitation to Further Thought Within the Framework of DEMATEL; Battelle Geneva Research Center: Geneva, Switzerland, 1972; Volume 1, pp. 12–14. [Google Scholar]
- Boutkhoum, O.; Hanine, M.; Nabil, M.; El Barakaz, F.; Lee, E.; Rustam, F.; Ashraf, I. Analysis and evaluation of barriers influencing blockchain implementation in Moroccan sustainable supply chain management: An integrated IFAHP-DEMATEL framework. Mathematics 2021, 9, 1601. [Google Scholar] [CrossRef]
- Yu, S.; Geng, X.; He, J.; Sun, Y. Evolution analysis of product service ecosystem based on interval Pythagorean fuzzy DEMATEL-ISM-SD combination model. J. Clean. Prod. 2023, 421, 138501. [Google Scholar] [CrossRef]
- Vuchic, V.R. Urban Transit Systems and Technology; John Wiley & Sons: Hoboken, NJ, USA, 2007. [Google Scholar]

| Linguistic Terms | Interval-Valued Pythagorean Numbers | |||
|---|---|---|---|---|
| Certainly Low Importance (CLI) | 0.0 | 0.0 | 0.9 | 1.0 |
| Very Low Importance (VLI) | 0.1 | 0.2 | 0.8 | 0.9 |
| Low Importance (LI) | 0.2 | 0.35 | 0.65 | 0.8 |
| Below Average Importance (BLI) | 0.35 | 0.45 | 0.55 | 0.65 |
| Equal Importance (EI) | 0.1965 | 0.1965 | 0.1965 | 0.1965 |
| Average Importance (AI) | 0.45 | 0.55 | 0.45 | 0.55 |
| Above Average Importance (AHI) | 0.55 | 0.65 | 0.35 | 0.45 |
| High Importance (HI) | 0.65 | 0.8 | 0.2 | 0.35 |
| Very High Importance (VHI) | 0.8 | 0.9 | 0.1 | 0.2 |
| Certainly High Importance (CHI) | 0.9 | 1.0 | 0.0 | 0.0 |
| Linguistic Terms | Interval-Valued Pythagorean Fuzzy Number |
|---|---|
| Very high influence | ([0.80, 0.95], [0.00, 0.10]) |
| High influence | ([0.60, 0.80], [0.10, 0.30]) |
| Low influence | ([0.40, 0.60], [0.30, 0.50]) |
| Very low influence | ([0.20, 0.40], [0.50, 0.70]) |
| No influence | ([0.00, 0.20], [0.70, 0.90]) |
| No DM | Job Position | Experience (Years) | Age | Educational Level |
|---|---|---|---|---|
| DM #1 | Head of the Depot | 26 | 51 | MSc |
| DM #2 | Senior Engineer | 20 | 45 | MSc |
| DM #3 | Senior Engineer | 18 | 42 | MSc |
| DM #4 | Technical Engineer | 5 | 25 | BSc |
| DM #5 | Technical Engineer | 4 | 27 | BSc |
| Critical Factor | Basic Event | BE Description |
|---|---|---|
| CF1 | BE1 | Failure of Transmission Computer |
| CF2 | BE2 | Failure of Transmission |
| CF3 | BE3 | Connection Misalignment of Transmission Cable |
| CF4 | BE4 | Failure of Transmission Speed Sensor |
| CF5 | BE6 | Failure of Water Tank Fan Pump Motor |
| CF6 | BE17 | Lack of Lubricating Oil |
| CF7 | BE18 | Failure of Ignition Switch Sensor |
| CF8 | BE20 | Failure of Engine Speed Sensor |
| CF9 | BE21 | Failure of Diesel Injector |
| CF10 | BE23 | Failure of Engine Cylinder |
| CF11 | BE24 | Failure of Turbocharger |
| CF12 | BE25 | Failure of High-Pressure Fuel Pump |
| CF13 | BE27 | Failure of ABS/ASR Sensor Circuit |
| CF14 | BE28 | Connection Misalignment of EBS Sensor Wire |
| CF15 | BE29 | Failure of EBS Valve |
| CF16 | BE31 | Failure of Brake System Air Hose |
| CF17 | BE32 | Failure of Air Brake Cylinder |
| CF18 | BE33 | Failure of Air Brake Dryer |
| CF19 | BE34 | Connection Misalignment of Handbrake/rear Transmission Safety Cable |
| CF20 | BE35 | Failure of Parking Handbrake Pump |
| CF21 | BE36 | Connection Misalignment of Balance Lever |
| CF22 | BE37 | Failure of Shock Absorber |
| CF23 | BE38 | Failure of Suspension Airbags |
| CF24 | BE39 | Failure of Power Steering Fluid Inlet Hard Hose |
| CF25 | BE40 | Failure of Power Steering Pump |
| CF26 | BE41 | Degradation of Battery |
| CF27 | BE42 | Failure of Alternator |
| CF28 | BE43 | Failure of Alternator Belt Components |
| CF29 | BE47 | Failure of Electrical Appliance Central Control System/line |
| CF30 | BE52 | Failure of Starter Motor |
| Critical Factors | D (Influence Degree) | C (Influenced Degree) | M = D + C (Centrality Degree) | R = D − C (Cause Degree) | Cause/Effect Groups Based on R Value | Ranking Based on M Value | Ranking Based on R Value |
|---|---|---|---|---|---|---|---|
| CF1 | 1.271729 | 1.503271 | 2.775000 | −0.231542 | Effect | 10 | 22 |
| CF2 | 0.917362 | 1.503316 | 2.420678 | −0.585954 | Effect | 13 | 26 |
| CF3 | 1.444551 | 0.897244 | 2.341796 | 0.547307 | Cause | 15 | 5 |
| CF4 | 1.149821 | 1.598771 | 2.748593 | −0.448950 | Effect | 11 | 24 |
| CF5 | 0.981939 | 1.408066 | 2.390005 | −0.426127 | Effect | 14 | 23 |
| CF6 | 1.280265 | 0.731577 | 2.011842 | 0.548688 | Cause | 19 | 4 |
| CF7 | 2.247947 | 1.260447 | 3.508394 | 0.987500 | Cause | 2 | 1 |
| CF8 | 1.920208 | 1.616124 | 3.536333 | 0.304084 | Cause | 1 | 9 |
| CF9 | 1.723379 | 1.691881 | 3.415260 | 0.031498 | Cause | 4 | 16 |
| CF10 | 1.796472 | 1.690464 | 3.486936 | 0.106008 | Cause | 3 | 13 |
| CF11 | 1.833694 | 1.495253 | 3.328947 | 0.338441 | Cause | 6 | 7 |
| CF12 | 0.923560 | 1.642029 | 2.565589 | −0.718469 | Effect | 12 | 27 |
| CF13 | 0.798804 | 1.530272 | 2.329076 | −0.731468 | Effect | 16 | 28 |
| CF14 | 0.872186 | 0.755319 | 1.627505 | 0.116867 | Cause | 21 | 11 |
| CF15 | 0.702164 | 0.565543 | 1.267707 | 0.136621 | Cause | 24 | 10 |
| CF16 | 0.593035 | 0.561935 | 1.154970 | 0.031100 | Cause | 28 | 17 |
| CF17 | 0.593295 | 0.643842 | 1.237137 | −0.050547 | Effect | 26 | 19 |
| CF18 | 0.617177 | 0.549447 | 1.166624 | 0.067731 | Cause | 27 | 14 |
| CF19 | 0.558750 | 0.683747 | 1.242497 | −0.124996 | Effect | 25 | 20 |
| CF20 | 0.558750 | 1.394440 | 1.953190 | −0.835689 | Effect | 20 | 29 |
| CF21 | 0.565621 | 0.506980 | 1.072601 | 0.058641 | Cause | 29 | 15 |
| CF22 | 0.737867 | 0.719515 | 1.457382 | 0.018352 | Cause | 22 | 18 |
| CF23 | 0.055525 | 0.518177 | 0.573701 | −0.462652 | Effect | 30 | 25 |
| CF24 | 0.606828 | 0.835935 | 1.442763 | −0.229107 | Effect | 23 | 21 |
| CF25 | 0.583098 | 1.556685 | 2.139784 | −0.973587 | Effect | 17 | 30 |
| CF26 | 1.986432 | 1.181203 | 3.167634 | 0.805229 | Cause | 7 | 3 |
| CF27 | 1.885019 | 1.460741 | 3.345760 | 0.424279 | Cause | 5 | 6 |
| CF28 | 1.495937 | 0.630901 | 2.126838 | 0.865036 | Cause | 18 | 2 |
| CF29 | 1.469081 | 1.353540 | 2.822621 | 0.115541 | Cause | 9 | 12 |
| CF30 | 1.615927 | 1.299762 | 2.915689 | 0.316166 | Cause | 8 | 8 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hou, Z.-F.; Lee, K.-M.; Keung, K.-L.; Huang, J.-Y. A Novel Multi-Criteria Decision-Making Framework of Vehicle Structural Factor Evaluation for Public Transportation Safety. Appl. Sci. 2025, 15, 3045. https://doi.org/10.3390/app15063045
Hou Z-F, Lee K-M, Keung K-L, Huang J-Y. A Novel Multi-Criteria Decision-Making Framework of Vehicle Structural Factor Evaluation for Public Transportation Safety. Applied Sciences. 2025; 15(6):3045. https://doi.org/10.3390/app15063045
Chicago/Turabian StyleHou, Zhe-Fan, Ka-Man Lee, Kin-Lok Keung, and Jing-Yuan Huang. 2025. "A Novel Multi-Criteria Decision-Making Framework of Vehicle Structural Factor Evaluation for Public Transportation Safety" Applied Sciences 15, no. 6: 3045. https://doi.org/10.3390/app15063045
APA StyleHou, Z.-F., Lee, K.-M., Keung, K.-L., & Huang, J.-Y. (2025). A Novel Multi-Criteria Decision-Making Framework of Vehicle Structural Factor Evaluation for Public Transportation Safety. Applied Sciences, 15(6), 3045. https://doi.org/10.3390/app15063045







