A Multi-Optimization Method for Capacity Configuration of Hybrid Electrolyzer in a Stand-Alone Wind-Photovoltaic-Battery System
Abstract
:1. Introduction
- (1)
- A hybrid electrolyzer scheme for hydrogen production, which combines the complementary advantages of AWE and PEME, was proposed and analyzed in depth. This analysis focused on the economic efficiency and production potential of hydrogen. The optimal ratio between the two types of electrolyzers within the hybrid system was also discussed.
- (2)
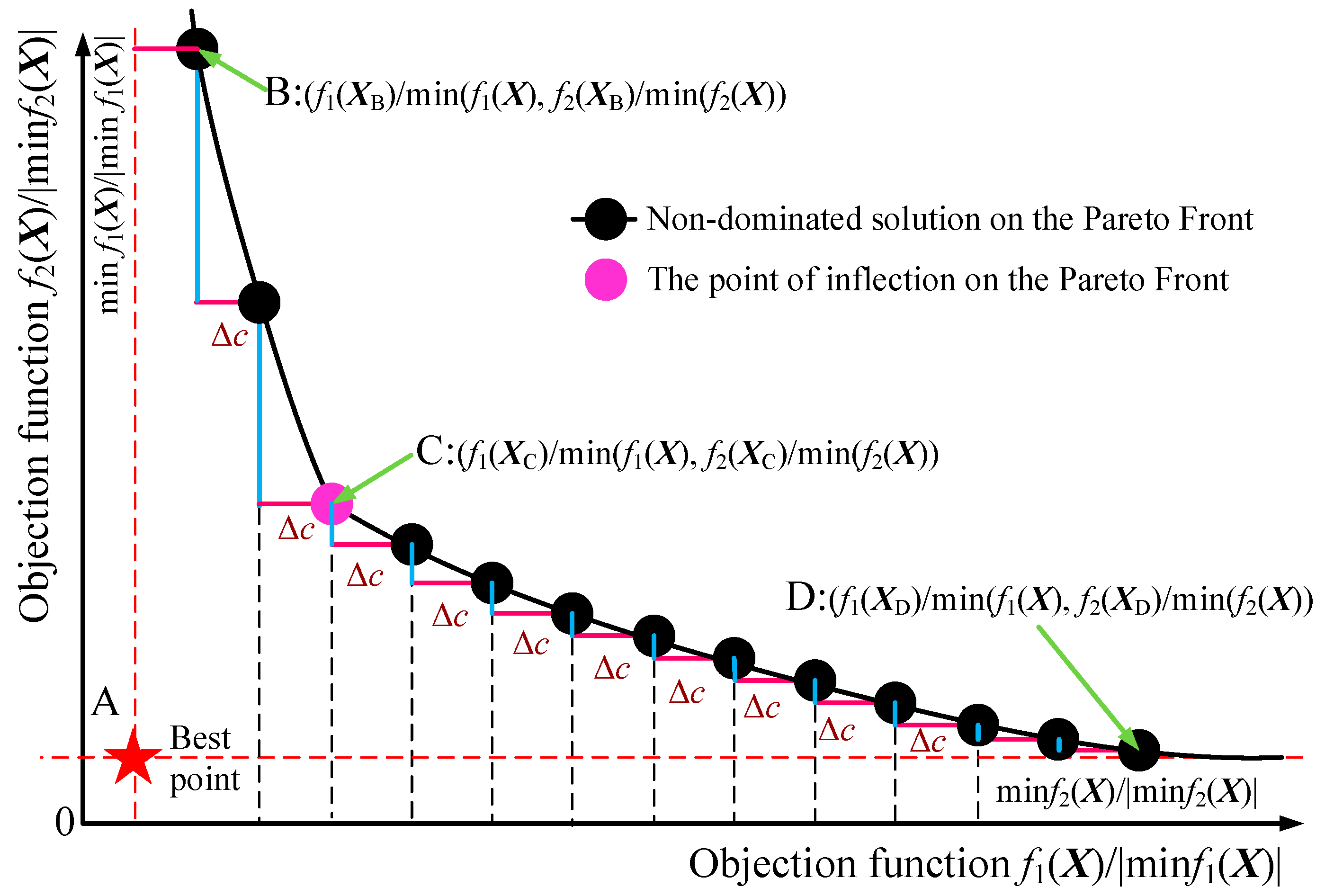
- A multi-objective optimization method based on the slope change of the Pareto front was presented, offering a new approach for selecting recommended solutions for multi-objective optimization problems.
- (3)
- Analysis of the relative values of AWE and PEME in hydrogen efficiency, unit cost, and unit investment price cost highlighted key factors affecting the hybrid electrolyzer’s rated power and mixing ratio. This will further enhance the hybrid electrolyzer’s application and development.
2. The Stand-Alone Wind-Photovoltaic-Battery System with the Hybrid Electrolyzer
2.1. Structure of Wind-Photovoltaic-Battery System with the Hybrid Electrolyzer
2.2. Mathematical Model of the Stand-Alone Wind-Photovoltaic-Battery System with the Hybrid Electrolyzer
- (1)
- The constraints of the real-time power balance of the system are expressed in Formula (1) and indicates the current balance of the system’s operating power in real-time. The system variables are defined as follows [31]: PPV(t)—photovoltaic generation output; PWIND(t)—wind turbine generation output; (t)—battery energy storage system discharge power; (t)—battery energy storage system charge power; PLoad(t)—active load demand; PAWE(t)—alkaline water electrolyzer hydrogen production power; PPEME(t)—proton exchange membrane electrolyzer power. (t) is negative, and the others are positive.
- (2)
- Formula (2) outlines the operation constraints of the PVGs and WTGs [25]. The power generation capacity of the renewable energy system is subject to operational constraints, where PPV(t) and (t) indicate the instantaneous output power and maximum available power from the PVGs, respectively, and PWIND(t) and (t) correspondingly represent these parameters for the WTGs. and refer to the rated power of the PVGs and WTGs, respectively. Additionally, δ1 represents the abandonment rate of the new energy source.
- (3)
- In the operation constraints of the BESS, there are specific relationships between the charging/discharging power and SOE of the BESS [31,32]. It outlines potential limitations regarding the BESS’s operating power and stored energy capacity. Formula (3) shows the initial, minimum, and maximum values of the SOE. Then, Formula (4) describes the BESS’s charging and discharging power range.where CSOE(t) represents the SOE of the BESS at time t. denotes the rated capacity of the BESS, while ηd and ηc are the discharge and charge efficiency of the BESS, respectively. The variables (t) and (t) are the binary optimization variables. If (t) = 1, it indicates that the BESS is discharging. Conversely, if (t) = 1, it indicates that the BESS is charging. The initial state of energy is specified as , with the minimum and maximum capacity limits defined as the CD SOE and , respectively. Additionally, Δt represents the sampling time, and T indicates the ending time.
- (4)
- The operation constraints of the production, storage, and sale of hydrogen units are defined as Formulas (5)~(8). The equation relationship between hydrogen production power and volume is Formula (5) [29]. Then, Formula (6) outlines the production, storage, and sale relationships among AWE, PEME, and HST [31,32]. The operation power range and climbing rate for AWE and PEME are illustrated in Formula (7) [28]. Finally, Formula (8) represents the range of hydrogen sales volume [32].where CSOH(t), VSELL(t), VAWE(t), and VPEME(t) represent the SOH of the HST, the volume of hydrogen sold, and the volume of hydrogen produced by AWE and PEME at time t, respectively. The hydrogen density (ρH2) is 0.9 kg/m3; is the rated capacity of the HST, and is the maximum volume of hydrogen sold. The parameters ηAWE, , αAWE, , , and represent the hydrogen production efficiency, electric hydrogen ratio, climbing rate, minimum power, maximum power, and rated power of AWE, respectively. Similarly, ηPEME, , αPEME, , , and reflect the corresponding properties for PEME. The initial, minimum, and maximum capacity values of the HST are represented by , , and , respectively.
- (5)
- The operation constraints of the load unit are presented in Formula (9). PLoad(t) and (t) refer to the load’s actual power and demand power, respectively. δ2 is the cut-off rate of the load.
- (1)
- This study examined the economic aspects of hydrogen production by analyzing the initial investment cost, hydrogen production cost, and sales revenue associated with AWE and PEME. The costs per kilowatt-hour (kWh) of the BESS, PVGs, and WTGs were considered. Subsequently, an objective function J1 was established to represent the economic viability of hydrogen production using a hybrid electrolyzer, as detailed in Formula (10) [25]. The investment cost is directly related to the rated power of the hybrid electrolyzer. In contrast, the hydrogen production cost and sales revenue depend on the actual output power of the electrolyzer, which is constrained by its rated capacity.
- (2)
- This study analyzed the energy loss and idle conditions associated with hydrogen production in a hybrid electrolyzer, focusing on its utilization efficiency. Then, another objective function, J2, was designed, as detailed in Formula (11), where Pi(t) (1 − ηi) and ( − Pi(t)) represent the energy loss and the idle power of hydrogen production using AWE or PEME at time t, respectively.where Pi(t) and VSELL(t) represent the hydrogen production power of AWE or PEME and the volume of hydrogen sold at time t; , Ni, , and ηi are the rated power, operation life, electric hydrogen ratio, and hydrogen production efficiency of AWE or PEME, respectively; , cWIND, and cBESS are the cost per kW/h of the PVGs, WTGs, and BESS; , , and are the investment cost coefficient, hydrogen production cost of AWE or PEME, and the hydrogen sales revenue, respectively; γ is the discount rate.
3. A Multi-Objective Optimization Problem and Solution for Hydrogen Production
| Algorithm 1. Pseudo code of the proposed method. | |
| Input: In a stand-alone wind-photovoltaic-battery system with the hybrid electrolyzer, the mathematical model is shown as Formulas (1)~(11) and (14). The step parameter and maximum iteration are defined as Δc and Nmax. Assuming that the number of iterations N is 0. The vector X includes PPV(t), PWIND(t), (t), (t), PLoad(t), PAWE(t), PPEME(t), (t), (t), CSOE(t), CSOH(t), VSELL(t), VAWE(t), and VPEME(t), t = 1, 2, …, T. | |
| 1 | Minimizing each single objective function J1(X) and J2(X) based on CPLEX optimization tool; |
| 2 | The minimum value of each optimization objective function is obtained by min(J1(X)) and min(J2(X)); |
| 3 | The control parameter c←Δc; |
| 4 | Based on Formula (14), min(J2(X)|c) is obtained; |
| 5 | Under the above parameter c condition, (X) is calculated; |
| 6 | While N <= Nmax |
| 7 | The number of iterations N ← N + 1; |
| 8 | The control parameter c ← c + Δc; |
| 9 | Based on Formula (14), min(J2(X)|c) is obtained; |
| 10 | Under the above parameter c condition, (X) and (X) are calculated; |
| 11 | Δ(X) ← |(X) − (X)|; |
| 12 | The SlopeN← Δ (X)/Δc; |
| 13 | end |
| 14 | index = argmax(SlopeN, N = 1, 2,…, Nmax) // argmax() is a function for finding an index at the maximum value of the variable |
| Output: ((X), (X)) and X under the parameter index × Δc condition | |
4. Case Analysis and Discussion
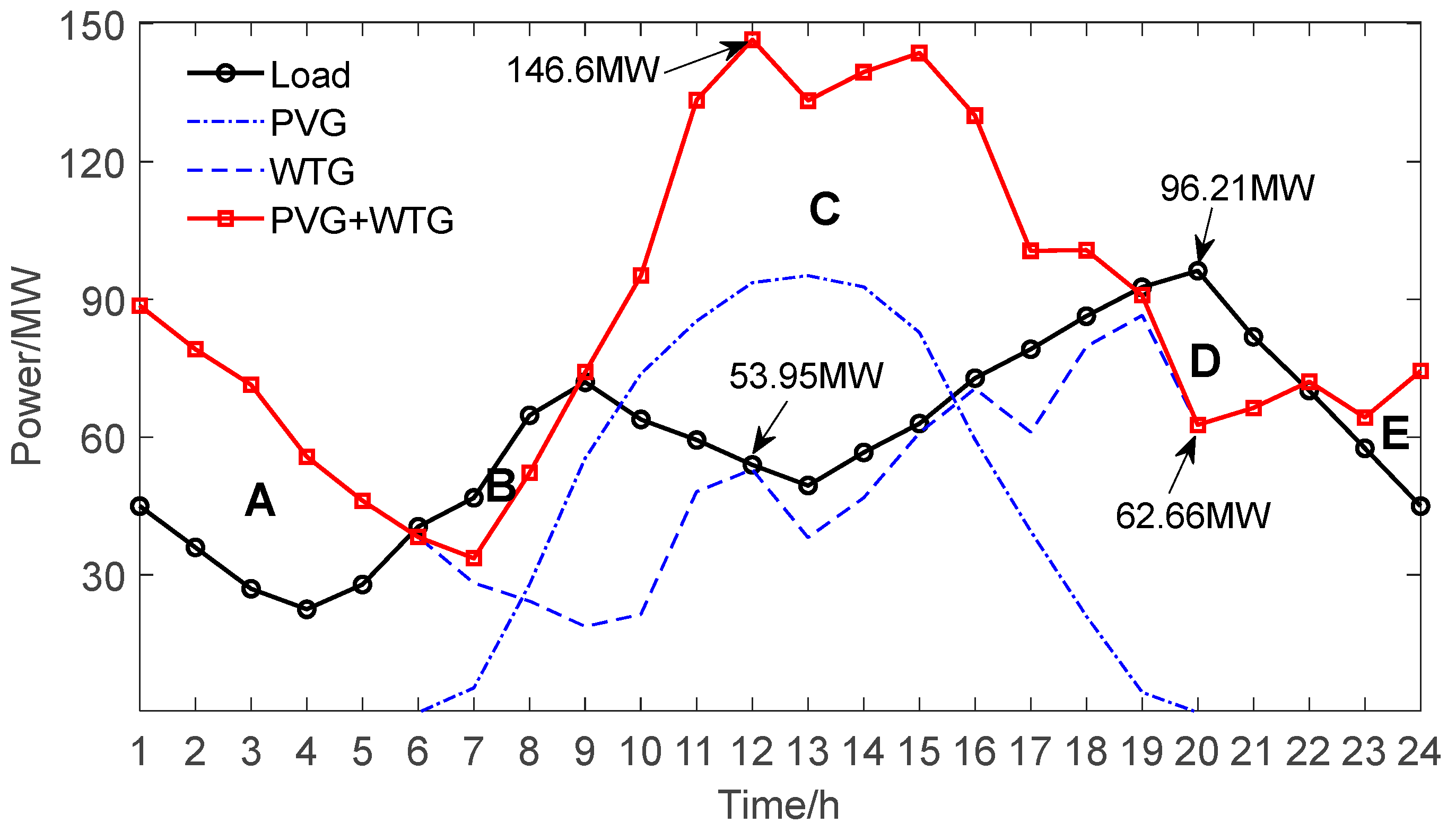
4.1. Parameter Description
4.2. Results Analysis
4.3. Discussion
5. Conclusions
- (1)
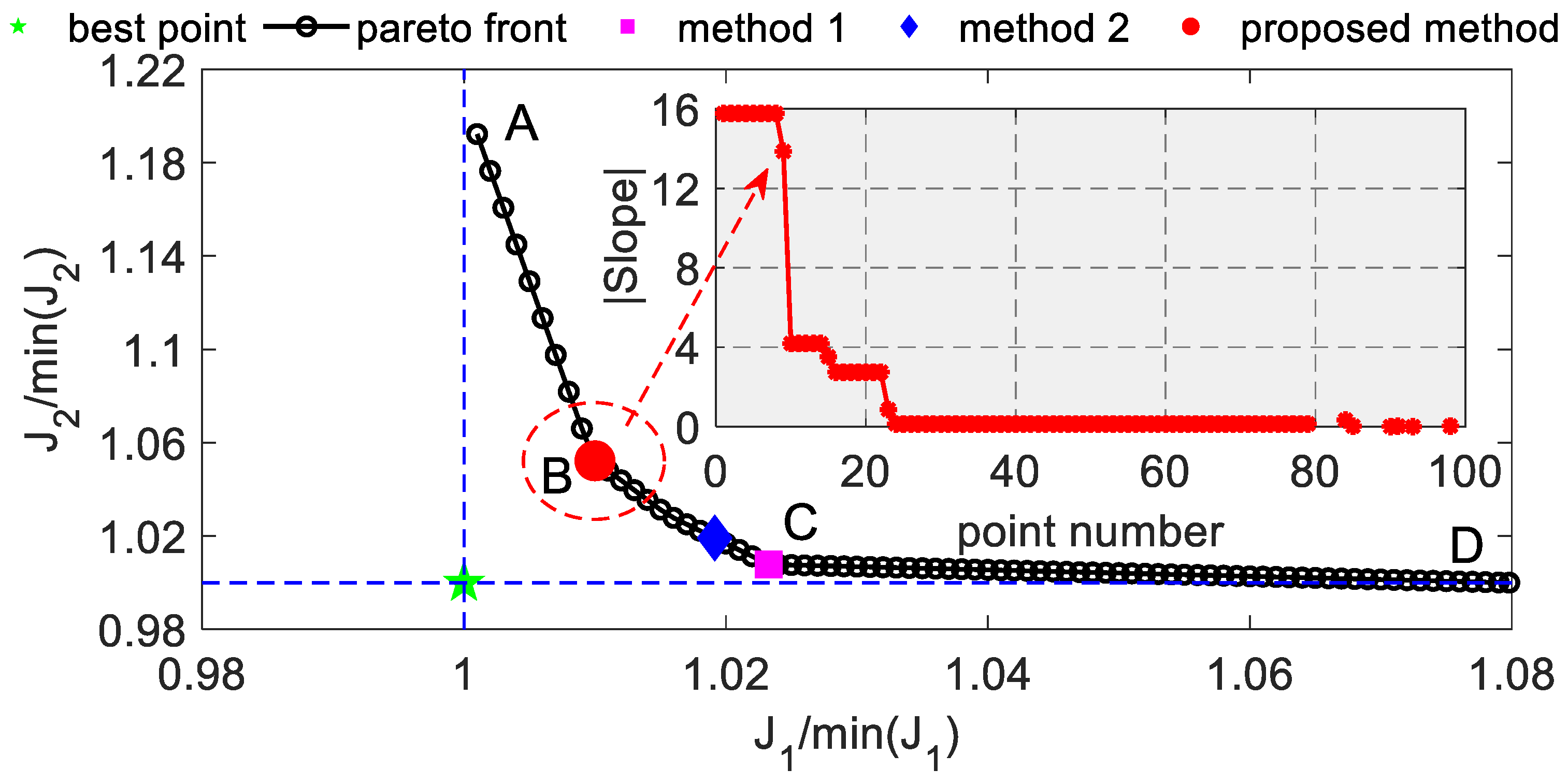
- An adjustable parameter was introduced to transform a multi-objective problem into a single-objective optimization problem with specific parameter constraints. This allowed for the effective and controllable drawing of the Pareto front associated with the multi-objective optimization problem. The adjustable parameter can be quantitatively modified by stepping; the non-dominated solution that exhibits the most significant change in slope is recommended as the optimal solution. This has provided a new approach for selecting recommended solutions for multi-objective optimization problems.
- (2)
- A hybrid electrolyzer that combines AWE and PEME can effectively balance the costs and losses of hydrogen production. This approach takes advantage of AWE’s lower production costs and PEME’s higher efficiency. In terms of the composition of hydrogen production, a hybrid electrolyzer based on AWE and PEME can better balance the economy and losses of hydrogen production. As a result, the complementary advantages of the hydrogen production cost of AWE and the hydrogen production efficiency of PEME can be fully leveraged. With the changing efficiency and costs of hydrogen production methods, particularly AWE and PEME, if AWE’s efficiency improves or if PEME’s costs decrease, the design of hydrogen production electrolyzers is likely to transition to a unified structure.
- (3)
- Under the structure of a hybrid electrolyzer compared with a single optimization objective function focused solely on minimizing the cost of hydrogen production, the proposed method achieved notable improvements. Specifically, this approach resulted in a 1.00% decrease in production costs while increasing hydrogen utilization by 21.71%. Additionally, compared with the single optimization objective function minimizing the loss of hydrogen production, the utilization and economy of hydrogen production were reduced by 5.22% and increased by 6.46%, respectively.
- (4)
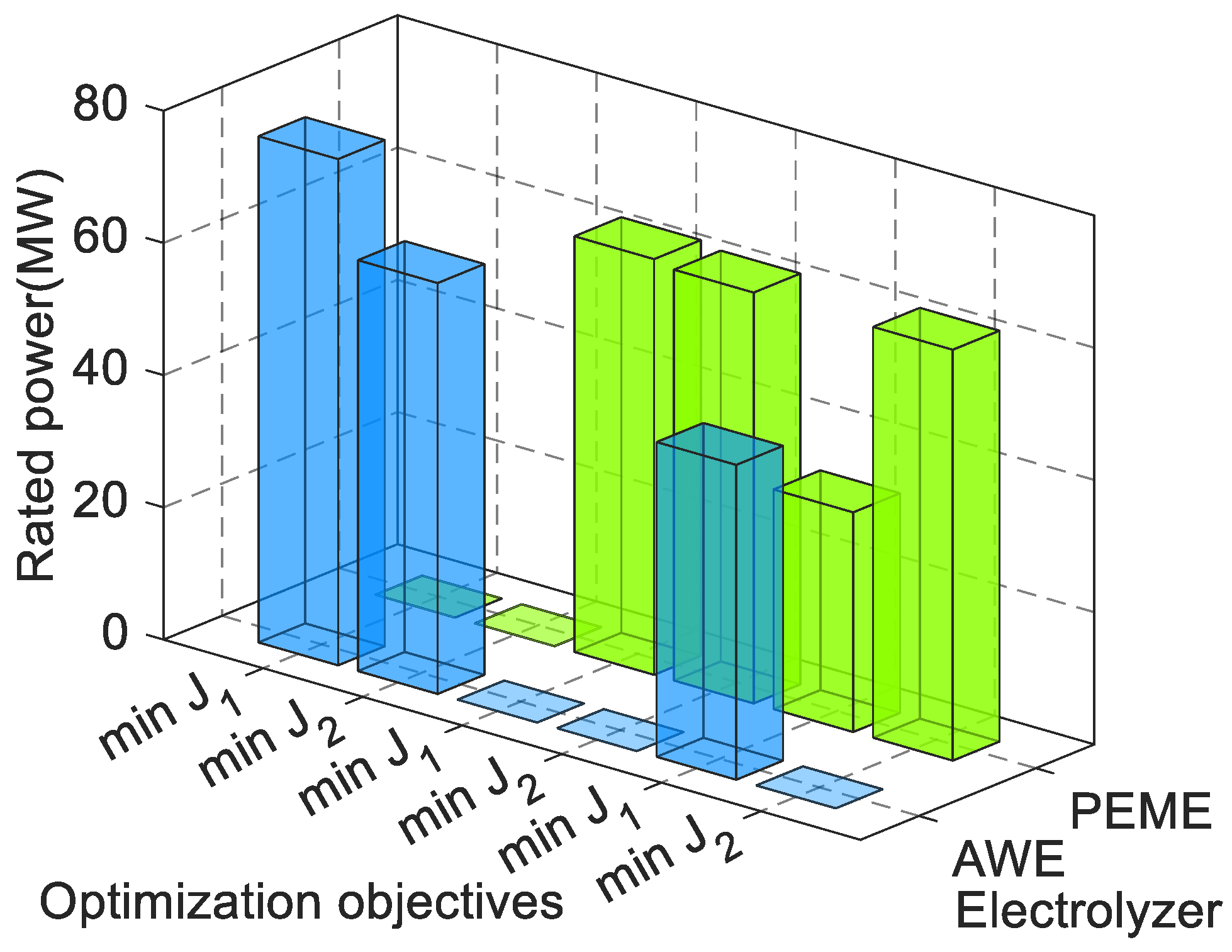
- In a stand-alone wind-photovoltaic-battery system with a hybrid electrolyzer, when the hydrogen production efficiency of AWE falls below 72%, the proportion of PEME will significantly increase. In terms of per unit hydrogen production and investment construction cost, the relative value between AWE and PEME is crucial in determining the composition of the hydrogen production electrolyzer. Furthermore, under stand-alone conditions, the relationship between the new energy source and load electricity consumption is a key factor influencing the hybrid electrolyzer’s total rated power and composition ratio.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| AWE | Alkaline electrolyzer | , | The lower and upper range of the SOE |
| PEME | Proton exchange membrane electrolyzer | CSOH | SOH of the HST |
| BESS | Battery energy storage system | VSELL | The volume of hydrogen sold |
| PVGs | Photovoltaic power generation system | VAWE, VPEME | The volume of hydrogen produced by AWE and PEME |
| WTGs | Wind turbine power generation system | ρH2 | Hydrogen density |
| SOE | State of energy | Rated capacity of the HST | |
| SOH | State of hydrogen | Maximum volume of hydrogen sold | |
| HST | Hydrogen storage tank | ηAWE, ηPEME | Hydrogen production efficiency of AWE and PEME |
| PPV | Actual output power of the PVGs | , | The electric hydrogen ratio of AWE and PEME |
| Rated power of PVGs | αAWE, αPEME | The climbing rate of AWE and PEME | |
| PWIND | Actual output power of the WTGs | , | Minimum and maximum power of AWE |
| Rated power of WTGs | , | Minimum and maximum power of PEME | |
| , | Discharging and charging power of the BESS | , | Rated power of AWE and PEME |
| PLoad | Active power of the load | , | Lower and upper range of the SOH |
| PAWE | Hydrogen production power of AWE | Initial SOH of the HST | |
| PPEME | Hydrogen production power of PEME | δ2 | Cut-off rate of load |
| δ1 | Abandonment rate of new energy source | , cWIND | Cost per kW/h of PVGs, and WTGs |
| CSOE | SOE of the BESS | cBESS | Cost per kW/h of BESS |
| Rated capacity of the BESS | The investment cost of AWE or PEME | ||
| ηd, ηc | Discharging and charging efficiency of the BESS | Hydrogen production cost of AWE or PEME | |
| , | Discharging and charging state of the BESS | Hydrogen sales revenue | |
| Initial SOE of the BESS | γ | Discount rate |
References
- Alanazi, K.; Mittal, S.; Hawkes, A.; Shah, N. Renewable hydrogen trade in a global decarbonised energy system. Int. J. Hydrogen Energy 2025, 101, 712–730. [Google Scholar] [CrossRef]
- Nasser, M.; Megahed, T.F.; Ookawara, S.; Hassan, H. A Review of Water Electrolysis-Based Systems for Hydrogen Production Using Hybrid/Solar/Wind Energy Systems. Environ. Sci. Pollut. Res. 2022, 29, 86994–87018. [Google Scholar] [CrossRef] [PubMed]
- Awad, M.; Said, A.; Saad, M.H.; Farouk, A.; Mahmoud, M.M.; Alshammari, M.S.; Omar, A.I. A Review of Water Electrolysis for Green Hydrogen Generation Considering Pv/Wind/Hybrid/Hydropower/Geothermal/Tidal and Wave/Biogas Energy Systems, Economic Analysis, and Its Application. Alex. Eng. J. 2024, 87, 213–239. [Google Scholar] [CrossRef]
- De León, C.M.; Ríos, C.; Brey, J.J. Cost of Green Hydrogen: Limitations of Production from A Stand-Alone Photovoltaic System. Int. J. Hydrogen Energy 2023, 48, 11885–11898. [Google Scholar] [CrossRef]
- Van, L.P.; Hoang, L.H.; Duc, T.N. A Comprehensive Review of Direct Coupled Photovoltaic-Electrolyser System: Sizing Techniques, Operating Strategies, Research Progress, Current Challenges, and Future Recommendations. Int. J. Hydrogen Energy 2023, 48, 25231–25249. [Google Scholar] [CrossRef]
- Escamilla, A.; Sánchez, D.; García-Rodríguez, L. Techno-economic study of Power-to-Power renewable energy storage based on the smart integration of battery, hydrogen, and micro gas turbine technologies. Energy Convers. Manag. X 2023, 18, 100368. [Google Scholar] [CrossRef]
- Barhoumi, E.M.; Belgacem, I.B.; Zghaibeh, M.; Tlili, I. Optimal Sizing of Photovoltaic Systems Based Green Hydrogen Refueling Stations Case Study Oman. Int. J. Hydrogen Energy 2022, 47, 31964–31973. [Google Scholar] [CrossRef]
- Lehmann, J.; Wabbes, A.; Gonzalez, E.M.; Scheerlinck, S. Levelized Cost of Hydrogen Calculation from Off-Grid Photovoltaic Plants Using Different Methods. Sol. RRL 2022, 6, 2100482. [Google Scholar] [CrossRef]
- Zhao, D.; Xia, Z.; Guo, M.; He, Q.; Xu, Q.; Li, X.; Ni, M. Capacity Optimization and Energy Dispatch Strategy of Hybrid Energy Storage System Based on Proton Exchange Membrane Electrolyzer Cell. Energy Convers. Manag. 2022, 272, 116366. [Google Scholar] [CrossRef]
- Escamilla, A.; Sánchez, D.; García-Rodríguez, L. Assessment of power-to-power renewable energy storage based on the smart integration of hydrogen and micro gas turbine technologies. Int. J. Hydrogen Energy 2022, 47, 17505–17525. [Google Scholar] [CrossRef]
- Molu, R.J.J.; Naoussi, S.R.D.; Wira, P.; Mbasso, W.F.; Kenfack, S.T.; Das, B.K.; Ali, E.; Alshareef, M.J.; Ghoneim, S.S.M. Optimizing Technical and Economic Aspects of Off-Grid Hybrid Renewable Systems: A Case Study of Manoka Island, Cameroon. IEEE Access 2023, 11, 130909–130930. [Google Scholar] [CrossRef]
- Mohammed, A. An Optimization-Based Model for A Hybrid Photovoltaic-Hydrogen Storage System for Agricultural Operations in Saudi Arabia. Processes 2023, 11, 1371. [Google Scholar] [CrossRef]
- Babatunde, O.M.; Munda, J.L.; Hamam, Y. Off-Grid Hybrid Photovoltaic-Micro Wind Turbine Renewable Energy System with Hydrogen and Battery Storage: Effects of Sun Tracking Technologies. Energy Convers. Manag. 2022, 255, 115335. [Google Scholar] [CrossRef]
- Moltames, R.; Assareh, E.; Mohammadi Bouri, F.; Azizimehr, B. Simulation and Optimization of a Solar Based Trigeneration System Incorporating PEM Electrolyzer and Fuel Cell. Sol. Energy 2021, 6, 664–677. [Google Scholar]
- Cecilia, A.; Carroquino, J.; Roda, V.; Costa-Castelló, R.; Barreras, F. Optimal Energy Management in a Standalone Microgrid, with Photovoltaic Generation, Short-Term Storage, and Hydrogen Production. Energies 2020, 13, 1454. [Google Scholar] [CrossRef]
- Wu, G.; Li, T.; Xu, W.; Xiang, Y.; Su, Y.; Liu, J.; Liu, F. Chance-Constrained Energy-Reserve Co-Optimization Scheduling of Wind-Photovoltaic-Hydrogen Integrated Energy Systems. Int. J. Hydrogen Energy 2023, 48, 6892–6905. [Google Scholar] [CrossRef]
- Menesy, A.S.; Almomin, S.; Sultan, H.M.; Habiballah, I.O.; Gulzar, M.M.; Alqahtani, M.; Khalid, M. Techno-Economic Optimization Framework of Renewable Hybrid Photovoltaic/Wind Turbine/Fuel Cell Energy System Using Artificial Rabbits Algorithm. IET Renew. Power Gener. 2024, 18, 2907–2924. [Google Scholar] [CrossRef]
- Ren, Y.; Jin, K.; Gong, C.; Hu, J.; Liu, D.; Jing, X.; Zhang, K. Modelling and Capacity Allocation Optimization of a Combined Pumped Storage/Wind/Photovoltaic/Hydrogen Production System Based on the Consumption of Surplus Wind and Photovoltaics and Reduction of Hydrogen Production Cost. Energy Convers. Manag. 2023, 296, 117662. [Google Scholar] [CrossRef]
- Ke, Y.; Tang, H.; Liu, M.; Meng, Q.; Xiao, Y. Optimal Sizing for Wind-Photovoltaic-Hydrogen Storage Integrated Energy System Under Intuitionistic Fuzzy Environment. Int. J. Hydrogen Energy 2023, 48, 34193–34209. [Google Scholar] [CrossRef]
- Ma, S.; Wu, Y.; Li, J.; Hou, X.; Li, D. Economic Planning Method of Energy Storage System to Improve Grid Reliability. Acta Energiae Solaris Sin. 2024, 45, 251–262. [Google Scholar]
- Meng, G.; Ding, Y.; Pau, G.; Yu, L.; Tan, W. Multi-Objective Capacity Optimization Configuration of Independent Wind-Photovoltaic-Hydrogen-Battery System Based on Improved Mossa Algorithm. Front. Energy Res. 2023, 10, 1077462. [Google Scholar]
- Mukoni, E.; Garner, K.S. Multi-Objective Non-Dominated Sorting Genetic Algorithm Optimization for Optimal Hybrid (Wind and Grid)-Hydrogen Energy System Modelling. Energy 2022, 15, 7079. [Google Scholar] [CrossRef]
- Niu, M.; Li, X.; Sun, C.; Xiu, X.; Wang, Y.; Hu, M.; Dong, H. Operation Optimization of Wind/Battery Storage/Alkaline Electrolyzer System Considering Dynamic Hydrogen Production Efficiency. Energy 2023, 16, 6132. [Google Scholar] [CrossRef]
- Li, Z.; Liu, Y.; Du, M.; Cheng, Y.; Shi, L. Modeling and Multi-Objective Optimization of a Stand-Alone Photovoltaic-Wind Turbine-Hydrogen-Battery Hybrid Energy System Based on Hysteresis Band. Int. J. Hydrogen Energy 2023, 48, 7959–7974. [Google Scholar] [CrossRef]
- Zhang, Y.; Sun, H.; Tan, J.; Li, Z.; Hou, W.; Guo, Y. Capacity Configuration Optimization of Multi-Energy System Integrating Wind Turbine/Photovoltaic/Hydrogen/Battery. Energy 2022, 252, 124046. [Google Scholar] [CrossRef]
- Attemene, N.S.; Agbli, K.S.; Fofana, S.; Hissel, D. Optimal Sizing of a Wind, Fuel Cell, Electrolyzer, Battery and Supercapacitor System for Off-Grid Applications. Int. J. Hydrogen Energy 2020, 45, 5512–5525. [Google Scholar] [CrossRef]
- Alili, H.; Mahmoudimehr, J. Techno-Economic Assessment of Integrating Hydrogen Energy Storage Technology with Hybrid Photovoltaic/Pumped Storage Hydropower Energy System. Energy Convers. Manag. 2023, 294, 117437. [Google Scholar] [CrossRef]
- Zheng, Y.; You, S.; Bindner, H.W.; Münster, M. Incorporating Optimal Operation Strategies into Investment Planning for Wind/Electrolyser System. CSEE J. Power Energy Syst. 2022, 8, 347–359. [Google Scholar]
- Tebibel, H. Methodology for multi-objective optimization of wind turbine/battery/electrolyzer system for decentralized clean hydrogen production using an adapted power management strategy for low wind speed conditions. Energy Convers. Manag. 2021, 238, 114125. [Google Scholar] [CrossRef]
- Su, W.; Li, Q.; Zheng, W.; Han, Y.; Yu, Z.; Bai, Z.; Han, Y. Enhancing Wind-Solar Hybrid Hydrogen Production Through Multi-State Electrolyzer Management and Complementary Energy Optimization. Energy Rep. 2024, 11, 1774–1786. [Google Scholar] [CrossRef]
- Guo, F.; Xu, G.; Wang, X.; Zhang, Y.; Xu, C.; Wang, Y. A Planning Method for Off-grid Wind-Solar Hydrogen Storage System based on 8760 Hours Production Simulation. Power Syst. Technol. 2024, 48, 2227–2235. [Google Scholar]
- Li, P.; Han, P.; Liu, S.; Zhang, J. Capacity Coordinated Optimization of Battery, Thermal and Hydrogen Storage System for Multi-energy Complementary Power System. In Proceedings of the 2023 IEEE 6th International Electrical and Energy Conference (CIEEC), Hefei, China, 12–14 May 2023. [Google Scholar]
- Ma, S.; Li, Y.; Jiang, Y.; Wu, Y.; Sha, G. The Multiobjective Control Based on Tolerance Optimization in a Multienergy System. Int. Trans. Electr. Energy Syst. 2024, 9991046. [Google Scholar] [CrossRef]
- Zhang, X.; Fan, X.; Wu, Z.; Zheng, L. Hydrogen Energy Supply Chain Cost Analysis and Suggestions. Chem. Ind. Eng. Prog. 2022, 41, 2364–2371. [Google Scholar]





| Simulation Parameter | Value | Simulation Parameter | Value |
|---|---|---|---|
| Rated power of the PVGs | 100 MW | Maximum power of AWE | 100 MW |
| Cost per kW/h of the PVGs | 0.359 ¥/kWh | Efficiency of AWE | 60% |
| Rated power of the WTGs | 100 MW | The investment cost of AWE | 1233.33 ¥/kWh |
| Cost per kW/h of the WTGs | 0.242 ¥/kWh | The hydrogen production cost of AWE | 22.425 ¥/kg |
| Rated power of the BESS | 20 MW | Energy consumption of AWE | 55.56 kWh/kg |
| Rated capacity of the BESS | 40 MWh | Operation life of AWE and PEME | 20 years |
| Cost per kW/h of the BESS | 0.7 ¥/kWh | Maximum power of PEME | 100 MW |
| Charging efficiency of the BESS | 95% | Efficiency of PEME | 90% |
| Discharging efficiency of the BESS | 92% | Investment cost coefficient of PEME | 4000 ¥/kWh |
| SOE range of the BESS | 10~90% | The hydrogen production cost of PEME | 29.903 ¥/kg |
| Initial SOE of the BESS | 50% | Energy consumption of PEME | 48.89 kWh/kg |
| Capacity of the HST | 20,000 m3 | Maximum hydrogen sales rate | 10,000 m3/h |
| SOH range of the HST | 10~90% | Hydrogen sales revenue | 50.4 ¥/kg |
| Initial SOH of the HST | 50% | Discount rate γ | 8% |
| The abandonment rate of new energy source δ1 | 5% | Initial stepper parameter Δc | 10−3 |
| Cut-off rate of load δ2 | 3% |
| Objective Function | AWE | PEME | AWE + PEME | |||
|---|---|---|---|---|---|---|
| J1 | J2 | J1 | J2 | J1 | J2 | |
| min(J1) | 450,244.91 | 1259.66 | 451,513.58 | 1033.22 | 442,790.62 | 1216.00 |
| min(J2) | 486,189.99 | 1101.03 | 478,127.59 | 905.29 | 478,127.59 | 905.29 |
| J1 | J2 | Rated Power of AWE (MW) | Rated Power of PEME (MW) | |
|---|---|---|---|---|
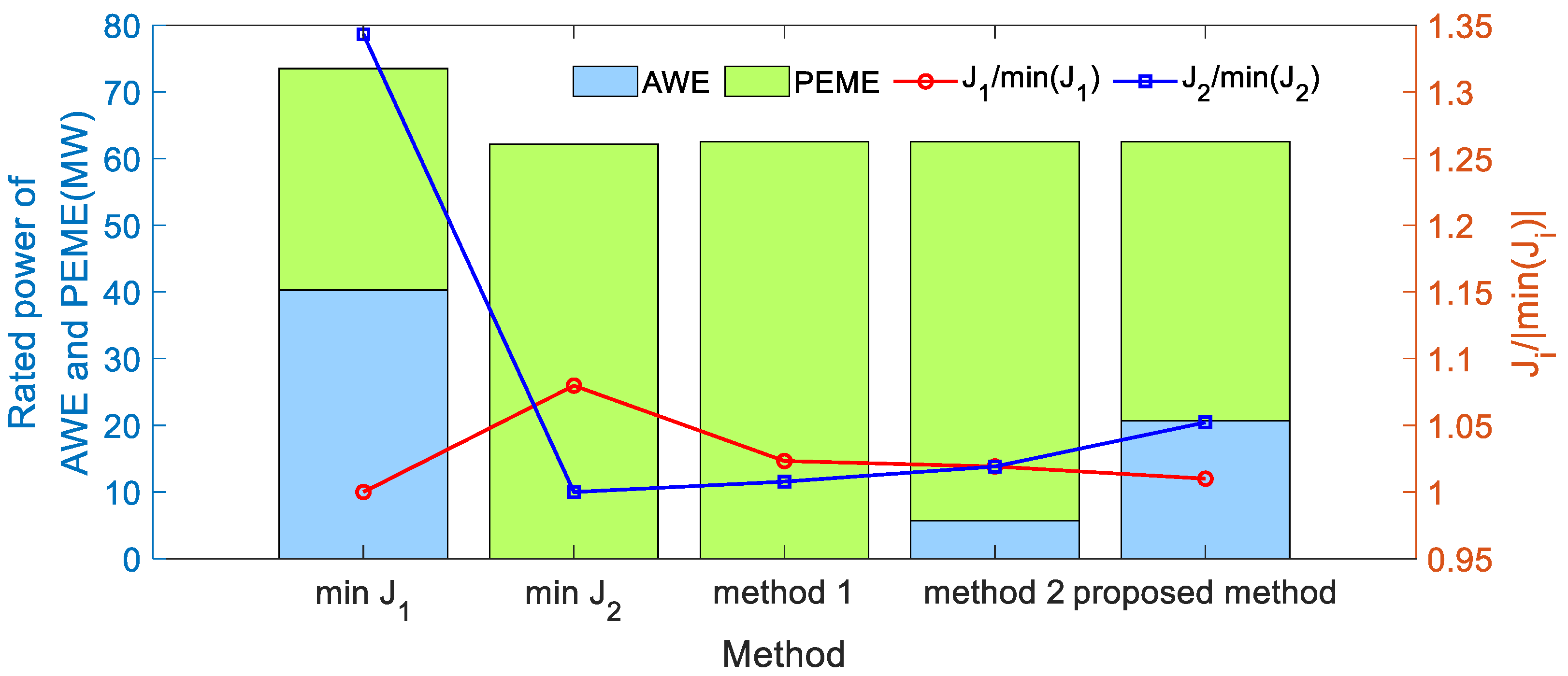
| min(J1) | 442,790.62 | 1216.00 | 40.27 | 33.23 |
| min(J2) | 478,127.59 | 905.29 | 0.00 | 62.15 |
| Method 1 | 453,097.09 | 912.35 | 0.00 | 62.51 |
| Method 2 | 451,268.28 | 922.62 | 5.70 | 56.81 |
| Proposed method | 447,218.53 | 952.56 | 18.87 | 43.64 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, S.; Meng, Z.; Mei, Y.; Chen, M.; Jiang, Y. A Multi-Optimization Method for Capacity Configuration of Hybrid Electrolyzer in a Stand-Alone Wind-Photovoltaic-Battery System. Appl. Sci. 2025, 15, 3135. https://doi.org/10.3390/app15063135
Ma S, Meng Z, Mei Y, Chen M, Jiang Y. A Multi-Optimization Method for Capacity Configuration of Hybrid Electrolyzer in a Stand-Alone Wind-Photovoltaic-Battery System. Applied Sciences. 2025; 15(6):3135. https://doi.org/10.3390/app15063135
Chicago/Turabian StyleMa, Suliang, Zeqing Meng, Yang Mei, Mingxuan Chen, and Yuan Jiang. 2025. "A Multi-Optimization Method for Capacity Configuration of Hybrid Electrolyzer in a Stand-Alone Wind-Photovoltaic-Battery System" Applied Sciences 15, no. 6: 3135. https://doi.org/10.3390/app15063135
APA StyleMa, S., Meng, Z., Mei, Y., Chen, M., & Jiang, Y. (2025). A Multi-Optimization Method for Capacity Configuration of Hybrid Electrolyzer in a Stand-Alone Wind-Photovoltaic-Battery System. Applied Sciences, 15(6), 3135. https://doi.org/10.3390/app15063135






