Deep Learning for Anomaly Detection in CNC Machine Vibration Data: A RoughLSTM-Based Approach
Abstract
:1. Introduction
2. Materials and Methods
2.1. Rough Set Theory
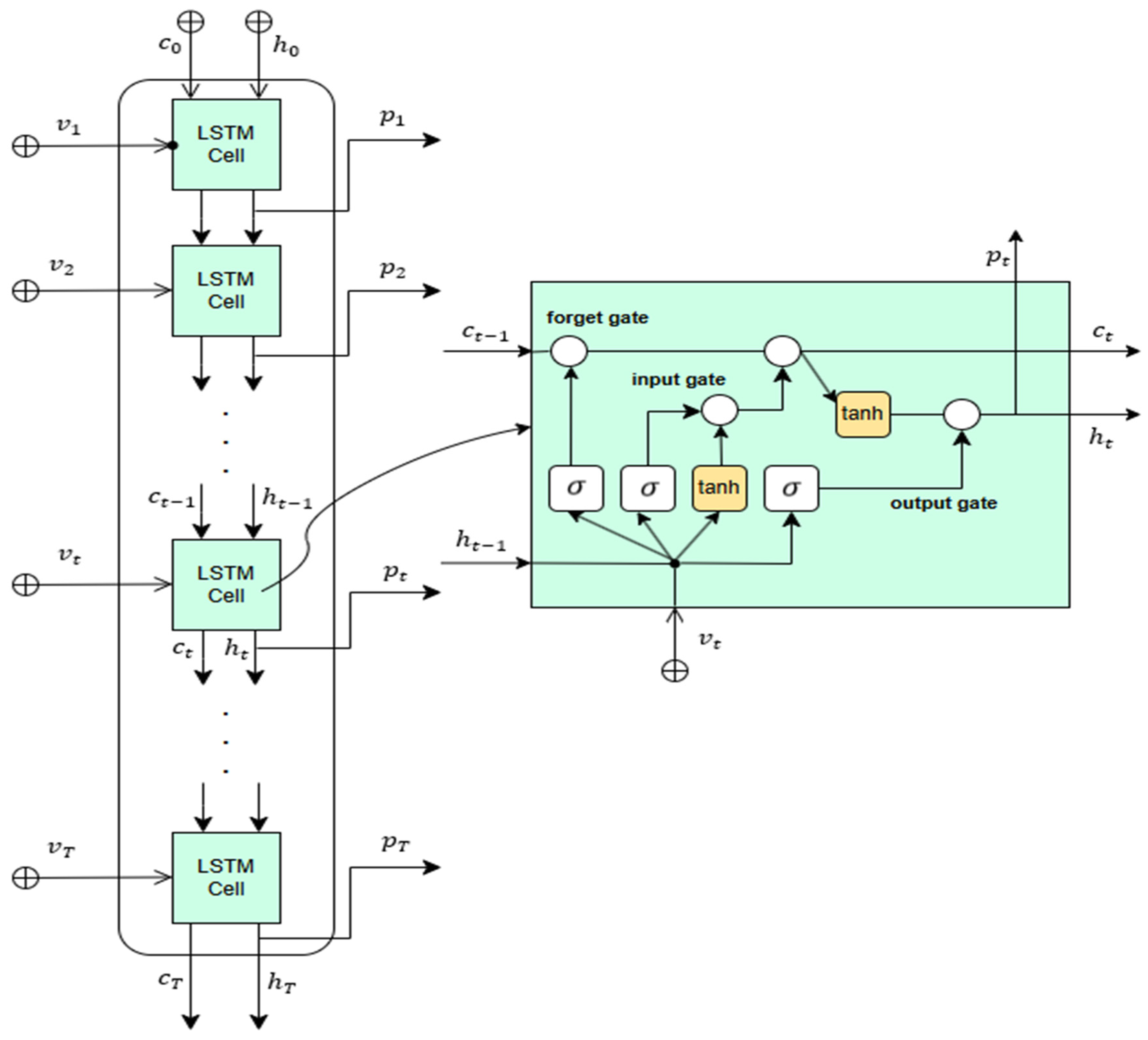
2.2. Long Short-Term Memory
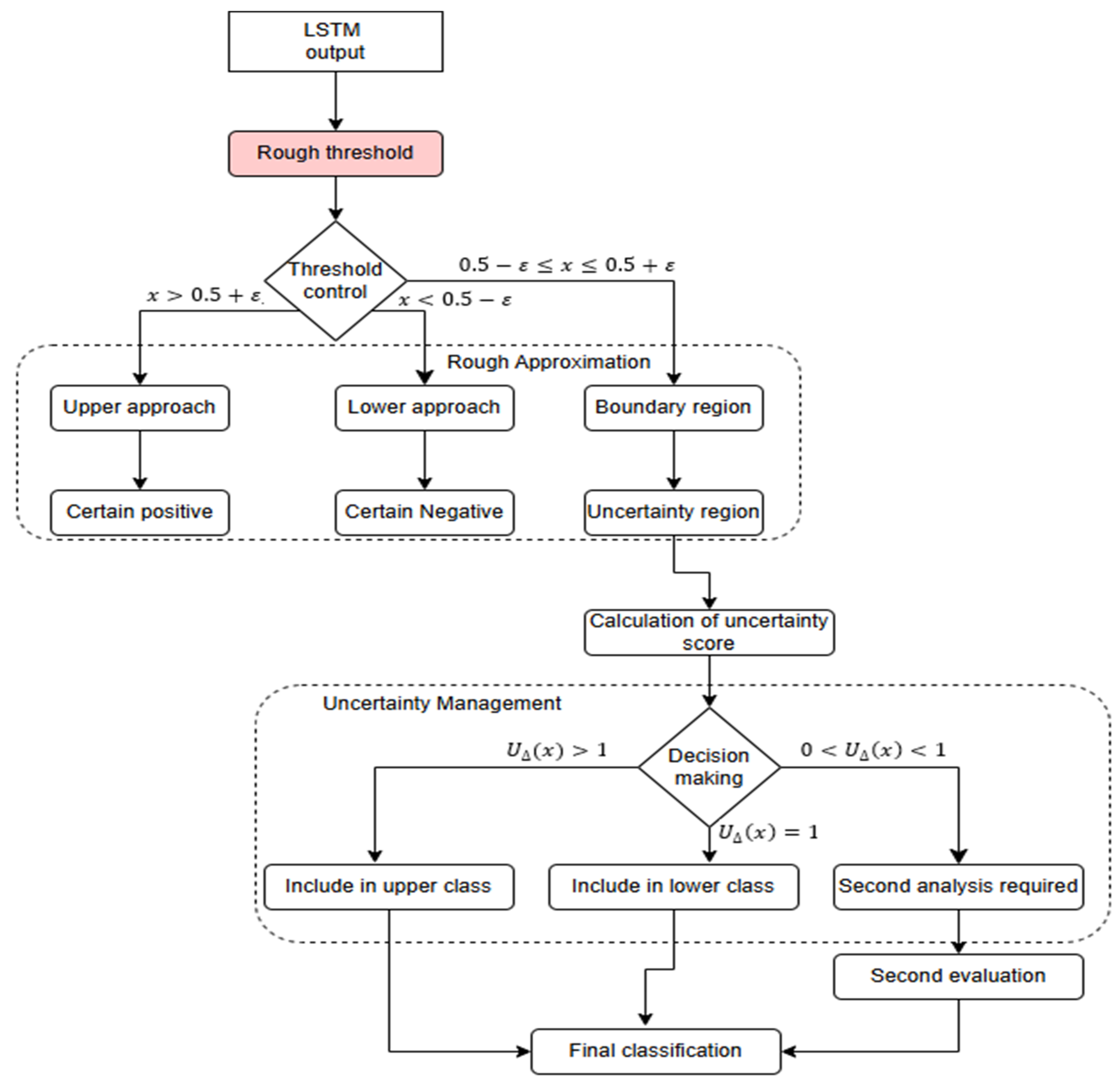
3. Proposed Model: RoughLSTM
- If , the sample is classified as an anomaly with high confidence.
- If , the sample is classified as normal with high confidence.
| Algorithm 1 RoughLSTM Pseudocode |
| 1: procedure RoughLSTM(signal, num samples, anomaly intervals) 2: Convert signal to double if necessary 3: Normalize signal |
| ▷ Windowing the Signal |
| 4: Define window size = 50, overlap = 25 5: Compute num windows 6: for i = 1 to num windows do 7: Extract window from signal 8: Check if window overlaps with any anomaly intervals 9: Label as normal (1) or anomalous (0) 10: end for |
| ▷ Rough Set Parameters |
| 11: Define ϵ = 0.1 (uncertainty threshold) 12: Generate additional noisy samples |
| ▷ Convert Data to LSTM Format |
| 13: Store augmented data 14: Convert each window to cell array format |
| ▷ Train-Test Split |
| 15: Shuffle data 16: Split into Train (70%), Validation (15%), and Test (15%) |
| ▷ Convert Labels to Categorical |
| 17: Convert 0 (Anomalous) and 1 (Normal) to categorical format |
| ▷ Define Rough-LSTM Model |
| 18: Define network layers (LSTM, Dropout, Rough Set Layer, Fully Con- nected) |
| ▷ Train the Model |
| 19: Train using Adam optimizer with 50 epochs |
| ▷ Testing and Post-processing |
| 20: Predict using trained model 21: Apply Rough Set Post-processin |
| ▷ Compute Accuracy |
| 22: Compare predictions with ground truth 23: Compute accuracy 24: return Y PredRoughLSTM, accuracyRoughLSTM 25: end procedure |
4. Experimental Results and Discussion
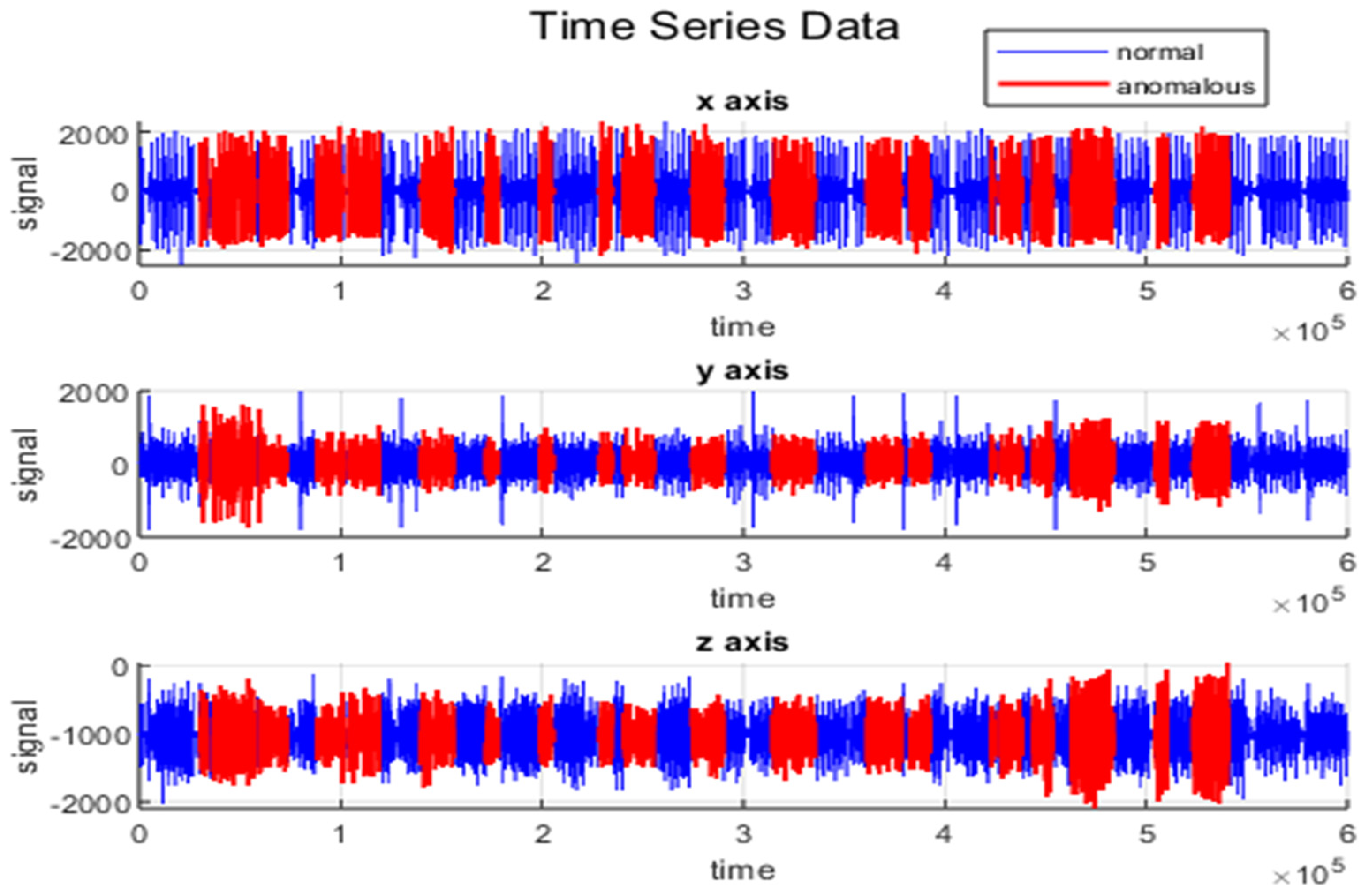
4.1. Dataset
4.2. Evaluation Metrics
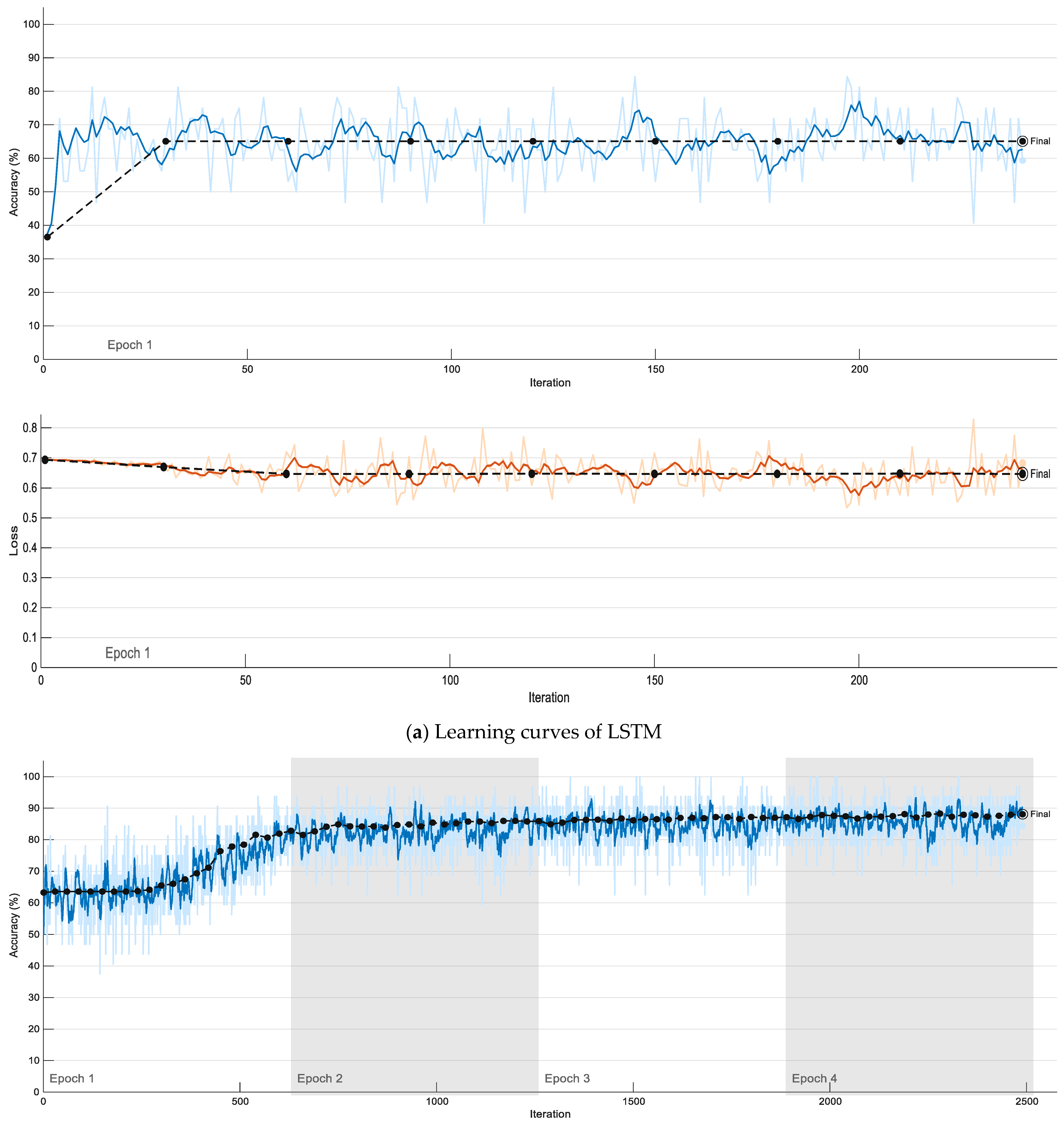
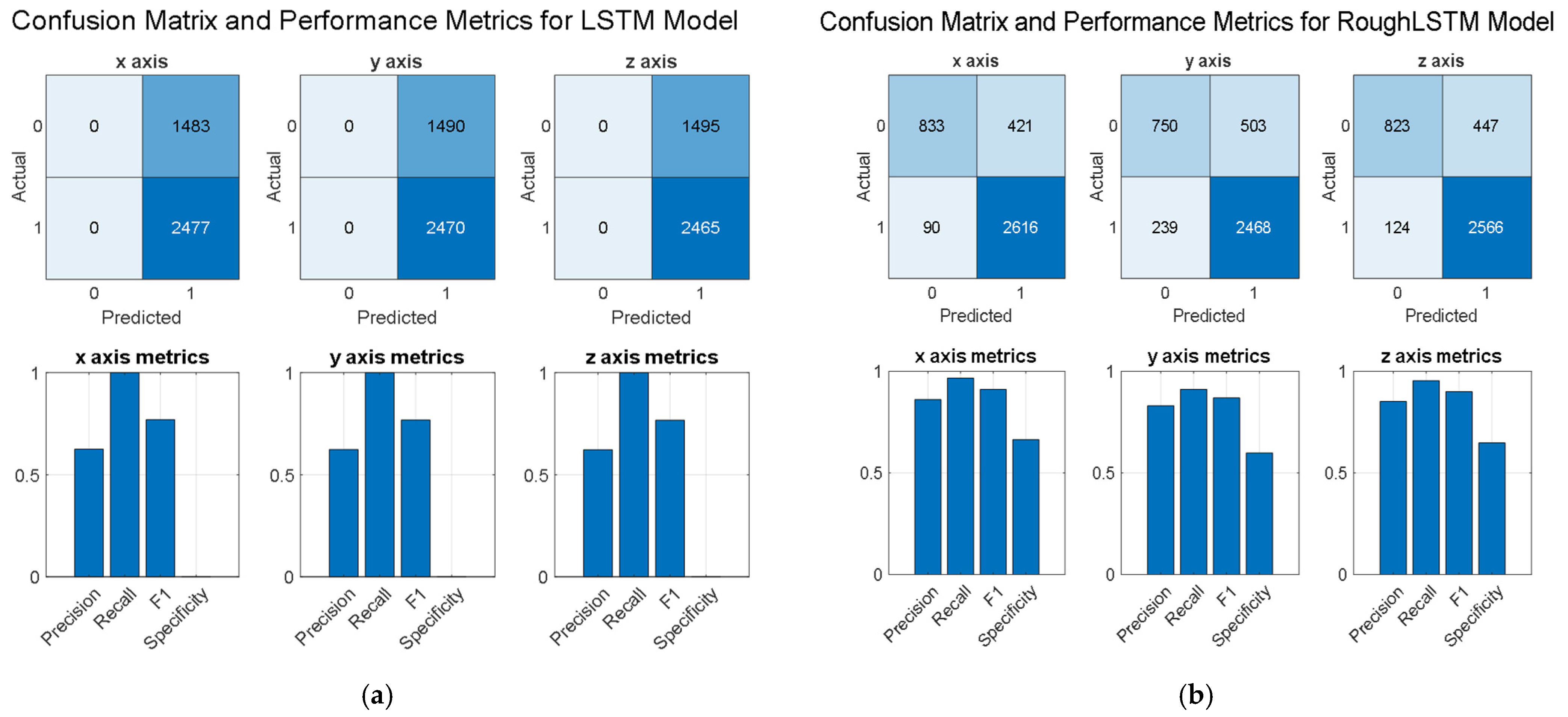
4.3. Performance Analysis
4.4. Comparative Performance Analysis
5. Conclusions
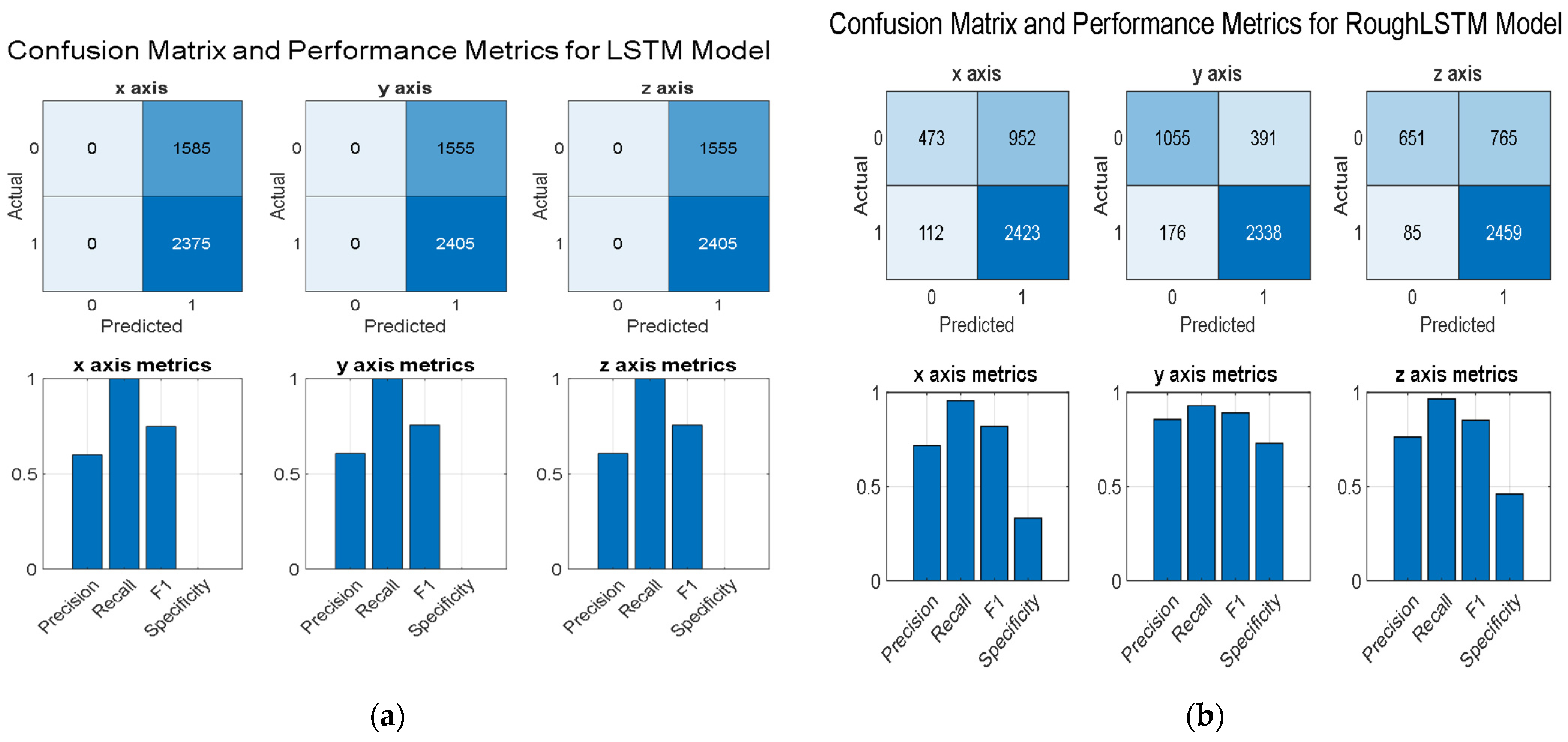
- Accuracy: RoughLSTM achieved a classification accuracy of 94.3%, compared to 78% for the conventional LSTM.
- False positive rate (FPR): RoughLSTM reduced the FPR to 3.7%, while the standard LSTM exhibited a much higher rate.
- False negative rate (FNR): The proposed model minimized the FNR to 2.0%, ensuring reliable detection of anomalies.
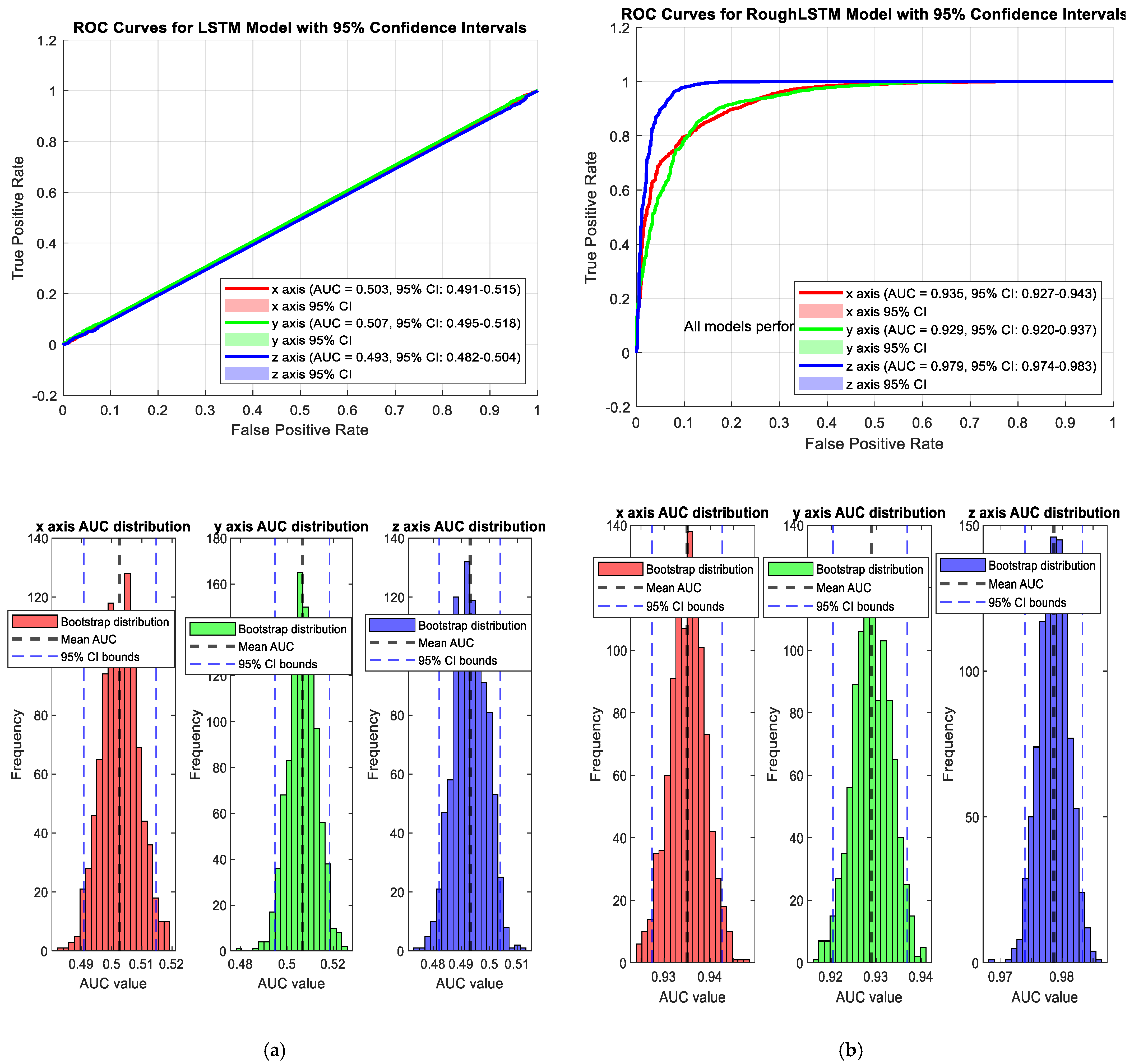
- AUC (area under the curve): RoughLSTM showed AUC values close to 0.95 across multiple operational scenarios, indicating strong classification performance.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Quatrano, A.; De Simone, M.C.; Rivera, Z.B.; Guida, D. Development and Implementation of a Control System for a Retrofitted CNC Machine by Using Arduino. FME Trans. 2017, 45, 565–571. [Google Scholar] [CrossRef]
- Lins, R.G.; Guerreiro, B.; Schmitt, R.; Sun, J.; Corazzim, M.; Silva, F.R. A Novel Methodology for Retrofitting CNC Machines Based on the Context of Industry 4.0. In Proceedings of the 2017 IEEE international systems engineering symposium (ISSE), Vienna, Austria, 11–13 October 2017; IEEE: New York, NY, USA, 2017; pp. 1–6. [Google Scholar]
- Yardımeden, A.; Turan, A. Farklı Kesme Parametreleriyle AISI 1040 Çeliğin Tornalanmasında Oluşan Titreşimlerin ve Yüzey Pürüzlülüğün Incelenmesi. Dicle Üniversitesi Mühendislik Fakültesi Mühendislik Derg. 2018, 9, 269–278. [Google Scholar]
- Nath, C. Integrated Tool Condition Monitoring Systems and Their Applications: A Comprehensive Review. Procedia Manuf. 2020, 48, 852–863. [Google Scholar] [CrossRef]
- Arriaza, O.V.; Tumurkhuyagc, Z.; Kim, D.-W. Chatter Identification Using Multiple Sensors and Multi-Layer Neural Networks. Procedia Manuf. 2018, 17, 150–157. [Google Scholar] [CrossRef]
- Yan, S.; Sun, Y. Early Chatter Detection in Thin-Walled Workpiece Milling Process Based on Multi-Synchrosqueezing Transform and Feature Selection. Mech. Syst. Signal Process. 2022, 169, 108622. [Google Scholar] [CrossRef]
- Fourlas, G.K.; Karras, G.C. A Survey on Fault Diagnosis and Fault-Tolerant Control Methods for Unmanned Aerial Vehicles. Machines 2021, 9, 197. [Google Scholar] [CrossRef]
- Park, J.; Jung, Y.; Kim, J.-H. Multiclass Classification Fault Diagnosis of Multirotor UAVs Utilizing a Deep Neural Network. Int. J. Control. Autom. Syst. 2022, 20, 1316–1326. [Google Scholar] [CrossRef]
- Zhang, X.; Zhao, Z.; Wang, Z.; Wang, X. Fault Detection and Identification Method for Quadcopter Based on Airframe Vibration Signals. Sensors 2021, 21, 581. [Google Scholar] [CrossRef]
- Altinors, A.; Yol, F.; Yaman, O. A Sound Based Method for Fault Detection with Statistical Feature Extraction in UAV Motors. Appl. Acoust. 2021, 183, 108325. [Google Scholar] [CrossRef]
- Han, Y.; Qi, Z.; Tian, Y. Anomaly Classification Based on Self-Supervised Learning and Its Application. J. Radiat. Res. Appl. Sci. 2024, 17, 100918. [Google Scholar] [CrossRef]
- Darban, Z.Z.; Webb, G.I.; Pan, S.; Aggarwal, C.C.; Salehi, M. CARLA: Self-Supervised Contrastive Representation Learning for Time Series Anomaly Detection. Pattern Recognit. 2025, 157, 110874. [Google Scholar] [CrossRef]
- Fatemifar, S.; Awais, M.; Akbari, A.; Kittler, J. Pure Anomaly Detection via Self-Supervised Deep Metric Learning with Adaptive Margin. Neurocomputing 2025, 611, 128659. [Google Scholar] [CrossRef]
- Han, H.; Fan, H.; Huang, X.; Han, C. Self-Supervised Multi-Transformation Learning for Time Series Anomaly Detection. Expert. Syst. Appl. 2024, 253, 124339. [Google Scholar] [CrossRef]
- Choubey, M.; Chaurasiya, R.K.; Yadav, J.S. Contrastive Learning for Efficient Anomaly Detection in Electricity Load Data. Sustain. Energy Grids Netw. 2025, 42, 101639. [Google Scholar] [CrossRef]
- Fadi, O.; Bahaj, A.; Zkik, K.; El Ghazi, A.; Ghogho, M.; Boulmalf, M. Smart Contract Anomaly Detection: The Contrastive Learning Paradigm. Comput. Netw. 2025, 260, 111121. [Google Scholar] [CrossRef]
- Chi, J.; Mao, Z. One-Classification Anomaly Detection: Utilizing Contrastive Transfer Learning. Measurement 2025, 242, 116173. [Google Scholar] [CrossRef]
- Xiao, B.W.; Xing, H.J.; Li, C.G. MulGad: Multi-Granularity Contrastive Learning for Multivariate Time Series Anomaly Detection. Inf. Fusion. 2025, 119, 103008. [Google Scholar] [CrossRef]
- Kang, H.; Kang, P. Transformer-Based Multivariate Time Series Anomaly Detection Using Inter-Variable Attention Mechanism. Knowl. Based Syst. 2024, 290, 111507. [Google Scholar] [CrossRef]
- Gao, R.; Wang, J.; Yu, Y.; Wu, J.; Zhang, L. Enhanced Graph Diffusion Learning with Dynamic Transformer for Anomaly Detection in Multivariate Time Series. Neurocomputing 2025, 619, 129168. [Google Scholar] [CrossRef]
- Sui, L.; Jiang, Y. Argo Data Anomaly Detection Based on Transformer and Fourier Transform. J. Sea Res. 2024, 198, 102483. [Google Scholar] [CrossRef]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep Learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef] [PubMed]
- Glaeser, A.; Selvaraj, V.; Lee, S.; Hwang, Y.; Lee, K.; Lee, N.; Lee, S.; Min, S. Applications of Deep Learning for Fault Detection in Industrial Cold Forging. Int. J. Prod. Res. 2021, 59, 4826–4835. [Google Scholar] [CrossRef]
- Glowacz, A.; Glowacz, W.; Kozik, J.; Piech, K.; Gutten, M.; Caesarendra, W.; Liu, H.; Brumercik, F.; Irfan, M.; Khan, Z.F. Detection of Deterioration of Three-Phase Induction Motor Using Vibration Signals. Meas. Sci. Rev. 2019, 19, 241–249. [Google Scholar] [CrossRef]
- Ruiz, M.; Mujica, L.E.; Alférez, S.; Acho, L.; Tutivén, C.; Vidal, Y.; Rodellar, J.; Pozo, F. Wind Turbine Fault Detection and Classification by Means of Image Texture Analysis. Mech. Syst. Signal Process. 2018, 107, 149–167. [Google Scholar] [CrossRef]
- Kounta, C.A.K.A.; Arnaud, L.; Kamsu-Foguem, B.; Tangara, F. Deep Learning for the Detection of Machining Vibration Chatter. Adv. Eng. Softw. 2023, 180, 103445. [Google Scholar] [CrossRef]
- Ozkat, E.C. Vibration Data-Driven Anomaly Detection in UAVs: A Deep Learning Approach. Eng. Sci. Technol. Int. J. 2024, 54, 101702. [Google Scholar] [CrossRef]
- Zhao, R.; Yan, R.; Chen, Z.; Mao, K.; Wang, P.; Gao, R.X. Deep Learning and Its Applications to Machine Health Monitoring. Mech. Syst. Signal Process. 2019, 115, 213–237. [Google Scholar] [CrossRef]
- Jang, D.; Jung, J.; Seok, J. Modeling and Parameter Optimization for Cutting Energy Reduction in MQL Milling Process. Int. J. Precis. Eng. Manuf.-Green. Technol. 2016, 3, 5–12. [Google Scholar] [CrossRef]
- Aydın, M.; Karakuzu, C.; Uçar, M.; Cengiz, A.; Çavuşlu, M.A. Prediction of Surface Roughness and Cutting Zone Temperature in Dry Turning Processes of AISI304 Stainless Steel Using ANFIS with PSO Learning. Int. J. Adv. Manuf. Technol. 2013, 67, 957–967. [Google Scholar] [CrossRef]
- Zuperl, U.; Cus, F.; Mursec, B.; Ploj, T. A Generalized Neural Network Model of Ball-End Milling Force System. J. Mater. Process. Technol. 2006, 175, 98–108. [Google Scholar] [CrossRef]
- Liao, Y.; Ragai, I.; Huang, Z.; Kerner, S. Manufacturing Process Monitoring Using Time-Frequency Representation and Transfer Learning of Deep Neural Networks. J. Manuf. Process. 2021, 68, 231–248. [Google Scholar] [CrossRef]
- Ismail Fawaz, H.; Lucas, B.; Forestier, G.; Pelletier, C.; Schmidt, D.F.; Weber, J.; Webb, G.I.; Idoumghar, L.; Muller, P.-A.; Petitjean, F. Inceptiontime: Finding Alexnet for Time Series Classification. Data Min. Knowl. Discov. 2020, 34, 1936–1962. [Google Scholar] [CrossRef]
- Sener, B.; Gudelek, M.U.; Ozbayoglu, A.M.; Unver, H.O. A Novel Chatter Detection Method for Milling Using Deep Convolution Neural Networks. Measurement 2021, 182, 109689. [Google Scholar] [CrossRef]
- Tran, M.-Q.; Liu, M.-K.; Tran, Q.-V. Milling Chatter Detection Using Scalogram and Deep Convolutional Neural Network. Int. J. Adv. Manuf. Technol. 2020, 107, 1505–1516. [Google Scholar] [CrossRef]
- Shi, F.; Cao, H.; Wang, Y.; Feng, B.; Ding, Y. Chatter Detection in High-Speed Milling Processes Based on ON-LSTM and PBT. Int. J. Adv. Manuf. Technol. 2020, 111, 3361–3378. [Google Scholar] [CrossRef]
- Vashisht, R.K.; Peng, Q. Online Chatter Detection for Milling Operations Using LSTM Neural Networks Assisted by Motor Current Signals of Ball Screw Drives. J. Manuf. Sci. Eng. 2021, 143, 011008. [Google Scholar] [CrossRef]
- Cui, Z.; Chen, W.; Chen, Y. Multi-Scale Convolutional Neural Networks for Time Series Classification. arXiv 2016, arXiv:1603.06995. [Google Scholar]
- Wang, Z.; Yan, W.; Oates, T. Time Series Classification from Scratch with Deep Neural Networks: A Strong Baseline. In Proceedings of the 2017 International Joint Conference on Neural Networks (IJCNN), Anchorage, AK, USA, 14–19 May 2017; IEEE: New York, NY, USA, 2017; pp. 1578–1585. [Google Scholar]
- Barzegar, R.; Aalami, M.T.; Adamowski, J. Short-Term Water Quality Variable Prediction Using a Hybrid CNN–LSTM Deep Learning Model. Stoch. Environ. Res. Risk Assess. 2020, 34, 415–433. [Google Scholar] [CrossRef]
- Su, S.; Zhao, G.; Xiao, W.; Yang, Y.; Cao, X. An Image-Based Approach to Predict Instantaneous Cutting Forces Using Convolutional Neural Networks in End Milling Operation. Int. J. Adv. Manuf. Technol. 2021, 115, 1657–1669. [Google Scholar] [CrossRef]
- Vaishnav, S.; Agarwal, A.; Desai, K.A. Machine Learning-Based Instantaneous Cutting Force Model for End Milling Operation. J. Intell. Manuf. 2020, 31, 1353–1366. [Google Scholar] [CrossRef]
- Qin, C.; Shi, G.; Tao, J.; Yu, H.; Jin, Y.; Lei, J.; Liu, C. Precise Cutterhead Torque Prediction for Shield Tunneling Machines Using a Novel Hybrid Deep Neural Network. Mech. Syst. Signal Process. 2021, 151, 107386. [Google Scholar] [CrossRef]
- Fu, S.; Wang, L.; Wang, D.; Li, X.; Zhang, P. Accurate Prediction and Compensation of Machining Error for Large Components with Time-Varying Characteristics Combining Physical Model and Double Deep Neural Networks. J. Manuf. Process. 2023, 99, 527–547. [Google Scholar] [CrossRef]
- Karim, F.; Majumdar, S.; Darabi, H.; Chen, S. LSTM Fully Convolutional Networks for Time Series Classification. IEEE Access 2017, 6, 1662–1669. [Google Scholar] [CrossRef]
- Li, B.; Liu, T.; Liao, J.; Feng, C.; Yao, L.; Zhang, J. Non-Invasive Milling Force Monitoring through Spindle Vibration with LSTM and DNN in CNC Machine Tools. Measurement 2023, 210, 112554. [Google Scholar] [CrossRef]
- Bai, Y.; Xie, J.; Wang, D.; Zhang, W.; Li, C. A Manufacturing Quality Prediction Model Based on AdaBoost-LSTM with Rough Knowledge. Comput. Ind. Eng. 2021, 155, 107227. [Google Scholar] [CrossRef]
- Liu, Z.; Zhang, D.; Jia, W.; Lin, X.; Liu, H. An Adversarial Bidirectional Serial–Parallel LSTM-Based QTD Framework for Product Quality Prediction. J. Intell. Manuf. 2020, 31, 1511–1529. [Google Scholar] [CrossRef]
- Zhou, J.-T.; Zhao, X.; Gao, J. Tool Remaining Useful Life Prediction Method Based on LSTM under Variable Working Conditions. Int. J. Adv. Manuf. Technol. 2019, 104, 4715–4726. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, J.; Wang, X. Bilateral LSTM: A Two-Dimensional Long Short-Term Memory Model with Multiply Memory Units for Short-Term Cycle Time Forecasting in Re-Entrant Manufacturing Systems. IEEE Trans. Ind. Inform. 2017, 14, 748–758. [Google Scholar] [CrossRef]
- Zhang, Q.; Xie, Q.; Wang, G. A Survey on Rough Set Theory and Its Applications. CAAI Trans. Intell. Technol. 2016, 1, 323–333. [Google Scholar] [CrossRef]
- Cekik, R.; Telceken, S. A New Classification Method Based on Rough Sets Theory. Soft Comput. 2018, 22, 1881–1889. [Google Scholar] [CrossRef]
- Pawlak, Z. Rough Set Theory and Its Applications to Data Analysis. Cybern. Syst. 1998, 29, 661–688. [Google Scholar] [CrossRef]
- Demirkiran, E.T.; Pak, M.Y.; Çekik, R. Multi-Criteria Collaborative Filtering Using Rough Sets Theory. J. Intell. Fuzzy Syst. 2021, 40, 907–917. [Google Scholar] [CrossRef]
- Staudemeyer, R.C.; Morris, E.R. Understanding LSTM--a Tutorial into Long Short-Term Memory Recurrent Neural Networks. arXiv 2019, arXiv:1909.09586. [Google Scholar]
- Lindemann, B.; Maschler, B.; Sahlab, N.; Weyrich, M. A Survey on Anomaly Detection for Technical Systems Using LSTM Networks. Comput. Ind. 2021, 131, 103498. [Google Scholar] [CrossRef]
- Tnani, M.-A.; Feil, M.; Diepold, K. Smart Data Collection System for Brownfield CNC Milling Machines: A New Benchmark Dataset for Data-Driven Machine Monitoring. Procedia CIRP 2022, 107, 131–136. [Google Scholar] [CrossRef]
- Çekik, R.; Kaya, M. A New Performance Metric to Evaluate Filter Feature Selection Methods in Text Classification. J. Univers. Comput. Sci. 2024, 30, 978. [Google Scholar] [CrossRef]


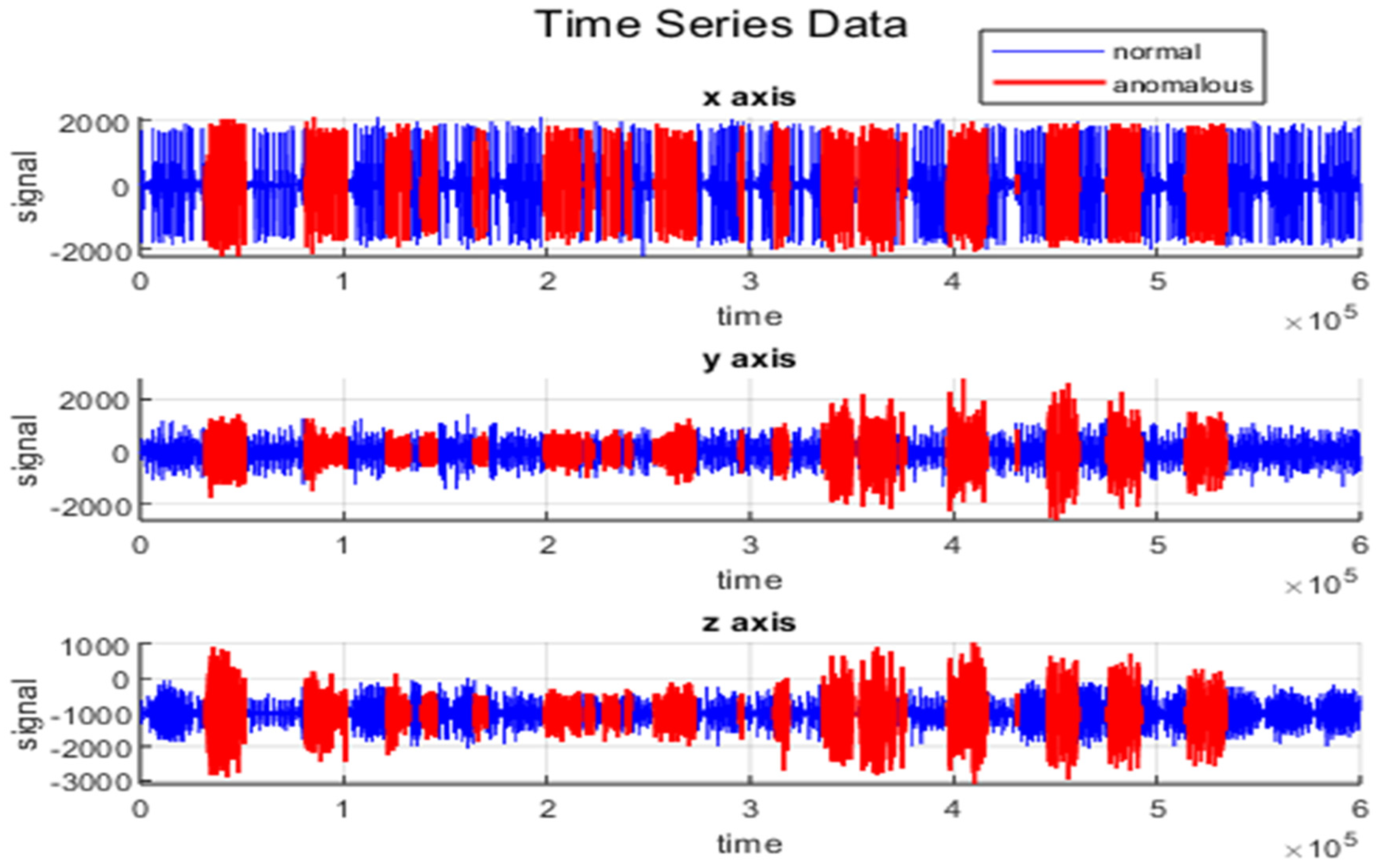


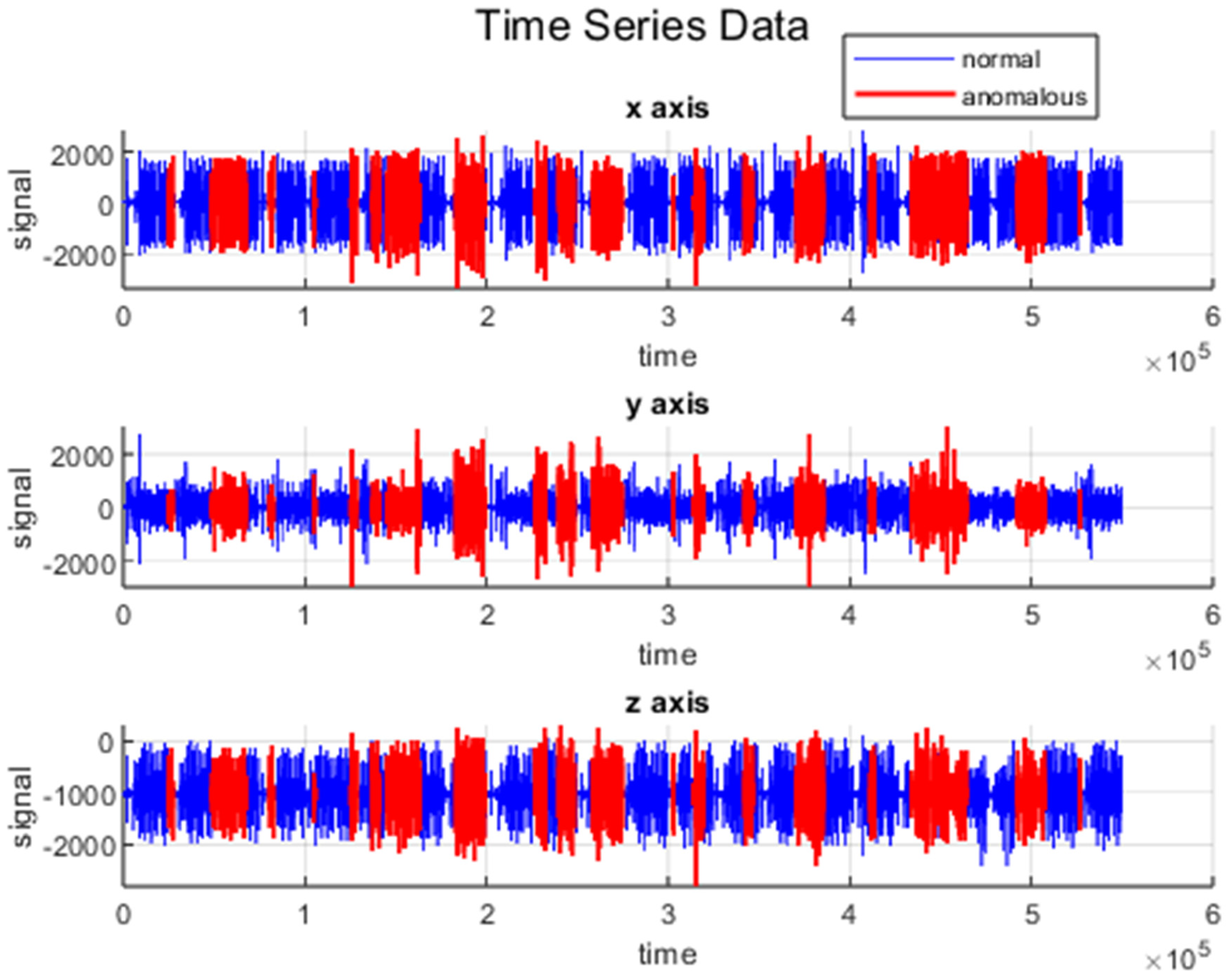

| Tool Operation | Description | Speed (RPM) | Feed (mm/s) | Duration (s) |
|---|---|---|---|---|
| OP00 | Step drill | 250 | ≈100 | ≈132 |
| OP01 | Step drill | 250 | ≈100 | ≈29 |
| OP02 | Drill | 200 | ≈50 | ≈42 |
| OP03 | Step drill | 250 | ≈330 | ≈77 |
| OP04 | Step drill | 250 | ≈100 | ≈64 |
| OP05 | Step drill | 200 | ≈50 | ≈18 |
| OP06 | Step drill | 250 | ≈50 | ≈91 |
| OP07 | Step drill | 200 | ≈50 | ≈24 |
| OP08 | Step drill | 250 | ≈50 | ≈37 |
| OP09 | Straight flute | 250 | ≈50 | ≈102 |
| OP10 | Step drill | 250 | ≈50 | ≈45 |
| OP11 | Step drill | 250 | ≈50 | ≈59 |
| OP12 | Step drill | 250 | ≈50 | ≈46 |
| OP13 | T-slot cutter | 75 | ≈25 | ≈32 |
| OP14 | Step drill | 250 | ≈100 | ≈34 |
| Actual Positive (1) | Actual Negative (0) | |
|---|---|---|
| Predicted Positive (1) | True Positive (TP) | False Positive (FP) |
| Predicted Negative (0) | False Negative (FN) | True Negative (TN) |
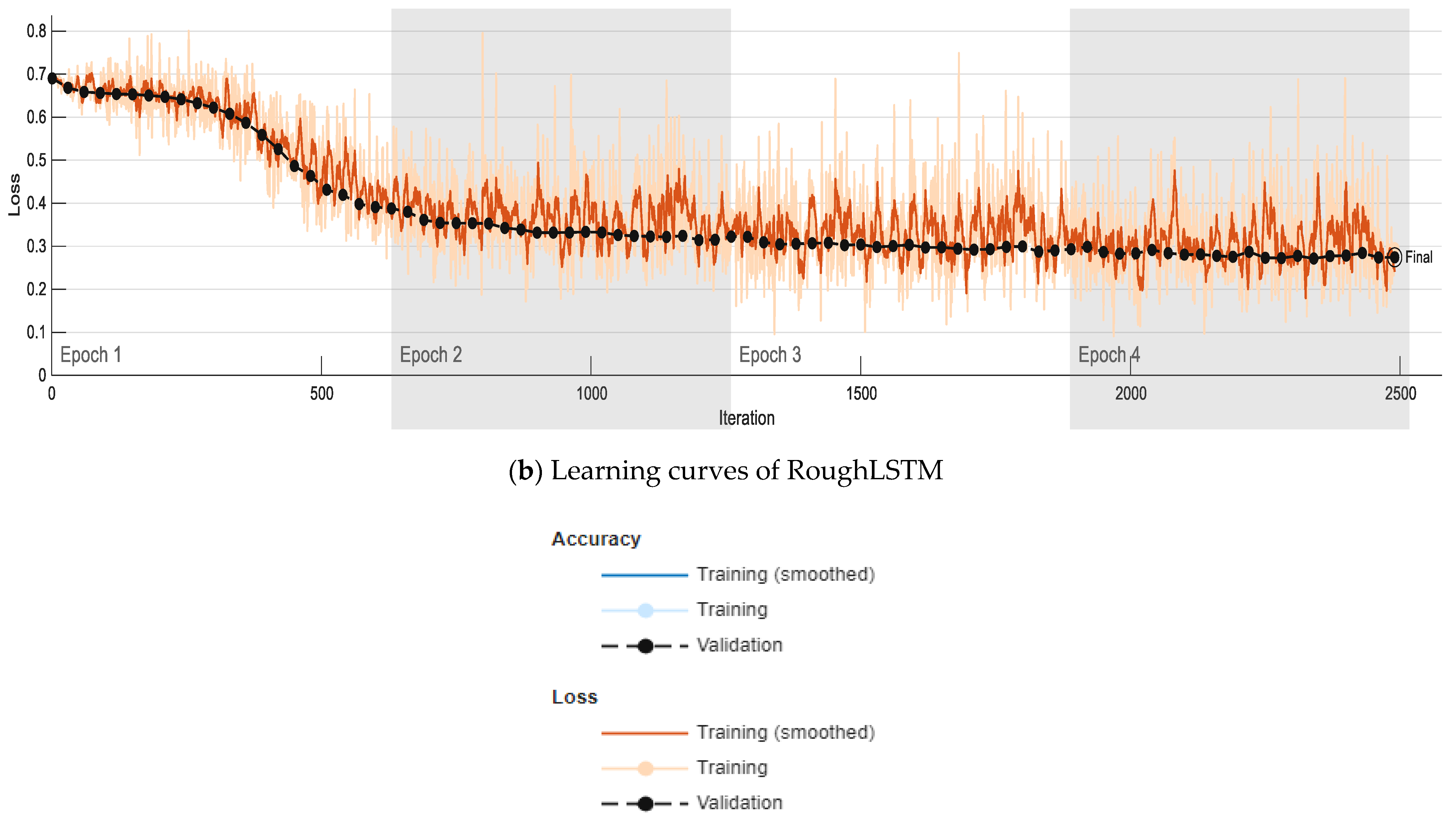
| Model | Average Training Accuracy | Average Validation Accuracy | Average Training Loss | Average Validation Loss | Standard Deviation of Accuracy | Standard Deviation of Loss |
|---|---|---|---|---|---|---|
| LSTM | ~%85 | ~%78 | ~0.35 | ~0.42 | 4.2 | 3.8 |
| RoughLSTM | ~%89 | ~%84 | ~0.28 | ~0.34 | 2.1 | 2.0 |
| (a) | |||||||
|---|---|---|---|---|---|---|---|
| AUC | AUC 95%CI | F1-Score | Precision | Recall | Specificity | Std (AUC) | |
| x axis | 0.503 | 0.491–0.515 | 0.731 | 0.576 | 1.000 | 0.000 | 0.006 |
| y axis | 0.507 | 0.495–0.518 | 0.732 | 0.577 | 1.000 | 0.000 | 0.006 |
| z axis | 0.493 | 0.482–0.504 | 0.733 | 0.578 | 1.000 | 0.000 | 0.006 |
| (b) | |||||||
| x axis | 0.935 | 0.927–0.943 | 0.852 | 0.800 | 0.911 | 0.676 | 0.004 |
| y axis | 0.929 | 0.920–0.937 | 0.860 | 0.822 | 0.902 | 0.722 | 0.004 |
| z axis | 0.979 | 0.974–0.983 | 0.942 | 0.928 | 0.956 | 0.894 | 0.002 |
| (a) | |||||||
|---|---|---|---|---|---|---|---|
| AUC | AUC 95%CI | F1-Score | Precision | Recall | Specificity | Std (AUC) | |
| x axis | 0.4950 | 0.483–0.507 | 0.751 | 0.600 | 1.000 | 0.000 | 0.006 |
| y axis | 0.4930 | 0.480–0.505 | 0.756 | 0.607 | 1.000 | 0.000 | 0.006 |
| z axis | 0.4930 | 0.480–0.505 | 0.756 | 0.607 | 1.000 | 0.000 | 0.006 |
| (b) | |||||||
| x axis | 0.8450 | 0.833–0.857 | 0.8200 | 0.8200 | 0.9560 | 0.3320 | 0.006 |
| y axis | 0.9520 | 0.946–0.958 | 0.8920 | 0.8570 | 0.9300 | 0.7300 | 0.003 |
| z axis | 0.8950 | 0.885–0.906 | 0.8530 | 0.7630 | 0.9670 | 0.4600 | 0.005 |
| (a) | |||||||
|---|---|---|---|---|---|---|---|
| AUC | AUC 95%CI | F1-Score | Precision | Recall | Specificity | Std (AUC) | |
| x axis | 0.512 | 0.500–0.524 | 0.770 | 0.626 | 1.000 | 0.000 | 0.006 |
| y axis | 0.489 | 0.477–0.501 | 0.766 | 0.624 | 1.000 | 0.000 | 0.006 |
| z axis | 0.495 | 0.483–0.508 | 0.767 | 0.622 | 1.000 | 0.000 | 0.006 |
| (b) | |||||||
| x axis | 0.943 | 0.933–0.951 | 0.911 | 0.861 | 0.967 | 0.664 | 0.006 |
| y axis | 0.918 | 0.908–0.927 | 0.869 | 0.831 | 0.912 | 0.599 | 0.003 |
| z axis | 0.912 | 0.901–0.923 | 0.900 | 0.852 | 0.954 | 0.648 | 0.005 |
| M01 | M02 | M03 | ||||
|---|---|---|---|---|---|---|
| OP02+OP05+OP08+OP11+OP14 | OP00+OP01+OP04+OP07+OP09 | OP01+OP02+OP04+OP07+OP10 | ||||
| LSTM | RoughLSTM | LSTM | RoughLSTM | LSTM | RoughLSTM | |
| x-axis | 0.65903 | 0.83079 | 0.61505 | 0.73056 | 0.68662 | 0.88712 |
| y-axis | 0.66319 | 0.84977 | 0.62014 | 0.86134 | 0.68182 | 0.83232 |
| z-axis | 0.66319 | 0.89722 | 0.61597 | 0.78727 | 0.69268 | 0.85126 |
| Operations | Axis | CNN–LSTM | WaveletLSTMa | LSTM | RoughLSTM |
|---|---|---|---|---|---|
| OP01+OP02 | x-axis | 0.7983 | 0.8283 | 0.7056 | 0.8425 |
| y-axis | 0.8400 | 0.8200 | 0.7069 | 0.8312 | |
| z-axis | 0.8100 | 0.8017 | 0.7153 | 0.8245 | |
| OP04+OP10 | x-axis | 0.7867 | 0.7167 | 0.5625 | 0.7633 |
| y-axis | 0.8100 | 0.8014 | 0.5417 | 0.8250 | |
| z-axis | 0.8183 | 0.8028 | 0.5417 | 0.8367 | |
| OP06+OP13 | x-axis | 0.8944 | 0.9200 | 0.7218 | 0.9150 |
| y-axis | 0.8736 | 0.9033 | 0.7139 | 0.8883 | |
| z-axis | 0.9183 | 0.9217 | 0.7312 | 0.9236 |
| Operations | Axis | CNN–LSTM | WaveletLSTMa | LSTM | RoughLSTM |
|---|---|---|---|---|---|
| OP02+OP08 | x-axis | 0.9400 | 0.9383 | 0.8694 | 0.9194 |
| y-axis | 0.9350 | 0.9233 | 0.8279 | 0.9389 | |
| z-axis | 0.9500 | 0.9350 | 0.8912 | 0.9514 | |
| OP04+OP09 | x-axis | 0.6783 | 0.6833 | 0.7194 | 0.7181 |
| y-axis | 0.7783 | 0.7900 | 0.7019 | 0.8028 | |
| z-axis | 0.8283 | 0.8400 | 0.7436 | 0.7972 | |
| OP07+OP11 | x-axis | 0.9317 | 0.9317 | 0.7994 | 0.9319 |
| y-axis | 0.9217 | 0.9200 | 0.8126 | 0.9347 | |
| z-axis | 0.9300 | 0.9500 | 0.8302 | 0.9542 |
| Operations | Axis | CNN–LSTM | WaveletLSTMa | LSTM | RoughLSTM |
|---|---|---|---|---|---|
| OP01+OP02 | x-axis | 0.8567 | 0.7542 | 0.7294 | 0.7792 |
| y-axis | 0.7883 | 0.8233 | 0.7305 | 0.7883 | |
| z-axis | 0.7736 | 0.7817 | 0.7128 | 0.7950 | |
| OP04+OP07 | x-axis | 0.8347 | 0.8433 | 0.7815 | 0.8750 |
| y-axis | 0.7917 | 0.8167 | 0.7664 | 0.7833 | |
| z-axis | 0.8097 | 0.8133 | 0.7700 | 0.8233 | |
| OP010+OP14 | x-axis | 0.8350 | 0.8233 | 0.7194 | 0.7181 |
| y-axis | 0.8433 | 0.8733 | 0.7678 | 0.8792 | |
| z-axis | 0.8517 | 0.8400 | 0.7408 | 0.7986 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Çekik, R.; Turan, A. Deep Learning for Anomaly Detection in CNC Machine Vibration Data: A RoughLSTM-Based Approach. Appl. Sci. 2025, 15, 3179. https://doi.org/10.3390/app15063179
Çekik R, Turan A. Deep Learning for Anomaly Detection in CNC Machine Vibration Data: A RoughLSTM-Based Approach. Applied Sciences. 2025; 15(6):3179. https://doi.org/10.3390/app15063179
Chicago/Turabian StyleÇekik, Rasım, and Abdullah Turan. 2025. "Deep Learning for Anomaly Detection in CNC Machine Vibration Data: A RoughLSTM-Based Approach" Applied Sciences 15, no. 6: 3179. https://doi.org/10.3390/app15063179
APA StyleÇekik, R., & Turan, A. (2025). Deep Learning for Anomaly Detection in CNC Machine Vibration Data: A RoughLSTM-Based Approach. Applied Sciences, 15(6), 3179. https://doi.org/10.3390/app15063179






