Abstract
Packaging design plays a crucial role in ensuring the protective performance of packages. Various factors must be considered to ensure package strength during the packaging design process. Understanding the relative importance of each influencing factor or design feature provides valuable insights for optimizing packaging designs. However, traditional methods such as testing and numerical analysis have limitations in evaluating the relative significance of these parameters. To address this challenge, this work applied four distinct Artificial Neural Network (ANN)-based approaches, including connection weights, gradient-based, permutation, and Shapley additive explanations (SHAP) values, to explore the relative importance of different packaging design features on a given packaging property. In this study, box compression strength (BCS) was used as a representative packaging property, and the relative importance of up to six BCS features (edge crush test (ECT), perimeter, thickness, depth, and flexural stiffness in both the machine and cross-machine directions) were evaluated. The findings of this study demonstrate the effectiveness of artificial neural network (ANN)-based approaches in evaluating the relative importance of packaging design features. This approach can be readily applied to assess other packaging design features’ importance beyond the studied features with significant potential for cost savings and material reduction in packaging design.
1. Introduction
Packaging design plays a vital role in ensuring packaging performance. Effective design can reduce costs by minimizing material usage and waste while protecting products during transportation, storage, and handling. To improve packaging performance, the design process must consider various influencing factors, each of which impacts specific packaging properties differently. Understanding the relative importance of these influencing factors for packaging design, or packaging design features, is crucial for enhancing packaging performance and maximizing cost savings.
The evaluation of packaging parameters (e.g., material properties, box dimensions, environmental conditions) influencing a specific packaging property still primarily relies on physical testing. However, physical testing has several drawbacks, especially considering the numerous factors involved in packaging design. One major issue is that it is time-consuming and costly, as it requires extensive material use and repetitive testing. Additionally, it is destructive, meaning that physical tests damage samples, making large-scale evaluations expensive. Moreover, the generalization of physical testing is limited due to the variability in board quality, adhesives, and other factors, which can lead to inconsistencies in the results. Several new methods for assessing the importance of packaging design features have emerged in recent years. Techniques such as analytical hierarchy process (AHP) [1,2] and finite element analysis (FEA) [3,4,5] have been developed to optimize different packaging systems. However, these methods are not consistently applied or fully integrated into industry practices. For instance, a primary disadvantage of AHP is expert subjectivity [6]. AHP relies on expert input for pairwise comparisons between options, where experts evaluate the relative importance or performance of one option over another. These judgments, being influenced by personal opinions, can introduce subjectivity [1]. On the other hand, FEA requires material properties that are challenging to obtain due to the anisotropic and non-linear mechanical behavior exhibited by paper fibrous material [7,8]. Additionally, there are limited applications of these methods for systematically evaluating the importance of packaging design features. Therefore, there is a significant opportunity to develop a more efficient approach for assessing the feature importance for packaging design.
Despite the limited advancement in methods for evaluating the feature importance of packaging design, researchers have extensively investigated various techniques for assessing the relative importance of input variables using machine learning (ML) techniques. According to a recent academic report, ML applications in the packaging industry highlight their transformative impact on operational optimization and process efficiency. Key application areas include packaging design optimization, quality control, predictive maintenance, and supply chain management. ML has significant potential to revolutionize traditional packaging processes by enhancing automation, precision, and decision-making [9]. In recent decades, artificial neural networks (ANNs), one subset of ML, have been a focal point due to their capability to generalize complex non-linear problems. ANNs are excellent at capturing non-linear relationships between input features and the outcomes. Compared with traditional physical testing methods or numerical (e.g., FEM) that might require explicit programming of relationships between features, ANN methods automatically learn the patterns in the data through training, which saves time and reduces the risk of human error in modeling complex engineering systems [10]. In recent years, ANNs have gained growing interest in various engineering and multidisciplinary research fields, such as the tourism industry [11], financial sector [12], and complex engineering applications [13], as well as the optimization of sustainable construction material and technique [14,15]. However, in the field of packaging, artificial neural networks (ANNs) have been applied in only a few areas, such as food packaging’s influence on food shelf life [16,17,18,19], estimating edge crush resistance and evaluating other packaging properties [20,21], with limited applications beyond these.
In principle, training an ANN model involves building a function that recognizes the underlying relationships between input variables and output variables. Several methods have been employed within ANN models to determine the relative importance of input variables. One commonly used method is the weight connections method [22]. In this method, the importance of input variables is determined by the connection strengths (weights) within a trained neural network [23]. In 1991, Garson et al. [23,24] proposed a method to determine the relative impact of each input variable by calculating the percentage of output weight values associated with the contribution of a single input across the entire network. This method was utilized by N.L. Da Costa et al. [22] to evaluate the contribution of inputs to outputs in trained neural networks for both classification and regression problems. Another widely used method is the gradient-based method [25]. A. Hill et al. [25] proposed a gradient-based method to identify the relative importance of influencing factors for robotic control by obtaining the gradient of the output with respect to any component of the neural network using the chain rule in 2020. K. Fukumizu et al. [26] conducted dimension reduction for both feature extraction and variable selection based on the gradient-based method in supervised learning. In addition, the sensitivity analysis [27] and SHAP (Shapley additive explanations) values [28] are also commonly applied. One of the most commonly used techniques within the sensitivity analysis is the permutation method. H. Mandler et al. [29] used the permutation method to measure the sensitivity of a model with the presence or absence of a feature to determine the importance scores of input features in fluid dynamics using a neural network-based turbulence model. Altmann et al. [30] estimated the distribution of measured importance for each variable in a non-informative setting based on the permutation method in random forest (RF) models. Regarding SHAP values, S.M. Lundberg et al. [28] presented a unified framework for interpreting predictions, assigning each feature an importance value for a particular prediction in a deep learning model. Ziqi Li [31] applied SHAP values to extract spatial effects for interpreting and visualizing complex geographical phenomena and processes in machine learning models.
Given ANNs’ effectiveness in evaluating input feature importance across various fields and the limitations of traditional methods in assessing packaging design features, ANNs show strong potential for application in evaluating the importance of input features in packaging design to support cost savings and minimize material usage. Therefore, this study explores the application of ANN models to assess the relative importance of packaging design features, providing valuable insights that can be directly applied to optimize the packaging design process. In this study, box compression strength (BCS) was used as an example packaging property, and the relative importance of up to six packaging design features was assessed using ANN-based methods. Two datasets were utilized: one synthetic dataset generated using a widely used mathematical model (the McKee formula) and one real dataset [32]. These datasets were used to train artificial neural networks (ANNs) to assess packaging design feature importance. Theoretical feature importance was calculated and compared with the feature importance from the ANN-based methods. This study demonstrates the feasibility of applying ANN approach for evaluating the relative importance of packaging design features.
2. Methods
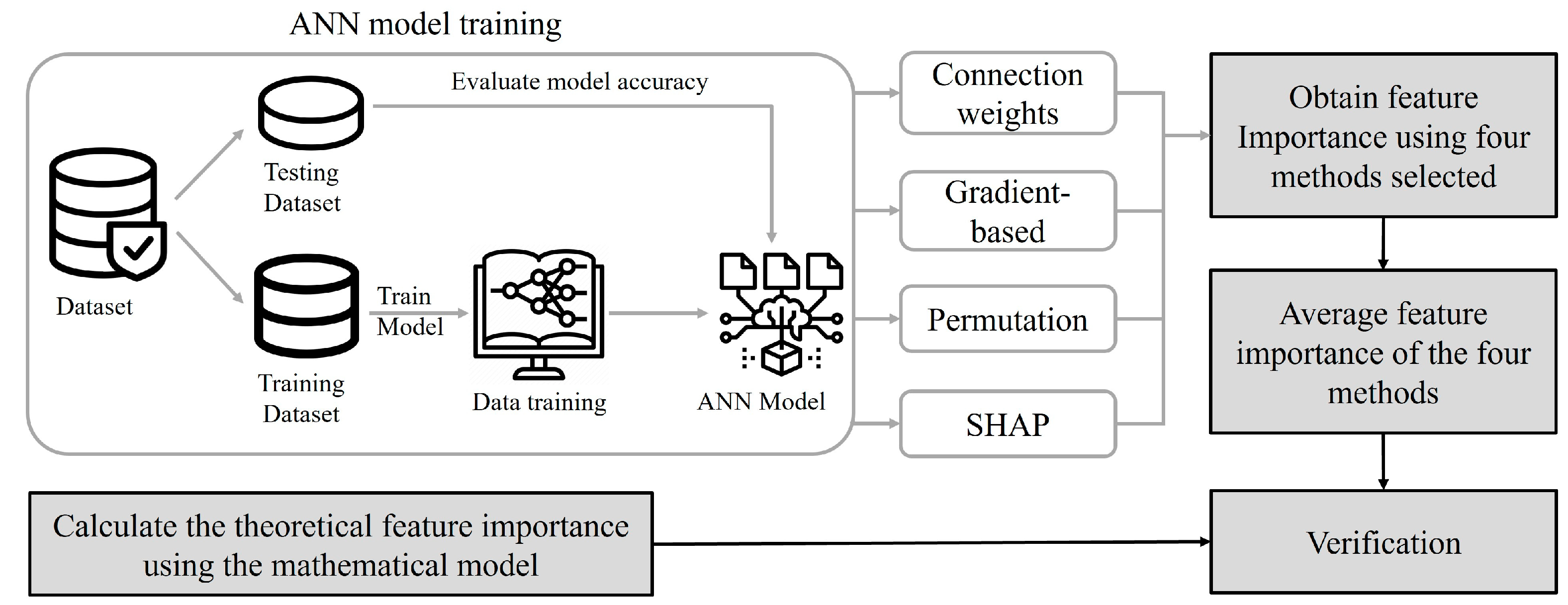
As mentioned above, ANNs have been widely used by researchers to evaluate the relative importance of input features [18,19,20,21,22,23,24]. By feeding the models with values of relevant input features and the corresponding output values of available data points, ANNs can be trained to learn the relationship between output(s) and their input features. Consequently, the trained ANN model can forecast the output values for new data points based on their input feature values as they become available. The process began with the construction of an ANN model through the training of available datasets, analogous to the procedure used for predicting output values. In this study, ANN models were initially developed by training on the available datasets. Then, the four aforementioned methods (the weight connections method, the permutation method, the gradient-based method, and SHAP values) were applied to assess the relative importance of various packaging design features within the trained ANN model. The results of the packaging design feature importance assessment were validated by comparing them with the theoretical feature importance calculated by an analytical method. Figure 1 illustrates the sequential procedure for mapping input feature importance within an ANN model, utilizing the four selected methods.
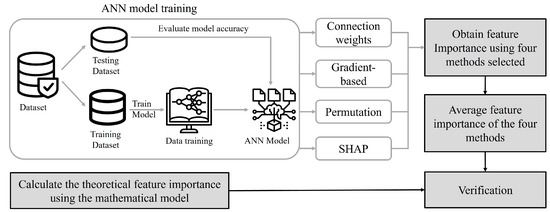
Figure 1.
Flow of mapping feature importance using four ANN-based methods.
2.1. ANN Neuron Number Determination in the Hidden Layer
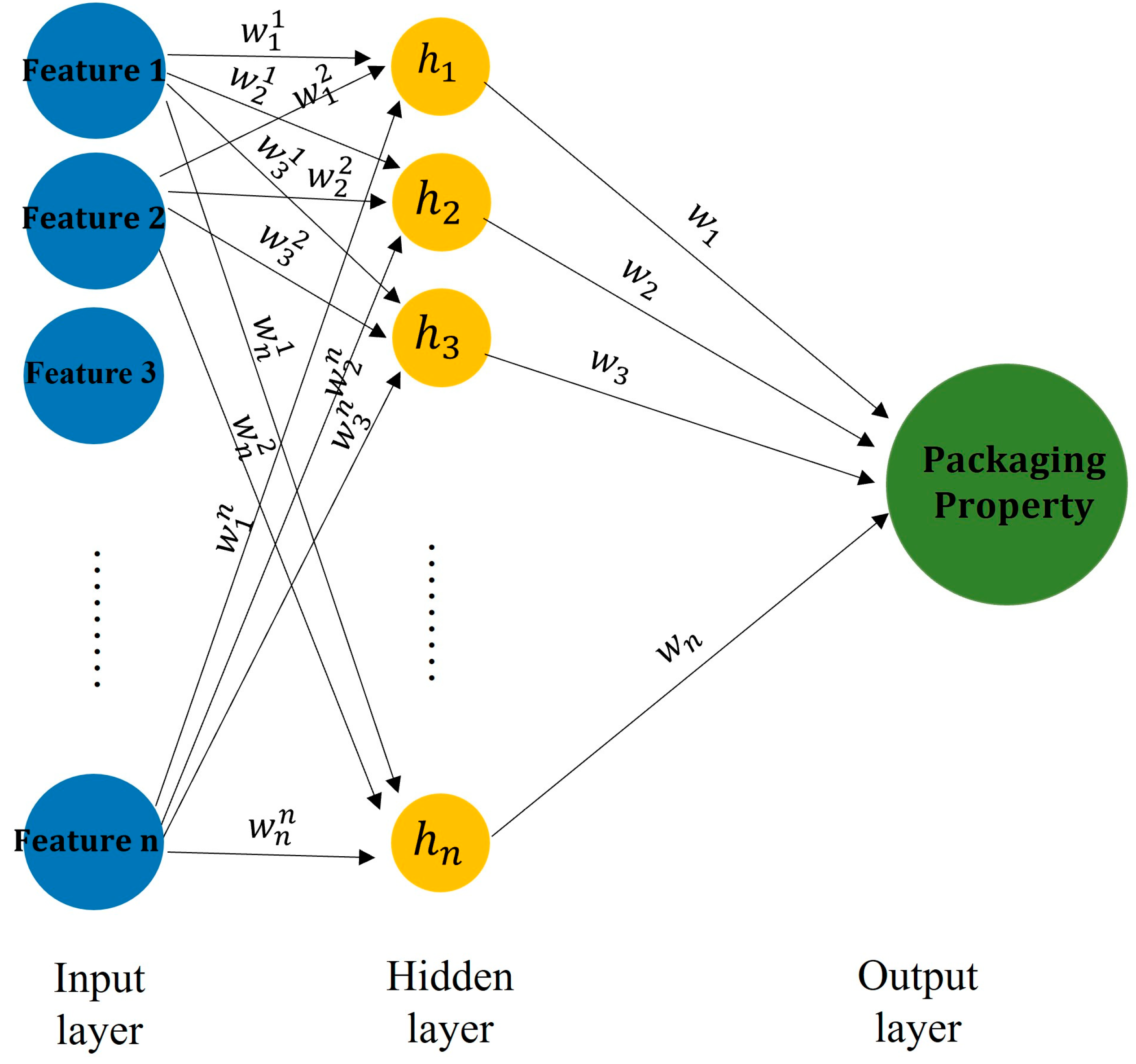
To obtain the feature importance through ANN approach, the first step is to build an ANN model. The dataset for training the ANN was randomly divided into two subsets: a training dataset for training the model and a testing dataset for assessing model accuracy. To construct the ANN model, the number of hidden layers and the neuron numbers for each layer were determined by balancing the model accuracy and computational efficiency. Figure 2 presents a conceptual diagram of the ANN structure developed in this study. In this study, five optimization methods were examined, each targeting the optimization of the hidden layer configuration. These methods included the Bayesian optimization method [33,34], information criteria the using Akaike information criterion (AIC) method [35], information criteria using the Bayesian information criterion (BIC) method [36], Hebb’s rule [37], and the optimal brain damage (OBD) rule [38]. The final hidden layer configuration was determined based on minimizing model error and maximizing computational efficiency through a comprehensive comparison of model errors across the five optimization methods mentioned above.
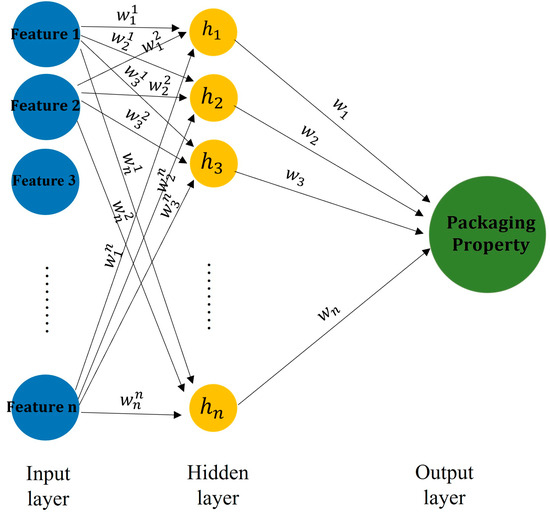
Figure 2.
A conceptual diagram of the ANN structure used in this study.
The number of epochs was determined based on the model loss (error) versus epoch plot. The epoch count was chosen when the model error decreased and reached a stable, plateaued level.
2.2. Methods for Evaluating Input Feature Importance
Based on the reliability of the packaging feature importance rankings of the synthetic dataset generated using the widely used mathematical model, four ANN-based methods were selected to evaluate the importance of the target packaging design features in this study. These four methods are the connection weights method, the gradient-based method, the permutation method, and SHAP values. The principles underlying each method for extracting input feature importance are explained in this section.
2.2.1. Connection Weights Method
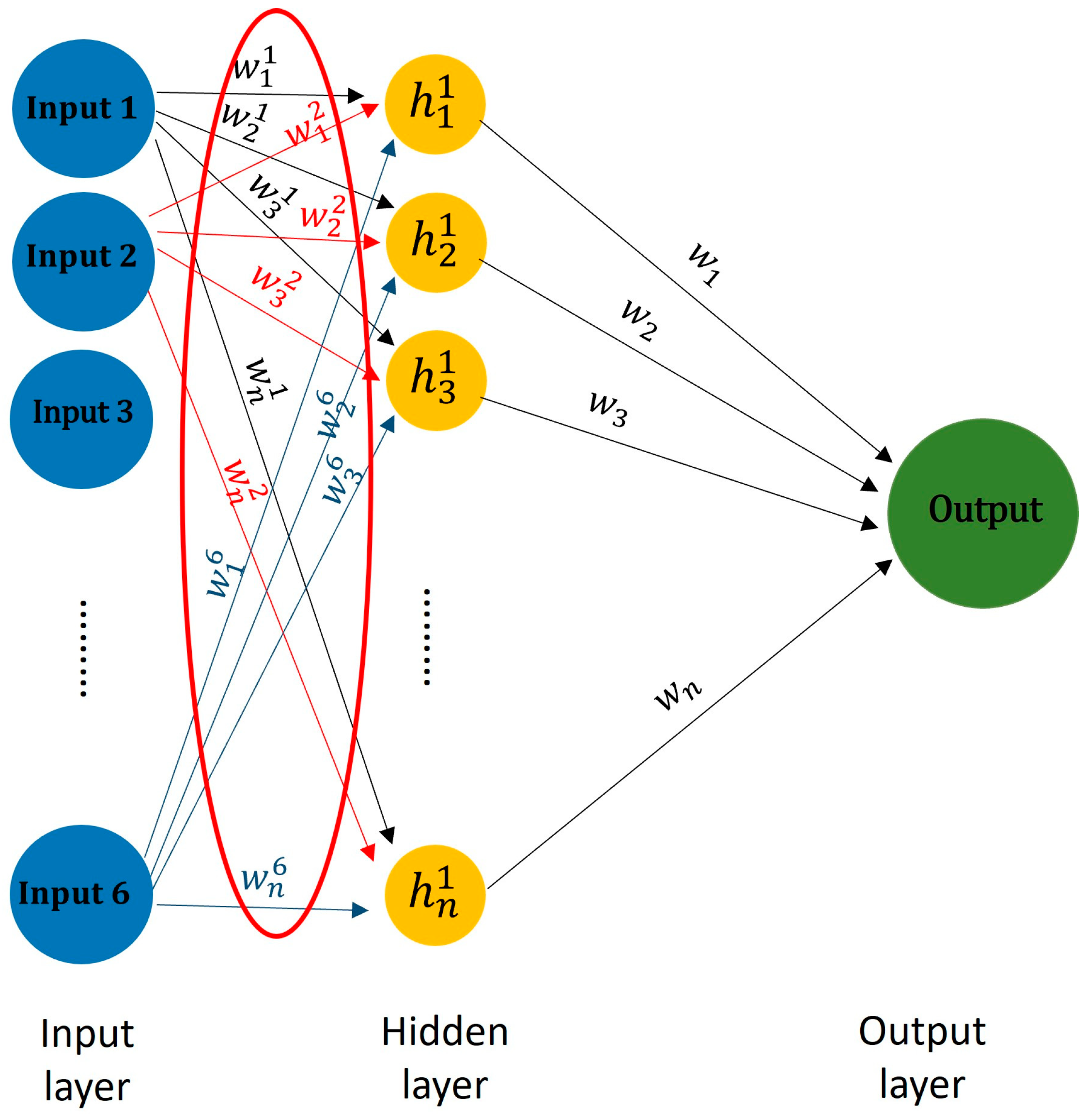
The connection weights method examines the weights between the neurons in an ANN structure to determine the relative significance of each input feature in relation to the output [22]. This approach derives the relative importance of input features by extracting these weights from the first layer, as illustrated in Equation (1) and Figure 3. The weight function was employed to extract the weights from the first layer of the ANN model.
where
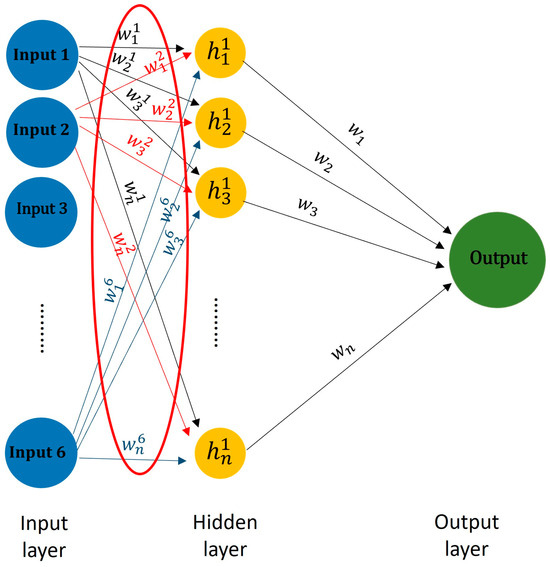
Figure 3.
The ANN structure and connection weights method extracts the weights in the first layer as the input feature importance.
- —The standard deviation of the ith input is equal to the ith input; subtract the mean of input features and divide it by the standard deviation of inputs features.
- —The ith input’s importance.
- —The number of hidden nodes in the first layer.
- —The weight connecting the ith input to the jth hidden node in the first layer.
2.2.2. Gradient-Based Method
The gradient-based method is a key technique for evaluating how a model’s outputs are influenced by its input features. It involves calculating the partial derivative of the output with respect to the input, which measures sensitivity. This approach is applicable in deep neural networks (DNNs), a specialized type of ANN [39]. Examining how variations in input features influence the predicted output can reveal insights into feature importance within ANN models. The gradient’s magnitude indicates the extent of change in the predicted output due to an infinitesimal alteration in the input feature [40]. The gradient of output with respect to input X is represented in Equation (2),
The differentiability of deep neural networks is determined by the activation function used. Activation functions like sigmoid, ReLU, and Tanh are differentiable almost everywhere. In this study, where the sigmoid function is utilized, a central difference method was applied to numerically approximate the gradient of F(X) at X, as defined in Equation (3).
where
- X + ,
- X − .
∈ R is the step size, and for all k = 1, …, d, ek ∈ Rd is the standard basis vector. The terms F(X (k+)) and F(X (k−)) are obtained from two forward passes of the model. The importance of the kth feature is then defined as the absolute value of the partial derivative with respect to xk. This gradient vector provides the feature importance for a single test sample. To determine the global feature importance, the feature importances for all samples in the test set SN were averaged, where N represents the number of samples in the test set [40], as outlined in Equation (4),
In this study, gradients were computed using tf.GradientTape(), a Python 3.11.5 tool that allows for nesting to calculate higher-order derivatives.
2.2.3. Permutation Method
The permutation method measures a feature’s importance by observing how model accuracy changes when the values of that feature are randomly shuffled while keeping other feature values intact. A feature with higher importance will have a greater effect on the model’s accuracy when its values are shuffled [29]. As detailed in Equation (5) and Table 1, to determine the feature importance of feature fj, the column corresponding to fj is randomly shuffled to generate a corrupted dataset Dkj. The ANN model is then trained on Dkj, and its accuracy is compared with the accuracy of the original models. The difference in accuracy scores indicates the importance of feature fj.
where

Table 1.
Principle of permutation feature importance.
- ij—Importance for feature fj.
- s—Reference score of the model m on dataset D.
- K—Repetition times for randomly shuffling column j of the dataset D to generate a corrupted version of the data named Dkj.
- skj—Score of the model on corrupted data Dkj.
In this study, the np.random.permutation() function from the NumPy library in Python 3.11.5 was utilized to randomly shuffle the input features in the ANN.
2.2.4. SHAP Values
SHAP (Shapley additive explanations) values use principles from game theory to measure the contribution of each feature to the final prediction [29,41]. They aim to fairly allocate the contributions of each feature towards achieving the overall result [31]. SHAP values can be applied in machine learning to measure the contribution of each feature to the model’s prediction, providing insights into how each feature collectively influences the final outcome [42]. In evaluating feature importance, SHAP values compare the model’s output with and without a specific feature for a given data point, accounting for all possible combinations of the other features. The average difference in the output is then computed. The SHAP value for feature Xj in a model is represented by Equation (6):
where
- p—The total number of features.
- N\{j}—A set of all possible combinations of features excluding Xj.
- S—A feature set in N\{j}.
- f(S)—The model prediction with features in S.
- f(S∪{j})—The model prediction with features in S plus feature Xj.
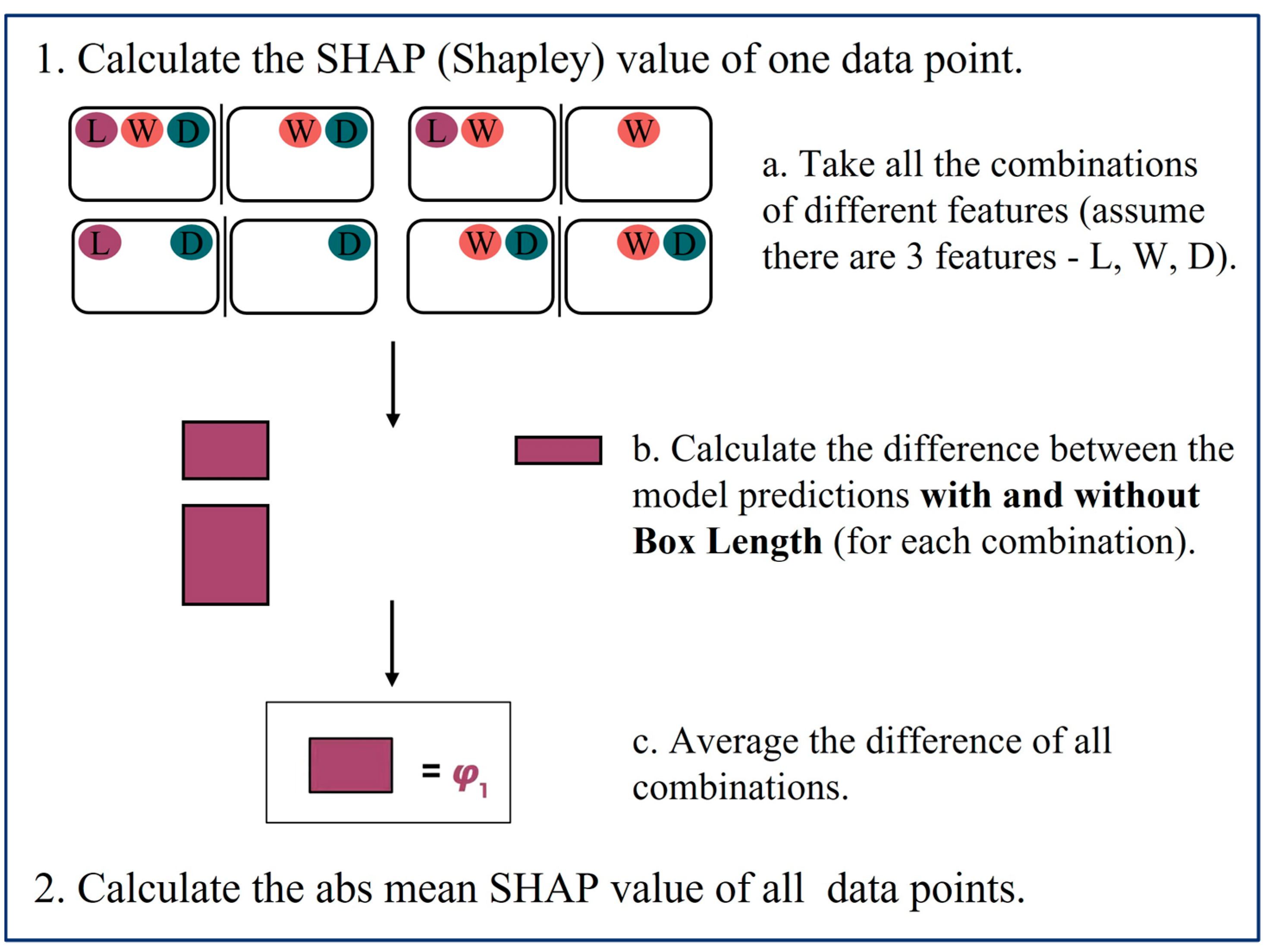
According to Equation (6), the SHAP value of a feature represents its marginal contribution to the model’s prediction, averaged across all possible models with varying combinations of features [42]. Equation (6) determines feature importance for a single data point. In our study, which involves multiple data points, this process is repeated for each data point. The average difference in output across all data points is then used to measure the importance of a single feature. The calculation process of SHAP values for multiple data points in our dataset is illustrated in Figure 4.
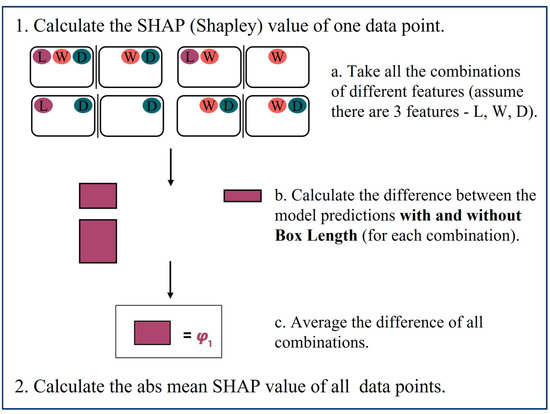
Figure 4.
Calculation process of SHAP values with multiple data points in a dataset.
In this study, the explainer.shap_values() function from the SHAP library in Python 3.11.5 was employed to compute the SHAP values for each BCS feature.
2.3. Final Relative Feature Importance Determination
With the optimal hidden neuron setting and the optimal epoch number, the packaging design features studied were incorporated into the ANN model. The relative importance of these packaging design features was evaluated using the previously mentioned methods. Each method provided importance scores for the studied packaging features, which were then normalized to a scale from 0 to 1 to account for differences in scaling. The theoretical feature importance of 0 for features not included in the mathematical model was used to identify and eliminate unreliable methods. In practice, researchers and practitioners often average feature importance scores from various methods to obtain a more stable or general feature ranking. Therefore, in this study, to produce a comprehensive measurement, the feature importance results from the reliable methods were averaged to determine the final importance of different packaging design features. To confirm the validity of these results, the averaged packaging design feature importance was compared with the theoretical feature importance calculated using the well-established mathematical model.
3. Results
Box compression strength (BCS) was used as a representative packaging property to validate the capability of an ANN approach to assess the relative importance of packaging design features. Two datasets (one synthetic and one real) were employed as case studies. Incorporating six input features: box perimeter, depth, ECT, thickness, and bending stiffness in both machine (EIx) and cross directions (EIy). The average feature importance of these BCS features, as determined by the four ANN approaches, were compared with the theoretical feature importance values derived from the McKee formula to verify the ANN assessment.
3.1. Case Study 1: Relative Feature Importance of the Synthetic Dataset
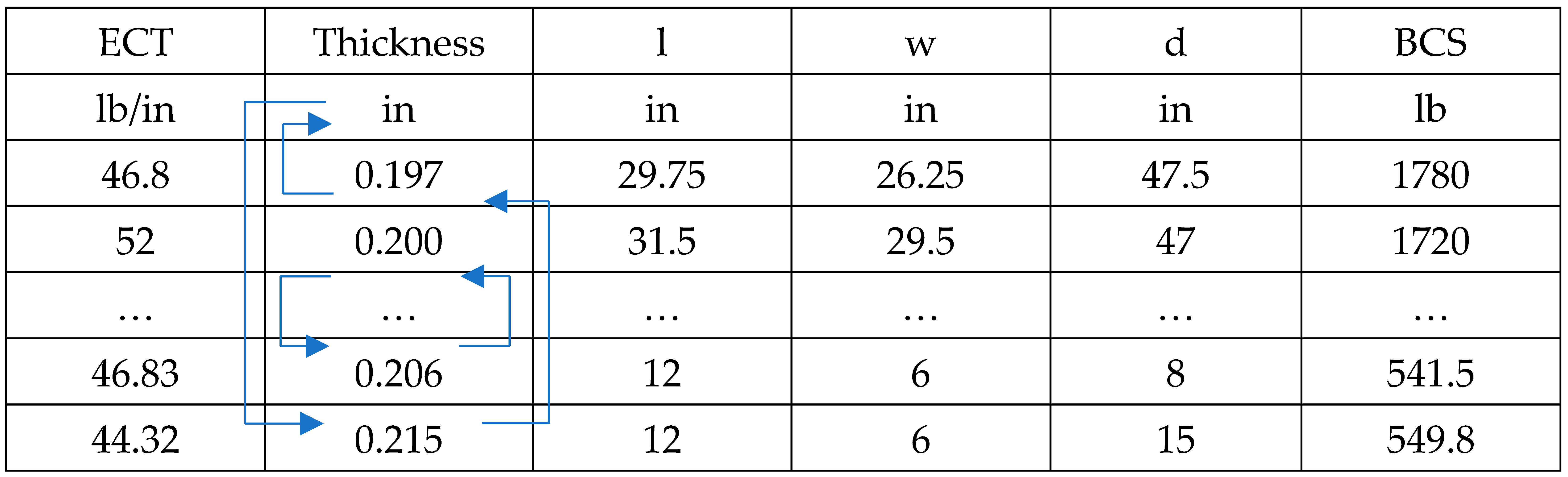
The synthetic dataset was created by inputting the box perimeters, depths, ECTs, and thicknesses of 3009 commonly used commercial boxes [43] into the simplified McKee formula, as detailed in Equation (7) [44] to compute the BCS values.
where
- ECT—Edge crush strength (lb/in).
- Thickness—Thickness of the corrugated board (in).
- P—Perimeter of the box (in).
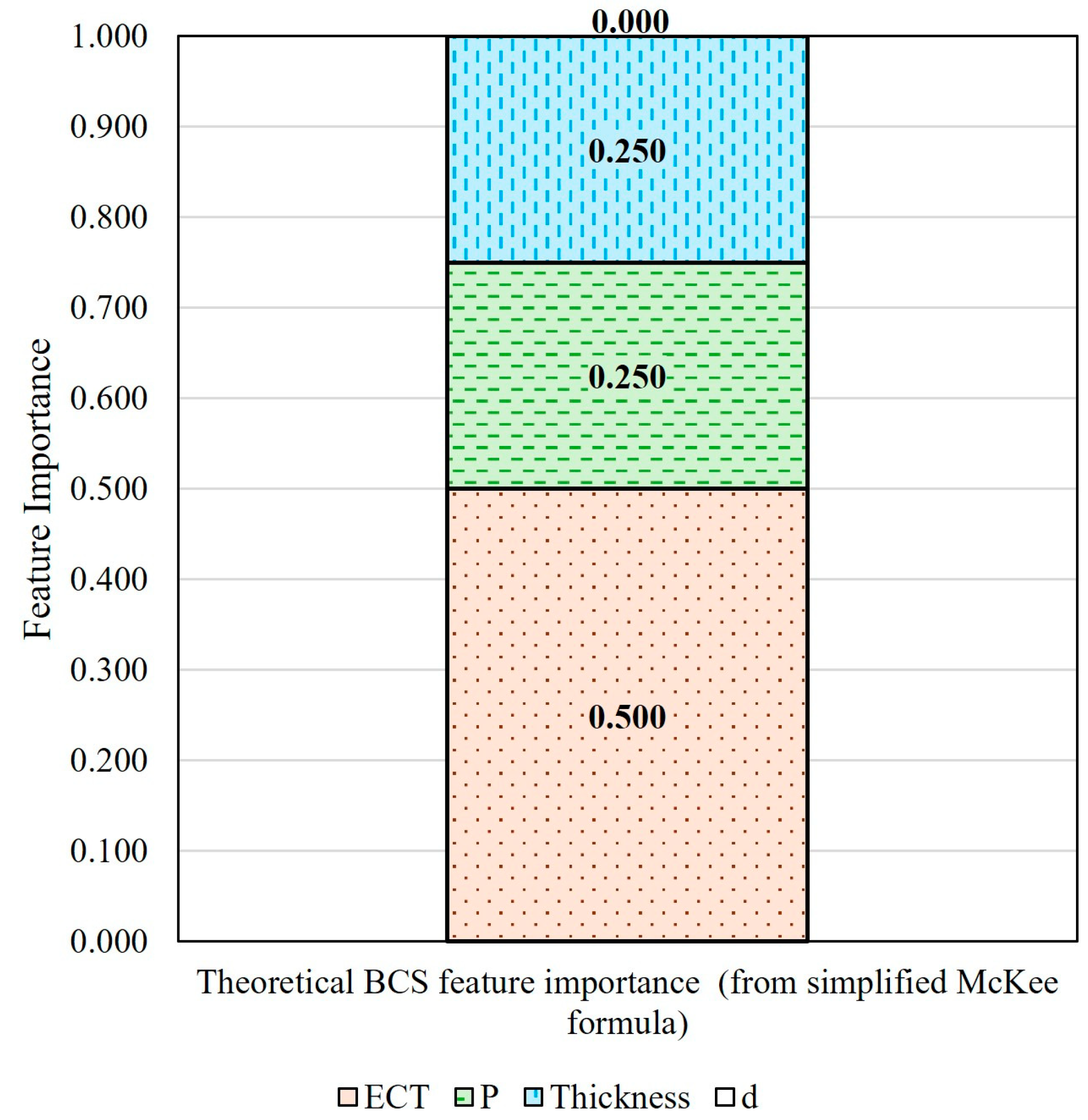
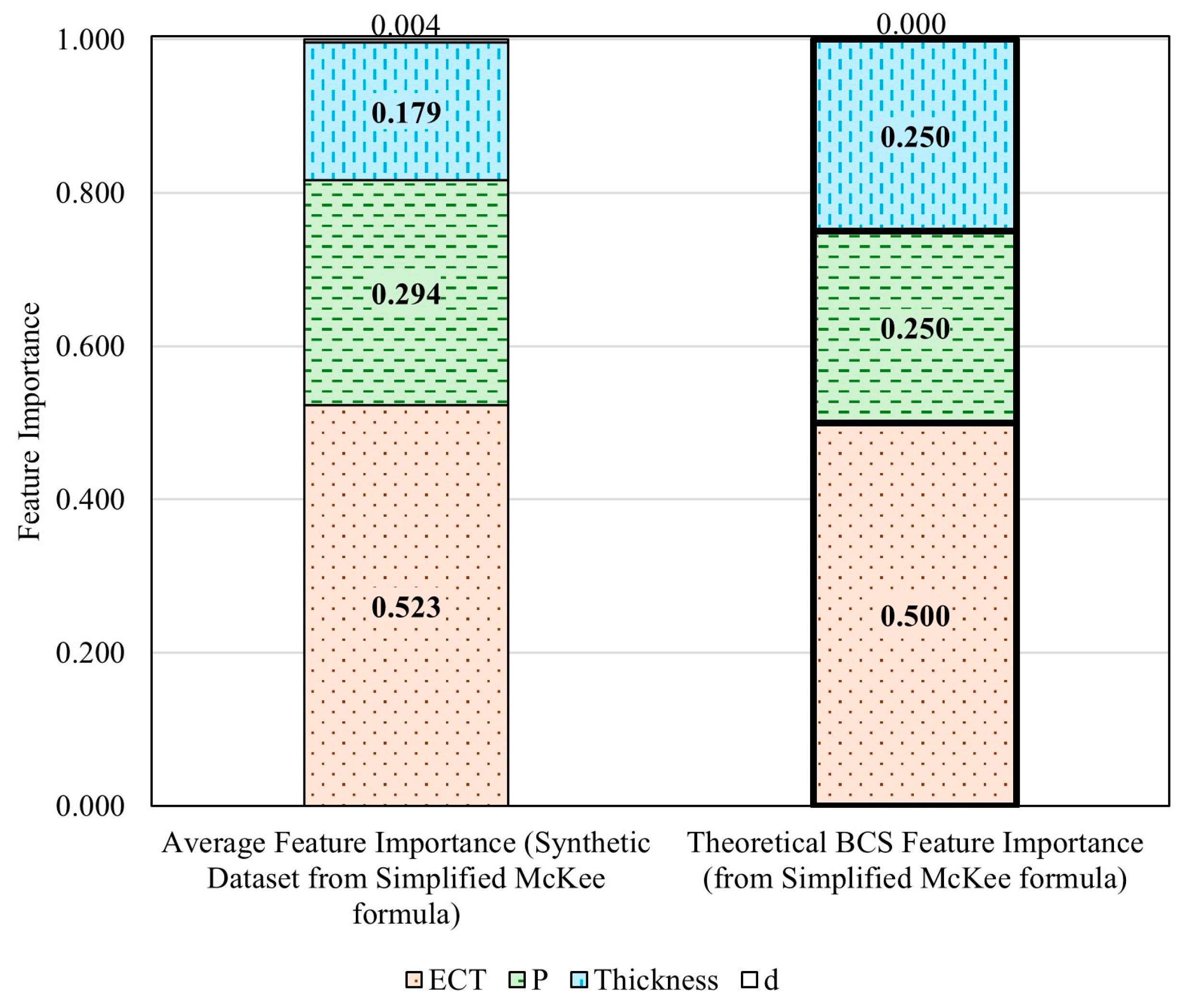
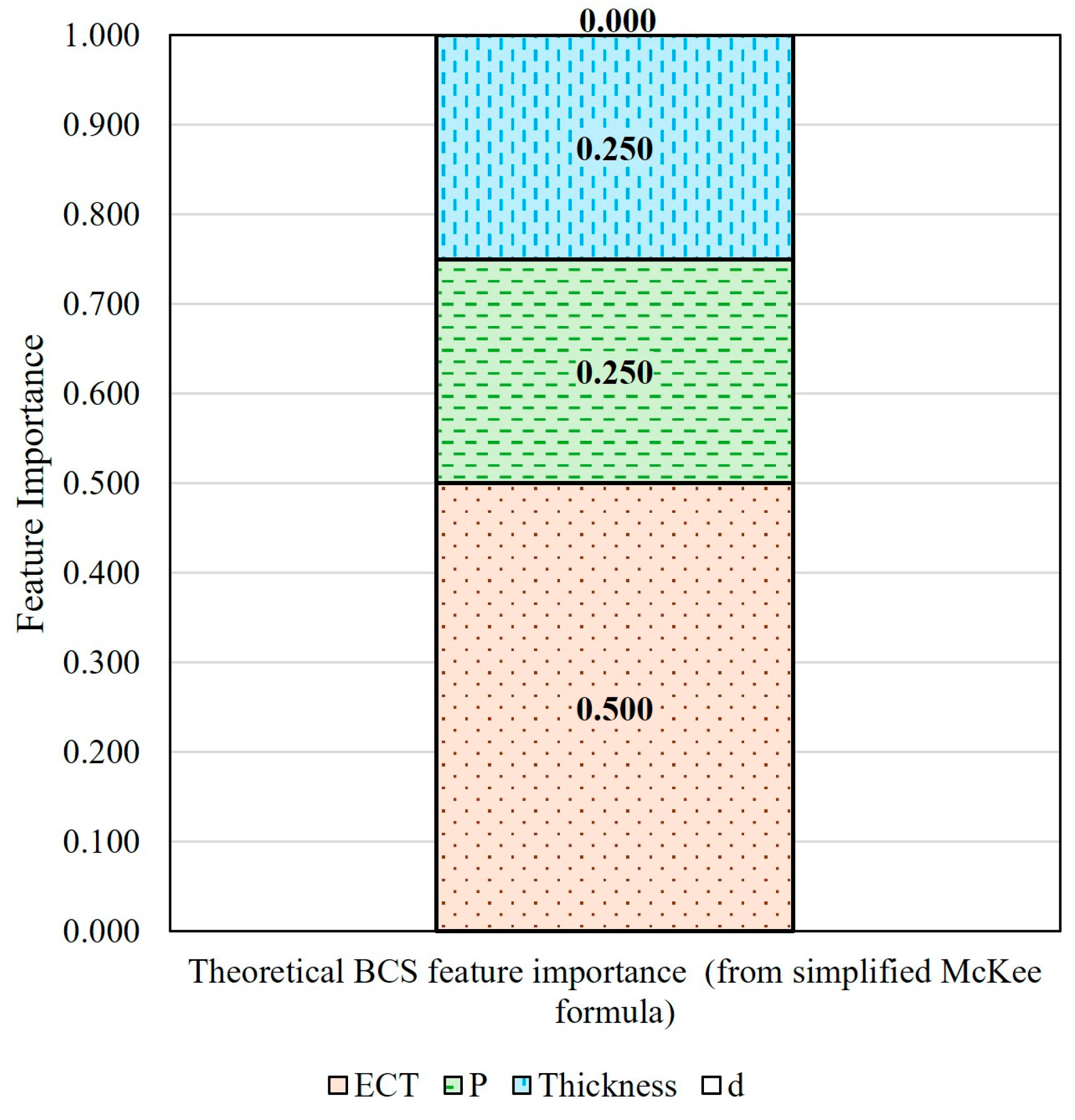
Using the simplified McKee formula and the concept of derivative, the theoretical relative importances of the four BCS features were calculated, as shown in Figure 5. ECT has a weight of 0.500, both perimeter and thickness have a weight of 0.250, and depth (abbreviated as d below) has no importance (0).
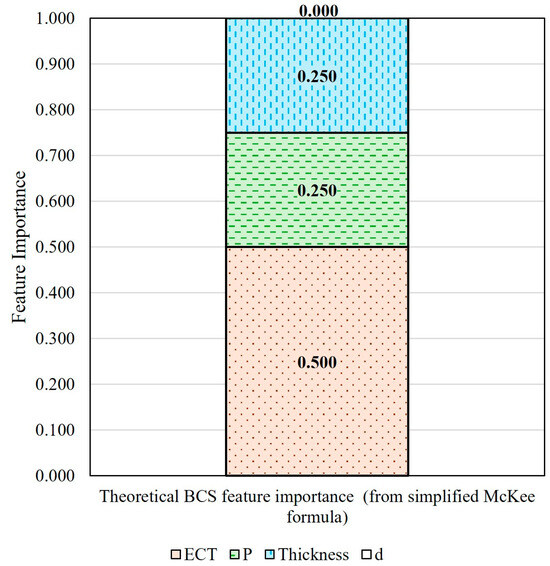
Figure 5.
Theoretical BCS feature importance calculated using the simplified McKee formula.
3.1.1. ANN Training Using the Synthetic Dataset
During the ANN model training process, the synthetic dataset with 3009 data points was randomly divided into two subsets: 70% of the data (2016 data points) for training the model and the remaining 30% (993 data points) for testing the model’s accuracy.
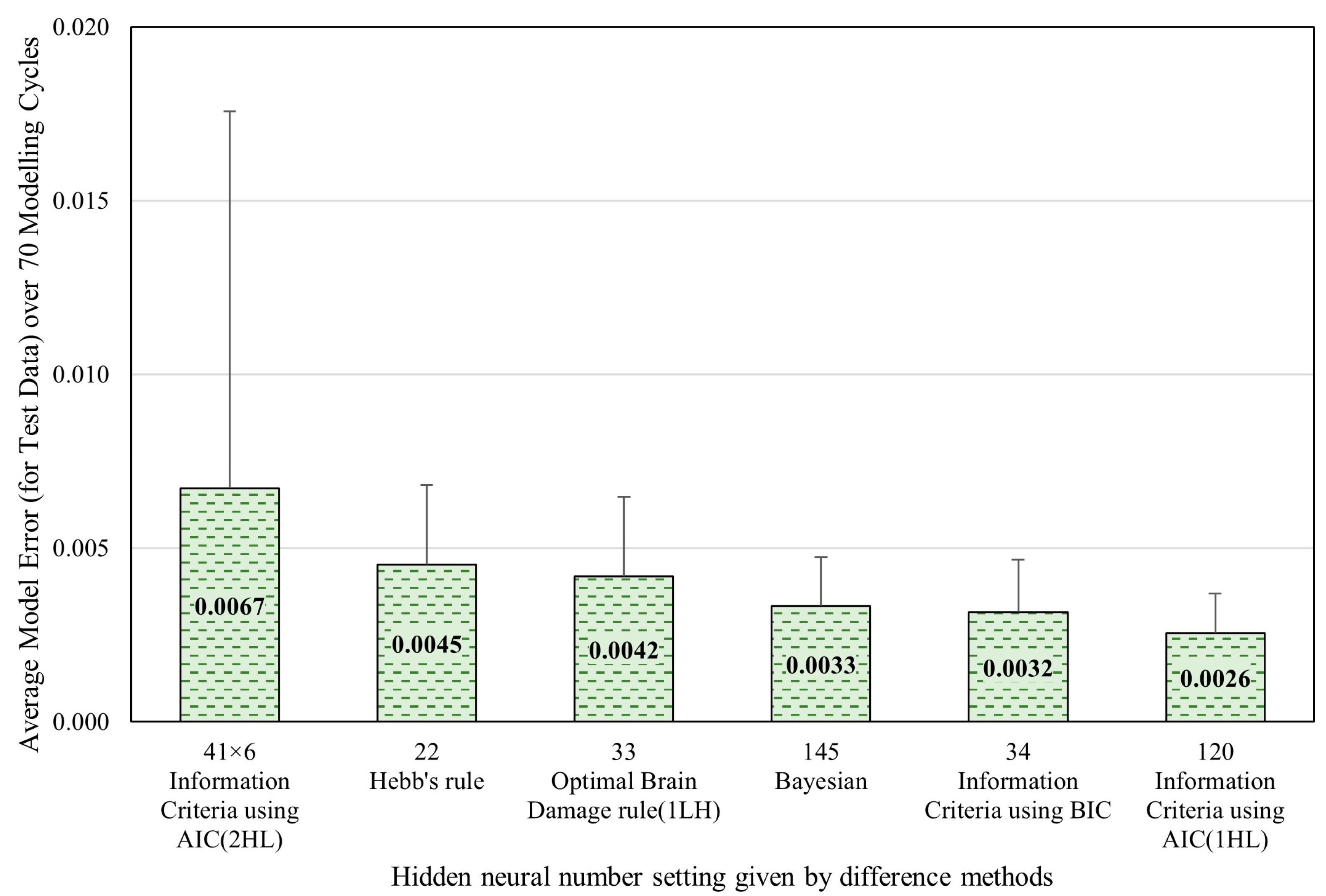
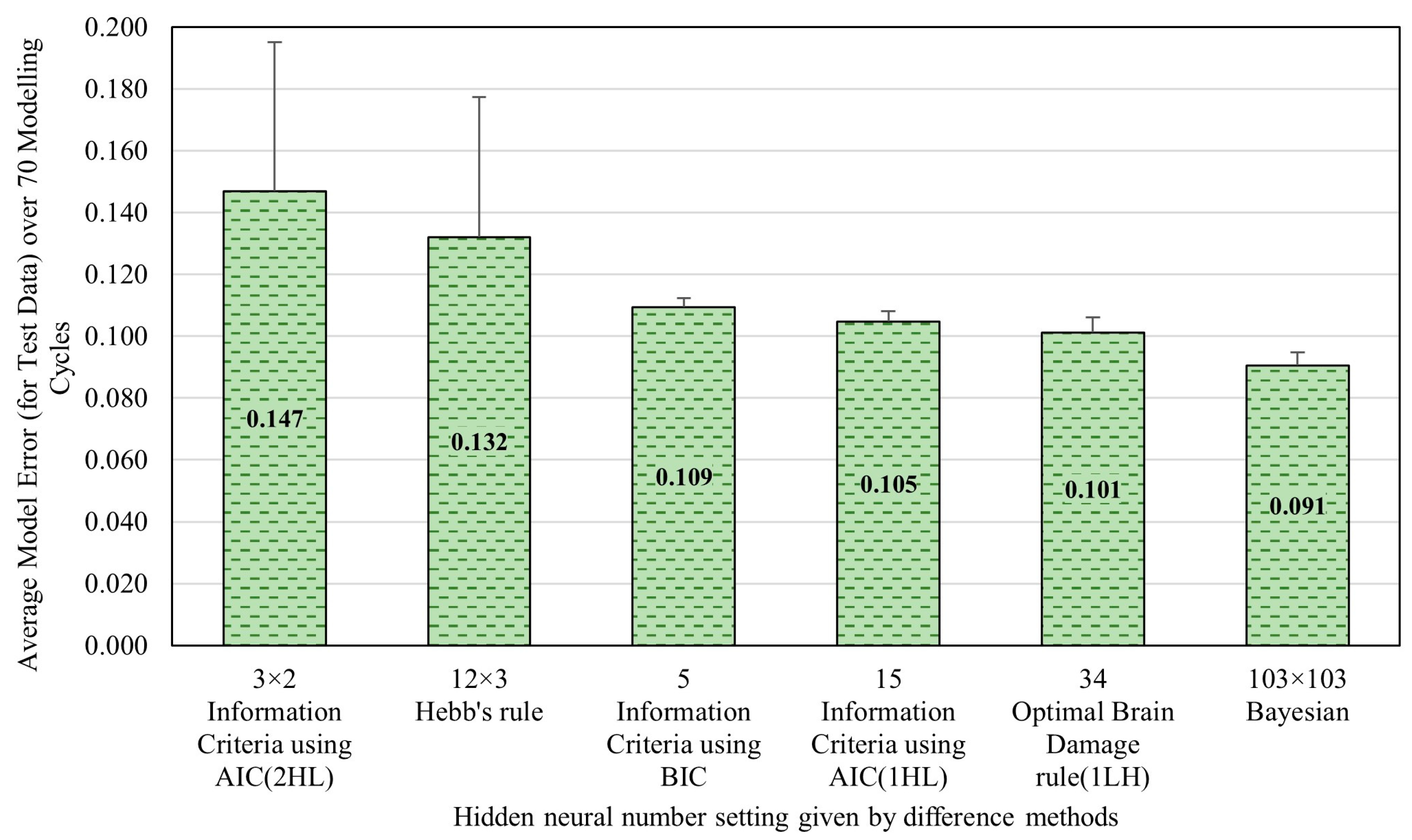
As previously mentioned, the hidden layer neuron number setting was determined through comparing the model errors obtained by the five optimization methods mentioned in Section 2.2 (including Bayesian optimization method, AIC method, BIC method, Hebb’s rule, and the OBD rule) to minimize the model error and maximize the computational efficiency. Figure 6 presents the optimal neuron settings for the hidden layer as determined by each method, along with their corresponding model errors in test data over 70 modeling cycles. The results showed that the AIC method achieved the lowest model errors with one hidden layer and 120 neurons. The BIC method produced the second-lowest model error, with one hidden layer and 34 neurons. The error difference between these two methods was no more than 0.0032, considering their 95% confidence intervals (0.0032 ± 0.0015 and 0.0026 ± 0.0011). This indicates that the more complex configuration suggested by the AIC method was not necessary. In contrast, the simple configuration of 34 provides slightly less accuracy but is significantly more efficient in terms of computational resources, making it the optimal choice for balancing model prediction accuracy and computational efficiency. Consequently, the neuron configuration proposed by the BIC rule was applied throughout the study for this dataset. Namely, the ANN model developed in this real dataset includes a single hidden layer with 34 neurons.
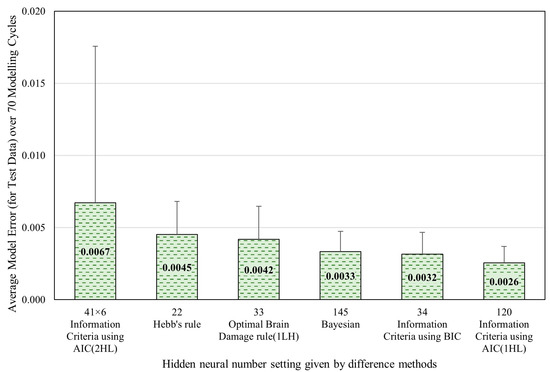
Figure 6.
Optimal neuron numbers in the hidden layer(s) determined by different methods for the synthetic dataset.
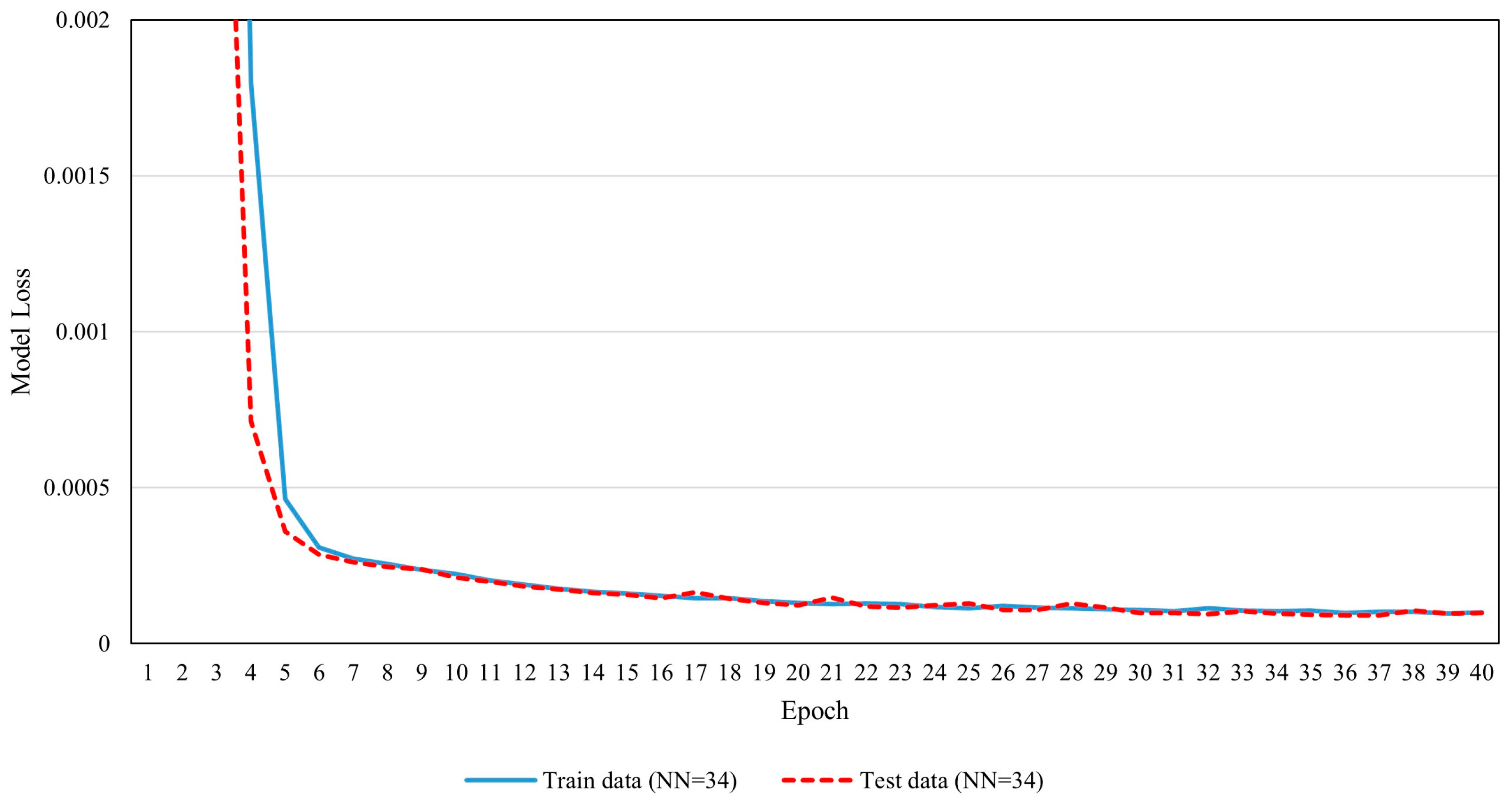
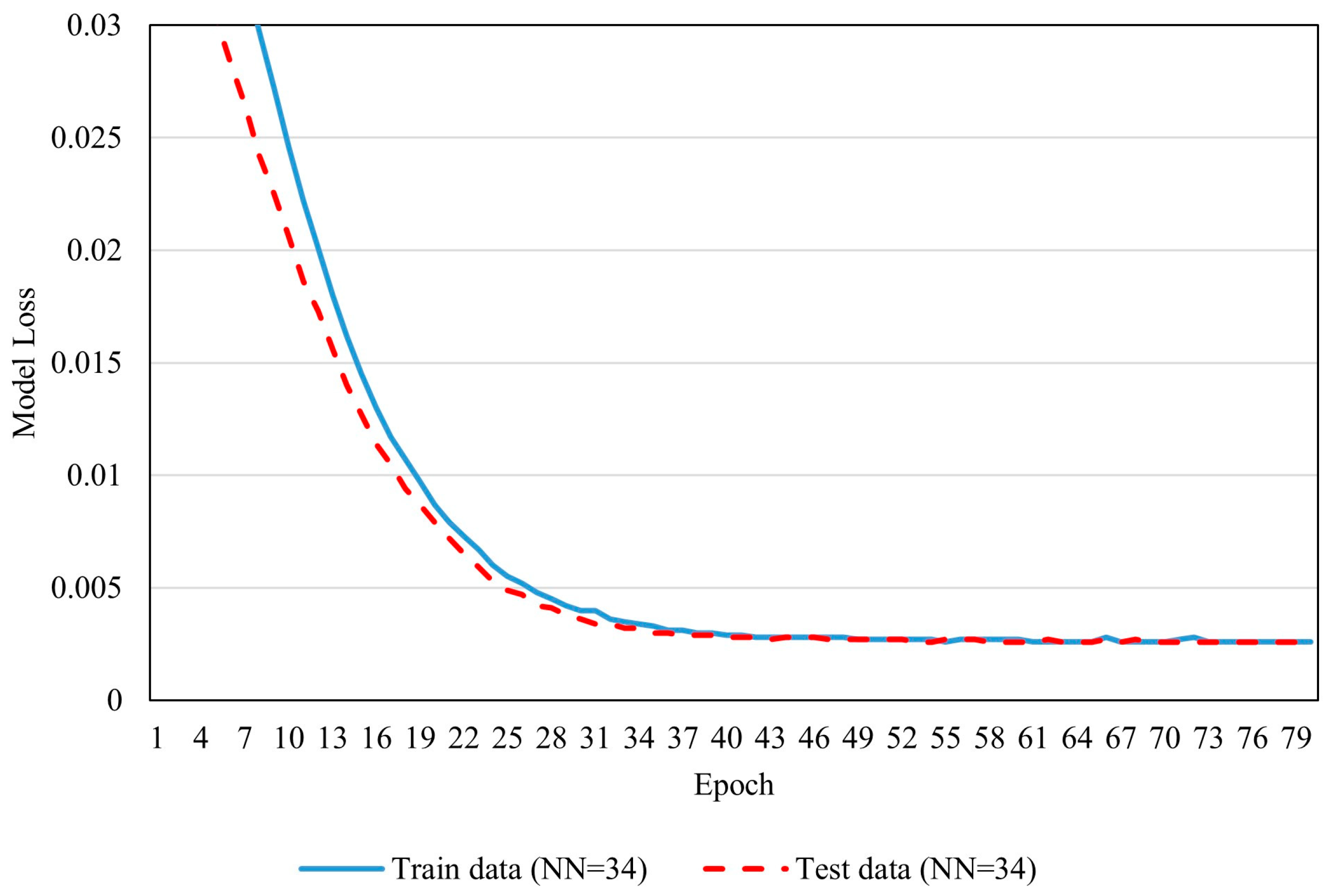
The number of epochs was determined based on the model loss (error) epoch plot (Figure 7), which showed that model error reduction plateaued after 25 epochs, but did not reach zero, meaning the error continued to decrease slowly for both training and test data. To balance high prediction accuracy with computational efficiency, a conservative approach was taken by extending the training for an additional 10 epochs beyond the plateau, resulting in a total of 35 epochs.
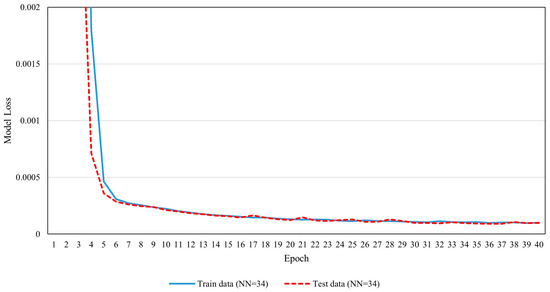
Figure 7.
Model loss (error) versus epoch plot with 34 neurons in the hidden layer.
The feature importance of 10 modeling cycles was averaged to obtain a relative reliable average feature importance.
3.1.2. Relative Feature Importance Analysis of the Synthetic Dataset
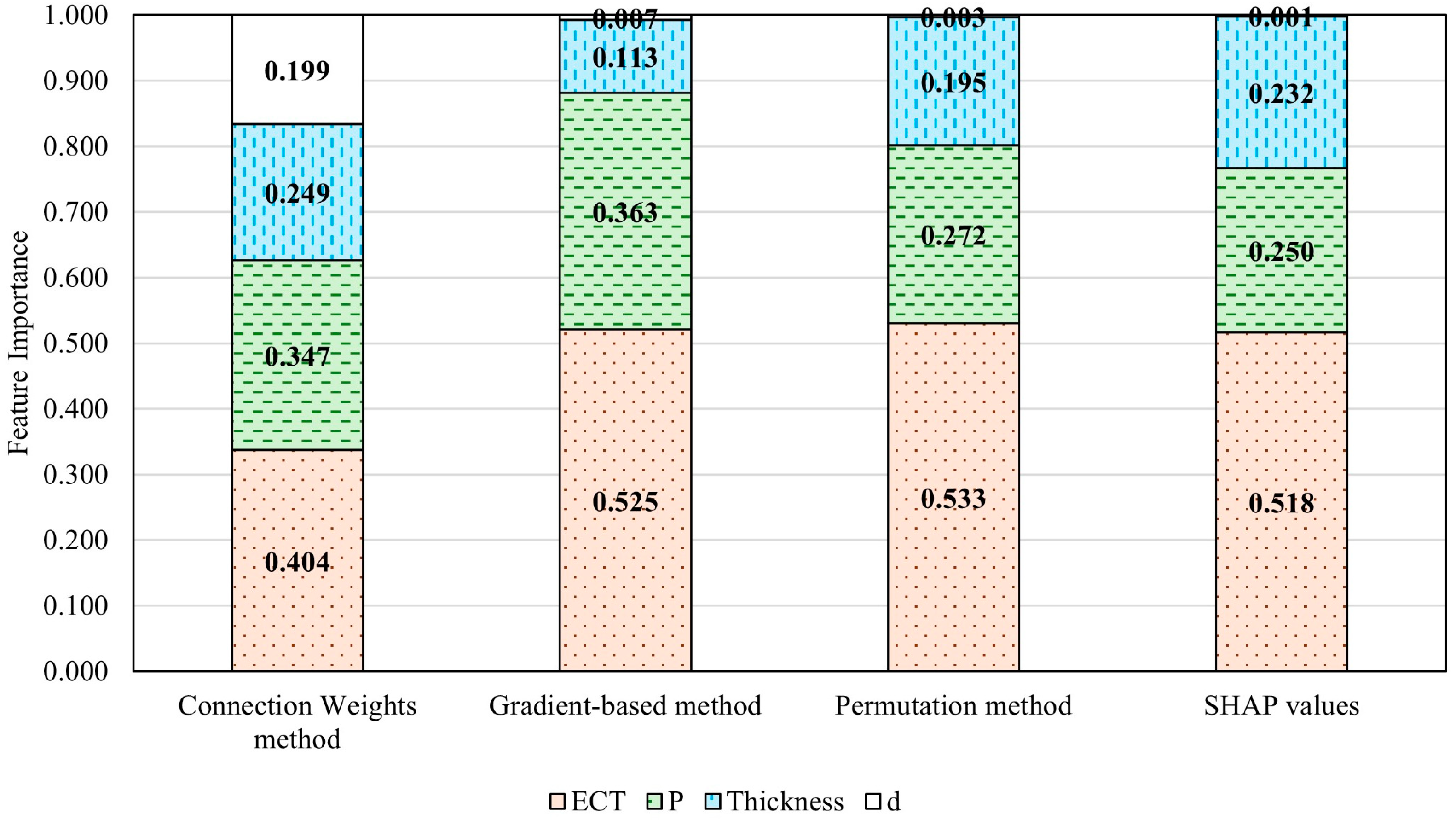
The BCS feature importance in this dataset was evaluated using the four methods mentioned earlier. Each method provided the relative importance of the four BCS features (ECT, thickness of the corrugated board, box perimeter, and box depth). To ensure comparability across methods, the BCS feature importances were normalized so that the sum of the importances for all four features equaled 1 within each method, as illustrated in Figure 8.
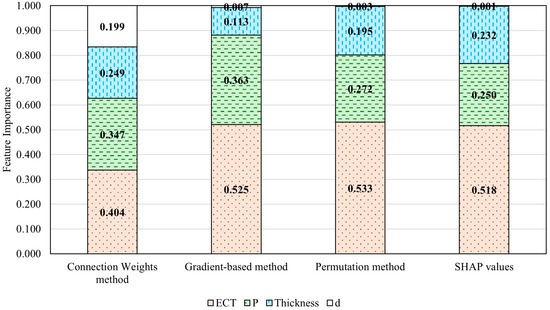
Figure 8.
ANN-evaluated BCS feature importance of the synthetic dataset generated using the simplified McKee formula.
The ranking of BCS feature importance consistently identified by the four methods is ECT > perimeter > thickness > depth. However, the connection weights method shows an unusually high importance for the depth feature, which deviates significantly from the expected value of zero given the synthetic dataset’s design (recall that this synthetic dataset was generated using the simplified McKee formula, which does not account for depth. Therefore, the influence of depth on BCS is theoretically zero for this dataset). This discrepancy renders the results from the connection weights method unreliable. Therefore, the feature importance results of the other three approaches were averaged to provide a comprehensive estimate of BCS feature importance. The average BCS feature importance from these three methods shows that ECT has a weight of 0.525, a perimeter of 0.295, a thickness of 0.180, and a depth of 0.004, as illustrated in Figure 9 (left). When compared to the theoretical BCS feature importance ranking calculated using the simplified McKee formula (depicted in Figure 9 (right)), the results from the three reliable methods are closely aligned. This highlights that the ANN approach is a highly promising and effective tool for evaluating the relative importance of packaging design features, offering significant potential to revolutionize the optimization process in packaging design.
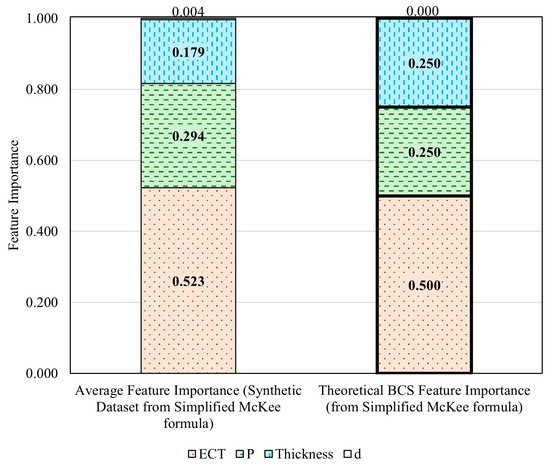
Figure 9.
Comparison of the average feature importance assessed by the selected ANN-based methods and theoretical BCS feature importance calculated using the simplified McKee formula.
3.2. Case Study 2: Relative Feature Importance of the Real Dataset
The real dataset comprises industry data on 429 commonly used commercial boxes, detailing five BCS features: box perimeters, depths, ECTs, and flexural stiffness in both the machine and cross-machine directions. These BCS values were obtained through actual testing, accurately reflecting real-world industry conditions. Since real-world data captures fluctuations in BCS feature values due to measurement inaccuracies and variations in material parameters, studying a real dataset from the industry is very meaningful to the feature importance assessment.
As with the first synthetic dataset, the theoretical relative importance of these five BCS features were calculated using the improved McKee formula (Equation (8)) [45], where the ECT has a weight of 0.500, the perimeter has a weight of 0.330, both stiffnesses EIx and EIy have a weight of 0.085, and depth has no importance (0), as shown in Figure 10.
where
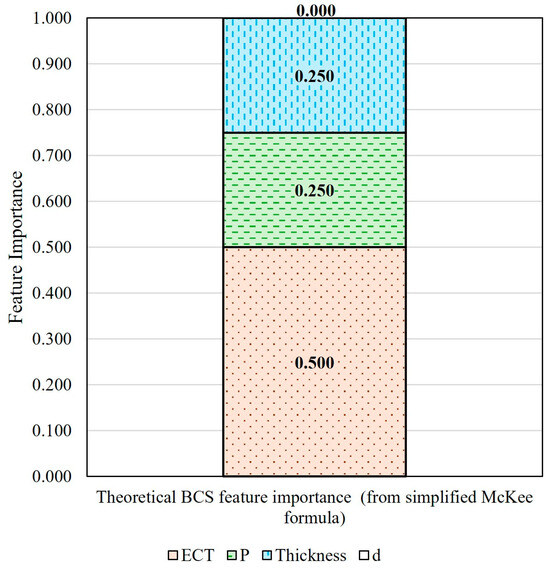
Figure 10.
Theoretical BCS feature importance calculated using the improved McKee formula.
- ECT—Edge crush strength (lb/in).
- EIx, EIy—Flexural stiffness in the machine direction and cross-machine directions of the corrugated board (lb×in).
- P—Perimeter of the box (in).
3.2.1. ANN Training Using the Real Dataset
During the ANN model training process, the real dataset with 429 data points was randomly divided into two subsets: 70% of the data (287 data points) for training the model and the remaining 30% (142 data points) for testing the model’s accuracy.
As with the synthetic dataset, the hidden layer neuron number setting was also determined through comparing the model errors given by the five optimization methods mentioned above (including Bayesian optimization method, AIC method, BIC method, Hebb’s rule, and the OBD rule) to minimize the model error and maximize the computational efficiency. Figure 11 presents the optimal neuron settings for the hidden layer as determined by each method, along with their corresponding model errors in test data over 70 modeling cycles. The results showed that Bayesian optimization achieved the lowest model errors with two hidden layers, each containing 103 neurons. The OBD rule produced the second-lowest model, with one hidden layer and 34 neurons. The error difference between these two methods was no more than 0.0191, considering their 95% confidence intervals (0.101 ± 0.0048 and 0.091 ± 0.0043). This indicates that the more complex configuration suggested by Bayesian optimization was not necessary. In contrast, the simple configuration of 34 provides nearly the same accuracy but is significantly more efficient in terms of computational resources, making it the optimal choice for balancing model prediction accuracy and computational efficiency. Consequently, the neuron configuration proposed by the OBD rule was applied throughout the study for this dataset. Namely, the ANN model developed in this real dataset includes a single hidden layer with 34 neurons.
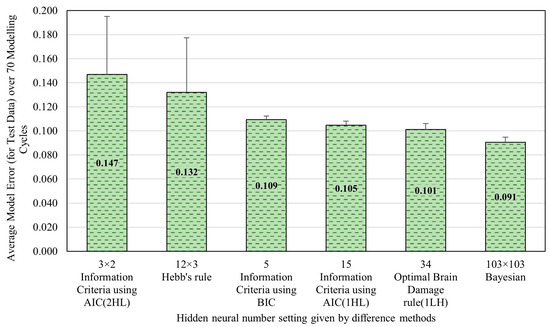
Figure 11.
Optimal neuron numbers in the hidden layer(s) determined by different methods for the real dataset.
The number of epochs was determined based on the model loss (error)-epoch plot (Figure 12), which showed that model loss (error) reduction plateaued after 40 epochs. To balance high prediction accuracy with computational efficiency while achieving a conservative result, the number of epochs was set to 50.
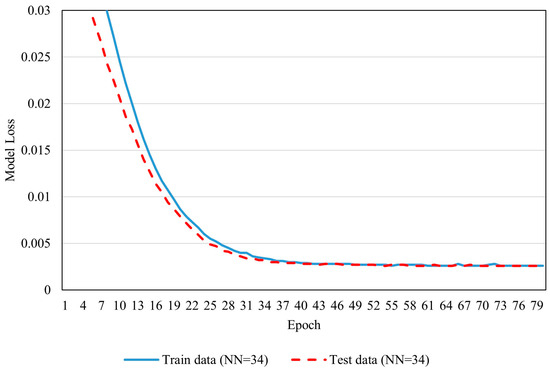
Figure 12.
Model mean squared error (MSE) versus epoch plot with 34 neurons in the hidden layer.
The feature importance of 10 modeling cycles was averaged to achieve a reliable average feature importance.
3.2.2. Relative Feature Importance Analysis of the Real Dataset
Given the unreliability of the connection weights method for assessing BCS feature importance, particularly for the depth feature, it was excluded from the analysis of the real dataset. Instead, the BCS feature importance for the real data were evaluated using the remaining three methods. Following the same procedure applied to the synthetic dataset, the BCS feature importances were normalized across these methods to ensure that the sum of the five BCS feature importances equaled 1 for each method, as illustrated in Figure 13.
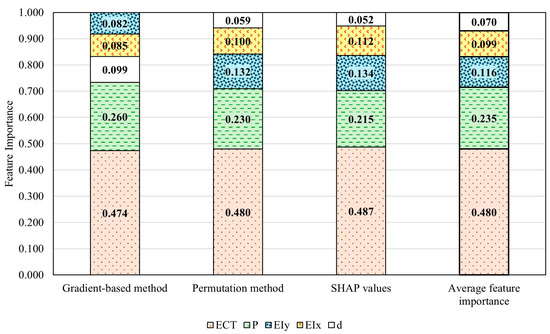
Figure 13.
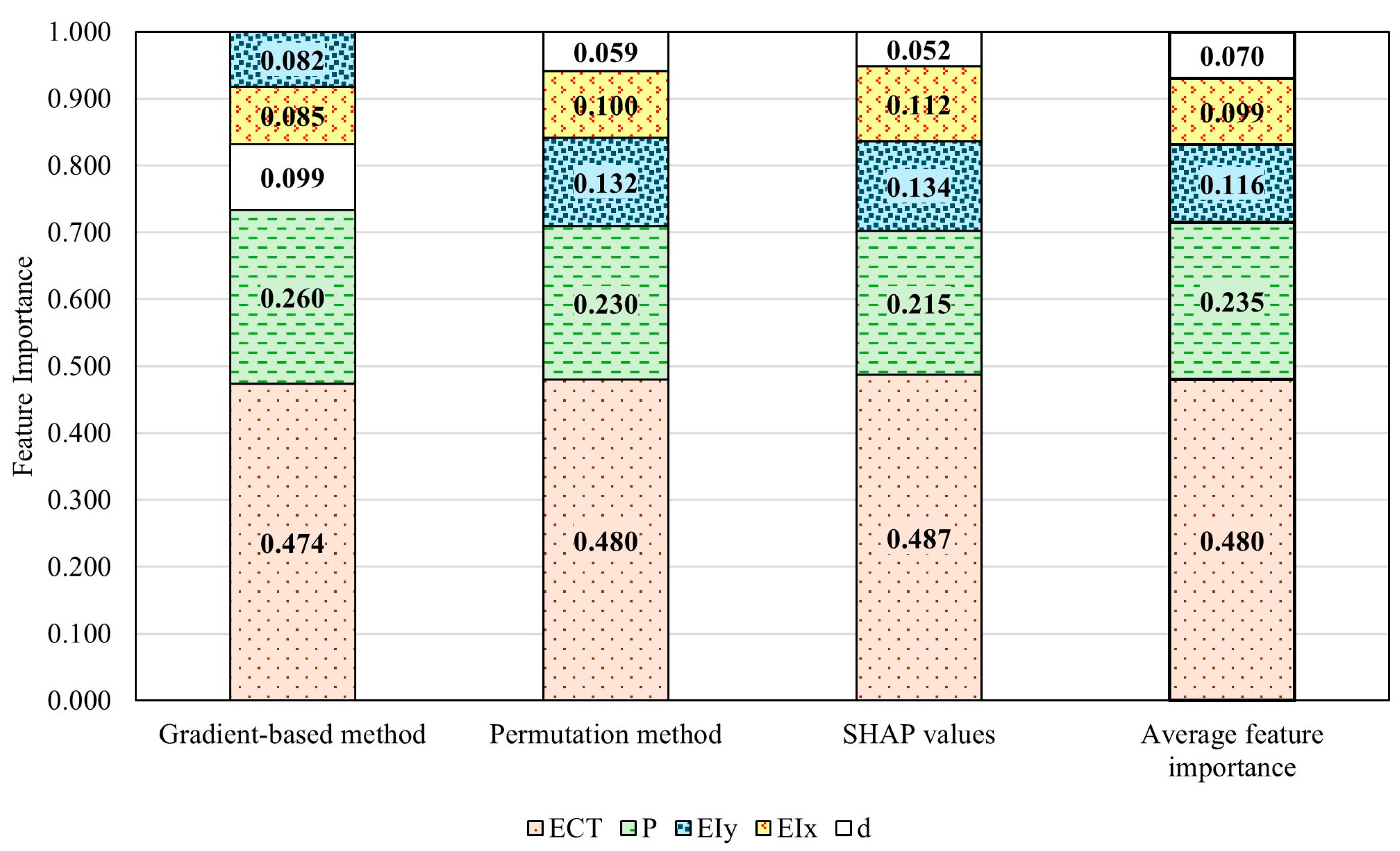
ANN-evaluated BCS feature importance of the real dataset.
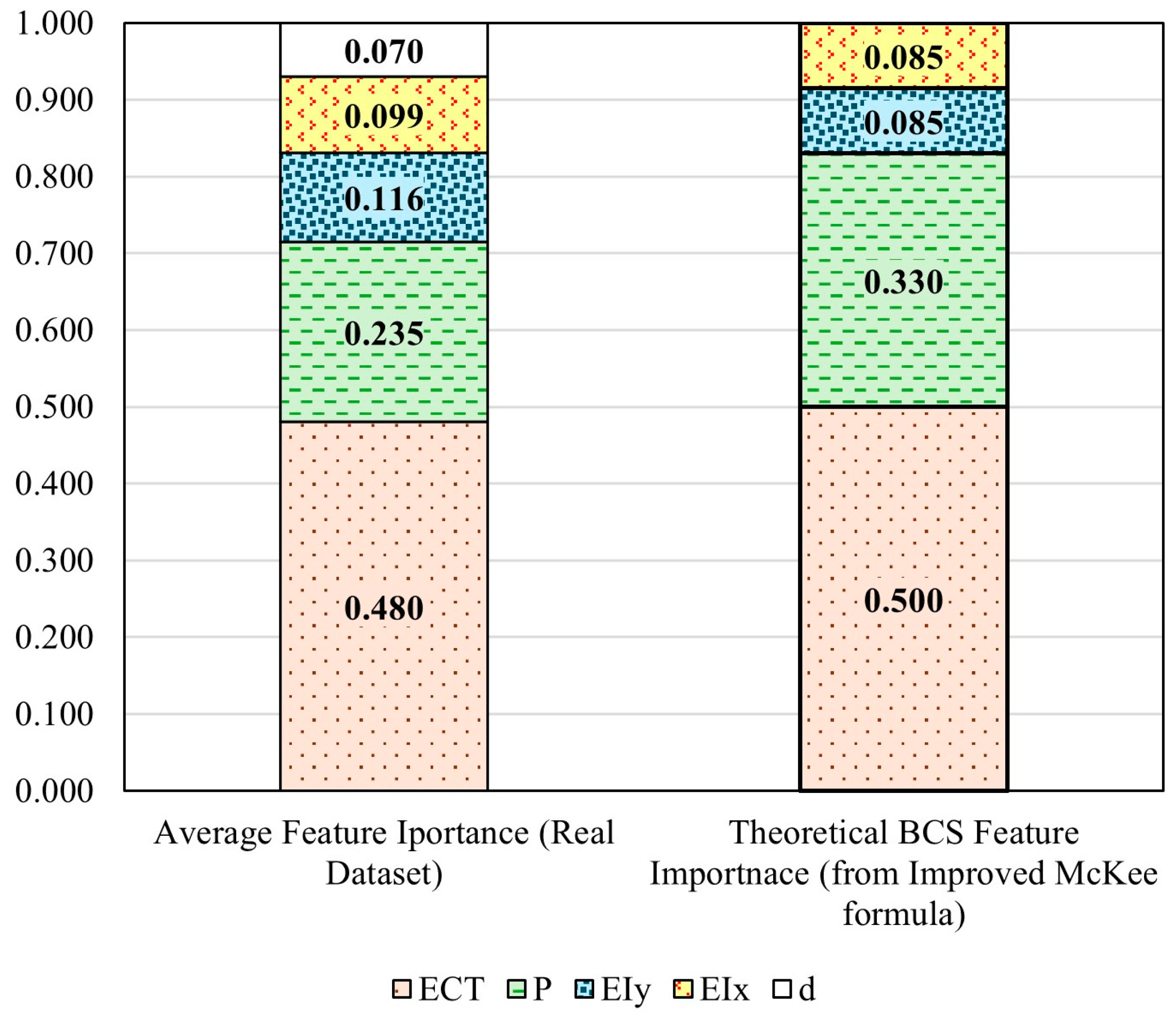
The results from the three methods demonstrate overall consistency and have been averaged to establish a comprehensive ranking of the five BCS feature importances. The average BCS feature importance is ranked as ECT > perimeter > EIy > EIx > depth, which aligns well with the theoretical BCS feature importance calculated using the mathematical model, as shown in Figure 14. The average BCS feature importance from these three methods shows that ECT has a weight of 0.480, perimeter has a weight of 0.235, EIy has a weight of 0.116, EIx 0.099, and depth has a weight of 0.070. The analysis of the real dataset reveals that, although depth is ranked last, it still has a notable influence. In general, depth remains an important factor in determining BCS (buckling compression strength). As the depth value increases, buckling theory suggests that depth can significantly affect compression strength, making it a critical consideration. Despite the McKee equation [20] theoretically assigns a zero-importance value to depth, the real-world data demonstrate that the depth’s effect should not be disregarded. Since the real dataset is derived from real-world scenarios, it naturally reflects various real-world influencing factors, including the buckling of the corrugated board under compression. Therefore, it is expected that the importance of depth is not zero. Our results emphasize the influence of depth, validating that the proposed methods for measuring feature importance accurately reflect practical applications. Furthermore, although the theoretical BCS feature importance ranks EIx EIy equally, the average importance ranking from the three methods shows a 0.017 difference between these two features. This small variation is understandable considering the fluctuations of measurement inaccuracies that mathematical models may not fully account for.
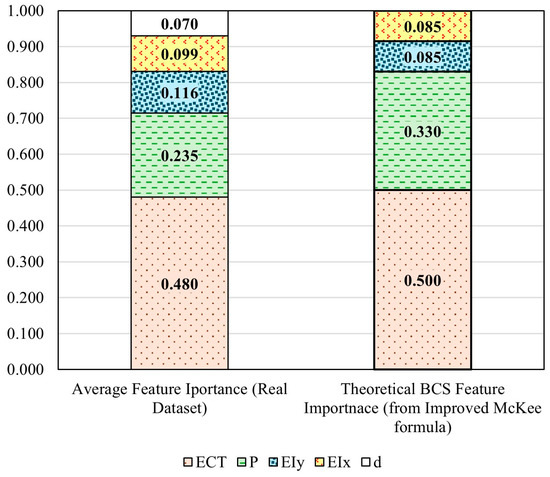
Figure 14.
Comparison of the average ANN-evaluated BCS feature importance of the real dataset and theoretical BCS feature importance calculated using the improved McKee formula.
In summary, the BCS feature importance ranking for the real dataset is consistent with the findings from the theoretical feature importance. The evaluation of the real dataset provides a real-world context to the findings and further demonstrates the capability of ANN approach in terms of feature importance evaluation for packaging design.
Based on the results of this study, there are practical implications for improving the packaging design process. On the one hand, packaging designers seeking to significantly enhance a package’s BCS can prioritize modifying key features with the greatest impact, such as the ECT of the corrugated board. A relatively small increase in ECT can enhance BCS more effectively than changes to other features, minimizing design effort. Understanding the relative importance of different factors helps designers avoid modifications with minimal impact, such as increasing the box’s depth, which has the lowest effect on BCS compared to features like ECT, perimeter, thickness, and flexural stiffness. On the other hand, when ECT is not changeable, to increase BCS, designers can first consider increasing the box dimensions for a minimal design effort and reducing material waste, rather than modifying the thickness or flexural stiffness, which would require changes to the materials or production process.
4. Discussion
The findings of this study demonstrate the effectiveness of artificial neural network (ANN)-based approaches in evaluating the relative importance of packaging design features. By applying four ANN-based methods—connection weights, gradient-based, permutation, and SHAP values, the study successfully assessed the significance of six design features influencing box compression strength (BCS). The validation of these ANN-derived feature importance rankings against theoretical values obtained from the McKee formula further supports the reliability of this approach.
The results consistently indicated that the edge crush test (ECT) is the most influential factor for BCS, followed by perimeter, thickness, and flexural stiffness in both machine and cross-machine directions. These rankings were largely consistent across the synthetic and real datasets, confirming the robustness of the ANN-based methods. Additionally, the study highlights that the permutation and gradient-based methods yield reliable rankings, whereas the connection weights method showed inconsistencies when applied to features theoretically deemed insignificant, such as depth.
Another strength lies in the versatility of the ANN framework. The adaptability of these methods enables their application beyond BCS to other packaging design properties, allowing for a more comprehensive and data-driven optimization of packaging performance. This approach could serve as a valuable tool for material cost reduction while maintaining structural integrity.
Despite the promising results, certain limitations exist. First, while the ANN-based feature importance rankings aligned well with theoretical calculations, the study was limited to six packaging design features. Other relevant factors, such as environmental conditions (humidity, temperature), dynamic load considerations, and secondary packaging influences, were not included in the analysis. Future studies should explore the integration of these additional variables to refine and enhance the accuracy of ANN-based feature importance evaluations.
Second, the study relied on two datasets—one synthetic and one real—but both were constrained to commonly used commercial packaging formats. The generalizability of the findings to more diverse or unconventional packaging structures remains uncertain. Expanding the dataset to include a broader range of packaging designs could further validate the applicability of the proposed methodology.
Additionally, while ANN models provide valuable insights into feature importance, they operate as “black box” models, making the direct interpretation of their inner workings challenging. The reliance on SHAP values and permutation techniques mitigates this issue to some extent, but further work is needed to enhance the interpretability of ANN-derived insights in the packaging domain.
For future research, several promising directions could further enhance packaging design optimization.
- Expanding Input Features: Incorporating additional packaging parameters, such as material properties, environmental factors, and manufacturing processes, could improve model accuracy and provide a more comprehensive understanding of factors influencing BCS. These aspects were not fully explored in this study but could significantly impact packaging performance.
- Enhancing Model Generalizability: Broadening the range of package types and materials in the dataset would improve the ANN model’s applicability across various industries, making it more versatile and widely usable.
- Improving Data Quality and Expanding Data: Utilizing numerical methods to generate higher-quality synthetic data or collecting real-world data from diverse sources, such as physical tested data from different companies, would enhance the model’s reliability and robustness.
- Exploring Hybrid Models: Combining ANN-based approaches with traditional simulation could yield more robust results, particularly in cases where input feature quality or dataset representativeness is a limiting factor.
- Integrating Real-Time Data and Machine Learning: Implementing real-time data collection and machine learning techniques would enable adaptive and dynamic packaging optimization, allowing designs to evolve based on continuous performance feedback.
- Incorporating Advanced Machine Learning Techniques: Utilizing advanced machine learning methods, such as reinforcement learning or other deep learning techniques, could further refine predictive accuracy and optimization, enabling a more automated and scalable approach to packaging engineering.
- Overfitting monitoring: Overfitting can lead to misleadingly high accuracy on training data but poor performance on test or validation data. In this study, overfitting was monitored and mitigated by identifying an early stopping point during training. However, future studies could incorporate additional techniques such as regularization, dropout, and cross-validation to further reduce the risk of overfitting and enhance the model’s real-world performance.
5. Conclusions
This study introduces a novel method for evaluating the importance of packaging design features using four ANN-based approaches: the connection weights method, the gradient-based method, the permutation method, and the SHAP values. Using BCS as a representative packaging design property, the relative importance of up to six BCS features was assessed through these ANN-based approaches. One synthetic dataset derived from the well-established mathematical model (McKee formula) and one real dataset were used as two case studies for training ANN model and obtaining the feature importance influencing BCS. The feature importance rankings provided by the ANN approaches were consistent with the theoretical feature importance calculated using the mathematical model across both datasets. This result highlights the effectiveness of the ANN approach in evaluating feature importance in packaging design, allowing for a more efficient and accurate assessment of the relative impact of various design features, positioning it as a transformative tool for optimizing packaging performance and material efficiency. This allows designers to focus on the most influential features, leading to reduced material usage and overall costs. For instance, to increase BCS, designers can first consider increasing the box dimensions for a minimal design effort and reduced material waste, rather than modifying the thickness or flexural stiffness, which would require changes to the materials or production process. Overall, this study offers a novel approach to assessing packaging design feature importance effectively through ANN techniques, providing practical insights for improving material efficiency and cost-effectiveness. This method can be easily applied to evaluate the relative importance of other packaging properties beyond BCS, making it a valuable tool for a wide range of packaging optimization tasks using ANN approaches.
Author Contributions
Conceptualization, E.L. and J.G.; Methodology, J.G. and E.L.; Software, J.G.; Formal Analysis, J.G. and E.L.; Investigation, J.G.; Data Curation, J.G.; Validation, E.L.; Visualization, J.G. and E.L.; Writing—original draft, J.G. and E.L.; Writing—review and editing, J.G. and E.L.; Supervision, E.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data that support the findings of this study are available on request from the corresponding author. The data are not publicly available due to privacy or ethical restrictions.
Acknowledgments
The author would like to thank the Packaging Corporation of America for providing the datasets used in this study, as well as for their valuable guidance and feedback on the writing and editing process.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Zhang, L.; Lu, J.; Cao, G.; Miao, H. Research on packaging evaluation system of fast moving consumer goods based on analytical hierarchy process method. In Advanced Graphic Communications and Media Technologies; Springer: Berlin/Heidelberg, Germany, 2017. [Google Scholar]
- Pérez, A.; Villena, J.; Matuk, D.; Luna, A.; Chong, M. An analytical hierarchy approach applied in the packaging supply chain. In Supply Chain Management and Logistics in Emerging Markets: Selected Papers from the 2018 MIT SCALE Latin America Conference; Emerald Publishing Limited: Warrington, UK, 2020. [Google Scholar]
- Fadiji, T.; Coetzee, C.J.; Berry, T.M.; Ambaw, A.; Opara, U.L. The efficacy of finite element analysis (FEA) as a design tool for food packaging: A review. Biosyst. Eng. 2018, 174, 20–40. [Google Scholar] [CrossRef]
- Hicks, B.J.; Mullineux, G.; Sirkett, D. A finite element-based approach for whole-system simulation of packaging systems for their improved design and operation. Packag. Technol. Sci. Int. J. 2009, 22, 209–227. [Google Scholar] [CrossRef]
- Park, J.; Park, M.; Choi, D.S.; Jung, H.M.; Hwang, S.W. Finite element-based simulation for edgewise compression behavior of corrugated paperboard for packaging of agricultural products. Appl. Sci. 2020, 10, 6716. [Google Scholar] [CrossRef]
- Nefeslioglu, H.A.; Sezer, E.A.; Gokceoglu, C.; Ayas, Z. A modified analytical hierarchy process (M-AHP) approach for decision support systems in natural hazard assessments. Comput. Geosci. 2013, 59, 1–8. [Google Scholar] [CrossRef]
- Nygårds, M.; Hallbäck, N.; Just, M.; Tryding, J. A finite element model for simulations of creasing and folding of paperboard. In Abaqus Users’ Conference; ABAQUS, Inc.: Stockholm, Sweden, 2005. [Google Scholar]
- Garbowski, T.; Gajewski, T.; Grabski, J.K. Estimation of the compressive strength of corrugated cardboard boxes with various perforations. Energies 2021, 14, 1095. [Google Scholar] [CrossRef]
- Alper, M.M.; Sezen, B.; Balcıoğlu, Y.S. Machine Learning Applications in Packaging Industry Optimization: A Systematic Literature Review and Future Research Directions. In International Newyork Congress Conference; BZT TURAN Publishing House: Baku, Azerbaijan, 2025. [Google Scholar]
- Kazeruni, M.; Ince, A. Data-driven artificial neural network for elastic plastic stress and strain computation for notched bodies. Theor. Appl. Fract. Mech. 2023, 125, 103917. [Google Scholar] [CrossRef]
- Tsaur, S.-H.; Chiu, Y.-C.; Huang, C.-H. Determinants of guest loyalty to international tourist hotels—A neural network approach. Tour. Manag. 2002, 23, 397–405. [Google Scholar] [CrossRef]
- Iqbal, J.; Saeed, A.; Khan, R.A. The relative importance of textual indexes in predicting the future performance of banks: A connection weight approach. Borsa Istanb. Rev. 2023, 23, 240–253. [Google Scholar] [CrossRef]
- Goh, A.T. Back-propagation neural networks for modeling complex systems. Artif. Intell. Eng. 1995, 9, 143–151. [Google Scholar] [CrossRef]
- Ombres, L.; Aiello, M.A.; Cascardi, A.; Verre, S. Modeling of steel-reinforced grout composite system-to-concrete bond capacity using artificial neural networks. J. Compos. Constr. 2024, 28, 04024034. [Google Scholar] [CrossRef]
- John, S.K.; Cascardi, A.; Nadir, Y.; Aiello, M.A.; Girija, K. A New Artificial Neural Network Model for the Prediction of the Effect of Molar Ratios on Compressive Strength of Fly Ash-Slag Geopolymer Mortar. Adv. Civ. Eng. 2021, 2021, 6662347. [Google Scholar] [CrossRef]
- Tavar, M.; Rabbani, H.; Gholami, R.; Ahmadi, E.; Kurtulmus, F. Investigating the Effect of Packaging Conditions on the Properties of Peeled Garlic by Using Artificial Neural Network (ANN). Packag. Technol. Sci. 2024, 37, 755–767. [Google Scholar] [CrossRef]
- Ahmed, A.R.; Aleid, S.M.; Mohammed, M. Impact of Modified Atmosphere Packaging Conditions on Quality of Dates: Experimental Study and Predictive Analysis Using Artificial Neural Networks. Foods 2023, 12, 3811. [Google Scholar] [CrossRef] [PubMed]
- El-Mesery, H.S.; Adelusi, O.A.; Ghashi, S.; Njobeh, P.B.; Hu, Z.; Kun, W. Effects of storage conditions and packaging materials on the postharvest quality of fresh Chinese tomatoes and the optimization of the tomatoes’ physiochemical properties using machine learning techniques. LWT 2024, 201, 116280. [Google Scholar] [CrossRef]
- Brazolin, I.F.; Sousa, F.M.M.; Dos Santos, J.W.S.; Concha, V.O.C.; Da Silva, F.V.; Yoshida, C.M.P. A method for pH food dependent shelf-life prediction of intelligent sustainable packaging device using artificial neural networks. J. Appl. Polym. Sci. 2024, 141, e55646. [Google Scholar] [CrossRef]
- Gajewski, T.; Grabski, J.K.; Cornaggia, A.; Garbowski, T. On the use of artificial intelligence in predicting the compressive strength of various cardboard packaging. Packag. Technol. Sci. 2024, 37, 97–105. [Google Scholar] [CrossRef]
- Malasri, S.; Rayapati, P.; Kondeti, D. Predicting corrugated box compression strength using an artificial neural network. Int. J. 2016, 4, 169–176. [Google Scholar] [CrossRef][Green Version]
- Da Costa, N.L.; De Lima, M.D.; Barbosa, R. Evaluation of feature selection methods based on artificial neural network weights. Expert Syst. Appl. 2021, 168, 114312. [Google Scholar] [CrossRef]
- Zobel, C.W.; Cook, D.F. Evaluation of neural network variable influence measures for process control. Eng. Appl. Artif. Intell. 2011, 24, 803–812. [Google Scholar] [CrossRef]
- Garson, G.D. Interpreting neural-network connection weights. AI Expert 1991, 6, 46–51. [Google Scholar]
- Hill, A.; Lucet, E.; Lenain, R. A novel gradient feature importance method for neural networks: An application to controller gain tuning for mobile robots. In Proceedings of the International Conference on Informatics in Control, Automation and Robotics, Online, 7–9 July 2020; Springer: Cham, Germany, 2020. [Google Scholar]
- Fukumizu, K.; Leng, C. Gradient-based kernel method for feature extraction and variable selection. Adv. Neural Inf. Process. Syst. 2012, 25, 2114–2122. [Google Scholar]
- Iooss, B.; Saltelli, A. Introduction to sensitivity analysis. In Handbook of Uncertainty Quantification; Springer: Cham, Germany, 2017; pp. 1103–1122. [Google Scholar]
- Lundberg, S.M.; Lee, S.-I. A unified approach to interpreting model predictions. Adv. Neural Inf. Process. Syst. 2017, 30, 4768–4777. [Google Scholar]
- Mandler, H.; Weigand, B. Feature importance in neural networks as a means of interpretation for data-driven turbulence models. Comput. Fluids 2023, 265, 105993. [Google Scholar] [CrossRef]
- Altmann, A.; Toloşi, L.; Sander, O.; Lengauer, T. Permutation importance: A corrected feature importance measure. Bioinformatics 2010, 26, 1340–1347. [Google Scholar] [CrossRef] [PubMed]
- Li, Z. Extracting spatial effects from machine learning model using local interpretation method: An example of SHAP and XGBoost. Comput. Environ. Urban Syst. 2022, 96, 101845. [Google Scholar] [CrossRef]
- Urbanik, T.J.; Frank, B. Box compression analysis of world-wide data spanning 46 years. Wood Fiber Sci. 2006, 38, 399–416. [Google Scholar]
- Frazier, P.I. A tutorial on Bayesian optimization. arXiv 2018, arXiv:1807.02811. [Google Scholar]
- Will, K. A Conceptual Explanation of Bayesian Hyperparameter Optimization for Machine Learning. Towards Data Sci. 2018, 24. Available online: https://medium.com/towards-data-science/a-conceptual-explanation-of-bayesian-model-based-hyperparameter-optimization-for-machine-learning-b8172278050f (accessed on 13 March 2025).
- Akaike, H. Information theory and an extension of the maximum likelihood principle. In Selected Papers of Hirotugu Akaike; Springer: New York, NY, USA, 1998; pp. 199–213. [Google Scholar]
- Schwarz, G. Estimating the Dimension of a Model. Ann. Stat. 1978, 6, 461–464. [Google Scholar] [CrossRef]
- Hebbian Theory. 11 January 2025 (UTC). Available online: https://en.wikipedia.org/wiki/Hebbian_theory (accessed on 20 December 2024).
- Lecun, Y.; Denker, J.; Solla, S. Optimal brain damage. In Proceedings of the 3rd International Conference on Neural Information Processing Systems; MIT Press: Cambridge, MA, USA, 1989; pp. 598–605. [Google Scholar]
- Jeon, G.; Jeong, H.; Choi, J. Distilled gradient aggregation: Purify features for input attribution in the deep neural network. Adv. Neural Inf. Process. Syst. 2022, 35, 26478–26491. [Google Scholar]
- Azmat, M.; Alessio, A.M. Feature Importance Estimation Using Gradient Based Method for Multimodal Fused Neural Networks. In Proceedings of the 2022 IEEE Nuclear Science Symposium and Medical Imaging Conference (NSS/MIC), Milano, Italy, 5–12 November 2022. [Google Scholar]
- Van Den Broeck, G.; Lykov, A.; Schleich, M.; Suciu, D. On the tractability of SHAP explanations. J. Artif. Intell. Res. 2022, 74, 851–886. [Google Scholar] [CrossRef]
- Štrumbelj, E.; Kononenko, I. Explaining prediction models and individual predictions with feature contributions. Knowl. Inf. Syst. 2014, 41, 647–665. [Google Scholar] [CrossRef]
- Gu, J.; Frank, B.; Lee, E. A comparative analysis of artificial neural network (ANN) architectures for box compression strength estimation. Korean J. Packag. Sci. Technol. 2023, 29, 163–174. [Google Scholar] [CrossRef]
- Mckee, R.; Gander, J.; Wachuta, J. Compression strength formula for corrugated boxes. Paperboard Packag. 1963, 48, 149–159. [Google Scholar]
- Pyr’yev, Y.; Kibirkštis, E.; Gegeckienė, L.; Vaitasius, K.; Venytė, I. Empirical models for prediction compression strength of paperboard carton. Wood Fiber Sci. 2022, 54, 60–73. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).