Assessment of Structural Integrity Through On-Site Decision-Making Analysis for a Jacket-Type Offshore Platform
Abstract
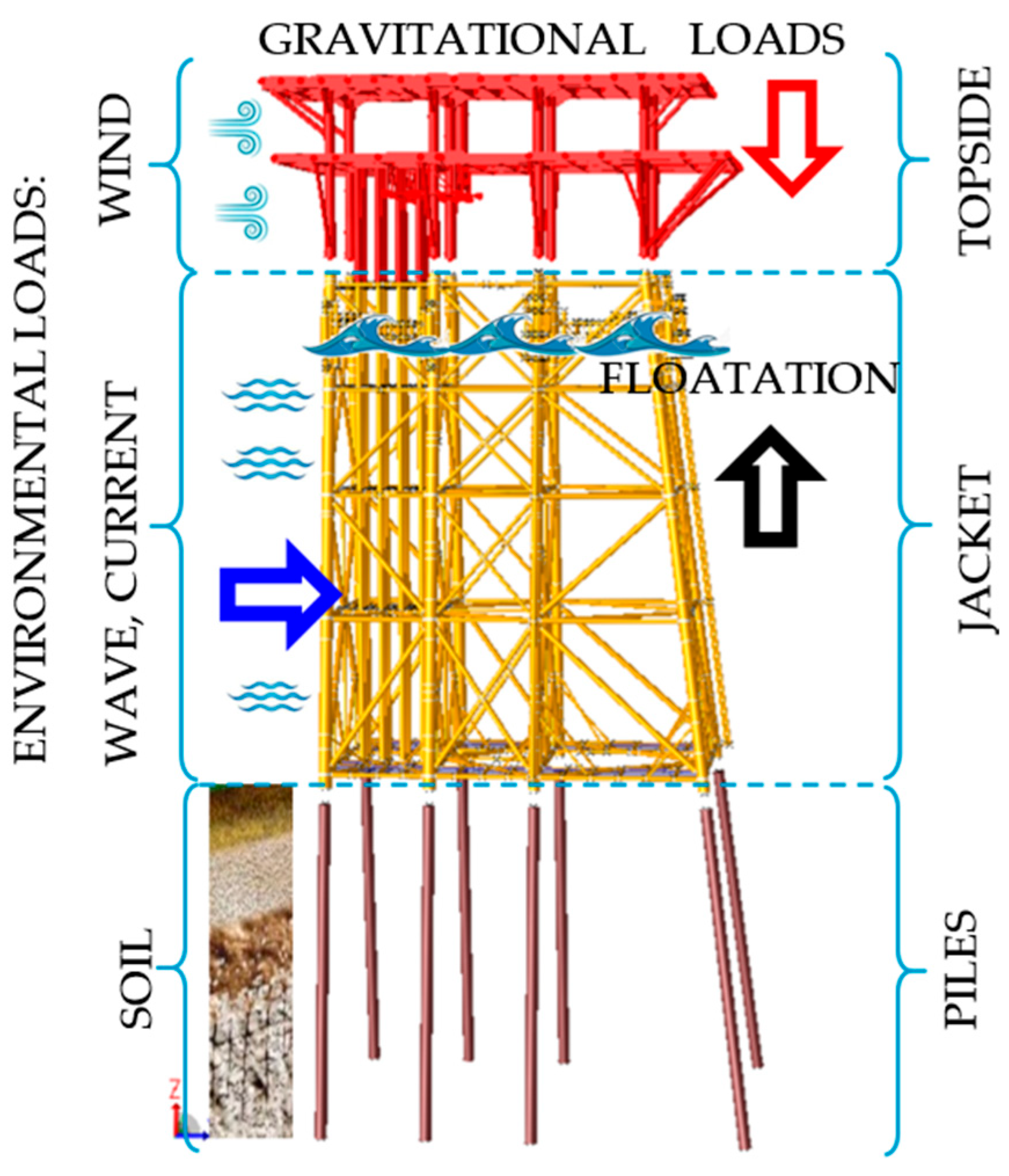
1. Introduction
2. Materials and Methods
3. Linear Analysis
3.1. Linearization of the Foundation (Applicable to Dynamic Storm, Seismic Resistance, and Fatigue Analysis)
3.2. Determination of Dynamic Properties (Applicable to Dynamic Storm, Seismic Resistance, and Fatigue Analysis)
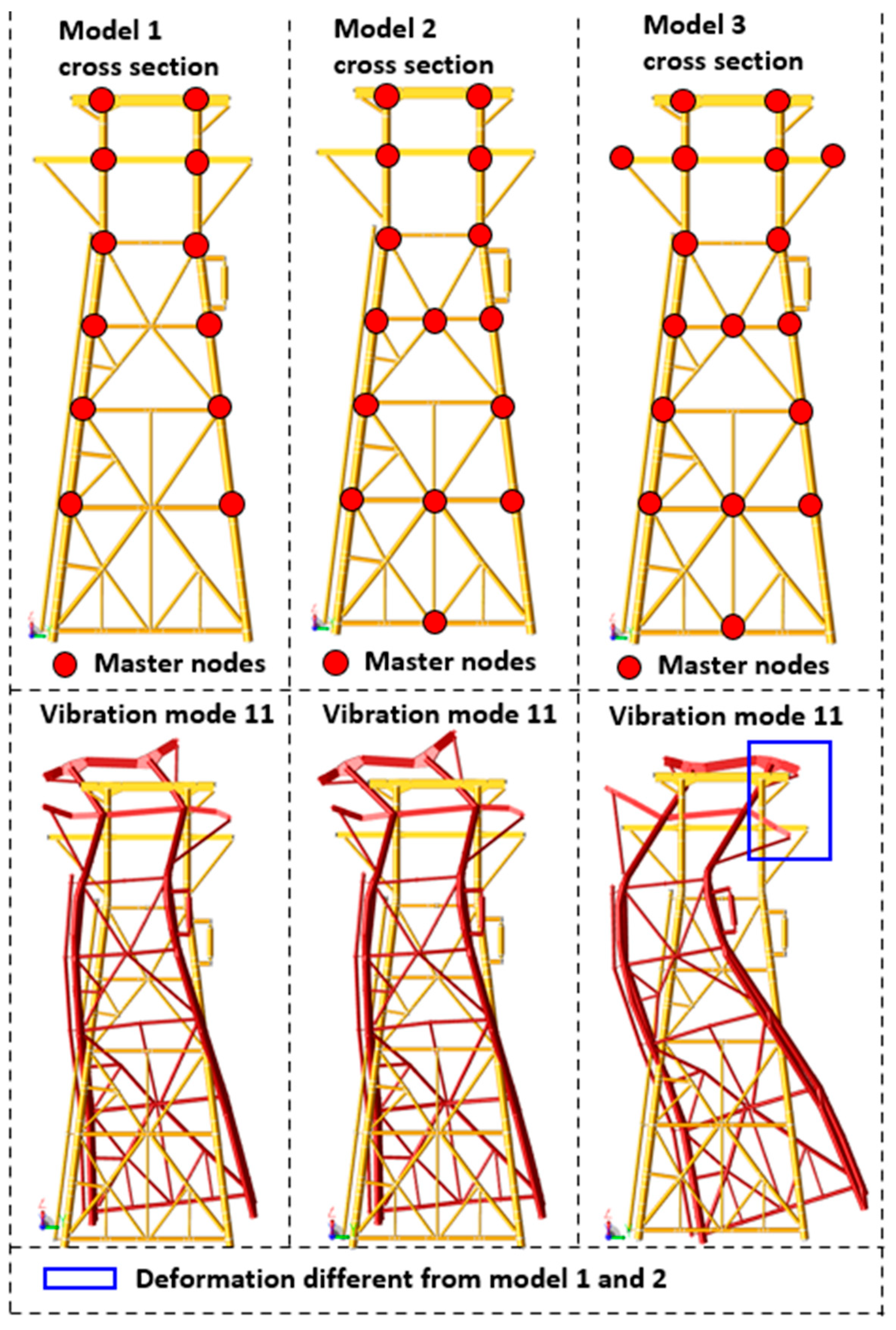
- Model 1: Masses concentrated solely at axis intersections.
- Model 2: Masses concentrated at axis intersections and x-brace connections of the jacket.
- Model 3: Similar to Model 2, but with additional mass concentrations on diagonal members supporting cantilevers in the topside (see Figure 4). This figure also illustrates the platform deformation in mode 11, revealing similar deformation patterns across models.
- The highest natural period across all models is 2.70 s along the X-axis, with mass participation factors exceeding 83%.
- Along the Y-axis, the highest period is approximately 2.5 s, with mass participation factors around 79%.
- In the Z-axis, the maximum mass participation factor occurs in mode 11 for Models 1 and 2, whereas for Model 3, it occurs in mode 12. These variations influence the final results, as detailed in Section 5.3.
3.3. Structural Evaluation Under Dynamic and Spectral Loading Conditions
3.3.1. Dynamic Storm Analysis—Wave Response
- Inertia loads are derived from modal accelerations.
- Hydrodynamic loads account for forces exerted by fluid motion and platform interaction.
3.3.2. Resistance-Level Analysis—Spectral Modal Seismic Analysis
3.3.3. Spectral Fatigue Analysis—Transfer Functions
- is the frequency-dependent transfer function.
- is the generalized stiffness.
- is the excitaion frequency.
- is the natural frequency of the system.
- is the damping ratio.
4. Nonlinear Analysis (Pushover)
4.1. Ultimate Wave Resistance Analysis
4.2. Seismic Analysis by Ductility
- The gravity load is incrementally applied in steps of 10% until reaching the total design gravity load (100%).
- The seismic load is then applied in 5% increments until reaching 100% of the prescribed seismic load. Subsequently, the incremental application of the seismic load continues at 5% intervals until the collapse mechanism of the structure is fully developed.
5. Results and Discussion
5.1. Operational and Static Storm Analysis
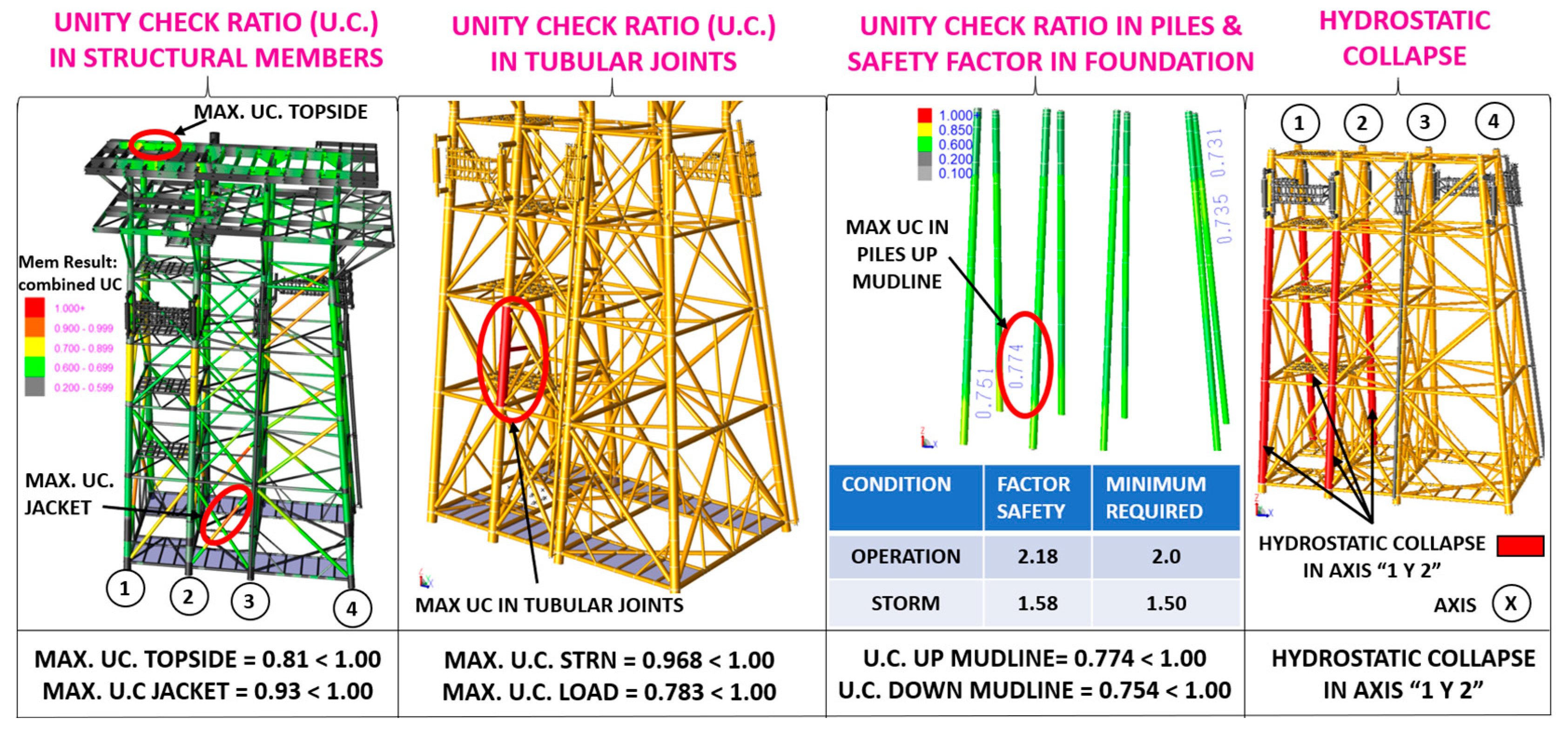
- Stress Interaction and Unity Check (UC) Analysis. The maximum UC in the substructure (jacket) was found to be 0.93, while the maximum UC in the superstructure (topside) was 0.81, both of which are below the threshold value of 1.0, ensuring compliance with regulatory standards.
- Tubular Joint Penetration Analysis. Tubular joints were evaluated for penetration load and structural resistance (STRN), with results of 0.968 and 0.783, respectively. Since both values are below unity, they comply with the current standards.
- Pile Stress Interaction and Load Safety Factors. The maximum UC for piles above the seabed (mudline) was 0.774, whereas for piles below the seabed, it was 0.754, both within the acceptable range. The axial load safety factors in the foundation exceeded the minimum regulatory requirements, with an operational value of 2.18 (>2.00 required) and storm condition value of 1.58 (>1.50 required), confirming compliance with industry standards.
- Hydrostatic Collapse Assessment and Mitigation Strategies. Localized overstress was identified in the columns along axes 1 and 2, necessitating corrective measures. The following solutions are recommended based on platform status:
- -
- For pre-installed but uninstalled structures: Reinforcement using 1.00-inch (25.4 mm) thick rings with a 12-inch (305 mm) spacing, as guided by SACS redesign recommendations. However, this approach may be impractical for installed structures due to the high cost of underwater welding.
- -
- For structures in the design phase: Modifications include increasing pipe thickness or incorporating anchor bolts to enhance structural resistance.
- -
- For installed structures: Cementing the affected elements can enhance structural properties and mitigate hydrostatic collapse risks.
5.2. Dynamic Storm Analysis
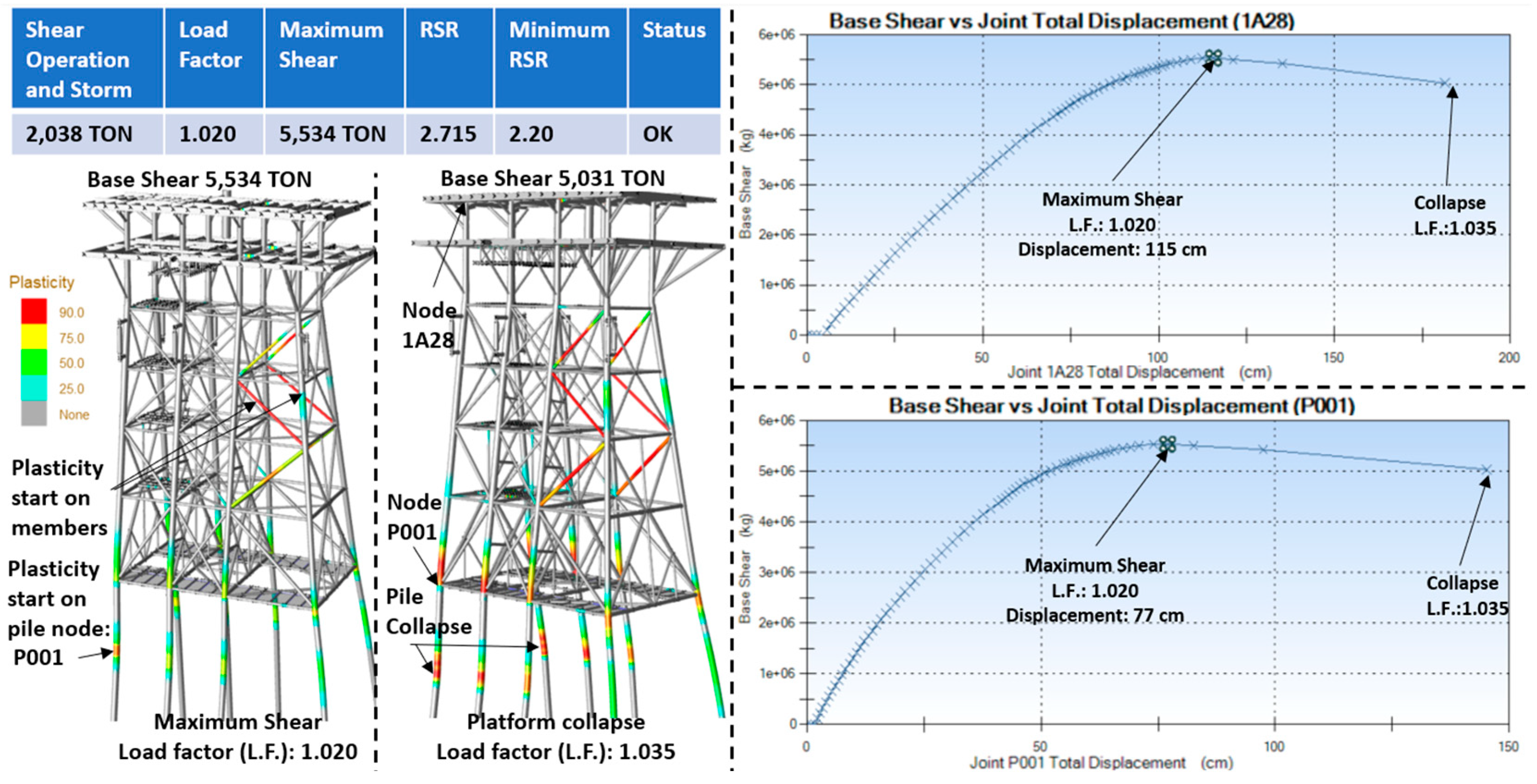
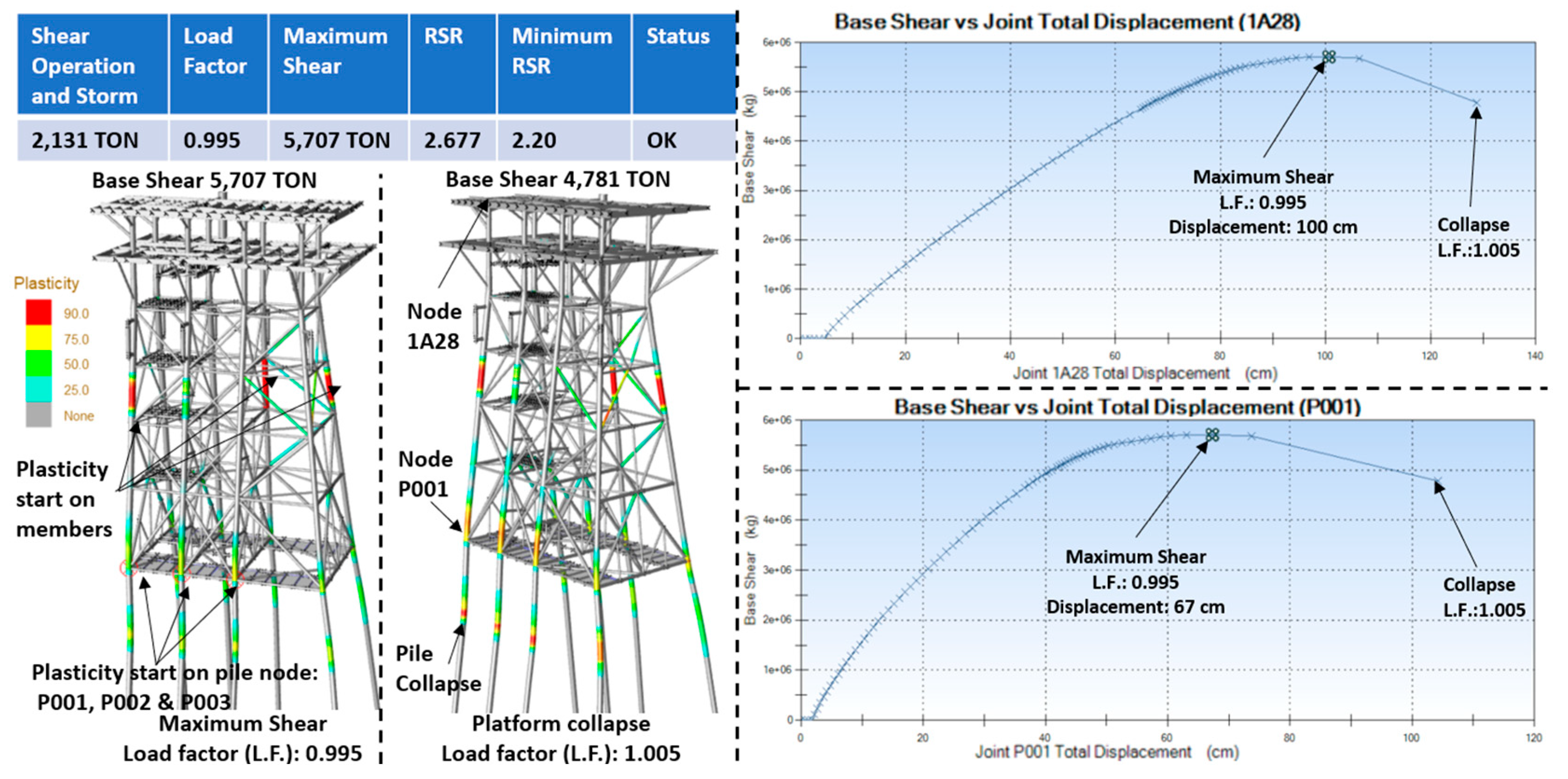
5.3. Seismic Resistance Analysis
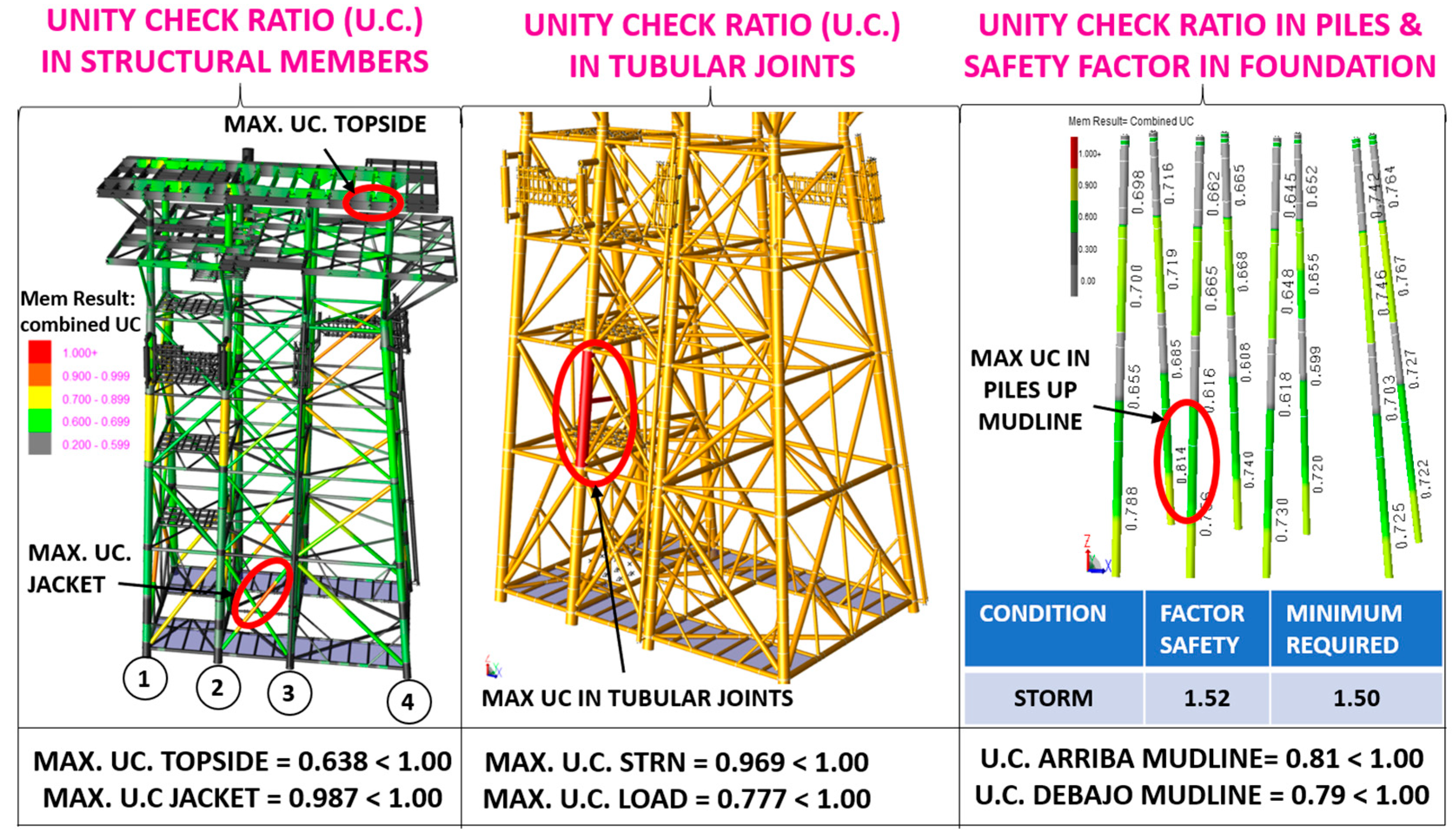
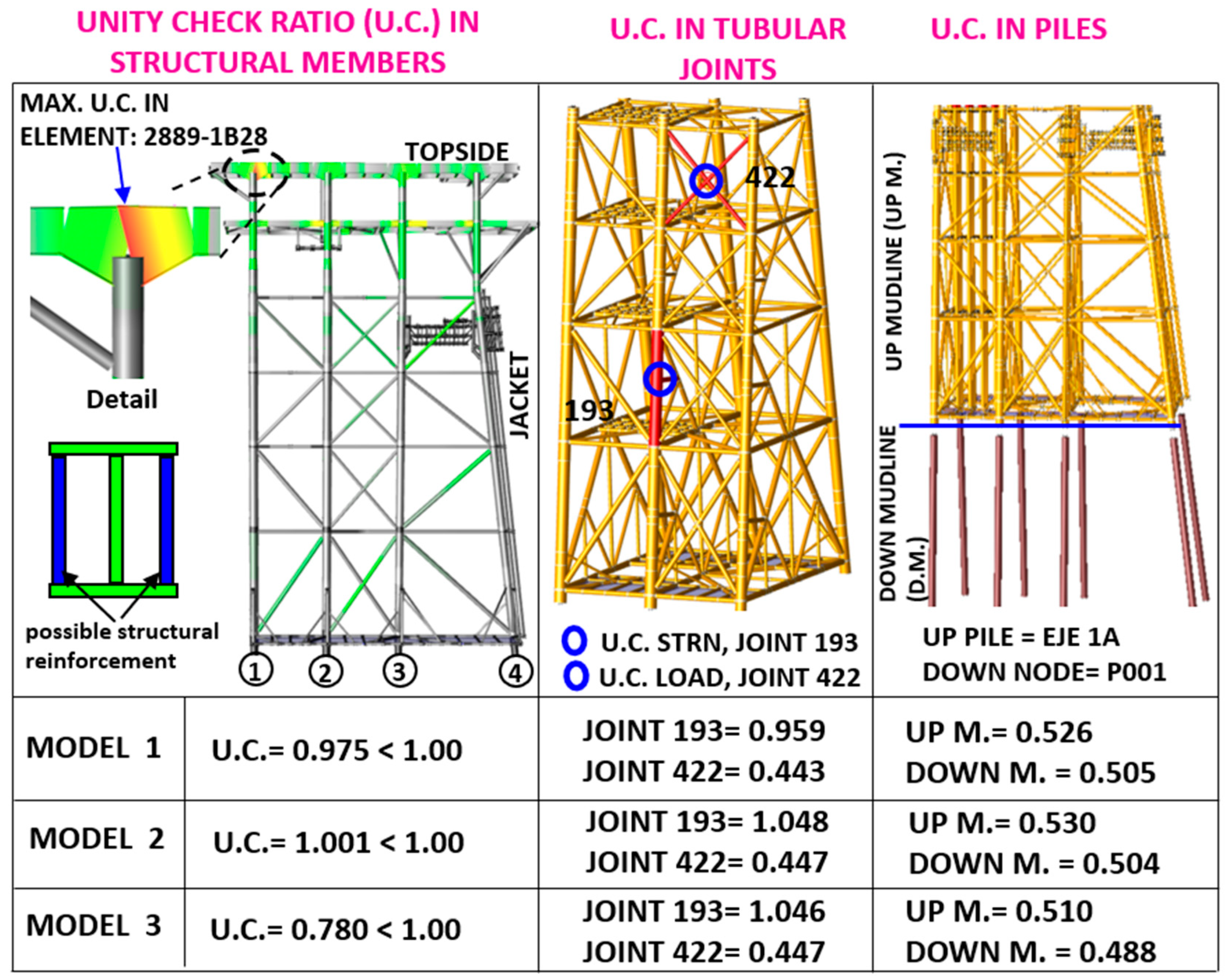
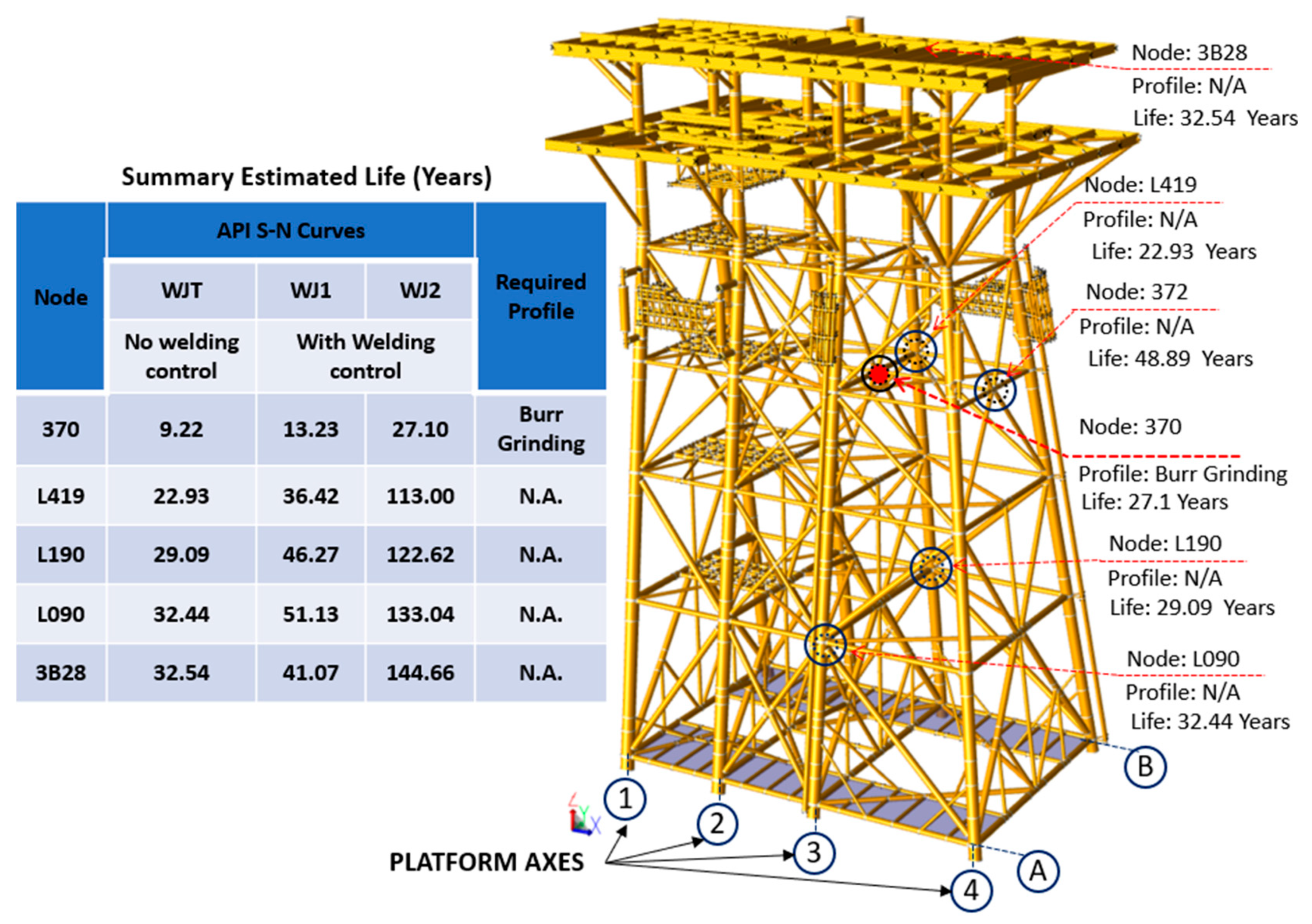
- The maximum unity check (UC) occurs in element 2289-1B28, with a value of 1.001 > 1.00 (exceeding the allowable limit). To address this, the following reinforcement strategies are proposed:
- ○
- Increasing the thickness of the web or flange.
- ○
- Encasing the section with lateral plates to form secondary and tertiary webs at the extremities.
- ○
- Enhancing the yield strength of the material.
- Regarding the assessment of tubular joints, joint 193 exhibits a U.C. of 1.048 > 1.00 (exceeding the allowable limit). The following strengthening solutions are recommended:
- ○
- Increasing the tube thickness.
- ○
- Reinforcing with stiffener plates.
- ○
- Injecting cementitious material inside the tube for additional stiffness and load-bearing capacity.
- U.C. in Piles and Load Safety Factors in the Foundation. The piles were assessed to ensure compliance with design requirements. The maximum U.C. for piles above the seabed (mudline) was 0.530, whereas for those below the seabed, it was 0.504, with both values being within acceptable limits. Furthermore, the safety factor for axial load in the piles was 2.04 > 2.00 (meeting the minimum required threshold). These results confirm that the foundation adheres to the parameters established in the applicable design standards, as illustrated in Figure 8.
5.4. Results of Seismic Ductility Analysis
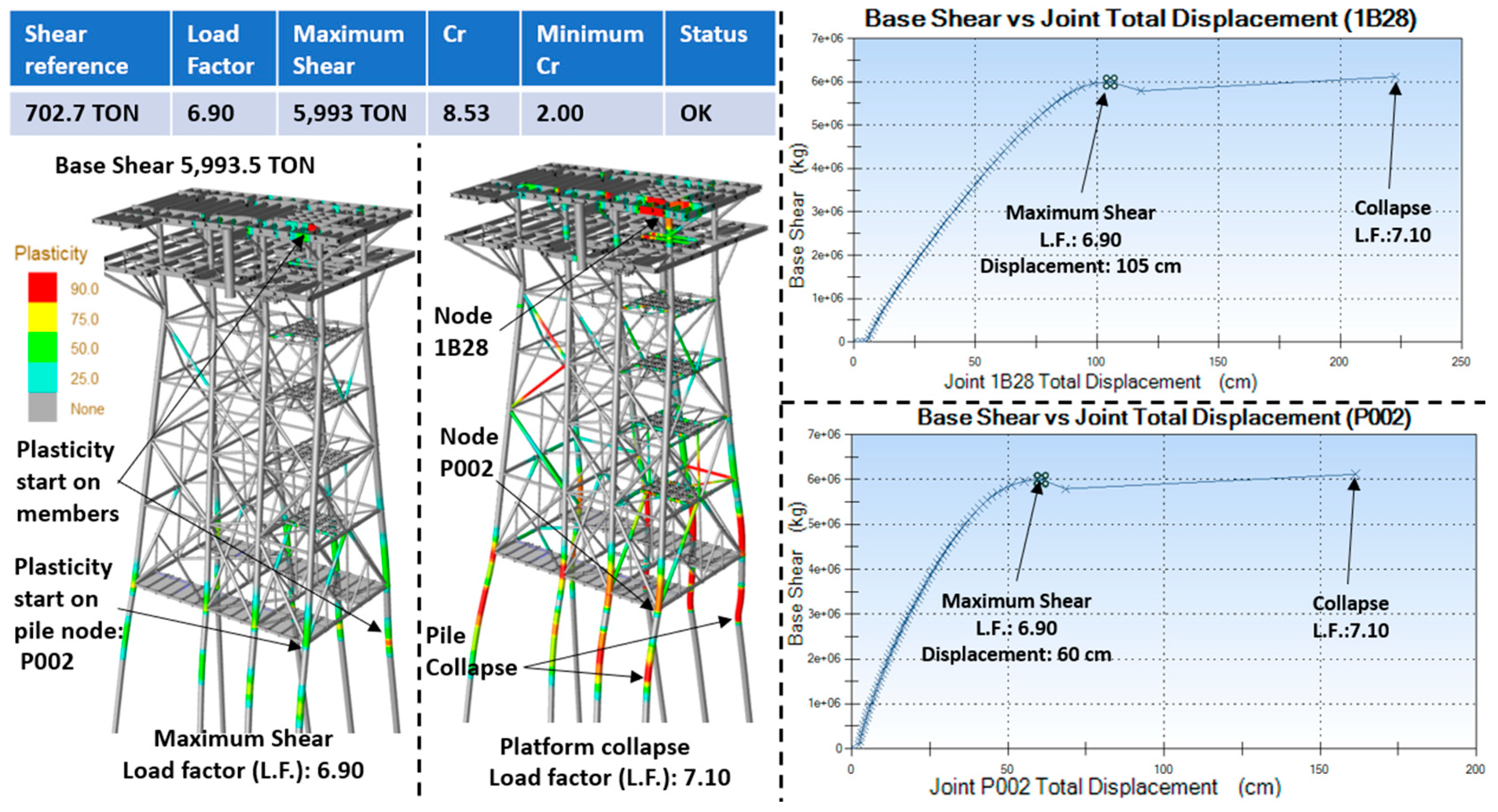
5.5. Results of Ultimate Resistance Analysis for Wave Loads
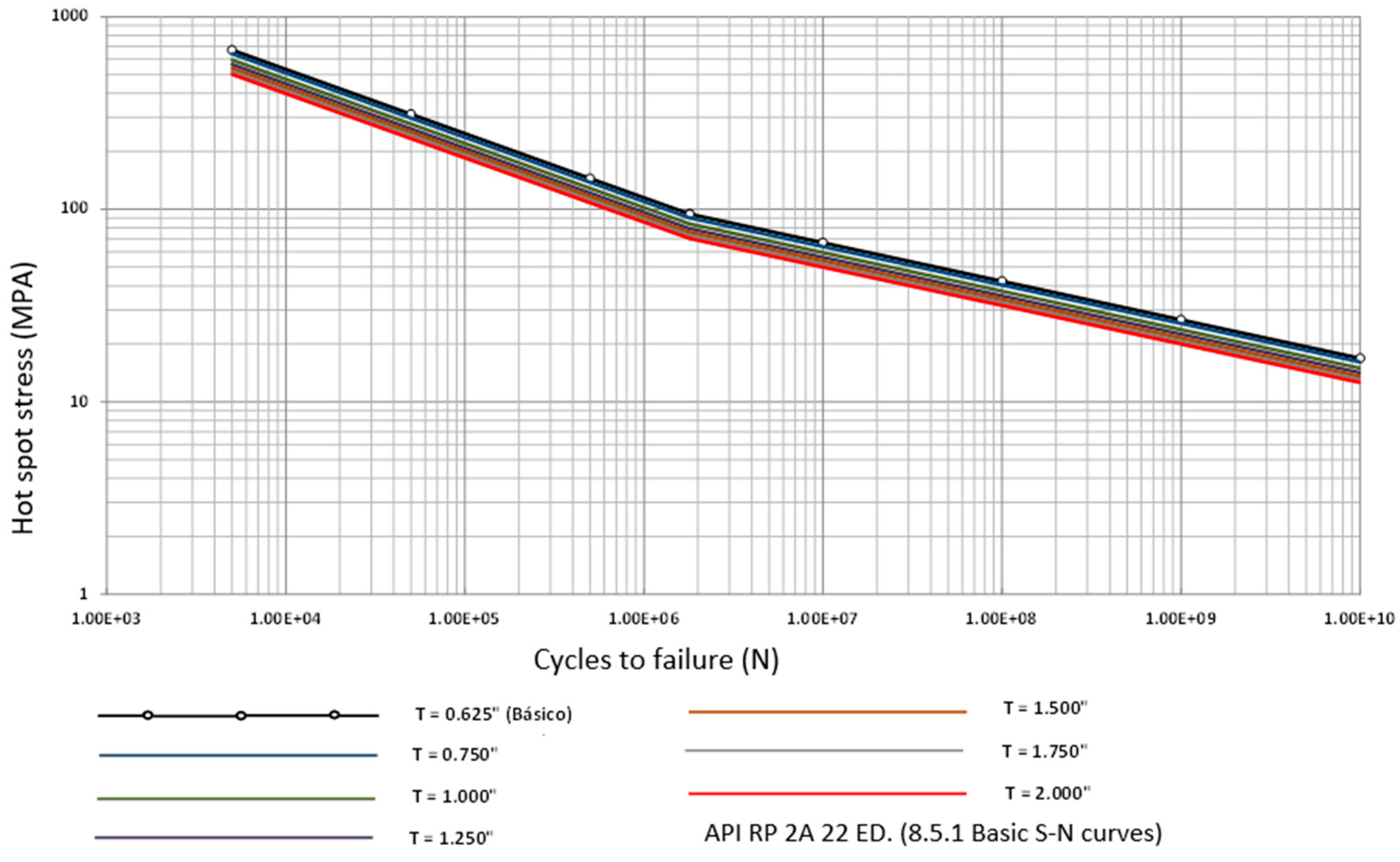
5.6. Spectral Fatigue Analysis
- For structures in the design phase: Increasing thickness, diameter, or yield strength, as well as reinforcing with internal plates or external ring-shaped stiffeners.
- For already constructed but uninstalled structures: Reinforcement using external ring plates.
- For installed offshore structures: The most frequently utilized method involves cement injection within the tubular section.
6. Conclusions
- The static operation and storm analysis includes the evaluation of unity checks (UCs) in structural elements, tubular joints, piles, and safety factors to ensure compliance with the design criteria.
- The dynamic storm analysis considers the influence of vibration modes and periods on the platform’s response. The findings indicate that this analysis results in more unfavorable conditions compared to the static operation and storm analysis.
- For the strength-level seismic analysis, different master node configurations were evaluated, highlighting their impact on U.C. assessments in structural elements, tubular joints, and piles. This study proposes reinforcement solutions for elements that do not meet the regulatory requirements.
- The seismic ductility analysis reveals that the collapse mechanism initiates in the topside structure, reaching the Cr factor in all analyzed directions.
- In the ultimate wave resistance analysis, the collapse mechanism is observed to originate in the jacket structure, with the platform meeting the required reserve strength ratio (RSR) in all eight analyzed directions.
- The spectral fatigue analysis provides insights into the behavior of tubular joints under different S–N curves. The results indicate that the fatigue life of all tubular joints is reached within the expected operational period.
- Through the execution of these analyses, the structural behavior of the platform under both linear and nonlinear static conditions can be assessed, allowing for the identification of critical zones requiring reinforcement. Furthermore, compliance with regulatory standards is verified to ensure the structural integrity and performance of the platform under various loading scenarios throughout its service life.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| SACS | Structural Analysis Computer System |
| U.C. | Unity checks |
| API | American Petroleum Institute |
| API RP 2A-WSD | Planning, Designing and Constructing Fixed Offshore Platforms—Working Stress Design |
| AISC | American Institute of Steel Construction |
| IMCA | Instituto Mexicano de la Construcción del Acero |
| Pemex | Petroleos Mexicanos |
| Cr | Ratio between the ultimate lateral load resisting the platform before collapse |
| RSR | Resistance Reserve Factor |
| S–N | Curve stress interval vs. number of cycles |
| DNV GL | DNV (Det Norske Veritas) y GL (Germanischer Lloyd) |
| FE | Finite element |
| ARMAX | Autoregressive moving average model with exogenous inputs |
| SCFs | Concentration factors |
| WAVEWATCH III | Wave data simulator |
| PoF | Probability of Failure |
| N | Order of the stream function |
| k | Wave number |
| TLP | Tension Leg Platform |
| CQC | Complete quadratic combination |
| SRSS | Square root of the sum of the squares |
| H(f) | Mechanical transfer function |
| Ki | Generalized stiffness |
| fn | Natural frequency |
| c | Percent damping |
| STRN | Strength |
| ISO | International Organization for Standardization |
| D | Fatigue damage |
References
- Petróleos Mexicanos. (s.f.). Estadísticas Petroleras. Available online: https://www.pemex.com/ri/Publicaciones/Paginas/IndicadoresPetroleros.aspx (accessed on 1 July 2023).
- Petróleos Mexicanos. (n.d.). Volumen de las Exportaciones de Petróleo Crudo. Available online: https://www.pemex.com/ri/Publicaciones/Indicadores%20Petroleros/evolexporta_esp.pdf (accessed on 4 November 2024).
- Petróleos Mexicanos. (n.d.). Valor de las Exportaciones de Petróleo Crudo. Available online: https://www.pemex.com/ri/Publicaciones/Indicadores%20Petroleros/evalorexporta_esp.pdf (accessed on 4 November 2024).
- Petróleos Mexicanos. Plan de Negocios 2023–2027. 2023. Available online: https://www.pemex.com/acerca/plan-de-negocios/Documents/pn_2023-2027_total.pdf (accessed on 4 November 2024).
- Ersdal, G.; Sharp, J.V.; Stacey, A. Ageing and Life Extension of Offshore Structures: The Challenge of Managing Structural Integrity, 1st ed.; John Wiley & Sons: Hoboken, NJ, USA, 2019; Available online: https://books.google.com.mx/books/about/Ageing_and_Life_Extension_of_Offshore_St.html?id=tzB6DwAAQBAJ&redir_esc=y (accessed on 4 November 2024).
- Vaz, M.A.; Cyrino, C.R.; Hernández, I.D. Experimental and numerical analyses of the ultimate compressive strength of perforated offshore tubular members. Mar. Struct. 2018, 58, 1–17. [Google Scholar] [CrossRef]
- Gao, S.; Guo, L.; Zhang, S.; Peng, Z. Performance degradation of circular thin-walled CFST stub columns in high-latitude offshore region. Thin-Walled Struct. 2020, 154, 106906. [Google Scholar] [CrossRef]
- Onoufriou, T. Reliability based inspection planning of offshore structures. Mar. Struct. 1999, 12, 521–539. [Google Scholar] [CrossRef]
- Lotsberg, I.; Sigurdsson, G.; Fjeldstad, A.; Moan, T. Probabilistic methods for planning of inspection for fatigue cracks in offshore structures. Mar. Struct. 2016, 46, 167–192. [Google Scholar] [CrossRef]
- Ramasamy, R.; Ibrahim, Z.; Chai, H.K. Screening method for platform conductor integrity assessment for life extension prioritisation. Mar. Struct. 2018, 58, 136–153. [Google Scholar] [CrossRef]
- Jimenez-Martinez, M. Fatigue of offshore structures: A review of statistical fatigue damage assessment for stochastic loadings. Int. J. Fatigue 2020, 132, 105327. [Google Scholar] [CrossRef]
- Muzaffer, S.; Chang, K.-H.; Hirohata, M. Fatigue Life Comparison of Tubular Joints in Tripod and Jacket Offshore Support Substructures Using 3D Fatigue FE Analysis. KSCE J. Civ. Eng. 2024, 28, 849–859. [Google Scholar] [CrossRef]
- Pachoud, A.J.; Manso, P.A.; Schleiss, A.J. Stress intensity factors for axial semi-elliptical surface cracks and embedded elliptical cracks at longitudinal butt welded joints of steel-lined pressure tunnels and shafts considering weld shape. Eng. Fract. Mech. 2017, 185, 214–238. [Google Scholar] [CrossRef]
- Liu, L.; Yang, D.Y.; Frangopol, D.M. Ship service life extension considering ship condition and remaining design life. Mar. Struct. 2021, 78, 102940. [Google Scholar] [CrossRef]
- Adamkowski, A.; Lewandowski, M.; Lewandowski, S. Fatigue life analysis of hydropower pipelines using the analytical model of stress concentration in welded joints with angular distortions and considering the influence of water hammer damping. Thin-Walled Struct. 2021, 159, 107350. [Google Scholar] [CrossRef]
- Mojtahedi, A.; Lotfollahi Yaghin, M.A.; Ettefagh, M.M.; Hassanzadeh, Y.; Fujikubo, M. Detection of nonlinearity effects in structural integrity monitoring methods for offshore jacket-type structures based on principal component analysis. Mar. Struct. 2013, 33, 100–119. [Google Scholar] [CrossRef]
- Ahmadi, H.; Zavvar, E. Stress concentration factors induced by out-of-plane bending loads in ring-stiffened tubular KT-joints of jacket structures. Thin-Walled Struct. 2015, 91, 82–95. [Google Scholar] [CrossRef]
- Ahmadi, H.; Mohammadi, A.H.; Yeganeh, A. Probability density functions of SCFs in internally ring-stiffened tubular KT-joints of offshore structures subjected to axial loading. Thin-Walled Struct. 2015, 94, 485–499. [Google Scholar] [CrossRef]
- Asgarian, B.; Aghaeidoost, V.; Rahman Shokrgozar, H. Damage detection of jacket type offshore platforms using rate of signal energy using wavelet packet transform. Mar. Struct. 2016, 45, 1–21. [Google Scholar] [CrossRef]
- Mohammad, S.F.; Galgoula, N.S.; Starossek, U.; Videiro, P.M. An efficient time domain fatigue analysis and its comparison to spectral fatigue assessment for an offshore jacket structure. Mar. Struct. 2016, 49, 97–115. [Google Scholar] [CrossRef]
- Pérez, R.; Rodríguez, R.; Vázquez-Hernández, A.O. Damage detection in offshore jacket platforms with limited modal information using the Damage Submatrices Method. Mar. Struct. 2017, 55, 78–103. [Google Scholar] [CrossRef]
- Aeran, A.; Siriwardane, S.C.; Mikkelsen, O.; Langen, I. A framework to assess structural integrity of ageing offshore jacket structures for life extension. Mar. Struct. 2017, 56, 237–259. [Google Scholar] [CrossRef]
- Dodaran, N.A.; Ahmadi, H.; Lotfollahi-Yaghin, M. Parametric study on structural behavior of tubular K-joints under axial loading at fire-induced elevated temperatures. Thin-Walled Struct. 2018, 130, 467–486. [Google Scholar] [CrossRef]
- Lotsberg, I.; Olufsen, O.; Solland, G.; Dalane, J.I.; Haver, S. Risk assessment of loss of structural integrity of a floating production platform due to gross errors. Mar. Struct. 2004, 17, 551–573. [Google Scholar] [CrossRef]
- Mousavi, M.; Gardoni, P. A simplified method for reliability- and integrity-based design of engineering systems and its application to offshore mooring systems. Mar. Struct. 2014, 36, 88–104. [Google Scholar] [CrossRef]
- Guédé, F. Risk-based structural integrity management for offshore jacket platforms. Mar. Struct. 2019, 63, 444–446. [Google Scholar] [CrossRef]
- Zeinoddini, M.; Yaghubi Namin, Y.; Nikoo, H.M.; Estekanchi, H.; Kimiaei, M. An EWA framework for the probabilistic-based structural integrity assessment of offshore platforms. Mar. Struct. 2018, 59, 60–79. [Google Scholar] [CrossRef]
- Leheta, H.W.; Badran, S.F.; Elhanafi, A.S. Ship structural integrity using new stiffened plates. Thin-Walled Struct. 2015, 94, 545–561. [Google Scholar] [CrossRef]
- Hüsken, G.; Shamsuddoha; Pirskawetz, S.; Hofmann, D.; Baeßler, M.; Kühne, H.-C. Potential of a repair system for grouted connections in offshore structures: Development and experimental verification. Mar. Struct. 2021, 77, 102934. [Google Scholar] [CrossRef]
- Amiri, N.; Shaterabadi, M.; Reza Kashyzadeh, K.; Chizari, M. A comprehensive review on design, monitoring, and failure in fixed offshore platforms. J. Mar. Sci. Eng. 2021, 9, 1349. [Google Scholar] [CrossRef]
- Sidiq, R.B.; Utomo, C.; Silvianita. Determining Factors of Fixed Offshore Platform Inspections in Indonesia. Appl. Sci. 2023, 13, 737. [Google Scholar] [CrossRef]
- Kazeminezhad, M.H.; Ghavanini, F.A. Operational wave forecasting for extreme conditions in the Arabian Sea—A comparison with buoy and satellite data. Ocean Eng. 2023, 275, 114152. [Google Scholar] [CrossRef]
- Tu, Y.; Cheng, Z.; Muskulus, M. A global slamming force model for offshore wind jacket structures. Mar. Struct. 2018, 60, 201–217. [Google Scholar] [CrossRef]
- Alizadeh, A.; Siriwardane, S.C.; Mikkelsen, O.; Mikkelsen, O.; Kazeminezhad, M.H. A framework for implementing structural integrity management of an aging fixed offshore platform using wave modeling for risk-based underwater inspection provision. Ocean Eng. 2024, 309, 118368. [Google Scholar] [CrossRef]
- API. American Petroleum Institute, Recommended Practice for Planning, Designing and Constructing Fixed Offshore Platforms–Working Stress Design, API RP 2A-WSD, Twenty-Second Edition, November 2014. Available online: https://store.accuristech.com/api/standards/api-rp-2a-wsd-r2020?product_id=1886617 (accessed on 1 July 2023).
- Diseño y Evaluación de Plataformas Marinas Fijas en el Golfo de México, Especificación Técnica Interna para Proyecto de Obras, “P.2.0130.01:2015” Segunda Edición, Agosto de 2015. Available online: https://es.scribd.com/document/389186286/P-2-0130-01-2015-CLASIFICADO (accessed on 1 December 2023).
- Fenton, J.D. A high-order cnoidal wave theory. J. Fluid Mech. 1979, 94, 129–161. [Google Scholar] [CrossRef]
- Atkins Engineering Services. Fluid Loading on Fixed Offshore Structures, OTH 90 322. 1990. Available online: https://core.ac.uk/download/pdf/237397122.pdf (accessed on 1 September 2023).
- Chakrabarti, S.K. Handbook of Offshore Engineering, 1st ed.; Elsevier: Plainfield, IL, USA, 2005; Available online: https://www.amazon.com.mx/Handbook-Offshore-Engineering-Subrata-Chakrabarti/dp/0080443818 (accessed on 1 November 2023).
- Tabeshpour, R.; Fatemi, M. Optimum arrangement of braces in jacket platform based on strength and ductility. Mar. Struct. 2020, 71, 102734. [Google Scholar] [CrossRef]
- Asgarian, B.; Shokrgozar, H.R.; Shahcheraghi, D.; Ghasemzadeh, H. Effect of soil pile structure interaction on dynamic characteristics of jacket type offshore platforms. Coupled Syst. Mech. 2012, 1, 381–395. [Google Scholar] [CrossRef]
- Serrano-Antoñanazas, A.; Serrano-Antoñanazas, M.; Sierra-Antoñanazas, S.; Sierra-Antoñanazas, A. Identification of Vibration Modes in Floating Offshore Wind Turbines. J. Mar. Sci. Eng. 2023, 11, 1893. [Google Scholar] [CrossRef]
- Xu, T.; Li, Y.; Leng, D. Mitigating jacket offshore platform vibration under earthquake and ocean waves utilizing tuned inerter damper. Bull. Earthq. Eng. 2023, 21, 1627–1650. [Google Scholar] [CrossRef]
- Viero, P.F.; Roitman, N. Application of some damage identification methods in offshore platforms. Mar. Struct. 1999, 12, 107–126. [Google Scholar] [CrossRef]
- ISO 19902; INTERNATIONAL STANDARD Petroleum and Natural Gas Industries—Fixed Steel Offshore Structures, Twenty-Second Edition. International Organization for Standardization: Geneva, Switzerland, November 2014. Available online: https://www.iso.org/standard/65688.html (accessed on 1 July 2023).



| Load Case | Load Case Description | Weight “Ton” |
|---|---|---|
| 1 | Self-weight structure (Does not include flotation or marine growth) | 3574.90 |
| 2 | Dead load on the jacket | 263.96 |
| 3 | Dead load on the topside (deck) | 405.92 |
| 4 | Live load on the topside (deck) | 1065.13 |
| 5 | Dead load of empty equipment on the topside (deck) | 464.69 |
| 6 | Live load of equipment on the topside (deck) | 274.57 |
| 7 | Piping, electrical, and instrumentation load on the topside | 36.30 |
| 8 | Dead load of equipment drilling | 2069.69 |
| 9 | Dead load of drilling tower at “Position 1” | 944.00 |
| 10 | Dead load of drilling tower at “Position 2” | 944.00 |
| 11 | Dead load of drilling tower at “Position 3” | 944.00 |
| 12 | Live load of equipment drilling | 1687.53 |
| 13 | Load increase per operation of drilling tower at “Position 1” | 796.00 |
| 14 | Load increase per operation of drilling tower at “Position 2” | 796.00 |
| 15 | Load increase per operation of drilling tower at “Position 3” | 796.00 |
| 16–23 | Wave, current, and wind @45°—operation | |
| 24–31 | Wave, current, and wind @45°—extreme storm | |
| R001–R008 | Wave, current, and wind @45°—ultimate resistance to waves | |
| S000–S342 | Seismic environmental loads |
| Description | Operation | Extreme | Pushover | ||||
|---|---|---|---|---|---|---|---|
| Parameter | Reference | Parameter | Reference | Parameter | Factor | Total | |
| Maximum wave height (m): | 7.60 | * Figure 20 | 16.20 | * Figure 13 | 16.20 | 1.38 | 22.36 |
| Wave period (s): | 8.20 | * Table 17 | 12.18 | * Section A.1.1 | 12.18 | 1.12 | 13.64 |
| Astronomical tide (m): | 0.76 | * Table 17 | 0.76 | * Section A.1.1 | 0.76 | 1.00 | 0.76 |
| Tide storm (m): | 0.30 | * Table 17 | 0.62 | * Figure 15 | 0.62 | 1.51 | 0.94 |
| Water depth (m): | 50.40 | 50.40 | 50.40 | 50.40 | |||
| Water depth including tides (m): | 51.46 | 51.78 | 51.78 | 52.10 | |||
| Wave theory | steam function 3 | steam function 5 | steam function 7 | ||||
| Current speed (cm/s): | |||||||
| At 0% depth: | 30.00 | * Figure 17 | 125.00 | * Figure 16 | 125.00 | 2.04 | 255.00 |
| At 50% depth: | 25.00 | 112.00 | 112.00 | 2.04 | 228.48 | ||
| At 95% depth: | 18.00 | 100.00 | 100.00 | 2.04 | 204.00 | ||
| Maximum wind speed at 10 m SNMM (m/s), 1 h average: | 14.00 | * Figure 17 | 31.00 | * Figure 14 | 31.00 | 1.40 | 43.40 |
| Coefficients | ||||||
|---|---|---|---|---|---|---|
| Wave kinematics coefficient: | 1.00 | * Section 8.3.2.2 | ||||
| Drag coefficient (Cd): | 1.05 | |||||
| Coefficient of inertia (cm.): | 1.20 | |||||
| Marine Growth | ||||||
| Elevation Interval Regarding NMM (m) | Hard Marine Growth Thickness (cm) | |||||
| (+) | 1.00 | A | (−) | 20.00 | 7.50 | * Table 3 |
| (−) | 20.00 | A | (−) | 50.00 | 5.50 | |
| (−) | 50.00 | A | (−) | 80.00 | 3.50 | |
| Blocking Factor for Currents | ||||||
| # Columns | Direction | Factor | ||||
| 8 | Longitudinal | 0.80 | ** Table 5.2 | |||
| Diagonal | 0.85 | |||||
| Crossover | 0.80 | |||||
| Wind Shape Coefficients | ||||||
| Area | Shape Coefficients | |||||
| Beams | 1.50 | ** Tabla 5.4 | ||||
| Module Surfaces | 1.50 | |||||
| Cylindrical Sections | 0.50 | |||||
| Total Platform Area | 1.00 | |||||
| Item | Description | Linear Analysis | Nonlinear Analysis | Predictive | |||
|---|---|---|---|---|---|---|---|
| 5.1 Operational and Static Storm | 5.2 Dynamic Storm | 5.3 Seismic Resistance | 5.4 Ultimate Wave | 5.5 Seismic Ductility | 5.6 Spectral Fatigue | ||
| 3.0 | Analysis static | X | |||||
| 3.1. | Pile supper element | X | X | X | |||
| 3.2. | Obtaining dynamic properties | X | X | X | |||
| 3.3.1 | Dynamic wave | X | |||||
| 3.3.2 | Seismic spectrum response | X | |||||
| 3.3.3 | Transfer function | X | |||||
| 4.0 | Analysis pushover | X | X | ||||
| 5.0 | Results | X | X | X | X | X | X |
| Mode | Frequencies and Generalized Mass | Mass Participation Factor Report Based on Expanded Degrees of Freedom | |||||||
|---|---|---|---|---|---|---|---|---|---|
| FREQ. (CPS) | Period (SECS) | Mass Participation Factors | Cumulative Factors | ||||||
| X | Y | Z | X | Y | Z | ||||
| Model 1 | 1 | 0.3698 | 2.7045 | 0.8379 * | 0.0003 | 0.0005 | 0.8379 | 0.0003 | 0.0005 |
| 2 | 0.3947 | 2.5336 | 0.0004 | 0.7951 ** | 0.0000 | 0.8382 | 0.7954 | 0.0005 | |
| 3 | 0.4790 | 2.0877 | 0.0016 | 0.0007 | 0.0000 | 0.8398 | 0.7961 | 0.0005 | |
| 4 | 1.0598 | 0.9436 | 0.0001 | 0.1803 | 0.0002 | 0.8399 | 0.9764 | 0.0008 | |
| 5 | 1.1257 | 0.8883 | 0.1405 | 0.0003 | 0.0014 | 0.9805 | 0.9768 | 0.0021 | |
| 6 | 1.2975 | 0.7707 | 0.0013 | 0.0032 | 0.0000 | 0.9818 | 0.9800 | 0.0021 | |
| 7 | 1.4572 | 0.6862 | 0.0001 | 0.0002 | 0.0003 | 0.9819 | 0.9802 | 0.0025 | |
| 8 | 1.6618 | 0.6017 | 0.0000 | 0.0000 | 0.0000 | 0.9819 | 0.9802 | 0.0025 | |
| 9 | 2.3835 | 0.4195 | 0.0011 | 0.0014 | 0.1039 | 0.9830 | 0.9815 | 0.1064 | |
| 10 | 2.4075 | 0.4154 | 0.0000 | 0.0124 | 0.0084 | 0.9830 | 0.9940 | 0.1148 | |
| 11 | 2.4145 | 0.4142 | 0.0072 | 0.0004 | 0.4464 *** | 0.9903 | 0.9944 | 0.5613 | |
| 12 | 2.5465 | 0.3927 | 0.0040 | 0.0001 | 0.3564 | 0.9943 | 0.9944 | 0.9177 | |
| 13 | 3.2880 | 0.3041 | 0.0001 | 0.0000 | 0.0016 | 0.9944 | 0.9944 | 0.9192 | |
| 14 | 3.4741 | 0.2878 | 0.0009 | 0.0000 | 0.0055 | 0.9952 | 0.9945 | 0.9247 | |
| 15 | 3.7416 | 0.2673 | 0.0000 | 0.0004 | 0.0004 | 0.9952 | 0.9949 | 0.9251 | |
| 30 | 4.1567 | 0.2406 | 0.0000 | 0.0000 | 0.0000 | 1.0000 | 0.9982 | 0.9254 | |
| Model 2 | 1 | 0.3698 | 2.7045 | 0.838 * | 0.000 | 0.001 | 0.8384 | 0.0003 | 0.0005 |
| 2 | 0.3947 | 2.5336 | 0.000 | 0.795 ** | 0.000 | 0.8388 | 0.7954 | 0.0005 | |
| 3 | 0.4790 | 2.0877 | 0.002 | 0.001 | 0.000 | 0.8404 | 0.7961 | 0.0005 | |
| 4 | 1.0598 | 0.9436 | 0.000 | 0.180 | 0.000 | 0.8405 | 0.9764 | 0.0008 | |
| 5 | 1.1257 | 0.8883 | 0.140 | 0.000 | 0.001 | 0.9808 | 0.9767 | 0.0021 | |
| 6 | 1.2975 | 0.7707 | 0.001 | 0.003 | 0.000 | 0.9821 | 0.9800 | 0.0021 | |
| 7 | 1.4572 | 0.6862 | 0.000 | 0.000 | 0.000 | 0.9822 | 0.9801 | 0.0025 | |
| 8 | 1.6618 | 0.6017 | 0.000 | 0.000 | 0.000 | 0.9822 | 0.9801 | 0.0025 | |
| 9 | 2.3835 | 0.4195 | 0.002 | 0.001 | 0.137 | 0.9838 | 0.9815 | 0.1396 | |
| 10 | 2.4075 | 0.4154 | 0.000 | 0.013 | 0.002 | 0.9839 | 0.9941 | 0.1416 | |
| 11 | 2.4145 | 0.4142 | 0.007 | 0.000 | 0.393 *** | 0.9909 | 0.9943 | 0.5350 | |
| 12 | 2.5465 | 0.3927 | 0.004 | 0.000 | 0.382 | 0.9945 | 0.9944 | 0.9172 | |
| 13 | 3.2880 | 0.3041 | 0.000 | 0.000 | 0.002 | 0.9946 | 0.9944 | 0.9189 | |
| 14 | 3.4741 | 0.2878 | 0.001 | 0.000 | 0.005 | 0.9955 | 0.9944 | 0.9241 | |
| 15 | 3.7416 | 0.2673 | 0.000 | 0.000 | 0.000 | 0.9955 | 0.9948 | 0.9245 | |
| 30 | 4.1567 | 0.2406 | 0.000 | 0.000 | 0.000 | 0.9989 | 0.9981 | 0.9249 | |
| Model 3 | 1 | 0.3697 | 2.7048 | 0.8382 * | 0.0004 | 0.0005 | 0.8382 | 0.0004 | 0.0005 |
| 2 | 0.3940 | 2.5379 | 0.0005 | 0.7934 ** | 0.0000 | 0.8387 | 0.7938 | 0.0005 | |
| 3 | 0.4754 | 2.1034 | 0.0016 | 0.0013 | 0.0000 | 0.8403 | 0.7951 | 0.0005 | |
| 4 | 1.0570 | 0.9461 | 0.0001 | 0.1805 | 0.0002 | 0.8404 | 0.9756 | 0.0008 | |
| 5 | 1.1255 | 0.8885 | 0.1402 | 0.0004 | 0.0013 | 0.9806 | 0.9760 | 0.0021 | |
| 6 | 1.2898 | 0.7753 | 0.0014 | 0.0038 | 0.0000 | 0.9821 | 0.9798 | 0.0021 | |
| 7 | 1.4553 | 0.6871 | 0.0001 | 0.0002 | 0.0004 | 0.9822 | 0.9800 | 0.0025 | |
| 8 | 1.5484 | 0.6458 | 0.0000 | 0.0000 | 0.0001 | 0.9822 | 0.9800 | 0.0026 | |
| 9 | 2.0832 | 0.4800 | 0.0000 | 0.0000 | 0.0007 | 0.9822 | 0.9800 | 0.0032 | |
| 10 | 2.3897 | 0.4185 | 0.0038 | 0.0070 | 0.3391 | 0.9860 | 0.9871 | 0.3423 | |
| 11 | 2.4012 | 0.4165 | 0.0042 | 0.0071 | 0.2197 | 0.9903 | 0.9942 | 0.5620 | |
| 12 | 2.5433 | 0.3932 | 0.0041 | 0.0001 | 0.3475 *** | 0.9943 | 0.9943 | 0.9095 | |
| 13 | 2.9545 | 0.3385 | 0.0000 | 0.0000 | 0.0013 | 0.9943 | 0.9943 | 0.9108 | |
| 14 | 3.2159 | 0.3110 | 0.0002 | 0.0000 | 0.0029 | 0.9945 | 0.9943 | 0.9137 | |
| 15 | 3.3119 | 0.3019 | 0.0007 | 0.0001 | 0.0094 | 0.9952 | 0.9944 | 0.9231 | |
| 30 | 4.1478 | 0.2411 | 0.0000 | 0.0000 | 0.0000 | 0.9989 | 0.9979 | 0.9245 | |
| Campeche Bay | |
|---|---|
| Period (second “s”) | Acceleration “α” (g’s) |
| 0.010–0.050 | 0.100 |
| 0.125–0.504 | 0.250 |
| 10 | 0.013 |
| Angle Deg | Damping 2% | Damping 5% | ||||
|---|---|---|---|---|---|---|
| Base Shear | Overturning Moment | Vertical Load | Base Shear | Overturning Moment | Vertical Load | |
| Ton | Ton-M | Ton | Ton | Ton-M | Ton | |
| 0 | 679.44 | 22,125.67 | 1314.98 | 687.62 | 22,511.32 | 1509.55 |
| 18 | 684.58 | 23,456.37 | 1314.98 | 696.19 | 24,285.96 | 1509.55 |
| 36 | 691.14 | 25,278.76 | 1314.98 | 704.34 | 26,822.54 | 1509.55 |
| 54 | 696.29 | 27,093.88 | 1314.98 | 708.53 | 29,189.43 | 1509.55 |
| 72 | 698.00 | 28,528.01 | 1314.98 | 706.65 | 30,995.49 | 1509.55 |
| 90 | 698.52 | 28,694.71 | 1314.98 | 702.72 | 31,175.57 | 1509.55 |
| 108 | 700.27 | 28,380.62 | 1314.98 | 708.20 | 30,864.82 | 1509.55 |
| 126 | 697.40 | 26,880.03 | 1314.98 | 709.17 | 29,026.76 | 1509.55 |
| 144 | 691.04 | 24,578.74 | 1314.98 | 704.21 | 26,117.74 | 1509.55 |
| 162 | 684.76 | 22,247.35 | 1314.98 | 696.73 | 23,031.73 | 1509.55 |
| 180 | 679.44 | 22,125.67 | 1314.98 | 687.62 | 22,511.32 | 1509.55 |
| 198 | 684.58 | 23,456.37 | 1314.98 | 696.19 | 24,285.96 | 1509.55 |
| 216 | 691.14 | 25,278.75 | 1314.98 | 704.34 | 26,822.54 | 1509.55 |
| 234 | 696.29 | 27,093.87 | 1314.98 | 708.53 | 29,189.42 | 1509.55 |
| 252 | 698.00 | 28,528.01 | 1314.98 | 706.65 | 30,995.49 | 1509.55 |
| 270 | 698.52 | 28,694.71 | 1314.98 | 702.72 | 31,175.57 | 1509.55 |
| 288 | 700.27 | 28,380.62 | 1314.98 | 708.20 | 30,864.82 | 1509.55 |
| 306 | 697.40 | 26,880.03 | 1314.98 | 709.17 | 29,026.76 | 1509.55 |
| 324 | 691.04 | 24,578.75 | 1314.98 | 704.21 | 26,117.74 | 1509.55 |
| 342 | 684.76 | 22,247.35 | 1314.98 | 696.73 | 23,031.73 | 1509.55 |
| maximum | 700.27 * | 28,694.71 ** | 1314.98 | 709.17 * | 31,175.57 ** | 1509.55 |
| Resistance Reserve Factor (RSR) | Collapse Mechanism | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Direction | Load Factor | Maximum Shear (Ton) | Shear (Ton) | RSR | RSR Minimum | Status | Collapse By | Pile Capacity | |||
| Plasticization of Elements | Pile Collapse | % | Pile | Type | |||||||
| 0° | 1.020 | 5517.15 | 2022.39 | 2.728 | 2.20 | OK | YES | NO | 81.7% | P008 | Compression |
| 45 | 1.005 | 5809.17 | 2130.64 | 2.726 | 2.20 | OK | YES | NO | 92.3% | P008 | Compression |
| 90 | 1.090 | 6596.93 | 2350.79 | 2.806 | 2.20 | OK | YES | NO | 71.8% | P008 | Compression |
| 135 | 1.005 | 5665.08 | 2080.09 | 2.723 | 2.20 | OK | YES | NO | 81.9% | P007 | Tension |
| 180 | 1.020 | 5534.18 | 2038.55 | 2.715 | 2.20 | OK | YES | NO | 63.1% | P007 | Tension |
| 225 | 0.995 | 5707.43 | 2131.81 | 2.677 | 2.20 | OK | YES | NO | 84.6% | P008 | Tension |
| 270 | 1.085 | 6573.62 | 2347.36 | 2.800 | 2.20 | OK | YES | NO | 71.2% | P005 | Compression |
| 315 | 1.035 | 5907.95 | 2062.58 | 2.864 | 2.20 | OK | YES | NO | 90.5% | P007 | Compression |
| Weld Improvement Technique | Improvement Factors for “S” | Improvement Factors for “N” | Type |
|---|---|---|---|
| Profile (see 14.1.3.4) * | varies | WJ1 | |
| Weld toe burr grinding | 1.25 | 2 | WJ2 |
| Hammer peening | 1.56 | 4 | WJ3 |
| Chord side only |
| Revision | (i) Operation and Static Storm | (ii) Dynamic Storm | (iii) Seismic Resistance | (iv) Seismic Ductility | (v) Ultimate Wave Resistance | (vi) Spectral Fatigue | Status |
|---|---|---|---|---|---|---|---|
| Reference value | UC < 1.00 | UC < 1.00 | UC < 1.00 | Cr > 2.0 | RSR > 2.20 | Life > 20 years | |
| Unity check (UC) ratio in structural members | TOPSIDE: UC = 0.81 | TOPSIDE: UC = 0.64 | TOPSIDE: * UC = 1.001 | — | — | — | OK |
| JACKET: UC = 0.93 | JACKET: UC = 0.99 | JACKET: UC = 0.631 | — | — | — | OK | |
| PILES: UP = 0.77 Down = 0.75 | PILES: UP = 0.81 Down = 0.79 | PILES: UP = 0.530 Down = 0.504 | — | — | — | OK | |
| Unity check (UC) ratio in tubular members | LOAD = 0.783 STR = 0.968 | LOAD = 0.777 STRN = 0.969 | LOAD = 0.447 * STRN = 1.048 | — | — | — | OK |
| Safety factor | Operation = 2.18 > 2.00 Storm = 1.58 > 1.50 | Storm = 1.52 > 1.50 | Seismic = 2.04 > 2.00 | — | — | — | OK |
| Hydrostatic collapse | * YES (strengthen) | * YES (strengthen) | * YES (strengthen) | — | — | — | Reinforce with Rings |
| RSR Cr (Seismic) | — | — | — | “Cr”: 8.53 | “RSR” 2.68 | — | OK |
| Minimum life in years Node 370 | — | — | — | — | — | WJ0 = 9.2 WJ1 = 13 WJ2 = 27 | Apply Burr Grinding in Node 370 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Martínez, R.D.Á.B.; Álvarez-Arellano, J.A.; El Hamzaoui, Y. Assessment of Structural Integrity Through On-Site Decision-Making Analysis for a Jacket-Type Offshore Platform. Appl. Sci. 2025, 15, 3418. https://doi.org/10.3390/app15073418
Martínez RDÁB, Álvarez-Arellano JA, El Hamzaoui Y. Assessment of Structural Integrity Through On-Site Decision-Making Analysis for a Jacket-Type Offshore Platform. Applied Sciences. 2025; 15(7):3418. https://doi.org/10.3390/app15073418
Chicago/Turabian StyleMartínez, Rodrigo Daniel Álvarez Bello, Juan Antonio Álvarez-Arellano, and Youness El Hamzaoui. 2025. "Assessment of Structural Integrity Through On-Site Decision-Making Analysis for a Jacket-Type Offshore Platform" Applied Sciences 15, no. 7: 3418. https://doi.org/10.3390/app15073418
APA StyleMartínez, R. D. Á. B., Álvarez-Arellano, J. A., & El Hamzaoui, Y. (2025). Assessment of Structural Integrity Through On-Site Decision-Making Analysis for a Jacket-Type Offshore Platform. Applied Sciences, 15(7), 3418. https://doi.org/10.3390/app15073418







