Numerical Analysis on the Performance of a Heat Pump Powered by Surface Water Freezing
Abstract
:1. Introduction
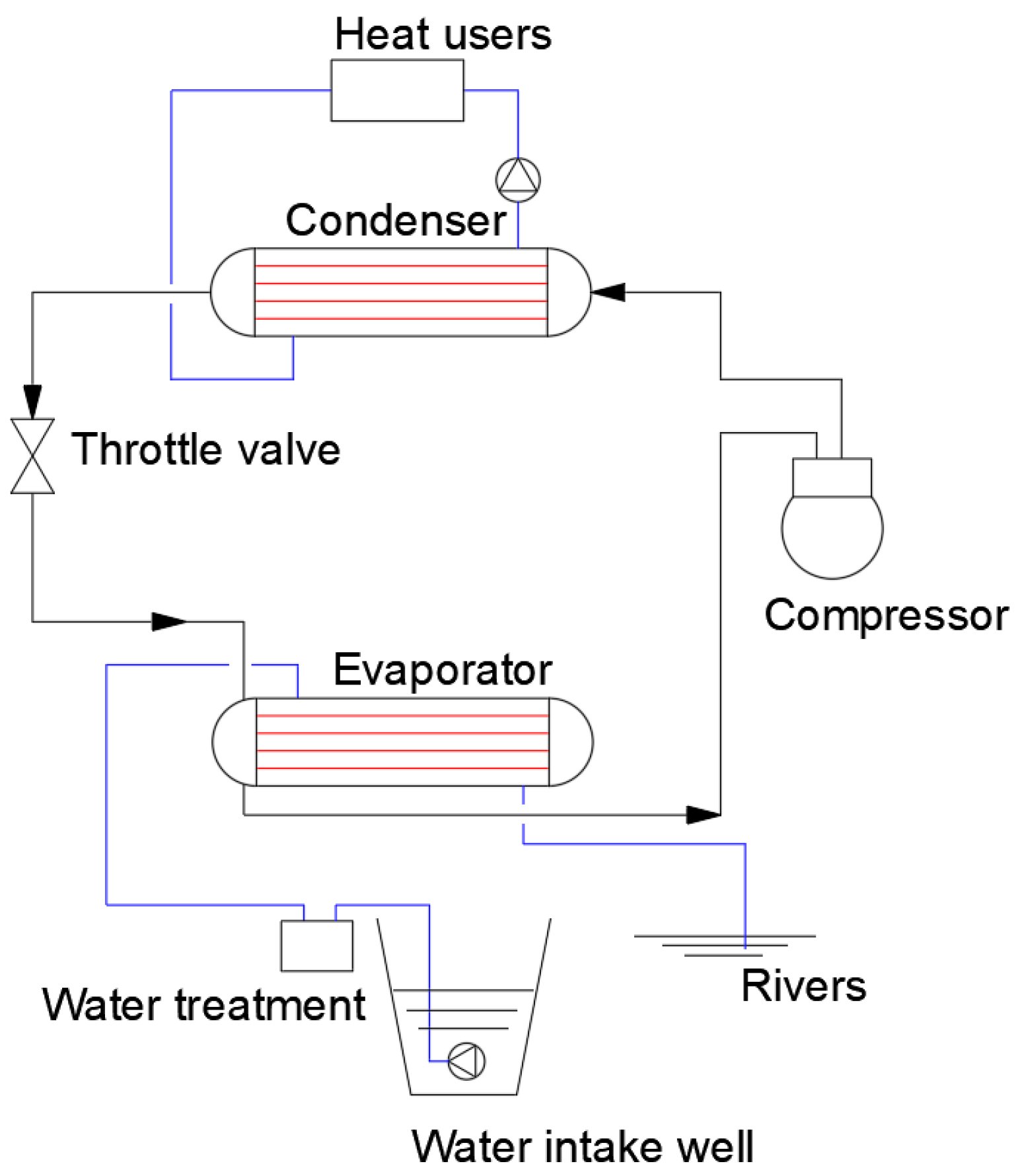
2. The Heat Pump System and Its Numerical Model
2.1. Evaporator Model
2.2. Compressor Simulation Model
- (1)
- The compression process is regarded as adiabatic compression, ignoring the heat exchange between the compressor shell and the surrounding environment.
- (2)
- Regardless of the pressure loss of the refrigerant at the inlet and outlet of the compressor, the evaporator outlet pressure is equal to the compressor suction pressure, and the condenser inlet pressure is equal to the compressor discharge pressure.
- (3)
- Do not consider the friction power consumption in the compressor, the influence of lubricating oil, etc.
2.3. Condenser Simulation Model
2.4. Simulation Modeling of Expansion Valve
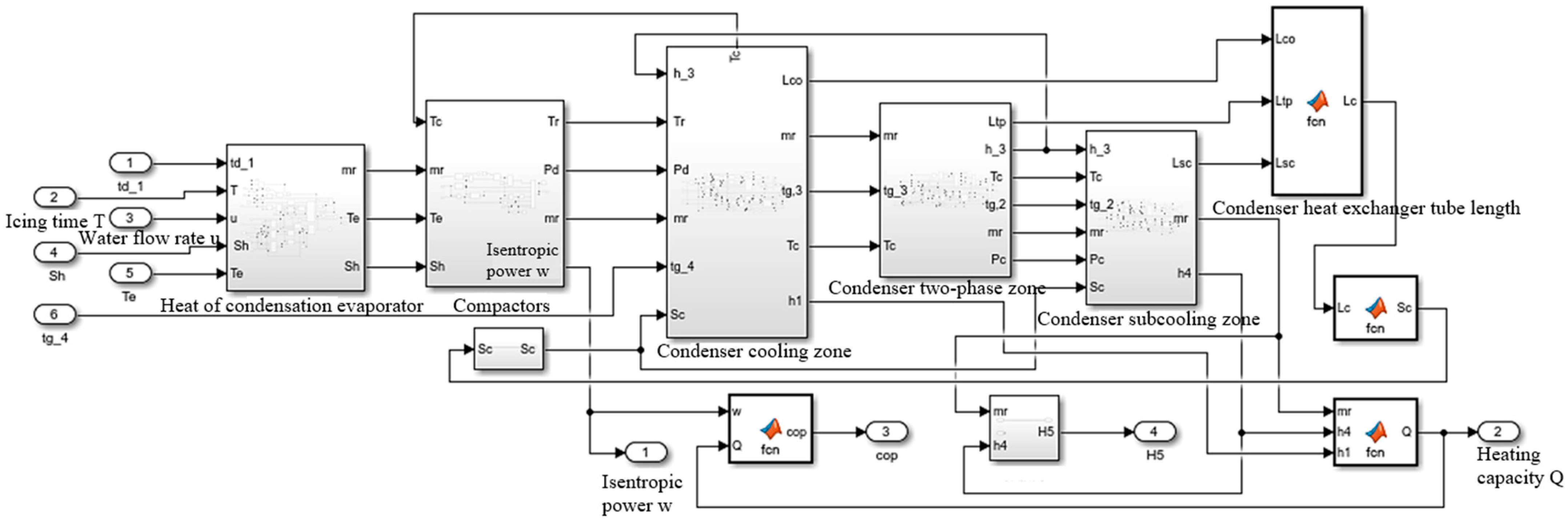
2.5. Simulation Model and Method of Heat Pump System
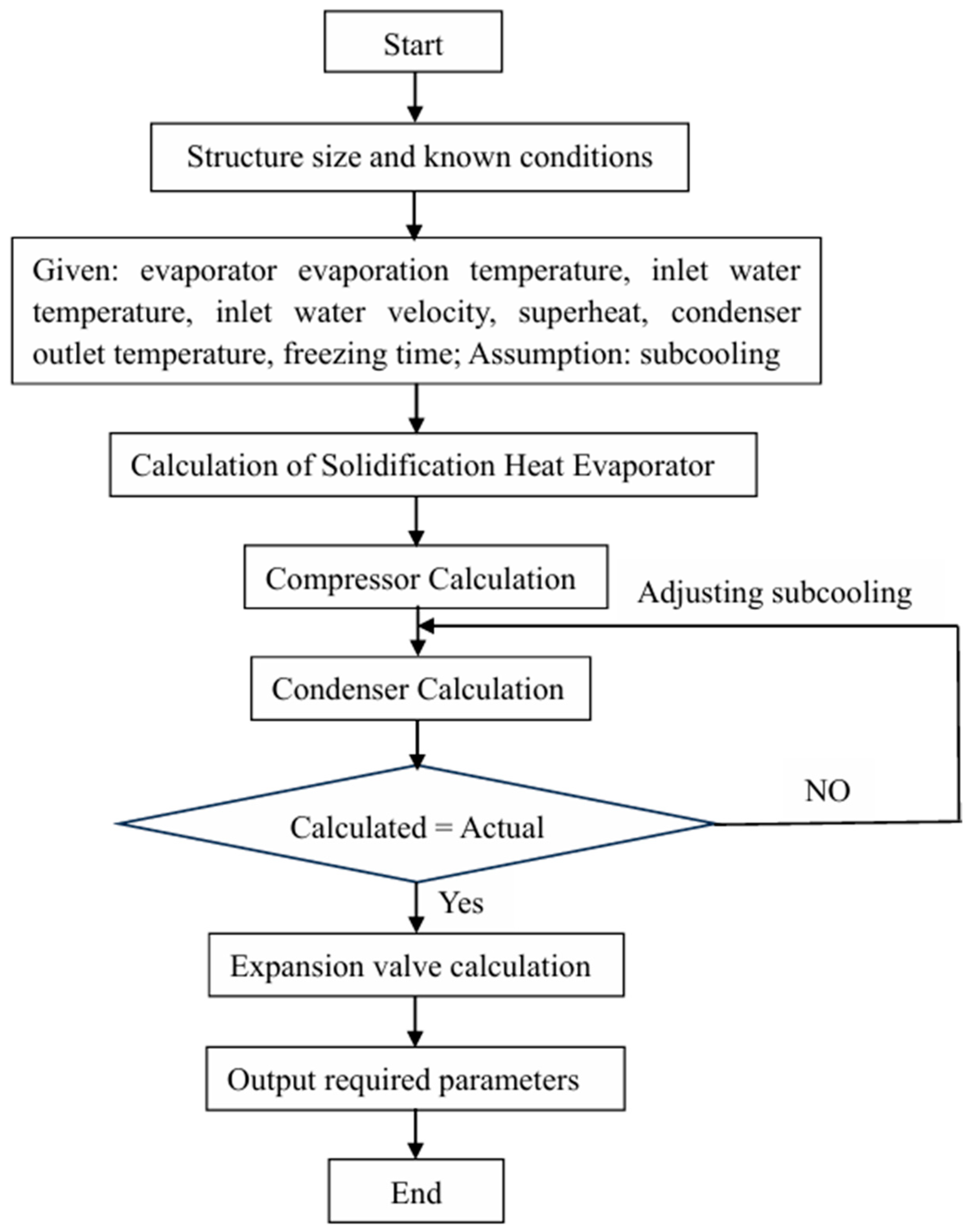
2.6. Validation of Simulation Models and Methods
3. Results and Analysis
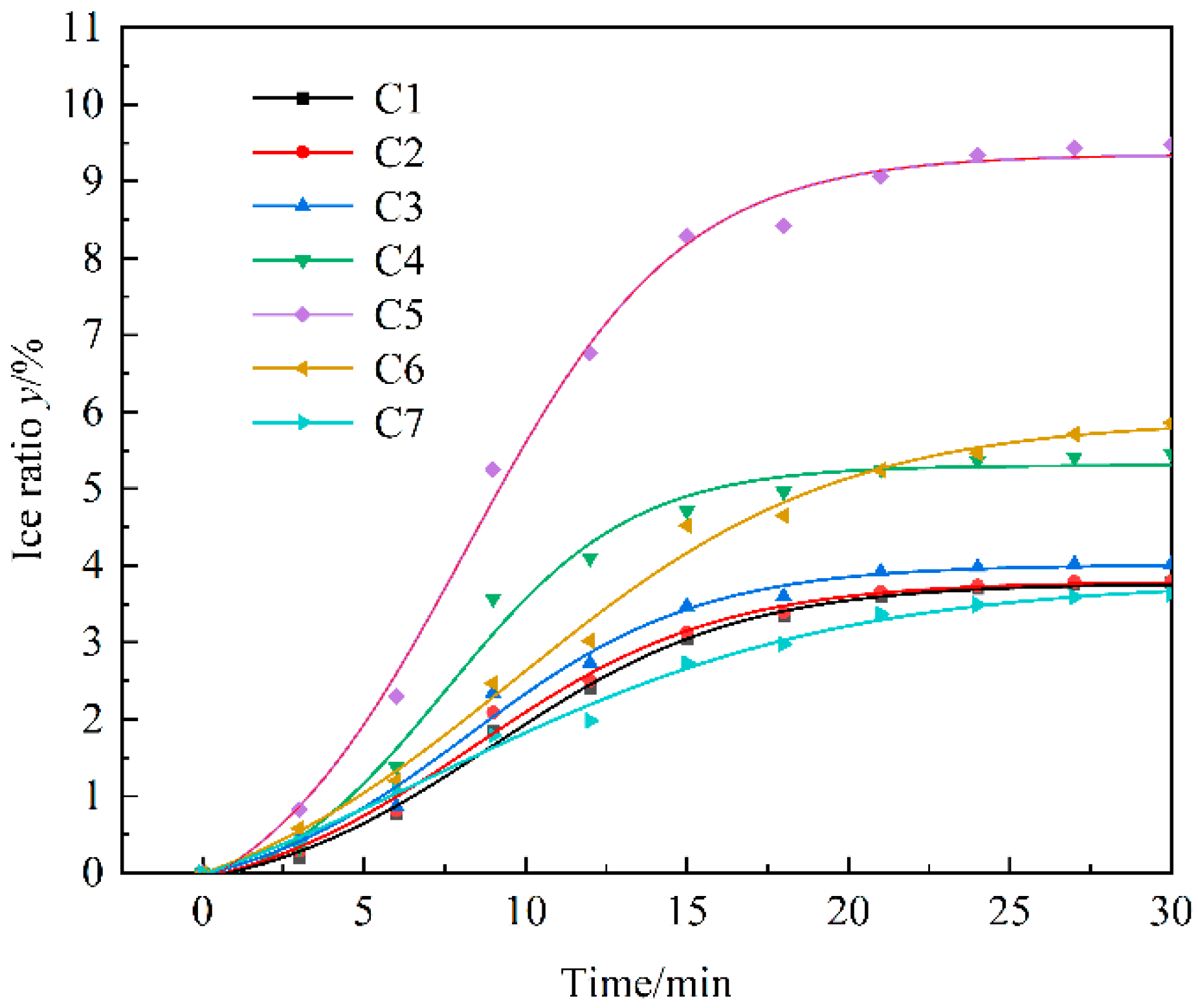
3.1. Analysis of Ice Rate of Water in Evaporator
3.2. Effect of Evaporation Temperature
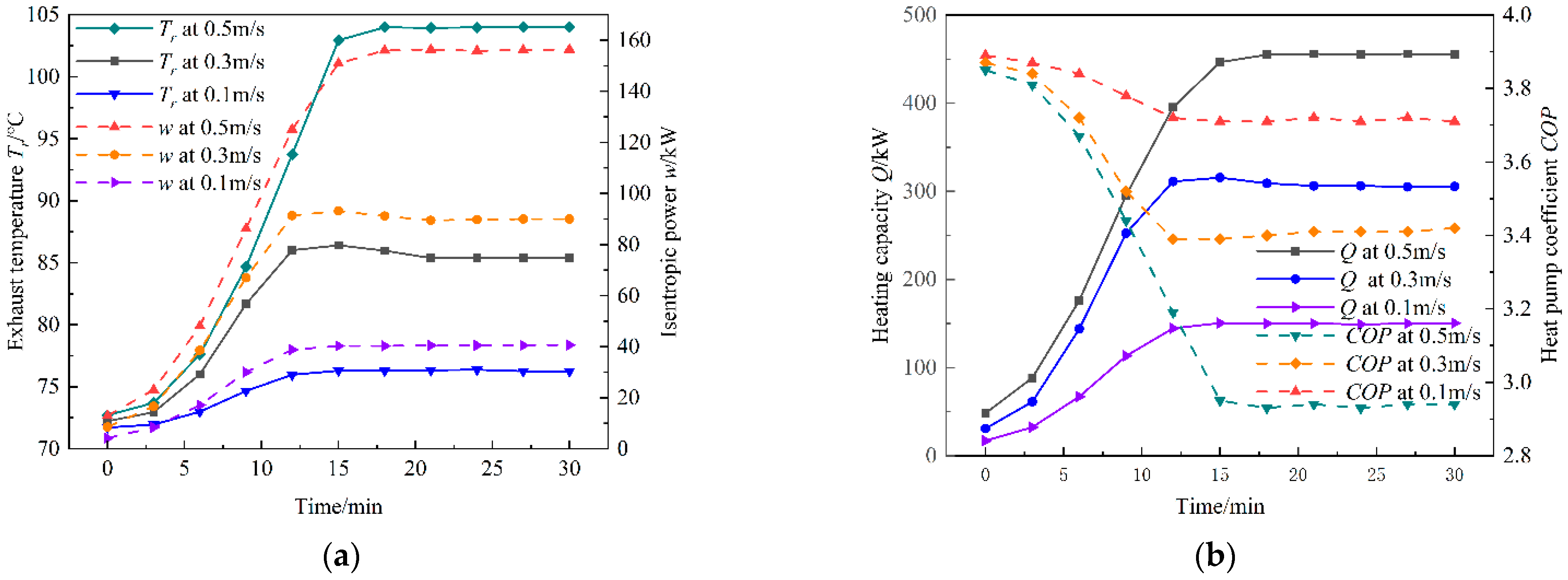
3.3. Effect of Water Velocity at Evaporator Inlet
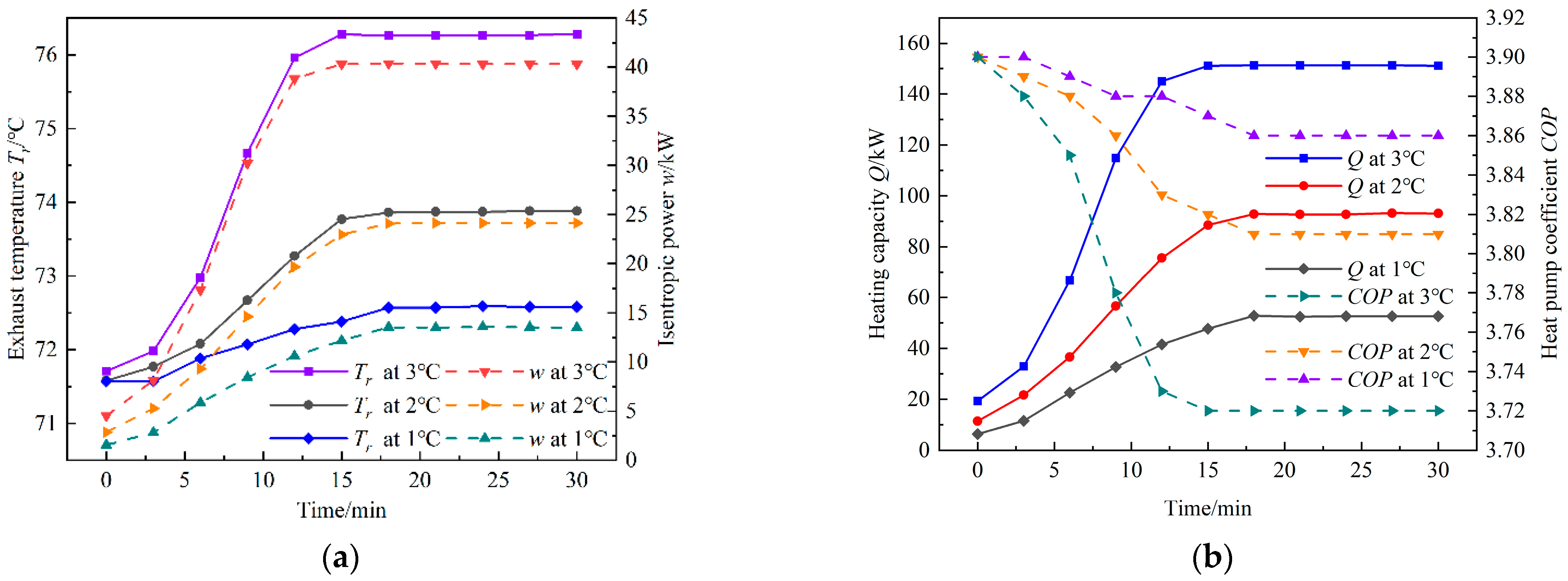
3.4. Influence of Water Temperature at Evaporator Inlet
4. Conclusions
- (1)
- The direct solidification heat source heat pump provided in this paper is simpler and more efficient, but its run-time should be about 15 min before once again deicing. Although its COP during the cold period is a little lower than that of the traditional surface water source heat pump due to a lower evaporative temperature, it can be used in all winter.
- (2)
- Based on Simulink software, the numerical model and method shown in this paper are verified and practicable.
- (3)
- The evaporation temperature is negatively correlated with the exhaust temperature, isentropic power, and heating capacity and positively correlated with COP. The water velocity at the evaporator inlet is negatively correlated with the exhaust temperature, isentropic power, and heating capacity and positively correlated with COP. The water temperature at the evaporator inlet is negatively correlated with the exhaust temperature, isentropic power, and heating capacity and positively correlated with COP. During the stable operation of the system, when the evaporation temperature is −3 °C, the evaporator inlet water velocity is 0.1 m/s, and the evaporator inlet water temperature is 1 °C, the COP has a maximum value, and the maximum values are 3.02 and 3.72 and 3.86, respectively.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| K | Total heat transfer coefficient/W/(m2·°C) |
| hd | Low-temperature heat source water-side convection heat transfer coefficient/W/(m2·°C) |
| Qg | High-temperature heat source water heat absorption/kJ/s |
| Qr | Refrigerant heat gain/kJ/s |
| Ql | Latent heat release from low-temperature heat source water/kJ/s |
| Qs | Apparent heat release from low-temperature heat source water/kJ/s |
| Qd | Water-side heat release from surface heat sources/kJ/s |
| h | Enthalpy of refrigerant/kJ/kg |
| t | Temperature of high-temperature heat source water/°C |
| Δtm | Logarithmic mean temperature difference between refrigerant and water/°C |
| td1 | Evaporator inlet heat source water temperature/°C |
| ti | Liquid–solid surface temperature, take 0 °C |
| l | Length of heat exchanger tubes, m |
| A | Heat transfer area per unit length of heat transfer tube/m2 |
| cp | Specific heat capacity of water at constant pressure, take 4.2 kJ/(kg·°C) |
| k | Multivariate index of the compression process, take 1.15 |
| x | Time/min |
| y | Ice content/% |
| vd | Compressor inlet volume flow rate/m3/kg |
| vr | Compressor outlet volume flow rate/m3/kg |
| Tr | Compressor discharge temperature/°C |
| Td | Compressor suction temperature/°C |
| Pd | Compressor suction pressure/Pa |
| Pr | Compressor discharge pressure/Pa |
| r | Latent heat of freezing of ice/kJ/kg |
| mr | Mass flow rate of refrigerant/kg/s |
| mg | Mass flow rate of low-temperature heat source water/kg/s |
| IPFs | Ice content of mobile ice/% |
| Subscripts | |
| sc | Supercooled zone |
| c | Cooling zone |
| tp | Two-phase zone |
| in | Inlet |
| out | Outlet |
| ev | Evaporator |
| sg | Saturated gaseous state |
| co | Condenser |
References
- Li, G. Anchoring the “dual carbon” goal and accelerating innovation. Workers’ Daily, 21 March 2023. [Google Scholar]
- Xu, X.; Fang, Z.; Wang, Z. Climatic division based on frosting characteristics of air source heat pumps. Energy Build. 2020, 224, 110219. [Google Scholar] [CrossRef]
- Tang, R.; Wang, F.; Wang, Z.; Yang, W. Division of Frosting Type and Frosting Degree of the Air Source Heat Pump for Heating in China. Front. Energy Res. 2021, 9, 708478. [Google Scholar]
- Shen, C.; Lei, Z.; Wang, Y.; Zhang, C.; Yao, Y. A review on the current research and application of wastewater source heat pumps in China. Therm. Sci. Eng. Prog. 2018, 6, 140–156. [Google Scholar]
- Shen, C.; Lei, Z.; Lv, G.; Ni, L.; Deng, S. Experimental performance evaluation of a novel anti-fouling wastewater source heat pump system with a wastewater tower. Appl. Energy 2019, 236, 690–699. [Google Scholar]
- Zhang, J. Development status and problems of surface water source heat pump. Refrig. Air Cond. Electr. Mach. 2007, 6, 73–77. [Google Scholar]
- Sun, D.; Zhang, C.; Wu, R.; Qian, J. Heat pump system and device using cold water to solidify heat. HVAC 2006, 7, 41–44. [Google Scholar]
- Qian, J.; Sun, D.; Meng, J. A simplified model of water temperature and heat load in winter for surface water source collection and solidification heat pump system. Energy Technol. 2007, 6, 483–485+521. [Google Scholar]
- Wu, X.; Wu, R.; Wu, H. Economic and energy consumption analysis of cold water phase change energy heat pump system. J. Qingdao Univ. (Atural Sci.) Ed. 2018, 2, 138–142. [Google Scholar]
- Xu, C.; Zhang, C.; Luo, J. Experimental research on casing phase change solidification heat exchange device and heat pump heating system for coal mines. Coal Eng. 2022, 12, 152–156. [Google Scholar]
- Zhen, Y.; Wu, Y.; Zhang, J. Experimental study on the performance of the extraction of solidification heat device. J. Harbin Univ. Commer. (Nat. Sci.) Acad. Ed. 2019, 35, 710–714. [Google Scholar]
- Wu, X.; Wu, R.; Wu, H. Experimental analysis of performance of chilled water phase change energy heat pump system. J. Qingdao Univ. (Eng. Technol. Ed.) 2019, 34, 105–110. [Google Scholar]
- Liu, Z.; Yue, Y.; Wu, R. Cold water phase change energy heat pump system and its heat transfer performance. HVAC 2020, 50, 94–98. [Google Scholar]
- Luo, D.; Zhou, M.; Tang, J. Simulation study on the influence of intermediate heat exchanger on COP of surface water source heat pump unit. Build. Therm. Energy Vent. Air Cond. 2022, 3, 62–64. [Google Scholar]
- Qian, J.; Sun, D.; Zhang, J. Novel Harvesting and Solidification Heat Pump Technology and System Comprehensive Heating Performance Analysis. Dalian J. Polytech. Univ. 2011, 51, 244–249. [Google Scholar]
- Zheng, J.; Wu, R. Technical scheme of heat pump system for extracting cold water solidification heat. HVAC 2016, 46, 140–142. [Google Scholar]
- Shi, Y. Technical scheme of heat pump system for extracting cold water solidification heat. Mod. Manuf. Technol. Equip. 2018, 5, 140–141. [Google Scholar]
- Liu, Z.; Wu, R.; Yu, H. Operation test of aqueous phase change energy heat pump heating system. HVAC 2019, 49, 96–100. [Google Scholar]
- Yue, Y. Operational Characteristics and Engineering Experimental Research of Cold Water Phase Change Energy Heat Pump System. Master’s Thesis, Qingdao University, Qingdao, China, 2020. [Google Scholar]
- Zhang, Y. Research on Unstable Working Conditions of Low-Temperature Phase Change Heat Source of Water Source Heat pump. Master’s Thesis, Yanshan University, Qinhuangdao, China, 2021. [Google Scholar]
- Qian, J.; Zhang, C.; Sun, D. Study on Enhanced Heat Transfer by Laminar Flow Condition of Acquisition and Solidification Heat Pump Technology. Fluid Mech. Eng. 2007, 35, 70–74. [Google Scholar]
- Qian, J.; Guo, Y.; Li, J. Analysis of Parameters and Conditions for Continuous Heat Intake in Acquisition and Solidification Heat Pump System. Harbin Commer. J. Chin. Univ. (Nat. Sci. Ed.) 2011, 27, 630–632. [Google Scholar]
- Zhang, C. Theory and Device of Heat Exchange for Extracting Latent Heat of Cold Water Solidification. Ph.D. Thesis, Harbin Institute of Technology, Harbin, China, 2008. [Google Scholar]
- Zhang, Y.; Shang, D. Research on core technology of ice water source heat pump. Sci. Technol. Innov. Appl. 2020, 8, 155–159. [Google Scholar]
- Han, S. Research on Modeling and Simulation of Direct Heating System of Wind Energy Heat Pump. Master’s Thesis, University of Chinese Academy of Sciences (CASA Engineering Heat Institute of Physics), Beijing, China, 2018. [Google Scholar]
- Yang, Z. Simulation Research on High-Temperature Heat Pump System Based on Waste Heat Utilization. Master’s Thesis, Harbin Institute of Technology, Harbin, China, 2020. [Google Scholar]
- Zhu, S. Study on Performance of Heat Pump Evaporator for Surface Water Solidification Heat Source. Master’s Thesis, Lanzhou Jiaotong University, Lanzhou, China, 2022. [Google Scholar]
- Wu, X. Simulation and Experimental Study of Cold Water Phase Change Energy Heat Pump System. Master’s Thesis, Qingdao University, Qingdao, China, 2019. [Google Scholar]




| Evaporator Structure Parameters | |||||
|---|---|---|---|---|---|
| Number of Round Tubes | 16 | Tube Length | 4 | Arrangement | Crossbar |
| Pipe spacing | 80 mm | Pipe diameter | 10 mm | Total length of heat exchanger tube | 110 m |
| Condition | Evaporation Temperature/°C | Inlet Water Temperature/°C | Inlet Water Velocity/(m/s) | A1 | A2 | x0 | dx |
|---|---|---|---|---|---|---|---|
| C1 | −3 | 3 | 0.5 | −0.44 ± 0.19 | 3.77 ± 0.06 | 3.81 ± 0.38 | 9.01 ± 0.47 |
| C2 | −5 | 3 | 0.5 | −0.49 ± 0.31 | 3.79 ± 0.09 | 8.41 ± 0.73 | 3.80 ± 0.57 |
| C3 | −7 | 3 | 0.5 | −0.43 ± 0.36 | 4.01 ± 0.10 | 8.21 ± 0.79 | 3.57 ± 0.62 |
| C4 | −5 | 3 | 0.3 | −0.53 ± 0.44 | 5.31 ± 0.13 | 7.55 ± 0.67 | 2.86 ± 0.52 |
| C5 | −5 | 3 | 0.1 | −0.92 ± 0.51 | 9.35 ± 0.15 | 8.17 ± 0.48 | 3.32 ± 0.37 |
| C6 | −5 | 2 | 0.1 | −0.86 ± 0.57 | 5.90 ± 0.19 | 9.68 ± 0.96 | 5.00 ± 0.82 |
| C7 | −5 | 1 | 0.1 | −1.27 ± 0.72 | 3.81 ± 0.15 | 7.16 ± 1.83 | 6.35 ± 1.20 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Y.; Mao, W.; Zhou, W.; Han, S.; Chu, X.; Li, X. Numerical Analysis on the Performance of a Heat Pump Powered by Surface Water Freezing. Appl. Sci. 2025, 15, 3421. https://doi.org/10.3390/app15073421
Chen Y, Mao W, Zhou W, Han S, Chu X, Li X. Numerical Analysis on the Performance of a Heat Pump Powered by Surface Water Freezing. Applied Sciences. 2025; 15(7):3421. https://doi.org/10.3390/app15073421
Chicago/Turabian StyleChen, Yuying, Wei Mao, Wenhe Zhou, Sen Han, Xingyu Chu, and Xiang Li. 2025. "Numerical Analysis on the Performance of a Heat Pump Powered by Surface Water Freezing" Applied Sciences 15, no. 7: 3421. https://doi.org/10.3390/app15073421
APA StyleChen, Y., Mao, W., Zhou, W., Han, S., Chu, X., & Li, X. (2025). Numerical Analysis on the Performance of a Heat Pump Powered by Surface Water Freezing. Applied Sciences, 15(7), 3421. https://doi.org/10.3390/app15073421





