A New Ground-Motion Prediction Model for Shallow Crustal Earthquakes in Türkiye
Abstract
1. Introduction
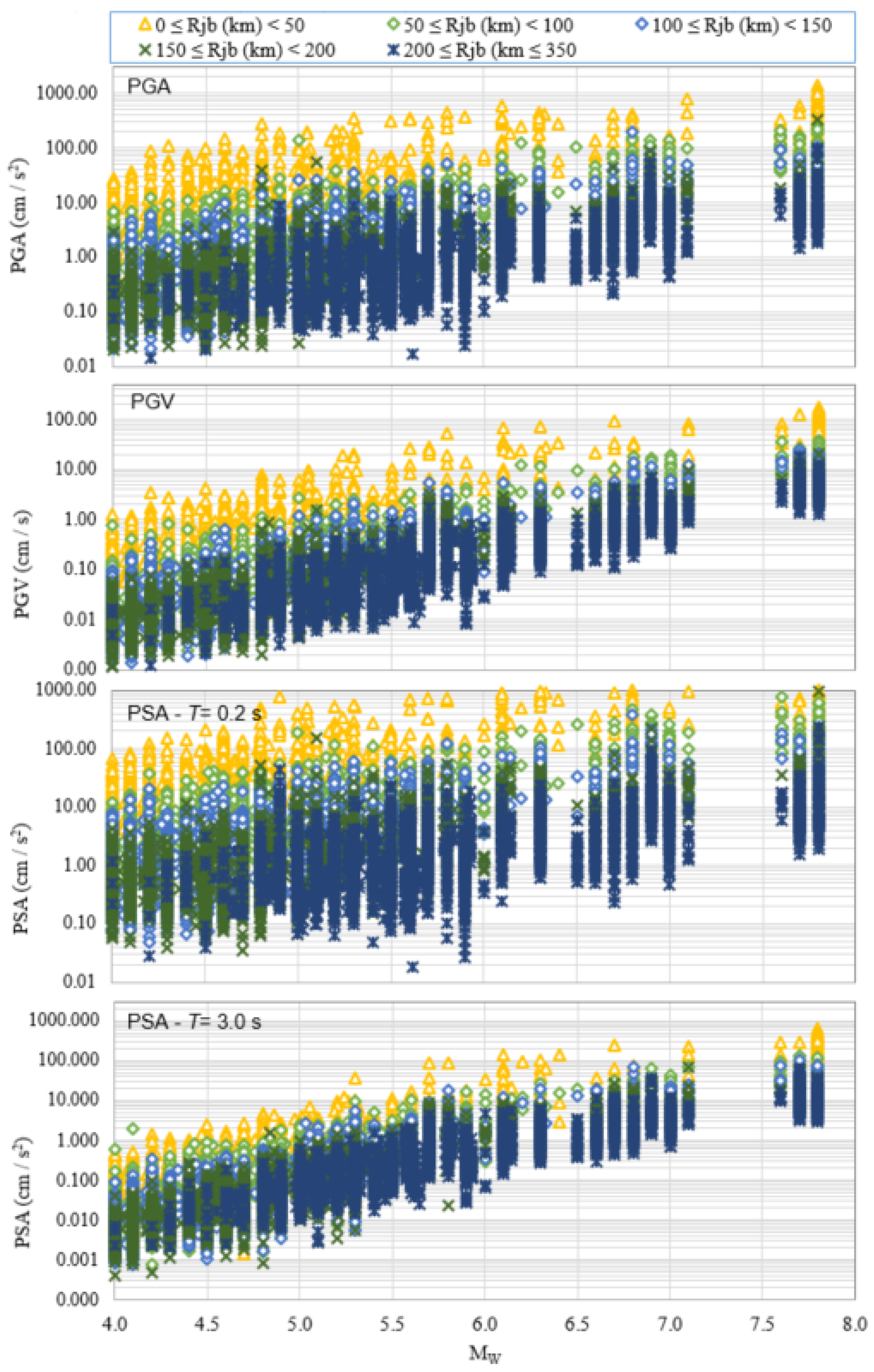
2. Database and Selection Criteria
- Moment magnitude (MW) ranging from 4.0 to 7.8 for shallow crustal earthquakes,
- Mainshock and aftershock events with focal depths ≤ 35 km,
- A source-to-site distance (RJB) ranging from 0 to 350 km,
- The used records are characterized by SS (9410), NS (9713), and RS (1050) fault types,
- The ground-motion data, obtained from the databases, consist of horizontal-component recordings that have been processed and converted to RotD50 [31]. The dataset includes PGA, PGV, and 5% damping PSA values for 36 different periods ranging from 0.01 to 10.0 s.
- Time-averaged 30 m shear-wave velocities of VS30 = 131 to 1862 m/s,
- The strong-motion records controlling our equations are derived principally only from Türkiye and were mostly obtained from high-resolution digital recorders in free-field stations, while a limited number of records before 2000 were provided from single-story buildings and analog instruments,
- Records with low resolution, noise, anormal peaks, or with S-triggers, and those containing consecutive earthquakes in the same series, have been excluded.
3. Ground-Motion Prediction Models (GMPMs)
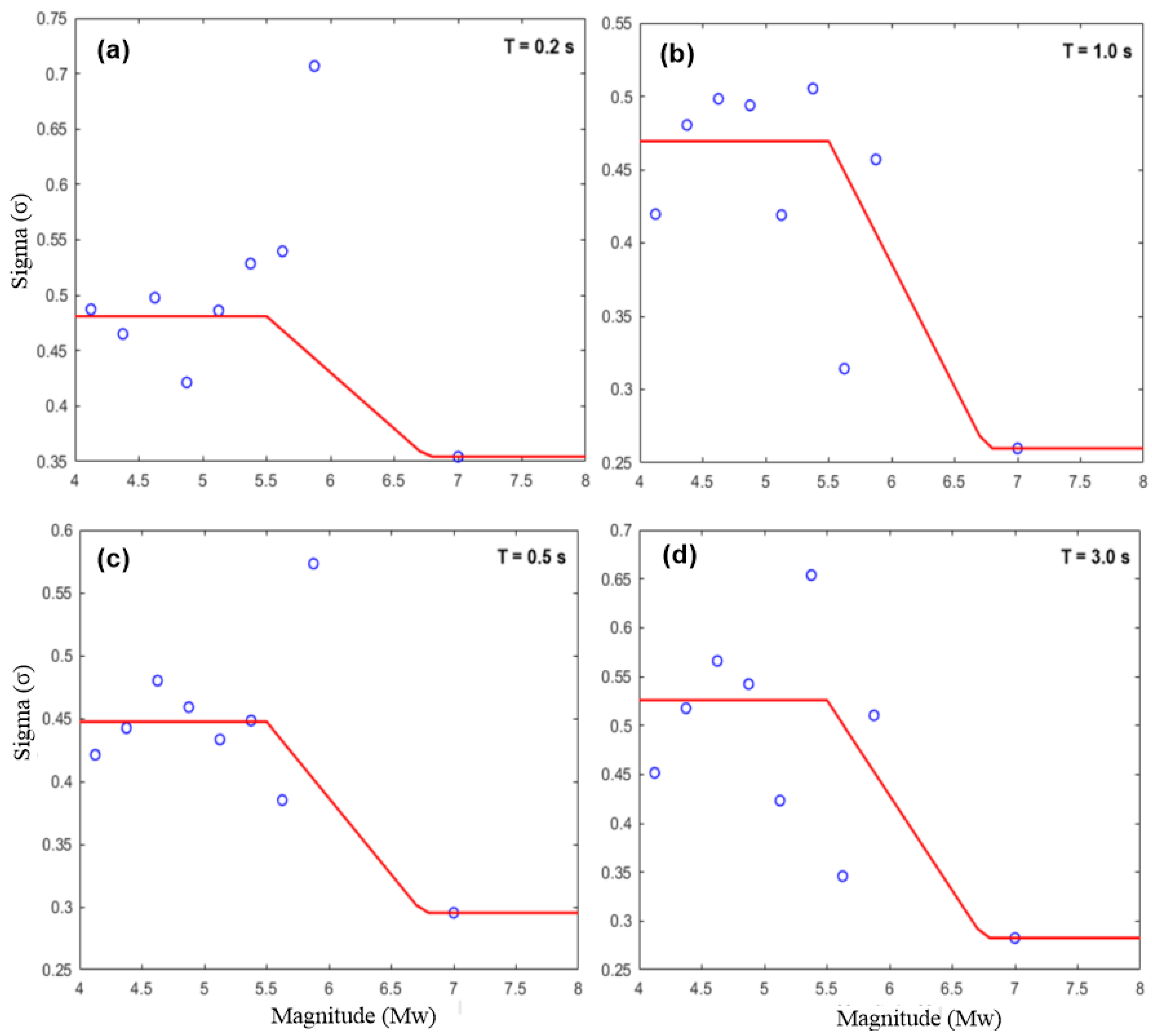
3.1. Aleatory Variability Model
3.2. Regression Analysis
3.3. Regression Coefficients and Residuals
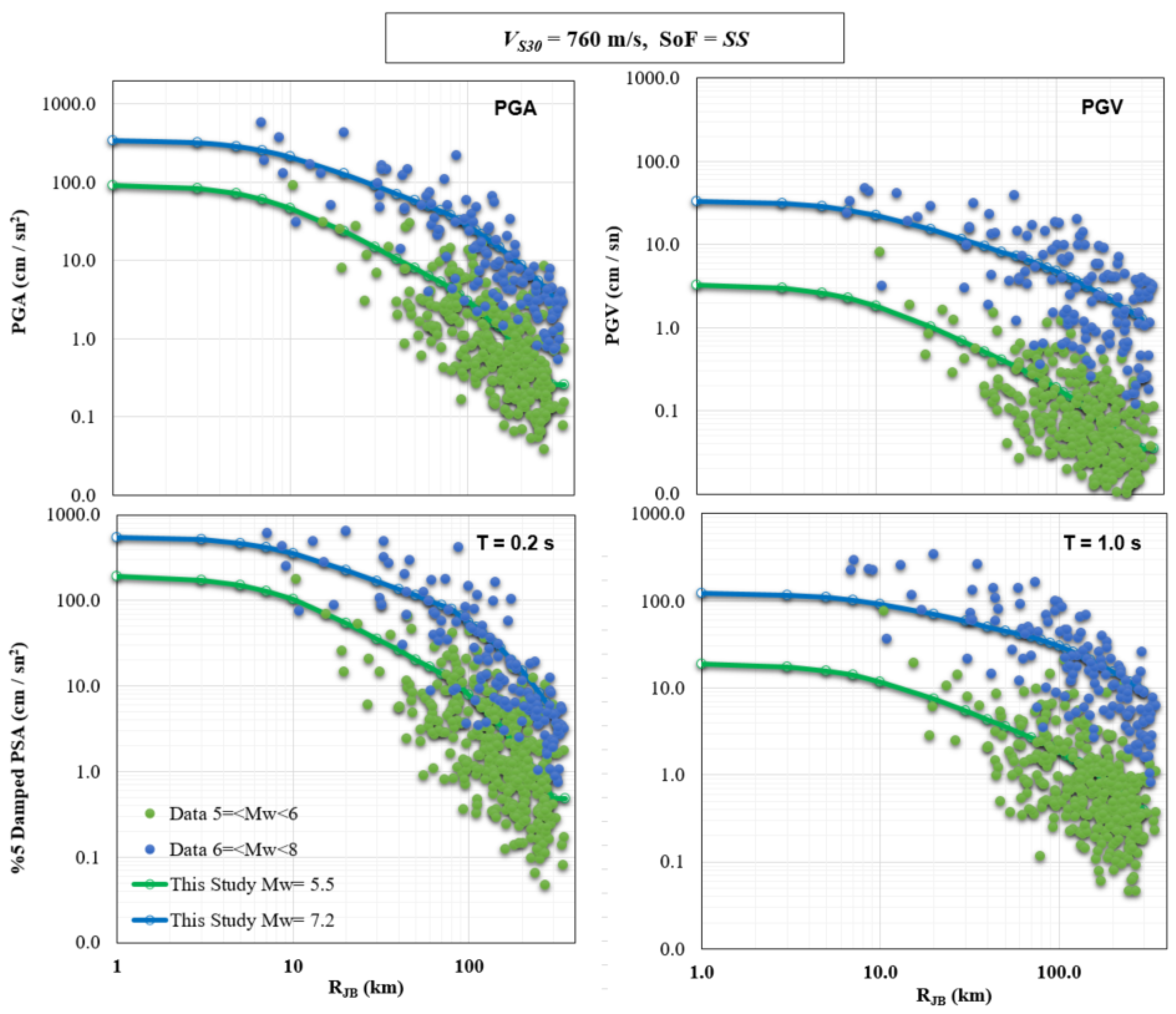
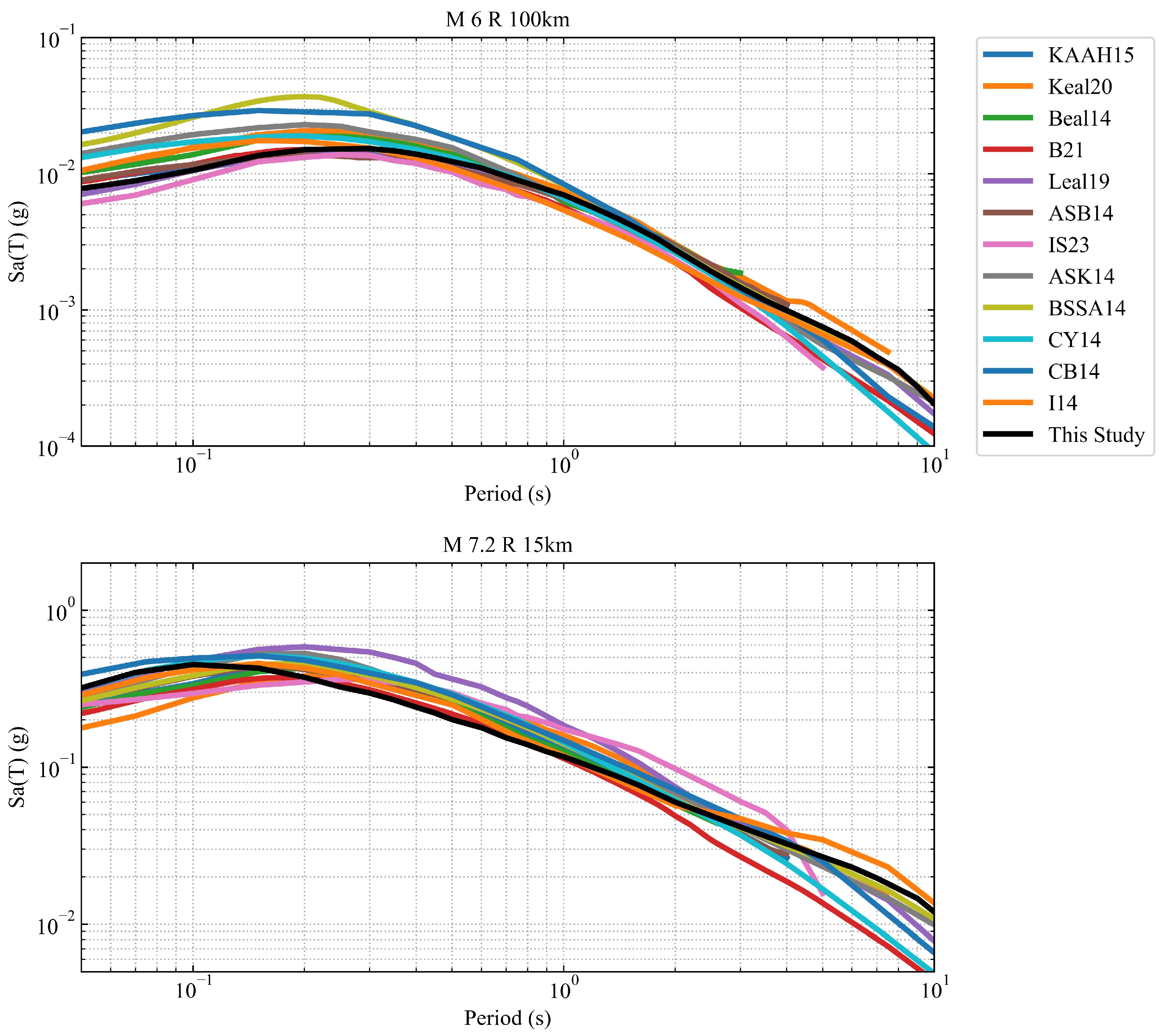
3.4. Comparisons
4. Results and Discussion
- The between-event residuals show no significant trends, though records from the Van earthquake (MW 7.1) fall below the median. This discrepancy is likely due to the interaction between the variable stress drop and the kappa term. The weak ground motions from the Van earthquake are inconsistent with finite-fault distance metrics.
- A strong correlation was found between one component of the standard deviation (between-event standard deviations) and magnitude. As the magnitude increases, τ decreases, and this pattern is independent of the period.
- By incorporating a heteroscedastic model for between-event variability, the GMPMs address the magnitude-dependent nature of ground-motion variability, particularly for large events (MW > 6.5).
- The inclusion of non-linear site amplification terms ensures accurate predictions for high-amplitude ground motions, particularly for soft soil conditions (low VS30 values).
- The models are validated for events ranging from MW 4.0 to 7.8 and source-to-site distances up to 350 km. These limits ensure their applicability for a wide range of engineering and seismic hazard scenarios.
- Magnitude (MW) range: 4.0–7.8,
- Events: mainshocks and aftershocks,
- Distance (RJB) range: 0–350 km,
- Event depth: shallower than 35 km,
- Style of faulting (SoF): SS, NS, and RS,
- Range of applicable site conditions (VS30): 131–1862 m/s,
- GMIMs (RotD50): PSA at 5% damping for 36 periods in the 0.01–10 s range, PGA and PGV.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bozkurt, E. Neotectonics of Turkey—A synthesis. Geodin. Acta 2001, 14, 3–30. [Google Scholar] [CrossRef]
- Douglas, J. Ground Motion Prediction Equations 1964–2023. 2024. Available online: https://figshare.com/authors/John_Douglas/4052182 (accessed on 19 March 2025).
- Kalkan, E.; Gülkan, P. Site-dependent spectra derived from ground motion records in Turkey. Earthq. Spectra 2004, 20, 1111–1138. [Google Scholar] [CrossRef]
- Akkar, S.; Cagnan, Z. A local ground-motion predictive model for Turkey and its comparison with other regional and global ground-motion models. Bull. Seismol. Soc. Am. 2010, 100, 2978–2995. [Google Scholar] [CrossRef]
- Zhao, J.X.; Zhou, S.; Zhou, J.; Zhao, C.; Zhang, H.; Zhang, Y.; Gao, P.; Lan, X.; Rhoades, D.; Fukushima, Y.; et al. Ground-motion prediction equations for shallow crustal and upper-mantle earthquakes in Japan using site class and simple geometric attenuation functions. Bull. Seismol. Soc. Am. 2016, 106, 1552–1569. [Google Scholar] [CrossRef]
- Bindi, D.; Massa, M.; Luzi, L.; Ameri, G.; Pacor, F.; Puglia, R.; Augliera, P. Pan-European ground-motion prediction equations for the average horizontal component of PGA, PGV, and 5%-damped PSA at spectral periods up to 3.0 s using the RESORCE dataset. Bull. Earthq. Eng. 2014, 12, 391–430. [Google Scholar] [CrossRef]
- Kale, Ö.; Akkar, S.; Ansari, A.; Hamzehloo, H. A ground-motion predictive model for Iran and Turkey for horizontal PGA, PGV and 5%-damped response spectrum: Investigation of possible regional effects. Bull. Seismol. Soc. Am. 2015, 105, 963–980. [Google Scholar]
- Lanzano, G.; Luzi, L.; Pacor, F.; Felicetta, C.; Puglia, R.; Sgobba, S.; D’Amico, M. A revised ground-motion prediction model for shallow crustal earthquakes in Italy. Bull. Seismol. Soc. Am. 2019, 109, 525–540. [Google Scholar] [CrossRef]
- Boore, D.M.; Stewart, J.P.; Skarlatoudis, A.A.; Seyhan, E.; Margaris, B.; Theodoulidis, N.; Scordilis, E.; Kalogeras, I.; Klimis, N.; Melis, N.S. A ground-motion prediction model for shallow crustal earthquakes in Greece. Bull. Seismol. Soc. Am. 2021, 111, 857–874. [Google Scholar]
- Özbey, C.; Sarı, A.; Manuel, L.; Erdik, M.; Fahjan, Y. An empirical attenuation relationship for northerwestern Turkey ground motion using a random effects approach. Soil Dynam. Earthq. Eng. 2004, 24, 115–125. [Google Scholar]
- Luzi, L.; Morasca, P.; Zolezzi, F.; Bindi, D.; Pacor, F.; Spallarossa, D.; Franceschina, G. Ground motion models for Molise region (southern Italy). In Proceedings of the First European Conference on Earthquake Engineering and Seismology (a Joint Event of the 13th ECEE & 30th General Assembly of the ESC, Geneva, Switzerland, 3–8 September 2006; p. 938. [Google Scholar]
- Akyol, N.; Karagöz, Ö. Empirical Attenuation Relationships for Western Anatolia, Turkey. Turk. J. Earth Sci. 2009, 18, 2. [Google Scholar] [CrossRef]
- Lanzano, G.; Luzi, L. A ground motion model for volcanic areas in Italy. Bull. Earthq. Eng. 2020, 18, 57–76. [Google Scholar] [CrossRef]
- Akkar, S.; Bommer, J.J. Empirical Equations for the Prediction of PGA, PGV, and Spectral Accelerations in Europe, the Mediterranean Region, and the Middle East. Seismol. Res. Lett. 2010, 81, 195–206. [Google Scholar] [CrossRef]
- Boore, D.M.; Stewart, J.P.; Seyhan, E.; Atkinson, G.A. NGA-West2 equations for predicting PGA, PGV, and 5% damped PSA for shallow crustal earthquakes. Earthq. Spectra 2014, 30, 1057–1085. [Google Scholar] [CrossRef]
- Chiou, B.S.-J.; Youngs, R.R. Update of the Chiou and Youngs NGA model for the average horizontal component of peak ground motion and response spectra. Earthq. Spectra 2014, 30, 1117–1153. [Google Scholar]
- Akkar, S.; Sandıkkaya, M.A.; Bommer, J.J. Empirical ground-motion models for point-and extended-source crustal earthquake scenarios in Europe and the Middle East. Bull. Earthq. Eng. 2014, 12, 359–387. [Google Scholar]
- Kotha, S.R.; Weatherill, G.; Bindi, D.; Cotton, F. A regionally-adaptable ground-motion model for shallow crustal earthquakes in Europe. Bull. Earthq. Eng. 2020, 18, 4091–4125. [Google Scholar] [CrossRef]
- İçen, A.; Sandikkaya, M.A. Region Specific Ground-Motion Predictive Models for Shallow Active Regions. J. Earthq. Eng. 2023, 27, 4449–4468. [Google Scholar] [CrossRef]
- Ulusay, R.; Tuncay, E.; Sönmez, H.; Gökçeoğlu, C. An attenuation relationship based on Turkish strong motion data and iso-acceleration map of Turkey. Eng. Geol. 2004, 74, 265–291. [Google Scholar]
- Akkar, S.; Çagnan, Z.; Yenier, E.; Erdogan, Ö.; Sandıkkaya, M.A.; Gülkan, P. The recently compiled Turkish strong-motion database: Preliminary investigation for seismological parameters. J. Seismol. 2010, 14, 457–479. [Google Scholar]
- Power, M.; Chiou, B.; Abrahamson, N.; Bozorgnia, Y.; Shantz, T.; Roblee, C. An overview of the NGA project. Earthq. Spectra 2008, 24, 3–21. [Google Scholar] [CrossRef]
- Ancheta, T.D.; Darragh, R.B.; Stewart, J.P.; Seyhan, E.; Silva, W.J.; Chiou, B.S.J.; Wooddell, K.E.; Graves, R.W.; Kottke, A.R.; Boore, D.M.; et al. NGA-West2 database. Earthq. Spectra 2014, 30, 989–1005. [Google Scholar]
- Luzi, L.; Puglia, R.; Russo, E.; D’Amico, M.; Felicetta, C.; Pacor, F.; Lanzano, G.; Çeken, U.; Clinton, J.; Costa, G.; et al. The Engineering Strong-Motion Database: A Platform to Access Pan-European Accelerometric Data. Seismol. Res. Lett. 2016, 87, 987–997. [Google Scholar] [CrossRef]
- Akkar, S.; Sandıkkaya, M.A.; Şenyurt, M.; Sisi, A.A.; Ay, B.Ö.; Traversa, P.; Douglas, J.; Cotton, F.; Luzi, L.; Hernandez, B.; et al. Reference Database for Seismic Ground-Motion in Europe (RESORCE). Bull. Earthq. Eng. 2014, 12, 311–339. [Google Scholar]
- Dogan, G.G.; Yalciner, A.C.; Yuksel, Y.; Ulutas, E.; Polat, O.; Güler, I.; Şahin, C.; Tarih, A.; Kânoğlu, U. The 30 October 2020 Aegean Sea Tsunami: Post-Event Field Survey Along Turkish Coast. Pure Appl. Geophys. 2021, 178, 785–812. [Google Scholar] [CrossRef] [PubMed]
- Ozer, C. 4-D tomographic change of Vp and Vp/Vs structure before destructive earthquakes: A case study of the Sivrice-Elazığ earthquake (MW = 6.8), Eastern Turkey. Nat. Hazards 2021, 108, 1901–1917. [Google Scholar] [CrossRef]
- Öztürk, S.; Alkan, H. Multiple parameter analysis for assessing and forecasting earthquake hazards in the Lake Van region, Turkey. Baltica 2023, 36, 133–154. [Google Scholar] [CrossRef]
- Paolucci, R.; Pacor, F.; Puglia, R.; Ameri, G.; Cauzzi, C.; Massa, M. Record processing in ITACA, the new Italian strong-motion database, in Earthquake Data in Engineering Seismology. In Geotechnical, Geological and Earthquake Engineering; Akkar, S., Gulkan, P., Van Eck, T., Eds.; Springer: Dordrecht, The Netherlands, 2011; Volume 14, pp. 99–113. [Google Scholar]
- Sandıkkaya, M.A.; Güryuva, B.; Kale, Ö.; Okçu, O.; İçen, A.; Yenier, E.; Akkar, S. An Updated Strong-Motion Database of Türkiye (SMD-TR). Earthq. Spectra 2024, 40, 847–870. [Google Scholar] [CrossRef]
- Boore, D.M. Orientation-independent, nongeometric-mean measures of seismic intensity from two horizontal components of motion. Bull. Seismol. Soc. Am. 2010, 100, 1830–1835. [Google Scholar]
- TBEC-2018; (Turkish Building Earthquake Code), Specifications for Buildings to be Built in Seismic Areas. Ministry of Public Works and Settlement: Ankara, Turkey.
- NEHRP. Recommended Provisions for Seismic Regulations for New Buildings; NEHRP: Gaithersburg, MD, USA, 2003; Fema450. [Google Scholar]
- Eurocode-8. Design Provisions for Earthquake Resistance of Structures. Seismic Actions and General Requirements of Structures; ENV 1998-1-1; European Committee for Standardization (CEN): Brussels, Belgium, 2002; CEN/TC 250, Draft. [Google Scholar]
- Sandıkkaya, M.A.; Yılmaz, M.T.; Bakır, B.S.; Yılmaz, O. Site classification of Turkish national strong-motion stations. J. Seismol. 2010, 14, 543–563. [Google Scholar]
- Kurtuluş, C.; Sertçelik, F.; Sertçelik, İ.; Kuru, T.; Tekin, K.; Ateş, E.; Apak, A.; Kökbudak, D.; Sezer, S.; Yalçın, D. Determination of site characterization in Turkey strong motion recording stations. J. Fac. Eng. Archit. Gazi Univ. 2020, 35, 1829–1846. [Google Scholar]
- Abrahamson, N.A.; Silva, W.J.; Kamai, R. Summary of the ASK14 ground motion relation for active crustal regions. Earthq. Spectra 2014, 30, 1025–1055. [Google Scholar]
- Campbell, K.W.; Bozorgnia, Y. NGA-West2 ground motion model for the average horizontal components of PGA, PGV, and 5% damped linear acceleration response spectra. Earthq. Spectra 2014, 30, 1087–1115. [Google Scholar]
- Al Atik, L.; Abrahamson, N.A.; Bommer, J.J.; Scherbaum, F.; Cotton, F.; Kuehn, N. The variability of ground-motion prediction models and its components. Seismol. Res. Lett. 2010, 81, 794–801. [Google Scholar]
- Bates, D.M.; Maechler, M.; Bolker, B. Lme4: Linear Mixed-Effects Models Using S4 Classes, R Manual. 2013. Available online: https://CRAN.R-project.org/package=lme4 (accessed on 10 December 2024).
- Pinheiro, J.; Bates, D.; DebRoy, S.; Sarkar, D.; R Core Team. nlme: Linear and Nonlinear Mixed Effects Models. R Package Version 3.1-155. 2022. Available online: https://CRAN.R-project.org/package=nlme (accessed on 10 December 2024).
- Abrahamson, N.A.; Gülerce, Z. Summary of the Abrahamson and Gulerce NGA-SUB ground-motion model for subduction earthquakes. Earthq. Spectra 2022, 38, 87552930221114374. [Google Scholar] [CrossRef]
- Idriss, I.M. An NGA-West2 empirical model for estimating the horizontal spectral values generated by shallow crustal earthquakes. Earthq. Spectra 2014, 30, 1155–1177. [Google Scholar] [CrossRef]
- Wessel, P.; Luis, J.F.; Uieda, L.A.; Scharroo, R.; Wobbe, F.; Smith, W.H.; Tian, D. The generic mapping tools version 6. Geochem. Geophys. Geosystems 2019, 20, 5556–5564. [Google Scholar]

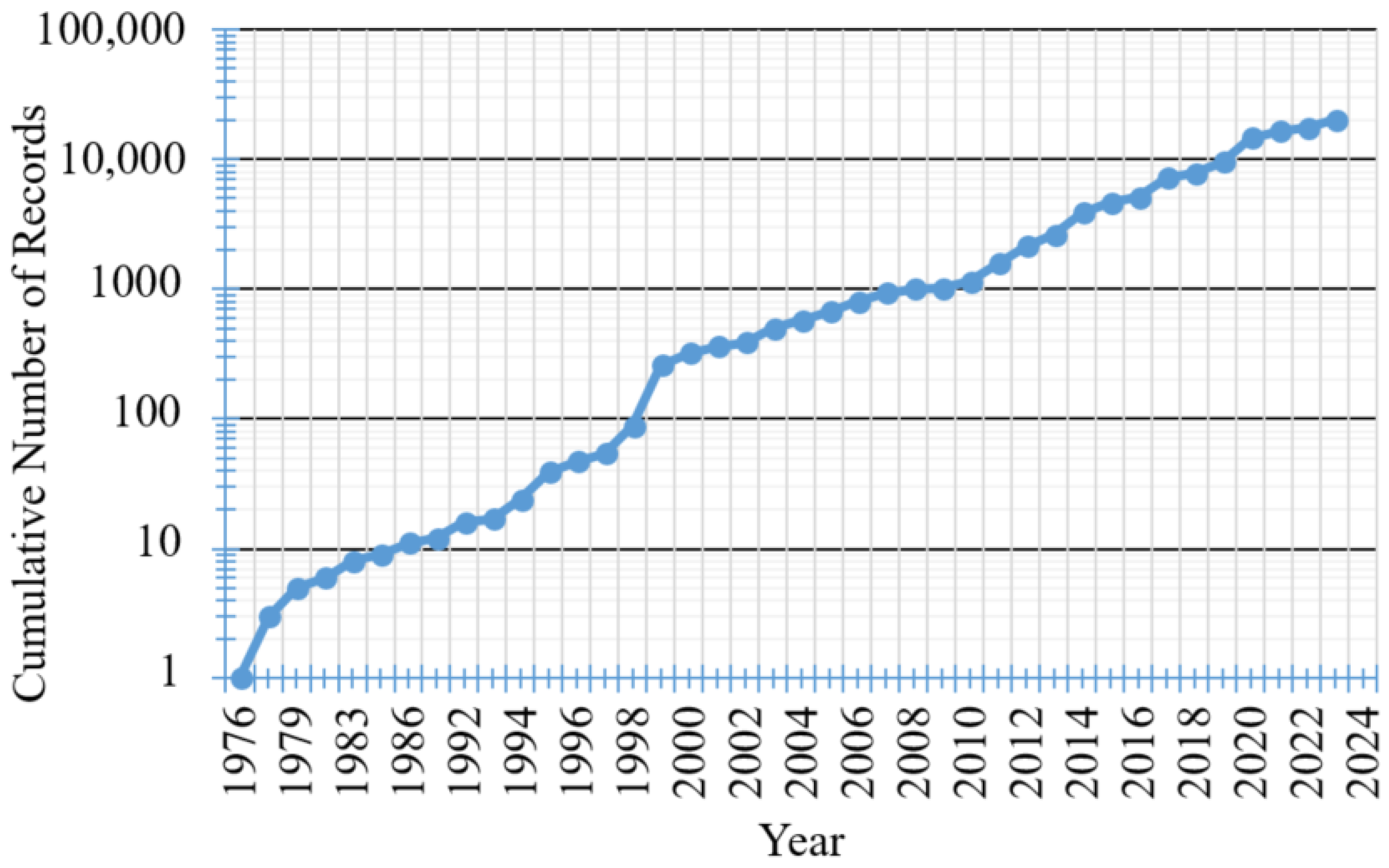
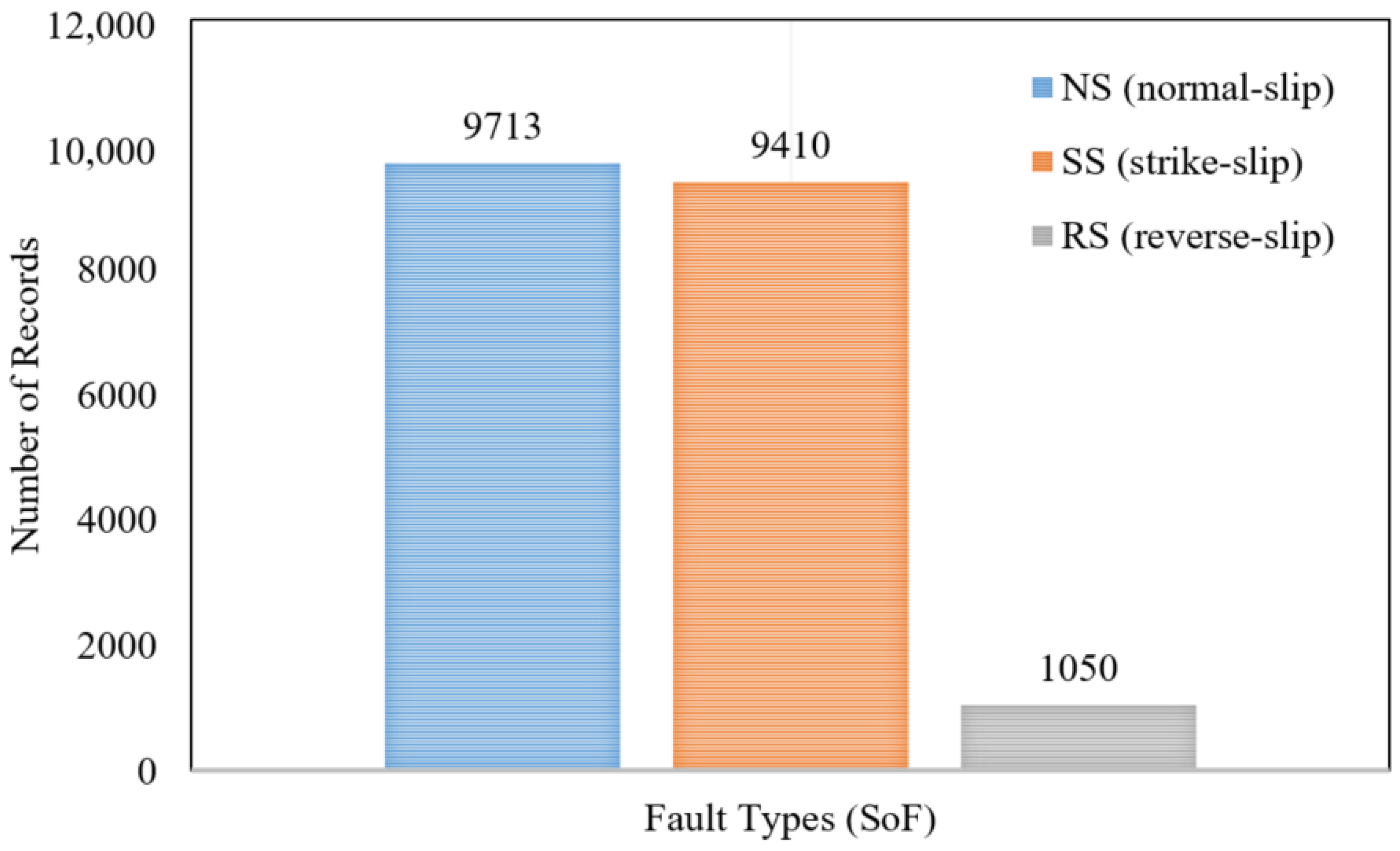



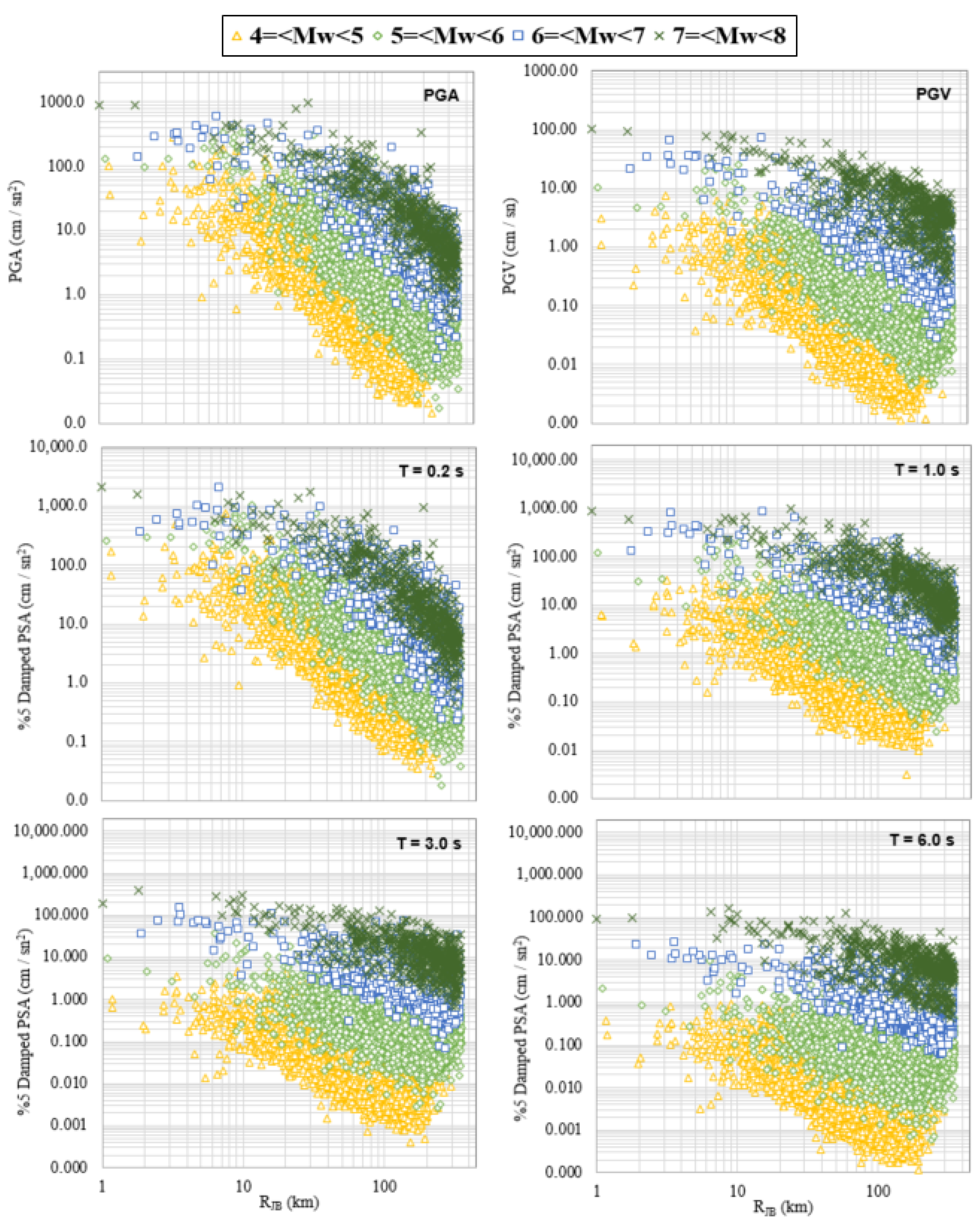
| Database Source | Abbr. | Event Range | Number of Events | Number of Records | Magnitude Range (MW) | Distance Range (RJB) (km) | SoF |
|---|---|---|---|---|---|---|---|
| Engineering Strong-Motion Database | ESM | 1976–2016 (1976–2006) (2006–2016) | 554 | 1736 (671) (1065) | 4.0–7.6 | 0–349 | SS: 938 NS: 664 RS: 134 |
| Updated Strong Motions Database of Türkiye | SMD-TR | 2006–2023 (2006–2016) (2016–2023) | 1149 | 18,437 (3333) (15,104) | 4.0–7.8 | 0–350 | SS: 8472 NS: 9049 RS: 916 |
| Period (s) | c1 | c2 | c3 | c4 | c5 | c6 | c7 | c8 | d1 | d2 | d3 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| PGV | 7.4200 | −4.1159 | 1.0709 | −1.0385 | −1.1349 | 0.0108 | −0.0120 | 0.0200 | −0.8183 | 0.2000 | −0.0026 |
| PGA | 2.4717 | −2.7927 | 0.7180 | −0.6765 | −0.9615 | 0.0163 | −0.0120 | 0.0200 | −1.0108 | 0.2000 | −0.0054 |
| 0.01 | 2.4722 | −2.7671 | 0.7171 | −0.6708 | −0.9463 | 0.0163 | −0.0120 | 0.0200 | −1.0138 | 0.2000 | −0.0054 |
| 0.03 | 2.5008 | −2.6916 | 0.6982 | −0.6520 | −0.8853 | 0.0161 | −0.0120 | 0.0200 | −1.0305 | 0.2000 | −0.0053 |
| 0.04 | 2.8840 | −2.7779 | 0.6495 | −0.6660 | −0.8936 | 0.0163 | −0.0120 | 0.0200 | −1.0980 | 0.2000 | −0.0051 |
| 0.05 | 3.2209 | −2.8597 | 0.6079 | −0.6822 | −0.9234 | 0.0163 | −0.0120 | 0.0200 | −1.1488 | 0.2000 | −0.0051 |
| 0.07 | 3.5751 | −2.8716 | 0.5338 | −0.6851 | −0.9305 | 0.0167 | −0.0120 | 0.0200 | −1.1931 | 0.2000 | −0.0057 |
| 0.10 | 3.3146 | −2.3686 | 0.5264 | −0.5778 | −0.7252 | 0.0184 | −0.0120 | 0.0200 | −1.1605 | 0.2000 | −0.0067 |
| 0.15 | 2.5614 | −1.7674 | 0.6121 | −0.4494 | −0.5501 | 0.0189 | −0.0120 | 0.0200 | −1.0156 | 0.2000 | −0.0077 |
| 0.20 | 2.0036 | −1.5234 | 0.7226 | −0.3983 | −0.5040 | 0.0193 | −0.0120 | 0.0200 | −0.9022 | 0.2000 | −0.0080 |
| 0.25 | 1.5687 | −1.3544 | 0.8164 | −0.3640 | −0.4465 | 0.0182 | 0.0000 | 0.0200 | −0.8233 | 0.2000 | −0.0078 |
| 0.30 | 1.6805 | −1.8930 | 0.8951 | −0.4798 | −0.7252 | 0.0170 | 0.0000 | 0.0200 | −0.7764 | 0.2000 | −0.0074 |
| 0.35 | 1.6229 | −2.1342 | 0.9499 | −0.5340 | −0.8441 | 0.0167 | 0.0000 | 0.0200 | −0.7392 | 0.2000 | −0.0070 |
| 0.40 | 1.6496 | −2.5115 | 1.0038 | −0.6139 | −0.9976 | 0.0159 | 0.0000 | 0.0170 | −0.7106 | 0.2000 | −0.0066 |
| 0.45 | 1.6080 | −2.6932 | 1.0443 | −0.6569 | −1.0700 | 0.0150 | 0.0000 | 0.0130 | −0.6860 | 0.2000 | −0.0063 |
| 0.50 | 1.6051 | −2.9406 | 1.0893 | −0.7118 | −1.1861 | 0.0143 | 0.0000 | 0.0100 | −0.6648 | 0.2000 | −0.0060 |
| 0.60 | 1.7622 | −3.4835 | 1.1674 | −0.8365 | −1.4512 | 0.0133 | 0.0000 | 0.0000 | −0.6424 | 0.2000 | −0.0054 |
| 0.70 | 1.7293 | −3.7962 | 1.2278 | −0.9071 | −1.5472 | 0.0116 | 0.0000 | 0.0000 | −0.6202 | 0.2000 | −0.0049 |
| 0.75 | 1.7602 | −3.8986 | 1.2494 | −0.9373 | −1.6284 | 0.0102 | 0.0000 | 0.0000 | −0.6149 | 0.2000 | −0.0047 |
| 0.80 | 1.7332 | −3.9058 | 1.2728 | −0.9485 | −1.6721 | 0.0095 | 0.0000 | 0.0000 | −0.6068 | 0.2000 | −0.0045 |
| 0.90 | 1.9534 | −4.5322 | 1.3179 | −1.0848 | −1.9409 | 0.0089 | 0.0000 | 0.0000 | −0.5950 | 0.2000 | −0.0042 |
| 1.00 | 2.1180 | −4.9821 | 1.3566 | −1.1867 | −2.1377 | 0.0090 | 0.0000 | 0.0000 | −0.5867 | 0.2000 | −0.0039 |
| 1.20 | 2.1639 | −5.2964 | 1.4327 | −1.2667 | −2.2765 | 0.0080 | 0.0000 | 0.0000 | −0.5862 | 0.2000 | −0.0032 |
| 1.40 | 2.1964 | −5.5681 | 1.4907 | −1.3350 | −2.3754 | 0.0079 | 0.0000 | 0.0000 | −0.5881 | 0.2000 | −0.0027 |
| 1.60 | 2.0974 | −5.6227 | 1.5441 | −1.3566 | −2.3645 | 0.0074 | 0.0000 | 0.0000 | −0.5864 | 0.2000 | −0.0024 |
| 1.80 | 2.2356 | −6.0418 | 1.5792 | −1.4514 | −2.5501 | 0.0067 | 0.0000 | 0.0000 | −0.5931 | 0.2000 | −0.0019 |
| 2.00 | 2.0771 | −5.9185 | 1.6095 | −1.4335 | −2.4513 | 0.0061 | 0.0000 | 0.0000 | −0.6026 | 0.2000 | −0.0016 |
| 2.50 | 2.1419 | −6.3343 | 1.6567 | −1.5360 | −2.5018 | 0.0047 | 0.0000 | 0.0000 | −0.6234 | 0.2000 | −0.0012 |
| 3.00 | 2.1283 | −6.6005 | 1.7053 | −1.6062 | −2.5294 | 0.0033 | 0.0000 | 0.0000 | −0.6266 | 0.2000 | −0.0008 |
| 3.50 | 1.9908 | −6.5981 | 1.7334 | −1.6241 | −2.4824 | 0.0026 | 0.0000 | 0.0000 | −0.6203 | 0.2000 | −0.0005 |
| 4.00 | 2.0597 | −6.8899 | 1.7536 | −1.7011 | −2.6062 | 0.0011 | 0.0000 | 0.0000 | −0.6143 | 0.2000 | 0.0000 |
| 5.00 | 2.0970 | −7.0547 | 1.7703 | −1.7478 | −2.6782 | 0.0017 | 0.0000 | 0.0000 | −0.6204 | 0.2000 | 0.0000 |
| 6.00 | 1.9158 | −6.8783 | 1.7855 | −1.7233 | −2.5327 | 0.0006 | 0.0000 | 0.0000 | −0.6256 | 0.2000 | 0.0000 |
| 7.00 | 1.8140 | −6.9570 | 1.8022 | −1.7555 | −2.4594 | 0.0002 | 0.0000 | 0.0000 | −0.6443 | 0.2000 | 0.0000 |
| 8.00 | 1.5010 | −6.6609 | 1.8011 | −1.7085 | −2.2424 | −0.0008 | 0.0000 | 0.0000 | −0.6603 | 0.2000 | 0.0000 |
| 9.00 | 1.2469 | −6.4606 | 1.7966 | −1.6775 | −2.1087 | −0.0005 | 0.0000 | 0.0000 | −0.6768 | 0.2000 | 0.0000 |
| 10.00 | 0.9173 | −6.1840 | 1.7716 | −1.6269 | −1.9417 | 0.0000 | 0.0000 | 0.0000 | −0.6938 | 0.2000 | 0.0000 |
| Period (s) | s1 | s2 | s3 | s4 | VC | τ1 | τ2 | Φs2s | Φss | τ | σ |
|---|---|---|---|---|---|---|---|---|---|---|---|
| PGV | −0.6153 | −0.0660 | −0.0090 | 5.0000 | 1418 | 0.4230 | 0.2348 | 0.4706 | 0.4680 | 0.3553 | 0.7528 |
| PGA | −0.5400 | −0.1780 | −0.0080 | 0.1460 | 1418 | 0.4546 | 0.2842 | 0.4930 | 0.5107 | 0.4108 | 0.8201 |
| 0.01 | −0.5379 | −0.1780 | −0.0080 | 0.1460 | 1418 | 0.4483 | 0.2839 | 0.4930 | 0.5114 | 0.4113 | 0.8208 |
| 0.03 | −0.5234 | −0.1910 | −0.0080 | 0.1710 | 1407 | 0.4478 | 0.2841 | 0.4909 | 0.5205 | 0.4108 | 0.8250 |
| 0.04 | −0.4952 | −0.2190 | −0.0080 | 0.1810 | 1395 | 0.4518 | 0.2827 | 0.4923 | 0.5335 | 0.4231 | 0.8403 |
| 0.05 | −0.4799 | −0.2560 | −0.0070 | 0.1920 | 1388 | 0.4580 | 0.2855 | 0.4986 | 0.5429 | 0.4437 | 0.8604 |
| 0.07 | −0.4672 | −0.2967 | −0.0070 | 0.2280 | 1373 | 0.4703 | 0.3001 | 0.5126 | 0.5428 | 0.4831 | 0.8892 |
| 0.10 | −0.4664 | −0.3210 | −0.0070 | 0.2710 | 1352 | 0.4864 | 0.3256 | 0.5268 | 0.5361 | 0.4893 | 0.8969 |
| 0.15 | −0.4970 | −0.3097 | −0.0070 | 0.3087 | 1318 | 0.4855 | 0.3497 | 0.5343 | 0.5349 | 0.4827 | 0.8970 |
| 0.20 | −0.5556 | −0.2900 | −0.0070 | 0.2900 | 1256 | 0.4811 | 0.3543 | 0.5285 | 0.5316 | 0.4688 | 0.8841 |
| 0.25 | −0.6022 | −0.2700 | −0.0080 | 0.2500 | 1200 | 0.4650 | 0.3528 | 0.5177 | 0.5332 | 0.4539 | 0.8708 |
| 0.30 | −0.6487 | −0.2460 | −0.0080 | 0.2150 | 1138 | 0.4614 | 0.3432 | 0.5142 | 0.5340 | 0.4411 | 0.8627 |
| 0.35 | −0.6774 | −0.2255 | −0.0080 | 0.1890 | 1085 | 0.4541 | 0.3295 | 0.5064 | 0.5312 | 0.4352 | 0.8533 |
| 0.40 | −0.7142 | −0.2050 | −0.0080 | 0.1630 | 1047 | 0.4509 | 0.3192 | 0.5066 | 0.5277 | 0.4317 | 0.8494 |
| 0.45 | −0.7327 | −0.1845 | −0.0085 | 0.1520 | 1016 | 0.4482 | 0.3081 | 0.5060 | 0.5226 | 0.4341 | 0.8471 |
| 0.50 | −0.7634 | −0.1640 | −0.0090 | 0.1410 | 989 | 0.4474 | 0.2954 | 0.5071 | 0.5186 | 0.4341 | 0.8453 |
| 0.60 | −0.7854 | −0.1373 | −0.0090 | 0.1250 | 945 | 0.4455 | 0.2988 | 0.5107 | 0.5108 | 0.4387 | 0.8451 |
| 0.70 | −0.8053 | −0.1137 | −0.0090 | 0.1110 | 912 | 0.4525 | 0.2859 | 0.5194 | 0.5013 | 0.4390 | 0.8449 |
| 0.75 | −0.8140 | −0.1033 | −0.0090 | 0.1050 | 899 | 0.4572 | 0.2817 | 0.5243 | 0.4945 | 0.4450 | 0.8471 |
| 0.80 | −0.8171 | −0.0930 | −0.0090 | 0.0990 | 888 | 0.4607 | 0.2774 | 0.5291 | 0.4873 | 0.4513 | 0.8492 |
| 0.90 | −0.8363 | −0.0795 | −0.0090 | 0.0900 | 872 | 0.4652 | 0.2699 | 0.5411 | 0.4815 | 0.4656 | 0.8610 |
| 1.00 | −0.8393 | −0.0660 | −0.0090 | 0.0810 | 862 | 0.4694 | 0.2598 | 0.5496 | 0.4760 | 0.4774 | 0.8698 |
| 1.20 | −0.8342 | −0.0513 | −0.0083 | 0.0663 | 855 | 0.4755 | 0.2809 | 0.5715 | 0.4661 | 0.4998 | 0.8909 |
| 1.40 | −0.8266 | −0.0393 | −0.0077 | 0.0527 | 850 | 0.4883 | 0.2644 | 0.5934 | 0.4551 | 0.5118 | 0.9062 |
| 1.60 | −0.8023 | −0.0300 | −0.0070 | 0.0400 | 845 | 0.4950 | 0.2555 | 0.6021 | 0.4495 | 0.5169 | 0.9120 |
| 1.80 | −0.7865 | −0.0250 | −0.0055 | 0.0335 | 840 | 0.5007 | 0.2677 | 0.6075 | 0.4446 | 0.5209 | 0.9154 |
| 2.00 | −0.7652 | −0.0200 | −0.0040 | 0.0270 | 835 | 0.5069 | 0.2708 | 0.6167 | 0.4389 | 0.5237 | 0.9205 |
| 2.50 | −0.7115 | −0.0130 | −0.0030 | 0.0190 | 830 | 0.5166 | 0.2776 | 0.6380 | 0.4296 | 0.5117 | 0.9238 |
| 3.00 | −0.6757 | −0.0080 | −0.0020 | 0.0150 | 810 | 0.5257 | 0.2825 | 0.6529 | 0.4266 | 0.4883 | 0.9202 |
| 3.50 | −0.6478 | −0.0040 | −0.0020 | 0.0115 | 800 | 0.5380 | 0.2850 | 0.6642 | 0.4251 | 0.4742 | 0.9202 |
| 4.00 | −0.6253 | 0.0000 | −0.0020 | 0.0080 | 780 | 0.5467 | 0.3026 | 0.6724 | 0.4242 | 0.4591 | 0.9181 |
| 5.00 | −0.6008 | 0.0000 | −0.0010 | 0.0070 | 760 | 0.5501 | 0.3271 | 0.6742 | 0.4238 | 0.4454 | 0.9125 |
| 6.00 | −0.5826 | 0.0000 | 0.0000 | 0.0063 | 760 | 0.5499 | 0.3491 | 0.6709 | 0.4270 | 0.4301 | 0.9041 |
| 7.00 | −0.5510 | 0.0000 | 0.0000 | 0.0057 | 760 | 0.5416 | 0.4130 | 0.6569 | 0.4369 | 0.4000 | 0.8845 |
| 8.00 | −0.5242 | 0.0000 | 0.0000 | 0.0050 | 760 | 0.5310 | 0.4293 | 0.6443 | 0.4459 | 0.3775 | 0.8697 |
| 9.00 | −0.5094 | 0.0000 | 0.0000 | 0.0045 | 760 | 0.5215 | 0.4216 | 0.6324 | 0.4565 | 0.3638 | 0.8606 |
| 10.00 | −0.5016 | 0.0000 | 0.0000 | 0.0040 | 760 | 0.5126 | 0.4200 | 0.6234 | 0.4630 | 0.3525 | 0.8528 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Çeken, U.; Sertçelik, F.; İçen, A. A New Ground-Motion Prediction Model for Shallow Crustal Earthquakes in Türkiye. Appl. Sci. 2025, 15, 3442. https://doi.org/10.3390/app15073442
Çeken U, Sertçelik F, İçen A. A New Ground-Motion Prediction Model for Shallow Crustal Earthquakes in Türkiye. Applied Sciences. 2025; 15(7):3442. https://doi.org/10.3390/app15073442
Chicago/Turabian StyleÇeken, Ulubey, Fadime Sertçelik, and Abdullah İçen. 2025. "A New Ground-Motion Prediction Model for Shallow Crustal Earthquakes in Türkiye" Applied Sciences 15, no. 7: 3442. https://doi.org/10.3390/app15073442
APA StyleÇeken, U., Sertçelik, F., & İçen, A. (2025). A New Ground-Motion Prediction Model for Shallow Crustal Earthquakes in Türkiye. Applied Sciences, 15(7), 3442. https://doi.org/10.3390/app15073442






