Research on the Aerodynamic–Propulsion Coupling Characteristics of a Distributed Propulsion System

Abstract

In recent years, the distributed propulsion system has received extensive attention due to its advantages such as high propulsion efficiency, low noise, high safety redundancy, and good flexibility and maneuverability. However, the interaction between the internal and external flow can limit the aerodynamic performance of the ducted fan. To investigate the influence of the internal and external flow interaction on the aerodynamic–propulsion coupling characteristics of the distributed propulsion system, an over-wing symmetric configuration with five distributed ducted fans was constructed, and numerical simulations were performed using a method based on the body force model. Results show that as the flight Mach number increases, the lift obtained by the wing increases, while the stall angle of attack decreases, and the stall angle of attack at a Mach number of 0.5 is reduced by 15° compared with a Mach number of 0.2. At large angles of attack, the edge fans have the strongest ability to resist airflow separation, while the middle fan has the weakest ability to resist airflow separation, and its fan performance index drops the fastest. When the Mach number is 0.4, the mass flow rate and thrust of the middle fan are reduced by 16% and 28%, respectively, compared with those when the Mach number is 0.2. The higher the flight Mach number, the larger the intake distortion degree of the ducted fans. The middle fan is most affected by total pressure distortion and least affected by swirl distortion, whereas the edge fans are least affected by total pressure distortion and most affected by swirl distortion.

1. Introduction

Due to the severe problems of air pollution and excessive consumption of fossil fuels caused by the rapid development of the aviation industry, an increasing number of countries are advocating for the development plan of “Green Aviation”. The National Aeronautics and Space Administration (NASA) of the United States has proposed the N + 3 development goal, requiring a 70% reduction in aircraft fuel consumption by 2030 [1,2,3]. However, it is difficult to meet the future requirements of aircraft in terms of energy conservation and emissions reduction merely by relying on existing technologies to improve traditional aircraft. Distributed electrical propulsion (DEP) has attracted much attention from scholars due to its advantages of low emissions, low consumption, and low noise [4,5,6,7].

DEP aircraft have become a research hotspot among scholars due to its favorable economic performance and propulsion advantages. Kim [8] and Fard [9] provided detailed introductions to distributed propulsion aircraft with different configurations and elucidated their potential aerodynamic-–propulsion advantages. Zhang [10] and Perry [11] conducted research on the aerodynamic–propulsion coupling characteristics of the DEP system through low-speed wind tunnel tests, revealing the potential benefits of this coupled layout for aerodynamic–propulsion interaction. Cui Rong [12] explored the influence of engine flow rate and the engine installation position on the aerodynamic performance of the blended wing body aircraft. Xu De [13] conducted research on the aerodynamic influence law and flow mechanism of the DEP system with the boundary layer ingestion (BLI) effect based on the two-dimensional calculation method and considering the influence of multiple variables. Gong Tianyu [14] revealed the influence law of the internal and external flow coupling effect on the aerodynamic performance and flow mechanism of the DEP system under different flight conditions. Zhou Fang [15] analyzed the coupling interference mechanism and law among ducted fans in the DEP system by combining experiments and numerical simulations. Dorfling [16] investigated the effects of different configurations, such as an isolated ducted fan layout, a single ducted fan and wing coupled layout, and a multi-ducted fan and wing coupled layout, on the performance of a single ducted fan through wind tunnel tests. The research showed that the coupling interference between the fan and the wing significantly disturbs the internal flow of the ducted fan, thus resulting in performance losses. Liu [17] and Kerho [18], respectively, carried out numerical studies on distributed ducted fans, focusing on the influence of the internal and external flow coupling effect on the aerodynamic performance of the coupled configuration. The above research results indicate that there is a significant coupling effect between aerodynamics and propulsion in the DEP system. Although many scholars at home and abroad have carried out research on the complex interactive coupling mechanism and aerodynamic–propulsion characteristics of the DEP system, few have paid attention to the influence law of the internal and external flow coupling effect on the performance of ducted fans, especially the influence of boundary layer ingestion on the intake distortion of ducted fans, as well as the relevant details of the flow field.

Therefore, this paper develops a body force model (BFM) which is capable of conducting rapid numerical simulations and calculations for complex rotating turbomachinery. And this model is applied to carry out numerical simulation research on an over-wing symmetric configuration with five distributed ducted fans. The influence of the internal and external flow coupling effect on the aerodynamic characteristics of the coupled configuration and the performance of the ducted fans is deeply explored. Meanwhile, the details of the external flow field of the wing and the internal flow field of the ducted fans are studied, and the performance variation laws of the ducted fans under the coupling effect of the internal and external flow are preliminarily summarized.

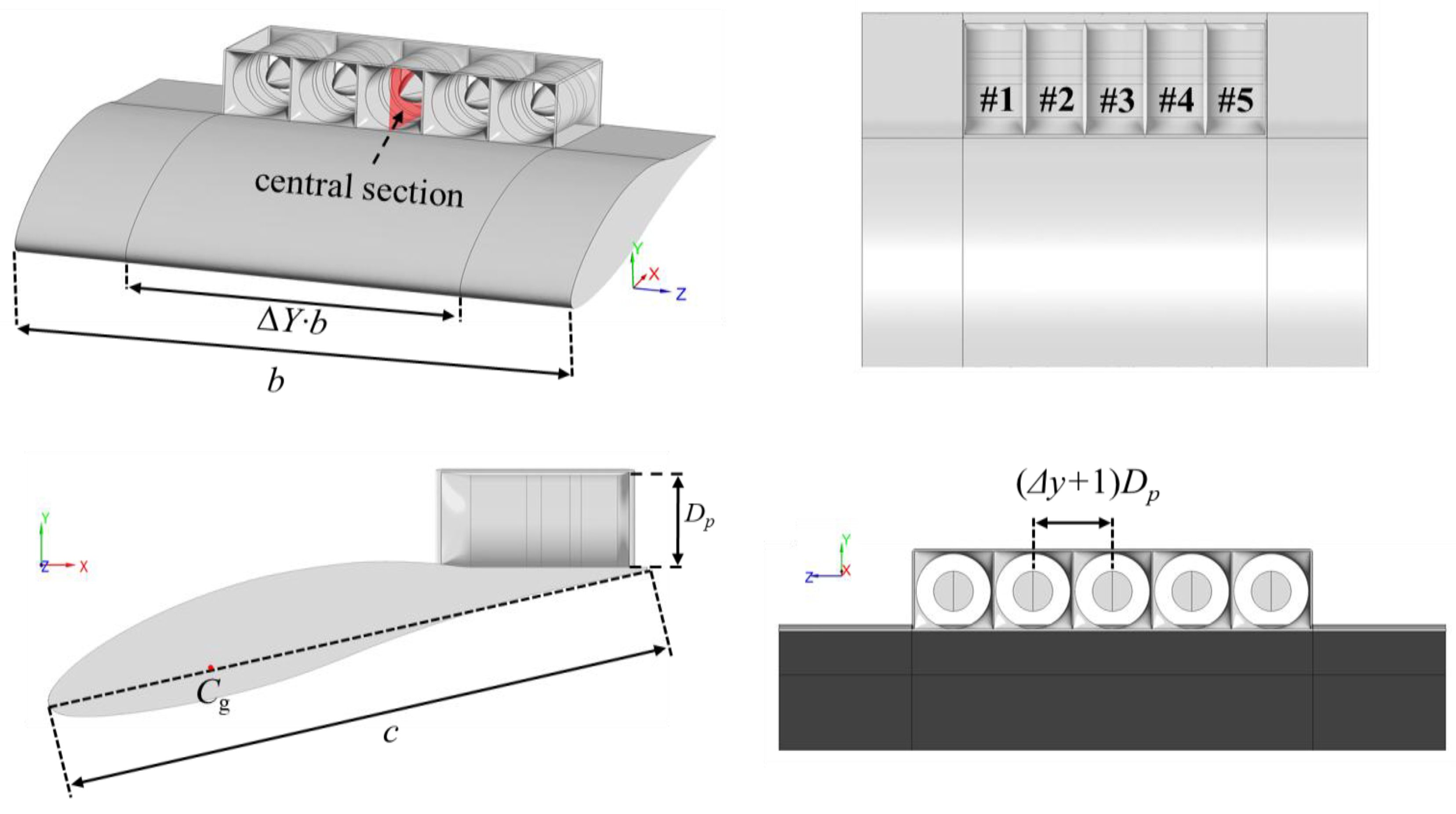
2. Materials and Methods

To achieve a rapid simulation of a distributed propulsion system, a circumferential body force model is established and validated.

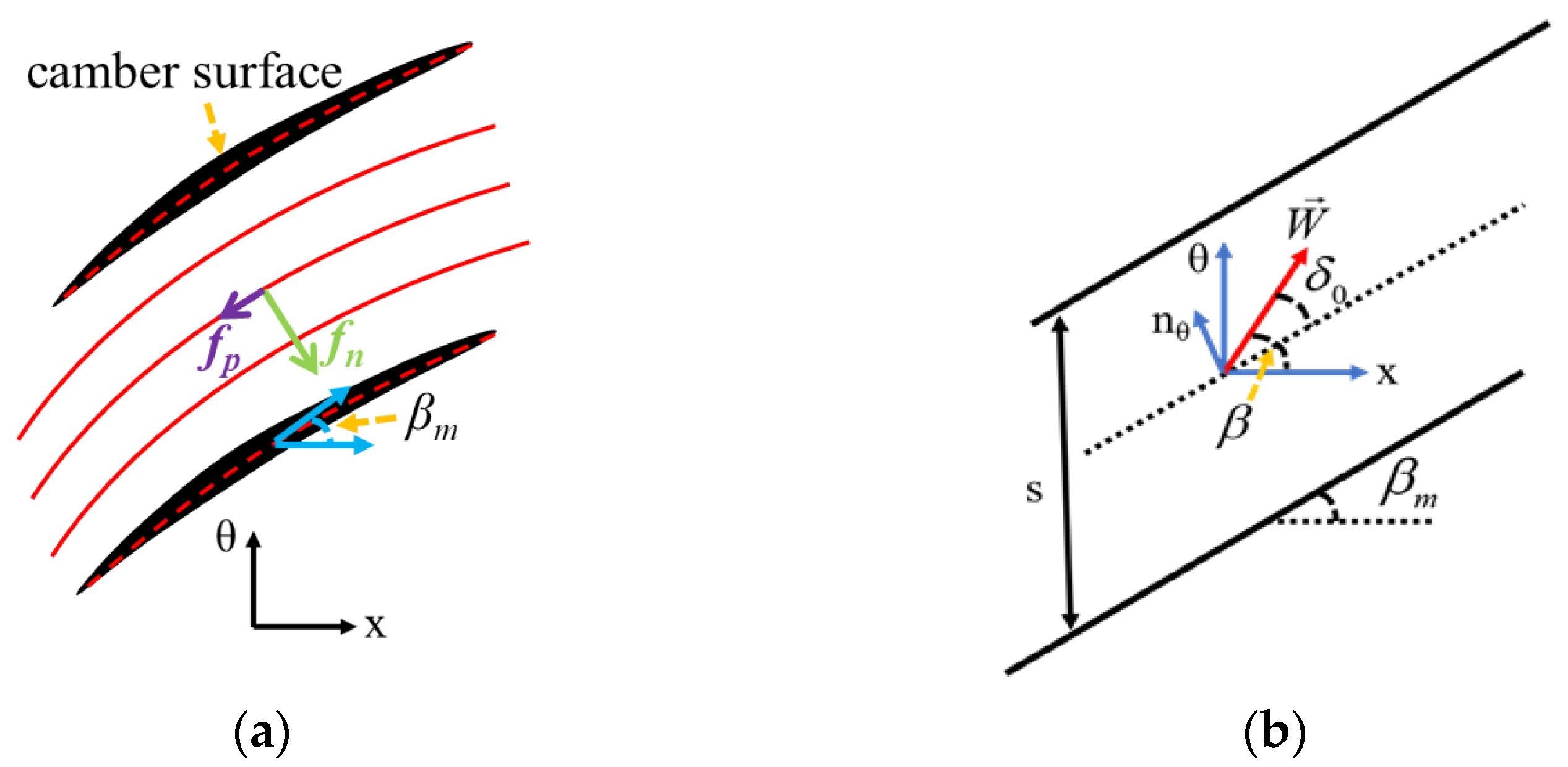
2.1. Development of Body Force Model

The concept of a body force model is that the blades of the rotating turbomachinery are replaced by source term distributions, and the reproduction of the effects of the blades on the work, deflection, and friction of the airflow is achieved [19]. Since there is no need to conduct mesh generation for the actual blades anymore, it can significantly improve the numerical simulation efficiency of turbomachinery and reduce the consumption of computational resources. In this paper, based on the model proposed by Hall [20] and considering the effect of compressibility [21], a circumferential body force model based on local flow field parameters has been developed. The governing equations including the body force source terms are expressed as follows:

$${\displaystyle \frac{\partial \rho }{\partial t}}+\nabla ·(\rho \overrightarrow{V})=-{\displaystyle \frac{1}{b}}(\rho \overrightarrow{V}·\overrightarrow{\nabla }b)$$

(1)

$${\displaystyle \frac{\partial (\rho \overrightarrow{V})}{\partial t}}+\nabla ·(\rho \overrightarrow{V}{\overrightarrow{V}}^t)+\overrightarrow{\nabla }(p)=\rho \overrightarrow{f}-{\displaystyle \frac{1}{b}}(\rho \overrightarrow{V}·\overrightarrow{\nabla }b)\overrightarrow{V}$$

(2)

$${\displaystyle \frac{\partial (\rho e_t)}{\partial t}}+\nabla ·(\rho h_t\overrightarrow{V})=\rho r\mathsf{\Omega }{f}_{\theta }-{\displaystyle \frac{1}{b}}(\rho h_t\overrightarrow{V}·\overrightarrow{\nabla }b)$$

(3)

where $-{\displaystyle \frac{1}{b}}\left(\rho \overrightarrow{V}·\nabla b\right)$ is used to simulate the blocking effect caused by the blade thickness and $b$ denotes the blockage factor, which is the ratio of the axial thickness of the blade $e_x$ to the blade pitch s [22,23]. And $\rho$ denotes the density of air, $\overrightarrow{V}$ denotes the absolute velocity and ${\overrightarrow{V}}^t$ denotes its transposition, $p$ denotes the static pressure, $e$ denotes the total energy per unit mass, $h_t$ denotes the enthalpy of stagnation per unit mass, $t$ denotes the time, and $\Omega$ denotes the angular velocity. $\overrightarrow{f}$ denotes the body force per unit mass and $f_{\theta }$ denotes the circumferential component of the body force per unit mass. In this study, the body force $\overrightarrow{f}$ is decomposed into two components $\overrightarrow{f}=\overrightarrow{f_p}+\overrightarrow{f_n}$, and the decomposition of body force $\overrightarrow{f}$ within the flow plane is illustrated in Figure 1. The force $f_p$ is parallel but opposite to the relative flow direction, which simulates the frictional drag and loss term due to the blade thickness. Meanwhile, the force $f_n$ is perpendicular to the relative flow direction, which simulates the load exerted by the actual blade on the airflow to achieve deflection of the airflow as well as the work performed on the airflow. In this BFM, the source term depends only on the local flow conditions and local geometry of the blade. The expressions of the body force components $f_n$ and $f_p$ are as follows [21,22]:

$$f_n=K_{\mathit{Mach}}{\displaystyle \frac{(2\pi \delta )(0.5{\overrightarrow{W}}^2/\left|n_{\theta }\right|)}{\mathit{sb}}}$$

(4)

$$f_p={\displaystyle \frac{0.5{\overrightarrow{W}}^2}{\mathit{sb}\left|n_{\theta }\right|}}[2C_f+2\pi K_{\mathit{Mach}}{(\delta -{\delta }_0)}^2]$$

(5)

in which

$$K_{\mathit{mach}}=\left\{\begin{array}{c}\min ({\displaystyle \frac{1}{\sqrt{1-M_{\mathit{rel}}^2}}},3),\begin{array}{c}{M}_{\mathit{rel}}<1\end{array}\\ \min ({\displaystyle \frac{4}{2\pi \sqrt{M_{\mathit{rel}}^2-1}}},3),\begin{array}{c}\end{array}\begin{array}{c}{M}_{\mathit{rel}}>1\end{array}\end{array}\right.$$

(6)

$$s={\displaystyle \frac{2\pi r}{B}}$$

(7)

$$C_f=0.0592R{e}_x^{-0.2}$$

(8)

$$R{e}_x={\displaystyle \frac{\rho Wx}{\mu }}$$

(9)

where ${2\pi K_{\mathit{mach}}({\delta -\delta }_0)}^2$ denotes the loss terms under off-design conditions. $K_{\mathit{mach}}$ denotes the compressibility coefficient, which is used for the correction of compressibility effects caused by the Mach number. $\delta$ denotes the local deviation angle, $\overrightarrow{W}$ denotes the relative velocity, $s$ denotes the blade pitch, $B$ denotes the blade number, $n_{\theta }$ denotes the unit normal vector of the blade local surface, $C_f$ denotes the local friction coefficient, $M_{\mathit{rel}}$ denotes the relative Mach number, $r$ denotes the radius, ${\mathit{Re}}_x$ denotes the Reynolds number based on the local relative velocity and axial chord, $x$ denotes the axial chord length of the blade, and $\mu$ denotes the air dynamic viscosity. The reference local deviation angle ${\delta }_0$ is defined as follows:

$${\delta }_0=\beta -{\beta }_m$$

(10)

where $\beta$ denotes the relative flow angle and ${\beta }_m$ denotes the blade metal angle, which is defined as the angle formed by the metal part of the blade and the reference axis [24]. The simplified geometric relationship is illustrated in Figure 1b. The reference local deviation angle ${\delta }_0$ is related to the rotation speed, and it is necessary to extract ${\delta }_0$ separately at different rotation speeds to obtain accurate simulation results.

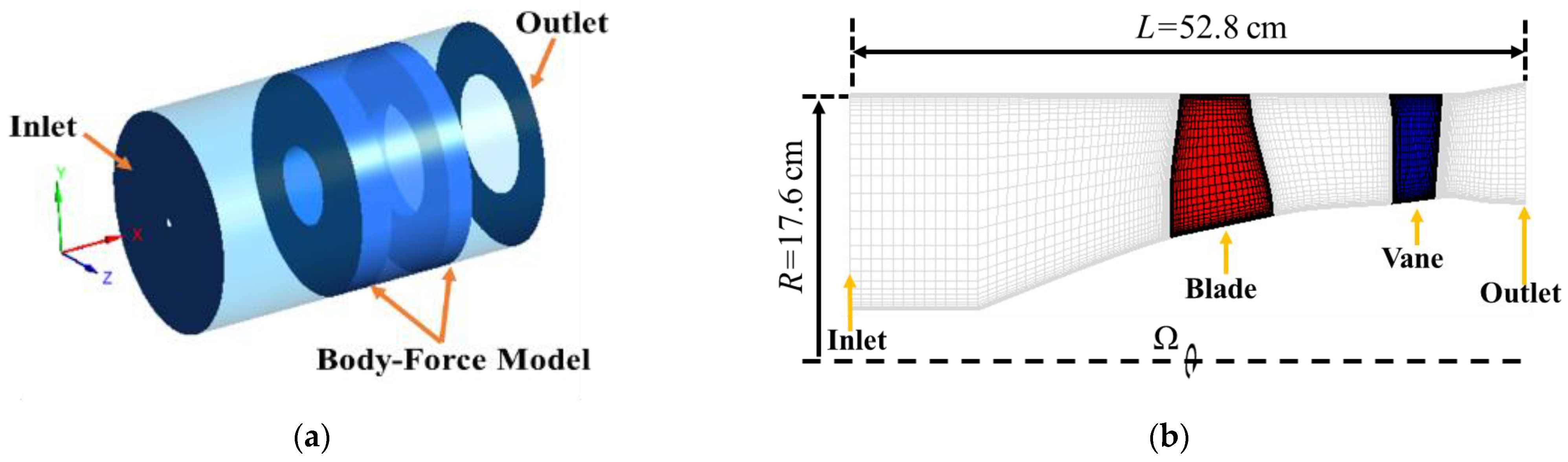
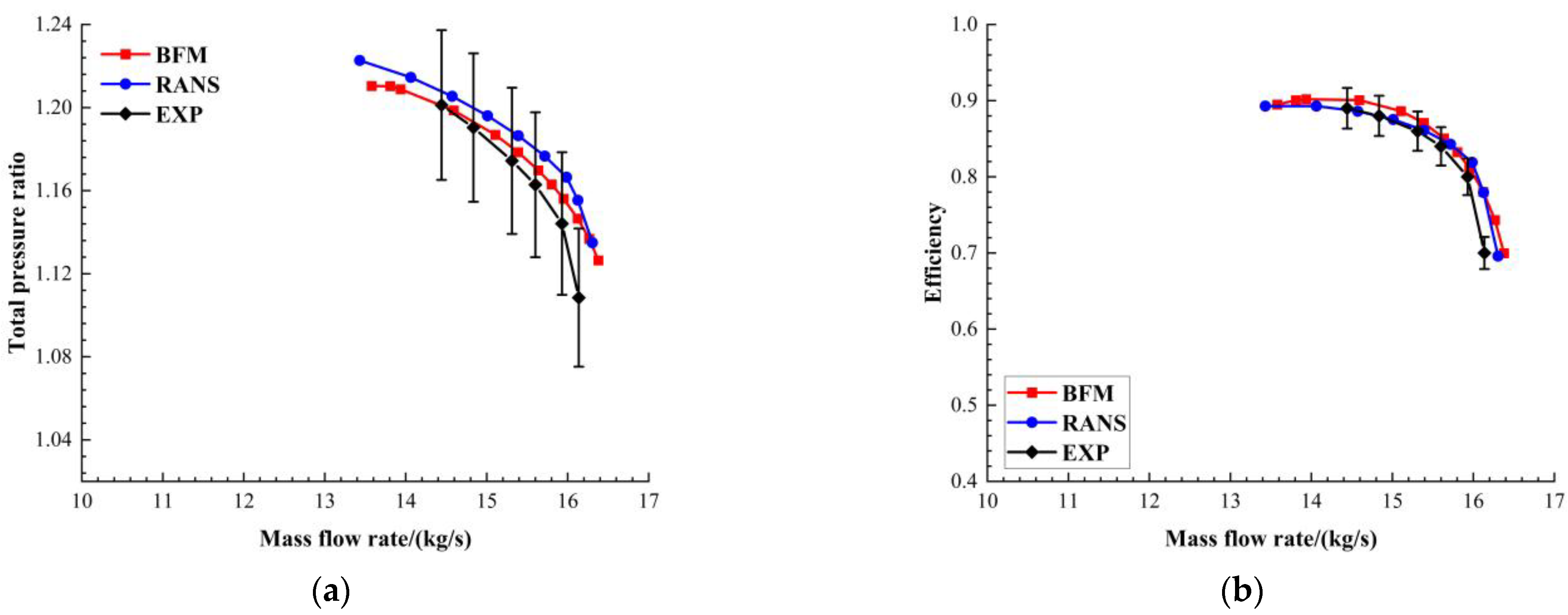
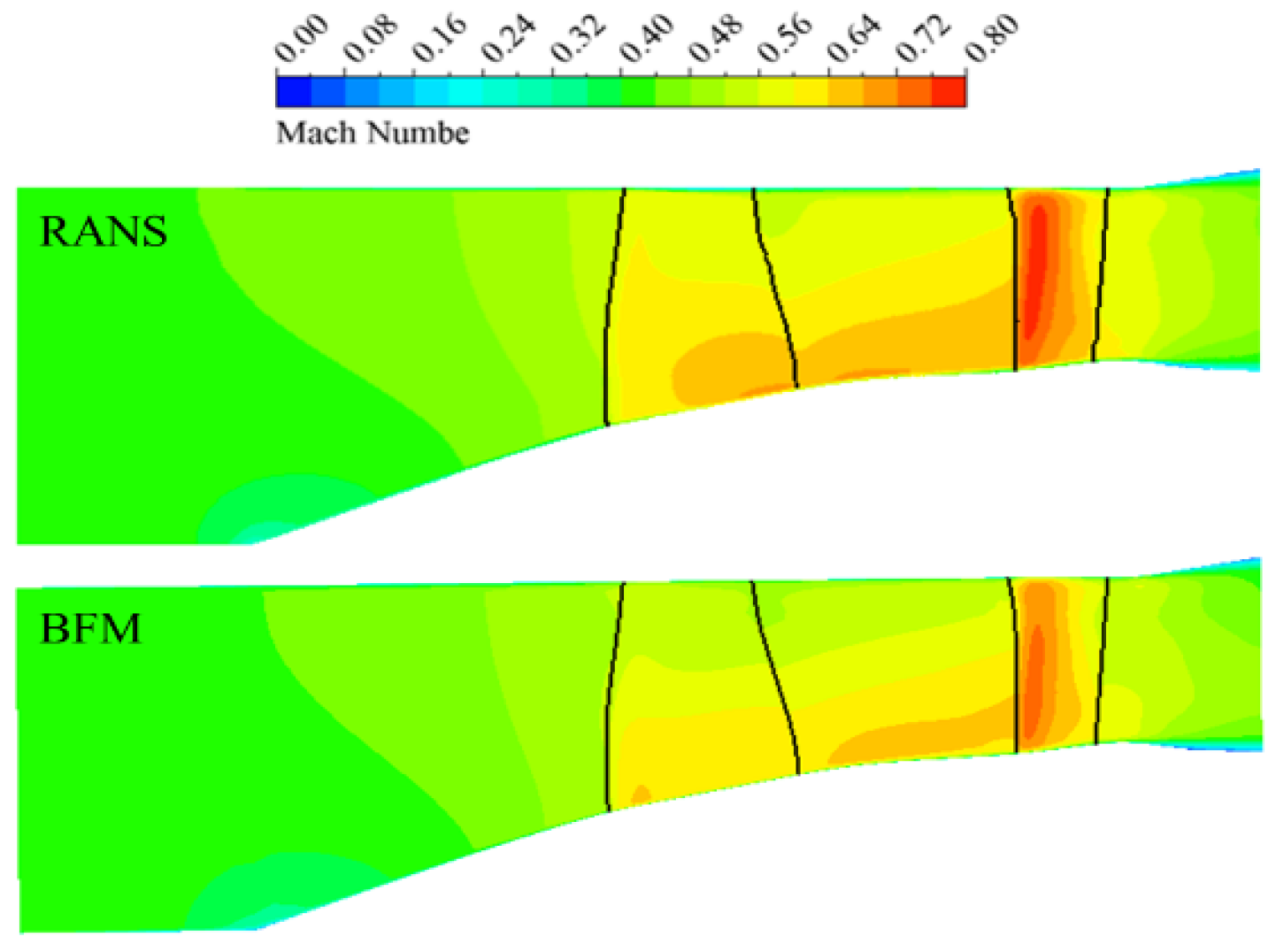
2.2. Validation of Body Force Model

The fan of the DGEN 380 engine at the Civil Aviation University of China was selected to validate the body force model [25]. The DGEN 380, a high-bypass-ratio turbofan engine featuring dual rotors and a separate exhaust system, measures 1346 mm in length and 352 mm in diameter. It has characteristics such as a small size, low pressure ratio, and high efficiency, which highly coincide with the design performance requirements of distributed ducted fans. Thus, subsequent research will select the fan of the DGEN 380 engine as the propulsion system to provide stable thrust support for the aircraft/engine integrated model. And the structures of the engine and fan are shown in Figure 2. The design parameters of the fan are listed in

Table 1. Design parameters of DGEN 380 fan.

Parameter	Value
Fan diameter	352 mm
Number of blades	14
Number of vanes	40
Rotation speed	13,150 r·min−1
Inlet total temperature	288.15 K
Inlet total pressure	101,325 Pa
Total pressure ratio	1.17
Equivalent flow rate	14.635 kg·s−1
Isentropic efficiency	0.87

.

The computational domain and meridional mesh based on the circumferential body force model solution are illustrated in Figure 3. The axial length of the computational domain was 52.8 cm, and the radius of the inlet was 17.6 cm. In FLUENT version 2022.R2 software, the body force model was employed to simulate the impact of blades on the airflow. Specifically, user-defined functions (UDFs) were utilized to load the body force source terms into the red region (blade) and the blue region (vane), despite the absence of physical blades within these two zones. In other regions, the three-dimensional steady Reynolds-averaged Navier–Stokes (RANS) equations were solved using the k-ω SST turbulence model. The number of grid nodes in the radial and axial directions of the blade region was 40 and 30, respectively, and the number in the circumferential direction was 90. Grid independence was verified using 0.55 million, 0.69 million, 0.80 million, and 0.92 million grids. When the grid number exceeded 0.69 million, the errors in total pressure ratio and isentropic efficiency remained within 0.2%. Therefore, 0.69 million grids were chosen for the numerical simulation. The total temperature and total pressure were imposed at the inlet, with a total pressure of 101,325 Pa and a total temperature of 288.15 K, and the operating point of the fan was controlled by changing the average static pressure at the outlet. The convergence time for a single case was approximately 40 min.

In order to validate the BFM method, a full three-dimensional numerical simulation was conducted to solve the three-dimensional steady RANS equations. The full-annulus computational domain and blade mesh of the fan stage are illustrated in Figure 4. The total number of grids was approximately 27.7 million. The boundary conditions were set to be consistent with those in the BFM calculation method. The rotor–stator interface was set as a mixing plane. The wall was set to a no-slip adiabatic wall. The convergence time of a single case based on the RANS method using the same computational resources was approximately 12 h. The convergence of the iterative solution was monitored by the residuals of the mass, momentum, energy, and turbulence model equations. The required root mean square (RMS) residual order of accuracy was less than 10⁻⁶.

The aerodynamic characteristics of the fan stage at design rotation speed (100% RPM) are presented in Figure 5. The experimental results were obtained from the test rig at the Civil Aviation University of China, with a relative error band of 3%. It can be found that the results obtained using the BFM method are in good agreement with the numerical simulation results (RANS) and experimental results (EXP). The isentropic efficiency obtained using the BFM method is slightly higher than that obtained using the RANS method. The maximum deviation is not more than 2 percentage points. This can be explained by the fact that only the work and deflection of the blade acting on the airflow are considered, and three-dimensional flow losses, such as tip leakage flow loss and secondary flow loss near the endwall region, are neglected. The mass flow rates at the near-choke point obtained using the numerical simulation method (both the BFM and RANS methods) are slightly higher than the experimental results. This can be attributed to the blockage effects of the centrifugal compressor, combustion chamber, and turbine in the DGEN 380 engine test, which lead to a reduction in the mass flow rate through the fan. Therefore, the experimental result of the mass flow rate at the near-choke point is slightly lower than that of the numerical simulations.

The Mach number contours in the meridional plane are illustrated in Figure 6. It can be observed that the results obtained using the BFM method agree well with the RANS results. The body force model can accurately simulate the work performed by the fan stage and the flow loss in the boundary layer near the endwall region. In the rotor and stator regions, the Mach numbers obtained by the BFM method are lower than those obtained by the RANS method. This is because the BFM method does not consider the effects of secondary flows, such as tip leakage flow and endwall passage vortex.

In general, the numerical simulation results obtained using the BFM method agree well with the RANS results, and the computational efficiency is markedly improved. Therefore, it is feasible to use the BFM method to simulate the blade force acting on the airflow.

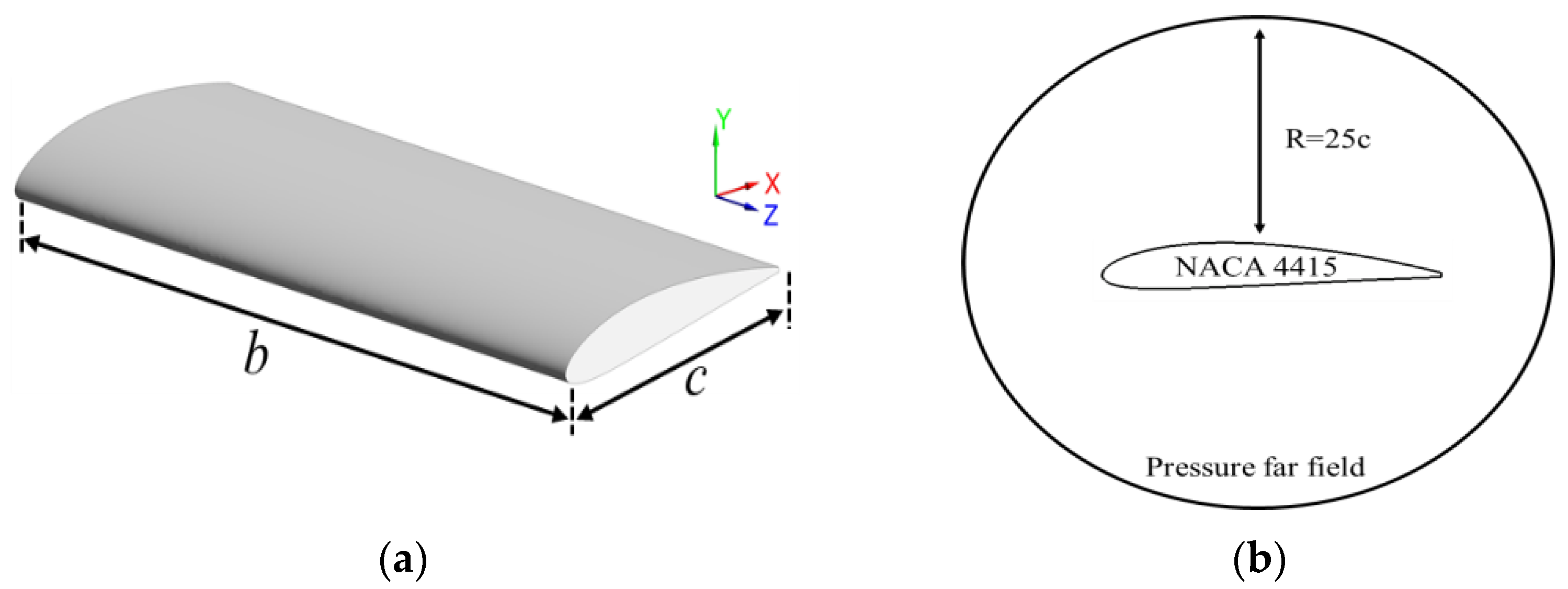
3. Numerical Method Validation and Grid Independence Validation

To investigate the influence of the internal and external flow coupling effect on the aerodynamic–propulsion coupling characteristics of the distributed propulsion system and consider the impact of boundary layer ingestion on the inlet distortion of the ducted fan, the NACA 643-618 airfoil and the DGEN 380 engine fan are integrated into a model with five ducted fans over the wing. The symmetrical integrated model is illustrated in Figure 7. The geometric parameters of the integrated model are listed in

Table 2. Geometric parameters of five-ducted-fan over-wing integrated model.

Parameter	Value
Chord/c	100 cm
Span/b	141.2 cm
Fan axial position/(x/c)	0.7
Fan diameter/DP	15.84 cm
Number of fans/N	5
Separation distance between neighboring fans/Δy·Dp	1.0 cm
Fraction of wingspan occupied by ducted fan array/ΔY	0.6

, with reference to the typical layout of distributed ducted fans [26]. The separation distance between the fans, $\Delta y·D_p$, is the minimum distance between two neighboring fans in the spanwise direction. To minimize the inlet flow velocity and improve the benefit of boundary layer ingestion, the ducted fan array is placed at the trailing edge of the upper surface of the wing at $x/c=0.7$. The ducted fans are numbered from left to right in the spanwise direction of the wing, in sequence from #1 to #5.

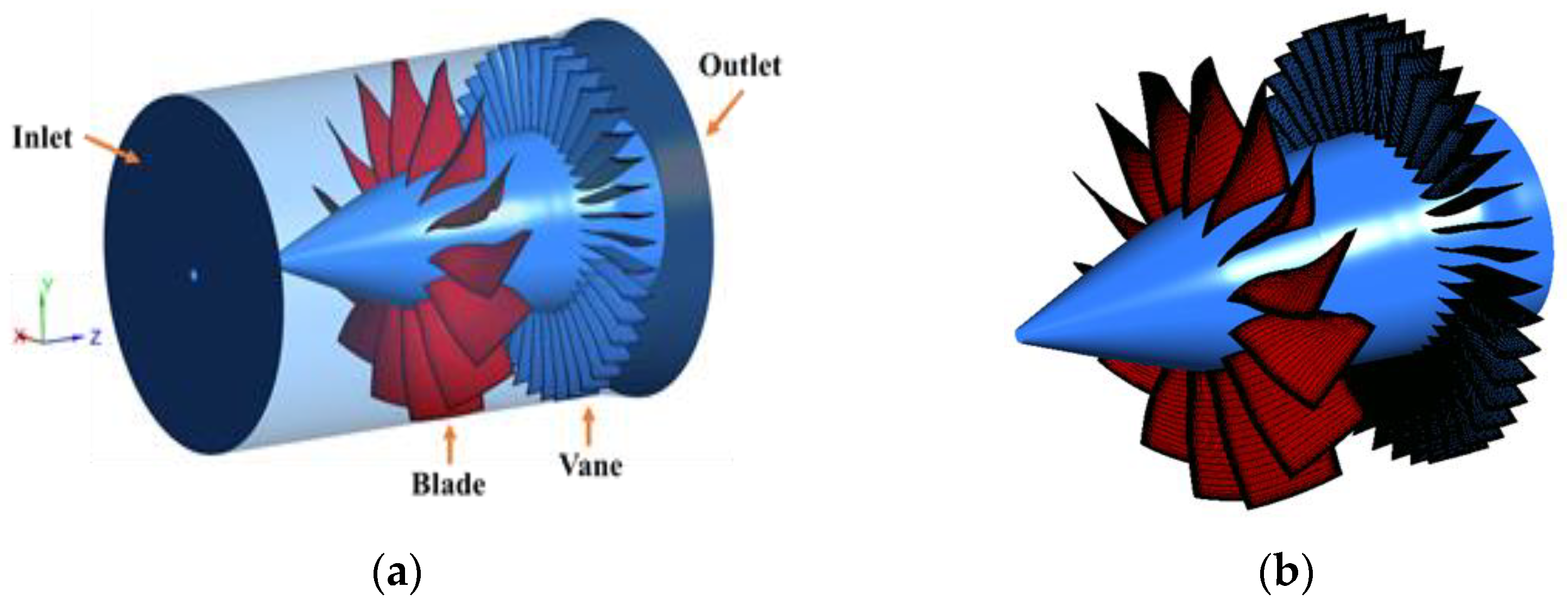
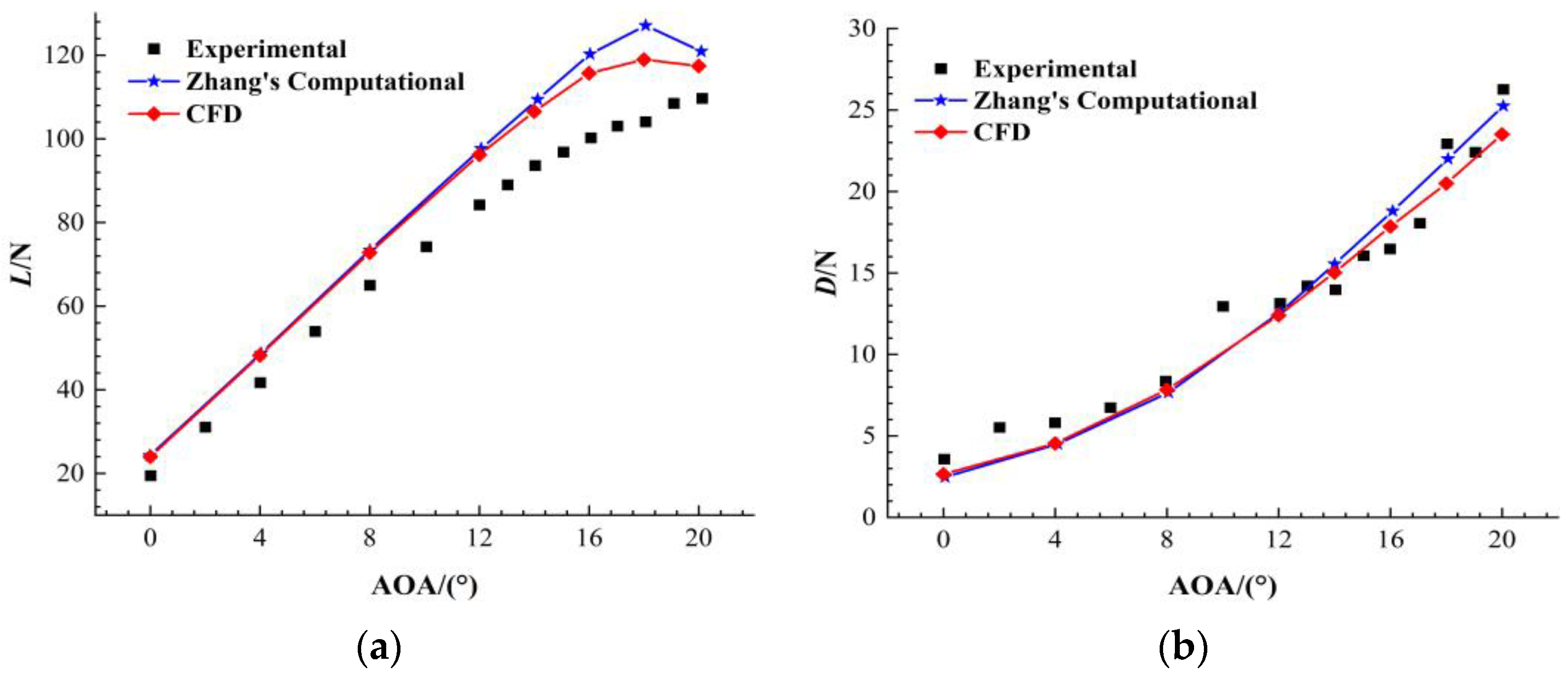
3.1. Validation of Numerical Method

The NACA 4415 airfoil is selected, and the numerical simulation method for the flow field of the wing is validated by comparing the numerical simulation results in the present study with the experimental results [10]. The geometric model and computational domain of the NACA 4415 wing are illustrated in Figure 8. The geometric parameters of the airfoil and the incoming flow conditions can be found in Reference [10]. The radius of the computational domain is 25 times the chord length of the airfoil and a pressure far-field boundary condition is applied. A density-based implicit coupling algorithm is selected to solve the three-dimensional steady RANS equations using the k-ω SST turbulence model. The height of the first layer of the boundary layer grid is 0.01 mm to ensure that y +≈ 1. The grid growth rate is 1.2, and the total number of grids in the boundary layers is 30. The wall was set to a no-slip adiabatic wall.

The variations in lift and drag with the inflow angle of attack (AOA) for the NACA 4415 wing are presented in Figure 9. It can be observed that the variations in the lift and drag with the angle of attack agree well with the experimental and numerical simulation results [10]. At low angles of attack, the numerical simulation results obtained in this study coincide with those reported in the literature. Near the critical angle of attack, there are slight deviations in lift due to the simplification of the wing model and CFD methods. However, the lift and drag values obtained in this study are closer to the experimental results. Overall, the numerical simulation method still has high reliability in rapidly evaluating the characteristics of wing flow fields.

3.2. Grid Independence Verification

The computational domain and mesh of the over-wing symmetric configuration with five distributed ducted fans are illustrated in Figure 10. The computational domain for the system is spherical, with a radius of 25 times the wing chord length. The coupled model is meshed using Pointwise version 18.4R3 and Meshing version 2022.R2 software. The ducted fan array is meshed with structured grids, while the external flow field of the wing is meshed with unstructured grids. A thorough inspection is carried out on metrics such as the element aspect ratio, skewness, and orthogonality. To verify the grid independence of the integrated model,

Table 3. Grid independence verification.

Number of Grids × 104	${\mathit{C}}_{\mathit{L}}$	${\mathit{C}}_{\mathit{D}}$	${\mathit{C}}_{\mathit{M}}$
836	0.314541	0.035984	−0.103817
1065	0.309606	0.035231	−0.100242
1392	0.310634	0.035205	−0.100418
1612	0.309065	0.035092	−0.100660

presents the comparison results of the lift coefficient $C_L$, the drag coefficient $C_D$, and the pitching moment coefficient $C_M$ for four different grids at an angle of attack of 0°. The height of the first layer of the four grids is 0.01 mm, with a grid growth rate of 1.2 and a total of 30 layers, satisfying y +≈ 1. It can be seen that when the number of grids increases to 10.65 million or more, the deviations among the lift coefficient, the drag coefficient, and the pitching moment coefficient are extremely small, fulfilling the requirement of grid independence. Considering both the computational accuracy and efficiency comprehensively, the total number of grids for the integrated model is selected to be approximately 10.65 million, as shown in Figure 10b.

4. Results and Discussion

The five-ducted-fan over-wing integrated model is numerically solved using FLUENT software. The circumferential body force model is used to simulate the force of the blades acting on the airflow, and the BFM is loaded in the red region, as shown in Figure 10b. For each iteration, the body force source term is updated accordingly. In other regions, the three-dimensional steady RANS equations are solved using the k-ω SST turbulence model, which has significant advantages in addressing near-wall and separated flows and can accurately capture complex flow. The air is modeled as an ideal gas following Sutherland’s law for viscosity. An implicit coupled density-based solver is employed, and the wall is set to a no-slip adiabatic wall. The far field is spatially discretized using the finite volume method, and the second-order upwind scheme is selected as the discretization scheme. Based on the designed cruise altitude of the DGEN 380 engine, the pressure far-field boundary condition is set at an altitude of 3 km, with the atmospheric pressure being 70,108 Pa and the atmospheric temperature being 268.65 K. The flight Mach number ranges from 0.2 to 0.5.

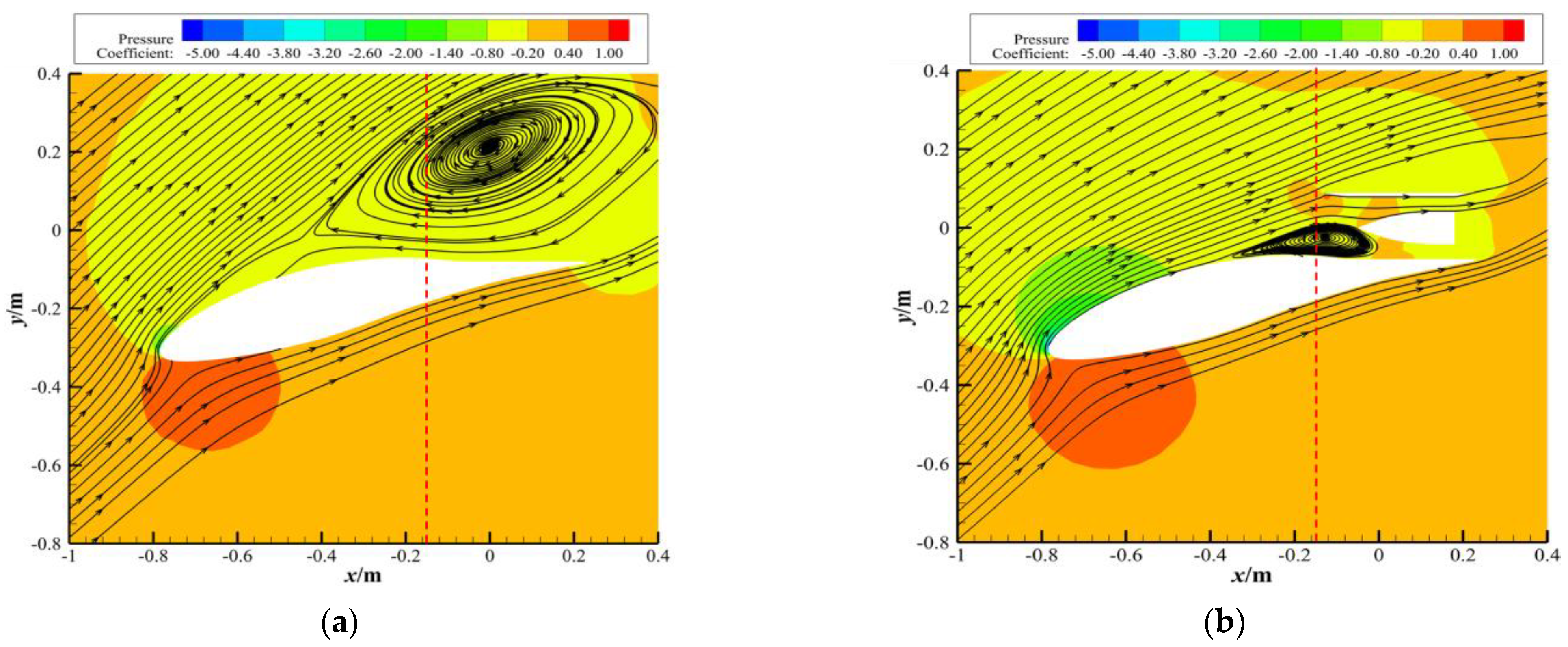
4.1. Wing Aerodynamic Performance

Under the condition that the physical rotational speed of the fan remains constant, Figure 11 presents the variation laws of the wing lift coefficient $C_L$ with the incoming angle of attack, the variation relationship between the lift coefficient and the drag coefficient $C_D$, the lift-to-drag ratio, and the variation relationship of the pitching moment coefficient $C_M$ with the lift coefficient in the Mach number range from 0.2 to 0.5. These coefficients are defined as follows:

$$C_L={\displaystyle \frac{L}{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.{\rho }_{\infty }{V}_{\infty }^{2}S}}$$

(11)

$$C_D={\displaystyle \frac{D}{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.{\rho }_{\infty }{V}_{\infty }^{2}S}}$$

(12)

$$C_M={\displaystyle \frac{M}{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.{\rho }_{\infty }{V}_{\infty }^{2}Sl}}$$

(13)

where $L$ denotes the lift, $D$ denotes the drag, and $M$ denotes the pitching moment. ${\rho }_{\infty }$ and $V_{\infty }$ denote the density and velocity of the air at infinity when Ma = 0.2. $S$ denotes the equivalent wing reference area, which is defined as $S=bc$. The reference point of the pitching moment is taken as the quarter chord length from the leading edge of the wing, as shown in the projection of point $C_g$ on the spanwise center plane of the wing in Figure 7.

It can be observed that the lift/drag characteristic curves of the wing are generally in agreement with the results predicted by the classical subsonic airfoil theory. In the distributed propulsion system, the suction and exhaust effects of the fans alter the local flow field around the wing. At small angles of attack, the fan suction accelerates the airflow on the upper surface of the wing, reducing the pressure and thereby increasing the lift coefficient. Meanwhile, the increase in the drag coefficient is relatively slow, leading to an increase in the lift-to-drag ratio. As the angle of attack continues to increase to the stall angle of attack, due to the increase in the adverse pressure gradient, the suction effect of the ducted fans on the airflow weakens. The airflow on the upper surface of the wing starts to separate, and even backflow occurs. The growth of the lift coefficient stagnates and then decreases, while the drag coefficient rises sharply. This causes the variation in the lift coefficient with the angle of attack, the variation in the lift-to-drag ratio with the lift coefficient, and the polar curve to exhibit a bell-shaped trend. As the flight Mach number increases, the lift and drag coefficients of the wing also increase. The maximum lift coefficients corresponding to the Mach numbers from 0.2 to 0.5 are 1.96, 3.81, 6.02, and 7.96, respectively. The maximum lift coefficient at a Mach number of 0.5 has increased by 306% compared with that at a Mach number of 0.2, and the drag coefficient corresponding to the maximum lift coefficient has increased by 97%.

However, the stall angle of attack of the wing during flight decreases as the flight Mach number increases. The stall angles of attack corresponding to the flight Mach numbers from 0.2 to 0.5 are 38°, 32°, 26°, and 23°, respectively. The stall angle of attack at a Mach number of 0.2 is 15° larger than that at a Mach number of 0.5. This is because the increase in the flight Mach number leads to a reduction in the inlet flow tube area of the fan, which in turn weakens the suction effect of the ducted fan on the airflow on the upper surface of the wing and enhances the drag effect of the fan casing. Meanwhile, the pressure difference resistance and frictional resistance borne by the airflow on the upper surface of the wing also increase accordingly. Under the combined effect of these factors, the airflow on the upper surface of the wing is more prone to separation or even backflow. Therefore, a higher flight Mach number invariably leads to a narrower flight margin.

As can be seen from Figure 11d, with the increase in the wing lift coefficient, the pitching moment coefficient (with the nose-up moment defined as positive) generally shows an upward trend; that is, the nose-down moment of the wing increases accordingly. As the flight Mach number increases, the variation range of the pitching moment coefficient with the lift coefficient becomes larger. This indicates that the Mach number has a significant impact on the longitudinal stability characteristics of the wing. That is, the higher the Mach number, the more significant the influence of the lift coefficient on the longitudinal stability. When the angle of attack of the incoming flow goes beyond the stall angle of attack, the airflow on the upper surface of the wing is compelled to separate due to the increased adverse pressure gradient. This separation then triggers a decrease in lift. Subsequently, the nose-down moment of the wing tends to either grow slowly or decline instead.

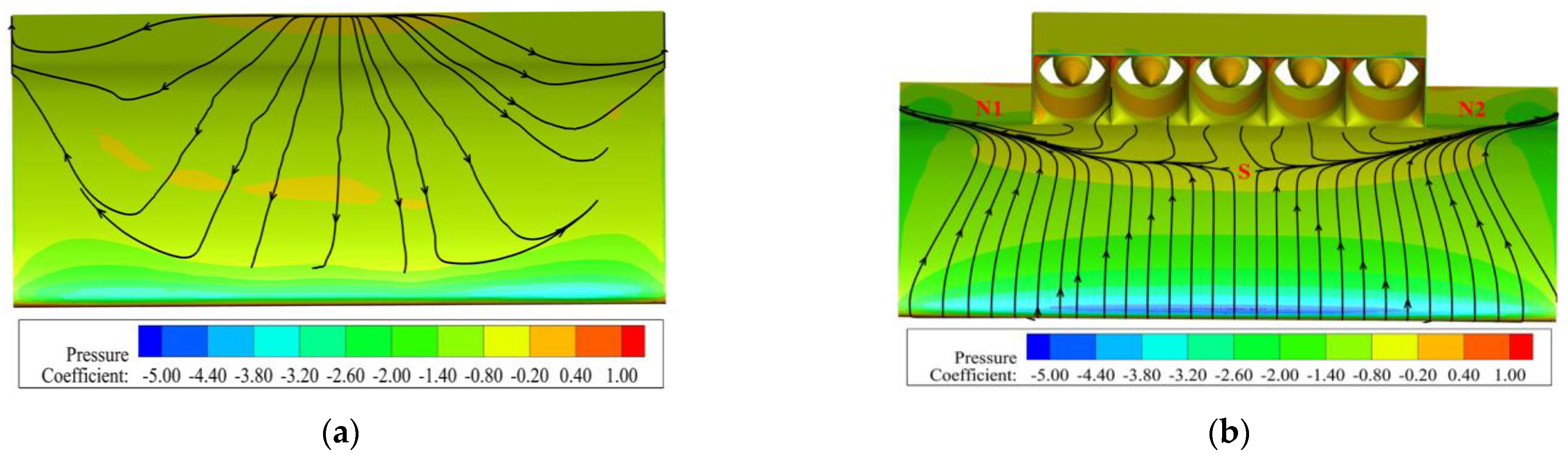
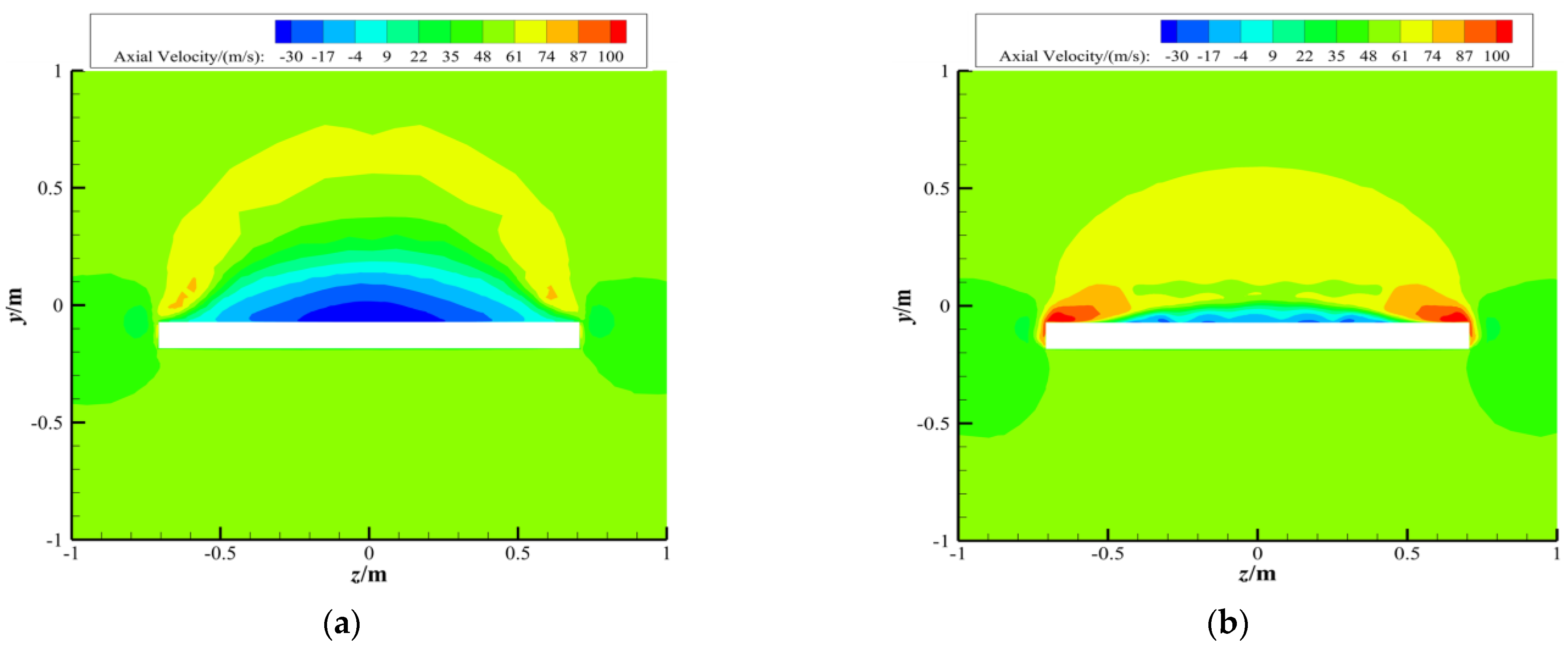
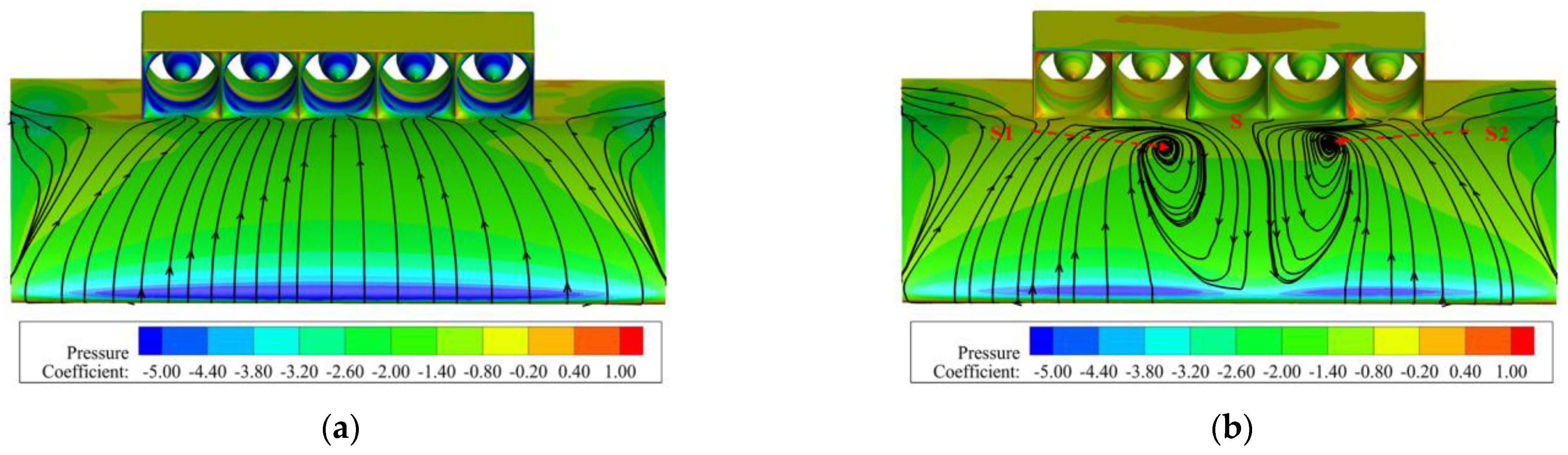
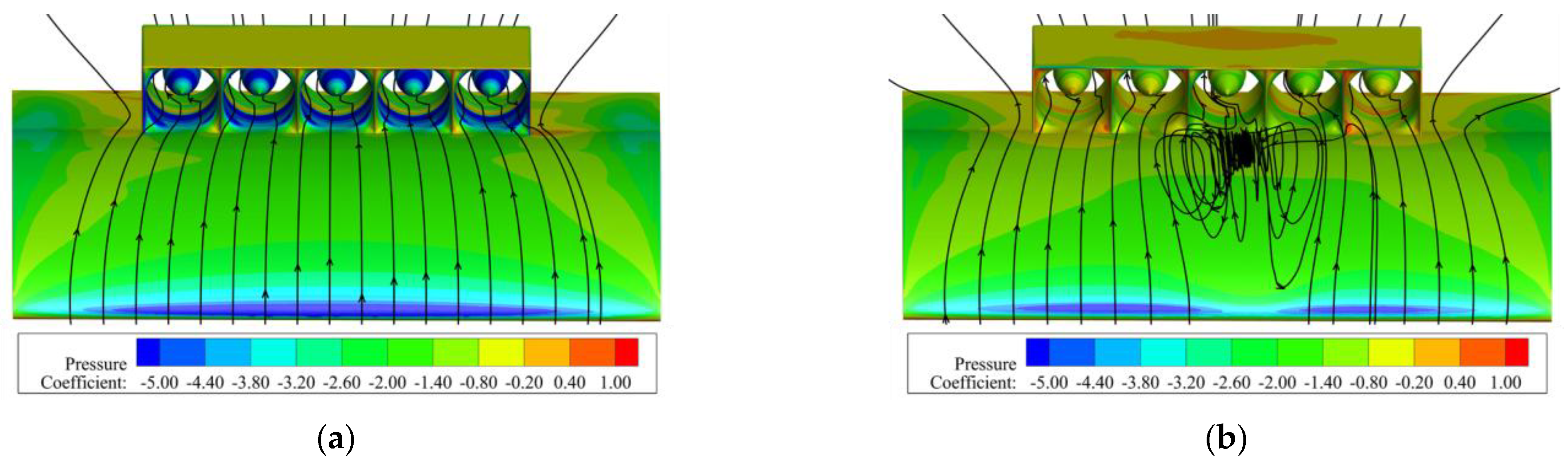
4.2. Influence of the Internal and External Flow Coupling Effect on the Performance of Ducted Fans

The variations in the mass flow rate and thrust of each ducted fan with the flight Mach number at an angle of attack of 26° are presented in Figure 12. The normalization of the mass flow rate and thrust is carried out with reference to the corresponding values of the middle fan (#3) when the angle of attack is 0° and the Mach number is 0.2.

It can be found that both the mass flow rate and thrust of the #1 and #5 fans increase with the increase in the flight Mach number at AOA = 26°. Taking the #5 fan as an example, the mass flow rate and thrust at a Mach number of 0.4 increase by 10% and 23%, respectively, compared with those at a Mach number of 0.2. However, when the Mach number is 0.4, the mass flow rate and thrust of fans #2, #3, and #4 are all smaller than those at a Mach number of 0.3. Among them, the mass flow rate and thrust of fan #3 are even smaller than those at a Mach number of 0.2, decreasing by 16% and 28%, respectively.

The results indicate that as the Mach number increases, the inlet flow tube area of the fan is reduced. This reduction then triggers the stagnation of the airflow, which consequently brings about a substantial decrease in both the mass flow rate and thrust of the fan. From the perspective of improving this situation, further explorations of the layout strategies of ducted fans can be carried out in follow-up studies. For example, considering increasing the spacing between fans or installing the fans on a lower surface of the wing, with the expectation of alleviating the adverse effects caused by the increase in Mach number, may achieve the optimization and improvement of the fan performance.

Figure 13, Figure 14 and Figure 15, respectively, present the flow characteristics of the NACA 643-618 clean airfoil and the coupled configuration without the fan suction effect under the conditions of a Mach number of 0.2 and an angle of attack of 26° from different perspectives. Figure 13 shows the static pressure coefficient contours and limiting streamlines on the upper surface of the wing, Figure 14 presents the streamline distribution at the middle section of the wingspan (as shown in the red section of Figure 7), and Figure 15 shows the axial velocity contours at the x = −0.15 m section (corresponding to the red dashed line in Figure 14). The static pressure coefficient $C_P$ is defined as follows in Equation (14):

$$C_p={\displaystyle \frac{p-p_{\infty }}{0.5{\rho }_{\infty }{V}_{\infty }^2}}$$

(14)

A comprehensive analysis reveals that when the Mach number is 0.2 and the angle of attack is 26°, the airflow undergoes severe separation on the upper surface of the clean wing, with the separation region nearly covering the entire upper surface. Meanwhile, a large-scale separation vortex forms near the trailing edge of the wing, and there is a distinct backflow close to the wing surface. For the coupled configuration without the fan suction effect, although airflow separation also occurs in the upstream region of the duct inlet, the separation degree is significantly lower than that of the clean wing. In this coupled configuration, the separation is the most severe in the upstream region of fan #3, while it is relatively less severe in the wingtip region. Moreover, a saddle node-type separation structure is observed, where the saddle point S and the two separation nodes N1 and N2 jointly form the separation line.

There are two main aspects contributing to the changes in the separation characteristics of these two configurations. On one hand, for the coupled configuration, when the airflow passes through the duct, the flow area suddenly decreases compared to the far field, leading to an increase in the flow velocity. As a result, the local static pressure drops, the adverse pressure gradient decreases, and the degree of airflow separation weakens. As shown in Figure 14, the separation zone is only concentrated in the lower half of the duct. It can also be seen from Figure 15 that for the coupled configuration, the axial velocity of the airflow at the duct inlet is significantly greater than that of the clean wing, which is the result of the airflow acceleration in the duct. On the other hand, the influence of the airflow acceleration process in the duct on the flow field propagates upstream against the direction of the incoming flow, thus affecting the airflow on the upper surface of the wing leading edge and improving the flow state near the leading edge.

Figure 16 and Figure 17 show the two-dimensional and three-dimensional streamline distributions on the upper surface of the wing of the coupled configuration, respectively. These distributions are obtained under the influence of the fan suction effect, at an angle of attack of 26° and Mach numbers of 0.2 and 0.4. As shown in Figure 16a and Figure 17a, the flow field on the upper surface of the wing is significantly improved after considering the suction effect of the ducted fans. The air intake of the ducted fan is uniform, and its aerodynamic performance is evenly distributed in the wingspan direction. This indicates that the suction of the ducted fan can accelerate the low-energy fluid in the boundary layer of the wing surface and effectively suppress the airflow separation. However, when the Mach number is 0.4, the inlet flow tube area of the fans shrinks due to the increase in the air velocity. Subsequently, the suction ability of the fans on the airflow on the wing surface weakens, while the drag of the fan casing increases, accompanied by a more pronounced adverse pressure gradient and frictional resistance. At the same time, the angle of attack of the incoming flow attains a critical value corresponding to a Mach number of 0.4. Under such circumstances, obvious separation of the airflow occurs in some areas on the upper surface of the wing, and even backflow is generated. As illustrated in Figure 17b, a distinct three-dimensional separated region emerges upstream of the inlet of fan #3. This gives rise to a significant blockage effect at the inlet of fan #3, severely affecting the aerodynamic performance. Moreover, it also has a partial impact on the adjacent fans #2 and #4. From the view of the distribution of the limiting streamlines on the wing surface, a saddle spiral node-type separation structure is observed. The saddle point S and the spiral nodes S1 and S2 form two separation spiral vortices of comparable size, which are approximately symmetrically distributed about the center position of the wing. Their spanwise span covers the upstream areas of fans #2 to #4.

There are two main reasons for the transformation from saddle node-type separation to saddle spiral node-type separation. Firstly, the Mach number of the incoming flow increases. With the increase in the Mach number, the adverse pressure gradient and friction resistance in the center area of the wing rise significantly, and the airflow velocity decreases sharply, which makes the airflow in this area extremely prone to separation. This, in turn, triggers a blockage phenomenon in the upstream area of the ducted fan. Secondly, the suction effect of the ducted fan has an influence. In the ducted fan array, the airflow upstream of fan #3 separates first. To maintain the flow rate required for its normal operation, it will draw in the airflow at the wingtip, which leads to the formation of a large velocity gradient in the wingspan direction, making it easy for the airflow on the upper surface of the wing to develop into large-scale separation spiral vortices, thus forming a saddle spiral node-type separation structure.

Figure 18 and Figure 19 present the pressure distribution curves and axial velocity profiles at different spanwise positions when the Mach number is 0.4 and the angle of attack is 26°, respectively. It can be observed that the pressure only varies along the spanwise direction in the areas near the inlets of #3, #4, and # 5, showing an increasing trend in sequence, while it is relatively uniformly distributed along the spanwise direction in other areas. This is consistent with the phenomenon in Figure 16b, where there is a spanwise movement trend in the flow near the inlets of the ducted fans, forming separation spiral vortices. The study of the airflow conditions upstream of each ducted fan reveals that the airflow upstream of fan #3 has undergone severe separation accompanied by a large-scale recirculation zone. The recirculation zone is concentrated in the interval of 10–60% of the wing chord length, corresponding to the coordinate range from x = −0.7 m to x = −0.2 m, and the separation is most significant near the position of 50% of the wing chord length (x = −0.3 m). It is worth noting that when being closer to the inlet of fan #3, the degree of airflow separation gradually decreases due to the acceleration effect brought about by the fan suction. Compared with fan #3, the separation degree of the airflow upstream of fan #4 is significantly weakened, and the range of the recirculation zone is reduced, while the airflow upstream of fan #5 has almost no separation. This is because fans #1 and #5 are closest to the wingtip positions and can ingest more wingtip fluid to compensate for their required flow rate. Therefore, their ability to resist the reduction in fan flow rate caused by airflow separation is the strongest. As a result, when the flight Mach number increases, the thrust they generate also increases. In contrast, fan #3 is the farthest from the wingtip position, and the airflow it inhales from the wingtip is far from enough to compensate for the sharp reduction in fan flow rate caused by airflow separation. Therefore, when the flight Mach number is 0.4, its performance drops significantly.

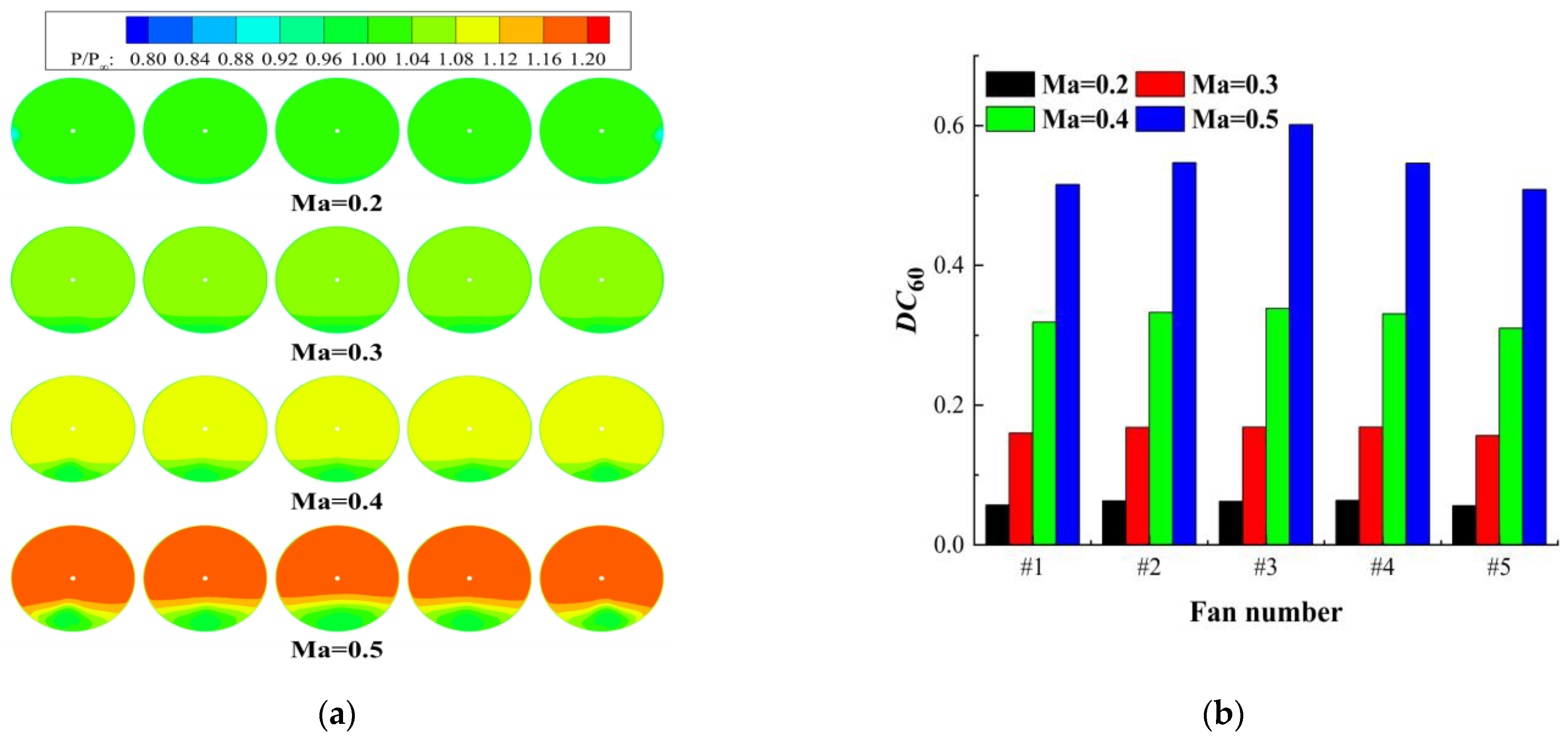
4.3. Intake Distortion of Ducted Fans

In order to explore the impact of the flight Mach number on the inlet distortion of ducted fans, this paper conducts a quantitative evaluation on the degree of inlet distortion of ducted fans by using two indicators, namely the total pressure distortion index ${DC}_{60}$ and the swirl distortion index ${SC}_{60}$ [27]. Their definitions formulas are as follows:

$$D{C}_{60}={\displaystyle \frac{\overline{P_{\mathrm{tot}}}-\overline{P_{\mathrm{tot},\min }(60)}}{\overline{q}}}$$

(15)

$$S{C}_{60}={\displaystyle \frac{\overline{V_{2,\max }(60)}-\overline{V_{2,\min }(60)}}{\overline{V}}}$$

(16)

where $P_{\mathit{tot}}$ denotes the total pressure, $q$ denotes the dynamic pressure, and $V_2$ denotes the secondary flow velocity. Figure 20 and Figure 21, respectively, show the variation in the total pressure distortion and the swirl distortion at the inlet section (1.4 times the axial chord length from the leading edge of the fan rotor) with the flight Mach number at AOA = 21°. And the swirl angle $\alpha$ is defined as the ratio of the circumferential velocity component $U_{\theta }$ of the airflow at the fan inlet to the axial velocity component $U_x$. A positive swirl angle indicates a positive pre-swirl, while a negative swirl angle represents a negative pre-swirl. The specific expression is as follows:

$$\alpha =\arctan ({\displaystyle \frac{U_{\mathsf{\theta }}}{U_{\mathrm{x}}}})$$

(17)

The perspective in the figures is from the fan inlet to the fan outlet, and clockwise is the positive direction. It can be seen from Figure 20 that as the flight Mach number increases, the intake uniformity of the ducted fan becomes worse. The total pressure loss at the inlet section becomes more severe, and the total pressure distortion area also expands accordingly. Taking fan #3 as an example, the ${\mathit{DC}}_{60}$ value at a flight Mach number of 0.5 has increased by 867% compared with that at a flight Mach number of 0.2.

When the flight Mach number ranges from 0.2 to 0.4, the angle of attack is far away from the stall angle of attack range, so the intake conditions among the ducted fans tend to be relatively consistent. Under the same Mach number, the ${\mathit{DC}}_{60}$ values of each ducted fan are nearly equivalent, which means that the total pressure losses of each ducted fan are basically the same.

When Ma = 0.5, it can be clearly observed that fan #3 has the largest total pressure loss, followed by fans #2 and #4, and fans #1 and #5 have the smallest total pressure losses. Compared with fan #5, the ${\mathit{DC}}_{60}$ value of fan #3 is 18% larger, indicating that the degree of total pressure distortion of fan #3 is the most severe. The reason for the differences in the degree of total pressure distortion among the ducted fan array lies in the fact that the angle of attack approaches the stall angle of attack corresponding to this flight Mach number. As elucidated in Section 4.2, under the influence of adverse pressure gradients and frictional resistance, the airflow first separates in the central area of the wing and even generates backflow, which leads to a significant reduction in the performance of fan #3, thereby making its total pressure loss reach the maximum.

From Figure 21, it can be seen that as the flight Mach number increases, the swirl distortion at the inlet section of the ducted fans also increases. Taking fan #1 as an example, the ${\mathit{SC}}_{60}$ value at a flight Mach number of 0.5 increases by 232% compared with that at a flight Mach number of 0.2. Meanwhile, the deviation of ${\mathit{SC}}_{60}$ values among different ducted fans increases. The swirl distortion at the inlet sections of fans #1 and #5 grows most rapidly, followed by fans #2 and #4, and fan #3 is the slowest. At Ma = 0.5, the ${\mathit{SC}}_{60}$ values of fans #1 and #5 are both 20% larger than that of fan #3. This is completely contrary to the trend of the total pressure distortion exhibited by the ducted fan array.

The reason for the differences in the degree of swirl distortion among the ducted fan array lies in the fact that under the suction effect of the ducted fans on the airflow at the wingtip, it is easy for a relatively large velocity gradient to form in the wingspan direction of the wing. Consequently, two vortices with comparable intensities, opposite directions (the one on the left is a clockwise vortex and the one on the right is a counterclockwise vortex), and symmetrical distribution about the central position of the wing are formed in the upstream area of the inlet of the ducted fans. Moreover, the closer to the wingtip, the stronger the intensity of the vortices. These vortices are ingested into the fans under the suction effect of the fans, further leading to the edge fans (#1 and #5) being most affected by swirl distortion, while the middle fan (#3) is least affected by swirl distortion.

5. Conclusions

In this study, a circumferential body force model based on local flow parameters was developed and validated. An over-wing symmetric configuration with five distributed ducted fans was constructed, and the impacts of the flight Mach number on the aerodynamic performance and flow field structure of the coupled configuration were investigated in detail. For the integrated configuration considered in this study, the main conclusions can be drawn as follows:

(1)

The higher the flight Mach number is, the greater the lift obtained by the wing is. When the Mach number is 0.5, the maximum lift coefficient of the wing increases by 306% compared with that at a Mach number of 0.2. However, the stall angle of attack of the wing during flight decreases as the flight Mach number increases. Under flight Mach numbers ranging from 0.2 to 0.5, the corresponding stall angles of attack are 38°, 32°, 26°, and 23°, respectively. The stall angle of attack at a Mach number of 0.5 decreases by 15° compared with that at a Mach number of 0.2.

(2)

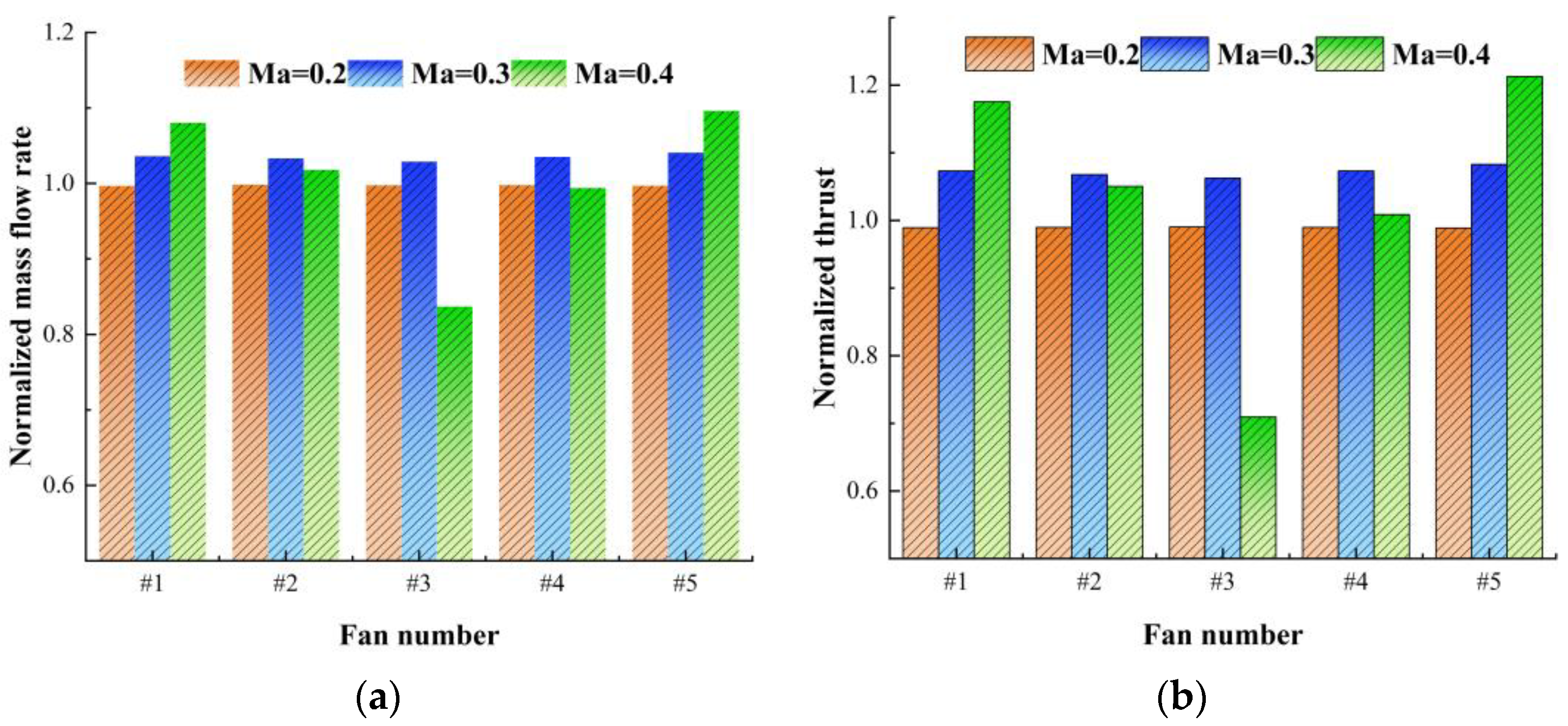
Fans #1 and #5 have the strongest ability to resist airflow separation, while fan #3 has the weakest ability. When the angle of attack is 26°, the mass flow rate and thrust of fans #1 and #5 increase with the increase in the flight Mach number. However, when the Mach number is 0.4, the mass flow rate and thrust of fan #3 decrease significantly. Compared with those at a Mach number of 0.2, the mass flow rate and thrust of fan #3 decrease by 16% and 28%, respectively.

(3)

The higher the flight Mach number is, the greater the degree of intake distortion of the ducted fans is. For total pressure distortion, as the Mach number increases, fan #3 is the most affected by total pressure distortion, followed by fans #2 and #4, and fans #1 and #5 are the least affected by total pressure distortion. For swirl distortion, as the Mach number increases, fans #1 and #5 are the most affected by swirl distortion, followed by fans #2 and #4, and fan #3 is the least affected by swirl distortion.

(4)

For the configuration studied in this paper, the fan located in the middle of the ducted fan array is most sensitive to changes in the angle of attack and the incoming flow velocity. At large angles of attack or high incoming velocities, the performance of the middle fan is significantly reduced. However, the edge fans are less affected by the incoming flow and exhibit a relatively stable aerodynamic performance.