Eccentric Compression Behavior of Coral Aggregate Geopolymer Concrete Columns Reinforced with Stainless-Steel Rebars
Abstract
:1. Introduction
2. Experimental Program
2.1. Raw Material and Mix Ratio of Concrete
2.2. Tensile Performance of SSRs
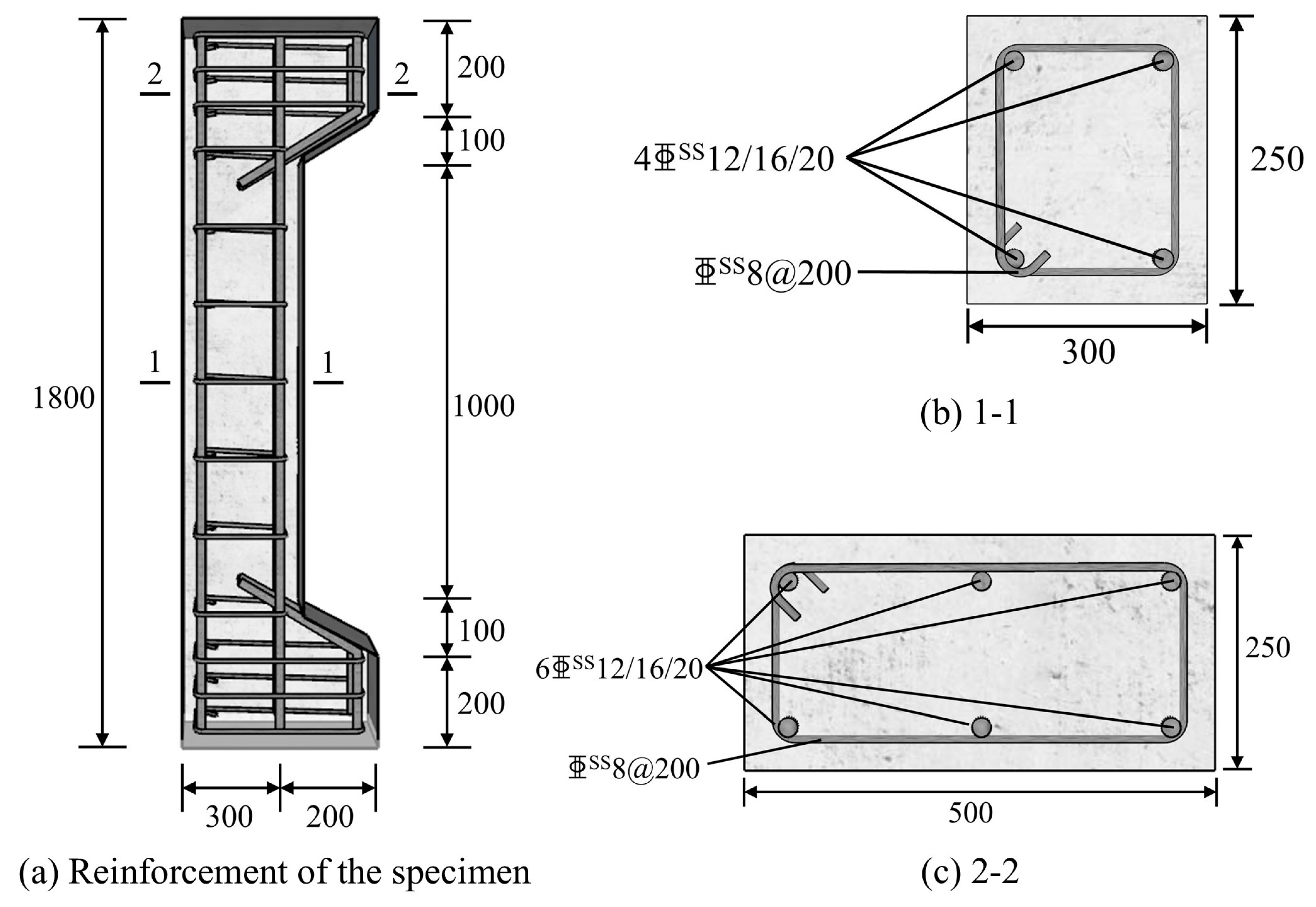
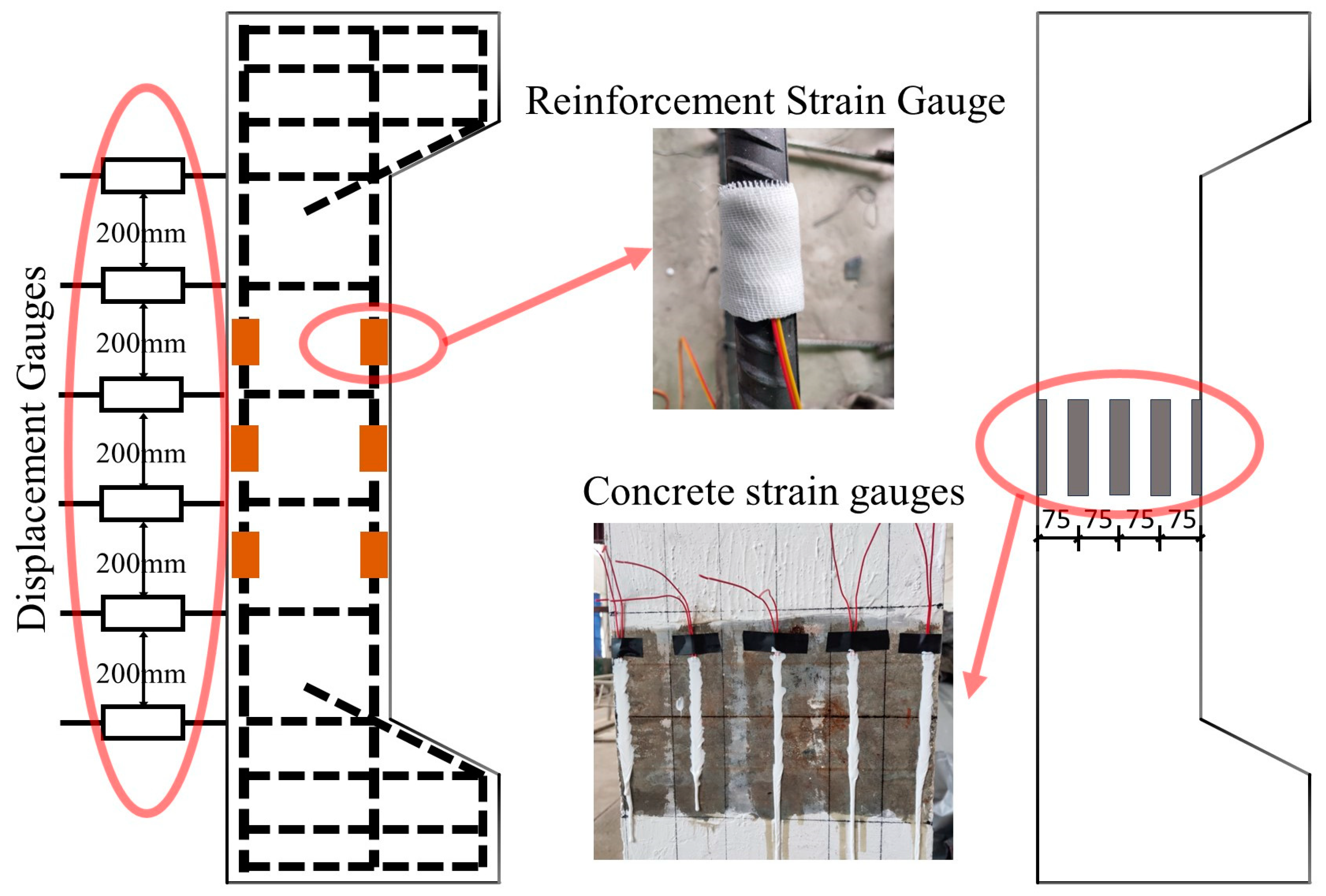
2.3. Eccentric Compression Column Design
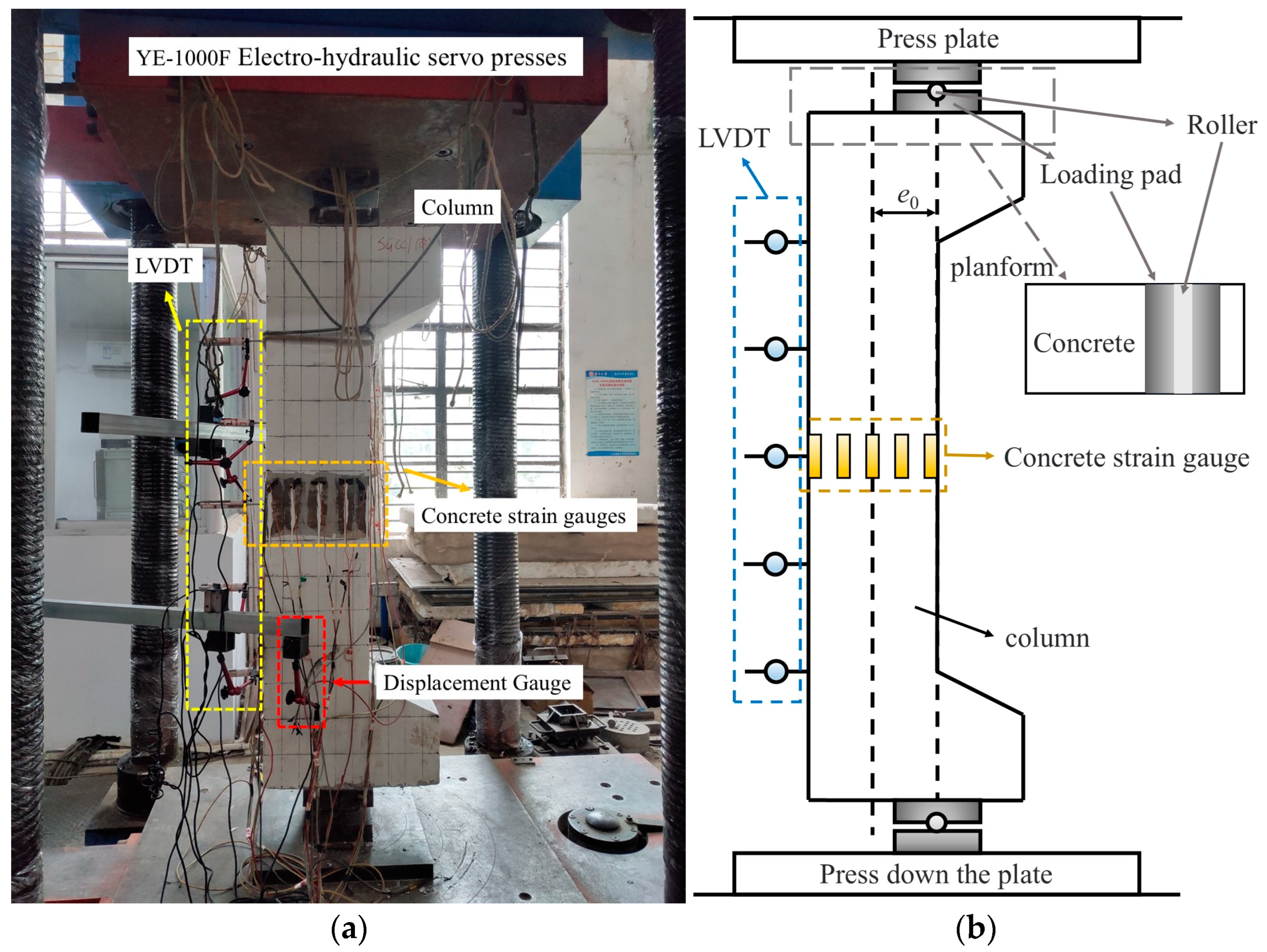
2.4. Test Setup
3. Test Result and Analysis
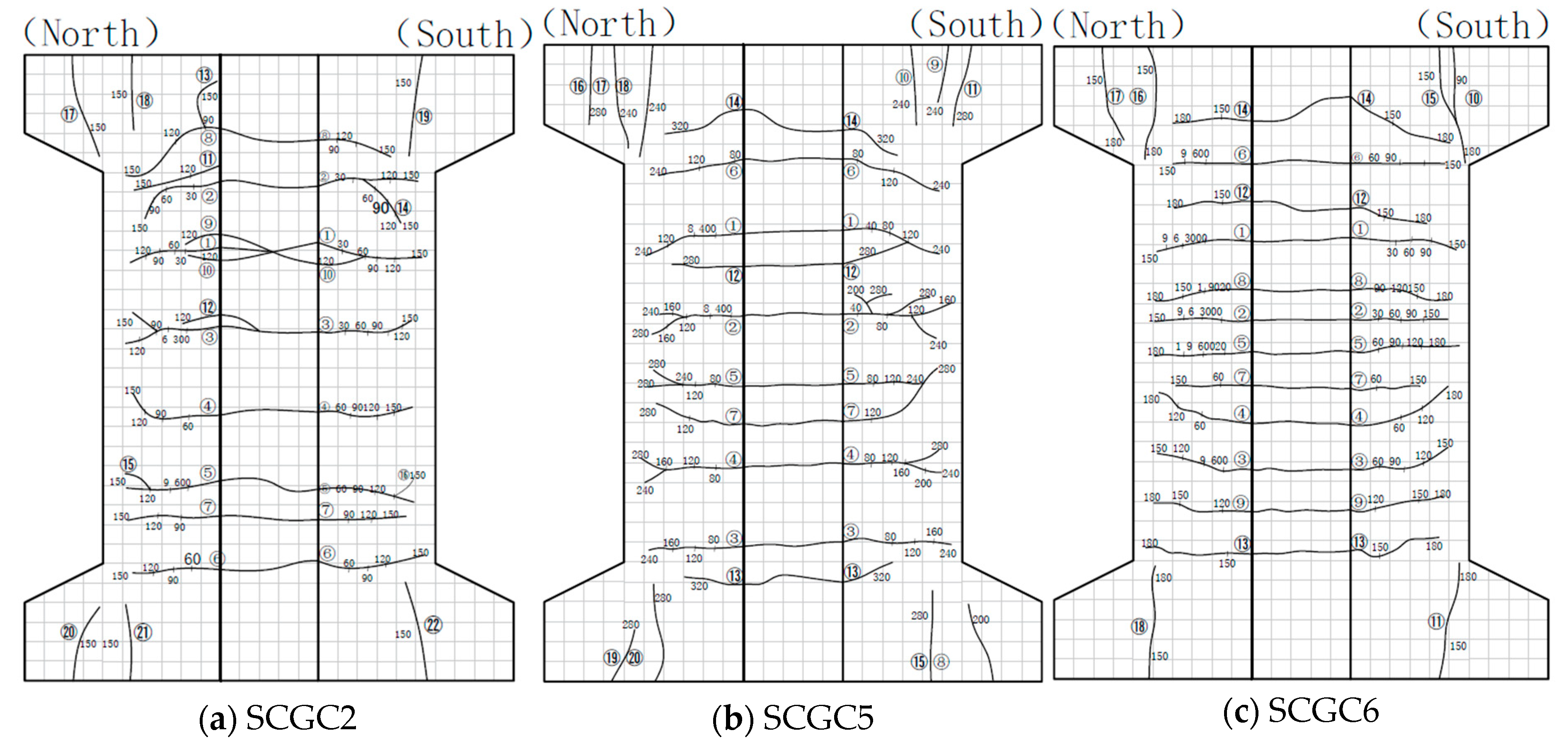
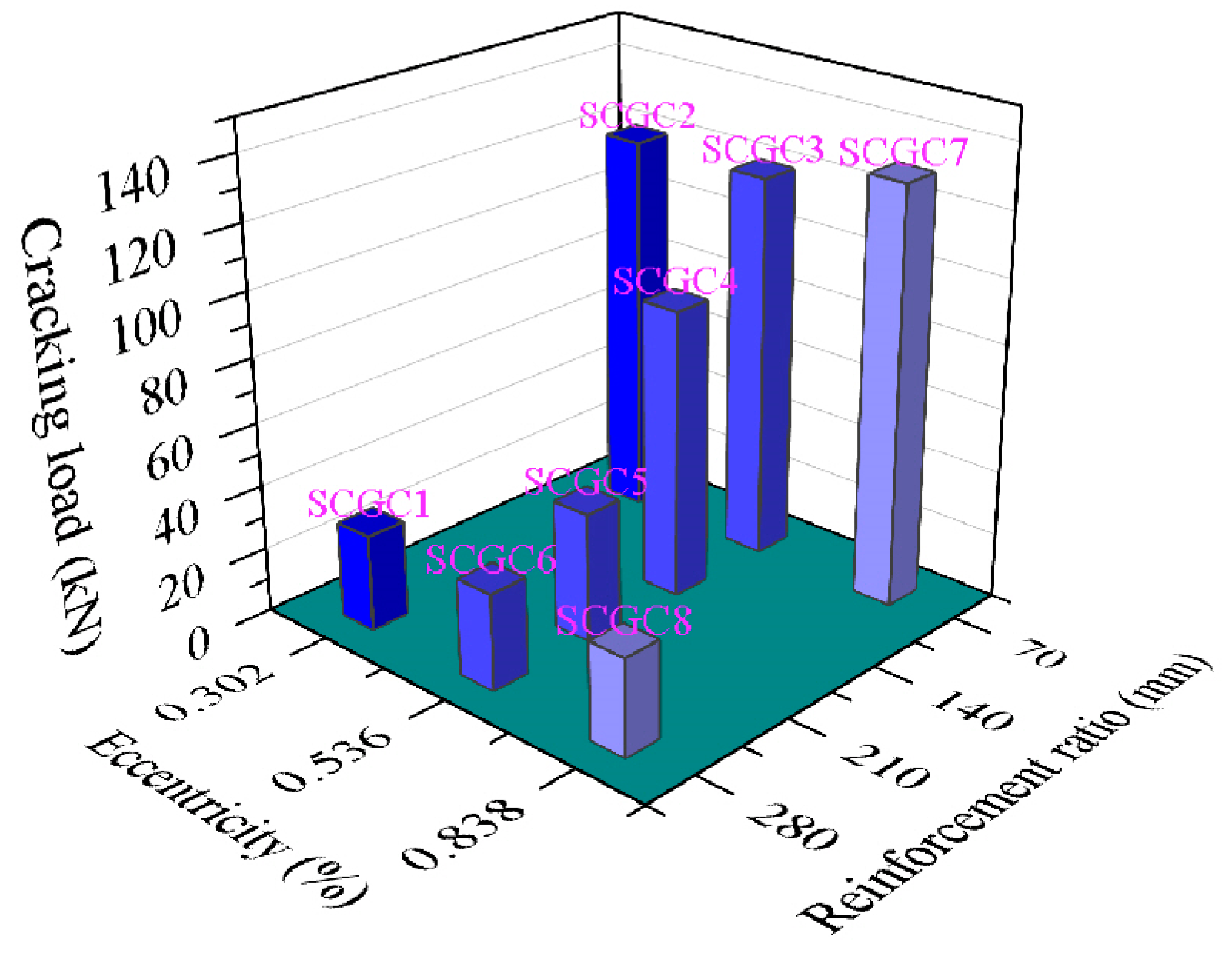
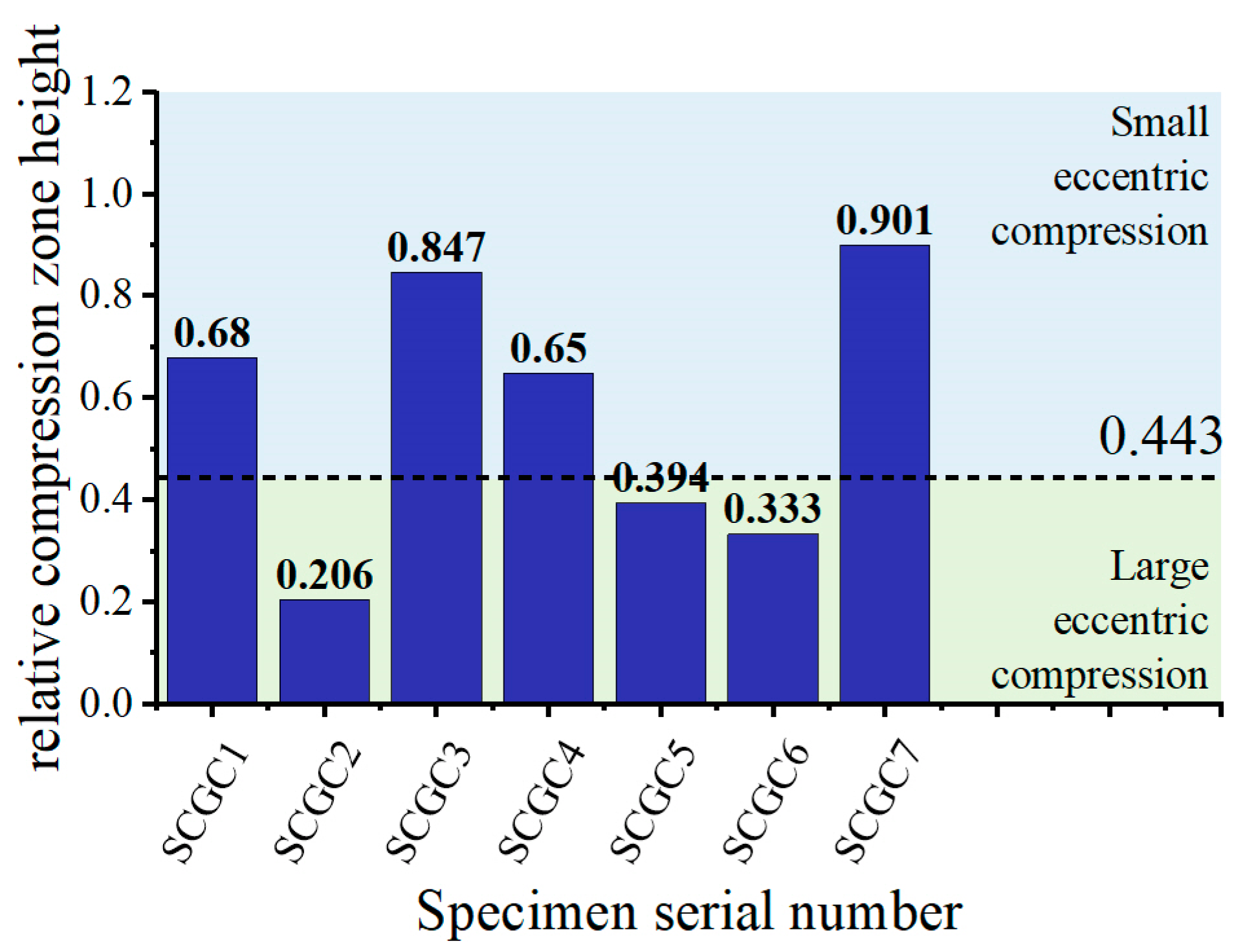
3.1. Failure Patterns and Crack Development
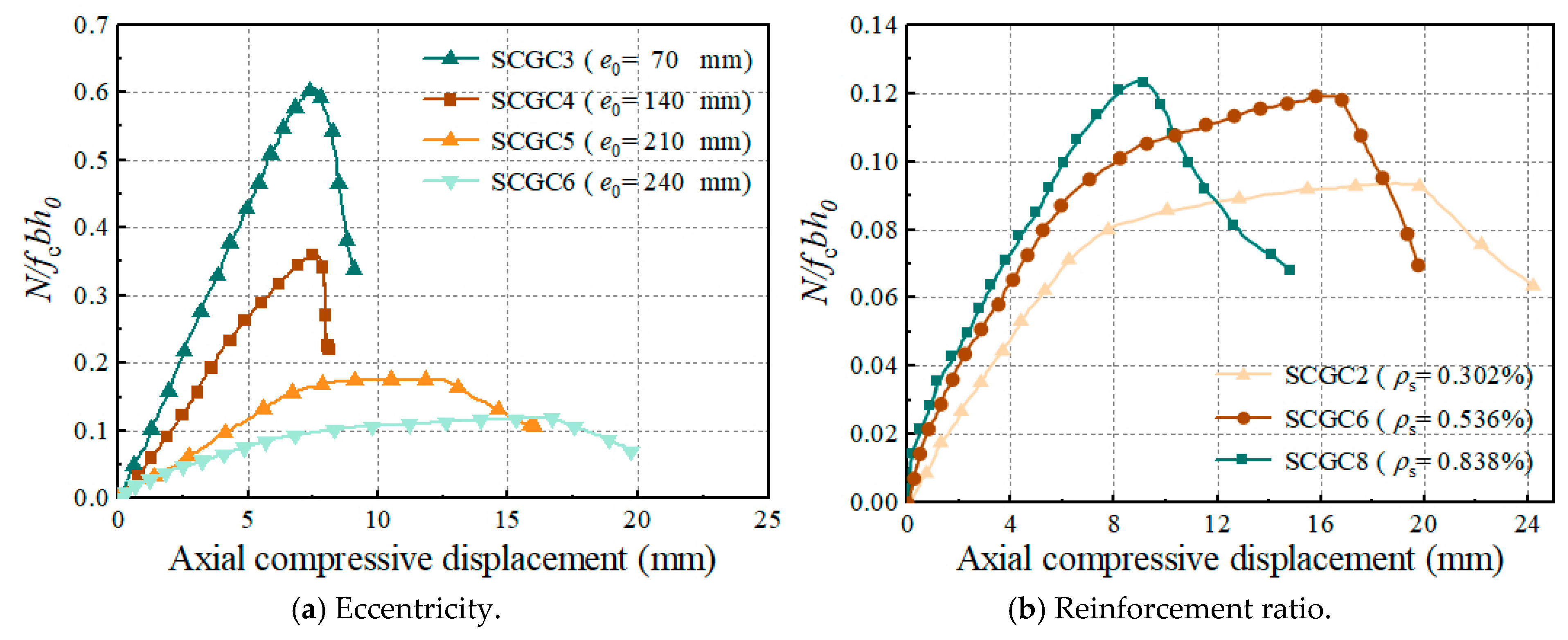
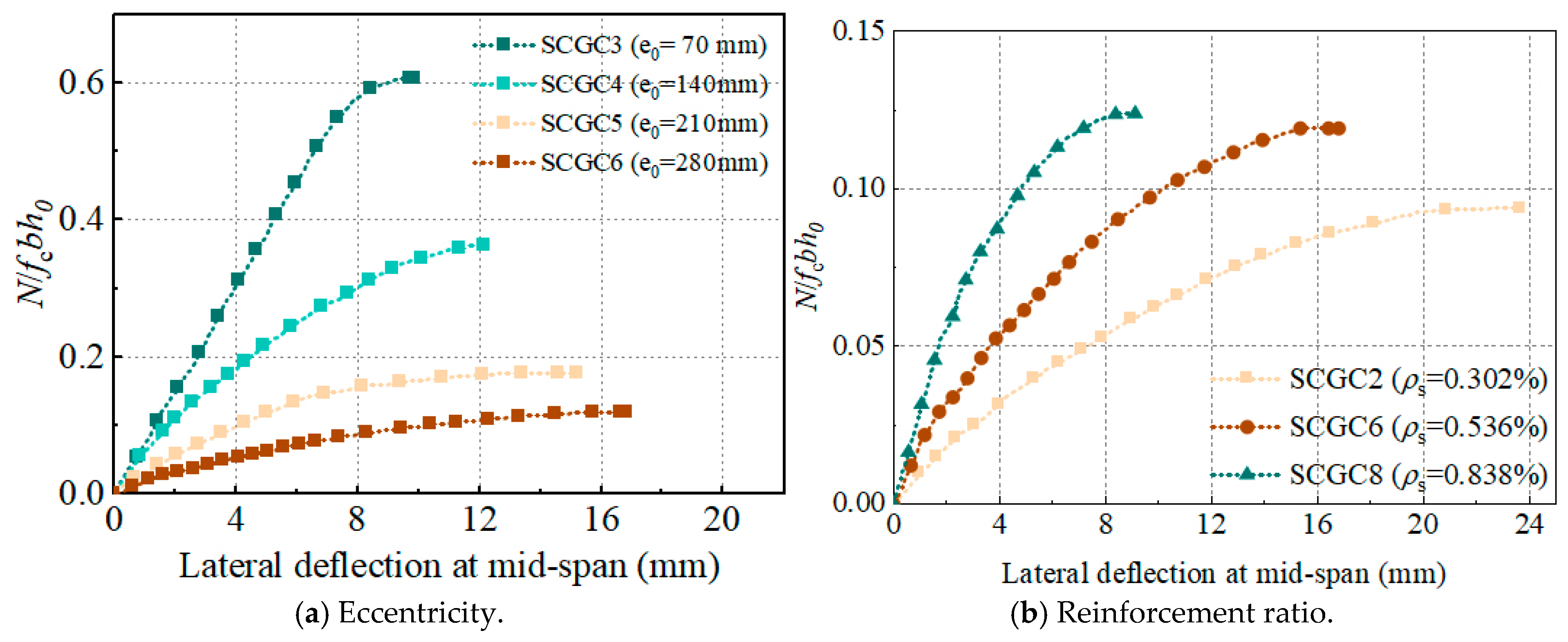
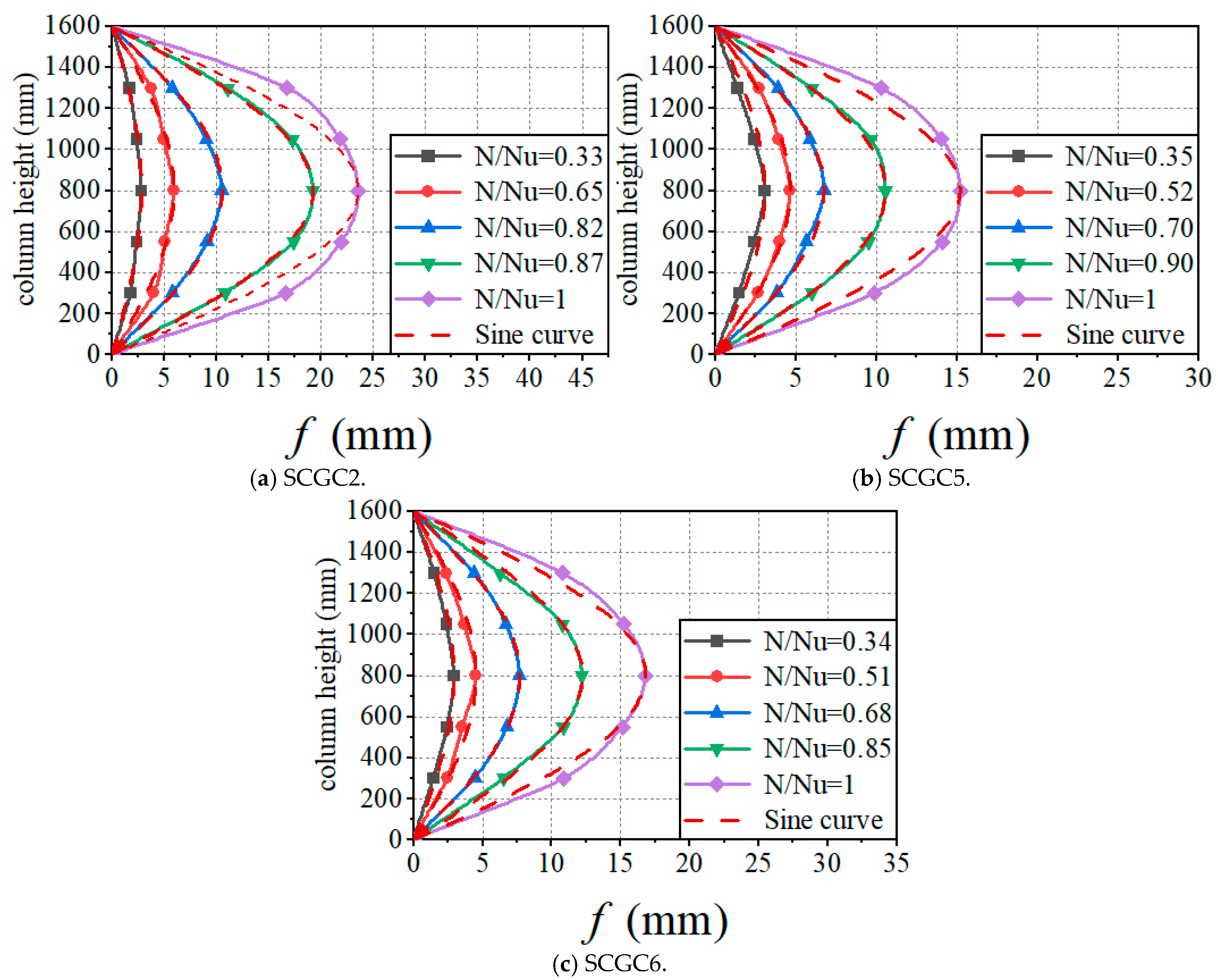
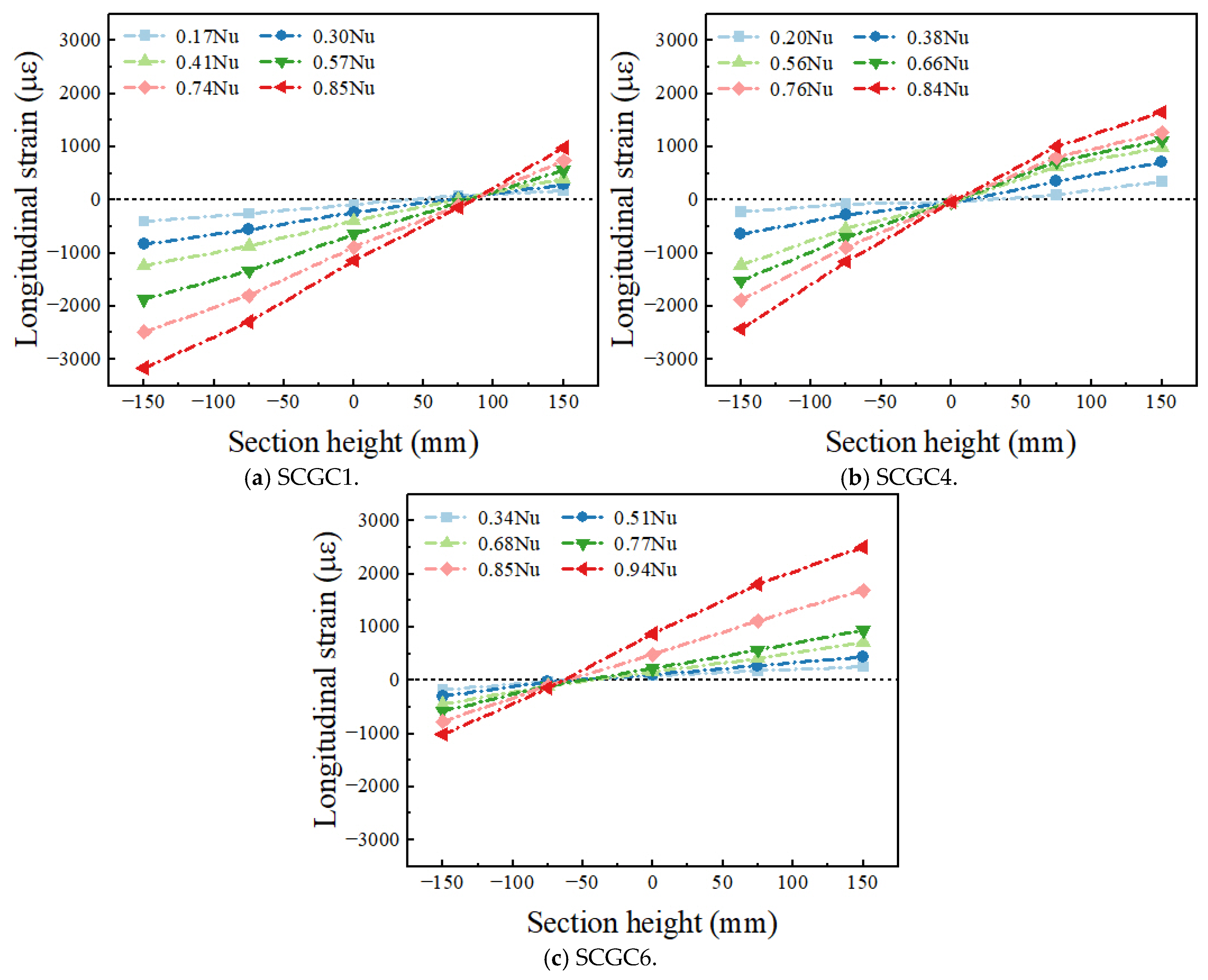
3.2. Deformation Analysis
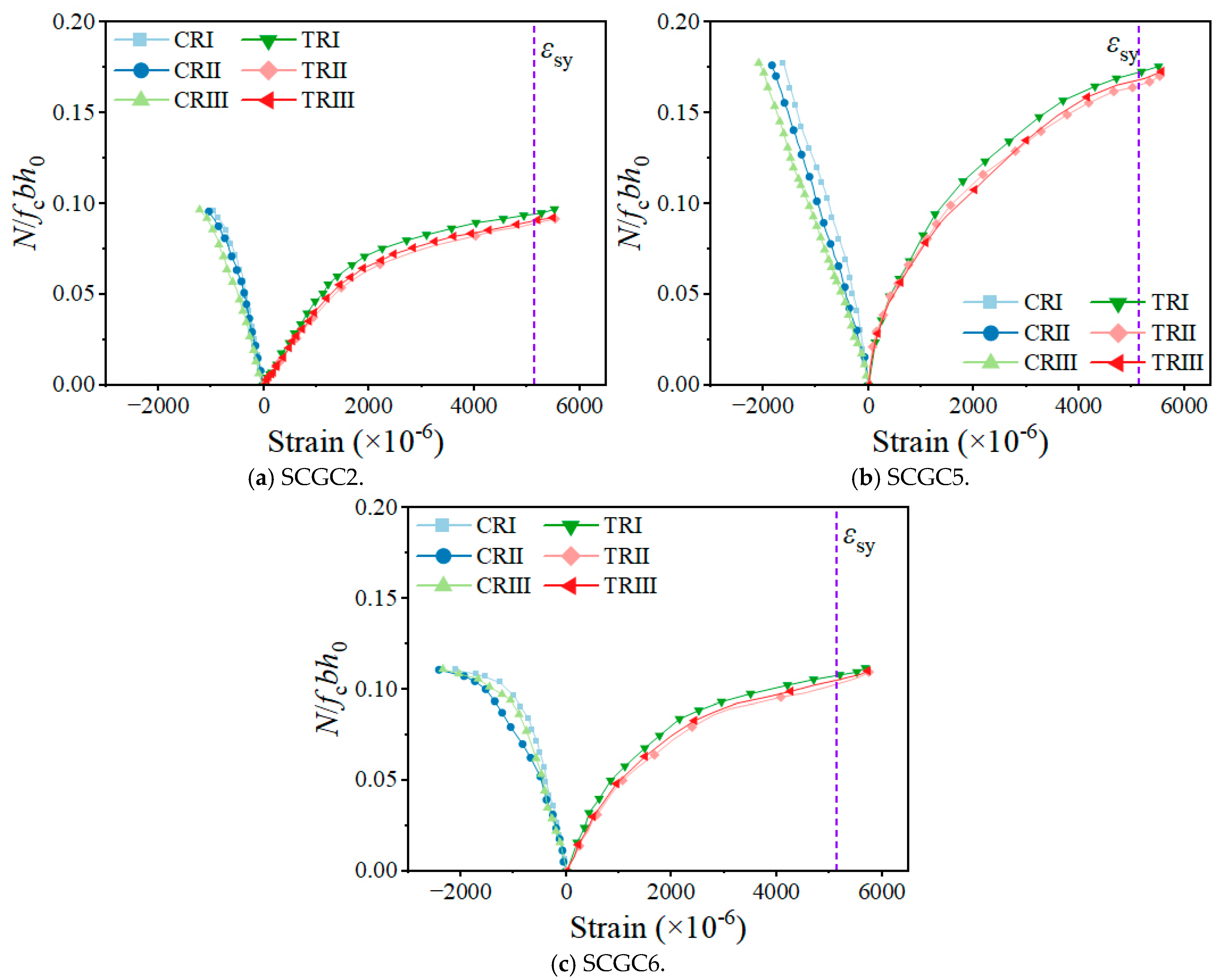
3.3. Strain Analysis
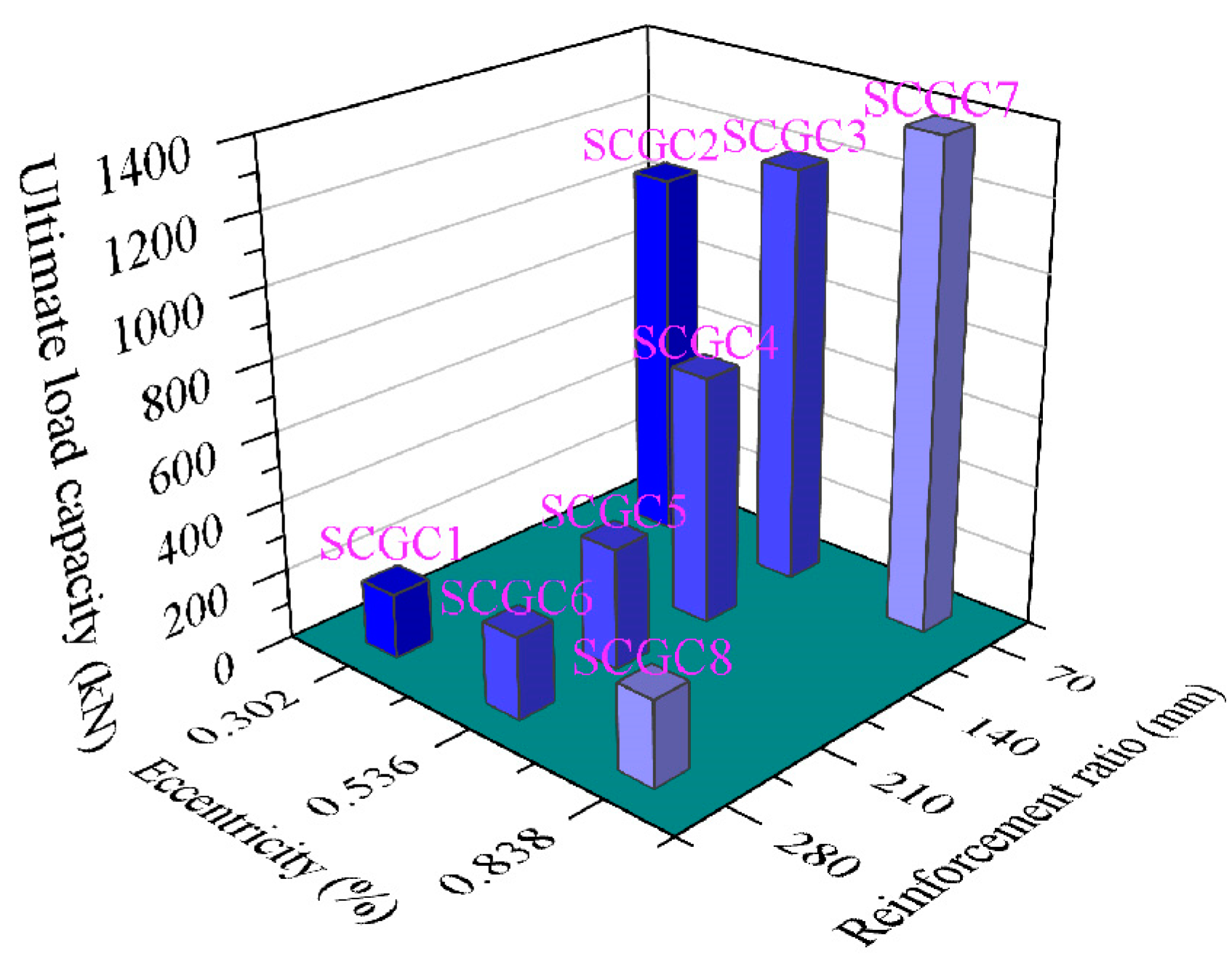
4. Analysis of the Bearing Capacity and Crack Width of SCGCs
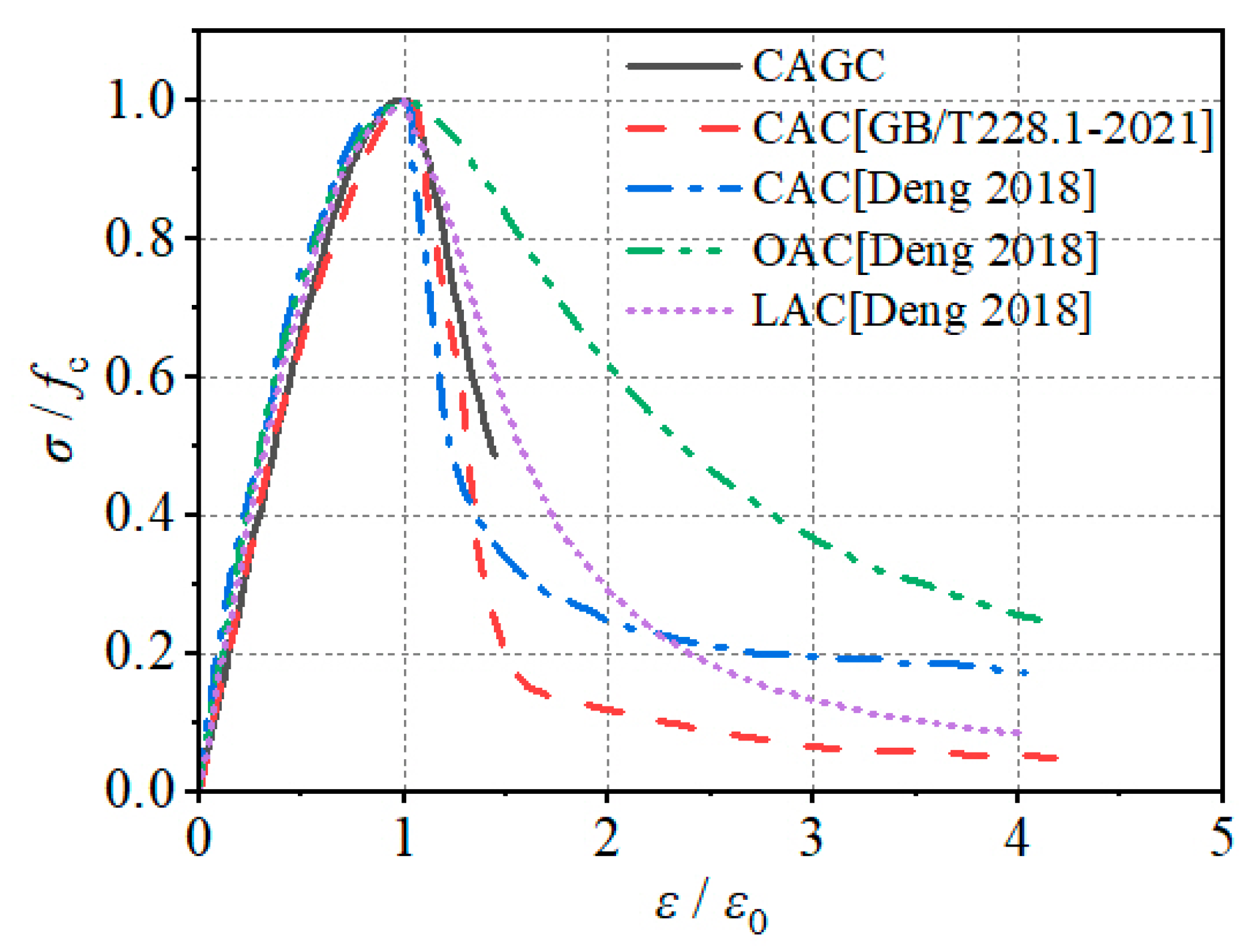
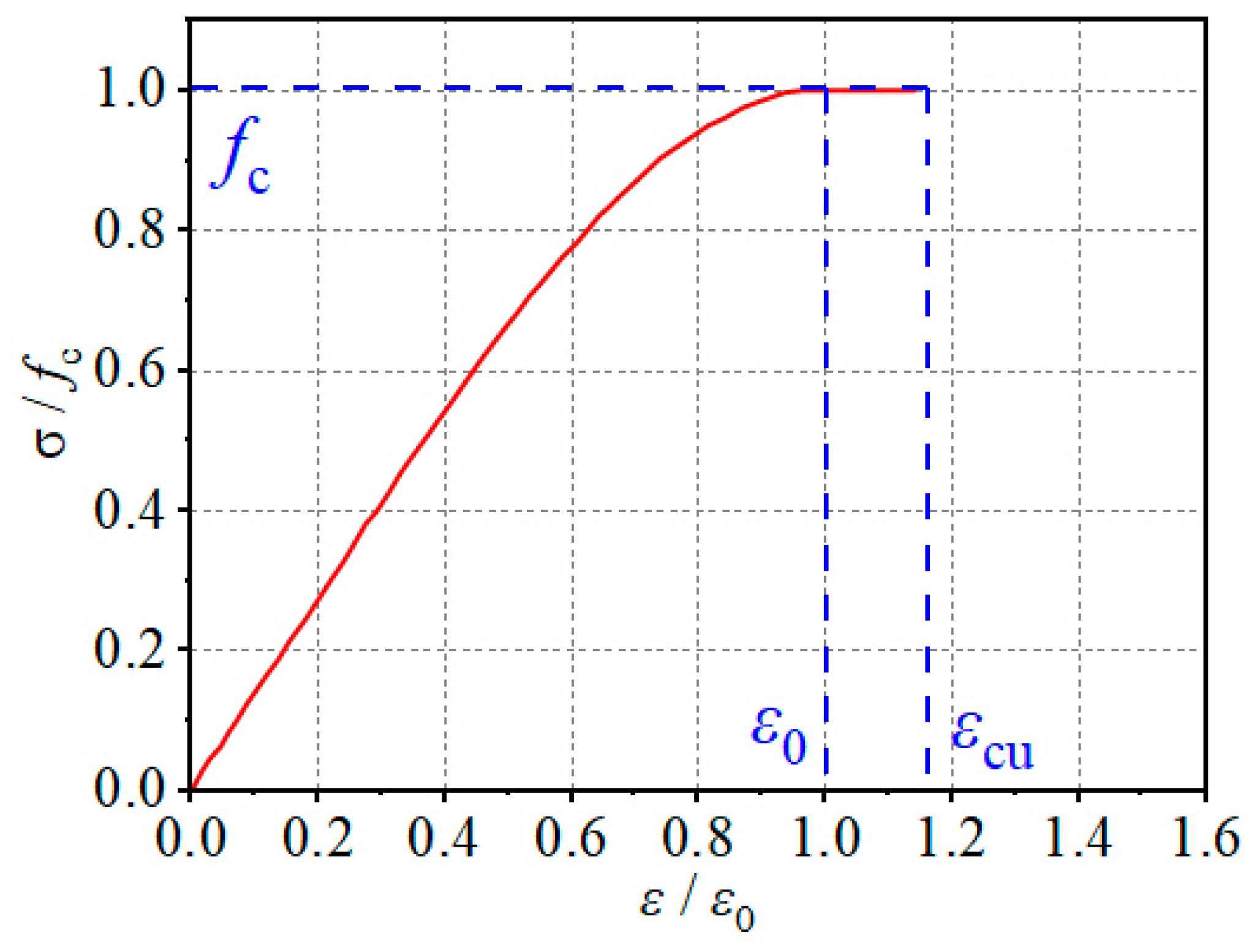
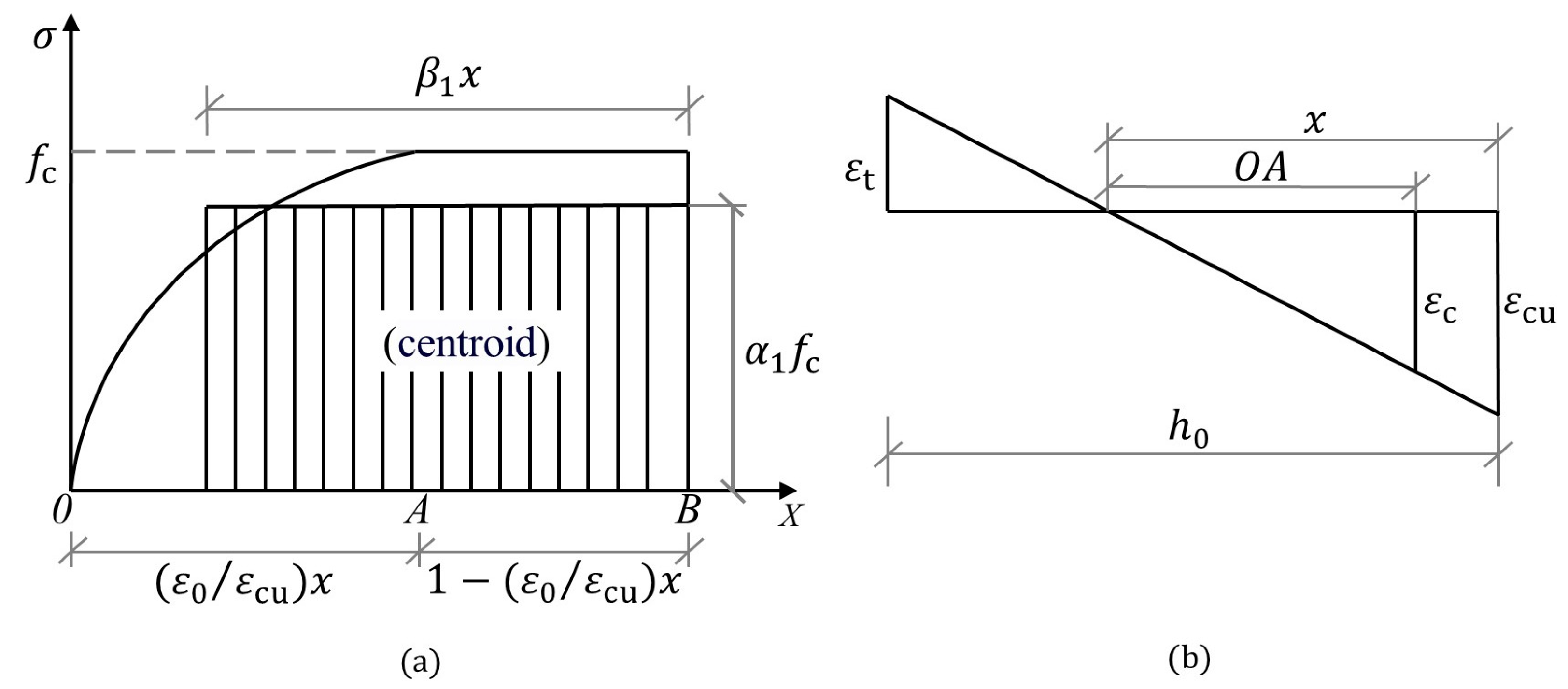
4.1. Constitutive Relationship of CAGC
4.2. Bearing Capacity
4.2.1. Calculation and Analysis of Nu
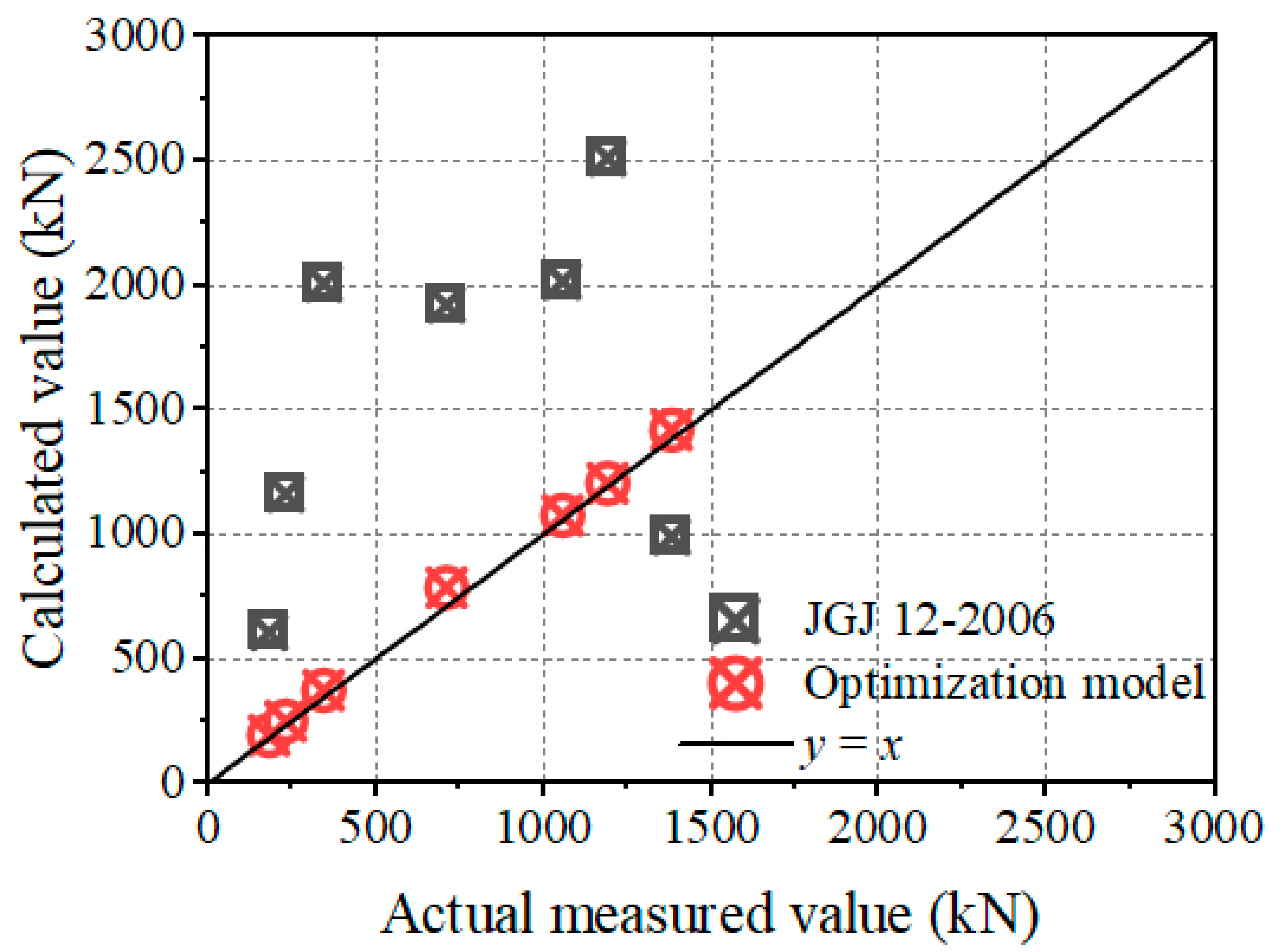
4.2.2. Model Optimization
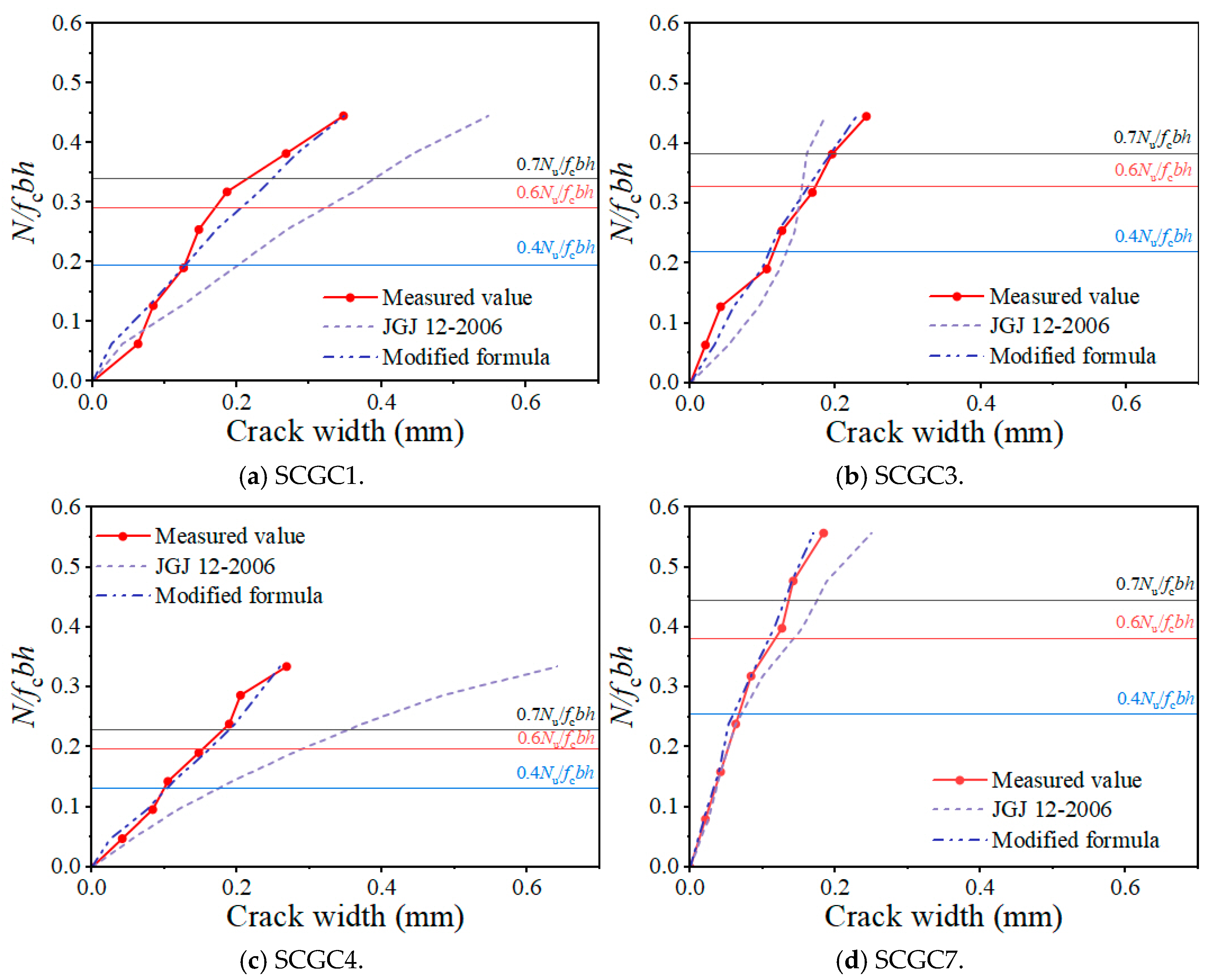
4.3. Crack Width
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ebead, U.; Lau, D.; Lollini, F.; Nanni, A.; Suraneni, P.; Yu, T. A review of recent advances in the science and technology of seawater-mixed concrete. Cem. Concr. Res. 2022, 152, 106666. [Google Scholar] [CrossRef]
- Da, B.; Yu, H.; Ma, H.; Tan, Y.; Mi, R.; Dou, X. Experimental investigation of whole stress-strain curves of coral concrete. Constr. Build. Mater. 2016, 122, 81–89. [Google Scholar] [CrossRef]
- Yang, H.; Li, M.; Jiang, J.; Zhang, Y.; Mei, J.; Deng, Z. Mechanical properties of steel reinforced coral aggregate concrete column under uniaxial compression. Constr. Build. Mater. 2023, 369, 130508. [Google Scholar] [CrossRef]
- Liang, X.; Yin, S.; Hu, C. Environmental reduction factors of BFRP bars in coral aggregate concrete in high temperature and high humidity environments. Structures 2021, 33, 3017–3024. [Google Scholar] [CrossRef]
- Zi, M.; Liu, K.; Liu, S.; Qin, M. Study on the basic properties of coral sand used as fine aggregate. Constr. Build. Mater. 2015, 5, 11–14. [Google Scholar]
- Zhao, Y.; Han, C.; Zhang, S.; Ge, R. Experimental study on the compression age strength of seawater coral concrete. Concrete 2011, 2, 43–45. (In Chinese) [Google Scholar]
- Liu, J.; Ou, Z.; Mo, J.; Chen, Y.; Guo, T.; Deng, W. Effectiveness of saturated coral aggregate and shrinkage reducing admixture on the autogenous shrinkage of ultrahigh performance concrete. Adv. Mater. Sci. Eng. 2017, 2017, 2703264. [Google Scholar] [CrossRef]
- Yang, H.; Mei, J.; Yang, Y. Bond strength and reliability analysis of stainless steel rebar embedded in fiber reinforced coral aggregate concrete. Constr. Build. Mater. 2022, 350, 128783. [Google Scholar] [CrossRef]
- Huang, D.; Niu, D.; Li, S.; Zheng, H.; Fu, Q.; Liu, Y. Effects of mineral admixtures on chloride diffusion in environment-friendly coral aggregate concrete. J. Renew. Mater. 2022, 10, 3477. [Google Scholar] [CrossRef]
- Ma, L.; Li, Z.; Wang, M.; Wei, H.; Fan, P. Effects of size and loading rate on the mechanical properties of single coral particles. Powder Technol. 2019, 342, 961–971. [Google Scholar] [CrossRef]
- Zhang, J.; Wu, Z.; Zhang, Y.; Fang, Q.; Yu, H.; Jiang, C. Mesoscopic characteristics and macroscopic mechanical properties of coral aggregates. Constr. Build. Mater. 2021, 309, 125125. [Google Scholar] [CrossRef]
- Wang, A.; Zhang, Z.; Liu, K.; Xu, H.; Shi, L.; Sun, D. Coral aggregate concrete: Numerical description of physical, chemical and morphological properties of coral aggregate. Cem. Concr. Compos. 2019, 100, 25–34. [Google Scholar] [CrossRef]
- Zhang, P.; Zheng, Y.; Wang, K.; Zhang, J. A review on properties of fresh and hardened geopolymer mortar. Compos. Part B Eng. 2018, 152, 79–95. [Google Scholar] [CrossRef]
- Van Jaarsveld, J.G.S.; Van Deventer, J.S.J.; Lorenzen, L. The potential use of geopolymeric materials to immobilise toxic metals: Part I. Theory and applications. Miner. Eng. 1997, 10, 659–669. [Google Scholar] [CrossRef]
- Zhang, B.; Zhu, H.; Lu, F. Fracture properties of slag-based alkali-activated seawater coral aggregate concrete. Theor. Appl. Fract. Mech. 2021, 115, 103071. [Google Scholar] [CrossRef]
- Zhang, B.; Zhu, H.; Shah, K.W.; Dong, Z.; Wu, J. Performance evaluation and microstructure characterization of seawater and coral/sea sand alkali-activated mortars. Constr. Build. Mater. 2020, 259, 120403. [Google Scholar] [CrossRef]
- Zhang, B.; Zhu, H.; Shah, K.W.; Dong, Z.; Wu, J. Design and properties of seawater coral aggregate alkali-activated concrete. J. Sustain. Cem.-Based Mater 2022, 11, 187–201. [Google Scholar] [CrossRef]
- Wu, W.; Wang, R.; Zhu, C.; Meng, Q. The effect of fly ash and silica fume on mechanical properties and durability of coral aggregate concrete. Constr. Build. Mater. 2018, 185, 69–78. [Google Scholar] [CrossRef]
- Yuan, J.; Ou, Z. Research progress and engineering applications of stainless steel-reinforced concrete structures. Adv. Civ. Eng. 2021, 2021, 9228493. [Google Scholar] [CrossRef]
- Jing, Q.; Fang, X.; Ni, J.; Tang, Y.; Fang, X. Use of 2304 Stainless steel reinforcement in Hong Kong-Zhuhai-Macau bridge-corrosion behaviours of 2304 stainless steel reinforcement. J. Highw. Transp. Res. Dev. 2017, 34, 51–56. [Google Scholar]
- Da, B.; Yu, H.F.; Ma, H.Y.; Wu, Z. Anti-corrosion performances of different types of rebars in coral aggregate seawater concrete. Mater. Rep. 2019, 33, 2002–2008. (In Chinese) [Google Scholar]
- Li, Q.; Kuang, Y.; Guo, W.; Zhang, Y. Experimental research on mechanical performance of SSRC columns under eccentric compression. Appl. Sci. 2020, 10, 5629. [Google Scholar] [CrossRef]
- Rabi, M.; Cashell, K.A.; Shamass, R. Flexural analysis and design of stainless steel reinforced concrete beams. Eng. Struct. 2019, 198, 109432. [Google Scholar] [CrossRef]
- Geromel, M.; Mazzarella, O. Experimental and analytical assessment of the behavior of stainless steel reinforced concrete beams. Mater. Struct. 2005, 38, 211–218. [Google Scholar] [CrossRef]
- Li, Q.; Guo, W.; Liu, C.; Kuang, Y.; Geng, H. Experimental and theoretical studies on flexural performance of stainless steel reinforced concrete beams. Adv. Civ. Eng. 2020, 2020, 4048750. [Google Scholar] [CrossRef]
- Rabi, M.; Cashell, K.A.; Shamass, R. Ultimate behaviour and serviceability analysis of stainless steel reinforced concrete beams. Eng. Struct. 2021, 248, 113259. [Google Scholar] [CrossRef]
- Khalifa, M. Heat of Hydration Thermal Performance and Flexural Capacity of Stainless-Steel Reinforced Concrete Sections. Master’s Thesis, The University of Western Ontario (Canada), London, ON, Canada, 2019. [Google Scholar]
- Zhang, G.; Zhang, Y.; Zhou, Y. Fatigue tests of concrete slabs reinforced with stainless steel bars. Adv. Mater. Sci. Eng. 2018, 2018, 5451398. [Google Scholar] [CrossRef]
- Fu, J.; Ge, X.; Li, J.; Sun, Z.; Wang, D. Seismic performance of concrete bridge piers reinforced by stainless steel bars: A quasi-static experimental study. Eng. Struct. 2022, 266, 114507. [Google Scholar] [CrossRef]
- Nicoletti, V.; Carbonari, S.; Gara, F. Nomograms for the pre-dimensioning of RC beam-column joints according to Eurocode 8. Structures 2022, 39, 958–973. [Google Scholar] [CrossRef]
- Zhou, Y.J.; Wang, X.T.; Sun, H.R.; Chen, X.; Wang, T. Residual seismic performance for damaged RC frame based on beam-to-column joint subassemblies. Structures 2025, 71, 107980. [Google Scholar] [CrossRef]
- JGJ51-2002; Technical Code for Lightweight Aggregate Concrete. China Architecture & Building Press: Beijing, China, 2002. (In Chinese)
- GB/T17431-2010; Lightweight Aggregate and Its Test Methods. Standards Press of China: Beijing, China, 2010. (In Chinese)
- JGJ52-2006; Standard for Quality and Testing Methods of Sand and Crushed Stone for Ordinary Concrete. China Architecture & Building Press: Beijing, China, 2006. (In Chinese)
- Liu, B.; Ye, J.; Liu, X.; Lin, W.; Deng, Z.; Liu, Q. Shear strength and failure criterion of carbon fiber reinforced coral concrete under combined compression-shear stresses. Constr. Build. Mater. 2022, 325, 126728. [Google Scholar] [CrossRef]
- GB/T228.1-2021; Tensile Testing of Metallic Materials-Part 1: Room Temperature Test Method. Standards Press of China: Beijing, China, 2021. (In Chinese)
- Deng, M.; Pan, J.; Liang, X. Uniaxial compressive test of high ductile fiber-reinforced concrete and damage constitutive model. Adv. Civ. Eng. 2018, 2018, 4308084. [Google Scholar] [CrossRef]
- Liu, B.; Zhou, J.; Wen, X.; Hu, X.; Deng, Z. Mechanical properties and constitutive model of carbon fiber reinforced coral concrete under uniaxial compression. Constr. Build. Mater. 2020, 263, 120649. [Google Scholar] [CrossRef]
- Da, B.; Chen, Y.; Yu, H.; Ma, H.; Chen, D.; Wu, Z.; Liu, J.; Li, Y. Preparation technology, mechanical properties and durability of coral aggregate seawater concrete in the island-reef environment. J. Clean. Prod. 2022, 339, 130572. [Google Scholar] [CrossRef]
- GB50010-2010; Code for Design of Concrete Structures. China Architecture & Building Press: Beijing, China, 2015. (In Chinese)
- JGJ12-2006; Technical Code for Lightweight Aggregate Concrete Structures. China Architecture & Building Press: Beijing, China, 2006. (In Chinese)
- GB50068-2018; Unified Standard for Reliability Design of Engineering Structures. China Architecture & Building Press: Beijing, China, 2018. (In Chinese)



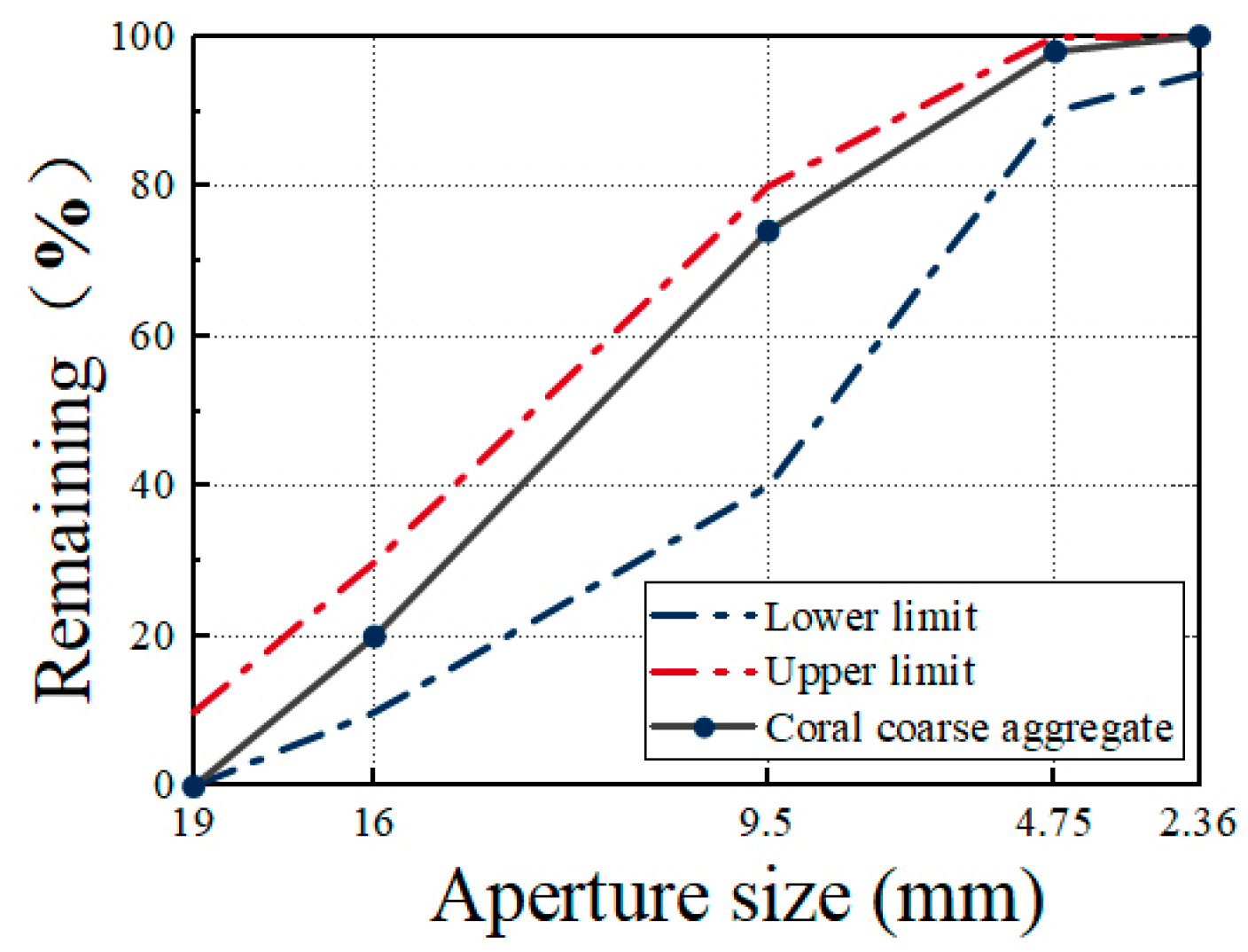
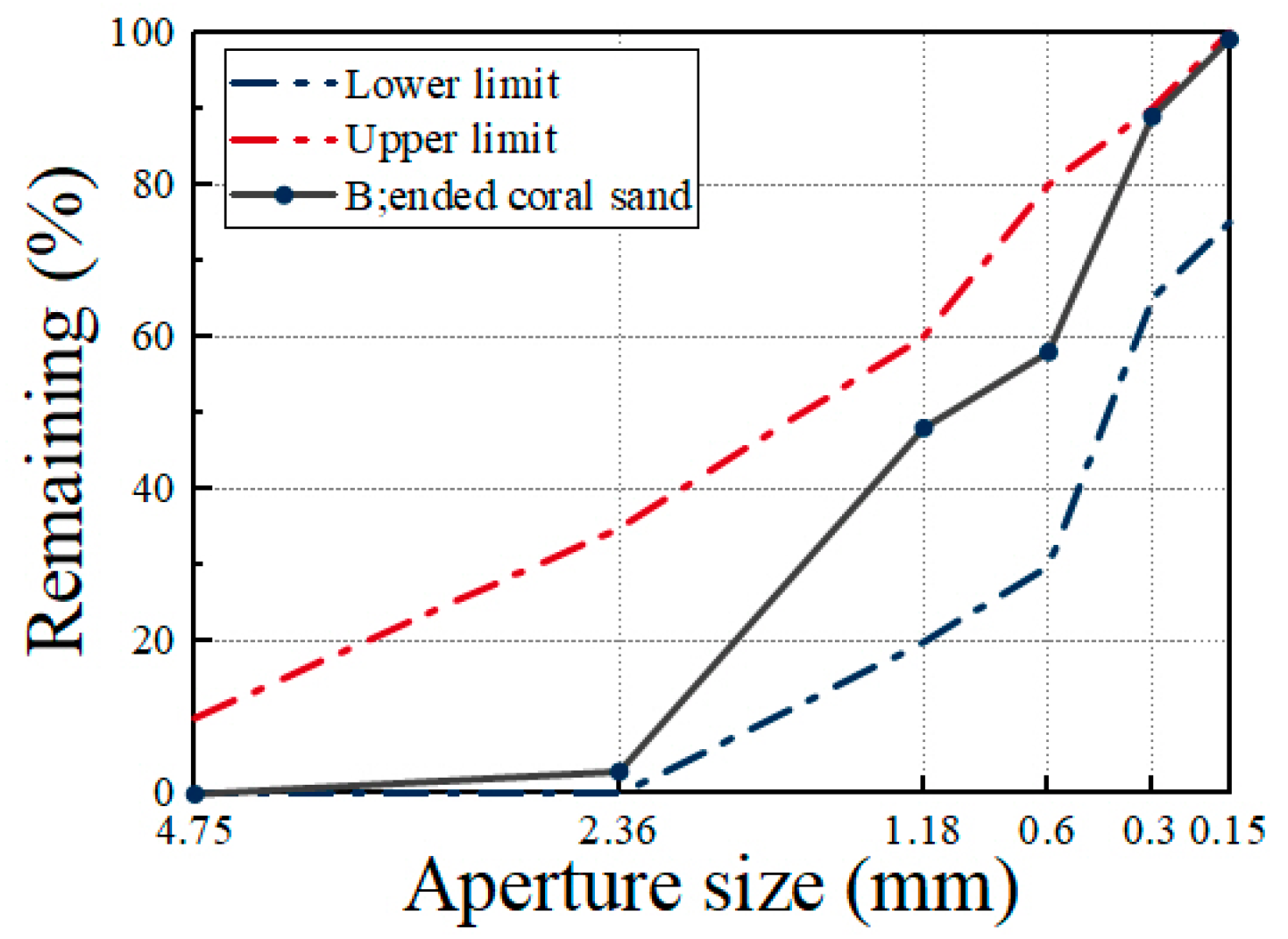






| No. | 1 h Water Absorption (%) | 24 h Water Absorption (%) | Bulk Density (kg/m3) | Apparent Density (kg/m3) | Cylinder Compressive Strength (MPa) | Silt Content (%) |
|---|---|---|---|---|---|---|
| Coral coarse aggregate | 7.82 | 8.13 | 882 | 2092 | 2.1 | 4.2 |
| No. | 1 h Water Absorption (%) | 24 h Water Absorption (%) | Bulk Density (kg/m3) | Apparent Density (kg/m3) | Moisture Content (%) | Silt Content (%) |
|---|---|---|---|---|---|---|
| Mixed coral sand | 3.52 | 3.73 | 1296 | 2707 | 2.87 | 0.5 |
| Coarse Aggregate (kg/m3) | Fine Aggregate | SL (kg/m3) | FA (kg/m3) | Alkali Activator | Seawater (kg/m3) | (MPa) | (MPa) | ||
|---|---|---|---|---|---|---|---|---|---|
| Coarse Sand (kg/m3) | Fine Sand (kg/m3) | Sodium Silicate (kg/m3) | NaOH Solution (kg/m3) | ||||||
| 711 | 336 | 336 | 167 | 250 | 142 | 127 | 60 | 37.6 | 29.0 |
| No. | NaCl | MgCl2•6H2O | Na2SO4 | CaCl2 |
|---|---|---|---|---|
| Content/(g/L) | 28.1 | 7.22 | 2.43 | 1.12 |
| No. | Ingredient Composition | |||||||
|---|---|---|---|---|---|---|---|---|
| Al2O3 (%) | SiO2 (%) | Fe2O3 (%) | CaO (%) | MnO (%) | MgO (%) | K2O (%) | Na2O (%) | |
| SL | 14.3 | 36.5 | 3.2 | 33.6 | 0.8 | 7.5 | \ | \ |
| FA | 28.1 | 50.8 | 6.2 | 3.7 | 1.2 | 28.1 | 0.6 | 1.2 |
| d (mm) | Nominal Yield Stress RP0.2 (MPa) | Ultimate Stress Rm (MPa) | Modulus of Elasticity Es (GPa) |
|---|---|---|---|
| 8 | 511.1 | 799.1 | 165.1 |
| 12 | 515.4 | 807.5 | 167.2 |
| 16 | 516.8 | 806.6 | 166.8 |
| 20 | 516.7 | 803.3 | 169.1 |
| No. | Strength Grade | Size (b × h × l) (mm) | e0 (mm) | d (mm) | ρs (mm) | Stirrup (mm) |
|---|---|---|---|---|---|---|
| SCGC1 | C30 | 250 × 300 × 1600 | 70 | 12 | 0.302 | 8@200 |
| SCGC2 | C30 | 250 × 300 × 1600 | 280 | 12 | 0.302 | 8@200 |
| SCGC3 | C30 | 250 × 300 × 1600 | 70 | 16 | 0.536 | 8@200 |
| SCGC4 | C30 | 250 × 300 × 1600 | 140 | 16 | 0.536 | 8@200 |
| SCGC5 | C30 | 250 × 300 × 1600 | 210 | 16 | 0.536 | 8@200 |
| SCGC6 | C30 | 250 × 300 × 1600 | 280 | 16 | 0.536 | 8@200 |
| SCGC7 | C30 | 250 × 300 × 1600 | 70 | 20 | 0.838 | 8@200 |
| SCGC8 | C30 | 250 × 300 × 1600 | 280 | 20 | 0.838 | 8@200 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, H.; Jiang, J.; Yang, C. Eccentric Compression Behavior of Coral Aggregate Geopolymer Concrete Columns Reinforced with Stainless-Steel Rebars. Appl. Sci. 2025, 15, 3570. https://doi.org/10.3390/app15073570
Xu H, Jiang J, Yang C. Eccentric Compression Behavior of Coral Aggregate Geopolymer Concrete Columns Reinforced with Stainless-Steel Rebars. Applied Sciences. 2025; 15(7):3570. https://doi.org/10.3390/app15073570
Chicago/Turabian StyleXu, Haiwen, Jiasheng Jiang, and Chao Yang. 2025. "Eccentric Compression Behavior of Coral Aggregate Geopolymer Concrete Columns Reinforced with Stainless-Steel Rebars" Applied Sciences 15, no. 7: 3570. https://doi.org/10.3390/app15073570
APA StyleXu, H., Jiang, J., & Yang, C. (2025). Eccentric Compression Behavior of Coral Aggregate Geopolymer Concrete Columns Reinforced with Stainless-Steel Rebars. Applied Sciences, 15(7), 3570. https://doi.org/10.3390/app15073570