Development of a Partial Clustering Model of Alloy Viscosity
Abstract
:1. Introduction
2. Materials and Methods
2.1. Concept of Chaotic Particles
2.2. Viscosity of Alloy and Its Partial Clustering Model
| N | Cu-w, % Sn | ||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
| Cu-Sn alloy | 0 | 10 | 25 | 30.6 | 38 | 58.6 | 92.4 | 99.3 | 100 |
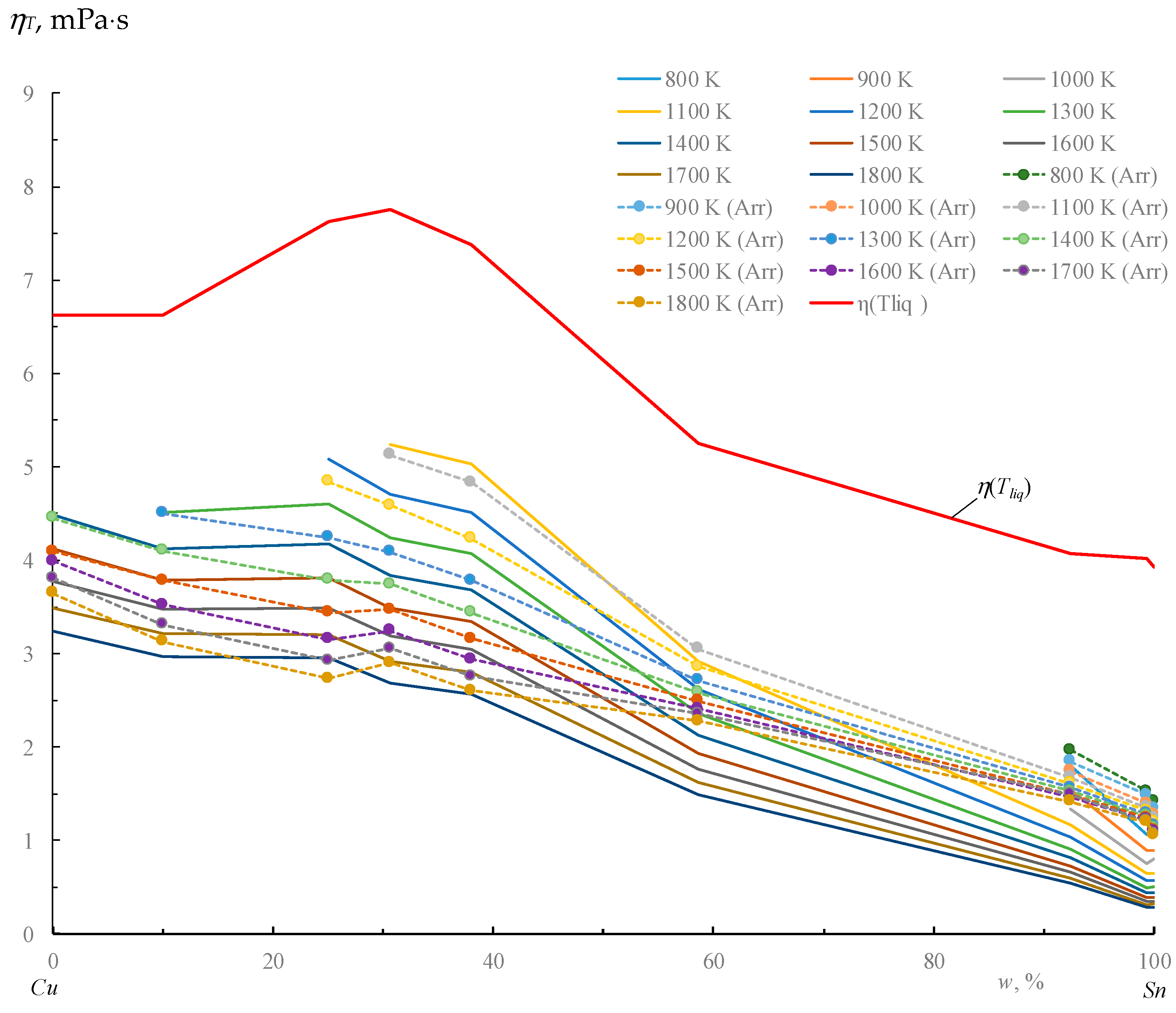
3. Results
- -
- A systematic deviation of one dependence from the other, with no prolonged overestimations or underestimations;
- -
- The closest alignment of data points at the boundaries of the comparable dependencies;
- -
- The largest divergence of points at corresponding extrema;
- -
- The absence of unpaired extrema;
- -
- Selection of “reference” dependencies based on their closest proximity to experimental definitions (in this case, thermal definitions are measured directly, while activation energy is determined only through a calculated linearization from the inverse absolute temperature);
- -
- Calculation of the nonlinear multiple correlation coefficient yields R = 0.729, with statistical significance according to Student’s t-test, tR = 6.05 > 2, for three factors (T, w, Tliq) with t being a probability of 0.9;
- -
- Full coverage of the Cu-Sn composition range (from 0 to 100% w Sn).
4. Discussion
- -
- Developing an optimal melting regime to prevent “freezing” of the melt in the ladle during technological transport;
- -
- Addressing “washout” of furnace linings during overheating;
- -
- Managing emergency situations related to casting speeds in continuous rolling mill lines;
- -
- Understanding lava flow dynamics during volcanic eruptions.
5. Conclusions
- A partial clustering model was obtained that includes the contribution of alloy components to its viscosity. In this model, the impact of clusters was compared with the energy barriers that can be calculated directly in formulas. This assumption can be considered as the fundamental significance of clusters for expressing viscosity, one of the most important properties of the liquid state.
- The new partial clustering model of viscosity was tested on the experimental data as an example of Cu-Sn alloy. The liquidus temperature was applied as a thermal barrier for the alloys. The high adequacy of the obtained results indicates the correctness of the proposed equation and possibility of its use based on the state diagram.
- The new partial clustering model of viscosity can be used for different alloys (two- and three-component) and to predict the behavior of this characteristic at the high temperatures, i.e., they face problems of difficulty in accurate measurement.
- A probabilistic interpretation of the cluster presence in a liquid can be appreciated as a contribution to the theory of the liquid state.
- The proposed model for the temperature dependence of dynamic viscosity is already suitable for practical application, particularly for extrapolation to temperatures above 1800 K. This temperature range is challenging to achieve experimentally, yet it is reliably represented in the model (13). Additionally, technological verification of the proposed model is feasible for viscosity-based control in the ultra-high temperature regime.
- The relationship of the concept of viscosity in the approximation of the Arrhenius physico-chemical model is revealed when comparing the activation energy of a viscous flow with the chaotic energy according to the partial clustering model, taking into account the thermal barrier along the liquidus line. This gives the proposed model fundamental importance.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Fu, Y.; Li, H.; Tang, K.; Yang, S.; Shi, Y.; Liu, B.; Luo, Q.; Zhang, L.; Li, Q.; Pan, F. Melt viscosity of light alloys: Progress and challenges. J. Mater. Sci. Technol. 2024, 183, 72–88. [Google Scholar] [CrossRef]
- Tolokonnikova, V.V.; Baisanov, S.O.; Saulebek, Z.K.; Orlov, A.S. Mathematical description of the lines of monovariant phase equilibria on the MnO-SiO2 phase equilibrium diagram. CIS Iron Steel Rev. 2023, 26, 105–110. [Google Scholar] [CrossRef]
- Terzieff, P. The viscosity of liquid alloys. J. Alloys Compd. 2008, 453, 233–240. [Google Scholar] [CrossRef]
- Dobosz, A.; Gancarz, T. Reference Data for the Density, Viscosity, and Surface Tension of Liquid Al–Zn, Ag–Sn, Bi–Sn, Cu–Sn, and Sn–Zn Eutectic Alloys. J. Phys. Chem. Ref. Data 2018, 47, 013102. [Google Scholar] [CrossRef]
- Rozhitsina, E.V.; Gruner, S.; Kaban, I.; Hoyer, W.; Sidorov, V.E.; Popel’, P.S. Dynamic viscosities of pure tin and Sn-Ag, Sn-Cu, and Sn-Ag-Cu eutectic melts. Russ. Metall. 2011, 2, 118–121. [Google Scholar] [CrossRef]
- Zhao, Y.; Hou, X. A Direct Correlation between Viscosity and Liquid Structure in Cu-Sn Alloys. Adv. Condens. Matter Phys. 2017, 1, 7536853. [Google Scholar] [CrossRef]
- Piatkowski, J.; Gajdzik, B.; Matula, T. Crystallization and Structure of Cast A390.0 Alloy with melt Overheating Temperature. Metalurgija 2012, 51, 321–324. Available online: https://hrcak.srce.hr/clanak/120265 (accessed on 10 March 2025).
- Lu, X.K.; Xiao, S.J.; He, W.Q.; Wang, J.J.; Ma, Y.M.; Zhang, H.H. Effect of melt overheating treatment on the microstructure and mechanical properties of Zn-Al alloy. Vacuum 2022, 201, 111071. [Google Scholar] [CrossRef]
- Nikulin, S.A.; Rogachev, S.O.; Prosvirnin, D.V.; Pivovarchik, S.V.; Belov, V.A.; Shplis, N.V.; Zadorozhnyy, M.Y.; Khatkevich, V.M. Influence of Overheating on High-Cycle Fatigue Characteristics of the Base Metal and Weld Metal of Low-Carbon Steel Welded Joints. Metals 2023, 13, 1707. [Google Scholar] [CrossRef]
- Liang, Y.; Guo, J.; Zhou, L.; Zhang, C.; Lin, J. Effect of overheating treatment on the microstructure of NiAl-based alloy. Mater. Lett. 2010, 64, 1707–1709. [Google Scholar] [CrossRef]
- Qiu, D.; Zhang, M.X.; Taylor, J.A.; Fu, H.M.; Kelly, P.M. A novel approach to the mechanism for the grain refining effect of melt superheating of Mg–Al alloys. Acta Mater. 2007, 55, 1863–1871. [Google Scholar] [CrossRef]
- Yin, F.S.; Sun, X.F.; Li, J.G.; Guan, H.R.; Hu, Z.Q. Effects of melt treatment on the cast structure of M963 superalloy. Scr. Mater. 2003, 48, 425–429. [Google Scholar] [CrossRef]
- Karyakin, N.V. Fundamentals of Chemical Thermodynamics; Textbook for Universities; Publishing House “Center Academy”: Moscow, Russia, 2003. [Google Scholar]
- Khrapak, S.A. Elementary vibrational model for transport properties of dense fluids. Phys. Rep. 2024, 1050, 1–29. [Google Scholar] [CrossRef]
- Ferkl, P.; Lu, X.; Kruger, A.A.; Vienna, J.D. Temperature and composition dependence modeling of viscosity and electrical conductivity of low-activity waste glass melts. J. Non-Cryst. Solids 2024, 640, 123119. [Google Scholar] [CrossRef]
- Malyshev, V.P.; Makasheva, A.M. Boltzmann distribution as the basis for a universal expression of the activation energy of viscous flow, chemical reactions and mechanical destruction. Russ. Non-Ferr. Met. 2018, 10, 6–12. [Google Scholar] [CrossRef]
- Kuhn, T. Structure of Scientific Revolutions; Progress: Moscow, Russia, 1975. [Google Scholar]
- Malyshev, V.P.; Nurmagambetova (Makasheva), A.M. The concept of chaotized particles as the basis for a unified representation of solid, liquid and gaseous states of matter. Bull. Kazakh Natl. Univ. Ser. Chem. 2004, 3, 53–67. [Google Scholar]
- Leontovich, M.A. Introduction to Thermodynamics. In Statistical Physics; Higher School: Moscow, Russia, 1983. [Google Scholar]
- Boltzmann, L. Selected Works. Molecular Kinetic Theory of Gases. Thermodynamics. Statistical Mechanics. Theory of Radiation. General Questions of Physics; Nauka: Moscow, Russia, 1984. [Google Scholar]
- Soroko, E.M. Structural Harmony of Systems; Nauka I Technika: Minsk, Belarus, 1984. [Google Scholar]
- Livio, M. φ is the Number of God. The Golden Ratio and the Formula of the Universe; AKT: Moscow, Russia, 2015. [Google Scholar]
- Craciun, I.; Inoan, D.; Popa, D.; Tudose, L. Generalized Golden Ratios defined by means. Appl. Math. Comput. 2015, 250, 221–227. [Google Scholar] [CrossRef]
- Korchemkina, N.V.; Pastukhov, E.A.; Selivanov, E.N.; Chentsov, V.P. Structure and Properties of Melts of Copper with Aluminum, Tin and Lead; UIPTs: Yekaterinburg, Russia, 2014. [Google Scholar]
- Arkharov, V.I.; Novokhatsky, I.A. On the quasi-polycrystalline model of melts. In Structure and Properties of Metal and Slag Melts: Scientific Report of the All-Union Conference on the Structure and Properties of Metal and Slag Melts; Publishing House of the Ural Polytechnic University: Yekaterinburg, Russia, 1974. [Google Scholar]
- M’chaar, R.; Sabbar, A.; Moudane, M.E. Temperature dependences of surface tension, density and viscosity study of Sn-Ag-Cu with Bi additions using theoretical models. Sci. Rep. 2019, 9, 14177. [Google Scholar] [CrossRef]
- Gancarz, T.; Gasior, W. Density, Surface Tension, and Viscosity of Liquid Pb–Sb Alloys. J. Chem. Eng. 2018, 63, 1471–1479. [Google Scholar] [CrossRef]
- Odusote, Y.A.; Popoola, A.I. Thermodynamic and surface properties of Cr-X, (X = Mo, Fe) liquid alloys. Am. J. Condens. Matter Phys. 2017, 7, 57–66. [Google Scholar] [CrossRef]
- Li, X.; Zuo, X.; Li, J.; Zeng, Y.; Long, J.; Chen, J.; Wu, L. Surface tension and viscosity of Zr–Ti–Cu liquid alloys. Vacuum 2024, 220, 112712. [Google Scholar] [CrossRef]
- Zhang, F.; Wen, S.; Liu, Y.; Du, Y.; Kaptay, G. Modelling the viscosity of liquid alloys with associates. J. Mol. Liq. 2019, 291, 111345. [Google Scholar] [CrossRef]
- Mao, T.; Bian, X.; Xue, X.; Zhang, Y.; Guo, J.; Sun, B. Correlation between viscosity of molten Cu-Sn alloys and phase diagram. Physica B 2007, 387, 1–5. [Google Scholar] [CrossRef]
- Ghosh, G.; Asta, M. Phase stability, phase transformations, and elastic properties of Cu6Sn5: Ab initio calculations and experimental results. J. Mater. Res. 2005, 20, 3102–3117. [Google Scholar]
- Jia, P.; Zhang, J.; Hu, X.; Li, C.; Zhao, D.; Teng, X.; Yang, C. Correlation between the resistivity and the atomic clusters in liquid Cu-Sn alloys. Physica B 2018, 537, 58–62. [Google Scholar] [CrossRef]
- Ghandili, A. Viscosity in Simple Fluids: A Different Perspective Based on the Thermodynamic Dimension. Fluid Phase Equilibria 2024, 585, 114178. [Google Scholar] [CrossRef]
- Fan, G.J.; Fecht, H.J. A cluster model for the viscous flow of glass-forming liquids. J. Chem. Phys. 2002, 116, 5002–5006. [Google Scholar] [CrossRef]
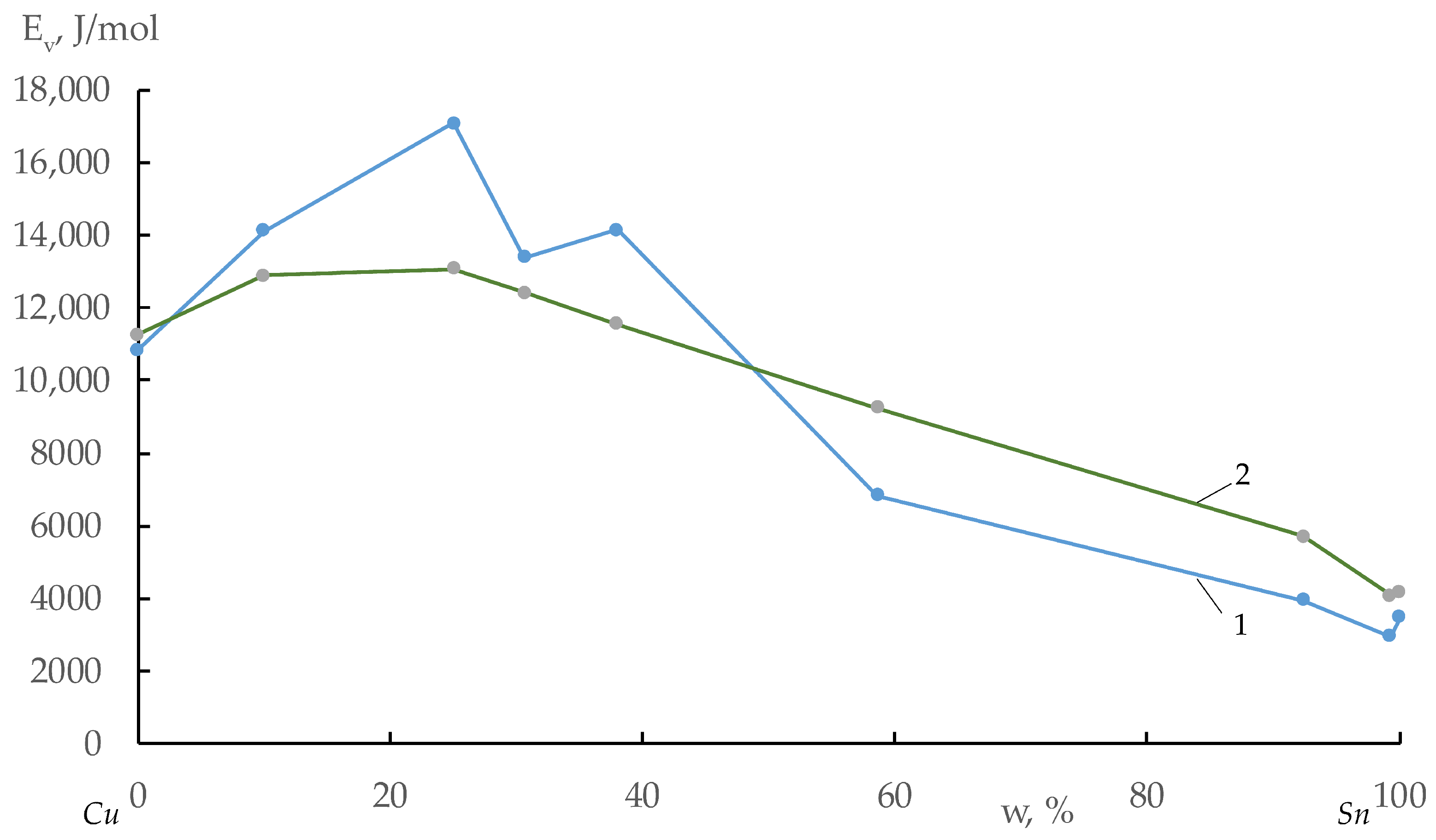
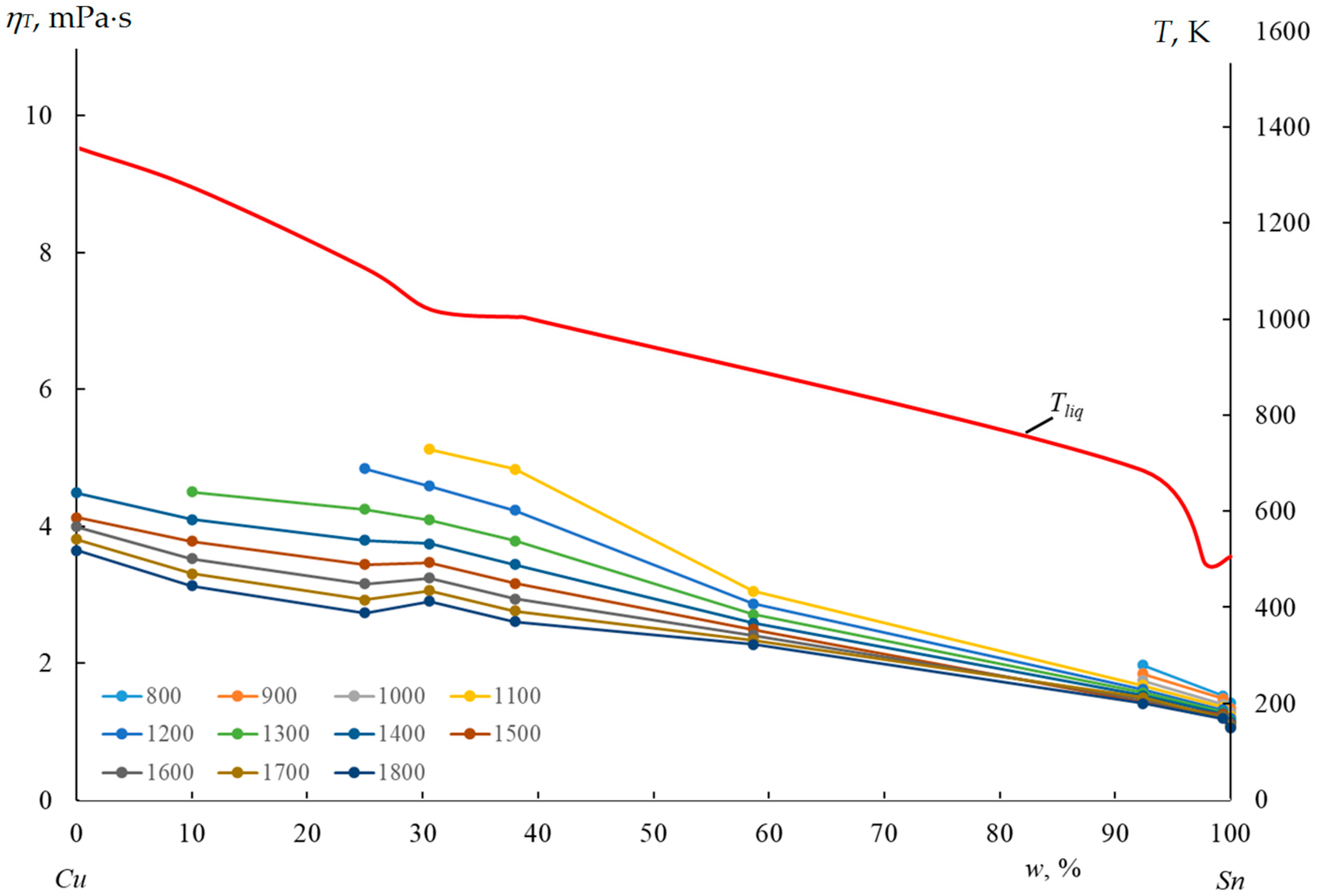
| N | Cu-Sn Alloy, w, % | A, mPa·s | Eν, J/mole | Tliq, K | ΔmixH, J/mole | ΔchH = RTliq + ΔmixH |
|---|---|---|---|---|---|---|
| 1 | Cu | 1.769 | 10,833.7 | 1356 | 0 | 11,274 |
| 2 | Cu-10% Sn | 1.219 | 14,116.8 | 1273 | 2300 | 12,884 |
| 3 | Cu-25% Sn | 0.874 | 17,080.8 | 1104 | 3900 | 13,079 |
| 4 | Cu-30.6% Sn | 1.187 | 13,373.8 | 1019 | 3950 | 12,422 |
| 5 | Cu-38% Sn | 0.988 | 14,151.8 | 1004 | 3200 | 11,548 |
| 6 | Cu-58.6% Sn | 1.436 | 6830.2 | 1004 | 900 | 9248 |
| 7 | Cu-92.4% Sn | 1.036 | 3953.8 | 684 | 30 | 5717 |
| 8 | Cu-99.3% Sn | 0.979 | 2963.0 | 490 | 10 | 4084 |
| 9 | Sn | 0.841 | 3488.8 | 505 | 0 | 4199 |
| N | , mPa·s | ηT, mPa·s, at T, K | Measurement Interval η, mPa·s | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 800 | 900 | 1000 | 1100 | 1200 | 1300 | 1400 | 1500 | 1600 | 1700 | 1800 | |||
| 1 | 4.624 | – | – | – | – | – | – | 4.489 4.449 | 4.129 4.093 | 3.776 3.994 | 3.492 3.807 | 3.237 3.648 | 4.0–4.7 |
| 2 | 4.626 | – | – | – | – | – | 4.507 4.500 | 4.123 4.099 | 3.782 3.781 | 3.480 3.523 | 3.212 3.309 | 2.971 3.131 | 3.8–4.7 |
| 3 | 5.619 | – | – | – | – | 5.081 4.842 | 4.599 4.244 | 4.180 3.791 | 3.812 3.438 | 3.489 3.156 | 3.204 2.926 | 2.952 2.736 | 4.5–6.3 |
| 4 | 5.754 | – | – | – | 5.245 5.123 | 4.708 4.585 | 4.245 4.091 | 3.844 3.743 | 3.485 3.469 | 3.190 3.244 | 2.923 3.058 | 2.687 2.901 | 4.3–5.8 |
| 5 | 5.383 | – | – | – | 5.036 4.831 | 4.516 4.232 | 4.069 3.784 | 3.682 3.438 | 3.346 3.164 | 3.053 2.942 | 2.796 2.759 | 2.569 2.606 | 4.1–5.8 |
| 6 | 3.255 | – | – | – | 2.916 3.050 | 2.615 2.865 | 2.356 2.716 | 2.132 2.586 | 1.938 2.495 | 1768 2410 | 1.619 2.358 | 1.487 2.276 | 3.0–3.7 |
| 7 | 2.076 | 1.803 1.968 | 1.548 1.842 | 1.341 1.743 | 1.171 1.673 | 1.031 1.614 | 0.914 1.566 | 0.816 1.525 | 0.733 1.491 | 0.661 1.468 | 0.600 1.496 | 0.546 1.414 | 1.8–2.1 |
| 8 | 2.026 | 1.059 1.528 | 0.890 1.485 | 0.758 1.398 | 0.652 1.354 | 0.568 1.318 | 0.498 1.288 | 0.440 1.263 | 0.392 1.242 | 0.351 1.223 | 0.307 1.207 | 0.287 1.193 | 1.65–2.0 |
| 9 | 4.624 | 1.057 1.421 | 0.890 1.340 | 0.798 1.279 | 0.654 1.232 | 0.569 1.193 | 0.500 1.161 | 0.442 1.135 | 0.394 1.112 | 0.354 1.093 | 0.319 1.076 | 0.289 1.062 | 1.5–1.9 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Issagulov, A.; Makasheva, A.; Malyshev, V.; Kvon, S.; Kulikov, V.; Bekbayeva, L.; Arinova, S. Development of a Partial Clustering Model of Alloy Viscosity. Appl. Sci. 2025, 15, 3601. https://doi.org/10.3390/app15073601
Issagulov A, Makasheva A, Malyshev V, Kvon S, Kulikov V, Bekbayeva L, Arinova S. Development of a Partial Clustering Model of Alloy Viscosity. Applied Sciences. 2025; 15(7):3601. https://doi.org/10.3390/app15073601
Chicago/Turabian StyleIssagulov, Aristotel, Astra Makasheva, Vitaliy Malyshev, Svetlana Kvon, Vitaliy Kulikov, Lazzat Bekbayeva, and Saniya Arinova. 2025. "Development of a Partial Clustering Model of Alloy Viscosity" Applied Sciences 15, no. 7: 3601. https://doi.org/10.3390/app15073601
APA StyleIssagulov, A., Makasheva, A., Malyshev, V., Kvon, S., Kulikov, V., Bekbayeva, L., & Arinova, S. (2025). Development of a Partial Clustering Model of Alloy Viscosity. Applied Sciences, 15(7), 3601. https://doi.org/10.3390/app15073601






