Accurate Rotor Temperature Prediction of Permanent Magnet Synchronous Motor in Electric Vehicles Using a Hybrid RIME-XGBoost Model
Abstract
:1. Introduction
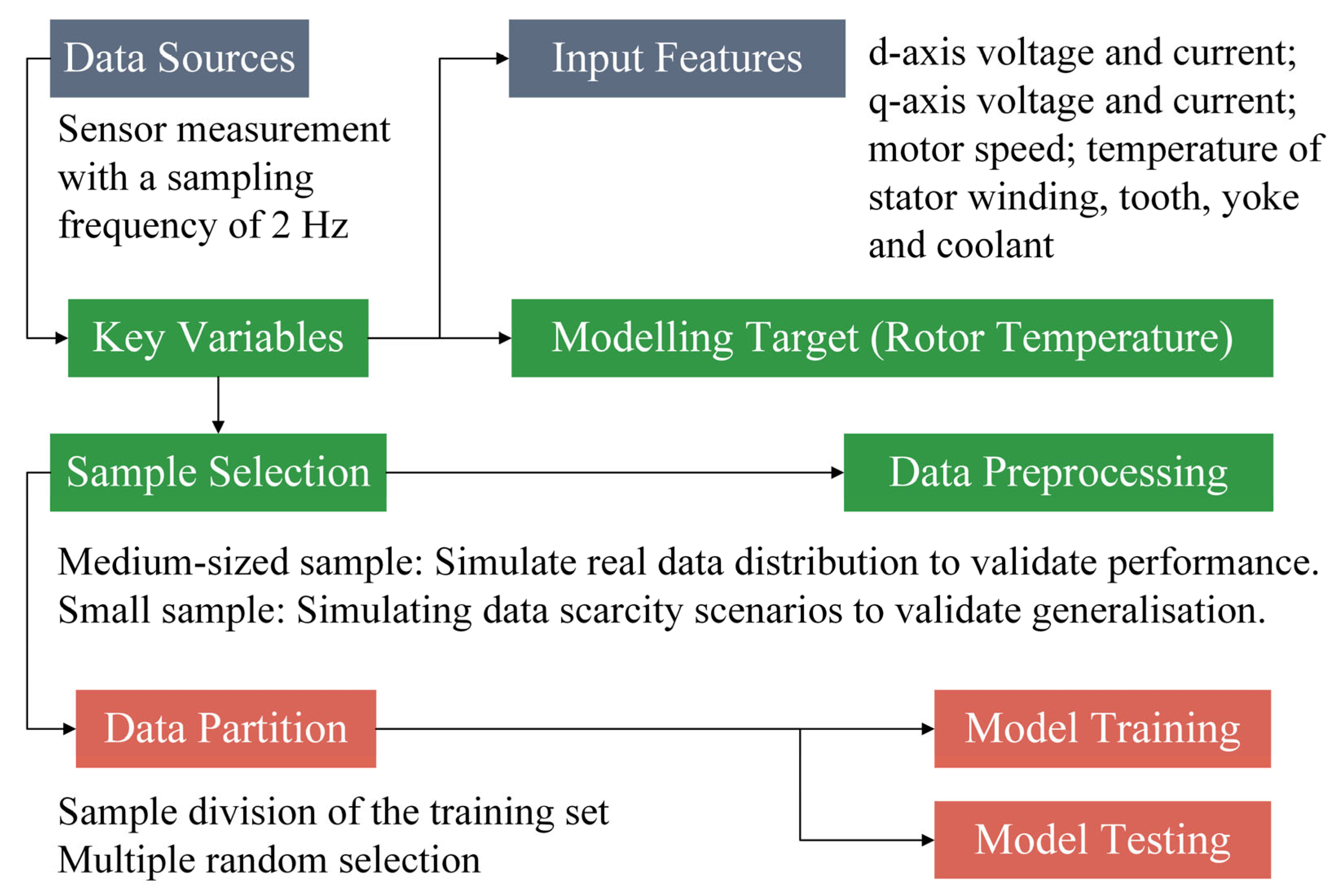
2. Data and Their Processing
2.1. Data Sources and Composition
2.2. Data Processing and Utilization
2.3. The Impact of Data Preprocessing on Model Performance
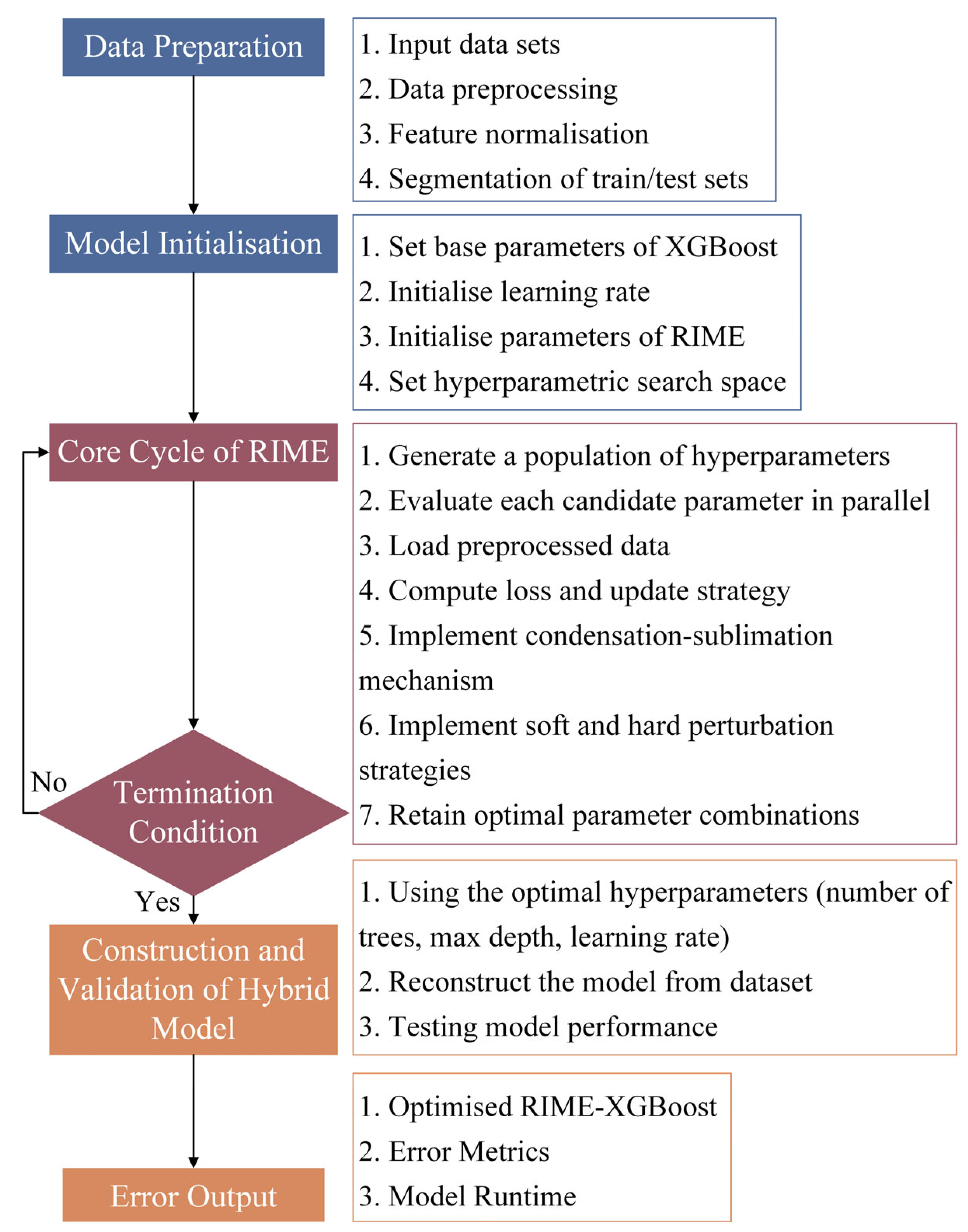
3. Algorithm Principles
3.1. Basic Principles of XGBoost
3.2. Introduction to RIME
3.3. RIME-Optimized XGBoost Hybrid Model
4. Comparative Study and Error Quantification
4.1. Comparative Methods
4.2. Error Measurement Metrics
5. Rotor Temperature Modeling and Prediction
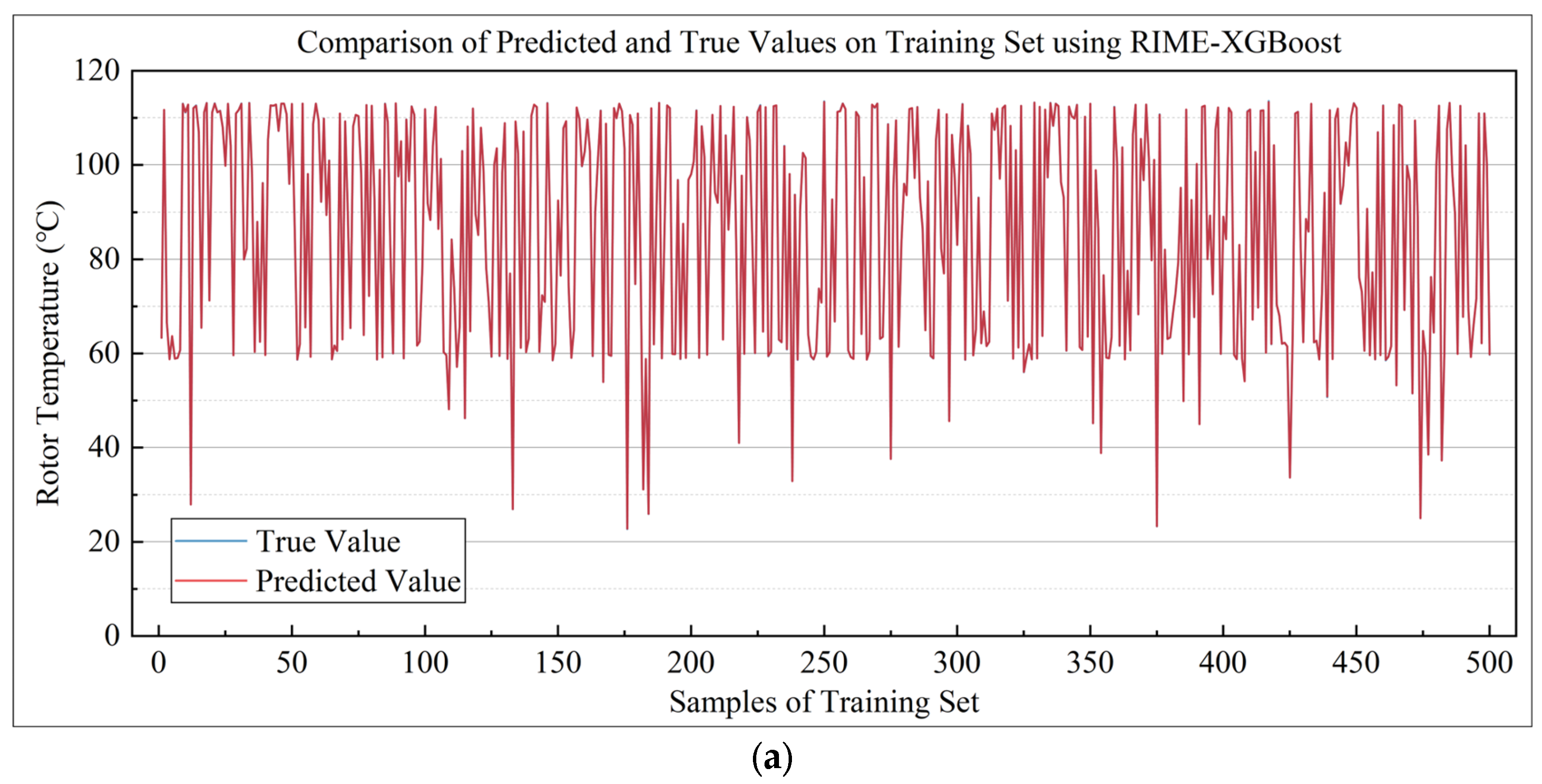
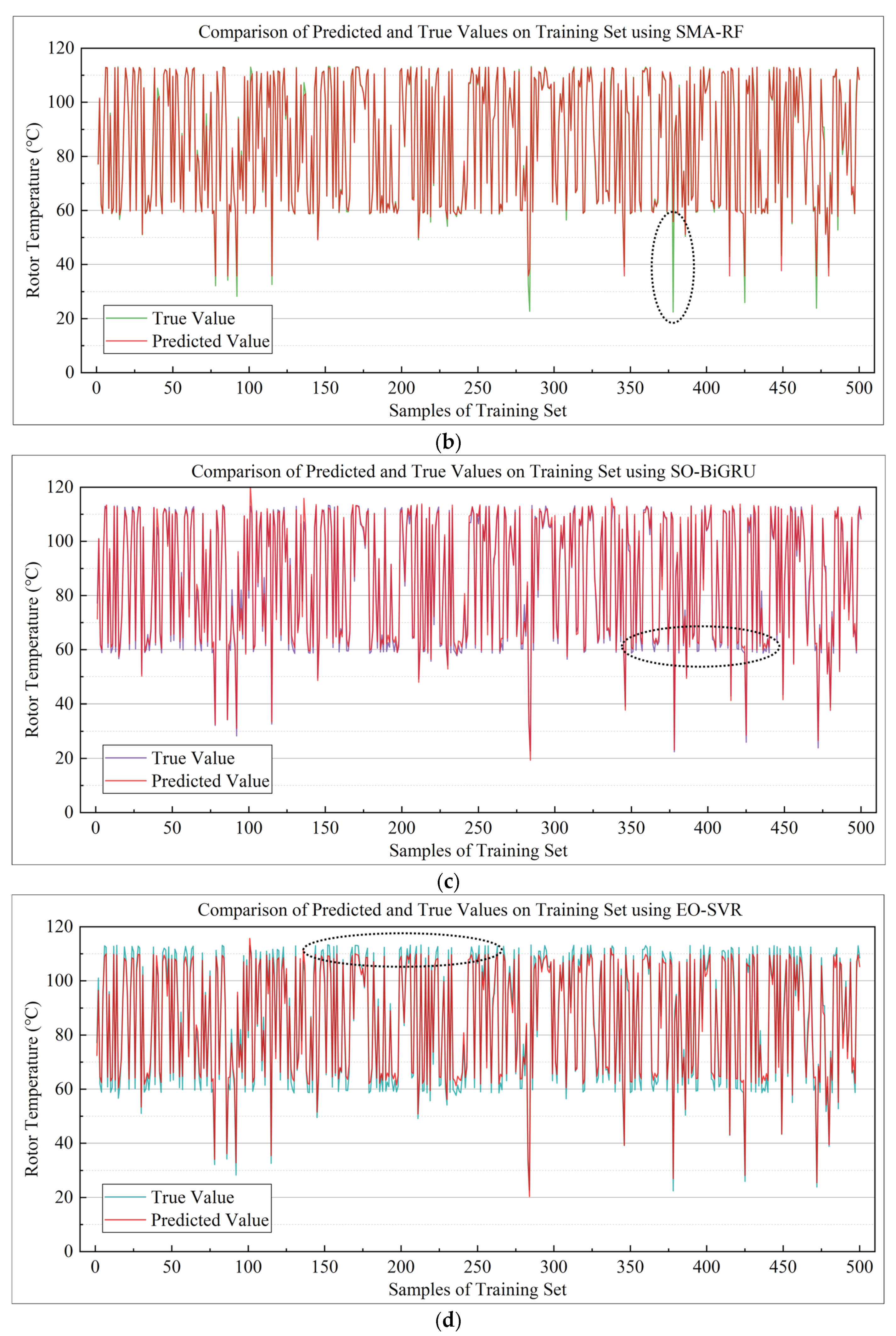
5.1. Rotor Temperature Prediction Experiment Under Medium-Sized Samples
5.2. Rotor Temperature Modeling and Prediction Under Small Samples
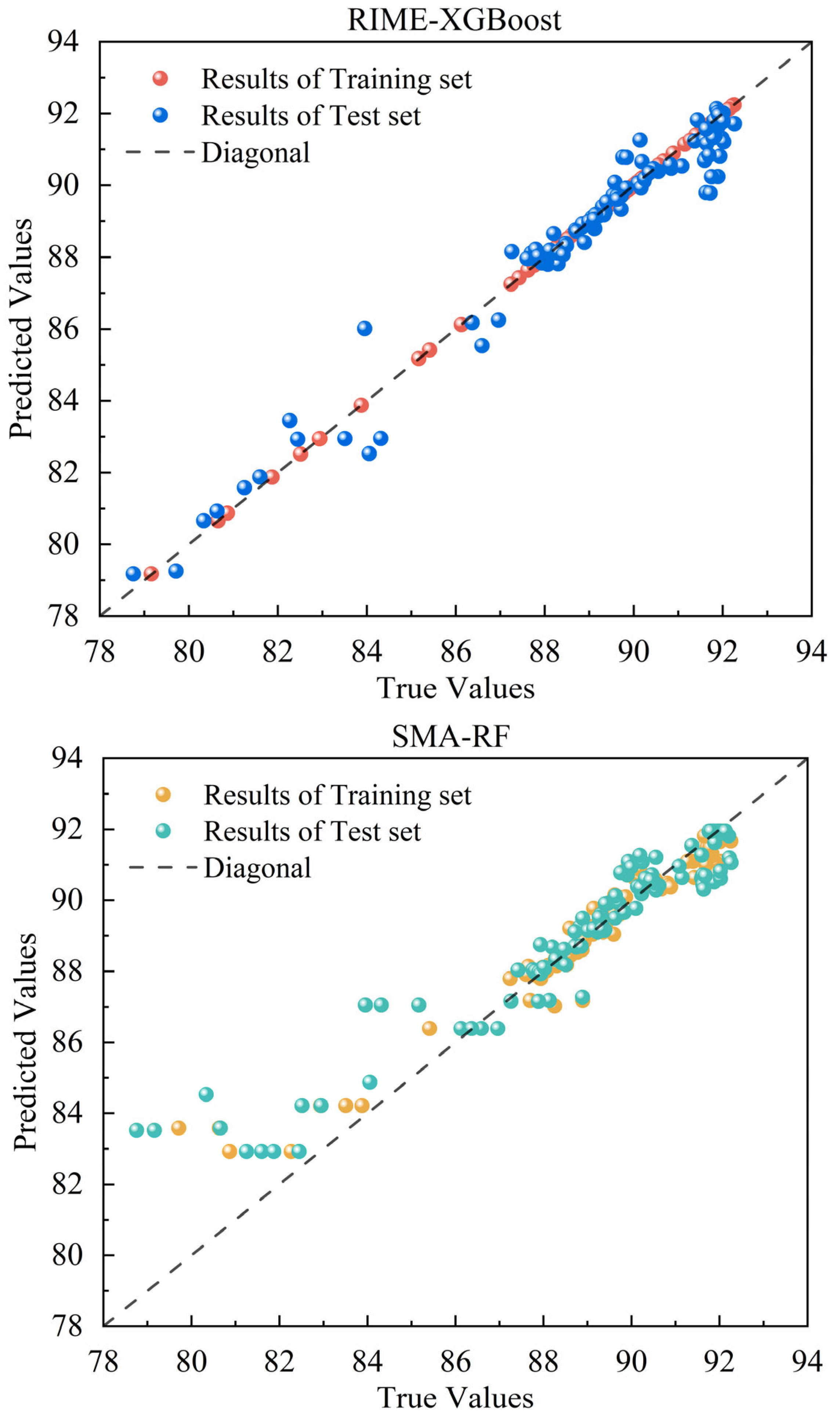
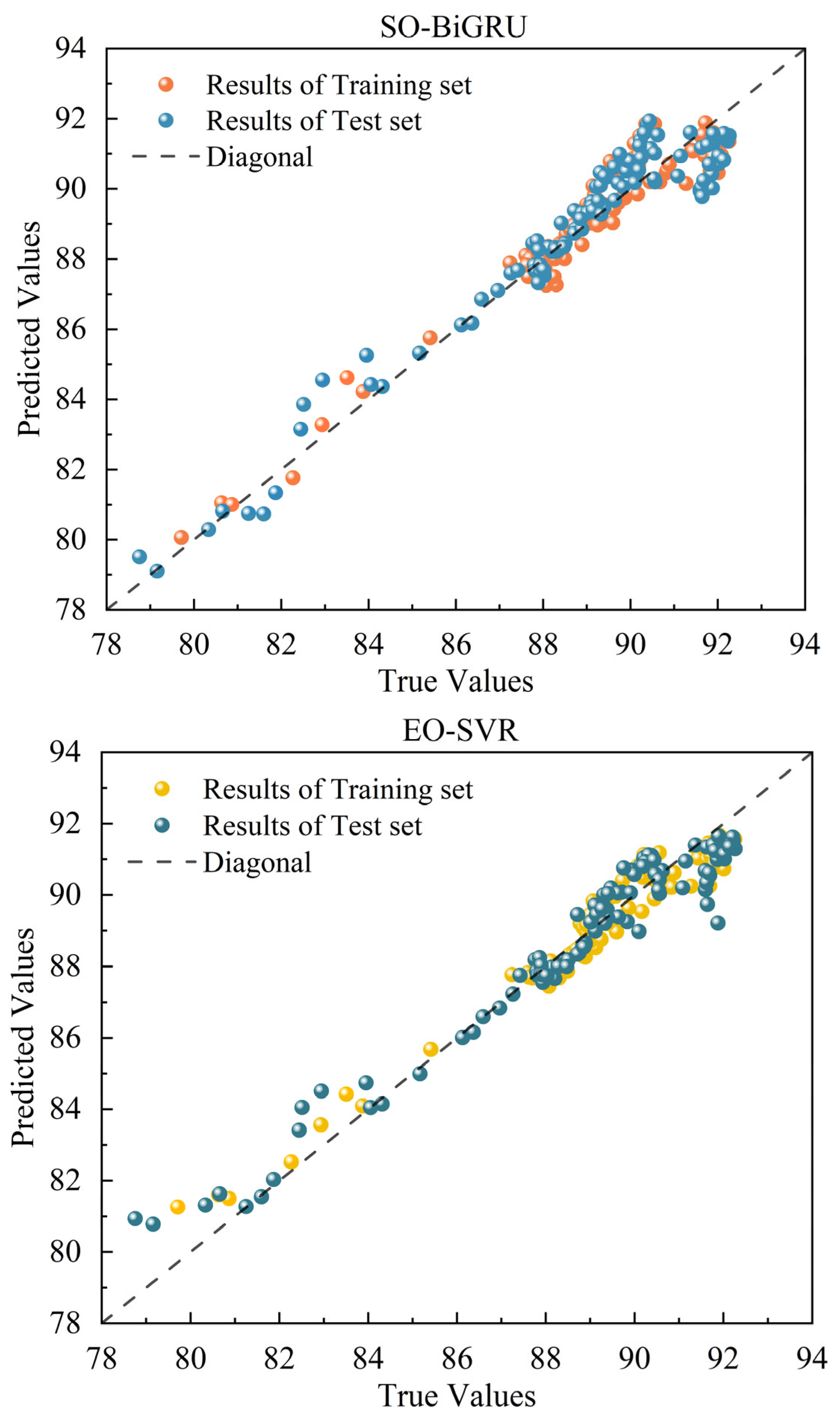
5.3. Performance Comparison Between RIME-XGBoost and Baseline XGBoost
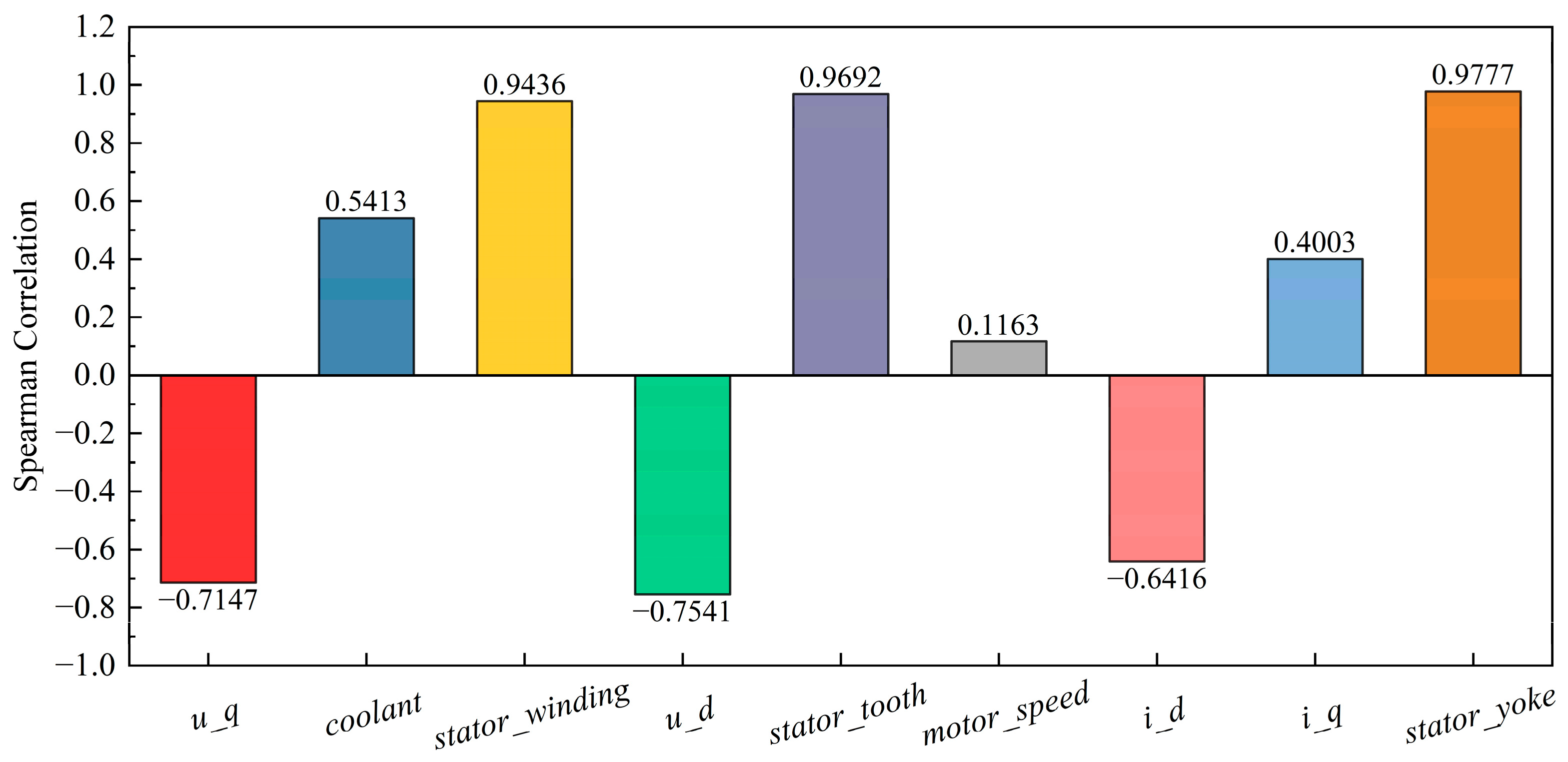
5.4. Spearman Correlation Analysis of Rotor Temperature Dependencies in PMSMs
5.5. Enhancement of Motor Optimization and Adaptability of RIME-XGBoost
5.6. In-Depth Discussion on Model Performance
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Littlejohn, C.; Proost, S. What Role for Electric Vehicles in the Decarbonization of the Car Transport Sector in Europe? Econ. Transp. 2022, 32, 100283. [Google Scholar] [CrossRef]
- Kubik, A.; Turoń, K.; Folęga, P.; Chen, F. CO2 Emissions—Evidence from Internal Combustion and Electric Engine Vehicles from Car-Sharing Systems. Energies 2023, 16, 2185. [Google Scholar] [CrossRef]
- Teng, Z.; Tan, C.; Liu, P.; Han, M. Analysis on Carbon Emission Reduction Intensity of Fuel Cell Vehicles from a Life-Cycle Perspective. Front. Energy 2024, 18, 16–27. [Google Scholar] [CrossRef]
- Ercan, T.; Onat, N.C.; Keya, N.; Tatari, O.; Eluru, N.; Kucukvar, M. Autonomous Electric Vehicles Can Reduce Carbon Emissions and Air Pollution in Cities. Transp. Res. Part D Transp. Environ. 2022, 112, 103472. [Google Scholar] [CrossRef]
- Akrami, M.; Jamshidpour, E.; Pierfederici, S.; Frick, V. Flatness-Based Trajectory Planning/Replanning for a Permanent Magnet Synchronous Machine Control. In Proceedings of the 2023 IEEE Transportation Electrification Conference & Expo (ITEC), Detroit, MI, USA, 21 June 2023; pp. 1–5. [Google Scholar]
- Song, Y.; Lu, J.; Hu, Y.; Wu, X.; Wang, G. Fast Calibration with Raw Data Verification for Current Measurement of Dual-PMSM Drives. IEEE Trans. Ind. Electron. 2024, 71, 6875–6885. [Google Scholar] [CrossRef]
- Rigatos, G.; Abbaszadeh, M.; Wira, P.; Siano, P. A Nonlinear Optimal Control Approach for Voltage Source Inverter-Fed Three-Phase PMSMs. In Proceedings of the IECON 2021—47th Annual Conference of the IEEE Industrial Electronics Society, Toronto, ON, Canada, 13 October 2021; pp. 1–6. [Google Scholar]
- Pandey, A.; Madduri, B.; Perng, C.-Y.; Srinivasan, C.; Dhar, S. Multiphase Flow and Heat Transfer in an Electric Motor. In Proceedings of the Volume 8: Fluids Engineering; Heat Transfer and Thermal Engineering. American Society of Mechanical Engineers: Columbus, OH, USA, 2022; p. V008T10A034. [Google Scholar]
- Liu, L.; Ding, S.; Liu, C.; Zhang, D.; Wang, Q. Electromagnetic Performance Analysis and Thermal Research of an Outer-rotor I-shaped Flux-switching Permanent-magnet Motor with Considering Driving Cycles. IET Electr. Power Appl. 2019, 13, 2052–2057. [Google Scholar] [CrossRef]
- Meiwei, Z.; Weili, L.; Haoyue, T. Demagnetization Fault Diagnosis of the Permanent Magnet Motor for Electric Vehicles Based on Temperature Characteristic Quantity. IEEE Trans. Transp. Electrif. 2023, 9, 759–770. [Google Scholar] [CrossRef]
- Lima, R.P.G.; Mauricio Villanueva, J.M.; Gomes, H.P.; Flores, T.K.S. Development of a Soft Sensor for Flow Estimation in Water Supply Systems Using Artificial Neural Networks. Sensors 2022, 22, 3084. [Google Scholar] [CrossRef]
- Ahmed, U.; Ali, F.; Jennions, I. Acoustic Monitoring of an Aircraft Auxiliary Power Unit. ISA Trans. 2023, 137, 670–691. [Google Scholar] [CrossRef]
- Gudur, B.R.; Poddar, G.; Muni, B.P. Parameter Sensitivity on the Performance of Sensor-Based Rotor Flux Oriented Vector Controlled Induction Machine Drive. Sādhanā 2023, 48, 169. [Google Scholar] [CrossRef]
- Hu, J.; Sun, Z.; Xin, Y.; Jia, M. Real-Time Prediction of Rotor Temperature with PMSMs for Electric Vehicles. Int. J. Therm. Sci. 2025, 208, 109516. [Google Scholar] [CrossRef]
- Kang, M.; Shi, T.; Guo, L.; Gu, X.; Xia, C. Thermal Analysis of the Cooling System with the Circulation between Rotor Holes of Enclosed PMSMs Based on Modified Models. Appl. Therm. Eng. 2022, 206, 118054. [Google Scholar] [CrossRef]
- Song, B.-K.; Chin, J.-W.; Kim, D.-M.; Hwang, K.-Y.; Lim, M.-S. Temperature Estimation Using Lumped-Parameter Thermal Network with Piecewise Stator-Housing Modules for Fault-Tolerant Brake Systems in Highly Automated Driving Vehicles. IEEE Trans. Intell. Transp. Syst. 2021, 22, 5819–5832. [Google Scholar] [CrossRef]
- Pereira, M.; Araújo, R.E. Model-Free Finite-Set Predictive Current Control with Optimal Cycle Time for a Switched Reluctance Motor. IEEE Trans. Ind. Electron. 2023, 70, 8355–8364. [Google Scholar] [CrossRef]
- Kumar, J.A.; Swaroopan, N.M.J.; Shanker, N.R. Prediction of Rotor Slot Size Variations in Induction Motor Using Polynomial Chirplet Transform and Regression Algorithms. Arab. J. Sci. Eng. 2023, 48, 6099–6109. [Google Scholar] [CrossRef]
- Ye, C.; Deng, C.; Yang, J.; Dai, Y.; Yu, D.; Zhang, J. Study on a Novel Hybrid Thermal Network of Homopolar Inductor Machine. IEEE Trans. Transp. Electrif. 2023, 9, 549–560. [Google Scholar] [CrossRef]
- Zhou, H.; Wang, X.; Zhao, W.; Liu, J.; Xing, Z.; Peng, Y. Rapid Prediction of Magnetic and Temperature Field Based on Hybrid Subdomain Method and Finite-Difference Method for the Interior Permanent Magnet Synchronous Motor. IEEE Trans. Transp. Electrif. 2024, 10, 6634–6651. [Google Scholar] [CrossRef]
- Bouziane, M.; Bouziane, A.; Naima, K.; Alkhafaji, M.A.; Afenyiveh, S.D.M.; Menni, Y. Enhancing Temperature and Torque Prediction in Permanent Magnet Synchronous Motors Using Deep Learning Neural Networks and BiLSTM RNNs. AIP Adv. 2024, 14, 105136. [Google Scholar] [CrossRef]
- Cuiping, L.; Pujia, C.; Shukang, C.; Feng, C. Research on Motor Iron Losses and Temperature Field Calculation for Mini Electric Vehicle. In Proceedings of the 2014 17th International Conference on Electrical Machines and Systems (ICEMS), Hangzhou, China, 22 October 2014; pp. 2380–2383. [Google Scholar]
- Ayvaz, S.; Alpay, K. Predictive Maintenance System for Production Lines in Manufacturing: A Machine Learning Approach Using IoT Data in Real-Time. Expert Syst. Appl. 2021, 173, 114598. [Google Scholar] [CrossRef]
- Kirchgassner, W.; Wallscheid, O.; Bocker, J. Data-Driven Permanent Magnet Temperature Estimation in Synchronous Motors with Supervised Machine Learning: A Benchmark. IEEE Trans. Energy Convers. 2021, 36, 2059–2067. [Google Scholar] [CrossRef]
- Zhang, X.; Hu, Y.; Zhang, J.; Xu, H.; Sun, J.; Li, S. Domain-Adversarial Adaptation Regression Model for IPMSM Permanent Magnet Temperature Estimation. IEEE Trans. Transp. Electrif. 2025, 11, 4383–4394. [Google Scholar] [CrossRef]
- Jing, H.; Chen, Z.; Wang, X.; Wang, X.; Ge, L.; Fang, G.; Xiao, D. Gradient Boosting Decision Tree for Rotor Temperature Estimation in Permanent Magnet Synchronous Motors. IEEE Trans. Power Electron. 2023, 38, 10617–10622. [Google Scholar] [CrossRef]
- Jing, H.; Xiao, D.; Wang, X.; Chen, Z.; Fang, G.; Guo, X. Temperature Estimation of Permanent Magnet Synchronous Motors Using Support Vector Regression. In Proceedings of the 2022 25th International Conference on Electrical Machines and Systems (ICEMS), Chiang Mai, Thailand, 29 November 2022; pp. 1–6. [Google Scholar]
- Zhang, Z.; Zhang, Y.; Wen, Y.; Ren, Y. Data-Driven XGBoost Model for Maximum Stress Prediction of Additive Manufactured Lattice Structures. Complex Intell. Syst. 2023, 9, 5881–5892. [Google Scholar] [CrossRef]
- Xu, H.-W.; Qin, W.; Sun, Y.-N. An Improved XGBoost Prediction Model for Multi-Batch Wafer Yield in Semiconductor Manufacturing. IFAC-PapersOnLine 2022, 55, 2162–2166. [Google Scholar] [CrossRef]
- Jin, R.; Huang, H.; Li, L.; Zuo, H.; Gan, L.; Ge, S.S.; Liu, Z. Artificial Intelligence Enabled Energy-Saving Drive Unit with Speed and Displacement Variable Pumps for Electro-Hydraulic Systems. IEEE Trans. Autom. Sci. Eng. 2024, 21, 3193–3204. [Google Scholar] [CrossRef]
- Li, D.; Zhu, D.; Tao, T.; Qu, J. Power Generation Prediction for Photovoltaic System of Hose-Drawn Traveler Based on Machine Learning Models. Processes 2023, 12, 39. [Google Scholar] [CrossRef]
- Pan, Z.; Fang, S. Torque Performance Improvement of Permanent Magnet Arc Motor Based on Two-Step Strategy. IEEE Trans. Ind. Inf. 2021, 17, 7523–7534. [Google Scholar] [CrossRef]
- Lin, B.; Wang, D.; Ni, Y.; Song, K.; Li, Y.; Sun, G. Temperature Prediction of Permanent Magnet Synchronous Motor Based on Data-Driven Approach. In Proceedings of the 2024 36th Chinese Control and Decision Conference (CCDC), Xi’an, China, 25 May 2024; pp. 3270–3275. [Google Scholar]
- Shimizu, Y.; Morimoto, S.; Sanada, M.; Inoue, Y. Using Machine Learning to Reduce Design Time for Permanent Magnet Volume Minimization in IPMSMs for Automotive Applications. IEEJ J. Ind. Appl. 2021, 10, 554–563. [Google Scholar] [CrossRef]
- Shimizu, Y. Efficiency Optimization Design That Considers Control of Interior Permanent Magnet Synchronous Motors Based on Machine Learning for Automotive Application. IEEE Access 2023, 11, 41–49. [Google Scholar] [CrossRef]
- Kirchgassner, W.; Wallscheid, O.; Bocker, J. Estimating Electric Motor Temperatures with Deep Residual Machine Learning. IEEE Trans. Power Electron. 2021, 36, 7480–7488. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. XGBoost: A Scalable Tree Boosting System. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco CA, USA, 13 August 2016; pp. 785–794. [Google Scholar]
- Su, H.; Zhao, D.; Heidari, A.A.; Liu, L.; Zhang, X.; Mafarja, M.; Chen, H. RIME: A Physics-Based Optimization. Neurocomputing 2023, 532, 183–214. [Google Scholar] [CrossRef]
- Khajavi, H.; Rastgoo, A. Predicting the Carbon Dioxide Emission Caused by Road Transport Using a Random Forest (RF) Model Combined by Meta-Heuristic Algorithms. Sustain. Cities Soc. 2023, 93, 104503. [Google Scholar] [CrossRef]
- Lei, W.; Gu, X.; Zhou, L. A Deep Learning Model Based on the Introduction of Attention Mechanism Is Used to Predict Lithium-Ion Battery SOC. J. Electrochem. Soc. 2024, 171, 070508. [Google Scholar] [CrossRef]
- Houssein, E.H.; Dirar, M.; Abualigah, L.; Mohamed, W.M. An Efficient Equilibrium Optimizer with Support Vector Regression for Stock Market Prediction. Neural Comput. Appl. 2022, 34, 3165–3200. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Schuster, M.; Paliwal, K.K. Bidirectional Recurrent Neural Networks. IEEE Trans. Signal Process. 1997, 45, 2673–2681. [Google Scholar] [CrossRef]
- Smola, A.J.; Schölkopf, B. A Tutorial on Support Vector Regression. Stat. Comput. 2004, 14, 199–222. [Google Scholar] [CrossRef]


| Variable Type | Variable | Description |
|---|---|---|
| Input Feature | u_q | The q-axis component of the voltage measured in the dq-coordinate system |
| coolant | The temperature of the coolant | |
| stator_winding | The temperature of the stator windings | |
| u_d | The d-axis component of the voltage | |
| stator_tooth | The temperature of the stator teeth | |
| motor_speed | The rotational speed of the motor | |
| i_d | The d-axis component of the current | |
| i_q | The q-axis component of the current | |
| stator_yoke | The temperature of the stator yoke | |
| Target | pm | The temperature of the permanent magnet |
| No. | Range | Count | No. | Range | Count | No. | Range | Count |
|---|---|---|---|---|---|---|---|---|
| 2 | 23.02 | 19,357 | 27 | 87.41 | 35,361 | 59 | 47.07 | 7475 |
| 3 | 6.26 | 19,248 | 29 | 75.60 | 21,358 | 60 | 49.64 | 14,543 |
| 4 | 76.47 | 33,424 | 30 | 30.39 | 23,863 | 61 | 31.82 | 14,516 |
| 5 | 14.05 | 14,788 | 31 | 78.07 | 15,587 | 62 | 53.21 | 25,600 |
| 6 | 69.16 | 40,388 | 32 | 67.13 | 20,960 | 63 | 44.21 | 16,668 |
| 7 | 10.79 | 14,651 | 36 | 26.01 | 22,609 | 64 | 43.03 | 6250 |
| 8 | 20.27 | 18,757 | 41 | 67.85 | 16,700 | 65 | 67.39 | 40,094 |
| 9 | 26.31 | 20,336 | 42 | 45.88 | 16,920 | 66 | 44.58 | 36,476 |
| 10 | 49.15 | 15,256 | 43 | 41.02 | 8443 | 67 | 39.69 | 11,135 |
| 11 | 32.88 | 7887 | 44 | 51.75 | 26,341 | 68 | 58.01 | 23,331 |
| 12 | 23.76 | 21,942 | 45 | 63.36 | 17,142 | 69 | 59.07 | 15,350 |
| 13 | 10.85 | 35,906 | 46 | 14.83 | 2180 | 70 | 42.50 | 25,677 |
| 14 | 36.00 | 18,598 | 48 | 33.44 | 21,983 | 71 | 54.60 | 14,656 |
| 15 | 72.79 | 18,124 | 49 | 42.17 | 10,816 | 72 | 41.07 | 15,301 |
| 16 | 23.15 | 20,645 | 50 | 41.19 | 10,810 | 73 | 63.41 | 16,786 |
| 17 | 45.32 | 15,964 | 51 | 52.88 | 6261 | 74 | 29.04 | 23,761 |
| 18 | 15.39 | 37,732 | 52 | 28.76 | 3726 | 75 | 70.31 | 13,472 |
| 19 | 72.31 | 10,410 | 53 | 37.90 | 32,442 | 76 | 51.12 | 22,188 |
| 20 | 82.41 | 43,971 | 54 | 47.44 | 10,807 | 78 | 46.76 | 8445 |
| 21 | 70.65 | 17,321 | 55 | 52.71 | 10,807 | 79 | 71.60 | 31,154 |
| 23 | 74.11 | 11,856 | 56 | 43.60 | 33,123 | 80 | 58.49 | 23,824 |
| 24 | 91.67 | 15,015 | 57 | 62.35 | 14,403 | 81 | 52.65 | 17,672 |
| 26 | 71.56 | 16,666 | 58 | 54.84 | 33,382 | / | / | / |
| Name (Abbreviation) | Advantages of Hybrid Modeling | Hyperparameter |
|---|---|---|
| SMA-RF | Reduce computational cost and improve generalization ability | Number of decision trees: [10, 300] Minimum number of leaf nodes: [10, 300] |
| SO-BiGRU | Enhance prediction accuracy and generalization ability and accelerate model convergence | Initial learning rate: [1 × 10−4, 1 × 10−1] Number of neurons in GRU layer: [3, 50] L2 regularization parameter: [1 × 10−6, 1 × 10−2] |
| EO-SVR | Escape local optima and better balance model complexity and fitting error | Penalty factor: [1, 2000] Radial basis function kernel parameter: [1 × 10−2, 10] |
| RIME-XGBoost | SMA-RF | SO-BiGRU | EO-SVR | |
|---|---|---|---|---|
| Population | 20 | 20 | 10 | 30 |
| Iteration | 20 | 30 | 5 | 50 |
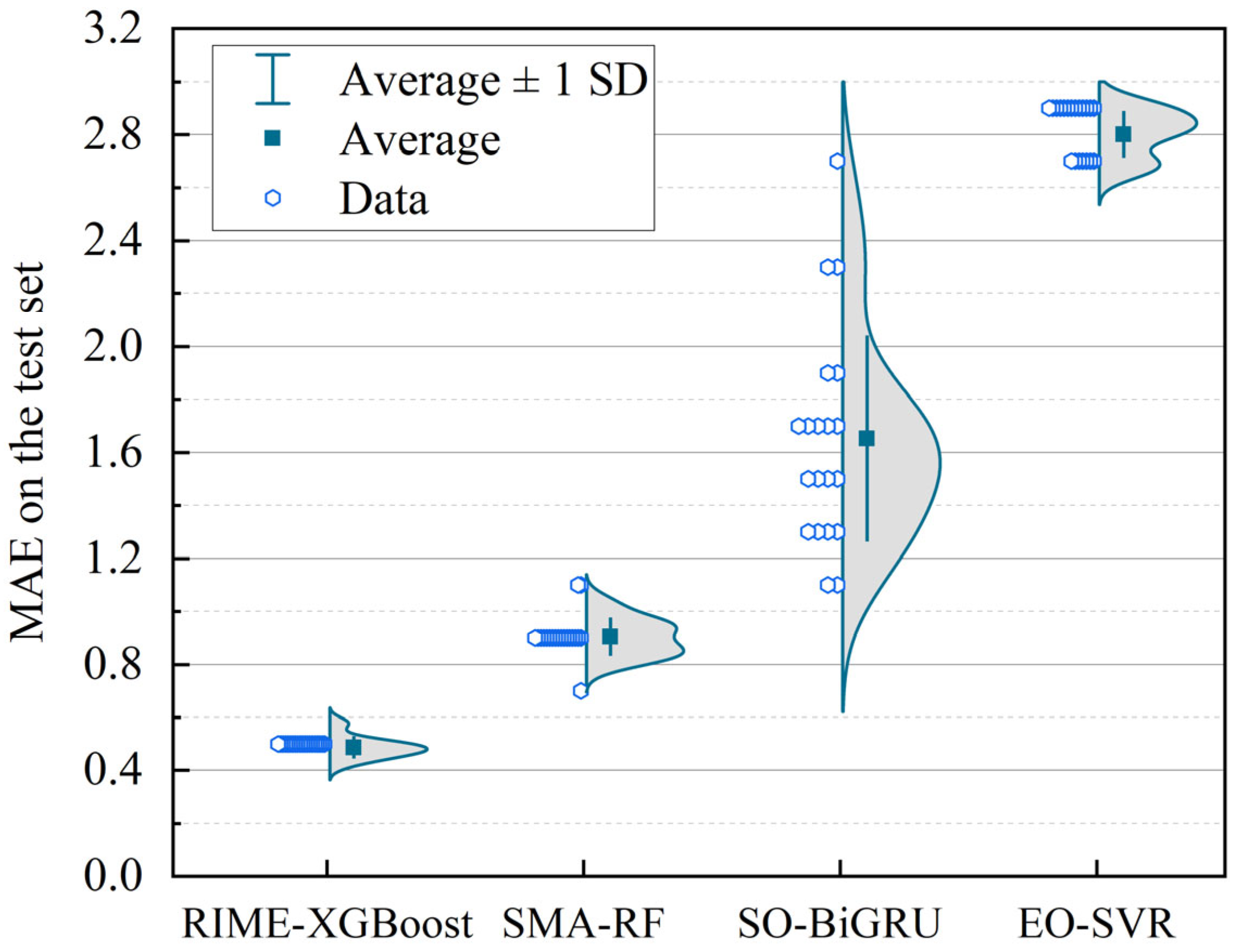
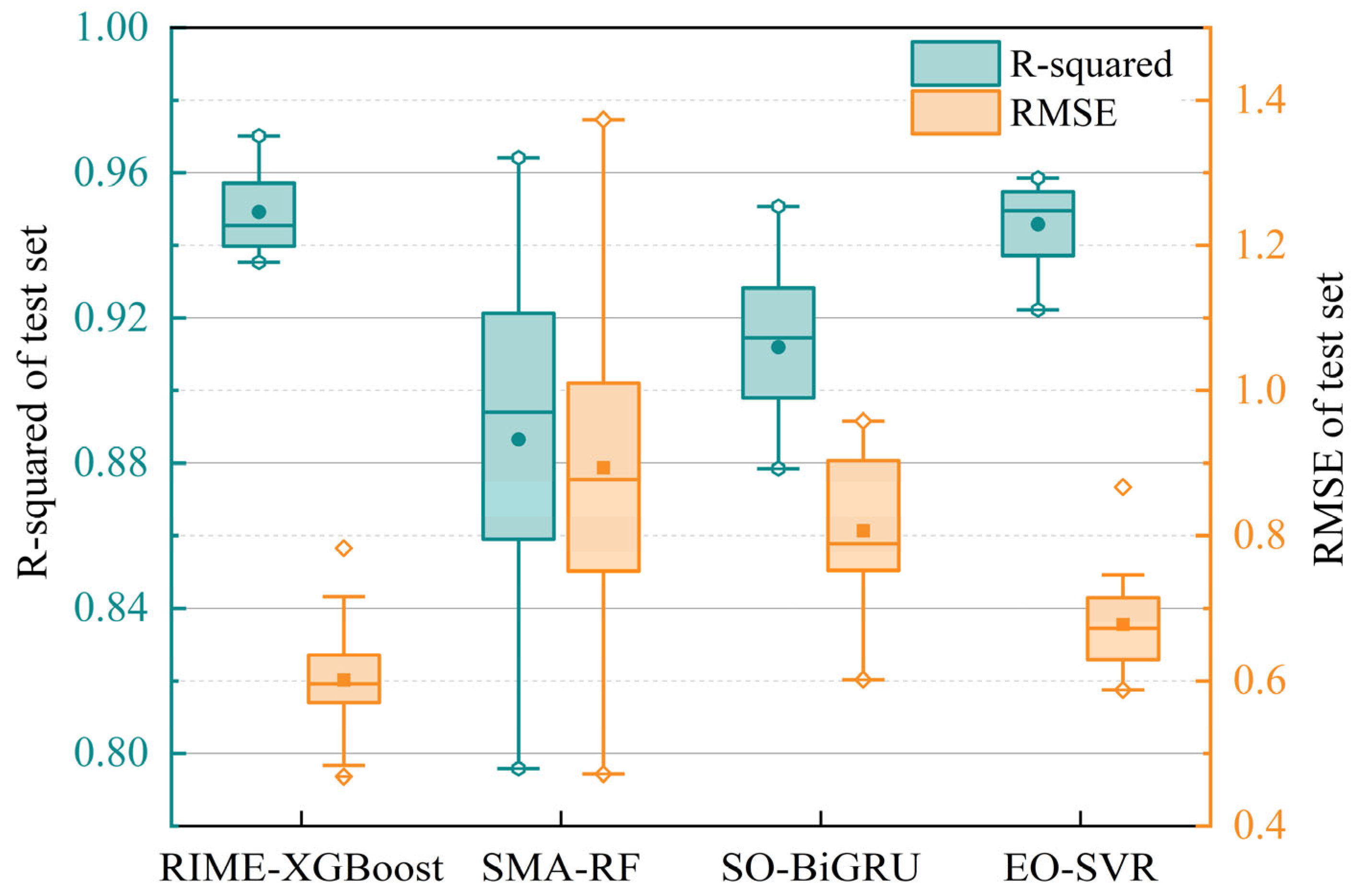
| Model | Stage | Error | Average | Median | Standard Deviation |
|---|---|---|---|---|---|
| RIME-XGBoost | Train | RMSE | 0.0440 | 0.0442 | 0.0016 |
| MSE | 0.0019 | 0.0020 | 0.0001 | ||
| MAE | 0.0318 | 0.0321 | 0.0013 | ||
| MBE | 2.84 × 10−5 | 9.42 × 10−6 | 5.53 × 10−5 | ||
| R-squared | 0.9999 | 0.9999 | 2.17 × 10−7 | ||
| Test | RMSE | 1.1555 | 1.0298 | 0.4079 | |
| MSE | 1.5016 | 1.0605 | 1.1670 | ||
| MAE | 0.4864 | 0.4782 | 0.0410 | ||
| MBE | −0.0227 | −0.0185 | 0.0478 | ||
| R-squared | 0.9972 | 0.9981 | 0.0021 | ||
| Total | Runtime | 52.9506 | 51.3548 | 4.9756 | |
| SMA-RF | Train | RMSE | 1.7814 | 1.7963 | 0.2987 |
| MSE | 3.2625 | 3.2269 | 1.0684 | ||
| MAE | 0.7109 | 0.7136 | 0.0706 | ||
| MBE | 0.0456 | 0.0463 | 0.0364 | ||
| R-squared | 0.9940 | 0.9942 | 0.0020 | ||
| Test | RMSE | 2.2036 | 2.0456 | 0.3157 | |
| MSE | 4.9554 | 4.1855 | 1.4704 | ||
| MAE | 0.9034 | 0.8913 | 0.0705 | ||
| MBE | 0.0689 | 0.0787 | 0.0936 | ||
| R-squared | 0.9909 | 0.9923 | 0.0027 | ||
| Total | Runtime | 28.3762 | 28.5778 | 1.8633 | |
| SO-BiGRU | Train | RMSE | 1.9903 | 2.0787 | 0.4596 |
| MSE | 4.1726 | 4.3210 | 2.0399 | ||
| MAE | 1.4642 | 1.4852 | 0.3535 | ||
| MBE | −0.0946 | −0.0334 | 0.4265 | ||
| R-squared | 0.9923 | 0.9920 | 0.0037 | ||
| Test | RMSE | 4.4236 | 3.4068 | 3.1639 | |
| MSE | 29.5780 | 11.6067 | 47.3067 | ||
| MAE | 1.6525 | 1.6125 | 0.3797 | ||
| MBE | −0.0933 | −0.0437 | 0.4356 | ||
| R-squared | 0.9457 | 0.9785 | 0.0867 | ||
| Total | Runtime | 302.5257 | 297.2967 | 17.3790 | |
| EO-SVR | Train | RMSE | 2.9917 | 3.0152 | 0.1205 |
| MSE | 8.9648 | 9.0911 | 0.7025 | ||
| MAE | 2.7001 | 2.7252 | 0.1351 | ||
| MBE | 0.0658 | 0.0417 | 0.1639 | ||
| R-squared | 0.9897 | 0.9898 | 0.0008 | ||
| Test | RMSE | 3.5104 | 3.3311 | 0.5031 | |
| MSE | 12.5763 | 11.0971 | 3.7286 | ||
| MAE | 2.8003 | 2.8138 | 0.0863 | ||
| MBE | 0.0854 | 0.1177 | 0.1648 | ||
| R-squared | 0.9835 | 0.9878 | 0.0074 | ||
| Total | Runtime | 25.1217 | 24.3481 | 2.4326 |
| RIME-XGBoost | SMA-RF | SO-BiGRU | EO-SVR | |
|---|---|---|---|---|
| Population | 20 | 50 | 10 | 30 |
| Iteration | 20 | 50 | 10 | 50 |
| Model | Stage | Error | Average | Median | Standard Deviation |
|---|---|---|---|---|---|
| RIME-XGBoost | Train | RMSE | 0.0068 | 0.0068 | 0.0004 |
| MSE | 0.0000 | 0.0000 | 0.0000 | ||
| MAE | 0.0050 | 0.0050 | 0.0003 | ||
| MBE | 1.23 × 10−6 | −1.04 × 10−6 | 7.08 × 10−6 | ||
| R-squared | 0.9999 | 0.9999 | 1.09 × 10−6 | ||
| Test | RMSE | 0.6010 | 0.5960 | 0.0741 | |
| MSE | 0.3667 | 0.3553 | 0.0913 | ||
| MAE | 0.4020 | 0.4015 | 0.0429 | ||
| MBE | 0.0149 | 0.0180 | 0.0748 | ||
| R-squared | 0.9491 | 0.9455 | 0.0107 | ||
| Total | Runtime | 47.4799 | 47.3804 | 1.5684 | |
| SMA-RF | Train | RMSE | 0.6295 | 0.5911 | 0.1417 |
| MSE | 0.4163 | 0.3494 | 0.2044 | ||
| MAE | 0.3941 | 0.3716 | 0.0773 | ||
| MBE | 0.0322 | 0.0217 | 0.0382 | ||
| R-squared | 0.9427 | 0.9504 | 0.0273 | ||
| Test | RMSE | 0.8937 | 0.8773 | 0.2180 | |
| MSE | 0.8463 | 0.7697 | 0.4081 | ||
| MAE | 0.6043 | 0.5951 | 0.1177 | ||
| MBE | 0.0508 | 0.0241 | 0.1763 | ||
| R-squared | 0.8865 | 0.8941 | 0.0486 | ||
| Total | Runtime | 47.0174 | 46.6430 | 6.1770 | |
| SO-BiGRU | Train | RMSE | 0.7036 | 0.6963 | 0.0818 |
| MSE | 0.5018 | 0.4849 | 0.1143 | ||
| MAE | 0.5591 | 0.5705 | 0.0754 | ||
| MBE | 0.0014 | 0.0008 | 0.0030 | ||
| R-squared | 0.9302 | 0.9294 | 0.0165 | ||
| Test | RMSE | 0.8069 | 0.7890 | 0.0914 | |
| MSE | 0.6594 | 0.6225 | 0.1459 | ||
| MAE | 0.6409 | 0.6314 | 0.0734 | ||
| MBE | 0.0087 | 0.0150 | 0.1145 | ||
| R-squared | 0.9119 | 0.9146 | 0.0214 | ||
| Total | Runtime | 176.0875 | 176.1744 | 1.4659 | |
| EO-SVR | Train | RMSE | 0.5598 | 0.5539 | 0.0282 |
| MSE | 0.3142 | 0.3068 | 0.0318 | ||
| MAE | 0.4820 | 0.4756 | 0.0286 | ||
| MBE | −0.0647 | −0.0602 | 0.0339 | ||
| R-squared | 0.9588 | 0.9582 | 0.0066 | ||
| Test | RMSE | 0.6777 | 0.6722 | 0.0639 | |
| MSE | 0.4634 | 0.4519 | 0.0908 | ||
| MAE | 0.5435 | 0.5429 | 0.0377 | ||
| MBE | −0.0631 | −0.0637 | 0.0992 | ||
| R-squared | 0.9458 | 0.9495 | 0.0109 | ||
| Total | Runtime | 6.2627 | 6.2731 | 0.6984 |
| Model | Number of Trees | Tree Depth | Learning Rate |
|---|---|---|---|
| XGBoost-Alpha | 50 | 5 | 0.05 |
| XGBoost-Beta | 300 | 15 | 0.005 |
| Model | Stage | Error | Average | Median | Standard Deviation |
|---|---|---|---|---|---|
| RIME-XGBoost | Train | RMSE | 0.0440 | 0.0442 | 0.0016 |
| MSE | 0.0019 | 0.0020 | 0.0001 | ||
| MAE | 0.0318 | 0.0321 | 0.0013 | ||
| MBE | 2.84 × 10−5 | 9.42 × 10−6 | 5.53 × 10−5 | ||
| R-squared | 0.9999 | 0.9999 | 2.17 × 10−7 | ||
| Test | RMSE | 1.1555 | 1.0298 | 0.4079 | |
| MSE | 1.5016 | 1.0605 | 1.1670 | ||
| MAE | 0.4864 | 0.4782 | 0.0410 | ||
| MBE | −0.0227 | −0.0185 | 0.0478 | ||
| R-squared | 0.9972 | 0.9981 | 0.0021 | ||
| Total | Runtime | 52.9506 | 51.3548 | 4.9756 | |
| XGBoost-Alpha | Train | RMSE | 2.3286 | 2.3308 | 0.0623 |
| MSE | 5.4261 | 5.4325 | 0.2887 | ||
| MAE | 1.9056 | 1.9028 | 0.0614 | ||
| MBE | 1.3008 | 1.3051 | 0.0903 | ||
| R-squared | 0.9900 | 0.9901 | 0.0005 | ||
| Test | RMSE | 2.7128 | 2.6569 | 0.2273 | |
| MSE | 7.4084 | 7.0594 | 1.2525 | ||
| MAE | 2.0269 | 2.0355 | 0.0432 | ||
| MBE | 1.2814 | 1.3351 | 0.1039 | ||
| R-squared | 0.9863 | 0.9870 | 0.0023 | ||
| Total | Runtime | 0.5361 | 0.3879 | 0.6124 | |
| XGBoost-Beta | Train | RMSE | 6.7034 | 6.6945 | 0.1096 |
| MSE | 44.9465 | 44.8168 | 1.4738 | ||
| MAE | 5.5201 | 5.5063 | 0.1260 | ||
| MBE | 3.9315 | 3.9234 | 0.1789 | ||
| R-squared | 0.9171 | 0.9172 | 0.0032 | ||
| Test | RMSE | 6.9004 | 6.8938 | 0.0993 | |
| MSE | 47.6243 | 47.5249 | 1.3725 | ||
| MAE | 5.6420 | 5.6478 | 0.0485 | ||
| MBE | 3.9833 | 3.9951 | 0.0793 | ||
| R-squared | 0.9122 | 0.9124 | 0.0024 | ||
| Total | Runtime | 0.5342 | 0.3799 | 0.6368 |
| Model | Stage | Error | Average | Median | Standard Deviation |
|---|---|---|---|---|---|
| RIME-XGBoost | Train | RMSE | 0.0068 | 0.0068 | 0.0004 |
| MSE | 0.0000 | 0.0000 | 0.0000 | ||
| MAE | 0.0050 | 0.0050 | 0.0003 | ||
| MBE | 1.23 × 10−6 | −1.04 × 10−6 | 7.08 × 10−6 | ||
| R-squared | 0.9999 | 0.9999 | 1.09 × 10−6 | ||
| Test | RMSE | 0.6010 | 0.5960 | 0.0741 | |
| MSE | 0.3667 | 0.3553 | 0.0913 | ||
| MAE | 0.4020 | 0.4015 | 0.0429 | ||
| MBE | 0.0149 | 0.0180 | 0.0748 | ||
| R-squared | 0.9491 | 0.9455 | 0.0107 | ||
| Total | Runtime | 47.4799 | 47.3804 | 1.5684 | |
| XGBoost-Alpha | Train | RMSE | 0.4443 | 0.4456 | 0.0251 |
| MSE | 0.1980 | 0.1986 | 0.0223 | ||
| MAE | 0.3575 | 0.3636 | 0.0229 | ||
| MBE | 0.2488 | 0.2526 | 0.0185 | ||
| R-squared | 0.9748 | 0.9753 | 0.0032 | ||
| Test | RMSE | 0.8240 | 0.7992 | 0.1017 | |
| MSE | 0.6888 | 0.6387 | 0.1770 | ||
| MAE | 0.6192 | 0.6087 | 0.0553 | ||
| MBE | 0.2720 | 0.2871 | 0.0990 | ||
| R-squared | 0.8977 | 0.9047 | 0.0177 | ||
| Total | Runtime | 0.3359 | 0.3276 | 0.0292 | |
| XGBoost-Beta | Train | RMSE | 1.0984 | 1.1127 | 0.0642 |
| MSE | 1.2104 | 1.2381 | 0.1367 | ||
| MAE | 0.9745 | 0.9871 | 0.0634 | ||
| MBE | 0.7655 | 0.7684 | 0.0599 | ||
| R-squared | 0.8373 | 0.8377 | 0.0184 | ||
| Test | RMSE | 1.2480 | 1.2134 | 0.1456 | |
| MSE | 1.5777 | 1.4723 | 0.3938 | ||
| MAE | 1.0448 | 1.0288 | 0.0958 | ||
| MBE | 0.7317 | 0.7591 | 0.1560 | ||
| R-squared | 0.7830 | 0.7918 | 0.0429 | ||
| Total | Runtime | 0.4117 | 0.2716 | 0.6223 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shan, J.; Che, Z.; Liu, F. Accurate Rotor Temperature Prediction of Permanent Magnet Synchronous Motor in Electric Vehicles Using a Hybrid RIME-XGBoost Model. Appl. Sci. 2025, 15, 3688. https://doi.org/10.3390/app15073688
Shan J, Che Z, Liu F. Accurate Rotor Temperature Prediction of Permanent Magnet Synchronous Motor in Electric Vehicles Using a Hybrid RIME-XGBoost Model. Applied Sciences. 2025; 15(7):3688. https://doi.org/10.3390/app15073688
Chicago/Turabian StyleShan, Jianzhao, Zhongyuan Che, and Fengbin Liu. 2025. "Accurate Rotor Temperature Prediction of Permanent Magnet Synchronous Motor in Electric Vehicles Using a Hybrid RIME-XGBoost Model" Applied Sciences 15, no. 7: 3688. https://doi.org/10.3390/app15073688
APA StyleShan, J., Che, Z., & Liu, F. (2025). Accurate Rotor Temperature Prediction of Permanent Magnet Synchronous Motor in Electric Vehicles Using a Hybrid RIME-XGBoost Model. Applied Sciences, 15(7), 3688. https://doi.org/10.3390/app15073688







