Deflection Modeling and Curvature Manipulation of a Variable-Stiffness Flexible Needle
Abstract
1. Introduction
2. Materials and Methods
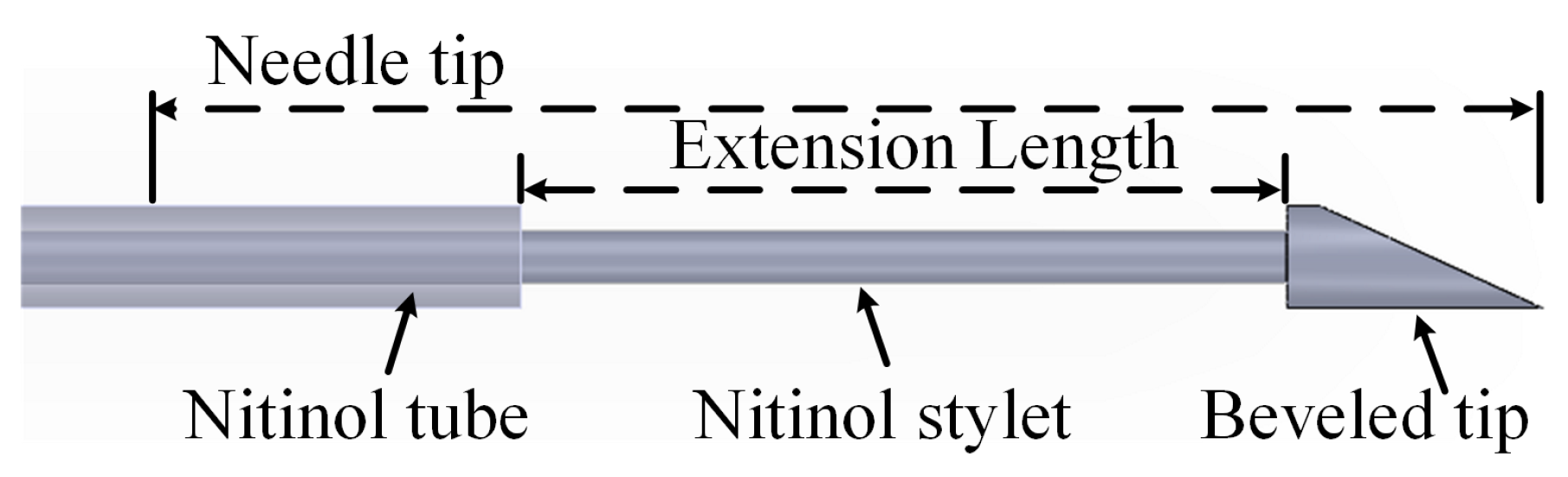
2.1. Design of the Stiffness-Tunable Needle
- Within certain limits, a thicker tip on the flexible needle results in greater extrusion deformation of the soft tissue after cutting. That means a greater deflection force, which the soft tissue can provide.
- A sharper flexible needle tip with a larger bevel will displace more tissue and generate a greater reaction force on the tip.
- If the body of the needle is too stiff or too thin, or if the tissue is unable to support the traversal of the body, it can slice through the tissue.
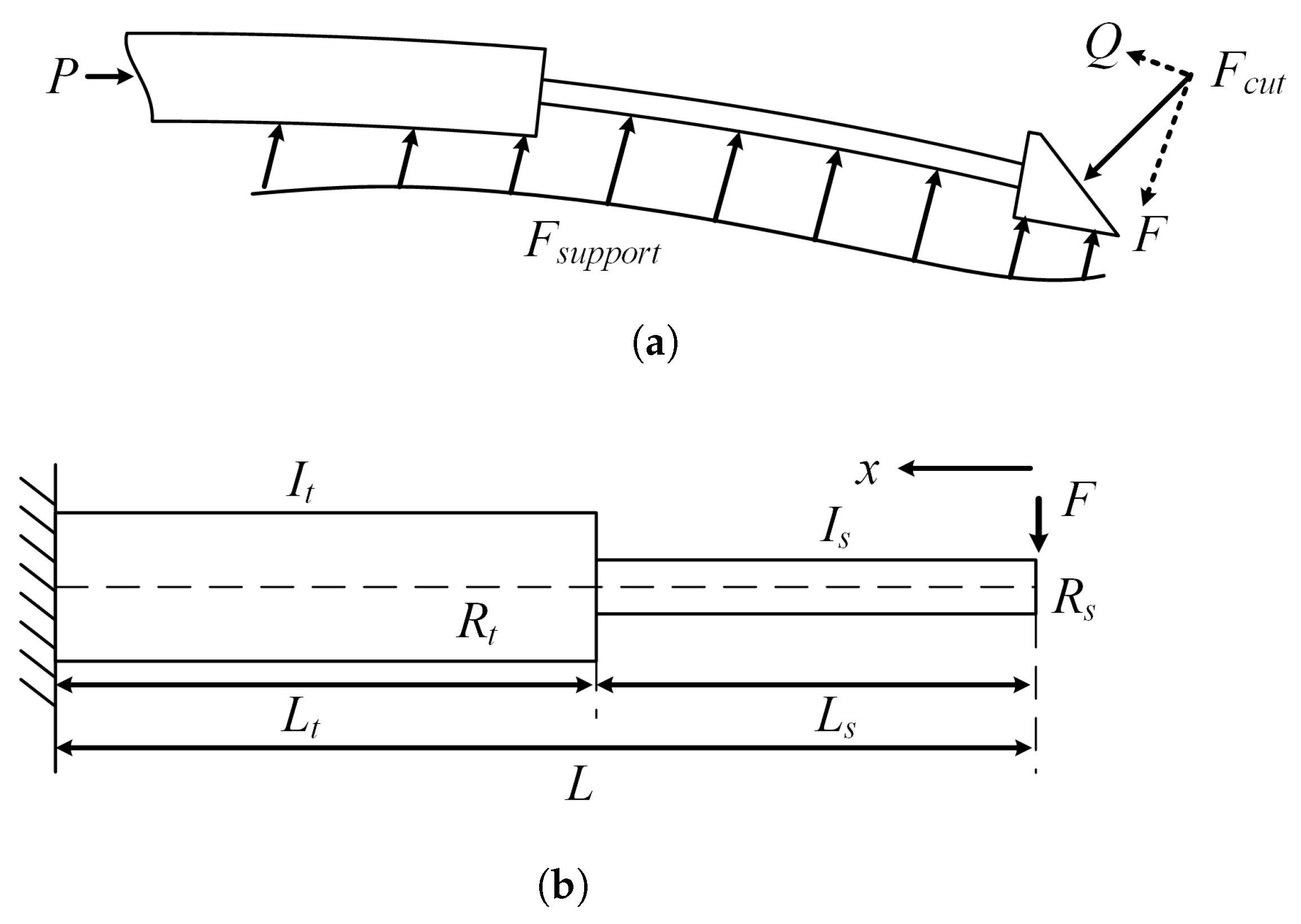
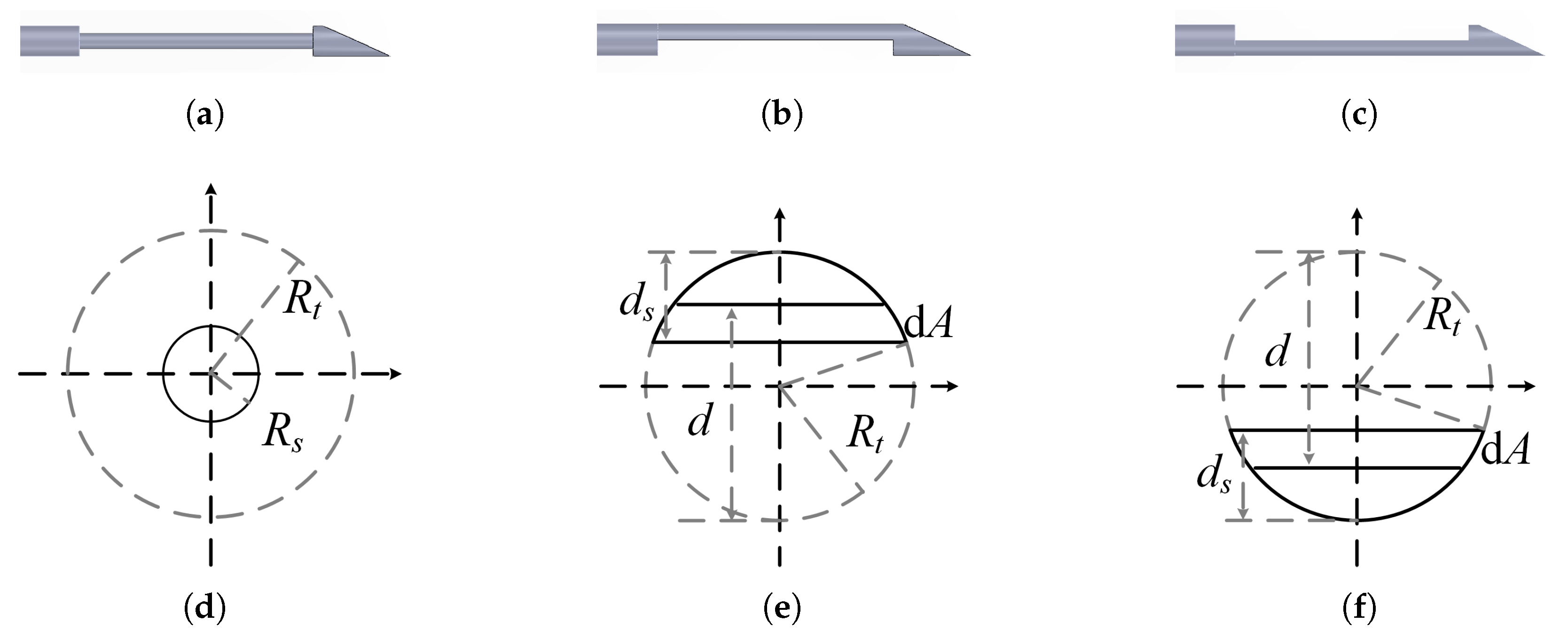
2.2. Model Analysis of Flexible Needle
- The beveled tip is designed to generate an asymmetric deflection force. In fact, it is possible to make the beveled tip very short without compromising the deflection force. Compared to the needle tip, which is several centimeters long, the beveled tip is relatively short (as short as 3 mm), and its effect on beam deflection is negligible.
- The variable-stiffness needle bends because the extending stylet adjusts the deflection of the needle, not because the beveled tip bends directly. The bending deformation of the beveled tip is minimal. Consequently, the beveled tip can be ignored when modeling the physics of the variable-stiffness needle.
- The cutting force is an equivalent force applied to the beveled tip. For uniform tissue, the cutting force is essentially constant during puncture, while for non-uniform tissue, this force varies. Based on the quasi-static assumption, a linear superposition can be applied to estimate the deflection estimation under a changing force.
- From our previous puncture force studies [24] and others’ puncture force simulations [25], it is clear that although bending occurs in the puncture, the cutting force is essentially constant in uniform tissue. The deformation of the beveled tip during puncture is so small that it can be neglected, and thus the partial forces F and Q are also essentially constant. The transverse force F is the key factor affecting deflection, while the axial force Q, transmitted through the stylet to the base of the needle, affects the insertion force.
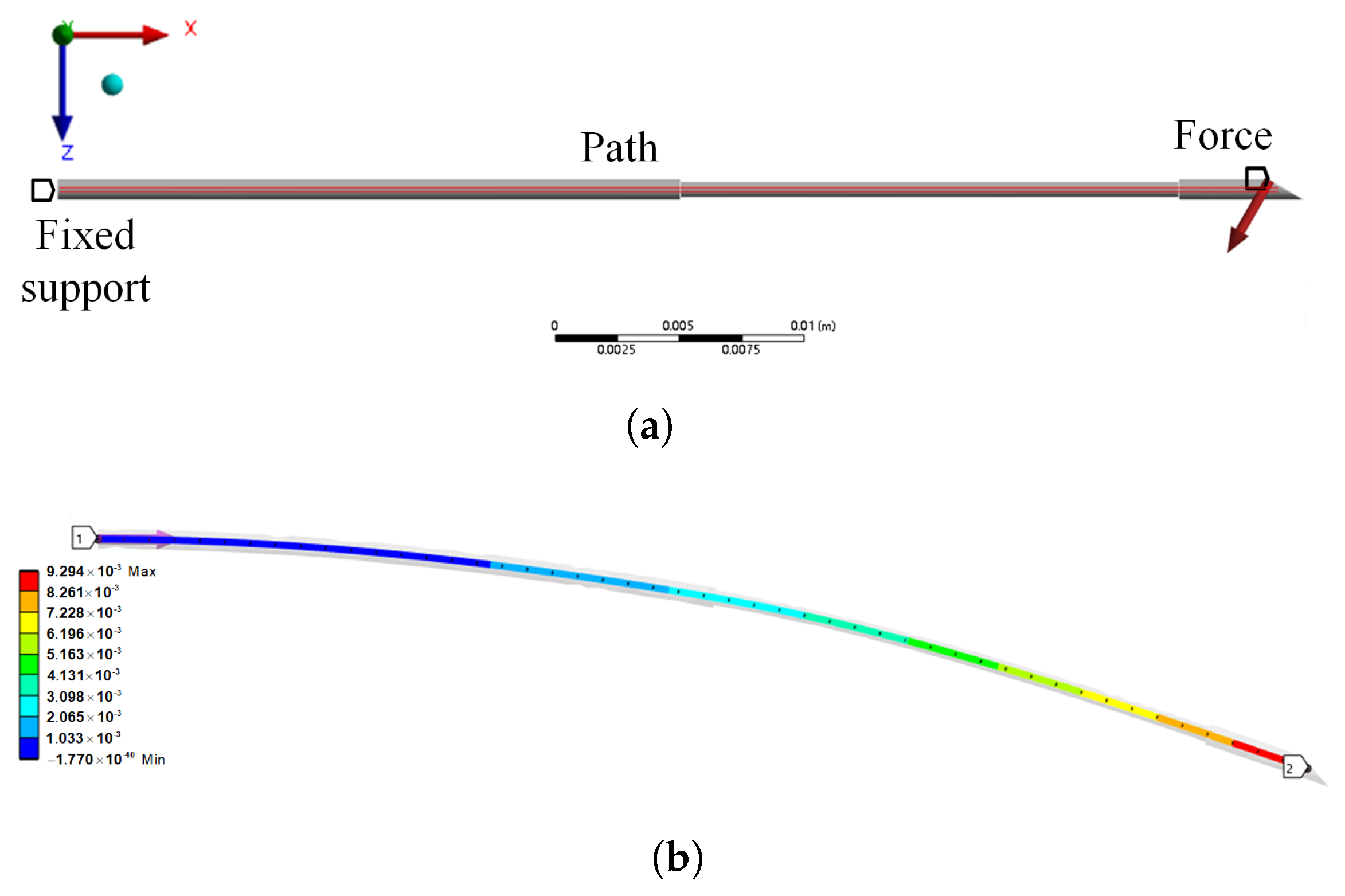
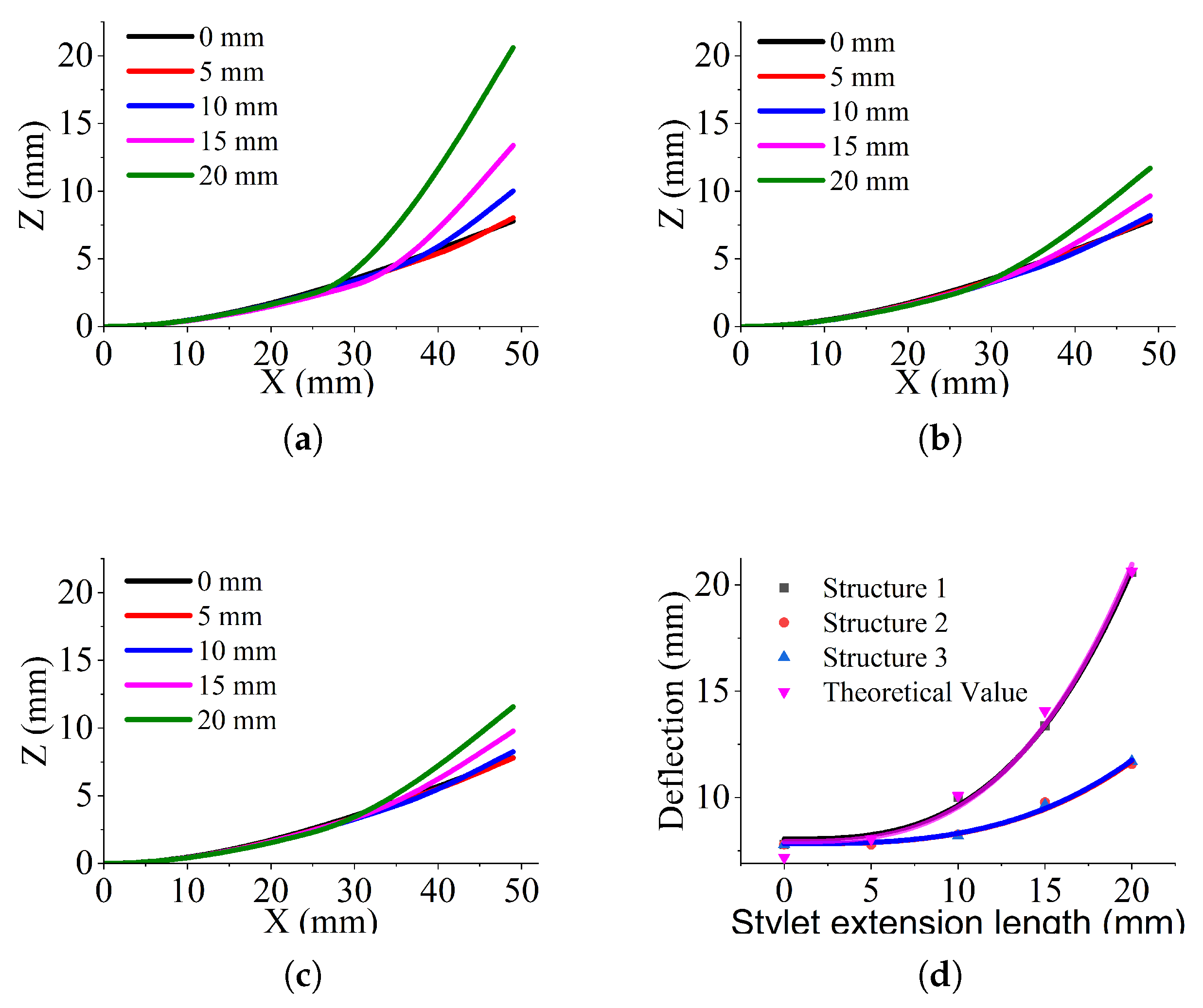
2.3. Simulation of the Effect of Stylet Diameter on Deflection
2.4. Simulation of the Effect of Stylet Extension Length on Deflection
3. Results
3.1. Experimental Setup
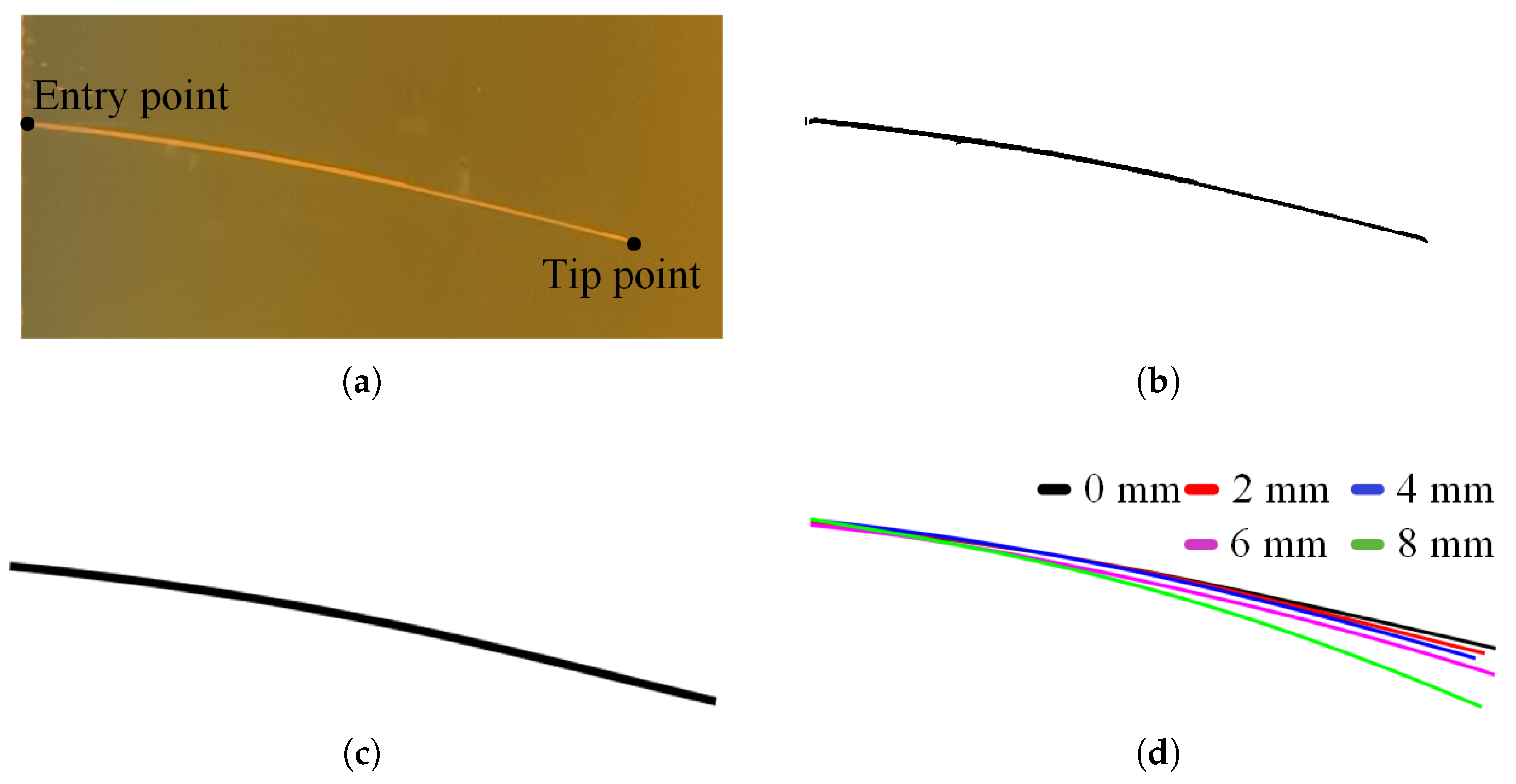
3.2. Effect of Needle Stiffness on Puncture Trajectory
- The insertion point was captured in MATLAB R2021b and the region within was intercepted, as demonstrated in Figure 9a.
- Binarization was performed with a threshold of 0.6 to extract the flexible needle, as in Figure 9b.
- Discrete points were fitted to minimize data loss during extraction and to remove shadow interference caused by gelatin damage. The curves after second-order Fourier fitting are plotted in Figure 9c.
- The increase in temperature of the gelatin affected its mechanical properties, even though the air conditioner had been set to 25 °C.
- Entry points and tip points are collected manually, which inevitably leads to errors.
- Feed errors were caused by motor vibration, motor temperature rise, low speed friction, etc. This effect is more pronounced with thin rods. This can be a key factor that leads to larger standard deviation at an extension length of 8 mm. However, these errors are acceptable.
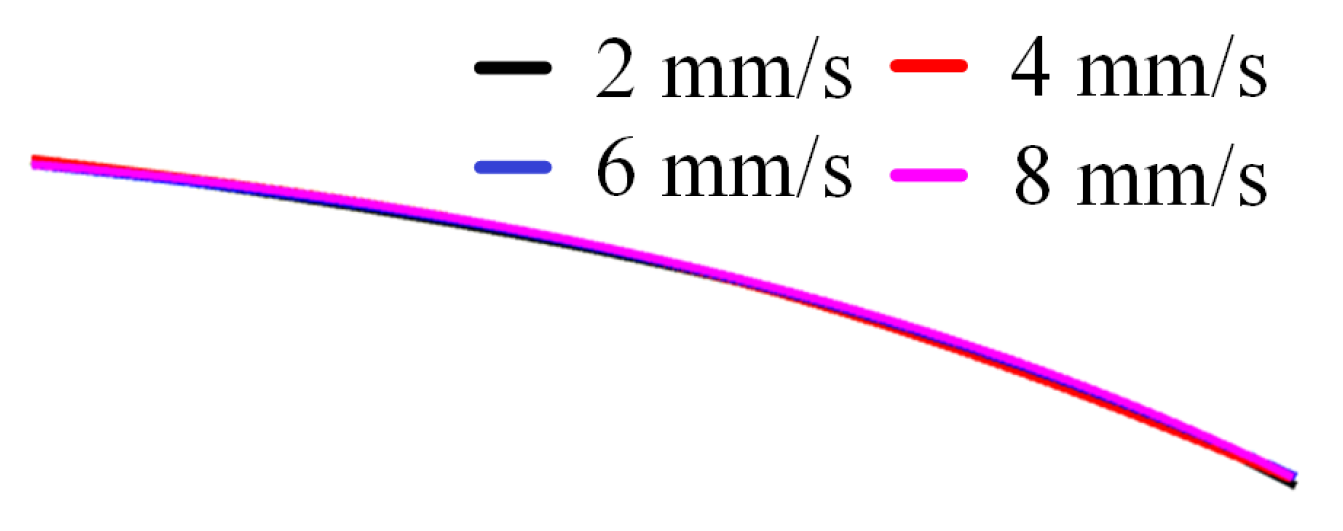
3.3. Effect of Puncture Speed on Puncture Trajectory
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Segato, A.; Di Marzo, M.; Zucchelli, S.; Galvan, S.; Secoli, R.; De Momi, E. Inverse reinforcement learning intra-operative path planning for steerable needle. IEEE Trans. Biomed. Eng. 2022, 69, 1995–2005. [Google Scholar] [CrossRef] [PubMed]
- Zhang, S.L.; Chen, J.C.; Sun, H.K.; Qi, Z.; Zhang, H. A scientometric review of medical flexible needle systems in surgery: Signal processing, navigation and control. Math. Biosci. Eng. 2024, 21, 627–642. [Google Scholar]
- Duan, Y.Z.; Ling, J.; Feng, Z.; Ye, T.T.; Sun, T.R.; Zhu, Y.C. A survey of needle steering approaches in minimally invasive surgery. Ann. Biomed. Eng. 2024, 52, 1492–1517. [Google Scholar] [PubMed]
- Lin, D.J.; Wang, J.Y.; Jiao, N.I.; Wang, Z.D.; Liu, L.Q. A flexible magnetically controlled continuum robot steering in the enlarged effective workspace with constraints for retrograde yntrarenal surgery. Adv. Intell. Syst. 2021, 3, 2000211. [Google Scholar]
- Adebar, T.K.; Fletcher, A.E.; Okamura, A.M. 3-D ultrasound-guided robotic needle steering in biological tissue. IEEE Trans. Biomed. Eng. 2014, 61, 2899–2910. [Google Scholar] [CrossRef]
- de Jong, T.L.; van de Berg, N.J.; Tas, L.; Moelker, A.; Moelker, A.; van den Dobbelsteen, J.J. Needle placement errors: Do we need steerable needles in interventional radiology. Med. Devices-Evid. Res. 2018, 11, 259–265. [Google Scholar]
- Li, A.D.R.; Liu, Y.; Plott, J.; Chen, L.; Montgomery, J.S.; Shih, A. Multi-bevel needle design enabling accurate insertion in biopsy for cancer diagnosis. IEEE Trans. Biomed. Eng. 2021, 68, 1477–1486. [Google Scholar]
- Gidde, S.T.R.; Ciuciu, A.; Devaravar, N.; Doracio, R.; Kianzad, K.; Hutapea, P. Effect of vibration on insertion force and deflection of bioinspired needle in tissues. Bioinspir. Biomim. 2020, 15, 054001. [Google Scholar]
- Favaro, A.; Secoli, R.; Baena, F.R.Y.; De Momi, E. Model-based robust pose estimation for a multi-segment, programmable bevel-tip steerable needle. IEEE Robot. Autom. Let. 2020, 5, 6780–6787. [Google Scholar] [CrossRef]
- Aktas, A.; Demircali, A.A.; Secoli, R.; Temelkuran, B.; Baena, F. Towards a procedure-optimised steerable catheter for deep-seated neurosurgery. Biomedicines 2023, 11, 2008. [Google Scholar] [CrossRef]
- Deaton, N.J.; Brumfiel, T.A.; Yamamoto, K.K.; Elliott, D.; Patel, P. Towards steering a high-dose rate brachytherapy needle with a robotic steerable stylet. IEEE T. Med. Robot. Bio. 2023, 5, 54–65. [Google Scholar]
- Deaton, N.J.; Brumfiel, T.A.; Sarma, A.; Desai, J.P. Simultaneous shape and tip force sensing for the COAST guidewire robot. IEEE Robot. Autom. Let. 2023, 8, 3725–3731. [Google Scholar]
- Zhang, J.Y.; Fang, Q.; Xiang, P.Y.; Liu, L.L.; Xiong, R.; Wang, Y.; Lu, H.J. Flexible biopsy robot with force sensing for deep lung examination. Adv. Intell. Syst. 2024, 6, 2300107. [Google Scholar]
- Lu, M.Y.; Zhang, Y.D.; Lim, C.M.; Ren, H.L. Flexible needle steering with tethered and untethered actuation: Current states, targeting errors, challenges and opportunities. Ann. Biomed. Eng. 2023, 51, 905–924. [Google Scholar] [CrossRef] [PubMed]
- Padasdao, B.; Konh, B. Shape memory alloy actuators in an active needle modeling, precise assembly and performance evaluation. J. Manuf. Sci. Eng. 2021, 143, 021003. [Google Scholar]
- Yan, K.; Yan, W.Q.; Zeng, W.H.; Ding, Q.P.; Chen, J.H.; Yan, J.Y.; Lam, C.P.; Wan, S.; Cheng, S.S. Towards a wristed percutaneous robot with variable stiffness for pericardiocentesis. IEEE Robot. Autom. Let. 2021, 6, 2993–3000. [Google Scholar]
- Bui, V.K.; Park, S.; Park, J.O.; Ko, S.Y. A novel curvature-controllable steerable needle for percutaneous intervention. Proc. Inst. Mech. Eng. Part H J. Eng. Med. 2016, 230, 727–738. [Google Scholar]
- Xu, B.X.; Ko, S.Y. Planar trajectory following control with a curvature-controllable steerable needle: Preliminary modeling and simulation. In Proceedings of the 18th International Conference on Control, Automation and Systems, PyeongChang, Republic of Korea, 17–20 October 2018. [Google Scholar]
- Xu, B.X.; Ko, S.Y. 3D feedback control using fuzzy logic for a curvature-controllable steerable bevel-tip needle. Mechatronics 2020, 68, 102368. [Google Scholar] [CrossRef]
- Jiang, S.; Li, P.; Yu, Y.; Liu, J.; Yang, Z.Y. Experimental study of needle–tissue interaction forces: Effect of needle geometries, insertion methods and tissue characteristics. J. Biomech. 2014, 47, 3344–3353. [Google Scholar]
- Jushiddi, M.G.; Cahalane, R.M.; Byrne, M.; Mani, A.; Silien, C.; Tofail, S.A.M.; Mulvihill, J.J.E.; Tiernan, P. Bevel angle study of flexible hollow needle insertion into biological mimetic soft-gel: Simulation and experimental validation. J. Mech. Behav. Biomed. Mater. 2020, 111, 103896. [Google Scholar]
- Rox, M.; Emerson, M.; Ertop, T.E.; Fried, I.; Fu, M.Y.; Hoelscher, J.; Kuntz, A.; Granna, J.; Mitchell, J.E.; Lester, M. Decoupling steerability from diameter: Helical dovetail laser patterning for steerable needles. IEEE Access 2022, 8, 181411–181419. [Google Scholar] [CrossRef] [PubMed]
- Misra, S.; Reed, K.B.; Schafer, B.W.; Ramesh, K.T.; Okamura, A.M. Mechanics of flexible needles robotically steered through soft tissue. Int. J. Robot. Res. 2010, 29, 1640–1660. [Google Scholar] [CrossRef] [PubMed]
- Wei, G.Z.; Jiang, Q. A temperature-compensated force sensor based on a cascaded FPI for needle force sensing. Measurement 2022, 202, 111748. [Google Scholar] [CrossRef]
- Jushiddi, M.G.; Mulvihill, J.J.E.; Chovan, D.; Mani, A.; Shanahan, C.; Silien, C.; Tofail, S.A.M.; Tiernan, P. Simulation of biopsy bevel-tipped needle insertion into soft-gel. Comput. Biol. Med. 2019, 111, 103337. [Google Scholar] [CrossRef]
- Abayazid, M.; Roesthuis, R.J.; Reilink, R.; Misra, S. Integrating deflection models and image feedback for real-time flexible needle steering. IEEE Trans. Robot. 2013, 29, 542–553. [Google Scholar] [CrossRef]
- Song, L.; Su, T.; Gao, L.Y.; Zhang, Q.H. Indentation tests based on gelatin phantom. In Proceedings of the 3rd International Conference on Mechanical Engineering, Materials and Energy, Changsha, China, 9–10 November 2013. [Google Scholar]



| Extension Length | 0 mm | 5 mm | 10 mm | 15 mm | 20 mm | |
|---|---|---|---|---|---|---|
| Deflection | ||||||
| Bending deflection (mm) | 7.1788 | 8.0402 | 10.0862 | 14.0704 | 20.6389 | |
| Shear deflection (mm) | 0.0008 | 0.0013 | 0.0015 | 0.0017 | 0.0020 | |
| Total deflection (mm) | 7.1796 | 8.0415 | 10.0877 | 14.0721 | 20.6409 | |
| Bending deflection/Total deflection | 99.99% | 99.98% | 99.99% | 99.99% | 99.99% | |
| Total Length (mm) | Tip Angle (°) | Tip Length (mm) |
| 50 | 30 | 5 |
| Tube Diameter (mm) | Stylet Diameter (mm) | Stylet Length (mm) |
| 0.8 | 0.8, 0.7, 0.6, 0.5, 0.4 | 0, 5, 10, 15, 20 |
| Young’s Modulus (MPa) | Poisson’s Ratio | Load (N) |
| 75,000 | 0.3 | 0.3 |
| Extension Length | 0 mm | 2 mm | 4 mm | 6 mm | 8 mm | |
|---|---|---|---|---|---|---|
| Deflection | ||||||
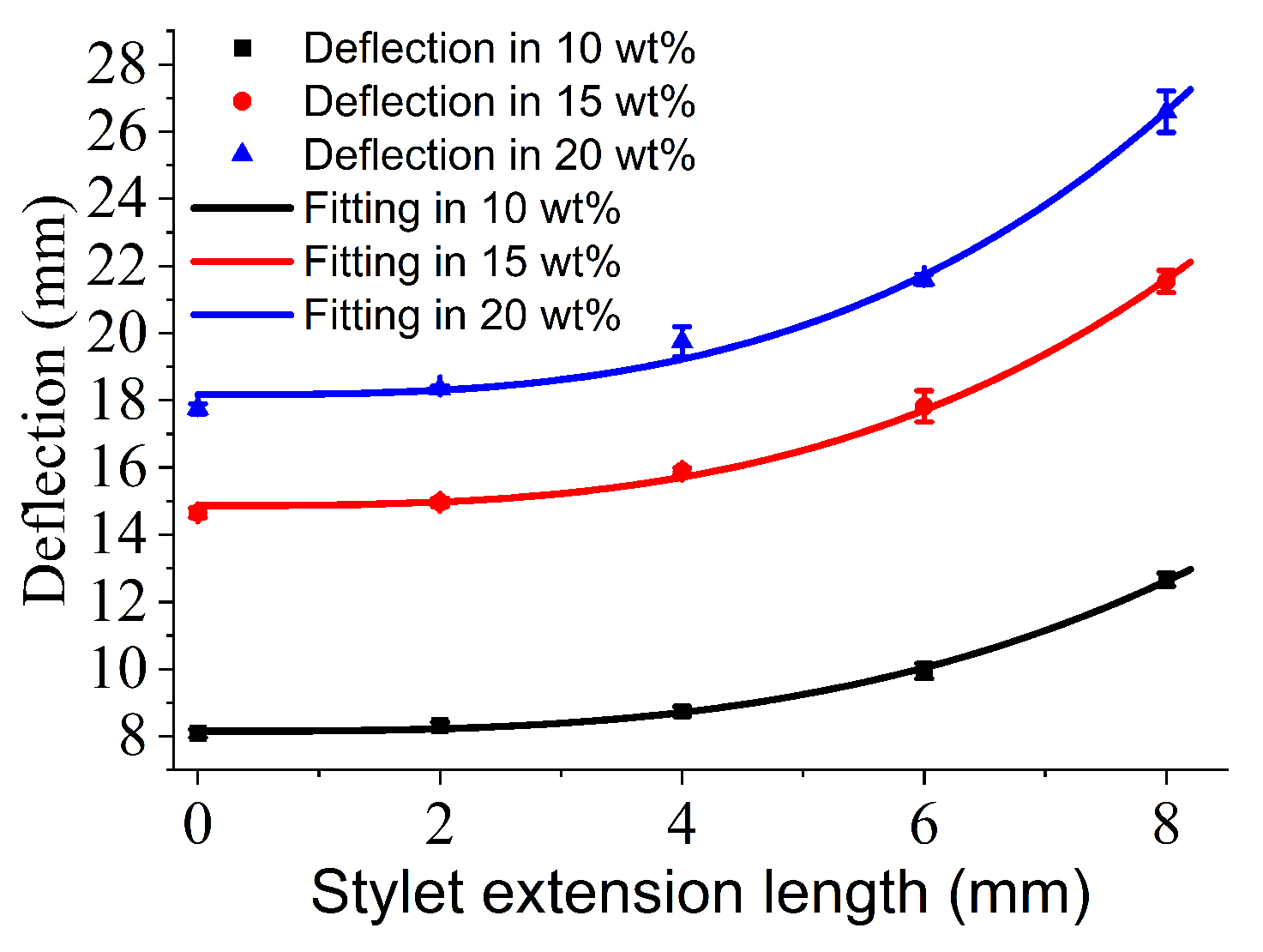
| Deflection1 (mm) | 17.716 | 18.232 | 20.296 | 21.672 | 27.520 | |
| Deflection2 (mm) | 17.888 | 18.232 | 19.608 | 21.672 | 25.800 | |
| Deflection3 (mm) | 17.888 | 18.404 | 19.436 | 21.672 | 26.488 | |
| Deflection4 (mm) | 17.716 | 18.404 | 19.264 | 21.672 | 26.488 | |
| Deflection5 (mm) | 17.544 | 18.404 | 20.124 | 21.328 | 26.66 | |
| Average (mm) | 17.750 | 18.335 | 19.746 | 21.603 | 26.591 | |
| SD (mm) | 0.144 | 0.094 | 0.445 | 0.154 | 0.615 | |
| Extension Length | 0 mm | 2 mm | 4 mm | 6 mm | 8 mm | |
|---|---|---|---|---|---|---|
| Deflection | ||||||
| Deflection1 (mm) | 14.448 | 15.136 | 15.824 | 17.028 | 20.984 | |
| Deflection1 (mm) | 14.792 | 14.964 | 15.824 | 17.888 | 21.844 | |
| Deflection1 (mm) | 14.792 | 14.964 | 15.996 | 17.888 | 21.500 | |
| Deflection1 (mm) | 14.620 | 14.792 | 15.824 | 18.060 | 21.672 | |
| Deflection1 (mm) | 14.620 | 14.964 | 15.996 | 18.232 | 21.672 | |
| Average (mm) | 14.654 | 14.964 | 15.893 | 17.819 | 21.534 | |
| SD (mm) | 0.144 | 0.122 | 0.094 | 0.465 | 0.331 | |
| Extension Length | 0 mm | 2 mm | 4 mm | 6 mm | 8 mm | |
|---|---|---|---|---|---|---|
| Deflection | ||||||
| Deflection1 (mm) | 8.084 | 8.428 | 8.772 | 9.804 | 12.384 | |
| Deflection2 (mm) | 8.256 | 8.256 | 8.772 | 10.148 | 12.728 | |
| Deflection3 (mm) | 7.912 | 8.256 | 8.600 | 9.632 | 12.728 | |
| Deflection4 (mm) | 8.084 | 8.256 | 8.944 | 10.148 | 12.900 | |
| Deflection5 (mm) | 8.084 | 8.428 | 8.600 | 9.976 | 12.556 | |
| Average (mm) | 8.084 | 8.325 | 8.738 | 9.942 | 12.659 | |
| SD (mm) | 0.122 | 0.094 | 0.144 | 0.224 | 0.196 | |
| Extension Length | 0 mm | 2 mm | 4 mm | 6 mm | 8 mm | |
|---|---|---|---|---|---|---|
| Puncture Speed | ||||||
| At 2 mm/s (mm) | 18.232 | 18.576 | 19.608 | 21.156 | 27.004 | |
| At 4 mm/s (mm) | 17.888 | 18.404 | 19.436 | 21.672 | 26.488 | |
| At 6 mm/s (mm) | 18.06 | 18.576 | 19.436 | 21.844 | 26.66 | |
| At 8 mm/s (mm) | 18.232 | 18.748 | 19.78 | 21.672 | 26.66 | |
| Average (mm) | 18.103 | 18.576 | 19.565 | 21.586 | 26.703 | |
| SD (mm) | 0.165 | 0.140 | 0.165 | 0.298 | 0.216 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wei, G.; Liu, Z.; Yu, H.; Zhang, Z.; Li, K. Deflection Modeling and Curvature Manipulation of a Variable-Stiffness Flexible Needle. Appl. Sci. 2025, 15, 3746. https://doi.org/10.3390/app15073746
Wei G, Liu Z, Yu H, Zhang Z, Li K. Deflection Modeling and Curvature Manipulation of a Variable-Stiffness Flexible Needle. Applied Sciences. 2025; 15(7):3746. https://doi.org/10.3390/app15073746
Chicago/Turabian StyleWei, Guozhao, Zhixing Liu, Hanwen Yu, Zhenzhong Zhang, and Kun Li. 2025. "Deflection Modeling and Curvature Manipulation of a Variable-Stiffness Flexible Needle" Applied Sciences 15, no. 7: 3746. https://doi.org/10.3390/app15073746
APA StyleWei, G., Liu, Z., Yu, H., Zhang, Z., & Li, K. (2025). Deflection Modeling and Curvature Manipulation of a Variable-Stiffness Flexible Needle. Applied Sciences, 15(7), 3746. https://doi.org/10.3390/app15073746






