Adaptive Beamforming Damage Imaging of Lamb Wave Based on CNN
Abstract
:1. Introduction
2. Beamforming Imaging Method
2.1. DAS Method
2.2. MVDR Method
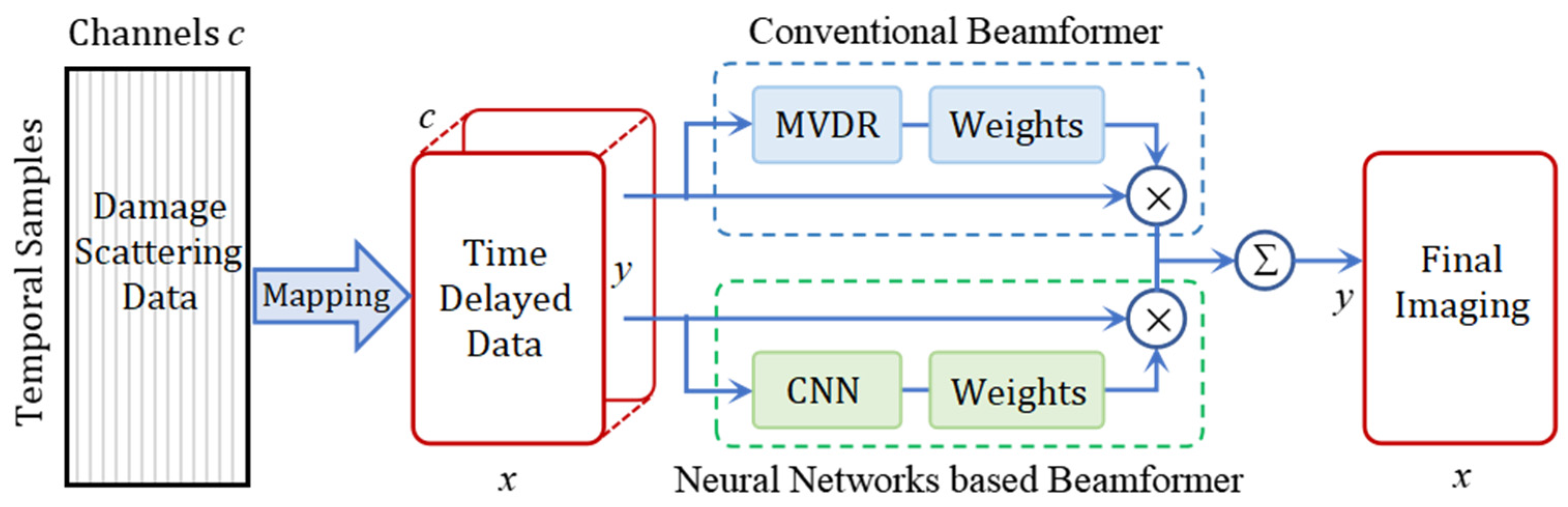
3. Adaptive Beamforming Model Based on CNN
3.1. Network Model Architecture
- (1)
- Preprocess input signals:
- –
- Apply Time-of-Flight Correction (ToFC) to align scattered signals.
- –
- Extract real and imaginary parts (channel dimension: 16 for 8 receivers).
- (2)
- Feed ToFC data into the CNN:
- –
- Input dimensions: 201 101 16.
- –
- Process through four convolutional layers (7 × 7 kernels, anti-rectifier activation).
- –
- Apply batch normalization and L2 regularization.
- (3)
- Predict apodization weights :
- –
- Softmax activation ensures .
- (4)
- Compute pixel values:
- –
- .
- (5)
- Generate the final image by aggregating pixel values across the grid.
3.2. Network Training Strategies
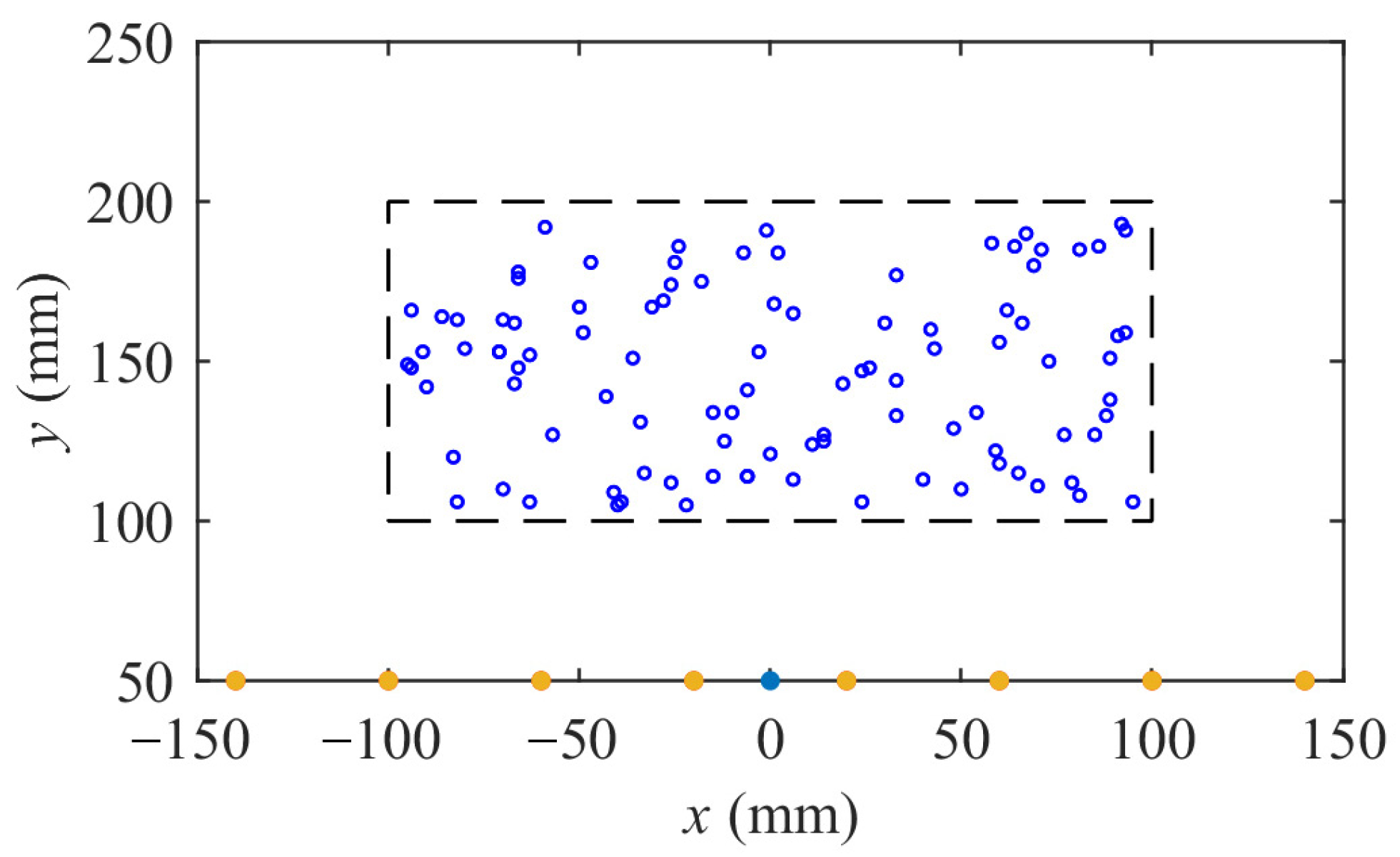
3.3. Acquisition of Training Data Sets
4. Discussion and Analysis of Results
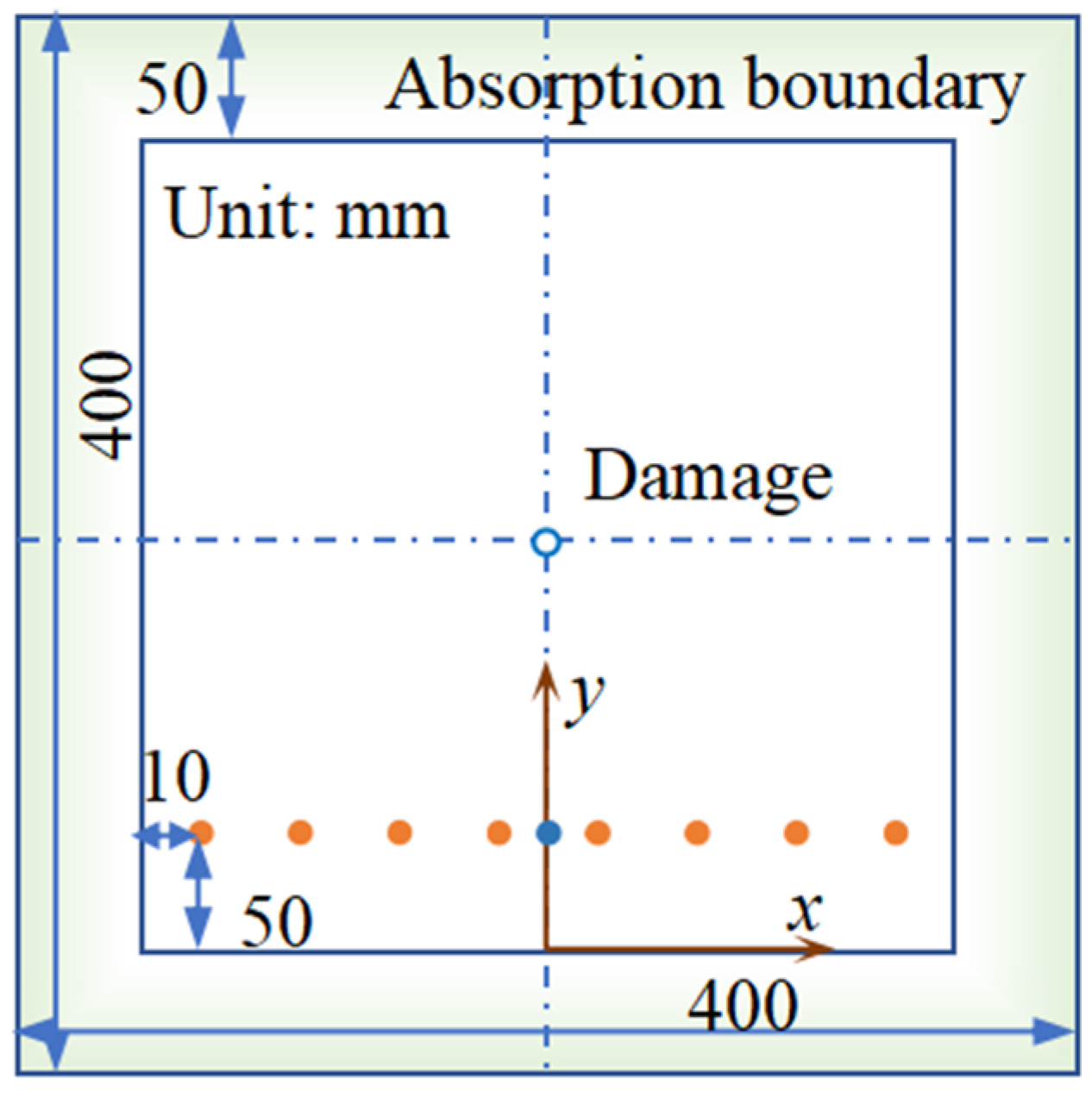
4.1. Finite Element Simulation Model
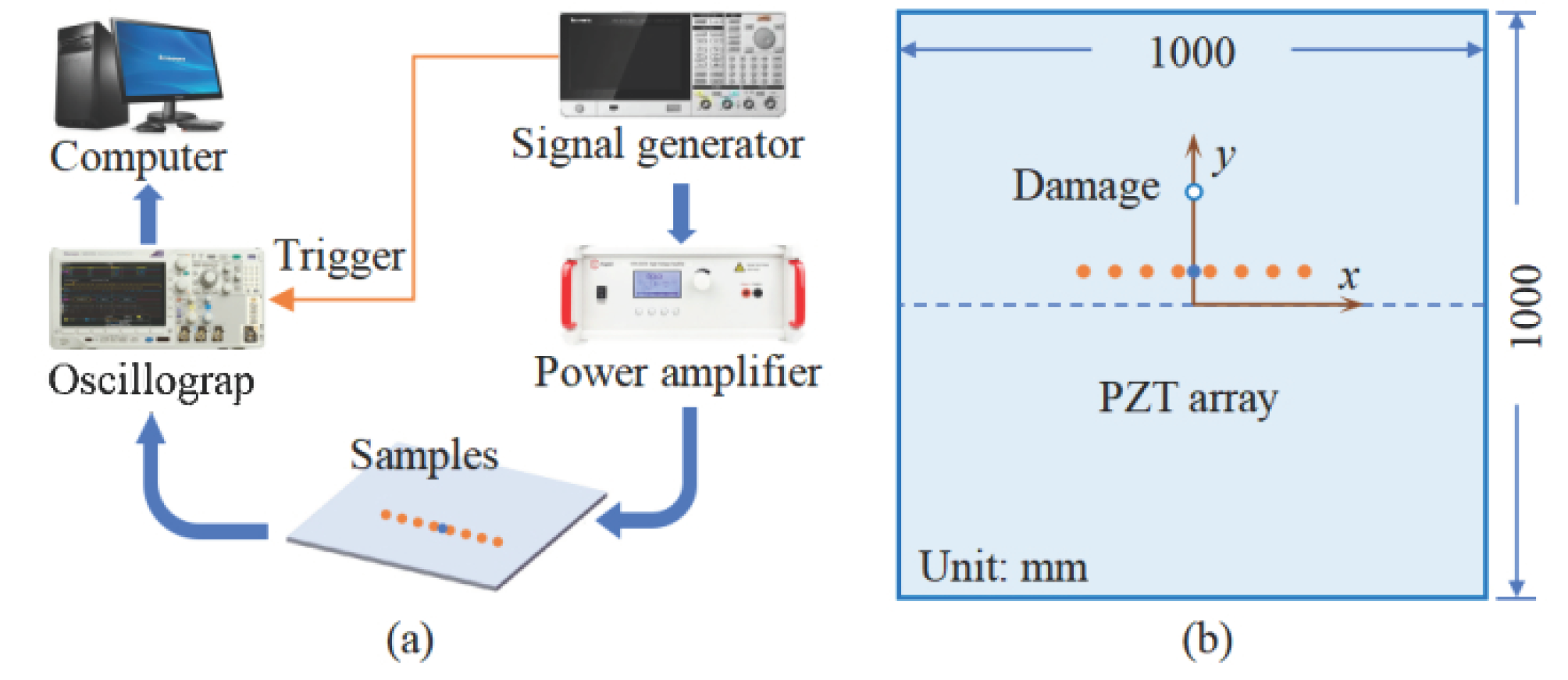
4.2. Construction of Experiment Platform
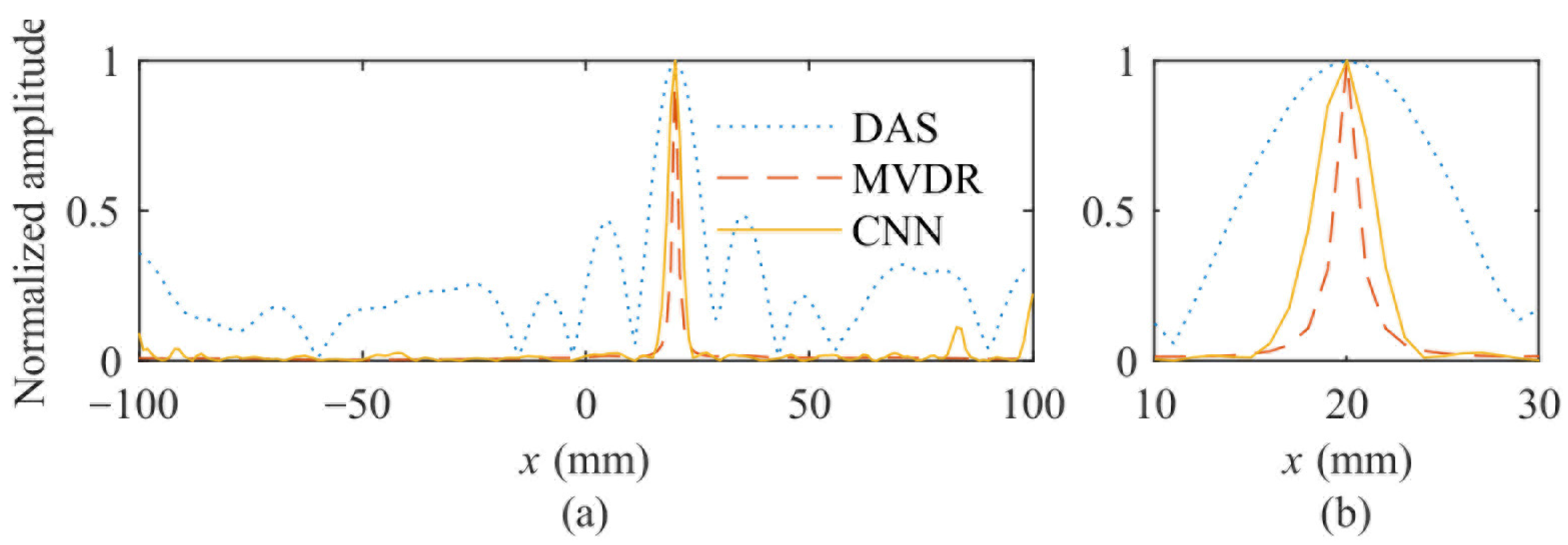
4.3. Quantitative Metrics of Imaging Results
4.4. Dataset Acquisition and Training
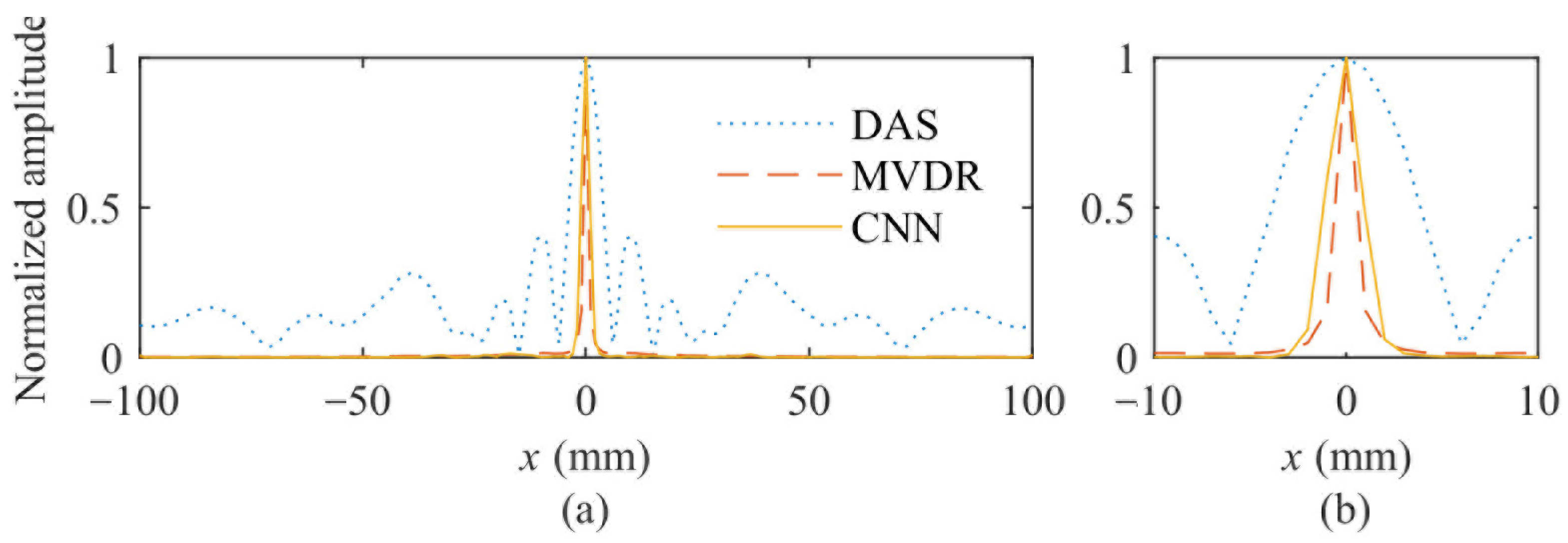
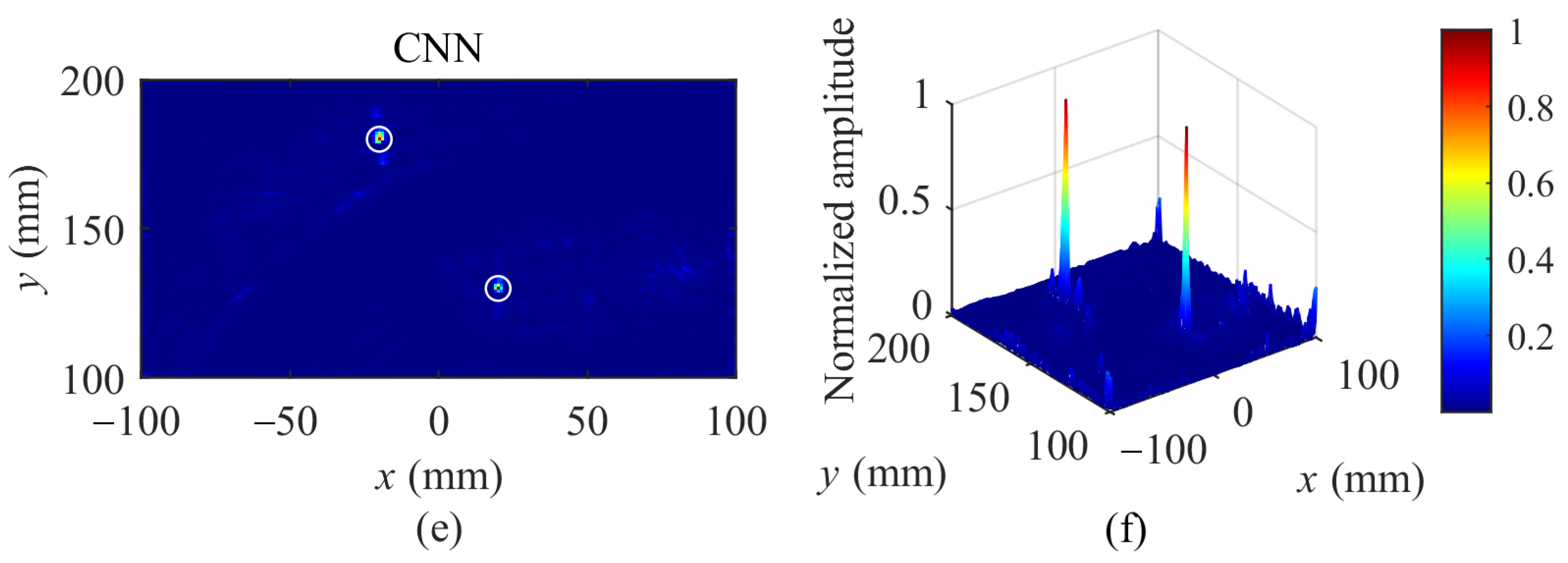
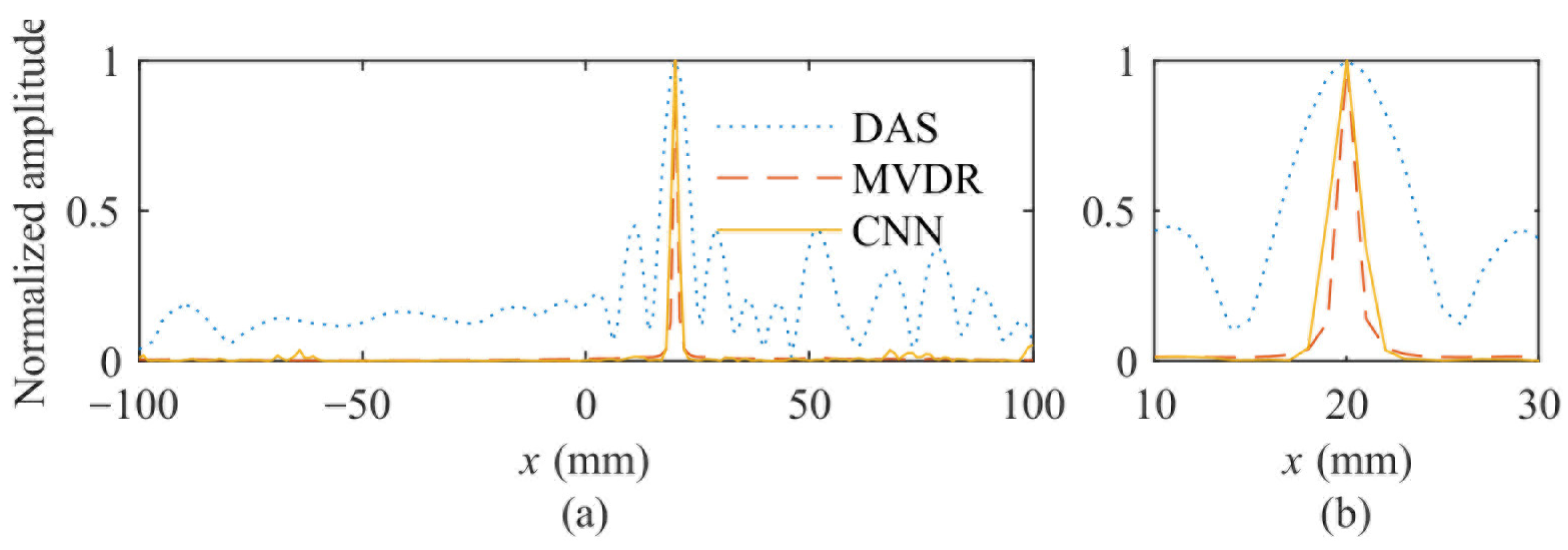
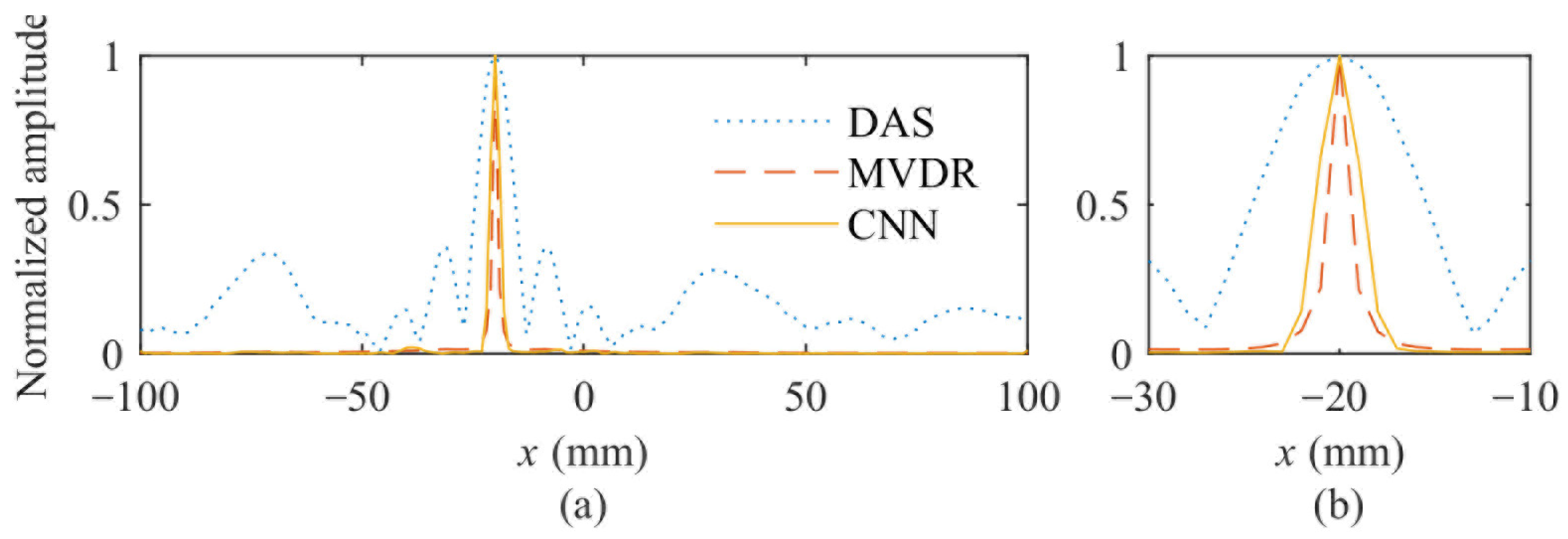
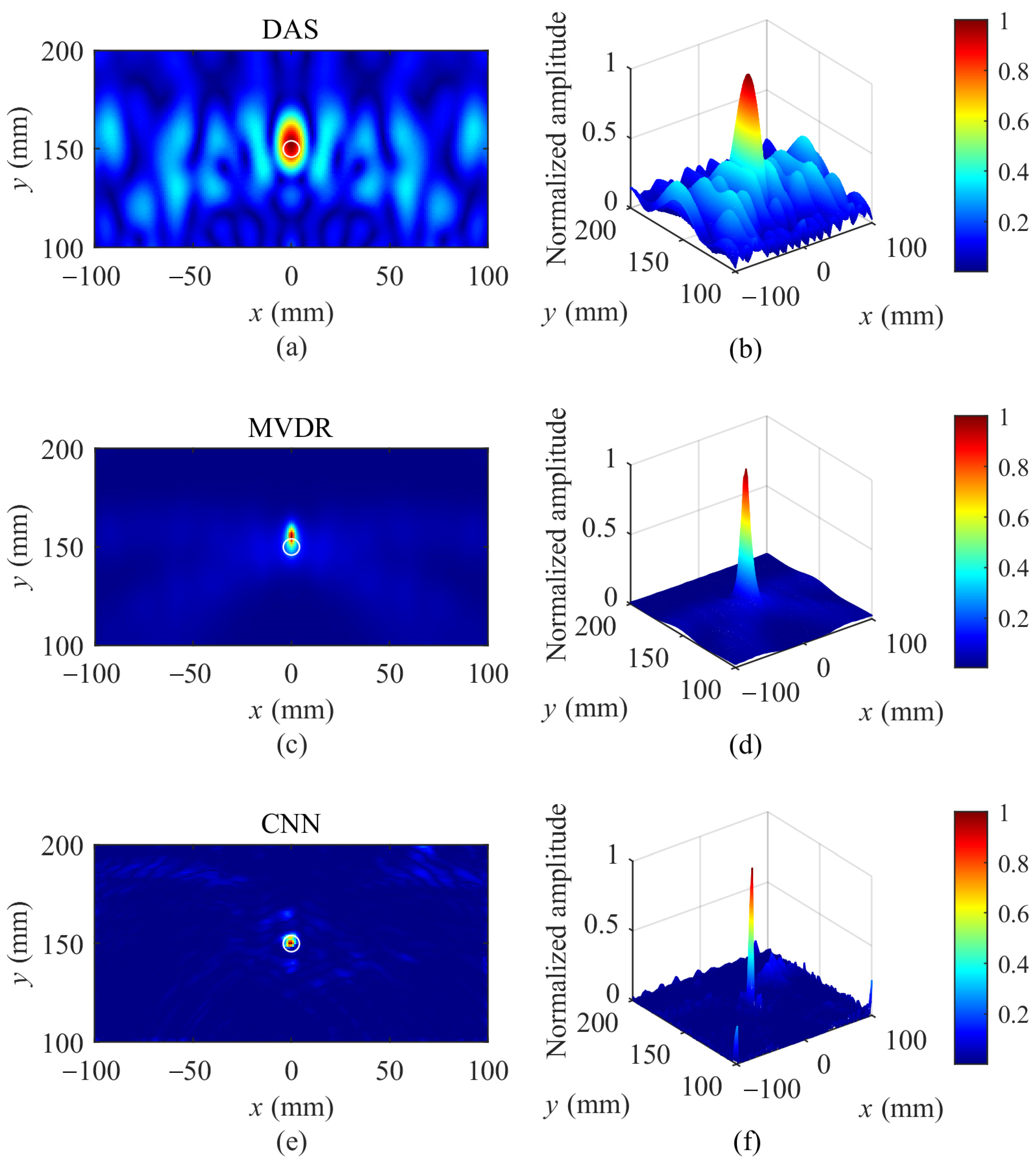
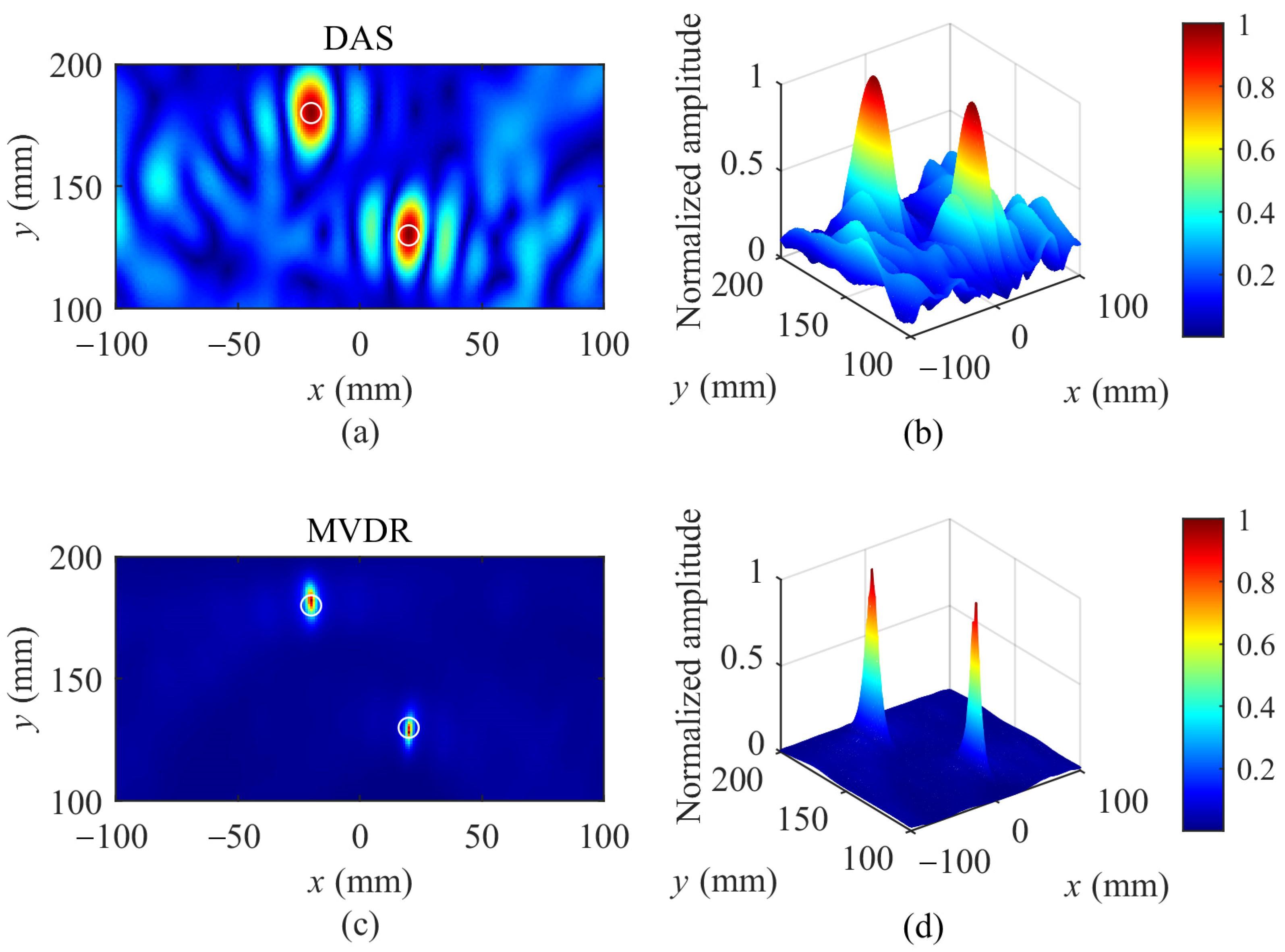
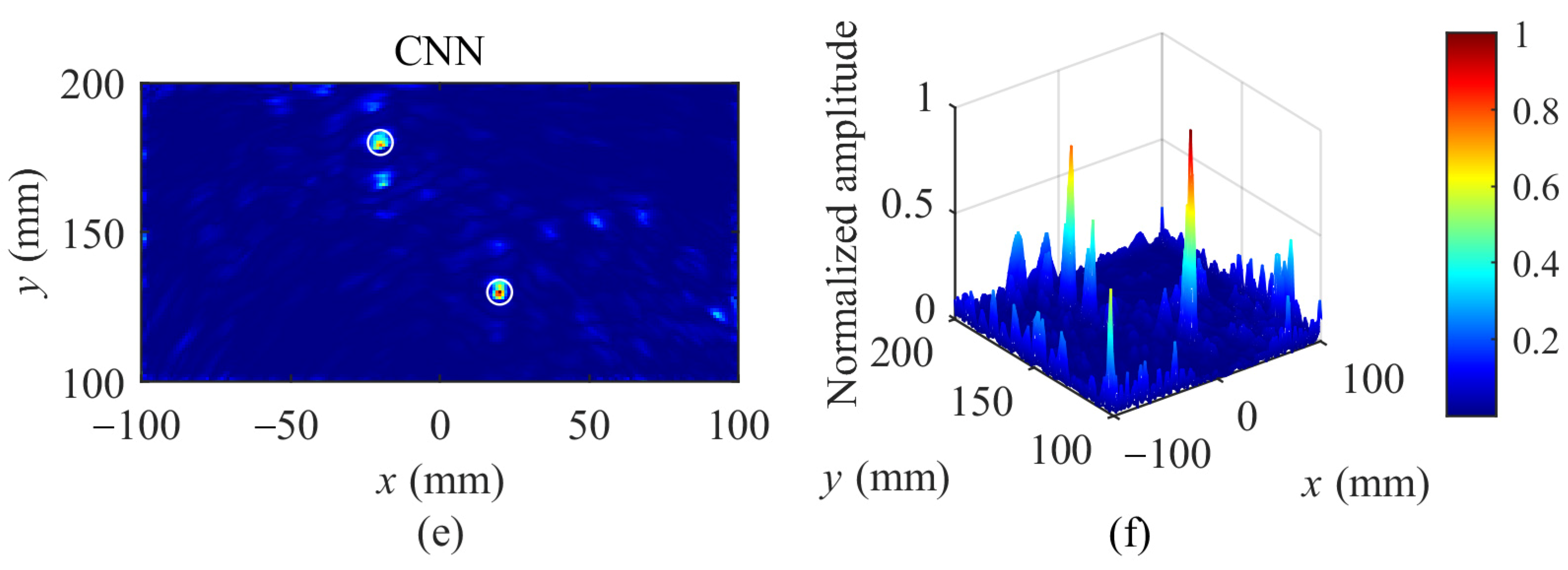
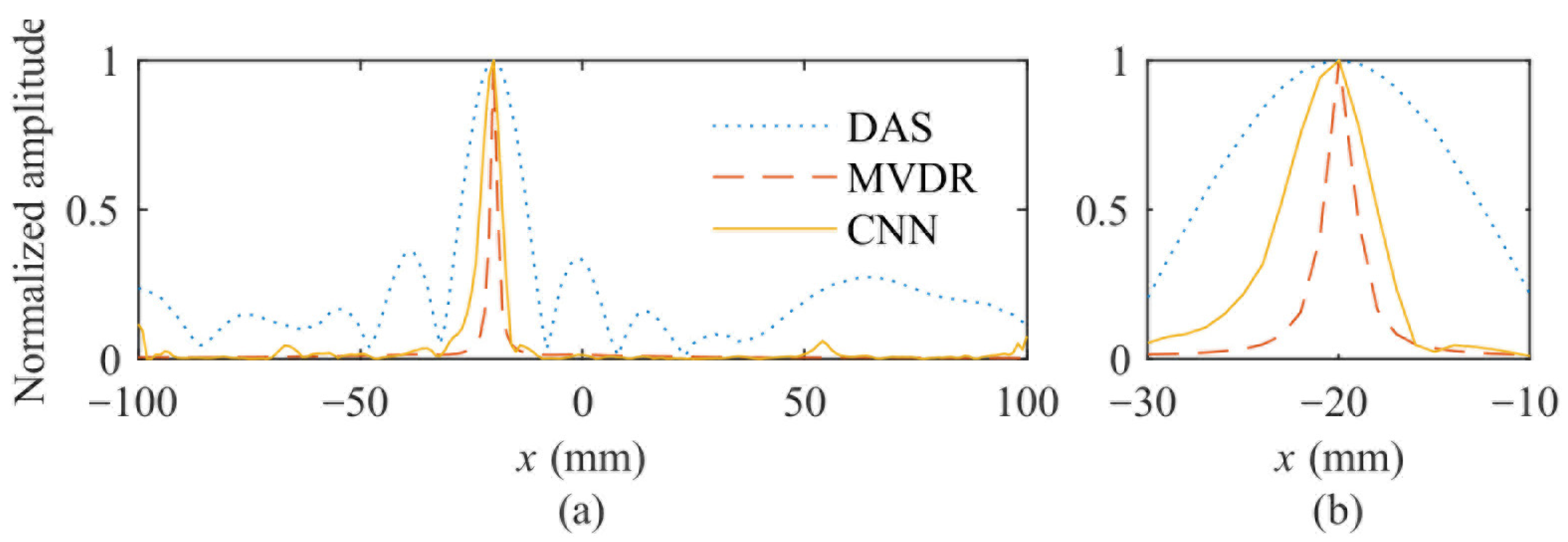
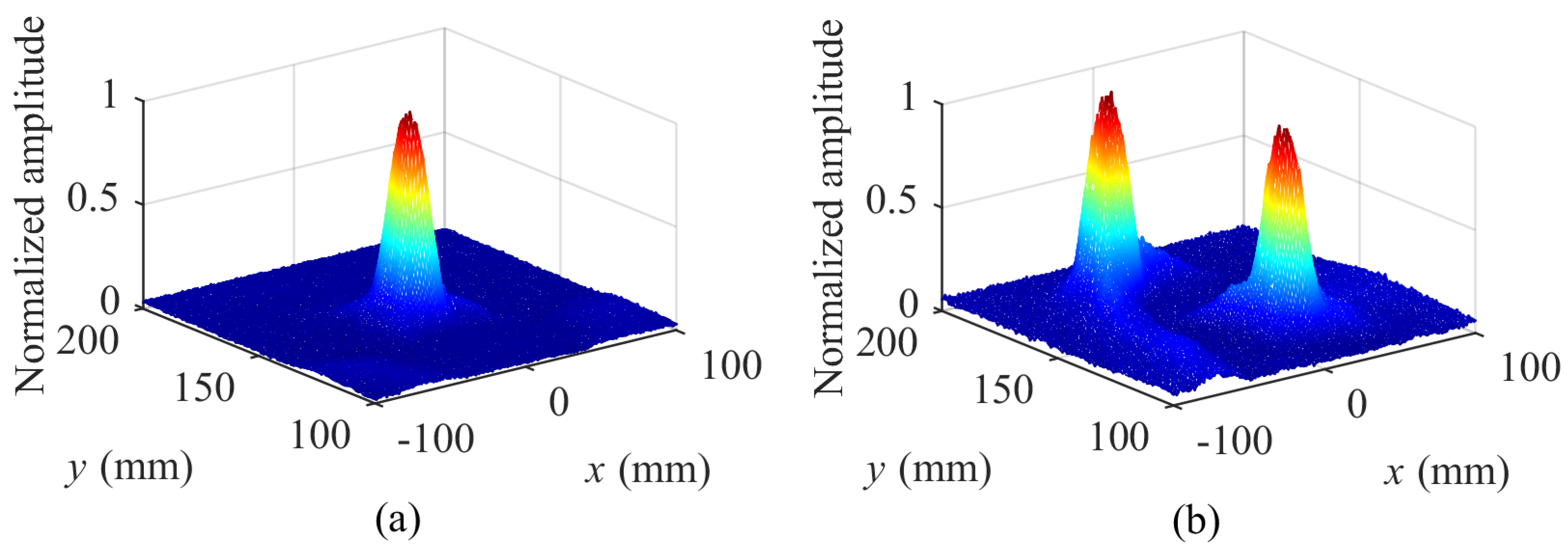
4.5. Simulation Results and Analysis
4.6. Experimental Results and Analysis
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Su, Z.; Ye, L. Identification of Damage Using Lamb Waves: From Fundamentals to Applications; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2009; Volume 48. [Google Scholar]
- Mitra, M.; Gopalakrishnan, S.J. Guided wave based structural health monitoring: A review. Smart Mater. Struct. 2016, 25, 053001. [Google Scholar] [CrossRef]
- Shan, S.; Qiu, J.; Zhang, C.; Ji, H.; Cheng, L.J. Multi-damage localization on large complex structures through an extended delay-and-sum based method. Struct. Health Monit. 2016, 15, 50–64. [Google Scholar] [CrossRef]
- Hua, J.; Zhang, H.; Miao, Y.; Lin, J.J. Modified minimum variance imaging of Lamb waves for damage localization in aluminum plates and composite laminates. NDT & E Int. 2022, 125, 102574. [Google Scholar]
- Liu, Z.; Sun, K.; Song, G.; He, C.; Wu, B.J. Damage localization in aluminum plate with compact rectangular phased piezoelectric transducer array. Mech. Syst. Signal Process. 2016, 70, 625–636. [Google Scholar] [CrossRef]
- Zhang, S.; Li, C.M.; Ye, W.J. Damage localization in plate-like structures using time-varying feature and one-dimensional convolutional neural network. Mech. Syst. Signal Process. 2021, 147, 107107. [Google Scholar] [CrossRef]
- Yu, L.; Giurgiutiu, V.J. In-situ optimized PWAS phased arrays for Lamb wave structural health monitoring. J. Mech. Mater. Struct. 2007, 2, 459–487. [Google Scholar]
- Veidt, M.; Ng, C.; Hames, S.; Wattinger, T.J. Imaging laminar damage in plates using Lamb wave beamforming. Adv. Mater. Res. 2008, 47, 666–669. [Google Scholar] [CrossRef]
- Sharif-Khodaei, Z.; Aliabadi, M.J. Assessment of delay-and-sum algorithms for damage detection in aluminum and composite plates. Smart Mater. Struct. 2014, 23, 075007. [Google Scholar] [CrossRef]
- Tian, Z.; Howden, S.; Ma, Z.; Xiao, W.; Yu, L. Pulsed laser-scanning laser Doppler vibrometer (PL-SLDV) phased arrays for damage detection in aluminum plates. Mech. Syst. Signal Process. 2019, 121, 158–170. [Google Scholar] [CrossRef]
- Michaels, J.E.; Hall, J.S.; Michaels, T.E. Adaptive imaging of damage from changes in guided wave signals recorded from spatially distributed arrays. In Proceedings of the Health Monitoring of Structural and Biological Systems 2009, San Diego, CA, USA, 9–12 March 2009; pp. 351–361. [Google Scholar]
- Hall, J.S.; Michaels, J.E. Minimum variance ultrasonic imaging applied to an in situ sparse guided wave array. IEEE Trans. Ultrason. Ferroelectr. Freq. Control. 2010, 57, 2311–2323. [Google Scholar] [CrossRef]
- Engholm, M.; Stepinski, T.J. Adaptive beamforming for array imaging of plate structures using lamb waves. IEEE Trans. Ultrason. Ferroelectr. Freq. Control. 2010, 57, 2712–2724. [Google Scholar] [CrossRef] [PubMed]
- Hua, J.; Lin, J.; Zeng, L.; Luo, Z.J. Minimum variance imaging based on correlation analysis of Lamb wave signals. Ultrasonics 2016, 70, 107–122. [Google Scholar]
- Xu, C.; Yang, Z.; Zuo, H.; Deng, M. Minimum variance Lamb wave imaging based on weighted sparse decomposition coefficients in quasi-isotropic composite laminates. Compos. Struct. 2021, 275, 114432. [Google Scholar]
- Peng, L.; Xu, C.; Gao, G.; Hu, N.; Deng, M. Lamb wave based damage imaging using an adaptive Capon method. Meas. Sci. Technol. 2023, 34, 125406. [Google Scholar] [CrossRef]
- Perfetto, D.; De Luca, A.; Perfetto, M.; Lamanna, G.; Caputo, F. Damage detection in flat panels by guided waves based artificial neural network trained through finite element method. Materials 2021, 14, 7602. [Google Scholar] [CrossRef]
- Humer, C.; Höll, S.; Kralovec, C.; Schagerl, M. Damage identification using wave damage interaction coefficients predicted by deep neural networks. Ultrasonics 2022, 124, 106743. [Google Scholar] [CrossRef]
- Ma, J.; Hu, M.; Yang, Z.; Yang, H.; Ma, S.; Xu, H.; Yang, L.; Wu, Z.J. An efficient lightweight deep-learning approach for guided Lamb wave-based damage detection in composite structures. Appl. Sci. 2023, 13, 5022. [Google Scholar] [CrossRef]
- Su, C.; Jiang, M.; Lv, S.; Lu, S.; Zhang, L.; Zhang, F.; Sui, Q.J. Improved damage localization and quantification of CFRP using Lamb waves and convolution neural network. IEEE Sens. J. 2019, 19, 5784–5791. [Google Scholar] [CrossRef]
- Song, H.; Yang, Y.J. Super-resolution visualization of subwavelength defects via deep learning-enhanced ultrasonic beamforming: A proof-of-principle study. NDT E Int. 2020, 116, 102344. [Google Scholar] [CrossRef]
- Zhang, B.; Hong, X.; Liu, Y.J. Deep convolutional neural network probability imaging for plate structural health monitoring using guided waves. IEEE Trans. Instrum. Meas. 2021, 70, 2510610. [Google Scholar]
- Wang, X.; Li, J.; Wang, D.; Huang, X.; Liang, L.; Tang, Z.; Fan, Z.; Liu, Y.J. Sparse ultrasonic guided wave imaging with compressive sensing and deep learning. Mech. Syst. Signal Process. 2022, 178, 109346. [Google Scholar] [CrossRef]
- Shen, R.H.; Zhou, Z.X.; Xu, G.D.; Zhang, S.; Xu, C.G.; Xu, B.Q.; Luo, Y. Adaptive Weighted Damage Imaging of Lamb Waves Based on Deep Learning. IEEE Access 2024, 12, 128860–128870. [Google Scholar] [CrossRef]
- Sternini, S.; Pau, A.; Di Scalea, F.L. Minimum-variance imaging in plates using guided-wave-mode beamforming. IEEE Trans. Ultrason. Ferroelectr. Freq. Control. 2019, 66, 1906–1919. [Google Scholar]
- Haskins, G.; Kruger, U.; Yan, P. Deep learning in medical image registration: A survey. Mach. Vis. Appl. 2020, 31, 8. [Google Scholar]
- Wei, A.; Guan, S.; Wang, N.; Lv, S. Damage detection of jacket platforms through improved stacked autoencoder and softmax classifier. Ocean. Eng. 2024, 306, 118036. [Google Scholar] [CrossRef]
- Xu, B.Q.; Shen, Z.H.; Ni, X.W.; Wang, J.J.; Guan, J.F.; Lu, J. Thermal and mechanical finite element modeling of laser-generated ultrasound in coating–substrate system. Opt. Laser Technol. 2006, 38, 138–145. [Google Scholar]
- Zhang, J.; Drinkwater, B.W.; Wilcox, P.D. Effects of array transducer inconsistencies on total focusing method imaging performance. NDT & E Int. 2011, 44, 361–368. [Google Scholar]
- Velichko, A.; Wilcox, P.D. An analytical comparison of ultrasonic array imaging algorithms. J. Acoust. Soc. Am. 2010, 127, 2377–2384. [Google Scholar]




| DAMAGE LOCATION (mm) | API | SNR (dB) | ||||
|---|---|---|---|---|---|---|
| DAS | MVDR | CNN | DAS | MVDR | CNN | |
| (0, 150) | 36.50 | 2.32 | 4.16 | 19.58 | 121.12 | 95.62 |
| (−20, 180) | 38.26 | 2.62 | 4.68 | 21.41 | 120.28 | 89.08 |
| (20, 130) | 35.32 | 2.26 | 5.03 | 20.35 | 119.53 | 93.16 |
| DAMAGE LOCATION (mm) | API | SNR (dB) | ||||
|---|---|---|---|---|---|---|
| DAS | MVDR | CNN | DAS | MVDR | CNN | |
| (0, 150) | 25.82 | 4.13 | 8.18 | 16.44 | 82.32 | 54.81 |
| (−20, 180) | 28.16 | 3.96 | 7.72 | 15.97 | 73.08 | 57.16 |
| (20, 130) | 26.36 | 4.08 | 7.69 | 15.85 | 70.29 | 55.38 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shen, R.; Zhou, Z.; Xu, G.; Zhang, S.; Xu, C.; Xu, B.; Luo, Y. Adaptive Beamforming Damage Imaging of Lamb Wave Based on CNN. Appl. Sci. 2025, 15, 3801. https://doi.org/10.3390/app15073801
Shen R, Zhou Z, Xu G, Zhang S, Xu C, Xu B, Luo Y. Adaptive Beamforming Damage Imaging of Lamb Wave Based on CNN. Applied Sciences. 2025; 15(7):3801. https://doi.org/10.3390/app15073801
Chicago/Turabian StyleShen, Ronghe, Zixing Zhou, Guidong Xu, Sai Zhang, Chenguang Xu, Baiqiang Xu, and Ying Luo. 2025. "Adaptive Beamforming Damage Imaging of Lamb Wave Based on CNN" Applied Sciences 15, no. 7: 3801. https://doi.org/10.3390/app15073801
APA StyleShen, R., Zhou, Z., Xu, G., Zhang, S., Xu, C., Xu, B., & Luo, Y. (2025). Adaptive Beamforming Damage Imaging of Lamb Wave Based on CNN. Applied Sciences, 15(7), 3801. https://doi.org/10.3390/app15073801





