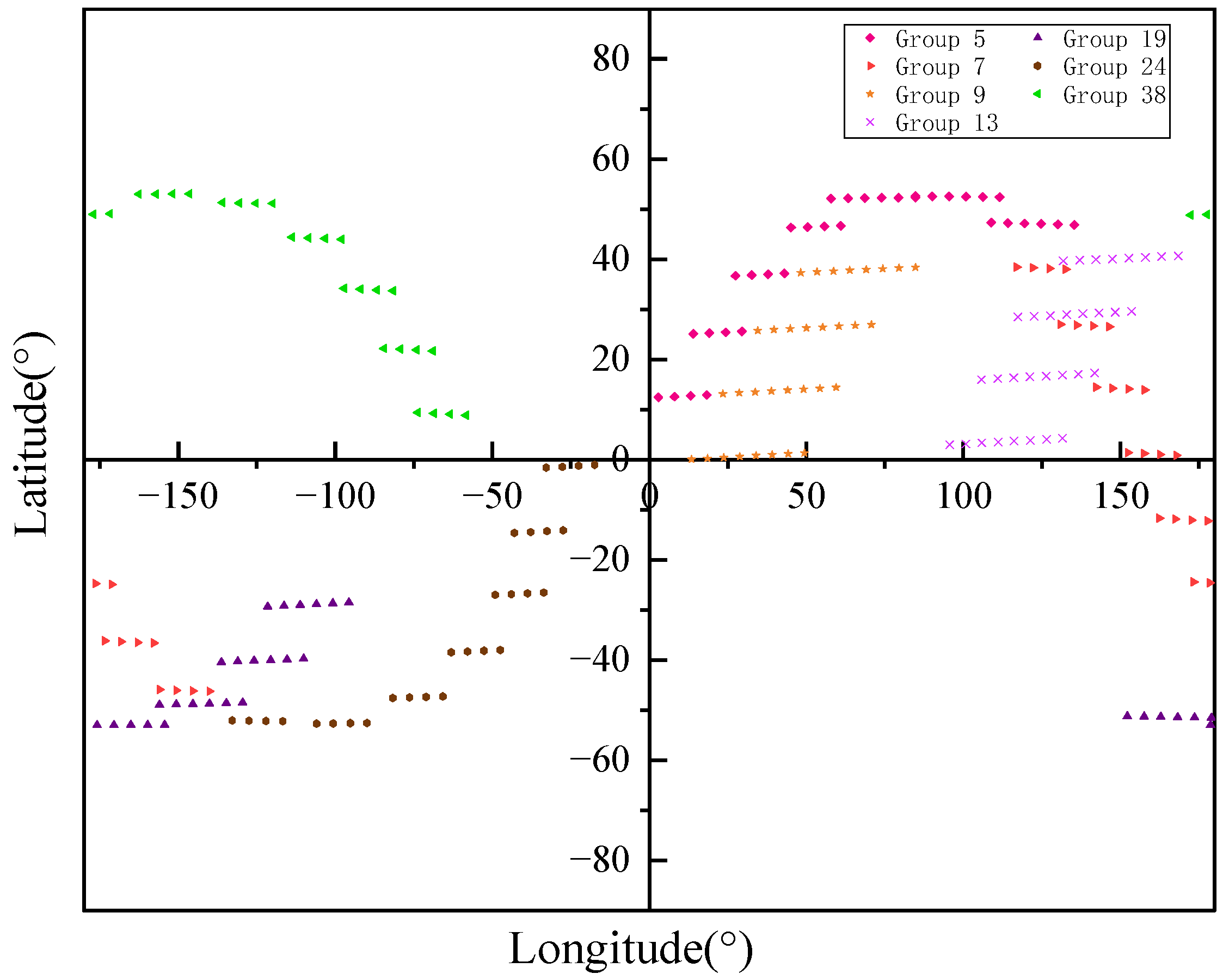Abstract
The development of low-orbit satellite communication networks marks the beginning of a new era in global communication. However, in the context of large-scale LEO satellite communication scenarios, the traditional adjacent connection transmission method limits the advantages of low latency in optical communication. Multi-hop transmission increases the number of hops and propagation distance, thereby affecting time-sensitive business transmissions. Therefore, based on the design of optical interconnect parallel subnetworks, this paper proposes a scheduling strategy for time-sensitive business transmissions between LEO satellites. Firstly, this strategy integrates the gate control scheduling mechanism from Time-Sensitive Networking (TSN) transmission in the interconnect parallel subnetwork scenario. Secondly, considering issues like queuing after subnetwork division, excessive burden, and algorithm complexity, mathematical problem abstraction modeling is applied to subsequent route scheduling, with reinforcement learning used to solve the problem. Through simulation experiments, it has been observed that compared to SPF (Shortest Path First) and ELB (Equal Load Balance), this approach can effectively enhance the control capability of end-to-end latency for TSN services in long-distance transmissions within Low Earth Orbit mega-constellations. The integration of reinforcement learning decision algorithms also reduces the complexity compared to traditional constraint-solving algorithms, ensuring a certain level of practicality. Overall, this solution can enhance the communication efficiency and performance of time-sensitive services between satellite constellations. By integrating time-sensitive network transmission technologies into optically interconnected subnets, further exploration and realization of low-latency and controllable latency satellite communication networks can be pursued.
1. Introduction
Despite the widespread development of technologies, such as 5G and optical transmission networks, the deployment of ground networks is still constrained by various factors, including geography, economics, and the environment. According to statistics from the International Telecommunication Union (ITU) [1], as of the end of 2022, approximately 5.3 billion people worldwide were using the Internet, while 2.7 billion people still did not have access to the Internet. Compared to traditional ground network solutions, satellite networks can provide broader coverage and can be applied in special scenarios, such as disaster relief and emergency communication. They can leverage satellite multi-beam capabilities to achieve large-scale flexible communication [2]. With these advantages, satellite networks serve as a flexible supplement and effective extension of ground mobile communication networks, integrating with ground networks to provide seamless coverage of network services. Low Earth Orbit (LEO) satellites, with their lower communication latency and superior signal quality, represent a key focus and important component of the current satellite industry.
However, current research on satellite networking methods is primarily based on existing microwave communication transmission technologies, focusing on small-scale networking and satellite–ground communication. The existing link scheduling schemes are not suitable for the context of Low Earth Orbit mega-constellations with inter-satellite laser interconnectivity. With the rapid increase in the number of satellites and the enlargement of network scales, as well as the expected use of laser communication schemes between satellites, in the context of tens of thousands of satellites, the increased routing hops and delays resulting from dense satellite networking may erode the advantages of laser communication [3]. Therefore, traditional satellite networking schemes fail to fully exploit the ultra-low latency advantages brought by networks of tens of thousands of satellites and inter-satellite laser communication. Simultaneously, as space communication tasks become increasingly complex, the demand for time-sensitive services continues to grow, posing new challenges for information transmission. On one hand, internal satellite systems are required to possess high bandwidth, reliability, and real-time capabilities. On the other hand, inter-satellite communication established through wireless links needs to have low latency and high reliability. However, when business data are forwarded within satellite nodes and transmitted via wireless links between satellites, congestion at nodes and uncontrollable transmission delays may occur, thus failing to meet the key requirements of real-time transmission and controllable latency for time-sensitive services.
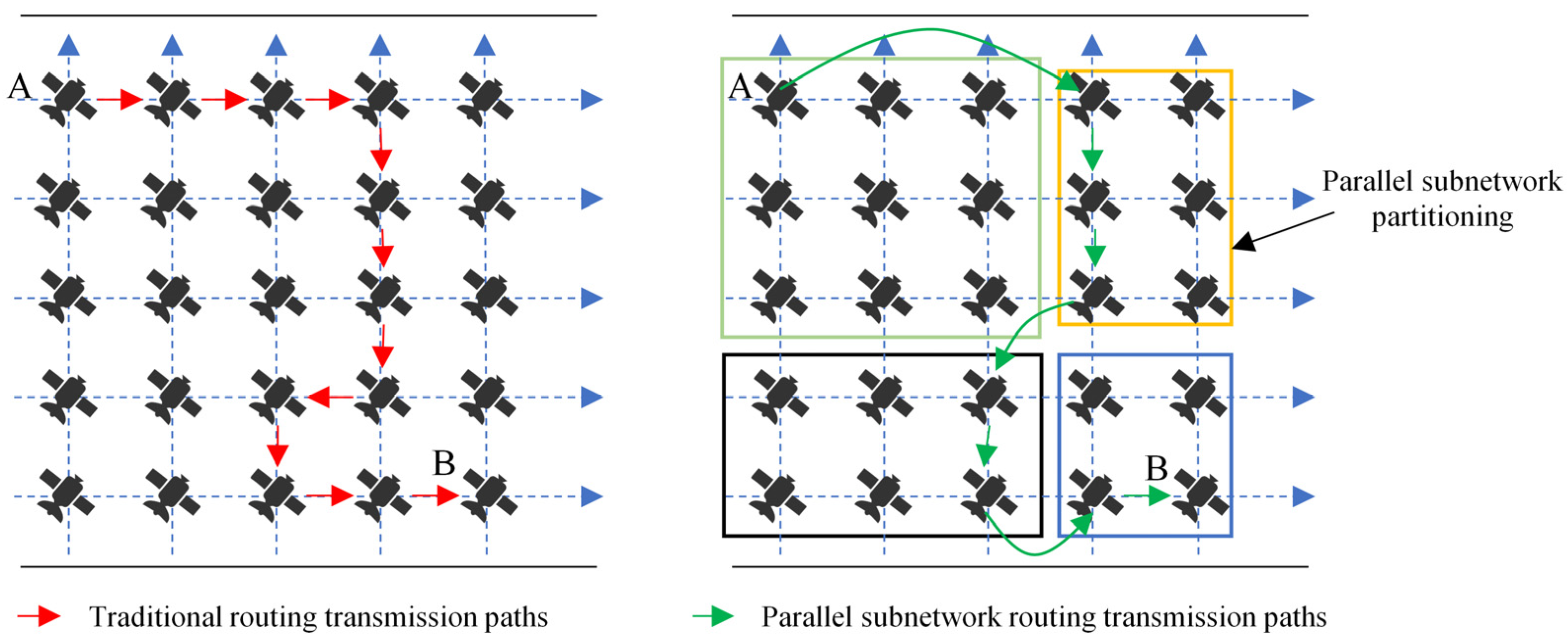
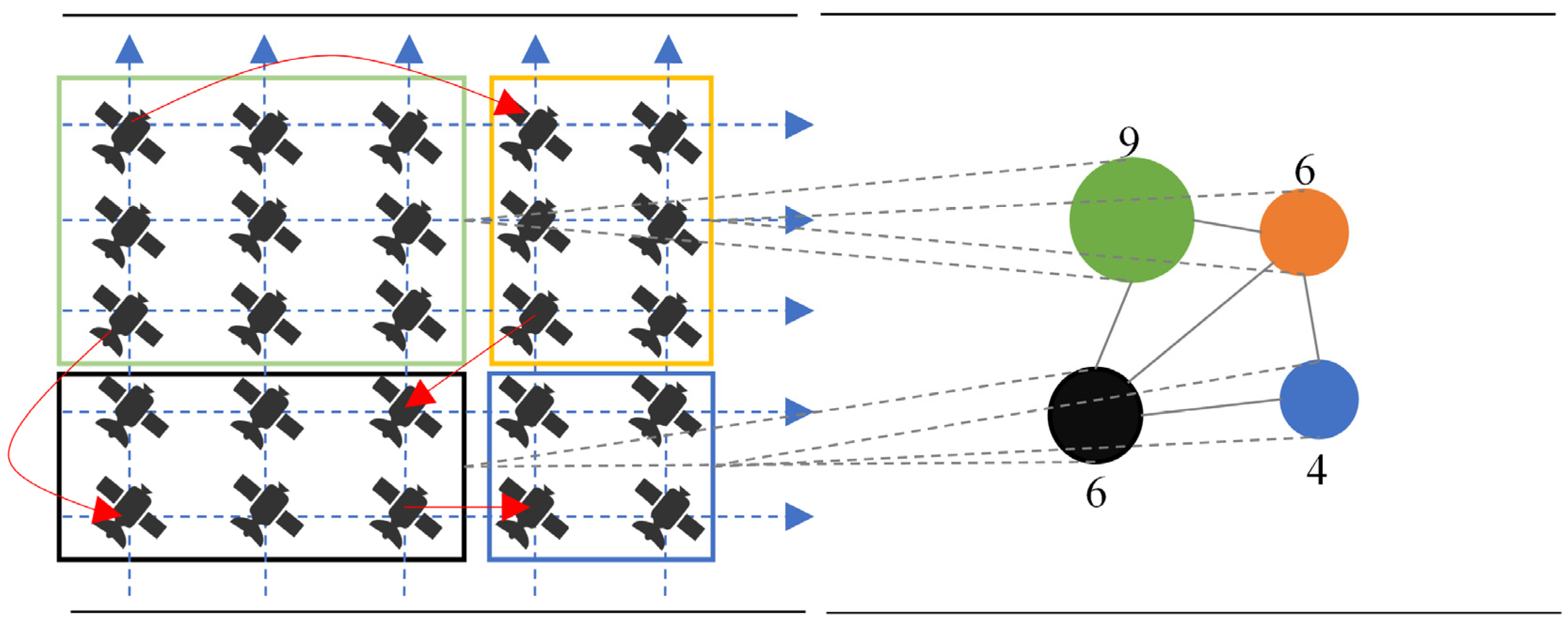
To simplify long-distance data business transfers, our team proposed a new solution based on optical interconnect parallel subnetworks for routing transmissions in earlier research [4]. Optical interconnect parallel subnetworks refer to dividing many satellites in the orbital plane of LEO satellites into multiple secondary subnetworks based on the spatial positions and link conditions of LEO satellites. The satellites within the same secondary subnetwork are closely related, and each secondary subnetwork is treated as a node [5], forming a new graph topology. This is known as the subdivided satellite network. Due to the small scale of the network and the lack of optical links, traditional satellite networks rely on routing communication with adjacent satellites, which poses challenges for long-distance transmission [6]. After subdividing into parallel subnetworks, communication within the network is based on optical links, with the lengths of adjacent satellite links within secondary subnetworks ranging from hundreds to thousands of kilometers. Additionally, there are adjacent satellite links and long-distance optical links between them, which can facilitate direct transmission using laser characteristics. The schematic difference between traditional satellite constellation routing and routing via parallel subnetworks is shown in Figure 1. The blue horizontal and vertical dashed arrows are the orbit of the satellite. Suppose there are two satellites A and B to transmit routing information. Clearly, after subdividing into parallel subnetworks, if time-sensitive services are being transmitted simultaneously within the same time frame, following traditional Dijkstra algorithms for routing within the subnetwork will inevitably lead to exceeding the time limit due to excessive hop counts, which does not meet the transmission requirements of time-sensitive services. Therefore, developing routing scheduling strategies to avoid queuing or worse scenarios for multiple time-sensitive service transmissions within the same time frame is a topic worthy of research.
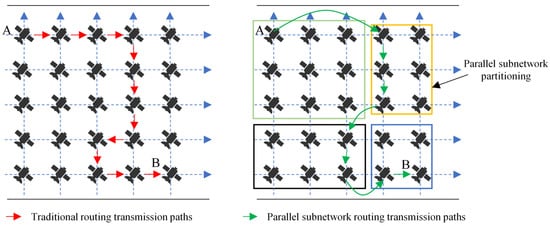
Figure 1.
The difference between traditional network routing and parallel subnetwork routing.
To ensure controlled latency, Time-Sensitive Networking (TSN) appears to be the most promising solution currently. TSN is an extension of traditional Ethernet, enhancing it with features like time synchronization mechanisms, credit-based traffic shaping mechanisms, time-based shaping mechanisms, gate control lists, and stream reservation while remaining fully compatible with traditional Ethernet. TSN and its extension into the wireless domain, such as 5G-TSN and WIFI-TSN, aim to provide deterministic communication for wireless mobile robotic arms and devices in cross-domain networks. The IEEE 802.1 [7] TSN Task Group (TG) is dedicated to developing a set of TSN standards, including sub-standards within IEEE 802.1 Ethernet. Therefore, TSN offers various sub-standards with diverse shaping and scheduling mechanisms, providing different levels of Quality of Service (QoS), such as Time-Aware Shaper (TAS), Asynchronous Traffic Shaper (ATS), and Credit-Based Shaper [8]. Among these mechanisms, TAS scheduling has been extensively researched over the years. TAS, through precise opening and closing of gates for Time-Triggered (TT) traffic types, offers time guarantees and zero jitters, facilitated by a gate mechanism known as Gate Control List (GCL). However, generating GCL for TAS is an NP-hard problem, with complexity increasing with network size and traffic volume. Therefore, various shaping mechanisms, like CBS, ATS, and CQF, have been proposed to alleviate TAS workload in mixed-criticality networks. Like TAS, CQF is also based on GCL. CQF is gaining popularity due to its simple GCL operations and direct computation of maximum and minimum jitter. While CQF does not provide the fine-grained scheduling of TAS, it offers a simple scheduling configuration with bounded delay and jitter. Hence, in mixed-criticality networks with diverse QoS requirements, selecting appropriate scheduling and shaping algorithms is becoming increasingly necessary.
Furthermore, research on integrating TSN technology into Low Earth Orbit (LEO) satellite constellation scenarios has only recently begun to emerge in the past few years. Existing studies on the IEEE 802.1Qbv gate scheduling mechanism primarily focus on wired networks, often assuming link delays as slow-changing or fixed values. References [9,10] propose gate scheduling models, but these models do not consider offsets in gate slots between neighboring nodes, assuming gate slot alignment. Reference [11] introduces a non-overlapping gate list window mechanism to enhance business curve rates and eliminate traffic congestion in TSN. Reference [12] considers the relative position relationships of gate slots between adjacent nodes, presenting a window-based flexible gate list scheduling model that reduces the latency jitter requirements for business flows. However, references [11,12] do not address scheduling strategies for time-sensitive service transmission as the number of satellites increases in LEO satellite constellations. In the LEO satellite constellation scenario, the unpredictable jitter in inter-satellite wireless link latency, which is far more complex than the predictable jitter in wired links, introduces deviations in gate openings between satellite nodes, posing significant challenges for the deterministic transmission of time-sensitive data. By the end of 2024, there was significant development in time-sensitive business transmission technologies based on Low Earth Orbit satellite constellations. For instance, Huawei has introduced the “Direct Satellite Connection for Mobile Phones” service, enabling users to access time-critical video and audio services directly through their mobile devices. SpaceX has also launched the “Star Shield” service, utilizing the Starlink constellation to rapidly access and transmit battlefield and security information.
Based on scenarios and emerging TSN technology for time-sensitive business transmission, the research work of this paper is as follows:
- (1)
- Establish a routing and scheduling model named parallel subnetworks—FJSP—Reinforcement Learning Scheduling, abbreviated as “PSFRS”, for time-sensitive business transmission in the scenario of optical interconnect parallel subnetworks. The objective is to minimize the multi-hop transmission delay for time-sensitive businesses, reduce resource consumption for satellite transmission, and adhere to constraints, such as the maximum number of simultaneous transmissions per satellite, the maximum number of hops for packet transmission, packet transmission interruption constraints, and the absence of priority constraints for time-sensitive business. Considering the characteristics of packet transmission in the objective function and constraints, we formulate the routing and scheduling strategy problem to achieve controllable multi-hop transmission delay in Low Earth Orbit satellite constellations. This problem involves multiple objective functions and coupled variables, making it challenging to obtain analytical solutions.
- (2)
- Address the potential queuing issues that may arise between subnetworks after reconfiguration in the optical interconnect parallel subnetwork. We utilize the controllability of delay in a single satellite using CQF gate scheduling in time-sensitive business transmission technology to extend the local end-to-end delay optimization problem to a global routing delay optimization problem. Consequently, the routing and scheduling problem in Low Earth Orbit satellite constellations transforms into a classic Flexible Job Scheduling Problem (FJSP). This transformation significantly enhances the feasibility of utilizing optical interconnect parallel subnetworks for time-sensitive business transmission and introduces a new approach for employing CQF gate scheduling for transmission in Low Earth Orbit satellite constellations.
- (3)
- Given the characteristic of optional selection for each hop in the routing of time-sensitive business transmission, we employ Q-learning-based reinforcement learning to solve the problems. This solution aligns with the requirements of routing and scheduling for time-sensitive business transmission in Low Earth Orbit constellations. Compared to traditional algorithms, this approach offers a superior solution to the NP-hard problem.
- (4)
- Building upon the previous work of the Optical Communication team at Shanghai University, simulations were conducted using existing simulation platforms and the specialized TSN simulation tool OMNET++ to validate the proposed models and routing scheduling strategies in time-sensitive business transmissions. The experiments focused on testing key metrics, such as algorithm complexity, constellation task burden, and end-to-end latency.
2. Related Work and Problem Description
In this section, the Low Earth Orbit satellite constellation scenario, parallel subnet architecture, and key technologies for time-sensitive business transmission data used in this paper will be introduced.
2.1. Low Earth Orbit Giant Constellation
The orbit height of satellites classifies them into four types: Geosynchronous Earth Orbit (GEO), Highly Elliptical Orbit (HEO), Medium Earth Orbit (MEO), and Low Earth Orbit (LEO). Each type of satellite has its own orbit height and functions, as shown in Table 1.

Table 1.
Satellite classification table based on orbital altitude.
Wu et al. [13] proposed a user mobility management mechanism based on the GEO/LEO architecture. Huang et al. [14] introduced an inter-layer link allocation scheme for MEO/LEO, aiming to maximize the utilization of inter-layer links. Truchly et al. [15] studied the impact of inter-layer connection modes in two-layer satellite systems (GEO/LEO, MEO/LEO, and MEO/LEO) on end-to-end latency. Jing et al. [16] presented a distributed routing algorithm based on the minimum evolving connected dominating set for GEO/MEO/LEO satellite networks. Building a satellite constellation with large exchange capacity, high communication rates, low transmission latency, and high security and reliability has become the development trend for next-generation satellite communications to achieve seamless global coverage of communication signals across the world [17].
GEO satellites orbit at an altitude of 35,786 km, moving at the same speed as the Earth’s rotation; hence, they are termed geosynchronous satellites. GEO satellites can establish stable, continuous, structurally simple, and wide-coverage satellite networks. However, due to the significant distance of GEO satellites from the Earth’s surface, they exhibit high link loss and communication delays, making them unsuitable for transmitting time-sensitive traffic, often limited to providing “bent-pipe” relay communication to the ground. Furthermore, the design, construction, and launch costs of GEO satellites are high. Consequently, more satellite communication companies and research institutions are shifting their focus towards LEO satellites, which offer lower launch costs, reduced communication delays, and lower power consumption [18]. This transition aims to achieve reduced round-trip delays between satellites and the ground and minimize inter-satellite transmission losses while enhancing the flexibility of satellite systems.
2.2. Low Earth Orbit Satellite Routing and Optical Laser Interconnection
In the past few decades, both domestic and international researchers have conducted extensive studies on satellite routing algorithms for Low Earth Orbit satellite constellations, making significant contributions to the continuous improvement and development of satellite routing. Early routing schemes can be mainly classified into two categories: virtual topology and virtual nodes.
Virtual topology involves the temporal virtualization of the network structure, discretizing the orbital motion into a series of time slots, with each time slot referred to as a snapshot. Within each snapshot, due to the short period, the topology of the satellite network is considered stable or quasi-static, with changes occurring only at the junctions of snapshots. In each snapshot, different satellite nodes are interconnected, indicating the establishment of communication links for data transmission. It is worth noting that each snapshot contains replicas of all satellite nodes, consuming a significant amount of onboard storage space. With the rapid increase in the number of satellites and the rapid expansion of constellation size, the interconnections between satellites have become more frequent, increasing the pressure on onboard storage and maintenance, leading to an increase in onboard task burden. This poses significant challenges and pressures on resource-constrained Low Earth Orbit small satellite networks. Reference [19] proposes a region-based satellite routing algorithm. Its core involves dividing satellite regions based on topological properties and implementing a distributed subdomain routing mechanism. Satellite nodes establish and maintain routing tables within domains and inter-domain routing tables. When there are topological changes, only a few intra-domain routing tables need to be updated, while inter-domain routing tables are updated only when inter-domain neighbor relationships change. This approach enables fast rerouting in dynamic networks.
Virtual nodes involve virtualizing the satellite network into fixed-coordinate virtual nodes, assuming that the entire Earth’s surface can be covered by the Low Earth Orbit satellite constellation. The logical positions within the constellation remain unchanged, and when a satellite is relocated, its position is inherited by the nearest satellite. Specific routing decisions are calculated by relevant controllers, but a potential issue that arises with a substantial increase in traffic is the occurrence of link congestion, resulting in a decline in algorithm performance [20]. In the context of virtual node technology, regarding the issue of link failures in satellite networks, Zhu et al. proposed a dual-layer satellite network routing algorithm based on priority and fault probability. This algorithm considers business classification and link failure probabilities to meet various Quality of Service (QoS) requirements for different services [21].
Inter-satellite links (ISLs) play a crucial role in satellite networks, with two methods of communication: microwave and laser communication. Compared to the former, laser inter-satellite links (LISLs) offer advantages, such as high transmission bandwidth, high channel throughput, strong anti-interference capabilities, high security, and confidentiality, making them an effective means for achieving high-speed satellite communication. In September 2020, Starlink first installed laser units on the 12th batch of satellites at a 53° inclination, and, starting from 13 November 2021, subsequent launches of the V1.5 version satellites have all been equipped with laser units [22]. Due to the small divergence angle of laser communication, precise alignment of communication components at the transmitting and receiving ends is required to establish inter-satellite links. Currently, laser inter-satellite links rely on Acquiring, Tracking, and Pointing (ATP) systems to achieve high-precision tracking and pointing assistance [22]. According to documents submitted by SpaceX to the FCC in 2018, each Starlink satellite is equipped with four laser units distributed on the front, back, left, and right sides of the satellite’s baseplate. Therefore, the satellite model used in the simulation in this paper is Starlink’s satellite, with inter-satellite communication in the directions of front, back, left, and right [23].
2.3. Parallel Subnetwork Routing Architecture
The introduction of the optical interconnection parallel subnetwork algorithm aims to address the issue of excessive hops in large Low Earth Orbit (LEO) constellations. The core idea of this algorithm is to partition these satellites into multiple secondary subnetworks based on the positional information and connectivity status of the LEO satellites. Subsequently, the algorithm establishes optical links within each subnetwork and between different subnetworks. The design of the secondary subnetworks and the scheduling of optical connections are based on snapshots of the satellite topology at specific time points. In theory, the partitioning of secondary subnetworks and the selection of connected satellite pairs will evolve with changes in the current link conditions. Due to the periodic nature of satellite movement, these changes exhibit periodic characteristics globally. Additionally, the fundamental requirement for establishing long-distance links is the presence of satellite pairs with line-of-sight visibility and sufficient available power in both subnetworks [4].
When applied to routing and transmission in Low Earth Orbit constellations, this algorithm only considers single services and single paths. However, in practical scenarios, especially in time-sensitive service transmission scenarios, multiple services and paths may exist simultaneously within the same period. Therefore, this paper has made improvements to the algorithm to account for these multi-service and multi-path transmission scenarios.
2.4. Time-Sensitive Network and Deterministic Network
Time-Sensitive Networking (TSN) is an extended standard Ethernet technology that is backward compatible with standard Ethernet. It enables us to achieve low jitter, low latency, and robust communication channels through standard Ethernet. As an IEEE standard, TSN will be a vital component of future real-time Ethernet communication [24]. TSN transmission technology is a protocol suite consisting of multiple sub-protocols, each serving different functions [25].
By providing determinism and high reliability through compatible collaboration for data transmission, TSN protocols offer low latency, low jitter, and extremely low data loss rates. Through techniques like clock synchronization, bandwidth reservation, gate operation mechanisms, flow filtering and policing, frame preemption, and cyclic queuing forwarding, TSN enhances the real-time capabilities of standard Ethernet, opening a new realm for real-time Ethernet communication.
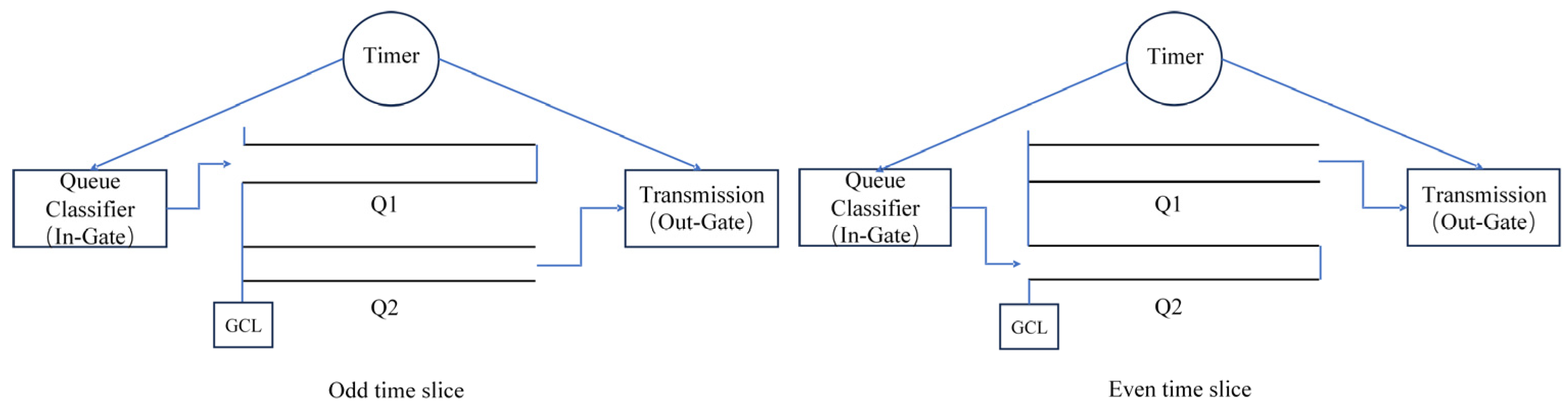
The CQF (Credit-Based Shaper with Queueing and Forwarding) gate control scheduling used on a single satellite in this paper is based on the IEEE 802.1Qch protocol. This protocol is widely employed in Deterministic Networking (DetNet) transmissions, aiming to provide deterministic quality of service guarantees for network services [26]. As depicted in Figure 2, each TSN switch applied to satellites with CQF functionality features two queues for the CQF mechanism: an even queue and an odd queue. Within a fixed time slot (T), one queue continuously receives and buffers incoming data frames, while the other queue transmits frames received in the previous time slot. The tasks performed by the two queues in alternating time slots are opposite. Clearly, utilizing this technology on each satellite within the parallel subnetwork architecture is beneficial for reducing latency jitter and uncertainty in multi-hop networks.
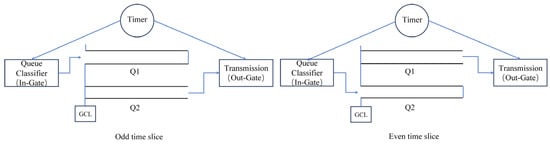
Figure 2.
CQF scheduling mechanism diagram.
2.5. Reinforcement Learning Algorithm
Reinforcement learning (RL), a field of study within machine learning, involves designing a class of learning algorithms that enable computers to start from scratch, learn through trial and error, discover patterns from mistakes, and eventually achieve goals. Inspired by human behavioral psychology, RL aims to make decisions that benefit the agent itself [27]. In RL, there is no concept of absolute right or wrong; instead, it relies on self-defined reward values to optimize its strategies. Therefore, this characteristic of reinforcement learning presents significant advantages in solving NP-hard problems [28].
There are four key concepts in reinforcement learning: reward, policy, agent, and environment.
- (1)
- Reward: The goal of reinforcement learning is to maximize rewards. The agent receives a reward after each interaction with the environment;
- (2)
- Policy: A policy refers to the action plan devised based on the current situation. In reinforcement learning, a policy indicates the probabilities that guide the agent in choosing actions in different environments;
- (3)
- Agent: In reinforcement learning, the agent plays the roles of observer, decision maker, and learner. Depending on the number of agents involved, reinforcement learning can be categorized into multi-agent and single-agent models;
- (4)
- Environment: The environment encompasses all aspects of reinforcement learning apart from the agent, including the current location and transition rules. It refers to the uncontrollable elements in the learning process.
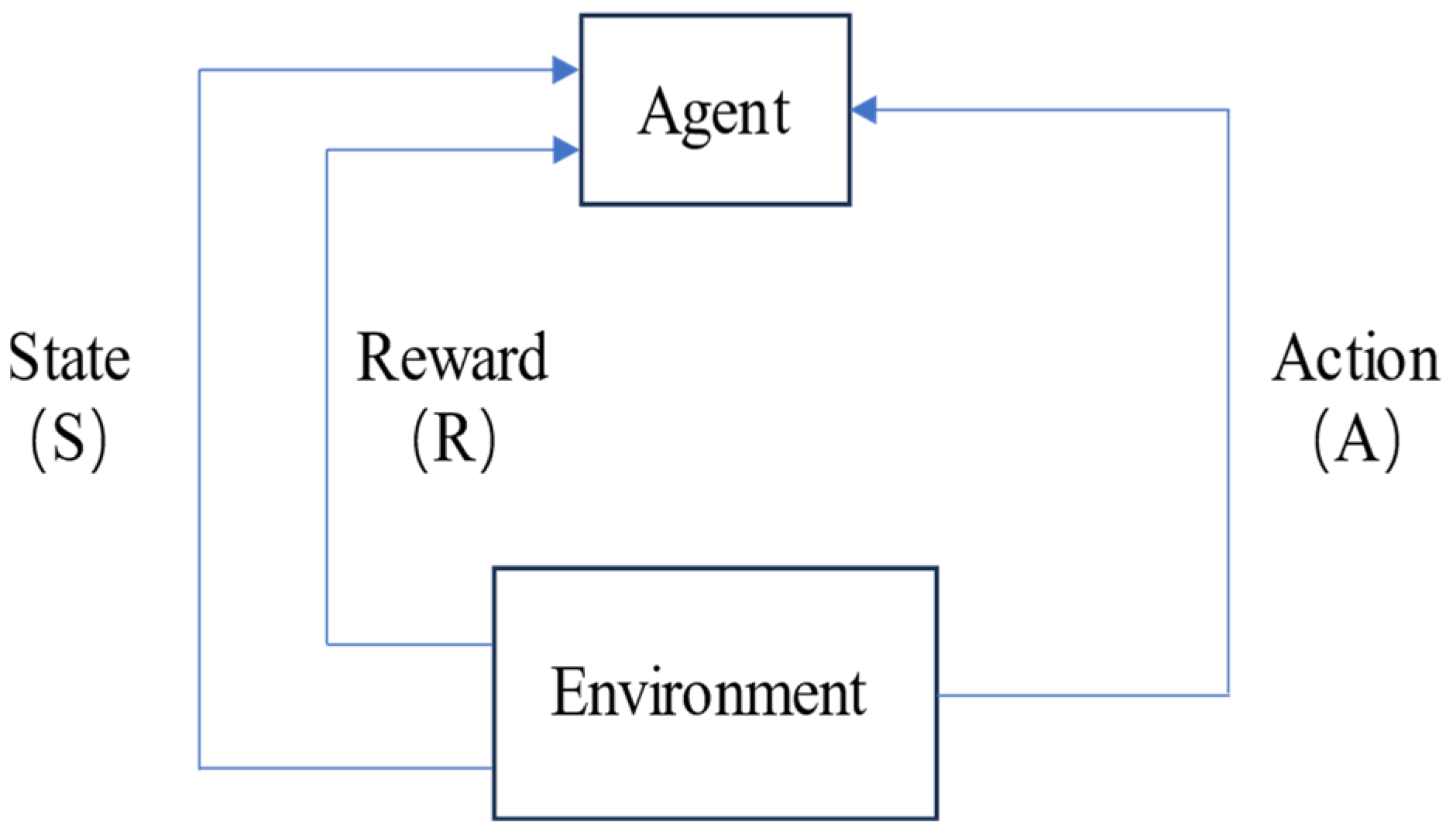
The interaction between the agent and the environment mainly consists of the following three steps:
- (1)
- The agent observes the current environment and obtains its own state S.
- (2)
- The agent makes decisions based on its current observations and its policy, selecting an action A to execute.
- (3)
- The agent changes its state based on the executed action through the environment and receives a reward R.
The basic logic diagram of reinforcement learning is shown in Figure 3.
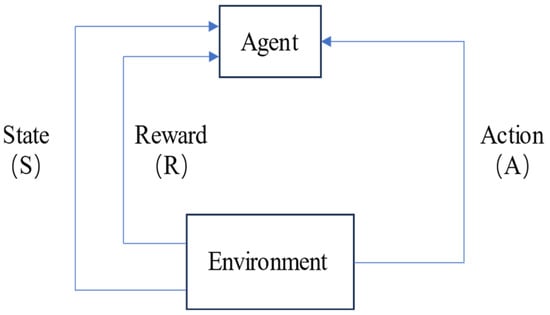
Figure 3.
Flowchart of reinforcement learning principles.
3. Materials and Methods
In this section, a detailed overview of the proposed structure of the time-sensitive business transmission model based on optical interconnect parallel subnets will be provided, elucidating the functions of its components.
3.1. The Structure of the Proposed Model
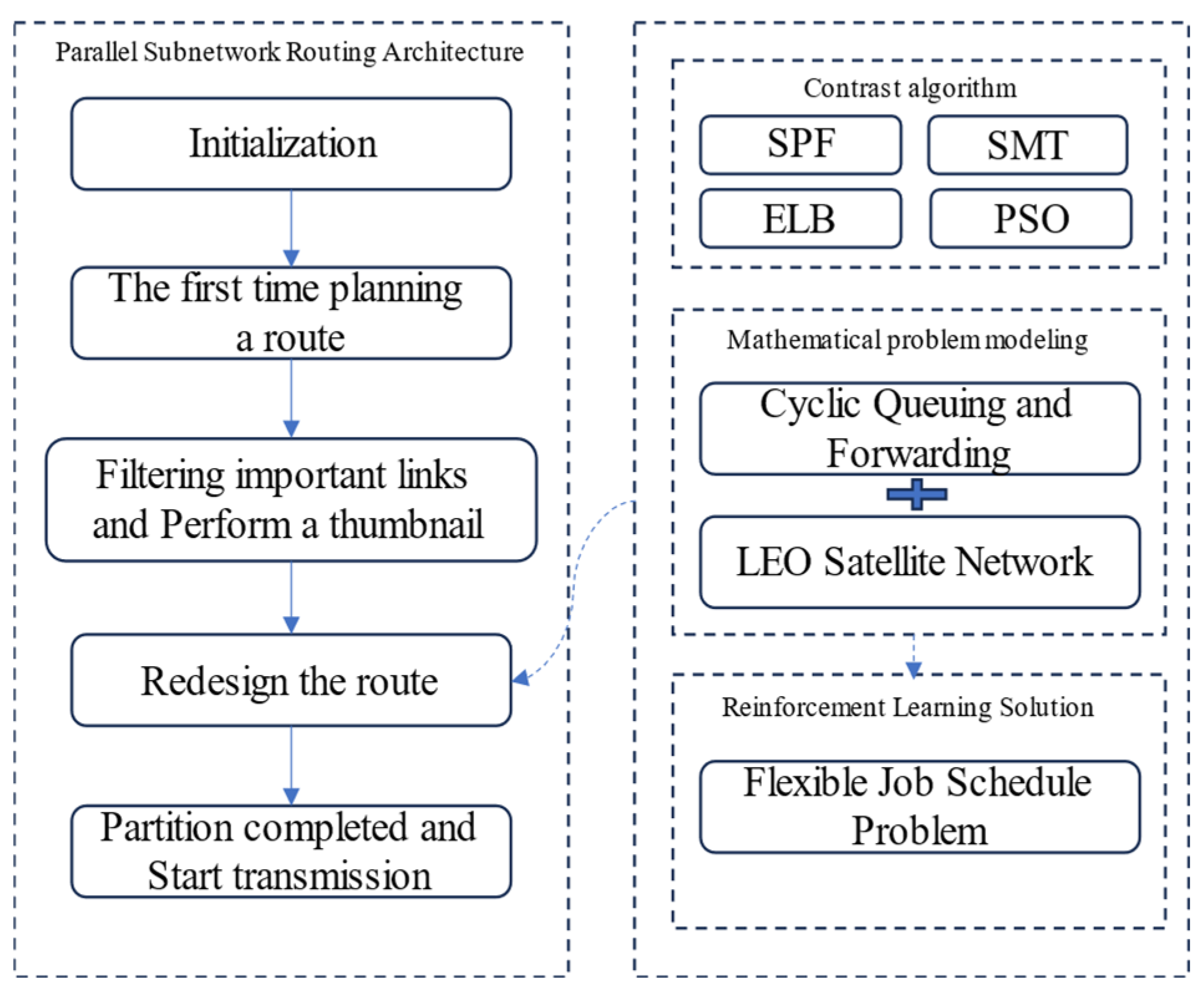
The architecture of the time-sensitive service transmission model based on the optical interconnect parallel subnet comprises two main components, as illustrated in the diagram below: the model construction part and the algorithm-solving part.
It is described in detail in Figure 4.
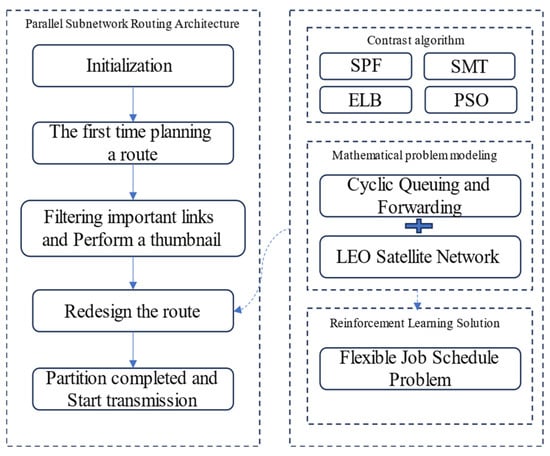
Figure 4.
The whole process of the model.
- (1)
- The introduction of the optical interconnect parallel subnet aims to overcome the limitations of traditional Low Earth Orbit constellation routing for the transmission of time-sensitive services. The latter faces some obstacles that are difficult to overcome at the transmission level. Detailed explanations of the optical interconnect parallel subnet can be found in Section 3.2.
- (2)
- The introduction of the CQF (Credit-based Queueing and Forwarding) gate control scheduling in TSN (Time-Sensitive Networking) technology aims to enhance the stability and controllability of time-sensitive service forwarding and processing in LEO (Low Earth Orbit) satellite networks. Detailed explanations of the CQF gate control schedule can be found in Section 3.3.
- (3)
- The mathematical modeling of routing in LEO satellite networks based on CQF scheduling is conducted because the various factors and constraints of this issue align with classical industrial processing control problems, making it amenable to transformation. Details of the mathematical modeling are discussed in Section 3.4.
- (4)
- The introduction of reinforcement learning for solving the satellite routing scheduling problem is aimed at leveraging scenarios that align with the application conditions of reinforcement learning, thereby reducing the likelihood of traditional solutions getting stuck in local optima. Detailed information on the utilization of reinforcement learning is provided in Section 3.5.
- (5)
- The performance of the time-sensitive service transmission model based on the optical interconnect parallel subnet is compared with traditional routing scheduling algorithms and conventional solving methods to demonstrate its advantages. Specific experimental results are presented in Section 4.
3.2. Detailed Description of the Routing Algorithm
In this paper, the entire LEO satellite optical interconnect network is graphically depicted as
where is the set of satellite nodes equipped with TSN forwarding switches and is the set of directed edges connecting two nodes, representing full-duplex optical interconnection physical connection paths between two nodes. Traditional inter-satellite links (ISLs) use microwave communication, while laser inter-satellite links (LISLs) utilize high-frequency lasers as carriers. The reason for choosing laser links in this paper is that the laser carrier frequency is 3 to 5 orders of magnitude higher than that of microwaves, allowing it to carry more information. Therefore, LISLs have higher signal bandwidth and antenna gain. Additionally, laser wavelengths are smaller than microwave wavelengths, and the optical antennas and other devices required for laser communication are lighter and smaller compared to those needed for microwaves, meeting the development requirements of satellite miniaturization and low orbit deployment [29].
Based on the team’s previous research [4], the process of dividing optical interconnection parallel subnets can be briefly outlined as follows. Obtain the IP addresses of each satellite and the laser connection information table. According to the laser connection information table, use the satellite’s logical address to find the preceding and succeeding satellites in the same orbit and neighboring satellites to the left and right. Connect the satellite node to these four adjacent satellites to complete the initialization. Repeat this process for each satellite to establish satellite connections with equal initial costs. Initiate connections between adjacent satellite nodes and plan routes using the traditional Dijkstra path algorithm. After selecting important links based on a set threshold, reduce the graph based on traffic weights and strong connectivity algorithms to divide the entire satellite constellation into several parallel subnets. Use cross-links between parallel subnets and strong connections within each subnet. Repeat the above steps to convert inter-subnet connections into long-distance connections to ensure specific services. Perform route replanning; use the original routing method for services within each subnet, and calculate link costs within the subnet; for inter-subnet services, use long-distance links to connect satellite nodes across the two subnets. After the partitioning is complete, the topological structure of a portion of the satellite network is transformed into Figure 5.
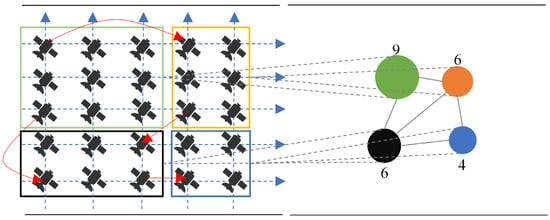
Figure 5.
Long-distance optical links and the division of primary and secondary parallel subnets.
3.3. CQF Scheduling Mechanism
For time-sensitive operations, utilizing a periodic cyclic scheduling and forwarding mechanism is a key technology for deterministic transmission. The satellite’s physical layer responsible for forwarding functions includes TSN switches that can handle time-sensitive business transmissions. Leveraging the characteristics of these switches, gate scheduling based on odd–even time slots with time-protected segments is employed for the transmission of time-sensitive operations.
In the CQF model, TSN switches are configured with a CQF scheduling mechanism that includes two queues (even and odd). The CQF mechanism operates using a single time slot , with a gate of length cyclically alternating its operation within each time slot. In each time slot of length , one queue receives data, while the other queue transmits data [30]. Furthermore, the timer module in the SW is utilized to control the opening and closing of transmission gates on the forwarding ports.
In some cases, TSN packets might be transmitted behind lower-priority traffic, and if lower-priority packets are too large, they may not meet the latency requirements of time-sensitive operations, potentially leading to congestion in time-sensitive operations.
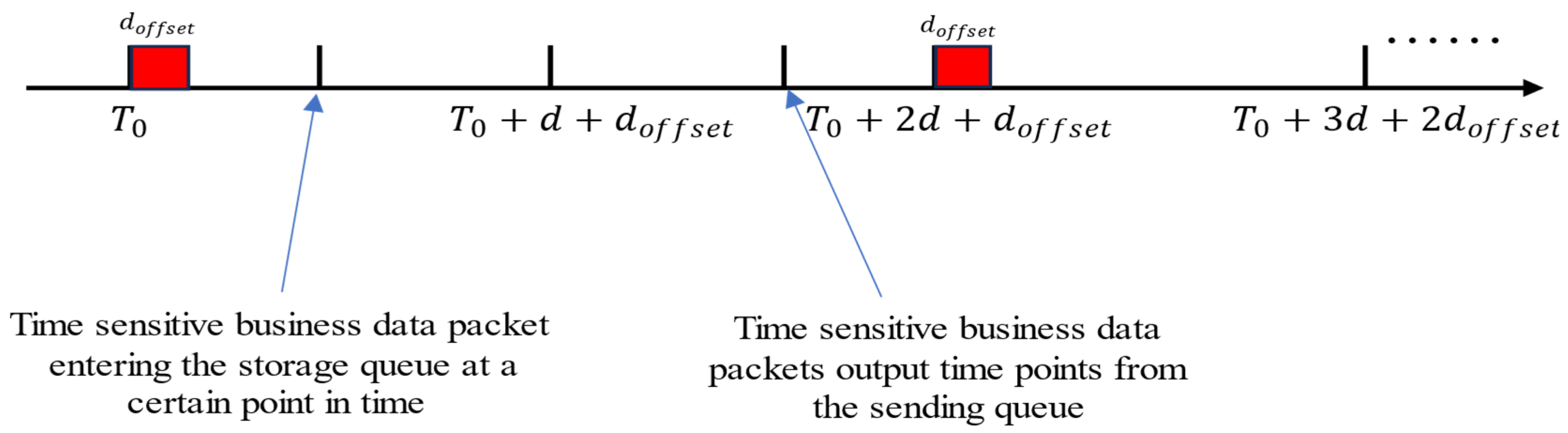
To address this issue, this paper proposes to allocate a period (typically equivalent to the transmission time of a standard Ethernet frame) before the scheduled transmission of time-sensitive operations, during which no lower-priority traffic can be transmitted. The time axis for gate-controlled switching in CQF forwarding within a single satellite is illustrated in the Figure 6.
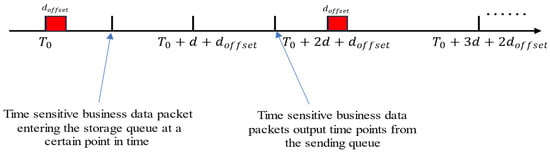
Figure 6.
Key time points in CQF gate scheduling.
Assuming the timer starts counting at , at this moment, Queue 1 in the SW opens for data transmission and closes for data writing, while Queue 2 opens for data writing and closes for data transmission. After a time period , when the timer module reaches the threshold , the states of the two queues are flipped: Queue 1 opens for data writing and closes for data sending, and Queue 2 closes for data writing and opens for data transmission. Therefore, the time point for the switch in the gate opening and closing transition becomes
Based on the key time points in the CQF gate scheduling diagram provided above, the switch in the previous hop satellite, upon receiving frame in time slot , will definitely be able to forward the arriving frame to the switch in the next hop satellite in time slot . Therefore, the maximum delay is from the beginning of the first time slot to the end of the last time slot, plus the width of the guard band, as follows:
The minimum delay is from the time node at the end of the starting time slot to the time node at the beginning of the next time slot, as follows:
Therefore, it can be inferred that the range of frame forwarding jitter on a single satellite is
Furthermore, it can be further deduced that the delay of forwarding utilizing the CQF cyclic gate control mechanism in a multi-hop satellite network can be expressed as
In the equation, represents the number of hops in the satellite network.
Based on the odd–even cycle gate scheduling, by combining the data frame guard band and cyclic forwarding mechanism, the forwarding delay of a single satellite becomes predictable and controllable. When extended to the entire network, it enhances the overall predictability and controllability of the satellite network transmission delay.
3.4. Mathematical Problem Modeling
Based on the CQF scheduling mechanism and the transmission mechanism of LEO satellite constellations mentioned above, this paper mathematically models the process of time-sensitive business transmission in Low Earth Orbit satellite constellations. Building upon the theory discussed earlier, the forwarding delay of a single satellite is controllable. Extending this to the initially partitioned parallel subnet, the transmission within the subnet transforms into a multi-objective optimization problem aimed at optimizing overall delay and energy consumption by controlling the flow of packet transmissions. This represents a classic Flexible Job Scheduling Problem (FJSP). In the context of the FJSP problem, where each workpiece can be processed on multiple machines for each operation, with processing times varying across machines, actual production can flexibly select resources based on the workload to enhance processing flexibility [31]. Therefore, it is evident that routing transmission and packet forwarding in Low Earth Orbit satellite constellations align with the elements and application scenarios of the FJSP problem, abstracting into an FJSP problem.
To solve the FJSP problem abstracted from time-sensitive business transmission in Low Earth Orbit satellite networks, the mathematical symbols and definitions of the variables involved in the FJSP problem are presented in Table 2.

Table 2.
Symbol definitions of FJSP.
Additionally, there are some constraint discriminants, as follows:
Typically, the general FJSP problem is subject to the following constraints:
Equations (10) and (11) represent the constraints on the sequence of each hop for each data packet. Equations (12) and (13) indicate that at any given time, a single satellite’s port can forward only one hop. Equation (14) signifies the machine constraint, meaning that at the same time, the same hop can only be forwarded by a single satellite port.
In the process of solving the FJSP, the evaluation of the quality of a feasible solution requires measurement through an objective function. Common optimization objectives found in the relevant literature include minimizing , minimizing total machine load, minimizing maximum machine load, and minimizing delay [32].
In this paper, the objective of solving the FJSP is to find a feasible solution that minimizes both the maximum transmission completion time and satellite buffer consumption simultaneously. In the method of solving multi-objective optimization functions, the use of a weighted sum has been verified as a viable approach, and the weights of each optimization objective can be adjusted based on the actual production requirements [33]. Therefore, the design of the objective optimization function in this paper is formulated as shown in Equation (15):
where denotes the maximum completion time value, denotes the total energy consumption required to complete all processes, and reflects the importance of each objective optimization target, with 0 < < 1.
3.5. Solution Based on Reinforcement Learning
In this paper, the classic Q-learning algorithm is used to solve the above problem. Q-learning is a reinforcement learning method where an agent takes actions based on the current state and the environment provides corresponding feedback signals based on the actions taken by the agent. The agent updates the Q-values stored in the Q-table according to this feedback and uses these continuous feedback values to determine changes in states. This process is repeated until the agent determines that the state is a final state, at which point the learning ends.
Simply put, at a given time t, the agent will receive a reward value from the environment and the next state S, and at time t + 1, the agent will provide an action A to the environment based on this information. This process continues iteratively until the agent can make the best decision.
The Q-learning algorithm selects actions in two ways. One is the greedy strategy, where decisions are made based on the maximum expected value in the Q-table; the other is the -greedy strategy. The Q-table is updated after each action selection, and its update formula is based on the Bellman equation [34], as shown in Equation (16):
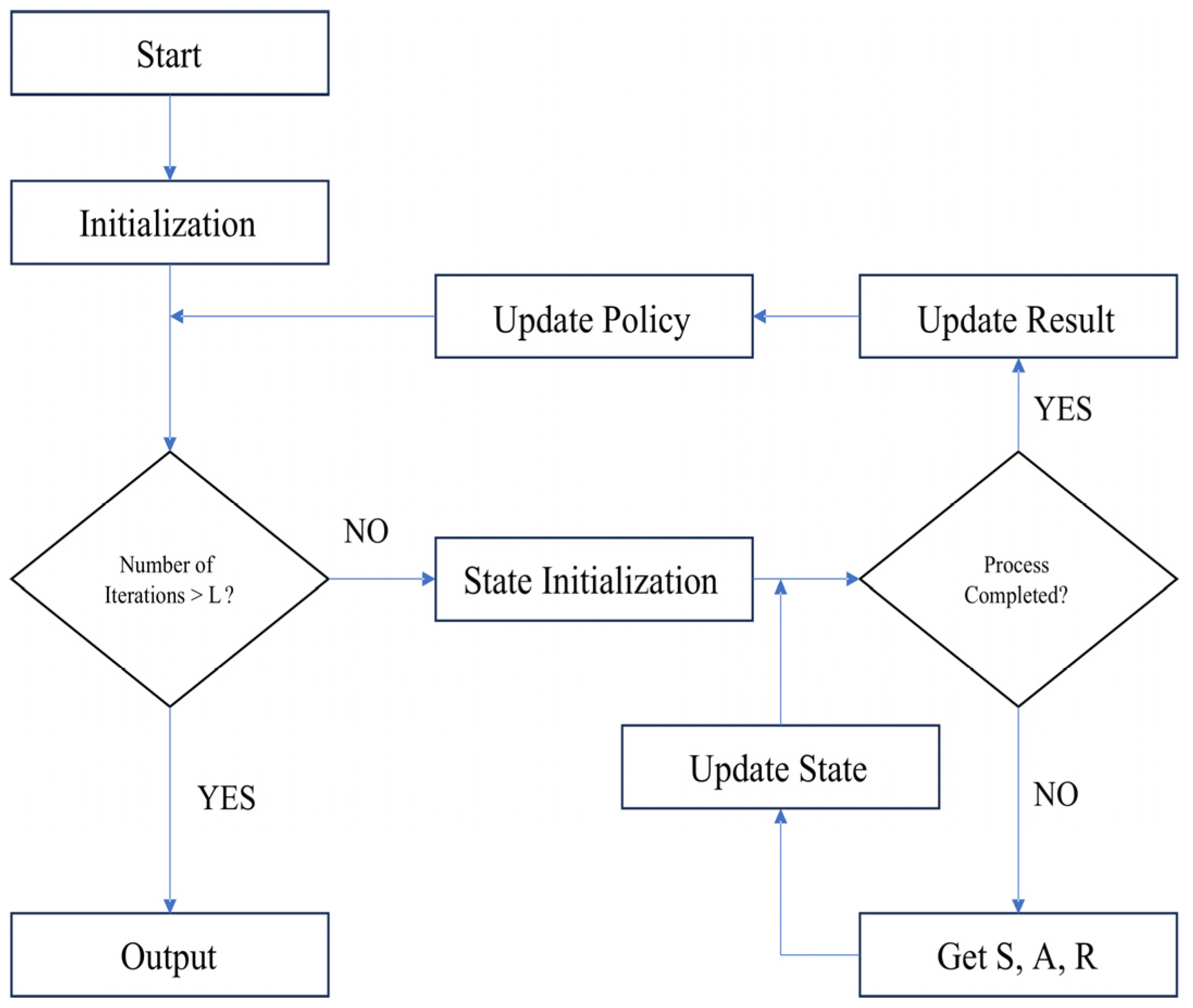
The specific algorithm flowchart is shown in Figure 7. This paper mainly introduces randomly generated feasible operation codes as prior knowledge of the algorithm while optimizing the maximum transmission time and satellite task burden. It mainly consists of the following five parts:
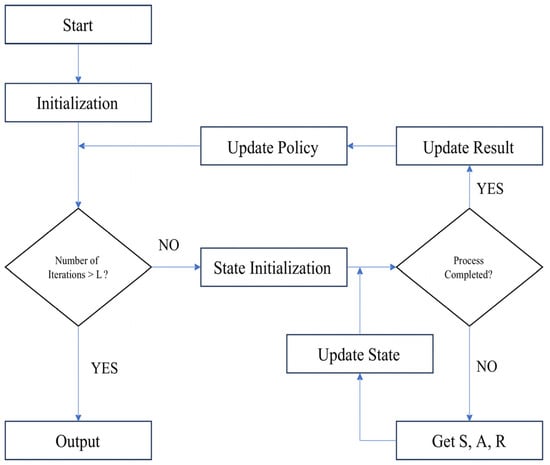
Figure 7.
Reinforcement learning algorithm flowchart.
- (1)
- State Space. The state space can be defined as a finite set of all jumps. To facilitate the representation of all states, coupling numbers can be used, where represents the packet number and represents the jump number.
- (2)
- Action Space. The agent selects a satellite for forwarding based on the current state, which includes each hop during forwarding and the satellite situation. In this problem, the total number of satellites is , so the action space is typically defined as a finite set of the number of satellites, denoted as .
- (3)
- Reward Function. The optimization goal is to minimize the maximum transmission time and minimize the total task burden. The larger the satellite task burden, the smaller the reward ; the longer the total transmission time of the satellite, the smaller the reward .
- (4)
- Selection Policy. When the agent is in a certain state S, taking an action will, with a probability of 1 − , choose the action corresponding to the maximum Q-value in the Q-list, and, with a probability of , randomly select an action.
- (5)
- Random Generation of Jump Codes. Randomly generate process codes. Under the constraints of the problem, feasible jump codes are randomly generated based on the number of packets and transmission hops as prior knowledge for the algorithm.
4. Experiment
4.1. Simulation Model Establishment
The experimental setup uses Windows 10 as the operating system, equipped with an AMD R5 4500 u CPU. Python 3.8 serves as the primary tool for reinforcement learning solutions. The parameters for reinforcement learning are set as follows: are commonly used numerical values in the Q-table update formula, and parameter is used for calculating actions during random selection in the algorithm iteration, indicating a higher weight on completion time. The reinforcement learning algorithm iterates 200 times.
The data packet format used in this paper is shown in Figure 8. Type is used to differentiate data packets, representing AF, BF, and EF types of data packets. In brief, different values indicate different priorities. Packet Length indicates the length of the data packet. Source and Destination represent the source satellite node and the destination node of the data packet, respectively. Data denote the contents being transmitted in the packet. Check Code is used to verify if any errors occurred during the data packet transmission process.

Figure 8.
Packet format.
The simulation of this paper adopts satellite constellations based on optical inter-satellite links using the Starlink mega-constellation as an example. The constellation consists of 1584 satellites, with an ideal inter-satellite distance of 60–300 km, considering the absence of reverse seams and pole issues, and the satellites are positioned at a height of 550 km above the ground. The inter-satellite optical link transmission speed is km. The gate control scheduling conversion time within a satellite is 400 . As shown in Figure 9, the 1584 satellite nodes are divided into 56 secondary subnetworks using the Louvain algorithm, from which 7 sets of subnetworks are extracted. For the sake of image simplification, this article only selects seven sets of satellites at mid-latitudes after division as examples. In addition to adjacent connections with neighboring subnetworks, each secondary subnetwork also establishes long-distance connections with visible subnetworks. Satellites in the 7th subnetwork have established long-distance connections with different satellites in the 5th, 9th, 13th, 19th, 24th, and 38th subnetworks. Subsequently, rerouting and data scheduling will be based on the new topology structure.
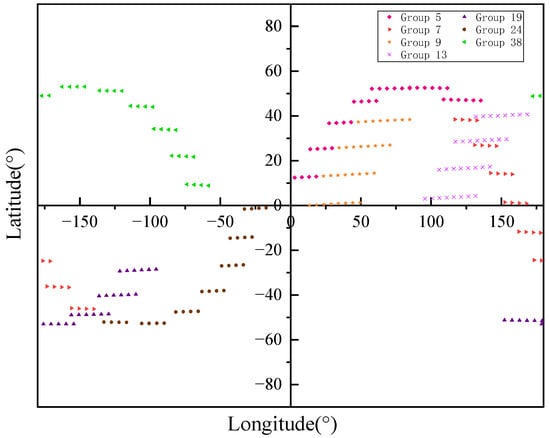
Figure 9.
Partially partitioned optical inter-satellite subnetwork.
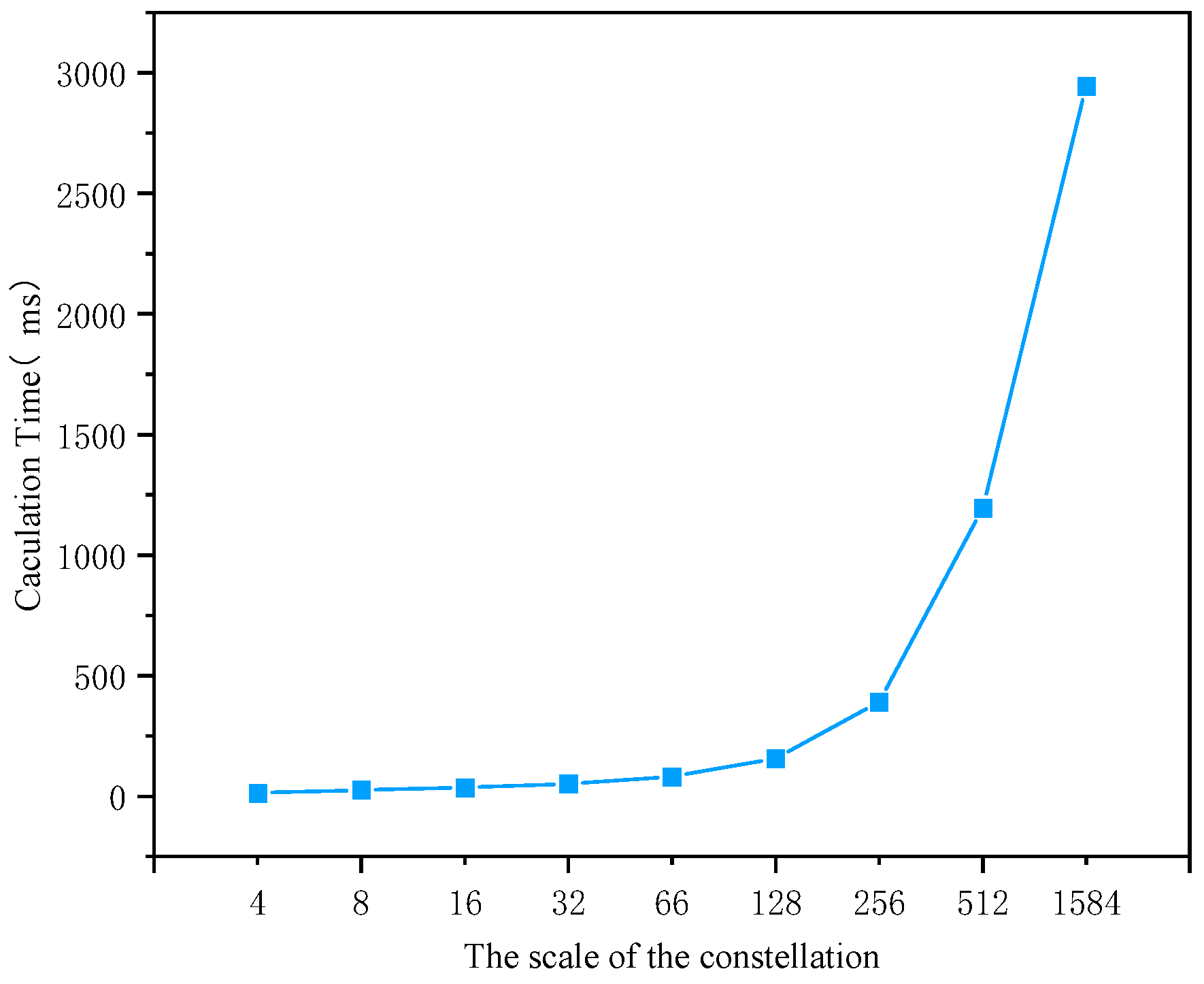
For constellation sizes of 4, 8, 16, 32, 66, 128, 512, and 1584 satellites, the computation time of the visibility model was recorded ten times each, and the average was calculated. The reason for selecting these constellation sizes is that they represent the number of satellites in satellite constellations that are suitable for different scenarios in practical applications. The experimental results are shown in Figure 10. It can be observed from the graph that when the constellation size is less than 100 satellites, the computation time of the visibility model is less than 100 ms. As the constellation size increases, the computation time of the visibility model also increases due to the need to traverse the visibility between all satellites. When the constellation size reaches 1584 satellites, the overall constellation computation time is 2.946 s, showing relatively low computational time. To simplify the complexity of this paper and reduce computation time, a pre-partitioned subnetwork is selected for the next step of routing scheduling and data transmission.
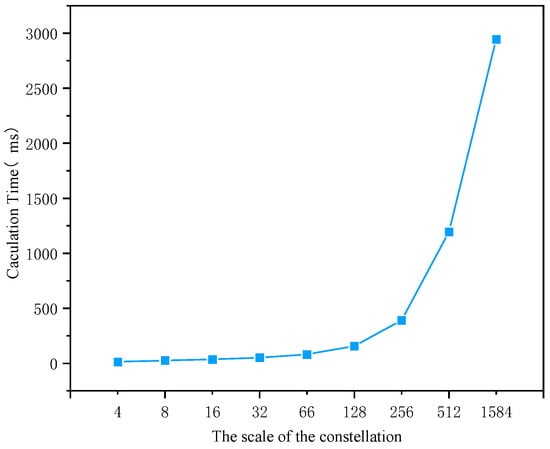
Figure 10.
Model computation time as a function of the number of satellites.
4.2. Experimental Results
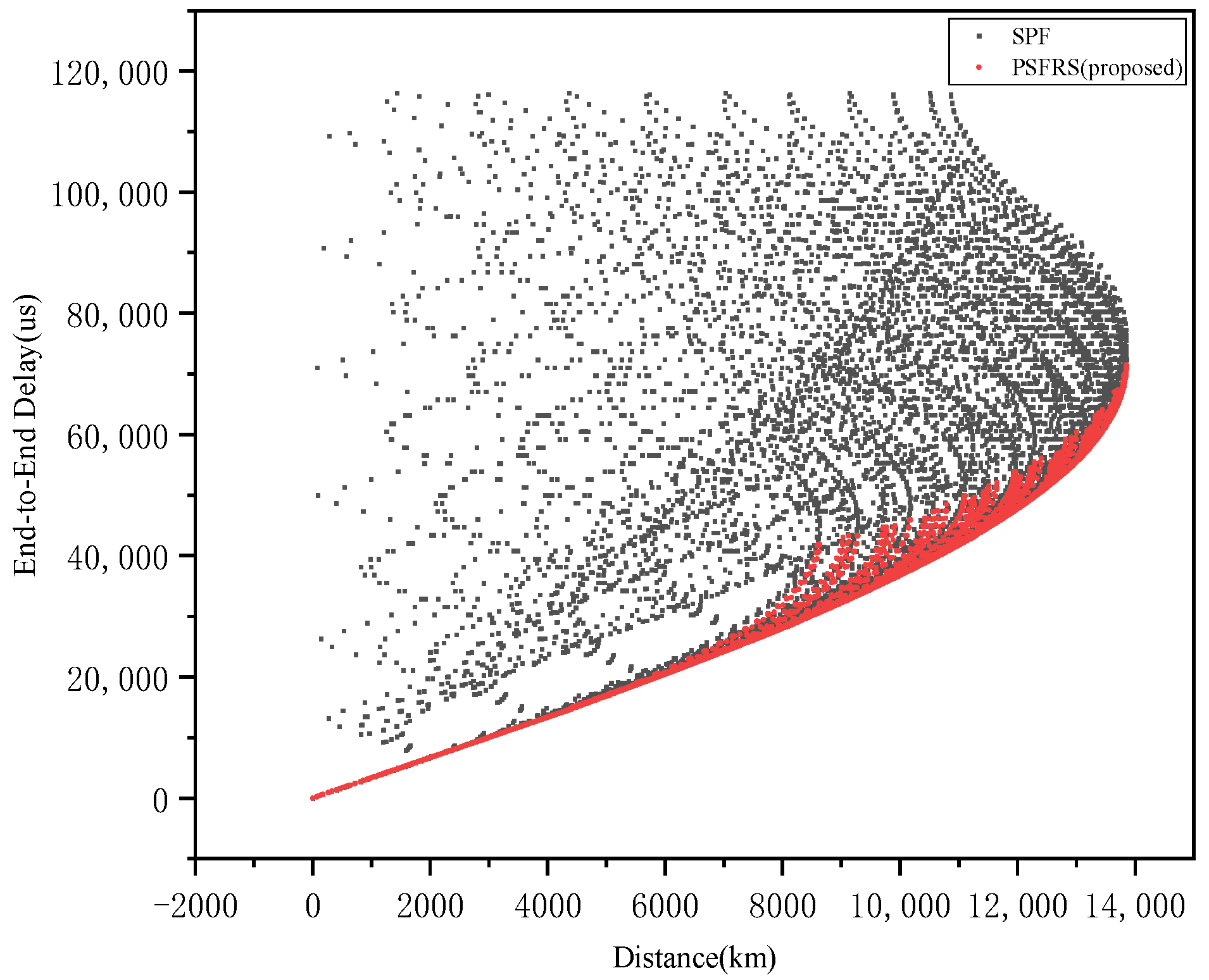
As shown in Figure 11, based on the topology resulting from the partitioning of optical interconnection parallel subnetworks, a simulation platform “Laser Communication Satellite Network Simulation Platform (LCSN-EP) [35]” for laser satellite interconnection was utilized, relying on the SGP4 model. This platform determined the end-to-end delay of satellite data transmission between parallel subnetworks that are visible and communicable to each other, as the optical link distance varied.
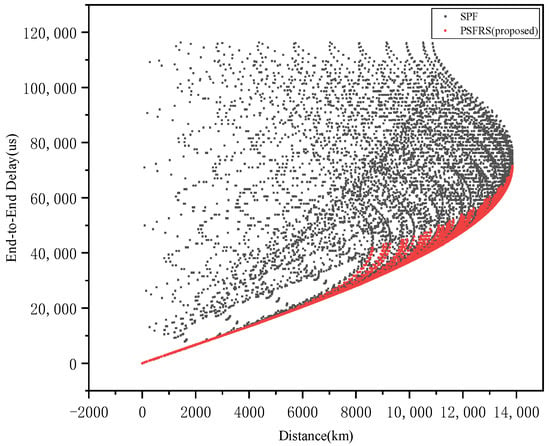
Figure 11.
Inter-subnet end-to-end latency for optical interconnection.
The data indicate that when the distance between satellites is large, data performance is excellent. This is because longer distances provide greater advantages for long-distance links by reducing the number of hops and propagation distances.
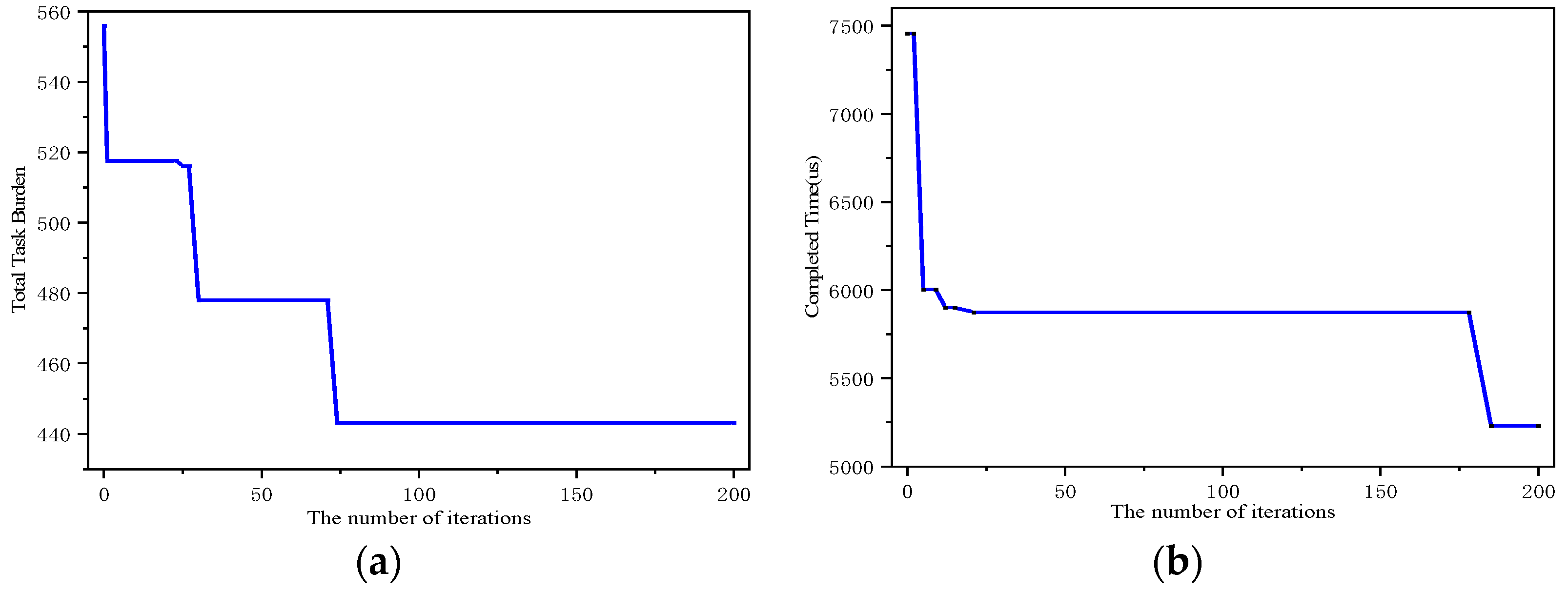
This paper solved the forwarding scheduling of data packets from two perspectives: optimizing the total task burden of the satellite constellation and the maximum completion time of packet forwarding within the satellite constellation. Figure 12a,b demonstrate the execution process of reinforcement learning in solving the transmission scheduling of satellite subnets. Initially, during the iterations, the algorithm’s initialization strategy randomly selected scheduling rules, leading to excessively large values for the total task burden and maximum completion time.
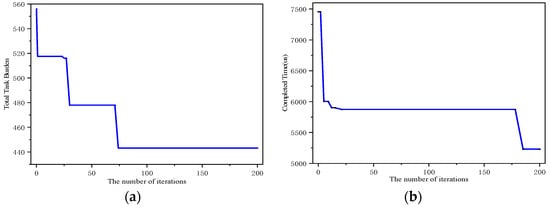
Figure 12.
(a) The total task burden as a function of the number of iterations. (b) The maximum completion time of forwarding as a function of the number of iterations.
As the number of iterations increased, the algorithm gradually improved its strategy, resulting in the optimal solution for the maximum completion time decreasing. The overall numerical trend exhibits a negative slope, indicating that the strategy optimized by the algorithm is effectively solving the FJSP. This discussion not only validates the effectiveness of the proposed framework for constructing inter-subnet scheduling strategies based on reinforcement learning but also confirms the convergence of reinforcement learning in solving the FJSP.
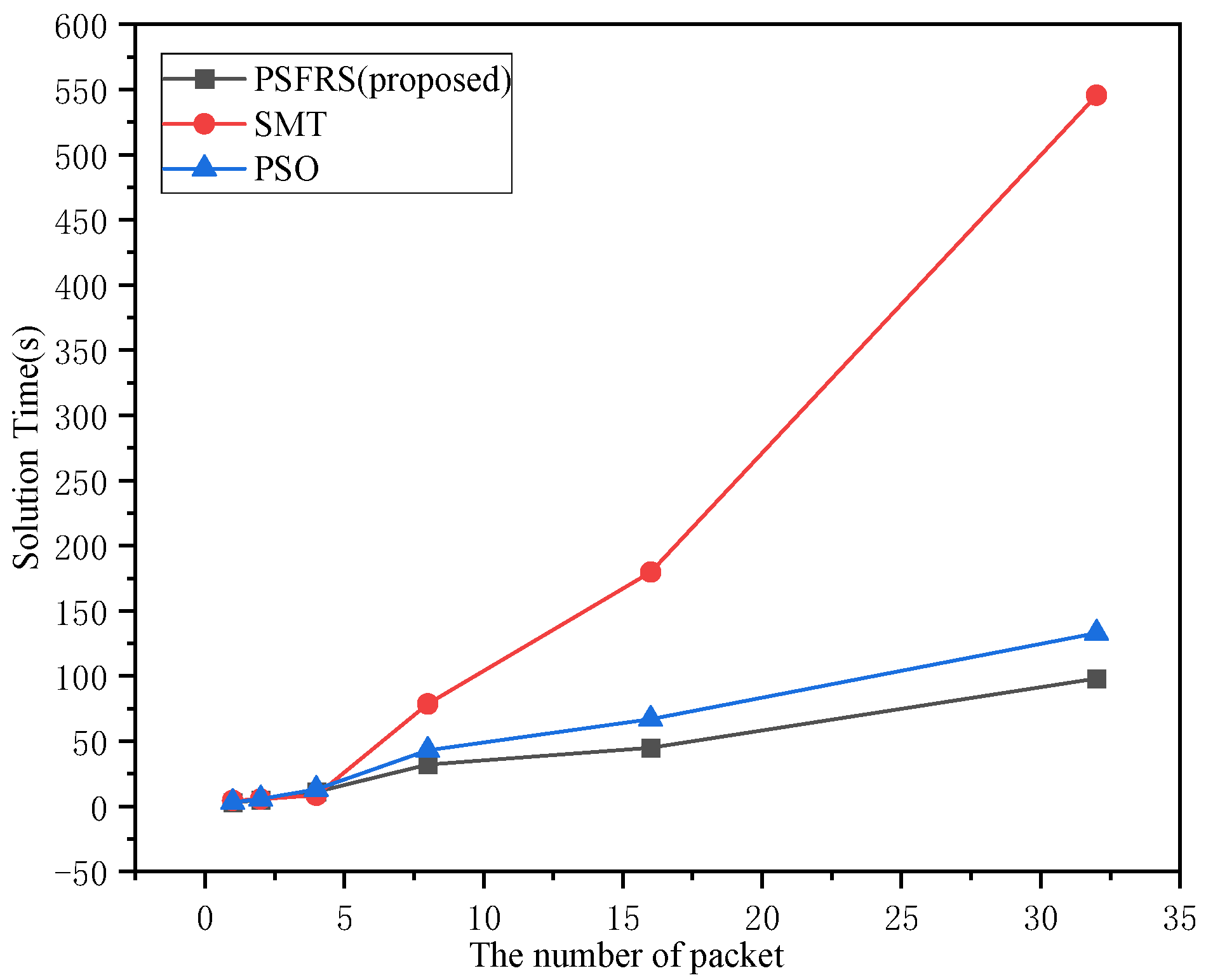
To evaluate the performance of the PSFRS algorithm used in this paper for solving large-scale network problems, experiments were conducted. The algorithm proposed in this paper was compared with the Satisfiability Modulo Theories (SMT) solving method and Particle Swarm Optimization (PSO). To ensure the reliability of the experiments, each solving method was used to schedule 0–32 data packets, with the completion time as the performance metric.
As shown in Figure 13, when solving the scheduling for fewer than five data packets, all three algorithms showed relatively low solving times. However, as the number of data packets to be scheduled increased, the performance of the SMT-solving method deteriorated significantly. This degradation can be attributed to the exponential increase in the exploration space of the SMT method as the number of packets to be solved increases. In comparison to the PSO algorithm, PSFRS used in this paper demonstrated superior solving time as the number of packets to be solved increased. This advantage can be attributed to the incremental updates and greedy strategy employed by Q-learning, where the algorithm selects the action with the maximum Q-value at each step, thus improving efficiency and shortening computation time.
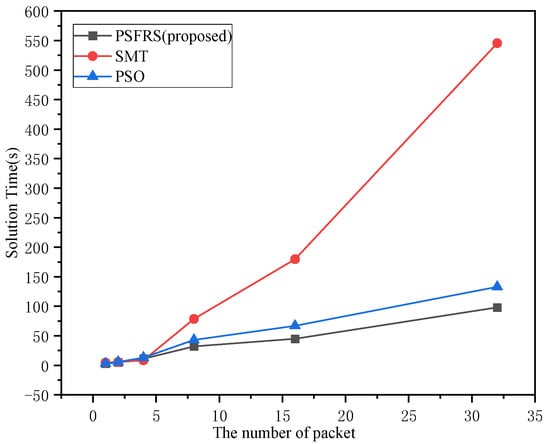
Figure 13.
The solving time of different algorithms as a function of the number of data packets.
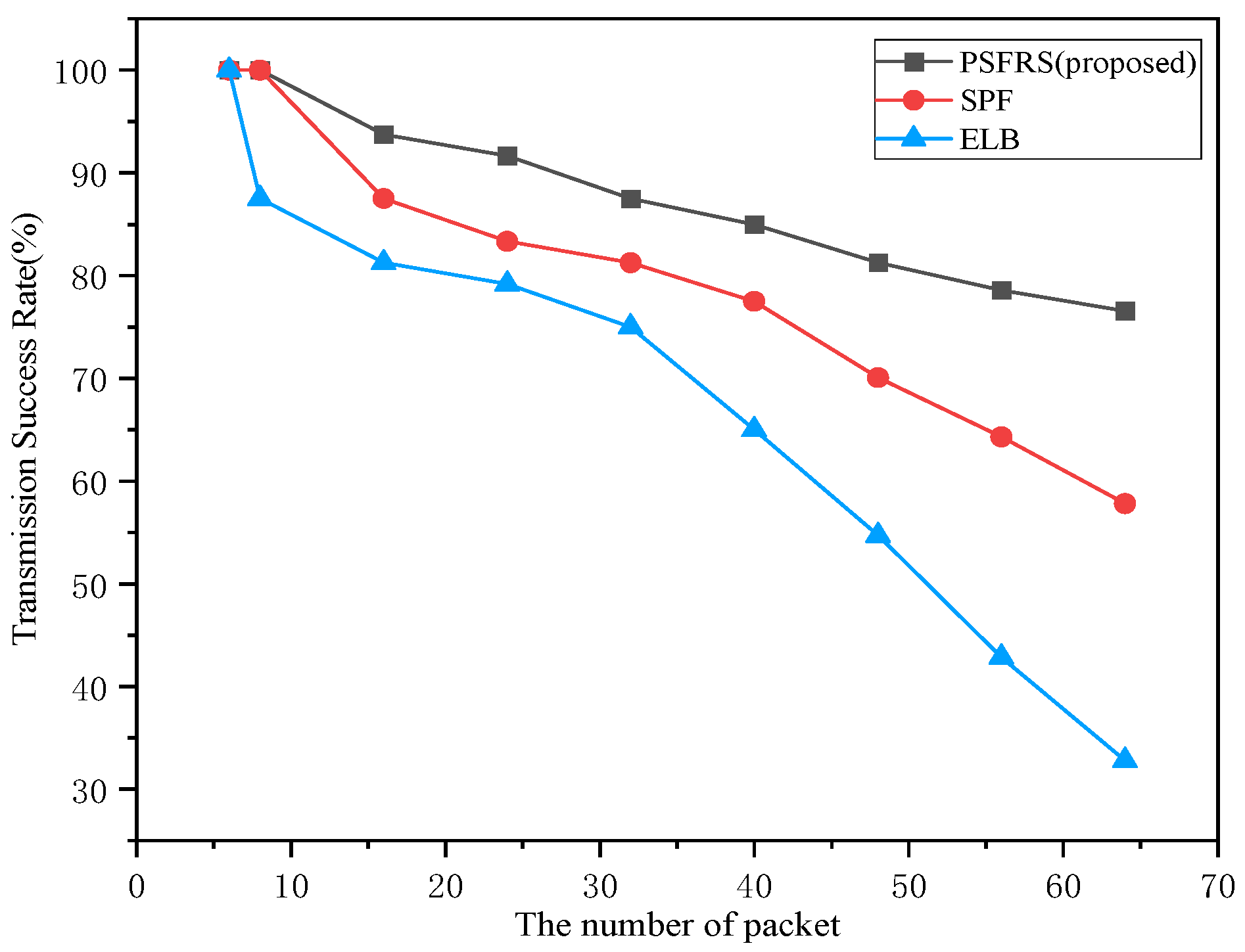
The success rate of transmission represents the proportion of successfully transmitted packets to the total number of packets sent during transmission. It is a crucial metric for evaluating the performance of routing algorithms and serves as an indicator of routing algorithm reliability. This paper focuses on time-sensitive operations, where the transmission time of packets is limited. To assess the transmission success rate of the routing scheduling algorithm employed in this paper, experiments were conducted.
As shown in the simulation results in Figure 14, the transmission success rate of all algorithms decreases as the number of data packets increases. This decrease is attributed to the higher queuing delays and increased likelihood of congestion as the number of packets grows, leading to more packets failing to meet the time-sensitive transmission requirements. The SPF (Shortest Path First) algorithm exhibits a relatively higher transmission success rate due to its characteristic of selecting paths with the shortest distance, which helps in routing packets through nodes with shorter propagation paths. While some congestion may occur, most packets are guaranteed timely delivery. On the other hand, the ELB (Equal Load Balancing) algorithm, which utilizes load-balancing mechanisms by perceiving neighboring node states and alternative paths, reduces the overall task burden. However, it may struggle to meet the transmission requirements of time-sensitive tasks, resulting in the lowest success rate. PSFRS proposed in this paper, leveraging reinforcement learning, balances the overall load and avoids nodes with excessively high forwarding delays. This approach satisfies the time-sensitive propagation delay requirements while effectively reducing the overall task burden.
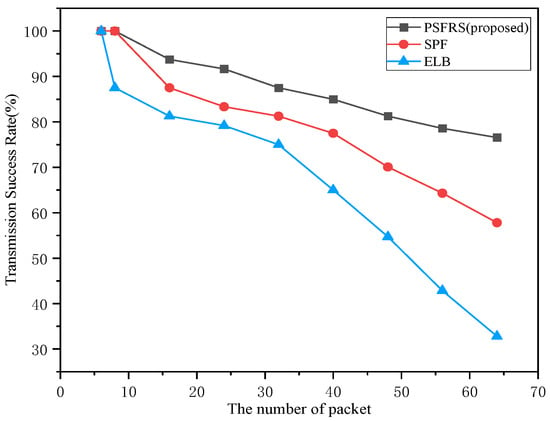
Figure 14.
The transmission success rate of different algorithms as the number of data packets increases.
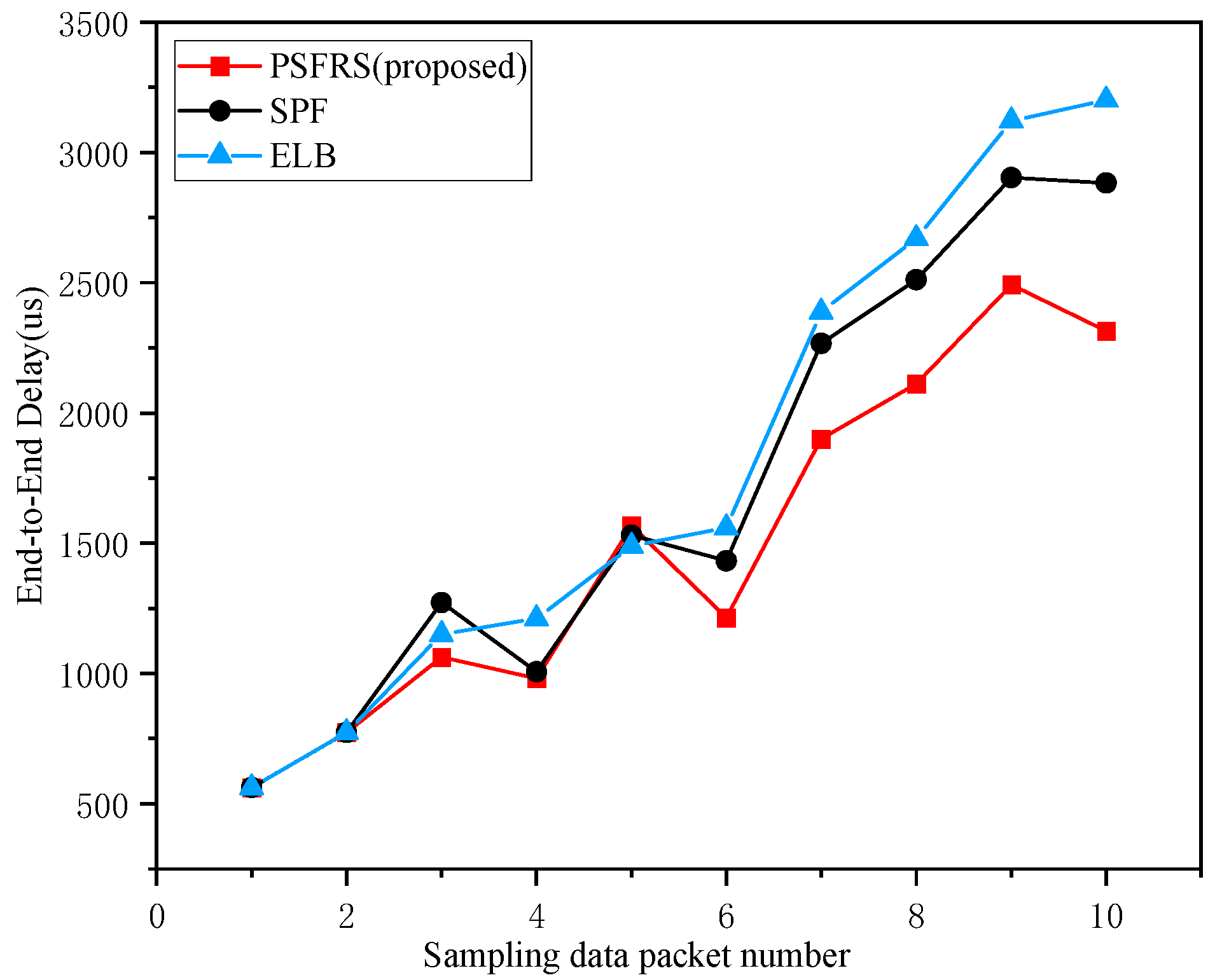
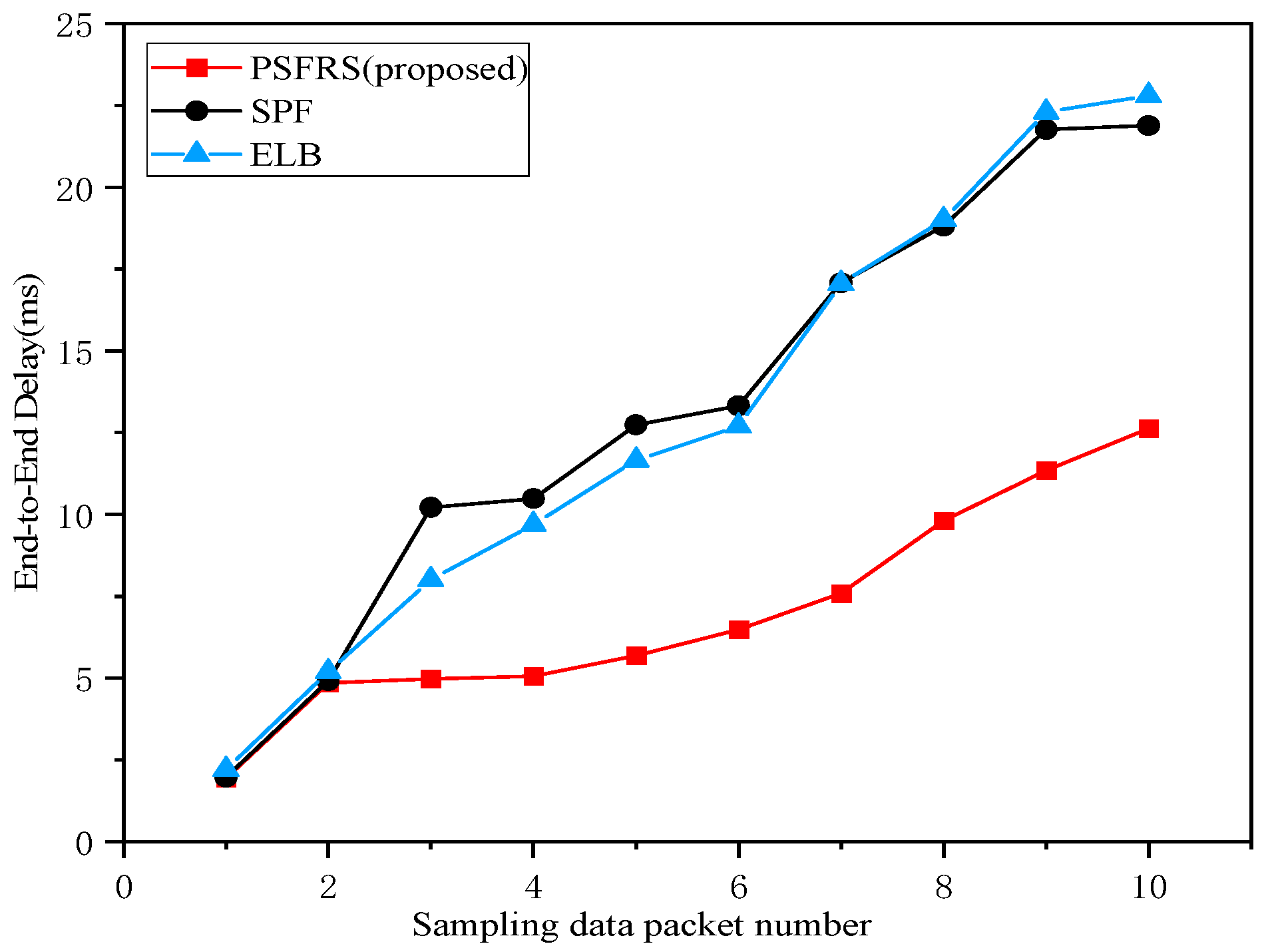
The most critical evaluation metric for satellite routing algorithms is the end-to-end delay, which is an important performance indicator for assessing Quality of Service (QoS) in computer networks. In this paper, based on the format of time-sensitive business packets, data packet types were classified into two categories; the first type is packets that are only transmitted within the subnet, where both the source and destination nodes are within the subnet, and the second type is packets that require cross-span transmission, where the source node is within the subnet and the destination node is outside of the subnet. Ten samples were taken from each of these two categories, totaling twenty data packets, with packet numbers marked in ascending order based on the number of hops traversed. For performance evaluation, comparisons were made with the SPF algorithm in terms of end-to-end delay, as shown in the simulation results in Figure 15 and Figure 16.
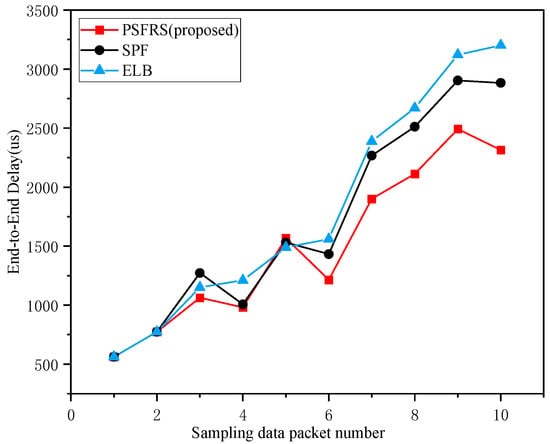
Figure 15.
The end-to-end delay of sampling data packets transmitted without cross-span.
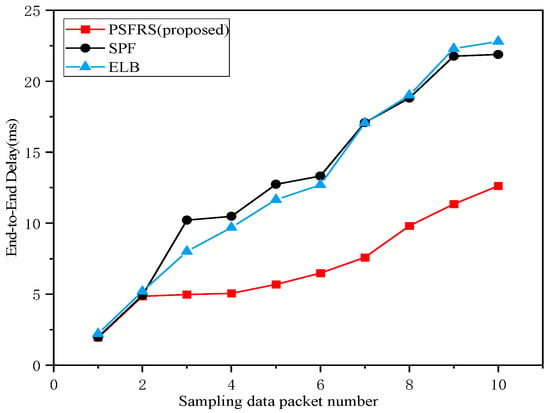
Figure 16.
The end-to-end delay of sampling data packets that require cross-span transmission.
Figure 15 indicates that at lower hop counts, there is not a significant difference in performance between the scheduling algorithm in this paper and the SPF algorithm. In some cases, the end-to-end delay of the SPF algorithm is even shorter than that of the algorithm presented in this paper. This is because the SPF algorithm emphasizes current local optimization, while the algorithm in this paper focuses on global optimization, sometimes sacrificing some delay in scheduling certain packets to achieve an overall optimal solution. As the number of hops increases, the end-to-end delay of data packets with the same source and destination nodes transmitted using the SPF algorithm will sharply rise. This is because the SPF algorithm does not consider congestion avoidance and only selects the nearest nodes for transmission based on a greedy strategy. Therefore, in the case of non-cross-span transmission, the PSFRS proposed in this paper performs better than the SPF algorithm. At the same time, this paper also compares the ELB algorithm with the proposed PSFRS algorithm. As shown in Figure 15, it can be observed that the end-to-end delay of the ELB algorithm is similar to that of the PSFRS algorithm during low-hop transmissions. With an increase in the number of hops, the overall transmission delay of the ELB algorithm shows an upward trend, similarly to the SPF algorithm, leading to a significant delay increase. This is because the ELB algorithm optimizes only based on node loads, which in some cases may result in packets taking longer routes for load balancing, thus encountering local optima. In comparison to the ELB algorithm, the PSFRS algorithm considers both load balancing and the necessary upper bound on delays, better meeting the transmission requirements of time-sensitive services.
Figure 16 shows that at lower hop counts and shorter linear distances, there is not a significant difference in end-to-end delay between the algorithm proposed in this paper and the SPF algorithm. However, as the number of hops and distances increase, the optical interconnect parallel subnet architecture and the reinforcement learning scheduling strategy utilized in this paper optimize both intra-subnet and inter-subnet transmissions, resulting in significantly better performance compared to the SPF algorithm. The reason behind this improvement is that the SPF algorithm may encounter congestion and jitter during long-distance inter-subnet transmissions, whereas the performance of long-distance branch line transmissions based on laser alignment is far superior. Similarly, compared to the ELB algorithm, the proposed PSFRS algorithm in this paper demonstrates superior performance in scenarios involving time-sensitive business transmissions across Low Earth Orbit satellite constellations. This is because during transmissions across distances, it is necessary to consider both intra-constellation transmission delays and inter-constellation transmission delays. The ELB algorithm focuses solely on balancing node loads to facilitate business transmissions. Consequently, in the context of LEO giant constellations, as the distance between source and destination nodes increases, the transmission delay of the ELB algorithm exhibits a sharp increase, failing to meet the transmission requirements of time-sensitive services.
Therefore, the parallel subnet architecture and intra-subnet scheduling transmission strategy employed in this paper exhibit excellent performance in large-scale satellite networks and provide valuable insights for further research and implementation.
5. Conclusions
This paper proposes a delay-driven optical interconnect Low Earth Orbit satellite constellation time-sensitive business routing and scheduling strategy named PSFRS, which is suitable for large-scale connections in a massive Low Earth Orbit constellation. Firstly, it introduces a parallel subnet long-distance transmission scheme based on optical interconnects to achieve low-latency data packet transmission and large-scale connections. Secondly, by incorporating CQF gate scheduling from TSN deterministic transmission technology to determine the transmission delay of a single satellite, this is then extended globally, transforming the transmission scheduling of the entire constellation into an FJSP problem. Finally, reinforcement learning is introduced for problem solving, where reinforcement learning is used to replan the scheduling of well-segmented inter-subnet routes. Simulation results in an LEO satellite constellation environment demonstrate that our proposed optical interconnect routing and scheduling strategy can rapidly compute inter-satellite visibility, effectively solve routing scheduling within the constellation, and improve transmission success rates while significantly reducing end-to-end delays by simultaneously considering load and latency. Furthermore, through comparative experiments, we validate the effectiveness and accuracy of the proposed evaluation standard model. In future research, through collaboration with the Optical Communication Laboratory at Shanghai University, we will further expand the model mentioned in this paper. Our team plans to include ground stations of PON networks in the research scope, study various paths for time-sensitive business transmission, and, ultimately, build an integrated air–ground–space time-sensitive business transmission model. Overall, the findings of this paper are crucial for assessing and optimizing performance in cross-span transmissions of time-sensitive services within large-scale LEO satellite constellations, providing a foundation for future research and development in optical interconnect constellation networks.
Author Contributions
Conceptualization, B.C. and X.F.; methodology, X.F.; validation, X.F. and Y.H.; formal analysis, B.C.; investigation, X.F.; writing—original draft preparation, X.F. and Y.H.; writing—review and editing, X.F. and Q.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by The National Key Research and Development Program of China (2021YFB2900800).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding authors.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- ITU. Internet. Access Statistics [EB/OL]. 2022. Available online: https://www.itu.int/en/ITU-D/Statistics/Pages/stat/default.aspx (accessed on 1 March 2023).
- Chen, Q.; Yang, L.; Guo, J.; Li, X. LEO mega-constellation network: Networking technologies and state of the art. J. Commun. 2022, 43, 177–189. [Google Scholar]
- Blondel, V.D.; Guillaume, J.L.; Lambiotte, R.; Lefebvre, E. Fast unfolding of communities in large networks. J. Stat. Mech. 2008, 2008, P10008. [Google Scholar] [CrossRef]
- Hong, Y.; Zhang, J.; Zang, J.; Fan, X.; Zhao, Q. Parallel Subnetwork Routing Algorithm for Inter-Satellite Optical Communication. In Proceedings of the 2023 Asia Communications and Photonics Conference/2023 International Photonics and Optoelectronics Meetings (ACP/POEM), Wuhan, China, 4–7 November 2023; pp. 1–3. [Google Scholar]
- Jing, Y.; Yi, L.; Zhao, Y.; Wang, H.; Wang, W.; Zhang, J. Deep-learning-based path computation without routing convergence in optical satellite networks. J. Opt. Commun. Netw. 2023, 15, 294–303. [Google Scholar] [CrossRef]
- Ruan, Y.J.; Hu, M.; Yun, C.M. Advances and prospects of the configuration design and control research of the LEO mega-constellations. Chin. Space Sci. Technol. 2022, 42, 1–15. [Google Scholar]
- IEEE 802.1; IEEE Standard for Local and Metropolitan Area Network–Bridges and Bridged Networks. IEEE Std 802.1Q-2018 (Revision of IEEE Std 802.1Q-2014). IEEE: New York, NY, USA, 2018; pp. 1–1993.
- Yan, J.; Quan, W.; Jiang, X.; Sun, Z. Injection Time Planning: Making CQF Practical in Time-Sensitive Networking. In Proceedings of the IEEE INFOCOM 2020—IEEE Conference on Computer Communications, Toronto, ON, Canada, 6–9 July 2020; pp. 616–625. [Google Scholar]
- Hellmanns, D.; Falk, J.; Glavackij, A.; Hummen, R.; Kehrer, S.; Dürr, F. On the performance of stream-based, class-based time-aware shaping and frame preemption in TSN. In Proceedings of the 2020 IEEE International Conference on Industrial Technology (ICIT), Buenos Aires, Argentina, 26–28 February 2020; IEEE Press: Piscataway, NJ, USA, 2020; pp. 298–303. [Google Scholar]
- Reusch, N.; Zhao, L.; Craciunas, S.S.; Pop, P. Window-based schedule synthesis for industrial IEEE 802.1Qbv TSN networks. In Proceedings of the 2020 16th IEEE International Conference on Factory, Porto, Portugal, 27–29 April 2020. [Google Scholar]
- Hasan, M.M.; Feng, H.; Khan, S.; Ullah, M.I.; Hasan, M.T.; Gain, B. Improve service curve using non-overlapped gate in time sensitive network switch. In Proceedings of the 2021 IEEE 21st International Conference on Communication Technology (ICCT), Tianjin, China, 13–16 October 2021; IEEE Press: Piscataway, NJ, USA, 2021; pp. 913–918. [Google Scholar]
- Zhao, L.; Pop, P.; Gong, Z.; Fang, B. Improving latency analysis for flexible window-based GCL scheduling in TSN networks by integration of consecutive nodes offsets. IEEE Internet Things J. 2021, 8, 5574–5584. [Google Scholar] [CrossRef]
- Wu, Z.; Hu, G.; Jin, F.; Song, Y.; Fu, Y.; Ni, G. A novel routing design in the IP-based GEO/LEO hybrid satellite networks. Int. J. Satell. Commun. Netw. 2017, 35, 179–199. [Google Scholar] [CrossRef]
- Huang, Y.; Feng, B.; Dong, P.; Tian, A.; Yu, S. A multi-objective based inter-layer link allocation scheme for MEO/LEO satellite networks. In Proceedings of the 2022 IEEE Wireless Communications and Networking Conference (WCNC), Austin, TX, USA, 10–13 April 2022; pp. 1301–1306. [Google Scholar]
- Truchly, P.; Vangel, M. Performance of multilayered satellite networks. In Proceedings of the ELMAR-2012, Zadar, Croatia, 12–14 September 2012; pp. 113–116. [Google Scholar]
- Jing, Y.; Yang, Z.; Liao, X.; Qi, X. A minimum connected dominating set based multicast routing algorithm in hybrid LEO/MEO/GEO constellation network. In Proceedings of the 2017 International Conference on Communications, Signal Processing, and Systems, Noida, India, 7–9 March 2019; Springer: Singapore, 2019; pp. 93–100. [Google Scholar]
- Cui, X.; Wu, J.; Zhou, Y.; Liu, L.; Pan, Z. Challenges of and Key Technologies for the Air-Space-Ground Integrated Network. J. Xidian Univ. 2023, 50, 1–11. [Google Scholar]
- Yang, F.; Zhao, J.; Yao, N.; Li, Z.; Jiang, H.; Wang, J.; Zhu, H.; Liu, S.; Wang, S.; Wang, X. System design and technical innovation of BJ-3A/B Satellites. Spacecr. Eng. 2023, 32, 7–15. (In Chinese) [Google Scholar]
- Zhang, X.; Yang, Y.; Xu, M.; Luo, J. ASER: Scalable Distributed Routing Protocol for LEO Satellite Networks. In Proceedings of the IEEE Conference on Local Computer Networks (LCN), Edmonton, AB, Canada, 4–7 October 2021; IEEE Press: Piscataway, NJ, USA, 2021; pp. 65–72. [Google Scholar]
- Zhu, Y.; Qian, L.; Ding, L.; Yang, F.; Zhi, C.; Song, T. Software defined routing algorithm in LEO satellite networks. In Proceedings of the 2017 International Conference on Electrical Engineering and Informatics (ICELTICs), Banda Aceh, Aceh, Indonesia, 18 October 2017. [Google Scholar]
- Zhu, Y.; Rui, L.; Qiu, X.; Huang, H. Double-Layer Satellite Communication Network Routing Algorithm Based on Priority and Failure Probability. In Proceedings of the International Wireless Communications and Mobile Computing Conference (IWCMC), Tangier, Morocco, 24–28 June 2019; pp. 1518–1523. [Google Scholar]
- Osoro, O.B.; Oughton, E.J. A techno-economic framework for satellite networks applied to low earth orbit constellations: Assessing Starlink, OneWeb and Kuiper. IEEE Access 2021, 9, 141611–141625. [Google Scholar]
- SpaceX. Starlink—starlink.com. March 2023. Available online: https://www.starlink.com/ (accessed on 31 March 2023).
- Nasrallah, A.; Thyagaturu, A.S.; Alharbi, Z.; Wang, C.; Shao, X.; Reisslein, M.; ElBakoury, H. Ultra-Low Latency (ULL) networks: The IEEE TSN and IETF DetNet standards and related 5G ULL research. IEEE Commun. Surv. Tutor. 2019, 21, 88–145. [Google Scholar]
- Liu, H.; Li, M.; Gu, F.; Li, Q.; Zhang, W.; Guo, S. End-to-end Flow Scheduling Optimization for Industrial 5G and TSN Integrated Networks. In Proceedings of the GLOBECOM 2024—2024 IEEE Global Communications Conference, Cape Town, South Africa, 8–12 December 2024; pp. 1797–1802. [Google Scholar] [CrossRef]
- Malis, A.; Geng, X.; Chen, M.; Varga, B.; Bernardos, C. Deterministic Networking (DetNet) Controller Plane Framework. Internet Engineering Task Force. 2023. Available online: https://datatracker.ietf.org/doc/draft-ietf-detnet-controller-plane-framework/ (accessed on 30 December 2024).
- Liu, F.; Zeng, G. Study of genetic algorithm with reinforcement learning to solve the TSP. Expert Syst. Appl. 2008, 36, 6995–7001. [Google Scholar]
- Naimi, R.; Nouiri, M.; Cardin, O. A Q-Learning Rescheduling Approach to the Flexible Job Shop Problem Combining Energy and Productivity Objectives. Sustainability 2021, 13, 13016. [Google Scholar] [CrossRef]
- Li, R.; Lin, B.; Liu, Y.; Dong, M.; Zhao, S. A survey on laser space network: Terminals, links, and architectures. IEEE Access 2022, 10, 34815–34834. [Google Scholar]
- Finn, N. Multiple Cyclic Queuing and Forwarding. 2021. Available online: https://www.ieee802.org/1/files/public/docs2021/new-finn-multiple-CQF-0921-v02.pdf (accessed on 4 February 2024).
- Bouazza, W.; Sallez, Y.; Beldjilali, B. A distributed approach solving partially flexible job-shop scheduling problem with a Q-learning effect. In Proceedings of the 20th World Congress of the International Federation of Automatic Control (IFAC), Toulouse, France, 14 July 2017; pp. 15890–15895. [Google Scholar]
- Zarrouk, R.; Bennour, I.E.; Jemai, A. A two-level particle swarm optimization algorithm for the flexible job shop scheduling problem. Swarm Intell. 2019, 13, 145–168. [Google Scholar] [CrossRef]
- Ye, J.; Wang, A.; Ge, Y.; Shen, X. An Improved Grey Wolf Optimizer for Flexible Job-shop Scheduling Problem. In Proceedings of the IEEE of the 11th International Conference on Mechanical and Intelligent Manufacturing Technologies, Cape Town, South Africa, 20–22 January 2020; pp. 213–217. [Google Scholar]
- Bellman, R. Dynamic Programming. Science 1966, 153, 34–37. [Google Scholar] [CrossRef] [PubMed]
- Xu, T.; Cao, B.; Hong, Y. Research on Constellation Network Simulation System Driven by Visibility Matrix. Ind. Control Comput. 2023, 36, 107–109. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).